Abstract.
Accurate tracking and localization of ultrasound (US) images are used in various computer-assisted interventions. US calibration is a preoperative procedure to recover the transformation bridging the tracking sensor and the US image coordinate systems. Although many calibration phantom designs have been proposed, a limitation that hinders the resulted calibration accuracy is US elevational beam thickness. Previous studies have proposed an active-echo (AE)-based calibration concept to overcome this limitation by utilizing dynamic active US feedback from a single PZT element-based phantom, which assists in placing the phantom within the US elevational plane. However, the process of searching elevational midplane is time-consuming and requires dedicated hardware to enable “AE” functionality. Extending this active phantom, we present a US calibration concept and associated mathematical framework enabling fast and accurate US calibration using multiple “active” points. The proposed US calibration can simplify the calibration procedure by minimizing the number of times midplane search is performed and shortening calibration time. This concept is demonstrated with a configuration mechanically tracking a US probe using a robot arm. We validated the concept through simulation and experiment, and achieved submillimeter calibration accuracy. This result indicates that the multiple active-point phantom has potential to provide superior calibration performance for applications requiring high tracking accuracy.
Keywords: ultrasound calibration, active-echo, calibration phantom
1. Introduction
Ultrasound (US) imaging has been widely used as a diagnostic imaging modality as well as a guidance tool for surgical interventions. Tracking US images adds substantial value to various applications, and it has been an active area of research to use this tracking information to assist image-guided interventions,1,2 to construct three-dimensional (3-D) US volumes,3 and to improve imaging field-of-view and image quality.4,5 To accurately track the US image, many tracking systems such as mechanical, optical, and electromagnetic trackers have been proposed and can be rigidly attached to the US probe. For most of them, a preoperative task, known as US calibration, is required to compute the unknown transformation bridging the tracker frame and the US image frame.6 Once calibration is complete, the computed transformation and associated tracking information can be used to locate the US image position and link a set of US images together. The performance of US tracking-based applications heavily depends on the accuracy of both the tracking system and US calibration.
US calibrations are generally performed using special calibration phantoms.6,7 Many US calibration phantom designs have been proposed, and these phantoms can be placed abstractly into two categories: point-based phantoms and structural phantoms. Point-based phantoms consist of a single point or multiple points in a three-dimensional (3-D) space and can be formed using a stylus8 or a cross wire.9,10 For a one-dimensional (1-D) array US probe, points seen in a US image slice are assumed to be in the US image plane, and its elevational component in a 3-D space is set to zero. Structures such as line- or wall-based phantoms, on the other hand, have their own predetermined structures, and the segmented feature(s) from a US image are registered back to the model structure to recover the US image pose with respect to the phantom.11 Point-based phantoms in general can provide superior accuracy compared with structural phantoms by avoiding the intermediate registration process but take a longer time for data collection because of the requirement to align the US midplane to the point. Additionally, calibration using point-based phantoms is difficult to automate due to the midplane alignment process. Structural phantoms are more flexible and easier to automate, because there is a larger set of valid poses for image acquisition.
Another strong distinction in these US calibration methods can be seen from a mathematical perspective. The methods available to compute the unknown transformation are restricted by the information accessible from the calibration phantom; for example, point-based phantoms are only capable of providing positional information of a point target, whereas structural phantoms can provide the full pose, both orientation and position, of the phantom. Information about the full pose from structural phantoms can be used to form an equation that has a closed-form solution. Therefore, by not requiring optimization, a computationally efficient solution is available and we will further elaborate in Sec. 2.1.
The goal of this work is to present a calibration concept and an associated algorithm to enable a fast and accurate US calibration. A point-based phantom is used as the base design to take advantage of its superiority in the elevational dimension position detection accuracy as compared with structural phantoms. Even with this improvement, the main source of error in US calibration using point-based phantoms remains its localization inaccuracy in the elevation dimension due to the US beam thickness. To improve conventional point-based phantoms such as the cross-wire phantom, Cheng et al. and Guo et al.12–14 have proposed an active-echo (AE) phantom approach to precisely find the midplane of the US beam. The AE phantom is made of a single piezoelectric (PZT) element, which receives a US signal from the probe, then responds by transmitting a US. The strength of the corresponding response echo received by the probe is correlated with the distance and angle of the US imaging plane to the PZT element. The maximum received response echo indicates optimal alignment of the US probe with respect to the PZT element with accuracy.15 However, repeating this midplane search for all imaging poses is time-consuming and this functionality requires a specialized on-board signal processing system to drive “receive and transmit” operations. We propose a calibration concept using multiple active-point (MAP) sources and active transmission of the US signal from these point sources. This can drastically speed up the calibration by minimizing the number of times that midplane detection must be performed. Compared with the AE phantom, the active phantom only requires a synchronized transmission board so the hardware is simplified. Also, multiple point acquisitions allow computation of full image poses enabling a closed-form solution that is not possible in single point-based phantoms. The proposed calibration concept can be applied to any US probe including dual-array transrectal US (TRUS) probes as well as classical monoarray probes. As proof of concept, we utilized two arrays on a TRUS probe to demonstrate the calibration performance of both monoarray and dual-array transducers.
This paper is structured as follows: we first introduce the theory behind US calibration and the proposed calibration method and algorithm. Then, we present the simulation and experimental setup to analyze the performance of the method. After that, the numerical simulation and experimental results are presented. Finally, we discuss this method’s limitations and its potential applications.
2. Theory
2.1. Solving Ultrasound Calibration Problem
US calibration is the process of solving for the rigid-body transformation, , spatially relating the US image coordinate system to the tracking sensor coordinate system. Various calibration phantom designs have been proposed with their corresponding formulations, for which and are the two most common ones, where , , , and SE(3) denotes the special Euclidean group in 3-D composed of rigid-body homogenous transformations. The details of each formulation are described in the following paragraphs.
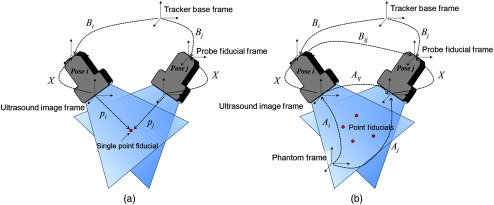
The formulation is generally used for point-based phantoms [Fig. 1(a) shows an example of the coordinate systems associated with a point-based phantom]. A single point or multiple point-like fiducials are imaged with a tracking sensor or marker-attached US probe multiple times from distinct poses, varying in both orientations and positions. is the sensor reading and denotes the homogenous transformation from the tracking base to the tracking sensor or marker. is the location of the point fiducial in the US image coordinates, segmented from the US image. Though the full 3-D position can be recovered when using dual-array probes, it sets the elevation dimension to be zero when using monoarray probes, making the assumption that the point is perfectly aligned at the midplane or the center of the US beam. For all combinations of and
| (1) |
must be satisfied, assuming that the point phantom’s location with respect to the tracking base frame is fixed and constant.
Fig. 1.
Illustration of coordinate systems on ultrasound calibration. (a) A single point target phantom, in which formulation is used. (b) The proposed MAP phantom, in which formulation is used.
is another formulation for solving the sensor calibration problem [Fig. 1(b) shows an example of the framework]. For all combinations of and ,
| (2) |
stands, where represents the relative rigid body transformation between two image poses, and . Similarly, is the relative transformation between two tracking poses, and . Subscript s such as and are the transformations from the US image frame to the phantom base frame for poses and , and subscript s are the tracking transformations as introduced in the formulation. In contrast to the formulation, the formulation has a closed-form solution.16 Thus, it is not possible to avoid solving an optimization problem in the formulation, increasing the computation time.16–20 In addition, probabilistic approaches that do not require a priori knowledge of the temporal correspondence between sensor measurements have also been proposed.21–23
The formulation can typically compute a better than the formulation due to its lower elevational dimension error when collecting data points. Acquiring the transformation in requires a phantom with structure(s) such as a line(s) or wall(s). While it is possible to avoid the time-consuming midplane search process required in point-based phantoms, these phantoms suffer from inaccurate feature segmentation due to the US elevational beam thickness and the insonification angle. Therefore, a calibration concept inheriting advantages from both types of phantoms is in need.
2.2. Ultrasound Calibration Using a Multiple Active-Point Phantom
An active-point target is defined as a point fiducial that can actively interact with the US receiver by transmitting acoustic waves. In general, calibration phantoms are passive, and their appearance in a US image is based on the acoustic wave transmitted and subsequently received by the US probe. Guo at al.12 proposed a realization of an active-point target by placing a piezoelectric element on a needle tip.14 The PZT element transmits acoustic signals with a large capture range and can be received by the US probe even if the target is positioned out of plane. Moreover, the active point provides background-free signals as the active point acts as the lone acoustic source, and minimizes the imaging artifacts such as reverberation. As the US line trigger is used to synchronize the acoustic signal transmission by the active point with the US probe data collection, the geometrical distance from the probe to the active point can be estimated based on the time-of-flight of the transmitted wave. This active-point phantom has been used to improve the midplane search process. In this work, we propose to distribute multiple active points in a 3-D space. Traditionally, only the formulation is feasible with point-based phantoms because rotational information of the point is undefined. A phantom with multiple active points can use these active points to define a coordinate frame, thus gaining the ability to recover both rotation and translation components, and enabling the formulation.
The concept of having multiple active points in a phantom is shown in Fig. 1(b). When calibrating a US probe with a two-dimensional (2-D) array such as a matrix-array probe or a dual-array transrectal probe, the 3-D locations of the point targets on the phantom as seen in the US images are segmented, and the transformation is recovered through a point cloud registration between the phantom model frame and the US image frame, as in Ref. 24:
| (3) |
where is the point position defined in the US image frame, and is the position defined in the phantom model frame.
Considering the case of monoarray probes, the signals from active-point targets appear in the channel data as 2-D information. When the -, -, and -axes are defined as the lateral, axial, and elevational dimensions from the US image coordinate frame, respectively, the position of the active-point target can be determined as
| (4) |
where is the unknown elevational component (Fig. 2). Here, is the distance from the target to the receiver based on the earliest time of arrival signal in the received channel data. When is used to solve for and the unknown for each pose, Eq. (3) returns , an with a one degree-of-freedom (DOF) unknown rotation, which is defined as
| (5) |
| (6) |
where is the ground truth, and the recovered contains an unknown one DOF rotation with magnitude in the lateral axis of the US image coordinate system. We define the as the partial . The true pose cannot be uniquely determined without knowing , because is variable for every pose. Based on Eq. (2), the formulation is
| (7) |
and combining this with Eq. (5) gives
| (8) |
Fig. 2.
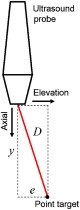
US image coordinate and associated position of the active-point target.
Equation (8) has eight unknown parameters: six unknowns in and one each in and . Thereby, the solution of Eq. (8) is with error, which is defined as
| (9) |
where is a one DOF rotation [proof is shown in Appendix A (Sec. 7)].
Although cannot be uniquely solved when has an unknown one DOF rotation, it is possible to recover these unknown rotations within all s using the Euclidean-Group invariants if at least one is fully known. From screw theory, the homogenous transformation can be written as
| (10) |
where is the matrix exponential on , is an identity matrix, and is the angle of rotation. In addition,
where denotes the unit vector representing the axis of rotation, and . are known as the Plücker coordinates of the screw motion. Two invariants and are defined as follows:
| (11) |
| (12) |
where and are the rotation and translation vectors of the matrix. When the relationship is kept, two invariants in matrix and are related as
| (13) |
As and here are relative poses resulting from a combination of two poses, if in one pose is fully known, then the other pose in the pair can also be recovered using Eq. (13).
In the MAP phantom, the all s can be fully recovered as long as at least one of the point targets is within the US plane for one of the imaging poses. By taking this one known , the remaining unknown s do not require an in-plane point and can be recovered using the invariants and described in Eqs. (11) and (12) by solving Eq. (14):
| (14) |
where is the known rotation components when aligning a point to the US midplane for the poses specific pose . Two functions and are defined to calculate and of a homogeneous transformation. Once all s are known, can be recovered by solving the problem.
3. Materials and Methods
3.1. Calibration Workflow
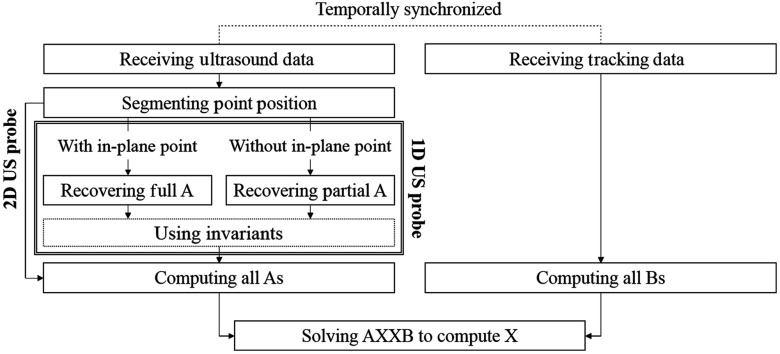
The algorithmic steps of US calibration using the MAP phantom are shown in Fig. 3. In its basic configuration, the phantom consists of three or more points, and the relative 3-D spatial location of these points is known prior to usage. These active points are placed sparsely as shown in Fig. 1(b), and the signals transmitted from all points are received by the US transducer using the channel data acquisition system. The tracking device is rigidly attached to the probe, and the tracking sensor information is temporally synchronized to the US data acquisition. These US and tracker readings are used to generate s and s, respectively, and to reconstruct . When the 3-D locations of the points are accessible, the full transformation of is recovered using Eq. (3), and is computed by solving the formulation.
Fig. 3.
Diagram illustrating ultrasound calibration procedure using MAP phantom.
When a 1-D array receiver is used, the elevational component cannot be determined from the recorded two-dimensional (2-D) US data. The lateral and axial components of the active point are segmented from the earliest time of arrival. The lateral position is determined by the element number and the pitch, and the axial position is calculated from converting time to distance based on
| (15) |
where denotes the temporal length from the probe to the active point, and SoS is the speed of sound in the medium. The obtained 2-D information and the predetermined point distribution on the phantom are used to recover partial s [Eq. (5)] using Eq. (3). When one of the active points is located in-plane, the elevational component is assumed to be zero. Thus, this property can be used to recover a full as the elevational component of being zero adds an additional constraint to Eq. (3). Although this approach uses only a single data point by segmenting the earliest time of flight as the axial component, an alternative approach using the entire waveform to recover is introduced in Appendix B (Sec. 8).
From the given partial s including at least one full s and s obtained from the tracker, the full s of remaining poses are recovered using the invariants. Equation (14) derives the one DOF unknown component in the partial s so that the full is . Once the corresponding s and s are recovered, the unknown transformation is solved using classical solvers.17,18
3.2. Simulation Setup
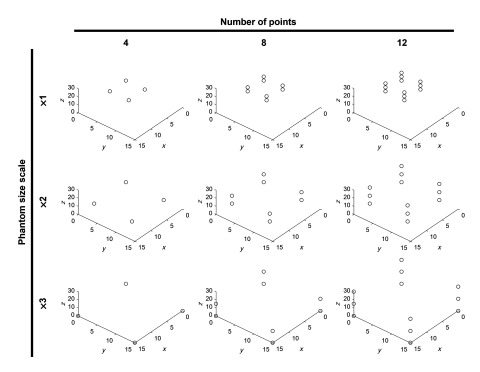
We conducted a geometrical simulation to evaluate the calibration performance of the proposed method under the presence of different error sources. For the simulation, a single point target was set as the phantom, and a linear array transducer with 128 elements and a 0.3-mm pitch was used as the receiver. To simulate midplane alignment where the US beam is across the point target, the elevational component of the point position was set to zero. For the simulation, a phantom consisting of multiple points was generated, and the other setup parameters were kept the same as the simulation. In the base configuration, four points were placed in a plane at 5-mm intervals. To evaluate the calibration accuracy under difference point configurations, the number of points (4, 8, 12) and the phantom size scale (1, 2, 3 times) were varied (Fig. 4). A total of 125 US probe poses were used, and the corresponding point position and tracking information were stored. From these poses, 60 of them were randomly chosen to be used for calibration, and another 60 from the remaining set of poses were randomly chosen for evaluation. The example simulation code with the proposed algorithm is available online (https://github.com/hzhang61/us_calibration).
Fig. 4.
Simulated phantom design. Four points separated by 5-mm distance was regarded as the base, the size scale of phantom (1, 2, 3 times), and the number of points (4, 8, 12) were varied. The unit was mm.
3.3. Experimental Implementation
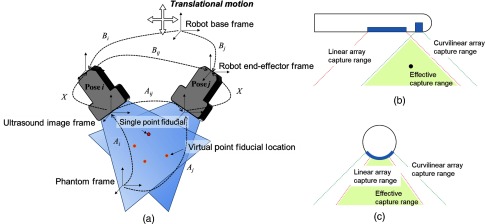
In this paper, we present an example configuration to realize the MAP phantom concept using a single PZT element as the active element and a robot arm as the tracker and the translation stage to virtually create multiple active points. The active element is made of disc-shaped 1-mm diameter PZT element, and it has a center frequency of 10 MHz [Fig. 5(a)]. A driving pulser was used to generate pulses with a minimum duration of 12.5 ns in the range between and 150 V.12 A transrectal probe (BPC8-4/10 & BPL9-5/55 Transrectal Bi-plane, Ultrasonix Corp. Richmond, Canada) with dual arrays is used as the US probe, and the linear array portion (BPL9-5/55) is used for the mono (1-D) array calibration [Fig. 5(b)]. The curvilinear part of the probe (BPC8-4/10) is used to obtain another set of position information, which is used to localize the 3-D location of the active element.25 The channel data were recorded with a DAQ device (SonixDAQ, Ultrasonix Corp. Richmond, Canada), and the data acquisition timing was synchronized by the line trigger from the US machine. In this experimental evaluation, we used a robot arm, the UR5 (Universal Robot) as a mechanical tracker. Instead of placing multiple active elements, we moved the robot arm in a translational motion from the robot base frame to emulate multiple point sources (Fig. 6). To collect a varied set of poses, the robot arm was moved to 125 different poses, where each rotation angle about each of the three axes was incremented by 5 deg with a total of five steps, to produce 125 unique poses. The translational component for each pose was then determined accordingly to let the probe stay within the range of the active element signals. The actual poses tracked are presented in the results section. For each of these poses, the robot arm applies five translational motions defined from the robot base coordinate system to the active element to emulate a multiple active elements phantom. To maintain compatibility with the data collected from the 125 robot poses, the data collected from these five translational motions are treated as if they were from a single fixed robot pose with the active element being the one that is moving. This virtually creates a MAP phantom with five points to be used for US calibration. The unknown was recovered through using a closed-form solution.17,18
Fig. 5.
Pictures of the experimental setup. (a) Active-point phantom and (b) transrectal probe mounted on the robot arm.
Fig. 6.
The experimental design (a) and the scanning field in the transrectal probe (b, c). (a) Ultrasound calibration was performed to the US probe held by a robot arm. An active-point target was used as the single point fiducial, and multiple active points were virtually created by applying pure-translation with the robot arm. (b) Lateral-axial view (with respect to linear array) of the transrectal US probe. (c) Elevation-axial view (with respect to linear array) of the transrectal probe. Two planes cover the save area that was regarded as the effective capture range, where 3-D position of a point target is accessible for reference.
3.4. Evaluation Methods
Calibration can be evaluated based on accuracy and precision. Accuracy is a direct metric presenting the distance error comparing the recovered point location and the true location for the same target, which is defined as
| (16) |
where is the ground-truth target point from the tracking base frame. Precision is a metric defined as
| (17) |
where is the mean of for all . Ideally, if no error is present, the true would cause all of the to equal and converge to a single point. However, when error is present, for all forms a point cloud instead of a single point, and the size of the point cloud is correlated to the precision of .
Although accuracy is a more reliable metric to evaluate , experimental analysis is often based on precision because the ground-truth point location is inaccessible. Instead, the simulation evaluates both metrics to compare their relevance.
4. Results
4.1. Geometrical Simulation
We conducted the geometrical simulation to review the effect of experimental errors on US calibration, to compare the and the mathematical frameworks using the point and the MAP phantoms, and to validate the MAP phantom using a 1-D array.
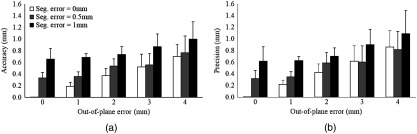
First, the error tolerance of the conventional formulation was evaluated. When a point target is scanned by a 1-D array US probe, we assume that there are two types of errors, the out-of-plane error and the point segmentation error. The out-of-plane error and the segmentation error were simulated as error biases added in the elevational axis and the image plane axes of the US image, respectively. In both cases, the parameter that was changed is the magnitude of the standard deviation (S.D.) when sampling the error value from a normal distribution, and the accuracy and precision of the calibration result, , were computed 20 times under each condition.
The mean and standard deviation of this study on error tolerance is shown in Fig. 7. The out-of-plane error caused the calibration error to increase linearly for small segmentation errors with 4 mm of out-of-plane error resulting in around 1-mm accuracy and precision. Segmentation error had a more significant effect on the calibration error compared with the out-of-plane error, especially when the out-of-plane error was small. When the out-of-plane error is large, the effects due to the segmentation error are relatively low. The calibration accuracy and precision metrics show similar trends and error values. This supports the use of precision to evaluate the experimental results. Note that experimentally, the precision will also include the tracking error in , which was not considered in this simulation to focus on the effect on the phantom .
Fig. 7.
(a) Accuracy and (b) precision of -based calibration for corresponding segmentation and elevational errors.
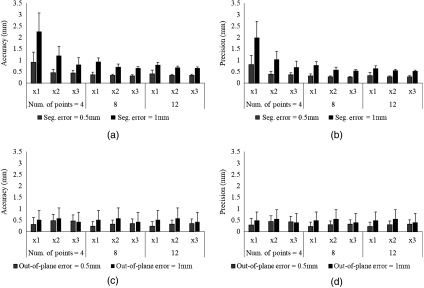
Next, the formulation based on the MAP phantom was evaluated (Fig. 8). Same with the formulation evaluation, a 1-D array US probe was used. The phantom design consists of four points separated by 5 mm (Fig. 4). To account for calibration performance under different phantom conditions, the separation of the points in the phantom was magnified by a phantom size scale factor (1, 2, and 3 times), and the number of points was also varied (4, 8, and 12 points). For each of the phantom conditions, segmentation error and out-of-plane errors were added independently, in which the magnitude of 0.5 and 1 mm was applied for each case. To satisfy the required condition using the MAP phantom, the 3-D location of the point in the first pose was known while partial s were used for the rest of poses, with the out-of-plane information being randomized to simulate the experimental scenario. Once simulation data were created, the unknown component of the s for all poses was recovered using the invariants and first, then the was reconstructed by solving the equation. This simulation computation was repeated 20 times, and the mean case and its standard deviation are shown in Fig. 8.
Fig. 8.
Calibration error of the when different number of points and sizes of an MAP phantom were used. (a–b) The accuracy (a) and precision (b) are shown when the segmentation error was added. (c–d) The accuracy (c) and precision (d) are shown when the out-of-plane error was added.
As the results in Fig. 8 show, all phantom conditions met submillimeter accuracy when the segmentation error was 0.5 mm. When the segmentation error was 1 mm, achieving submillimeter accuracy required either the phantom size to be or the number of points to be 12. The effect of the out-of-plane error was smaller than the segmentation error and was independent from the phantom configuration. When more than 12 points were used with a phantom size of on the MAP phantom, the accuracy of the formulation was superior to the formulation.
4.2. Experimental Results
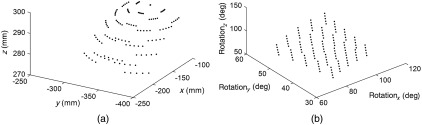
To confirm the robot poses during the experiment, the position and vectorized orientations of the robot end-effector were shown in Fig. 9. The US data of the active points were recorded using both of the arrays on the transrectal probe. Two nonparallel arrays give a unique 3-D localization of the active points, and this information was used for both and calibrations. The experimental results are shown in Table 1. From a total of five active-point targets, four of them were used in the calibration formulation, and the unknown transformation was computed from each active-point target. The internal precision indicates the reconstruction precision computed on the points used for calibration. The external precision is the reconstruction precision when the fifth independent point is used for evaluation. In the calibration, four points were used to calibrate , and the reconstruction precision computed based on the translation component of the recovered s is shown as the internal precision . The same fifth independent point used in the analysis was used to compute the external precision . The results show that the formulation could recover an that minimized the internal precision well, whereas the external precision was not as good as the formulation. This indicates that the formulation recovers an optimized to the areas near the points used for calibration, whereas it does not provide as good of an estimate for the areas that are far from these points. On the contrary, the formulation could keep low reconstruction precisions even on the independent evaluation point by incorporating both the position and the orientation of the phantom.
Fig. 9.
(a) Translation and (b) vectorized orientation of robot tracking information for all poses.
Table 1.
The experimental results.
| Calibration | Internal precision c (mm) | External precision c (mm) | |
|---|---|---|---|
| Dual array (biplane) | BXp Point #1 | 0.77 | 2.55 |
| BXp Point #2 | 0.68 | 1.56 | |
| BXp Point #3 | 0.79 | 3.59 | |
| BXp Point #4 | 0.66 | 2.60 | |
| AXXB | 0.60 | 0.67 | |
| Mono (1-D) array | AXXB | 0.93 | 0.98 |
| Control (BXp)14 | CW/AE | 1.72 | — |
| AE/CW | 1.00 | — |
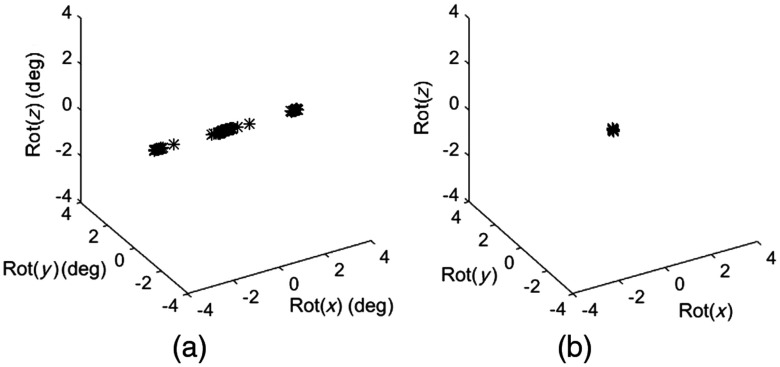
For mono 1-D array calibration, only the linear array portion of the transrectal probe was used for calibration. The intermediate step of recovering is shown in Fig. 10. The error magnitude presents the rotational difference between the recovered s using the monoarray and the s from the ground-truth data using two arrays. The relative matrix between these two s was calculated, and then the vectorized rotational component is shown in an Euler angle representation. Before recovering the one DOF unknown rotation using the invariants, the rotational error is distributed in the rotation around the axis as expected [Fig. 10(a)]. After the invariant-based compensation, the error was substantially improved [Fig. 10(b)].
Fig. 10.
The error magnitude of comparing s from 1-D array and from 2-D array as the ground truth. The rotational error before (a) and after (b) recovering the unknown rotation is shown. If rotational components between them are identical, all axis should be zero.
Using the recovered , the computed reconstruction precision using the formulation was 1 mm with the internal precision and 0.93 mm for the external precision . Although the result was slightly worse compared with the calibration using a US probe with two arrays, the calibration precision with the mono array was still in the submillimeter range of despite having much more limited information in comparison with the dual-array case.
5. Discussion
In the proposed calibration method using the formulation, the phantom size is crucial to the resulting calibration accuracy. From our simulation study, a bigger phantom provides a more reliable , which can eventually be used to solve for a more precise . Therefore, a larger size of the phantom design should be considered when fabricating an MAP phantom. The phantom parameters such as the number of points and the size scale of the phantom can be easily adjusted if the phantom is constructed by multiple virtual points created by the translation of the tracking base frame as presented in the experiments shown in this work. The ability to adjust and customize the phantom design is an advantage over conventional point-based phantoms, where the target and imaging poses are heavily constrained such that the single point must be aligned with the US probe in its midplane.
Comparing and evaluating different US calibration approaches is not a simple task because the performance can be affected by so many factors including the US imaging environment, tracking devices, and calibration phantom designs.7,26 Among various methods used in prior literature, we used accuracy and precision as the metrics to show the calibration performance in simulation. Though accuracy is desired as it reflects the calibration error directly, obtaining the true accuracy is challenging or may even be impossible, because the process of defining the true reference position may introduce other additional errors. On the contrary, the precision metric is based on the same experimental setting as the actual calibration, and subjective evaluation is possible because the datasets used for calibration and evaluation are independent. Our simulation results present a similar numerical outcome with both metrics, and it indicates that precision could be a good indicator of calibration performance when the true accuracy is inaccessible.
To provide a direct comparison with previously proposed approaches, the calibration results using the conventional method is shown in Table 1.14 The same robot arm and geometry of the US probe (linear array, 0.3-mm pitch) as the proposed method was used. Two calibration phantoms, a cross wire and the AE phantom, were used for reconstruction and evaluation, and cross-validation was performed between these two phantoms. When the cross-wire phantom points were used for solving for and the AE points were used for evaluation, the reconstruction prevision had a value of 1.72 mm. When the AE points were used for solving for , and the cross-wire phantom points were used for evaluation, the reconstruction precision was 1.00 mm. This result reconfirms that the proposed method can produce the equivalent or improved calibration performance while substantially reducing the number of midplane detection processes necessary thus decreasing the data acquisition time during US calibration.
Nevertheless, there are some shortcomings that should be noted. The fabrication of a MAP phantom requires a special hardware setup including multiple active US elements. The most direct way of fabrication is to build a phantom consisting of multiple active elements with known geometric relationships. Alternatively, realization of the MAP phantom concept requires at least one active element transmission system with translational motion applied to the phantom using a 2-D translational stage or a robot arm as demonstrated in this paper. For US researchers or researchers conducting image-guided intervention research, having access to a single element transducer is not difficult, and it can be purchased from commercial vendors. In addition to the phantom fabrication, another requirement is that the US machine must have access to a line trigger to initiate the active US element. In addition, to accurately estimate the time of flight of the US signal, access to raw US radio frequency (RF) data is preferred. Usually, US machines designed for interventional applications can meet these requirements due to the need for synchronization with other medical tools and devices.
When US calibration is required in a procedure, the user can choose from calibration phantoms with a wide range of options based on their application and available equipment. For applications in which a coarse calibration with error on the order of several millimeters is acceptable, the phantom position estimation error due to the US beam thickness is negligible, and structural phantoms are suitable due to its rapid calibration time without requiring the midplane detection step as such required in point-based phantoms. For applications that are highly sensitive to accuracy and require submillimeter errors, then calibration methods using point-based phantoms such as the AE system that can minimize the error from the US beam thickness are preferred. The MAP phantom can perform calibrations with the advantages from both types of phantoms.
6. Conclusions
We proposed a US calibration concept utilizing an MAP phantom, which combines high submillimeter calibration accuracy with a quick calibration process. The proposed concept was derived in theory and was demonstrated through simulation and experiment. For future work, the proposed MAP phantom can be simplified and integrated into a compact package that is readily available for calibration. The presented method still requires one midplane detection step that acts as the reference for the rest of the out-of-plane search procedures. This calibration uses only the time-of-flight information, and we envision incorporating intensity information to completely avoid midplane detection.
7. Appendix A: Recovering A Using Multiple Active-Point Phantom Involves One DOF Deficiency
Equations (6)–(9) can be rewritten as
| (18) |
Rearranging Eq. (18) gives
| (19) |
By defining and :
| (20) |
This is another correct formulation bounding and .
Equation (18) is a case of Eqs. (19) and (20) when is identity matrix. When we have poses, Eq. (19) contains unknown, in which unknown in unknown rotation , and one DOF known is , and five DOF in . However, as Eq. (20), we only can solve for DOF because unknown rotation and share the same rotation axis, and these will be solved as one DOF . Therefore, we miss the last one DOF to solve all unknowns.
8. Appendix B: Alternative Approach for Recovering A Using Multiple Active-Point Phantom
Here, we will discuss the way of computing from the channel data. The difference compared with previous approach is that instead of using the earliest arrival data, using the entire wave form could provide more information to localize the point segmentation. The time-of-flight map of the segmented waveform will be obtained. Next, using phantom point location and the corresponding distance (computed from time-of-flight), the position of US array element position from phantom coordinate can be calculated through trilateration.
Each US array element can be computed as
| (21) |
where is the number of phantom points and is the point position from the phantom frame.
The transformation of the US array from phantom coordinate to US image coordinate is computed through point cloud registration. Note that the recovered is not fully true because the US array model is a line, and one DOF rotation is undefined:
| (22) |
s from different poses can be computed through previous steps, but we need to know one fully defined to solve . When one of the poses is forcing the probe to capture the midplane of the active point, the unknown one DOF can be recovered as
| (23) |
where the elevational dimension of is zero.
Acknowledgments
H. K. Zhang was supported by the CDMRP, through the Prostate Cancer Research Program, Early Investigator Research Award under Award No. W81XWH1810188. Additional financial supports were provided by Johns Hopkins University internal funds, NSF Grant RI-Medium No. IIS-1162095, NIH Grant No. R21CA202199, NIBIB-NIH Grant No. EB015638, NIGMS-/NIBIB-NIH Grant No. 1R01EB021396, and NSF Grant No. IIS-1653322.
Biographies
Haichong K. Zhang received his MS and PhD degrees from Johns Hopkins University in 2015 and 2017, respectively. Prior to that, he earned his BS and MS degrees from Kyoto University in 2011 and 2013, respectively. His research interests include advanced medical imaging techniques such as robotic ultrasound and translational photoacoustic imaging of brain and cancer. Currently, he is a postdoctoral fellow in the Laboratory for Computational Sensing and Robotics at Johns Hopkins University.
Alexis Cheng received his BASc from the University of British, Columbia, in 2011 and his MSc and PhD degrees from the Johns Hopkins University in 2013 and 2017, respectively. He has coauthored more than 30 peer-reviewed conference papers and journal articles in the fields of surgical guidance, medical robotics, interventional ultrasound, and photoacoustic imaging. His current research interests include surgical robotics and instrumentation, deep learning in medicine, and ultrasound imaging.
Younsu Kim is a PhD student in the Department of Computer Science at Johns Hopkins University. Prior to joining PhD program at Johns Hopkins, he worked as a research engineer at in LG Electronics Inc, Korea. He received his BE degree in microelectrical engineering from Tsinghua University, Beijing, China, in 2008. His research interests include ultrasound thermal monitoring and ultrasound guided tracking technologies for interventions.
Qianli Ma received his MS degree in robotics from Johns Hopkins University. He graduated with a PhD in mechanical engineering from Johns Hopkins University in 2017. He was affiliated with the Laboratory for Computational Sensing and Robotics under the guidance of Professor Gregory S. Chirikjian. His primary research areas are kinematics of robotics, path planning problems and sensor calibration of robotic systems. He is now working as a senior self-driving car engineer in Aptiv.
Gregory S. Chirikjian received undergraduate degrees from Johns Hopkins University in 1988, and the PhD from the California Institute of Technology, Pasadena, in 1992. Since 1992, he has been on the faculty of the Department of Mechanical Engineering, Johns Hopkins University, where he has been a full professor since 2001. His research interests include robotics, applications of group theory in a variety of engineering disciplines, and the mechanics of biological macromolecules.
Emad M. Boctor joined the Russell H. Morgan Department of Radiology and Radiological Science at the Johns Hopkins Medical Institute in 2007. His research focuses on image-guided therapy, advanced interventional ultrasound imaging and surgery. He is an Engineering Research Center investigator and holds a primary appointment as an assistant professor in the Department of Radiology and a secondary appointment in both the computer science and electrical engineering departments at Johns Hopkins.
Disclosures
No conflicts of interest, financial or otherwise, are declared by the authors.
References
- 1.Okumura Y., et al. , “Three-dimensional ultrasound for image-guided mapping and intervention methods, quantitative validation, and clinical feasibility of a novel multimodality image mapping system,” Circ. Arrhythm. Electrophysiol. 1(2), 110–119 (2008). 10.1161/CIRCEP.108.769935 [DOI] [PubMed] [Google Scholar]
- 2.Hu Y., et al. , “MR to ultrasound registration for image-guided prostate interventions,” Med. Image Anal. 16(3), 687–703 (2012). 10.1016/j.media.2010.11.003 [DOI] [PubMed] [Google Scholar]
- 3.Wachinger C., Wein W., Navab N., “Three-dimensional ultrasound mosaicking,” Lect. Notes Comput. Sci. 4792, 327–335 (2007). 10.1007/978-3-540-75759-7 [DOI] [PubMed] [Google Scholar]
- 4.Zhang H. K., et al. , “Synthetic tracked aperture ultrasound imaging: design, simulation, and experimental evaluation,” J. Med. Imaging 3(2), 027001 (2016). 10.1117/1.JMI.3.2.027001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bottenus N., et al. , “Feasibility of swept synthetic aperture ultrasound imaging,” IEEE Trans. Med. Imaging 35(7), 1676–1685 (2016). 10.1109/TMI.2016.2524992 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Melvær E. L., et al. , “A motion constrained cross-wire phantom for tracked 2D ultrasound calibration,” Int. J. Comput. Assisted Radiol. Surg. 7(4), 611–620 (2012). 10.1007/s11548-011-0661-6 [DOI] [PubMed] [Google Scholar]
- 7.Mercier L., et al. , “A review of calibration techniques for freehand 3-D ultrasound systems,” Ultrasound Med. Biol. 31(4), 449–471 (2005). 10.1016/j.ultrasmedbio.2004.11.015 [DOI] [PubMed] [Google Scholar]
- 8.Hsu P.-W., et al. , “Comparison of freehand 3-D ultrasound calibration techniques using a stylus,” Ultrasound Med. Biol. 34(10), 1610–1621 (2008). 10.1016/j.ultrasmedbio.2008.02.015 [DOI] [PubMed] [Google Scholar]
- 9.Detmer P. R., et al. , “3D ultrasonic image feature localization based on magnetic scanhead tracking: in vitro calibration and validation,” Ultrasound Med. Biol. 20, 923–936 (1994). 10.1016/0301-5629(94)90052-3 [DOI] [PubMed] [Google Scholar]
- 10.Trobaugh J. W., Trobaugh D. J., Richard W. D., “Three-dimensional imaging with stereotactic ultrasonography,” Comput. Med. Imaging Graphics 18, 315–323 (1994). 10.1016/0895-6111(94)90002-7 [DOI] [PubMed] [Google Scholar]
- 11.Boctor E., et al. , “A novel closed form solution for ultrasound calibration,” in 2nd IEEE Int. Symp. on Biomedical Imaging: Nano to Macro (2004). 10.1109/ISBI.2004.1398591 [DOI] [Google Scholar]
- 12.Guo X., et al. , “Active echo: a new paradigm for ultrasound calibration,” Lect. Notes Comput. Sci. 8674, 315–323 (2014). 10.1007/978-3-319-10470-6_50 [DOI] [PubMed] [Google Scholar]
- 13.Aalamifar F., et al. , “Robot assisted automatic ultrasound calibration,” Int. J. Comput. Assisted Radiol. Surg. (IJCARS) 11(10), 1821–1829 (2016). 10.1007/s11548-015-1341-8 [DOI] [PubMed] [Google Scholar]
- 14.Cheng A., et al. , “Active phantoms: a new paradigm for ultrasound calibration using phantom feedback,” J. Med. Imaging 4(3), 035001 (2017). 10.1117/1.JMI.4.3.035001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Guo X., et al. , “Active ultrasound pattern injection system (AUSPIS) for interventional tool guidance,” PLoS One 9(10), e104262 (2014). 10.1371/journal.pone.0104262 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Horn B. K., et al. , “Closed-form solution of absolute orientation using orthonormal matrices,” J. Opt. Soc. Am. A 5(7), 1127–1135 (1988). 10.1364/JOSAA.5.001127 [DOI] [Google Scholar]
- 17.Tsai R., Lenz R., “A new technique for fully autonomous and efficient 3D robotics hand/eye calibration,” IEEE Trans. Rob. Autom. 5(3), 345–358 (1989). 10.1109/70.34770 [DOI] [Google Scholar]
- 18.Shiu Y., Ahmad S., “Finding the mounting position of a sensor by solving a homogeneous transform equation of the form AX = XB,” in IEEE Int. Conf. on Robotics and Automation, Vol. 4, pp. 1666–1671 (1987). 10.1109/ROBOT.1987.1087758 [DOI] [Google Scholar]
- 19.Chen H. H., “A screw motion approach to uniqueness analysis of head-eye geometry,” in IEEE Conf. on Computer Vision and Pattern Recognition, pp. 145–151 (1991). 10.1109/CVPR.1991.139677 [DOI] [Google Scholar]
- 20.Park F. C., Martin B. J., “Robot sensor calibration: solving AX = XB on the Euclidean Group,” IEEE Trans. Rob. Autom. 10(5), 717–721 (1994). 10.1109/70.326576 [DOI] [Google Scholar]
- 21.Ackerman M. K., et al. , “Sensor calibration with unknown correspondence: solving AX = XB using euclidean-group invariants,” in IEEE/RSJ Int. Conf. on Intelligent Robots and Systems (IROS’13), pp. 1308–1313 (2013). 10.1109/IROS.2013.6696518 [DOI] [Google Scholar]
- 22.Ma Q., Li H., Chirikjian G. S., “New probabilistic approaches to the AX = XB hand-eye calibration without correspondence,” in IEEE Int. Conf. on Robotics and Automation, pp. 4365–4371 (2016). 10.1109/ICRA.2016.7487635 [DOI] [Google Scholar]
- 23.Ackerman M. K., Chirikjian G. S., “A probabilistic solution to the AX = XB problem: sensor calibration without correspondence,” Lect. Notes Comput. Sci. 8085, 693–701 (2013). 10.1007/978-3-642-40020-9 [DOI] [Google Scholar]
- 24.Arun K. S., Huang T. S., Blostein S. D., “Least-squares fitting of two 3-D point sets,” IEEE Trans. Pattern Anal. Mach. Intell. PAMI-9(5), 698–700 (1987). 10.1109/TPAMI.1987.4767965 [DOI] [PubMed] [Google Scholar]
- 25.Cheng A., et al. , “Ultrasound to video registration using a bi-plane transrectal probe with photoacoustic marker,” Proc. SPIE 9786, 97860J (2016). 10.1117/12.2216644 [DOI] [Google Scholar]
- 26.Hsu P. W., et al. , “Freehand 3D ultrasound calibration: a review,” in Advanced Imaging in Biology and Medicine, pp. 47–84, Springer, Berlin Heidelberg: (2009). [Google Scholar]