Learning Gene Regulatory Networks from Next Generation Sequencing Data

Summary:

In recent years, next generation sequencing (NGS) has gradually replaced microarray as the major platform in measuring gene expressions. Compared to microarray, NGS has many advantages, such as less noise and higher throughput. However, the discreteness of NGS data also challenges the existing statistical methodology. In particular, there still lacks an appropriate statistical method for reconstructing gene regulatory networks using NGS data in the literature. The existing local Poisson graphical model method is not consistent and can only infer certain local structures of the network. In this paper, we propose a random effect model-based transformation to continuize NGS data, and then we transform the continuized data to Gaussian via a semiparametric transformation and apply an equivalent partial correlation selection method to reconstruct gene regulatory networks. The proposed method is consistent. The numerical results indicate that the proposed method can lead to much more accurate inference of gene regulatory networks than the local Poisson graphical model and other existing methods. The proposed data-continuized transformation fills the theoretical gap for how to transform discrete data to continuous data and facilitates NGS data analysis. The proposed data-continuized transformation also makes it feasible to integrate different types of data, such as microarray and RNA-seq data, in reconstruction of gene regulatory networks.

1. Introduction

The emergence of high-throughput technologies has made it feasible to measure the activities of thousands of genes simultaneously, which provides scientists with a major opportunity to infer global gene regulatory networks (GRNs). Accurate inference of global GRNs is pivotal to gaining a systematic understanding of the molecular mechanism, to shedding light on the mechanisms of diseases that occur when cellular processes are dysregulated, and to further identifying potential therapeutic targets for diseases. Given the high dimensionality and complexity of high-throughput data, inference of global GRNs largely relies on the advance of computational statistical methods.

Gaussian graphical models.

The traditional methods for learning GRNs include Boolean networks, Bayesian networks and differential equation models. See Karlebach and Shamir (2008) for an overview. Since these methods are not scalable, they are usually only applicable to small sets of genes. For large sets of genes, the GRN can be constructed based on Gaussian graphical models (GGMs). The idea underlying GGMs is to use the partial correlation coefficient as a measure of dependency of any two variables (referred to as genes in GRNs). A zero partial correlation coefficient indicates conditional independence of the two variables. A variety of methods have been proposed for constructing GGMs from observed data. A popular method is covariance selection (Dempster, 1972), which identifies the non-zero elements in the concentration matrix (i.e., inverse of the covariance matrix) because the non-zero entries in the concentration matrix correspond to conditionally dependent variables. However, this approach cannot be applied to the case of p > n, where the sample covariance matrix is singular and thus the concentration matrix can no longer be directly estimated. To tackle this difficulty, regularization methods such as nodewise regression (Meinshausen and Bühlmann, 2006) and graphical Lasso ( Yuan and Lin, 2007; Friedman et al., 2008) have been proposed. Nodewise regression uses Lasso (Tibshirani, 1996) as a variable selection method to identify the neighborhood of each variable, and thus the nonzero elements of the concentration matrix. A neighborhood is the set of predictor variables with nonzero coefficients in a regression model estimated separately for each variable. Meinshausen and Bühlmann (2006) showed that this method asymptotically recovers the true graph. To avoid estimating a large number of regressions, Yuan and Lin (2007) proposed to directly estimate the concentration matrix using the regularization method with a l₁-penalty. Soon, this method was accelerated by Friedman et al. (2008) using a coordinate descent algorithm that was originally designed for Lasso regression, and this led to the so-called graphical Lasso algorithm. Quite recently, Liang et al. (2015) proposed the ψ-learning method, which works based on an equivalent measure of partial correlation coefficients calculated with reduced conditional sets. The nodewise regression, graphical Lasso and ψ-learning methods can generally work well for Gaussian data, such as the gene expression data measured in DNA microarray.

RNA-seq Data and Poisson Graphical Models.

In recent years, next generation sequencing (NGS) has gradually replaced microarray as the major platform in transcriptome studies, say, through sequencing RNAs (RNA-seq). RNA-seq uses counts of reads to quantify gene expression levels. Compared to microarray data, RNA-seq data have many advantages, such as providing digital rather than analog signals of expression levels, dynamic and wider ranges of measurements, less noise, higher throughput, etc. However, their discreteness also challenges the existing statistical methods. In practice, RNA-seq data are often modeled using Poisson (Sultan et al., 2008) or negative-binomial distributions (Robinson and Oshlack, 2010; Anders and Huber, 2010), but difficulties often arise in the computation or knowing the properties of the statistics based on these distributions.

Let Y = (Y₁,…Y_p) denote a p-dimensional Poisson random vector associated with a graphical model G. It is natural to assume that all the node-conditional distributions, i.e., the conditional distribution of one variable given all other variables, are Poisson with the distribution given by

$$\begin{gathered} P\left(Y_j|Y_k,\forall k\ne j;{\text{Θ}}_j\right)=\exp \left[{\theta }_j{Y}_j-\log \left(Y_j!\right)+\sum _{k\ne j}{\theta }_{jk}{Y}_j{Y}_k \\ -A\left({\theta }_j,{\theta }_{jk}\right)\right], \end{gathered}$$ (1)

where Θ_j = {θ_j, θ_jk, k ≠ j}, and A(θ_j, θ_jk) is the log-partition function of the Poisson distribution. Following from the Hammersley-Clifford theorem (Besag, 1974), the node-conditional distributions combine to yield the joint Poisson distribution

$$P\left(\mathit{Y},\Theta \right)=\exp \left[\sum _{j=1}^p\left({\theta }_j{Y}_j-\log \left(Y_j!\right)\right)+\sum _{j\ne k}{\theta }_{jk}{Y}_j{Y}_k-\varphi \left(\Theta \right)\right],$$ (2)

where Θ = (Θ_1,…, Θ_p) and ϕ(Θ) is the normalizing term ensuring the properness of this distribution. However, the Poisson graphical model suffers from a major caveat: the interaction parameters θ_jk must be non-positive for all j ≠ k to ensure ϕ(Θ) to be finite and thus the distribution P (Y; Θ) to be proper (Besag, 1974; Yang et al., 2012). Therefore, the Poisson graphical model only permits negative conditional dependencies, which is a severe limitation in practice. As shown in Patil and Joshi (1968), the negative binomial graphical model also suffers from the same limitation.

To relax this limitation, Allen and Liu (2013) proposed a local Poisson graphical model (LPGM), which ignores the joint distribution of Y_j’s, and works by finding a local model for each gene using a regularization method based on the conditional distribution (1) and then defining the network structure as the union of the local models. To account for the high dispersion of the NGS data when the inter-sample variance is greater than the sample mean, Gallopin et al. (2013) proposed a hierarchical log-normal Poisson model which assumes Y_ij ~ Poisson(λ_ij) with $\log ({\lambda }_{ij})={\sum }_{{}_{k\ne j}}{\beta }_{jk}{\tilde{y}}_{ik}+{ϵ}_{ij}$ for j = 1,…,n, where ϵ_ij is a Gaussian random variable, and ${\tilde{y}}_{ik}$ denotes the standardized, log-transformed data. For each variable Y_i, the local model can be found via a regularization approach for the log-normal Poisson regression. Quite a few related models have been proposed along this direction, including the truncated PGM, quadratic PGM, sub-linear PGM and square-root PGM. Refer to Yang et al. (2013) and Inouye et al. (2016) for the detail. However, these LPGM-based methods are not consistent due to their ignorance of the joint distribution of Y_j’s. Without the joint distribution, the conditional dependence $Y_k\cancel{\perp }{Y}_j|Y_{V\backslash \left\{k,j\right\}}$ is not well defined and thus the theoretical basis $Y_k\cancel{\perp }{Y}_j|Y_{V\backslash \left\{k,j\right\}}\iff {\theta }_{kj}\ne 0$ and θ_jk ≠ 0 of nodewise regression (Meinshausen and Bühlmann, 2006; Ravikumar et al., 2009) does not hold, where θ_kj and θ_jk are defined in (1). Hence, linking the Poisson graphical model to nodewise Poisson regression will not lead to a consistent estimate for the underlying network.

In this paper, we propose a random effect model-based transformation for RNA-seq data. This transformation transforms count data to continuous data, which can then be further transformed to Gaussian data via a semiparametric transformation as prescribed in Liu et al. (2009). Then, we adopt the ψ-learning method developed in Liang et al. (2015) to construct GGMs for the transformed data. Under mild regularity and sparsity conditions, we show that the proposed method is consistent. Transforming count data to continuous data greatly facilitates the analysis of NGS data.

The remainder of this paper is organized as follows. Section 2 describes the random effect model-based transformation, and gives a brief review for the semiparametric transformation of Liu et al. (2009) and the ψ-learning method of Liang et al. (2015). Section 3 illustrates the proposed method using simulated data along with comparisons with gLasso, nodewise regression, LPGM, and some other existing methods. Section 4 applies the proposed method to two real data examples. Section 5 concludes the paper with a brief discussion.

2. Method

The proposed method consists of three steps: (i) data-continuized transformation, (ii) data-Gaussianized transformation, and (iii) ψ-learning, which are described in sequel as follows.

2.1. Data-Continuized Transformation

To continuize the RNA-seq data, we propose a random effect model-based transformation. Let Y_ij denote the RNA-seq expression of gene i from subject j for i = 1,…,p and j = 1,…,n, where p denotes the number of genes and n denotes the number of subjects. We assume that

$$Y_{ij}\sim Poisson\left({\theta }_{ij}\right),{\theta }_{ij}\sim Gamma\left({\alpha }_i,{\beta }_i\right),$$ (3)

where α_i and β_i are two parameters of the Gamma distribution. It is easy to see that (3) forms a random effect model with the gene-specific random effect modeled by a Gamma distribution. If we integrate out θ_ij from the joint distribution $f\left(Y_{ij},{\theta }_{ij}|{\alpha }_i,{\beta }_i\right),$ we will have Y_ij distributed according to a negative binomial distribution N B(r; q) with r = β_i and q = α_i/(1 + α_i). Hence, the model (3) is quite flexible, which accommodates potential overdispersion of the data.

To avoid an explicit specification for the values of α_i and β_j, we conduct a Bayesian analysis for the model. For this purpose, we let α_i and β_i be subject to the prior distributions:

$${\alpha }_i\sim Gamma\left(a_1,b_1\right),{\beta }_i\sim Gamma\left(a_2,b_2\right),$$

where a₁, b₁, a₂ and b₂ are prior hyperparameters. By assuming that αi and β_i are a priori independent, the full conditional posterior distributions of θ_ij, α_i and β_i are given as follows:

$$\begin{gathered} f\left({\alpha }_i\left|{\theta }_{ij},{\beta }_i,{\mathit{y}}_i\right.\right)\propto \frac{{\alpha }_i^{a_1-1}}{{\Gamma }^n\left({\alpha }_i\right)}{e}^{{\alpha }_i\left(-b_1+n\log {\beta }_i+{\sum }_{j=1}^n\log {\theta }_{ij}\right)}, \\ f\left({\beta }_i\left|{\alpha }_i,{\theta }_{ij},{\mathit{y}}_i\right.\right)\propto {\beta }_i^{n{\alpha }_i+a_2-1}{e}^{-{\beta }_i\left({\sum }_{j=1}^n{\theta }_{ij}+b_2\right)} \\ \propto Gamma(n{\alpha }_i+a_2,\sum _{j=1}^n{\theta }_{ij}+b_2), \\ f\left({\theta }_{ij}\left|{\alpha }_i,{\beta }_i,{\mathit{y}}_i\right.\right)\propto {\theta }_{ij}^{y_{ij}+{\alpha }_i-1}{e}^{-{\theta }_{ij}\left(1+{\beta }_i\right)} \\ \propto Gamma\left(y_{ij}+{\alpha }_i,{\beta }_i+1\right), \end{gathered}$$ (4)

where y_i = {y_ij : j = 1; 2,…,n}. Regarding the choice of prior hyperparameters, we establish the following lemma, whose proof is given in the supplementary material.

Lemma 1:

If a₁ and a₂ take small positive values, then for all i and j, the posterior mean of θ_ij, denoted by E[θ_ij|y_i], will converge to y_ij as b₁ → ∞ and b₂ → ∞.

Suppose that a MCMC algorithm, e.g., the Metropolis-within-Gibbs sampler (Müller, 1993), was used to simulate from the posterior distribution (4). Let ${\theta }_{ij}^{\left(t\right)}$ denote the posterior samples of θ_ij for = 1, 2, …, and let ${\widehat{\theta }}_{ij}^{\left(T\right)}={\sum }_{t=1}^T{\theta }_{ij}^{\left(t\right)}/T$ denote the Monte Carlo estimator of $E\left[{\theta }_{ij}|{\mathit{y}}_i\right]$. Then, following from the standard theory of MCMC, we have ${\widehat{\theta }}_{ij}^{\left(T\right)}\stackrel{p}{\to }E\left[{\theta }_{ij}|y_i\right]$ as T → ∞, where $\stackrel{p}{\to }$ denotes convergence in probability. To ensure the convergence ${\widehat{\theta }}_{ij}^{\left(T\right)}\stackrel{p}{\to }{y}_{ij}$ hold in a rigorous manner, the iteration number T and the prior hyperparameters b₁ and b₂ need to go to infinity simultaneously. To achieve this goal, we let b₁ and b₂ increase with iterations. Let $b_1^{\left(t\right)}$ and $b_2^{\left(t\right)}$ denote the respective values of b₁ and b₂ taken at iteration t, and we set

$$b_1^{(t)}=b_1^{(t-1)}+\frac{c}{t^{\zeta }},\hspace{0.17em}\hspace{0.17em}{b}_2^{(t)}=b_2^{(t-1)}+\frac{c}{t^{\zeta }},\hspace{0.17em}\hspace{0.17em}t=1,2,\dots ,$$ (5)

where $b_1^{(0)}$ and $b_2^{(0)}$ are fixed large constants, c > 0 is a small constant, and 0 < ζ ≤ 1. Under this setting, the MCMC sampler for (4) forms an adaptive Markov chain for which the target distribution gradually shrinks toward a Dirac delta measure defined on (α_i, β_i, θ_ij) = (0; 0; y_ij). For simplicity in theoretical development (see supplementary material), we assume that a random walk proposal is used in simulating from the conditional posterior distribution $f\left({\alpha }_i|\cdot \right)$, i.e., the proposal distribution $q\left({\alpha }_i^{\prime }|{\alpha }_i^{\left(t\right)}\right)=q\left(\left|{\alpha }_i^{\prime }-{\alpha }_i^{(t)}\right|\right)$ depends on $\left|{\alpha }_i^{\prime }-{\alpha }_i^{(t)}\right|$ only. In summary, we have the following lemma, whose proof is given in the supplementary material.

Lemma 2:

If a random walk proposal is used in simulating from $f\left({\alpha }_i|\cdot \right)$ and the prior hyperparameters are chosen in (5), then ${\widehat{\theta }}_{ij}^{\left(T\right)}\stackrel{p}{\to }{y}_{ij}$ for all i and j as $T\to \infty$, where ${\widehat{\theta }}_{ij}^{\left(T\right)}={\sum }_{t=1}^T{\theta }_{ij}^{\left(t\right)}/T$ and ${\theta }_{ij}^{\left(t\right)}$ denotes the posterior sample of θ_ij generated at iteration t.

Lemma 2 implies that the statistical inference for y_ij’s can be approximately made using ${\widehat{\theta }}_{ij}^{\left(T\right)}$’s as T → ∞. The validity of the approximation can be argued as follows: Let $\mathbb{F}\left({\widehat{\theta }}_1^{(T)},\dots ,{\widehat{\theta }}_p^{(T)}\right)$ denote the empirical CDF of p-continuized random variables. Let $\mathbb{F}({\mathit{y}}_1,\dots ,{\mathit{y}}_p)$ denote the empirical CDF of (Y_1,…,Y_p). It is easy to see that the convergence ${\widehat{\theta }}_{ij}^{\left(T\right)}\stackrel{p}{\to }{y}_{ij}$ implies ${\sup }_{\mathit{t}\in {ℝ}^p}\Vert {\mathbb{F}}_{{\widehat{\theta }}_1^{(T)},\dots ,{\widehat{\theta }}_p^{(T)}}(\mathit{t})-{\mathbb{F}}_{y_1,\dots ,y_p}(\mathit{t})\Vert \stackrel{p}{\to }0$ as T → ∞. Further, as the sample size n → ∞, ${\sup }_{\mathit{t}\in {ℝ}^p}\Vert {\mathbb{F}}_{y_1},\dots {,}_{y_p}(\mathit{t})-F_{Y_1,\dots ,Y_p}(\mathit{t})\Vert \stackrel{a.s.}{\to }0$ holds under some regularity and sparsity conditions, where F_Y1,…,Yp(t) denotes the CDF of Y_i’s, and $\stackrel{a.s.}{\to }$ denotes almost sure convergence. For example, we can assume that for each Y_i, the number of variables that Y_i depends on is upper bounded by n / log(n). In summary, we have ${\sup }_{\mathit{t}\in {ℝ}^p}\Vert {\mathbb{F}}_{{\widehat{\theta }}_p^{(T)},\dots ,{\widehat{\theta }}_p^{(T)}}(\mathit{t})-F_{Y_1,\dots ,Y_p}(t)\Vert \stackrel{p}{\to }0$ as T → ∞ and n → ∞, which implies that a consistent estimate can be formed based on the continuized data for each conditional probability used for inference of the network structure underlying Y_1,…,Y_p. That is, the conditional independence relations among Y_1,…,Y_p can be learned from the continuized data ${\widehat{\theta }}_1^{(T)},\dots ,{\widehat{\theta }}_p^{(T)}$ in a consistent manner.

2.2. Data Gaussianized transformation

Since GGMs have been extensively studied, we seek for a transformation that transforms the continuized data to be Gaussian, while maintaining the conditional independence relations among the variables. The semiparametric Gaussian copula transformation, the so-called nonparanormal transformation, proposed by Liu et al. (2009) satisfies this requirement. It can be described as follows.

Let X = (X_1,…,X_p)^T be a continuous p-dimensional random vector. It is said that X has a nonparanormal distribution if there exist functions ${\left\{f_j\right\}}_{j=1}^p$ such that Z = f(X) ~ N(μ, ∑), where f(X) = (f₁(X₁),…,f_p(X_p))^T. We write X ~ N P N(μ, ∑, f). It is known that if f_j’s are monotone and differentiable, the joint probability density function of X is given by

$$\begin{gathered} P_X(x)=\frac{1}{{(2\pi )}^{p/2}{\left|\Sigma \right|}^{1/2}}\exp \left\{-\frac{1}{2}{(f(x)-\mu )}^T{\Sigma }^{-1}(f(x)-\mu \right\} \\ \cdot \prod _{j=1}^p\left|f_j^{\prime }(x_j)\right|. \end{gathered}$$ (6)

Based on this formula, Liu et al. (2009) argued that if X ~ N P N(μ, ∑, f) and each f_j is monotone and differentiable, then $X_i\perp X_j\left|X_{V\backslash \left\{i,j\right\}}\iff Z_i\perp Z_j\right|Z_{V\backslash \left\{i,j\right\}}.$ With the similar argument, we can have that for any triple of disjoint sets $A,B,C\subseteq V,X_A\perp X_B\left|X_C\iff Z_A\perp Z_B\right|Z_C.$ In other words, the nonparanormal transformation preserves the conditional independence structure of the original graphical model formed by X. Liu et al. (2009) further showed that $f_j(x)={\mu }_j+{\sigma }_j{\Phi }^{-1}(F_j(x))$ is such a monotone and differentiable transformation, where μ_j is the mean of X_j, ${\sigma }_j^2$ is the variance of X_j, and F_j(x) is the CDF of X_j. For the high dimensional case where p is greater than and can increase with n, F_j(x) can be replaced by a truncated or Winsorized estimator of the marginal empirical distribution of X_j in order to reduce the variance of the estimate.

2.3. ψ-Learning for Gaussian Graphical Models

There are several methods for learning the structure of Gaussian graphical models, such as gLasso, nodewise regression, and ψ-learning. In this paper ψ-learning is adopted, which, as shown in Liang et al. (2015), tends to have better numerical performance and less CPU cost than gLasso and nodewise regression. The ψ-learning method consists of three steps:

• (a)
  (Correlation screening) Determine the neighborhood for each vertex (or variable) X_i.

  • (i)
    Conduct a multiple hypothesis test to identify the pairs of variables for which the empirical correlation coefficient is significantly different from zero. This step results in a so-called empirical correlation network.
  • (ii)
    For each vertex X_i, identify its neighborhood in the empirical correlation network, and reduce the size of the neighborhood to O(n= log(n)) by removing the variables having lower correlation (in absolute value) with X_i. This step results in a so-called reduced correlation network.
• (b)(ψ-calculation) For each pair of vertices i and j, identify a separator S_ij based on the reduced correlation network resulted in step (a) and calculate ${\Psi }_{ij}={\rho }_{ij|S_{ij}},$ where ${\rho }_{ij|S_{ij}}$ denotes the partial correlation coefficient of X_i and X_j conditioned on the variables {X_k : k ∈ S_ij}. For a pair of vertices i ≠ j, a set of vertices is called a separator of i and j if all paths from vertex i to vertex j have at least one vertex in the set.
• (c)(ψ-screening) Conduct a multiple hypothesis test to identify the pairs of vertices for which ψ_ij is significantly different from zero, and set the corresponding element of the adjacency matrix to be 1.

Under mild conditions, Liang et al. (2015) showed that the ψ-partial correlation coefficient is equivalent to the true partial correlation coefficient in determining the structure of GGMs in the sense that

$${\Psi }_{ij}=0\iff {\rho }_{ij|V\backslash \left\{i,j\right\}}=0,$$ (7)

where ${\rho }_{ij|V\backslash \left\{i,j\right\}}$ denotes the partial correlation coefficient of X_i and X_j conditioned on all other variables in the set V. As implied by (7), the key to the success of the ψ-learning method is that it has reduced the computation of partial correlation coefficients from a high dimensional problem to a low dimensional problem. In general, the cardinality of the set V \ {i,j} can be much higher than the sample size n, while the cardinality of S_ij is upper bounded by O(n/log(n)). As shown in Liang et al. (2015), the Ψ-learning method is consistent, i.e., the network produced by it will converge to the true one as the sample size n → ∞.

The multiple hypothesis tests involved in the correlation screening and Ψ-screening steps can be done using an empirical Bayes method developed in Liang and Zhang (2008). The advantage of this method is that it allows for the general dependence between test statistics. Other multiple hypothesis tests which accounts for the dependence between test statistics, e.g., Benjamini et al. (2006), can also be applied here. The performance of multiple hypothesis tests depend on their significance levels. Following the suggestion of Liang et al. (2015), we set the significance level of correlation screening to be α₁ = 0:2 and that of Ψ-screening to be α₂ = 0:05. In general, a high significance level of correlation screening will lead to a slightly large separator set S_ij, which reduces the risk of missing some important variables in the conditioning set. Including a few false variables in the conditioning set will not hurt much the accuracy of Ψ-partial correlation coefficients.

2.4. Consistency

In summary, the proposed method consists of three steps: (i) data-continuized transformation, (ii) data-Gaussianized transformation, and (iii) Ψ-learning for Gaussian graphical models. From Lemma 2 and the followed arguments, we can conclude that the network structure of Y_1,…,Y_p can be consistently learned from the continuized data ${\widehat{\theta }}_1^{(T)},\dots ,{\widehat{\theta }}_p^{(T)}$. Liu et al. (2009) showed that the data-Gaussianized transformation preserves the network structure underlying the data, and Liang et al. (2015) showed that the Ψ-learning method is consistent in recovering the underlying network structure. Therefore, the consistency also holds for the proposed method; that is, the true gene regulatory relations can be recovered from the RNA-seq data using the proposed method when the sample size becomes large.

3. Simulation Studies

To illustrate the performance of the proposed method, we consider some simulation examples with the known conditional independence structure. Since the most NGS data tend to be zero-inflated and highly over-dispersed, the data were simulated from a multivariate zero-inflated negative binomial (ZINB) distribution. The ZINB distribution contains three parameters, λ, k and ω, which controls its mean, dispersion and degree of zero-inflation, respectively. The algorithm developed by Yahav and Shmueli (2012) was adopted to simulate the data, which works via an inverse nonparanormal transformation as follows:

• (a)Simulate a random sample of n multivariate Gaussian random variables with the known concentration matrix. Denote the random sample by (X_1,…,X_p), where each variable X_i = (X_i1,…,X_in)^T consists of n realizations.
• (b)For each variable X_i, find its empirical CDF based on the n realizations and calculate the cumulative probability value for each realization X_ij.
• (c)Generate a random sample of n zero-inflated negative binomial random variables with pre-specified parameters λ, k and ω by inverting the cumulative probability values obtained in (b).

In our simulations, we set the concentration matrix as follows:

$$C_{i,j}=\{\begin{array}{c}0.5,\\ 0.25,\\ 1,\\ 0,\end{array}\begin{array}{c}\text{if}\left|j-i\right|=1,i=2,\dots ,(p-1),\\ \text{if}\left|j-i\right|=2,i=3,\dots ,(p-2),\\ \text{if}\hspace{0.17em}i=j,i=1,\dots ,p,\\ \text{otherwise}.\end{array}$$ (8)

This matrix has been used by quite a few authors to demonstrate their GGM algorithms, say, Yuan and Lin (2007), Mazumder and Hastie (2012), and Liang et al. (2015). To make the simulation similar to the real world, we set the parameters λ, k and ω of the ZINB distribution to their estimates from a real dataset, Acute myeloid leukemia(AML) mRNA sequencing data, which is available on The Cancer Genome Atlas(TCGA) data portal. We estimated these parameters using the function “glm.nb” in R for each gene, and then set the simulation parameters to the medians of the estimates: λ = 515; 743, k = 3:304 and ω = 0:003. For the other parameters, we set n = 100 and p = 200. We then applied the proposed method to the simulated data, which went through the steps of data-continuized transformation, nonparanormal transformation, and ψ-learning. To measure the performance of the method, we plot the precision-recall curve (defined in the supplementary material) in Figure 2, which is drawn by fixing the significance level of correlation screening to α₁ = 0.2 and varying the value of α₂, the significance level of ψ-screening.

Figure 2.

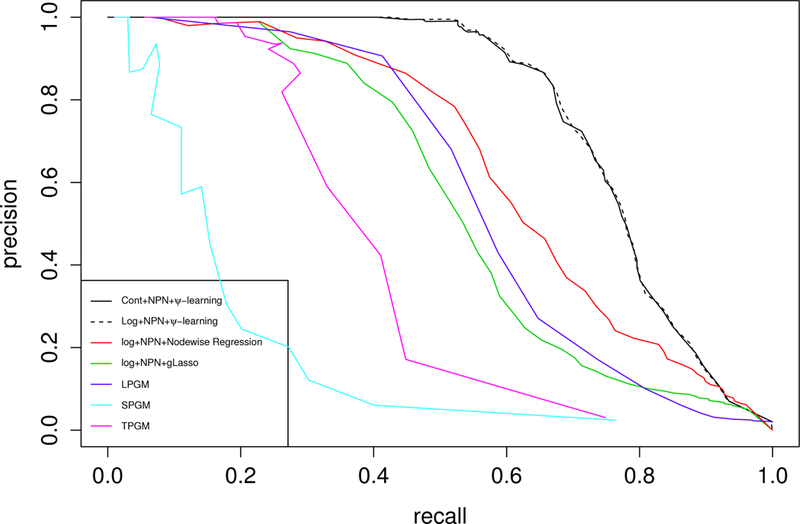
Precision-recall curves produced by the proposed method (Cont+NPN+Ψ-learning), log transformation-based Ψ-learning (Log+NPN+Ψ-learning), log transformation-based gLasso (Log+NPN+gLasso), log transformation-based nodewise regression (Log+NPN+nodewise Regression), LPGM SPGM, TPGM for the simulated data with (n, p) = (100, 200).

To conduct the data-continuized transformation, the Metropolis-within-Gibbs sampler was run for 10000 iterations for this dataset, where the first 1000 iterations were discarded for the burn-in process and the remaining iterations were used for inference. The total CPU time cost by the sampler was 39.0 seconds on a personal computer with 2.8GHz Intel Core i7. On average, it cost less than 0.2 seconds per variable. For this transformation, we set α₁ = α₂ = 1, $b_1^{(0)}=b_2^{(0)}$ = 10000, c = 1 and ς = 1, the default setting of the prior hyperparameters used throughout the paper. The left panel of Figure 1 shows the scatter plot of the continuized data versus raw counts for one variable, and the right panel shows the Q-Q plot of the Gaussianized data for the variable. The scatter plot indicates that the continuized data and the raw counts are very close to each other. To have a thorough exploration for the data-continuized transformation, we reported in Table 2 of the supplementary material the posterior mean and standard deviation of α_i, β_i, θ_ij and the AUC value, i.e., the area under the precision-recall curve, for measuring the performance of the proposed method. The results indicate again that θ_ij can be very close to y_ij and our method is robust to the choice of (a₁, a₂, $b_1^{(0)},b_2^{(0)}$). The data-continuized transformation does not lose much information of the raw counts.

Figure 1.

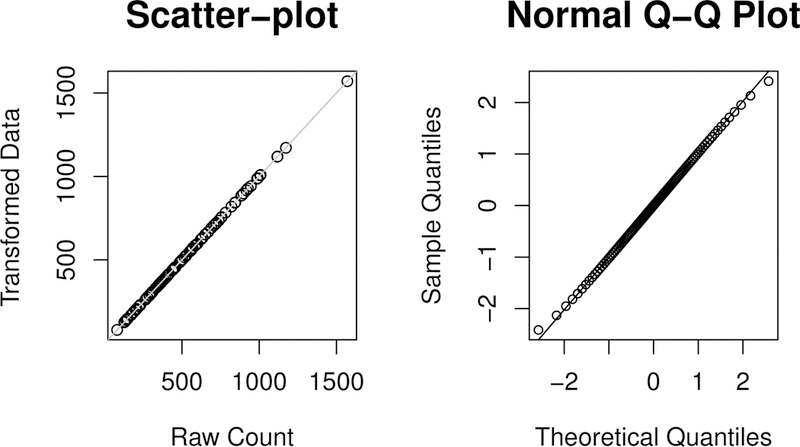
Left: Scatter plot of the continuized data versus raw counts for one variable. Right: QQ-plot of the Gaussianized data for one continuized variable.

For comparison, we have applied the existing methods, including gLasso, nodewise regression, Local Poisson Graphical Model (LPGM), Truncated Poisson Graphical Model (TPGM) and Sublinear Poisson Graphical Model (SPGM) to the simulated data. For gLasso and node-wise regression, the simulated ZINB data first went through the logarithm transformation and nonparanormal transformation, which have been widely used in RNA-seq data analysis, and then the methods were applied. The gLasso and nodewise regression methods have been implemented in the R-package huge (Zhao et al., 2015). In our applications, the stability approach was used to determine their regularization parameters. The stability approach selects the network with the smallest amount of regularization that simultaneously makes the network sparse and replicable under random sampling. For LPGM, we used the method proposed by Allen and Liu (2013). For SPGM and TPGM, we used the method proposed by Yang et al. (2013). The three methods have been implemented in the R-package XMRF (Wan et al., 2015). Besides these existing method, we also compared the proposed method with the one without data-continuized process, i.e., ψ-learning with logarithmic and non-paranormal transformations, which is labeled as “Log+NPN+ψ-Learning” in Figure 2.

The comparison indicates that the proposed method significantly outperforms other meth-ods, although the improvement mainly comes from ψ-learning. The data-continuized transformation does not loss the information of the data, and it provides a justification for the empirical use of treating log-NGS data as continuous. Multiple datasets have been tried, the results are very similar. Note that LPGM is an extension of the nodewise regression method (Meinshausen and Bühlmann, 2006) to multivariate Poisson. Both the LPGM and nodewise regression methods are based on the idea of neighborhood selection. This experiment also shows that the data-continuized transformation and nonparanormal transformation improves the performance of the neighborhood selection method. Based on this experiment, we suspect that the graph consistency established in Meinshausen and Bühlmann (2006) for nodewise normal regression might not hold for LPGM.

We have also considered several common network structures such as hub, scale-free, small-world and random. The multivariate Gaussian random variables given these structures can be generated by functions provided in “huge” package. Then we continue steps (b) and (c) of Yahav and Shmueli’s algorithm to get ZINB samples with the same parameters as used before, i.e., (n, p) = (100, 200), λ = 515; 743, k = 3:304 and ω = 0:003. The results are summarized in Figure 3. It shows that the proposed method significantly outperforms all other methods for the scale-free, small world and random structures, and performs similarly to gLasso and nodewise regression for the hub structure. To have a thorough comparison with the existing methods, we also considered the scenario of n > p with the results reported in the supplementary material.

Figure 3.

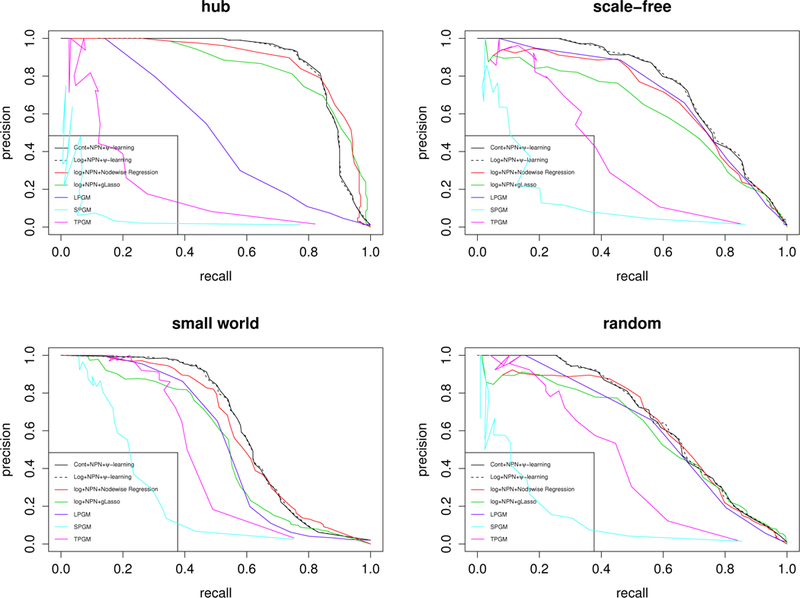
Precision-recall curves of each method for different type of structures with (n, p) = (100, 200). Upper left: hub; upper right: scale-free; lower left: small-world; lower right: random. Refer to the legend of Figure 2 for the labels.

4. Real Data Examples

4.1. Liver cytochrome P450s subnetwork

Liver cytochrome P450s play critical roles in drug metabolism, toxicology, and metabolic processes. They form a superfamily of monooxygenases critical for anabolic and catabolic metabolism in all organisms characterized so far (Nelson et al., 1996; Aguiar et al., 2005; Plant, 2007). Specifically, P450 enzymes are involved in the metabolism of various endogenous and exogenous chemicals, including steroids, bile acids, fatty acids, eicosanoids, xenobiotics, environmental pollutants, and carcinogens (Ortiz, 2005). Through experimental work, Yang et al. (2010) determined the human liver transcriptional network structure, uncovered subnet-works representative of the P450 regulatory system, and identified novel candidate regulatory genes. Our goal is to recover the P450s gene regulatory subnetwork, as shown in the left panel of Figure 4, using the RNA-seq data generated at Dr. Lamba’s lab. In the plot, the P450 genes and the known P450 regulators are highlighted as red circles and blue squares, respectively.

Figure 4.

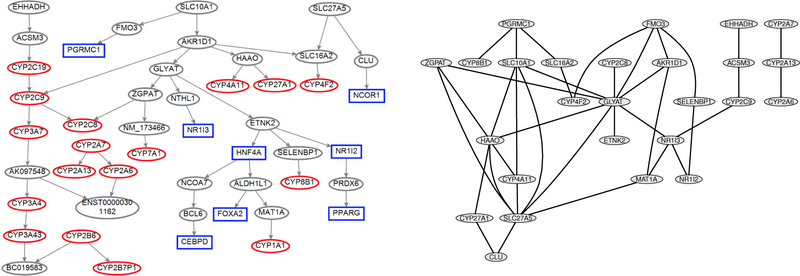
Left: P450 gene regulatory subnetwork reproduced from Yang et al. (2010), where the known regulators and P450 genes are shown as blue rectangles and red ovals, respectively. Right: the subnetwork produced by the proposed method.

The original dataset consisted of 100 samples, and each sample consisted of 22337 genes. In our study, we only considered the genes shown in the left panel of Figure 4. The genes “AK097548s”, “BC019583”, “ENST00000301162” and “NM 173466” have been excluded from our study, as they are not protein-coding genes and their expression data are not available in the original dataset. According to the proposed method, we first applied the data-continuized transformation to the RNA-seq data. After the data-continuized transformation, we adjusted some effects that potentially affect the distribution of the data, including the age, gender and batch of data collection, through linear regression. Then, we applied the nonparanormal transformation and Ψ-learning method to the adjusted data. Figure 4 shows the resulting subnetwork.

The subnetwork published in Yang et al. (2010) contains 48 genes, and the subnetwork produced by the proposed method contains 26 genes which are connected to some other genes. Although the two subnetworks contain different numbers of genes, they share very similar relations for gene regularations. For example, in the subnetwork by Yang et al. (2010), the gene GLYAT connects to the genes ZGPAT, ETNK2, and AKR1D1; gene HAAO connects to gene CYP27A1; gene CYP2A7 connects to gene CYP2A13; gene CLU connects to SLC27A5; gene ACSM3 connects to EHHADH, and gene CYP4F2 connects to gene SLC16A2. All these connections have been recovered in our subnetwork. Although the rest connections in the two subnetworks do not match exactly, they show some similar dependence. For example, gene CYP2A7 connects to both CYP2A6 and CYP2A13 in the subnetwork by Yang et al. (2010), our subnetwork also shows that they are dependent. This example indicates the validity of the proposed method.

4.2. Acute myeloid leukemia mRNA sequencing network

This example illustrates the performance of the proposed method in the small-n-large-p scenario. The dataset is the mRNA sequencing data from acute myeloid leukemia (AML) patients and available at The Cancer Genome Atlas(TCGA) data portal (http://cancergenome.nih.gov/). In this study, we directly worked on the raw count data, which contains 179 patients and 19990 genes. In preprocessing the data, we filtered out some low expression genes: we first excluded the genes with at least one zero count, and then selected 500 genes with the largest inter-sample variance as suggested by Gallopin et al. (2013). The selected genes are more likely linked to the development of acute myeloid leukemia as their expression levels are highly variable.

Figure 5 shows the GRN produced by the proposed method for the AML RNA-seq data. Through this network, we can identify some hub genes that are likely related to AML. A hub gene refers to a gene which has strong connectivity to other genes. Our finding is pretty consistent with the existing knowledge. For example, the hub gene MKI67 is a well known tumor proliferation marker. The prognostic value of the MKI67 protein expression has been reported for many types of malignant tumors including brain, breast, and lung cancer, with only a few exceptions for certain types of tumors (Mizuno et al., 2009). Another example is the gene KLF6. Humbert et al. (2011) showed the expression patterns of KLFs with a putative role in myeloid differentiation in a large cohort of primary AML patient samples, CD34+ progenitor cells and granulocytes from healthy donors. They found that KLF2, KLF3, KLF5 and KLF6 are significantly lower expressed in AML blast and CD34+ progenitor cells compared to normal granulocytes, and that KLF6 is upregulated by RUNX1-ETO and participates in the RUNX1-ETO gene regulation. This finding provides new insights into the under-studied mechanism of RUNX1-ETO target gene upregulation and identifies KLF6 as a potentially important protein for further study in AML development (DeKelver et al., 2013). The biological functions of other hub genes, such as H3F3B and TMC8, will be further studied.

Figure 5.

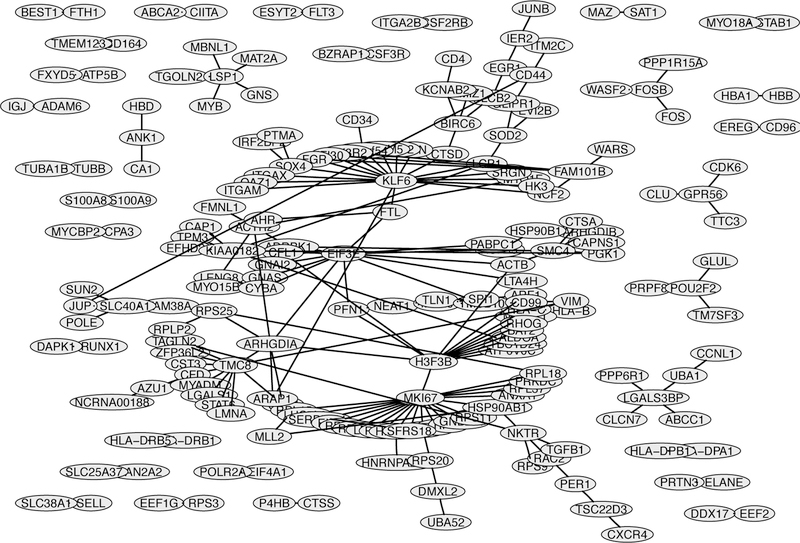
Gene regulatory network produced by the proposed method for the acute myeloid leukemia RNA-seq data with (n, p) = (179, 500).

For comparison, gLasso, nodewise regression and LPGM have been applied to this dataset. They were run as for the simulated examples. Nodewise regression and gLasso were run using the package huge under their default setting, but the regularization parameter was determined using the stability approach. LPGM was run using the package XMRF under its default setting. All these methods produced much denser networks than the proposed method. To assess the quality of the networks produced by different methods, the power law curve (see, e.g., Kolaczyk 2009, pp.80–85) was t to them. A nonnegative random variable X is said to have a power-law distribution if

$$P(X=x)\propto ~x^{-\upsilon },$$ (9)

for some positive constant ν. The power law states that the majority of vertices are of very low degree, although some are of much higher degree. A network whose degree distribution follows the power law is called a scale-free network and it has been verified that many biological networks are scale-free, e.g., gene expression networks, protein-protein interaction networks, and metabolic networks (Barabási and Albert 1999). Figures 6 show the log-log plots of the degree distributions of the networks generated by four methods, where the curves are fitted by the loess function in R. It shows that the network produced by the proposed method approximately follows the power law, while those by gLasso, nodewise regression and LPGM do not.

Figure 6.

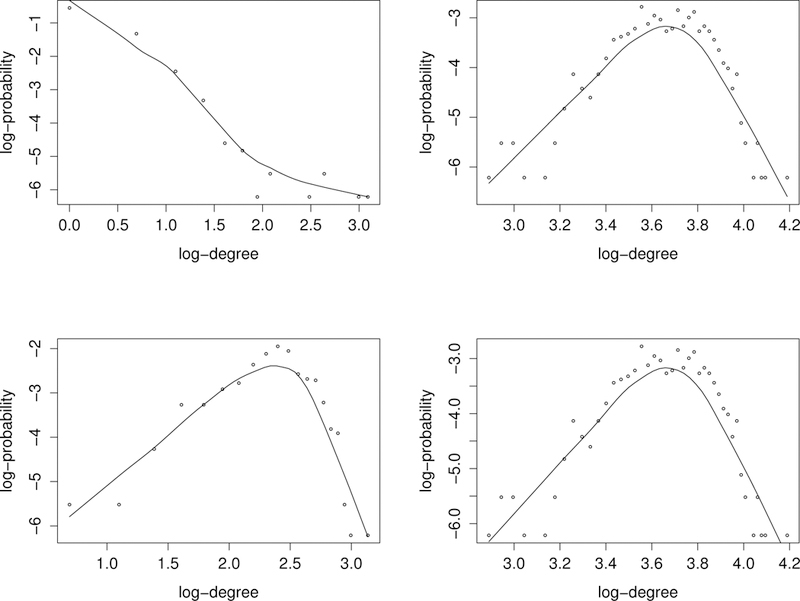
Log-log plots of the degree distributions of the four networks generated by the proposed method (upper left), gLasso (upper right), nodewise regression (lower left), and LPGM (lower right).

5. Discussion

We have proposed a method for learning gene regulatory networks from RNA-seq data. The proposed method is a combination of a random effect model-based data-continuized transformation, the nonparanormal transformation, and the ψ-learning algorithm. The proposed method is consistent in the sense that the true gene regulatory networks can be recovered from the RNA-seq data when the sample size becomes large. The major contribution of this paper lies on the data-continuized transformation, which fills the theoretical gap of how to transform NGS data to continuous data and facilitates learning of gene regulatory networks.

The proposed data-continuized transformation involves an adaptive Markov chain. We proved the convergence and the weak law of large numbers for the adaptive Markov chain under the framework provided by Liang et al. (2016). A strong law of large numbers (SLLN) can potentially be proved for the algorithm under the framework provided by Fort (2011). With the SLLN, some stronger theoretical properties might be obtained for the resulting networks.

In practice, some authors treated the logarithm of the RNA-seq data as continuous, though not rigorous. The proposed method provides a justification for this use, which is necessary and important given the popularity of NGS techniques. As discussed in Liang et al. (2015), the ψ-learning algorithm provides a general framework for how to integrate multiple sources of data in reconstructing Gaussian graphical networks, where it is proposed to use a meta-analysis method to combine the ψ-partial correlation coefficients calculated from different sources of data. Similarly, with the proposed method, we can integrate different types of omics data, such as the RNA-seq and microarray data, to improve inference for gene regulatory networks. We expect that this method will be widely used in the near future.

Finally, we note that alternative to the LPGM method, an existing method that can potentially be used for Poisson graphical modeling is the latent copula Gaussian graphical modeling method (Ho , 2007; Dobra and Lenkoski, 2011). The basic idea of this method is to introduce Gaussian latent variables in place of discrete random variables in the Poisson network inference. Since the method involves imputation for a large number of latent variables, it is very slow and can only be applied to the problems with a small set of genes.