Microtubule Dynamics, Kinesin-1 Sliding, and Dynein Action Drive Growth of Cell Processes

Abstract

Recent experimental studies of the role of microtubule sliding in neurite outgrowth suggested a qualitative model, according to which kinesin-1 motors push the minus-end-out microtubules against the cell membrane and generate the early cell processes. At the later stage, dynein takes over the sliding, expels the minus-end-out microtubules from the neurites, and pulls in the plus-end-out microtubules that continue to elongate the nascent axon. This model leaves unanswered a number of questions: why is dynein unable to generate the processes alone, whereas kinesin-1 can? What is the role of microtubule dynamics in process initiation and growth? Can the model correctly predict the rates of process growth in control and dynein-inhibited cases? What triggers the transition from kinesin-driven to dynein-driven sliding? To answer these questions, we combine computational modeling of a network of elastic dynamic microtubules and kinesin-1 and dynein motors with measurements of the process growth kinetics and pharmacological perturbations in Drosophila S2 cells. The results verify quantitatively the qualitative model of the microtubule polarity sorting and suggest that dynein-powered elongation is effective only when the processes are longer than a threshold length, which explains why kinesin-1 alone, but not dynein, is sufficient for the process growth. Furthermore, we show that the mechanism of process elongation depends critically on microtubule dynamic instability. Both modeling and experimental measurements show, surprisingly, that dynein inhibition accelerates the process extension. We discuss implications of the model for the general problems of cell polarization, cytoskeletal polarity emergence, and cell process protrusion.

Introduction

One of the main questions in cell biology is how cytoskeleton dynamics causes cell polarization (1). For example, cellular polarization is vital for proper maturation and function of neurons (2). The polarization of neurons starts without directional external cues in a stochastic manner when several finger-like projections emerge from the body of the cell. Of these processes, called neurites, only one turns into a long axon; others become short dendrites (3).

This polarization process involves a complex crosstalk between several length-dependent feedbacks, molecular pathways, and transport phenomena (4, 5), but here we focus on the role of cytoskeletal mechanics identified to be of critical importance for neuronal polarization (6). Current data suggests that actin polymerization is important for the neurite’s initiation and elongation (7, 8), whereas intermediate filaments are critical for their maturation (9). However, several studies have demonstrated that it is the third major cytoskeletal component, microtubules (MTs), that determine the initial neuronal polarization. For example, neurite formation and outgrowth correlate with the formation of MT bundles at the core of axons and dendrites (10, 11). In this study, we restrict our attention to mechanics of MTs and MT-associated molecular motors driving the growth of the cell processes.

In mature neurons, the MT organization is different between axons and dendrites: the majority of the MTs in axons have their plus ends facing out from the cell body toward the growth cone (10), whereas the MTs have their minus ends facing out in dendrites of neurons in Drosophila and Caenorhabditis elegans (12). On the contrary, dendrites in mammalian neurons have mixed MT polarity (13, 14). Thus, in addition to the whole-cell polarization problem, there is the problem of the cytoskeletal polarization: what are the molecular mechanisms underlying the MT polarity sorting, and does this polarity sorting play a role in the whole-cell polarization? The MT polarity sorting problem is not restricted to the neuronal cell (15): for example, such sorting is crucial for assembly of meiotic spindles (16).

Theoretical predictions and in vitro observations pointed out that the MT polarity sorting is generated by the sliding of the MTs by molecular motors of the kinesin and dynein families (17, 18, 19). A number of studies showed that MT sliding by kinesins and cytoplasmic dynein contributes crucially to mitotic spindle maintenance (20, 21) and muscle cell development (22). Motor-generated MT sliding was also demonstrated to be important in the MT polarity organization in long axons (23) and to drive the MT polarity sorting in neurites (24).

In this study, we focus on the actions of cytoplasmic dynein and kinesin-1. Dynein complex binds to cortical F-actin and slides MTs, which is crucial for the MT organization in axons (25, 26), in particular for the axon initiation (27) and for MT transport (28). Kinesin-1, previously thought to be deployed only in organelle transport, was recently shown to bind one MT with its cargo domain and to slide another MT relative to the first one (29, 30). This kinesin-1-powered sliding leads to an extension of MT arrays that appears to press against the expanding distal tip of nascent neurites and to generate a force for the initial axonal extension (29, 30).

Neurons contain both stable and dynamic MTs (14, 31). Inhibition of the MT dynamics does not abolish the neurite extension in Drosophila neurons (29) but slows it down, and so the MT dynamics, in addition to the motor action, is likely to play a role in the axon initiation and maintenance. However, the respective mechanisms are currently not known (32).

Our recent experimental work on formation and extension of the cell processes in Drosophila neuronal and S2 cells demonstrated the following:

• 1)In Drosophila S2 cells, inhibition of centripetal actomyosin flow results in formation of multiple radial processes filled with MTs (33).
• 2)At the initial stage, MTs have mixed polarity, with minus ends being pushed out against the plasma membrane. Growing neurites and processes of S2 cells contain comets of MT plus-end-binding protein EB1 moving in both anterograde and retrograde directions (34).
• 3)The fraction of retrograde EB1 comets starts to decline after the initial stage. At the next stage, the growing processes are mostly filled with plus-end-out MTs (34).
• 4)At this later stage, the MT minus ends are scattered throughout the length of the processes. However, inactivation of dynein results in a dramatic accumulation of the minus ends at the processes’ tips (34).
• 5)Cytoplasmic dynein has to be anchored at the cell cortex or on the membrane for the MT polarity to change at the later stage (34). Dynein is dispensable for the process outgrowth (29, 33, 34).
• 6)Kinesin-1 slides apart antiparallel MT pairs and bundles and is essential for the process outgrowth (29, 33, 34).

These observations led us to the following qualitative model (11, 34): in the early stages of neuronal process outgrowth, kinesin-1-generated MT sliding drives initial process extensions, with the MT minus ends pushing out the plasma membrane at the tips. Later, cytoplasmic dynein associates with the actin cortex in longer processes and expels the minus-end-out MTs into the cell body, establishing the uniform (plus-ends-out) orientation of the MTs.

A few questions have to be answered to verify this model. Why is dynein unable to generate processes alone without kinesin-1 action? What is the role of the MT dynamics during initial process outgrowth and subsequent maturation? Can the model correctly predict the rates of process outgrowth? Why does dynein start working only later? What triggers the transition from the kinesin-driven to the dynein-driven sliding?

Computational modeling of dynamic MT-motor networks complemented by comparison with experimental data has a long history of being able to answer such questions (35, 36, 37, 38). In this study, we develop a computational model of a network of elastic dynamic MTs and kinesin-1 and dynein motors in a symmetric cell with flexible membrane. The model parameters were estimated from published data. The simulations based off these estimations correctly reproduced the dynamic MT polarity in the growing processes. This model makes to our knowledge novel predictions about the rates of process growth in control and in dynein-inhibited and/or MT-dynamics-inhibited Drosophila S2 cells. We find that the MT dynamics enhances the process elongation, but counterintuitively, dynein inhibition accelerates the process extension. We verify these predictions and test the model by measuring the rates under these conditions. Our results support the qualitative model of the process extension, explain the role of the MT dynamics in the process elongation, and shed light on the mechanism of the switch from kinesin- to dynein-dominated protrusion.

Materials and Methods

Computational model

MTs

Based on experimental images (33, 34), we consider the cell body as a two-dimensional disk (Fig. 1 A), with a finite number of MTs that are treated as semiflexible elastic rods. Specifically, following established previous models ((39, 40, 41, 42, 43); see also Figs. S3 and S4), we simulate each MT as an end-to-end chain of segments connected by elastic angular springs at the nodes. Angular spring stiffness is calibrated so that MT persistence length agrees with that measured in vitro. The segments themselves are very stiff elastic springs with a finite rest length to account for the fact that the MT lattice is almost incompressible and inextensible. Besides the elastic forces that arise from MT deformations, we consider the following forces applied to the MTs (respective math is explained in the Supporting Materials and Methods): 1) movement of MT in the lab coordinate system generates an effective viscous drag force per unit MT length. We approximate this drag with a low-Reynolds-number hydrodynamic formula for movement of cylindrical MT segments through the cytoskeletal/cytosolic gel with viscosity on the order of 10³-fold that of water (44). 2) Thermal forces generate Brownian movements of the MT nodes. 3) There is an effective steric repulsion force preventing the MTs from penetrating the cell boundary. 4) Dynein and kinesin-1 motors apply forces to the MTs as described below. The sum of all these forces balances to zero.

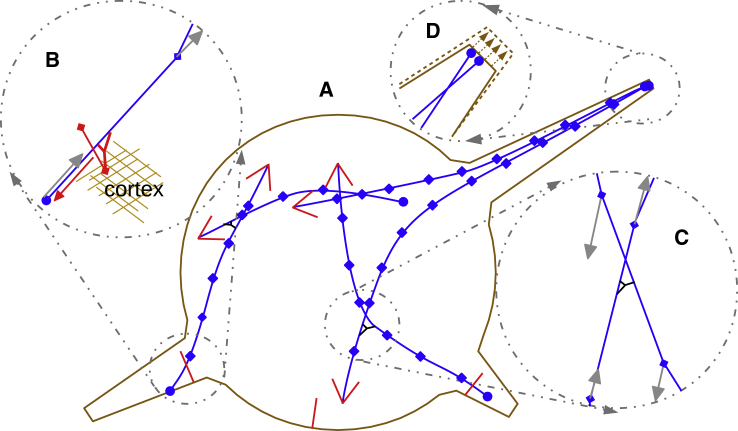
Figure 1.

Overview of the model elements. (A) MTs within the discoid cell body, some of which protrude into three processes, are shown in blue as chains of segments between the nodes. Large arrows show the plus ends. (B) Cortex-anchored dynein (red) moves toward the MT minus end (red arrow), which causes MT transport in the direction of its plus end (gray arrows). (C) Kinesin (black) is attached to a pair of intersecting MTs; one MT connects to the cargo domain of the motor and is moved toward the plus end of another MT. The MT to which kinesin connects with its motor domain is shifted toward its minus end. This causes relative sliding of MTs (gray arrows). Note that in the model, kinesin action is distributed to two pairs of nodes at the ends of two overlapping MT segments and that the magnitudes of the opposing forces on two MTs are equal. (D) Process elongation in response to MT pushing against the tip of the processes is shown. To see this figure in color, go online.

MT dynamics

MT minus ends in the model are not dynamic. In the numerical experiments with inhibited MT dynamics, plus ends are not dynamic either; otherwise, the plus ends undergo a dynamic instability process with given rates of growth, shortening, catastrophe, and rescue. Specifically, the growth and shortening are implemented by adding and deleting the MT segments, respectively, with constant rates. A switch from the shortening to growth takes place with a constant rescue rate. However, if an MT shortens to a single segment, this segment switches to growth instantly and is randomly relocated within the cell and rotated. This ensures conservation of the total MT number. Experimental observations showed that short MTs sometimes undergo rotations (45); in the simulations, MTs shorter than 1 μm change their orientation randomly in the cell body and flip their orientation in the process at a slow rate.

An MT switches from growth to shortening with a constant catastrophe rate as long as its plus end is not pressing against the cell boundary. Otherwise, the component of the force F on the MT plus end parallel to the MT tip increases the catastrophe rate by an exponential factor exp(F/F_halt), where F_halt is a parameter. For computational convenience, we introduce short pauses between the periods of growth and shortening. The pause duration is much shorter than that of the growth and shortening periods; numerical tests showed that these brief pauses do not affect the model behavior. According to our observations, the EB1 comet signal associated with the growing plus ends is lost right after the growing ends run into the cell boundary. Accordingly, we stop the MT elongation when the plus end runs into the cell boundary. At that moment, the plus end becomes static, and the next event is the catastrophe with the rate described above. Thus, in the model, only motor forces ultimately push on the cell boundary, not the MT polymerization force.

Kinesin

In the model, a kinesin-1 motor attach to a point of intersection between two MTs and exert a force there (Fig. 1 C). The cargo domain of the motor attaches to one of the MTs, chosen at random between the two, while the motor domain pulls another MT in the tangential direction. The MT is pulled in the direction of its minus end (Fig. 1 C). The force magnitude is determined by the linear force-velocity relation, as explained in the Supporting Materials and Methods. As the motor domain applies the force to one of the MTs, the opposite force is applied to another MT to which the cargo domain is bound. Computationally, we distribute these two opposing forces to four MT nodes (two nodes for each MT of the pair), which are the ends of two intersecting MT domains (Fig. 1 C). Note that this implicitly assumes that the force does not depend on the angle between two intersecting MTs. The situation can become more complex when two MTs are parallel and close together because in that case, multiple motors can associate with such an MT pair, effectively sliding apart the antiparallel MTs and locking together parallel MTs (11). In our simulations, this problem is circumvented because in the model, the MTs are never exactly parallel even in the cell processes and because the effective number of acting motors is relatively small. In the model, there is a conserved constant number of acting kinesin-1 motors with the following kinetics. The motors unbind (both cargo and motor domains unbind simultaneously) at a constant rate or at an instant when the MT pair does not intersect anymore. A detached motor reattaches immediately to a random intersection of any two intersecting MT pairs.

Dynein

In the model, the dynein motors bind and unbind with their cargo domains at the cell boundary. The motors dissociate with a constant rate and associate at random locations along the boundary at a rate that is proportional to the total boundary length so that the average total motor number per unit boundary length is a constant. Therefore, the number of attached dynein motors is increased as the processes’ elongation increases the perimeter of the cell. We model the interactions of dyneins with MTs as follows: a dynein at the boundary attaches with its motor domain instantly to any MT intersecting with the segment of a constant length representing the spatial range at which the motor domain can act. One end of the segment—the cargo domain—always locates to the cell boundary, and the segment is locally normal to the boundary. The MT intersecting with such a segment stops interacting with the respective motor (the motor detaches) at a constant rate or as soon as the MT does not overlap with the segment anymore. As long as the motor and MT interact, a force is applied to the MT at the MT intersection with the segment. Computationally, the force is distributed equally to two MT nodes at the ends of the MT domain intersecting with the motor (Fig. 1 B)). The force is applied tangentially to the MT domain in the direction of the plus end. The force magnitude is determined by the linear force-velocity relation, as explained in the Supporting Materials and Methods. This force is balanced by the opposing force on the cell cortex at the boundary, which is not modeled explicitly because we assume that all such forces are transduced to cell adhesions and ultimately all dynein-generated forces are balanced by cell traction forces.

Cell boundary

The cell boundary is modeled as a chain of straight segments without any elastic or viscous forces associated with this chain. All forces applied to the cell boundary are assumed to be transduced to the adhesions and to be balanced by the cell traction forces, which are not modeled explicitly. We simulate changes of the cell shape as follows. If the sum of the forces exerted by MTs on a single cell boundary segment exceeds a threshold force, which is a constant parameter, this segment is moved in the radial direction by a constant increment. This increment is equal to a constant protrusion rate times the time-step duration; numerical experiments showed that variation of the protrusion rate value up to an order of magnitude does not affect the model behavior, as the process length is basically determined by the force balance: if the process elongates too much, the pushing MTs lag behind and protrusion stops. This segment turns into the tip of the process, and further process elongation in the radial direction proceeds by shifting this segment by the same increment at each computational step whenever the sum of the forces exerted by MTs at the tip exceeds the threshold value (Fig. 1 D). The ends of the boundary segments neighboring the process tip are shifted slightly in the radial direction at each step in linear proportion to the tip shifts (details in the Supporting Materials and Methods).

Estimating model parameters

The model parameters are listed in the Supporting Materials and Methods. Here, we discuss five groups of parameters that determine the system behavior: 1) MT dynamics parameters, 2) motor and MT numbers, 3) cell boundary mechanics, 4) motor mechanical parameters, and 5) MT mechanical parameters. Two out of these five groups—motor and MT mechanical parameters (stall force, force-free speed, dissociation rates for the motors; MT bending elasticity and drag coefficients)—are well characterized in vitro, and we use the published data for these parameters’ values.

MT dynamics

The dynamic instability parameters were measured many times in different systems. Expectedly, the measurements varied greatly. However, there are only two principal scales that determine main features of the MT dynamics: average MT length and mean characteristic duration of the dynamic instability cycle. The question about the average MT length is whether it is comparable to the cell radius (∼10 μm) or much shorter than that. Microscopy lacks resolution to answer this question definitively, and so we simulated the model with both short and long MTs. When the MTs were short, with a typical length of 5 μm or less, we found that the MT-motor network exhibited a fluid-like behavior with rapid local streams and vortices, characteristic for some dense in vitro systems (18) but not observed in our Drosophila cells. Besides, we found that in this regime, kinesin-1 was unable to establish long and narrow processes. On the other hand, the model with long MTs successfully reproduced many observed phenomena. Next, we varied the mean characteristic duration of the dynamic instability cycle. When this cycle was faster than ∼10 s, the ability of kinesin-1 to establish processes deteriorated: MTs turned over before the motors had time to slide the MTs significantly. When the cycle was slower than ∼100 s, new growing plus ends were entering the processes and generating new MT-MT intersections too infrequently, and the rate and extent of the process growth approached those in the case of completely stable MTs. Interestingly, many studies (see the Supporting Materials and Methods) report the dynamic instability parameters such that the average MT length is, in fact, on the order of 1–10 microns, and the mean characteristic duration of the dynamic instability cycle is between 10 and 100 s. These arguments informed the choice of this group of parameters.

MT and motor numbers

The number of long MTs has been frequently estimated in the range of hundreds per cell, and this is the order of magnitude that we can glean from the S2 cell images. Also, this is the number for which our computational code runs one simulation on a reasonable (a few hours) timescale. Most of the computational time goes into simulation of the MT deformations and forces, and if the MT number is on the order of a thousand, the simulation time becomes prohibitive. Most importantly, an MT number in the low hundreds results in the observed characteristic number (∼10) of processes per cell. All these considerations led us to choose an MT number ∼150.

We estimated the characteristic number of working kinesin-1 motor proteins, which is unknown from experiments, from our previously published data on MT mobility in control cells (33). Namely, MT movement was quantified by applying fiduciary marks to MTs in Drosophila S2 cells. Fluorescent MT segments then spread in random, seemingly uncorrelated directions on a micron length scale and a minute timescale (Fig. S1). Simulations with varying kinesin-1 motor numbers and ∼100 long MTs exhibited a similar mobility pattern (Fig. S1) under the condition that only ∼25% of MTs are being slid by the motors at any given time and that typically only one kinesin-1 motor is acting on a given pair of MTs at a time. Thus, this data is consistent with ∼20 working kinesin-1 motors. This estimate seems quite low; however, there were reports in studies of the axonal MT transport suggesting that though the total number of the motors is large, each individual motor operates only very infrequently (46).

After deciding on the number of kinesin motors, we estimated the characteristic density of working dynein motor proteins per unit length of the cell boundary, which is unknown from experiments, by varying this number and finding which value of this parameter predicts the characteristic elongation rate and saturation length of the processes that are consistent with semiquantitative data from (33).

Cell boundary mechanics

The only parameter of major importance for the cell boundary deformations is the characteristic threshold force necessary to deform and protrude the membrane at the cell boundary. By analogy with much-studied filopodial protrusions, this force, from physical considerations, is on the order of ∼10 pN (47). We experimented numerically with varying this parameter, aiming to find a parameter value predicting the characteristic elongation rate of the short processes observed in (33). We found that the force of ∼3 pN, consistent with the physical estimates, leads to good fits with the data.

Results

Kinesin-1 motors initiate the processes by sliding long minus-end-out MTs in the cell body

In the description of the numerical experiments, we adopt the following terminology: “control” means that both dynein and kinesin are functional and MTs undergo the dynamic instability. In “dynein-” or “kinesin-inhibited” cells, the respective motor is switched off. In “MT-dynamics-inhibited” cells, the MTs undergo dynamic instability until equilibrium MT length distribution is reached, after which the MTs do not change anymore. Simulations of control cells revealed that initiation of the processes as well as elongation of short processes is driven by the MT minus ends (Fig. 2 A, inset arrow a) pushing on the cell boundary. The pushing forces typically originated from kinesin-1 sliding minus-end-out MTs against other MTs in the cell body (MTs being pushed by kinesin are shown in dark blue in Fig. 2 A). Occasionally, MTs were also pushed with their plus ends out against the tip of a process (Fig. 2 A, inset arrow b)—not by the polymerization force that is absent in the model, but because these MTs interacted with another MT in the cell body, which in turn interacted with yet another MT, and the resulting complex sliding geometry led to an occasional MT with its plus end out. These numerical observations confirm the results reported in our earlier experimental study (34): in the short processes, the majority of MT ends at the tips are minus ends. Simulations also showed that the processes were initiated with the minus-end-out MTs in dynein-inhibited cells.

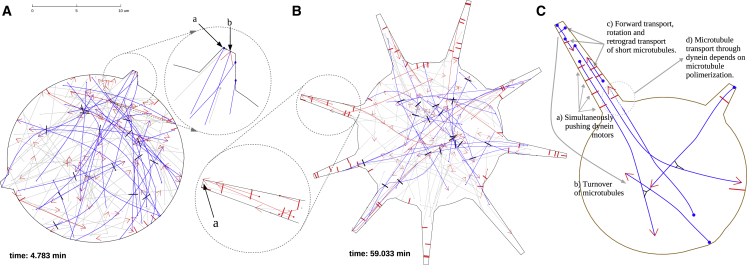
Figure 2.

Simulation of the process initiation in control cells. (A) MTs are dark blue if slid by kinesin, red if slid by dynein, and otherwise gray. Kinesins are represented as black rods, and dyneins as red, cortex-anchored rods. MT minus ends are thick dots. Polymerizing MT plus ends are red arrows; nonpolymerizing ends are not marked. The inset shows that process formation is driven by kinesins sliding MTs. Most MTs are pushed against the leading edge of the process with their minus ends forward (a), but some are pushed with their plus ends forward (b). (B) Simulation of the process elongation in control cells is shown. Dynein pushes MTs against the tip of the process with their plus ends forward (arrow a). Note that MTs are shown in red if currently pushed by dynein and in dark blue if currently pushed by kinesin. (C) For geometric reasons, dynein can only be effective in long processes in which several dynein motors cooperate to overcome pushing by cytoplasmic kinesin (a). Note that MTs would accumulate at the process’s tip through dynein forward transport unless they are redistributed by random turnover (b) or turned around by random forces and transported back into the cell body by dynein (c). Polymerization of MT plus ends into processes increases the polarity sorting effect of dynein (d). To see this figure in color, go online.

The simulations also highlighted the important roles of MT bending and elasticity. We observed that when we simplified the model drastically by making the MTs stiff rods, the MTs were not able to squeeze into the longer processes and reach their tips unless they originated from the center of the cell. Also, importantly, the simulations showed that kinesin-1 often buckled the MTs, the elastic energy of which was stored first and then released into pushing against the cell boundary. This is consistent with the experimental observations demonstrating MT bending and buckling at the process tips (29). Lastly, in the cell body, the MTs bend and buckle often, making it hard to initiate a process. Only kinesin-1 action on a minus-end-out MT relatively normal to the boundary and close to the boundary led to the process initiation. While within the process, MTs were prevented from buckling by confinement in the process.

Dynein alone is unable to initiate cell processes

Simulations of kinesin-inhibited cells showed that dynein alone does not initiate processes because, for geometric reasons, the forces dynein exerts are mainly oriented tangential to the cell boundary. The simulations showed that dynein mainly transported the MTs along the boundary (Fig. 3 A). The reason is that when a single dynein motor “grabs” an MT near its plus end and pushes it against the boundary, the single dynein motor force is insufficient to make a protrusion. Instead, a torque that the motor exerts on the MT often turns this MT parallel to the boundary, after which the motor propels the MT along the boundary.

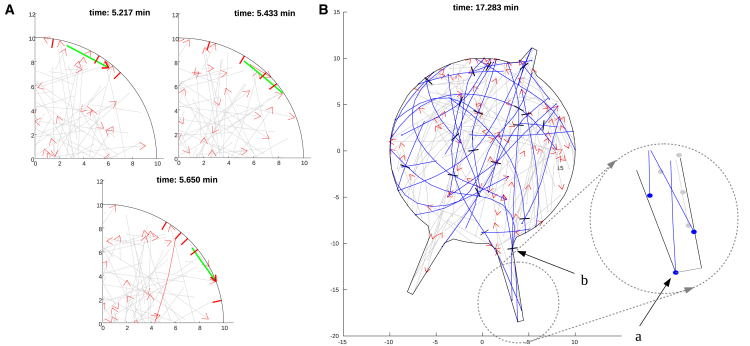
Figure 3.

Simulations of motor-perturbed cells. (A) Simulations of cells after kinesin inhibition are shown. Cortex-bound dynein motors push MTs tangentially along the cortex and therefore do not initiate processes. One MT that is being slid by dynein along the cell boundary in this simulation is shown in green. One MT starts to interact with a dynein motor at the later time and is shown in red. (B) Process elongation driven by kinesins (black bars) in dynein-inhibited cells is shown. Kinesin motors, such as the one shown in (b), push against the process tips through MT minus ends (filled circles at the MT ends in the inset marked in (a)). MTs being pushed by kinesin are shown in blue. In both (A) and (B), MTs not interacting with the motors are shown in gray; growing MT plus ends are indicated by the red arrows. To see this figure in color, go online.

Dynein in longer processes changes MT polarity

We earlier reported (34) that dynein motors in long processes promote the MT polarity sorting changing the polarity from the minus end out in short processes to the plus end out in long processes. Simulations confirm this hypothesis and reveal the mechanism of this phenomenon: in processes that are long enough, dynein acts as a gatekeeper preventing the minus-end-out MTs from penetrating the processes (Fig. 2 B). Here is the physical explanation: the stall force of kinesin is significantly higher than the stall force of dynein (Supporting Materials and Methods). Therefore, several dynein motor proteins need to act in concert to overcome the pushing force exerted by one kinesin motor. These simultaneously pushing dynein motors have to be colocated in a single process. Such a concentration of dynein motors is far more likely in longer processes, whereas in short processes, typically only a few dynein motors will exert the force at a time (Fig. 2 C).

These numerical results are consistent with the experimental data on the minus- and plus-end-out MTs at the process tips. Fig. 4 A indicates that at the initial phase of the process growth, the minus ends at the tip dominate. This phase is also characterized by the fast process outgrowth (Fig. 4 A(i)). As the threshold process length of about 3 μm is achieved, the fraction of the minus ends at the tips declines rapidly. At the later stage, when the process length reaches about 5 μm, only a few minus ends occasionally reach the tip, whereas the plus ends are present at the tip sporadically during the entire time. The plus ends appear to drive much slower process growth once the minus ends are absent from the tip (Fig. 4 A(i) and (iii)).

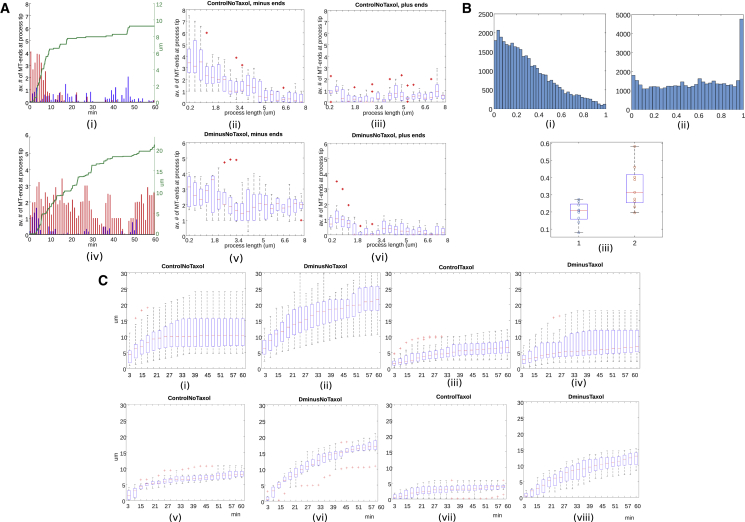
Figure 4.

Dynamic changes of the process length and MT polarity. (A) Length of simulated processes versus number of MT ends at the process tips is shown. We average the number of MT plus and minus ends located within a narrow 1 μm stripe at the tip of a process during 1 min time intervals and compare the simulation of a control cell (upper row) to the simulated dynein-inhibited cell (lower row). (i and iv) For a single simulated process (control and dynein-inhibited, respectively), these diagrams show process length (green), minus-end numbers at the tip (red bars), and plus-end numbers at the tip (blue bars) as functions of time. (ii and iii) Boxplots show distributions of minus-end (ii) and plus-end (iii) numbers at the process tips of the simulated control cell as functions of the process length. (v and vi) Distributions of minus- (v) and plus-end (vi) numbers at the process tips of the simulated dynein-inhibited cell are shown. (B) Distribution of the MT minus ends and of polymerizing plus ends in the processes longer than 6 μm is shown. We show statistics extracted from single simulation snapshots at intervals of 5 s from two 50-min-long simulations (of control and dynein-inhibited cells, respectively), with nine processes each. The positions are normalized to the interval between 0 (base) and 1 (tip). The vertical axes in histograms show the number of the minus-ends. (i) Histogram of relative minus-end positions in control show monotonic decrease toward the process tip, with relatively few minus ends at the tip. (ii) In the absence of dynein, minus ends are uniformly distributed along processes with a peak at the process tip. (iii) Percentage of retrograde plus-end-trajectories in control (1) and dynein-inhibited (2) cells is shown. Circles show the fraction of the retrograde plus ends in single processes; boxplots visualize their distributions. Mean fractions in control and dynein-inhibited cells are significantly different, with p-value p = 0.0086. (C) The upper row shows experimentally measured growth of the processes’ length (length versus time; time is measured for each individual process starting from the process initiation; see also Fig. S2). The lower row shows simulated process growth: (i and v) control; (ii and vi) dynein-inhibited; (iii and vii) control with taxol; (iv and viii) dynein-inhibited with taxol. To see this figure in color, go online.

As a consequence of the dynein’s gatekeeper function, it is not surprising that in the simulated control cells, the distribution of the minus ends is biased toward the base of the processes (Fig. 4 B(i)). In dynein-inhibited cells, the minus ends are uniformly present everywhere within the processes at a low density, and their number is very high at the tips (Fig. 4 B(ii)). Both of these numerical results agree with the experimental observations (34) of the fluorescent minus ends at the tips of the control and dynein-inhibited cells. The simulations also are consistent with the experimental results (34), according to which trajectories of polymerizing plus ends are bidirectional in the dynein-inhibited cells, whereas they are unidirectionally oriented toward the cell body in the control cells (Fig. 4 B(iii)). The physical explanation is that there are plus-end-out trajectories due to polymerization of the MTs that dynein is pulling into the processes in the control cells. Dynein does not allow MT minus ends to enter the processes; hence the absence of the plus-end-inward trajectories. In dynein-inhibited cells, some polymerizing plus ends enter the processes from the cell body before being slowly expelled back by kinesin; in addition, plus-end-inward trajectories are generated by polymerizing MTs, the minus ends of which accumulate at the tips of the processes.

In the absence of dynein, process elongation is driven by kinesin-1 faster than in control. Simulations of the dynein-inhibited cells show that, in the absence of dynein, even elongation of the long processes is driven by the minus-end-forward MTs slid by kinesins in the cell body (Fig. 3 B). Quantitative analysis of the presence of MT minus ends and plus ends at the process tips of a simulated dynein-inhibited cell (Fig. 4 A, lower row) reveals that indeed, minus ends are consistently present and dominate at the tip of the simulated processes, whereas the plus ends reach the tip of processes only sporadically. This does not change as the processes grow.

One reason for the lower presence of the plus ends at the tips is that in the dynein-inhibited cells, kinesins tend to expel the plus-end-out MTs from the processes. In addition, in the context of our model, the MTs pushed into the tips with their plus ends out are more likely to undergo a catastrophe (Fig. S4). This limits the impact of the MT plus ends and therefore the ability of the dynein motors in the control cells to protrude the processes over extended periods of time. As a consequence, simulated process growth is significantly faster in the dynein-inhibited cells than in the control cells (Fig. 4, A(iv) and C, lower row).

We confirmed these observations experimentally by measuring lengths of the growing processes in the control and dynein-inhibited cells as functions of time (Fig. S2). Comparison of the growth profiles (Fig. 4 C(i) and (ii) shows that the processes indeed grow faster in the absence of the dynein action (Fig. 4 C(v) and (vi)).

MT dynamic instability makes the process elongation more efficient

We simulated the MT dynamics-inhibited cells and found that the processes in these cells grow slower and to a lesser extent (Fig. 4 C(vii) and (viii)), both with and without functional dynein. We used the cytoskeleton drug taxol, which largely reduces the dynamic instability and thus stabilizes the MTs (48), to test this prediction, and found, in a good quantitative agreement between the experiment (Fig. 4 C(iii) and (vi)) and theory (Fig. 4 C(vii) and (viii)), that taxol slows down the elongation.

According to the simulations, slower process growth in the dynein-inhibited cells treated with taxol is caused by fewer intersections of the minus-ends-out MTs at the process tips with other MTs in the cell body. In control cells treated with taxol, this effect is smaller because dynein restricts the effect of kinesin to shorter processes. Nevertheless, further process elongation by dynein is less effective if the MTs are stabilized because this process relies on availability of the plus-end-out MTs in the processes. In control cells without taxol, the dynamic instability guarantees that the plus ends frequently enter the processes, where dynein can grab them and push them further into the process. Under the effect of taxol, however, dynein motor proteins within the processes rarely encounter the plus-end-out MTs because kinesin would typically pull them back into the cell body.

Discussion

We combined computer simulations with experimental measurements of MT-motor sliding and cell process growth in both control Drosophila S2 cells and dynein-inhibited and/or MT-stabilized cells. The simulation results confirmed a qualitative model that emerged from our experimental studies (29, 33, 34). Namely, at the early stage, kinesin-1 slides the minus-end-out MTs against the oppositely oriented MTs in the cell body. This sliding generates the pushing force that bends the cell membrane and creates early cell processes. At the later stage, dynein takes over, expels the minus-end-out MTs from the processes, pulls in the plus-end-out MTs, and pushes them against the processes’ tips, continuing the elongation.

The model demonstrates that the switch from the kinesin-dominated protrusion with the minus-end-forward MTs to the dynein-dominated protrusion with the plus-end-forward MTs emerges from the simple mechanical-length-dependent feedback: the longer the process becomes, the more dynein motors operate along the cortex in the process, overpowering kinesin-1 action. The model also explains why dynein cannot generate the processes alone: the forces dynein exerts are mainly tangential relative to the cortex, propelling MTs along the cell boundary rather than pushing them outward, unless the dyneins are in a process of a threshold length.

The model and measurements demonstrate that the MT dynamic instability plays an important role by delivering MTs into the growing processes and creating antiparallel MT overlaps in the cell body where kinesin-1 can generate sliding. After the model was calibrated by using available published data, the model correctly predicted the rates of the process growth in Drosophila S2 cells in four cases: in control, when dynein is inhibited, when MT dynamics are inhibited, and when both MT dynamics and dynein are inhibited. The processes grow rapidly at earlier stages and slowly later; the growth follows kinetics with saturation. Both modeling and experimental measurements show, surprisingly, that dynein inhibition accelerates the process extension. The reason, according to the model, is that dyneins within the processes rarely encounter the plus-end-out MTs because kinesins would typically pull such MTs back into the cell body. Inhibition of the MT dynamics expectedly slows down the process growth either with functional dynein or without it. Without dynein, absence of the MT dynamics shortens the average overlaps between the antiparallel MTs in the cell body needed for kinesin-1 sliding action. With dynein and without the MT dynamic instability, the plus-end-out MTs rarely reach the processes.

Our model is not limited to the neurite’s emergence. MT transport and dynamics have long been implicated in axonal elongation (49). Recently, it was shown both in vivo and in silico that dynein-mediated transport of MTs can establish the polar MT organization in mature axons only if a kinesin motor and a static cross-linker protein are also at play (37, 38). Specifically, dynein-powered sliding dominates in this case, but kinesin can slide MTs if dynein is weakened (37, 38). Moreover, motor sliding of MT bundles plays key roles in other systems. This sliding could be the mechanism of protrusion in cell motility of some cancer cells (50). Bone marrow megakaryocytes extend long cytoplasmic protrusions (ultimately producing platelets from their tips) by dynein-powered MT sliding (51). Other examples of physiologically important phenomena based on motor-powered MT sliding include process formation in renal glomerular podocytes (52) and in generating cytoplasmic streaming (53).

Our model leaves many aspects of the motor-powered MT sliding and resulting process growth unexplored. In principle, multiple kinesins may cross-link long parallel MTs in the processes and lock these MTs together (11), but a tug-of-war between the kinesins could also create a winner-takes-all effect, leading to sliding of the parallel MTs. There are also many subtle interactions between the motors and MTs that could have significant effects: dynein could capture MT plus ends and delay catastrophes (54), and MT stability and chemical state could affect the type of motors associated with MT bundles in axons and dendrites (14). Moreover, other motors, i.e., kinesins 5, 6, and 12, are also at work in axons (15). Kinesin-6, for example, was reported to negatively regulate kinesin-1-driven sliding in older neurites (55). Selective stabilization of plus-end-out MTs in axons could be an important additional mechanism of the MT polarity sorting in growing axons (13). The roles of cross-links (22, 37, 38) and microtubule associated proteins (MAPs) (56), especially MAP-regulated MT severing (13), could be much more complex than simply creating effective drag between the MTs. The nature of the force extending the processes and of regulation upstream of this force requires much additional research (11).

Last but not least, one of the most poignant questions is why only one of the growing processes becomes an axon and what are the similarities and differences between the MT-motor sliding in axons and dendrites (15). We and others have demonstrated that cytoplasmic dynein is required for the uniform MT polarity in axons and that cortical recruitment of dynein is required for this process (55, 57). Therefore, we speculate that dynein is recruited to the cortex only in the axon but not in dendrites. This selective recruitment could potentially be explained by axon-specific signaling mechanisms that cause selective localization of the dynein regulators NDEL1 and LIS1 and related scaffold protein ankyrin-G to the axon initial segment (58, 59). Furthermore, as the axon continues to grow, transport of mitochondria and other organelles and membrane vesicles into the axon becomes an important factor in the axon’s growth and maturation (60).

One of the most important open future problems is the interplay between actin and MT dynamics, both of which are involved in various stages of axon formation. Their respective contributions to the axon’s development remain unclear (61). One recent study, in fact, suggests that the neurite outgrowth is driven by actin polymerization (7). Another one argued that actin waves stochastically migrate from the cell body toward neurite tips and widen the neurite shaft to allow MT polymerization and kinesin-based transport to drive the neurite extension (8). This study hints at multiple feedback links between dynamic actin and MTs, the unraveling of which will require combined modeling and experimental effort.

Conclusions

The growth of cell processes starts with kinesin-1 motors pushing the minus-end-out MTs against the cell membrane. When a process reaches a critical length, dynein force becomes greater than kinesin force and dynein takes over the sliding, expels the minus-end-out MTs, and pulls in the plus-end-out MTs. However, kinesin-1 alone is sufficient for the process elongation, and in fact, dynein inhibition accelerates the process extension. The mechanism of elongation depends critically on MT dynamic instability.

Author Contributions

D.B.O. derived the model equations, developed the computational tools, and ran the simulations. D.B.O. and A.M. wrote the manuscript. U.d.C. and V.I.G. obtained the experimental results. D.B.O., U.d.C., V.I.G., and A.M. developed the model and analyzed the results.

Editor: Stanislav Shvartsman.

Supporting Citations

References (62, 63, 64, 65, 66, 67, 68, 69, 70) appear in the Supporting Material.