Modeling Structure, Stability, and Flexibility of Double-Stranded RNAs in Salt Solutions

Abstract

Double-stranded (ds) RNAs play essential roles in many processes of cell metabolism. The knowledge of three-dimensional (3D) structure, stability, and flexibility of dsRNAs in salt solutions is important for understanding their biological functions. In this work, we further developed our previously proposed coarse-grained model to predict 3D structure, stability, and flexibility for dsRNAs in monovalent and divalent ion solutions through involving an implicit structure-based electrostatic potential. The model can make reliable predictions for 3D structures of extensive dsRNAs with/without bulge/internal loops from their sequences, and the involvement of the structure-based electrostatic potential and corresponding ion condition can improve the predictions for 3D structures of dsRNAs in ion solutions. Furthermore, the model can make good predictions for thermal stability for extensive dsRNAs over the wide range of monovalent/divalent ion concentrations, and our analyses show that the thermally unfolding pathway of dsRNA is generally dependent on its length as well as its sequence. In addition, the model was employed to examine the salt-dependent flexibility of a dsRNA helix, and the calculated salt-dependent persistence lengths are in good accordance with experiments.

Introduction

RNAs play a pervasive role in gene regulation and expression. In addition to single-stranded (ss) RNAs such as mRNAs and tRNAs, double-stranded (ds) RNAs are widespread in cells and are involved in a variety of biological functions (1, 2, 3). For examples, small noncoding dsRNAs can play a critical role in mediating neuronal differentiation (4), dsRNA segments of special lengths can inhibit the translation of mRNA molecules into proteins through attaching to mRNAs (5, 6), and dsRNAs of more than 30 basepair (bp) length can be key activators of the innate immune response against viral infections (7). Generally, dsRNAs realize their biological functions through becoming partially melted or changing their conformations (2, 3, 4, 5, 6, 7, 8, 9). Furthermore, the interchain interactions in stabilizing structures of dsRNAs are very sensitive to the environment (e.g., temperature and ion conditions) (10, 11, 12, 13, 14). Thus, a full understanding of dsRNA-mediated biology would require the knowledge of three-dimensional (3D) structures, structural stability, and flexibility of dsRNAs in ion solutions.

The 3D structures of RNAs, including dsRNAs, can be measured by several experimental methods such as x-ray crystallography, NMR spectroscopy, and cryo-electron microscopy. However, it is still technically challenging and expensive to experimentally derive 3D structures of RNAs at high resolution, and the RNA structures deposited in the Protein Data Bank (PDB) are still limited (15). Therefore, as complementary methods, some computational models have been developed in recent years, aiming to predict RNA 3D structures in silico (16, 17, 18, 19, 20, 21, 22, 23). The fragment assembly models (24, 25, 26, 27, 28, 29, 30, 31) such as MC-Fold/MC-Sym pipeline (24), 3dRNA (25, 26, 27), RNAComposer (28), and Vfold3D (29, 30) can successfully predict 3D structures of RNAs, including even large RNAs, at fast speed; however, these methods are generally based on given secondary structures and the limited known RNA 3D structures deposited in the PDB. Although the fragment assembly method of fragment assembly of RNA (FARNA) (31) can predict 3D structures for RNAs from sequences, it can only be efficient for small RNAs because of its full-atomic resolution. In parallel ways, some coarse-grained (CG) models (32, 33, 34, 35, 36, 37, 38, 39, 40, 41) such as iFold (42), SimRNA (43), HiRE-RNA (44), and RACER (45, 46) have been proposed to predict 3D structures for RNAs with medium length from their sequences based on knowledge-based statistical potentials and/or experiential parameters. However, these existing 3D-structure prediction models seldom make quantitative predictions for thermodynamic stability and flexibility of RNAs.

Simultaneously, some models have been employed to predict the thermodynamics of RNAs. Vfold2D/VfoldThermal (29, 30) with involving thermodynamic parameters can make reliable predictions on the free-energy landscape of RNAs, including pseudoknots, at the secondary structure level. The model proposed by Denesyuk and Thirumalai (47, 48) can predict the thermodynamics of small RNAs well, whereas such a structure-based (Gö-like) model could not predict 3D structures of RNAs solely from the sequences. Although other models such as iFold (42), HiRE-RNA (44), oxRNA (49), and NARES-2P (50, 51) may give melting curves of RNAs, there is still a lack of extensive experimental validation for these models.

Furthermore, RNAs are highly charged polyanionic molecules, and RNA structure and stability are generally sensitive to solution ion conditions, especially multivalent ions such as Mg²⁺ (8, 10, 11, 12, 13, 14). The role of ions in RNA structure and stability—especially the role of Mg²⁺, which is generally beyond the mean field descriptions (52, 53)—is seldom involved in the existing 3D-structure prediction models. To predict the 3D structures and stability of RNAs in ion solutions, we have developed a CG model with implicit electrostatic potential (54, 55), and the model has been validated through making reliable predictions on 3D structures and stability of RNA hairpins and pseudoknots as well as the ion effect on their stability. However, the model of the previous version was developed to predict the 3D structure and stability of ssRNA and cannot be directly employed to simulate the folding of RNAs with multiple strands because the translational entropy change of RNA strands during structure formation was not taken into account in the model. Unlike ssRNAs, the structure folding and stability of RNAs with multiple strands would be strongly dependent on strand concentration, which can make predictions on folding of dsRNAs very inefficient, especially for predicting dsRNA stability at (low) experimental strand concentration.

In this work, we further developed our previous three-bead CG model for ssRNAs to predict the 3D structure and stability of dsRNAs from their sequences by involving strand translations associated with strand concentration. For predicting stability of dsRNAs, we involved a correction of finite size effect (56) for dsRNA with two strands in a simulation box and introduced a technique of transforming melting curves of dsRNAs at high strand concentrations to those at low strand concentrations (57, 58) to promote the simulation efficiency of the model. Furthermore, an implicit structure-based electrostatic potential is introduced to capture the effect of ions such as Mg²⁺ on 3D structures and stability of dsRNAs. As compared with the extensive experimental data, this model can predict the 3D structures, stability, and flexibility of various dsRNAs with high accuracy, and the effects of monovalent/divalent ions on the stability and flexibility of dsRNAs can be well captured by this model. Additionally, our further analyses show that the thermally unfolding pathway of dsRNA is dependent on not only its length but also its sequence.

Methods

CG structure model and energy function

To reduce the complexity of nucleotides, in our CG model, one nucleotide is represented by three beads: the phosphate bead (P), sugar ring bead (C), and base bead (N) (54, 55). The P and C beads are placed at the P and C4′ atom positions, and the base bead (N) is placed at N9 atom position for purine or N1 for pyrimidine; see Fig. 1. The three beads are treated as van der Waals spheres with the radii of 1.9, 1.7, and 2.2 Å, respectively (54, 55).

Figure 1.

(A) The CG representation for one fragment of dsRNA superposed on an all-atom representation. The beads of P (orange) and C (green) are located at the P atom in the phosphate group and the C4′ atom in the sugar ring, respectively. The beads of N (blue) are located at the N9 atom position for purine or N1 atom position for pyrimidine. (B) A schematic representation for pseudobonds (solid lines), base pairing (dashed lines), and base stacking (dash-dotted line) in our model. (C and D) An illustration for the folding process of a typical dsRNA (PDB: 2JXQ) in our model. (C) The system energy (top), number of basepairs (middle), and the RMSD (bottom) along the simulated annealing MC simulation. The inset is the zoomed RMSD of the structure in the refinement procedure at the end of the simulation. (D) The four typical conformation states in the folding procedure. The structures are shown with PyMol (http://www.pymol.org). To see this figure in color, go online.

The potential energy of a CG dsRNA is composed of two parts, bonded potential U_bonded and nonbonded potential U_nonbonded (54, 55):

$$U_{total}=U_{bonded}+U_{nonbonded}.$$ (1)

The bonded potential U_bonded represents the energy associated with pseudocovalent bonds between contiguous CG beads within any single chain, which includes bond-length energy U_b, bond-angle energy U_a, and dihedral-angle energy U_d:

$$U_{bonded}=U_b+U_a+U_d.$$ (2)

The initial parameters of these potentials were derived from the statistical analysis on the available 3D structures of RNA molecules in the PDB (http://www.rcsb.org/pdb/home/home.do), and two sets of parameters Para_helical and Para_nonhelical were provided for stems and single strands/loops, respectively. Note that only Para_nonhelical is used in the folding process and both Para_helical and Para_nonhelical are used in structure refinement (54, 55). The nonbonded potential U_nonbonded in Eq. 1 includes the following five components:

$$U_{nonbonded}=U_{bp}+U_{bs}+U_{cs}+U_{exc}+U_{el}.$$ (3)

U_bp is the base-pairing interaction between Watson-Crick (G-C and A-U) and wobble (G-U) basepairs. U_bs and U_cs are sequence-dependent base stacking and coaxial stacking interactions between two neighbor basepairs and between two neighbor stems, respectively. The strengths of U_bs and U_cs were derived from the combined analysis of available thermodynamic parameters and Monte Carlo (MC) simulations (54, 55). U_exc represents the excluded volume interaction between two CG beads, and it is modeled by a purely repulsive Lennard-Jones potential.

The last term U_el in Eq. 3 is a structure-based electrostatic energy for an RNA, which is newly refined in the model to better capture the contribution of monovalent and divalent ions to RNA 3D structures. The electrostatic potential is treated as a combination of Debye-Hückel approximation and the counterion condensation theory (52, 53, 54, 55),

$$U_{el}=\frac{Q_i{Q}_j{e}^2}{4\pi {\mathit{ϵ}}_0\mathit{ϵ}{r}_{ij}}{e}^{-\frac{r_{ij}}{l_D}},$$ (4)

where r_ij is the distance between the i-th and j-th P beads, each of which carries a unit negative charge (−e). l_D is the Debye length of ion solution. ${\mathit{\epsilon }}_0$ is the permittivity vacuum, and ε is the effective temperature-dependent dielectric constant of water (54, 55). The reduced negative charge Q_i on the i-th P bead is given by

$$Q_i=1-f_i,$$ (5)

where f_i is the fraction of ion neutralization. In this model, beyond the assumption of uniform distribution of binding ions along RNA chain in our previous model, f_i is dependent on RNA 3D structure and includes the contributions of monovalent and divalent ions

$$f_i=x{f}_i^1+\left(1-x\right)f_i^2.$$ (6)

Here, x and 1 − x represent the contribution fractions from monovalent and divalent ions, which can be derived from the tightly bound ion model (55, 59, 60, 61, 62, 63).$f_i^{\text{ν}}\left(\nu =\mathrm{1,2}\right)$ is the binding fraction of ν-valent ions and is given by

$$f_i^{\nu }=\frac{N{\overline{f}}_i^{\nu }}{{\sum }_N{e}^{-\beta \nu {\varphi }_i}}{e}^{-\beta \nu {\varphi }_i},$$ (7)

where N is the number of P beads. ${\overline{f}}_i^{\nu }$ represents the average charge-neutralization fraction of ions, and the counterion condensation theory gives that (52, 53, 54, 55) ${\overline{f}}_i^{\nu }=1-\left(b/\nu l_B\right)$, where b is the average charge spacing on RNA backbone and l_B is the Bjerrum length. ϕ_i in Eq. 7 is the electrostatic potential at the i-th P bead and can be approximately calculated by

$${\varphi }_i=\sum _{j\ne i}^N\frac{l_B{Q}_j}{r_{ij}}{e}^{-\frac{r_{ij}}{l_D}}.$$ (8)

Equations 5, 6, 7, and 8 show that the structure-based reduced charge fraction Q_i needs to be obtained through an iteration process: 1) use ion-neutralization fraction $f_i^{\nu }$ to calculate f_i through Eq. 6, where the initial $f_i^{\nu }={\overline{f}}_i^{\nu }$; 2) calculate Q_i through Eq. 5 and substitute Q_i in Eq. 8 to calculate ϕ_i; 3) calculate (renew) $f_i^{\nu }$ of ν-valent ions through Eq. 7; 4) repeat 1–3 until $f_i^{\nu }$ becomes converged. See more details in the Supporting Materials and Methods.

The detailed descriptions of the CG energy function as well as the parameters for the potentials in Eqs. 1, 2, and 3 can be found in the Supporting Materials and Methods.

Simulation algorithm

To effectively avoid the traps in local energy minima, the MC simulated annealing algorithm is used to sample conformations for dsRNA at given monovalent/divalent ion conditions. Based on the sequence of dsRNA, two initial random CG chains can be generated and be separately placed in a cubic box, the size of which is determined by concentration of ssRNA. Generally, the simulation of a dsRNA system with a given ion condition is performed from a high temperature (e.g., 110°C) to the target temperature (e.g., room/body temperature). At each temperature, the conformations of the dsRNA are sampled by intrastrand pivot moves and interstrand translation/rotation through the Metropolis algorithm until the system reaches enough equilibrium. In this process, the newly refined electrostatic potential U_el is involved (see Eq. 4), and U_el can only be obtained after an iterative process for Q_i. In practice, U_el is renewed over every 20 MC steps, and generally, U_el can be obtained through ∼4 times iterations for converged Q_i. Thus, the increase in computation cost due to involving the newly refined U_el is negligible compared to the whole simulation cost. The equilibrium conformations of the system at each temperature can be saved to obtain 3D structures and structural properties of the dsRNA at each temperature.

Calculation of melting temperature

The stability of dsRNAs generally depends on strand concentration due to the contribution of translation entropy of melted ssRNA chains (64). However, for dsRNA with low strand concentrations (e.g., 0.1 mM in experiments), a very long simulation time is generally required to reach equilibrium for the dsRNA system. To make our calculation efficient, the simulations for dsRNAs can be performed at relatively high strand concentrations $C_s^h$ (44, 65). To avoid the boundary effect, we generally took a suitable high strand concentration $C_s^h$ (e.g., 10 mM for dsRNA ≤6 bp and 1 mM for dsRNA >6 bp). Correspondingly, the volume of dsRNAs can become negligible compared to the simulation boxes, e.g., dsRNAs of 6 and 14 bp only occupy the simulation boxes with side length of ∼70 and ∼150 Å by ∼2 and ∼0.4% in volume, respectively. Based on the equilibrium conformations at each temperature T, the fraction Φ(T) of unfolded state characterized as a completely dissociated ss chain can be obtained at T. Because the small system of the simulation (two strands in a simulational box) can lead to a significant finite size effect (56), the predicted Φ(T) needs to be further corrected to the fraction θ_h(T) of unfolded state at the high bulk strand concentration $C_s^h$ (56):

$${\theta }_h\left(T\right)=1-\left(1+\frac{\mathit{\Phi }\left(T\right)}{2a\left(1-\mathit{\Phi }\left(T\right)\right)}\right)+\sqrt{{\left(1+\frac{\mathit{\Phi }\left(T\right)}{2a\left(1-\mathit{\Phi }\left(T\right)\right)}\right)}^2-1},$$ (9)

where a = 1 and 2 for non-self-complementary and self-complementary sequences, respectively (56). Afterwards, based on θ_h(T) at the high strand concentration, the fraction θ(T) of unfolded state at an experimental strand concentration C_s (e.g., ∼0.1 mM) can be calculated by (57, 58)

$$\theta \left(T\right)=\frac{\lambda {\theta }_h\left(T\right)}{1+\lambda {\theta }_h\left(T\right)-{\theta }_h\left(T\right)},$$ (10)

where $\lambda =C_s^h/C_s$. Finally, the fractions θ(T) of unfolded state can be fitted to a two-state model to obtain the melting temperature T_m (54, 55, 57),

$$\theta \left(T\right)=1-\frac{1}{1+e^{\left(T-T_m\right)/dT}},$$ (11)

where dT is an adjustable parameter. More details about the calculation of melting temperature are given in the Supporting Materials and Methods. For long dsRNAs whose unfolding can be a non-two-state transition, we still used the above formulas to estimate their melting temperatures, in analogy to related experiment (66).

Results and Discussion

In this section, our model was first employed to predict 3D structures of extensive dsRNAs in monovalent/divalent ion solutions. Afterwards, the model was used to predict stability of extensive dsRNAs and the effects of monovalent/divalent ions and further to analyze the thermally unfolding pathway of various dsRNAs. Finally, the model was employed to examine the salt-dependent flexibility of a dsRNA helix. Our predictions and analyses were extensively compared with the available experiments and existing models.

Structure predictions for dsRNAs in ion solutions

Two sets of available dsRNAs were used in this work on 3D structure prediction. One set includes 16 dsRNAs whose structures were determined by x-ray experiments (defined as the x-ray set), and the other set contains 10 dsRNAs whose structures were determined by NMR experiments in ion solutions (defined as the NMR set). The PDB codes as well as the descriptions of the dsRNAs in two sets are shown in Tables 1 and S3, respectively. In the following, because of the lack of ionic conditions for dsRNAs in the x-ray set, we first made the predictions on 3D structures for 26 dsRNAs in the x-ray set and NMR set at high salt (e.g., 1 M Na⁺), i.e., assuming dsRNAs are nearly fully neutralized and consequently ignoring electrostatic contribution to the predicted structures. Afterwards, we further employed our model to predict 3D structures for dsRNAs in NMR set at their respective experimental ion conditions to examine whether the model with structure-based electrostatic potential can improve 3D structure predictions for dsRNAs in ion solutions.

Table 1.

10 dsRNAs in the NMR Set for Structure Prediction at Respective Salt Conditions

PDB	Descriptiona	Length (nt)	[Na+]/[Mg2+] mM/mMb	Mean/Minimal RMSDs (Å)c
				In 1M [Na+]	In Experimental Solution
2GM0	I	70	250/0.1	7.8/3.5	6.1/3.1
2M1O	H	14	80/0.1	2.4/1.1	2.0/0.7
1TUT	I	22	80/3	3.9/2.2	3.2/1.7
2KYD	H	40	150/10	3.8/1.2	3.7/1.2
2D1A	I	78	50/0	7.4/4.1	6.9/3.8
2DD1	I	20	90/0	3.7/1.5	3.3/1.5
2K7E	I	24	110/0	2.8/1.2	2.4/1.3
2LX1	I	22	90/0	5.6/3.3	4.8/2.4
2JXQ	H	20	60/0	2.1/0.8	2.0/0.8
1F5G	I	20	80/0	3.2/1.9	2.8/1.7

^aH stands for dsRNAs of complementary duplex, and I stands for dsRNAs with internal loop.

^bThe experimental ion conditions for structure determination by NMR method.

^cThe RMSDs are calculated over all three CG beads of predicted structures by our model from the corresponding atoms of the native structures.

Structure predictions for dsRNAs at 1M [Na⁺]

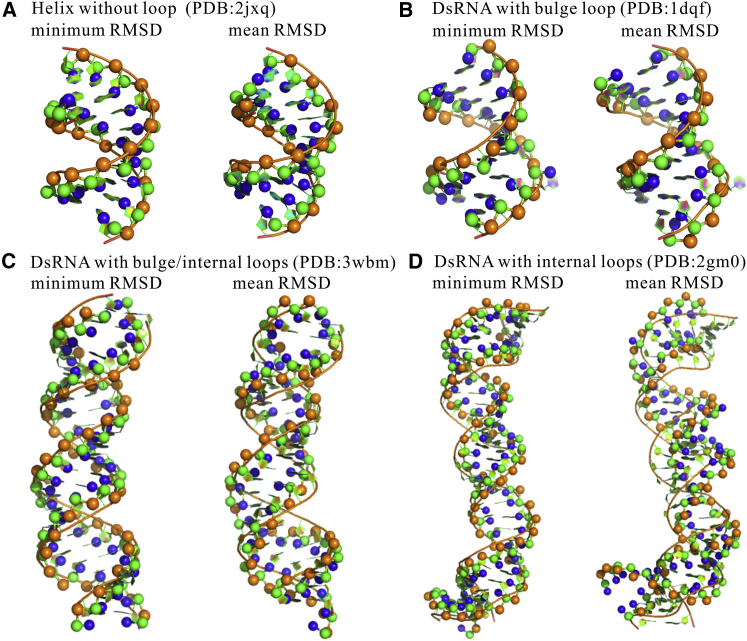
For 26 dsRNAs in the x-ray set and NMR set, the 3D structures were predicted from sequences with strand concentration of 1 mM at high salt concentration (e.g., 1 M Na⁺), regardless of possible ion effects. In the following, we used a paradigm dsRNA (PDB: 2JXQ; shown in Table 1) to show the structure predicting process of dsRNA with our model, which is shown in Fig. 1 C. First, the energy of the system reduces with the decrease of temperature (from 100°C to room temperature), and the dsRNA folds into native-like structures (e.g., structure c in Fig. 1 D) from an initial random configuration (e.g., structure a in Fig. 1 D). Second, a further structure refinement (∼1.2 × 10⁷ MC steps) is performed at the target temperature (e.g., room temperature), in which the last predicted structure from the annealing process is taken as input and the parameters Para_nonhelical of bonded potentials are replaced by Para_helical for the base-paired regions to better capture the geometry of helical stems (54, 55). Finally, an ensemble of refined 3D structures (∼10,000 structures) can be obtained over the last ∼1 × 10⁶ MC steps, and these structures can be evaluated by the root mean-square deviation (RMSD) values calculated over all the beads in predicted structures from the corresponding atoms in the native structures in the PDB (67). As shown in Figs. 1 C and 2, for the dsRNA of PDB: 2JXQ, the mean RMSD (the averaged value over the refined structures) and the minimal RMSD (from the structure closest to the native one) are 2.1 and 0.8 Å, respectively.

Figure 2.

The predicted 3D structures (ball-stick) with mean/minimal RMSDs in comparison with the corresponding native structures (cartoon) for four typical dsRNAs. (A) dsRNA helix without loop (PDB: 2JXQ) with mean/minimal RMSDs of 2.0 Å/0.8 Å. (B) dsRNA containing a bulge loop (PDB: 1DQF) with mean/minimal RMSDs of 2.5 Å/1.6 Å. (C) dsRNA containing two bulge loops and two internal loops (PDB: 3WBM) with mean/minimal RMSDs of 5.4 Å/2.3 Å. (D) dsRNA containing four internal loops (PDB: 2GM0) with mean/minimal RMSDs of 6.1 Å/3.1 Å. The structures are shown with PyMol (http://www.pymol.org). To see this figure in color, go online.

Following the above process, the 3D structures of 26 dsRNAs, including 15 dsRNAs with bulge/internal loops, were predicted by this model with an overall mean RMSD of ∼3.3 Å and an overall minimal RMSD of ∼1.8 Å; see Figs. 2, 3, and Table S1. This shows that our model with coaxial/base stacking can reliably capture the 3D shapes of various dsRNAs, including those with bulge/internal loops. For 13 dsRNAs with internal loops, the overall mean RMSD is ∼4.2 Å, which is slightly larger than that (∼3.3 Å) of all the 26 dsRNAs. This is because large internal loops generally contain noncanonical basepairs, which is ignored in this model. For example, the dsRNA of PDB: 3WBM contains two internal loops with several noncanonical basepairs to keep the helix more continuous than the predicted one; see Fig. 2 C.

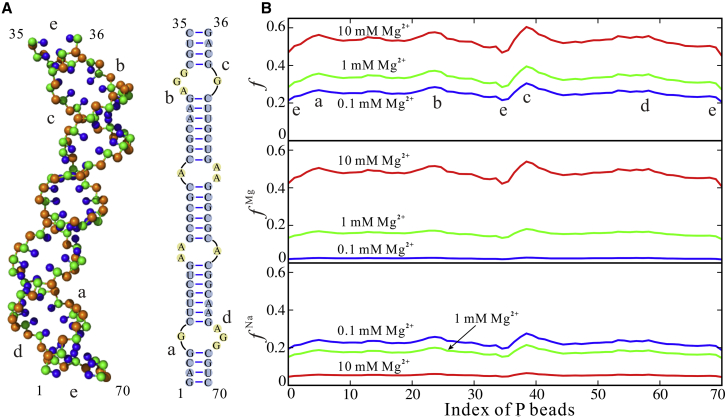
Figure 3.

(A) The predicted 3D structure (left, shown with PyMol) and secondary structure (right) of dsRNA (PDB: 2GM0). (B) The calculated ion-charge-neutralization fractions along P beads of the predicted structure of the dsRNA at different ion conditions; see Eq. 6. f, the total ion-neutralization fractions (top); f^Mg, neutralization fractions of Mg²⁺ (middle); f^Na, neutralization fractions of Na⁺ (bottom). The blue, green, and red lines denote the cases of the dsRNA in 150 mM Na⁺ solutions mixed with 0.1, 1, and 10 mM Mg²⁺, respectively. The two bent regions labeled with (a, d) and (b, c) induced by the internal loops correspond to the ion-neutralization-fraction peaks in (B), and two helical ends of the dsRNA labeled with (e) correspond to the ion-neutralization-fraction troughs in (B). To see this figure in color, go online.

Structure predictions for dsRNAs in respective ion solutions

Because RNA structures can be strongly influenced by ions (10, 11, 12, 13, 14), we introduced the structure-based electrostatic potential in our model to improve the 3D structure prediction for dsRNAs at the respective ion conditions. In the following, we first examined the structure-based electrostatic potential through the charge-neutralization fractions f^Na and f^Mg of Na⁺ and Mg²⁺ along with an example dsRNA (PDB: 2GM0) in mixed Na⁺/Mg²⁺ solutions. As shown in Fig. 3 B, f^Na and f^Mg appear dependent on Na⁺/Mg²⁺ concentrations as well as dsRNA structures: 1) as Mg²⁺ concentration increases, f^Mg increases and f^Na decreases because of the competition between Mg²⁺ and Na⁺ in binding to an RNA and the lower binding-entropy penalty for Mg²⁺ at higher Mg²⁺ concentration (10, 11, 12, 13, 14, 59, 60, 61, 62, 63); 2) f^Na and f^Mg are larger at bent regions and appear less at two ends, which is attributed to the higher charge density of P beads at bending regions and lower charge density of P beads at two ends of the dsRNA. Therefore, the newly refined electrostatic potential (Eqs. 4, 5, 6, 7, and 8) can capture the structure-based ion binding and the competitive binding between Na⁺ ions and Mg²⁺ ions to dsRNAs.

To examine whether the involvement of the implicit structure-based electrostatic potential (Eqs. 4, 5, 6, 7, and 8) and corresponding ion conditions can improve 3D structure prediction for dsRNAs, we further predicted the 3D structures for 10 dsRNAs in the NMR set at their respective experimental ion conditions. For the 10 dsRNAs, the overall mean RMSD between predicted structures in ion solutions and the native structures is ∼3.7 Å, which is visibly smaller than that (∼4.3 Å) of the predictions at 1 M [Na⁺]; see Table 1. This suggests that the inclusion of structure-based electrostatic potential can account for ionic conditions for RNAs and the implementation of the corresponding experimental ion conditions can improve the predictions on 3D structures for dsRNAs in ion solutions. Furthermore, Table 1 also shows that such improvement appears more pronounced for the dsRNAs with internal loops and for the ion conditions containing Mg²⁺, e.g., the mean RMSDs of the dsRNA of 2GM0 and 1TUT decrease from 7.8 and 3.9 Å to 6.1 and 3.2 Å, respectively. This indicates that the newly refined electrostatic potential can effectively involve the RNA structure information and the effect of ions such as Mg²⁺. In addition, we have further predicted 3D structures for dsRNAs in NMR set using our model in the previous version and for several ssRNAs including hairpins and pseudoknots involved in (55, 68) using our model; see Table S4. The comparisons between predictions from our model and its previous version show a visible improvement (∼0.4 Å in mean RMSD) on predicting RNA structures, including both dsRNAs and ssRNAs (55, 69). This indicates that the inclusion of the newly refined structure-based electrostatic potential can better capture RNA structures at their respective ion conditions.

Comparisons with other models

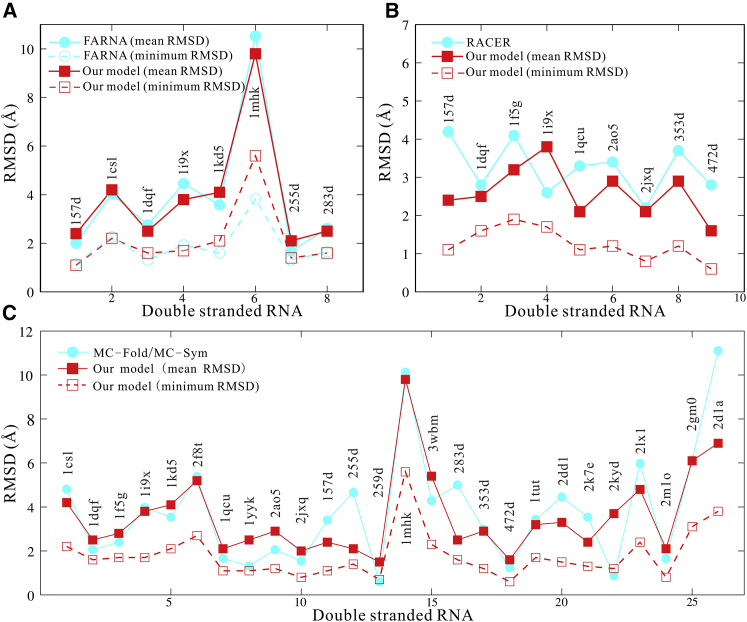
To further examine our model, we made extensive comparisons with three existing RNA-structure-prediction models: FARNA (31), RACER (45, 46), and MC-Fold/MC-Sym pipeline (24). FARNA is a fragment-assembly model with high resolution for small RNAs (31). As shown in Fig. 4 A, the average mean RMSD (∼3.9 Å) from our model is very slightly smaller than that (∼4.1 Å) from FARNA. Afterwards, we made the comparison with a newly developed CG model, RACER (45). As shown in Fig. 4 B, the mean RMSD of the predictions from our model (∼2.6 Å) is slightly smaller than that (∼3.2 Å) from RACER. Furthermore, we made the extensive comparison with MC-Fold/MC-Sym pipeline (24), a well-established RNA 2D/3D structure prediction model with a web server (http://www.major.iric.ca/MC-Pipeline). We used the web server of MC-Fold/MC-Sym pipeline to predict the structures of all the dsRNAs involved in our structure prediction and chose the top predicted structure to make comparisons with our model. As shown in Fig. 4 C, the average mean RMSD (∼3.3 Å) of the predictions from our model is slightly smaller than that (∼3.8 Å) of the top structure from MC-Fold/MC-Sym pipeline. Therefore, the above comparisons show that our model can be reliable in predicting the 3D structures of dsRNAs. Beyond 3D structure predictions, our model can also predict the stability and flexibility of dsRNAs in ion solutions. It should be noted that the computational cost of our model is comparable with that of RACER (46) but much higher than that of the fragment-assembly methods such as MC-Fold/MC-Sym (24) because our model and RACER both involved conformation sampling, unlike fragment-assembly methods. For example, for dsRNA with 20 nt, it takes ∼3 h for our model to predict its 3D structure with one thread on the early generation Intel i7 central processing unit and takes ∼10 min by MC-Fold/MC-Sym on its server. However, compared with the existing models, our model can also predict the 3D structures at different temperatures and can estimate thermodynamic stability for dsRNAs simultaneously.

Figure 4.

The comparisons of the predicted 3D structures between our model and the existing models: (A) FARNA (31), (B) RACER (45, 46), and (C) MC-Fold/MC-Sym pipeline (24). The RMSDs of structures predicted by FARNA are calculated over the C4′ atom (31). The RMSDs of structures predicted by RACER, MC-Fold/MC-Sym pipeline, and our model are calculated over all CG beads (24, 45). The data of FARNA and RACER are taken from (31) to (45), respectively. To see this figure in color, go online.

Stability of dsRNAs in ion solutions

Stability of dsRNAs with various sequences

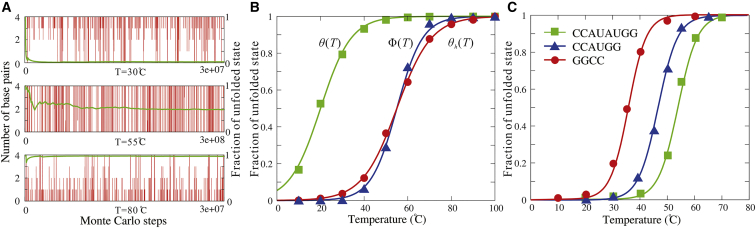
As described in Methods, for dsRNA with a given strand concentration, the melting curve as well as the melting temperature T_m can be calculated with our model. For example, for the sequence (CGCG)₂, the melting curve of the dsRNA with a high strand concentration of 10 mM can be predicted based on the fractions of unfolded state at different temperatures, and the melting curve as well as the melting temperature T_m of the dsRNA at low experimental strand concentration (0.1 mM) can be calculated through Eqs. 9, 10, and 11; see Fig. 5, A and B. As shown in Fig. 5, A and B, the predicted T_m of the sample sequence (CGCG)₂ with experimental strand concentration of 0.1 mM is ∼19.5°C, which agrees well with the corresponding experimental value (∼19.3°C). Furthermore, we further predicted the thermodynamic stability of 22 dsRNAs (from 4-bp to 14 bp) with various complementary sequences; see Table 2. Here, dsRNAs are assumed in solutions of 1 M [Na⁺] to solely examine the stabilities of dsRNAs of various sequence and make comparisons with extensive experimental data (58, 66, 70, 71, 72). As shown in Table 2, the T_m values of extensive dsRNAs from our model are in good agreement with the corresponding experimental data with the mean deviation ∼1.3°C and maximal deviations <2.5°C. Such agreement indicates that the sequence-dependent base-pairing and base-stacking interactions in our model can capture the stability of dsRNAs of extensive sequences and different lengths well (58, 66, 70, 71, 72).

Figure 5.

(A) The time evolution of the number of basepairs (vertical or red lines) and the average fractions of unfolded state (transverse or green lines) for the sample dsRNA of (CGCG)₂ at 30°C (top), 55°C (middle), and 80°C (bottom). (B) The fractions of unfolded state as functions of temperature for the dsRNA of (CGCG)₂. Symbols show the predicted data at different temperatures: blue triangle, at high strand concentration (10 mM); red circle, corrected value of θ_h(T) by Eq. 9; and green square, at experimental strand concentration (0.1 mM) derived by Eq. 10. Lines are the fitted melting curve to the predicted data through Eq. 11. More details can be found in the Supporting Materials and Methods. (C) The fractions of unfolded states for three dsRNAs with 0.1 mM strand concentration as functions of temperature. Symbols are the predicted data and lines are the fitted curves for the three dsRNAs through Eq. 11. To see this figure in color, go online.

Table 2.

The Melting Temperature T_m Values for 20 dsRNAs in 1 M [Na⁺] Solution

	Sequencea	Length (bp)	Expt. (°C)d	Pred. (°C)	Deviation (°C)
1	CGCG	4	19.9	19.5	−0.4
2	GGCC	4	34.3	35.1	+0.8
3	GCGC	4	26.6	28.1	+1.5
4	CCGG	4	27.2	26.6	−0.6
5	CGCGCG	6	57.8	58.5	+0.7
6	CCGCGG	6	59.8	61.2	+1.4
7	CCAUGG	6	46.4	45.3	−1.1
8	GUCGAC	6	45.3	46.8	+1.5
9	AGCGCU	6	50.2	51.1	+0.9
10	UCAUGA	6	27.2	25.7	−1.5
11	GAGGAG	6	50.9	52.0	+1.1
12	AACUAGUU	8	45.7	45.5	−0.2
13	ACUUAAGU	8	40.3	41.3	+1.0
14	ACCUUUGG	8	56.3	54.8	−1.5
15	GCCAUGGC	8	71.4	69.5	−1.9
16	GCUGCGAC	8	67.9	65.8	−2.1
17	CCAUAUGG	8	57.0	59.1	+2.1
18	GAACGUUC	8	52.3	53.6	+1.3
19	AAGGUUGGAA	10	66.5	64.1	−2.4
20	AUUGGAUACAAAb	12	55.4	58.1	+2.7
21	AAAAAAAUUUUUUUc	14	33.2	35.0	+1.8
22	CCUUGAUAUCAAGG	14	76.7	74.3	−2.4

^aThere is only one sequence for dsRNA, and the other is complementary to the shown one. The strand concentrations are 0.1 mM.

^bThe strand concentration of AUUGGAUACAAA is 8 μM.

^cThe strand concentration of AAAAAAAUUUUUUU is 3.9 μM.

^dThe experimental data are from (66, 70, 71, 72).

Thermally unfolding pathways of dsRNAs

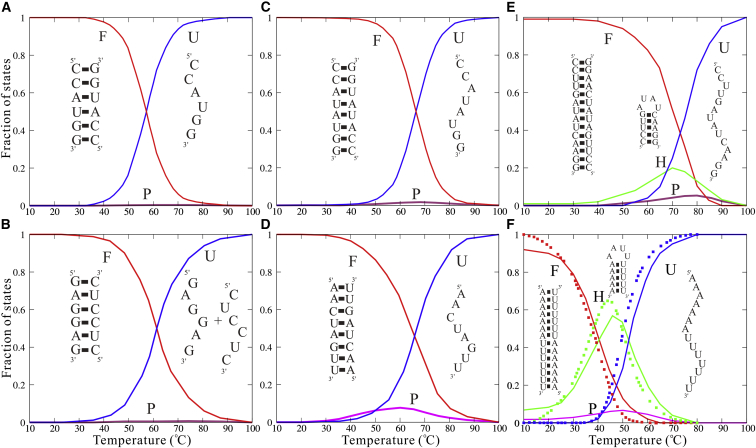
Because intermediate states of RNAs can be important to their functions (1, 2, 3, 10, 68, 69), we made further analyses of thermally unfolding pathways for different dsRNAs. To distinguish the possible different states of dsRNAs at different temperatures in our simulations, all the states for dsRNA were more detailedly divided into unfolded state (U, two disassociated single strands), possible hairpin state (H, with at least one hairpin), folded helix state (F, with the formation of all basepairs except for the two end ones), and partially folded helix state (P, other conformations besides U, F, and H states).

As shown in Fig. 6, the unfolding pathways of dsRNAs are dependent on their length as well as sequences. For short sequences (≤6 bp), dsRNAs undergo the standard two-state melting transitions and there are almost no intermediate states such as P and H states (see Fig. 6, A and B), which is consistent with the previous experiments (66). As chain length increases to ∼8 bp, P states begin to appear and can become visible at ∼T_m; see Fig. 6, C and D. Figs. 6, C and D also show that the unfolding pathways of dsRNAs with the same chain length but different sequences would be slightly different, e.g., the fraction of P state of (AACUAGUU)₂ with end A-U basepairs is slightly higher than that of (CCAUAUGG)₂ with end G-C basepairs. This is because the unstable end A-U basepairs can induce more notable P states than stable end G-C basepairs; see Fig. S1.

Figure 6.

The fractions of F (folded, red lines), P (partially folded, pink lines), H (hairpin, green lines), and U (unfolded, blue lines) states as functions of temperature for the unfolding of (CCAUGG)₂ (A), (GAGGAG, CUCCUC) (B), (CCAUAUGG)₂ (C), (AACUAGUU)₂ (D), (CCUUGAUAUCAAGG)₂ (E), and (AAAAAAAUUUUUUU)₂ (F). The full symbols in (F) are the corresponding experimental data from (71). The insets illustrate the typical predicted secondary structures for F, U, and H states. To see this figure in color, go online.

For dsRNAs with more than 10 bp, their thermally unfolding pathways become more complex and interesting because their ss chain may fold to hairpin structures. As shown in Fig. 6, E and F for the dsRNA of (CCUUGAUAUCAAGG)₂ and (AAAAAAAUUUUUUU)₂, the fractions of F state are near unity at low temperature. As temperature increases, the dsRNAs begin to melt and H states would form from the melted ssRNAs with the maximal fractions of ∼0.2 and ∼0.5 for the two dsRNAs, respectively. At higher temperatures, the dsRNAs become almost completely melted as the U state. Notably, as shown in Fig. 6 F, the unfolding pathway of (AAAAAAAUUUUUUU)₂ predicted by our model is very close to the corresponding experiments (66, 71), suggesting that the melting pathways of dsRNAs can be well captured by our analyses with this model. The difference on unfolding pathways between the two dsRNAs is attributed to the different sequences, i.e., G-C content, especially at two ends. Specifically, the fractions of states follow the order of $\text{F}>U\mathrm{\gtrsim }H>P$ for (CCUUGAUAUCAAGG)₂ at ∼70°C, whereas for (AAAAAAAUUUUUUU)₂ at ∼45°C, such an order becomes $\text{H}>F\mathrm{\gtrsim }U>P$. To reveal what determines the order, we calculated the stability for the states with Mfold (73). We found that the order of state fractions is in agreement with that of state stability. For example, the formation free energies for F, H, and P states are ∼−0.5, ∼0.2, and ∼1.5 kcal/mol for (CCUUGAUAUCAAGG)₂ at ∼70°C, respectively. For (AAAAAAAUUUUUUU)₂ at ∼45°C, the formation free energies for H, F, and P states are ∼−0.8, ∼−0.1, and ∼0.6 kcal/mol. This indicates that the unfolding pathway of dsRNA is dependent on the stability of possible states.

Although unfolding of long dsRNAs can be non-two-state transitions, in analogy to experiments (66), we can still estimate their melting temperatures by assuming strands completely disassociated state as U state (66); see Eq. 11 in Methods.

Stability of dsRNAs with bulge/internal loops

Beyond the dsRNAs with complementary sequences shown above, the stability of other eight dsRNAs with bulge/internal loops was examined by our model. As shown in Table 3, for the dsRNAs with single/double-bulge loops of different loop lengths (sequences 1–6) and the dsRNAs with internal loops (sequences seven and eight), the mean deviation between the predicted T_m values and the experimental data (74, 75, 76, 77, 78, 79, 80) is ∼2.6°C, which indicates that our model with the coaxial stacking potential can roughly estimate the stability of dsRNAs with bulge/internal loops. However, such predictions, especially for dsRNAs with long bulge/internal loops, are not as precise as those for dsRNAs without loops. The detailed comparisons with experimental data show that the predicted T_m values for the dsRNAs with a one-nucleotide (nt) bulge loop are slightly higher than experimental data, whereas our model underestimates the stability of dsRNAs with longer bulge loops, which may suggest that the coaxial stacking potential U_cs involved in our model may slightly overestimate the coaxial interaction strength while underestimating the coaxial interaction range. For the dsRNAs with an internal loop (e.g., AA/AA or AAA/AAA), our model underestimates their stability, which may be attributed to the ignorance of noncanonical basepairs in this model (80).

Table 3.

The Melting Temperatures T_m for Eight dsRNAs with Bulge/Internal Loop in 1 M Na⁺ Solution

	Sequencea	Descriptionb	Experiment (°C)c	Prediction (°C)	Deviation (°C)
1	UGACGCUCA, ACUG GAGU	B	42.2	45.0	+2.8
2	GACUAUGUC, CUGA ACAG	B	34.2	36.1	+1.9
3	GACUAGUGUC, CUGA ACAG	B	31.9	29.5	−2.4
4	GACUCAUCCUG, CUGG GGAC	B	40.7	37.9	−2.8
5	GCAGUUCACG, CG CAAG GC	B	35.5	36.8	+1.3
6	CGAGUAC CG, GC CAUGAGC	B	43.6	41.5	−2.1
7	CGC AA GCG, GCG AA CGC	I	35.5	33.2	−2.3
8	CGCAAAGGC, GCGAAACCG	I	38.5	33.1	−5.4

^aThe strand concentrations are 0.1 mM.

^bB stands for dsRNA with bulge loop, and I stands for dsRNA with internal loop.

^cThe experimental data are from (74, 75, 76, 77, 78, 79, 80).

Effects of monovalent and divalent ions

The thermal stability of RNA molecules is generally sensitive to the ionic conditions (10, 11, 12, 13, 14, 59, 60, 61, 62, 63). Particularly, Mg²⁺ is efficient in neutralizing the negative charges on the RNA molecule and generally plays an important role in RNA folding (14, 59, 60, 61, 62, 63, 81, 82, 83, 84). However, most of the existing structure prediction models cannot quantitatively predict the stability of dsRNAs in ion solutions, especially in the presence of Mg²⁺. Here, we employed our model to examine the stability for dsRNAs over a wide range of monovalent and divalent ion concentrations.

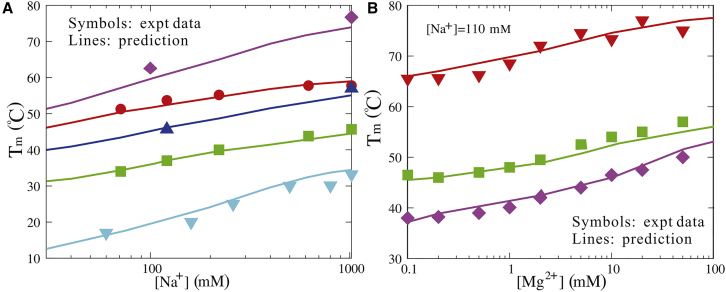
First, we examined the effect of monovalent ions on the stability of dsRNAs. As shown in Fig. 7 A, for five dsRNAs with different sequences and lengths, the predicted melting temperature T_m values from our model agree well with the experimental data (58, 66, 70, 71, 72, 84), with a mean deviation <2°C over the wide range of [Na⁺]. As [Na⁺] increases from 10 mM to 1 M, T_m values of the dsRNAs obviously increase, which is attributed to lower ion-binding entropy penalty and stronger ion neutralization for basepair formation at higher [Na⁺]; see also Fig. S1. Furthermore, Fig. 7 A shows that the [Na⁺]-dependence of T_m is stronger for longer dsRNAs. This is because basepair formation of longer dsRNAs causes larger buildup of negative charges and consequently causes stronger [Na⁺]-dependent ion binding.

Figure 7.

(A) The predicted melting temperatures T_m and corresponding experimental data (58, 66, 70, 71, 72, 84) as functions of [Na⁺] for sequences CCUUGAUAUCAAGG, CGCGCG, CCAUAUGG, AACUAGUU, and AAAAAAAUUUUUUU (from top to bottom). (B) The predicted melting temperatures T_m and corresponding experimental data (84) as functions of [Mg²⁺] for sequences CCUUGAUAUCAAGG, CCAUAUGG, and CCAUGG (from top to bottom). Note that the solutions contain 110 mM Na⁺ as background (84). To see this figure in color, go online.

Second, we examined the stability of dsRNAs in mixed monovalent and divalent ion solutions. As shown in Fig. 7 B, for three different dsRNAs, the predicted T_m values are in good accordance with the experimental data over the wide range of [Mg²⁺] (84). Fig. 7 B also shows that there are three ranges in T_m-[Mg²⁺] curves: 1) at low [Mg²⁺] (relatively to [Na⁺]), the stability of the dsRNAs is dominated by the background [Na⁺] and T_m values of the dsRNAs are almost the same as the corresponding pure [Na⁺]; 2) with the increase of [Mg²⁺], Mg²⁺ ions begin to play a role and T_m increases correspondingly; and 3) when [Mg²⁺] becomes very high (relatively to [Na⁺]), the stability is dominated by Mg²⁺. Furthermore, it is shown that Mg²⁺ is very efficient in stabilizing dsRNAs. Even in the background of 110 mM Na⁺, ∼1 mM Mg²⁺ begins to enhance the stability of dsRNAs, and 10 mM Mg²⁺ (+110 mM background Na⁺) can achieve the similar stability to 1 M Na⁺ for dsRNAs; see sequences of CCUUGAUAUCAAGG and CCAUAUGG in Fig. 7, A and B. This is attributed to the high ionic charge of Mg²⁺ and the consequent efficient role in stabilizing dsRNAs (58, 59, 60, 61, 62, 63, 81, 82, 83, 84).

Flexibility of dsRNA in ion solutions

DsRNAs generally are rather flexible in ion solutions because of their polymeric nature, and the flexibility is extremely important for their biological functions. Additionally, dsRNA flexibility is highly dependent on solution ion conditions (85, 86, 87, 88, 89, 90, 91, 92, 93). In this section, we further employed our model to examine the flexibility of a 40-bp RNA helix in ion solutions. The sequence of the dsRNA helix, which is selected according to a previous study (91), is 5′-CGACUCUACGGAAGGGCAUCCUUCGGGCAUCACUACGCGC-3′, with 57% CG content in its central 30-bp segment and the other chain being fully complementary to it. First, we predicted the 3D structures for the dsRNA helix from the sequence at 25°C, and afterwards, we performed further simulations for the dsRNA helix at various ion conditions based on the predicted structures. Enough conformations at equilibrium at each ion condition were used to analyze the salt-dependent flexibility of the dsRNA helix; see Fig. S2.

Structure fluctuation of dsRNA in ion solutions

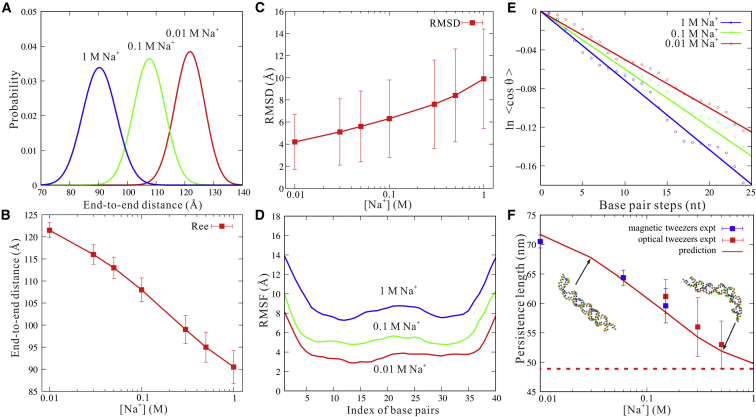
In the following, we first examined the structure fluctuation of the dsRNA helix through calculating end-to-end distance, RMSD variance, and root mean-square fluctuation (RMSF) at different [Na⁺] values (85). As [Na⁺] increases, the end-to-end distance of the dsRNA helix decreases, e.g., from ∼125 Å at 10 mM [Na⁺] to ∼90 Å at 1 M [Na⁺], and simultaneously, the variance of end-to-end distance increases; see Fig. 8, A and B. This indicates the stronger bending conformations and the higher bending fluctuation for the dsRNA helix at higher ion concentrations, which are attributed to the stronger ion neutralization on P bead charges and consequently the reduced electrostatic repulsion due to bending (86, 87, 88, 89, 90, 91, 92, 93, 94). The RMSD variance of the dsRNA helix at different [Na⁺] values calculated based on the conformation-averaged reference structure also indicates that the dsRNA helix would become more flexible with the increase of [Na⁺]; see Fig. 8 C. To examine local structure fluctuation, we further calculated the RMSF of the centers of each basepair of the dsRNA helix at different [Na⁺] values. As shown in Fig. 8 D, the RMSF increases as [Na⁺] increases from 0.01 to 1 M, which is because the stronger ion binding and charge neutralization on P beads enable the larger fluctuation of basepairs along the helix (94). Additionally, end effect contributes to an extra increase of RMSF at the two helical ends (94).

Figure 8.

(A) The distributions of end-to-end distance for the 40-bp dsRNA helix at 1, 0.1, and 0.01 M [Na⁺], respectively. (B) The mean end-to-end distances of the 40-bp dsRNA helix as a function of [Na⁺]. Here, the error bars denote the variance for the end-to-end distances. (C) The RMSD of the 40-bp dsRNA helix calculated based on the conformation-averaged reference structure of the respective simulation as a function of [Na⁺]. Here, the error bars denote the variances for the RMSDs. (D) The RMSF of basepairs along the 40-bp dsRNA helix from simulated ensembles at 1, 0.1, and 0.01 M [Na⁺] values. (E) The fitting curves for l_p through Eq. 12 for the 40-bp dsRNA helix at 1, 0.1, and 0.01 M [Na⁺] values. (F) The predicted persistence length l_p (lines) for the 40-bp dsRNA helix as a function of [Na⁺]. Blue squares, experimental data from magnetic tweezers method (93); red squares, experimental data from optical tweezers method (93). The dashed line in (F) shows the predicted l_p assuming all P beads are electrically neutral. To see this figure in color, go online.

Persistence length of dsRNA helix in ion solutions

Generally, the flexibility of a polymer can be described by its persistence length l_p (95), and l_p can be calculated by the following (96):

$$\cos {\theta }_i=\text{exp}\left(-\frac{ib}{l_p}\right),$$ (12)

where $\cos {\theta }_i={\hat{r}}_i\cdot {\hat{r}}_0$ and ${\hat{r}}_0$ and ${\hat{r}}_i$ are the first and i-th bond-direction vectors, respectively. b in Eq. 12 is the average bond length. According to Eq. 12, l_p of the dsRNA helix can be obtained through modeling the dsRNA helix as a bead chain composed of the central beads of basepairs; see Fig. 8 E. To avoid the end effect (94), the first and last five basepairs were excluded in our calculations and the bond vectors are selected as those over every five continuous basepairs (91).

As shown in Fig. 8 F, the persistence lengths of the 40-bp dsRNA helix at different [Na⁺] values predicted by our model are in quantitative agreement with the corresponding experimental data (93). For example, the deviation of l_p between prediction and experiments is less than ∼2 nm over the wide range of [Na⁺]. As [Na⁺] increases from 0.01 to 1 M, l_p of the dsRNA helix decreases from ∼70 to ∼50 nm. This is because more binding ions neutralize the negative P bead charges on the dsRNA helix more strongly and can reduce the electrostatic bending repulsion along the strands more strongly, causing stronger bending flexibility at high [Na⁺]. Additionally, we have taken out the representative structures at 0.1 mM [Na⁺] and have calculated the ion-charge-neutralization fractions along the structures. As shown in Fig. S3, the ion-charge-neutralization fraction changes as RNA structure is changed, especially in the bending regions.

Conclusions

Knowledge of the 3D structures and thermodynamic properties of dsRNAs are crucial for understanding their biological functions. In this work, we have further developed our previous CG model by introducing a structure-based electrostatic potential and employed the model to predict 3D structures, stability, and flexibility of dsRNAs in monovalent/divalent ion solutions. Our predictions were extensively compared with experimental data, and the following conclusions have been obtained:

• 1)Our model can predict 3D structures from sequences for extensive dsRNAs with/without bulge/internal loops in monovalent/divalent ion solutions well with overall mean RMSD <3.5 Å, and the involvement of the structure-based electrostatic potential and corresponding experimental ion conditions generally improves the structure predictions with smaller RMSDs for dsRNAs in ion solutions.
• 2)Our model can make good predictions for the stability for dsRNAs with extensive sequences over wide ranges of monovalent/divalent ion concentrations with mean deviation <2°C, and our analyses show that the thermally unfolding pathway of dsRNA is dependent on its length as well as its sequence.
• 3)Our model can well capture the salt-dependent flexibility of dsRNAs, and the predicted salt-dependent persistence lengths are in good accordance with experiments.

Although our predictions agree well with the extensive experimental data on 3D structure, stability and flexibility of dsRNAs, there are still several limitations in our model. First, despite the fact that the structure-based electrostatic potential can efficiently capture the effects of monovalent/divalent ions on the structure, stability, and flexibility of dsRNAs, the model was not examined for RNAs with more complex structures, and the model cannot consider concrete ion distribution and specific ion binding around an RNA. Further development of this model may need to involve the effect of ions through an implicit-explicit combined treatment for ions (54). Second, the model only involves canonical and wobble basepairs (A-U, G-C, and G-U) and ignores noncanonical basepairs because over ∼90% basepairs in the ds stems of natural RNAs are canonical ones (97). However, noncanonical basepairs are usually found in RNAs of complex structures, e.g., in interhelical junction loops (98), and for those dsRNAs with bulge/internal loops, the ignorance of noncanonical basepairs may (only) slightly affect the predictions on the structure and stability (97). The noncanonical basepairs can also be possibly involved in the model for predicting RNAs of complex structures at the level of three CG beads through two treatments: 1) derive the (local) bond energy parameters for noncanonical basepairs based on the corresponding structures in the PDB and involve them in Eqs. S3–S5 (54); or 2) given Turner’s nearest-neighbor thermodynamic parameters for noncanonical base stacking (99), derive the basepair/stacking parameters for noncanonical basepairs based on the corresponding structures in the PDB (54) and involve these parameters in Eqs. S7–S9. Finally, our model is a CG model, and it is still necessary to rebuild all-atom structures based on predicted CG ones. Nevertheless, our model can predict the 3D structures, stability, and flexibility of dsRNAs over the wide ranges of monovalent/divalent ion concentrations well and can be a good basis for further development for a predictive model with higher accuracy.

Author Contributions

Z.-J.T., L.J., and Y.-Z. S. designed the research. L.J., Y.-Z.S., and C.-J.F. performed the simulation. Z.-J.T., L.J., and Y.-L.T. analyzed the data. L.J., Y.-Z.S., and Z.-J.T. wrote the manuscript. All authors discussed the result and reviewed the manuscript.

Editor: Tamar Schlick.