Reversible Stochastically-Gated Diffusion-Influenced Reactions

Abstract

An approximate but accurate theory is developed for the kinetics of reversible binding of a ligand to a macromolecule when either can stochastically fluctuate between reactive and unreactive conformations. The theory is based on a set of reaction-diffusion equations for the deviations of the pair distributions from their bulk values. The concentrations are shown to satisfy non-Markovian rate equations with memory kernels that are obtained by solving an irreversible geminate (i.e., two-particle) problem. The relaxation to equilibrium is not exponential but rather a power law. In the Markovian limit, the theory reduces to a set of ordinary rate equations with renormalized rate constants.

Graphical Abstract

Introduction

In an influential paper,¹ McCammon and Northrup generalized the Smoluchowski theory² of diffusion-controlled irreversible reactions to the case when the reactivity turns on and off in a deterministic fashion. Specifically, they calculated the diffusive flux into a sphere, which changes from partially absorbing to reflecting at regular time intervals. Since this problem could not be solved analytically, it was subsequently modified³ so that the reactivity fluctuated stochastically. The transitions between “open” and “closed” states were described by two-state chemical kinetics. The resulting steady-state rate constant was then expressed in terms of the Laplace transform of the Smoluchowski time-dependent rate coefficient for an ungated irreversible reaction evaluated at the sum of the opening and closing rate constants.

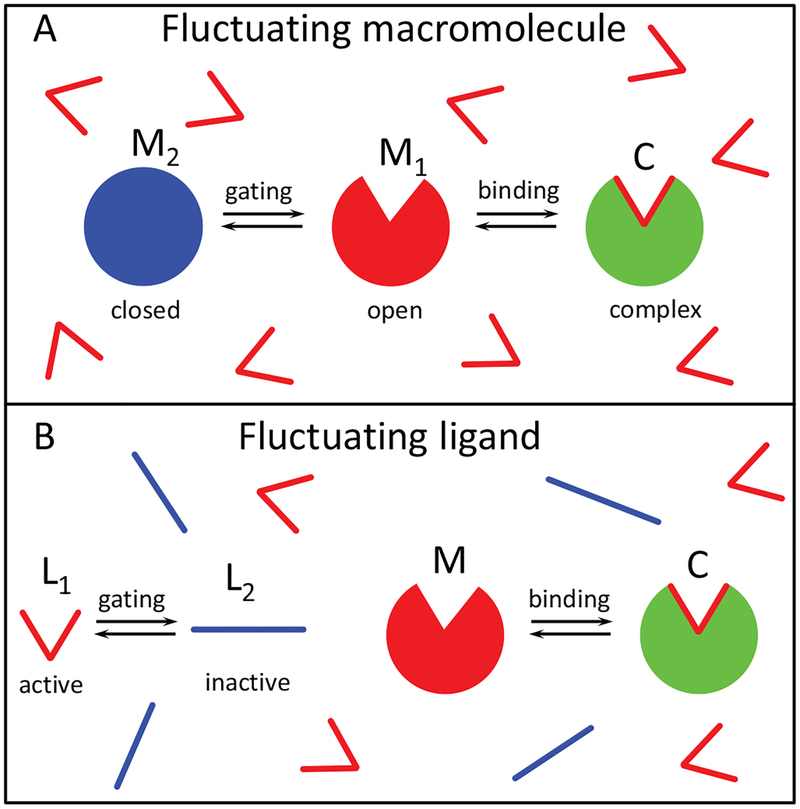
For the geminate reaction between an isolated macromolecule-ligand pair, it does not matter which partner is gated. However, in the pseudo-first order limit where the ligands are in excess, this is not the case for many-particle systems.⁴ The problem where the macromolecule’s binding site fluctuates between reactive and unreactive conformations turned out to be more difficult and a simple but rather ad hoc theory was proposed.⁴ The two cases considered here are shown in Fig. 1. A macromolecule reversibly binds to a ligand and the ligands are in excess. Figure 1A illustrates the case of gated macromolecules, where the macromolecule’s binding site switches between “open” (reactive) and “closed” (unreactive) states. The binding occurs only when the binding site is open. Figure 1B illustrates the situation where it is the ligands that switch between active and inactive states. The binding occurs only when a ligand is in its active conformation.

Figure 1:

Reversible binding with stochastic gating. (A) A macromolecule fluctuates between the open, M₁ (red), and closed, M₂ (blue), states. A ligand L reversibly binds to the macromolecule in the open state M₁ and forms a complex C. (B) A ligand fluctuates between the reactive, L₁ (red), and unreactive, L₂ (blue), states. The ligand in the reactive state L₁ binds to the macromolecule M and forms a complex C. The open (or reactive) states are labeled by the index “1”.

The purpose of this paper is to bring the full machinery of the modern theory of reversible diffusion-influenced reactions^5–32 on both these problems. We will use a generalization of our particular formulation of the theory^21,30,32 where the only approximation made is to assume that the deviation of the distribution functions from their bulk values satisfy reaction-diffusion equations with a physically transparent structure. This formalism is exact at short times and has been shown to give the exact long-time behavior of the concentrations for the reactions A + B ⇌ C and A + B ⇌ C + D.^21,33,34 At the intermediate times, the simplest version of the theory has been found^10,21 by comparison with simulations³⁵ to be pretty accurate as long as the concentrations are not too large.

When we applied this formalism to the A + B ⇌ C reaction with B being in great excess, we noticed²¹ that the final result involved a quantity that had the same structure as the Laplace transform of the stochastically-gated rate coefficient of an irreversible reaction.^3,4 We suggested that, since A can react with B, but C cannot, then in some sense A is an “open” state and C is a “closed” one. In this paper we shall make this analogy more precise.

The outline of the paper is as follows. In the next section we consider fluctuating macromolecules and explain the key ideas behind the formalism. In Sec. III, the reversible non-Markovian rate equations for the concentrations are derived and the corresponding memory kernels are expressed in terms of the time-dependent rate coefficients for a certain irreversible stochastically gated reaction. Fluctuating ligands are considered in Sec. IV. Section V presents the results of illustrative calculations and some concluding remarks are made in Sec. VI. In Appendix A, our formalism is derived starting from the exact many-particle equations corresponding to our microscopic model. In Appendix B, the stochastically-gated time-dependent rate coefficient for a system with 1 open and N – 1 closed states is expressed in terms of the rate coefficient that describes the simplest irreversible reaction, M + L → C.

Gated Macromolecules

We consider the binding of a ligand L to a macromolecule M with fluctuating reactivity (Figure 1A). The macromolecule can be in an open (reactive) and a closed (unreactive) state, which we denote as M₁ and M₂, respectively. The interconversion of these states are described by the rate constants a (M₁ → M₂) and b (M₂ → M₁). The corresponding chemical kinetics scheme is

$$\begin{array}{r}\hfill M_1+L\underset{{\kappa }_r}{\overset{{\kappa }_f}{\rightleftharpoons }}C\\ \hfill M_1\underset{b}{\overset{a}{\rightleftharpoons }}{M}_2\end{array}$$ (1)

where κ_f and κ_r are the intrinsic forward (binding) and reverse (dissociation) rate constants. In the pseudo-first order limit when the ligand concentration is so high that it does not appreciably change with time, the corresponding rate equations for the concentrations, in matrix form, are:

$$\frac{d}{dt}\left(\begin{array}{c}\left[M_1\right]\\ \left[M_2\right]\\ [C]\end{array}\right)=\left(\begin{array}{ccc}-\left(a+{\kappa }_f[L]\right)& b& {\kappa }_r\\ a& -b& 0\\ {\kappa }_f[L]& 0& -{\kappa }_r\end{array}\right)\left(\begin{array}{c}\left[M_1\right]\\ \left[M_2\right]\\ [C]\end{array}\right)$$ (2)

This description is valid only in the limit that the reactants diffuse so fast that there are many encounters between the reactants before the reaction actually occurs.

To see how diffusion influences the kinetics of this reaction, we adopt the simplest possible microscopic model. All reactants are spherical and have the same diffusion coefficients. When M₁ and L come in contact and are separated by a distance r_c independent of their orientation, they can react to form C with rate constant κ_f. The complex C can dissociate to form a contact pair with rate constant κ_r.

The exact rate equations that determine the bulk concentrations can be obtained from eq 2 by simply replacing the bimolecular term [M₁][L] by the pair distribution function between M₁ and L at contact, ${\rho }_{M_{1}L}\left(r_c,t\right)$:

$$\begin{gathered} \frac{d\left[M_1\right]}{dt}=-a\left[M_1\right]-{\kappa }_f{\rho }_{M_{1}L}\left(r_c,t\right)+b\left[M_2\right]+{\kappa }_r[C] \\ \frac{d\left[M_2\right]}{dt}=a\left[M_1\right]-b\left[M_2\right] \\ \frac{d[C]}{dt}={\kappa }_f{\rho }_{M_{1}L}\left(r_c,t\right)-{\kappa }_r[C] \end{gathered}$$ (3)

The pair distribution function ${\rho }_{M_{1}L}(r,t)$ is the probability density of finding a macromolecule in the reactive state in one volume element and a ligand in another, a distance r apart, which has units (concentration)². As r → ∞, macromolecules and ligands are uncorrelated, so that ${\rho }_{M_{1}L}(r,t)\to \left[M_1\right][L]$. In Appendix A, we derive this equation starting from the many-particle description of the model.

The problem is to find ${\rho }_{M_{1}L}\left(r_c,t\right)$, but unfortunately no closed equation exists for this quantity even for our simple microscopic model. However, the boundary condition that must be satisfied by this distribution function can be found exactly by equating the diffusive flux at contact to the rate of complex formation and dissociation:

$$D4\pi r_c^2\frac{\partial }{\partial r}{\rho }_{M_{1}L}{(r,t)|}_{r=r_c}={\kappa }_f{\rho }_{M_{1}L}\left(r_c,t\right)-{\kappa }_r[C]$$ (4)

where D is the sum of diffusion coefficients of M₁ and L.

The pair distribution function changes because of the relative diffusion of the reactants. It also changes because of reaction. For example, if M₁ is transformed to M₂, then the M₁ − L pair is changed into the M₂ − L pair. Similarly, if the macromolecule in a M₁ − L pair reacts with a ligand from the bulk, then it is converted into a C − L pair. Thus we need to consider not only ${\rho }_{M_{1}L}(r,t)$, but also ${\rho }_{M_{2}L}(r,t)$ and ρ_CL(r, t). Instead of trying to find an equation for the pair distribution functions themselves, we consider the difference between these functions and their values in the bulk, δρ_XL(r, t) = ρ_XL(r, t) − [X][L], X = M₁, M₂, C. Since X and L become uncorrelated at large r, ρ_XL(r, t) → [X][L] and thus δρ_XL(r, t) → 0 as r → ∞. The deviations δρ_XL can be regarded as the fluctuation of the pair distribution function from its bulk value. In the spirit of Onsager’s Regression Hypothesis, we assume that these fluctuations relax due to reaction in the same way as the corresponding bulk concentrations do.^36,37 The simplest description of the time course of the bulk concentrations is ordinary chemical kinetics. Then it follows that, in the framework of this approximation, the fluctuations of the pair distribution functions satisfy

$$\frac{\partial }{\partial t}\left(\begin{array}{c}\delta {\rho }_{M_{1}L}\\ \delta {\rho }_{M_{2}L}\\ \delta {\rho }_{CL}\end{array}\right)=D{\nabla }^2\left(\begin{array}{c}\delta {\rho }_{M_{1}L}\\ \delta {\rho }_{M_{2}L}\\ \delta {\rho }_{CL}\end{array}\right)+\left(\begin{array}{ccc}-\left(a+{\kappa }_f[L]\right)& b& {\kappa }_r\\ a& -b& 0\\ {\kappa }_f[L]& 0& -{\kappa }_r\end{array}\right)\left(\begin{array}{c}\delta {\rho }_{M_{1}L}\\ \delta {\rho }_{M_{2}L}\\ \delta {\rho }_{CL}\end{array}\right)$$ (5)

The term involving the Laplacian describes changes of the pair distribution functions due to diffusion, while the other term describes changes due to reaction. Note that the above rate matrix is identical to that in eq 2, which describes the evolution of the bulk concentrations according to ordinary chemical kinetics.

This equation has a simple physically transparent structure and can be formally derived in a number of ways. Perhaps the simplest way is to truncate the hierarchy of equations satisfied by the many-particle distributions using a linearized superposition approximation. For the simpler reaction A+B ⇌ C, this was implicitly done in Ref.¹⁰ The triple distribution function involving a molecule X (X = M₁, M₂, C) and two ligands separated from X by distances r₁ and r₂ is denoted by ρ_XLL(r₁, r₂, t). The standard superposition approximation is^8,38–40 [X]ρ_XLL(r₁, r₂, t) = ρ_XL(r₁, t)ρ_XL(r₂, t) = (δρ_XL(r₁, t) + [X][L])(δρ_XL(r₂, t) + [X][L]). The linearized superposition approximation neglects the non-linear term δρ_XL(r₁, t)δρ_XL(r₂, t) and thus can be written as ρ_XLL(r₁, r₂, t) = (δρ_XL(r₁, t) + δρ_XL(r₂, t))[L] + [X][L]². Using this to close the equations satisfied by the pair distribution functions leads to eq 5 as shown in Appendix A. Another way to get the above approximation for ρ_XLL(r₁, r₂, t) is based on the cluster representation of the distribution functions.⁴¹ This representation has been used in the development of various forms of encounter theory.^24,42,43

The above formalism is the simplest one that leads to the correct power-law time course of the concentrations as they relax to equilibrium. This was rigorously proved for A+B ⇌ C and A+B ⇌ C +D for all possible values of the diffusion coefficients of the reactants.³⁴ The formalism based on eqs 3–5 can be improved by using a better description of how the pair distribution functions change because of chemical reaction. The simplest way of doing this is to replace the chemical rate constants κ_f and κ_r in eq 5 by effective rate constants k_f and k_r. To find these, we need two conditions. The first is to insist that the equilibrium constant is unchanged: k_f/k_r = κ_f/κ_r. The second condition²¹ is to require that the relaxation time calculated from chemical kinetics is the same as that obtained from the diffusion-influenced formalism. This leads a non-linear equation that must be solved iteratively to obtain self-consistent values of the effective rate constants.

Rate Equations with Memory

Our problem is to solve eqs 3 and 5 subject to the boundary condition for ${\rho }_{M_{1}L}(r,t)$ in eq 4. In addition, since M₂ and C cannot bind a ligand, both ${\rho }_{M_{2}L}$ and ρ_CL satisfy reflecting boundary conditions at contact, $\partial {\rho }_{M_{2}L}(r,t)/\partial r=\partial {\rho }_{CL}(r,t)/\partial r=0$ at r = r_c. Initially all reactants are uncorrelated and uniformly distributed, so that $\delta {\rho }_{M_{1}L}(r,0)=\delta {\rho }_{M_{2}L}(r,0)=\delta {\rho }_{CL}(r,0)=0$. We shall now reduce the solution of this problem to that of finding the time-dependent stochastically-gated rate constant for an irreversible reaction involving one open state (M₁) and two closed states (M₂ and C).

This can be done most simply in Laplace space where $\widehat{f}(r,s)={\int }_0^{\infty }f(r,t)\text{exp}(-st)dt$ for any function f. The Laplace transform of eq 3 that determines the bulk concentrations can be written in matrix form as

$$s\widehat{c}-c_0=K\widehat{c}+E\delta \widehat{\rho }\left(r_c,s\right)$$ (6)

where $\widehat{c}(s)$ is a column vector of the concentrations $[{\widehat{M}}_1]$, $[{\widehat{M}}_2]$ and $[\widehat{C}]$, c₀ is the vector of initial concentrations, $\delta \widehat{\rho }\left(r_c,s\right)$ is the vector of pair distribution deviations at contact with elements $\delta {\widehat{\rho }}_{M_{1}L}$, $\delta {\widehat{\rho }}_{M_{2}L}$, and $\delta {\widehat{\rho }}_{CL}$, K is the rate matrix of chemical kinetics and E is a matrix defined as follows:

$$K=\left(\begin{array}{ccc}-\left(a+{\kappa }_f[L]\right)& b& {\kappa }_r\\ a& -b& 0\\ {\kappa }_f[L]& 0& -{\kappa }_r\end{array}\right),E=\left(\begin{array}{ccc}-{\kappa }_f& 0& 0\\ 0& 0& 0\\ {\kappa }_f& 0& 0\end{array}\right)$$ (7)

When $\delta \widehat{\rho }=0$ in eq 6, we recover the ordinary chemical kinetics. Laplace transforming eq 5, we find that $\delta \widehat{\rho }(r,s)$ satisfies

$$s\delta \widehat{\rho }=D{\nabla }^2\delta \widehat{\rho }+K\delta \widehat{\rho }$$ (8)

subject to the boundary condition that

$$D4\pi r_c^2\frac{\partial }{\partial r}\delta {\widehat{\rho }|}_{r=r_c}=v{\kappa }_f\left(\delta {\widehat{\rho }}_{M_{1}L}\left(r_c,s\right)+{[\widehat{M}]}_1[L]-{\kappa }_r[\widehat{C}]/{\kappa }_f\right)$$ (9)

where v is a column vector with elements 1, 0, 0.

The above boundary condition is unusual because the right hand side contains both δρ and the Laplace transforms of the bulk concentrations. One can eliminate the latter in both eqs 8 and 9 using the transformation $\delta \widehat{\rho }(r,s)=\widehat{h}(r,s)\left([{\widehat{M}}_1][L]-{\kappa }_r[\widehat{C}]/{\kappa }_f\right)$. However, the boundary condition remains unusual because the right hand side is of the form $v{\kappa }_f\left({\widehat{h}}_1+1\right)$. Because the derivative of a constant is zero, the substitution $\widehat{h}\to \widehat{g}-1$ would cast the boundary condition into a standard form, but would mess up eq 8 because now it would have the strange term K1. However, if 1 were replaced by a vector proportional to the equilibrium probability distribution, p, that satisfies Kp = 0, this difficulty would disappear. This suggests that we try a substitution of the form $\widehat{h}=\alpha \widehat{f}+\beta p$ and choose α and β so that both eqs 8 and 9 are nice. In this way one can show that the transformation

$$\delta \widehat{\rho }(r,s)=\frac{s\widehat{f}(r,s)-p}{p_1}\left([{\widehat{M}}_1][L]-{\kappa }_r[\widehat{C}]/{\kappa }_f\right)$$ (10)

reduces the problem to solving an irreversible stochastically-gated problem for an isolated ligand-macromolecule pair. Here p₁ = [M₁]_eq = (1 + a/b + κ_f[L]/κ_r)⁻¹, p₂ = [M₂]_eq = p₁a/b, and p₃ = [C]_eq = p₁κ_f[L]/κ_r.

Substituting eq 10 into eq 8 and using Kp = 0, we find that the new function $\widehat{f}$ satisfies

$$s\widehat{f}-p=D{\nabla }^2\widehat{f}+K\widehat{f}$$ (11)

In the time domain, this equation implies that f(r, t) satisfies the equilibrium initial condition, f(r, 0) = p. Substituting eq 10 into eq 9, we find that ${\widehat{f}}_2$ and ${\widehat{f}}_3$ satisfy reflecting boundary conditions and ${\widehat{f}}_1$ satisfies the “radiation” or partially absorbing boundary condition

$$D4\pi r_c^2\frac{\partial }{\partial r}{{\widehat{f}}_1|}_{r=r_c}={\kappa }_f{\widehat{f}}_1\left(r_c,s\right)$$ (12)

Unlike eq 9, this boundary condition does not involve bulk concentrations. It is the same as the boundary condition introduced by Collins and Kimball⁴⁴ to generalize Smoluchowski’s work² from diffusion-controlled to irreversible diffusion-influenced reactions.

By substituting the transformation in eq 10 into eq 6, one finds that the rate equations can be rewritten as

$$s\widehat{c}-c_0=\widehat{\mathcal{K}}\widehat{c}$$ (13)

where

$$\widehat{\mathcal{K}}=\left(\begin{array}{ccc}-\left(a+{\widehat{\mathcal{K}}}_f(s)[L]\right)& b& {\widehat{\mathcal{K}}}_r(s)\\ a& -b& 0\\ {\widehat{\mathcal{K}}}_f(s)[L]& 0& -{\widehat{\mathcal{K}}}_r(s)\end{array}\right)$$ (14)

Here we have defined

$$\begin{gathered} {\widehat{\mathcal{K}}}_f(s)={\kappa }_{f}s{\widehat{f}}_1\left(r_c,s\right)/p_1 \\ {\widehat{\mathcal{K}}}_r(s)={\widehat{\mathcal{K}}}_f(s){\kappa }_r/{\kappa }_f={\kappa }_{r}s{\widehat{f}}_1\left(r_c,s\right)/p_1 \end{gathered}$$ (15)

Note that $\widehat{\mathcal{K}}(s)$ can be obtained from the chemical kinetics rate matrix, K, eq 7, by simply replacing κ_f by ${\widehat{\mathcal{K}}}_f(s)$ and κ_r by ${\widehat{\mathcal{K}}}_r(s)$. Since these kernels satisfy ${\widehat{\mathcal{K}}}_f(s)/{\widehat{\mathcal{K}}}_r(s)={\kappa }_f/{\kappa }_r$, it follows that the equilibrium solution of eq 13 is the same as that found from chemical kinetics.

In the time domain, the rate equations in eq 13 are non-Markovian involving the memory kernels ${\mathcal{K}}_f(t)$ and ${\mathcal{K}}_r(t)$. Since the inverse Laplace transform of $\widehat{f}(s)\widehat{g}(s)$ is ${\int }_0^{t}f(t-\tau )g(\tau )d\tau$, it follows that in the time domain

$$\frac{dc}{dt}=\left(\begin{array}{ccc}-a& b& 0\\ a& -b& 0\\ 0& 0& 0\end{array}\right)c+{\int }_0^t\left(\begin{array}{ccc}-{\mathcal{K}}_f(t-\tau )[L]& 0& {\mathcal{K}}_r(t-\tau )\\ 0& 0& 0\\ {\mathcal{K}}_f(t-\tau )[L]& 0& -{\mathcal{K}}_r(t-\tau )\end{array}\right)c(\tau )d\tau$$ (16)

The first term on the right-hand side, which describes gating, is the same as in the conventional rate equations, eq 2. The terms corresponding to association and dissociation are replaced by convolutions with memory kernels, which depend both on diffusion and gating. The memory kernels appear because different M – L pairs need different times to diffuse together and react.

The reaction kernels ${\widehat{\mathcal{K}}}_f(s)$ and ${\widehat{\mathcal{K}}}_r(s)$ are related to the function ${\widehat{f}}_1$ (see eq 15), which is found by solving eqs 11 and 12. This function also describes an irreversible geminate reaction between a ligand and macromolecule with one open state (labelled by the index “1”) and N – 1 closed (unreactive) states that interconvert via an N × N rate matrix K. For the model without any closed states (K = 0), the Collins-Kimball time-dependent rate coefficient, k_irr(t), is κ_f f₁(r_c, t). This theory was extended to the simplest irreversible stochastically-gated reaction (where K is a 2 × 2 matrix) in Refs.,^3,4 where the Laplace transform of the stochastically-gated rate coefficient k_sg(t) was defined as

$${\widehat{k}}_{sg}(s)={\kappa }_f{\widehat{f}}_1\left(r_c,s\right)$$ (17)

Thus by solving eq 11 subject to the initial condition f(r, 0) = p and the boundary condition in eq 12, we can find the rate coefficient for an irreversible stochastically-gated reaction, in which there is one open but many closed states interconverting via a rate matrix K. In Appendix B we show that when the open state is speci ed by the index “1”, then

$$\frac{p_1}{s{\widehat{k}}_{sg}(s)}=\sum _{i=1}^N\frac{{[T]}_{1i}{\left[T^{-1}\right]}_{i1}}{\left(s+{\lambda }_i\right){\widehat{k}}_{irr}\left(s+{\lambda }_i\right)}$$ (18)

where T is the transformation that diagonalizes K, KT = TɅ, where Ʌ is a diagonal matrix with elements −λ_i, and ${\widehat{k}}_{irr}(s)$ is the Laplace transform of rate coefficient k_irr(t) for simple diffusion-influenced irreversible binding. For uniformly reactive spheres, it is the Collins-Kimball rate coefficient given later in eq 36. However, it is shown in Appendix B that this relation between k_sg and k_irr remains valid in the presence of an interaction potential and for long-range (i.e., non-contact) as well as anisotropic reactivities within the framework of the Wilemski-Fixman⁴⁵ or the constant flux^46,47 approximations.

After this aside, let us return to the reaction kernels. They are simply related to the stochastically-gated rate coefficient, as follows from eqs 15 and 17:

$${\widehat{\mathcal{K}}}_f(s)=s{\widehat{k}}_{sg}(s)/p_1$$ (19)

and consequently,

$$\frac{1}{{\widehat{\mathcal{K}}}_f(s)}=\sum _{i=1}^N\frac{{[T]}_{1i}{\left[T^{-1}\right]}_{i1}}{\left(s+{\lambda }_i\right){\widehat{k}}_{irr}\left(s+{\lambda }_i\right)}$$ (20)

Now for the gated model described by the kinetic scheme in eq 1 (N = 3) one can show after a bit of algebra that

$$\frac{1+a/b+K_{eq}[L]}{{\widehat{\mathcal{K}}}_f(s)}=\frac{1}{{\widehat{\mathcal{K}}}_{irr}(s)}+\frac{a/b+x}{{\widehat{\mathcal{K}}}_{irr}\left(s+k_g-k\right)}+\frac{K_{eq}[L]-x}{{\widehat{\mathcal{K}}}_{irr}\left(s+k_0+k\right)}$$ (21)

where

$$\begin{gathered} K_{eq}={\kappa }_f/{\kappa }_r \\ {k}_g=a+b \\ {k}_0={\kappa }_f[L]+{\kappa }_r \\ 2k=k_g-k_0+\sqrt{{\left(k_g-k_0\right)}^2+4a{\kappa }_f[L]} \\ x=\frac{(k-a)K_{eq}[L]-\left(k+{\kappa }_f[L]\right)a/b}{k_0-k_g+2k} \end{gathered}$$ (22)

where we have defined

$${\widehat{\mathcal{K}}}_{irr}(s)=s{\widehat{k}}_{irr}(s)$$ (23)

As mentioned above, these results are not restricted to uniformly reactive spheres, but under certain conditions are valid quite generally (i.e., for anisotropic reactivity where only a part of the macromolecular surface is active as depicted in Fig. 1).

An interesting prediction of this theory is that the concentrations relax to equilibrium as a power law rather than exponentially as expected from the ordinary chemical kinetics. To find the long-time behavior, we expand the Laplace transforms of the kernels ${\widehat{\mathcal{K}}}_{irr}(s)$, eq 23, and ${\widehat{\mathcal{K}}}_f(s)$, eq 21, about s = 0, collecting the terms involving $\sqrt{s}$. For a simple irreversible reaction, it has been shown quite generally^47,48 that

$$\underset{s\to 0}{\text{lim}}{\widehat{\mathcal{K}}}_{irr}(s)={\widehat{\mathcal{K}}}_{irr}(0)+{\widehat{\mathcal{K}}}_{irr}{(0)}^2\frac{\sqrt{s/D}}{4\pi D}$$ (24)

Using this in eq 21, we find

$$\underset{s\to 0}{\text{lim}}{\widehat{\mathcal{K}}}_f(s)={\widehat{\mathcal{K}}}_f(0)+{\widehat{\mathcal{K}}}_f{(0)}^2\frac{\sqrt{s/D}}{4\pi D\left(1+a/b+K_{eq}[L]\right)}$$ (25)

Finally, using this in eq 13 and the fact that ${\widehat{\mathcal{K}}}_f(0)/{\widehat{\mathcal{K}}}_r(0)=K_{eq}$, we find that as t → ∞ the concentrations decay to their equilibrium values as

$$\begin{array}{l}\frac{\left[M_1(t)\right]-{\left[M_1\right]}_{eq}}{{[C]}_{eq}-[C(0)]}~\frac{K_{eq}}{{\left(1+a/b+K_{eq}[L]\right)}^2}\frac{1}{{(4\pi Dt)}^{3/2}}\\ \frac{\left[M_2(t)\right]-{\left[M_2\right]}_{eq}}{{[C]}_{eq}-[C(0)]}~\frac{K_{eq}a/b}{{\left(1+a/b+K_{eq}[L]\right)}^2}\frac{1}{{(4\pi Dt)}^{3/2}}\\ \frac{[C(t)]-{[C]}_{eq}}{{[C(0)]-[C]}_{eq}}~\frac{K_{eq}(1+a/b)}{{\left(1+a/b+K_{eq}[L]\right)}^2}\frac{1}{{(4\pi Dt)}^{3/2}}\end{array}$$ (26)

While the above formalism leads to analytic expressions for the concentrations in the Laplace domain, it is of interest to obtain approximations that can be implemented more easily. The most straightforward one is the so-called Markovian approximation where ${\widehat{\mathcal{K}}}_f(s)$ and ${\widehat{\mathcal{K}}}_r(s)$ are replaced by their values at s = 0, ${\widehat{\mathcal{K}}}_f(0)$ and ${\widehat{\mathcal{K}}}_r(0)$. Within the framework of this approximation, the concentrations can be calculated just as in chemical kinetics after κ_f and κ_r are replaced by ${\widehat{\mathcal{K}}}_f(0)$ and ${\widehat{\mathcal{K}}}_r(0)$. To make contact with the original paper on stochastic gating,³ let us take the low concentration limit of these effective rate constants. When [L] → 0, it follows from eq 21 (x → 0, k → 0 when k_g < k₀, or x → −a/b, k → k_g − k₀ when k_g > k₀) that

$$\underset{[L]\to 0}{\text{lim}}{\widehat{\mathcal{K}}}_f(0)=(1+a/b)k_{sg}$$ (27)

where k_sg is given by

$$\frac{1}{k_{sg}}=\frac{1}{k_{\infty }}+\frac{a/b}{(a+b){\widehat{k}}_{irr}(a+b)}$$ (28)

where ${\widehat{k}}_{irr}$ is the Laplace transform of the rate coefficient of irreversible binding without gating, and $k_{\infty }={\text{lim}}_{s\to 0}s{\widehat{k}}_{irr}(s)=k_{irr}(\infty )$. The above expression for k_sg turns out to be identical to the stochastically-gated rate constant of reference.³ In this approximation, the concentrations are calculated as in chemical kinetics but with κ_f replaced by k_sg/(1 + a/b) and κ_r by κ_rk_sg/[κ_f(1 + a/b)]. It is interesting that this low concentration result is different from the “naïve” approximation in which the chemical forward and reverse rate constants are simply replaced by their diffusion-influenced counterparts (κ_f → k_irr(∞) and κ_r →κ_rk_irr(∞)/κ_f) for an ungated reaction.

Gated Ligands

Now we consider the case where it is the ligand that can be in two conformational states, L₁ and L₂. The ligand can bind to the receptor and form a ligand-receptor complex C only when it is in the open or active (L₁) state. The transitions between these states are described by two rate constants, a (L₁ → L₂) and b (L₂ → L₁). This process corresponds to the kinetic scheme

$$\begin{array}{r}\hfill M+L_1\underset{{\kappa }_r}{\overset{{\kappa }_f}{\rightleftharpoons }}C\\ \hfill L_1\underset{b}{\overset{a}{\rightleftharpoons }}{L}_2\end{array}$$ (29)

If we assume as before that the ligands are in excess and initially in equilibrium, then their concentrations do not change with time, [L₁] = [L₂]b/a. The rate equations for the macromolecule and complex concentrations in the presence of diffusion are, as before, obtained by replacing [M][L₁] in the ordinary rate equations by ${\rho }_{M{L}_1}\left(r_c,t\right)$:

$$\begin{gathered} \frac{d[M]}{dt}=-{\kappa }_f{\rho }_{M{L}_1}\left(r_c,t\right)+{\kappa }_r[C] \\ \frac{d[C]}{dt}={\kappa }_f{\rho }_{M{L}_1}\left(r_c,t\right)-{\kappa }_r[C] \end{gathered}$$ (30)

where ${\rho }_{M{L}_1}(r,t)$ is the pair distribution function of the macromolecule M and a ligand in the open state, L₁, separated by distance r. The boundary condition for ${\rho }_{M{L}_1}(r,t)$ is the same as eq 4 since M − L₁ can react at contact:

$$D4\pi r_c^2\frac{\partial }{\partial r}\delta {\rho }_{M{L}_1}{(r,t)|}_{r=r_c}={\kappa }_f{\rho }_{M{L}_1}\left(r_c,t\right)-{\kappa }_r[C]$$ (31)

The pair function ${\rho }_{M{L}_1}(r,t)$ is coupled to three other pair functions, ${\rho }_{M{L}_2}(r,t)$, ${\rho }_{C{L}_1}(r,t)$, and ${\rho }_{C{L}_2}(r,t)$, that satisfy reflecting boundary condition at contact since the partners cannot react.

The equations for the deviations of the pair distribution functions from their bulk values, $\delta {\rho }_{M{L}_j}(r,t)={\rho }_{M{L}_j}(r,t)-[M][L_j]$ and $\delta {\rho }_{C{L}_j}(r,t)={\rho }_{C{L}_j}(r,t)-[C][L_j],j=1,2$, are analogous to the corresponding equation for gated receptors, eq 5. The deviations of the pair distribution functions change due to diffusion, ligand interconversion between open and closed states and reaction with the ligands in the bulk. For example, the macromolecule from the M − L₁ pair can react with some other ligand in the active state to generate a C − L₁ pair. The latter may disappear due to dissociation of C, producing an M − L₁ pair. Thus the Laplace transform of the vector of deviations δρ(r, t) with the elements ($\delta {\widehat{\rho }}_{M{L}_1}$, $\delta {\widehat{\rho }}_{M{L}_2}$, $\delta {\widehat{\rho }}_{C{L}_1}$, $\delta {\widehat{\rho }}_{C{L}_2}$) satisfies eq 8, but now K is the 4 × 4 rate matrix:

$$K=\left(\begin{array}{cccc}-\left(a+{\kappa }_f\left[L_1\right]\right)& b& {\kappa }_r& 0\\ a& -\left(b+{\kappa }_f\left[L_1\right]\right)& 0& {\kappa }_r\\ {\kappa }_f\left[L_1\right]& 0& -\left(a+{\kappa }_r\right)& b\\ 0& {\kappa }_f\left[L_1\right]& a& -\left(b+{\kappa }_r\right)\end{array}\right)$$ (32)

Using a similar substitution as in eq 10 (with $[{\widehat{M}}_1]\to [\widehat{M}]$ and [L] → [L₁]), it can be shown that the rate equations in the Laplace space are the same as eq 13, where $\widehat{c}$ is a vector with elements $[\widehat{M}]$ and $[\widehat{C}]$ and

$$\mathcal{K}=\left(\begin{array}{cc}-{\widehat{\mathcal{K}}}_f(s)\left[L_1\right]& {\widehat{\mathcal{K}}}_r(s)\\ {\widehat{\mathcal{K}}}_f(s)\left[L_1\right]& -{\widehat{\mathcal{K}}}_r(s)\end{array}\right)$$ (33)

Here the reaction kernels ${\widehat{\mathcal{K}}}_f(s)={\kappa }_{f}s{\widehat{f}}_1\left(r_c,s\right)/p_1$ and ${\widehat{\mathcal{K}}}_r(s)={\kappa }_{r}s{\widehat{f}}_1\left(r_c,s\right)/p_1$ are again related by detailed balance and are given by eq 20, where T is the matrix of the eigenvectors of the 4 × 4 matrix in eq 32 and −λ_i are the corresponding eigenvalues. One can show after a bit of algebra that

$$\frac{\left(1+a/b+K_{eq}[L]\right)}{{\widehat{\mathcal{K}}}_f(s)}=\frac{1}{{\widehat{\mathcal{K}}}_{irr}(s)}+\frac{a/b}{{\widehat{\mathcal{K}}}_{irr}\left(s+k_g\right)}+\frac{K_{eq}\left[L_1\right]}{{\widehat{\mathcal{K}}}_{irr}\left(s+k_0\right)}+\frac{K_{eq}\left[L_1\right]a/b}{{\widehat{\mathcal{K}}}_{irr}\left(s+k_g+k_0\right)}$$ (34)

where k_g = a + b, k₀ = κ_f[L₁] + κ_r, with ${\widehat{\mathcal{K}}}_{irr}$ given by eq 23, and [L] is the total ligand concentration (i.e., [L₁] = b[L]/(a+b)). This expression for the reaction kernel for fluctuating ligands differs from eq 21 for fluctuating macromolecules. However, in the limit of small ligand concentration, it can be shown that they are the same.

Relaxation to equilibrium at long times is a power law

$$\frac{[M(t)]-{[M]}_{eq}}{[M(0)]-{[M]}_{eq}}=\frac{[C(t)]-{[C]}_{eq}}{{[C(0)]-[C]}_{eq}}~\frac{K_{eq}(1+a/b)}{{\left(1+a/b+K_{eq}[L]\right)}^2}\frac{1}{{(4\pi Dt)}^{3/2}}$$ (35)

Note that the amplitude of the relaxation of the bound state [C] is the same as that for fluctuating macromolecule given in eq 26.

Illustrative Calculations

As an illustration, consider the kinetics of binding to fluctuating macromolecules. The kinetics are found by solving the equations for the Laplace transform of the concentrations, eqs 13–14, with the kernels ${\widehat{\mathcal{K}}}_f(s)$ and ${\widehat{\mathcal{K}}}_r(s)={\widehat{\mathcal{K}}}_f(s)/K_{eq}$ in eqs 21–23. For uniformly reactive spheres, ${\widehat{k}}_{irr}(s)$ is given by the Collins-Kimball rate coefficient:⁴⁴

$$\frac{1}{s{\widehat{k}}_{irr}(s)}=\frac{1}{{\kappa }_f}+\frac{1}{4\pi D{r}_c\left(1+\sqrt{s{r}_c^2/D}\right)}$$ (36)

Solving eq 13 for the concentrations and inverting the Laplace transform numerically, say, by using the Stehfest algorithm,⁴⁹ one can find the time dependence of the concentrations.

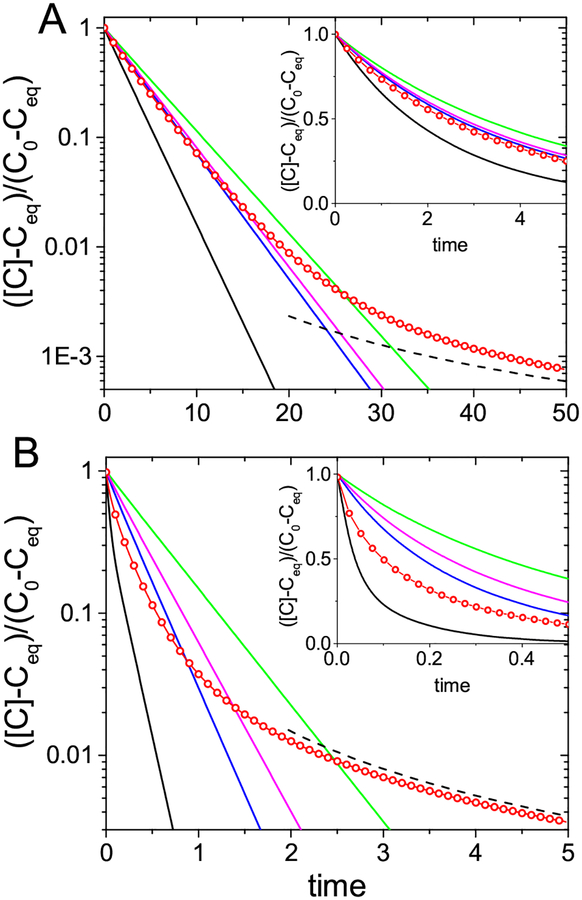
Figure 2 shows the time dependence of the relaxation function, ([C(t)] − [C]_eq)/([C(0)] − [C]_eq), obtained using time-dependent memory kernels (red circles). Initially, all macromolecules are unbound and at equilibrium, [M₁(0)]/[M₂(0)] = b/a, [C(0)] = 0. The kinetics is compared with that obtained using conventional rate equations, eq 2, with various sets of modified forward, k_f, and reverse, k_r, rate constants. These include the intrinsic rate constants k_f = κ_f (black), the diffusion-influenced rate constants, k_f = κ_f4πr_cD/(κ_f + 4πr_cD) (green), the stochastically-gated rate constants, k_f = (1 + a/b)k_sg with k_sg obtained from eqs 28 and 36 (magenta), and the Markovian limit (blue), $k_f={\widehat{\mathcal{K}}}_f(0)$. The reverse rate constant in all cases is found using detailed balance, k_r = k_fκ_r/κ_f. When the ligand concentration is small (Fig. 2A), the rate equations with the stochastically-gated rate constants provide an accurate description of the kinetics at short and intermediate times. The naive approach of simply using diffusion-influenced rate constants performs surprisingly poorly. At long times, the relaxation becomes a power law (dashed lines) (see eq 25). At a high ligand concentration (see Fig. 2B), the kinetics is intrinsically non-Markovian, so descriptions with time-independent rate constants are inadequate essentially at all times (see Fig. 2B).

Figure 2:

Relaxation function of reversible binding to a fluctuating macromolecule. The relaxation function ([C(t)] − [C]_eq)=([C(0)] − [C]_eq) is calculated using eqs 13–14 (red circles) and plotted against dimensionless time t/τ_D, where ${\tau }_D=r_c^2/D$. It is compared with the relaxation function obtained from conventional chemical kinetics with various choices for the rate constants: intrinsic (black), diffusion-influenced (green), diffusion-influenced with stochastic gating (magenta), Markovian limit (blue). The black dashed lines show the power-law asymptotics, eq 26. The insets show behavior at short times. The parameters are (A) v[L] = 0.1, κ_f/k_D = 1, aτ_D = bτ_D = 1, and (B) v[L] = 0.5, κ_f/k_D = 10, aτ_D = bτ_D = 5, where $v=4\pi r_c^3/3$ and k_D = 4πDr_c = 3v/τ_D. In both plots, K_eq[L] ≡ κ_f[L]/κ_r = 1, all macromolecules are initially unbound with equal population in the open and closed states.

Concluding Remarks

In this paper we derived non-Markovian rate equations that describe the kinetics of reversible ligand binding when the reactivity of either the macromolecule (see eq 1) or the ligand (see eq 29) fluctuates. We were able to express the memory kernels for association and dissociation in terms of the time-dependent rate coefficient that describes the simplest irreversible binding reaction. Consequently, our formalism is not restricted to reactants that are non-interacting spheres with isotropic reactivity. One can immediately handle any geometry for which the time-dependent rate coefficient for the irreversible reaction between two species is known to a good approximation. These include reactive sites of arbitrary shape embedded in an otherwise inert planar surface,⁵⁰ the presence of an arbitrary centrosymmetric interaction potential,⁵¹ a buried active site connected to the surface of the macromolecule by a tunnel,⁵² and, finally, reactive patches on a plane, cylinder and sphere in the presence of surface diffusion due to nonspecific binding.²³

Appendix A: Many-Particle Formulation with the Superposition and Linearised Superposition Approximations

Consider a reversible ligand binding to a macromolecule fluctuating between open (M₁) and closed (M₂) states. In the open state, it can bind a ligand L. Ligands are in excess, so that we can consider just one macromolecule in states M₁, M₂, and C surrounded by many (N) ligands in a volume V. We will be interested in the thermodynamic limit, where N → ∞, V → ∞ in such a way that N/V approaches to the ligand concentration, [L]. The many-body problem in this case simplifies because only the state of the macromolecule (i.e., open, closed, or bound) changes. For simplicity, we assume that the system is homogeneous, the macromolecule is at the center and does not move, the ligands are noninteracting points diffusing with diffusion coefficient D.

Let $P_{M_1}\left(r_1,\dots ,r_N,t\right)\left(P_{M_2}\left(r_1,\dots ,r_N,t\right)\right)$ be the probability densities that the macromolecule is in state M₁ (M₂) and the ligands are located at distances r₁,…,r_N from the center of a spherical macromolecule. P_Ci(r₁,…, r_{i −1}; r_i+1,…, r_N, t) is the probability density that the macromolecule is bound to the ith ligand. The normalization condition is

$$\int \left(P_{M_1}+P_{M_2}\right)d{r}_1\dots d{r}_N+\sum _{i=1}^N\int P_{Ci}d{r}_1\dots d{r}_{i-1}d{r}_{i+1}\dots d{r}_N=1$$ (37)

where $d{r}_i=4\pi r_i^{2}d{r}_i$, so that ∫ dr_i = V.

The intrinsic association rate constant at contact (i.e., when r_i = r_c) is κ_f. The macromolecule bound to the ith ligand can dissociate with the rate constant κ_r, leading to the appearance of the ligand i at contact. M₁ and M₂ interconvert with rate constants a and b. The probability densities satisfy the master equations:

$$\frac{\partial }{\partial t}{P}_{M_1}=\sum _{i=1}^{N}D{\nabla }_i^2{P}_{M_1}-a{P}_{M_1}+b{P}_{M_2}$$ (38a)

$$\frac{\partial }{\partial t}{P}_{M_2}=\sum _{i=1}^{N}D{\nabla }_i^2{P}_{M_2}+a{P}_{M_1}-b{P}_{M_2}$$ (38b)

$$\frac{\partial }{\partial t}{P}_{Ci}=\sum _{j=1,j\ne i}^{N}D{\nabla }_j^2{P}_{Ci}+{\kappa }_f{P_{M_1}|}_{r_i=r_c}-{\kappa }_r{P}_{Ci}$$ (38c)

with the boundary conditions

$$D{\nabla }_i{P_{M_1}|}_{r_i=r_c}={\kappa }_f{P_{M_1}|}_{r_i=r_c}-{\kappa }_r{P}_{Ci}$$ (39a)

$${\nabla }_i{P_{M_2}|}_{r_i=r_c}=0$$ (39b)

$${\nabla }_i{P_{Cj}|}_{r_i=r_c}=0,i\ne j$$ (39c)

Here ${\nabla }_i^2$ and ∇_i are the three-dimensional Laplacian and gradient in polar coordinates of the ith ligand. Eq 39a means that the diffusive and reactive fluxes are equal at contact. The two other boundary conditions imply that neither M₂ or C can react with a ligand. At this stage, the volume of the system is finite, so that the above probability distributions obey reflecting boundary conditions at the outer boundary.

The concentrations are related to the probability densities by

$$\left[M_1(t)\right]=M_{tot}\underset{N,V\to \infty }{\text{lim}}\int P_{M_1}d{r}_1\dots d{r}_N$$ (40a)

$$\left[M_2(t)\right]=M_{tot}\underset{N,V\to \infty }{\text{lim}}\int P_{M_2}d{r}_1\dots d{r}_N$$ (40b)

$$[C(t)]=M_{tot}\underset{N,V\to \infty }{\text{lim}}\sum _{i=1}^N\int P_{Ci}d{r}_1\dots d{r}_{i-1}d{r}_{i+1}\dots d{r}_N$$ (40c)

where M_tot = [M₁] + [M₂] + [C] is the total macromolecule concentration, which does not change. Here the limit N → ∞ and V → ∞ is taken in such a way that N/V = [L] = const. The initial conditions for the P’s in terms of the initial concentrations are $P_{M_1}(t=0)=V^{-N}\left[M_1(0)\right]/M_{tot}$, $P_{M_2}(t=0)=V^{-N}\left[M_2(0)\right]/M_{tot}$, $P_{Ci}(t=0)=V^{-(N-1)}[C(0)]/\left(M_{tot}N\right)$.

The pair distribution functions are defined as

$$4\pi r^2{\rho }_{M_{1}L}(r,t)=M_{tot}\underset{N,V\to \infty }{\text{lim}}\int \sum _{i=1}^N\delta \left(r-r_i\right)P_{M_1}d{r}_1\dots d{r}_N$$ (41a)

$$4\pi r^2{\rho }_{M_{2}L}(r,t)=M_{tot}\underset{N,V\to \infty }{\text{lim}}\int \sum _{i=1}^N\delta \left(r-r_i\right)P_{M_2}d{r}_1\dots d{r}_N$$ (41b)

$$4\pi r^2{\rho }_{CL}(r,t)=M_{tot}\underset{N,V\to \infty }{\text{lim}}\int \sum _{i,j=1,i\ne j}^N\delta \left(r-r_i\right)P_{Cj}d{r}_1\dots d{r}_{j-1}d{r}_{j+1}\dots d{r}_N$$ (41c)

where δ(r) is the one-dimensional delta function, $\int \delta \left(r-r_i\right)4\pi r_i^{2}d{r}_i=4\pi r^2$. Note that ρ_XL(r, 0) = [X(0)]N/V = [X(0)][L], where X = M₁, M₂, C, which follows from eq 41 using the initial values for P’s.

We will also use the three-particle distribution function:

$${\left(4\pi r{r}^{\prime }\right)}^2{\rho }_{M_{1}LL}\left(r,r^{\prime },t\right)=M_{tot}\underset{N,V\to \infty }{\text{lim}}\int \sum _{i,j=1;i\ne j}^N\delta \left(r-r_i\right)\delta \left(r^{\prime }-r_j\right)P_{M_1}d{r}_1\dots d{r}_N$$ (42)

Now we derive the exact equations for the concentrations and pair distributions. Multiplying the master equation for $P_{M_1}$ in eq 38 by M_tot, integrating with respect to all ligand coordinates and using eq 40a, we get the rate equation for [M₁]. To simplify the right-hand side, we use the following two equalities that can be derived using eqs 39a, 40c, and 41a:

$$\begin{gathered} D\int {\nabla }_i^2{P}_{M_1}d{r}_i=-D{\nabla }_i{P_{M_1}|}_{r_i=r_c}=-{\kappa }_f{P_{M_1}|}_{r_i=r_c}+{\kappa }_r{P}_{Ci} \\ {M}_{tot}\sum _{i=1}^N\int \left({\kappa }_f{P_{M_1}|}_{r_i=r_c}-{\kappa }_r{P}_{Ci}\right)d{r}_1\dots d{r}_{i-1}d{r}_{i+1}\dots d{r}_N={\kappa }_f{\rho }_{M_{1}L}\left(r_c,t\right)-{\kappa }_r[C] \end{gathered}$$ (43)

The equation for [M₂] is found similarly but using the reflecting boundary condition in eq 39b. To find the equation for [C], one needs to integrate the equation for P_Ci over all coordinates except i and to sum over i (see eq 40c). In this way, we find that the concentrations [M₁(t)], [M₂(t)], and [C(t)] satisfy:

$$\begin{gathered} \frac{d\left[M_1\right]}{dt}=-{\kappa }_f{\rho }_{M_{1}L}\left(r_c,t\right)+{\kappa }_r[C]-a\left[M_1\right]+b\left[M_2\right] \\ \frac{d\left[M_2\right]}{dt}=a\left[M_1\right]-b\left[M_2\right] \\ \frac{d[C]}{dt}={\kappa }_f{\rho }_{M_{1}L}\left(r_c,t\right)dr-{\kappa }_r[C] \end{gathered}$$ (44)

in agreement with eq 3 of the main text.

These equations involve the pair distribution function ${\rho }_{M_{1}L}\left(r_c,t\right)$ in contact. The equation for ${\rho }_{M_{1}L}(r,t)$ is obtained by multiplying eq 38a for $P_{M_1}$ by M_tot ∑_j δ(r − r_j)/4πr² and integrating with respect to all coordinates (see eq 41a). In the right-hand side, the terms $M_{tot}{\sum }_{i\ne j}\int \delta \left(r-r_j\right)D{\nabla }_i^2{P}_{M_1}d{r}_1\dots d{r}_N/4\pi r^2$ are rearranged using eqs 41c, 42, and 43 and result in the term $-{\kappa }_f{\rho }_{M_{1}LL}\left(r,r_c,t\right)+{\kappa }_r{\rho }_{CL}(r,t)$. The terms with i = j can be simplified using ${\sum }_i\int \delta \left(r-r_i\right)D{\nabla }_i^2{P}_{M_1}d{r}_1\dots d{r}_N=D{\nabla }_r^2{\sum }_i\int \delta \left(r-r_i\right)P_{M_1}d{r}_1\dots d{r}_N$. This leads to the term $D{\nabla }^2{\rho }_{M_{1}L}$ in the right-hand side. The equations for ${\rho }_{M_{1}L}$ and ρ_CL are obtained similarly, so we have:

$$\begin{gathered} \frac{\partial }{\partial t}{\rho }_{M_{1}L}(r,t)=D{\nabla }^2{\rho }_{M_{1}L}-{\kappa }_f{\rho }_{M_{1}LL}\left(r,r_c,t\right)+{\kappa }_r{\rho }_{CL}-a{\rho }_{M_{1}L}+b{\rho }_{M_{2}L} \\ \frac{\partial }{\partial t}{\rho }_{M_{2}L}(r,t)=D{\nabla }^2{\rho }_{M_{2}L}+a{\rho }_{M_{1}L}-b{\rho }_{M_{2}L} \\ \frac{\partial }{\partial t}{\rho }_{CL}(r,t)=D{\nabla }^2{\rho }_{CL}+{\kappa }_f{\rho }_{M_{1}LL}\left(r,r_c,t\right)-{\kappa }_r{\rho }_{CL} \end{gathered}$$ (45)

The boundary condition for ${\rho }_{M_{1}L}$ is found by integrating eqs 39 with respect to all coordinates except r_i, summing over i and then using eqs 40c and 41a. In this way we find

$$D\nabla {{\rho }_{M_{1}L}|}_{r=r_c}={\kappa }_f{\rho }_{M_{1}L}\left(r_c,t\right)-{\kappa }_r[C]$$ (46)

in agreement with eq 4 in the main text. Similarly, we find that ${\rho }_{M_{2}L}$ and ρ_CL satisfy reflecting boundary conditions at contact.

Equations 44–46 couple concentrations and pair distribution functions to the three-particle distribution function ${\rho }_{M_{1}LL}\left(r,r_c,t\right)$ of the macromolecule and two ligands located in r and r_c. These equations are exact for the model adopted above.

To obtain a closed equation for the three-particle distributions, we use the so-called superposition approximation:

$${\rho }_{M_{1}LL}\left(r,r^{\prime },t\right)\approx \frac{{\rho }_{M_{1}L}(r,t){\rho }_{M_{1}L}\left(r^{\prime },t\right)}{\left[M_1(t)\right]}$$ (47)

Using this in eq 45 leads to a rather ugly set of non-linear equations. The same is true if they are written in terms of the pair correlation functions, g_XL(r, t) (X = M₁, M₂, C), defined as ρ_XL(r, t) = g_XL(r, t)[X(t)][L].¹⁰ However, the corresponding equations for the deviations of the pair distribution functions from their bulk values,

$$\delta {\rho }_{XL}={\rho }_{XL}-[X][L],X=M_1,M_2,C$$ (48)

turn out to have remarkably simple structure:

$$\frac{\partial }{\partial t}\left(\begin{array}{c}\delta {\rho }_{M_{1}L}\\ \delta {\rho }_{M_{2}L}\\ \delta {\rho }_{CL}\end{array}\right)=D{\nabla }^2\left(\begin{array}{c}\delta {\rho }_{M_{1}L}\\ \delta {\rho }_{M_{2}L}\\ \delta {\rho }_{CL}\end{array}\right)+\left(\begin{array}{ccc}-\left(a+k_f(t)[L]\right)& b& {\kappa }_r\\ a& -b& 0\\ k_f(t)[L]& 0& -{\kappa }_r\end{array}\right)\left(\begin{array}{c}\delta {\rho }_{M_{1}L}\\ \delta {\rho }_{M_2}L\\ \delta {\rho }_{CL}\end{array}\right)$$ (49)

where we have defined a time-dependent association rate coefficient k_f(t) by

$$k_f(t)\equiv {\kappa }_f\frac{{\rho }_{M_{1}L}\left(r_c,t\right)}{\left[M_1(t)\right][L]}$$ (50)

In terms of this rate coefficient, eq 44, which exactly describes the time evolution of the concentrations, can be rewritten as:

$$\frac{d}{dt}\left(\begin{array}{c}\left[M_1\right]\\ \left[M_2\right]\\ [C]\end{array}\right)=\left(\begin{array}{ccc}-\left(a+k_f(t)[L]\right)& b& {\kappa }_r\\ a& -b& 0\\ k_f(t)[L]& 0& -{\kappa }_r\end{array}\right)\left(\begin{array}{c}\left[M_1\right]\\ \left[M_2\right]\\ [C]\end{array}\right)$$ (51)

Note that the matrices in eqs 49 and 51 are the same. Thus, the deviations of the pair distribution functions from their bulk values relax due to reaction (eq 49) in precisely the same way as do the bulk concentrations (eq 51).

For an irreversible reaction (κ_r = 0), k_f(t) can be interpreted as the diffusion-modified association rate coefficient. However, for reversible reactions, this interpretation cannot be correct because it implies a violation of detailed balance.

Since k_f(0) = κ_f, if we were to replace k_f(t) by its initial value in eq 51, we would recover the rate equations of ordinary chemical kinetics, eq 2. The same approximation (k_f(t) → κ_f) in eq 49 that determines the pair distribution function would lead to the set of linear equations, eq 5, in the main text. To obtain this approximation directly, one can use the linearized version of the superposition approximation in eq 45:

$${\rho }_{M_{1}LL}\left(r,r^{\prime },t\right)=\left[M_1\right]{[L]}^2+\delta {\rho }_{M_{1}L}(r,t)[L]+\delta {\rho }_{M_{1}L}\left(r^{\prime },t\right)[L]$$ (52)

This approximation can be obtained by rewriting the superposition approximation in eq 47 in terms of $\delta {\rho }_{M_{1}L}$ and then neglecting the nonlinear term $\delta {\rho }_{M_{1}L}(r,t)\delta {\rho }_{M_{1}L}\left(r^{\prime },t\right)$ as mentioned in the main text.

Appendix B: Stochastic gating with N states

In this Appendix we derive eq 18, which expresses the stochastically gated rate coefficient ${\widehat{k}}_{sg}(s)$ for a system with one open state and N − 1 closed states in terms of the rate coefficient ${\widehat{k}}_{irr}(s)$ for the much simpler system where there is only a single open state. For uniform reactivity at contact and noninteracting particles, this amounts to solving eq 11 for ${\widehat{f}}_1(r,s)$ subject to the boundary condition in eq 12. Here we will show that eq 18 holds more generally. Specifically, we assume that all pairs interact with the same potential U(x), where x can depend both on distance and orientation. The dynamics (including rotational diffusion) of all pairs is described by an operator $\mathcal{L}$ with the property that $\mathcal{L}\text{exp}(-\beta U(x))=0$. Finally, we describe the reactivity of the open state by a non-local sink function σ(x), which is normalized ∫ σ(x)dx = 1. This sink function can depend, say, exponentially on r or be localized in a small region of configuration space. For isotropic reactivity, the boundary condition in eq 12 is equivalent to the sink function $\sigma (r)=\delta \left(r-r_c\right)/4\pi r_c^2$ in conjunction with a reflecting boundary condition at contact.⁵³ For this microscopic model, eq 11 must be replaced by

$$s\widehat{f}-p{e}^{-\beta U(x)}=\mathcal{L}\widehat{f}+K\widehat{f}-{\kappa }_f\sigma (x)v\widehat{f}$$ (53)

with reflecting boundary conditions at contact. Here p is the equilibrium distribution corresponding to K (i.e., Kp = 0) and v is a vector with its first element equal to 1 and the rest equal to 0. The Laplace transform of the stochastically gated rate coefficient is given by

$${\widehat{k}}_{sg}(s)={\kappa }_f\int \sigma (x){\widehat{f}}_1(x,s)dx$$ (54)

By introducing the matrix Green’s function $\widehat{G}(x,s|x^{\prime })$ that satisfies

$$s\widehat{G}-I\delta \left(x-x^{\prime }\right)=\mathcal{L}\widehat{G}+K\widehat{G}$$ (55)

where I is the identity matrix, one can recast eq 53 into the integral equation

$${\widehat{f}}_1(x,s)=p_1{e}^{-\beta U(x)}/s-\int {\widehat{G}}_{11}(x,s|x^{\prime }){\kappa }_f\sigma \left(x^{\prime }\right){\widehat{f}}_1\left(x^{\prime },s\right)d{x}^{\prime }$$ (56)

where ${\widehat{G}}_{11}$ is a matrix element of $\widehat{G}$.

In general, eq 56 can be solved analytically only using the Wilemski-Fixmann approximation.⁴⁵ In this approximation, the dependence of ${\widehat{f}}_1$ on x and s is decoupled assuming that the equilibrium distribution is maintained in the volume where the reaction occurs, but with s-dependent amplitude. This amounts to replacing f₁ under the integral sign in eq 56 by

$${\widehat{f}}_1(x,s)\approx e^{-\beta U(x)}\frac{\int \sigma \left(x^{\prime }\right){\widehat{f}}_1\left(x^{\prime },s\right)d{x}^{\prime }}{\int \sigma \left(x^{\prime }\right)e^{-\beta U\left(x^{\prime }\right)}d{x}^{\prime }}$$ (57)

This approximation is exact for the contact reactivity.

Multiplying eq 56 by κ_fσ(x), integrating it with respect to x, and using eq 57 in the right hand side of this equation, we get an algebraic equation for ${\widehat{k}}_{sg}(s)$, defined in eq 54:

$${\widehat{k}}_{sg}(s)=\langle {\kappa }_f\rangle p_1/s-\langle {\kappa }_f\rangle \widehat{\Gamma }(s){\widehat{k}}_{sg}(s)$$ (58)

where we have defined 〈κ_f〉 as

$$\langle {\kappa }_f\rangle ={\kappa }_f\int \sigma (x)e^{-\beta U(x)}dx$$ (59)

and $\widehat{\Gamma }(s)$ is the Laplace transform of the sink-sink autocorrelation function:

$$\widehat{\Gamma }(s)=\frac{{\kappa }_f^2}{{\langle {\kappa }_f\rangle }^2}\int \sigma (x){\widehat{G}}_{11}(x,s|x^{\prime })\sigma \left(x^{\prime }\right)e^{-\beta U\left(x^{\prime }\right)}dxd{x}^{\prime }$$ (60)

Rearranging eq 58, we find

$$\frac{p_1}{s{\widehat{k}}_{sg}(s)}=\frac{1}{\langle {\kappa }_f\rangle }+\widehat{\Gamma }(s)$$ (61)

which determines the stochastically-gated rate coefficient.

To proceed further, we diagonalize the rate matrix, K = T Diag(−λ_i)T⁻¹, where Diag(−λ_i) is the diagonal matrix of eigenvalues −λ_i defined so that λ_i are positive or 0. Then it follows from eq 55 that $G=T\text{Diag}\left(\widehat{g}\left(s+{\lambda }_i\right)\right)T^{-1}$, where the diagonal elements are $\widehat{g}\left(s+{\lambda }_i\right)\equiv \widehat{g}\left(x,s+{\lambda }_i|x^{\prime }\right)$, where $\widehat{g}(x,s|x^{\prime })$ satisfies eq 55 with K = 0:

$$s\widehat{g}-\delta \left(x-x^{\prime }\right)=\mathcal{L}\widehat{g}$$ (62)

with reflecting boundary condition at contact.

Using this representation in eqs (60)–(61), we get

$$\frac{p_1}{s{\widehat{k}}_{sg}(s)}=\frac{1}{\langle {\kappa }_f\rangle }+\sum _{i=1}^N{[T]}_{1i}{\left[T^{-1}\right]}_{i1}\widehat{\gamma }\left(s+{\lambda }_i\right)$$ (63)

where $\widehat{\gamma }(s)$ is given, similar to eq 60, by

$$\widehat{\gamma }(s)=\frac{{\kappa }_f^2}{{\langle {\kappa }_f\rangle }^2}\int \sigma (x)\widehat{g}(x,s|x^{\prime })\sigma \left(x^{\prime }\right)e^{-\beta U\left(x^{\prime }\right)}dxd{x}^{\prime }$$ (64)

The stochastically-gates rate coefficient in eq 63 can be related to the Laplace transform of the rate coefficient ${\widehat{k}}_{irr}(s)$ for the irreversible binding without gating (i.e., to the open state with index 1). ${\widehat{k}}_{irr}(s)$ can be obtained using eqs 53 and 54 with K set to 0. In the framework of the Wilemski-Fixmann approximation, it is given by eq 63 with N = 1, p₁ = 1, and T = I:

$$\frac{1}{s{\widehat{k}}_{irr}(s)}=\frac{1}{\langle {\kappa }_f\rangle }+\widehat{\gamma }(s)$$ (65)

Using this in eq 64 and noting that Σ_i[T]_1i[T⁻¹]_i1 = 1, we recover eq 18 in the main text.