SCALPEL: EXTRACTING NEURONS FROM CALCIUM IMAGING DATA

Abstract

In the past few years, new technologies in the field of neuroscience have made it possible to simultaneously image activity in large populations of neurons at cellular resolution in behaving animals. In mid-2016, a huge repository of this so-called “calcium imaging” data was made publicly available. The availability of this large-scale data resource opens the door to a host of scientific questions for which new statistical methods must be developed.

In this paper we consider the first step in the analysis of calcium imaging data—namely, identifying the neurons in a calcium imaging video. We propose a dictionary learning approach for this task. First, we perform image segmentation to develop a dictionary containing a huge number of candidate neurons. Next, we refine the dictionary using clustering. Finally, we apply the dictionary to select neurons and estimate their corresponding activity over time, using a sparse group lasso optimization problem. We assess performance on simulated calcium imaging data and apply our proposal to three calcium imaging data sets.

Our proposed approach is implemented in the R package scalpel, which is available on CRAN.

1. Introduction.

The field of neuroscience is undergoing a rapid transformation; new technologies are making it possible to image activity in large populations of neurons at cellular resolution in behaving animals [Ahrens et al. (2013), Prevedel et al. (2014), Huber et al. (2012), Dombeck et al. (2007)]. The resulting calcium imaging data sets promise to provide unprecedented insight into neural activity. However, they bring with them both statistical and computational challenges.

While calcium imaging data sets have been collected by individual labs for the past several years, up until quite recently large-scale calcium imaging data sets were not publicly available. Thus, attempts by statisticians to develop methods for the analysis of these data have been hampered by limited data access. However, in July 2016, the Allen Institute for Brain Science released the Allen Brain Observatory, which contains 30 terabytes of raw data cataloguing 25 mice over 360 different experimental sessions [Shen (2016)]. This massive data repository is ripe for the development of statistical methods, which can be applied not only to the data from the Allen Institute but also to calcium imaging data sets collected by individual labs worldwide.

We now briefly describe the science underlying calcium imaging data. When a neuron fires, voltage-gated calcium channels in the axon terminal open and calcium floods the cell. Therefore, intracellular calcium concentration is a surrogate marker for the spiking activity of neurons [Grienberger and Konnerth (2012)]. In recent years genetically encoded calcium indicators have been developed [Chen et al. (2013), Looger and Griesbeck (2012), Rochefort, Jia and Konnerth (2008)]. These indicators bind to intracellular calcium molecules and fluoresce. Thus, the locations of neurons and the times at which they fire can be seen through a sequence of two-dimensional images taken over time, typically using two-photon microscopy [Svoboda and Yasuda (2006), Helmchen and Denk (2005)].

A typical calcium imaging video consists of a 500 × 500 pixels frame over one hour sampled at 15–30 Hz. A given pixel in a given frame is continuous valued, with larger values representing higher fluorescent intensities due to greater calcium concentrations. An example frame from a calcium imaging video is shown in Figure 1(a). We have posted snippets of the three calcium imaging videos analyzed in this paper at www.ajpete.com/software.

Fig. 1.

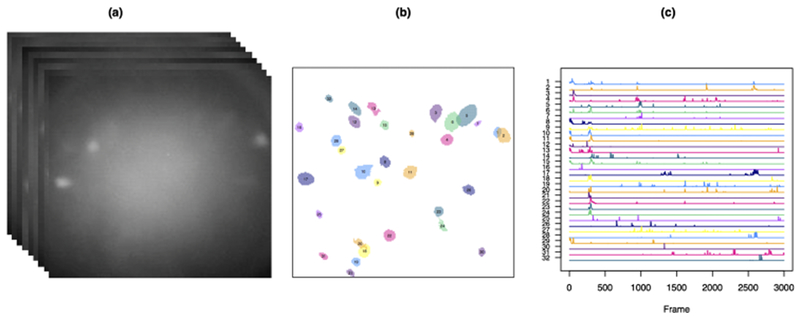
In (a), we display sample frames from the raw calcium imaging video described in the text in Section 4, and analyzed in greater detail in Section 6.2. We wish to construct a spatial map of the neurons, like that shown in (b). As a by-product, we will also obtain a crude estimate of the calcium trace for each neuron over time, as shown in (c).

On the basis of a calcium imaging video, two goals are typically of interest:

• Neuron identification: The goal is to assign pixels of the image frame to neurons. Due to the thickness of the brain slice captured by the imaging technology, neurons can overlap in the two-dimensional image. This means that a single pixel can be assigned to more than one neuron. This step is sometimes referred to as region of interest identification or cell sorting. An example of neurons identified from a calcium imaging video is shown in Figure 1(b).

• Calcium quantification: The goal is to estimate the intracellular calcium concentration for each neuron during each frame of the movie. An example of these estimated calcium traces is shown in Figure 1(c).

To a certain extent, these two goals can be accomplished by visual inspection. However, visual inspection suffers from several shortcomings:

• It is subjective, and it is not reproducible. Two people who view the same video may identify a different set of neurons or different firing times.

• It does not yield numerical information regarding neuron firing times, which may be needed for downstream analyses.

• It may be inaccurate; for instance, a neuron that is very dim or that fires infrequently may not be identified by visual inspection.

• It is not feasible on videos with very large neuronal populations or very long durations. In fact, a typical calcium imaging video contains 250,000 pixels and more than 50,000 frames, making visual inspection essentially impossible.

In this paper we propose a method that identifies the locations of neurons. Previous proposals to automatically accomplish this task have been proposed in the literature and are reviewed in Section 3. However, our method has several advantages over competing approaches. Unlike many existing approaches, it:

• Involves few tuning parameters, which are themselves interpretable to the user, can for the most part be set to default values and can be varied independently;

• Yields results that are stable across a range of tuning parameters;

• Is computationally feasible even on very large data sets; and

• Uses spatial and temporal information to resolve individual neurons from sets of overlapping neurons without postprocessing.

The methods proposed in this paper can be seen as a necessary step that precedes downstream modeling of calcium imaging data. For instance, there is substantial interest in modeling functional connectivity among populations of neurons or using neural activity to decode stimuli [see, e.g., Ko et al. (2011), Mishchencko, Vogelstein and Paninski (2011), Paninski, Pillow and Lewi (2007)]. However, before either of those tasks can be carried out, it is necessary to first identify the neurons; this is the task that we consider in this paper.

The remainder of this paper is organized as follows. We introduce notation in Section 2. In Section 3 we review related work. We present our proposal in Section 4 and discuss the selection of tuning parameters in Section 5. We apply our method to three calcium imaging videos in Section 6 and assess performance using simulated calcium imaging data in Section 7. We close with a discussion in Section 8. Proofs are in the Supplementary Material [Petersen, Simon and Witten (2018)].

2. Notation.

Let P denote the total number of pixels per image frame and T the number of frames of the video. We define Y to be a P × T matrix for which the (i, j)th element, y_i,j, contains the fluorescence of the ith pixel in the jth frame. We let y_i,·= (y_i,1, y_i,2 … y_i,T)^⊺ represent the fluorescence of the ith pixel at each of the T frames. We let y_·,j = (y_1,j y_2,j … y_P,j)^⊺ represent the fluorescence of all P pixels during the jth frame. We use the same subscript conventions in order to reference the elements, rows and columns of other matrices.

The primary goal of our work is to identify the locations of the neurons; as a by-product we will also obtain a crude estimate of their calcium concentrations over time: we view these tasks in the framework of a matrix factorization problem. We decompose Y into a matrix of spatial components, $\mathit{A}\in {ℝ}^{P\times K}$ and a matrix of temporal components, $\mathit{Z}\in {ℝ}^{K\times T}$, such that

$$\mathit{Y}\approx \mathit{AZ},$$ (1)

where K is the total number of estimated neurons. Note that a_·,k specifies which of the P pixels of the image frame are mapped to the kth neuron, and z_k,· quantifies the calcium concentration for the kth neuron at each of the T video frames. We note that the true number of neurons is unknown and must be determined as part of the analysis. The vectorization of the image frames in Y is simply for notational convenience. In estimating A we will use spatial information from the two-dimensional structure of the image frames.

3. Related work.

There are two distinct lines of work in this area. The first focuses on simply identifying the regions of interest in the video and then subsequently estimating the calcium traces. The second aims to simultaneously identify neurons and quantify their calcium concentrations.

Methods that focus solely on region of interest identification typically construct a summary image for the calcium imaging video and then segment this image using various approaches. For example, Pachitariu et al. (2013) calculate the mean image of the video and then apply convolutional sparse block coding to identify regions of interest. Alternatively, Smith and Hausser (2010) calculate a local cross-correlation image, which is then thresholded using a locally adaptive filter to extract the regions of interest. Similar approaches have been used by others [Ozden et al. (2008), Mellen and Tuong (2009)]. These region of interest approaches often do not fully exploit temporal information; furthermore, they typically are unable to resolve spatially-overlapping neurons.

We now focus on methods that simultaneously identify neurons and estimate calcium concentrations. One of the first methods in this area was proposed by Mukamel, Nimmerjahn and Schnitzer (2009). This method first applies principal component analysis to reduce the dimensionality of the data, followed by spatio-temporal independent component analysis to produce spatial and temporal components that are statistically independent of one another. Though this method is widely used, it often requires heuristic postprocessing of the spatial components, and typically fails to distinguish between spatially overlapping neurons [Pnevmatikakis et al. (2016)].

To better handle overlapping neurons, Maruyama et al. (2014) proposed a non-negative matrix factorization approach, which estimates A and Z in (1) by solving

$$\underset{\mathit{A}\ge 0,\mathit{Z}\ge 0,{\mathit{a}}_b\ge 0}{\text{minimize}}\frac{1}{2}{\parallel \mathit{Y}-\mathit{AZ}-{\mathit{a}}_b{\mathit{z}}_b^{⊺}\parallel }_F^2.$$ (2)

In (2), the term ${\mathit{a}}_b{\mathit{z}}_b^{⊺}$ is a rank-one correction for background noise; ${\mathit{z}}_b\in {ℝ}^T$ is a temporal representation of the background noise (known as the bleaching line and estimated using a linear fit to average fluorescence over time of a background region), and ${\mathit{a}}_b\in {ℝ}^P$ is a spatial representation of the background noise. Elementwise positivity constraints are imposed on A, Z and a_b in (1). While (2) can handle overlapping neurons, there is no constraint on the sparsity of Z, and no effort to ensure that the nonzero elements of A are sparse and spatially contiguous. Thus, the estimated temporal components are very noisy, and the estimated spatial components often require heuristic postprocessing.

To overcome these shortcomings, Haeffele, Young and Vidal (2014) modify (2) so that the temporal components A are sparse, and the spatial components Z are sparse and have low total variation. Recently, Pnevmatikakis et al. (2016) further refine (2) by explicitly modeling the dynamics of the calcium when estimating the temporal components Z and combining a sparsity constraint with intermediate image filtering when estimating the spatial components A. Zhou et al. (2016) extend the work of Pnevmatikakis et al. (2016) to better handle one-photon imaging data by: (i) modeling the background in a more flexible way, and (ii) introducing a greedy initialization procedure for the neurons that is more robust to background noise. Related approaches are taken by Diego et al. (2013), Diego and Hamprecht (2014), Friedrich et al. (2015). Other recent approaches consider using convolutional networks trained on manual annotation [Apthorpe et al. (2016)] and multilevel matrix factorization [Diego and Hamprecht (2013)].

While these existing approaches show substantial promise and are a marked improvement over manual identification of neurons from the calcium imaging videos, they also suffer from some shortcomings:

• The optimization problems [see, e.g., (2)] are biconvex. Thus, algorithms typically get trapped in unattractive local optima. Furthermore, the results strongly depend on the choice of initialization.

• Each method involves several user-selected tuning parameters. There is no natural interpretation to these tuning parameters which leads to challenges in selection. Furthermore, the tuning parameters are highly interdependent, so that changing one tuning parameter may necessitate updating all of them. Moreover, there is no natural nesting with respect to the tuning parameters. A slight increase or decrease in one tuning parameter can lead to a completely different set of identified neurons.

• The number of neurons K must be specified in advance, and the estimates obtained for different values of K will not be nested: two different values of K can yield completely different answers.

• Postprocessing of the identified neurons is often necessary.

• Implementation on very large data sets can be computationally burdensome.

To overcome these challenges, instead of simultaneously estimating A and Z in the model (1), we take a dictionary learning approach. We first leverage spatial information to build a preliminary dictionary of spatial components, which is then refined using a clustering approach to give an estimate of A. We then use our estimate of A to obtain an accurate estimate of the temporal components Z, while simultaneously selecting the final set of neurons in A. This dictionary learning approach allows us to recast (1), a very challenging unsupervised learning problem, into a much easier supervised learning problem. Compared to existing approaches, our proposal is much faster to solve computationally, involves more interpretable tuning parameters and yields substantially more accurate results.

4. Proposed approach.

Our proposed approach is based on dictionary learning. In Figure 2, we summarize our Segmentation, Clustering and Lasso Penalties (SCALPEL) proposal, which consists of four steps:

Fig. 2.

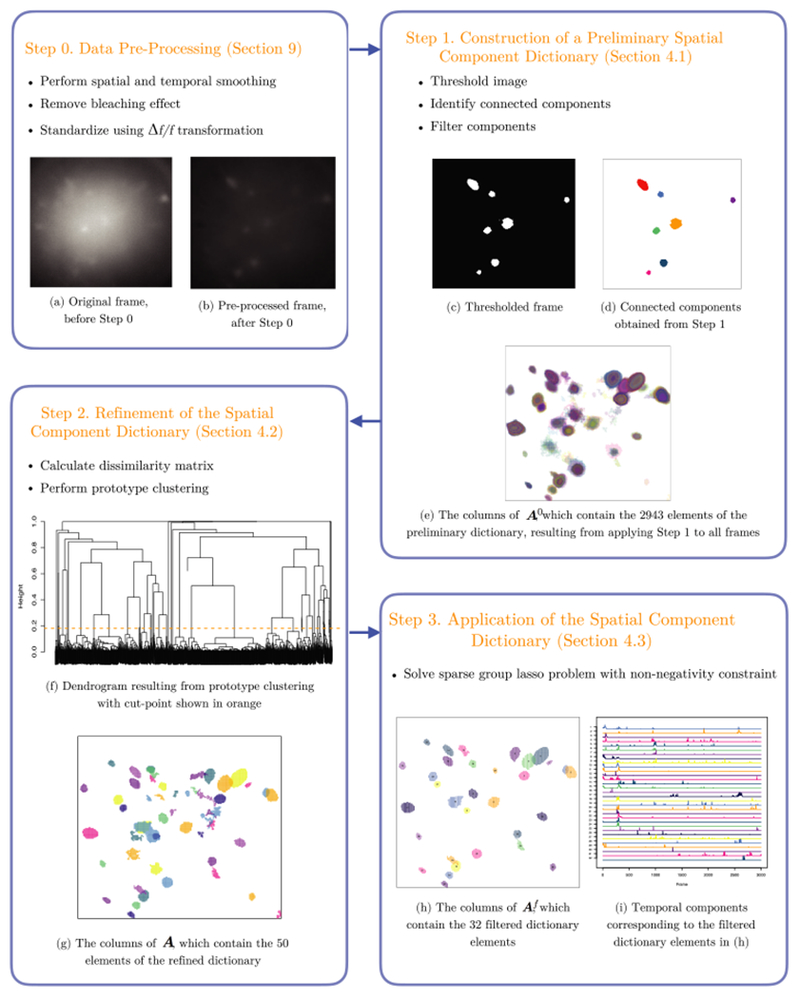
A summary of the SCALPEL procedure, along with the results of applying each step to an example data set with 205 × 226 pixels and 3000 frames, described in the text in Section 4, and analyzed in greater detail in Section 6.2.

Step 0. Data preprocessing: We apply standard preprocessing techniques to smooth the data both temporally and spatially, remove the bleaching effect and calculate a standardized fluorescence. Details are provided in Section 9 of the Supplementary Material [Petersen, Simon and Witten (2018)]. In what follows, Y refers to the calcium imaging data after these three preprocessing steps have been performed.

Step 1. Construction of a preliminary spatial component dictionary: We apply a simple image segmentation procedure to each frame of the video to derive a spatial component dictionary, which is used to construct the matrix ${\mathit{A}}^0\in {ℝ}^{P\times K^0}$ with $a_{j,k}^0=1$ if the jth pixel is contained in the kth preliminary dictionary element and $a_{j,k}^0=0$ otherwise. This is discussed further in Section 4.1.

Step 2. Refinement of the spatial component dictionary: To eliminate redundancy in the preliminary spatial component dictionary, we cluster together dictionary elements that colocalize in time and space. This results in a matrix $\mathit{A}\in {ℝ}^{P\times K}$ where K < K⁰: a_j,k = 1 if the jth pixel is contained in the kth dictionary element, and a_j,k = 0 otherwise. More details are provided in Section 4.2.

Step 3. Application of the spatial component dictionary: We remove dictionary elements corresponding to clusters with few members resulting in a filtered dictionary ${\mathit{A}}^f\in {ℝ}^{P\times K_f}$, which contains a subset of the columns of A. We then estimate the temporal components Z corresponding to the filtered elements of the dictionary by solving a sparse group lasso problem with a nonnegativity constraint. The kth row of $\widehat{\mathit{Z}}$ is the estimated calcium trace corresponding to the kth filtered dictionary element; if this is entirely equal to zero, then the kth dictionary element in A^f has been eliminated. Thus, in this step we finalize our estimates of the neurons’ locations, and as a by-product obtain a crude estimate of the temporal components associated with each estimated neuron. Additional details are in Section 4.3.

Step 1 is applied to each frame separately and thus can be efficiently performed in parallel across the frames of the video. Similarly, parts of Step 0 can be parallelized across frames and across pixels.

Throughout this section we illustrate SCALPEL on an example one-photon calcium imaging data set that has 205 × 226 pixels and 3000 frames sampled at 10 Hz and collected in the lab of ilana Witten at the Princeton Neuroscience institute. Figures 1–8, as well as Figures S1, S2 and S4-S9 in the Supplementary Material [Petersen, Simon and Witten (2018)], involve this data set. In Section 6 we present a more complete analysis of this data set along with analyses of additional data sets.

Fig. 8.

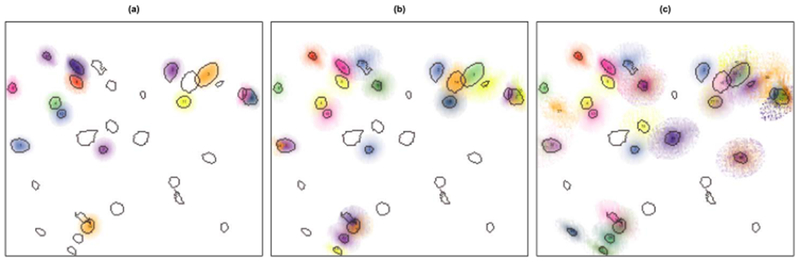
We display the estimated neurons that result from applying a competitor method, CNMF-E [Zhou et al. (2016)], to the calcium imaging video considered in Section 6.2 for (a) the default parameters c_min = 0.85 and α_min = 10, (b) the parameters c_min = 0.6 and α_min = 7 and (c) the parameters c_min = 0.5 and α_min = 3. The variation in darkness of the neurons estimated by CNMF-E is due to the fact that they take on continuous values compared to the binary masks produced by SCALPEL. In each plot the true neurons identified by SCALPEL are outlined in gray. Regardless of the tuning parameters used, CNMF-E yields a substantial number of false positives and false negatives.

4.1. Step 1: Construction of a preliminary spatial component dictionary.

In this step we identify a large set of preliminary dictionary elements, by applying a simple image segmentation procedure to each frame separately:

1. Threshold image: We create a binary image by thresholding the image frame. Figure 3(b) displays the binary image that results from thresholding the frame shown in Figure 3(a).

Fig. 3.

In (a), we display a single frame of the example calcium imaging video after performing the preprocessing described in Section 9 of the Supplementary Material [Petersen, Simon and Witten (2018)]. In (b), we show the binary image that results after thresholding using the negative of the 0.1% quantile of the video’s elements. In (c), we display the seven connected components from the image in (b) that contain at least 25 pixels.

2. Identify connected components: We identify the connected components of the thresholded image using the notion of 4-connectivity. Connected pixels are pairs of white pixels that are immediately to the left, right, above or below one another [Sonka, Hlavac and Boyle (2014)]. Some of these connected components may represent neurons, whereas others are likely to be noise artifacts or snapshots of multiple nearby neurons.

3. Filter components: To eliminate noise, we filter components based on their overall size, width and height. In the examples in this paper, we discard connected components of fewer than 25 or more than 500 pixels, as well as those with a width or height larger than 30 pixels.

We now discuss the choice of threshold used above. After performing Step 0, we expect that the intensities of “noise pixels” (i.e., pixels that are not part of a firing neuron in that frame) will have a distribution that is approximately symmetric and approximately centered at zero. In contrast, nonnoise pixels will have larger values. This implies that the noise pixels should have a value no larger than the negative of the minimum value of Y. Therefore, we threshold each frame using the negative of the minimum value of Y. We also repeat this procedure using a threshold equal to the negative of the 0.1% quantile of Y, as well as with the average of these two threshold values. In Section 5.1, we discuss alternative approaches to choosing this threshold.

The K⁰ connected components that arise from performing Step 1 on each frame, for each of the three threshold values, form a preliminary spatial component dictionary. We use them to construct the matrix ${\mathit{A}}^0\in {ℝ}^{P\times K^0}$. The kth column of A⁰ is a vector of 1’s and 0’s, indicating whether each pixel is contained in the kth preliminary dictionary element.

4.2. Step 2: Refinement of the spatial component dictionary.

We will now refine the preliminary spatial component dictionary obtained in Step 1 by combining dictionary elements that are very similar to each other, as these likely represent multiple appearances of a single neuron. We proceed as follows:

1. Calculate dissimilarity matrix: We use a novel dissimilarity metric, which incorporates both spatial and temporal information, to calculate the dissimilarity between every pair of dictionary elements. More details are given in Section 4.2.1.

2. Perform prototype clustering: We use the aforementioned pair-wise dissimilarities to perform prototype clustering of dictionary elements [Bien and Tibshirani (2011)]. We also identify a representative dictionary element for each cluster. More details are given in Section 4.2.2.

These elements of this refined dictionary make up the columns of the matrix A, which will be used in Step 3 and discussed in Section 4.3.

4.2.1. Choice of dissimilarity metric.

Before performing clustering, we must decide how to quantify similarity between the K⁰ elements of the preliminary dictionary obtained in Step 1. Dictionary elements that correspond to the same neuron are likely to have: (i) similar spatial maps and (ii) similar average fluorescence over time. To this end, we construct a dissimilarity metric that leverages both spatial and temporal information.

We define $p_{i,j}={({\mathit{a}}_{\cdot ,i}^0)}^{⊺}{\mathit{a}}_{\cdot ,j}^0$, the number of pixels shared between the ith and jth dictionary elements. When i = j, p_i,i is simply the number of pixels in the ith dictionary element. We then define the spatial dissimilarity between the ith and jth dictionary elements to be

$$d_{i,j}^s=1-\frac{p_{i,j}}{\sqrt{p_{i,i}{p}_{j,j}}}.$$ (3)

Thus, $d_{i,j}^s=1$ if and only if the ith and jth elements are nonoverlapping in space, and $d_{i,j}^s=0$ if and only if they are identical. Note that $d_{i,j}^s$ is known as the cosine dissimilarity or Ochiai coefficient [Gower (2006)].

We now define the matrix Y^B, a thresholded version of the preprocessed data matrix Y (obtained in Step 0), with elements of the form

$${[{\mathit{Y}}^B]}_{j,k}=\{\begin{array}{cc}{[\mathit{Y}]}_{j,k}\hfill & \text{if}{[\mathit{Y}]}_{j,k}>-{\text{quantile}}_{0.1\%}(\mathit{Y}),\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$

Note that when a value other than the negative of the 0.1% quantile is used for image segmentation in Step 1, this value can also be used to threshold Y above. The temporal dissimilarity between the ith and jth dictionary elements is defined as

$$d_{i,j}^t=1-\frac{{({\mathit{a}}_{\cdot ,i}^0)}^{⊺}{\mathit{Y}}^B{({\mathit{Y}}^B)}^{⊺}{\mathit{a}}_{\cdot ,j}^0}{{\parallel ({\mathit{Y}}^B){}^{⊺}{\mathit{a}}_{\cdot ,i}^0\parallel }_2{\parallel ({\mathit{Y}}^B){}^{⊺}{\mathit{a}}_{\cdot ,j}^0\parallel }_2}.$$ (4)

[Note that the elements of ${({\mathit{Y}}^B)}^{⊺}{\mathit{a}}_{\cdot ,i}^0\in {ℝ}^T$ represent the thresholded fluorescence of each time frame summed over all pixels in the ith preliminary dictionary element.] We threshold Y before computing this dissimilarity, because: (i) we are interested in the extent to which there is agreement between the peak fluorescences of the ith and jth preliminary dictionary elements; and (ii) the sparsity induced by thresholding is computationally advantageous.

Finally, the overall dissimilarity is

$$d_{i,j}=\omega d_{i,j}^s+(1-\omega )d_{i,j}^t,$$ (5)

where ω ∈ [0 , 1] controls the relative weightings of the spatial and temporal dissimilarities. We use ω = 0.2 to obtain the results shown throughout this paper. While we wish to incorporate the spatial and temporal information equally, the magnitudes of the two dissimilarity measures translate to different degrees of similarity. That is, a pair of neurons will tend to have a larger spatial dissimilarity than temporal dissimilarity. Therefore, we weight the temporal information more heavily. A detailed justification for ω = 0.2 is given in Section 10 of the Supplementary Material [Petersen, Simon and Witten (2018)]; furthermore, a sensitivity analysis for the value of ω is presented in Section 7.3.

In Figure 4 we illustrate pairs of preliminary dictionary elements with various dissimilarities for ω = 0.2.

Fig. 4.

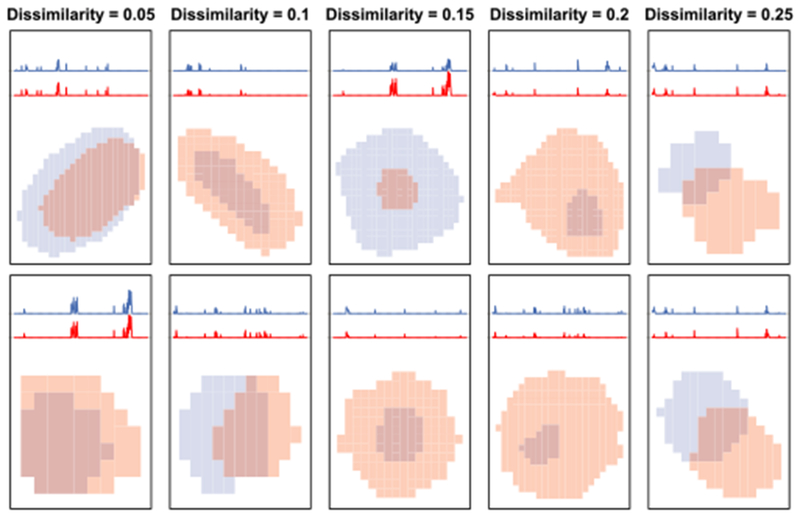
Each column displays two pairs of preliminary dictionary elements with overall dissimilarities, as defined in (5), of 0.05, 0.1, 0.15, 0.2 and 0.25. For each preliminary dictionary element, the average thresholded fluorescence over time and the (zoomed-in) spatial map are shown. These results are based on the example calcium imaging video.

4.2.2. Prototype clustering.

We now consider the task of clustering the elements of the preliminary dictionary. To avoid prespecifying the number of clusters and to obtain solutions that are nested as the number of clusters is varied, we opt to use hierarchical clustering [Hastie, Tibshirani and Friedman (2009)].

In particular we use prototype clustering, proposed in Bien and Tibshirani (2011), with the dissimilarity given in (5). Prototype clustering guarantees that at least one member of each cluster has a small dissimilarity with all other members of the cluster. To represent each cluster using a single dictionary element, we choose the member with the smallest median dissimilarity to all of the other members. Then we combine the representatives of the K clusters to obtain a refined spatial component dictionary. We can represent this refined dictionary with the matrix $\mathit{A}\in {ℝ}^{P\times K}$, defined as follows: a_j,k = 1 if the jth pixel is contained in the kth cluster’s representative, and a_j,k = 0 otherwise.

We apply prototype clustering to the example calcium imaging data set using the R package protoclust [Bien and Tibshirani (2015)]. The resulting dendrogram is in Figure 5(a). In Section 5.2, we discuss choosing the cutpoint, or height, at which to cut the dendrogram. Results for different cutpoints are displayed in Figures 5(b)–(e). An additional example is provided in Section 11 of the Supplementary Material [Petersen, Simon and Witten (2018)], and a sensitivity analysis indicating that the results of SCALPEL are insensitive to the choice of cutpoint is presented in Section 7.3.

Fig. 5.

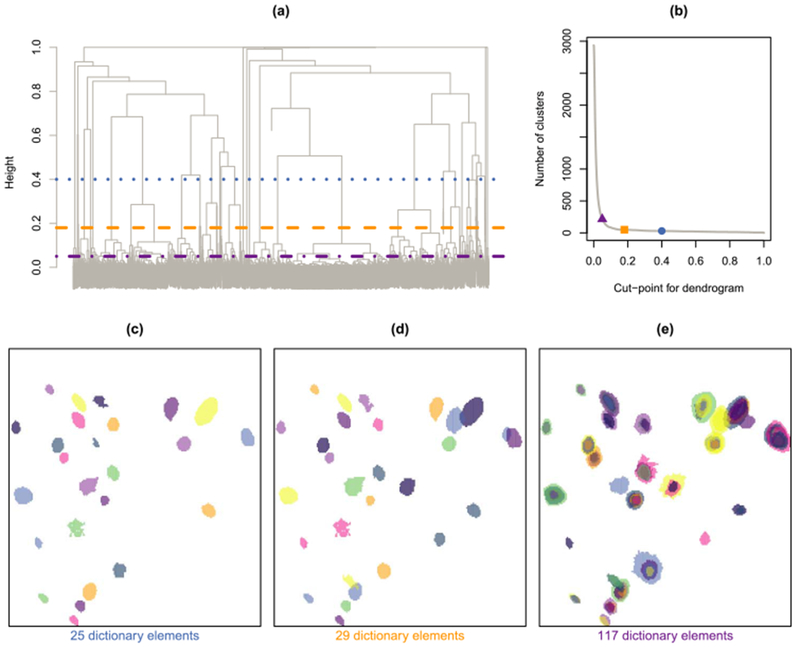
In (a), we display the dendrogram that results from applying prototype clustering to the example calcium imaging data set. Three different cutpoints are indicated: 0.05 (), 0.18 () and 0.4 (). In (b), we display the number of clusters that result from these three cutpoints. In (c)–(e), we show the refined dictionary elements that result from using these three cutpoints. For simplicity, we only display dictionary elements corresponding to clusters with at least five members.

4.3. Step 3: Application of the spatial component dictionary.

In this final step we optionally filter the K refined dictionary elements and then estimate the temporal components associated with this filtered dictionary. We recommend performing the optional filtering of the dictionary elements based on the number of members in the cluster, as clusters with a larger number of members are more likely to be true neurons. This filtering process is discussed more in Section 12 of the Supplementary Material [Petersen, Simon and Witten (2018)]. After this filtering we construct the filtered dictionary, ${\mathit{A}}^f\in {ℝ}^{P\times K_f}$, which contains the retained columns of A.

We estimate the temporal components associated with the K_f elements of the final dictionary by solving a sparse group lasso problem with a nonnegativity constraint,

$$\underset{\mathit{Z}\in {ℝ}^{K_f\times T},\mathit{Z}\ge 0}{\text{minimize}}\frac{1}{2}{\parallel \mathit{Y}-{\tilde{\mathit{A}}}^f\mathit{Z}\parallel }_F^2+\lambda \alpha \sum _{k=1}^{K_f}{\parallel {\mathit{z}}_{k,\cdot }\parallel }_1+\lambda (1-\alpha )\sum _{k=1}^{K_f}{\parallel {\mathit{z}}_{k,\cdot }\parallel }_2,$$ (6)

where α ∈ [0, 1] and λ > 0 are tuning parameters, and ${\tilde{\mathit{A}}}^f$ is defined as ${\tilde{\mathit{a}}}_{\cdot ,k}^f={\mathit{a}}_{\cdot ,k}^f∕{\parallel {\mathit{a}}_{\cdot ,k}^f\parallel }_2^2$. This scaling of A^f is justified in Section 13.3 of the Supplementary Material [Petersen, Simon and Witten (2018)].

The first term of the objective in (6) encourages the spatiotemporal factorization (1) to fit the data closely. The two penalty terms in (6) were specifically chosen to accomplish two goals:

• Temporal components should be nonzero for a small number of frames: The second term in (6) is a lasso penalty on each of the temporal components. A lasso penalty on a vector encourages a subset of the individual elements of the vector to be exactly zero [Tibshirani (1996)]. In our application this element-wise sparsity translates to each neuron being estimated to be active in a small number of frames, which fits with the scientific understanding of the activity of neurons.

• Unneeded neurons should be removed: The third term in (6) is a group lasso penalty on each of the temporal components. A group lasso penalty on a vector encourages the entire vector to equal zero [Yuan and Lin (2006)]. This group-wise sparsity on the temporal components leads to selection of dictionary components. For λ(1 − α) sufficiently large, only a subset of the K_f elements in the filtered dictionary will have a nonzero temporal component. This penalty is especially useful for removing any dictionary elements that are a combination of neighboring neurons; we elaborate on this point in Section 13.5 of the Supplementary Material [Petersen, Simon and Witten (2018)].

In Section 13 of the Supplementary Material [Petersen, Simon and Witten (2018)], we discuss the technical details related to solving (6). We summarize the practical implications of these results here:

• Feasible computational time: We show that solving (6) is decomposable into spatially overlapping groups of neurons. Furthermore, in many cases a closed-form solution is available. These two results greatly reduce the computational time required in Step 3. See Sections 13.1 and 13.2 of the Supplementary Material [Petersen, Simon and Witten (2018)] for details.

• Scaling of the columns of A^f : In Section 13.3 of the Supplementary Material [Petersen, Simon and Witten (2018)], we discuss how to scale the columns of A^f, so that the optimization problem (6) is invariant to the sizes of the dictionary elements.

• Ease of tuning parameter selection: Our results in Section 13.4 of the Supplementary Material [Petersen, Simon and Witten (2018)] allow us to determine the largest value of λ to consider when selecting λ by cross-validation.

• Zeroing out of double neurons: Some of the preliminary dictionary elements in Step 1 may be double neurons, that is, elements that are a combination of two neighboring neurons that happened to be active during the same frame. In Step 2, these double neurons are unlikely to cluster with elements representing either of the individual neurons they represent, and thus these double neurons may remain in the filtered set of dictionary elements, A^f, used in Step 3. Fortunately, as detailed in Section 13.5 of the Supplementary Material [Petersen, Simon and Witten (2018)], the group lasso penalty in (6) zeroes out these double neurons.

5. Tuning parameter selection.

SCALPEL involves a number of tuning parameters:

• Step 1: Quantile thresholds for image segmentation.

• Step 2: Cutpoint for dendrogram and dissimilarity weight ω.

• Step 3: λ and α for equation (6).

However, in marked contrast to competing methods (such as matrix factorization approaches) that involve a number of interdependent tuning parameter values, the tuning parameters in SCALPEL can be chosen independently at each step and are very interpretable to the user. We provide recommendations for fixed default values for all but the choice of λ in Step 3. We recommend that users first run SCALPEL using the default values. Then, if needed to accommodate differences between labs, experimental conditions, brain regions or calcium indicators, those default values can be modified. Furthermore, a sensitivity analysis showing that SCALPEL is robust to modest changes in the values of the tuning parameters will be presented in Section 7.3.

We note that in a typical statistical problem, tuning parameters must be carefully chosen using cross-validation or a validation set approach to avoid overfitting. By contrast, the goal of SCALPEL is to identify neurons in the video at hand rather than in a future video. Furthermore, true positives and false positives can be assessed by visual inspection on a frame-by-frame basis. Thus, tuning parameter selection in SCALPEL is more straightforward than in a typical statistical problem.

5.1. Tuning parameters for Step 1.

The tuning parameters in Step 1 are the quantile thresholds used in image segmentation. In analyzing the example video considered thus far in this paper, we used three different threshold values to segment the video: the negative of the minimum value of Y, the negative of the 0.1% quantile of Y and the average of these two values. In principle, these quantile thresholds may need to be adjusted; however, it is straightforward to select reasonable thresholds by visually examining a few frames and their corresponding binary images, as in Figures 3(a) and (b). Furthermore, the results of SCALPEL are insensitive to the exact values of these threshold values, as they serve only to generate a preliminary dictionary. We illustrate the robustness of the results to modest changes in the values of the quantile thresholds in Section 7.3 and Section 14 of the Supplementary Material [Petersen, Simon and Witten (2018)].

5.2. Tuning parameters for Step 2.

In Step 2, we must choose a height h ∈ [0, 1] at which to cut the hierarchical clustering dendrogram, as shown in Figure 5(a). Fortunately, the cutpoint has an intuitive interpretation which can help guide our choice. If we cut the dendrogram at a height of h, then each cluster will contain an element of the preliminary dictionary that has dissimilarity no more than h with each of the other members of that cluster. Figure 4 displays pairs of preliminary dictionary elements with a given dissimilarity. We have used a fixed cutpoint of 0.18 to obtain all of the results shown in this paper. An investigator can either choose a cutpoint by visual inspection of the resulting refined dictionary elements, or can simply use a fixed cutpoint, such as 0.18. We recommend choosing a outpoint less than the dissimilarity weight ω in (5), as this guarantees that the dictionary elements within each cluster will have spatial overlap. We recommend using ω = 0.2, as discussed in Section 10 of the Supplementary Material [Petersen, Simon and Witten (2018)]. Furthermore, in Section 7.3 and Section 14 of the Supplementary Material we show that the results are robust to modest changes in the values of ω and the cutpoint.

5.3. Tuning parameters for Step 3.

In Step 3, we must choose values of λ and α in (6). We suggest using a fixed value of α = 0.9, which is known to work well in settings like this with a high level of element-wise sparsity [Simon et al. (2013)]. To select the value of λ, we use cross-validation. We illustrate this approach in Section 6, and provide further details in Section 13.6 of the Supplementary Material [Petersen, Simon and Witten (2018)]. Alternatively, both α and λ can be chosen by cross-validation on a two-dimensional grid.

6. Results for calcium imaging data.

In this section we compare SCALPEL’s performance to that of competitor methods on three calcium imaging data sets. In Section 6.1, we detail how we assess performance in this setting. We consider one-photon and two-photon calcium imaging data sets in Sections 6.2 and 6.3 respectively. In Section 6.4, we compare the running times for the various methods. Additional results for these three calcium imaging videos are available at www.ajpete.com/software.

6.1. Assessment of performance.

Given that we are in an unsupervised setting in which both A and Z are unknown, performance cannot be assessed in a traditional manner, such as cross-validation error. Instead, we will assess whether identified neurons are true positives or false positives by visually inspecting a small number of frames in which they are estimated to be active. In SCALPEL, these active frames can be chosen in one of two ways: (i) the frames in which the element was originally derived in Step 1 of SCALPEL, or (ii) the frames for which the corresponding temporal component is estimated to be the largest in Step 3 of SCALPEL. We can then visually examine these frames to see if the fluorescence is consistent with the presence of a neuron.

We now briefly comment on the use of visual inspection to determine whether an estimated neuron is a true or false positive. We believe that if the goal were to identify neurons in a single calcium imaging frame, then visual inspection would be the gold standard. However, while it is feasible to identify neurons in a single frame by visual inspection, it would not be possible to identify neurons in an entire movie by visual inspection, because a movie consists of O(10⁵) frames, and because of difficulties in aligning neurons between frames (i.e., determining whether two neurons identified in different frames are in fact the same neuron). Thus, while we can confirm or disprove the presence of a given potential neuron by visual inspection, an automated procedure such as SCALPEL is needed to estimate neurons throughout the entire video.

6.2. Application to one-photon calcium imaging data.

We now present the results Section 4. This one-photon video, collected by the lab of Ilana Witten at the Princeton Neuroscience Institute, has 3000 frames of size 205 × 226 pixels sampled at 10 Hz. We used the default tuning parameters to analyze this video. Using from applying SCALPEL to the calcium imaging video used as an example in the default quantile thresholds that corresponded to thresholds of 0.0544, 0.0743 and 0.0942, Step 1 of SCALPEL resulted in a preliminary dictionary with 2943 elements, which came from 997 different frames of the video. Using a cutpoint of 0.18 in Step 2 resulted in a refined dictionary that contained 50 elements. In Step 3, we discarded the 21 components corresponding to clusters with fewer than five preliminary dictionary elements assigned to them and then fit the sparse group lasso model with α = 0.9 and λ = 0.0416, which was chosen using the validation set approach described in Section 13.6 of the Supplementary Material [Petersen, Simon and Witten (2018)]. This resulted in 29 estimated neurons. The results are shown in Figures 6(a) and (b). In Figure 6(c), we compare the estimated neurons to a pixel-wise variance plot of the calcium imaging video. We expect pixels that are part of true neurons to have higher variance than pixels not associated with any neurons. Indeed, we see that many of the estimated neurons coincide with regions of high pixel-wise variance. However, some estimated neurons are in regions with low variance. Examining the frames from which the dictionary elements were derived can provide further evidence as to whether an estimated neuron is truly a neuron. For example, in Figure 7(a) we show that one of the estimated neurons in a low-variance region does indeed appear to be a true neuron, while Figure 7(b) shows evidence that one of the estimated neurons (element 22 in Figure 6) is not truly a neuron. Repeating this process for all of the estimated neurons, we see that element 22 in Figure 6 is the only estimated neuron that does not appear to be a true neuron.

Fig. 6.

In (a), we plot the spatial maps for the 29 elements of the final dictionary for the calcium imaging video considered in Section 6.2. In (b), we plot their estimated intracellular calcium concentrations corresponding to λ chosen via a validation set approach. In (c), we compare the outlines of the 29 dictionary elements from (a) to a heat map of the pixel-wise variance of the calcium imaging video. That is, we plot the variance of each pixel over the 3000 frames with whiter points indicating higher variance.

Fig. 7.

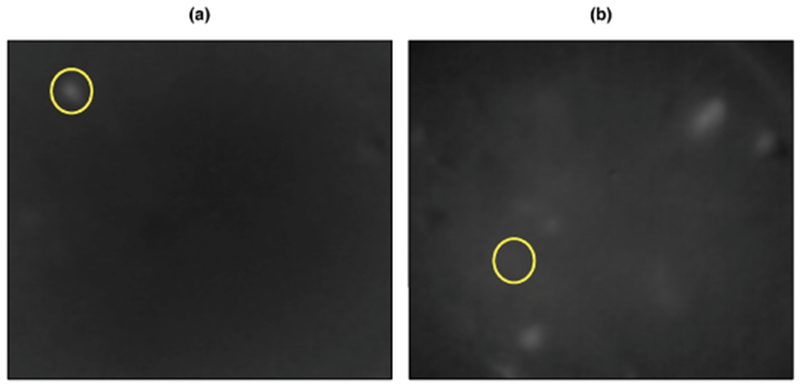
In (a), we see that one of the estimated neurons in a low-variance region in Figure 6(c) does correspond to a true neuron. In (b), we see a frame in which one of the estimated neurons was identified, though there does not appear to be a true neuron.

We compare the performance of SCALPEL to that of CNMF-E [Zhou et al. (2016)], a proposal for the analysis of one-photon data that takes a matrix factorization approach as described in Section 3. The tuning parameters we consider are those noted in Algorithm 1 of Zhou et al. (2016)—the average neuron size r and the width of the 2D Gaussian kernel σ, which relate to the spatial filtering, and the minimum local correlation c_min and the minimum peak-to-noise ratio α_min, which relate to initializing neurons. We choose r = 11 in accordance with the average diameter of the neurons identified using SCALPEL. The default values suggested for the other tuning parameters are σ = 3, c_min = 0.85 and α_min = 10. We present the results for these default values in Figure 8(a). Only 14 of the 29 neurons identified using SCALPEL were found by CNMF-E using these default parameters. To increase the number of neurons found, we consider lower values for c_min and α_min. We fit CNMF-E for all combinations of c_min = 0.5, 0.6,0.7 and α_min = 3,5, 7. To assess the performance of these nine combinations of tuning parameters, we reviewed each estimated neuron for evidence of whether or not it appeared to be a true neuron by visually inspecting the frames in which the neuron was estimated to be most active. In Figure 8(b), we present the results, chosen from the nine combinations of tuning parameter values considered, that has the smallest number of false positive neurons (i.e., estimated neurons that are noise or duplicates of other estimated neurons). These results consist of 24 estimated neurons; 21 elements correspond to neurons identified using SCALPEL. One element [element 23 in Figure 8(b)] corresponds to a neuron not identified using SCALPEL, and two elements [elements 22 and 24 in Figure 8(b)] appear to be duplicates of other estimated neurons. In Figure 8(c), we present the results, chosen from the nine combinations of tuning parameter values considered, with the highest number of true positive neurons (i.e., neurons that were identified by CNMF-E that appear to be real). These results consist of 41 estimated neurons; 25 elements correspond to neurons identified using SCALPEL. Two elements [elements 27 and 34 in Figure 8(c)] correspond to neurons not identified using SCALPEL, 11 elements appear to be duplicates of other estimated neurons and three elements [elements 39, 40 and 41 in Figure 8(c)] appear to be noise. So while this pair of tuning parameter values resulted in the identification of most of the neurons, it also resulted in a number of false positives. Some of the estimated neurons in Figure 8(c) are large and diffuse making them difficult to interpret.

6.3. Application to two-photon calcium imaging data.

We now illustrate SCALPEL on two calcium imaging videos released by the Allen Institute as part of their Allen Brain Observatory. In addition to releasing the data, the Allen Institute also made available the spatial masks for the neurons they identified in each of the videos, using their own in-house software for this task. Thus, we compare the estimated neurons from SCALPEL to those from the Allen Institute analysis. The two-photon videos we consider are those from experiments 496934409 and 502634578. The videos contain 105,698 and 105,710 frames respectively, of size 512 × 512 pixels. In their analyses, the Allen Institute downsampled the number of frames in each video by a factor of eight; we did the same in our analysis. For these videos we found that using a value slightly smaller than the negative of the 0.1% quantile for the smallest threshold value in Step 0 was preferred based on visual inspection of the thresholding via the plotThresholdedFrame function in the SCALPEL R package. Otherwise, default values were used for all of the tuning parameters.

6.3.1. Allen Brain Observatory experiment 496934409.

Using thresholds of 0.250, 0.423 and 0.596, Step 1 of SCALPEL resulted in a preliminary dictionary with 68,630 elements, which came from 11,739 different frames of the video. After refining the dictionary via clustering in Step 2, we were left with 544 elements. In the analysis by the Allen Institute, neurons near the boundary of the field of view were eliminated from consideration. Thus we filtered out 259 elements that contained pixels outside of the region considered by the Allen Institute. Of the remaining 285 elements, 32 of these were determined to be dendrites, 131 were small elements not of primary interest and 10 were duplicates of other neurons found. Thus in the end, we identified the same 87 neurons that the Allen Institute did in addition to 25 potential neurons not identified by the Allen Institute. In Figure 9(a), we show the neurons identified by both SCALPEL and the Allen Institute. In Figure 9(b), we show the potential neurons uniquely identified by SCALPEL, along with evidence that they are, in fact, neurons in Figure 9(c).

Fig. 9.

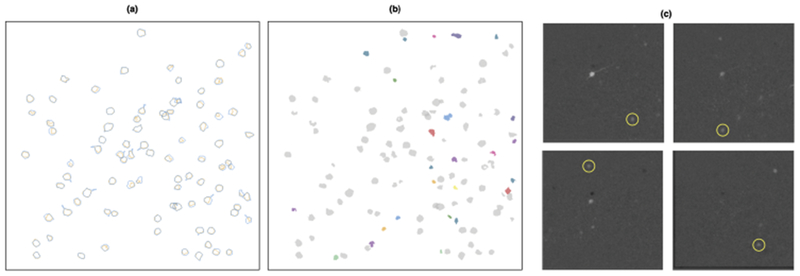
We present the results for the calcium imaging video analyzed in Section 6.3.1. In (a), we plot the outlines of the neurons identified by the Allen Institute in blue, along with the outlines of the corresponding SCALPEL neurons in orange. In (b), we plot the 25 potential neurons uniquely identified by SCALPEL in color, along with the SCALPEL neurons also identified by the Allen Institute in gray. In (c), we provide evidence for four of the 25 unique neurons. Similar plots for all of the potential neurons uniquely identified by SCALPEL are available at www.ajpete.com/software.

6.3.2. Allen Brain Observatory experiment 502634578.

Using thresholds of 0.250, 0.481 and 0.712, Step 1 of SCALPEL resulted in a preliminary dictionary with 84,996 elements, which came from 12,272 different frames of the video. After refining the dictionary via clustering in Step 2, we were left with 1297 elements. Once again, we filtered out the 390 elements that contained pixels outside of the region considered by the Allen Institute. Of the remaining 907 elements, 22 of these were determined to be dendrites, 382 were small elements not of primary interest and 39 were duplicates of other neurons found. Thus in the end, we identified 370 of the 375 neurons that the Allen Institute did, in addition to 94 potential neurons not identified by the Allen Institute. Note that the five neurons identified by the Allen Institute, but not SCALPEL, each appear to be combinations of two neurons. SCALPEL did identify the 10 individual neurons of which these five Allen Institute neurons were a combination. In Figure 10(a), we show the neurons jointly identified by SCALPEL and the Allen Institute. In Figure 10(b), we show the potential neurons uniquely identified by SCALPEL, along with evidence that they are, in fact, real neurons in Figure 10(c).

Fig. 10.

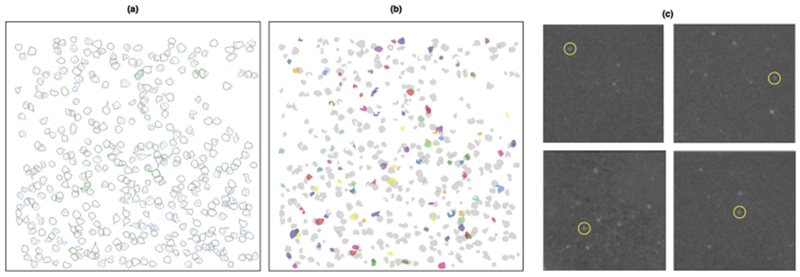
We present the results for the calcium imaging video analyzed in Section 6.3.2. In (a), we plot the outlines of the neurons identified by the Allen Institute in blue, along with the outlines of the corresponding SCALPEL neurons in orange. Those shown in green are the Allen Institute neurons that appear to actually be a combination of two neurons. In (b), we plot the 94 potential neurons uniquely identified by SCALPEL in color, along with the SCALPEL neurons also identified by the Allen Institute in gray. In (c), we provide evidence for four of the 94 unique neurons. Similar plots for all of the potential neurons uniquely identified by SCALPEL are available at www.ajpete.com/software.

6.4. Timing results.

All analyses were run on a Macbook Pro with a 2.0 GHz Intel Sandy Bridge Core i7 processor. Running the SCALPEL pipeline on the one-photon data presented in Section 6.2 took 6 minutes for Step 0 and 2 minutes for Steps 1–3. Running CNMF-E on the one-photon data presented in Section 6.2 took 5,5 and 7 minutes for the analyses with a single set of tuning parameters presented in Figures 8(a), 8(b) and 8(c) respectively. Running the SCALPEL pipeline on the two-photon data presented in Section 6.3.1 took 12.85 hours for Step 0, 2.33 hours for Step 1, and 0.42 hours for Step 2. Running the SCALPEL pipeline on the two-photon data presented in Section 6.3.2 took 12.50 hours for Step 0, 2.55 hours for Step 1 and 0.43 hours for Step 2.

Further computational gains could be made by parallelizing the implementation of SCALPEL Steps 0 and 1. Also, recall that SCALPEL’s most time-intensive step, Step 0, is only ever run a single time for each data set regardless of whether the user wishes to fit SCALPEL for different tuning parameters.

7. Results for simulated calcium imaging data.

In this section we apply SCALPEL and CNMF-E [Zhou et al. (2016)] to simulated calcium imaging data to assess performance under a range of noise settings. In Section 7.1, we discuss the process of generating the data and assessing performance. In Section 7.2, we present the results comparing SCALPEL to CNMF-E. In Section 7.3, we consider the impact on performance of using nondefault tuning parameters.

7.1. Data generation and performance metrics.

We generate simulated calcium imaging videos with 200 × 200 pixels and 1000 frames by combining the true signal with independent noise and spatially correlated noise, that is, Y = AZ + E_in + E_sc, using the notation from (1). In each replicate the true A matrix includes 100 neurons, whose shapes are based on actual calcium imaging data and are available in the ADINA toolbox [Diego et al. (2013)]. The calcium traces that make up the true Z are constructed to have 1–3 spikes per neuron, with each spike producing a nonzero calcium concentration for a period of 50 frames. The elements are E_in are independent Uniform draws. To construct the spatially correlated noise E_sc, we generate a spatially correlated two-dimensional image (i.e., a random field) whose intensity peaks and recedes over a span of 75 frames. There are 20 of these spatially correlated noise patterns in each video. We vary the strength of the noise patterns to explore different signal to noise ratios. We define the signal to noise ratio as the ratio of the peak intensity of the spiking neurons to the peak absolute intensity of the noise. We consider two noise scenarios. In the first we keep the signal to independent noise ratio fixed at 1.5 and consider values of 1, 1.5 and 2 for the signal to spatially correlated noise ratio. In the second we keep the signal to spatially correlated noise ratio fixed at 1.5 and consider values of 0.5, 1, 1.5 and 2 for the signal to independent noise ratio. In order to understand the difficulty of identifying neurons in this simulated data, example frames from each of these noise scenarios are shown in Figure 11. Further details needed to replicate the generation of this simulated data are provided in the R code available at www.ajpete.com/software.

Fig. 11.

We illustrate the various noise scenarios that we consider for the simulated calcium imaging data described in Section 7.1. We vary the signal to spatially correlated noise (SSCN) ratio and the signal to independent noise (SIN) ratio. We show the simulated neurons truly active during a particular frame, along with the simulated data for that frame for each of the noise scenarios. The top row of frames has a variable strength of spatially correlated noise with a fixed strength of independent noise (SIN = 1.5), and the bottom row of frames has a variable strength of independent noise with a fixed strength of spatially correlated noise (SSCN = 1.5).

We measure performance in terms of sensitivity, defined as the percent of true neurons detected, and precision, defined as the percent of neurons detected that are true neurons. We consider a detected neuron to be a match to a true neuron when: (i) the pixels of the detected neuron contain at least 50% of the true neuron’s total intensity, and (ii) no more than 20% of the detected neuron’s intensity is contained in pixels not belonging to the true neuron. When more than one detected neuron matches these criteria for a true neuron, we match the detected neuron that captures the highest percentage of the true neuron’s intensity. We chose these fairly liberal matching criteria as to not put the competitor method, CNMF-E, at a disadvantage, since it tends to estimate more diffuse neuron masks than SCALPEL.

7.2. Comparison of methods.

We applied SCALPEL and CNMF-E [Zhou et al. (2016)] to the simulated calcium imaging data. For all noise scenarios SCALPEL was fit using the default tuning parameter values. We found that the default tuning parameter values performed poorly for the competitor method, CNMF-E. Thus we fit CNMF-E for all combinations of c_min = 0.5,0.6, 0.7,0.85 and α_min = 3, 5,7,10 on five replicates of data for each noise scenario. For each noise scenario, we choose the tuning parameter combination that had the highest sum of the average sensitivity and average precision such that the average sensitivity was within 5% of the maximum average sensitivity. We then used this selected tuning parameter combination to analyze the remaining replicates of data for that noise scenario. Note that we used knowledge of the true neurons to select the tuning parameter values for CNMF-E so that we can compare SCALPEL’s performance to the best possible performance of CNMF-E in these settings. By contrast, no knowledge of the true neurons was used when applying SCALPEL, for which we just used the default tuning parameter values.

In Figure 12, we present the performance of SCALPEL and CNMF-E on the simulated calcium imaging data. In Figure 12(a), we see that sensitivity of SCALPEL improves as the strength of the spatially correlated noise is reduced, while the precision is fairly constant. Both the sensitivity and precision of CNMF-E improve as the strength of the spatially correlated noise is reduced. However, SCALPEL outperforms CNMF-E on both metrics under all noise scenarios. In Figure 12(b), we see that the sensitivity of SCALPEL is fairly constant as the strength of the independent noise is varied. However, the precision of SCALPEL drops as the strength of independent noise is reduced. While this might seem counterintuitive at first, the strong independent noise effectively counteracts the spatially correlated noise, since the former prevents spatial noise artifacts from being misconstrued as neurons. With the lowest strength of independent noise, CNMF-E has slightly higher precision, but still lower sensitivity than SCALPEL.

Fig. 12.

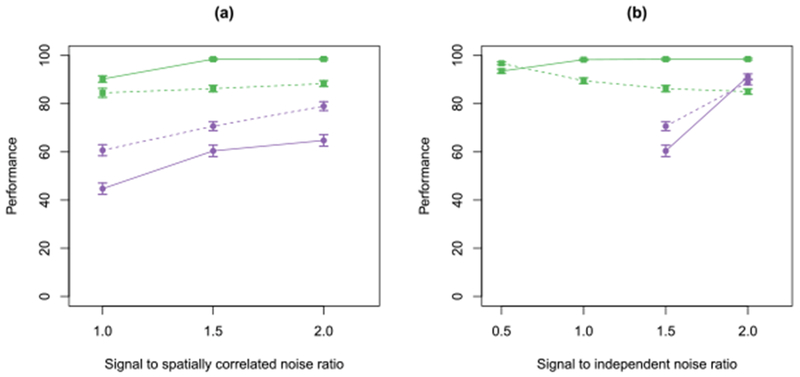
We illustrate the performance of SCALPEL () and CNMF-E [Zhou et al. (2016)] () in terms of the average sensitivity (percent of true neurons detected; shown as a solid line) and precision (percent of neurons detected that are true neurons; shown as a dashed line) for the simulated calcium imaging data described in Section 7.1. For both, 95% confidence intervals are shown. In (a), we consider the performance for a fixed signal to independent noise ratio of 1.5 and varying signal to spatially correlated noise ratio. In (b), we consider the performance for a fixed signal to spatially correlated noise ratio of 1.5 and varying signal to independent noise ratio. Note that CNMF-E was unable to initialize neurons in the presence of a high amount of independent noise, so the CNMF-E results are omitted for ratios of 0.5 and 1 in (b).

7.3. Sensitivity of results to tuning parameter selection.

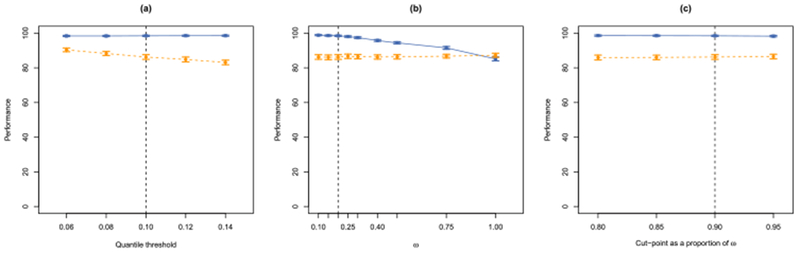
In Section 7.2, we presented the results for SCALPEL with all tuning parameters set to their default values. To determine how sensitive the results are to changes in the tuning parameters, we now consider the performance of SCALPEL for varied tuning parameter selections. In particular, we investigate the impact of modifying the quantile threshold in Step 1, the dissimilarity weight ω in Step 2, and the dendrogram cutpoint in Step 2. The panels of Figure 13 plot the sensitivity and precision of SCALPEL when one of the tuning parameters is varied and the others are kept fixed at their default values. Note that the results presented are for a signal to spatially correlated noise ratio of 1.5 and a signal to independent noise ratio of 1.5. In Figure 13(a), we see that a high sensitivity is maintained regardless of the quantile threshold. Precision is slightly higher when a lower quantile threshold is used. In Figure 13(b), we see that the choice of ω does not have an impact on the precision, but choosing a large ω near 1 results in finding a lower percentage of the true neurons. Recall that when ω equals 1, only spatial information is used to cluster the preliminary dictionary elements. Without the benefit of temporal information, we are likely to erroneously cluster together spatially overlapping neurons, resulting in reduced sensitivity. In Figure 13(c), we see that the performance is robust to modest variations in the dendrogram cutpoint. These simulations illustrate that the performance of SCALPEL does not diminish with modest variations in the values of the tuning parameters. In Section 14 of the Supplementary Material [Petersen, Simon and Witten (2018)], we investigate the robustness of the results to modest changes in the tuning parameters for the one-photon data analyzed in Section 6.2.

Fig. 13.

We present the sensitivity of SCALPEL’s performance to changes in the tuning parameters for the simulated calcium imaging data described in Section 7.1. In all panels, we plot the average sensitivity () and precision (), along with 95% confidence intervals, as a function of the tuning parameter value. The dashed line indicates the default value of the tuning parameter. In (a), we consider the value of the quantile threshold used to construct the preliminary dictionary in Step 1. In (b), we consider the value of the dissimilarity weight ω in Step 2. In (c), we consider the value of the dendrogram cutpoint in Step 2, as a proportion of ω = 0.2.

8. Discussion.

We have presented SCALPEL, a method for identifying neurons from calcium imaging data. SCALPEL takes a dictionary learning approach. We segment the frames of the calcium imaging video to construct a large preliminary dictionary of potential neurons, which is then refined through the use of clustering using a novel dissimilarity metric that leverages both spatial and temporal information. We then solve a sparse group lasso problem with a nonnegativity constraint to obtain a final estimate of the neurons in the data, and to obtain a crude estimate of the calcium concentrations for these neurons.

Future work could consider alternative ways of deriving a preliminary dictionary in Step 1. Currently, we perform image segmentation via thresholding with multiple quantiles. This approach assumes that active neurons will have brightness, relative to their baseline fluorescence levels, that is within the range of our image segmentation threshold values. In practice there is evidence that some neurons have comparatively lower fluorescence following spiking, which presents a challenge for optimal identification. Though SCALPEL performed well on the one-photon calcium imaging video we considered in Section 6.2, other one-photon videos may have more severe background effects. If this is the case, it may be desirable to incorporate more sophisticated modeling of the background noise, like that employed in Zhou et al. (2016). Additionally, in future work we could modify Step 3 of SCALPEL to make use of a more refined model for neuron spiking, as in Friedrich, Zhou and Paninski (2017), Vogelstein et al. (2010), Jewell and Witten (2018).

Our SCALPEL proposal is implemented in the R package scalpel, which is available on CRAN. A vignette illustrating how to use the package, and code to reproduce all results presented in this paper, are available at ajpete.com/software.