Abstract
Favorable steric and electrostatic fit of a ligand to a receptor is of central interest in theoretical drug design. This paper considers the effects of non-protic solvents, in comparison with the gas phase, on the preferred conformation of the XCYCH3 moiety of simple aliphatic esters and heterocyclic methyl ethers with all combinations of the X and Y atoms as oxygen and sulfur. An IEF-PCM/B97D/aug-cc-pv(t+d)z continuum dielectric solvent study in chloroform and acetonitrile explores the through-space polarization effect of the environment on the conformational preference, not affected by possible solute-solvent hydrogen bond formation. The inherently favored structure for the present molecules is important, since the hypothetical oxygen and sulfur lone-pairs point approximately in opposite directions in the cis conformation of esters, whereas the trans and gauche conformations for the methyl group in ethers define nearly parallel or perpendicular directionality for the lone pairs of the ring heteroatoms and the O or S atoms connecting to the ring. These different preferences for the studied two families of compounds allow for designing formation of hydrogen bonds with a protein in fairly different regions of the latter still within the ligand-binding cavity. For a fine-tuning of these hydrogen bonds, a replacement of an oxygen atom of the ligand by a sulfur atom could be a straightforward possibility.
Keywords: B97D/aug-cc-pvtz, IEF-PCM, cis-trans conformation equilibrium, atomic charges
1. Introduction
One of the major problems throughout the theoretical design of a drug candidate is the choice for a ligand structure that would optimally fit to the targeted receptor. Optimal fit is meant here as the best compromise for the steric and electrostatic complementarity in the ligand-biomacromolecule complex, as well as the matching of their hydrophobic sites [1]. By means of the structure based design (SBD), the procedure becomes feasible if the tertiary structure of an enzyme or a protein receptor is known, which is more and more available recently on the basis of their determined crystal structures.
Esters and ethers are frequently appearing substructures in drug molecules. In the common oxo-esters there are two oxygen atoms acting as possible hydrogen-bonding acceptor sites. Heterocyclic ethers with an O-C-O substructure (see 2-OCH3 furan in the present study) could be an alternative for the O=C-O moiety in a drug candidate. Previous investigations predicted that both types of molecules are good hydrogen bond acceptors [2,3,4]. For ester/ether ligands, a possible way for fine-tuning the hydrogen bond is the replacement of an oxygen atom by a sulfur atom. There are four possible combinations when O and S atoms are considered in an XCYCH3 moiety, namely XY = OO, OS, SO, and SS. The most important issue in this respect is that the favored conformation in the XCYCH3 moiety could be more or less different. Diversities in the molecular geometries, lone-pair orientations and atomic charges could help optimizing the ligand-protein interactions.
Correct determination of the relative conformational energies for drug candidates is the basic need in SBD. The primary question is: what are the reasonable theoretical method and level? Semi-empirical quantum chemical methods could provide useful information for some structures, whereas they fail properly working for other systems (see below). Thus the present theoretical study is a high-level conformational investigation of a simple aliphatic ester, methyl acetate, its thio- and dithio- analogues, as well as for the 2-OCH3 and 2SCH3 furan and thiophene ethers. Potential energy curves for the rotation about the C-Y bond in the gas phase were compared with those in chloroform and acetonitrile in order to characterize the effects of the solvent on the in-solution optimized molecular geometry and relative conformer energy. These solvents were chosen to avoid the possible effect of the solute-solvent hydrogen bond formation, thus the results reflect the “inherent” conformational preference of the solute in two, non-protic solvents with considerably different dielectric constants.
If one intends to compare conformational energies for a set of molecules, the same theoretical level and basis set are to be used. The goal of the present study is to point out the solvent effect on the relative conformer energies. Thus even if a number of gas-phase studies are available for some of the present eight molecules, they could be considered only for a partial comparison. Such comparison has become possible for CH3COOCH3 and CH3COSCH3, based on some former publications [2,5,6,7,8]. These papers also reported different solvent-effect calculations using different theoretical methods and basis sets. Thus they cannot serve as a basis for a consistent comparison regarding the present target molecules, mainly not since no solvent-effect calculations have been found in the literature for the conformational preferences of the 2-OCH3 and 2-SCH3 heterocyclic ethers. For furan and thiophene derivatives in solution, only some review works have been identified [9,10]. However, from the point of view of an SBD, relative free energies are meaningful only as existing in some environment, namely in a protein cavity that could be characterized by low, although inhomogeneous dielectric constant.
2. Methods and Calculations
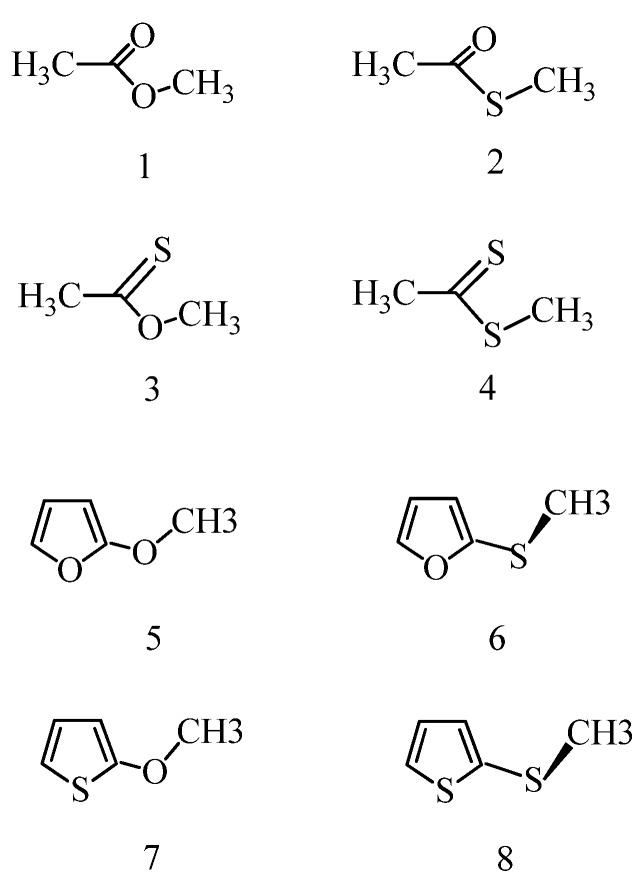
Investigated species, structures 1–8 in their most stable conformations are shown in Figure 1. The calculations were performed by means of the Gaussian 09 package [11] running on the platform of the Ohio Supercomputer Center. Symmetry-unrestricted geometry optimizations in the gas phase were performed by means of the B97D density functional method [12] using the aug-cc-pvtz [13,14,15] basis set and aug-cc-pv(t+d)z basis set [16] for S containing molecules. Reoptimizations in chloroform and acetonitrile, with dielectric constants accepted as 4.71 and 35.7 at T = 298 K°, respectively, were performed by using the integral equation formalism of the polarizable continuum method, IEF-PCM [17,18] at the above-indicated theoretical level. Cavity radii for the C, O, S atoms were set to scaled Bondi values [19,20], and the united CH3 and CH group approach was applied in other cases [20]. This latter approximation has minimal effect on the optimized geometry [21]. Local energy minima were identified by all positive vibrational frequencies. The relative internal Gibbs free energy, ΔGint is the sum of the relative internal energy, ΔEint and the relative thermal correction, ΔGth, where ΔGth was calculated in the rigid-rotor, harmonic-oscillator approach at T = 298 K° and p = 1 atm [22]. The relative solvent-effect related free energy contribution, ΔG(solv) was calculated as the sum of ΔGelst for the relative solute-solvent electrostatic interaction free energy and of ΔGdrc, standing for the relative solute-solvent dispersion + repulsion free energies, plus for the difference in the cavitation free energy upon the conformer transformation. ΔGdrc generally amounts only to about 0–0.2 kcal/mol, in comparison with ΔGelst up to several kcal/mol in the present calculations. The total relative free energy is ΔGtot = ΔEint + ΔGth + (ΔGelst + ΔGdrc) = ΔEint + ΔGth + ΔG(solv). Applied formulae were described earlier [23,24].
Figure 1.
Compound structures: methyl acetate (1); S-methyl thioacetate (2); O-methyl thioacetate (O-methyl ethanethioate, 3); dithioacetic acid methyl ester (4); 2-methoxyfuran (5); 2-methylthiofuran (6); 2-methoxythiophene (7); 2-methylthiothiophene (8). The indicated conformation of the esters 1–4 is the most stable cis form. For 2-methoxyfuran (5) and 2-methoxythiophene (7) the most stable form is trans, and for 2-methylthiofuran (6) and 2-methylthiothiophene (8) the most stable form is gauche.
Optimized geometric parameters show a remarkable basis set dependence in general. It was revealed from recent calculations [23,24,25] that the calculated relative free energy in conformational/tautomeric equilibria is also subject to the basis set effect, even if the relative internal energies are calculated at the aug-cc-pvdz level. B97D/aug-cc-pvtz relative internal energies are, however, close to the complete basis set limit [23], thus ΔE and ΔG values were calculated at this level in the present study as nearly converged values. Nonetheless, the aug-cc-pvtz basis set still may not be large enough for S containing molecules. Calculated bond lengths to the sulfur atom in some heterocyles could be considerably ameliorated by considering “d” orbitals on S [26,27]. Accordingly, the aug-cc-pv(t+d)z basis set was eventually used in the present optimizations for the thio- dithio- ester analogues, the furan thiomethyl ether, and the thiophene derivatives. For comparison, some gas-phase calculations with geometry optimization were performed at the MP2 level [28] with the same basis set as used with B97D, and semi-empirical calculations at the PM3, PM6, and PDDG/PM3 levels [29,30,31] were carried out for some gas-phase CH3COSCH3 conformers.
Due to the large number of the needed structure optimizations and especially the lengthy determination of the TS (transition state) structures, torsional potential curves were approached upon considering only a limited number of torsion angles for the XCYC moiety. The energy for the top of barrier was approximated generally by the value calculated at XCYC = 90°. More precise torsion potential curves for CH3COOCH3 (structure 1) and CH3CSSCH3 (structure 4) (see below) support this approach.
3. Results and Discussion
When conformational equilibria are studied, relative energies/free energies are always to be considered. These values could be relevant even if the underlying optimized geometries and individual energy terms are only moderately correct. Thus equilibrium calculations could lead to valuable conclusions despite some possible systematic error in the applied theoretical method and/or due to the incompleteness of the basis set. If reasonable trends are noted for the individual species by applying gradually increasing theoretical level through the investigations, and the calculated relative values show convergence, the obtained results may be acceptable. Still, however, it is not easy to verify that the predicted relative free energies and the concomitantly derived equilibrium composition are correct.
In cases, experimental information is available regarding the structure and the equilibrium composition. Experimental data are mostly available for gas-phase systems, and generally only for the structure of the predominant conformer. Even less is known for in-solution equilibria and related conformer structures. Theoretical calculations become of paramount interest in these cases. Since no experimental data have been found for the in-solution structure and equilibrium of the eight target molecules in the present study, the trends for their conformational preferences may provide useful information regarding their behavior through in-solution reactions and interactions with protein receptors in a binding cavity.
3.1. Geometries
Optimized molecular geometric parameters are compared with available experimental values for furan and thiophene (Table 1) and for methyl acetate (structure 1) and thioacetic acid S-methyl ester (structure 2) (Table 2). The calculated bond distances were estimated in remarkably better accord with the experimental values when the aug-cc-pvTz basis set rather than the aug-cc-pvDz set was used (Table 1). However, the O-C distance in furan is still overestimated by 0.008 Å even when the larger basis set is used [32]. (From experimental data, the symmetry of the furan and thiophene molecules is C2v, thus symmetry-restricted geometry optimizations were performed in these cases.) For thiophene, the calculated S-C distance improves by more than 0.02 Å with increasing basis sets. The bond angles are in good agreement with the experimental values at any calculation level [33]. For the present purposes, however, the main goal is not achieving very high precision in individual geometries. As emphasized in the Introduction, this study aims to point out the trends of the changes in molecular conformations and relative free energies, affected by the solvent. Table 1 indicates negligible solvent effect for ring structures.
Table 1.
C2v symmetry restricted optimized geometries at the B97D/aug-cc-pvXz level for furan and thiophene a.
| Gas | CHCl3 | CH3CN | Exp b | |||
|---|---|---|---|---|---|---|
| X = D | X = T | X = T | X = T | |||
| Furan | ||||||
| OC | 1.375 | 1.370 | 1.373 | 1.374 | 1.362 | |
| X = D | X = T | X = T + d | X = T + d | X = T + d | ||
| Thiophene | ||||||
| SC | 1.745 | 1.730 | 1.723 | 1.724 | 1.725 | 1.714 |
Table 2.
Geometric parameters optimized at the B97D/aug-cc-pvTz and B97D/aug-cc-pv(T+d)z levels for methyl acetate and thioacetic acid S-methyl ester, respectively a.
| Gas | CHCl3 | CH3CN | Exp. | |
|---|---|---|---|---|
| CH3COOCH3, cis b | ||||
| C-C | 1.514(1.500) | 1.511 | 1.510 | 1.496 |
| CH3COOCH3, trans | ||||
| C-C | 1.519 | 1.514 | 1.511 | |
| CH3COSCH3, cis c | ||||
| C-C | 1.520(1.507) | 1.517 | 1.516 | 1.499 |
| CH3COSCH3, trans | ||||
| C-C | 1.518 | 1.514 | 1.511 | |
a Distances in Å, angles in degrees. Cis and trans structures correspond to O=C-X-C (X=O, S) torsional angles of very close to 0° and 180°, respectively, heavy atoms are nearly coplanar. Values in parentheses from MP2 optimization with the same basis set. B97D parameters with characteristic changes in the transition state geometry or for the X=C-Y-C = 90° structures (rot 90°) are indicated. b Experimental data from ref. [32]. Corrected geometric parameters based on gas electron diffraction experiment. c Experimental data from gas electron diffraction, ref. [33].
Table 2, Table S1 summarize the calculated characteristic geometric parameters for simple esters. All results were obtained from symmetry-unrestricted optimizations starting from some structure of C1 symmetry. The symmetry of the converged cis and trans structures corresponds only nearly to Cs, the torsional angles for the heavy atoms deviate from 0 or 180° by some hundredths of a degree (achievement of a perfect symmetry plane is almost impossible when the standard convergence thresholds are used in a symmetry-unrestricted energy minimization in Gaussian. The symmetry-unrestricted optimization assures, however, that the structure does not remain stuck in some transition state if the starting geometry is wrongly chosen; a possible source for defining a transiton state when the methyl group is set in an improper rotational position). It reveals from cases when comparison with experimental values is possible (Table 2) that the gas-phase B97D single bonds are overestimated by up to 0.02 Å for methyl acetate [34] and thioacetic acid S-methyl ester [35]. The largest overestimation was noted for the C-C bond, which probably has, however, minor effect on the conformational equilibria. For the thioacetic acid S-methyl ester, the C-S and S-C distances are too long by up to 0.016 Å. The calculated bond angles for the cis conformers agree within 1° with the corresponding experimental values.
The most conspicuous changes of the geometric parameters upon the cis to trans transformation were noted for some bond angles. For the two esters in Table 2, the O=C-X angles decrease and the C-X-CH3 (X=O, S) bond angles increase by about 5° in the gas phase. For the C=S containing esters (Table S1) the S=C-X angles decrease by 7–8°, and the S-CH3 distance increases in the trans conformer of the dithioacetic acid ester by more than 0.02 Å.
The H-C-C=O torsion angles are about 0 and 180° for the cis CH3COOCH3 and CH3COSCH3 conformers, respectively, both at the B97D and MP2 levels. The experimental value for CH3COOCH3 was not provided by Pyckhout et al. [34]. The torsional angle is 143.1° (without refinement) for CH3COSCH3 from gas electron-diffraction measurements by Della Védova et al. [35]. This torsion angle was calculated at 180° and 178.8° using the B97D and MP2 method, respectively, and applying the aug-cc-pv(t+d)z basis set. It is remarkable that the H-C-C=O torsion angle changes to 0° for the trans conformer.
The solvent effects are small and consistent for any geometric parameters. By consistency the finding is meant that the geometric parameters monotonically decrease or increase with increasing polarity of the environment in the gas-phase, chloroform and acetonitrile series. Remarkable changes were found for some atom distances, which were larger by up to 0.017 Å in acetonitrile compared to those in the gas phase.
3.2. Energy Results for Esters
Relative energy/free energy components of ΔGtot for the studied esters are compared in Table 3. Due to the practically achieved symmetry plane for the molecules in their cis and trans conformations, and the energy equivalence of the clockwise and anticlockwise rotation about the C-Y bond, these structures must correspond to either a local energy minimum or a transition state. Non-planar structures exist in two mirror image forms, and for their ΔGtot value the entropy of mixing term, -RT ln 2 = −0.41 kcal/mol is to be considered. Table 3, Table 4 include the ΔGth values for the local-energy- minimum and TS structures in both solvents, and accordingly the correct ΔGtot = ΔEint + ΔGth + ΔG(solv) was calculated. For torsional rotamers corresponding neither to energy minima nor TS structures, only the ΔEint + ΔG(solv) term could be reasonably compared.
Table 3.
Relative energies for esters as the function of the rotation about the C-O and C-S bonds a.
| Gas | Chloroform | Acetonitrile | |
|---|---|---|---|
| ΔEint | ΔEint + ΔG(solv) | ΔEint + ΔG(solv) | |
| O=C-O-C | |||
| 0 | 0.0 | 0.0 + 0.0 = 0.0 | 0.0 + 0.0 = 0.0 |
| 30 | 2.88 | 2.91 − 0.04 = 2.87 | 2.95 − 0.12 = 2.83 |
| 60 | 8.76 | 8.85 − 0.13 = 8.72 | 8.96 − 0.35 = 8.61 |
| TS(95.4, 92.2, 90.7) | 12.40 | 12.59 − 0.75 = 11.84 | 12.80 − 1.29 = 11.51 |
| 120 | 11.15 | 11.54 − 1.57 = 9.97 | 11.98 − 2.61 = 9.37 |
| 150 | 7.00 | 7.96 − 2.48 = 5.48 | 8.59 − 4.02 = 4.57 |
| 180 | 5.71 | 6.37 − 2.86 = 3.51 | 7.09 − 4.59 = 2.50 |
| ΔGth | 0.89 | 1.09 | 1.10 |
| ΔGth(TS) | 0.44 | 0.48 | 0.40 |
| O=C-S-C | |||
| 0 | 0.0 | 0.0 + 0.0 = 0.0 | 0.0 + 0.0 = 0.0 |
| 30 | 2.72 | 2.76 + 0.02 = 2.78 | 2.80 − 0.03 = 2.77 |
| 60 | 8.86 | 8.93 − 0.12 = 8.81 | 9.00 − 0.32 = 8.68 |
| 90 | 12.16 | 12.34 − 0.61 = 11.73 | 12.55 − 1.17 = 11.38 |
| 120 | 10.27 | 10.60 − 1.10 = 9.50 | 10.89 − 1.87 = 9.02 |
| 150 | 5.63 | 6.08 − 1.62 = 4.46 | 6.57 − 2.72 = 3.85 |
| 180 | 3.35 | 3.86 − 1.89 = 1.97 | 4.42 − 3.12 = 1.30 |
| ΔGth | 1.18 | 1.29 | 1.31 |
| S=C-O-C | |||
| 0 | 0.0 | 0.0 + 0.0 = 0.0 | 0.0 + 0.0 = 0.0 |
| 30 | 2.83 | 2.84 + 0.00 = 2.84 | 2.86 − 0.04 = 2.82 |
| 60 | 8.95 | 8.98 + 0.00 = 8.98 | 9.02 − 0.11 = 8.91 |
| 90 | 12.94 | 13.04 − 0.35 = 12.69 | 13.17 − 0.72 = 12.45 |
| 120 | 11.61 | 11.94 − 1.37 = 10.57 | 12.33 − 2.32 = 10.01 |
| 150 | 7.81 | 8.44 − 2.64 = 5.80 | 9.14 − 4.30 = 4.84 |
| 180 | 6.25 | 7.00 − 3.19 = 3.81 | 7.83 − 5.13 = 2.70 |
| ΔGth | 0.10 | 0.42 | 0.51 |
| S=C-S-C | |||
| 0 | 0.0 | 0.0 + 0.0 = 0.0 | 0.0 + 0.0 = 0.0 |
| 30 | 3.02 | 3.00 − 0.15 = 2.85 | 3.03 − 0.28 = 2.75 |
| 60 | 9.96 | 9.86 + 0.12 = 9.98 | 9.76 + 0.16 = 9.92 |
| TS(90.6, 89.7, 89.0) | 14.30 | 14.27 + 0.07 = 14.34 | 14.24 − 0.10 = 14.14 |
| 120 | 11.40 | 11.52 − 0.93 = 10.59 | 11.71 − 1.55 = 10.16 |
| 150 | 5.60 | 6.03 − 1.92 = 4.11 | 6.62 − 3.20 = 3.42 |
| 180 | 3.10 | 3.65 − 2.05 = 1.60 | 4.30 − 3.42 = 0.88 |
| ΔGth | 0.16 | 0.80 | 1.10 |
| ΔGth(TS) | 0.47 | 0.85 | 1.16 |
a Energies in kcal/mol, torsion angles in deg. Local-energy-minima torsion angles are underscored.
Table 4.
Torsion barrier energies relative to the cis conformation in the gas phase a.
| CH3COOCH3 | CH3COSCH3 | |
|---|---|---|
| B3LYP/6-311++G** b | 13.35 | 11.80 |
| B97D/aug-cc-pvtz c | 12.40 | 12.16 |
| MP2/6-311++G** b | 13.45 | 11.18 |
| MP2/aug-cc-pv(t+d)z | 11.98 | |
| INDO d | 29.10 | 14.06 |
| PM3 | 6.05 | |
| PM6 | 6.53 | |
| PDDG/PM3 | 4.87 |
The theoretical results could be summarized as follows. The X=C-Y-CH3 cis conformers are more stable than the trans forms for all four studied esters in the gas phase. ΔEint is considerably larger for OCH3 esters compared with SCH3 esters. The B97D/aug-cc-pvtz level, however, probably underestimates the cis-trans energy difference for methyl acetate as of ΔH = ΔEint + ΔHth = 5.71 − 0.07 = 5.64 kcal/mol. Here ΔHth is the thermal enthalpy correction (including relative zero-point energies) at T = 298 K° and p = 1 atm. The total relative free energy is remarkably larger, 5.71 + 0.89 = 6.60 kcal/mol. Blom and Günthard [36] estimated the enthalpy difference as 8.5 ± 1 kcal/mol and commented that there was a very small band in the matrix IR spectra, and “it is possible that this band is due to the methyl acetate”. The equilibrium composition depends on the relative total free energy. If, as calculated here, ΔGtot is as large as 6.6 kcal/mol, the trans conformer could be hardly observed. Pyckhout et al. [34] calculated ΔE = 10.3 kcal/mol at the ab initio 4-21G level. Nagy et al. [7] obtained ΔH = 7.8–8.2 kcal/mol at the MP2 and B3LYP levels, using the 6-311++G** basis sets, whereas the G3B3 [37] ΔH value by Terhorst and Jorgensen is 7.46 kcal/mol [8]. Although the aug-cc-pvtz basis set was applied presently in geometry optimizations, which is considerably larger than in any former study, the author has no good explanation for the underestimation of ΔH for methyl acetate.
Della Vedova found only one conformation in the sample of CH3COSCH3, assigning it to the cis conformation [35]. Table 3 predicts ΔGtot = 4.53 kcal/mol for the trans conformer (4.60 kcal/mol in ref. [8]), a value large enough for preventing the presence of this conformer at an experimentally observable concentration in the gas-phase mixture. Overall, gas-phase calculation results suggest that ΔGtot is prohibitively large for the observation of the trans CH3 position in any studied X=C-Y- CH3 ester moiety. The question is, whether the solvent effects could modify this equilibrium ratio.
The conclusion about the solvent effect for esters (always talking about the four studied prototypes) is that the cis conformer remains the prevailing conformation, although the cis-trans free energy difference could be largely decreased in comparison with the gas phase. The 0° and 180° torsion angles are underscored in Table 3, indicating local energy minima both in chloroform and the acetonitrile solvents. Adding ΔGth to the 180° ΔEint + ΔG(solv) value, the obtained ΔGtot (in the order of the appearance of the structures in Table 3) are 4.60, 3.26, 4.23, and 2.40 kcal/mol in chloroform, and 3.60, 2.61, 3.21, and 1.98 kcal/mol in acetonitrile. The in-acetonitrile values are consistently smaller than those with chloroform solvent, but even the smallest calculated ΔGtot value for CH3CSSCH3 in acetonitrile allows for a trans-cis ratio of only about 4:96 at T = 298 K. This ratio was calculated by using the relationship −RT ln K = ΔG°, where ΔG° was accepted to be equal to the calculated ΔGtot, and the concentration related activity coefficients were accepted to be equal for the two conformers in very dilute solution as modeled by IEF-PCM. [39,40]. Thus one may conclude that the effect of a non-protic solvent on the cis-trans equilibrium of esters is small, but may not be negligible for esters mainly with the –SCH3 group.
Another important question is: how can the esters reach the equilibrium composition? For compounds with a polar hydrogen atom, even conformational equilibration could be reached by the catalytic involvement of a protic solvent [41,42]. For esters in a non-protic solvent, this reaction path does not seem to be travelable. The straightforward mechanism is, of course, the rotation about the C-Y (Y = O, S) bond. This is a simple mechanism if the barrier to the rotation is energetically affordable. The transition states were identified for CH3COOCH3 and CH3CSSCH3 in all three environments, and the energy values for the barrier scatter in the 11.5–14.3 kcal/mol range. The barrier tops are close to 90°. The activation free energy for passing the barrier can be obtained by adding ΔGth(TS) to the TS energy, and subtracting 0.41 kcal/mol for the entropy of mixing for the TS optical antipodes. Still one is left in the range of ΔGtot = 11–15 kcal/mol. For the other two molecules, the 90° relative energies are also in this latter range. This activation free energy may be considered fairly large, although, e.g., Lunazzi et al. [43] found experimentally the successful annular tautomerizations of azoles in DMSO, THF and CD2Cl2, with activation free energies of 11–14 kcal/mol. Even though the chemical problem studied by Lunazzi et al. is quite different, an activation free energy in the indicated range seems to be affordable for structural transformations in solution. Then this author considers the cis-trans equilibration for simple esters in solution via the rotation of the methyl group about the C-Y bond.
Components of the ΔEint + ΔG (solv) term as the function of the X=C-Y-CH3 torsion angle are provided in the 0–180° range in Table 3. ΔEint, compared with the corresponding gas-phase value, changes only slightly up to about 90° torsion, but conspicuously and unanimously increases after then in solution in comparison with the gas phase. What could be the explanation?
The PCM optimization procedure (keeping only the X=C-Y-CH3 torsion angle at the set value with the exception for the local-minimum-energy conformers) seeks the structure corresponding to the minimum of the Eint+Gelst term. The solvent polarizes the solute’s electron distribution and slightly modifies the geometry throughout the optimization. The internal energy itself, Eint necessarily increases, whereas a more and more negative Gelst is being developed in parallel, and the Eint+Gelst minimum for the considered conformer is ultimately reached. As long as ΔG(solv) is only of a few tenths of a kcal/mol for different conformers as calculated in the 0–60° torsion range, ΔEint changes only moderately compared with it in the gas phase. However, the stiffness of the PES depends on the course of ΔEint in the given environment and could be considered moderate only up to about 30°. ΔEint is here about 3 kcal/mol for all studied esters both in the gas phase and solution, but increases to 8.8–10.0 kcal/mol at torsion angle of 60°.
ΔEint(solution), as the relative internal energy in solution, could both increase and decrease compared with ΔEint(gas) depending on the sensitivity of the internal energy itself on the solvent effect for the cis conformer compared with a torsioned structure. When, however, ΔGelst can become remarkable, due to, e.g., the increase of dipole moment, the molecular structure gets distorted accordingly. Table 3 shows that ΔG(solv) is at least about –1 kcal/mol starting at X=C-Y-CH3 = 120°.
Overall, the question can be raised: how reliable is the calculated torsion potential curve for ΔEint? This is an important issue, since molecular modelers may want to develop torsional potential parameters for esters/ethers to be utilized in Monte Carlo and/or molecular mechanics/dynamic theoretical binding studies. Unfortunately, no experimental torsion barrier data are available for the molecules under scrutiny. To get some information about the stability of the calculated data, MP2/aug-cc-pv(t+d)z calculations in addition to the B97D calculations have been carried out for the cis and 90° rotated CH3COSCH3 structures in the gas phase and are compared with PM3, PM6 and PDDG/PM3 results based on symmetry-unrestricted geometry optimizations. Former INDO [38] and B3LYP/MP2 studies [7] have been also considered.
INDO geometries are fairly good for the cis CH3COOCH3, but cannot be reasonably judged for CH3COSCH3, where the authors did not optimize the S-C bond length and the C-S-C bond angle. Using the sp basis set, the C(O)-S bond length was underestimated by 0.05 Å, with the spd set the C=O became even further away from the experimental value. In the torsion energy barrier calculation they considered a rigid rotation, whereas Table 2 of this paper shows that the C-S bond length increases by about 0.09 Å. PM3 finds the C-S bond length longer than that for S-C and the CSC angle is too large by about 6° for the cis ester conformer. With PM6, the two C-S bonds are still only equally long, the CSC angle is too large by 4°, and the CCO angle was overestimated by about 5°. All these parameters are close to the experimental values from PDDG/PM3 optimizations, although the trans hydrogens of the ester methyl group was found 23° out of the heavy-atom plane. Furthermore, all three optimizations predicted eclipsed HCCO arrangements in contrast to the experimental.
Still the main problem is related to the predicted torsion barrier. The results indicate (Table 4) that the DFT and MP2 energy barriers are similar; they scatter in a range of about 1 kcal/mol. In contrast, the INDO barrier is about the double of the DFT/MP2 values for CH3COOCH3, whereas PM3, PM6, PDDG/PM3 give barrier heights about the half of the DFT/MP2 values. All these findings together suggest that consistent, numerically stable potential curves could be probably only obtained based on large-basis-set calculations.
3.3. Energy Results for Ethers
Relative energies are provided in Table 5 with respect to the actually lowest-energy conformer. In contrast to esters, the relative energy/free energy of two local energy minimum structures are relatively small, up to about 2 kcal/mol. The solvent can both increase (OCH3) and decrease (SCH3) the energy separations for the local-minimum-energy ether structures in comparison with the gas phase. The X-C-Y-C torsional angle in the lowest-energy conformation is 180° for the 2-OCH3 ethers. The second local energy minimum is, however, largely different: XCOC is about 50° and 6° for the furan and thiophene derivative, respectively. The most stable conformation for the furan-2SCH3 thioether is a gauche form with OCSC = 69–76°, whereas for the second stable structure OCSC = 180°. The most complicated equilibrium was found for the thiophene-2SCH3 thioether. None of the stable conformers adopt a coplanar heavy-atom arrangement. As mentioned above, if conformers with a molecular symmetry plane, as in this case with XCYC torsion angles of 0° and 180°, do not correspond to local energy minima, then they must exhibit a transition state structure due to the equivalence of the clockwise and anti-clockwise rotation. For the 2-SCH3 thiophene, in-solution minimum-energy structures adopt XCYC torsion angles of 83–84° and ~172°. There must be a local energy maximum around 120°–150° (see Table 5), thus this potential curve has two minima and three TS structures in the 0–180° range of the XCYC rotation. The subtle effect of the solvents indicates that the marginal ΔEint+ΔG(solv) preference for the two minimum-energy structures is reversed in the two solvents.
Table 5.
Relative energies for ethers as the function of the rotation about the C-O and C-S bonds a.
| Gas | Chloroform | Acetonitrile | |
|---|---|---|---|
| ΔEint | ΔEint + ΔG(solv) | ΔEint + ΔG(solv) | |
| Furan, O-C-O-C | |||
| 0 | 1.53 | 1.38 + 0.72 = 2.10 | 1.18 + 1.16 = 2.32 |
| Furan, O-C-S-C | |||
| 0 | 1.92 | 1.83 − 0.06 = 1.77 | 1.70 + 0.10 = 1.80 |
| Thiophene, S-C-O-C | |||
| 0 | 0.87 | 0.81 + 0.17 = 0.98 | 0.70 + 0.36 = 1.06 |
| Thiophene, S-C-S-C | |||
| 0 | 1.10 | 1.06 − 0.52 = 0.54 | 1.01 − 0.55 = 0.46 |
a Energies in kcal/mol, torsion angles in deg. See also the footnotes for Table 3.
In general, ΔGtot is small for any studied ether in solution. Considering ΔGth and –0.41 kcal/mol for the entropy of mixing for non-planar structures, ΔGtot for the less stable conformer is (in the order of the structure appearance in Table 5) 0.34, 1.11, 0.39, and 0.64 kcal/mol in chloroform, and 1.10, 1.40, 0.24, and 0.58 kcal/mol in acetonitrile. Considering the moderate rotational barriers, equilibration of the stable conformers via C-Y rotation at T = 298 K° would not be hindered. Provided the thermodynamic control for the conformer equilibration, structures with different orientations for the lone pairs of the O and S atoms in the methyl ether and thiomethyl ether groups are expected in the solution. This is a remarkable difference in comparison with esters, where the prevailing lone pair arrangements are determined by the XCYC cis conformation. For esters, the lone pairs of the X atom point approximately toward northwest and east, and those for Y about toward southwest if the CH3-C axis points from west to east (Figure 1). Thus the lone pairs point in fairly opposite directions in this case. For furan and thiophene ethers, the lone pair of the X heteroatom (nearly) in the ring plane points south. Due to fairly unhindered rotation of the CH3 group about the C-Y bond, the lone pairs of Y would point in many different directions, including orientations basically parallel or antiparallel with those on X. This variety of the lone pair directionality could be expediently utilized through drug design, as hinted for in the Introduction section.
3.4. Atomic Charges
In molecular mechanics, Monte Carlo or molecular dynamics studies utilizing some effective pair potential for calculating the interaction energy for a ligand-macromolecule complex, one of the most important issue is the proper estimation of the electrostatic component. This energy is generally represented, at least as the leading term of an expanded series, by the sum of Coulomb energies of effective net atomic charges. There are a number of different methods known in the literature for deriving these charges, and the applied force field parameters must be harmonized with the actually derived charge sets. The charges presented in Table 6 were derived by means of the CHELPG procedure [44], fitting the in-solution atomic charges to the corresponding molecular electrostatic potential.
Table 6.
Net atomic charges fitted to the B97D/aug-cc-pv(t+d)z molecular electrostatic potential by means of the CHELPG procedure a.
| Gas | CHCl3 | CH3CN | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X | Y | DM | X | Y | DM | X | Y | DM | ||||
| CH3C(O)OCH3 | ||||||||||||
| cis | −0.55 | −0.40 | 1.87 | −0.61 | −0.41 | 2.33 | −0.63 | −0.42 | 2.53 | |||
| CH3C(O)SCH3 | ||||||||||||
| cis | −0.45 | −0.25 | 1.30 | −0.51 | −0.26 | 1.71 | −0.53 | −0.26 | 1.93 | |||
| CH3C(S)OCH3 | ||||||||||||
| cis | −0.32 | −0.29 | 2.32 | −0.39 | −0.30 | 3.07 | −0.42 | −0.30 | 3.41 | |||
| CH3C(S)SCH3 | ||||||||||||
| cis | −0.28 | −0.16 | 2.01 | −0.35 | −0.15 | 2.84 | −0.39 | −0.13 | 3.27 | |||
| Furan-2OCH3 | ||||||||||||
| OCOC = 45–54° | −0.14 | −0.37 | 1.13 | −0.15 | −0.41 | 1.35 | −0.16 | −0.43 | 1.49 | |||
| Furan-2SCH3 | ||||||||||||
| OCSC = 69–76° | −0.17 | −0.25 | 1.56 | −0.20 | −0.30 | 2.04 | −0.21 | −0.33 | 2.29 | |||
| Thiophene-2OCH3 | ||||||||||||
| SCOC = 0–6° | −0.04 | −0.31 | 1.11 | −0.05 | −0.34 | 1.30 | −0.04 | −0.35 | 1.37 | |||
| Thiophene-2SCH3 | ||||||||||||
| SCSC = 83–84° | −0.03 | −0.24 | 1.63 | −0.03 | −0.30 | 2.10 | −0.03 | −0.32 | 2.33 | |||
a Charges in atomic charge units, DM is the dipole moment in debye.
a Charges in atomic charge units, DM is the dipole moment in debye.
The derived charges are, however, fitting method and theoretical level dependent. In a recent publication by Nagy et al. [27], the CHELPG charges were compared for 3,5-dimethoxy-1,2,4-thiadiazole calculated in tetrahydrofuran solvent. Non-negligible differences were noticed in the charges derived at different theoretical levels, although the trends were generally preserved. Monti and Nagy [21,45] compared CHELPG and RESP [46] atomic charges for the trimethyl- and dimethylammonium cations at different theoretical levels. Non-negligible differences were noticed in some cases also in these studies. These findings confirm that the charge derivation by different methods and/or at different theoretical levels generally lead more or less different charge sets. Charges in Table 6 were derived on the basis of large-basis-set calculations, where the molecular electrostatic potential utilized in the atom-charge fitting process was generated by means of a wave function reflecting the electron correlation for the target molecule. Although the present study represents high-level calculations and probably provides fairly relevant charges, the primary goal of the comparison in Table 6 is to point out the sensitivity of the obtained charges to the conformation and solvent effects.
A physically measurable structure characteristic is the dipole moment (DM). No proper experimental data have been found for the present molecules, the only available experimental value is 1.72 ± 0.09 D for the liquid methyl acetate, probably assignable to the cis form [47]. Table 6 shows that the quantum-mechanical DM is both conformation and environment dependent. The dipole moment gradually increases when the dielectric constant of the solvent increases compared to the gas phase (with unit dielectric constant). This finding emphasizes the polarization effect of the environment because geometries have only slightly changed upon solvation. The conformation is inherently a major determinant of the molecular dipole, as reveals from their large changes mainly for esters.
The dipole moment is capable only for an overall characterization of the molecule in the given environment, whereas effective pair-potentials need individual atom charges. It is to be emphasized, however, that atom charges have no physical meaning; they facilitate a simple way to calculate molecular electrostatic interactions in the system. It is important to know, how well they would reproduce the overall, physically meaningful dipole moment of the molecule calculated quantum mechanically. Not indicated in Table 6, but the dipoles calculated by means of net atomic charges deviate by less than 0.13 D from the corresponding exact B97D/aug-cc-pvtz values (as an exception, the difference amounted to 0.17 D for 2SCH3 thiophene in solution). Thus the dipoles calculated by means of net atomic charges approach the exact values satisfactorily in general, crediting the underlying atom-charge distribution.
Changes in the corresponding atomic charge values (if the change is larger than 0.01 units thus larger than the rounding error) are gradual: from left to right the negative charges monotonically vary; generally increase in accord with the increasing dipole moments. The trend in the change for a specific atom in different conformations (upper line compared to the lower line) is generally the same in all three environments. All these findings together indicate that one has to consider conformation dependent charges, and they have to be determined in the specific solvent for providing Monte Carlo or molecular dynamics atom-charge parameters for explicit solvent simulations.
3.5. Vibrational Frequencies
Hernandez et al. [48] presented some parts of the IR spectra for methyl acetate and its deuterated forms recorded in dilute CCl4. These authors also performed 6-31** theoretical calculations, and assigned the six C-H stretching frequencies and IR intensities to the acetyl methyl and the ester methyl groups. The dielectric constant of the used solvent is 2.23 [47], thus the results could be relevantly compared with our calculated C-H stretching frequencies for the gas phase and in chloroform solution with ε = 4.71.
The presently calculated B97D frequencies for CH3COOCH3 and CH3CSSCH3, both for their cis and trans conformations are summarized in Table 7. The X=C-Y-C torsion frequencies for the cis forms are also provided. The corresponding vibrations in the trans forms are strongly coupled with both methyl torsions.
Table 7.
B97D frequencies and IR intensities for CH3COOCH3 and CH3CSSCH3 a.
| Gas | CHCl3 | CH3CN | Exp b | ||||
|---|---|---|---|---|---|---|---|
| ω | Int | ω | Int | ω | Int | ||
| CH3COOCH3, cis | |||||||
| C-H stretching | |||||||
| acetyl methyl | 3088 | 8.3 | 3080 | 9.2 | 3077 | 5.2 | 2844–3026 |
| 3041 | 6.5 | 3034 | 3.2 | 3031 | 1.9 | ||
| 2967 | 5.8 | 2960(c) | 5.0 | 2956(c) | 13.3 | ||
| ester methyl | 3080 | 15.3 | 3079 | 10.2 | 3079 | 12.3 | |
| 3045 | 23.1 | 3046 | 20.8 | 3046 | 20.1 | ||
| 2961 | 33.0 | 2957 | 26.5 | 2955(c) | 15.5 | ||
| torsional | |||||||
| O=C-O-CH3 | 177 | 6.0 | 196 | 8.4 | 197 | 9.5 | |
| CH3COOCH3, trans | |||||||
| C-H stretching | |||||||
| acetyl methyl | 3092 | 6.0 | 3085 | 4.3 | 3082 | 3.4 | |
| 3031(c) | 14.7 | 3026 | 0.9 | 3022 | 0.3 | ||
| 2961 | 7.7 | 2955 | 3.0 | 2952(c) | 4.4 | ||
| ester methyl | 3067 | 18.5 | 3073 | 13.5 | 3074 | 11.6 | |
| 3020(c) | 24.8 | 3036 | 22.5 | 3041 | 15.9 | ||
| 2941 | 35.6 | 2948 | 27.9 | 2949 | 21.0 | ||
| CH3CSSCH3, cis | |||||||
| C-H stretching | |||||||
| acetyl methyl | 3042 | 5.1 | 3032 | 7.4 | 3027 | 10.7 | |
| 3025 | 9.4 | 3022 | 8.5 | 3021 | 5.3 | ||
| 2945 | 9.4 | 2939 | 3.4 | 2936 | 1.9 | ||
| ester methyl | 3070 | 4.0 | 3064 | 1.9 | 3061 | 1.0 | |
| 3063 | 3.0 | 3058 | 1.4 | 3056 | 0.8 | ||
| 2969 | 11.7 | 2953 | 5.0 | 2950 | 2.8 | ||
| torsional | |||||||
| S=C-S-CH3 | 220 | 4.3 | 191 | 7.3 | 188 | 8.3 | |
| CH3CSSCH3, trans | |||||||
| C-H stretching | |||||||
| acetyl methyl | 3069 | 3.7 | 3063(c) | 2.8 | 3061(c) | 2.8 | |
| 3003 | 7.8 | 2999 | 2.7 | 2995 | 0.8 | ||
| 2938 | 10.5 | 2933 | 2.6 | 2929 | 0.3 | ||
| ester methyl | 3064 | 5.6 | 3062(c) | 2.7 | 3061 | 0.6 | |
| 3061 | 6.9 | 3062(c) | 2.5 | 3060(c) | 1.8 | ||
| 2960 | 2960 | 2955 | 5.2 | 2952 | 1.9 | ||
a Frequencies (ω) in cm−1. Letter “c” in parentheses refers to non-negligible coupling with displacements in the other methyl group. b Ref. [48], data recorded in dilute CCl4 solution.
Our frequencies have been calculated in the harmonic oscillator approximation [22]. As it is known, the calculated high-frequency stretching values are generally larger than the anharmonic frequencies [28], which are probably observed in the experimental spectra. Then it is not surprising that the present C-H stretching frequencies are higher by 60–120 cm−1 than the experimental values. Although Cappelli et al. [49] developed recently a perturbative methodology considering nonequibrium solvation conditions for evaluating anharmonic vibrational frequencies in solution, the method is not available in Gaussian 09. Nonetheless, assignment of the C-H stretching frequencies to vibrations of the two methyl groups is still possible.
Solvation generally results in a gradual decrease of the C-H frequencies. Shifts in ω are up to about 20 cm−1. However, these frequencies for the ester methyl group of CH3COOCH3 are hardly sensitive to the solvent effects in the cis conformation, and remarkably increase in the trans form with increasing solvent polarity. No such “out of trend” behavior has been calculated for CH3CSSCH3, where, however, the ester group shows insensitivity for the solvent effects in the trans conformation.
In accord with the conclusions of Hernandez et al. above, the IR intensities of the C-H stretching frequencies are consistently higher for the ester rather than for the acetyl methyl group for CH3COOCH3. This conclusion is valid for the series calculated both for the cis and the trans conformers, both in the gas-phase and in solution. For CH3CSSCH3, no such clear-cut trend was calculated, the IR intensities are of the same order of magnitude for the C-H vibrations of the two methyl groups. In comparison with the experiment for CH3COOCH3 it has to be mentioned, however, that the largest intensities were observed in the middle of the spectrum, whereas the largest intensities were theoretically calculated at the low-frequency site both here and in ref. [48].
The X=C-Y-CH3 torsional frequencies were assigned to 177–197 cm−1 vibrations for CH3COOCH3 and to 188–220 cm−1 for CH3CSSCH3. The IR intensities increase for both molecules in their cis form with increasing polarity of the environment. However, the theoretical frequencies increase in this series for CH3COOCH3 but decreases for CH3CSSCH3, further emphasizing the structural differences for XY=OO and XY=SS esters.
4. Conclusions
Simple aliphatic esters and 2-substituted heterocyclic ethers have two local-energy-minimum conformations when the methyl group of the XCYCH3 moiety (X, Y = O, S) is rotated from 0 to 180°. Due to molecular symmetries, clockwise and anticlockwise rotations in the indicated torsional energy range are equivalent. The minimum-energy torsion angles could deviate by up to about 10° when the gas-phase molecule is dissolved in chloroform or acetonitrile. Bond lengths and bond angles change by up to 0.017 Å and a few degrees, respectively, as calculated at the B97D/aug-cc-pv(t+d)z theoretical level (d orbitals only for S containing molecules) and considering the IEF-PCM continuum dielectric solvent approximation for the in-solution geometry optimization.
In contrast to the small effect on the geometry, the solvent has remarkable effects on relative conformer energies for the stable species. Although the prevailing conformation is always cis for the studied esters with practically coplanar heavy atom skeleton, the energy separations of the cis and trans conformers decrease by 1–3 kcal/mol in solution compared with the gas phase. The smallest free energy difference was calculated at 1.98 kcal/mol, allowing for a trans-cis ratio of 4:96 at T = 298 K°. The barriers for the rotation about the C-Y bonds are in the range of 11–15 kcal/mol, which can be overridden as concluded from comparisons with experimental results found for successful in-solution equilibration for azoles. Thus one may expect that esters could conformationally equilibrate under the thermodynamic control.
2-Methoxy and 2-thiomethyl furan and thiophene ethers exhibit also two local-energy-minimum conformations for which the methyl group can have different favorable rotational positions in the 0–180° range for the XCYCH3 torsion angle. The aromatic rings take practically coplanar structures, whereas the methyl group favors XCYCH3 = 0–6° cis, 45–84° gauche, and 172–180° trans conformations in different environments for different ethers. The two locally stable conformers are separated in free energy only by 0.2–1.4 kcal/mol, and the barrier to rotation is about 2–3 kcal/mol at most. Thus conformer equilibration is also feasible under thermodynamic control. The various favorable ether conformations allow different relative orientations of the lone pairs for the ring heteroatoms and the 2Y (Y = O,S) atoms from nearly parallel to antiparallel combinations. In contrast, the lone pair orientations are fairly antiparallel in the almost exclusively prevailing cis conformation for esters. This possible difference of the lone-pair orientations for ethers and esters could be deliberately utilized in structure based drug design in order to provide favorable hydrogen-bond acceptor sites in a protein binding cavity. Furthermore, the distance of the head atoms in a ligand-protein hydrogen bond could be remarkably changed by the replacement of an O atom by an S atom.
Solvent effects are considerable on the dipole character of both esters and ethers. With increasing polarity for the solvent, the dipole moment monotonically increases in comparison with the gas-phase value. Molecular electrostatic potential fitted atomic charges reproduce well the quantum mechanical, exact dipole values. Since the derived charges show conformation and solvent dependence, charges for each conformer should be separately fitted in the specific solvent in order to obtain reliable charge parameters for Monte Carlo or molecular dynamics, explicit solvent simulations.
In summary, this study has called attention to the need for theoretical exploration of possible structural differences for chemical systems with formal substructure similarity. The conformation analysis has revealed large differences for the pairs of the corresponding esters and ethers with equal XCYC substructures. The obtained results could usefully be applied throughout the structure-based design of a related drug candidate.
Acknowledgments
The author thanks the Ohio Supercomputer Center the granted computer time.
Supplementary Materials
Detailed optimized geometric parameters for the CH3CSOCH3 and CH3CSSCH3 molecules in the gas-phase, chloroform, and acetonitrile are provided.
Supplementary materials can be accessed at: http://www.mdpi.com/1420-3049/18/7/8063/s1.
Conflicts of Interest
The authors declare no conflict of interest.
Footnotes
Sample Availability: Not available.
References
- 1.Náray-Szabó G., Nagy P. Electrostatic complementarity in molecular aggregates. 9: Protein-ligand complexes. Int. J. Quant. Chem. 1989;35:215–221. doi: 10.1002/qua.560350114. [DOI] [Google Scholar]
- 2.Evanseck J.D., Houk K.N., Briggs J.M., Jorgensen W.L. Quantification of solvent effects on the acidities of Z and E esters from fluid simulations. J. Am. Chem. Soc. 1994;116:10630–10638. doi: 10.1021/ja00102a032. [DOI] [Google Scholar]
- 3.Lommerse J.P.M., Price S.L., Taylor R. Hydrogen bonding of carbonyl, ether, and ester oxygen atoms with alkanol hydroxyl groups. J. Comput. Chem. 1997;18:757–774. [Google Scholar]
- 4.Nagy P.I., Erhardt P.W. Ab initio study of hydrogen-bond formation between cyclic ether and selected amino acid side chains. J. Phys. Chem. A. 2006;110:13923–13932. doi: 10.1021/jp061113t. [DOI] [PubMed] [Google Scholar]
- 5.Briggs J.M., Nguyen T.B., Jorgensen W.L. Monte Carlo simulations of liquid acetic acid and methyl acetate with OPLS potential functions. J. Phys. Chem. 1991;95:3315–3322. doi: 10.1021/j100161a065. [DOI] [Google Scholar]
- 6.Byun K., Mo Y., Gao J. New insight on the origin of the unusual acidity of Meldrum’s acid from ab initio and combined QM/MM simulation study. J. Am. Chem. Soc. 2001;123:3974–3979. doi: 10.1021/ja001369r. [DOI] [PubMed] [Google Scholar]
- 7.Nagy P.I., Tejada F.R., Sarver J.G., Messer W.J., Jr. Conformational analysis and derivation of molecular mechanics parameters for esters and thioesters. J. Phys. Chem. A. 2004;108:10173–10185. doi: 10.1021/jp0490251. [DOI] [Google Scholar]
- 8.Terhorst J.P., Jorgensen W.L. E/Z Energetics for Molecular Modeling and Design. J. Chem. Theory Comput. 2010;6:2762–2769. doi: 10.1021/ct1004017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Krygowski T.M., Cyranski M.K., editors. Aromaticity in Heterocyclyc Compounds. Springer-Verlag; Berlin, Germany: 2009. [Google Scholar]
- 10.Katritzky A.R., Ramsden C.A., Joule J.A., Zhdankin V.V. Handbook of Heterocyclic Chemistry. 3rd ed. Elsevier; Amsterdam, The Netherlands: 2010. [Google Scholar]
- 11.Frisch M.J., Trucks G.W., Schlegel H.B., Scuseria G.E., Robb M.A., Cheeseman J.R., Scalmani G., Barone V., Mennucci B., Petersson G.A., et al. Gaussian 09. Gaussian, Inc.; Wallingford, CT, USA: 2010. Revision C.01. [Google Scholar]
- 12.Grimme S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006;27:1787–1799. doi: 10.1002/jcc.20495. [DOI] [PubMed] [Google Scholar]
- 13.Dunning T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989;90:1007–1023. doi: 10.1063/1.456153. [DOI] [Google Scholar]
- 14.Kendall R.A., Dunning T.H., Jr. Harrison Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992;96:6796–6806. [Google Scholar]
- 15.Peterson K.A. Gaussian basis sets exhibiting systematic convergence to the complete basis set limit. Annu. Rep. Comput. Chem. 2007;3:195–206. doi: 10.1016/S1574-1400(07)03011-3. [DOI] [Google Scholar]
- 16.Dunning T.H., Jr., Peterson K.A., Wilson A.K. Gaussian basis sets for use in correlated molecular calculations. X. The atoms aluminum through argon revisited. J. Chem. Phys. 2001;114:9244–9253. [Google Scholar]
- 17.Miertus S., Scrocco E., Tomasi J. Electrostatic interaction of a solute with a continuum. A direct utilization of ab intio molecular potentials for the prevision of solvent effects. Chem. Phys. 1981;55:117–129. [Google Scholar]
- 18.Tomasi J., Mennucci B., Cammi R. Quantum mechanical continuum solvation models. Chem. Rev. 2005;105:2999–3094. doi: 10.1021/cr9904009. [DOI] [PubMed] [Google Scholar]
- 19.Bondi A. Van der Waals volumes and radii. J. Phys. Chem. 1964;68:441–451. [Google Scholar]
- 20.Nagy P.I., Alagona G., Ghio C. Theoretical investigation of tautomeric equilibria for isonicotinic acid, 4-pyridone, and acetylacetone in vacuo and in solution. J. Chem. Theory Comput. 2007;3:1249–1266. doi: 10.1021/ct6002252. [DOI] [PubMed] [Google Scholar]
- 21.Nagy P.I. Structure simulations for the 0.22 and 1 molar aqueous dimethylammonium chloride solutions. Phys. Chem. Chem. Phys. 2012;14:849–857. doi: 10.1039/c1cp22604e. [DOI] [PubMed] [Google Scholar]
- 22.McQuarrie D.A. Statistical Mechanics. University Science Books; Sausalito, CA, USA: 2000. [Google Scholar]
- 23.Nagy P.I. Theoretical studies of the solvent effect on the conformation of the HO-C-C-X (X = F, NH2, NO2) moiety with competing intra- and intermolecular hydrogen bonds. J. Phys. Chem. A. 2012;116:7726–7741. doi: 10.1021/jp304164g. [DOI] [PubMed] [Google Scholar]
- 24.Nagy P.I. Theoretical study of the gauche-trans equilibrium with and without an intramolecular hydrogen bond for +H3NCH2CH2X systems (X = OH, NH2, COO−) in solution. Phys. Chem. Chem. Phys. 2012;14:13955–13962. doi: 10.1039/c2cp42240a. [DOI] [PubMed] [Google Scholar]
- 25.Nagy P.I., Erhardt P.W. On the interaction of aliphatic amines and ammonium ions with carboxylic acids in solution and in receptor pockets. J. Phys. Chem. A. 2012;116:5425–5436. doi: 10.1021/jp300588q. [DOI] [PubMed] [Google Scholar]
- 26.Pasinszki T., Krebsz M., Vass G. Ground and ionic states of 1,2,5-thiadiazoles: An UV-photoelectron spectroscopic and theoretical study. J. Mol. Struct. 2010;966:85–91. doi: 10.1016/j.molstruc.2009.12.013. [DOI] [Google Scholar]
- 27.Nagy P.I., Tejada F.R., Kim Y.W., Messer W.J., Jr. Theoretical studies of the solvent effect on conformational equilibria and atomic charges for isolated and hydrogen-bonded dimethoxy thiadiazoles. Comput. Theor. Chem. 2011;966:194–206. doi: 10.1016/j.comptc.2011.02.034. [DOI] [Google Scholar]
- 28.Hehre W.J., Radom L., Schleyer P.V.R., Pople J.A. Ab Initio Molecular Orbital Theory. Wiley; New York, NY, USA: 1986. [Google Scholar]
- 29.Stewart J.J.P. Optimization of parameters for semiempirical methods I. Method. J. Comput. Chem. 1989;10:209–220. doi: 10.1002/jcc.540100208. [DOI] [Google Scholar]
- 30.Stewart J.J.P. Optimization of parameters for semiempirical methods V: Modification of NDDO approximations and application to 70 elements. J. Mol. Model. 2007;13:1173–1213. doi: 10.1007/s00894-007-0233-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tubert-Brohman I., Guimarães C.R., Jorgensen W.L. Extension of the PDDG/PM3 semiempirical molecular orbital method to sulfur, silicon, and phosphorus. J. Chem. Theory Comput. 2005;1:817–823. doi: 10.1021/ct0500287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Bak B., Christensen D., Dixon W.B., Hansen-Nygaard L., Rastrup-Andersen J., Schottländer M. The complete structure of furan. J. Mol. Spectrosc. 1962;9:124–129. [Google Scholar]
- 33.Bak B., Christensen D., Hansen-Nygaard L., Rastrup-Andersen J. The structure of tiophene. J. Mol. Spectrosc. 1961;7:58–63. [Google Scholar]
- 34.Pyckhout W., Van Alsenoy C., Geise H.J. Structure of gaseous methyl acetate as determined by joint analysis of electron diffraction, microwave and infrared spectroscopy, supplemented by a valance force field and constraints from geometry relaxed ab initio calculations. J. Mol. Struct. 1986;144:265–279. [Google Scholar]
- 35.Della Védova C.O., Romano R.M., Oberhammer H. Gas electron diffraction analysis on S-methyl thioacetate, CH3C(O)SCH3. J. Org. Chem. 2004;69:5395–5398. doi: 10.1021/jo0493828. [DOI] [PubMed] [Google Scholar]
- 36.Blom C.E., Günthard H.H. Rotational isomerism in methyl formate and methyl acetate; a low-temperature matrix infrared study using thermal molecular beams. Chem. Phys. Lett. 1981;84:267–271. doi: 10.1016/0009-2614(81)80342-9. [DOI] [Google Scholar]
- 37.Baboul A.G., Curtiss L.A., Redfern P.C., Raghavachari K. Gaussian-3 theory using density functional geometries and zero-point energies. J. Chem. Phys. 1999;110:7650–7657. doi: 10.1063/1.478676. [DOI] [Google Scholar]
- 38.Hilal R., El-Aaser A.M. A comparative quantum chemical study of methyl acetate and S- methyl thioacetate. Toward an understanding of the biochemical reactivity of esters of Coenzyme A. Biophys. Chem. 1985;22:145–150. doi: 10.1016/0301-4622(85)80036-3. [DOI] [PubMed] [Google Scholar]
- 39.Nagy P.I., Maheshwari A., Kim Y.W., Messer W.S., Jr. Theoretical and experimental studies of the isomeric protonation in solution for a prototype aliphatic ring containing two nitrogens. J. Phys. Chem. B. 2010;114:349–360. doi: 10.1021/jp9082085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Nagy P.I. Combined ab initio/DFT and Monte Carlo calculation of relative standard chemical potentials in solution. J. Phys. Chem. B. 2011;115:9634–9645. doi: 10.1021/jp204018s. [DOI] [PubMed] [Google Scholar]
- 41.Tsuchida N., Yamabe S. Reaction paths of tautomerization between hydroxypyrimidines and pyridones. J. Phys. Chem. A. 2005;109:1974–1980. doi: 10.1021/jp040451w. [DOI] [PubMed] [Google Scholar]
- 42.Nagy P.I. Theoretical calculations on the conformational/tautomeric equilibria for small molecules in solution. Biochem. Pharmacol. 2013 in press. [Google Scholar]
- 43.Lunazzi L., Parisi F., Macciantelli D. Conformational studies by dynamic nuclear magnetic resonance spectroscopy. Part 27. Kinetics and mechanism of annular tautomerism in isomeric triazoles. J. Chem. Soc. Perkin Trans. 2. 1984;1984:1025–1028. [Google Scholar]
- 44.Breneman C.M, Wiberg K.B. Determining atom-centered monopoles from molecular electrostatic potentials. The need for high sampling density in formamide conformational analysis. J. Comput. Chem. 1990;11:361–373. [Google Scholar]
- 45.Monti S., Nagy P.I. Molecular dynamics and Monte Carlo simulations for the structure of the aqueous trimethylammonium chloride solution in the 0.2–1 molar range. Phys. Chem. Chem. Phys. 2011;13:6270–6279. doi: 10.1039/c0cp02898c. [DOI] [PubMed] [Google Scholar]
- 46.Cornell W., Cieplak P., Bayly C.I., Gould I.R., Merz K.M., Ferguson D.M., Spellmeyer D.C., Fox T., Caldwell J.W., Kollman P.A. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 1995;117:5179–5197. doi: 10.1021/ja00124a002. [DOI] [Google Scholar]
- 47.Haynes W.M., editor. CRC Handbook of Chemistry and Physics. 91st ed. CRC Press Taylor and Francis Group; Boca Raton, FL, USA: pp. 2010–2011. [Google Scholar]
- 48.Hernandez V., Castiglioni C., Zerbi G. Hyperconjugation from infrared intensities: the case of methyl acetate and of its selectively deuterated derivatives. J. Mol. Struct. 1994;324:189–198. doi: 10.1016/0022-2860(94)08239-1. [DOI] [Google Scholar]
- 49.Cappelli C., Lipparini F., Bloino J., Barone V. Towards an accurate description of anharmonic infrared spectra in solution within the polarizable continuum model: Reaction field, cavity field and nonequilibrium effects. J. Chem. Phys. 2011;135:104505. doi: 10.1063/1.3630920. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.