Efficient Data Augmentation for Fitting Stochastic Epidemic Models to Prevalence Data

Abstract

Stochastic epidemic models describe the dynamics of an epidemic as a disease spreads through a population. Typically, only a fraction of cases are observed at a set of discrete times. The absence of complete information about the time evolution of an epidemic gives rise to a complicated latent variable problem in which the state space size of the epidemic grows large as the population size increases. This makes analytically integrating over the missing data infeasible for populations of even moderate size. We present a data augmentation Markov chain Monte Carlo (MCMC) framework for Bayesian estimation of stochastic epidemic model parameters, in which measurements are augmented with subject–level disease histories. In our MCMC algorithm, we propose each new subject–level path, conditional on the data, using a time–inhomogeneous continuous–time Markov process with rates determined by the infection histories of other individuals. The method is general, and may be applied to a broad class of epidemic models with only minimal modifications to the model dynamics and/or emission distribution. We present our algorithm in the context of multiple stochastic epidemic models in which the data are binomially sampled prevalence counts, and apply our method to data from an outbreak of influenza in a British boarding school.

1. Introduction

Stochastic epidemic models (SEMs) are classic tools for modeling the spread of infectious diseases. A SEM represents the time evolution of an epidemic in terms of the disease histories of individuals as they transition through disease states. Incorporating stochasticity into epidemic models is important when the disease prevalence is low or when the population size is small. In both cases, the stochastic variability in the evolution of an epidemic greatly influences the probability and severity of an outbreak, as well as the conclusions we draw about its dynamics (Keeling and Rohani, 2008, Allen, 2008). Moreover, many questions — e.g., what is the outbreak size distribution? What is the probability that a disease has been eradicated? — cannot be answered using deterministic methods (Britton, 2010).

The task of fitting a SEM is typically complicated by the limited extent of epidemiological data, which are recorded at discrete observation times, commonly describe just one aspect of the disease process, e.g., infections, and usually capture only a fraction of cases. Complete subject–level data, which would consist of the exact times at which individuals transition through disease states, are of-ten unavailable (O’Neill, 2010). Fitting SEMs in the absence of complete subject–level data presents a complicated latent variable problem since it is usually impossible to analytically integrate over the missing data (O’Neill, 2002). This makes the observed data likelihood for a SEM intractable.

Existing approaches to fitting SEMs with intractable likelihoods have largely fallen into four groups: martingale methods, approximation methods, simulation based methods, and data augmentation (DA) methods (O’Neill, 2010). Martingale methods estimate the parameters of interest using estimating equations based on martingales for the counting processes within the SEM, e.g., infections and recoveries (Becker, 1977, Watson, 1981, Sudbury, 1985, Andersson and Britton, 2000, Linden-strand and Svensson, 2013). These methods are not easily implemented for SEMs with complex dynamics fit to partially observed count data. Approximation methods replace the SEM, typically represented as a Markov jump process, with a simpler model whose likelihood is more tractable. For example, Roberts and Stramer (2001) and Cauchemez and Ferguson (2008) use diffusion processes that approximate the SEM dynamics, while Jandarov et al. (2014) use a Gaussian process approximation of a related gravity model. Another typical simplification is to discretize time and to construct a transition model for the population flow between model compartments at successive times (Longini Jr. and Koopman, 1982, Held et al., 2005, Lekone and Finkensta¨dt, 2006, Held and Paul, 2012). These methods are computationally efficient and in many cases yield sensible estimates. However, the simplifying assumptions used in the various approximations are not always appropriate. For instance, the diffusion approximation may not be valid in small populations where the system is far from its deterministic limit (Andersson and Britton, 2000), while the discretization of time makes it awkward to approximate systems in which the observation times are not evenly spaced or the rates of transition events span several orders of magnitude (Glass et al., 2003, Shelton and Ciardo, 2014). Simulation based methods use the underlying SEM to generate epidemic paths that serve as the basis for inference. This class of methods includes approximate Bayesian computation (ABC) methods (McKinley et al., 2009, Toni et al., 2009), pseudo–marginal methods (McKinley et al., 2014), and sequential Monte Carlo (or particle filter) methods (Toni et al., 2009, Andrieu et al., 2010, Ionides et al., 2011, Dukic et al., 2012, Koepke et al., 2016). Within this class of methods, the particle marginal Metropolis–Hastings algorithm of Andrieu et al. (2010) stands out in being a general method for Bayesian inference and is used as a benchmark method in this paper. Although simulation–based methods have been used to fit complex models, they are computationally intensive and suffer from well known pitfalls. ABC methods are sensitive to the choice of summary statistic, rejection threshold, and prior (Toni et al., 2009). Sequential Monte Carlo methods, on which pseudo–marginal methods often rely, are prone to “particle impoverishment” problems (Capp´e et al., 2006, Dukic et al., 2012).

Traditional agent–based DA methods for fitting SEMs, first presented by O’Neill and Roberts (1999) and Gibson and Renshaw (1998), target the joint posterior distribution of the missing data and model parameters to obtain a tractable complete data likelihood. That the augmentation is agent–based refers to the fact that subject–level disease histories, rather than population–level epidemic paths, are introduced as latent variables in the model. The advantage of the agent– based approach is that household structure and subject–level covariates may be incorporated into the model (Auranen et al., 2000, Höhle and Jørgensen, 2002, Cauchemez et al., 2004, Neal and Roberts, 2004, O’Neill, 2009). Development of DA methods for SEMs is of continuing interest, and recent works by Pooley et al. (2015), Qin and Shelton (2015), and Shestopaloff and Neal (2016) have presented methods that could possibly be applied to epidemic count data. However, their algorithms forgo the flexibility of agent–based DA, and in the case of the latter two papers have not been applied to SEMs.

We present an agent–based DA Markov chain Monte Carlo (MCMC) framework for fitting SEMs to time series count data. We obtain a tractable complete data likelihood by augmenting the data with subject–level disease histories. Our MCMC targets the joint posterior distribution of the latent epidemic process and the model parameters as we alternate between updating subject– level paths and model parameters. We propose each new subject–path, conditionally on the data, using a time–inhomogeneous continuous–time Markov chain (CTMC) with rates determined by the disease histories of the other individuals. These data–driven path proposals result in highly efficient perturbations to the latent epidemic path, and enable us to analyze epidemic count data in the absence of any subject–level information. In contrast, traditional agent–based DA MCMC algorithms rely on data–agnostic trans–dimensional proposals and suffer from convergence issues as the fraction of missing information becomes large (Roberts and Stramer, 2001, McKinley et al., 2014, Pooley et al., 2015). The de facto need for some subject–level data has precluded the use of classical DA machinery in many settings. Thus, our MCMC algorithm enables exact Bayesian inference for SEMs fit to datasets that would have been impossible to study with existing agent– based DA methods. Finally, our algorithm is not specific to any particular SEM dynamics or measurement process, and may be applied, with minimal modifications, to a broad class of SEMs.

2. The Data Augmentation Algorithm for an SIR Model

For concreteness and clarity of exposition, we present our Bayesian DA algorithm (BDA) in the context of fitting a stochastic Susceptible–Infected–Recovered (SIR) model to binomially distributed prevalence counts. We also use our algorithm to fit Susceptible–Exposed–Infected–Recovered (SEIR) and Susceptible–Infected–Recovered–Susceptible (SIRS) models in Sections 3.1, 3.2, and 4, and out-line the minimal adaptations required for these models in Section S6 of Supplementary Materials.

The SIR model describes the time evolution of an epidemic in terms of the disease histories of individuals as they transition through three states — susceptible (S), infected/infectious (I), and recovered (R). Under simple SIR dynamics, each individual becomes infectious immediately upon becoming infected, and acquires lifelong immunity upon recovery. For simplicity, we assume that the population is closed and mixes homogeneously, and that there is no external force of infection. Therefore, the epidemic ceases once the pool of infectious individuals is depleted.

2.1. Measurement process and data

Our data, Y = {Y₁,…,Y_L}, are disease prevalence counts recorded at times t₁,…,t_L ∈ [t₁,t_L]. It should not beggar belief that the data could be subject to measurement error, for example underreporting in settings where asymptomatic individuals escape detection. Let S_τ, I_τ, and R_τ denote the total susceptible, infected, and recovered people at time τ. We model the observed prevalence as a binomial sample, with constant detection probability ρ, of the true prevalence at each observation time. Thus,

$$Y_{\ell }|I_{t_{\ell }},\rho \sim \text{Binomial}\left(I_{t_{\ell }},\rho \right).$$ (1)

2.2. Latent epidemic process

The data are sampled from a latent epidemic process, X={X₁,…,X_N}, that evolves continuously in time as individuals become infected and recover. The state space of this process is $\mathcal{S}$ = {S,I,R}^N, the Cartesian product of N state labels taking values in {S,I,R}. The state space of a single subject, X_j, is ${\mathcal{S}}_j$ = {S,I,R}, and a realized subject–path is of the form

$${\mathbf{x}}_j(\tau )=\{\begin{array}{ll}S,& \tau <{\tau }_{\text{I}}^{(j)},\\ I,& {\tau }_{\text{I}}^{(j)}⩽\tau <{\tau }_{\text{R}}^{(j)}\\ R,& {\tau }_{\text{R}}^{(j)}⩽\tau ,\end{array},$$ (2)

where ${\tau }_{\text{I}}^{(j)}$ and ${\tau }_{\text{R}}^{(j)}$ are the infection and recovery times for subject j (though subject j may also never become infected or recover, or may become infected or recover outside of the observation period [t₁,t_L]). We write the configuration of X at time τ as X(τ) = (X₁(τ),…,X_N(τ)), and adopt the convention that X(τ) and derived quantities, e.g., I_τ, depend on the configuration just before τ. We use τ⁺ for quantities evaluated just after a particular time. The waiting times between transition events are taken to be exponentially distributed, and we denote by β and μ the per–contact infectivity and recovery rates. Thus, the latent epidemic process evolves according to a time–homogeneous CTMC, with transition rate from configuration X to X′ given by

$${\lambda }_{\mathbf{X},{\mathbf{X}}^{\prime }}=\{\begin{array}{l}\beta I,\text{if}\mathbf{X}\text{and}{\mathbf{X}}^{\prime }\text{differ}\text{only}\text{in}\text{subject}j,\text{with}{\mathbf{X}}_j=S,\text{and}{\mathbf{X}}_j^{\prime }=I,\\ \mu ,\text{if}\mathbf{X}\text{and}{\mathbf{X}}^{\prime }\text{differ}\text{only}\text{in}\text{subject}j,\text{with}{\mathbf{X}}_j=I,\text{and}{\mathbf{X}}_j^{\prime }=R,\\ 0,\text{for}\text{all}\text{other}\text{configurations}\mathbf{X}\text{and}{\mathbf{X}}^{\prime }.\end{array}$$ (3)

At the first observation time, we let $\mathbf{X}(t_1)|{\mathbf{p}}_{t_1}\sim \text{Categorical}(\{S,I,R\},{\mathbf{p}}_{t_1})$, where ${\mathbf{p}}_{t_1}$ = (p_S,p_I,p_R) are the probabilities that an individual is susceptible, infected, or recovered. Let τ = {τ₀,…,τ_K+1}, where t₁ ≡ τ₀ and t_L ≡ τ_K+1, be the (ordered) set of K infection and recovery times of all individuals along with the endpoints of the observation period [t₁,t_L]. Let Ⅱ $\left({\tau }_k\stackrel{\wedge}{=}I\right)$ and Ⅱ $\left({\tau }_k\stackrel{\wedge}{=}R\right)$ indicate whether τ_k is an infection or recovery time, and let 𝜃 = (β,μ,ρ, ${\mathbf{p}}_{t_1}$) denote the vector of unknown parameters. The complete data likelihood is

$$\begin{gathered} L(\mathbf{X},\mathbf{Y}|\theta )=\mathrm{Pr}(\mathbf{Y}|\mathbf{X},\rho )\times \mathrm{Pr}(\mathbf{X}(t_1)|{\mathbf{p}}_{t_1})\times \pi (\mathbf{X}|\mathbf{X}\left(t_1\right),\beta ,\mu ) \\ =\left[\prod _{l=1}^L\left(\begin{array}{c}{I}_{t_{\ell }}\\ Y_{\ell }\end{array}\right){\rho }^{Y_{\ell }}{(1-\rho )}^{I_{t_{\ell }}-Y_{\ell }}\right]\times \left[p_S^{S_{t_1}}{p}_I^{I_{t_1}}{p}_R^{R_{t_1}}\right] \\ \times \prod _{k=1}^K\left\{\left[\beta I_{{\tau }_k}\times \mathbb{I}\left({\tau }_k\widehat{=}I\right)+\mu \times \mathbb{I}\left({\tau }_k\widehat{=}R\right)\right]\exp \left[-\left({\tau }_k-{\tau }_{k-1}\right)\left(\beta I_{{\tau }_k}{S}_{{\tau }_k}+\mu I_{{\tau }_k}\right)\right]\right\} \\ \times \exp \left[-\left(t_L-{\tau }_K\right)\left(\beta I_{{\tau }_K^{+}}{S}_{{\tau }_K^{+}}+\mu I_{{\tau }_K^{+}}\right)\right]. \end{gathered}$$ (4)

We briefly reconcile what might seem like a discrepancy between the SIR model presented above and the lumped construction of the SIR model (see Andersson and Britton (2000)), which, for a number of computational and analytical reasons, is somewhat more common. Our model describes the time evolution of the subject–level collection of disease histories, and thus evolves on the state space of individual disease labels. The lumped SIR model describes the time evolution of the vector of compartment counts, the state space of which is defined as the partition of the original state space obtained by aggregating the individuals in each of the model compartments. The lumped construction would have been appropriate had we chosen to augment the data with the compartment counts (for example, as in Pooley et al. (2015)). Nonetheless, inference based on the full subject– level model will exactly match inference based on the lumped model. We discuss this further in Section S1 of Supplementary Materials.

2.3. Subject–path proposal framework

The observed data likelihood in the posterior $\pi (\mathit{\theta }|\mathbf{Y})\propto \pi (\mathbf{Y}|\mathit{\theta })\pi (\mathit{\theta })=\int L(\mathbf{Y}|\mathbf{X},\mathit{\theta })\pi (\mathbf{X}|\mathit{\theta })\pi (\mathit{\theta })\text{d}\pi (\mathbf{X})$ is analytically intractable for even moderately sized N as it involves an extremely high dimensional integral over the collection of subject–paths, X. The strategy employed in DA methods is to introduce the subject–paths, X, as latent variables in the model. This enables us to work with the tractable complete data likelihood given by (4). The joint posterior distribution is

$$\pi (\mathit{\theta },\mathbf{X}|\mathbf{Y})\propto \mathrm{Pr}(\mathbf{Y}|\mathbf{X},\rho )\times \pi (\mathbf{X}|\mathbf{X}\left(t_1\right),\beta ,\mu )\times \mathrm{Pr}(\mathbf{X}(t_1)|{\mathbf{p}}_{t_1})\times \pi (\beta )\pi (\mu )\pi (\rho )\pi ({\mathbf{p}}_{t_1}),$$ (5)

where π(β), π(μ), π(ρ), and $\pi \left({\mathbf{p}}_{t_1}\right)$ are prior densities. Our MCMC targets the joint posterior distribution, given by (5), as we alternate between updating X|𝜃, Y and 𝜃|X,Y.

Given the current collection of subject–paths, x^cur, we propose x^new by sampling the path of a single subject X_j, conditionally on the data, using a time–inhomogeneous CTMC with state space ${\mathcal{S}}_j$ and rates conditioned on the collection of disease histories of the other individuals, x_(-j) = {x₁,…,x_j−1,x_j+1,…,x_N}. The proposed collection of paths is accepted or rejected in a Metropolis–Hastings step.

Let ${\mathit{\tau }}^{(j)}=\{{\tau }_{\text{I}}^{(j)},{\tau }_{\text{R}}^{(j)}\}$ be the (possibly empty) set of infection and recovery times for subject j, and define ${\mathit{\tau }}^{(-j)}=\left\{\mathit{\tau }\backslash {\mathit{\tau }}^{(j)}\right\}=\left\{{\tau }_0^{(-j)},{\tau }_1^{(-j)},\dots ,{\tau }_M^{(-j)},{\tau }_{M+1}^{(-j)}\right\}$, where $t_1\equiv {\tau }_0^{(-j)}$ and $t_L\equiv {\tau }_{M+1}^{(-j)}$, to be the set of M ⩽ K (ordered) times at which other subjects become infected or recover, along with t₁ and t_L. Let $\mathcal{I}=\{{\mathcal{I}}_1,\dots ,{\mathcal{I}}_{M+1}\}$ be the intervals that partition [t₁,t_L], i.e. ${\mathcal{I}}_1=\left[{\tau }_0^{(-j)},{\tau }_1^{(-j)}\right)$, ${\mathcal{I}}_2=\left[{\tau }_1^{(-j)},{\tau }_2^{(-j)}\right)$, …, ${\mathcal{I}}_{M+1}=\left[{\tau }_M^{(-j)},{\tau }_{M+1}^{(-j)}\right)$. Let $I_{\tau }^{(-j)}={\sum }_{i\ne j}^{}\mathbb{I}\left({\mathbf{X}}_i(\tau )=I\right)$ be the prevalence at time τ, excluding subject j. Let ${\mathbf{\Lambda }}^{(-j)}(\mathit{\theta })=\left\{{\mathbf{\Lambda }}_1^{(-j)}(\mathit{\theta }),\dots ,{\mathbf{\Lambda }}_{M+1}^{(-j)}(\mathit{\theta })\right\}$ be the sequence of rate matrices corresponding to each interval in $\mathcal{I}$, where for m = 1,…,M + 1,

$${\mathbf{\Lambda }}_m^{(-j)}(\mathit{\theta })=\begin{array}{c}S\\ I\\ R\end{array}\left(\begin{array}{ccc}S& I& R\\ -\beta I_{{\tau }_m}^{(-j)}& \beta I_{{\tau }_m}^{(-j)}& 0\\ 0& -\mu & \mu \\ 0& 0& 0\end{array}\right).$$ (6)

We can construct the transition probability matrix for subject j over interval I_m,

$${\mathbf{P}}^{(j)}\left({\tau }_{m-1},{\tau }_m\right)={\left(p_{a,b}^{(j)}\left({\tau }_{m-1},{\tau }_m\right)\right)}_{a,b\in {\mathcal{S}}_j},$$

where $p_{a,b}^{(j)}\left({\tau }_{m-1},{\tau }_m\right)=\mathrm{Pr}\left({\mathbf{X}}_j\left({\tau }_m\right)=b|{\mathbf{X}}_j\left({\tau }_{m-1}\right)=a,\mathit{\theta }\right)$, using the matrix exponential

$${\mathbf{P}}^{(j)}\left({\tau }_{m-1},{\tau }_m\right)=\exp \left[\left({\tau }_m-{\tau }_{m-1}\right){\mathbf{\Lambda }}_m^{(-j)}(\mathit{\theta })\right].$$

This computation requires an eigen–decomposition of each rate matrix. We may reduce the total computational burden by computing the eigen decompositions analytically, and by caching the decompositions to avoid duplicate computations. One additional point is that while the eigen– values of any SIR rate matrix are always real valued, this is not generally true, e.g., it is possible for the rate matrix of an SIRS model to have complex eigenvalues. In this case, we obtain a real valued transition probability matrix by first applying a rotation to each rate matrix with complex eigenvalues to obtain its real canonical form (Hirsch et al., 2013). This is discussed in Section S2 of Supplementary Materials.

By the Markov property, the time–inhomogeneous CTMC density over the observation period [t₁,t_L], denoted $\pi \left({\mathbf{X}}_j|{\mathbf{x}}_{(-j)},\mathit{\theta }\right)\equiv \pi \left({\mathbf{X}}_j|{\mathbf{\Lambda }}^{(-j)}(\mathit{\theta });\mathcal{I}\right)$, can be written as a product of time–homogeneous CTMC densities over the inter–event intervals ${\mathcal{I}}_1,\dots ,{\mathcal{I}}_M$. Thus,

$$\mathrm{\pi }\left({\mathbf{X}}_j|{\mathbf{\Lambda }}^{(-j)};\mathcal{I}\right)=\mathrm{Pr}\left({\mathbf{X}}_j\left(t_1\right)|{\mathbf{p}}_{t_1}\right)\prod _{m=1}^M\pi \left({\mathbf{X}}_j|{\mathbf{x}}_j\left({\tau }_{m-1}\right),{\mathbf{\Lambda }}_m^{(-j)}(\mathit{\theta });{\mathcal{I}}_m\right).$$ (7)

Similarly, the transition probability matrix over an interval ${\mathcal{I}}_{\ell }=[t_{\ell -1},t_{\ell }]$ can be written as the product of transition probability matrices over the sub–intervals in ${\mathcal{I}}_{\ell }$, within which the subject– level CTMC is time–homogeneous. Thus, the transition probability matrix over an inter–observation interval, ${\mathcal{I}}_{\ell }=[t_{\ell -1},t_{\ell }]$, partitioned by S transition events that define inter–event intervals with endpoints given by times $t_{\ell -1}\equiv {\tau }_{\ell ,0}^{(-j)}<{\tau }_{\ell ,1}^{(-j)}<\cdots <{\tau }_{\ell ,S-1}^{(-j)}<{\tau }_{\ell ,S}^{(-j)}\equiv t_{\ell }$, is constructed as

$${\mathbf{P}}^{(j)}\left(t_{\ell -1},t_{\ell }\right)=\prod _{s=1}^S{\mathbf{P}}^{(j)}\left({\tau }_{\ell ,s-1}^{(-j)},{\tau }_{\ell ,s}^{(-j)}\right).$$

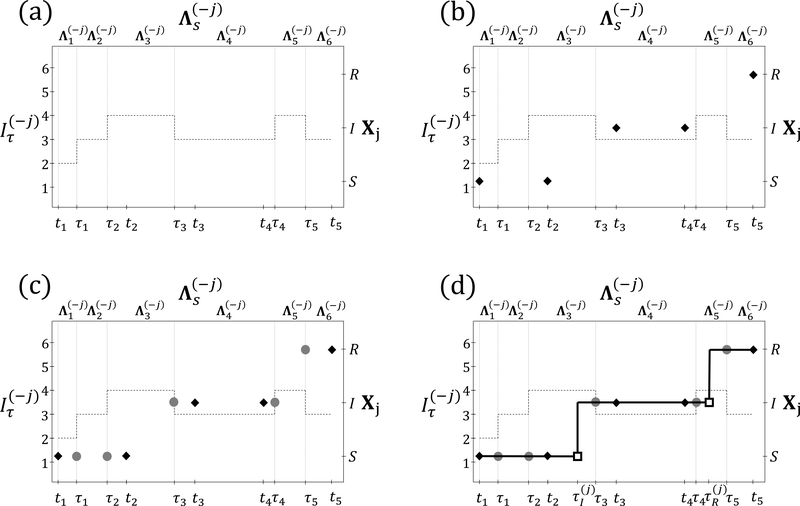
The MCMC algorithm for constructing a subject–path proposal proceeds in three steps (Figure 2):

Figure 2:

Procedure for constructing a subject–path proposal with SIR dynamics. (a) The dashed line depicts the number of infected individuals, excluding X_j, the subject whose path is being sampled. The observation times, t₁,…,t₅, and times at which other subjects change disease states, τ₁,…,τ₅, are shown on the bottom axis. Rate matrices of the time–inhomogeneous CTMC (top axis) are constant within inter–event intervals (vertical lines). The state space of the subject–level process, X_j, is shown on the right axis. (b) HMM step: Sample the state of X_j at t₁,…,t₅, conditional on the data and on the disease histories of other subjects. (c) Discrete time skeleton step: Sample the infection status at τ₁,…,τ₅, conditional on the sequence of states sampled in the HMM step. (d) Event time step: Sample the infection and recovery times from endpoint-conditioned time–homogeneous CTMC distributions, conditional on the sequence of disease states sampled in the HMM and discrete time skeleton steps.

1. H4MM step: sample the disease state of the subject under consideration at the observation times, conditional on the data and disease histories of other subjects.

2. Discrete time skeleton step: sample the state at times when the time–inhomogeneous CTMC rates change, conditional on the states sampled in the HMM step.

3. Event time step: sample the exact times of transition events conditional on the sequence of states sampled in the previous steps.

2.3.1. HMM step

The key to sampling a sequence of disease states at the observation times is to rewrite the emission probability, given by (1), as

$$Y_{\ell }|X_j\left(t_{\ell }\right),I_{t_{\ell }}^{(-j)},\rho \sim \text{Binomial}(\mathbb{I}(X_j\left(t_{\ell }\right)=I)+I_{t_{\ell }}^{(-j)},\rho ).$$ (8)

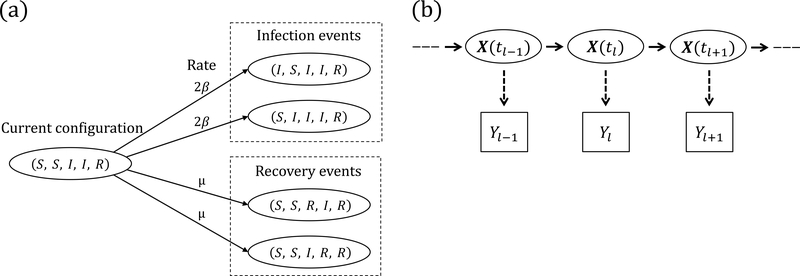
The emission probability in (8) only depends on whether subject j is infected at time t_ℓ, since we treat the paths of all other subjects, and the parameters, as fixed. Furthermore, the data are conditionally independent of one another, given x and 𝜃, which induces a hidden Markov model (HMM) over the joint distribution X and Y (Figure 1b).

Figure 1:

(a) SIR dynamics in a population of five subjects. The number of infecteds can increase from two to three via an infection of the first or second subject, reaching each of those configurations at rate 2β. The number of recovered individuals can increase from one to two via a recovery of the third or fourth subject, reaching each of those configurations at rate μ. (b) Hidden Markov model for the joint distribution of the latent epidemic process and the data. The observations, Y_ℓ, ℓ = 1,…,L, are conditionally independent given X(t), and ${\mathbf{Y}}_{\ell }|I_{t_{\ell }}$, ρ ∼ Binomial($I_{t_{\ell }}$, ρ).

We sample the discrete path of X_j at times t₁,…,t_L from the conditional distribution of X_j, denoted π(X_j|Y,x_(-j),𝜃;t₁,…,t_L), using the stochastic forward–backward algorithm (Scott, 2002). The algorithm efficiently computes the conditional probabilities of the paths that X_j can take through S_j in the forward recursion. A discrete path is then sampled in the backward recursion. We provide details about the HMM sampling step in Supplementary Material Section S3.

2.3.2. Discrete-time skeleton step

It would be straightforward to sample the exact infection and recovery times of subject j, conditional on the sequence of states at times t₁,…,t_L, if the subject–level CTMC rates did not possibly vary over each inter–observation interval. We may reduce our problem to the time–homogeneous case by first sampling the disease state at the intermediate event times when the CTMC rates change, and then sampling the full path within each inter–event interval. Consider an inter–observation interval, ${\mathcal{I}}_{\ell }=[t_{\ell -1},t_{\ell }]$, containing inter–event intervals whose endpoints are given by times $t_{\ell -1}\equiv {\tau }_{\ell ,0}^{(-j)}<{\tau }_{\ell ,1}^{(-j)}<\cdots <{\tau }_{\ell ,n-1}^{(-j)}<{\tau }_{\ell ,n}^{(-j)}\equiv t_{\ell }$. Let ${\tilde{\tau }}_i={\tau }_{l,i}^{(-j)}$ and $x_i={\mathbf{x}}_j({\tau }_{\ell ,i}^{(-j)})$. We recursively sample X_j at each intermediate event time, beginning at ${\tilde{\tau }}_1$, from the discrete distribution with masses

$$\begin{gathered} \mathrm{Pr}\left({\mathbf{X}}_j\left({\tilde{\tau }}_i\right)=x_i|{\mathbf{X}}_j\left({\tilde{\tau }}_{i-1}\right)=x_{i-1},{\mathbf{X}}_j\left({\tilde{\tau }}_n\right)=x_n\right) \\ =\frac{\mathrm{Pr}\left({\mathbf{X}}_j\left({\tilde{\tau }}_i\right)=x_i,{\mathbf{X}}_j\left({\tilde{\tau }}_{i-1}\right)=x_{i-1},{\mathbf{X}}_j\left({\tilde{\tau }}_n\right)=x_n\right)}{\mathrm{Pr}\left({\mathbf{X}}_j\left({\tilde{\tau }}_{i-1}\right)=x_{i-1},{\mathbf{X}}_j\left({\tilde{\tau }}_n\right)=x_n\right)} \\ =\frac{\mathrm{Pr}\left({\mathbf{X}}_j\left({\tilde{\tau }}_i\right)=x_i|{\mathbf{X}}_j\left({\tilde{\tau }}_{i-1}\right)=x_{i-1}\right)\mathrm{Pr}\left({\mathbf{X}}_j\left({\tilde{\tau }}_n\right)=x_n|{\mathbf{X}}_j\left({\tilde{\tau }}_i\right)=x_i\right)}{\mathrm{Pr}\left({\mathbf{X}}_j\left({\tilde{\tau }}_n\right)=x_n|{\mathbf{X}}_j\left({\tilde{\tau }}_{i-1}\right)=x_{i-1}\right)} \\ =\frac{{\left[{\mathbf{P}}^{(j)}\left({\tilde{\tau }}_{i-1},{\tilde{\tau }}_i\right)\right]}_{x_{i-1},x_i}{\left[{\prod }_{k=i}^{n-1}{\mathbf{P}}^{(j)}\left({\tilde{\tau }}_k,{\tilde{\tau }}_{k-1}\right)\right]}_{x_i,x_n}}{{\left[{\prod }_{k=i-1}^{n-1}{\mathbf{P}}^{(j)}\left({\tilde{\tau }}_k,{\tilde{\tau }}_{k+1}\right)\right]}_{x_{i-1},x_n}}. \end{gathered}$$ (9)

2.3.3. Event time step

The final step in constructing a subject–path is to sample the exact infection and recovery times given the discrete sequence of states obtained in the previous two steps. This amounts to simulating the path of an endpoint–conditioned time–homogeneous CTMC, a task for which there exist a variety of efficient methods (Hobolth and Stone, 2009). When fitting the SIR model, we chose to use modified rejection sampling, a modification of Gillespie’s direct algorithm (Gillespie, 1976) that explicitly avoids simulating constant paths. This method is known to be efficient when the states differ at the endpoints of small time intervals. We used uniformization–based sampling (Hobolth and Stone, 2009) when fitting SEIR and SIRS models, which was more robust when sampling paths in intervals with multiple transitions. Fast implementations of these methods are available in the ECctmc package in R (Fintzi, 2016). We briefly summarize the algorithms in Section S4 of Supplementary Materials.

2.3.4. Metropolis–Hastings step

Having constructed a complete subject–path proposal, we decide whether to accept or reject the proposal via a Metropolis–Hastings step. It is important to understand that the true distribution of X_j|x_(-j),𝜃 is neither Markovian nor analytically tractable, and therefore, does not match the time– inhomogeneous CTMC in our proposal. Suppressing the dependence on 𝜃, the target distribution of the subject–path proposal is $\pi (\mathbf{X}|\mathbf{Y})\propto \pi (\mathbf{Y}|\mathbf{X})\pi (\mathbf{X})$. Thus, we accept a proposed subject–path with probability

$$\begin{gathered} a_{{\mathbf{x}}^{\text{cur}}\to {\mathbf{x}}^{\text{new}}}=\min \left\{\frac{\pi \left({\mathbf{x}}^{\text{new}}|\mathbf{y}\right)}{\pi \left({\mathbf{x}}^{\text{cur}}|\mathbf{y}\right)}\frac{q\left({\mathbf{x}}^{\text{cur}}|{\mathbf{x}}^{\text{new}},\mathbf{y}\right)}{q\left({\mathbf{x}}^{\text{new}}|{\mathbf{x}}^{\text{cur}},\mathbf{y}\right)},1\right\} \\ =\min \left\{\frac{\pi \left({\mathbf{x}}^{\text{new}}\right)}{\pi \left({\mathbf{x}}^{\text{cur}}\right)}\frac{\pi \left({\mathbf{x}}_j^{\text{cur}}|{\mathbf{\Lambda }}^{(-j)};\mathcal{I}\right)}{\pi \left({\mathbf{x}}_j^{\text{new}}|{\mathbf{\Lambda }}^{(-j)};\mathcal{I}\right)},1\right\}. \end{gathered}$$ (10)

Hence, the Metropolis–Hastings ratio is equal to the ratio of population-level time–homogeneous CTMC densities, multiplied by the ratio of time–inhomogeneous CTMC proposal densities (see Supplementary Material Section S5 for the derivation).

2.3.5. Initializing the collection of subject–paths

We initialize the collection of subject paths at the start of our MCMC by simulating paths using Gillespie’s direct algorithm (Gillespie, 1976) until we have found one under which the data have non–zero probability. A sufficient condition for this under the binomial sampling model is that the number of infected individuals is greater than the observed prevalence at each observation time.

2.4. Parameter updates

One MCMC iteration includes a number of subject–path updates, followed by a set of parameter updates. The optimal number of subject–path updates per MCMC iteration is specific to the dynamics of the SEM and the epidemic setting (e.g., endemic vs. epidemic, high vs. low escape probability), but ultimately boils down to the cost of subject–path updates vis–a–vis parameter updates. We discuss this further in Section S7 of Supplementary Materials. In the case of the SIR model, as well as the other models we will fit in subsequent sections, conjugate priors are available for all our model parameters. Thus, we use Gibbs sampling to draw new parameter values from their univariate full conditional distributions (see Supplementary Material Section S8).

2.5. Implementation

We provide the R and C++ code base for this paper, along with examples and the code for reproducing the results we present in the following sections, in the form of an R package in a stable GitHub repository (https://github.com/fintzij/BDAepimodel). Future implementations, including ex-tensions to the algorithm presented in this paper, along with improvements to the implementation, will be incorporated into the stemr package (https://github.com/fintzij/stemr).

3. Simulation Results

3.1. Inference under various epidemic dynamics

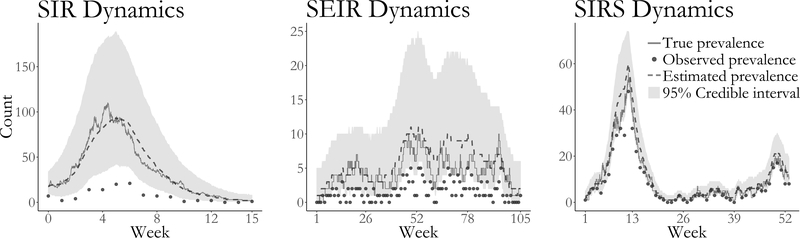
We fit SIR, SEIR, and SIRS dynamics to binomially distributed prevalence counts sampled from epidemics simulated under corresponding dynamics in populations of 750, 500, and 200 individuals (details provided in Supplementary Material Section S9). Priors for the rate parameters and binomial sampling probability were chosen so that the priors spanned reasonable ranges of values (e.g. recovery durations ranging from days to weeks/months rather than seconds to eons under extremely diffuse priors), but were otherwise only mildly informative, while the initial distribution parameters were assigned informative priors (see Supplementary Tables S4, S6, and S8). The three datasets, depicted in Figure 3 along with the estimated pointwise posterior prevalence, presented a range of challenges. The SIR example was arguably the most “standard” example as the observation period captured the exponential growth and decline of the epidemic. Thus, much of the curvature in the latent path was reflected in the data. In contrast, data from the outbreak simulated under near–endemic SEIR dynamics contained very little information about the shape of the epidemic curve. The task of disentangling whether the data were sampled with low probability from a high–prevalence outbreak, or visa–versa, was further complicated by the inclusion of an additional disease state — the exposed state — that was not directly observed. Finally, the SIRS model was more computationally challenging for two reasons. First, the recurrent nature of the disease process demanded that the disease state at each event time, and the path within each inter–event interval, be sampled in the subject–path proposal. Second, it was possible for CTMC rate matrices to have complex eigen–decompositions, which made computing transition probability matrices more expensive. This affected the optimal number of subject–path updates per MCMC iteration (see Supplementary Material Section S7 for further discussion of this point). Simulation details, along with minor adaptations to our algorithm for fitting the SEIR and SIRS models, are presented in Supplementary Material Section S6.

Figure 3:

Estimated latent posterior distributions of disease prevalence in outbreaks simulated under SIR (left), SEIR (middle), and SIRS (right) dynamics. Depicted are the true unobserved prevalence (solid line), observed data (dots), pointwise posterior median prevalence (dashed line), and pointwise 95% credible intervals (shaded region). Latent posterior estimates are based on a thinned sample, with every 250^th sample retained.

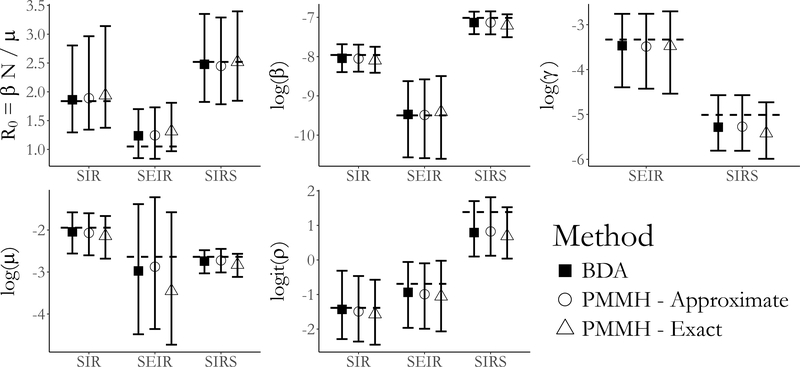
The true epidemic paths and parameter values fell well within the 95% Bayesian credible intervals in all three simulations (Figure 3 presents the estimated latent posterior prevalence; Figure 4 presents posterior estimates of model parameters; Supplementary Material Figure S12 presents estimated latent posterior distributions and true epidemic paths for all model compartments). The acceptance rates for subject–path proposals were roughly 92% for the SIR model, 91% for the SEIR model, and 77% for the SIRS model. Our posterior estimates of the model parameters also closely match estimates obtained using the particle marginal Metropolis–Hastings (PMMH) algorithm of Andrieu et al. (2010), implemented using the pomp package in R (King et al., 2016). We simulated particle paths in the PMMH algorithm in two ways; exactly using Gillespie’s direct algorithm (Gillespie, 1976), and approximately using a multinomial modification of τ–leaping (Bretó and Ionides, 2011). In these small population examples, the exact algorithm is arguably more appropriate, as the leap conditions for τ–leaping may not be met in small populations, but it is also substantially slower. In these simple settings, PMMH tended to outperform our algorithm in terms of log–posterior effective sample size (ESS) per CPU time. When PMMH particle paths were simulated by τ–leaping, the average ESS per CPU compared to BDA was roughly 350× greater for the SIR model, 4.4× greater for the SEIR model, and 13× greater for the SIRS model. Exact simulation of PMMH particle paths reduced the computational advantage of PMMH substantially. In this case, the average log– posterior ESS per CPU time was 10.5× greater for PMMH in fitting the SIR model, 2× for the SEIR model, and 0.7× for the SIRS model. These comparisons did not include the time required to tune the MCMC for PMMH, which was nontrivial. In contrast, our algorithm required no tuning beyond selecting the number of subject–paths to update per MCMC iteration. We also note that in fitting the models using PMMH, we were required to make several implementation decisions to prevent particle degeneracy and to balance speed with precision. These included selecting the number of particles and the time–step in the approximate τ–leaping algorithm. For example, when using τ–leaping to simulate particle paths, the number of particles required to obtain good mixing for the SIRS model fit with PMMH was much higher than for the other two models. Details of the PMMH implementations and further results are discussed in Supplementary Material Section S9.

Figure 4:

Posterior medians and 95% credible intervals of parameters in the SIR, SEIR, and SIRS models fit with Bayesian data augmentation (BDA) and particle marginal Metropolis– Hastings (PMMH) with particle paths simulated approximately (using τ–leaping) and exactly (using Gillespie’s direct algorithm). Displayed are estimates of the basic reproductive number, R₀, the rate parameters, and the binomial sampling probability. In all models, β is the per–contact infectivity rate, μ is the recovery rate, and ρ is the binomial sampling probability. In the SEIR model, γ denotes the rate at which an exposed individual becomes infectious, while in the SIRS model γ denotes the rate at which immunity is lost.

3.2. Inference under model misspecification

In practice, every stochastic epidemic model is misspecified with respect to the real world epidemic process from which the data arise, and the malignancy of the model misspecification is often imposible to diagnose a priori. We can build up an understanding of an epidemic’s dynamics by fitting SEMS under a range of dynamics, beginning with simple, easily interpretable models. The results of each model are interpretted counterfactually — e.g. “If the true epidemic followed SIR dynamics, our best guess of the dynamics that gave rise to the data would be…”. The iterative nature of epidemic modeling suggests that some minimal criteria for the usefulness of any computational algorithm would be that, for a reasonable model, the MCMC should converge to the posterior of the model parameters, and that the estimated latent posterior distribution under the hypothetical dynamics should reflect the true epidemic.

However, it is precisely the inherent misspecification of SEMs that leads simulation–based methods to struggle in many instances, and it is here that we highlight a critical advantage of our DA algorithm. Our subject–path proposals are driven, not just by the SEM dynamics, but also by the data. This enables us to overcome model misspecification in situations in which simulation–based methods degenerate due to their reliance on an adequately accurate model for simulating epidemic paths. We demonstrate this in a simple example in which we fit SIR and SEIR models to four years of weekly prevalence data sampled from an epidemic simulated under time–varying SEIR dynamics, where the latent period, infectious period, and per–contact infectivity rate were modulated over four discrete epochs (depicted in Figure 5, details presented in Supplementary Material Section S10).

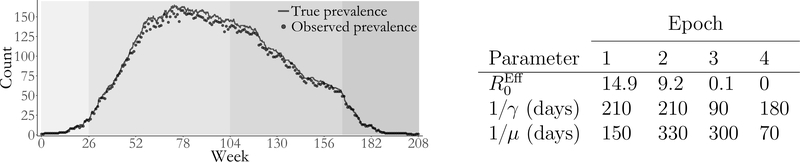
Figure 5 & Table 1:

Simulated outbreak with SEIR dynamics that varied over four epochs (shaded regions). Weekly prevalence counts (points) were binomially sampled with sampling probability ρ “ 0.95 from the true unobserved prevalence (solid line). The table presents the effective reproductive number computed based on the number of susceptibles at the beginning of each epoch, $R_0^{\text{Eff}}=\beta (\tau )S(\tau )/\mu (\tau )$, the mean latent period, 1/γ, and the mean infectious period, 1/μ.

We fit SIR and SEIR models to the data using our DA algorithm, and using PMMH with 2,500 particles, the paths for which were simulated approximately via τ–leaping with a time–step of 1 day. We assigned weakly informative priors for the rate parameters governing the epidemic dynamics in both models, and informative priors for the binomial sampling probability and the initial state probabilities (Supplementary Material Table S11). The MCMC chains for models fit with PMMH suffered from severe particle degeneracy and did not converge (see Supplementary Material Figures S13 and S15).

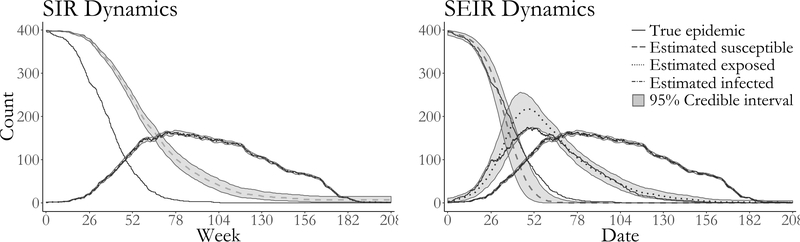
Both models fit via DA yield reasonable estimates for the within–subject disease dynamics (i.e. the infectious period, as well as the latent period in the case of the SEIR model). The posterior median average infectious period duration was estimated to be 292 days (95% BCI: 263 days, 323 days) under SIR dynamics, and 287 days (95% BCI: 260 days, 318 days) under SEIR dynamics. The posterior median average latent period under SEIR dynamics was 211 days (95% BCI: 165 days, 260 days). The posterior median estimate of R₀ under SIR dynamics was 4.05 (95% BCI: 3.40, 4.81), while under SEIR dynamics, the posterior median estimate of R₀ was 23.8 (95% BCI: 15.1, 37.0). While the true prevalence fell well within the pointwise 95% credible interval for both models (Figure 6), we notice that the degree of model misspecification drastically affected our ability to estimate the history of the numbers of noninfectious people over the course of the epidemic. Under SIR dynamics, we drastically overestimate the number of susceptible individuals. The SEIR model much more closely resembles the time–varying SEIR model used to simulate the epidemic. Although the true path for the number of susceptible still falls outsize the 95% credible interval at times, we are still able to reconstruct a reasonabe range of paths for the number of exposed individuals. This contrasts with the models fit in Section 3.1, which were not misspecified with respect to the true epidemic dynamics. In that case, the complete path of the epidemic fell well within the estimated credible intervals for all disease states for all three models (Supplementary Material Figure S12). Therefore, we advise caution in reconstructing the epidemic history for disease states that were not measured, particularly when severe model misspecification is suspected.

Figure 6:

True epidemic path (solid lines), pointwise posterior median estimate of the numbers of susceptibles (dashed line), exposed (dotted line), and infected individuals (dash–dotted line) and pointwise 95% credible intervals (shaded regions) under SIR and SEIR dynamics.

3.3. Inference under population size misspecification

Model misspecficiation often extends not only to the SEM dynamics, but also to the assumed population size. This is often the case in settings where subject–level data is unvailable, for example, in resource limited settings or surveillance settings, and may result in biased estimates of the SEM dynamics. This bias is the result of a missmatch between the intensive dynamics of the epidemic process, which are a function of the fractions of people in the population in each disease state, and the extensive scale of prevalence counts, which are not normalized by the population size. Without knowing the true population size, it is difficult to know whether the scale of the observed counts reflects a high prevalence/low detection rate setting, or visa–versa. Moreover, wrongly assuming too large, or too small, of a population size could bias posterior inference of the epidemic dynamics.

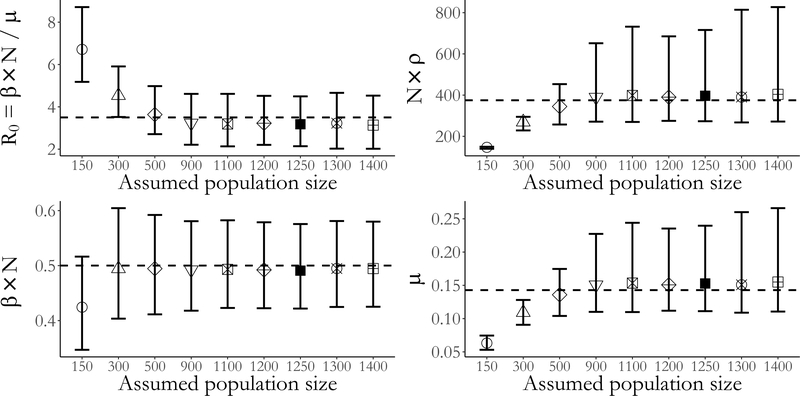
We simulated weekly prevalence counts under a binomial measurement process with detection probability ρ = 0.3 from an epidemic with SIR dynamics in a population of N = 1,250 individuals. We then fit SIR models using a series of assumed population sizes under a flat prior for the binomial sampling probability and diffuse priors for the epidemic dynamics (see Supplementary Material Section S11 for complete simulation details and prior specifications), and compared the resulting scaled parameter estimates. The per–contact infectivity rate, β, was rescaled by the population size, N, so that it could be interpreted as the rate of disease transmission. We computed R₀ using the assumed population size. Finally, we scaled the binomial sampling probability by the assumed population size to give the expected number of observed infections in a completely infected population.

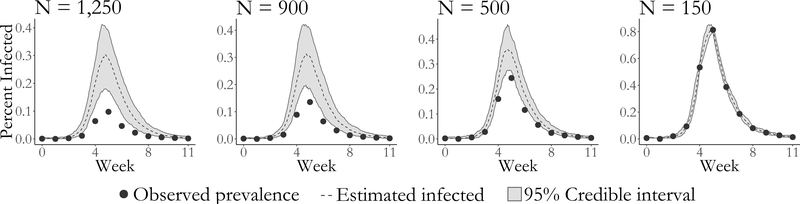
We are able to obtain approximately valid inference under moderate misspecification of the population size. However, estimates of the epidemic dynamics and the case detection probability become severely biased as the magnitude of the misspecification increases. Furthermore, the widths of the credible intervals for the model parameters shrink as misspecification of the population size becomes more severe. The constrained ranges of model dynamics also manifest in a narrowing of the widths of the pointwise credible intervals for disease prevalence (Figure 8). Under severe misspecification of the population size (N = 150), the latent posterior distribution has 95% of its mass within only a narrow band of epidemic paths. In contrast, under moderate misspecification of the population size, the widths of the latent posterior credible intervals are quite similar to the estimated range using the true population size.

Figure 8:

Estimated latent posterior distributions of disease prevalence under SIR dyamics. The true population size is 1,250. Depicted are the observed prevalence (dots), pointwise posterior median prevalence (dashed line), and pointwise 95% credible intervals (shaded region) all scaled by the assumed population size. Latent posterior estimates are based on a thinned sample, with every 250^th sample retained.

There are two final points that we wish to make based on this simulation. The first is that it might be possible to deliberately misspecify the true population size in order to speed up computation time and still obtain approximately valid inference. The average run time using the true population size of 1250 individuals was roughly 2× and 7× longer than the average run times in populations of 900 and 500 individuals. Yet, posterior inferences about the epidemic dynamics were not substantially affected. Longer run times in large populations result from having to sample more subject–paths per MCMC iteration at a relatively higher cost per subject–path. The second point is that in situations where the true population size is unknown, SEM likelihood–based inference has some robustness to misspecification of the population size, at least in a neighborhood of population sizes around the true number of individuals. Thus, comparing posterior inferences under a range of population sizes could be a useful heuristic diagnostic for population size misspecification.

3.4. Effect of prior specification on posterior inference

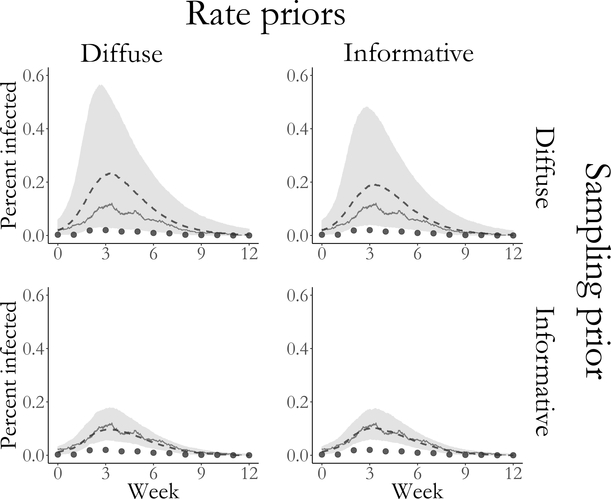
Given the relatively limited extent of aggregated prevalence counts compared to a setting in which subject–level data are available, we must consider how our choices of prior distributions influence our posterior inferences. We simulated an outbreak with SIR dynamics in a population of 750 individuals for which R₀ = β ×763/μ ≈ 1.84 and the mean infectious period was 1/μ = 7 days. We fit SIR models to binomially distributed weekly prevalence data, sampled with detection probability ρ = 0.2, under the following four prior regimes: Regime 1 — informative priors for all model parameters; Regime 2 — vague priors for the rate parameters and an informative prior for the sampling probability; Regime 3 — informative priors for the rate parameters and a flat prior for the sampling probability; Regime 4 — vague priors for the rate parameters and a flat prior for the sampling probability. The same prior for the initial state probabilities was used in all four regimes. Complete simulation details and convergence diagnostics are supplied in Section S12.

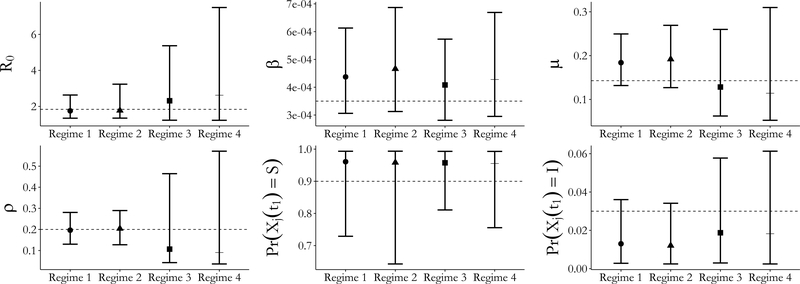
The true values for all model parameters fell within the 95% credible intervals under all four prior regimes. Unsurprisingly, informative priors tended to result in narrower credible intervals for the parameters (Figure 9) as well as for the latent process (Figure 10). The strength of prior information about the sampling probability affected the widths of credible intervals to a much greater extent than the priors for the rate parameters. Strong prior information about the sampling probability also resulted in substantially narrower credible intervals for disease prevalence under each of the prior regimes for the rate parameters. In contrast, informative priors for the rate parameters yielded only slightly narrower credible intervals for disease prevalence when holding constant the strength of the sampling probability prior. The effects on the initial state probability parameters seem to reverse this pattern, although we caution against overinterpretion given the paucity of data available for estimating those parameters. MCMC chains with strong priors for the binomial sampling probability also appeared to mix somewhat better than chains with diffuse priors for the sampling probabilty (see traceplots in Supplementary Material Section S12.

Figure 9:

Posterior median estimates and 95% credible intervals for all SIR model parameters under four different prior regimes (Table S14). Regimes 1 and 3 set informative priors for the per–contact infectivity and recovery rates. Regimes 1 and 2 set informative priors for the binomial sampling probability. The same mildly informative prior for the initial state probabilities was used in all four regimes.

Figure 10:

Estimated latent posterior distributions of disease prevalence in outbreaks simulated under four prior regimes for SIR model rate parameters and the binomial sampling probability. Depicted are the true unobserved prevalence (solid line), observed data (dots), pointwise posterior median prevalence (dashed line), and pointwise 95% credible intervals (shaded region). Latent posterior estimates are based on a thinned sample, with every 250^th sample retained.

4. Influenza in a British boarding school

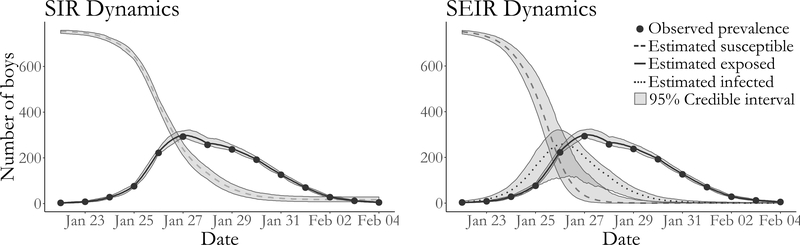
As an application, we analyze data from an outbreak of influenza in a British boarding school (Anon., 1978, Davies et al., 1982). This outbreak took place shortly after the Easter term began in January 1978, and was estimated to eventually infect roughly 90% of the 763 boys aged 10–18. Daily counts of the boys who were confined to the infirmary from January 22^nd through February 4^th were accessed via the pomp package in R (King et al., 2016), and are displayed in Figure 11.

Figure 11:

Boarding school data, pointwise posterior median estimates and pointwise 95% credible intervals (grey shaded areas) under SIR and SEIR dynamics of the numbers of susceptible boys (dashed line), exposed boys (dotted line), and infected boys (solid line). Posterior estimates based on a thinned sample, with every 250^th configuration retained.

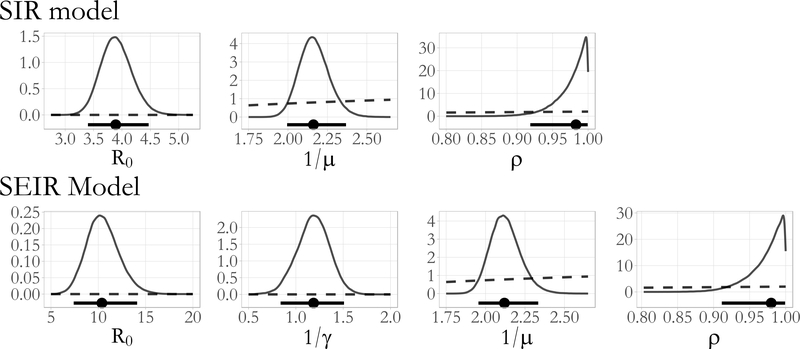
We used our DA algorithm and PMMH to fit SIR and SEIR models with a binomial emission distribution to the data (see Supplementary Material Section S13 of the supplement for complete details). All of the parameters were assigned diffuse priors, which are plotted over the posterior ranges in Figure 12. The PMMH algorithm failed to converge for both models, which we suspect was due to a combination of model misspecification and the constrained state space of the binomial measurement process. We also fit a set of supplementary SIR and SEIR models in Section S13.2, in which we assumed a negative–binomial emission distribution. This was done in order to facilitate comparison with PMMH, although we feel that a negative binomial emission distribution is not appropriate in such a closely monitored outbreak setting since it does not rule out over–reporting of cases.

Figure 12:

Posterior density estimates for R₀ = βN/μ, the mean latent and infectious periods, 1/γ and 1/μ, and the binomial sampling probability, ρ, from SIR and SEIR model parameters fit to the British boarding school data (solid lines). The posterior median and 95% Bayesian credible intervals are drawn below the density plots (solid lines with circles). The implied prior densities (dashed lines) for R₀ and the latent and infectious periods, and the prior density for the binomial sampling probability, are plotted over the posterior ranges.

Together, the SIR and SEIR models suggest that cases were detected with high probability and that the outbreak, though aggressive, was not atypical given the closed environment in which it occurred. The posterior median estimates of the detection probability, roughly 0.98 for both models (SIR 95% BCI: 0.92, 1.00; SEIR 95% BCI: 0.91, 1.00), suggested that while almost all of the infectious boys were detected, a handful of cases went unnoticed. The posterior median recovery rate under SIR dynamics corresponds to an average period of 2.16 days (95% BCI: 1.99, 2.37) during which an infectious boy could transmit an infection to other boys before being confined to the infirmary. Under SEIR dynamics, the posterior median average infectious period was 2.12 days (95% BCI: 1.95, 2.33), and the posterior median average latent period was 1.19 days (95% BCI: 0.84, 1.51). These results are consistent with the typical progression of influenza, in which individuals typically incubate for between one to four days before symptoms manifest, and are typically infectious for one day before, and up to a week after, symptom onset (Centers for Disease Control and Prevention, 2014). The posterior median estimates of R₀ were 3.89 (95% BCI: 3.40, 4.47) under SIR dynamics, and 10.38 (95% BCI: 7.40, 14.11) under SEIR dynamics. Previous analyses of this dataset with trajectory matching estimate R₀ to be roughly 3.7 for the SIR model and 35.9 for the SEIR model (Wearing et al., 2005, Keeling and Rohani, 2008), though we note that these estimates are based on deterministic models that do not properly account for distributional properties of the data. Our results for both models are also in agreement with estimates of SIR and SEIR model dynamics under a negative binomial emission distribution (see Section S13.2).

5. Conclusion

We have presented an agent–based Bayesian DA algorithm for fitting SEMs to disease prevalence time series counts. This was previously difficult, if not computationally infeasible, to carry out using traditional agent–based DA methods in the absence of subject–level data. Although we outlined the algorithm in the context of fitting an SIR model to binomially distributed prevalence data, our algorithm represents a general solution for fitting SEMs to prevalence counts. In simulations and the applied example, we fit SEIR and SIRS models to prevalence data, and in the supplement also fit SIR and SEIR models with a negative binomial emission distribution to the British boarding school data. We have demonstrated that our algorithm yields approximately valid inference when the population size is misspecified. Moreover, our algorithm is usable in settings in which simulation– based methods, such as PMMH, break down due to misspecification of the SEM. Finally, our DA algorithm is carried out entirely at the subject level, making it possible to also incorporate subject–level covariates and household structure, or to fit models to subject–level data.

There are two fundamental limitations of agent-based DA methods from which our algorithm is not excepted. First, the bookkeeping required to track the collection of subject–paths increases in size and complexity as the number of events grows large. Attempts to fit stochastic epidemic models in large populations using agent-based DA may be thwarted by prohibitive computational overhead. MCMC run times using our implementation, which was coded for reliability rather than speed, substantially degraded once the assumed population size was greater than a few thousand people. Second, we suspect that MCMC mixing in large populations could eventually become too slow for agent–based DA to be of practical use, even if solutions could be found for the computational bottlenecks. As the population size gets large, perturbations to the likelihood from re-sampling one subject at a time become relatively less significant. For this reason, we view extensions for jointly sampling multiple subject–paths as a critical step in mitigating slow MCMC mixing in large populations.

Finally, we would like to comment on directions for future work that we intend to pursue. The DA algorithm in this paper addresses the problem of fitting SEMs to prevalence data. This type of data summarizes total number of infections in the population at a particular time. However, outbreak data often consist of incidence counts, which are the number of new cases accumulated in each inter-observation interval. Extending our DA algorithm to accommodate incidence data is an important next step and should be straightforward in situations where the state space for the subject level process is finite — for instance, if a subject cannot become reinfected more than once or twice in a given inter-observation interval. We also believe it is important to investigate whether there is a way to make our DA algorithm more efficient by selecting the subjects whose paths are resampled in each iteration in a way that maximizes the perturbation to the population–level path and does not invalidate the MCMC. Designing an optimal schedule of subject–path updates could be critical to being able to use our algorithm in fitting more complex models to data from epidemics in large, structured populations.

Figure 7:

Posterior medians and 95% credible intervals for the basic reproductive number, R₀, infectivity rate, recovery rate, and binomial sampling probability scaled by the assumed population size. The dashed lines indicate the true values in the population of size 1,250. The population size, N, indicates the assumed population size used in fitting the model.