Abstract
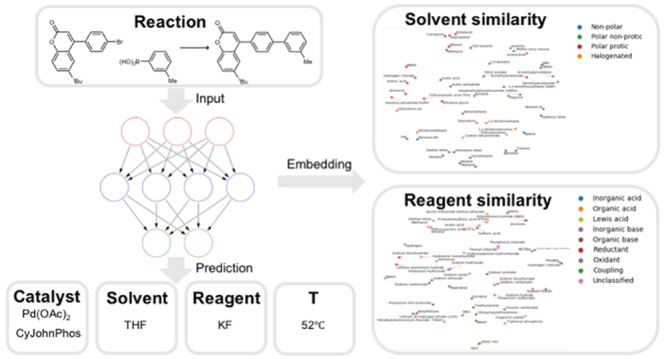
Reaction condition recommendation is an essential element for the realization of computer-assisted synthetic planning. Accurate suggestions of reaction conditions are required for experimental validation and can have a significant effect on the success or failure of an attempted transformation. However, de novo condition recommendation remains a challenging and under-explored problem and relies heavily on chemists’ knowledge and experience. In this work, we develop a neural-network model to predict the chemical context (catalyst(s), solvent(s), reagent(s)), as well as the temperature most suitable for any particular organic reaction. Trained on ∼10 million examples from Reaxys, the model is able to propose conditions where a close match to the recorded catalyst, solvent, and reagent is found within the top-10 predictions 69.6% of the time, with top-10 accuracies for individual species reaching 80–90%. Temperature is accurately predicted within ±20 °C from the recorded temperature in 60–70% of test cases, with higher accuracy for cases with correct chemical context predictions. The utility of the model is illustrated through several examples spanning a range of common reaction classes. We also demonstrate that the model implicitly learns a continuous numerical embedding of solvent and reagent species that captures their functional similarity.
Short abstract
Machine learning model predicts conditions for organic synthesis reactions and quantifies solvent and reagent similarity.
Introduction
Retrosynthetic planning is the process of proposing pathways to synthesize target molecules from available starting chemicals, and has demonstrated its importance and success in the chemical industry.1,2 While retrosynthesis traditionally requires extensive training and expertise of a chemist, recent years have seen renewed interest in computer-assisted synthetic planning (CASP).3−7 With the application of powerful machine learning techniques to large data sets of organic reactions like Reaxys8 and the USPTO database,9 there have been major advances both in searching for possible retrosynthetic pathways10−16 and in evaluating the feasibility of the proposed reactions.5,17−22
While existing tools have been demonstrated to predict the likelihood of success of reactions with good accuracy,20 one obstacle to experimentally validating computer-proposed reactions is the specification of reaction conditions, including chemical context (catalyst, reagent, solvent) and other operating conditions (e.g., temperature, pressure). In some cases, small changes in reaction conditions can lead to drastically different reaction outcomes. Therefore, recent work on reaction outcome prediction has started to include reaction conditions to improve the accuracy and specificity of predictions.20,21 More importantly, reaction conditions are necessary to evaluate opportunities for one-pot synthesis, telescoping in flow, and amenability to the use of “green” solvents for sustainability.
Extensive work has been done on the optimization of conditions for specific reaction classes, using a combination of domain knowledge and empirical optimization techniques to automatically identify the best reaction condition.23−27 Nevertheless, the initial guess of reaction conditions for a new reaction is predominantly considered a human task. Chemists use heuristics and perceived similarity of new reactions to ones they are familiar with to propose candidate conditions. However, this approach has its limitations and challenges. The recommendation might be biased by chemists’ preference and familiarity with certain types of reactions; the heuristic rules might not be all-encompassing or too abstract to narrow down to specific chemicals, and conditions of a precedent reaction may not be applicable to the new reactions even if the reactants are structurally similar.
In addition to the potential utility of in silico condition recommendation tools to practicing synthetic chemists, they are a necessary component of computer-aided synthesis planning. With thousands of plausible reactions generated in a few minutes or even seconds, it would be impossible to rely on manual input for suggesting reaction conditions. Research has shown that failure to specify appropriate reaction conditions might result in false prediction of reaction outcomes.21
However, computational condition recommendation remains a rarely addressed and complex challenge. Most existing work focuses only on specific elements of the chemical context (e.g., only reagents or only solvents), or specific reaction classes. Solvent selection, for instance, has been widely studied as a standalone problem.28 Struebing et al. combined quantum mechanical (QM) calculations with a computer-aided molecular design procedure to identify solvents that accelerate reaction kinetics.29 This approach was demonstrated to be effective for specific examples, yet it is difficult to apply at a larger scale due to the high computational cost of QM calculations.
Data-driven approaches have been employed to recommend conditions for specific types of reactions. Marcou et al.30 built an expert system to predict the type of catalyst and solvent used for Michael additions, trained on 198 known reactions. The problem was formulated as multiple binary classification subproblems of whether a certain type of solvent/catalyst would be suitable for a specific Michael reaction. However, on an external test set, only 8 out of 52 reactions had both predicted solvent and catalyst matching the true context. Lin et al. used a similarity-based approach to recommend catalysts for desired deprotection reactions, and demonstrated the approach in catalytic hydrogenation reactions.31
A study by Segler and Waller tackles a broader scope of reactions using a knowledge graph model of organic chemistry to infer complementary and analogous reactivity.32 Novel reactions are treated as missing links in this graph. Reaction context is taken as the combination of the first reactions that are linked with reactant molecules. They tested this approach on 11 reactions from the literature, and for most of them the model was able to identify the exact same or similar reagent/catalyst as used in the literature. This work demonstrated the feasibility of reaction context inference based on reaction patterns, yet context compatibility and temperature prediction are not taken into consideration.
Similar to the aforementioned approach, one straightforward method for identifying reasonable reaction conditions is to find a similar reaction in the literature and simply employ exactly the same reaction conditions reported for that precedent, referred to as the nearest-neighbor approach. Indeed this is an approach that many chemists may use implicitly. This can be successful with a database of known reactions that is sufficiently large and densely populated, but computationally, a nearest-neighbor search against millions of species is RAM- and CPU-intensive, even with optimized search strategies (e.g., using a ball tree). Furthermore, if some information in the nearest-neighbor reaction is not present (i.e., data is incomplete), that information cannot be inferred. The rigidity of this approach precludes asking questions essential to synthesis planning, such as whether the reaction could proceed in a particular replacement solvent.
In summary, we identify some primary limitations of existing approaches:
-
(1)
There has not been a published method that accurately predicts complete reaction conditions (catalysts, solvents, reagents, and temperature) suitable for use with a very large reaction corpus.
-
(2)
The compatibility and interdependence of chemical context and temperature are not taken into account in previous approaches.
-
(3)
No previous studies have performed quantitative evaluation of reaction condition predictions on a large-scale reaction data set. There are two major challenges which have impeded progress: (i) There is not a machine readable large data set available with catalysts/solvents/reagents classified into different types. (ii) For the similarity-based approaches it is difficult to quantitatively assess the level of “correctness” of conditions when comparing entire sets of conditions associated with different literature reactions.
-
(4)
Closer attention should be paid to balancing the generality/specificity of representing chemical context. If the representation is too general, such as manually encoded types/groups, it might not fully characterize functionality, and if it is too specific, e.g., copy–pasting the entire conditions from other reactions, it does not provide further information about chemical similarity.
New tools are needed that propose reaction conditions intelligently and can handle a broad scope of reaction classes. In this work we develop a neural-network-based model to predict suitable reaction conditions for arbitrary organic transformations. The model is trained on roughly 10 million examples from the Reaxys8 database to predict the chemical species used as catalysts, solvents, reagents, and an appropriate temperature for the reaction. Prediction results are evaluated both quantitatively, using a variety of accuracy metrics, and qualitatively, using multiple sets of representative examples. It is also demonstrated that the model learns the similarity of the chemical context (e.g., different solvents/reagents) exclusively from reaction data.
Results and Discussion
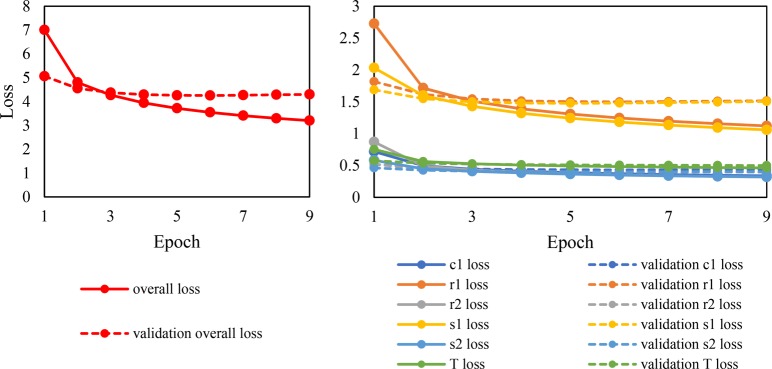
A neural network model is trained to predict up to one catalyst, two solvents, two reagents, and the temperature for a given organic reaction. Detailed data processing and model formulation steps are described in the Methods section. The training process is essentially a multiobjective optimization that minimizes the overall loss function which is a weighted sum of the loss for each individual objective (namely, catalyst, solvent 1, solvent 2, reagent 1, reagent 2, and temperature). The progress of training is reflected in the change of the overall and individual loss, which is shown in Figure 1. Validation loss (dashed red line) decreases for 2 epochs and then reaches a plateau and stays higher than the training loss (solid red line). Based on the plotted losses in Figure 1 the first solvent (s1, yellow lines) and the first reagent (r1, orange lines) are the most difficult to predict, with a significantly higher loss value than the other objectives (not including temperature). There is a large fraction of reactions which do not have a second solvent (s2, blue lines) or reagent (r2, gray lines), in which cases the model only needs to predict the NULL class, making these second predictions easier to classify. The same principle applies to catalyst, where many reactions do not use a catalyst, and others have catalysts frequently recorded as reagents. The mean squared error for temperature (T loss, green lines) decreases steadily over the epochs, ending in 0.46 for the training set and 0.50 for the validation set (after scaling by a factor of 0.001 K−2).
Figure 1.
Change of the loss functions with the number of epochs (left figure, overall; right figure, chemical context and temperature).
Statistical Analysis
Evaluating the results of chemical context prediction is a nontrivial task, mainly because it is a combination of individual chemicals, and because we lack a standard way of quantifying the “closeness” of the prediction when each exact chemical is not predicted. Since there is often more than one possible context combination suitable for a reaction, we do not want to focus exclusively on the top-one prediction, but also want to examine other highly ranked suggestions. However, the number of total combinations grows in a polynomial way (to the fifth power) with the increase of number of candidates to include for every individual element; e.g., if the top-three candidates are to be examined for the catalyst, both solvents, and both reagents, the total number of combinations is 243 (35), which is almost impossible to evaluate manually, and difficult to analyze. Since the data for catalyst, solvent 2 and reagent 2 are much more sparse than solvent 1 and reagent 1, there is likely more value in examining longer candidate list for the latter two. Therefore, we use the top-three reagent 1 predictions and top-three solvent 1 predictions along with the top-two catalyst, top-one solvent 2, and top-one reagent 2 to construct 18 top combinations, from which we can pick the top-three or top-10 combinations with the highest overall scores, calculated as the product of softmax probabilities for each individual element. The number of top candidates is a heuristic choice and can be tailored by model users for specific needs (e.g., the user can explore a longer list of catalyst candidates instead of only the top-two choices).
Evaluation is performed on the entire test set, and the accuracy values described in the Methods section are shown in Table 1. For the most difficult tasks of predicting solvent 1 and reagent 1, the frequency with which the recorded chemical is found in the top-10 combinations is 83.0% and 83.1%, respectively. After including those close match predictions (defined in the Methods section), the accuracy for solvent 1 increases by a margin of 2.4%, and the accuracy for reagent 1 increases by 1.8%. This suggests that, though not explicitly coded, the model learns the chemical similarity of solvents/reagents/catalysts which tend to be used in closely related reactions.
Table 1. Accuracy of Prediction of the Chemical Context by the Condition Recommendation Modela.
| Prediction task | Top-3 exact matches | Top-10 exact matches | Top-3 close matches | Top-10 close matches |
|---|---|---|---|---|
| c | 93.6% | 94.9% | 94.9% | 96.4% |
| s1 | 75.8% | 83.0% | 78.2% | 85.4% |
| s2 | 90.1% | 91.7% | 90.2% | 91.9% |
| r1 | 73.2% | 83.1% | 74.8% | 84.9% |
| r2 | 89.3% | 91.8% | 89.3% | 92.1% |
| c, s1, r1 | 57.3% | 66.0% | 60.4% | 69.6% |
| c, s1, s2, r1, r2 | 50.1% | 57.3% | 53.2% | 60.3% |
c, s1, s2, r1, and r2 refer to catalyst, solvent 1, solvent 2, reagent 1, and reagent 2, respectively.
Compared to the high accuracies for the individual prediction tasks, the top-three accuracy for the full condition recommendation (catalyst, two solvents, two reagents) is 50.1%, and the top-10 accuracy is 57.3% (53.2% and 60.3% when including close match predictions). However, given that these numbers represent the requirement to predict the full combination (all five elements) of the exact recorded context, it is expected to be more challenging than predicting individual elements. We further computed the top-10 accuracy of a subset of the combinations—catalyst, solvent 1, and reagent 1—as 66.0% and 69.6% for exact matches and close match predictions, respectively.
To evaluate the meaningfulness of the accuracies given in Table 1, we compared the trained model with a baseline model, where top-10 combinations are chosen based on the frequencies of the catalysts, solvents, and reagents (Supporting Information, Table S1). Detailed comparisons and statistical parameters are given in the Supporting Information, Table S2. It can be seen that 87.3% of the reactions do not use a catalyst; 85.6% of the reactions do not use a second solvent, and 82.3% of the reactions do not use a second reagent. For these tasks, predicting the NULL class can achieve relatively high accuracy, but the trained model still performs better by a significant margin. Meanwhile, the top-3 accuracy for predicting the correct combination of chemical context is only 4.7%, compared to 50.1% in the trained model, indicating that simply using the most frequent combination of chemical context is not an effective method.
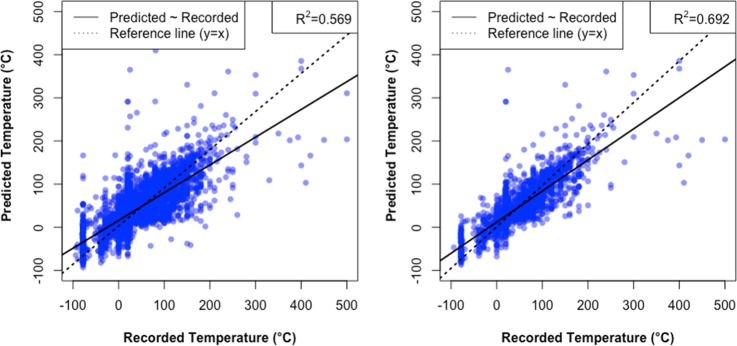
The evaluation of temperature is less straightforward than it seems, because the prediction of temperature is dependent on the chemical context, which means, in the top-10 temperature predictions, at least nine of them are based on chemical contexts that are at least partially different from the recorded context. Practically speaking, however, temperature is relatively easy to change and test in experiments, so suggesting an approximate initial guess of the temperature would be sufficiently helpful for the setup of experiments. The top-one temperature prediction falls within the ±10 or ±20 °C range of the recorded temperature in 36.7% and 57.7% of test cases, respectively. If we isolate reactions whose predicted chemical context matches the recorded chemical context, these accuracies increase to 42.6% and 65.9%. The mean absolute error (MAE) of temperature prediction for all reactions in the data set is 25.5 °C, and when the correct chemical context is found the MAE is 19.4 °C. Figure 2 visualizes this by plotting the predicted temperature against the recorded temperature for a 1% sample of the testing set. The fact that the quality of temperature prediction is significantly improved with correctly predicted chemical context demonstrates that the prediction of temperature accounts for the compatibility with the chemical context. This performance is also compared with a baseline model that predicts the most frequent temperature (20 °C) for every reaction in the Supporting Information. Figure S4 shows the distribution of temperature for the test set. While a majority of reactions use 20 °C, the distribution spans a wide range, and simply predicting the room temperature (20 °C) will result in a mean absolute error of 35.3 °C, which is significantly larger than the prediction given by the trained model and would be misleading for reactions that require high or low temperatures.
Figure 2.
Relationship between the true temperature and the top-one predicted temperature (left panel), and predicted temperature if the predicted context matches the chemical context (right panel).
Qualitative Evaluation of Reaction Examples
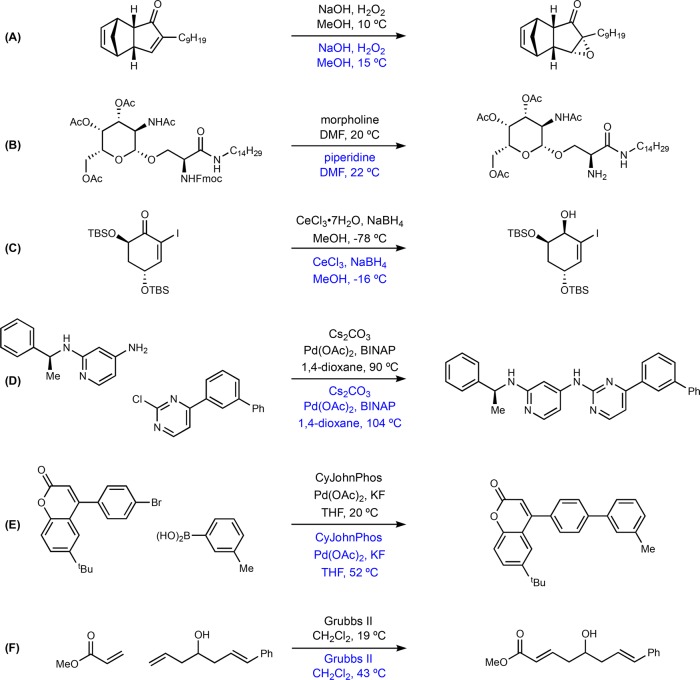
In addition to the statistical analyses, qualitative evaluation of reaction examples helps provide chemical insight in the model predictions. We select reactions from a variety of common types of organic reactions to evaluate the quality of model predictions. We randomly select example reactions that are labeled by reaction type (around five for each type) and compare the true condition, top-one prediction, and the closest prediction within top-10 candidates. The closest prediction is defined as the prediction that has the largest number of chemical elements exactly matching the true chemical context. The reaction types we choose to test include hydrolysis, esterification, alkylation, epoxidation, Wittig, reduction, oxidation, deprotection, Suzuki–Miyaura coupling, Grubbs metathesis, and Buchwald–Hartwig amination. Due to space limitation, we only place a small part of the examples here in the main text with the top-one prediction (Figure 3) and the rest in the Supporting Information (Table S3) with both the top-one prediction and the closest prediction.
Figure 3.
Example of model predictions compared with recorded context (temperature rounded to the closest integer; black text represents the recorded conditions, and blue text represents the predicted conditions). (A) Nucleophilic epoxidation. (B) Deprotection of fluorenylmethyloxycarbonyl (Fmoc). (C) Luche reduction of eneone, TBS = tert-butyl(dimethyl)silyl. (D) Buchwald–Hartwig aryl amination, BINAP = 2,2′-bis(diphenylphosphino)-1,1′-binaphthyl. (E) Suzuki-Miyaura coupling, CyJohnPhos = (2-biphenyl)dicyclohexylphosphine. (F) Hoveyda–Grubbs cross metathesis.
Figure 3A is an epoxidation reaction where two C=C bonds are present.33 The recorded reagents for a nucleophilic epoxidation, selective for the electron deficient alkene, are correctly predicted by the model. Figure 3B shows a Fmoc deprotection reaction where either acidic or basic conditions can be used. In this case, basic conditions are proposed by the model for removal of the Fmoc group which does not affect the other acetate protecting groups in the molecule.34 Notably, the predicted reagent (piperidine) is highly similar structurally and functionally to the recorded reagent (morpholine), demonstrating the model’s ability to capture chemical similarity. Figure 3C is a Luche reduction that needs a Lewis acid catalyst to selectivity reduce the carbonyl, and the model recognizes this specificity by suggesting cerium(III).35Figure 3D is a Buchwald–Hartwig aryl amination that uses BINAP as the ligand.36 The metal atoms, ligands, the base, and the solvents are all correctly predicted by the model. Figure 3E,F is a Suzuki–Miyaura coupling reaction37 and Grubbs metathesis,38 respectively, for which the model also successfully predicts the exact chemical context.
It is worth pointing out the success of predicting the context of catalytic reactions is partially attributable to a data cleaning step that moves transition metal compounds from the reagents field to the catalyst field. This only increases the overall accuracy by a small margin (∼0.5%), but it significantly improves the quality of model predictions for catalytic reactions in the case studies. For example, before data cleaning, Figure 3D had the catalyst predicted as a reagent, and Figure 3E missed the catalyst entirely. A complete list of 62 reactions from 11 reaction types can be found in the Supporting Information, Table S3. Finally, temperature is predicted within a reasonable error from the true temperature (Figure 3 and Supporting Information, Table S3), and examples with large deviations are mostly cases with chemical contexts predicted different from the recorded ones.
As mentioned in the Introduction, we also performed a nearest-neighbor search for these reaction examples, shown in the Supporting Information. The nearest-neighbor search is analogous to searching for similar reactions in reaction databases such as Reaxys or SciFinder. Results in the Supporting Information, Table S6, show that the nearest-neighbor method works comparably well in giving the first suggestion for many examples, but it is more than 10 000 times slower than the neural network method presented here. Therefore, it is prohibitively expensive to evaluate the nearest-neighbor approach on the entire test set, and only a qualitative comparison is given on the examples described above. This suggests that using the trained neural-network model can achieve significantly faster speed in finding reasonable condition recommendations compared to the nearest-neighbor search method, and thus can be better integrated with computer-assisted retrosynthetic programs.
The results in Figure 3 and the Supporting Information, Table S3, show selected results pulled out of the test set of some common classes of reactions such as oxidations, reductions, and coupling reactions. Although these are common reaction classes, there is much diversity in specific conditions to achieve the desired reactivity depending on the structure of the starting materials. The results in Figure 3 demonstrate that specific conditions can be chosen by the model for many reaction classes. We also include in the Supporting Information, Table S4, 100 completely random examples from the test set that will not have the restriction of the 11 reaction classes that we initially pulled examples from. It can be seen that the prediction performance is good for most of these random cases.
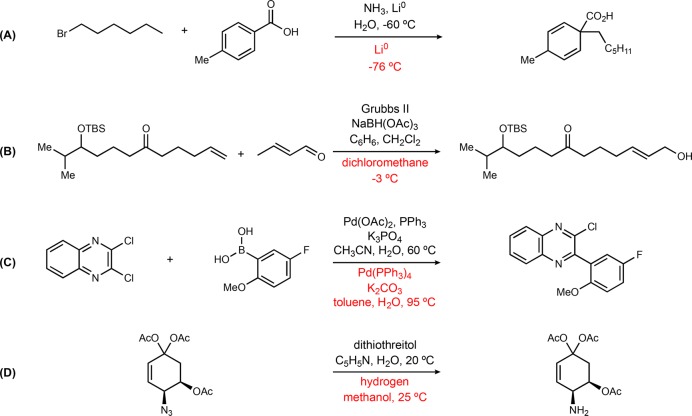
Nevertheless, it is important to also analyze examples with the most incorrect predictions. We calculate the sum of binary variables indicating whether the correct or similar c, s1, s2, r1, and r2 are predicted and use it as a crude measure of “correctness”. The test results are sorted in ascending order of this sum, and examples are drawn from the first 10 000 entries (this is about 1% of reactions from the test set with the quantitatively worst predictions) in the reaction types described above (five for each type, for some types fewer than five as the reactions with labeled reaction types are sparse in the database). A list of 40 reactions are generated and listed in the Supporting Information, Table S5 (part of the examples shown in Figure 4). Even in these ostensibly “worst” cases, many predictions are not unreasonable. Figure 4A represents a common type of data quality issue in the data set, where water is used to quench the reaction but recorded in the same way as other reagents, despite being incompatible and explosive with alkali metals in their pure form.39 However, the model recommends reagents that are commonly used for a dissolving metal reduction reaction. Figure 4B represents another type of problem observed in the data set, where a multistage reaction is recorded as a single transformation.40 In the original reference, the Grubbs reaction and reduction are two isolated steps, which is probably a rare case in the database, and the model fails to recognize these two reactions simultaneously. The top suggestion is indeed poor, whereas the 6th to 10th suggestions all recognize the Grubbs reaction and suggest a Grubbs catalyst (see the Supporting Information, Table S5). In Figure 4C, the model suggests using tetrakis palladium(0) where the true context is palladium(II) and triphenylphosphine which is commonly used to form palladium(0) in situ, so the prediction seems to be a viable context combination for the reaction.41Figure 4D is a case of an azide reduction reaction.42 The model recognizes a reductant is needed, and suggests hydrogen as a first choice. The fourth suggestion of the model include two reagents: 1,3-propanedithiol and triethylamine (Supporting Information, Table S5), which is a more plausible alternative to the recorded reagent. More examples can be found in the Supporting Information, Table S5, and many of the “poorly matching” results are not close to the published procedures but are not altogether unreasonable suggestions.
Figure 4.
Examples of the reactions with the fewest chemical elements matching the recorded context (temperature rounded to the nearest integer; black text represents the recorded conditions, and red text represents the predicted conditions). (A) Birch alkylation. (B) Hoveyda–Grubbs cross metathesis, TBS = tert-butyl(dimethyl)silyl. (C) Suzuki-Miyaura coupling. (D) Azide reduction.
In addition, we include a test of predicting context for Michael addition reactions that are the same as used by Marcou et al.,30 which shows significant improvement; results are presented in the Supporting Information.
Learned Embedding of Solvents and Reagents
While no explicit relationship between chemical species is included in the model, it implicitly learns the functional similarity of solvents and reagents through training, as it can suggest similar chemicals for the same reaction. Taking solvent as an example, the similarity information can be extracted from the neural network, specifically the weight matrix in the last hidden layer before the final likelihood prediction and softmax activation. If two rows in the weight matrix are similar, the model will tend to predict similar scores for the corresponding two solvents. In other words, each solvent can be represented by its corresponding row from the weight matrix. This representation contains information about how it is used in different reactions and can be used to characterize functional similarity, implicitly averaged over all training reactions. This is analogous to the word embedding in natural language modeling where discrete words are converted to vectors of real numbers which contain similarity information (word2vec),43 though we arrive at the representation indirectly, so we call the vector “solvent embedding”.
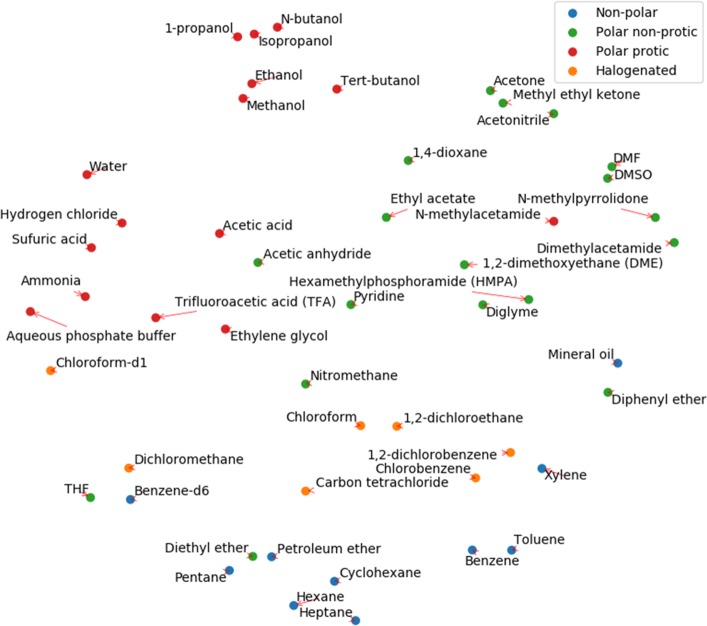
To visualize the embedding of solvents, the top 50 solvents with the highest frequency in the data set are selected, and labeled manually into four types (nonpolar, polar nonprotic, protic, and halogenated). The embeddings of the solvents are normalized to account for their frequency of use and projected into a 2-D space using the t-distributed stochastic neighbor embedding (t-SNE)44 technique, shown in Figure 5. It is worth noting that the solvent embedding vectors do not have a physical interpretation, and t-SNE is a technique that aims to preserve the similarity of the data points in a visualized low-dimensional space. Therefore, the axes on Figure 5 do not have direct meaningful representation. Nevertheless, it can be seen that the solvents of the same type are clustered in the same part of the graph, and we can even observe some chemically reasonable trend across clusters (e.g., increasing polarity from the bottom right to upper left). Some “close-neighbor” pairs agree well with chemical knowledge (e.g., benzene and toluene, methanol and ethanol). The model is not supplied with any information about polarity or other electronic properties, but it learns the difference by the ways that solvents are used in various reactions.
Figure 5.
Embedding of the most common 50 solvents projected onto a two-dimensional space using t-SNE. Solvents are naturally clustered into their corresponding classes (manually annotated).
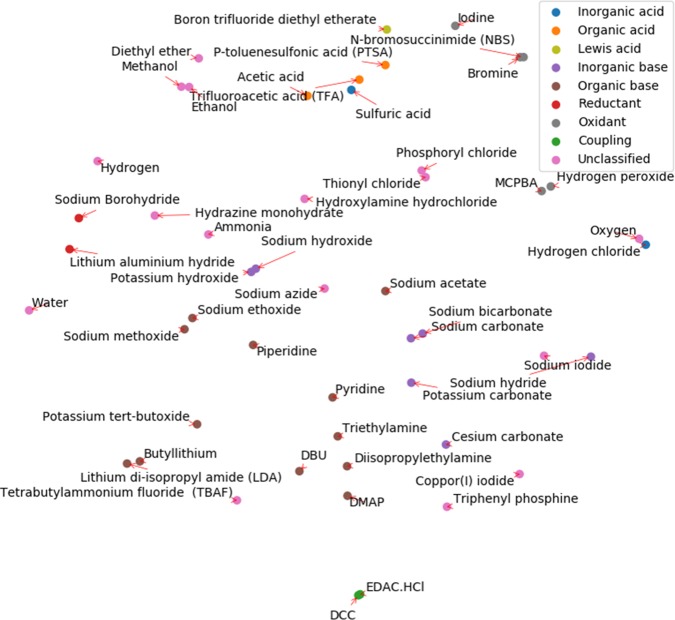
The same plot for the most common 50 reagent embedding is shown in Figure 6. The functionality of reagents is more diverse than solvents, and the label list includes inorganic acid, organic acid, Lewis acid, inorganic base, organic base, reductant, oxidant, and activating reagents. While a 2-D projection might be insufficient to fully represent the variance of functionality, it can be observed that reagents of similar function are reasonably clustered in the same area of the plot. Additionally, incompatible reagents are segregated from each other (e.g., acids and bases, reductants and oxidants) demonstrating the ability of the model to not only recommend similar reagents but also lower the chance of recommending reagents that will likely to be reactive with one another.
Figure 6.
Embedding of the most common 50 reagents projected onto a two-dimensional space using t-SNE. Reagents are naturally clustered into their corresponding classes (manually annotated).
The solvent and reagent embeddings extracted from the condition recommendation model demonstrate the possibility of understanding chemical functionality through reaction data, and have many potential applications. Most directly, it can be used as a tool to identify the closest alternative for the currently used solvents/reagents that are, for example, less toxic, cheaper, etc. It can also be used as input features for other machine learning problems that are context dependent, e.g., evaluation of reaction outcomes and solvent/reagent property estimation.
Strengths and Limitations
The neural-network model developed in this work overcomes many of the challenges described in the Introduction as summarized below:
-
(1)
By training on ∼10 million reactions from Reaxys, the model covers a wide range of organic reactions.
-
(2)
With a hierarchical neural network, the model predicts all the elements in the reaction condition sequentially with interdependence and relatively high accuracy.
-
(3)
The chemicals are not precategorized into classes so predictions can point to the specific chemicals that might, for example, be used as either an acid or an oxidant based on the reaction (e.g., sulfuric acid). On the other hand, individual chemical species are modeled as separate entities so that functional similarity can be learned during training and extracted from the model.
-
(4)
The model recommends reaction conditions much faster (less than 100 ms for one reaction) than nearest-neighbor search methods, and allows quantitative evaluation of model predictions on a large scale. It can also be used for efficient condition recommendation for a large number of reactions suggested by computer-assisted retrosynthetic analysis. The reaction conditions can be utilized by forward evaluation tools to better predict reactivity, especially for condition dependent reactions. In addition, the learned embeddings of solvents and reagents can be used to quantify similarity of conditions of sequential reactions to estimate separation requirements, and to find potential green alternatives to toxic solvents/reagents, both of which are helpful for pathway-level route screening and prioritization.
Meanwhile, the current model also has some limitations, as summarized below:
-
(1)
Since the chemical context is predicted in a sequential manner, we must limit number of predictions at each stage to obtain approximate top-10 combinations in a short time period (similar to a beam search).
-
(2)
Truncating the data based on minimal frequencies of catalysts, reagents, and solvents lowers the total number of trainable parameters and avoids data sparsity issues during training, but also limits the ability to predict rare contexts that are used by highly specific reactions.
-
(3)
There are various other limitations imposed by the imperfection of the training data. For example, even after filtering, some reactions with multiple transformations remain which confuses model prediction, and the labeling of reagents is sometimes misleading (e.g., quenching chemicals included as a reagent); there are some duplicated records or different labels for the same chemical. While these situations are relatively uncommon in the entire data set, a better curated data set can potentially further improve the model performance.
Methods
Overview
The task of condition prediction can be divided into two parts: chemical context prediction (catalysts, solvents, reagents) is treated as a set of multiclass classification problems (i.e., choosing chemical species from a fixed list), while temperature prediction is treated as a regression problem. Pressure is not considered in this scope because the majority of published reactions of interest are run at atmospheric pressure, and databases often do not record pressure for such cases. Concentration is also not considered because it is excluded from tabulated reaction databases, although sparse information is available in the form of mass or volume of some chemical species. As mentioned in the introduction, all these parts should be linked together in one model to solve these classification and regression problems in a hierarchical formulation to account for the interconnectedness of, e.g., solvent and catalyst selection. We choose to use neural networks to construct the model architecture, because of their flexibility to recognize highly nonlinear relationships and because the size and diversity of the data warrant a high-capacity model. The model is trained on published reaction data from Reaxys8 to predict the recorded reaction conditions, after which we are able to infer suitable reaction conditions for novel reactions.
Data
We construct our training set starting from the Reaxys reaction database that consists of 53 million reaction records. The information we use includes the simplified molecular-input line-entry system (SMILES) strings of the reactants and products, the Reaxys chemical ID and SMILES (if available) or name for the catalysts, solvents and reagents, and the temperature for the reactions. Note that in this context reagents are explicitly distinct from reactants, with the former generally not contributing carbon atoms to the reaction (typical reagents include acids, bases, oxidants, reductants, etc.). We restrict our analysis to single-product and single-step reactions to better align with the application to computer-aided synthesis planning. In this context, single-product reactions are defined as Reaxys reaction entries with only one recorded major product. Few entries have multiple products (e.g., specifying all outcomes in cases of ambiguous site selectivity), only 6.3% in this data set. Reactions are preannotated to specify the number of reaction steps associated with the recorded transformation; this attribute is used to filter out all multistep reactions. Some reaction examples passing this filter could still be considered as requiring multiple steps (as shown in the Results section), but it is otherwise hard to systematically distinguish between single- and multi-step reactions purely based on reactant and product structures. Reactions without recorded structures (half reactions) or with structures that could not be parsed by RDKit45 are removed. We also discard reaction entries with no reaction condition information (i.e., no catalyst, no solvent, no reagent, and no temperature), and restrict the maximum number of unique solvents and reagents per reaction to two per category, which will be further explained in the Model Structure section. We also note that there is some ambiguity between catalysts and reagents in Reaxys—many catalysts are recorded as reagents, causing the data to be sparser for catalysts and increasing the number of distinct reagents. This issue can hardly be eliminated completely since a strict separation between reagents and catalyst is difficult to achieve. As a data cleaning step to mitigate this issue, all chemicals that appear as catalysts or reagents that include transition metals in the name are marked as “catalyst exclusive” and consolidated to the catalyst field.
For the remaining 12.1 million reaction examples, we analyze the frequency of each solvent, reagent, and catalyst species. A minimum frequency filter is applied to remove rare catalysts, solvents, and reagents. Rare chemical species significantly increase the number of classes over which the condition prediction will be made, introducing concerns over data sparsity, and including them contributes little to model coverage (frequency vs rank plots for catalysts, reagents, and solvents are provided in the Supporting Information, Figures S1–S3). A minimum frequency of 100 is applied to solvents, reagents, and catalysts. The final number of classes—distinct chemical species—for solvents is 232, for reagents is 2247, and for catalysts is 803; this is an appreciable reduction from the original 11 246, 151 214, and 10 323, respectively. Meanwhile, the number of reactions filtered out by this criterion is only 676 848, around 5% of the total reactions. The number of reactions filtered out by each criterion is listed in Table 2.
Table 2. Number of Reactions by Each Filter Criterion.
| criterion | number of reactions |
|---|---|
| originally from Reaxys | 53 143 003 |
| temperature out of range | 56 235 |
| multistep | 23 536 281 |
| multiproduct | 3 335 439 |
| missing SMILES (including half reactions) | 92 472 |
| cannot be sanitized by RDKit | 1 693 625 |
| no condition information | 9 684 738 |
| exceeding one catalyst, two solvents, or two reagents | 2 645 058 |
| using rare catalysts, solvents, or reagents | 676 848 |
| final data set | 11 422 307 |
Temperature is treated as a continuous variable. For those reactions whose temperature is recorded as a range (e.g., 0–20 °C), the midpoint of the range is used. We require the reaction temperature to be within −100 and 500 °C, which comfortably contains the vast majority of organic transformations and only excludes chemistry outside the scope of this study (e.g., hydrocarbon cracking). After the full data preprocessing pipeline, there are a total of 11.4 M reaction records that result in the final data set.
Molecular Representation
Morgan circular fingerprints, as implemented in RDKit (with radius 2, calculated as bit vectors with length 16 384, stereochemistry information included, and feature-based invariants are not used),45 are used to represent reactants and product species, as they are a commonly used descriptor of organic molecules.11,15,46 Catalysts, solvents, and reagents are directly represented as one-hot vectors, with each different chemical species (more precisely, each chemical entity with a unique ID in Reaxys) representing a unique class. A NULL class is added for each element, to represent reactions where the corresponding element is not recorded (e.g., no reagent, etc.). The lack of a well-defined chemical structure for certain species (e.g., air) precludes a richer descriptor-based representation, and we find a one-hot representation to work well in practice.
Model Structure
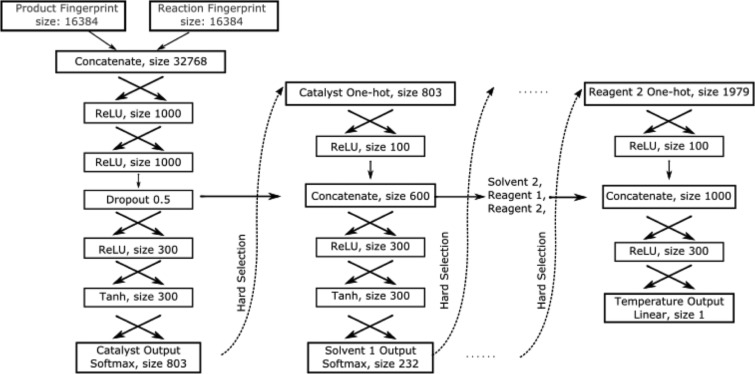
The neural network takes the product fingerprint and reaction fingerprint as two inputs. A reaction fingerprint is calculated as the difference between product fingerprint and reactant fingerprint, which represents the substructures that change during the reaction.46 Predictions are made sequentially so that information from precedent elements can be incorporated into the prediction of subsequent elements (e.g., the prediction of solvent will depend on what catalyst is chosen). Temperature is the final output of the model, such that it relies on the chemical context recommendations. The workflow of the model (shown graphically in Figure 7) is as follows:
-
(1)
Reaction and product fingerprints are concatenated and passed through two fully connected layers (ReLU activation, size 1000; ReLU activation, size 1000, with a 0.5 dropout) to generate a dense representation of the fingerprints (referred to as Dense FP).
-
(2)
Dense FP is passed through two fully connected layers (ReLU activation, size 300; Softmax activation, size 803) to predict the catalyst (or NULL) for the reaction.
-
(3)
The one-hot vector of the catalyst prediction is then concatenated with Dense FP and passed through two fully connected layers (ReLU activation, size 300; Softmax activation, size 232) to predict the first solvent (or NULL).
-
(4)
Step 3 is repeated for prediction of the second solvent (size 228), the first reagent (size 2240), and the second reagent (size 1979). The numbers are smaller than the total class of solvents/reagents because some solvents/reagents are only present in one of the fields (i.e., only as Solvent/Reagent 1 or Solvent/Reagent 2).
-
(5)
One-hot vectors of the catalyst, solvents, and reagents and Dense FP are all concatenated and passed through two fully connected layers (ReLU activation, size 300; Linear activation, size 1) to predict the temperature.
Figure 7.
Graphical representation of the neural-network model for context recommendation (“Hard Selection” refers to setting the value of the maximal element to one and zero for the rest, although the output of each classification task is a probability distribution).
Notable features of the model construction are as follows:
-
(1)
One feature is the order of the prediction tasks. The earlier it appears in the model, the more that task is able to be performed solely based on the reaction, independent of the other predictions. We experimented with predicting single elements using fingerprint information only and found that the validation accuracy (top-one accuracy) is highest for catalyst (92.1%), and similar for solvent and reagent (60.6% and 60.6%, respectively). This is consistent with how chemists generally approach this problem manually, i.e., identify if the reaction requires a catalyst. Reagents are placed last in the sequential prediction, so that information about catalyst and solvent selection is included in predicting reagents, which have the most unique possibilities and a greater level of flexibility even when the catalysts and solvents are fixed.
-
(2)
Another feature is the number of catalysts, solvents, and reagents for each reaction. Most of the reactions in the data set have no catalyst or at most one catalyst recorded, so the number of catalysts is limited to one. A majority of reactions use one solvent, but there are still many examples that use multiple solvent or multiple reagent combinations. Few reactions in the data set use three or more solvents or reagents, so limiting the number of solvents and reagents to two for each category keeps the model in a reasonable size. The final model has 38 M parameters.
Training and Evaluation
The data set is split randomly into training/validation/test sets with a ratio of 80/10/10. The time-split strategy is not used because, in practice, the model for condition recommendation is likely to be mainly used for interpolating and generalizing historical condition information to new substrates, but not designing fundamentally novel conditions that have not been previously discovered. It is worth noting that there can be multiple records for the same reaction, possibly happening under different conditions. When multiple records of the same reaction exist (i.e., if multiple reactions share the same reactants and products, which is quite common), they are grouped during shuffling to guarantee that the reactions in the test set are not present in the training set. Our model has intermediate outputs (catalysts, solvents, and reagents) that are used as input for the next prediction, which resembles the features of a recurrent neural network, so we apply the teacher forcing technique47 during training. It takes the ground truth output, instead of the predicted ones, as the input for the next prediction task. This technique has been shown to increase stability and accuracy of the training. Categorical cross-entropy is used as the loss function for the classification problems (i.e., catalysts, solvents, and reagents), and mean squared error is used for regression (i.e., temperature). A weighting factor of 0.001 is applied to temperature so that the numeric values of the loss functions are approximately on the same scale. Training continues until the validation loss does not improve over five epochs.
Evaluation is performed both quantitatively and qualitatively. We calculated the accuracy of the true combined chemical context as well as individual elements to be within the top-three and top-10 predicted combinations. Additionally, we extend this accuracy calculation to include some “close match” predictions. The similarity of solvents is characterized by the Euclidean distance between the Abraham parameters28 of the two solvents if the parameters are available, and otherwise only exact matches are considered. The methanol–ethanol pair is used as a threshold to identify solvents that are close matches. Catalysts and reagents are classified as close matches if they have the same metal atoms (for organometallic compounds) or if their feature-based Morgan fingerprints are exactly the same. The feature definitions are as implemented in RDKit, adapted from the definitions in Gobbi et al.,48 which define some invariants that share the same feature, such as “halogen” (e.g., −Cl and −Br), “hydrogen bond donor” (−SH and −OH), and unusual atoms (not H, C, N, O, F, S, Cl, Br, I; e.g., Na+ and K+). A complete table of feature definitions is included in the Supporting Information (Table S8).
For temperature, we calculated the percentage of cases when the temperature is predicted to be within ±10 and ±20 °C of the recorded temperature.
Besides the quantitative analysis, examples were chosen from common types of chemical reactions to demonstrate the wide applicability of the model and provide more insights into the model prediction characteristics. Successful and unsuccessful predictions in the test set are presented and analyzed to demonstrate the performance of the model. In comparison, the performance of the nearest-neighbor model on these reactions is also tested, and results are discussed in the Supporting Information.
This is a computational study, and we do not expect high safety hazards to be encountered.
Conclusion
A neural network model was developed for the task of reaction condition recommendation. Using a hierarchical design and training on about 10 million reactions from Reaxys, the model gives recommendations on the catalyst, solvent, reagent, and temperature to be used for any organic reaction. The model is tested on 1 million reactions outside the training set, and is able to recover a context combination with the catalyst and at least one solvent and reagent close to the true context in the top-10 predictions in 69.6% of those cases. Qualitative evaluation on common types of reactions reveals that the model can predict the exact conditions or predict conditions that have the same functionality as the true conditions. Many failed predictions are due to highly specific reactivity or data inconsistencies. Solvent and reagent embeddings are extracted from the trained model, and the visualization of them demonstrates that these representations capture the functional similarity. The context information generated by this tool can be used to aid experimental design, improve accuracy of in silico evaluation of reactivity and pathway-level evaluation, and improve chemical synthesis processes.
Acknowledgments
This work was supported by the DARPA Make-It program under Contract ARO W911NF-16-2-0023. We thank Elsevier for the permission to access the Reaxys API to obtain detailed information on the reaction records. The code and models are available online at https://github.com/Coughy1991/Reaction_condition_recommendation. A user-friendly web module is available at http://askcos.mit.edu/context.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.8b00357.
Description of computational methods, frequency vs rank plots, extended lists of reaction examples, and comparison of the model performance against baseline models (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Robinson R. LXIII.–A Synthesis of Tropinone. J. Chem. Soc., Trans. 1917, 111 (0), 762–768. 10.1039/CT9171100762. [DOI] [Google Scholar]
- Corey E. J.; Wipke W. T. Computer Assisted Design of Complex Organic Syntheses. Science (Washington, DC, U. S.) 1969, 166 (3902), 178–192. 10.1126/science.166.3902.178. [DOI] [PubMed] [Google Scholar]
- Cook A.; Johnson A. P.; Law J.; Mirzazadeh M.; Ravitz O.; Simon A. Computer-Aided Synthesis Design: 40 Years On. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2 (1), 79–107. 10.1002/wcms.61. [DOI] [Google Scholar]
- Warr W. A. A Short Review of Chemical Reaction Database Systems, Computer-Aided Synthesis Design, Reaction Prediction and Synthetic Feasibility. Mol. Inf. 2014, 33 (6–7), 469–476. 10.1002/minf.201400052. [DOI] [PubMed] [Google Scholar]
- Engkvist O.; Norrby P. O.; Selmi N.; Lam Y. H.; Peng Z.; Sherer E. C.; Amberg W.; Erhard T.; Smyth L. A. Computational Prediction of Chemical Reactions: Current Status and Outlook. Drug Discovery Today 2018, 23 (6), 1203–1218. 10.1016/j.drudis.2018.02.014. [DOI] [PubMed] [Google Scholar]
- Coley C. W.; Green W. H.; Jensen K. F. Machine Learning in Computer-Aided Synthesis Planning. Acc. Chem. Res. 2018, 51 (5), 1281–1289. 10.1021/acs.accounts.8b00087. [DOI] [PubMed] [Google Scholar]
- Goodman J. M. Reaction Prediction and Synthesis Design. Appl. Chemoinformatics Achiev. Futur. Oppor. 2018, 86–105. 10.1002/9783527806539.ch4b. [DOI] [Google Scholar]
- Reaxys. https://new.reaxys.com/ (accessed on Sept 28, 2017).
- Lowe D. M.Patent Reaction Extractor (v1.0); 2014.
- Szymkuć S.; Gajewska E. P.; Klucznik T.; Molga K.; Dittwald P.; Startek M.; Bajczyk M.; Grzybowski B. A. Computer-Assisted Synthetic Planning: The End of the Beginning. Angew. Chem., Int. Ed. 2016, 55 (20), 5904–5937. 10.1002/anie.201506101. [DOI] [PubMed] [Google Scholar]
- Segler M. H.S.; Preuss M.; Waller M. P.. Learning to Plan Chemical Syntheses. 2017, arXiv:1708.04202. arXiv.org e-Print archive. https://arxiv.org/abs/1708.04202.
- Law J.; Zsoldos Z.; Simon A.; Reid D.; Liu Y.; Khew S. Y.; Johnson A. P.; Major S.; Wade R. A.; Ando H. Y. Route Designer: A Retrosynthetic Analysis Tool Utilizing Automated Retrosynthetic Rule Generation. J. Chem. Inf. Model. 2009, 49 (3), 593–602. 10.1021/ci800228y. [DOI] [PubMed] [Google Scholar]
- Liu B.; Ramsundar B.; Kawthekar P.; Shi J.; Gomes J.; Luu Nguyen Q.; Ho S.; Sloane J.; Wender P.; Pande V. Retrosynthetic Reaction Prediction Using Neural Sequence-to-Sequence Models. ACS Cent. Sci. 2017, 3 (10), 1103–1113. 10.1021/acscentsci.7b00303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bøgevig A.; Federsel H.-J.; Huerta F.; Hutchings M. G.; Kraut H.; Langer T.; Löw P.; Oppawsky C.; Rein T.; Saller H. Software Tool as an Idea Generator for Synthesis Prediction. Org. Process Res. Dev. 2015, 19 (2), 357–368. 10.1021/op500373e. [DOI] [Google Scholar]
- Coley C. W.; Rogers L.; Green W. H.; Jensen K. F. Computer-Assisted Retrosynthesis Based on Molecular Similarity. ACS Cent. Sci. 2017, 3 (12), 1237–1245. 10.1021/acscentsci.7b00355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Segler M. H.S.; Preuss M.; Waller M. P. Planning Chemical Syntheses with Deep Neural Networks and Symbolic AI. Nature 2018, 555 (7698), 604–610. 10.1038/nature25978. [DOI] [PubMed] [Google Scholar]
- Kayala M. A.; Baldi P. F. Learning to Predict Chemical Reactions. J. Chem. Inf. Model. 2011, 51 (9), 2209–2222. 10.1021/ci200207y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kayala M. A.; Baldi P. ReactionPredictor: Prediction of Complex Chemical Reactions at the Mechanistic Level Using Machine Learning. J. Chem. Inf. Model. 2012, 52 (10), 2526–2540. 10.1021/ci3003039. [DOI] [PubMed] [Google Scholar]
- Segler M. H.S.; Waller M. P. Neural-Symbolic Machine Learning for Retrosynthesis and Reaction Prediction. Chem. - Eur. J. 2017, 23 (25), 5966–5971. 10.1002/chem.201605499. [DOI] [PubMed] [Google Scholar]
- Jin W.; Coley C. W.; Barzilay R.; Jaakkola T.. Predicting Organic Reaction Outcomes with Weisfeiler-Lehman Network, 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA; 2017; pp 2604–2613.
- Coley C. W.; Barzilay R.; Jaakkola T. S.; Green W. H.; Jensen K. F. Prediction of Organic Reaction Outcomes Using Machine Learning. ACS Cent. Sci. 2017, 3 (5), 434–443. 10.1021/acscentsci.7b00064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwaller P.; Laino T.. “Found in Translation”: Predicting Outcomes of Complex Organic Chemistry Reactions Using Neural Sequence-to-Sequence Models. 2017, arXiv:1711.04810. arXiv.org e-Print archive. https://arxiv.org/abs/1711.04810. [DOI] [PMC free article] [PubMed]
- Reizman B. J.; Jensen K. F. Simultaneous Solvent Screening and Reaction Optimization in Microliter Slugs. Chem. Commun. 2015, 51 (68), 13290–13293. 10.1039/C5CC03651H. [DOI] [PubMed] [Google Scholar]
- Sans V.; Porwol L.; Dragone V.; Cronin L. A Self Optimizing Synthetic Organic Reactor System Using Real-Time In-Line NMR Spectroscopy. Chem. Sci. 2015, 6 (2), 1258–1264. 10.1039/C4SC03075C. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmes N.; Akien G. R.; Savage R. J.D.; Stanetty C.; Baxendale I. R.; Blacker A. J.; Taylor B. A.; Woodward R. L.; Meadows R. E.; Bourne R. A. Reaction Chemistry & Engineering Online Quantitative Mass Spectrometry for the Reactors †. React. Chem. Eng. 2016, 1 (1), 96–100. 10.1039/C5RE00083A. [DOI] [Google Scholar]
- Reizman B. J.; Jensen K. F. Feedback in Flow for Accelerated Reaction Development. Acc. Chem. Res. 2016, 49 (9), 1786–1796. 10.1021/acs.accounts.6b00261. [DOI] [PubMed] [Google Scholar]
- Baumgartner L. M.; Coley C. W.; Reizman B. J.; Gao K. W.; Jensen K. F. Optimum Catalyst Selection over Continuous and Discrete Process Variables with a Single Droplet Microfluidic Reaction Platform. React. Chem. Eng. 2018, 3 (3), 301–311. 10.1039/C8RE00032H. [DOI] [Google Scholar]
- Kamlet M. J.; Abboud J. L.M.; Abraham M. H.; Taft R. W. Linear Solvation Energy Relationships. 23. A Comprehensive Collection of the Solvatochromic Parameters,.Pi.*,.Alpha., and.Beta., and Some Methods for Simplifying the Generalized Solvatochromic Equation. J. Org. Chem. 1983, 48 (17), 2877–2887. 10.1021/jo00165a018. [DOI] [Google Scholar]
- Struebing H.; Ganase Z.; Karamertzanis P. G.; Siougkrou E.; Haycock P.; Piccione P. M.; Armstrong A.; Galindo A.; Adjiman C. S. Computer-Aided Molecular Design of Solvents for Accelerated Reaction Kinetics. Nat. Chem. 2013, 5 (11), 952–957. 10.1038/nchem.1755. [DOI] [PubMed] [Google Scholar]
- Marcou G.; Aires De Sousa J.; Latino D. A.R.S.; De Luca A.; Horvath D.; Rietsch V.; Varnek A. Expert System for Predicting Reaction Conditions: The Michael Reaction Case. J. Chem. Inf. Model. 2015, 55 (2), 239–250. 10.1021/ci500698a. [DOI] [PubMed] [Google Scholar]
- Lin A. I.; Madzhidov T. I.; Klimchuk O.; Nugmanov R. I.; Antipin I. S.; Varnek A. Automatized Assessment of Protective Group Reactivity: A Step toward Big Reaction Data Analysis. J. Chem. Inf. Model. 2016, 56 (11), 2140–2148. 10.1021/acs.jcim.6b00319. [DOI] [PubMed] [Google Scholar]
- Segler M. H.S.; Waller M. P. Modelling Chemical Reasoning to Predict and Invent Reactions. Chem. - Eur. J. 2017, 23 (25), 6118–6128. 10.1002/chem.201604556. [DOI] [PubMed] [Google Scholar]
- Mikie Kanada R.; Taniguchi T.; Ogasawara K. Asymmetric Hydrogen Transfer Protocol for a Synthesis of (+)-Frontalin and (−)-Malyngolide. Tetrahedron Lett. 2000, 41 (19), 3631–3635. 10.1016/S0040-4039(00)00430-5. [DOI] [Google Scholar]
- Faroux-Corlay B.; Clary L.; Gadras C.; Hammache D.; Greiner J.; Santaella C.; Aubertin A. M.; Vierling P.; Fantini J. Synthesis of Single- and Double-Chain Fluorocarbon and Hydrocarbon Galactosyl Amphiphiles and Their Anti-HIV-1 Activity. Carbohydr. Res. 2000, 327 (3), 223–260. 10.1016/S0008-6215(00)00055-0. [DOI] [PubMed] [Google Scholar]
- Wang H.; Yu S. Synthesis of Isoquinolones Using Visible-Light-Promoted Denitrogenative Alkyne Insertion of 1,2,3-Benzotriazinones. Org. Lett. 2015, 17 (17), 4272–4275. 10.1021/acs.orglett.5b01960. [DOI] [PubMed] [Google Scholar]
- Li K.; Zeng Y.; Neuenswander B. Sequential Pd (II) -Pd (0) Catalysis for the Rapid Synthesis of Coumarins. J. Org. Chem. 2005, 70 (16), 6515–6518. 10.1021/jo050671l. [DOI] [PubMed] [Google Scholar]
- Mavunkel B.; Xu Y.; Goyal B.; Lim D.; Lu Q.; Chen Z.; Wang D.-X.; Higaki J.; Chakraborty I.; Liclican A. Pyrimidine-Based Inhibitors of CaMKIIδ. Bioorg. Med. Chem. Lett. 2008, 18 (7), 2404–2408. 10.1016/j.bmcl.2008.02.056. [DOI] [PubMed] [Google Scholar]
- Lautens M.; Maddess M. L. Chemoselective Cross Metathesis of Bishomoallylic Alcohols : Rapid Access to Fragment A of the Cryptophycins. Supplementary Material The Following Includes Representative Experimental Procedures and Details for Isolation of Compounds. Full Characterisat. Org. Lett. 2004, 6 (12), 1883–1886. 10.1021/ol049883f. [DOI] [PubMed] [Google Scholar]
- Krüger T.; Vorndran K.; Linker T. Regioselective Arene Functionalization: Simple Substitution of Carboxylate by Alkyl Groups. Chem. - Eur. J. 2009, 15 (44), 12082–12091. 10.1002/chem.200901774. [DOI] [PubMed] [Google Scholar]
- Palmes J. A.; Paioti P. H.S.; De Souza L. P.; Aponick A. PdII-Catalyzed Spiroketalization of Ketoallylic Diols. Chem. - Eur. J. 2013, 19 (35), 11613–11621. 10.1002/chem.201301723. [DOI] [PubMed] [Google Scholar]
- Liu J.; Fitzgerald A. E.; Mani N. S. Facile Assembly of Fused Benzo[4,5]Furo Heterocycles. J. Org. Chem. 2008, 73 (7), 2951–2954. 10.1021/jo8000595. [DOI] [PubMed] [Google Scholar]
- Schaub C.; Müller B.; Schmidt R. R. Sialyltransferase Inhibitors Based on CMP-Quinic Acid. Eur. J. Org. Chem. 2000, 2000 (9), 1745–1758. . [DOI] [PubMed] [Google Scholar]
- Mikolov T.; Sutskever I.; Chen K.; Corrado G. S.; Dean J.. Distributed Representations of Words and Phrases and Their Compositionality. In Advances in neural information processing systems; NIPS: Lake Tahoe, 2013; pp 3111–3119.
- García-Alonso C. R.; Pérez-Naranjo L. M.; Fernández-Caballero J. C. Multiobjective evolutionary algorithms to identify highly autocorrelated areas: the case of spatial distribution in financially compromised farms. Ann. Oper. Res. 2014, 219 (1), 187–202. 10.1007/s10479-011-0841-3. [DOI] [Google Scholar]
- Open-source. RDKit: Open-Source Cheminformatics Software, 2006. (accessed on Sept 28, 2017).
- Schneider N.; Lowe D. M.; Sayle R. A.; Landrum G. A. Development of a Novel Fingerprint for Chemical Reactions and Its Application to Large-Scale Reaction Classification and Similarity. J. Chem. Inf. Model. 2015, 55 (1), 39–53. 10.1021/ci5006614. [DOI] [PubMed] [Google Scholar]
- Williams R. J.; Zipser D. A Learning Algorithm for Continually Running Fully Recurrent Neural Networks. Neural Comput. 1989, 1 (2), 270–280. 10.1162/neco.1989.1.2.270. [DOI] [Google Scholar]
- Gobbi A.; Poppinger D. Genetic Optimization of Combinatorial Libraries. Biotechnol. Bioeng. 1998, 61 (1), 47–54. . [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.