Soft-Tissue Aberration Correction for Histotripsy

Abstract

Acoustic aberrations caused by natural heterogeneities of biological soft-tissue are a substantial problem for histotripsy, a therapeutic ultrasound technique that uses acoustic cavitation to mechanically fractionate and destroy unwanted target tissue without damaging surrounding tissue. These aberrations, primarily caused by sound speed variations, result in severe defocusing of histotripsy pulses thereby decreasing treatment efficacy. The gold standard for aberration correction (AC) is to place a hydrophone at the desired focal location to directly measure phase aberrations, which is a method that is infeasible in vivo. We hypothesized that the acoustic cavitation emission (ACE) shockwaves from the initial expansion of inertially cavitating microbubbles generated by histotripsy can be used as a point source for AC. In this study, a 500-kHz, 112-element histotripsy phased array capable of transmitting and receiving ultrasound on all channels was used to acquire ACE shockwaves. These shock-waves were first characterized optically and acoustically. It was found that the shockwave pressure increases significantly as the source changes from a single bubble to a dense cavitation cloud. The first arrival of the shockwave received by the histotripsy array was from the outer-most cavitation bubbles located closest to the histotripsy array. Hydrophone and ACE AC methods were then tested on ex vivo porcine abdominal tissue samples. Without AC, the focal pressure is reduced by 49.7% through the abdominal tissue. The hydrophone AC approach recovered 55.5% of the lost pressure. Using the ACE AC method, over 20% of the lost pressure was recovered, and the array power required to induce cavitation was reduced by approximately 31.5% compared to without AC. These results supported our hypothesis that the ACE shockwaves coupled with a histotripsy array with transmit and receive capability can be used for aberration correction for histotripsy through soft-tissue.

I. Introduction

The speed of sound in biological soft-tissue can vary by over 10% between tissue types [1,2,3]. These variations, caused by natural heterogeneities in tissue, result in phase aberrations of ultrasound pulses. For therapeutic ultrasound, phase aberrations are the primary source of overall acoustic aberration and can cause severe decorrelation of transmit waveforms thus altering the arrival time of ultrasound pulses emitted by different portions of a therapy array [4]. This effect can reduce the treatment efficacy and, in some cases, prevents treatment altogether [5,6].

Many aberration correction techniques have been developed for therapeutic ultrasound, and these typically fall into two categories. The first involves using an alternative imaging modality to ultrasound, e.g., magnetic resonance imaging (MRI) or x-ray computed tomography (CT), to obtain pre-operative information about the tissue overlying the target treatment area [7,8,9,10]. This tissue information is then used to estimate sound speed variations across the flight-path of the therapy array and then correct for these variations by applying appropriate phase delays across the elements of a therapy array. While these techniques have been shown to be somewhat successful, especially for transcranial therapies due to the highly aberrating nature of the skull, the efficacy of aberration correction using these methods is less than desired for several reasons. First, these methods only measure the tissue thickness, so several assumptions need to be made to estimate the sound speed. However, the speed of sound for a specific tissue (e.g., skin, skull, liver) varies across patients and even across locations within the same patient [3]. Second, the corrections acquired from these techniques degrade if the patient moves with respect to the ultrasound therapy array. The second category involves using point targets to correct for acoustic aberrations. These techniques were originally developed for ultrasound imaging [2,11,12,13,14,15] and rely on the existence of sparse, point scatters or sources in the area being imaged, which is not typically the case in biological tissues. By measuring the arrival time variations of sound from a point source across all elements of an ultrasound array, the overall time-of-flight variation from the location of the point source to each element can be accurately estimated. From this information, an ultrasound array can be phased to correct for these variations. It has been shown that cavitation bubbles could be used as a point source for this method [6]. However, cavitation can be difficult to control and maintain in both ultrasound imaging and thermally-based ultrasound therapies, which typically aim to reduce cavitation [16,17]. Others have suggested a similar approach in which liquid perfluorocarbon droplets are used as point-targets via acoustic droplet vaporization (ADV) [18,19]. However, this technique requires the injection of the droplet contrast agent, which is neither always desirable nor always feasible depending on the treatment and location. Furthermore, it is difficult to guarantee that the droplets will be in the precise location at which aberration correction is needed.

Histotripsy is a therapeutic ultrasound technique that employs the mechanical forces of highly controlled acoustic cavitation to non-invasively and non-thermally destroy unwanted target tissue [20,21,22,23]. When used via the intrinsic threshold mechanism, histotripsy initiates a cloud of cavitating microbubbles by transmitting a 1–2 cycle length ultrasound pulse with a high-amplitude negative phase, which exceeds an intrinsic threshold to generate cavitation in the target tissue (~28 MPa peak negative (rarefactional) pressure in water-based soft tissue) [24,25]. When a histotripsy pulse arrives at the focus of the array, existing cavitation nuclei in the target medium rapidly expand to multiple orders of magnitude larger than their original size [26,27]. For a single bubble, it is known that this rapid period of expansion emits a shockwave that is focused about the center of the bubble [28,29,17]. For a cloud of cavitating bubbles generated with histotripsy, the same shockwave phenomenon is observed and is known as the acoustic cavitation emission (ACE), but less is known about the nature of this construct of shockwaves [30,31]. It is possible that the cavitation bubbles generated by histotripsy could be used as a point source for aberration correction. However, while the point-source methods for aberration correction are applicable to histotripsy, these methods would require that the histotripsy array be able to receive signals. Histotripsy arrays are traditionally transmit-only systems.

Partially due to this lack of receiver technology, little has been done to correct for acoustic aberrations for histotripsy therapy in real time without a priori knowledge of the propagation medium [32]. The majority of the work on aberration correction for histotripsy has involved placing a hydrophone at the target location and directly measuring the phase aberrations of the pulses emitted by each histotripsy element [33]. This technique has also been previously explored for aberration correction for ultrasonic hyperthermia [34,35]. While this method has shown success for treatments in which a hydrophone can be placed at the target location such as transcranial histotripsy using a catheterized hydrophone [36], this method is infeasible for the majority of histotripsy therapies including most of those in the abdomen and also prevents histotripsy from being a noninvasive surgery. Without aberration correction, histotripsy has been used to produce lesions in in vivo large animal studies [37,38,39], but it is known that overlying soft-tissue causes severe acoustic aberrations resulting in focal pressure loss and reduction in treatment efficacy [40] [41,42,15,43].

Recently, we have developed receive-capable histotripsy arrays, which has enabled the exploration of aberration correction methods. Based on the fact that the histotripsy bubble cloud emits a construct of shockwaves from the target location during the initial phase of bubble cloud expansion, we hypothesize that these shockwaves can be detected by a receive-capable histotripsy array and used as a point-source signal for aberration correction. We further hypothesize that this will result in a significant recovery of pressure at the array focus and a reduction of array power required to initiate the cavitation bubble cloud. In this study, we test these hypotheses through two sets of experiments. In Experiment 1, we characterize the ACE expansion shockwaves from single bubbles and cavitation clouds generated by histotripsy via optical and acoustic measurements. In Experiment 2, we test the efficacy of using the ACE expansion shockwave from a histotripsy cavitation cloud as a point-source for aberration correction through ex vivo multi-layer heterogeneous porcine abdominal tissue.

II. Methods

A. Receive-Capable Histotripsy System

A 112-element, 500-kHz histotripsy array with a 15-cm radius of curvature and 27-cm aperture [44] was used for all experiments in this study. A custom-built, 112-channel, high-voltage pulsing system that generated 1.5-cycle, 3-us sinusoidal pulses was used to drive the transmit portion of the histotripsy array. The array was fired at 1 Hz pulse repetition frequency (PRF) throughout this study. Each transducer element had a diameter of 2 cm. The 112 elements of the histotripsy array were organized into five rings at angles of 20, 30, 40, 50, and 60 degrees relative to the axis of the array with the 20-degree ring being the inner-most ring. From inner-most to outer-most, these five rings consisted of 12, 16, 24, 28, and 32 elements. The histotripsy array was placed facing upwards in a tank filled with filtered, degassed, and deionized water (Fig. 1A) with the surface of the water approximately 6.5 cm above the array focus. The driving system was controlled by a system of field programmable gate arrays (FPGAs), which allowed each array element to be individually addressable to change the phase of the firing pulse across all elements of the array. The array was calibrated using a custom-built fiber optic probe hydrophone (FOPH) with a 100-μm sensing tip [45]. The FOPH measured a free-field −6 dB focal zone beamwidth of 1.65 mm laterally and 6.50 mm axially when measured in the acoustically linear regime at 10 MPa peak-negative pressure (P-). Above this linear region, the pressure could not be measured directly due to cavitation on the FOPH tip. To estimate the P- greater than 10 MPa, the array was fired in subaperture slices that were driven and measured separately and then summed together. The minimum number of subaperture slices was chosen at each measured pressure level to prevent cavitation on the FOPH tip. This subaperture calibration was performed to better estimate the effects of nonlinear propagation at high pressure levels [46]. This calibration was performed up to the maximum output of the array, which resulted in an estimated focal P- pressure of 63 MPa. It should be noted that this focal pressure is an overestimation as it does not completely account for non-linear propagation.

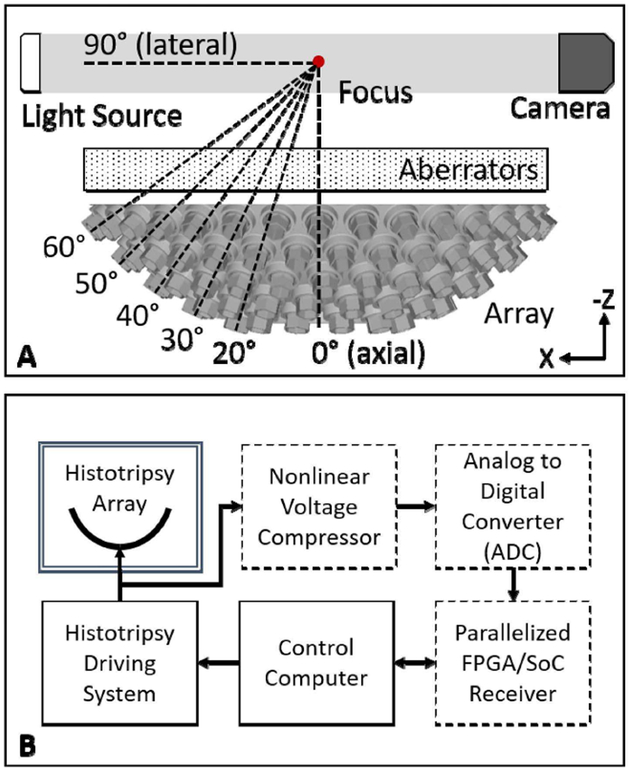
Fig. 1.

(A) 3D rendering of 112-element 500-kHz transducer with angles of each ring relative to the array axis indicated. A light source and camera were placed coaxially along the 90°-axis of the array. For all experiments, aberrators were placed between the array and the focus such that the focal region could be imaged and measured with a hydrophone. (B) High-level overview of receive-capable histotripsy system. A pre-existing histotripsy array was retrofitted with receiver components (dashed line boxes) including the nonlinear voltage compressor, ADCs, and FPGA/SoC-controlled custom receiver.

To enable the array to receive acoustic signals on all channels, the histotripsy system was retrofitted with an in-house, custom-built, 112-channel receiving system (Fig. 1B). Each channel of the receiver was directly connected to one channel of the histotripsy array such that the receiver could record both transmit and receive signals on all channels. To protect sensitive downstream electronics in the receiver, a nonlinear voltage compression isolation circuit was placed on the front-end of each channel of the receiver to attenuate high voltage driving signals (2–3 kV/channel) while preserving low voltage ACE signals (10–20 V/channel). The first component of the compressor was a capacitive voltage divider that attenuated all incoming signals to approximately 10%. The second component was a diode-resistor voltage divider that provided nonlinear attenuation to compress signals above approximately 0.7 Volts. Unlike a typical hard-clipping diode voltage-limiting circuit, the diode-resistor simply compressed the signals thus preserving all information within the waveform. Each receiver channel was then digitized by an 8-bit analog-to-digital converter (ADC) with a 20-MHz sampling rate (ADC1173, Texas Instruments, Inc., Dallas, TX, USA). The digitized signals were received by an FPGA/System-on-a-Chip (SoC) embedded processor (Cyclone V SoC, Intel Corporation, Santa Clara, CA, USA) that was integrated with an off-the-shelf hardware platform (DE0-nano-SoC, Terasic, Inc., Hsinchu, Taiwan, China), which interfaced the FPGA/SoC with requisite peripherals and memory including Ethernet hardware. Each FPGA/SoC system was able to receive digitized signals from eight channels of the histotripsy array. Therefore, the receiver system consisted of fourteen FPGA/SoC systems running in parallel. Each FPGA/SoC was routed via Ethernet to the master control computer that was also controlling the driving system. Thus, both the driving and receiving components of this histotripsy system were controlled from one computer. In this system, the control computer was able to control triggering, sample rate, and record length of the receiver system. For all experiments in this study, 400 μs of data were recorded on all elements of the array at a 20-MHz sampling rate, and all receive channels were triggered simultaneously with the transmit pulse.

B. Experiment 1: Acoustic Cavitation Emission (ACE) Expansion Shockwave Investigation

1). Hydrophone Shockwave Investigation:

ACE expansion shockwaves were investigated acoustically and optically. To investigate their acoustic nature, a low-frequency calibrated, broadband hydrophone (HGL-0085, Onda Corporation, Sunnyvale, CA, USA) was placed at the axial (0°) and lateral (90°) positions relative to the histotripsy array at a distance of 15-cm from the focus. Shockwaves were generated by bubble clouds that were initiated with estimated free-field focal pressures between 33 and 63 MPa (max power) P- pressure. Shockwave pressures and arrival times were recorded at all pressure levels.

2). Optical Shockwave Investigation:

The nature of the shockwaves was investigated optically to better understand the early stages of shockwave initiation, how they change depending on the size of the bubble cloud, and the impacts of these changes on the acoustic nature of the shockwaves. To optically investigate the nature of the shockwaves, a camera (Point Grey Chameleon 3, FLIR Systems, Inc., Richmond, BC, Canada) and macro lens (Macro 100 F2.8D, Tokina Co., Ltd., Tokyo, Japan) were used to acquire shadowgraph images of the bubble cloud with an effective resolution of 14.4 μm/pixel. Shadowgraph imaging is a technique that reveals perturbations in transparent media caused by localized heterogeneities in the refractive index typically due to abrupt temperature or pressure gradients [47]. The camera was back-lit by a custom-built, collimated, high-speed LED light source with a pulse width of approximately 20 ns. Shadowgraph images of bubble clouds and shockwaves were acquired at estimated P- histotripsy focal pressures that generated single cavitation bubbles (28 MPa), multi-bubble clouds (30 MPa), and full-sized, large bubble clouds (63 MPa). The large bubble clouds were the largest bubble clouds that could be generated by the array without risking damaging the array itself, i.e., at maximum power. It should be noted that large bubble clouds can be generated at P- pressures less than 63 MPa, but the aim of this experiment was to show a full range of possibilities across the output range of a typical histotripsy array. Fifteen shadowgraph images were acquired at each pressure level. From these images, the location of the leading-edge of the shockwaves emitted by the expansion of the bubble clouds was measured at angular increments of 10 degrees between the axial and lateral axes of the histotripsy array to investigate the propagation of different regions of the shockwaves for different types of bubble clouds. Reported distances between the focus and the measured portions of the shockwaves were normalized relative to the distance between the focus and the lateral-axis point of the shockwave to provide a metric for propagation difference across the front edge of the shockwaves. Image analysis was performed using custom image processing software (Matlab, The MathWorks, Natick, MA, USA). Differences in shockwave arrival time across all angles for the three bubble cloud types were statistically analyzed using one-way ANOVA with Tukey’s HSD test.

3). Receive-Capable Histotripsy Array Shockwave Investigation:

The nature of the ACE expansion shockwaves was also investigated using the receive-capable histotripsy array. Histotripsy bubble clouds were generated with estimated P-focal pressures between 30 and 63 MPa. Both the amplitude and phase (in cycles) of the leading shockwaves were analyzed for fifteen bubble clouds and compared across pressure levels. Amplitude was defined as the peak-to-peak pressure amplitude of the first shockwave to arrive at each element. Phase was defined as the shockwave arrival time difference across all elements of the array converted to 500 kHz wavelength cycles. The method of phase calculation for the leading ACE shockwave is further discussed in the following section.

C. Experiment 2: Aberration Correction Testing

1). Hydrophone-Based Aberration Correction Method:

Two soft-tissue aberration correction methods were used in this study. In the first method, the same broadband, low-frequency calibrated hydrophone from Experiment 1 was placed at the focus of the histotripsy array. The time-of-flight for the ultrasound pulse to travel from each element of the histotripsy array to the focus was measured by the hydrophone, which was then used for aberration correction. To ensure placement at the focus of the array, the hydrophone was manually positioned at the area of highest pressure when firing in the linear regime at approximately 2 MPa P- pressure on the entire array combined – a pressure safe for use with this hydrophone. The correct position of the hydrophone was also optically confirmed using live images on the camera from Experiment 1 that were marked with the central location of the bubble cloud. To acquire the hydrophone-based phase aberration correction for the histotripsy array, each histotripsy element was fired individually at approximately 200 kPa P- pressure. The raw phases, φ_i, of signals, s_i, received on the hydrophone from each element, i, were determined by calculating the lag required to achieve maximum correlation between the signals, given by

$${\phi }_i=\underset{\tau }{\mathrm{argmax}}\left(s_i*s_{\mathit{max}}\right)(\tau )\left(\frac{f_c}{f_s}\right)$$ (1)

where s_max is the signal from the element that generated the highest peak-to-peak pressure, τ is the cross correlation lag, and ∗ indicates the cross correlation operation. The $\underset{\tau }{\mathrm{argmax}}()(\tau )$ operation, or the arguments of the maxima operation, finds the value, τ, that maximizes the argument in parentheses. Phases were converted from samples to cycles by multiplying by the array center frequency, f_c (500 kHz), divided by the sampling frequency of the hydrophone, f_s (50 MHz). The phases were then inverted such that the uncorrected histotripsy element that emitted the pulse that arrived first at the focus was fired last when aligned, given by

$$p_i=\left|{\phi }_i-\underset{\tau }{\max }\left({\phi }_i\right)\right|.$$ (2)

The inverted phases, p_i, were then used to alter the phases of the elements in the histotripsy array such that the pulses from each element in the array arrived at the focus simultaneously. This inversion is similar to that used in the time-reversal acoustics method [48]. While this hydrophone-based method is infeasible in an in vivo setting as a hydrophone generally cannot be placed at the target location, it was treated as our gold standard method because it should result in the optimal delays required to align the waveforms to the hydrophone location.

2). ACE Aberration Correction Method:

The second aberration correction method employed the histotripsy receiver system and the ACE signals. By assuming the ACE expansion shockwave to be a spherical shockwave emitted from a point source, the front-edge of this shockwave received by each element of the histotripsy array can be used to correct for phase misalignment due to sound speed variations along the flight-path of each array element [2,49,50,18]. Bubble clouds were generated at maximum array power. It should be noted that the array power cavitation threshold was less than the maximum output of the array in all cases in this study. Thus, a lower pressure level could have been used for ACE aberration correction. However, maximum power bubble clouds were used here to provide the most high-intensity and consistent shockwaves possible. The round-trip time for sound to travel from the array to the focus and back was approximately 200 μs, so our signal processing was windowed to a region between 190–215 μs to ensure that the signals analyzed principally originated from the ACE expansion shockwave and not reflections in the water tank. Prior to experimentation, signals acquired between 190–215 μs when firing the array at a pressure level just below the intrinsic cavitation threshold level were checked to ensure that signals being used for aberration correction were indeed ACE signals and not reflections from the setup. The ACE shockwave signals from ten histotripsy bubble clouds were then averaged to account for minor pulse- to-pulse differences in shock arrival times due to the stochastic nature of the formation of individual bubbles within each generated bubble cloud. The raw signal phases (converted from samples to cycles) were calculated by finding arrival time of the 50% front-edge of the signal envelope acquired via the Hilbert transform, given by

$${\phi }_i=\underset{t}{\mathrm{argmax}}\left|H\left[s_i(t)\right]-\frac{1}{2}\max \left(H\left[s_i\right]\right)\right|\left(\frac{f_c}{f_r}\right)$$ (3)

where H indicates the Hilbert transform operation, and f_r is the sampling frequency of the receiver system ADCs (20 MHz). Phases were then inverted using (2) and used as the phase alignment on the histotripsy array to align the pulses at the focus. The cross-correlation method used for the hydrophone alignment method given by (1) could not be reliably used for the receiver-based aberration correction because the signals after the front-edge of the shockwave were not identical across all elements of the histotripsy array.

3). Comparison between Hydrophone and ACE Aberration correction methods:

The efficacy of the two aberration correction techniques was evaluated by placing aberrators between the array and the focus. Two methods are used for evaluation:1) measuring the focal pressure through the aberrator(s) after aberration correction using the same driving voltage to the histotripsy array, and 2) measuring the histotripsy array driving system power that is required to generate cavitation through the aberrator after aberration correction. For the first method, the array was driven well below the cavitation threshold in the acoustically linear regime, and the peak-to-peak focal pressure was directly measured via low-frequency calibrated hydrophone. The percent of pressure recovered, p_recovered, was calculated by dividing the pressure difference between aberration correction, p_AC, and no aberration correction, p_NAC, through tissue by the pressure difference between the free-field pressure without pre-focal aberrators, p freefield, and no aberration correction through tissue, given by,

$$p_{re\mathrm{cov}ered}=\frac{p_{AC}-p_{NAC}}{p_{freefield}-p_{NAC}}\times 100\%.$$ (4)

Beam profiles were also acquired at this pressure level in the x-, y- (lateral) and z- (axial) directions for ±5-mm in0.5-mm increments. The (0,0,0)-mm location was set to the focus of the hydrophone-aligned pulse. For the second method, the cavitation initiation thresholds were determined for both hydrophone and ACE aberration correction methods. This threshold was defined as the driving system power required to initiate cavitation with a 50% probability [24]. To find the cavitation threshold power, the histotripsy array was pulsed at 1-Hz PRF at a driving system power well below the cavitation threshold for each method, i.e., a point at which no cavitation was observed. The high-voltage power supply that powered the pulser was then increased in increments of 1 Volt, and 30 images were acquired at each increment with the same high-speed optical imaging setup from Experiment 1. The camera shutter was opened 50 μs prior to the arrival of the histotripsy pulse at the focus and was left open for 1 ms. The LED backlight was then triggered for each histotripsy pulse at the time corresponding to the time of maximum bubble expansion, which was determined prior to the experiment. The power was increased until cavitation was observed on all 30 frames. The percentage of frames that included cavitation in the focus for each frame was treated as the probability for cavitation at each threshold [51]. A sigmoid curve given by

$$v(t)=\frac{\alpha }{1+e^{-\beta t}}$$ (5)

was then fit to the cavitation probabilities at each power level with α and β being fitting parameters. The 50% probabil ity level on the curve was determined to be the cavitation threshold [52]. Cavitation power thresholds of all aberration correction methods were reported as a percentage of the cavitation power threshold through the aberrator without aberration correction.

4). Acrylic Disc Aberration Correction Testing:

To test the effectiveness of our histotripsy receiver system and ACE aberration correction algorithm to correctly identify phase aberrations across the array, two polymethyl methacrylate (acrylic) discs (McMaster-Carr Supply Company, Aurora, OH, USA) were placed between the histotripsy array and the focus covering approximately 30% of the elements in the array. The discs were 6.35 mm in thickness with diameters of 152.4 mm (disc A) and 101.6 mm (disc B). With an estimated sound speed of 2700 m/s [53,54], we anticipated a phase shift of approximately one cycle for the covered elements. Bubble clouds were generated with maximum power, and ACE expansion shockwave signals were acquired on the histotripsy array. Phases acquired from the ACE aberration correction method were subtracted from the free-field ACE aberration correction method phases acquired using bubble clouds generated with the same pressure to identify the total phase shift on each element due solely to the acrylic discs. These phases were then projected onto a rendering of the histotripsy array to visualize the areas of aberration.

5). Ex Vivo Porcine Tissue Testing:

Both aberration correction techniques were tested on four ex vivoporcine tissue samples. Tissue was acquired from four pigs that were a part of a separate, unrelated study approved by the University of Michigan Institutional Animal Care and Use Committee. Tissue was acquired from the entire middle abdominal region of the pigs laterally to the transverse processes of the lumbar vertebrae. These samples consisted of tissue from the complete abdominal wall including skin, subcutaneous fat, muscle, connective tissue, and the peritoneum. No internal organs were included in these tissue samples. Samples ranged between 25–50 mm in thickness throughout each sample and were approximately 200 mm in length and width. Samples were placed directly on a thin sheet of flexible plastic that was fixed in the water tank just above the histotripsy array such that the samples rested directly in the aberrator region shown in Figure 1A. For each sample, tissue impeded the paths between all elements of the histotripsy array and the focus. All tissue samples were harvested immediately after the pigs were sacrificed and used within three days of harvest. Samples were refrigerated and stored in 0.9% sodium chloride solution, USP (Baxter Healthcare Corporation, Deerfield, IL, USA), prior to experiments.

III. Results

A. Experiment 1: ACE Expansion Shockwave Investigation

1). Hydrophone Shockwave Investigation:

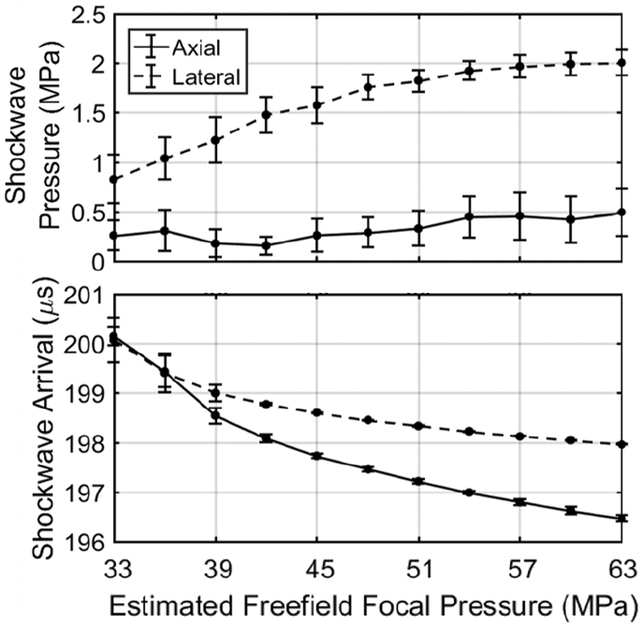
ACE expansion shockwaves generated across a range of transducer power levels were acquired via hydrophone to investigate their dependence on focal pressure. Mean ACE expansion shockwave pressures and arrival times acquired via hydrophone at the axial and lateral positions approximately 15-cm from the focus over a range of estimated free-field focal pressures are shown in Fig. 2. At the axial position, the shockwave pressure was measured between approximately 0.25 and 0.5 MPa between estimated focal pressures of 33 and 63 MPa. At the lateral position, the shockwave amplitude started at approximately0.8 MPa at the lowest tested focal pressure of 33 MPa and increased linearly to approximately 1.8 MPa at a focal pressure of 48 MPa. Increasing the focal pressure above this point resulted in moderate, logarithmic increases in shockwave pressure, which appeared to reach a saturation pressure of 2 MPa at a histotripsy focal pressure of 63 MPa. This indicates that increasing the focal pressure results in a compounding effect on shockwave pressure that does not occur in the axial direction.

Fig. 2.

Shockwave pressure (top) and arrival time (bottom) along the axial (0°) and lateral (90°) axes of the array measured with a low-frequency calibrated hydrophone. Shockwave pressure increased significantly with increasing focal pressure along the lateral direction but not along the axial direction. The shockwaves arrived at the hydrophone increasingly earlier with increasing focal pressure along both the axial and lateral directions. The shockwave arrival time also increased in consistency from pulse-to-pulse with increasing focal pressure.

At low amplitude, the shockwave arrival times on the hydrophone at both the axial and lateral positions were recorded at 200±0.2 μs, which is the round-trip travel time between the array elements and the focus. With increasing focal pressure and therefore increasing bubble cloud size, both hydrophone locations exhibited a decrease in arrival time of the first shockwave front. These results indicate outward growth of the portion of the bubble cloud that generates the front-edge shockwave. The axial position exhibited a larger decrease in shockwave arrival time totaling approximately 3.5 μs at a focal pressure of 63 MPa, while the lateral position exhibited a total shift of 2 μs at the same focal pressure. This is due to the larger size increase of the cavitation cloud in the axial direction than the lateral direction.

2). Optical Shockwave Investigation:

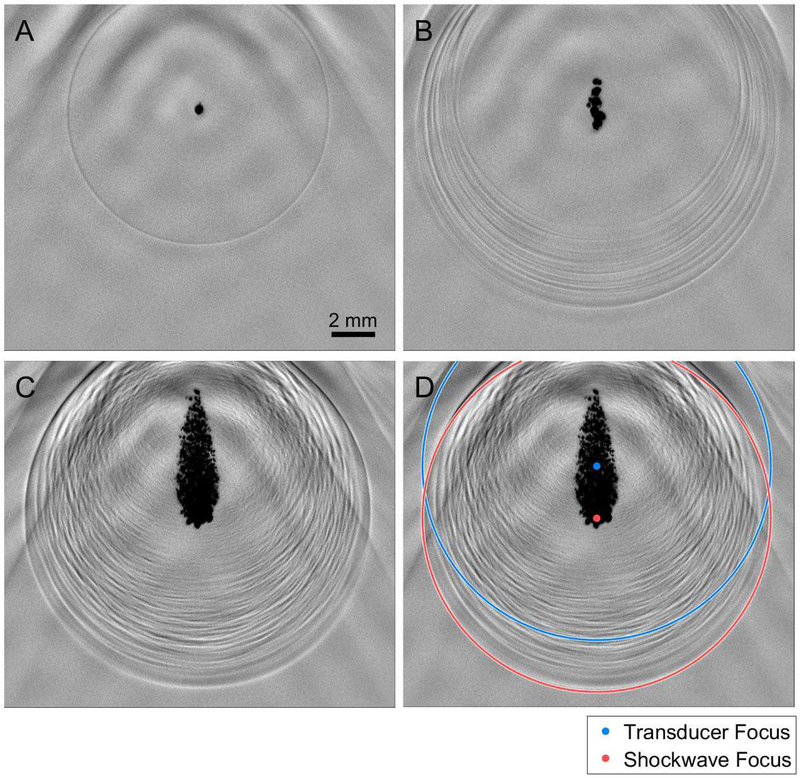
Bubble cloud shock-waves were investigated optically to analyze their spatial variations at all angles between the axial and lateral directions. Shadowgraph images of single-bubble, multi-bubble, and full-sized bubble cloud events are shown in Fig. 3A, B, and C, respectively. In all panels, histotripsy pulses were transmitted from below the frame with the axis of the array aligned with the center of the bubble clouds. In Fig. 3A, a single-cycle shockwave emitted by the expansion of a single inertial cavitation bubble is observed and appears to be perfectly circular indicating that the bubble emitted a spherical shockwave during its initial expansion. The remainder of the histotripsy pulse propagating past the focus is observable as low frequency oscillations in the background of the frame. In the multi-bubble case (Fig. 3B), which appears to include approximately 10–20 cavitation bubbles in a well-confined region, there are approximately 10–20 circular shockwaves surrounding the bubble cloud. However, the shockwaves are not co-aligned to one central location. The first arrival of the shockwave front to the array element location is consistently from the outer-most bubble (closest to the histotripsy array). Furthermore, the distance between the inner-most (closest to the bubble cloud) and front-edge shockwaves is larger in the axial direction than the lateral direction. In the robust bubble cloud case (Fig. 3C), which includes hundreds to thousands of bubbles densely packed into a confined area, a complex, layered shockwave construct surrounds the bubble cloud. The front-edge shockwave is not centered about the center of the bubble cloud, which is also the geometric center (focus) of the histotripsy array. Instead, it appears to be centered about the lowest portion of the bubble cloud (the portion closest to the histotripsy array). A high-speed video that captures the development of the bubble cloud in Fig. 3C and resulting shockwave construct is available in the online edition of this manuscript. In Fig. 3D, a blue circle indicates the expected location of the shockwave from Fig. 3C at this time point if the shockwave was emitted from the focus of the array. The actual location of the front-edge of the shockwave construct is fit with a red circle with the center of that circle is also indicated in red. In this panel, it is clear that the front edge of the shockwave construct appears to have been emitted from the frontal region of the bubble cloud with an axial shift of approximately 2.5 mm from the geometric focus. The layers of shockwaves following in the wake of the front-edge shockwave vary continuously between the axial and lateral axes of the array indicating that highly varied signals are expected to be acquired by the elements of the histotripsy array after the signal generated by the front-edge shockwave. These results corroborate the hydrophone results and indicate that shockwave arrival times for larger bubble clouds correspond to an emission from the outer-most bubbles closest to the histotripsy array.

Fig. 3.

Representative shadowgraph images of histotripsy-induced (A) single-bubble (28 MPa P-), (B), multi-bubble (30 MPa P-), and (C) robust bubble clouds (63 MPa P-) in the free-field with no pre-focal aberration medium. Single-cycle shockwaves released by the expansion of cavitation bubbles are shown as circular rings centered about the cavitation bubble that generated them. In the single-bubble case, only one shockwave is visible. (D) A ring centered about the transducer focus (blue) at the radius of the front edge of the expansion shockwaves and a ring centered about the estimated focus of the front edge of the expansion shockwave (red) are overlaid onto the robust bubble cloud shadowgraph image in (C).

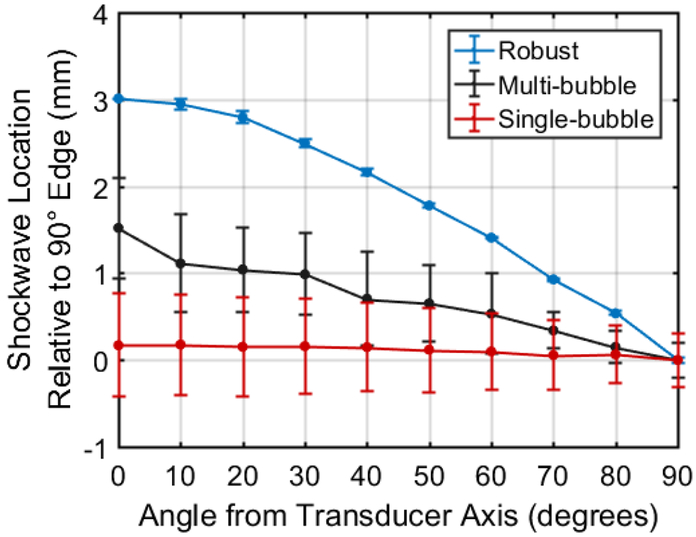
Shadowgraph images were then quantitatively analyzed. The location of the front-edge of the bubble cloud shockwaves acquired from shadowgraph images of 15 bubble clouds for single-bubble, multi-bubble, and full-sized bubble cloud events are shown in Fig. 4. Distances between the geometric focus of the array and the front-edge of the shockwave construct were normalized relative to the lateral axis such that the lateral portion of the shockwave was at a distance of 0 mm. This was done to allow for a more direct comparison of shockwave distances between the different bubble cloud sizes. For single bubbles, no significant difference (p=0.992) in shockwave distance relative to the 90° axis of the array was observed across all angles measured. However, all angles exhibited a high standard deviation of shockwave distance at each angle (≥0.31 mm). This was due to the fact that the single bubbles were rarely initiated at exactly the same location. Rather, they were initiated randomly in a small region near the focus (approximately ±0.5 mm axially and laterally) thus resulting in inconsistent shockwave locations. For the multi-bubble clouds, the front-edge of the shockwave was measured to be approximately 1.5 mm farther from the array focus at the 0° axis than the 90° axis indicating a pre-focal shift of the front edge of the shockwave construct. However, all angles still exhibited a relatively high standard deviation (≥0.19 mm). No neighboring angle measurements, e.g., 0° vs 10°, exhibited significant difference in shockwave distance (p>0.972). For the large cloud, the shockwave location exhibited a 3-mm difference between the 0° and 90° axes and decreased linearly between 20° and 60°. The standard deviation of the shockwave location was relatively small (≤0.07 mm) across all measured angles for the large bubble cloud. In the case of the robust bubble cloud, shockwave formation was highly consistent and resulted in nearly identical front-edge shockwave propagation from one cloud to the next. Importantly, a significant difference in shockwave arrival time was observed between all angles (p<0.001) thus indicating that each ring of the histotripsy array is expected to exhibit a significant difference in arrival time between all rings.

Fig. 4.

Optically measured location of the front edge of the cavitation expansion shockwave relative to the 90° axis of the histotripsy transducer. Single-bubble cavitation exhibited no significant change in shockwave edge across all measured angles but also exhibited high standard deviation due to inconsistency of the location of cavitation initiation. The multi-bubble cloud exhibited slight increase in shockwave front edge location and with increasing angle from transducer axis but also exhibited relatively high standard deviation across all angles. The robust (63 MPa P-) histotripsy cloud exhibited significant increase in shockwave edge distance with decreasing angle from axial direction of the transducer also exhibited very low standard deviation of shockwave location across all angles.

3). Receive-Capable Histotripsy Array Shockwave:

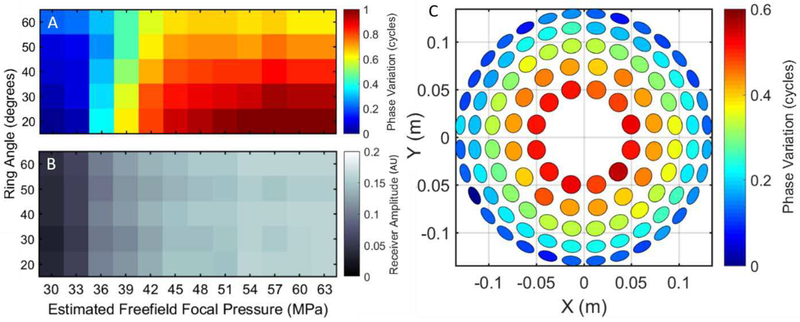
Bubble cloud shockwaves were measured with the histotripsy array to confirm the hydrophone and optical shockwave investigations. Shockwave phase variations measured with the receive-capable histotripsy array for estimated free-field focal pressures between 30 and 63 MPa are shown in Fig. 5A. For reference, a full one-cycle phase shift equals a 2-us temporal shift in water at 500 kHz. The receiver indicated that shock-wave phases increased on all array elements with increasing focal pressure (i.e., the shockwaves arrived earlier). However, this increase was nonlinearly correlated between elements on different rings of the array, and the elements in the innermost ring exhibited the largest phase increases. No differences in arrival time were observed between elements within the same ring for all focal pressures. For focal pressures at and above 48 MPa, the mean phases of each ring of the array were significantly different from all other rings (p<0.001). This is due to the fact that the shockwave front is formed by the outer-most bubbles that are closest to the array, and the elliptical-shaped cavitation cloud has a larger width in the axial direction than the lateral direction.

Fig. 5.

Free-field histotripsy receiver phase variation (A) and amplitude (B) across rings at varying histotripsy focal pressures. Receiver amplitude increased linearly across all rings of the histotripsy array with increasing focal pressure, but shockwave arrival increased non-linearly with increasing focal pressure with upwards of a half-wavelength difference between the outer- and inner-most rings at the highest focal pressure. Phase differences in shockwave arrival (generated with a 63 MPa focal pressure bubble cloud) are projected onto a rendering of the histotripsy array (C). Each ring exhibited low phase variance indicating a pre-focal shift of origin of the front edge of the shockwave.

Shockwave peak-positive amplitude variations measured with the array at estimated focal pressures between 30 and 63 MPa are shown in Fig. 5B. The receiver amplitude was found to increase linearly across all elements of the array with the highest receive amplitudes at the highest free-field focal pressure of 63 MPa. At any given focal pressure, the shock-wave amplitude differences between all array elements were insignificant. This indicates that shockwave signal intensity is expected to be the same on all elements of the array at any focal pressure.

To visualize the phase variation across the array at high focal pressures, the phase data from the 63 MPa estimated focal pressure bubble cloud data in Fig. 5A is projected onto a rendering of the array in Fig. 5C. The mean shift across all elements in each ring at this pressure level was found to be0.51±0.03, 0.43±0.02, 0.33±0.02, 0.21±0.03, and 0.12±0.04 cycles for rings one (20°) through five (60°), respectively. This further supports the notion that the shockwaves from bubble clouds generated at higher focal pressures are emitted from a pre-focal location without much shift in the transverse plane.

B. Experiment 2: Aberration Correction Testing

1). Acrylic Disc Aberration Correction Testing:

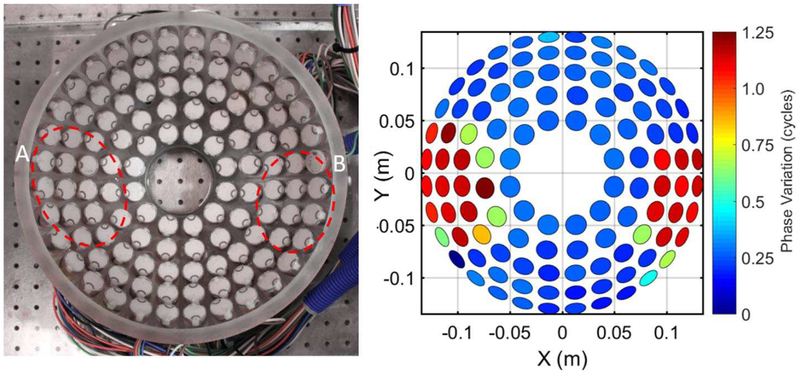
The ability of the receive-capable histotripsy array and ACE aberration correction algorithm to accurately detect phase aberrations was first tested by placing two acrylic discs aberrators between the array and the focus covering approximately 30% of the elements. The acrylic discs were expected to result in a phase shift of approximately 1 cycle for covered elements with normal incidence with the discs. The phase shifts of the ACE expansion shockwaves due to the discs are projected onto a rendering of the histotripsy array in Fig. 6. The mean phase shift of the elements covered by the discs was 1.04 ± 0.2 cycles with a median of 1.13 cycles. No completely uncovered elements exhibited a significant change in phase. These results indicate that the receiver system can accurately measure phase aberrations.

Fig. 6.

Picture of histotripsy array (left) with areas covered by acrylic discs outlined and phase projection (right) of ACE emission signal arrival time difference between disk phantom and free field measurements illustrating the resulting phase aberration. Both disc phantoms were circular with a thickness of 6.35 mm. Diameters of discs A and B were 152.4 mm and 101.6 mm, respectively.

2). Ex Vivo Porcine Tissue Testing:

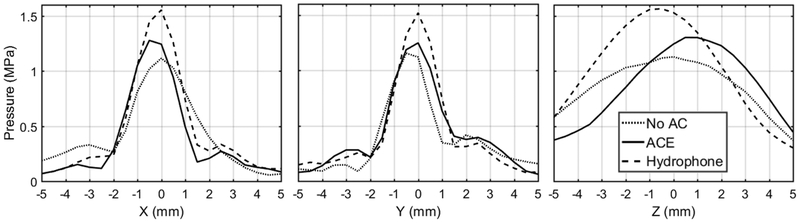
Both aberration correction methods were then tested using four porcine abdominal tissue samples. The average maximum phase shift across all tissue samples was 1.5 ± 0.16 cycles for both AC methods. Both aberration correction methods resulted in significant increases in focal pressure through the porcine tissue using the same transducer driving power compared to the focal pressure without aberration correction. Focal pressures and the percent pressure recovered with each aberration correction method, given by (4), are summarized in Table I. In the absence of tissue or any other aberrating medium, the array produced a peak-to-peak focal pressure of 2.19 MPa when tested at a sub-cavitation threshold array power level. At the same power level, this pressure level dropped to 1.09 ± 0.05 MPa in the presence of tissue, a reduction of approximately 50%. Using the hydrophone aberration correction method, the focal pressure recovered to 1.70 ± 0.10 MPa recovering approximately 55% of the lost pressure. When using the ACE-based aberration correction method, the focal pressure was found to be 1.32 ± 0.03, which corresponds to a pressure recovery of approximately 21%. Beam profiles (Fig. 7) tested at the same focal pressure level indicated that the ACE aberration correction method shifted the focus to a pre-focal location by 2–3 mm. Little to no shift in the x- and y-directions was observed.

TABLE I.

Focal Pressures Through Tissue

Treatment method	Focal Pressure (MPa)	% Recovered
Baseline pressure without tissuea	2.19	100.0%
No Aberration Correction	1.09 ± 0.05	0.0%
With Hydrophone AC	1.70 ± 0.10	55.5%
With ACE AC	1.32 ± 0.03	20.9%

^aPressure at the focus of the histotripsy array aligned with the hydrophone method in the free-field without any pre-focal aberration medium

Fig. 7.

Sub-cavitation threshold beam profiles in x-, y-, and z-directions with no aberration correction (AC), ACE AC, and hydrophone AC acquired through one tissue sample acquired with a low-frequency calibrated hydrophone.

The electric power input to the array required to generate cavitation was recorded for the case with the tissue aberrator in place for 1) without aberration correction, 2) using hydrophone aberration correction, and 3) with ACE aberration correction (Table II). The hydrophone and ACE methods both resulted in a statistically significant decreases in cavitation threshold power through the porcine tissue compared to that without aberration correction (p<0.001, p=0.007, respectively). The array power required to generate cavitation without aberration correction was normalized and referred to as 100% power. The hydrophone method reduced the cavitation threshold power to approximately 49.8% while the ACE method reduced this threshold to approximately 68.5%. For comparison, in the absence of tissue, cavitation threshold power was 33.2% relative to the normalized 100% power with tissue and no aberration correction. Therefore, since the hydrophone aberration correction reduced the threshold power to approximately 50%, a majority of the increase in cavitation threshold through tissue was due to phase aberrations and not scattering or absorption.

TABLE II.

Percent of Power Required to Induce Cavitation Through Tissue Aberrators

Without Aberration Correction	100%
Hydrophone	49.8 ± 6.8%
ACE	68.5 ± 12.9%
Free-field baseline powera	33.2%

^aPower required to induce cavitation in the free-field without pre-focal aberration media relative to average power required to induce cavitation through tissue without aberration correction

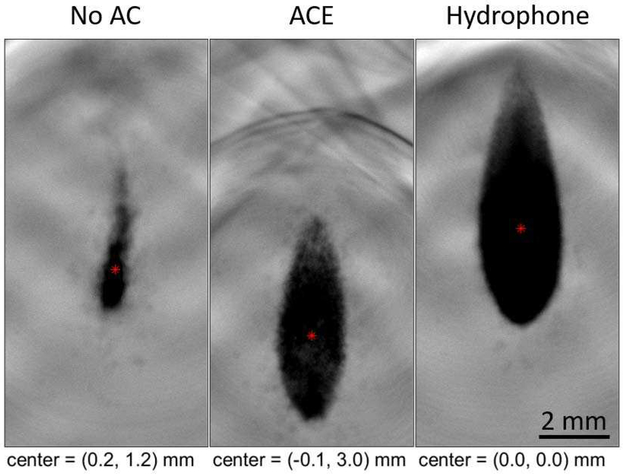
Representative average bubble cloud images generated through a tissue aberrator are shown in Fig. 8 for 1) without aberration correction, 2) using hydrophone aberration correc tion, and 3) with ACE aberration correction. Using the same electric power to drive the histotripsy array, the cavitation clouds generated without aberration correction were observed to be much smaller than the cavitation clouds generated using hydrophone and ACE aberration correction methods. This difference is due to the lower pressure and defocusing without aberration correction. The cavitation cloud generated after aberration correction using the hydrophone and ACE methods were more characteristic of a bubble cloud formed in the free-field (e.g., Fig. 3C). However, the cavitation clouds generated by ACE aberration correction exhibited a pre-focal shift of approximately 3 mm.

Fig. 8.

Average of 30 images of bubble clouds generated through one tissue sample at an estimated free-field P- pressure of 63 MPa using no aberration correction (AC), ACE AC, hydrophone AC. Bubble cloud foci are shown in red and are relative to the hydrophone-aligned bubble cloud center. The ACE-aligned bubble cloud exhibited a 3-mm pre-focal shift. Both aberration correction methods resulted in significantly larger bubble clouds than the unaligned treatment with the hydrophone method producing the largest, followed by ACE.

IV. Discussion

In this study, we developed and tested the first receive-capable histotripsy array to measure shockwaves emitted by the initial expansion of inertially cavitating bubbles generated by histotripsy to correct for phase aberrations due to ultrasound propagation through heterogeneous tissue without additional imaging equipment such as secondary ultrasound images, CT, or MRI. Furthermore, rather than simply receiving reflections of ultrasound from pre-existing bubbles or point scatterers, the array in this study was used to generate a point-source construct of shockwaves at a specific location that were received and analyzed for aberration correction. These techniques could potentially be used for all cavitation-based ultrasonic therapies including histotripsy.

Experiment 1 revealed that the front edge of the ACE signal originates from the bubbles of the cavitation cloud closest to the transducer rather than the geometric focus of the histotripsy array when initiating a robust bubble cloud. This result supports previous findings that the source of the acoustic emission from the bubble cloud is due to emitted shockwaves [30]. This phenomenon is important for bubble cloud localization and aberration correction, as the arrival time of shockwave to each element of the histotripsy array is determined by the distance between these cavitation bubbles and each element. Although it can be expected that the front edge of the shockwave construct will be emitted prefocally, it is difficult to estimate the extent of this shift (i.e., size of the cavitation cloud) without optical imaging. A single bubble would be the ideal point source for aberration correction. However, Experiment 1 shows that the location of the single bubble generation is not consistently at the geometrical focus of the histotripsy array, and the shockwave amplitude from the single bubble emission is low. Therefore, the benefit of using a robust bubble cloud is that the central location of shockwave formation is more consistent from one cloud to the next as opposed to the single bubbles. Another benefit of using a robust bubble cloud is that higher pressure shockwaves are emitted and are thus more easily detected through tissue. We hypothesize that the higher pressure is due to a layering effect of shockwaves that only occurs at non-axial locations. Due to the nature of the formation of the bubble cloud, the front-edge shockwave appears to experience constructive interference in the non-axial direction that increases the overall amplitude as more shockwaves are generated with more bubbles. Therefore, a robust cavitation cloud is used for ACE aberration correction for this study.

In Experiment 2, using robust bubble clouds, we hypothesized that the front edge of the shockwave construct can be used as a point source for aberration correction through soft tissue aberrators by calculating a phase correction using a receive-capable histotripsy system. Results showed significant pressure loss was induced by the 2.5- to 5-cm thick, multi-layered soft tissue aberrators. The phase aberrations appear to have a larger impact on histotripsy focal pressure than attenuation due to absorption and scattering because the hydrophone method was able to recover approximately 55% of the lost pressure in the linear regime. By correcting the phase aberrations, we were able to regain a significant amount of pressure and significantly reduce the overall power required to induce cavitation.

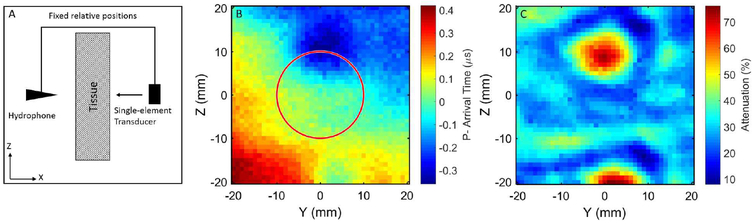
The ACE method recovered approximately 21% of the lost pressure in the linear regime. This demonstrates the proof-of-concept method of using cavitation shockwaves and a receive-capable histotripsy array for aberration correction, but the regained pressure was much less compared to the hydrophone method. We hypothesize that the primary reason for this discrepancy is due to the size of the elements in this histotripsy array. The aperture of the hydrophone used in this study was 85 μm in diameter while each histotripsy element was 2 cm in diameter. Therefore, because tissue sound speed may vary significantly over a small area, the hydrophone should allow for a much finer resolution correction. To briefly test this hypothesis, one element from the histotripsy array was co-axially aligned with the hydrophone at a distance of approximately 15 cm, and one sample of porcine abdominal tissue was placed between them, as shown in Fig. 9A. The hydrophone and histotripsy element were then scanned over a 40×40-mm grid with 1-mm spacing using an automated positioner, and an average of 30 pulses were acquired at each location. Arrival times of the P- portion of the average pulse from the single element at each location are shown in Fig. 9B and are overlaid with a red circle indicating the size of one histotripsy element. The percent acoustic attenuation at each location relative to the same measurements in the absence of tissue are shown in Fig. 9C. From this preliminary experiment, we can see that there is close to a 1-us worst-case difference in P- arrival time across the face of one 2-cm histotripsy element. This difference could erroneously put a 500-kHz histotripsy element completely out of phase. Furthermore, this effect could worsen in vivo with more overlying tissue and less consistent surface geometries. While it appears that, in general, the phase aberration changes gradually across tissue, this effect will likely worsen in vivo when there is even more overlying tissue. Therefore, smaller elements are likely to drastically improve the abilities to use the ACE method for aberration correction. The average percent attenuation shown in Fig. 9C was found to be 30.6±10.3%. From the ex vivo porcine tissue testing in Experiment 2, it was found that the focal pressure through tissue using the hydrophone-based aberration correction (1.70±0.1 MPa) exhibited approximately a 22% attenuation from the freefield measurement (2.19 MPa). These data support the notion that the hydrophone-based aberration correction method recovered virtually all of the attenuation due to phase aberration with the remainder being due to absorption and scattering. Therefore, the hydrophone-based method acts as a suitable gold-standard against which to compare the ACE-based aberration correction.

Fig. 9.

Spatial variation of soft-tissue induced ultrasonic aberration measured via transmission A-line imaging. Experimental setup (A) included a low-frequency calibrated hydrophone that was co-axially aligned with and rigidly fixed to a single-element histotripsy transducer. The hydrophone-transducer construct was scanned over a 40×40-mm area using an automated positioning system. The resulting raster scan image (B) indicates significant variation in sound speed across this area. The red circle indicates the size of one 20-mm histotripsy element from the 112-element array used in this study. When compared to the same measurements in the absence of tissue, the acoustic attenuation across this section of tissue (C) was found to vary between approximately 10–75%.

While the estimated P- focal pressure for the robust bubble clouds was reported to be 63 MPa, this is likely an overestimation of the actual focal pressure with pre-focal tissue aberrators. This pressure was used to cover the range of cavitation events that can be used for aberration correction, but this high level of pressure used to generate a large, dense bubble cloud, is not necessary to perform the proposed ACE aberration correction. The results in this study suggest that the most important feature of the bubble clouds used for ACE aberration correction is that they are consistent from one cloud to the next, thus emitting consistent shockwaves.

When used in vivo where severe phase aberrations occur resulting in poorly formed bubble clouds, this method may reduce treatment times and improve the range of electronic focal steering [55] thereby increasing the ability of histotripsy to treat larger and deeper targets. The reduction in array power to initiate cavitation is also important for reducing unwanted tissue heating.

The ACE aberration correction method resulted in a pre-focally generated bubble cloud. For the majority of histotripsy therapies, this is not a problem as the desired treatment volume typically consists of 1000 or more treatment locations. Therefore, treating a 2–3 mm boundary around a target area, e.g., a liver tumor, would likely not introduce any major complication. However, for histotripsy therapies that require very high precision, e.g., thrombolysis or brain therapies, one potential solution to get a better estimation of pre-focal shockwave formation could be to use a B-mode ultrasound imager to estimate the bubble cloud size. This could then be used to apply a more appropriate phase calibration to shift the ACE-corrected bubble cloud back to the focus. Another option for bubble cloud refocusing is to subtract the phase delays that would be used to steer the array prefocally. Since this method would only apply an axial shift, it may over-generalize the phase correction on the array thus reducing focal pressure and bubble cloud size. However, it would likely increase the accuracy of bubble cloud placement. These methods and others will be explored in future studies.

A different method for reducing the effects of the pre-focal shockwave formation is to use the shockwave from a single bubble as a point source for aberration correction rather than a large bubble cloud. Currently, this potential method has two problems. First, as shown in Fig. 4, when the histotripsy array is fired at the cavitation threshold where a single bubble is only formed approximately 50% of the time, the bubble tends to move about the focus substantially (~ ±0.5 mm). While this motion is bounded to within the dimensions of the transducer focus, this results in an inconsistent formation of the shockwave making it difficult to correct to one specific location. Second, the pressure of the single-bubble shockwave was found to be less than half the pressure of the shockwave emitted by the large bubble cloud. Due to attenuation in the tissue, single-bubble shockwaves were nearly impossible to detect with our current array hardware. These issues could be solved via hardware improvements and more advanced signal processing methods, which will both be explored in future studies.

V. Conclusions

This study demonstrated that the shockwaves generated by the initial expansion of inertially cavitating microbubbles received by a histotripsy array can be used for the ACE aberration correction. It was found that phase aberration induces significant reduction of histotripsy focal pressure. These results show that the ACE aberration correction method can be used for phase aberration correction to recover substantial pressure loss for histotripsy through soft-tissue.