Abstract
A crucial step for accelerating tuberculosis drug development is bridging the gap between preclinical and clinical trials. In this study, we developed a preclinical model‐informed translational approach to predict drug effects across preclinical systems and early clinical trials using the in vitro‐based Multistate Tuberculosis Pharmacometric (MTP) model using rifampicin as an example. The MTP model predicted rifampicin biomarker response observed in 1) a hollow‐fiber infection model, 2) a murine study to determine pharmacokinetic/pharmacodynamic indices, and 3) several clinical phase IIa early bactericidal activity (EBA) studies. In addition, we predicted rifampicin biomarker response at high doses of up to 50 mg/kg, leading to an increased median EBA0‐2 days (90% prediction interval) of 0.513 log CFU/mL/day (0.310; 0.701) compared to the standard dose of 10 mg/kg of 0.181 log/CFU/mL/day (0.076; 0.483). These results suggest that the translational approach could assist in the selection of drugs and doses in early‐phase clinical tuberculosis trials.
Study Highlights.
WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?
☑ The current treatment paradigm (drugs and doses) used in treatment of tuberculosis is not based on pharmacokinetic and pharmacodynamic (PK/PD) principles.
WHAT QUESTION DID THIS STUDY ADDRESS?
☑ How to optimally select clinical antituberculosis drug doses from preclinical studies using a translational pharmacometric approach.
WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?
☑ The study describes a model‐informed, in vitro‐based, translational approach to accurately predict the biomarker response across other preclinical systems and phase IIa early bactericidal activity studies using rifampicin as an example.
HOW MIGHT THIS CHANGE CLINICAL PHARMACOLOGY OR TRANSLATIONAL SCIENCE?
☑ The approach described in the study may help to inform decision‐making for dose selection in the planning of phase II studies using tuberculosis in vitro information. In addition, the effects of high‐dose rifampicin were evaluated suggesting a clinical potential for doses up to 50 mg/kg considering only efficacy and not safety/toxicity.
The current treatment paradigm for drugs and doses used in the treatment of tuberculosis (TB) is not based on pharmacokinetic and pharmacodynamic (PK/PD) principles.1 To make progress more rapid, we need to harness the power of PK/PD principles when developing new regimens. The Multistate Tuberculosis Pharmacometric (MTP) model is a semimechanistic pharmacometric model describing the growth and drug effects on different bacterial substates, including phenotypically resistant nonculturable (dormant) bacteria.2, 3 This transient phenotypic resistance allows the bacteria to persist under drug exposure, to a much larger degree than bacteria that exhibit active multiplication, and is thus thought to be a cause of patient relapse.4 As such, the estimation and prediction of drug effects on this phenotypic resistant subpopulation is crucial in order to develop and predict a successful treatment regimen. The MTP model was developed using in vitro information from classical time‐kill experiments and has been successful in describing the effects after exposure to rifampicin, not only for in vitro in monotherapy but also for assessing efficacy of drug combinations in vitro together with the General Pharmacodynamic Interaction model,5, 6 in vivo monotherapy,7 in vivo assessment of drug combinations,8 and clinical settings9 suggesting its value for describing drug effects as well as for translational applications.
Phase IIa is the first trial conducted in patients for TB drug development. These trials are most often monotherapy trials designed to provide information on a compounds' bactericidal activity after different doses.10, 11, 12 Traditionally, the measure of activity is early bactericidal activity (EBA), which is the daily decrease in log10 colony forming units (CFU) during the first 2 days of treatment (EBA0‐2) or the first 14 days of treatment (EBA0‐14).13 The currently employed approach to dose selection for phase IIa trials is based on targeting a PK/PD index using probability of target attainment (PTA) where the target often is defined from long‐term mouse experiments.14 Quantitative information on the PK/PD relationship for the antibiotics is ignored by using such summary variables as PK/PD index. This may be particularly important in the field of TB, where the effect is not immediate but takes a long time until cure is reached, i.e., the response cannot only be predicted using drug exposure and sensitivity (MIC) but biomarker response needs to be incorporated into the predictions. The MTP model has been shown to be superior in defining statistically significant drug effects in early clinical trials in TB drug development compared to standard approaches.15
The in vitro hollow fiber system model of TB (HFS‐TB) is an in vitro preclinical system that has shown accuracy in predicting PK/PD indices16 and which recently received a positive qualification opinion by the European Medicines Agency's Committee for Medicinal Products for Human Use for exploring dose and regimen selection in anti‐TB drug development programs.17
In this work, we aimed to develop a translation approach using in vitro information in order to predict biomarker response in other preclinical systems and in early clinical trials using the MTP model as a framework.18 Finally, a sensitivity analysis was performed to explore the impact of the translational factors on the predictions of biomarker response in preclinical systems and in EBA trials.
RESULTS
The translational MTP model
All model components, i.e., the human rifampicin PK model,19 the epithelial lining fluid model (ELF) model,20 and the MTP model2 were developed earlier and linked in this work (Figure 1). All parameter values used for the translational predictions are presented in Table 1. The following translational factors were included in the linked models, which were required to accurately predict the target systems (hollow‐fiber infection model, murine lung infection model, and clinical phase IIa early bactericidal activity study):
-
1
The minimal inhibitory concentration (MIC); We developed an MIC scaling term to account for differences in mycobacterial susceptibility between the mycobacterial isolates used in the different systems. The MIC scaling term was used to scale the drug potency measures (EC50 or slope) of the MTP model to predict from the original system to the target system.
-
2
The postantibiotic effect (PAE); i.e., persistent drug effects that are present after removal of the drug. The PAE model was developed in this work using PAE information from Gumbo et al.21 The final PAE model consisted of an effect compartment with a fast zero‐order rate (ke,in) from the rifampicin concentrations into the effect compartment and a saturable Michaelis–Menten kinetics (parameterized by ke,out,max and ke,out,50) describing the elimination from the effect compartment. This model had a 12‐point lower Akaike Information Criteria compared to a model with first‐order linear equilibrium rate constant. Predicted PAE vs. observed PAE values are presented in Table 2.
-
3
Differences in the maximum bacterial burden (Bmax) in the target system; The estimate for Bmax was obtained from Gumbo et al.21 for prediction of the hollow‐fiber study and estimated for the murine lung infection model from the digitalized experimental data of the mouse study.22 For the prediction of the clinical phase IIa EBA study, Bmax was set to the value obtained in vitro due to the lack of this information in EBA studies, as bacterial burden without drug treatment is commonly not obtained due to ethical reasons.
-
4
The bacterial growth state, which was controlled by the preincubation period before rifampicin treatment was initiated, which was 4 days and 30 days for the hollow‐fiber system and mouse study, respectively. For prediction of the phase IIa EBA study, a period of 150 days was assumed before treatment was initiated. The linked models (PK, ELF, MTP) including all translational factors is referred to as the translational MTP model in the following. A detailed description of the components of the translation MTP model is given in the Methods section.
Figure 1.
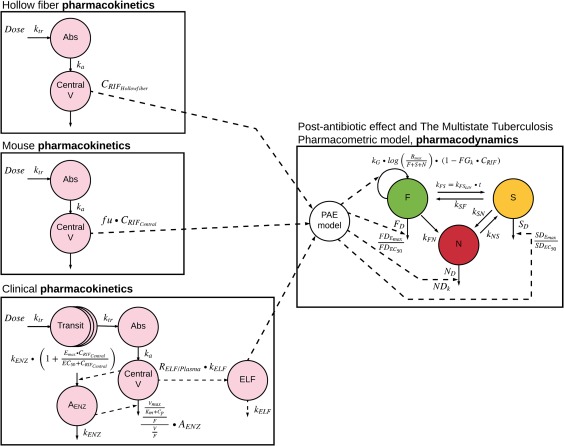
Compartmental sketch of the translational Multistate Tuberculosis Pharmacometric (MTP) model; left: pharmacokinetic models of each target system; right: pharmacodynamic MTP model; abbreviations are explained in the article text and in Table 1.
Table 1.
Parameters of the translational Multistate Tuberculosis Pharmacometric (MTP) model used for the translational predications into the target systems
| Parameter | Description | Value | Source reference |
|---|---|---|---|
| Pharmacodynamics (MTP model) | |||
| kFN [days−1] | Transfer rate from fast‐ to non‐multiplying state | 0.897 × 10−6 | (4) |
| kSN [days−1] | Transfer rate from slow‐ to non‐multiplying state | 0.186 | (4) |
| kSF[days−1] | Transfer rate from slow‐ to fast‐multiplying state | 0.0145 | (4) |
| kNS [days−1] | Transfer rate from non‐ to slow‐multiplying state | 0.123 × 10−2 | (4) |
| kFS,lin [days−2] | Time‐dependent transfer rate from fast‐ to slow‐multiplying state | 0.166 × 10−2 | (4) |
| S0 [mL−1] | Initial bacterial number of slow‐multiplying state | 9770 9770·50 (hollow‐fiber) | (4) scaled up from (4) |
| kG [days−1] | Fast‐multiplying bacterial growth rate | 0.150 (hollow‐fiber) 0.206 (mice) 0.206 (human) | estimated (4) (4) |
| F0 [mL−1] | Initial bacterial number of fast‐multiplying state | 4.1 4.1·50 (hollow‐fiber) | (4) scaled up from (4) |
| Bmax [mL−1] | System carrying capacity | 2.02·109 (hollow‐fiber) 4·106 (mice) 2.42·108 (human) | (17) estimated from (39) (4) |
| FGk [L·mg−1] | Linear inhibition of fast‐multiplying bacterial growth | 0.017 | (4) |
| FDEmax [days−1] | Maximal fast‐multiplying bacterial death rate | 2.15 | (4) |
| FDEC50 [mg·L−1] | Rifampicin concentration at which half FDEmax is reached | 0.52 | (4) |
| SDEmax [days−1] | Maximal slow‐multiplying bacterial death rate | 1.56 | (4) |
| SDEC50 [mg·L−1] | Rifampicin concentration at which half SDEmax is reached | 13.4 | (4) |
| NDk [L·mg·days‐1 | Linear non‐multiplying death rate | 0.24 | (4) |
| Link between pharmacokinetics and pharmacodynamics | |||
| ke,in [days−1] | Transfer rate constant into the effect compartment | 150 | estimated from (22) |
| ke,out, max [days−1] | Maximal transfer rate from the effect compartment | 1.091 | estimated from (22) |
| ke,out,50 [mg·L−1] | Rifampicin concentration at which half ke,out,max is reached | 0.662 | estimated from (22) |
| Pharmacokinetics Hollow fiber system | |||
| t1/2 [h] | Half‐life of elimination | 3 | (22) |
| fu [‐] | Fraction unbound | 0.2 | (22) |
| Vd [L] | Volume of distribution | 60 | (22) |
| Murine lung infection model | |||
| CL [L·days−1] | Clearance | 0.66 (dose ≤ 1 mg/kg) 1.03 (1 mg/kg < dose < 90 mg/kg) 2.29 (dose ≥ 90 mg/kg) | estimated from (39) |
| ka [days−1] | Absorption rate constant | 19.6 | estimated from (39) |
| Vd [L·kg−1] | Volume of distribution | 1.3 | estimated from (39) |
| fu [‐] | Fraction unbound | 0.03 | (40) |
| Clinical phase IIa | |||
| Vmax [mg·h−1·70 kg−1] | Maximal elimination rate | 525 | (20) |
| km [mg·L−1] | Rifampicin concentration at which half Vmax is reached | 35.3 | (20) |
| Vd [L·70 kg−1] | Volume of distribution | 87.2 | (20) |
| ka [h−1] | Absorption rate constant | 1.77 | (20) |
| MTT [h] | Mean transit time | 0.513 | (20) |
| NN [‐] | Number of transits | 23.8 | (20) |
| Emax [‐] | Maximal increase in enzyme production rate | 1.16 | (20) |
| EC50 [mg·L−1] | Rifampicin concentration at which half the Emax is reached | 0.0699 | (20) |
| kENZ [h−1] | First‐order rate constant for enzyme pool degradation | 0.00603 | (20) |
| Fmax [‐] | Maximal increase in relative bioavailability at doses above 450 mg | 0.504 | (20) |
| ED50 [mg] | Difference in dose above 450 mg at which half the Fmax is reached | 67.0 | (20) |
| IIV Vmax [%] | Interindividual variability in Vmax | 30.0 | (20) |
| IIV km [%] | Interindividual variability in km | 35.8 | (20) |
| IIV Vd [%] | Interindividual variability in Vd | 7.86 | (20) |
| IIV ka [%] | Interindividual variability in ka | 33.8 | (20) |
| IIV MTT [%] | Interindividual variability in MTT | 38.2 | (20) |
| IIV NN [%] | Interindividual variability in NN | 77.9 | (20) |
| IOV km [%] | Interoccasion variability in km | 18.9 | (20) |
| IOV ka [%] | Interoccasion variability in ka | 31.4 | (20) |
| IOV MTT [%] | Interoccasion variability in MTT | 56.4 | (20) |
| IOV F [%] | Interoccasion variability in F | 15.7 | (20) |
| Correlation Vmax‐km [%] | 38.9 | (20) | |
| fu [‐] | Fraction unbound | 0.2 | (21) |
| kELF [h−1] | Transfer rate constant from plasma to epithelial lining fluid | 41.58 | (21) |
| RELF/plasma [‐] | Epithelial lining fluid/plasma concentration ratio | 0.26 | (21) |
IIV, interindividual variability; IOV, interoccasion variability.
Table 2.
Observed (in vitro) vs. predicted postantibiotic effects (PAE) obtained after exposure to various rifampicin concentrations (0–14 mg/L) for 0–7 h
| Time; concentration | Observed PAE [days] | Predicted PAE [days] |
|---|---|---|
| 0; 0 | 0 | 0 |
| 7 h; 2 mg/L | 5.3 | 5.2 |
| 1 h; 7 mg/L | 12.3 | 12.0 |
| 2 h; 7 mg/L | 12.3 | 12.9 |
| 0.5 h; 14 mg/L | 19.9 | 19.3 |
Observed data from Ref. 22.
All predictions were made using the translational MTP model with translational factors and with no parameters estimated from the target experimental or clinical data apart from the bacterial growth properties for the hollow‐fiber system and the mouse experiments.
Prediction of hollow‐fiber experiments
The predictions of the different hollow fiber experiments with and without rifampicin (growth control, 600 mg once daily, 2,100 mg twice weekly, or 4,200 mg once weekly) using the H37Ra in vitro strain is presented in Figure 2. The translational MTP model predicted the hollow‐fiber regimens very well apart from some overprediction at >4 days after start of rifampicin treatment in the once‐weekly scenario.
Figure 2.
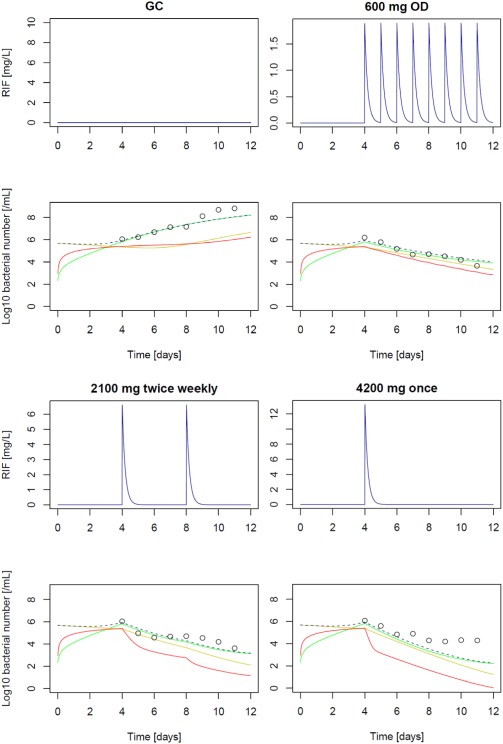
Prediction of hollow‐fiber system experiments with rifampicin against M. tuberculosis H37Ra; GC: growth control experiment; 600 mg once daily (OD) dosing, 2,100 mg twice daily; 4,200 mg once weekly; unbound rifampicin (RIF) pharmacokinetics (upper panels) and pharmacodynamic effect over time (lower panels); circles (experimental data, CFU/mL); predictions of the N state (red), S state (yellow), F state (green) and CFU/mL (black dashed; sum of F+S).
Prediction of PK/PD indices in a murine lung infection model
The rifampicin drug effect at day 6 in a murine lung infection model (Figure 3, upper panel) correlated best with the PK/PD index AUC0‐8/MIC (R² = 0.93) and Cmax/MIC (R² = 0.78). The patterns of the predicted PK/PD indices by the translational MTP model (Figure 3, lower panel) were in good agreement with the observed PK/PD indices and identified the same indices to be correlated with the effect of rifampicin (AUC0‐8/MIC: R² = 0.97, Cmax/MIC: R² = 0.97, %T>MIC: R² = 0.67). Moreover, the translational MTP model also predicted the magnitude of the observed in vivo effects. For instance, for a half‐maximum reduction of log CFU/mL in the mice, a Cmax/MIC of 58 or an AUC0‐8/MIC of 4,320 was required, whereas a Cmax/MIC of 168 or an AUC0‐8/MIC of 2,040 was predicted by the translational MTP model.
Figure 3.
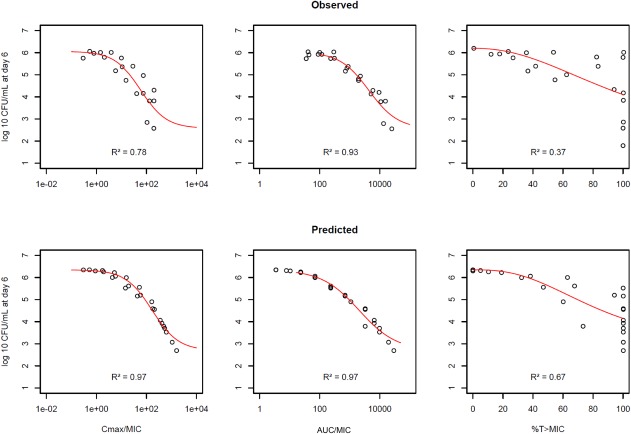
Prediction (upper panel) of PK/PD indices Cmax/MIC, AUC0‐8/MIC, and %T>MIC of rifampicin as observed (lower panel) in a murine lung infection model at day 6; red line represents regression line from an inhibitory sigmoidal maximum effect model.
Prediction of clinical early bactericidal activity phase IIa studies
The translational MTP model including variability of rifampicin in PK and PD predicted the clinical dose–response curve for up to 14 days as observed in EBA trials (Figure 4 a). For EBA0‐2days and a dose of 10 mg/kg, a median EBA (90% prediction interval) of 0.181 log CFU/mL/day (0.076; 0.483) was predicted. The EBA0‐5days was 0.201 (0.078; 0.484), and the EBA0‐14days was 0.202 (0.087; 0.343) for the 10 mg/kg rifampicin dose. The EBA0‐2 days for 35 mg/kg high dose regimen23 was 0.442 log CFU/mL/day (0.238; 0.674). The EBA0‐5days was 0.465 (0.259; 0.682), and the EBA0‐14days was 0.327 (0.227; 0.677) for the 35 mg/kg rifampicin dose. The predictions of the translational MTP model were in accordance with the results of several clinical trials14, 23, 24, 25, 26, 27 (Figure 4 a).
Figure 4.
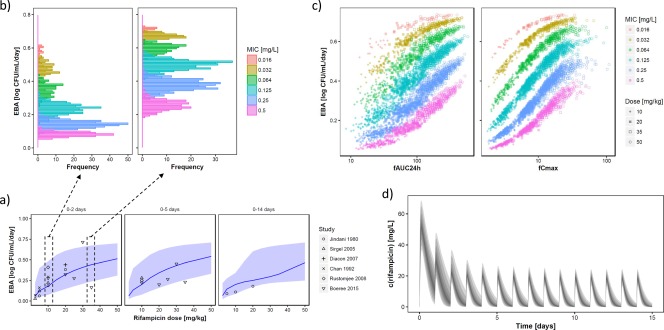
(a) Prediction (median, 10th to 90th percentile) of clinical early bactericidal activity (EBA0‐2days, EBA0‐5days, EBA0‐14days) for rifampicin doses of 2.5 to 50 mg/kg and observed EBA (points) for clinical trials. (b) Predicted impact of the mycobacterial minimum inhibitory concentration (MIC) on the obtained EBA for the 10 mg/kg dose (left) and the 25 mg/kg dose (right). (c) Predicted impact of pharmacokinetic variability (expressed as fAUC24h and fCmax) on the obtained EBA of rifampicin. (d) Pharmacokinetic variability of rifampicin exemplified for the 35 mg/kg dose.
We also assessed a further increased rifampicin dose to 50 mg/kg, which exceeds the current clinically investigated dose range capped at 35 mg/kg. The 50 mg/kg dose was predicted to yield an EBA0‐2 days of 0.513 log CFU/mL/day (0.310; 0.701), i.e., a modest increase compared to the 35 mg/kg dose. The EBA0‐5days was 0.542 (0.333; 0.711), and the EBA0‐14days was 0.465 (0.249; 0.711) for the 50 mg/kg rifampicin dose, where a more substantial increase in the EBA0‐14days was observed compared to the 35 mg/kg dose.
The MIC as a source of interindividual variability in EBA is depicted in Figure 4 b. The predicted median EBA0‐2days at 10 mg/kg and an MIC value of 0.125 mg/L was 0.235 log CFU/mL/day (0.175; 0.286). However, a much lower median EBA0‐2days of 0.083 log CFU/mL/day (0.062; 0.103) was predicted for MIC values of 0.5 mg/L at a dose of 10 mg/kg daily. An increased dose of 35 mg/kg predicted a higher EBA and might be particularly beneficial for patients with high MIC, where a median EBA0‐2days of 0.254 log CFU/mL/day (0.203; 0.297) was predicted for MIC values of 0.5 mg/L (Figure 4 b).
Another source of variability in EBA originated from interindividual differences in rifampicin PK (Figure 4 c,d). It is evident that the interindividual variability in rifampicin concentrations is particularly high during the first days of rifampicin treatment due to interindividual variability in onset of enzyme autoinduction processes (Figure 4 d).
An outline of the different components of the final preclinical to clinical forecasting in tuberculosis drug development using the translational MTP model approach is seen in Figure 5.
Figure 5.
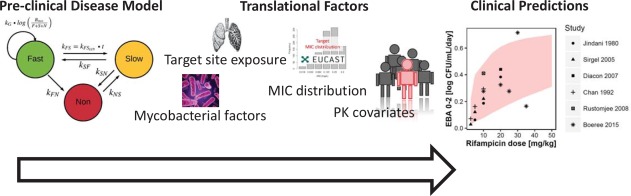
An outline of the different components of the final preclinical to clinical forecasting in tuberculosis drug development using the translational MTP model approach.
Sensitivity analysis
A sensitivity analysis was performed to assess the impact of the translational factors on the predictions. Each of the translational factors was excluded one at a time. Omitting a translational factor did not negatively influence the translational predictions in all target systems similarly, but resulted in worse predictive performance in at least one target system.
Exclusion of the PAE model substantially affected the predictions of the hollow‐fiber system (underprediction of the effect, Figure S1) and the clinical phase IIa EBA trial (underprediction of the median effect, Figure S4a), while the impact on the PK/PD index study in mice was less pronounced (Figure S3a).
Exclusion of the MIC scaling term or a wrong MIC scaling affected the PK/PD index study (underprediction of the effect, Figure S3b) and the phase IIa trial (underprediction of variability, Figure S4b), while the hollow‐fiber system (Figure S2) was least affected.
When a wrong preincubation period was used, all target systems were affected. When the preincubation period was wrongly set to 150 days instead of 4 days in the hollow‐fiber prediction, a tendency to a lower drug effect was observed due to the lower susceptibility due to the higher abundance of S and N state mycobacteria (Figure S5). Conversely, if a preincubation period of 4 days instead of 30 days was used for the prediction of the murine lung infection model, a tendency to overprediction of the antibacterial effects was observed (Figure S6). For clinical prediction, a preincubation period of 4 days instead of 150 days particularly affected the prediction of EBA0‐5days and EBA0‐14days, where even a negative EBA was predicted at low doses due to the active growth of the mycobacteria (Figure S7). In the clinical data, no variability of ELF penetration was quantifiable due to the study design; however, assumption of 30% variability in RELF/plasma only marginally increased the variability in EBA (Figure S8).
DISCUSSION
In this study we developed a model‐informed MTP translational approach for predicting biomarker response from in vitro time‐kill studies, while taking into account differences in drug susceptibility, postantibiotic effect, PK, and target site distribution along with innovative and quantitative PK/PD modeling methods. We were able to demonstrate a good predictive performance for this innovative translational approach, since it correctly predicted the results from other preclinical systems (hollow‐fiber model and murine lung infection model) and phase IIa dose ranging studies using rifampicin as a model drug.
The good predictive performance of our approach for predicting important preclinical and clinical phase IIa TB trials suggest that this approach can be used prospectively to design several key studies in TB drug development, and might be even more useful when extended to drug combinations. Optimization of doses and combinations prior to phase III is still a critical obstacle in the TB drug development pathway. Although the acceptance of PK/PD methods throughout drug development is increasing, the reliance on traditional methods for assessing drug effects is troublesome. This is especially worrying for diseases with weak market incentives and few active drug development programs, such as TB, where failure due to clinically unpredictive methods is unacceptable, which makes our suggested approach a relevant tool to aid in TB drug development.
The current employed approach for dose selection in phase II for antibiotics relies on the use of PK/PD indices that have been shown to be sensitive to both experimental design, MIC, and PK, suggesting that this approach may not be optimal for dose selection for early clinical trials.28, 29, 30, 31 For TB, this may be particularly relevant due to the difficulty in validating PK/PD indices in the clinic, requiring extensive trial durations for studying relapse (18 months) and the general high treatment success rate for the standard treatment regimen (95%). Further, only considering drug exposure and bacterial susceptibility (MIC) might be a too simplistic approach in the field of TB, where cure occurs after a long treatment period as compared to more general infections with a much shorter treatment period and where the aim is to “hit hard and fast.”
What differentiates this translational framework from previous more simplistic preclinical to clinical prediction efforts32 are mainly that our translational MTP approach is driven by target site concentration together with human plasma concentrations instead of only the latter, and consideration of MIC strain differences according to EUCAST published distributions as well as dynamic drug exposure by inclusion of PAE. In future studies, the PAE model may be refined by estimating its parameters from measured CFU vs. time curves instead of using the rather imprecise PAE itself. This requires a slightly more labor‐intense setup of the PAE experiment, but will increase the precision of the parameters of the PAE model in further applications of our approach. Moreover, optimally designed ELF studies are highly warranted to better characterize the variability of ELF penetration. However, perhaps the most important aspect is that the MTP model allows for quantification of drug effects on nonmultiplying (dormant) bacteria.2 Nonmultiplying bacteria can be quantified using resuscitation promoting factors (RPFs).33 The MTP model approach allows for a correct estimation of drug effect against nonmultiplying bacteria, which is crucial for a model‐based translational approach. This aspect will be particularly important when the approach will be extended to prediction of later endpoints such as the occurrence of relapse or to explore shortening of the treatment duration, which were not addressed in the present study.
Rifampicin was used as model drug in this work, which is relevant because rifampicin is part of current core treatment for susceptible TB and is under current clinical investigation for increasing the dose. A wide dose range of rifampicin has been studied and our predictions were validated against results of contemporary high‐dose rifampicin studies of up to 35 mg/kg daily. In addition, the response following 50 mg/kg was predicted—a dose level not yet studied. These predictions indicate that a further, but modest, increase in rifampicin EBA might be attainable at 50 mg/kg compared to 35 mg/kg. Although the concentrations achieved with a 50 mg/kg dose were covered by the PD side of our approach, PK was formally only studied up to 40 mg/kg,19 and hence our predictions represent a slight extrapolation out of the data space. As the maximum effects of all identified nonlinearities in rifampicin PK have been well captured, the accuracy of the extrapolation might be acceptable in this case. Although our prediction of 50 mg/kg rifampicin is encouraging, it should be highlighted that our suggested approach only predicts the bacteriological response and does not incorporate safety/toxicity components that could limit the use of even higher doses, as, e.g., the occurrences of flu‐like symptoms observed with large intermittent dosing of rifampicin or yet unknown adverse effects. In future studies, our approach might be also useful to help in the identification of an intermittent dosing regimen that provides similar efficacy as daily dosing regimens.
METHODS
The MTP model
The MTP model was previously developed based upon the hypoxia‐driven in vitro information described above.2 The mathematical model consists of three bacterial states: fast (F), slow (S), and nonmultiplying (N) bacteria. In the MTP model, the sum of F and S is assumed to represent culturable bacteria, i.e., CFU, while N represents a nonculturable state of the mycobacteria that does not appear on solid media.2, 33 The differential equation systems for F (Eq. 1), S (Eq. 2) and N (Eq. 3) bacterial states were as follows:
| (1) |
| (2) |
| (3) |
The definitions and values of parameters used are listed in Table 1.
Pharmacokinetics of rifampicin in the different target systems
To account for PK differences between the in vitro system used to estimate drug effects in the MTP model and the target systems for translational prediction, i.e., hollow‐fiber infection model, mouse and human, a relevant PK model of the target system was linked to the MTP model. For the hollow‐fiber system, the PK parameters were obtained from Gumbo et al.21 and are presented in Table 1. For predictions in the mouse, the unbound murine plasma concentration–time profiles were linked to the MTP model. The murine PK parameters were estimated from digitalized PK data from Jayaram et al.22 and are presented in Table 1. For prediction of the clinical phase IIa EBA study, the concentration–time profile in the epithelial lining fluid, predicted using the General Pulmonary Distribution model20 and a human plasma PK model,19 were linked to the MTP model. The covariates of the human PK rifampicin model (weight and height) were set to values typically observed in TB patients19 and sampled from log‐normal distributions with a geometric mean of 60 kg for weight and 1.75 m for height. Geometric standard deviation was set to 10% for weight and 7.5% for height, respectively.
Translational factors and development of the translational MTP model
The PK model for each translational target, as described above, was linked to the MTP model. The following translational factors were accounted for in the MTP model in order to create the model‐informed MTP translational approach: PAE, mycobacterial susceptibility, bacterial carrying capacity, and the bacterial growth phase. An outline of the translational MTP model is presented in Figure 1.
We utilized the MIC to account for differences in mycobacterial susceptibility between the in vitro system and the predicted target systems (hollow‐fiber system, mouse, and human). The MIC values in the target system (MICtarget) in relation to the MIC in the in vitro system used to estimate drug effects (MICorigin) were used to scale the parameters for drug effects in the target system, i.e., EC50target (Eq. 4) or slopetarget (Eq. 5) from the parameters obtained from the in vitro data (EC50origin or slopeorigin):
| (4) |
| (5) |
The uncertainty in MIC determination is usually assumed to be within ±1 log2 units, also for mycobacteria.34 In order not to bias our predictions by the use of a singular MIC value, we performed a literature search for the two common preclinical strains H37Ra (used in the hollow‐fiber study21) and H37Rv (used for development of the MTP model2) and determined the most‐likely ratio, i.e., the mode of MICtarget/MICorigin distribution by means of bootstrapping.35 The MIC distributions used for bootstrapping are presented in Figure S9. For prediction of clinical phase IIa EBA studies, the EUCAST clinical MIC distribution of rifampicin was used36 from which random samples were drawn to parameterize the MICtarget/MICorigin ratio.
An effect compartment model, here termed the PAE model, was developed which was linked to the PK and the MTP model to account for persistent drug effects after removal or decline of rifampicin concentrations. The PAE model was developed by modeling the PAE experiment data described in Gumbo et al.21 and derived the time to grow 1 log CFU/mL as a function of drug concentration and exposure time. Different parametrizations of the PAE model (first‐order or zero‐order effect delay rate constants) were evaluated to describe the PAE of rifampicin. The final PAE model accounted for a rapid equilibrium of rifampicin in the effect compartment with rifampicin concentrations at the target site (CPAE), followed by a Michaelis–Menten type decay of the concentrations in the PAE compartment:
| (6) |
and where ke,out,max is the maximal elimination rate from the PAE compartment, ke,put,50 is the concentration at which 50% of the ke,out,max is seen, and ke,in is the rate constant for rifampicin entering into the PAE compartment.
For differences in the maximal growth capacity in the system, the bacterial carrying capacity parameter Bmax was adapted to the target system (Table 1). The bacterial growth phase of the target system was accounted for by simulating a preincubation period before rifampicin treatment was initiated. The simulated preincubation period was identical to the experimentally employed preincubation periods in the target systems, which were 4 days and 30 days for hollow‐fiber system and mouse study, respectively. For prediction of the phase IIa EBA study, a period of 150 days was assumed before treatment was initiated to simulate an established infection.
Translational prediction from in vitro to the target systems
The translational MTP model was utilized to predict three typically used systems in preclinical and early clinical TB drug development: 1) the hollow‐fiber infection model, 2) the murine‐based PK/PD indices, and 3) clinical EBA studies. The model parameters used for the translational predictions into the three systems are presented in Table 1.
For translational prediction of rifampicin in hollow‐fiber experiments,21 several scenarios were predicted: a growth control (GC), 600 mg rifampicin once daily, 2,100 mg rifampicin twice weekly, and 4,200 mg rifampicin once weekly, each over a period of 7 days.
For prediction of a murine dose fractionation study,22 total doses of 2, 6, 18, 60, 180, 540, 1,080, or 1,620 mg/kg rifampicin were fractionated as either one, three, or six times in a treatment period of 144 hours. Doses of 4,860 or 3,240 mg/kg were not included in the simulations as in the original study for toxicity reasons.22 Three different PK/PD indices: Cmax/MIC, AUC0‐8/MIC, and %T>MIC were calculated from the simulations as in the original study22 using the noncompartmental PK estimates presented in the original article22 in order to ascertain comparability. The model‐predicted PK/PD indices were then compared to the indices observed in mice. Nonlinear regression analysis was utilized to assess the correlation between log CFU/mL at day 6 and the predicted PK/PD indices by the coefficient of determination (R²). For a quantitative comparison, the PK/PD index at half of the maximum reduction of log CFU/mL was calculated for the observed and predicted PK/PD indices.
The predicted clinical phase IIa EBA study consisted of 14 days of rifampicin once daily of monotherapy at 2.5, 5, 10, 15, 20, 25, 30, 35, or 50 mg/kg. Early bactericidal activity was calculated as the difference in log10 CFU/mL before treatment and at 2, 5, or 14 days. The predicted EBA was compared to observed EBA 0–2 days, 0–5 days and 0–14 days from numerous clinical studies.14, 23, 24, 25, 26, 27
Sensitivity analysis
To explore the impact of the translational factors on prediction of the three translational target systems, a sensitivity analysis was performed by excluding or modifying one translational factor at a time from the final translational MTP model.
Software, estimation, and simulation
All modeling and simulation tasks were performed in “R” (v. 3.3.3). Differential equation systems were solved using the lsoda routine of the “deSolve” package (v. 1.14). The predictions in “R” were successfully crossvalidated against NONMEM (7.3, ICON, Hanover, MD) and the results were identical to 1e‐8. “ggplot2” (v. 2.2.1) was used for generating plots. Parameters of the PAE model (kin, kout,max, kout,50) and murine PK parameters (CL, ka, Vd, cf. Table 1) were estimated using the R package “optim” using extended least squares regression. Nested models were compared using the likelihood ratio test, e.g., a 3.84 difference in the objective function value was required to select a more complex model for one degree of freedom and at a significance level of 5%. For comparison of nonnested models, the Akaike criterion was used,37 where a lower Akaike score is favorable.
FUNDING
The Swedish Research Council (grant number 521‐2011‐3442) and the Innovative Medicines Initiative Joint Undertaking (http://www.imi.europe.eu) under grant agreement 115337, resources of which are composed of financial contribution from the European Union's Seventh Framework Programme (FP7/2007‐2013) and EFPIA companies' in kind contribution.
CONFLICT OF INTEREST
The authors declare no competing interests for this work.
AUTHOR CONTRIBUTIONS
S.G.W., O.C., R.J.S., S.H.G., Y.H., A.R.M.C., and U.S.H.S. wrote the article; S.G.W., O.C., R.J.S., S.H.G., Y.H., A.R.M.C., and U.S.H.S. designed the research; S.G.W., O.C., R.J.S., S.H.G., Y.H., A.R.M.C., and U.S.H.S. performed the research; S.G.W., O.C., R.J.S., S.H.G., Y.H., A.R.M.C., and U.S.H.S. analyzed the data.
Supporting information
Supporting Information 1
Supporting Information 2
Supporting Information 3
Supporting Information 4
Supporting Information 5
Supporting Information 6
Supporting Information 7
Supporting Information 8
Supporting Information 9
ACKNOWLEDGMENTS
The research leading to these results has received funding from the Swedish Research Council (grant number 521‐2011‐3442) and the Innovative Medicines Initiative Joint Undertaking (http://www.imi.europe.eu) under grant agreement 115337, resources of which are composed of financial contribution from the European Union's Seventh Framework Programme (FP7/2007‐2013) and EFPIA companies' in kind contribution.
References
- 1. van Ingen, J. et al Why do we use 600 mg of rifampicin in tuberculosis treatment? Clin. Infect. Dis. 52, e194–e199 (2011). [DOI] [PubMed] [Google Scholar]
- 2. Clewe, O. , Aulin, L. , Hu, Y. , Coates, A.R.M. & Simonsson, U.S.H. A multistate tuberculosis pharmacometric model: a framework for studying anti‐tubercular drug effects in vitro. J. Antimicrob. Chemother. 71, 964–974 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Lipworth, S. et al Defining dormancy in mycobacterial disease. Tuberculosis 99, 131–142 (2016). [DOI] [PubMed] [Google Scholar]
- 4. Hu, Y. et al Detection of mRNA transcripts and active transcription in persistent Mycobacterium tuberculosis induced by exposure to rifampicin or pyrazinamide. J. Bacteriol. 182, 6358–6365 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Wicha, S.G. , Chen, C. , Clewe, O. & Simonsson, U.S.H. A general pharmacodynamic interaction model identifies perpetrators and victims in drug interactions. Nat. Commun. 8, (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Clewe, O. , Wicha, S.G. , Vogel, C.P. de , Steenwinkel, J.E.M. de & Simonsson, U.S.H. A model‐informed preclinical approach for prediction of clinical pharmacodynamic interactions of anti‐TB drug combinations. J. Antimicrob. Chemother. 73, 437–447 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Chen, C. et al The multistate tuberculosis pharmacometric model: a semi‐mechanistic pharmacokinetic‐pharmacodynamic model for studying drug effects in an acute tuberculosis mouse model. J. Pharmacokinet. Pharmacodyn. 44, 133–141 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Chen, C. et al Assessing pharmacodynamic interactions in mice using the multistate tuberculosis pharmacometric and general pharmacodynamic interaction models. CPT Pharmacometrics Syst. Pharmacol. 6, 787–797 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Svensson, R.J. & Simonsson, U.S.H. Application of the multistate tuberculosis pharmacometric model in patients with rifampicin‐treated pulmonary tuberculosis. CPT Pharmacometrics Syst. Pharmacol. 5, 264–273 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Diacon, A.H. et al 14‐day bactericidal activity of PA‐824, bedaquiline, pyrazinamide, and moxifloxacin combinations: a randomised trial. Lancet 380, 986–993 (2012). [DOI] [PubMed] [Google Scholar]
- 11. Heinrich, N. et al Early phase evaluation of SQ109 alone and in combination with rifampicin in pulmonary TB patients. J. Antimicrob. Chemother. 70, 1558–1566 (2015). [DOI] [PubMed] [Google Scholar]
- 12. Diacon, A.H. et al Bactericidal activity of pyrazinamide and clofazimine alone and in combinations with pretomanid and bedaquiline. Am. J. Respir. Crit. Care Med. 191, 943–953 (2015). [DOI] [PubMed] [Google Scholar]
- 13. Donald, P.R. & Diacon, A.H. The early bactericidal activity of anti‐tuberculosis drugs: a literature review. Tuberculosis 88, S75–S83 (2008). [DOI] [PubMed] [Google Scholar]
- 14. Rustomjee, R. et al Early bactericidal activity and pharmacokinetics of the diarylquinoline TMC207 in treatment of pulmonary tuberculosis. Antimicrob. Agents Chemother. 52, 2831–2835 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Svensson, R.J. , Gillespie, S.H. & Simonsson, U.S.H. Improved power for TB Phase IIa trials using a model‐based pharmacokinetic‐pharmacodynamic approach compared with commonly used analysis methods. J. Antimicrob. Chemother. 72, 2311–2319 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Gumbo, T. et al Selection of a moxifloxacin dose that suppresses drug resistance in Mycobacterium tuberculosis, by use of an in vitro pharmacodynamic infection model and mathematical modeling. J. Infect. Dis. 190, 1642–1651 (2004). [DOI] [PubMed] [Google Scholar]
- 17. European Medicines Agency Qualification opinion on in vitro hollow‐fibre‐system model of tuberculosis (HFS‐TB) (2014).
- 18. Cohrs, R.J. et al Translational medicine definition by the European Society for Translational Medicine. New Horizons Transl. Med. 2, 86–88 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Svensson, R.J. et al A population pharmacokinetic model incorporating saturable pharmacokinetics and autoinduction for high rifampicin doses. Clin. Pharmacol. Ther. 103, 674–683 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Clewe, O. , Goutelle, S. , Conte, J.E. & Simonsson, U.S.H. A pharmacometric pulmonary model predicting the extent and rate of distribution from plasma to epithelial lining fluid and alveolar cells—using rifampicin as an example. Eur. J. Clin. Pharmacol. 71, 313–319 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Gumbo, T. et al Concentration‐dependent mycobacterium tuberculosis killing and prevention of resistance by rifampin. Antimicrob. Agents Chemother. 51, 3781–3788 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Jayaram, R. et al Pharmacokinetics‐pharmacodynamics of rifampin in an aerosol infection model of tuberculosis. Antimicrob. Agents Chemother. 47, 2118–2124 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Boeree, M. J. et al A dose‐ranging trial to optimize the dose of rifampin in the treatment of tuberculosis. Am. J. Respir. Crit. Care Med. 191, 1058–1065 (2015). [DOI] [PubMed] [Google Scholar]
- 24. Jindani, A. , Aber, V.R. , Edwards, E.A. & Mitchison, D.A. The early bactericidal activity of drugs in patients with pulmonary tuberculosis. Am Rev Respir Dis 121, 939–949 (1980). [DOI] [PubMed] [Google Scholar]
- 25. Sirgel, F.A. et al The early bactericidal activities of rifampicin and rifapentine in pulmonary tuberculosis. Am. J. Respir. Crit. Care Med. 172, 128–135 (2005). [DOI] [PubMed] [Google Scholar]
- 26. Diacon, A.H. et al Early bactericidal activity of high‐dose rifampidin in patients with pulmonary tuberculosis evidenced by positive sputum smears. Antimicrob. Agents Chemother. 51, 2994–2996 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Chan, S.L. et al The early bactericidal activity of rifabutin measured by sputum viable counts in Hong Kong patients with pulmonary tuberculosis. Tuber. Lung Dis. 73, 33–38 (1992). [DOI] [PubMed] [Google Scholar]
- 28. Kristoffersson, A.N. et al Simulation‐based evaluation of PK/PD indices for meropenem across patient groups and experimental designs. Pharm. Res. 33, 1115–1125 (2016). [DOI] [PubMed] [Google Scholar]
- 29. Nielsen, E.I. , Cars, O. & Friberg, L.E. Pharmacokinetic/pharmacodynamic (PK/PD) indices of antibiotics predicted by a semimechanistic PKPD model: a step toward model‐based dose optimization. Antimicrob. Agents Chemother. 55, 4619–4630 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Nielsen, E.I. & Friberg, L.E. Pharmacokinetic‐pharmacodynamic modeling of antibacterial drugs. Pharmacol. Rev. 65, 1053–1090 (2013). [DOI] [PubMed] [Google Scholar]
- 31. Müller, M. , Peña, A. dela & Derendorf, H. Issues in pharmacokinetics and pharmacodynamics of anti‐infective agents: distribution in tissue. Antimicrob. Agents Chemother. 48, 1441–1453 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Bartelink, I. et al New paradigm for translational modeling to predict long‐term tuberculosis treatment response. Clin. Transl. Sci. doi: 10.1111/cts.12472 [Epub ahead of print]. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Hu, Y. et al High‐dose rifampicin kills persisters, shortens treatment duration, and reduces relapse rate in vitro and in vivo. Front. Microbiol. 6, 641 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Schön, T. et al Evaluation of wild‐type MIC distributions as a tool for determination of clinical breakpoints for Mycobacterium tuberculosis. J. Antimicrob. Chemother. 64, 786–793 (2009). [DOI] [PubMed] [Google Scholar]
- 35. Efron, B. The Jackknife, the Bootstrap and Other Resampling Plans. (Society for Industrial and Applied Mathematics, 1982).
- 36.EUCAST Rifampicin — Rationale for clinical breakpoints version 1.0. 1–14 (2010).
- 37. Akaike, H. A new look at the statistical model identification In: Sel. Pap. Hirotugu Akaike (Parzen E., Tanabe K. &. Kitagawa G., eds.) 215–222 (Springer, New York, 1974). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information 1
Supporting Information 2
Supporting Information 3
Supporting Information 4
Supporting Information 5
Supporting Information 6
Supporting Information 7
Supporting Information 8
Supporting Information 9


