Accelerating compressed sensing in parallel imaging reconstructions using an efficient circulant preconditioner for cartesian trajectories

Abstract

Purpose

Design of a preconditioner for fast and efficient parallel imaging (PI) and compressed sensing (CS) reconstructions for Cartesian trajectories.

Theory

PI and CS reconstructions become time consuming when the problem size or the number of coils is large, due to the large linear system of equations that has to be solved in ${\ell }_1$ and ${\ell }_2$‐norm based reconstruction algorithms. Such linear systems can be solved efficiently using effective preconditioning techniques.

Methods

In this article we construct such a preconditioner by approximating the system matrix of the linear system, which comprises the data fidelity and includes total variation and wavelet regularization, by a matrix that is block circulant with circulant blocks. Due to this structure, the preconditioner can be constructed quickly and its inverse can be evaluated fast using only two fast Fourier transformations. We test the performance of the preconditioner for the conjugate gradient method as the linear solver, integrated into the well‐established Split Bregman algorithm.

Results

The designed circulant preconditioner reduces the number of iterations required in the conjugate gradient method by almost a factor of 5. The speed up results in a total acceleration factor of approximately 2.5 for the entire reconstruction algorithm when implemented in MATLAB, while the initialization time of the preconditioner is negligible.

Conclusion

The proposed preconditioner reduces the reconstruction time for PI and CS in a Split Bregman implementation without compromising reconstruction stability and can easily handle large systems since it is Fourier‐based, allowing for efficient computations.

1. INTRODUCTION

The undersampling factor in parallel imaging (PI) is in theory limited by the number of coil channels.1, 2, 3, 4 Higher factors can be achieved by using compressed sensing (CS) which estimates missing information by adding a priori information.5, 6 The a priori knowledge relies on the sparsity of the image in a certain transform domain. It is possible to combine PI and CS, for example, Refs. 7 and 8 achieving almost an order of magnitude speed‐up factors in cardiac perfusion MRI and enabling free‐breathing MRI of the liver.9

CS allows reconstruction of an estimate of the true image even in the case of considerable undersampling factors, for which the data model generally describes an ill‐posed problem without a unique solution. This implies that the true image cannot be found by directly applying Fourier transforms. Instead, regularization is used to solve the ill‐posed problem by putting additional constraints on the solution. For CS, such a constraint enforces sparsity of the image in a certain domain, which is promoted by the ${\ell }_0$‐norm.6, 10, 11 However, practically the ${\ell }_1$‐norm is used instead as it is the closest representation that is numerically feasible to implement. The wavelet transform and derivative operators, integrated in total variation regularization, are examples of sparsifying transforms that can be used in the spatial direction8, 12, 13, 14, 15, 16 and temporal dimension,9 respectively.

Although CS has led to a considerable reduction in acquisition times either in PI applications or in single coil acquisitions, the benefit of the ${\ell }_1$‐norm regularization constraint comes with the additional burden of increased reconstruction times, because ${\ell }_1$‐norm minimization problems are in general difficult to solve. Many methods have been proposed that solve the problem iteratively.12, 14, 17, 18, 19, 20, 22, 23, 50 In this work, we focus on the Split Bregman (SB) approach because of its computational performance, and its well‐established track record.14, 24, 25, 26, 27, 28 SB transforms the initial minimization problem, containing both ${\ell }_1$ and ${\ell }_2$‐norm terms, into a set of subproblems that either require solving an ${\ell }_2$‐norm or an ${\ell }_1$‐norm minimization problem, each of which can be approached using standard methods.

The most expensive step in SB, which is also present in many other methods, is to solve an ${\ell }_2$‐norm minimization problem, which can be formulated as a linear least squares problem.29 The system matrix of the least squares problem remains constant throughout the SB iterations and this feature has shown to be convenient for finding an approximation of the inverse system matrix as is done in for example, Ref. 30. This approach eliminates the need for an iterative scheme to solve the ${\ell }_2$‐norm minimization problem, but for large problem sizes the initial computational costs are high, making it less profitable in practice.

An alternative approach for eliminating the iterative scheme to solve the ${\ell }_2$‐norm minimization problem was demonstrated in Ref. 31. In this approach, extra variable splitting is introduced to separate the coil sensitivity matrices from the Fourier transforms, such that all individual subproblems can be solved directly in the case of Cartesian sampling. This can lead to a considerable reduction in reconstruction time, provided that the reconstruction parameters are optimized. Simulations and in vivo experiments showed significant improvements in convergence compared to nonlinear conjugate gradient and a monotone fast iterative shrinkage‐thresholding algorithm. The extra variable splitting introduces penalty parameters, however, and unstable behavior can occur for certain parameter choices due to nontrivial null‐spaces of the operators.31, 32, 33 This can be seen as a drawback of this approach. Furthermore, determining the extra parameters is obviously nonunique. Considering the fact that each image slice would be reconstructed optimally with possibly different reconstruction parameters, we prefer the more straightforward SB scheme. Moreover, for non‐Cartesian trajectories, direct solutions are no longer possible and iterative schemes are needed.

Alternatively, to keep the number of reconstruction parameters to a minimum and to minimize possible stability issues, preconditioners can be used to reduce the number of iterations required for solving the least squares problem.34 The incomplete Cholesky factorization and hierarchically structured matrices are examples of preconditioners that reduce the number of iterations drastically in many applications.35, 36 The drawback of these type of preconditioners is that the full system matrix needs to be built before the reconstruction starts, which for larger problem sizes can only be done on a very powerful computer due to memory limitations. Although in Refs. 37, 38, 39 a penta‐diagonal matrix was constructed as a preconditioner, solving such a system is still relatively expensive. In addition, before constructing the preconditioner, patient‐specific coil sensitivity profiles need to be measured, which often leads to large initialization times. In Refs. 31 and 40, the extra variable splitting enables building a preconditioner independent of coil sensitivity maps, resulting in a preconditioner for non‐Cartesian reconstructions, but one that is not applicable for the more stable SB scheme.

In this work, we design a Fourier transform‐based preconditioner for PI–CS reconstructions and Cartesian trajectories in a stable SB framework, that takes the coil sensitivities on a patient‐specific basis into account, has negligible initialization time and which is highly scalable to a large number of unknowns, as often encountered in MRI.

2. THEORY

In this section we first describe the general PI and CS problems. Subsequently, the Split Bregman algorithm, which is used to solve these problems, is discussed. Hereafter, weintroduce the preconditioner that is used to speed up the PI–CS algorithm and elaborate on its implementation and complexity.

2.1. Parallel imaging reconstruction

In PI with full k‐space sampling the data, including noise, is described by the model

$$\mathrm{F}{\mathrm{S}}_i\mathbf{x}={\mathbf{y}}_{\text{full},i}\hspace{1em}\text{for}\hspace{0.17em}i=1,\dots ,{\mathrm{N}}_{\mathrm{c}}$$ (1)

where the ${\mathbf{y}}_{\text{full},i}\in {ℂ}^{N\times 1}$ are the fully sampled k‐space data sets containing noise for $i\in \{1,\mathrm{..},{\mathrm{N}}_{\mathrm{c}}\}$, with ${\mathrm{N}}_{\mathrm{c}}$ the number of coil channels, and $\mathbf{x}\in {ℂ}^{N\times 1}$ is the true image.3 Here, $N=m·n$, where m and n define the image matrix size in the x‐ and y‐directions, respectively, for a 2D sampling case. Furthermore, ${\mathrm{S}}_i\in {ℂ}^{N\times N}$ are diagonal matrices representing complex coil sensitivity maps for each channel. Finally, $\mathrm{F}\in {ℂ}^{N\times N}$ is the discrete two‐dimensional Fourier transform matrix. In the case of undersampling, the data is described by the model

$$\mathrm{RF}{\mathrm{S}}_i\mathbf{x}={\mathbf{y}}_i\hspace{1em}\text{for}\hspace{0.17em}i=1,\dots ,{\mathrm{N}}_{\mathrm{c}},$$ (1)

where ${\mathbf{y}}_i\in {ℂ}^{N\times 1}$ are the under sampled k‐space data sets for $i\in \{1,\mathrm{..},{\mathrm{N}}_{\mathrm{c}}\}$ with zeros at nonmeasured k‐space locations. The undersampling pattern is specified by the binary diagonal sampling matrix $\mathrm{R}\in {ℝ}^{N\times N}$, so that the under sampled Fourier transform is given by $\mathrm{RF}$. Here it is important to note that $\mathrm{R}$ reduces the rank of $\mathrm{RF}{\mathrm{S}}_i$, which means that solving for x in Equation 1 is in general an ill‐posed problem for each coil and a unique solution does not exist. However, if the individual coil data sets are combined and the undersampling factor does not exceed the number of coil channels, the image x can in theory be reconstructed by finding the least squares solution, that is, by minimizing

$$\widehat{\mathbf{x}}=\underset{\mathbf{x}}{\text{argmin}}\left\{{\displaystyle \sum _{i=1}^{{\mathrm{N}}_{\mathrm{c}}}{\Vert \mathrm{RF}{\mathrm{S}}_i\mathbf{x}-{\mathbf{y}}_i\Vert }_2^2}\right\},$$ (2)

where $\widehat{\mathbf{x}}\in {ℂ}^{N\times 1}$ is an estimate of the true image.

2.2. Parallel imaging reconstruction with compressed sensing

In the case of higher undersampling factors, the problem of solving Equation 2 becomes ill‐posed and additional regularization terms need to be introduced to transform the problem into a well‐posed problem. Since MR images are known to be sparse in some domains, ${\ell }_1$‐norm terms are a suitable choice for regularization. The techniques of PI and CS are then combined in the following minimization problem

$$\widehat{\mathbf{x}}=\underset{\mathbf{x}}{\text{argmin}}\left\{\frac{\mu }{2}{\displaystyle \sum _{i=1}^{{\mathrm{N}}_{\mathrm{c}}}{\Vert \mathrm{RF}{\mathrm{S}}_i\mathbf{x}-{\mathbf{y}}_i\Vert }_2^2}+\frac{\lambda }{2}\left({\Vert {\mathrm{D}}_x\mathbf{x}\Vert }_1+{\Vert {\mathrm{D}}_y\mathbf{x}\Vert }_1\right)+\frac{\gamma }{2}{\Vert \mathrm{W}\mathbf{x}\Vert }_1\right\},$$ (3)

with $\mu ,\lambda$, and γ the regularization parameters for the data fidelity, the total variation, and the wavelet, respectively.8 A total variation regularization constraint is introduced by the first‐order derivative matrices ${\mathrm{D}}_x,\hspace{0.17em}{\mathrm{D}}_y\in {ℝ}^{N\times N}$, representing the numerical finite difference scheme

$${D_x(x)|}_{i,j}=x_{i,j}-x_{i-1,j}\hspace{1em}i=2,\mathrm{..},m,\hspace{1em}j=1,\mathrm{..},n$$

$${D_y(x)|}_{i,j}=x_{i,j}-x_{i,j-1}\hspace{1em}i=1,\mathrm{..},m,\hspace{1em}j=2,\mathrm{..},n$$

with periodic boundary conditions

$${D_x(x)|}_{1,j}=x_{1,j}-x_{m,j}\hspace{1em}j=1,\mathrm{..},n$$

$${D_y(x)|}_{i,1}=x_{i,1}-x_{i,n}\hspace{1em}i=1,\mathrm{..},m$$

so that ${\mathrm{D}}_x$ and ${\mathrm{D}}_y$ are circulant. A unitary wavelet transform $\mathrm{W}\in {ℝ}^{N\times N}$ further promotes sparsity of the image in the wavelet domain.

2.3. Split Bregman iterations

Solving Equation 3 is not straightforward as the partial derivatives of the ${\ell }_1$‐norm terms are not well‐defined around 0. Instead, the problem is transformed into one that can be solved easily. In this work, we use Split Bregman to convert Equation 3 into multiple minimization problems in which the ${\ell }_1$‐norm terms have been decoupled from the ${\ell }_2$‐norm term, as discussed in detail in Refs. 14 and 24. For convenience, the Split Bregman method is shown in Algorithm 1. The Bregman parameters ${\mathbf{b}}_x,{\mathbf{b}}_y,{\mathbf{b}}_w$ are introduced by the Bregman scheme and auxiliary variables ${\mathbf{d}}_x,{\mathbf{d}}_y,{\mathbf{d}}_w$ are introduced by writing the constrained problem as an unconstrained problem. The algorithm consists of two loops: an outer loop and an inner loop. In the inner loop (steps 4–11), we first compute the vector b that serves as a right‐hand side in the system of equations of step 5. Subsequently, the ${\ell }_1$‐norm subproblems are solved using the shrink function in steps 6–8. Hereafter, the residuals for the regularization terms are computed in steps 9–11 and are subsequently fed back into the system by updating the right‐hand side vector b in step 5. Steps 4–11 can be repeated several times, but one or two inner iterations are normally sufficient for convergence. Similarly, the outer loop feeds the residual encountered in the data fidelity term back into the system, after which the inner loop is executed again.

The system of linear equations,

$$\mathrm{A}\widehat{\mathbf{x}}=\mathbf{b},$$ (4)

in line 5 of the algorithm follows from a standard least squares problem, where the system matrix is given by

$$\mathrm{A}=\mu {\displaystyle \sum _{i=1}^{{\mathrm{N}}_{\mathrm{c}}}{\left(\mathrm{RF}{\mathrm{S}}_i\right)}^H}\mathrm{RF}{\mathrm{S}}_i+\lambda \left({\mathrm{D}}_x^H{\mathrm{D}}_x+{\mathrm{D}}_y^H{\mathrm{D}}_y\right)+\gamma {\mathrm{W}}^H\mathrm{W}$$

with right‐hand side

$$\mathbf{b}=\mu {\displaystyle \sum _{i=1}^{{\mathrm{N}}_{\mathrm{c}}}{\left(\mathrm{RF}{\mathrm{S}}_i\right)}^H}{\mathbf{y}}_i+\lambda \left[{\mathrm{D}}_x^H\left({\mathbf{d}}_x^k-{\mathbf{b}}_x^k\right)+{\mathrm{D}}_y^H\left({\mathbf{d}}_y^k-{\mathbf{b}}_y^k\right)\right]+\gamma {\mathrm{W}}^H\left({\mathbf{d}}_w^k-{\mathbf{b}}_w^k\right).$$

In this work we focus on solving Equation 4, which is computationally the most expensive part of Algorithm 1. It is important to note that the system matrix $\mathrm{A}$ remains constant throughout the algorithm and only the right‐hand side vector b changes, which allows us to efficiently solve Equation 4 by using preconditioning techniques.

Algorithm 1. Split Bregman Iteration.

1: Initialize $\begin{array}{c}{\mathbf{y}}_i^{[1]}={\mathbf{y}}_i\hspace{0.17em}\text{for}\hspace{0.17em}i=1,\dots ,{\mathrm{N}}_{\mathrm{c}},\hspace{0.17em}{\mathbf{x}}^{[1]}=\text{Sum}\hspace{0.5em}\text{of}\hspace{0.5em}\text{Squares}({\mathrm{F}}^H{\mathbf{y}}_i,i=1,\dots ,{\mathrm{N}}_{\mathrm{c}})\end{array}$,

Initialize

${\mathbf{b}}_x^{[1]},{\mathbf{b}}_y^{[1]},{\mathbf{b}}_w^{[1]},{\mathbf{d}}_x^{[1]},{\mathbf{d}}_y^{[1]},{\mathbf{d}}_w^{[1]}=0$

2: for j = 1 to nOuter do

3: for k = 1 to nInner do

4: $\mathbf{b}=\mu {\displaystyle \sum _{i=1}^{{\mathrm{N}}_{\mathrm{c}}}{\mathrm{S}}_i^H}{\mathrm{F}}^H{\mathrm{R}}^H{\mathbf{y}}_i^{[j]}+\lambda \left[{\mathrm{D}}_x^H({\mathbf{d}}_x^{[k]}-{\mathbf{b}}_x^{[k]})+{\mathrm{D}}_y^H({\mathbf{d}}_y^{[k]}-{\mathbf{b}}_y^{[k]})\right]+\gamma {\mathrm{W}}^H({\mathbf{d}}_w^{[k]}-{\mathbf{b}}_w^{[k]})$

5: solve $\mathrm{A}{\mathbf{x}}^{[k+1]}=\mathbf{b}$ with ${\mathbf{x}}^{[k]}$ as initial guess

6: ${\mathbf{d}}_x^{[k+1]}=\text{shrink}\left({\mathrm{D}}_x{\mathbf{x}}^{[k+1]}+{\mathbf{b}}_x^{[k]},\frac{1}{\lambda }\right)$

7: ${\mathbf{d}}_y^{[k+1]}=\text{shrink}\left({\mathrm{D}}_y{\mathbf{x}}^{[k+1]}+{\mathbf{b}}_y^{[k]},\frac{1}{\lambda }\right)$

8: ${\mathbf{d}}_w^{[k+1]}=\text{shrink}\left(\mathrm{W}{\mathbf{x}}^{[k+1]}+{\mathbf{b}}_w^{[k]},\frac{1}{\gamma }\right)$

9: ${\mathbf{b}}_x^{[k+1]}={\mathbf{b}}_x^{[k]}+{\mathrm{D}}_x{\mathbf{x}}^{[k+1]}-{\mathbf{d}}_x^{[k+1]}$

10: ${\mathbf{b}}_y^{[k+1]}={\mathbf{b}}_y^{[k]}+{\mathrm{D}}_y{\mathbf{x}}^{[k+1]}-{\mathbf{d}}_y^{[k+1]}$

11: ${\mathbf{b}}_w^{[k+1]}={\mathbf{b}}_w^{[k]}+\mathrm{W}{\mathbf{x}}^{[k+1]}-{\mathbf{d}}_w^{[k+1]}$

12: end for

13: for i = 1 to ${\mathrm{N}}_{\mathrm{c}}$ do

14: ${\mathbf{y}}_i^{[j+1]}={\mathbf{y}}_i^{[j]}+{\mathbf{y}}_i^{[1]}-\mathrm{RF}{\mathrm{S}}_i{\mathbf{x}}^{[k+1]}$

15: end for

16: end for

2.4. Structure of the system matrix $\mathrm{A}$

The orthogonal wavelet transform is unitary, so that ${\mathrm{W}}^H\mathrm{W}=\mathrm{I}$. Furthermore, the derivative operators are constructed such that the matrices ${\mathrm{D}}_x,{\mathrm{D}}_y,{\mathrm{D}}_x^H$, and ${\mathrm{D}}_y^H$ are block circulant with circulant blocks (BCCB). The product and sum of two BCCB matrices is again BCCB, showing that ${\mathrm{D}}_x^H{\mathrm{D}}_x+{\mathrm{D}}_y^H{\mathrm{D}}_y$ is also BCCB. These types of matrices are diagonalized by the two‐dimensional Fourier transformation, that is,

$${\mathrm{D}}_1=\mathrm{FC}{\mathrm{F}}^H\hspace{1em}\text{or}\hspace{1em}{\mathrm{D}}_2={\mathrm{F}}^H\mathrm{CF}$$

where $\mathrm{C}$ is a BCCB matrix and ${\mathrm{D}}_1$ and ${\mathrm{D}}_2$ are diagonal matrices. This motivates us to write the system matrix $\mathrm{A}$ in Equation 4 in the form

$$\begin{array}{l}\mathrm{A}={\mathrm{F}}^H\mathrm{FA}{\mathrm{F}}^H\mathrm{F}\\ ={\mathrm{F}}^H\mathrm{KF}\end{array}$$ (5)

with $\mathrm{K}\in {ℂ}^{N\times N}$ given by

$$\mathrm{K}=\mu \underset{{\mathrm{K}}_c}{\underbrace{{\displaystyle \sum _{i=1}^{{\mathrm{N}}_{\mathrm{c}}}\mathrm{F}}{\mathrm{S}}_i^H{\mathrm{F}}^H{\mathrm{R}}^H\mathrm{RF}{\mathrm{S}}_i{\mathrm{F}}^H}}+\lambda \underset{{\mathrm{K}}_d}{\underbrace{ \mathrm{F}\left({\mathrm{D}}_x^H{\mathrm{D}}_x+{\mathrm{D}}_y^H{\mathrm{D}}_y\right){\mathrm{F}}^H}}+\gamma \underset{{\mathrm{K}}_w}{\underbrace{\mathrm{ I }}}.$$ (6)

The term ${\mathrm{D}}_x^H{\mathrm{D}}_x+{\mathrm{D}}_y^H{\mathrm{D}}_y$ is BCCB, so that ${\mathrm{K}}_d$ in $\mathrm{K}$ becomes diagonal. If there is no sensitivity encoding, that is ${\mathrm{S}}_i\hspace{0.17em}=\hspace{0.17em}\mathrm{I}\forall i\in \{1,\mathrm{..},{\mathrm{N}}_{\mathrm{c}}\}$, the entire $\mathrm{K}$ matrix becomes diagonal in which case the solution $\widehat{\mathbf{x}}$ can be efficiently found by computing

$$\widehat{\mathbf{x}}={\mathrm{A}}^{-1}\mathbf{b}={\mathrm{F}}^H{\mathrm{K}}^{-1}\mathrm{F}\mathbf{b}$$ (7)

for invertible $\mathrm{K}$. In practice, Fast Fourier Transforms (FFTs) are used for this step. With sensitivity encoding, ${\mathrm{S}}_i\ne \mathrm{I}$ and ${\mathrm{S}}_i^H{\mathrm{F}}^H{\mathrm{R}}^H\mathrm{RF}{\mathrm{S}}_i$ is not BCCB for any i, hence matrix $\mathrm{K}$ is not diagonal. In that case we prefer to solve Equation 4 iteratively, since finding ${\mathrm{K}}^{-1}$ is now computationally too expensive. It can be observed that the system matrix $\mathrm{A}$ is Hermitian and positive definite, which motivates the choice for the conjugate gradient (CG) method as an iterative solver.

2.5. Preconditioning

A preconditioner $\mathrm{M}\in {ℂ}^{N\times N}$ can be used to reduce the number of iterations required for CG convergence.41 It should satisfy the conditions

1. ${\mathrm{M}}^{-1}\mathrm{A}\approx \mathrm{I}$ to cluster the eigenvalues of the matrix pair around 1, and

2. determination of ${\mathrm{M}}^{-1}$ and its evaluation on a vector should be computationally cheap.

Ideally, we would like to use a diagonal matrix as the preconditioner as this is computationally inexpensive. For this reason, the Jacobi preconditioner is used in many applications with the diagonal elements from matrix $\mathrm{A}$ as the input. However, for the current application of PI and CS the Jacobi preconditioner is not efficient since it does not provide an accurate approximate inverse of the system matrix $\mathrm{A}$. In this work, we use a different approach and approximate the diagonal from $\mathrm{K}$ in Equation 6 instead. The motivation behind this approach is that the Fourier matrices in matrix $\mathrm{K}$ center a large part of the information contained in ${\mathrm{S}}_i^H{\mathrm{F}}^H{\mathrm{R}}^H\mathrm{RF}{\mathrm{S}}_i$ around the main diagonal of $\mathrm{K}$, so that neglecting off‐diagonal elements of $\mathrm{K}$ has less effect than neglecting off‐diagonal elements of $\mathrm{A}$.

For the preconditioner used in this work we approximate ${\mathrm{A}}^{-1}$ by

$${\mathrm{M}}^{-1}={\mathrm{F}}^H\text{diag}{\left\{\mathbf{k}\right\}}^{-1}\mathrm{F},$$ (8)

where $\text{diag}\left\{\right\}$ places the elements of its argument on the diagonal of a matrix. Furthermore, vector k is the diagonal of matrix $\mathrm{K}$ and can be written as

$$\mathbf{k}=\mu {\mathbf{k}}_c+\lambda {\mathbf{k}}_d+\gamma {\mathbf{k}}_w,$$ (9)

where ${\mathbf{k}}_c,\hspace{0.17em}{\mathbf{k}}_d$, and ${\mathbf{k}}_w$ are the diagonals of ${\mathrm{K}}_c,\hspace{0.17em}{\mathrm{K}}_d$, and ${\mathrm{K}}_w$, respectively. Note that ${\mathrm{K}}_d$ and ${\mathrm{K}}_w$ are diagonal matrices already, so that only ${\mathbf{k}}_c$ will result in an approximation of the inverse for the final system matrix $\mathrm{A}$.

2.6. Efficient implementation of the preconditioner

The diagonal elements ${\mathbf{k}}_{c;i}$ of ${\mathrm{K}}_{c;i}=\underset{{\mathrm{C}}_i^H}{\underbrace{\mathrm{F}{\mathrm{S}}_i^H{\mathrm{F}}^H}}\underset{\mathrm{R}}{\underbrace{\mathrm{ }{\mathrm{R}}^H\mathrm{R }}}\underset{{\mathrm{C}}_i}{\underbrace{\mathrm{F}{\mathrm{S}}_i{\mathrm{F}}^H}}$ for a certain i are found by noting that ${\mathrm{C}}_i=\mathrm{F}{\mathrm{S}}_i{\mathrm{F}}^H$ is in fact a BCCB matrix. The diagonal elements ${\mathbf{k}}_{c;i}$ of ${\mathrm{K}}_{c;i}$ can now be found on the diagonal of ${\mathrm{C}}_i^H\mathrm{R}{\mathrm{C}}_i$, so that

$${\mathbf{k}}_{c;i}={\displaystyle \sum _{j=1}^N{\mathbf{e}}_j}\left({\mathbf{c}}_{j;i}^H\mathrm{R}{\mathbf{c}}_{j;i}\right),$$

with ${\mathbf{c}}_{j;i}^H$ being the jth row of matrix ${\mathrm{C}}_i^H$ and ${\mathbf{e}}_j$ the j^th standard basis vector. Note that the scalar $\left({\mathbf{c}}_{j;i}^H\mathrm{R}{\mathbf{c}}_{j;i}\right)$ is the j^th entry of vector ${\mathbf{k}}_{c;i}$. Since $\mathrm{R}$ is a diagonal matrix which can be written as $\mathrm{R}=\text{diag}\left\{\mathbf{r}\right\}$, we can also write

$$\begin{array}{l}{\mathbf{k}}_{c;i}={\displaystyle \sum _{j=1}^N{\mathbf{e}}_j}\left({\mathbf{c}}_{j;i}^H°{\mathbf{c}}_{j;i}^T\right)\mathbf{r}\\ =\left[\begin{array}{c}{\mathbf{c}}_{1;i}^H°{\mathbf{c}}_{1;i}^T\\ {\mathbf{c}}_{2;i}^H°{\mathbf{c}}_{2;i}^T\\ ⋮\\ {\mathbf{c}}_{N;i}^H°{\mathbf{c}}_{N;i}^T\end{array}\right]\mathbf{r}\\ =\left({\mathrm{C}}_i^H°{\mathrm{C}}_i^T\right)\mathbf{r},\end{array}$$ (10)

where $°$ denotes the element‐wise (Hadamard) product. Since the element‐wise product of two BCCB matrices is again a BCCB matrix, the circular convolution theorem tells us42, 43 that

$$\mathrm{F}{\mathbf{k}}_{c;i}=\mathrm{F}\left[{\left({\mathbf{c}}_{1;i}^H°{\mathbf{c}}_{1;i}^T\right)}^T\ast \mathbf{r}\right]=\mathrm{F}\left[{\left({\mathbf{c}}_{1;i}^H°{\mathbf{c}}_{1;i}^T\right)}^T\right]°\mathrm{F}\mathbf{r}.$$

The resulting matrix vector product in Equation 10 can now be efficiently computed as

$${\mathbf{k}}_{c;i}={\mathrm{F}}^H\left\{\left[\mathrm{F}{\left({\mathbf{c}}_{1;i}^H°{\mathbf{c}}_{1;i}^T\right)}^T\right]°\mathrm{F}\mathbf{r}\right\}.$$ (11)

Finally, the diagonal elements d of the diagonal matrix $\mathrm{D}$ with structure $\mathrm{D}=\mathrm{FC}{\mathrm{F}}^H$ can be computed efficiently by using $\mathbf{d}=\mathrm{F}{\mathbf{c}}_1$, where ${\mathbf{c}}_1$ is the first row of $\mathrm{C}$. Therefore, the first row ${\mathbf{c}}_{1;i}^H$ of matrix ${\mathrm{C}}_i^H$ is found as ${\left({\mathbf{c}}_{1;i}^H\right)}^T={\mathrm{F}}^H{\left({\mathbf{s}}_i^H\right)}^T$, with ${\mathbf{s}}_i^H$ a row vector containing the diagonal elements of matrix ${\mathrm{S}}_i$. For multiple coils Equation 11 becomes

$${\mathbf{k}}_c={\mathrm{F}}^H\left\{\left[\mathrm{F}{\displaystyle \sum _{i=1}^{{\mathrm{N}}_{\mathrm{c}}}{\left({\mathbf{c}}_{1;i}^H°{\mathbf{c}}_{1;i}^T\right)}^T}\right]°\mathrm{F}\mathbf{r}\right\},$$ (12)

where the action of the Fourier matrix on a vector can be efficiently computed using the FFT.

Since ${\mathrm{D}}_x^H{\mathrm{D}}_x+{\mathrm{D}}_y^H{\mathrm{D}}_y$ is BCCB, the elements of ${\mathbf{k}}_d$ can be quickly found by evaluating ${\mathbf{k}}_d=\mathrm{F}{\mathbf{t}}_1$, where ${\mathbf{t}}_1$ is the first row of ${\mathrm{D}}_x^H{\mathrm{D}}_x+{\mathrm{D}}_y^H{\mathrm{D}}_y$. Finally, the elements of ${\mathbf{k}}_w$ are all equal to one, since ${\mathrm{K}}_{\mathrm{\omega }}$ is the identity matrix.

Alternatively, in Equation 2 the summation over the coil sensitivity matrices can be removed by stacking the matrices. The derivation following this approach can be found online as supporting information.

2.7. Complexity

For every inner‐iteration of the Split Bregman algorithm we need to solve the linear system given in Equation 4, which is done iteratively using a Preconditioned Conjugate Gradient method (PCG). In this method, the preconditioner constructed above is used as a left preconditioner by solving the following system of equations:

$${\mathrm{M}}^{-1}\mathrm{A}\widehat{\mathbf{x}}={\mathrm{M}}^{-1}\mathbf{b},$$ (13)

where $\widehat{\mathbf{x}}$ is the approximate solution constructed by the PCG algorithm. In PCG this implies that for every iteration the preconditioner should be applied once on the residual vector $\mathbf{r}=\mathrm{A}\widehat{\mathbf{x}}-\mathbf{b}$. The preconditioner $\mathrm{M}$ can be constructed beforehand since it remains fixed for the entire Split Bregman algorithm as the regularization parameters μ, λ, and γ are constant. As can be seen in Table 1, ${\mathrm{M}}^{-1}$ is constructed in $(3+2{\mathrm{N}}_{\mathrm{c}})N+(4+{\mathrm{N}}_{\mathrm{c}})N\log N$ FLOPS. Evaluation of the diagonal preconditioner ${\mathrm{M}}^{-1}$ from Equation 8 on a vector amounts to two Fourier transforms and a single multiplication, and therefore requires $N+2N\log N$ FLOPS.

Table 1.

FLOPS required for construction of ${\mathrm{M}}^{-1}$ and for evaluation of $\mathrm{A}$ on a vector.

	Operation	FLOPS
Construction of ${\mathrm{M}}^{-1}$	${\left({\mathbf{c}}_i^H\right)}^T={\mathrm{F}}^H{\left({\mathbf{s}}_i^H\right)}^T\forall i\in \{1,\mathrm{..},{\mathrm{N}}_{\mathrm{c}}\}$,	${\mathrm{N}}_{\mathrm{c}}N\log N$
	${\displaystyle \sum _i^{{\mathrm{N}}_{\mathrm{c}}}{\left({\mathbf{c}}_{1;i}^H°{\mathbf{c}}_{1;i}^T\right)}^T}$	$2{\mathrm{N}}_{\mathrm{c}}N-N$
	${\mathrm{F}}^H\left[\mathrm{F}(\dots )°\mathrm{F}(\dots )\right]$	$N+3N\log N$
	${\mathbf{k}}_d={\mathrm{F}}^H{\mathbf{t}}_1$	$N\log N$
	$\mathbf{k}={\mathbf{k}}_c+{\mathbf{k}}_d+{\mathbf{k}}_w$	2N
	${\mathbf{k}}^{-1}$	N
	Total	$(3+2{\mathrm{N}}_{\mathrm{c}})N+(4+{\mathrm{N}}_{\mathrm{c}})N\log N$
Evaluation $\mathrm{A}$ on vector	${\displaystyle \sum _{i=1}^{{\mathrm{N}}_{\mathrm{c}}}{\left(\mathrm{RF}{\mathrm{S}}_i\right)}^H}\mathrm{RF}{\mathrm{S}}_i$	${\mathrm{N}}_{\mathrm{c}}(3N+2N\log N)+{\mathrm{N}}_{\mathrm{c}}N-N$
	${\mathrm{D}}_x^H{\mathrm{D}}_x+{\mathrm{D}}_y^H{\mathrm{D}}_y$	5N
	${\mathrm{W}}^H\mathrm{W}$	0
	Summation of the three terms above	2N
	Total	$(6+4{\mathrm{N}}_{\mathrm{c}})N+2{\mathrm{N}}_{\mathrm{c}}N\log N$

To put this into perspective, evaluation of matrix $\mathrm{A}$ on a vector requires $(6+4{\mathrm{N}}_{\mathrm{c}})N+2{\mathrm{N}}_{\mathrm{c}}N\log N$ FLOPS, as shown in Table 1. The upper bound on the additional costs per iteration relative to the costs for evaluating $\mathrm{A}$ on a vector is therefore

$$\underset{N\to \infty }{\lim }\frac{N+2N\log N}{(6+4{\mathrm{N}}_{\mathrm{c}})N+2{\mathrm{N}}_{\mathrm{c}}N\log N}=\frac{1}{{\mathrm{N}}_{\mathrm{c}}},$$

showing that the preconditioner evaluation step becomes relatively cheaper for an increasing number of coil elements. The scaling of the complexity with respect to the problem size is depicted in Figure 1 for a fixed number of coils ${\mathrm{N}}_{\mathrm{c}}=12$.

Figure 1.

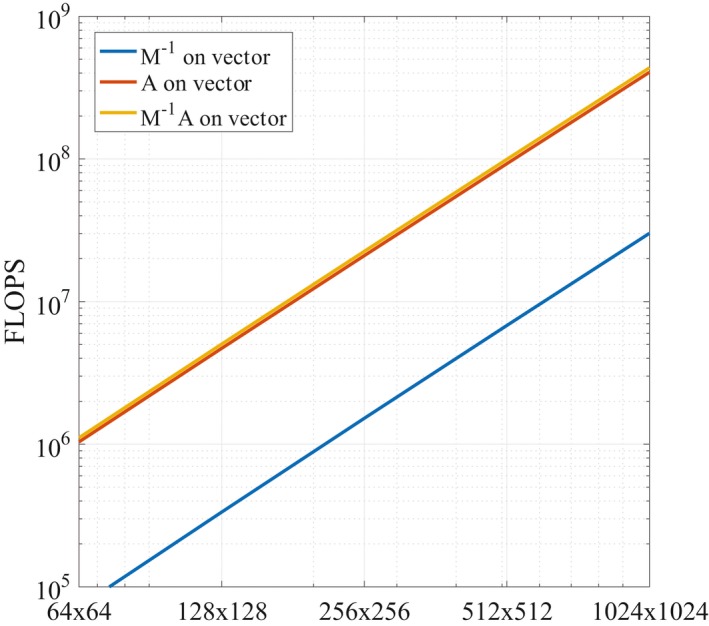
The complexity for different problem sizes. The number of FLOPS for the action of the preconditioner $\mathrm{M}$ on a vector (blue), $\mathrm{A}$ on a vector (red), and the combination of the two (yellow) are depicted for ${\mathrm{N}}_{\mathrm{c}}=12$.

3. Methods

3.1. MR data acquisition

Experiments were performed on healthy volunteers after giving informed consent. The Leiden University Medical Center Committee for Medical Ethics approved the experiment. An Ingenia 3T dual transmit MR system (Philips Healthcare) was used to acquire the in vivo data. A 12‐element posterior receiver array, a 15‐channel head coil, a 16‐channel knee coil (also used for transmission) and a 16‐element anterior receiver array were used for reception in the spine, the brain, the knee and the lower legs, respectively. The body coil was used for RF transmission, except for the knee scan.

For the spine data set, T₁‐weighted images were acquired using a turbo spin‐echo (TSE) sequence with the following parameters: field of view (FOV) = 340 × 340mm²; in‐plane resolution 0.66 × 0.66mm²; 4mm slice thickness; 15 slices; echo time (TE)/repetition time (TR)/TSE factor = 8 ms/648 ms/8; flip angle (FA) = 90°; refocusing angle = 120°; water–fat shift (WFS) = 1.5 pixels; and scan time = 2:12 minutes. T₂‐weighted TSE scans had parameters: FOV = 340 × 340mm²; in‐plane resolution 0.66 × 0.66mm²; 4mm slice thickness; 15 slices; TE/TR/TSE factor = 113 ms/4008 ms/32; FA = 90°; WFS = 1.1 pixels; and scan time = 3:36 minutes.

For the brain data set, T₁‐weighted images were acquired using an inversion recovery turbo spin‐echo (IR TSE) sequence with parameters: FOV = 230 × 230mm²; in‐plane resolution 0.90 × 0.90mm²; 4mm slice thickness; 24 slices; TE/TR/TSE factor = 20 ms/2000 ms/8; refocusing angle = 120°; IR delay: 800 ms; WFS = 2.6 pixels; and scan time = 05:50 minutes. T ${}_2^{\ast }$‐weighted images were measured using a gradient echo (FFE) sequence with parameters: FOV = 230 × 230mm²; in‐plane resolution 0.90 × 0.90mm²; 4mm slice thickness; 28 slices; TE/TR = 16 ms/817 ms; FA = 18°; WFS = 2 pixels; and scan time = 3:33 minutes.

For the knee data set, T₁‐weighted images were acquired using an FFE sequence with parameters: FOV = 160 × 160mm²; in‐plane resolution 1.25 × 1.25mm²; 3mm slice thickness; 32 slices; TE/TR = 10 ms/455 ms; FA = 90°; WFS = 1.4 pixels; and scan time = 1:01 minutes.

For the calf data set, T₁‐weighted images were acquired using an FFE sequence with parameters: FOV = 300 × 300mm²; in‐plane resolution 1.17 × 1.17mm²; 7mm slice thickness; 24 slices; TE/TR = 16 ms/500 ms; FA = 90°; WFS = 1.5 pixels; and scan time = 2:11 minutes.

The different acquisitions techniques (TSE, FFE) were chosen to address different basic contrasts used in daily clinical practice. Undersampling in the case of nonstationary echo signals, such as during a T₂‐decaying TSE train, can result in image quality degradation. This effect can be mitigated, for example, in TSE scans using variable refocusing angle schemes as outlined in Ref. 44.

To show the performance of the preconditioner also in the presence of these and similar effects, scans in the brain were acquired directly in undersampled mode employing a simple variable density sampling pattern, with acceleration factors R = 2 and R = 3. To validate the results, fully sampled data is acquired as well in a separate scan. Data for a T₂‐weighted TSE scan (R = 2, FOV = 230 × 230mm²; in‐plane resolution 0.90 × 0.90mm²; 4mm slice thickness; 1 slice; TE/TR/TSE factor = 80 ms/3000 ms/16; refocusing angle = 120°; WFS = 2.5 pixels; and scan time = 00:30 minutes), a FLAIR scan (R = 2, FOV = 240 × 224mm²; in‐plane resolution 1.0 × 1.0mm²; 4mm slice thickness; 1 slice; TE/TR/TSE factor = 120 ms/9000 ms/24; IR delay = 2500 ms; refocusing angle = 110°; WFS = 2.7 pixels; and scan time = 01:30 minutes) and a 3D magnetization prepared T₁‐weighted turbo field echo (TFE) scan (R = 3, FOV = 250 × 240 × 224mm²; 1.0mm³ isotropic resolution; TE/TR = 4.6 ms/9.9 ms; TFE factor = 112; TFE prepulse delay = 1050 ms; flip angle = 8°; WFS = 0.5 pixels; and scan time = 04:17 minutes).

3.2. Coil sensitivity maps

Unprocessed k‐space data was stored per channel and used to construct complex coil sensitivity maps for each channel.45 Note that the coil sensitivity maps are normalized such that

$$\widehat{S_i}={\left[{\displaystyle \sum _{j=1}^{{\mathrm{N}}_{\mathrm{c}}}{S}_j^H{S}_j}\right]}^{-\frac{1}{2}}{S}_i\hspace{1em}\text{for}\hspace{0.17em}i=1,\dots ,{\mathrm{N}}_{\mathrm{c}}.$$

The normalized coil sensitivity maps were given zero intensity outside the subject, resulting in an improved SNR of the final reconstructed image. For the data model to be consistent, also the individual coil images were normalized according to

$$m_i={\widehat{S}}_i{\displaystyle \sum _{j=1}^{{\mathrm{N}}_{\mathrm{c}}}{\widehat{S}}_j^H}{m}_j\hspace{1em}\text{for}\hspace{0.17em}i=1,\dots ,{\mathrm{N}}_{\mathrm{c}}.$$

3.3. Coil compression

Reconstruction of the spine data set was performed with and without coil compression. A compression matrix was constructed as in Ref. 46 and multiplied by the normalized individual coil images and the coil sensitivity maps, to obtain virtual coil images and sensitivity maps. The six least dominant virtual coils were ignored to speed up the reconstruction.

3.4. Undersampling

Two variable density undersampling schemes were studied: a random line pattern in the foot‐head direction, referred to as structured sampling, and a fully random pattern, referred to as random sampling. Different undersampling factors were used for both schemes.

3.5. Reconstruction

The Split Bregman algorithm was implemented in MATLAB (The MathWorks, Inc.). All image reconstructions were performed in 2D on a Windows 64‐bit machine with an Intel i3–4160 CPU @ 3.6GHz and 8 GB internal memory.

Reconstructions were performed for reconstruction matrix sizes of 128 × 128, 256 × 256, and 512 × 512, and the largest reconstruction matrix was interpolated to obtain a simulated data set of size 1024 × 1024 for theoretical comparison. For prospectively undersampled scans, additional matrix sizes of 240 × 224 were acquired. For the 3D scan, an FFT was first performed along the readout direction, after which one slice was selected. To investigate the effect of the regularization parameters on the performance of the preconditioner, three different regularization parameter sets were chosen as:

1. set 1 $\mu ={10}^{-3},\hspace{0.17em}\lambda =4·{10}^{-3}$, and $\gamma ={10}^{-3}$

2. set 2 $\mu ={10}^{-2},\hspace{0.17em}\lambda =4·{10}^{-3}$, and $\gamma ={10}^{-3}$

3. set 3 $\mu ={10}^{-3},\hspace{0.17em}\lambda =4·{10}^{-3}$, and $\gamma =4·{10}^{-3}.$

The Daubechies 4 wavelet transform was used for $\mathrm{W}$. Furthermore, the SB algorithm was performed with an inner loop of one iteration and an outer loop of 20 iterations. The tolerance (relative residual norm) in the PCG algorithm was set to $ϵ={10}^{-3}$.

4. RESULTS

Figure 2 shows the T₁‐weighted TSE spine images for a reconstruction matrix size of 512 × 512, reconstructed with the SB implementation for a fully sampled data set and for undersampling factors of four (R = 4) and eight (R = 8), where structured Cartesian sampling masks were used. The quality of the reconstructed images for R = 4 and R = 8 demonstrate the performance of the CS algorithm. The difference between the fully sampled and undersampled reconstructed images are shown (magnified five times) in Figure 2D,E for R = 4 and R = 8, respectively.

Figure 2.

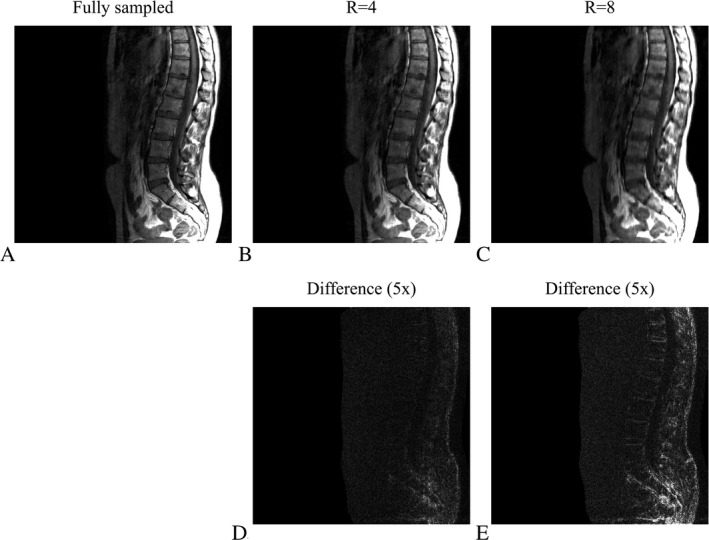
Reconstruction results for different structured Cartesian undersampling factors. (A) shows the fully sampled scan as a reference, whereas (B) and (C) depict the reconstruction results for undersampling factors four (R = 4) and eight (R = 8), respectively. The absolute difference, magnified five times, is shown in (D) and (E) for R = 4 and R = 8, respectively. The reconstruction matrix has dimensions 512 × 512. Regularization parameters were set to $\mu =1·{10}^{-3},\lambda =4·{10}^{-3}$, and $\gamma =1·{10}^{-3}$.

The fully built system matrix $\mathrm{A}={\mathrm{F}}^H\mathrm{KF}$ is compared with its circulant approximation ${\mathrm{F}}^H\text{diag}\left\{\mathbf{k}\right\}\mathrm{F}$ in Figure 3A for both structured and random Cartesian undersampling in the spine, without regularization to focus on the approximated term containing the coil sensitivities. The elements of $\mathrm{A}$ contain many zeros due to the lack of coil sensitivity in a large part of the image domain when using cropped coil sensitivity maps. These zeros are not present in the circulant approximation, since the circulant property is enforced by neglecting all off‐diagonal elements in $\mathrm{K}$. The entries introduced into the circulant approximation do not add relevant information to the system, because the image vector on which the system matrix acts contains zero signal in the region corresponding with the newly introduced entries. For the same reason, the absolute difference maps in the bottom row were masked by the coil‐sensitive region of $\mathrm{A}$, showing that the magnitude and phase are well approximated by assuming the circulant property. Figure 3B‐D show the same results for the brain, the knee and the calves, respectively, demonstrating the generalizability of this approach to different coil set‐ups and geometries.

Figure 3.

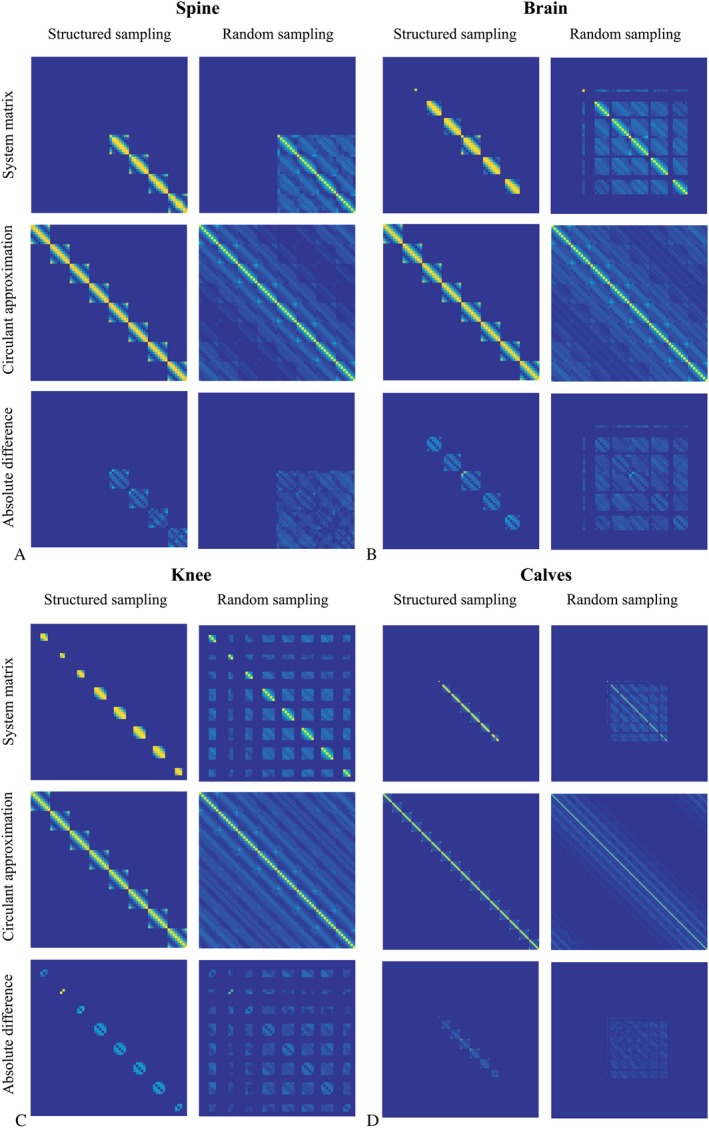
System matrix and its circulant approximation. The first and the second columns show the system matrix elements for structured and random undersampling and R = 4, respectively, for the spine (A), the brain (B), the knee (C), and the calves (D). The top row depicts the elementwise magnitude for the true system matrix $\mathrm{A}$, the second row depicts the elementwise magnitude for the circulant approximated system matrix and the bottom row shows the absolute difference between the true system matrix and the circulant approximation. The difference maps were masked by the nonzero‐region of $\mathrm{A}$, since only elements in the coil‐sensitive region of the preconditioner describe the final solution.

The product of the inverse of the preconditioner ${\mathrm{M}}^{-1}$ and the system matrix $\mathrm{A}$ is shown for the spine, the brain, the knee and the calves in Figure 4A‐D, respectively. Different regularization parameter sets show that the preconditioner is a good approximate inverse, suggesting efficient convergence.

Figure 4.

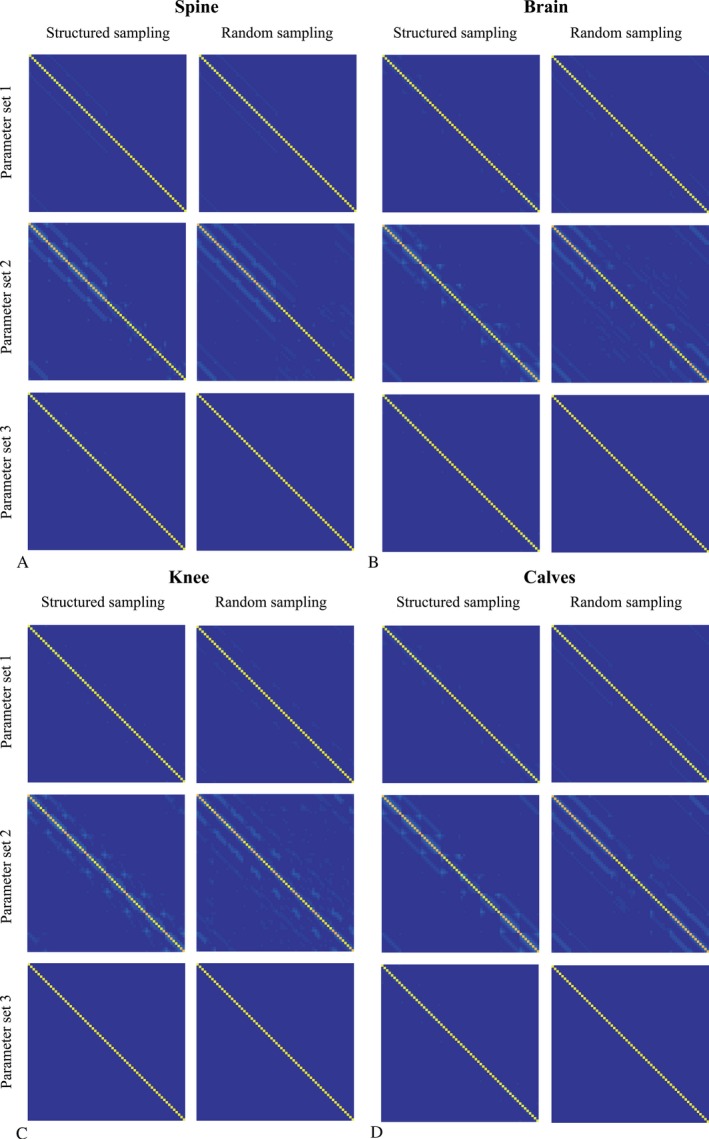
The new system matrix. The first column and the second column show the elements of the effective new system matrix ${\mathrm{M}}^{-1}\mathrm{A}$ for structured and random undersampling and R = 4, respectively, for the spine (A), the brain (B), the knee (C), and the calves (D). The rows show this result for the three studied regularization parameter sets.

Table 2 reports the number of seconds needed to build the circulant preconditioner in MATLAB before the reconstruction starts, for different orders of the reconstruction matrix. Note that the actual number of unknowns in the corresponding systems is equal to the number of elements in the reconstruction matrix size, which leads to more than 1 million unknowns for the 1024 × 1024 case. For all matrix sizes the initialization time is negligible compared with the image reconstruction time.

Table 2.

Initialization times for constructing the preconditioner for different problem sizes.

Problem size	128 × 128	256 × 256	512 × 512	1024 × 1024
Initialization time (s)	0.0395	0.0951	0.3460	1.3371
Additional costs (%)	1.7	0.85	0.52	0.48

Even for very large problem sizes the initialization time does not exceed 2 seconds.

Additional costs are given as percentage of the total reconstruction time without preconditioning.

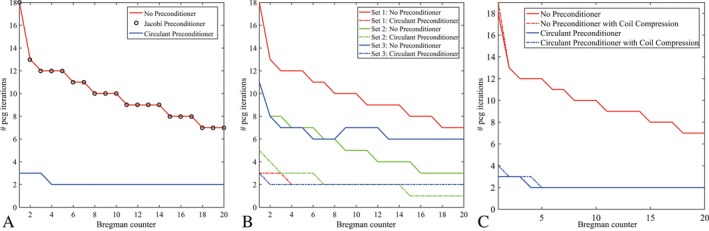
Figure 5A shows the number of iterations required for PCG to converge in each Bregman iteration without preconditioner, with the Jacobi preconditioner and with the circulant preconditioner for regularization parameters $\mu ={10}^{-3},\lambda =4·{10}^{-3}$, and $\gamma ={10}^{-3}$ and a reconstruction matrix size of 256 × 256. The Jacobi preconditioner does not reduce the number of iterations, which shows that the diagonal of the system matrix $\mathrm{A}$ does not contain enough information to result in a good approximation of ${\mathrm{A}}^{-1}$. Moreover, it shows that the linear system is invariant under scaling. The circulant preconditioner, however, reduces the number of iterations considerably, leading to a total speed‐up factor of 4.65 in the PCG part.

Figure 5.

Number of iterations needed per Bregman iteration. The circulant preconditioner reduces the number of iterations considerably compared with the nonpreconditioned case. The Jacobi preconditioner does not reduce the number of iterations due to the poor approximation of the system matrix’ inverse. (A) depicts the iterations for Set 1: $\left(\mu =1·{10}^{-3},\lambda =4·{10}^{-3},\gamma =1·{10}^{-3}\right)$, whereas (B) depicts the iterations for Set 1, Set 2: $\left(\mu =1·{10}^{-2},\lambda =4·{10}^{-3},\gamma =1·{10}^{-3}\right)$, and Set 3: $\left(\mu =1·{10}^{-3},\lambda =4·{10}^{-3},\gamma =4·{10}^{-3}\right)$ The preconditioner shows the largest speed up factor when the regularization parameters are well‐balanced. (C) Shown are the number of iterations needed per Bregman iteration with and without coil compression applied. The solid lines and the dashed lines depict the results with and without coil compression, respectively.

The effect of the reduced number of PCG iterations can directly be seen in the computation time for the reconstruction algorithm, plotted in Figure 6 for different problem sizes. Figure 6A shows the total PCG computation time when completing the total SB method, whereas Figure 6B shows the total computation time required to complete the entire reconstruction algorithm. A fivefold gain is achieved in the PCG part by reducing the number of PCG iterations, which directly relates to the results shown in Figure 5A. The overall gain of the complete algorithm, however, is a factor 2.5 instead of 5, which can be explained by the computational costs of the update steps outside the PCG iteration loop (see Algorithm 1). Figure 6C also shows the error, defined as the normalized 2‐norm difference with respect to the fully sampled image, as a function of time. The preconditioned SB scheme converges to the same accuracy as the original SB scheme, since the preconditioner only affects the required number of PCG iterations.

Figure 6.

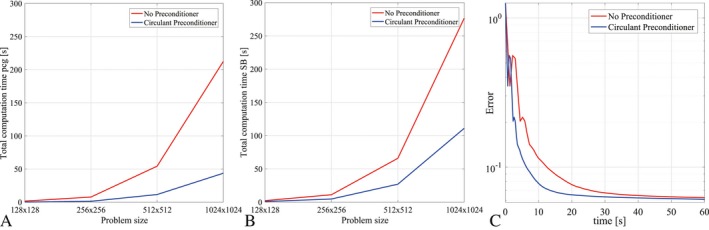
Computation time for 20 Bregman iterations and different problem sizes. (A) Using the preconditioner, the total computation time for the PCG part in 20 Bregman iterations is reduced by more than a factor of 4.5 for all studied problem sizes. (B) The computation time for 20 Bregman iterations of the entire algorithm also includes the Bregman update steps, so that the total speedup factor is approximately 2.5 for the considered problem sizes. (C) The two methods converge to the same solution, plotted here for R = 4 and a reconstruction matrix size 256 × 256.

The number of iterations required by PCG for each Bregman iteration is shown in Figure 5B for the three parameter sets studied. The preconditioned case always outperforms the nonpreconditioned case, but the speed up factor depends on the regularization parameters. Parameter set 1 depicts the same result as shown in Figure 5A and results in the best reconstruction of the fully sampled reference image. In parameter set 2 more weight is given to the data fidelity term by increasing the parameter μ. Since the preconditioner relies on an approximation of the data fidelity term, it performs less optimally than for smaller μ (such as in set 1) for the first few Bregman iterations, but there is still a threefold gain in performance. This behavior was already predicted in Figure 4. Finally, there is very little change between parameter set 3 and parameter set 1, because the larger wavelet regularization parameter γ gives more weight to a term that was integrated in the preconditioner in an exact way, as for the total variation term, without any approximations.

Figure 5C illustrates the required iterations when half of the coils are taken into account by coil compression. Only a small discrepancy is encountered for the first few iterations, since the global structure and content of the system matrix A remain the same, which demonstrates that coil compression and preconditioning can be combined to optimally reduce the reconstruction time.

The method also works for different coil configurations. In Figure 7 the result is shown when using the 15‐channel head coil for the brain scans, the 16‐channel knee coil for a knee scan and the 16‐channel receive array for the calf scan. The circulant preconditioner clearly reduces the number of iterations, with an overall speed‐up factor of 4.1/4.4 and 4.5 in the PCG part for the brain (TSE/FFE) and the knee, respectively.

Figure 7.

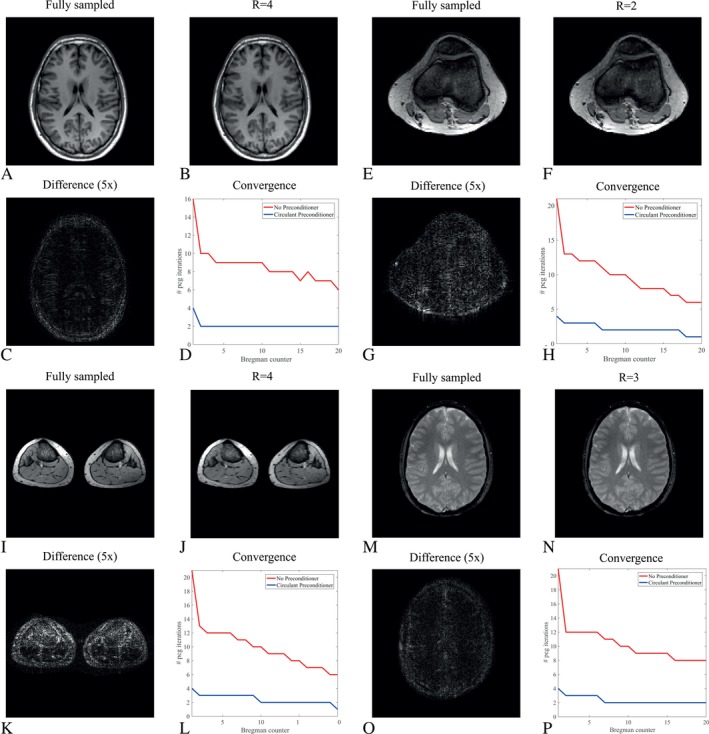
Reconstruction results for different anatomies. (A) shows the fully sampled scan as a reference for the brain, whereas (B) depicts the reconstruction results for an undersampling factor of four (R = 4). The absolute difference, magnified five times, is shown in (C). The reconstruction matrix has dimensions 256 × 256 and regularization parameters were chosen as $\mu =1·{10}^{-3},\lambda =4·{10}^{-3}$, and $\gamma =2·{10}^{-3}$. The convergence results for the PCG part with and without preconditioner are plotted in (D), showing similar reduction factors as with the posterior coil. Results for the knee are shown in (E)‐(F) for a reconstruction matrix size 128 × 128 and an undersampling factor of 2 (R = 2). Regularization parameters were chosen as $\mu =0.1,\lambda =0.4$, and $\gamma =0.1$. Results for the calves are shown in (I)‐(L) for a reconstruction matrix size 256 × 256 and R = 4. Regularization parameters were chosen as $\mu =0.1,\lambda =0.4$, and $\gamma =0.1$. Results for the brain FFE scan are shown in (M)‐(P) for a reconstruction matrix size 256 × 256 and R = 3. Regularization parameters were chosen as $\mu =1,\lambda =4$, and .

Figure 8 shows reconstruction results for scans where the data was directly acquired in under sampled mode instead of retrospectively undersampled, for a T₂‐weighted TSE scan, a FLAIR scan and a 3D magnetization prepared T₁‐weighted TFE scan, leading to PCG acceleration factors of 4.2, 5.1, and 5.4, respectively. The convergence behavior is similar to the one observed for the retrospectively undersampled data, demonstrating the robustness of the preconditioning approach in realistic scan setups.

Figure 8.

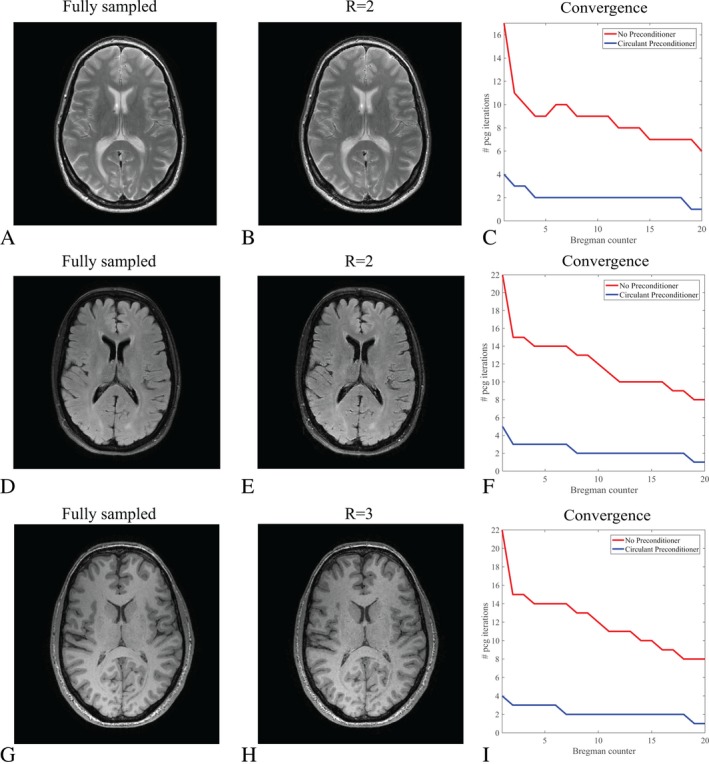
Reconstruction results for data acquired in fully and undersampled mode. (A) shows a fully sampled scan as a reference for a T₂‐weighted TSE scan in the brain, whereas (B) depicts the reconstruction results for a prospectively undersampled scan with an acceleration factor of two (R = 2). The reconstruction matrix has dimensions 256 × 256 and regularization parameters were chosen as $\mu =1,\lambda =4$, and γ = 1. The convergence results for the PCG part with and without preconditioner are plotted in (C). Results for the FLAIR brain scan are shown in (D)‐(F) for a reconstruction matrix size 240 × 224 and R = 2. Regularization parameters were chosen as $\mu =1.4·{10}^2,\lambda =5.7·{10}^2$, and $\gamma =1.4·{10}^2$. Results for a 3D magnetization prepared T₁‐weighted TFE scan in the brain are shown in (G)‐(I) for a reconstruction matrix size 240 × 224 and R = 3. Regularization parameters were chosen as $\mu =0.5,\lambda =2$, and $\gamma =0.5$. Note that the data in the left column stem from a different measurement as the data in the middle column

The performance of the preconditioner is also stable in the presence of different noise levels, as shown by experiments in which the excitation tip angle was varied from 10° to 90° in a TSE sequence, and results can be found online in Supporting Information Figure S1.

5. DISCUSSION AND CONCLUSIONS

In this work we have introduced a preconditioner that reduces the reconstruction times for CS and PI problems, without compromising the stability of the numerical SB scheme. Solving an ${\ell }_2$‐norm minimization problem is the most time‐consuming part of this algorithm. This ${\ell }_2$‐norm minimization problem is written as a linear system of equations characterized by the system matrix $\mathrm{A}$. The effectiveness of the introduced preconditioner comes from the fact that the system matrix is approximated as a BCCB matrix. Both the total variation and the wavelet regularization terms are BCCB, which means that only the data fidelity term, which is not BCCB due to the sensitivity profiles of the receive coils and the undersampling of k‐space, is approximated by assuming a BCCB structure in the construction of the preconditioner. This approximation has been shown to be accurate for CS–PI problem formulations. The efficiency of this approach comes from the fact that BCCB matrices are diagonalized by Fourier transformations, which means that the inverse of the preconditioner can simply be found by inverting a diagonal matrix and applying two additional FFTs.

With the designed preconditioner the most expensive ${\ell }_2$‐norm problem was solved almost five times faster than without preconditioning, resulting in an overall speed up factor of about 2.5. The discrepancy between the two speed up factors can be explained by the fact that apart from solving the linear problem, update steps also need to be performed. Step 4 and steps 13–15 of Algorithm 1 are especially time consuming since for each coil a 2D Fourier transform needs to be performed. Furthermore, the wavelet computation in steps 4, 8, and 11 are time consuming factors as well. Therefore, speed up factors higher than 2.5 are expected for an optimized Bregman algorithm. Further acceleration can be obtained through coil compression,46, 47 as the results in this study showed that it has negligible effect on the performance of the preconditioner.

The time required to construct the preconditioner is negligible compared with the reconstruction times as it involves only a few FFTs. The additional costs of applying the preconditioner on a vector is negligible as well, because it involves only two Fourier transformations and an inexpensive multiplication with a diagonal matrix. Therefore, the method is highly scalable and can handle large problem sizes.

The preconditioner works optimally when the regularization terms in the minimization problem are BCCB matrices in the final system matrix. This implies that the total variation operators should be chosen such that the final total variation matrix is BCCB, and that the wavelet transform should be unitary. Both the system matrix and the preconditioner can be easily adjusted to support single regularization instead of the combination of two regularization approaches.

The BCCB approximation for the data fidelity term supports both structured and random Cartesian undersampling patterns and works well for different undersampling factors. The performance of the preconditioner was experimentally validated using a variable density sampling scheme to prospectively undersample the data. The convergence behavior shows similar results as the retrospectively undersampled case.

The regularization parameters were shown to influence the performance of the preconditioner. Since the only approximation in the preconditioner comes from the approximation of the data fidelity term, the preconditioner results in poorer performance if the data fidelity term is very large compared with the regularization terms. In practice, such a situation is not likely to occur if the regularization parameters are chosen such that an optimal image quality is obtained in the reconstructed image. In this work, the regularization parameters were chosen empirically and were kept constant throughout the algorithm. For SB‐type methods, however, updating the regularization parameters during the algorithm makes the performance of the algorithm less dependent on the initial choice of the parameters.48 Moreover, it might result in improved convergence, from which our work can benefit.

This work focused on the linear part of the SB method, in which only the right‐hand side vector changes in each iteration and not the system matrix. Other ${\ell }_1$‐norm minimization algorithms exist that require a linear solver,49 such as IRLS or Second‐Order Cone Programming. For those type of algorithms linear preconditioning techniques can be applied as well. Although the actual choice for the preconditioner depends on the system matrix of the linear problem, which is in general different for different minimization algorithms, similar techniques as used in the current work can be exploited to construct a preconditioner for other minimization algorithms.

As outlined earlier in the introduction, there are alternative approaches to eliminating the iterative scheme to solve the ${\ell }_2$‐norm minimization problem. Although a detailed comparison of techniques is difficult due to the required choice of reconstruction parameters, it is worth noting that in Ref. 31 a comparison was made between the nonpreconditioned SB scheme that we also use as comparison in our work, and the authors’ extra variable splitting method. Their results suggest that the preconditioned SB scheme with an acceleration factor of 2.5 is very similar to the performance of the method adopting extra variable splitting. Moreover, variable splitting is not possible for non‐Cartesian data acquisition but is easily incorporated into the preconditioned SB approach. In this extension, the block circulant matrix with circulant blocks is replaced by the block Toeplitz matrix with Toeplitz blocks.40 Given the promising results for Cartesian trajectories, future work will therefore focus on including non‐Cartesian data trajectories into a single unified preconditioned SB framework.

Another large group of reconstruction algorithms involve gradient update steps; examples in this group are the Iterative Shrinkage‐Thresholding Algorithm (ISTA), FISTA, MFISTA, and BARISTA.50, 51, 52, 53 In Ref. 53 it was discussed that the performance of FISTA, for which convergence depends on the maximum sum of squared absolute coil sensitivity value, can be poor due to large variations in coil sensitivities. In our work, however, the coil sensitivity maps were normalized such that the corresponding sum‐of‐squares map is constant and equal to one in each spatial location within the object region. The normalization of these coil sensitivities might therefore lead to acceleration of FISTA‐type algorithms. Thus, it would be interesting to compare the performance of the preconditioned SB algorithm with the performance of FISTA when incorporating normalized coil sensitivities into both algorithms.

In conclusion, the designed FFT‐based preconditioner reduces the number of iterations required for solving the linear problem in the SB algorithm considerably, resulting in an overall acceleration factor of 2.5 for PI–CS reconstructions. The approach works for different coil‐array configurations, MR sequences, and nonpower of two acquisition matrices, and the time to construct the preconditioner is negligible. Therefore, it can be easily used and implemented, allowing for efficient computations.

Supporting information

FIGURE S1 The performance of the preconditioner for different SNR levels. Prospectively undersampled data sets were obtained for different SNR levels by varying the flip angle from 10 to 90 degrees in a TSE sequence. The difference in the number of CG iterations needed until convergence with and without preconditioner for different SNR levels is negligible.

Koolstra K, van Gemert J, Börnert P, Webb A, Remis R. Accelerating compressed sensing in parallel imaging reconstructions using an efficient circulant preconditioner for cartesian trajectories. Magn Reson Med. 2019;81:670–685. 10.1002/mrm.27371