Field responsive mechanical metamaterials

We present a new class of architected materials that exhibit rapid, reversible, and sizable changes in effective stiffness.

Abstract

Typically, mechanical metamaterial properties are programmed and set when the architecture is designed and constructed, and do not change in response to shifting environmental conditions or application requirements. We present a new class of architected materials called field responsive mechanical metamaterials (FRMMs) that exhibit dynamic control and on-the-fly tunability enabled by careful design and selection of both material composition and architecture. To demonstrate the FRMM concept, we print complex structures composed of polymeric tubes infilled with magnetorheological fluid suspensions. Modulating remotely applied magnetic fields results in rapid, reversible, and sizable changes of the effective stiffness of our metamaterial motifs.

INTRODUCTION

Cellular materials can be highly mechanically efficient, especially for coupled properties that often require trade-offs (1). For example, random cellular structures found in nature, such as teeth, bone, and bird beaks, have excellent strength and toughness relative to their density (2, 3). These stochastic cellular structures are often imitated in synthetic materials such as polymeric and metallic foams used for structural and functional applications (4). Ordered cellular structures can outperform their stochastic counterparts (5), with nature creating periodic architectures via evolutionary design (and, in some cases, directly competing designs). For example, a mollusk’s defensive armor shell is partly composed of strong and tough brick-and-mortar arrangements found in the inner nacreous layers (6). In response, the mantis shrimp has evolved offensive dactyl clubs that penetrate mollusk shells with high-speed impacts, and these clubs are partly composed of helicoidal stackups of mineralized fibers that resist fracture (7). Periodic and hierarchical architectures are also found in large-scale, manufactured structures such as truss bridges and the Eiffel tower (8). Now, additive manufacturing and three-dimensional (3D) printing techniques are being used to create cellular structures with nano-, micro-, meso-, and macro-length-scale features that exhibit unique mechanical, functional, and thermal property combinations (9). These material classes are often referred to as metamaterials—specific mechanical metamaterial demonstrations include lightweight yet stiff and strong architectures (10–12), forms with high mechanical resilience (13–16), structures with negative Poisson’s ratio (17–20), elastomechanical “unfeelability” cloaks (21), and multimaterial layouts that have negative coefficients of thermal expansion (22–24). For these examples, the material and architecture are fixed (in time) after fabrication, which limits their ability to respond and adapt to changing conditions.

To create more responsive and adaptable materials, so-called 4D printing has emerged as a new research area, where the fourth dimension represents time. The term “4D” stems from the fact that these materials are 3D printed and change their shape or function in response to changing conditions or stimuli. 4D-printed materials have been shown to reconfigure themselves due to mechanical force, temperature, swelling, and magnetic fields, causing color (25) or shape (26–34) changes. Yet, to date, these demonstrations suffer from a lack of highly deterministic control of mechanical properties or exhibit long response times due to transport limitations or slow kinetics of chemical transformations. Here, we present a new class of 3D-printed, field responsive mechanical metamaterials (FRMMs) that exhibit programmable, predictive, and highly controlled changes in mechanical properties with large dynamic range and rapid and reversible response by facile application of a remote magnetic field.

RESULTS AND DISCUSSION

To obtain FRMMs with dynamically tunable stiffness, we incorporate magnetorheological (MR) fluid suspensions into the core of 3D-printed polymer tubes (ala vasculature), which are the building blocks of unit cells and lattices. MR fluids, which consist of ferromagnetic microparticles suspended in nonmagnetic liquids, quickly change viscosity in response to an applied magnetic field. In the absence of a magnetic field, the MR fluid behaves as a liquid wherein the suspended particles are randomly distributed and the suspension freely flows to form a pool when deposited on a planar substrate (Fig. 1A). When a magnetic field is applied, the suspended particles align into chains along the field lines to form an array of spicular, blade-like structures that resemble stalactite deposits (Fig. 1B). As the particles of the MR fluid order under a magnetic field, the fluid viscosity monotonically increases until reaching a saturation point, where further strengthening the applied field has no additional rheological effect due to maximal structure development of the particles (35–37). Figure 1C shows that the relative increase in viscosity of our MR fluid begins to plateau at a magnetic field strength of approximately 0.3 T, yet some increase in viscosity remains evident even through the maximum tested field strength of 1.0 T (Fig. 1D).

Fig. 1. Structure onset and rheological tests of MR fluids in response to applied magnetic field.

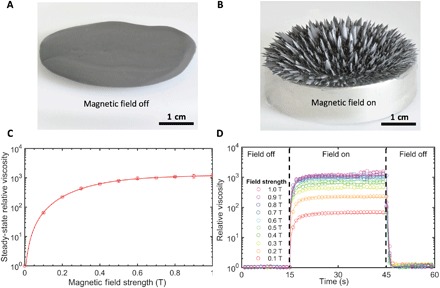
(A) Optical image of the MR fluid forming a liquid pool on a planar substrate in the absence of a magnetic field. (B) Optical image of the MR fluid forming ordered, blade-like columns in the presence of a magnetic field. (C) Rheological plot of the MR fluid’s relative steady-state viscosity, which increases with increasing applied magnetic field strength. The field off steady-state viscosity is 140 cP. (D) Rheological plot demonstrating the response time of the MR fluid at various magnetic field strengths.

To achieve deterministic design and programming of our FRMMs, we sought to develop a predictive modeling capability. This model starts with a representation of the mechanical response of a single strut as a frame element that resists combined axial compression, transverse bending, and torsional deformation (fig. S1). The magnetomechanical behavior exhibits directional dependence. For the purposes of model construction, we assume that the largest change in effective stiffness of the MR fluid–filled strut occurs when the field is applied parallel to the direction of deformation (38). For uniaxial compression tests, the strut stiffness will increase when the magnetic field is the same direction as the compressive load, whereas a field applied transverse to the applied force will exhibit no stiffening effect (Fig. 2A). For cantilevered bending tests, the strut shear stiffness will increase when the magnetic field is applied along the same direction as the bending displacement, whereas a field applied along the strut length will have no stiffening effect (Fig. 2B). We have confirmed the assumption that the change in effective stiffness is largest with a field applied parallel to the direction of the force, as in fig. S2, where it can be seen that a compression test of a strut with a perpendicular field of 0.4 T provides less mechanical stiffness than a compression test of a strut with a parallel field of 0.25 T at strains up to 10%. Since we are mechanically testing at small strains of 2.5%, we assume that the effect of the perpendicular field is negligible in our analytical model. To capture the constituent material behavior for our model, we first printed hollow struts of defined wall thickness and aspect ratio and infilled and sealed these struts with MR fluid for mechanical testing in both uniaxial compression and cantilevered bending. It was important that the single struts used to calibrate the model had the same length and cross-sectional shape (and area) as those in the final lattice structure to provide the most accuracy for the predicted response of the FRMMs. To carry out this calibration study, we constructed hollow 5-mm-long struts that had circular cross sections with 1.1-mm outer diameter and 1.0-mm inner diameter to yield 50-μm-thick walls (Fig. 2C). If lattices were created with a new strut geometry, then the model would need to be recalibrated with new struts. Each cylinder was filled with commercially available MR fluid (MRF-122EG, LORD Corporation) consisting of 50% by volume carbonyl iron particles with diameters of 4 to 20 μm suspended with a particle stabilizer in a hydrocarbon oil (Fig. 2D). We designed a custom, test apparatus to vary the magnetic field strength during mechanical testing of the struts by holding a permanent (neodymium) magnet at different distances from the sample with the magnetic field measured at the center of the sample with a Gaussmeter. Each magnetomechanical test was repeated at several different magnetic field strengths, where the field was aligned parallel to the direction of the applied force. The experimental data consist of a series of force-displacement curves at several values of magnetic field strengths from 0 to 0.21 T for compression (Fig. 2E and fig. S3A) and from 0 to 0.12 T for cantilever bending (Fig. 2F and fig. S3B). We note that the maximum magnetic field strengths vary between the mechanical tests due to the distance from the magnet to the center of the sample that is allowed by our experimental test setup. The mechanical test results were used to calibrate the model, with the aim of ultimately predicting the field responsive behavior of lattices composed of similar strut-like elements.

Fig. 2. Single strut characterization.

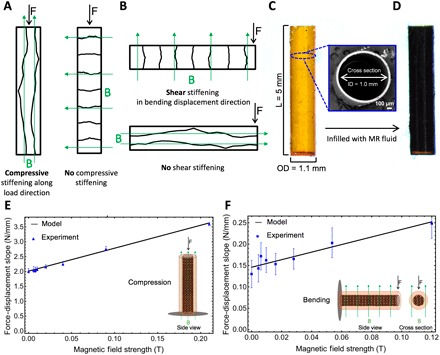
(A and B) Schematic illustrations of how the magnetic field application direction affects the stiffening of a strut. (A) In the axial case, a magnetic field applied transverse to the strut will produce no increase in axial stiffness, regardless of field strength applied. (B) In the bending case, a magnetic field applied perpendicular to the displacement will have no effect on bending stiffness, regardless of the field strength applied. (C) Side view optical image of the hollow polymer strut before infilling with MR fluid. Inset is a scanning electron microscopy micrograph of the hollow polymer strut cross section. (D) Side view optical image after infilling with MR fluid. The strut dimensions are 1.0-mm inner diameter (ID), 1.1-mm outer diameter (OD), 50-μm wall thickness, and 5-mm length (L). (E and F) Force-displacement slope versus magnetic field strength plots. (E) Uniaxial compression showing experimental results and model calibration. Inset is a schematic illustration of the experimental setup from the side view. (F) Cantilevered bending showing experimental results and model calibration. Inset is a schematic illustration of the experimental setup from the side and cross-sectional views.

Unlike typical frame elements used to model the response of lattice materials (10), the elastic stiffness of these struts changes with the application of an external magnetic field. Our model uses the composite beam theory to represent the increase in strut stiffness as the applied magnetic field increases the Young’s and shear moduli of the MR fluid–filled core. As a first approximation, we assume a linear relation between the magnetic field and the core Young’s and shear moduli, which is consistent with the behavior of MR fluid under moderate magnetic field strengths (36, 39). We note that the MR fluid core also has some initial stiffness, because the fluid is in a sealed system and will develop hydrostatic stress under load, even without an applied field. Calibrating the model required determination of six parameters: E_bulk, G_bulk, E_min, k_E, G_min, and k_G, where E_bulk is the Young’s modulus of the as-cured polymer resin, G_bulk is the shear modulus of the as-cured polymer resin, E_min is the effective Young’s modulus of the MR fluid–filled polymer strut with no applied field, G_min is the effective shear modulus of the MR fluid–filled polymer strut with no applied field, k_E is the increase in effective Young’s modulus of the MR fluid–filled polymer strut per tesla, and k_G is the increase in effective shear modulus of the MR fluid–filled polymer strut per tesla. Using the effective elastic stiffness of the MR fluid and the stiffness of the polymer, the standard composite beam theory was used to derive a model of the composite strut element, where the analysis assumes the Euler-Bernoulli bending theory.

These experimental force-displacement slopes (dF/dd) are used in combination with the analytically obtained slope of the force-displacement curve for the composite frame under uniaxial compression (Eq. 1)

$$\frac{\mathit{d}\mathit{F}}{\mathit{d}\mathit{d}}=\frac{\mathrm{\pi }\{({\mathit{r}}_{\mathit{o}}^2-{\mathit{r}}_{\mathit{i}}^2){\mathit{E}}_{\text{bulk}}+{\mathit{r}}_{\mathit{i}}^2{\mathit{E}}_{\text{MR}}\}}{\mathit{L}}$$ (1)

and the force-displacement relation for a linear elastic cantilever (Eq. 2)

$$\frac{\mathit{d}\mathit{F}}{\mathit{d}\mathit{d}}=\frac{3\mathrm{\pi }({\mathit{E}}_{\text{bulk}}{\mathit{r}}_{\mathit{o}}^4-({\mathit{E}}_{\text{bulk}}-3{\mathit{G}}_{\text{MR}}){\mathit{r}}_{\mathit{i}}^4)}{4{\mathit{L}}^3}$$ (2)

with

$${\mathit{E}}_{\text{MR}}={\mathit{E}}_{\text{min}}+{\mathit{k}}_{\mathit{E}}\mathit{B}$$ (3)

$${\mathit{G}}_{\text{MR}}={\mathit{G}}_{\text{min}}+{\mathit{k}}_{\mathit{G}}\mathit{B}$$ (4)

We solve for the unknown material constants, E_min, G_min, k_E, and k_G. E_bulk is the known Young’s modulus of the bulk as-cured polymer found through compression tests, and G_bulk is calculated from E_bulk assuming a Poisson’s ratio of ν = 0.45. The single strut responses under compression and bending with zero applied field are used to solve for E_min and then G_min directly. Nonlinear optimization was used to find the best fit for first k_E and then k_G by comparing the analytical force-displacement slope computed from the model to the experimental data. Table 1 summarizes the calibrated material constants. It is apparent that the sensitivity of effective shear modulus per tesla (k_G) is higher than the sensitivity of effective Young’s modulus per tesla (k_E). It can also be seen that the MR fluid adds more mechanical strength in bending with the field off (G_min) than it does under compression (E_min). However, the increase in the strut stiffness per tesla from the initial stiffness with no applied field is higher in magnitude for struts experiencing mechanical compression (67.5× increase in stiffness) than the increase in stiffness per tesla for struts experiencing mechanical bending (7.7× increase in stiffness). It is possible that this difference is due to the average chain length (and extent of formation) that develops in each orientation. To illustrate, in compression, the magnetic field is applied along the length of the strut, allowing the particles to form ~5-mm-long chains (Fig. 2E, inset), whereas in bending, the magnetic field is applied transverse to the strut length, which constrains particle movement and chain formation to a maximum length equal to the 1-mm inner diameter of the strut (Fig. 2F, inset). A comparison of how the experimental results and model capture the increase in force-displacement slope with applied magnetic field can be seen in Fig. 2E for compression and Fig. 2F for cantilever bending. The magnetomechanical strut tests show no obvious signs of saturation; thus, the analytical model assumes a linear relationship between mechanical strength and increase in magnetic field. However, it was previously demonstrated in Fig. 1 that the MR fluid used in these experiments starts to saturate around 0.3 T; therefore, we kept additional experiments below this threshold value.

Table 1. A summary of the calibrated material constants.

Property	Description	Value
Ebulk	Young’s modulus of the as-cured polymer resin	57.6 MPa
Emin	Young’s modulus of the MR fluid–filled strut with no applied field	0.725 MPa
kE	Magnetic field–dependent Young’s modulus of the MR fluid–filled strut	49.0 MPa/T
Gbulk	Shear modulus of the as-cured polymer resin	19.9 MPa
Gmin	Shear modulus of the MR fluid–filled strut with no applied field	32.4 MPa
kG	Magnetic field–dependent shear modulus of MR fluid–filled strut	250.6 MPa/T

Our collection of 3D structures, including struts, unit cells, and lattices, were produced using large area projection microstereolithography (LAPμSL), which is a photochemical additive manufacturing technique that scans ultraviolet light, patterned with a digital micromirror device, through a series of optics and exposes the free surface of a photocurable liquid resin (Fig. 3A) to produce a solidified 2D layer. Next, the substrate is lowered into the resin bath, and the subsequent image in the stack is scanned to form the next layer. This process proceeds until a 3D part is generated. The LAPμSL approach has been used to produce centimeter-scale structures with feature sizes down to tens of micrometers (15). We harnessed the high resolution of LAPμSL to create complex polymer architectures composed of uniform, thin-walled tubes (Fig. 2C). To demonstrate the feasibility of our fabrication and mechanical testing approach for complex architectures, we first printed cuboctahedron unit cells (Fig. 3B). These unit cells were drained of the prepolymer liquid resin, affixed to syringes (Fig. 3C), and injected with MR fluid (Fig. 3D). We determined that the unit cells exhibited an increasing degree of MR fluid filling as the separation between the inlet-to-outlet ports increased from one strut (Fig. 3E) to two struts (Fig. 3F) to a maximum separation of three struts (Fig. 3G) within the unit cell, with the latter case exhibiting almost complete filling. In addition, the infill procedure was most successful when the inlet hole was oriented below the outlet hole, with gravity helping to minimize the occurrence of entrapped gas bubbles.

Fig. 3. 3D printing and MR fluid infilling of unit cells.

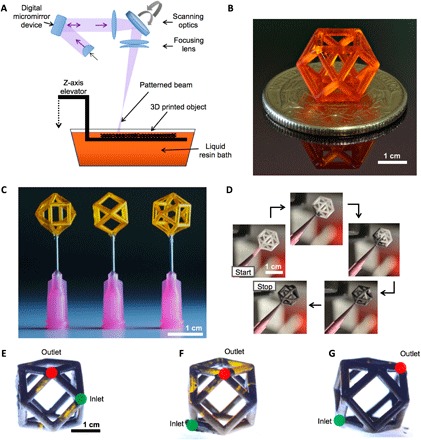
(A) Schematic illustration of the LAPμSL 3D printing process used to build struts, unit cells, and lattices. (B) Optical image of a resin-filled polymer cuboctahedron unit cell. (C) Optical image of drained (hollow) unit cells affixed with a dissolvable wax to syringe nozzles for infilling. (D) Optical images from a time-lapse recording of the MR fluid infilling process. (E to G) Optical image of the unit cell with inlet (green) and outlet (red) ports separated by various strut lengths. (E) Ports separated by one strut. (F) Ports separated by two struts. (G) Ports separated by three struts with the highest degree of infilling.

The cuboctahedron unit cells were tested in a custom apparatus that allowed for control of magnetic field strength by varying the distance of the magnet to the unit cell structure (Fig. 4A). The relationship between the effective Young’s modulus and magnetic field strength of the unit cell was found through compression tests at magnetic fields up to 0.18 T. Under uniaxial compression, we observed a 62% enhancement of effective stiffness between the field off and maximum applied field on states (Fig. 4B and fig. S4). The reversibility of the magnetomechanical results was also tested (fig. S5) by cycling three unit cells two times each from 0 to 0.11 T, and the SE was shown to be ±0.0006 for the Young’s modulus at 0 T and ±0.0005 for the Young’s modulus at 0.11 T. To determine the response time of the unit cell, we measured how quickly the mechanical properties changed in response to the application and removal of a magnetic field. This was done via a strain-controlled measurement where the cell was cycled between field off and field on states while under 10% compressive strain (Fig. 4C). There are several reported methods to calculate the response time of MR fluid and MR fluid systems (40, 41), and we calculated the response time of our MR fluid–filled architectures as the time from the initial, steady-state stiffness (either with field off or on) to 95% of the stiffness in the plateau region in the final state (after application or removal of the field). The average field on response time of four samples was found to be 0.83 ± 0.05 s (SEM), and the average field off response time was found to be 0.23 ± 0.06 s. The difference between the on and off response times suggests that it is faster for the magnetic particles to go from a state of order to a state of disorder when the magnetic field is removed than it is for the particles to go from a state of disorder to a state of order when the magnetic field is applied, as schematically illustrated in Fig. 4D. We hypothesize that, for the field on-to-off scenario, a relatively small number of particles must disengage from the chain network to destroy its load-carrying capability, whereas for the field off-to-on scenario, a relatively large number of disordered particles must move into position, overcoming steric or excluded volume effects that occur in particle-to-particle and particle-to-wall interactions, to form load-carrying chains that increase the stiffness of the overall composite. Literature reports typical response times for (unconstrained) MR fluids as between 0.001 and 0.1 s (42). While our measured response times are at the high end of this range, we note that our case is not only dependent on the MR fluid properties but is also affected by the surrounding (and constraining) polymer structure, the magnetomechanical test method, and the ultimate magnetic field strength we can achieve.

Fig. 4. Magnetomechanical characterization of cuboctahedron unit cells.

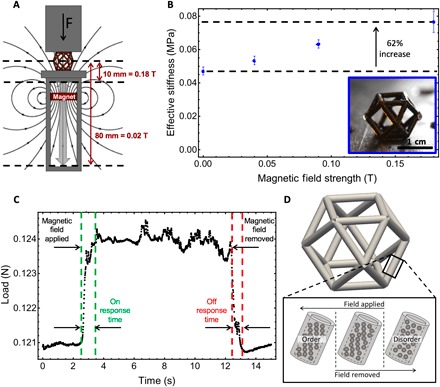
(A) Schematic illustration of the experimental setup for mechanical testing of MR fluid–filled samples with magnetic field strength controlled by translating a permanent magnet close to or away from the sample while measuring mechanical properties. (B) Plot of effective stiffness versus magnetic field strength for the cuboctahedron unit cell showing a 62% increase in stiffness from 0 to 0.18 T. Inset is an optical image of the MR fluid–filled unit cell. (C) Load versus time plot for one example of cycling a unit cell between field off (0.0 T) and field on (0.10 T) states to measure response times. (D) Schematic illustration of how the particles switch from ordered to disordered structures within the MR fluid–filled struts of the unit cells during field application or removal.

To demonstrate a predictive modeling capability for lattices, we created a system model of individual MR fluid–filled frame elements assembled into a lattice using the direct stiffness method of structural analysis (43). The system model predicts the linear elastic response of a lattice, constructed by tessellating a unit cell in 3D space, under a combination of mechanical loading and applied external magnetic field. The individual matrices describing the generalized force-displacement relation of each member were assembled into a global matrix describing the force-displacement relation for the lattice structures and boundary conditions applied to this matrix description. The resulting system of linear equations was solved for the unknown joint displacements and rotations given the value of the applied field, and the forces in each member were calculated by applying the element stiffness matrix to the element generalized displacements. The final model describes the response of a lattice composed of MR fluid–filled struts given the applied forces, displacements, and magnetic field vector. Our magnetomechanical model predicts the mechanical response of lattice architectures under arbitrary magnetic field strengths, with the assumption that the magnetic field is uniform over the entire structure. As a test case, we chose to fabricate a lattice by tessellating cuboctahedron unit cells (44, 45). We chose the cuboctahedron for multiple reasons including manufacturability for 3D printing and infilling and because it is periodically rigid (46, 47); hence, these structures could represent a variety of lattice structures by displaying a nonrigid behavior as a single unit cell to a rigid behavior when arranged in a lattice.

Next, we demonstrated viability of creating larger-area (and volume) FRMMs by printing a cuboctahedron lattice composed of a 2 by 2 by 2 arrangement of unit cells. We chose to fabricate lattices of this size because our predictive model assumes infinite periodic response, which is not applicable to single cells. Previous work has shown that it only takes specimens with two to three cells in each direction for infinite periodic models to approximate the observed behavior (48). In addition, because we are investigating mechanical metamaterial behavior, which is typically more than one cell, a predictive model for a single unit cell was not necessary. To produce these specimens, the drained, hollow lattices were injected with MR fluid using two syringes attached to each unit cell level with the inlet ports separated by a maximum distance and number of struts to the outlet ports (Fig. 5A and movie S1). We measured the stiffness response of the lattice as a function of magnetic field strength (Fig. 5B and fig. S6), where the maximum magnetic field strength was limited to 0.11 T (versus 0.18 T in the unit cells) due to the larger distance from the magnet to the centerline of the lattice in our custom test apparatus (Fig. 4A). In general, the model agreed well with the experiment and accurately predicted the response at field strengths above 0.02 T, whereas when the field strength increases, the measured effective stiffness becomes approximately linear with field strength. The difference between the model and the experiment at field strengths under 0.02 T may be due to the model assumption that the magnetic field is uniform throughout the sample and parallel to the applied compressive force, among other assumptions (see the supplementary materials for more details). At low fields, when the magnet is farthest away from the sample, the field lines may not be fully parallel to the applied compressive force. At the maximum applied magnetic field strength of 0.11 T, the model predicts the lattice stiffness increases by 22% from the initial stiffness (at zero applied field), whereas the experimentally observed stiffness enhancement is 35% with the difference due to the underprediction at low field strengths. The field responsive stiffness enhancement of these structures could be increased further, perhaps beyond an order of magnitude, with additional magnetic field strength since the applied fields in both the lattice and unit cell cases are well below the plateau region of the viscosity enhancement of the MR fluid (Fig. 1C). In addition, the lattice displays higher overall absolute stiffness than the unit cell and exhibits a lower magnetic field stiffness sensitivity (318% per tesla) compared to the unit cell (344% per tesla). This behavior may be due to the additional constraints imposed upon the nodes and shared edges in the lattice geometry. Previous reports indicate that bend-dominated structures, such as the cuboctahedron (44, 45), exhibit an increase in Young’s modulus as the lattice size, or number of unit cells, increases (46–48). Last, to visually illustrate the field response effect of our mechanical metamaterial lattice, we placed a static load (10-g mass) on the lattice with an initial condition of maximum applied magnetic field (0.11 T) (Fig. 5C). Upon slowly removing the magnet (and lowering the magnetic field strength), the effective stiffness decreases and the lattice deforms under the load (Fig. 5D) and continues to compress and bend (Fig. 5E) until, upon complete removal of the magnet, the structure collapses and the mass slides off the lattice surface (movie S2). Hence, we have demonstrated changing load-carrying ability without changing form factor in a strain-controlled experiment (Fig. 4C), and we have shown the ability to change form factor by changing stiffness in a stress-controlled experiment (Fig. 5, C to E), and achieved both solely by facile adjustment of the magnetic field.

Fig. 5. Infilling and magnetomechanical behavior of cuboctahedron lattices.

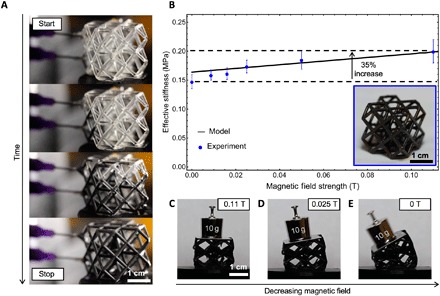
(A) Optical images showing a time lapse of the infilling process for a cuboctahedron lattice composed of a 2 by 2 by 2 unit cell arrangement. (B) Plot of the effective stiffness versus magnetic field strength for the cuboctahedron lattice showing a 35% increase in stiffness for 0 to 0.11 T. Inset is an optical image of the MR fluid–filled lattice. (C to E) Optical images of the MR fluid–filled lattice supporting a 10-g weight under various magnetic field strengths. (C) MR fluid–filled lattice supporting a static 10-g mass with a maximum magnetic field of 0.11 T applied. (D) Compression of the lattice as the applied field is reduced. (E) Bending of the lattice structure under the weight of the 10-g mass as the magnetic field is removed.

CONCLUSIONS

This work demonstrates the first tunable FRMMs that have a large dynamic range with rapid and reversible mechanical response to remotely applied magnetic fields. Via fabrication and testing of single MR fluid–filled struts, we have developed an empirically calibrated model that predicts the magnetomechanical response of FRMM lattices—this model will underpin future design optimization efforts. In addition, we have used an agile and simple fabrication process flow, founded upon 3D printing technologies combined with controlled fluid delivery methods, to demonstrate MR fluid–filled unit cells and lattices for ultimate creation of a new class of microarchitected mechanical metamaterials. Future FRMMs may be composed of actively addressed microfluidic networks wherein the MR fluid composition can be spatially and temporally modulated to further expand the design and accessible property space. In addition, magnetic field shaping could enhance directional control for a wider variety of deformation modes and application environments. Ultimately, we envision FRMMs being used for a broad array of emerging applications including actuatable soft robotics, rapidly adaptive helmets, and smart wearables with vibration-canceling behavior.

MATERIALS AND METHODS

MR characterization of MR fluid suspensions

Rheology measurements were performed on a TA Instruments DHR-1 rotational rheometer with an MR measurement accessory, using a 20-mm parallel plate setup. The sample thickness (spacing between the plates) was set to 500 μm. The magnetic field was applied through an integrated electromagnetic coil located below the sample. The coil delivers a homogeneous magnetic field normal to the plate surface, and real-time measurements and closed loop control of the sample field were achieved by inserting a Hall probe in a groove below the bottom sample plate and reading the output from the software interface. The temperature of the sample was kept at 25°C using an external thermostat to circulate water through the cooling jacket of the cell. Ink viscosities were measured at shear rates ranging from 0.01 to 100 s⁻¹ at magnetic field strengths up to 1.0 T in 0.1-T increments. Field response measurements were performed at a low shear rate (0.1 s⁻¹) by turning the field on and off at desired intensities and time intervals while measuring the corresponding viscosity response.

3D printing of struts, unit cells, and lattices

All test structures were fabricated with LAPμSL. The LAPμSL system is a custom, top-down, layer-by-layer 3D printing system that projects dynamic ultraviolet light patterns onto a photocurable resin. The photocurable resin solidifies where the light pattern is projected, and then an elevator lowers the substrate below the resin surface and the next pattern is projected. This process continues in a layer-by-layer fashion until a 3D structure is fabricated from a stack of 2D images. More information can be found on this process in the article published by Zheng et al. (15). Cuboctahedron unit cells and lattice computer-aided design files (.stl) were created in NetFabb. The cuboctahedron unit cells were designed as 10 mm by 10 mm by 10 mm cubes composed of tubular struts with 1.1-mm outer diameter, 1.0-mm channel inner diameter, and 50-μm-thick walls. All structures were fabricated out of 1,6-hexanediol diacrylate (HDDA) with 1.2 weight % (wt %) photoabsorber [phenylbis(2,4,6-trimethylbensoyl)phosphine oxide] and 2 wt % photoinitator (Sudan 1). All chemicals were purchased from Sigma-Aldrich. To prepare the resin formulation, HDDA, photoabsorber, and photoinitiator were mixed and stirred overnight. The LAPμSL build chamber was purged with inert gas to create a low-oxygen atmosphere that would not inhibit the free radical polymerization process. After printing, ethanol was used to clean the samples and remove the excess uncured resin. After cleaning, the samples were imaged with a tabletop scanning electron microscope (Phenom Pro, Phenom World), and important dimensions were measured.

Infilling with MR fluid suspensions

After fabrication, inlet and outlet holes were opened on opposing sides of the tubular polymer structures, and nozzles were affixed with dissolvable wax adhesive (CrystalBond 509). The nozzles were then connected to a syringe barrel with a mounted micronozzle (Nordson 7018178) to inject the MR fluid (LORD Corporation, MRF-122EG) into the core of the polymer structure. After complete infilling, the nozzle was removed, and the inlet and outlet holes were sealed with a wax adhesive. This approach was used to create the strut, unit cell, and lattice structures. The lattice was infilled using two syringes. The best orientation for infilling the structures was in a vertical alignment with the outlet hole directly below the inlet hole and separated by the maximum number of struts and distance (Fig. 3G).

Magnetomechanical testing

All compression and cantilever bending tests were performed using an Instron 5943 equipped with Bluehill data acquisition software and a 5-N load cell. Custom, nonmagnetic anvils were fabricated to test the structures under various magnetic fields by allowing a magnet to be placed at varying distances from the sample, with the magnetic field primarily aligned with the direction of applied force during mechanical testing. The maximum magnetic field applied to the unit cell and lattice was 0.18 and 0.11 T, respectively, and measured with an Alpha Labs, Model GM1-ST Gaussmeter. The difference in maximum field strength of each test was due to the distance from the magnet to the center of the sample allowed by the test setup. Each cuboctahedron structure was tested with the (100) plane aligned in the direction of the applied force and compressed three times to rule out any strain softening caused by the strain history–dependent Mullin’s effect (49). The Young’s modulus of the test structures was found by taking the slope of the unloading curve of the third cycle of the stress-strain curve (fig. S2). The unloading curve was used instead of the loading curve to mitigate loading imperfections such as sample misalignment and partial contact of the sample with the platens. All structures were compressed to a strain of 2.5% at a rate of 20 μm/s. The response times of the structures were determined as the time required for the structure to reach 95% of the final stiffness value from the initial state. Response time measurements were acquired from a strain-controlled test, with a static strain of 10% applied to the cuboctahedron unit cell while placing a neodymium magnet (K&J Magnetics) underneath the sample. Four samples were tested.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/12/eaau6419/DC1

Supplementary Text

Fig. S1. Assumptions made when assembling the frame element describing a single strut.

Fig. S2. Mechanical testing of MR fluid–filled struts under varying magnetic field orientations.

Fig. S3. Mechanical testing of MR fluid–filled struts under varying magnetic field strengths.

Fig. S4. Mechanical testing of MR fluid–filled cuboctahedron unit cells under varying magnetic field strengths.

Fig. S5. Mechanical testing for reversibility of MR fluid–filled cuboctahedron unit cell.

Fig. S6. Mechanical testing of MR fluid–filled cuboctahedron lattice under varying magnetic field strengths.

Movie S1. Video of infilling a cuboctahedron lattice composed of a 2 by 2 by 2 arrangement of unit cells.

Movie S2. Video of a cuboctahedron lattice with a 10-g mass placed on its top surface and the magnetic field strength gradually lowered by slowly removing a magnet.

Reference (49)