Skip to main content
PMC home page
Heredity logoLink to Heredity
. 2018 Jul 2;122(1):29–40. doi: 10.1038/s41437-018-0106-x

The relative contribution of natural landscapes and human-mediated factors on the connectivity of a noxious invasive weed

Diego F Alvarado-Serrano 1,✉, Megan L Van Etten 1, Shu-Mei Chang 2, Regina S Baucom 1
PMCID: PMC6288146  PMID: 29967398

Abstract

Examining how the landscape may influence gene flow is at the forefront of understanding population differentiation and adaptation. Such understanding is crucial in light of ongoing environmental changes and the elevated risk of ecosystems alteration. In particular, knowledge of how humans may influence population structure is imperative to allow for informed decisions in management and conservation as well as to gain a better understanding of anthropogenic impacts on the interplay between gene flow, genetic drift, and selection. Here, we use genome-wide molecular markers to characterize the population genetic structure and connectivity of Ipomoea purpurea (Convolvulaceae), a noxious invasive weed. We, likewise, assess the interaction between natural and human-driven influences on genetic differentiation among populations. Our analyses find that human population density is an important predictor of pairwise population differentiation, suggesting that the agricultural and/or horticultural trade may be involved in maintaining some level of connectivity across distant agricultural fields. Climatic variation appears as an additional predictor of genetic connectivity in this species. We discuss the implications of these results and highlight future research needed to disentangle the mechanistic processes underlying population connectivity of weeds.

Subject terms: Genetic variation, Plant molecular biology

Introduction

Elucidating routes and levels of migration between populations is essential to understand the forces that shape its evolutionary trajectory (Barrowclough 1980; Slatkin 1985). Landscape features, such as rivers, mountain ranges, crop fields, and urban areas, can impact levels of gene flow between populations by determining dispersal rates and routes (McRae 2006; Cushman et al. 2006) as well as influence the likelihood of successful establishment of immigrants (Wang and Bradburd 2014; Sexton et al. 2014). Landscape features can also indirectly condition the effect of gene flow by influencing local effective population sizes (Wright 1949; Slatkin 1985). Consequently, the landscape, loosely defined as an area with spatially variable biotic and abiotic factors (Holderegger et al. 2010), influences the levels of effective gene flow among populations (Clobert et al. 2012). In this way, the landscape plays a pivotal role in the evolution of species.

In contrast to species that depend almost exclusively on natural dispersal agents, species in heavily human-dominated ecosystems may exploit human activities to maintain gene flow among populations and expand their ranges (Everman and Klawinski 2013; Fountain et al. 2014). Such species may be capable of maintaining population connectivity over vast geographic ranges (Trakhtenbrot et al. 2005) by overcoming landscape features that would otherwise represent natural barriers. Such species would, thus, be able to attain dispersal distances that could be orders of magnitude greater than those dependent primarily on natural dispersal agents (Mack and Lonsdale 2001; Ricciardi 2007). By facilitating dispersal, humans have the potential to condition the balance between drift and selection (Slatkin 1985; Lenormand 2002), introduce genetic variation to local populations (Kolbe et al. 2004), prevent local extinction or favor recolonization (Fountain et al. 2014), and alter the overall genetic constitution of populations (Bataille et al. 2011). Human-aided migration—intentional or unintentional—is particularly prevalent in plants (Hodkinson et al. 1997; Auffret and Cousins 2013), where it has had major impacts on the distribution of species and stability of communities (Simberloff 2013 and references therein). Despite our knowledge of both human and natural factors influencing dispersal, there remains a gap in our understanding of the relative influence of each on the distribution of genetic variation among populations of many (if not most) plant species.

A particularly amenable study system to fill this knowledge gap comes from agricultural weed populations. Agricultural weeds experience a highly dynamic landscape characterized by frequent spatial rearrangements and changes in the physical environment (e.g., expansion of agricultural front, increased fragmentation, crop rotation, agricultural chemical use) (Menchari et al. 2007; Meehan et al. 2011). At the same time, natural features such as climate, soil type, and topography likely also play a significant role in structuring populations (Cimalová and Lososová 2009; Navas 2012). Under these conditions, human-aided migration may be critical for weedy plant success (Epperson and Clegg 1986). However, we have limited knowledge of how or if weedy plant populations are able to maintain connectivity through the complex landscape matrix. Addressing this limitation would improve our understanding of the underlying processes governing connectivity of weed populations and also offer practical tools to deal with the economic problems that weeds impose (on the order of 33B USD per year in US agriculture alone; Pimentel et al. 2005).

As a first step into investigating the interplay between natural factors and human activities on structuring genetic diversity in weed populations, we estimate the intensity and extent of migration and evaluate how multiple landscape features influence genetic connectivity of Ipomoea purpurea, one of the most troublesome weeds in US agriculture (Webster and Nichols 2012). Specifically, we ask the following questions: (1) what is the overall population structure of I. purpurea, and (2) which natural and/or human-influenced landscape features—soils, elevation, climate, landcover, crop types, human population density—may act to promote or constrain genetic connectivity between populations of this weed? Answering these questions offers a deeper understanding of the multiplicity of population structure drivers that influence noxious weeds.

Materials and methods

Study system

Ipomoea purpurea, the common morning glory, is a noxious agricultural weed (Defelice 2001; Fang et al. 2013) that has a widespread distribution across highly heterogeneous landscapes in the Eastern, South- and Mid-western regions of the United States (Culpepper 2006; Webster and Nichols 2012). It is a self-compatible annual bumblebee-pollinated vine and is found primarily in agricultural fields and disturbed areas (Tiffin and Rausher 1999; Baucom 2008), as well as cultivated flower gardens and yards (Defelice 2001). I. purpurea is one of the most problematic agricultural weeds of southeastern agriculture (Webster and Nichols 2012), and exhibits variable levels of resistance to the commonly used herbicide glyphosate (Kuester et al. 2015). This species is also a major concern for conservation given its naturalization in multiple regions throughout the world and its aggressiveness as an invasive (Chaney and Baucom 2012; Fang et al. 2013).

Data compilation

To capture the plausible effect of both natural and disturbed landscapes on structuring genetic diversity in I. purpurea, we compiled a diverse set of GIS data for the continental US from a variety of sources (Table S1). These data include human activities (human population density—estimated by imposing a 10 × 10 km grid on the 2010 Census Blocks’ population count, U.S. Census Bureau, Department of Commerce, landcover, planted crops, and roads) as well as natural factors such as elevation, climate (19 variables summarizing central tendencies and variability patterns in temperature and precipitation), and soil characteristics (8 variables summarizing the texture, pH, and organic and inorganic content of the top 20 cm of soil). Focusing on both sets of data allowed us to assess the relative influence of natural and human effects on structuring I. purpurea’s populations. We, first, processed all these data into landscape layers at a common spatial resolution of 10 km2 and a common spatial extent around the US states with available samples (Fig. 1). This spatial resolution was chosen to maintain a practical balance between scale and analytical manageability given available computational resources. To reduce dimensionality, we opted to perform two separate Principal Component Analyses on the 19 climatic and 8 soil layers, respectively. We opted to examine all variables, despite their wide range of autocorrelation with each other, to avoid introducing any a priori bias in our variable selection. For all subsequent analyses we kept the resulting first two principal components of each of these analyses, which accounted for over 78% of the variance in each case, and primarily summarized temperature temporal gradients and precipitation seasonality, and soils’ pH, sandiness, and grain size, respectively (Table S2).

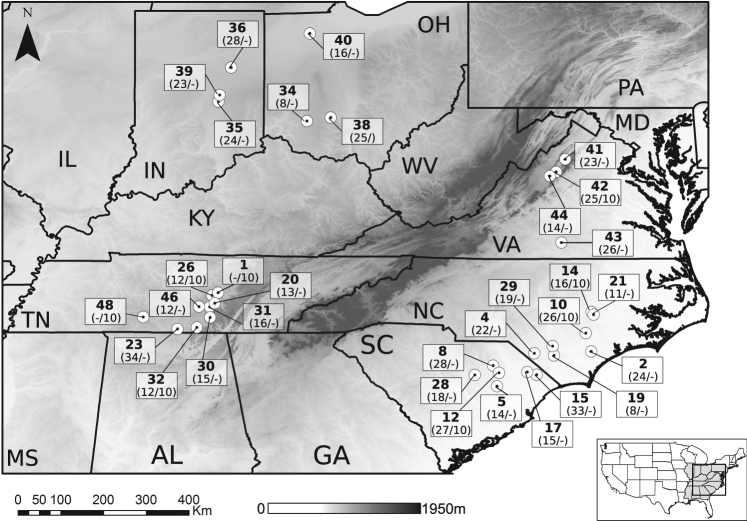
Fig. 1.

Fig. 1

Open in a new tab

Distribution of Ipomoea purpurea’s sampled localities. Sample sizes for both SSR (left) and SNP (right) datasets are indicated in parentheses (locality numbers are given in squares). Elevation is provided as background. IN Indiana, NC North Carolina, OH Ohio, SC South Carolina, TN Tennessee, VA: Virginia

We compiled data from a panel of 15 previously optimized Simple Sequence Repeats (SSR) loci (Molecular Ecology Resources Primer Development Consortium et al. 2013) to examine the genetic connectivity of populations of I. purpurea. These data (Kuester et al. 2015) encompass a total of 597 individuals from 31 localities (with a minimum of 8 individuals per locality) (Fig. 1; Table S3), collected in 2012 from farms across the range of I. purpurea in the United States (Kuester et al. 2015). In addition, to obtain a more comprehensive representation of the genome of I. purpurea, we generated a Next Generation Sequencing (NGS) dataset from an additional set of individuals (10 individuals each from 6 localities represented in the SSR dataset, plus 2 additional localities in close geographic proximity to localities in the SSR dataset, for a total of 8 populations; Fig. 1).

To generate the NGS dataset, we constructed a genome-wide Genotype By Sequencing (GBS) library. DNA was extracted using a standard CTAB protocol (Doyle and Doyle 1987) from leaf or cotyledon tissue. A nextRAD GBS library was developed by SNPsaurus (Oregon, USA). Seven ng of genomic DNA per sample were first fragmented using a Tagment DNA Enzyme (Illumina; California, USA) and then ligated to short adapter and barcode sequences using a partial Nextera® reaction (Illumina; California, USA) before being amplified using Phusion® Hot Start Flex DNA Polymerase (New England Biolabs; Massachusetts, USA). The PCR program used includes an initial step of 3 min at 72 °C, followed by 30 s at 98 °C, and five cycles of denaturation at 98 °C for 10 s, annealing at 63 °C for 30 s, and extension at 72 °C for 3 min. The 80 dual-barcoded PCR-amplified samples were pooled and the resulting libraries were purified using AMPure XP beads (Agencourt Bioscience Corporation; Massachusetts, USA) at 0.7 × . The purified library was then size selected to 350-800 base pairs and sequenced using two runs of an Illumina NextSeq500 sequencer (Genomics Core Facility, University of Oregon).

The resulting sequences were analytically processed using the SNPsaurus nextRAD pipeline (SNPsaurus, Oregon, USA; Siliceo-Cantero et al. 2016). Specifically, reads of 16 randomly selected individuals (of the 80 sequenced) were combined to create a pseudo-reference genome. This was done after removing loci with read counts above 20,000, which presumably corresponded to repetitive genomic material, and loci with read counts below 100, which presumably corresponded to off-target or read errors. The filtered reads were aligned to each other using BBMap (Bushnell 2014). All parameters were set to default values with the exception of minimum alignment identity, which was set to 0.93 to identify alleles, as this threshold has been found to work well for non-reference species (SNPsaurus, Oregon, USA). A single read instance was chosen to represent the locus in the pseudo-reference. This resulted in a total of 263,658 loci. All reads from each of the 80 individuals were then aligned to the pseudo-reference using BBMap (Bushnell 2014) and converted to a vcf genotype table, using default settings in Samtools (Li et al. 2009) and bcftools (Li 2011) except for quality score (we filtered out nucleotides with a quality score of 10 or worse). The resulting vcf table, which contained 9774 GBS tags, was further filtered using vcftools (Danecek et al. 2011) to remove tags with less than 5 high quality base calls and with more than 20% missing data or an average of less than 20 high quality base calls. We then called single nucleotide polymorphisms (SNPs) on this dataset using vcftools (Danecek et al. 2011) keeping only those with a minimum minor allele frequency of 0.02, a minimum read depth per individual of 5, and a maximum 15% of missing data. This resulted in a final panel of quality-vetted 8210 SNPs (Fig. S1) that we used in all subsequent analyses.

Population structure analyses

We first conducted a series of analyses to characterize the overall genetic structure of I. purpurea populations. All analyses were run separately for the SSR and SNP datasets given their intrinsic differences and distinct geographic coverage (Fig. 1; Table S3). In addition, we repeated all population structure analyses using just the subset of 6 localities where SSR and SNP datasets are both available. Running separate analyses using these two reduced datasets that include only localities in common for both marker sets (referred as SSRc and SNPc, hereafter) allowed us to determine if the differences between marker types was due to differences in sample size (SSR = 24 localities; SNP = 8 localities) or geographic coverage (Fig. 1). Similarly, to determine if the differences uncovered between marker types were due to SNP sequencing or genotyping error, we repeated all population genetic analyses after doing a more stringent SNP quality filtering by removing SNPs with a genotype quality score below 20 or a minimum read depth of 10. After having done this, we checked again for the amount of missing data per SNP locus and remove those with more than 15% missing individuals.

We then assessed population structure independently for all five different datasets (full SSR and SNP datasets, common-localities-only SSRc and SNPc datasets, and the more stringent SNP dataset). First, to characterize population differentiation we estimated expected and observed heterozygosity (He and Ho, respectively), and FST using GenAlEx v6.5 (Peakall and Smouse 2012) (because similar global FST and RST estimates were obtained for the SSR datasets, we opted to report FST values only to allow direct comparisons with the SNP datasets). We also tested for significant deviations from Hardy–Weinberg equilibrium in Arlequin (Excoffier and Lischer 2010) and for genetic neutrality using PopGenome (Pfeifer et al. 2014) in R (R Core Development Team 2016). We then estimated contemporary effective population size for each sampled locality in NeEstimator v2 using the excess heterozygous method (Do et al. 2014). We performed this latter analysis to assess the possibility that differences in local population size underlie differences in genetic variability (Weckworth et al. 2013) and/or promote asymmetric effective migration rate (Nm).

In addition, to further examine genetic structure we assessed population admixture and spatial genetic clustering using TESS (Chen et al. 2007). For this, as suggested in TESS’ documentation, we first added small random noise to the geographic coordinates of each individual using its “Generate Spatial Coordinates” function. TESS was then run using the admixture algorithm and a BYM model (Durand et al. 2009a, 2009b) with 10 runs per K value, and without using geographic weights. The TESS model with the lowest Deviance Information Criterion (DIC) at which the DIC-vs-K curve plateaus was chosen as the optimal model (Durand et al.2009a, 2009b). K values tested ranged from two to the maximum number of sampled localities. Additionally, following Wang et al. (2009), we complemented these analyses with Analyses of Molecular Variance (AMOVA; Excoffier et al. 1992) run in GenAlEx (Peakall and Smouse 2012) using 9999 permutation replicates. We ran these AMOVAs either partitioning the variance into regions based on the spatial genetic clusters previously identified—to quantify the fraction of the genetic variance explained by these clusters, or leaving it ungrouped (i.e., no regions), for comparison. Specifically, for the 4-level AMOVAs, the region assigned to each population corresponded to the most frequent spatial cluster (i.e., geographical assignment output; Durand et al. 2009a, 2009b) among those assigned to the individuals pertaining to that population.

Additionally, we investigated population connectivity by estimating levels of recent migration between sampled localities through the identification of individuals of mixed ancestry using BayesAss (Wilson and Rannala 2003). BayesAss is a program that uses individual multilocus genotypes and a Markov Chain Monte Carlo (MCMC) algorithm to probabilistically distinguish between immigrants and long-term native individuals (Wilson and Rannala 2003). We ran BayesAss for 6 million generations using default parameter settings, and discarded the first two million generations as burn-in (Dyer 2009). For each marker dataset, we repeated this analysis three times (for a total of 18 million generations) and combined the results from the three replicates for our final inference. Then, using a posterior probability cut-off of 0.75 we assign individuals’ ancestry. We chose this cut-off value as a minimum credibility score to simultaneously maximize sample size and reliability (more stringent thresholds show similar differences between marker sets; results not shown). It is important to note that because of computational limits we had to randomly subsample our set of SNPs to 400 SNPs for this analysis. The same subsampled set was used for the full and reduced (SNPc) analyses.

Landscape genetics analyses

To identify the likely landscape features underlying overall population structure of I. purpurea, we evaluated the association between landscape features and genetic differentiation based on the full datasets. First, we estimated conditional genetic distances (Dyer et al. 2010) using GeneticStudio (Dyer 2009). Briefly, conditional genetic distances are measures of pairwise genetic distance derived from population networks, constructed based on the degree of genetic similarity between sampled localities (Dyer and Nason 2004). They reflect genetic similarity between localities that better capture direct gene flow (i.e., direct migration) as opposed to connectivity driven by step-wise migration through intervening localities (Dyer 2015). The complexity of the associated conditional genetic network was summarized by their vertex connectivity (White and Harary 2001), whereas the congruence between networks derived from different marker sets was measured by their structural congruence (a measure of whether the number of congruent edges between networks is greater than expected by chance) (Dyer 2009).

To assess the association between landscape features and population differentiation, we first converted each landscape layer (climate, crops, elevation, landcover, population density, roads, and soils layers; Table S1) into landscape resistance layers. To do this, each landscape feature in these layers was assigned a resistance value that reflects the difficulty that each feature offers to the movement of gametes or individuals. In contrast to previous studies that typically rely on expert opinion for resistance assignment, we utilized an unbiased statistical optimization to avoid the sensitivity of results to subjective resistance assignment (Spear et al. 2010). Specifically, resistance values were optimized through a genetic algorithm approach (Mitchell 1996). Briefly, in this search algorithm a population of individuals with traits encoded by unique combinations of model parameters (resistance assignment proposals in our case) is allowed to compete with each other based on the fitness associated with the traits it carries (Peterman et al. 2014). Specifically, in Peterman’s (8) implementation of this algorithm, which we followed here, individuals’ fitness is estimated by the relative quality of a MLPE.lmm model (Maximum Likelihood Population Effects—Linear Mixture Model). This model evaluates the association between pairwise genetic distance and landscape cumulative resistance between localities, estimated in Circuitscape (Shah and McRae 2008). Individuals with parameter settings (i.e., resistance assignments) that result in better models, as measured by a DIC score, are preferentially represented in the following generation. Offspring modifications introduced by mutations (i.e., small resistance assignment perturbations) allow for exploration of the parameter space. The algorithm was stopped once 25 generations have passed without significant improvement in fitness.

We implemented Peterman’s (8) algorithm (package ResistanceGA; Peterman 8) in R (R Core Development Team 2016) allowing for the independent optimization of each of our landscape layers. The optimal resistance landscapes identified in this way were then used to run a final univariate MLPE.lmm model to characterize the association between landscape features and conditional genetic distances between localities. Because the roads-associated resistance was not recovered as significant for either marker dataset, we dropped this layer for all subsequent analyses. Finally, to identify the simultaneous contribution of natural and human-driven landscape features to population differentiation in I. purpurea we ran Multiple Regression on Distance Matrices (MRDM; Legendre et al. 1994). Before running these MRDM models, we standardized all optimized resistance layers to mean of zero and variance of one (Dyer et al. 2010). These final regressions included geographic distance as a null model predictor as well as effective population size and were run in R (package ecodist; Goslee and Urban 2007) using 10,000 permutations to assess significance. We accounted for multiple testing by applying a false recovery rate correction (Benjamini and Hochberg 1995) using the function p.adjust in R (R Core Development Team 2016).

These landscape genetic analyses, aimed at identifying the relative influence of natural and human-related landscape features on I. purpurea’s connectivity, show several differences between SSR and SNP datasets (see below). Nonetheless, we expect that association patterns that are robust between datasets should accurately reflect the impact of landscape features on gene flow, independent of possible biases introduced by marker idiosyncrasies. Therefore, we focus below on the common biological findings between marker types, while also denoting the most relevant differences.

Results

Population structure

The initial genetic analyses indicated that I. purpurea sampled localities were not in violation of Hardy–Weinberg equilibrium (Fig. S1c, d), as evidenced by the small difference between expected and observed heterozygosity (mean He = 0.294 ± 0.014 and 0.250 ± 0.001; mean Ho = 0.291 ± 0.009 and 0.260 ± 0.001, respectively, for SSR and SNP datasets). Levels of expected and observed heterozygosity for the SSR dataset were only slightly greater than those estimated for the SNP dataset. Likewise, the estimated mean effective population size per sampled locality was only slightly greater and more variable for the SSR dataset than for the SNP dataset (13.71 ± 5.59, 9.49 ± 0.13, respectively), but in neither case was there salient evidence of a plausible source-sink dynamic, as judged by the similar effective sizes among populations. Average pairwise FST estimates between datasets were also similar (0.151 and 0.140, respectively, for SSR and SNP datasets; Fig. S2).

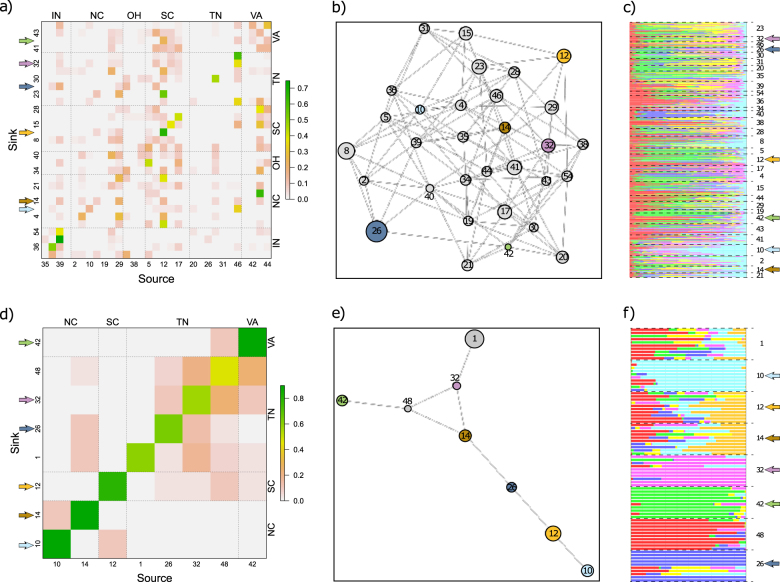
Interestingly, we found that estimates of recent ancestry differed between SSR and SNP datasets. The analysis of the SSR dataset indicated that recent migration among localities seems to be more widespread, with only four localities being primarily constituted of native individuals (Fig. 2a). Across localities, on average 73.65% of individuals were inferred to be 1st or 2nd generation immigrants. In comparison, analysis of the SNP dataset showed that most populations seem to have a more limited number of recent immigrants, and that the relatively few inferred immigrants (on average 27.42% of individuals) did not come exclusively from geographically proximate localities (Fig. 2d). Accordingly, pruned (i.e., with non-informative branches removed) SSR and SNP conditional genetic networks (Dyer and Nason 2004) indicated different underlying patterns of genetic connectivity (structural congruence = 0.108; Fig. 2b, e). While both were fully closed, the SSR-based network was more interconnected (vertex connectivity: 5) than the SNP-based network (vertex connectivity: 0). Further, based on the best TESS models (Fig. S3), widespread admixture was recovered in the SSR dataset (median individual maximum Q-score = 0.51), whereas minimal admixture was identified in the SNP dataset (median individual maximum Q-score = 0.73) (Fig. 2c, f). It is important to note that this latter result was consistent across models for different K values (Fig. S4 and S5). Finally, grouping individuals according to the corresponding TESS-identified spatial genetic clusters in AMOVA analyses only slightly reduced the variance explained solely by geographic location in both datasets (Table 1).

Fig. 2.

Fig. 2

Open in a new tab

Inferred population connectivity. The recent immigration history of each sampled locality (sink) is depicted according to the locality they were inferred to have originated from (source) (a, d). The grayscale of each cell in these plots depicts the relative proportion of individuals in the sink population that were estimated to be recent immigrants from each locality along the x-axis. Cells on the minor diagonal correspond to the proportion of native individuals. Pruned conditional genetic networks (b, e) and posterior estimates of admixture proportion identified by TESS analysis (c, f) are also displayed. The top row shows SSR-based results, the bottom shows the SNP-based results. Locality numbers follow Fig. 1. Localities shared between SSR and SNP datasets are denoted by gray-shaded arrows (for a similar figure based exclusively on these shared localities, see Fig. S6)

Table 1.

Analysis of molecular variance (AMOVA) of SSR and SNP data

Effect F-statistic Variance explained F-value P-value
SSR SNP SSR SNP SSR SNP
Regions F RT 0.61% 8.51% 0.006 0.085 0.001 0.001
Localities F SR 10.53% (11.06%) 6.10% (13.02%) 0.106 0.067 0.001 0.001
Individuals (among) F ST 38.27% (38.33%) 24.85% (25.31%) 0.112 (0.111) 0.146 (0.130) 0.001 (0.001) 0.001 (0.001)
Individuals (within) F IS 50.56% (50.61%) 60.54% (61.67%) 0.431 (0.431) 0.291 (0.291) 0.001 (0.001) 0.001 (0.001)
Total F IT 100% (100%) 100% (100%) 0.494 (0.494) 0.395 (0.383) 0.001 (0.001) 0.001 (0.001)
Open in a new tab

The contribution of spatial clusters (regions), localities, and individuals is shown. For comparison, results from an AMOVA analysis with no region category defined are presented in parentheses

Similar to our results from the entire datasets, when we subset the SSR and SNP dataset to the 6 localities in common (SSRc and SNPc datasets), we found no major differences in genetic estimates between the SSRc and SNPc datasets (Table S4), and we again identified differences in the underlying population structure (Fig. S6). Specifically, the SNPc dataset was characterized by a smaller percentage of recent immigrants (28.25%) than the SSRc dataset (44.93%) (Fig. S6a, d), and the corresponding genetic networks were also different from each other (structural congruence = 0.002)—with the SSR-based network being more connected (vertex connectivity = 2) than the SNPc-based network (vertex connectivity = 0) (Fig. S6b, e). Finally, as for the full data, a more admixed genetic composition of individuals was recovered in the SSRc dataset (median individual maximum Q-score = 0.71) than in the SNPc dataset (median individual maximum Q-score = 0.85) (Fig. S6c, f). Also, further confirming the limited spatial structure in this species, using TESS-identified spatial genetic clusters as regions in AMOVA analyses barely reduced the variance explained solely by geographic location when compared to a null model with no regions assigned (Tables S5).

Similarly, when using a more stringently filtered SNP dataset, which comprised 5811 SNPs, we found that this reduced dataset produced highly similar results to the original SNP dataset (percentage of recent immigrants = 25.94%, genetic network vertex connectivity = 0, average individual maximum Q-score = 0.71, and percentage explained by TESS-groupings = 7.31%). Hence, these results using a more rigorous SNP dataset further support the differences in population structure inferences between SSR and SNP data.

Landscape genetics

Both the SNP and SSR datasets provide evidence that human-impacted landscapes play an important role in shaping genetic connectivity in I. purpurea. In both sets of MLPE.lmm models, null (geographic distance), natural (climate, elevation, and soils), and human-related landscapes (landcover and human population density) were identified as significant (p < = 0.05) or marginally significant (0.05 < p < = 0.1) predictors of genetic differentiation between localities. Interestingly, the variables with the greatest association coefficient and lowest AICc value in both the SSR and SNP models were human-related variables (landcover and human population density, respectively; Table 2). However, when considering all variables together in a multivariate manner—while accounting for geographic distance—human population density, local effective population size, and different aspects of climate were the only variables that remained as significant or marginally significant predictors of genetic differentiation across both SSR and SNP datasets (Table 2). In contrast, elevation and soil were identified as significant or marginally significant predictors only in the SNP dataset. Both multivariate regressions also differed in the proportion of the variance explained (MRDM R2 for SSR and SNP dataset were 0.109 (F1,29 = 3.654, p-val. = 0.063) and 0.532 (F1,6 = 1.932, p-val. = 0.113), respectively). While some caution is needed when interpreting these multivariate models given the range of autocorrelation among predictor variables, their general agreement with our univariate models further support these latter results.

Table 2.

Summary of landscape genetics models

Feature MLPE.lmm MRDM
SSR SNP SSR SNP
Intrinsic variables
Geographic distance 0.187* (0.052) / 12.303 [8] 0.780* (0.055) / 0.396 [4] 0.051 (0.121) 0.255* (0.056)
Population size (Ne) – – -0.550 (0.001) -2.650* (0.051)
Natural environment variables
Climate PC1 0.243 (0.034) / 10.356 [3] 0.967 (0.045) / 0.032 [2] 0.533* (0.064) 1.782 (0.517)
Climate PC2 0.205 (0.048) / 12.030 [7] 0.814* (0.055) / 1.560 [7] -0.029 (0.978) 21.443* (0.075)
Elevation 0.244 (0.034) / 10.742 [4] 0.840* (0.054) / 1.423 [6] -0.607 (0.480) -31.789* (0.095)
Soil PC1 0.208 (0.039) / 11.378 [6] 1.044 (0.045) / 0.471 [5] 0.305 (0.510) 15.789 (0.038)
Soil PC2 0.320 (0.018) / 8.139 [2] 0.941 (0.045) / 0.284 [3] 0.187 (0.703) -6.838 (0.476)
Human-impact variables
Crops -0.226 (0.134) / 14.491 [9] 0.858* (0.054) / 15.371 [8] 0.154 (0.526) 0.360 (0.840)
Landcover 0.582 ( < 0.001) / 0 [1] 1.358 (0.003) / 39.775 [9] 0.340 (0.218) 3.887 (0.184)
Population density 0.227 (0.034)  10.821 [5] 0.912 (0.045) / 0 [1] -0.519* (0.095) -3.271 (0.037)
Open in a new tab

Model coefficients are reported followed by associated p-value (in parenthesis) and, for MLPE.lmm models, followed by AICc difference and ranking (in square brackets). Significant coefficients are in bold, marginally significant coefficients are marked with an asterisk.

In summary, across datasets, results indicated that human-population-density resistance was robustly associated with differentiation among I. purpurea’s populations, with sparsely to moderately populated areas identified as more conducive areas for migration and potential corridors available between all regions (Fig. S7b). In contrast, climatic variables produced potential barriers to gene flow, with temperature temporal gradients isolating the northernmost localities from the rest in the SSR dataset, and precipitation seasonality isolating the eastern and western localities in the SNP dataset (Fig. S7a). Finally, local effective population size was also a significant predictor in both datasets, with population size inversely associated with genetic differentiation (Table 2).

DISCUSSION

Our results reveal that broadly distributed populations of I. purpurea are not genetically isolated from each other. They also suggest the existence of long-distance and putatively human-mediated migration between localities. At the scale of our analyses, the regional agricultural matrix does not seem to have an overarching impact on population connectivity in this species, despite I. purpurea’s tight link to agricultural fields. Instead, genetic connectivity in this species seems to be primarily influenced by climate and human population density. Effective population size (Ne) also appears to influence population connectivity in this species, which suggests a plausible additional effect of genetic drift on the effectiveness of gene flow (Weckworth et al. 2013). Taken together, these results highlight the significant interplay between human-driven and natural landscapes in structuring I. purpurea populations.

Population connectivity patterns

Despite I. purpurea’s expected low natural seed dispersal, due to heavy, gravity-dispersed seeds, and large and patchy distribution, we found evidence of limited genetic differentiation through the species’ range and overall weak geographic structure. In fact, population differentiation was uneven (pairwise FST values ranged from 0.02 to 0.24), and only partially dependent on the geographic distance between populations. Further, genetic networks for both datasets were fully closed, suggesting the existence of direct or indirect gene flow among all sampled populations. In line with this finding, admixed individuals were present in all sampled localities (although levels of admixture vary for SSR and SNP datasets), and several instances of recent short- and long-distance migration were recovered. Nevertheless, the evidence of interconnectedness we uncovered is likely also influenced by the shared evolutionary history of populations and, thus, shared ancestral genetic variation likely confounds our estimates of genetic differentiation (Marko and Hart 2011). Given the relatively recent invasion of the US by I. purpurea and its inclusion in horticultural trade (Fang et al. 2013), it is possible that historical connectivity between populations due to human transport maintained gene flow between populations after its introduction into the US (Mack 1991). Alternatively, recurrent colonization from few genetically similar sources might instead have resulted in partial homogenization of otherwise isolated populations (Dlugosch and Parker 2008). To disentangle the relative contribution of recent gene flow from that of historical patterns of population connectivity, empirical estimates of inter-population migration (e.g., through the use of pollen traps) or direct measurements of gene flow (e.g., paternity analysis) would be needed.

Our estimates of differentiation as well as heterozygosity and allelic richness differ from other agricultural weedy species. Specifically, our estimates suggest that I. purpurea has lower genetic diversity (as measured by allelic richness, Rs, and/or heterozygosity, He) than primarily outcrossing annual weeds (e.g., ragweed [Rs: 5.85, He: 0.76] Genton et al. 2005, and annual sunflower [Rs: 4.05, He: 0.51] Muller et al. 2011), including many broadly distributed invasives (Dlugosch and Parker 2008). Its genetic diversity is also lower than other mixed-mating species such as downy yellow violet [He: 0.32] (Culley and Wolfe 2001) and common lungwort [Rs: 3.41, He: 0.60] (Meeus et al. 2012). This finding is potentially explained by both differences in the specifics of the reproduction system, as outcrossing and primarily outcrossing plants often show greater genetic diversity than plants with mixed or primarily selfing reproduction (Hamrick and Godt 1996), and the recent population bottlenecks likely experienced by I. purpurea (Kuester et al. 2016).

Genetic differentiation found in this study (as measured by FST), on the other hand, was relatively low for a broadly distributed gravity-dispersed plant (Hamrick and Godt 1996). This contrasts with many broadly distributed weeds, which show moderate to high FST values (0.15–0.48) likely due to dispersal limitations over distances above those commonly allowed by natural dispersal agents (Schmidt et al. 2009; Treier and Müller-Schärer 2011). This is the case, for example, of invasive weeds such as weedy Silene (Barluenga et al. 2011) that rely on specialist pollinators or seed dispersers that might not be present in the invaded range. Considering the natural history of I. purpurea—heavy seeds, bumblebee pollination (Osborne et al. 1999; Schulke and Waser 2001), and strong agricultural and horticultural ties (Defelice 2001), this finding suggests that human-aided dispersal presumably contributes to maintain connectivity in this species.

Landscape features influencing population connectivity

Our assessment of the association between population differentiation and landscape resistance identified several predictors of population connectivity. Of the landscape features examined, climate and human population density are the only robust predictors, suggesting a role for both human activities and climatic barriers in shaping population connectivity in this species. Specifically, our results suggest that while climatic variables provide some resistance to migration, scarcely to moderately populated areas (i.e., those corresponding with rural areas) offer potential corridors between all sampled regions. The existence of climatic dispersal barriers presumably arises in response to physiological preferences or local adaptations of the species (Cimalová and Lososová 2009); humans seem to oppose these natural limitations and help I. purpurea overcome climatic barriers (e.g., by allowing dispersal between northern and southern populations that are separated by areas of high temperature-related resistance to gene flow). Indeed, human-mediated migration is expected to be particularly prevalent among wild populations of species with commercial value such as I. purpurea (Mack 1991; Defelice 2001).

Population connectivity of species in human-dominated environments is potentially also affected by human-induced changes in population size (Méndez et al. 2014). Specifically, by influencing population size, anthropogenic activities condition the effectiveness of migration as it depends on migration relative rate (Nm) (Wright 1931). Furthermore, population size differences influence the overall dispersal spatial dynamics because the number and direction of migrants depend on local population sizes (e.g., proportionately greater number of migrants move from densely to sparsely populated areas than vice versa; Lenormand 2002). In line with these expectations, we found that effective population size is also a significant predictor of population differentiation in this species. Considering the prevalence of weed management practices (e.g., tillage, herbicide application) and their effect on weed populations (Kuester et al. 2016), it is likely that these anthropogenic activities play a significant role in controlling the rate of population differentiation in weeds by manipulating population size. Thus, all evidence suggests a predominant role of human activities in shaping I. purpurea’s current genetic structure.

Relatively few studies have explored how landscape features impact population connectivity in weeds at large spatial scales, making it hard to evaluate how distinctive I. purpurea’s response to climatic and anthropogenic factors may be from that of other weeds. Yet, simulations modeling short-distance dispersal based on spatial distances and landscape configuration have identified dispersal capabilities and landscape use (including availability of disturbed habitats and distribution of crop types) to be the most prevalent determinants of local level connectivity in several weed systems (Woolcock and Cousens 2000; Fénart et al. 2007; Will and Tackenberg 2008). For instance, using a ~10 km2 aerial photograph to inform a spatial mechanistic model of Canadian horseweed’s interfield dispersal, Dauer et al. (2009) showed that distribution of suitable habitat primarily determined the rate and extent of this weed’s dispersal at this spatial scale. In agreement with these predictions, empirical data show that local dispersal in mountain pasture weed is heavily influenced by the spatial distribution of human-dominated landscapes and the opportunities for interfield contamination (Treier and Müller-Schärer 2011). Yet, while neither landcover nor crop types distribution were identified as significant predictors in our multivariate analyses, we cannot rule out the possibility of high local gene flow at the scale of contiguous agricultural fields mediated by these landscape features given the scale of our analyses.

Marker-specific inferences

Our results identified interesting differences between marker types in terms of the inferred population structure of I. purpurea. The differences uncovered between datasets are at first glance unexpected as all loci in a species’ genome evolve under a common evolutionary history (Payseur and Cutter 2006). Nevertheless, differences between marker types have been similarly observed in other studies (Dixon et al. 2011; Martin et al. 2016). For example, several studies have recovered FST estimate differences when using SNP or SSR loci on the same set of samples (Coates et al. 2009; Gärke et al. 2012), presumably due to mutation rates and genomic representation differences of SSR and SNP loci (Payseur and Cutter 2006; Coates et al. 2009). Here, the population structure differences we uncovered may likewise be related to marker-specific rates of mutation, drift and/or marker-specific biases—such as greater ascertainment bias on SSR data (Väli et al. 2008; Defaveri et al. 2013)—and not likely caused by the different SSR and SNP dataset sampling. Because of these intrinsic marker differences, both markers could provide complementary information (Payseur and Cutter 2006). While our identification of robust environmental predictors of genetic differentiation for SSR and SNP datasets—despite differences in underlying population genetic patterns—is encouraging, further work is needed to reconcile traditional landscape genetics studies based on a few highly variable markers with increasing landscape genomics studies based on thousands of SNPs.

Conclusions

While our results suggest that I. purpurea experiences moderate inter-population connectedness and potential long-distance dispersal, we cannot rule out the influence of historical relatedness on the observed genetic patterns. To determine the amount of current-day gene flow that occurs between populations, direct estimates of gene flow need to be examined. Regardless, the limited population structure recovered as well as the identification of human population density as a significant predictor of population differentiation calls attention to the need for investigating the possible impact of human-mediated gene flow on the evolutionary path of this species—including its response to selection and the likelihood of further naturalization. In particular, it remains to be investigated whether the pattern of maintained connectivity we identify here could facilitate the success of this weed (e.g., by introducing relevant genetic variants; Kolbe et al. 2004) or reduce the fitness of local populations (Keller et al. 2000). What seems clear from this study is that human-aided migration presumably is an important component of gene flow between populations, which may counter the isolating effects of natural environmental barriers and genetic drift.

Data archiving

All data available from the Dryad Digital Repository: 10.5061/dryad.6rc405m.

Electronic supplementary material

41437_2018_106_MOESM1_ESM.docx (18.3KB, docx)

Supplemental material - titles/legends for supplemental figures and tables

Supplemental Figure 1 (7.1MB, pdf)
Supplemental Figure 2 (1.2MB, pdf)
Supplemental Figure 3 (1.3MB, pdf)
Supplemental Figure 4 (2.1MB, pdf)
Supplemental Figure 5 (419.6KB, pdf)
Supplemental Figure 6 (191.5KB, pdf)
Supplemental Figure 7 (2MB, pdf)
41437_2018_106_MOESM9_ESM.docx (24.7KB, docx)

Supplementary material - supplemental tables

Acknowledgements

The authors thank Adam Kuester for seed collecting and for contributing valuable data for this study. The authors also thank Ariana Wilson, Eva Fall, and Dan York for tissue collection. This research was funded by USDA NIFA grants 04180 and 07191 to R.S.B.

Compliance with ethical standards

Conflict of interest

The authors declare that they have no conflict of interest.

Electronic supplementary material

The online version of this article (10.1038/s41437-018-0106-x) contains supplementary material, which is available to authorized users.

References

  1. Auffret AG, Cousins SAO. Humans as long-distance dispersers of rural plant communities. PLoS ONE. 2013;8:1–7. doi: 10.1371/journal.pone.0062763. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Barluenga M, Austerlitz F, Elzinga JA, Teixeira S, Goudet J, Bernasconi G. Fine-scale spatial genetic structure and gene dispersal in Silene latifolia. Heredity. 2011;106:13–24. doi: 10.1038/hdy.2010.38. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Barrowclough GF. Gene flow, effective population sizes and genetic variance components in birds. Evolution. 1980;34:789–798. doi: 10.1111/j.1558-5646.1980.tb04018.x. [DOI] [PubMed] [Google Scholar]
  4. Bataille A, Cunningham AA, Cruz M, Cedeño V, Goodman SJ. Adaptation, isolation by distance and human-mediated transport determine patterns of gene flow among populations of the disease vector Aedes taeniorhynchus in the Galapagos Islands. Infect Genet Evol. 2011;11:1996–2003. doi: 10.1016/j.meegid.2011.09.009. [DOI] [PubMed] [Google Scholar]
  5. Baucom RS, Mauricio R. The evolution of novel herbicide tolerance in a noxious weed: the geographic mosaic of selection. Evol Ecol. 2008;22:85–101. doi: 10.1007/s10682-007-9160-1. [DOI] [Google Scholar]
  6. Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J R Stat Soc B. 1995;57:289–300. [Google Scholar]
  7. Bushnell B (2014). BBMap short read aligner. http://sourceforge.net/projects/bbmap/.
  8. Chaney L, Baucom RS. The evolutionary potential of Baker’s weediness traits in the common morning glory, Ipomoea purpurea (Convolvulaceae) Am J Bot. 2012;99:1524–1530. doi: 10.3732/ajb.1200096. [DOI] [PubMed] [Google Scholar]
  9. Chen C, Durand E, Forbes F, François O. Bayesian clustering algorithms ascertaining spatial population structure: a new computer program and a comparison study. Mol Ecol Notes. 2007;7:747–756. doi: 10.1111/j.1471-8286.2007.01769.x. [DOI] [Google Scholar]
  10. Cimalová Scaron, Lososová Z. Arable weed vegetation of the northeastern part of the Czech Republic: effects of environmental factors on species composition. Plant Ecol. 2009;203:45–57. doi: 10.1007/s11258-008-9503-1. [DOI] [Google Scholar]
  11. Clobert J, Baguette M, Benton TG, Bullock JM. Dispersal ecology and evolution. 1st edn. Oxford: Oxford University Press; 2012. [Google Scholar]
  12. Coates BS, Sumerford DV, Miller NJ, Kim KS, Sappington TW, Siegfried BD, et al. Comparative performance of single nucleotide polymorphism and microsatellite markers for population genetic analysis. J Hered. 2009;100:556–564. doi: 10.1093/jhered/esp028. [DOI] [PubMed] [Google Scholar]
  13. Culley TM, Wolfe AD. Population genetic structure of the cleistogamous plant species Viola pubescens Aiton (Violaceae), as indicated by allozyme and ISSR molecular markers. Heredity. 2001;86:545–556. doi: 10.1046/j.1365-2540.2001.00875.x. [DOI] [PubMed] [Google Scholar]
  14. Culpepper AS. Glyphosate-induced weed shifts. Weed Technol. 2006;20:277–281. doi: 10.1614/WT-04-155R.1. [DOI] [Google Scholar]
  15. Cushman SA, McKelvey KS, Hayden J, Schwartz MK. Gene flow in complex landscapes: testing multiple hypotheses with causal modeling. Am Nat. 2006;168:486–499. doi: 10.1086/506976. [DOI] [PubMed] [Google Scholar]
  16. Danecek P, Auton A, Abecasis G, Albers CA, Banks E, DePristo MA, et al. The variant call format and VCFtools. Bioinformatics. 2011;27:2156–2158. doi: 10.1093/bioinformatics/btr330. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Dauer JT, Luschei EC, Mortensen DA. Effects of landscape composition on spread of an herbicide-resistant weed. Landsc Ecol. 2009;24:735–747. doi: 10.1007/s10980-009-9345-9. [DOI] [Google Scholar]
  18. Defaveri J, Viitaniemi H, Leder E, Merilä J. Characterizing genic and nongenic molecular markers: comparison of microsatellites and SNPs. Mol Ecol Resour. 2013;13:377–392. doi: 10.1111/1755-0998.12071. [DOI] [PubMed] [Google Scholar]
  19. Defelice MS. Tall morningglory, Ipomoea purpurea (L.) roth-flower or foe? Weed Technol. 2001;15:601–606. doi: 10.1614/0890-037X(2001)015[0601:TMIPLR]2.0.CO;2. [DOI] [Google Scholar]
  20. Dixon CJ, Kapralov MV, Filatov DA. Gene flow and species cohesion following the spread of Schiedea globosa (Caryophyllaceae) across the Hawaiian Islands. J Evol Biol. 2011;24:1–11. doi: 10.1111/j.1420-9101.2010.02128.x. [DOI] [PubMed] [Google Scholar]
  21. Dlugosch KM, Parker IM. Founding events in species invasions: genetic variation, adaptive evolution, and the role of multiple introductions. Mol Ecol. 2008;17:431–449. doi: 10.1111/j.1365-294X.2007.03538.x. [DOI] [PubMed] [Google Scholar]
  22. Do C, Waples RS, Peel D, Macbeth GM, Tillett BJ, Ovenden JR. NeEstimatorv2: re-implementation of software for the estimation of contemporary effective population size (Ne) from genetic data. Mol Ecol Resour. 2014;14:209–214. doi: 10.1111/1755-0998.12157. [DOI] [PubMed] [Google Scholar]
  23. Doyle JJ, Doyle JL. A rapid DNA isolation procedure for small quantities of fresh leaf tissue. Phytochem Bull. 1987;19:11–15. [Google Scholar]
  24. Durand E, Chen C, Francois O (2009a). Tess version 2.3—Reference Manual, 1–30. http://www-timc.imag.fr/Olivier.Francois/tess.htm
  25. Durand E, Jay F, Gaggiotti OE, François O. Spatial inference of admixture proportions and secondary contact zones. Mol Biol Evol. 2009;26:1963–1973. doi: 10.1093/molbev/msp106. [DOI] [PubMed] [Google Scholar]
  26. Dyer RJ. GeneticStudio: a suite of programs for spatial analysis of genetic-marker data. Mol Ecol Resour. 2009;9:110–113. doi: 10.1111/j.1755-0998.2008.02384.x. [DOI] [PubMed] [Google Scholar]
  27. Dyer RJ. Population graphs and landscape genetics. Annu Rev Ecol Evol Syst. 2015;46:327–342. doi: 10.1146/annurev-ecolsys-112414-054150. [DOI] [Google Scholar]
  28. Dyer RJ, Nason JD. Population graphs: the graph theoretic shape of genetic structure. Mol Ecol. 2004;13:1713–1727. doi: 10.1111/j.1365-294X.2004.02177.x. [DOI] [PubMed] [Google Scholar]
  29. Dyer RJ, Nason JD, Garrick RC. Landscape modelling of gene flow: improved power using conditional genetic distance derived from the topology of population networks. Mol Ecol. 2010;19:3746–3759. doi: 10.1111/j.1365-294X.2010.04748.x. [DOI] [PubMed] [Google Scholar]
  30. Epperson BK, Clegg MT. Spatial-autocorrelation analysis of flower color polymorphisms within substructured populations of morning glory (Ipomoea purpurea) Am Nat. 1986;128:840–858. doi: 10.1086/284609. [DOI] [Google Scholar]
  31. Everman E, Klawinski P. Human-facilitated jump dispersal of a non-native frog species on Hawai’i Island. J Biogeogr. 2013;40:1961–1970. [Google Scholar]
  32. Excoffier L, Lischer HEL. Arlequin suite ver 3.5: a new series of programs to perform population genetics analyses under Linux and Windows. Mol Ecol Resour. 2010;10:564–567. doi: 10.1111/j.1755-0998.2010.02847.x. [DOI] [PubMed] [Google Scholar]
  33. Excoffier L, Smouse PE, Quattro JM. Analysis of molecular variance inferred from metric distances among DNA haplotypes: application to human mitochondrial DNA restriction data. Genetics. 1992;491:479–491. doi: 10.1093/genetics/131.2.479. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Fang Z, Gonzales AM, Durbin ML, Meyer KKT, Miller BH, Volz KM, et al. Tracing the geographic origins of weedy Ipomoea purpurea in the Southeastern United States. J Hered. 2013;104:666–677. doi: 10.1093/jhered/est046. [DOI] [PubMed] [Google Scholar]
  35. Fénart S, Austerlitz F, Cuguen J, Arnaud JF. Long distance pollen-mediated gene flow at a landscape level: the weed beet as a case study. Mol Ecol. 2007;16:3801–3813. doi: 10.1111/j.1365-294X.2007.03448.x. [DOI] [PubMed] [Google Scholar]
  36. Fountain T, Duvaux L, Horsburgh G, Reinhardt K, Butlin RK. Human-facilitated metapopulation dynamics in an emerging pest species, Cimex lectularius. Mol Ecol. 2014;23:1071–1084. doi: 10.1111/mec.12673. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Gärke C, Ytournel F, Bed’Hom B, Gut I, Lathrop M, Weigend S, et al. Comparison of SNPs and microsatellites for assessing the genetic structure of chicken populations. Anim Genet. 2012;43:419–428. doi: 10.1111/j.1365-2052.2011.02284.x. [DOI] [PubMed] [Google Scholar]
  38. Genton BJ, Shykoff JA, Giraud T. High genetic diversity in French invasive populations of common ragweed, Ambrosia artemisiifolia, as a result of multiple sources of introduction. Mol Ecol. 2005;14:4275–4285. doi: 10.1111/j.1365-294X.2005.02750.x. [DOI] [PubMed] [Google Scholar]
  39. Goslee SC, Urban DL. The ecodist package for dissimilarity-based analysis of ecological data. J Stat Softw. 2007;22:1–19. doi: 10.18637/jss.v022.i07. [DOI] [Google Scholar]
  40. Hamrick JL, Godt MJW. Effects of life history traits on genetic diversity in plant species. Philos Trans R Soc B Biol Sci. 1996;351:1291–1298. doi: 10.1098/rstb.1996.0112. [DOI] [Google Scholar]
  41. Hodkinson DJ, Thompson K. Plant dispersal: the role of man. J Appl Ecol. 1997;34:1484–1496. doi: 10.2307/2405264. [DOI] [Google Scholar]
  42. Holderegger R, Buehler D, Gugerli F, Manel S. Landscape genetics of plants. Trends Plant Sci. 2010;15:675–683. doi: 10.1016/j.tplants.2010.09.002. [DOI] [PubMed] [Google Scholar]
  43. Keller M, Kollmann J, Edwards PJ. Genetic introgression from distant provenances reduces fitness in local weed populations. J Appl Ecol. 2000;37:647–659. doi: 10.1046/j.1365-2664.2000.00517.x. [DOI] [Google Scholar]
  44. Kolbe JJ, Glor RE, Rodríguez Schettino L, Lara AC, Larson A, Losos JB. Genetic variation increases during biological invasion by a Cuban lizard. Nature. 2004;431:177–81. doi: 10.1038/nature02807. [DOI] [PubMed] [Google Scholar]
  45. Kuester A, Chang SM, Baucom RSnbsp. The geographic mosaic of herbicide resistance evolution in the common morning glory, Ipomoea purpurea: evidence for resistance hotspots and low genetic differentiation across the landscape. Evol Appl. 2015;8:821–833. doi: 10.1111/eva.12290. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Kuester A, Wilson A, Chang SM, Baucom RS. A resurrection experiment finds evidence of both reduced genetic diversity and potential adaptive evolution in the agricultural weed Ipomoea purpurea. Mol Ecol. 2016;25:4508–4520. doi: 10.1111/mec.13737. [DOI] [PubMed] [Google Scholar]
  47. Legendre P, Lapointe FJ, Casgrain P. Modeling brain evolution from behavior: a permutational regression approach. Evolution. 1994;48:1487–1499. doi: 10.1111/j.1558-5646.1994.tb02191.x. [DOI] [PubMed] [Google Scholar]
  48. Lenormand T. Gene flow and the limits to natural selection. Trends Ecol Evol. 2002;17:183–189. doi: 10.1016/S0169-5347(02)02497-7. [DOI] [Google Scholar]
  49. Li H. A statistical framework for SNP calling, mutation discovery, association mapping and population genetical parameter estimation from sequencing data. Bioinformatics. 2011;27:2987–2993. doi: 10.1093/bioinformatics/btr509. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Li H, Handsaker B, Wysoker A, Fennell T, Ruan J, Homer N, et al. The Sequence Alignment/Map format and SAMtools. Bioinformatics. 2009;25:2078–2079. doi: 10.1093/bioinformatics/btp352. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Mack RN. The commercial seed trade: An early disperser of weeds in the United States. Econ Bot. 1991;45:257–273. doi: 10.1007/BF02862053. [DOI] [Google Scholar]
  52. Mack RN, Lonsdale WM. Humans as global plant dispersers: getting more than we bargained for. Bioscience. 2001;51:95–102. doi: 10.1641/0006-3568(2001)051[0095:HAGPDG]2.0.CO;2. [DOI] [Google Scholar]
  53. Marko PB, Hart MW. The complex analytical landscape of gene flow inference. Trends Ecol Evol. 2011;26:448–456. doi: 10.1016/j.tree.2011.05.007. [DOI] [PubMed] [Google Scholar]
  54. Martin MD, Olsen MT, Samaniego JA, Zimmer EA, Gilbert MTP. The population genomic basis of geographic differentiation in North American common ragweed (Ambrosia artemisiifolia L.) Ecol Evol. 2016;6:3760–3771. doi: 10.1002/ece3.2143. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. McRae B. Isolation by resistance. Evolution. 2006;60:1551–1561. doi: 10.1111/j.0014-3820.2006.tb00500.x. [DOI] [PubMed] [Google Scholar]
  56. Meehan TD, Werling BP, Landis DA, Gratton C. Agricultural landscape simplification and insecticide use in the Midwestern United States. Proc Natl Acad Sci USA. 2011;108:11500–11505. doi: 10.1073/pnas.1100751108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Meeus S, Honnay O, Brys R, Jacquemyn H. Biased morph ratios and skewed mating success contribute to loss of genetic diversity in the distylous Pulmonaria officinalis. Ann Bot. 2012;109:227–235. doi: 10.1093/aob/mcr272. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Menchari Y, Délye C, Le Corre V. Genetic variation and population structure in black-grass (Alopecurus myosuroides Huds.), a successful, herbicide-resistant, annual grass weed of winter cereal fields. Mol Ecol. 2007;16:3161–3172. doi: 10.1111/j.1365-294X.2007.03390.x. [DOI] [PubMed] [Google Scholar]
  59. Méndez M, Vögeli M, Tella JL, Godoy JA. Joint effects of population size and isolation on genetic erosion in fragmented populations: finding fragmentation thresholds for management. Evol Appl. 2014;7:506–518. doi: 10.1111/eva.12154. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Mitchell M. An introduction to genetic algorithms. Cambridge, MA: MIT Press; 1996. [Google Scholar]
  61. Molecular Ecology Resources Primer Development Consortium, Aksoy S, Almeida-Val VMF, Azevedo VCR, Baucom RS, Bazaga P et al. (2013) Permanent genetic resources added to Molecular Ecology Resources Database 1 October 2012–30 November 2012. Mol Ecol Resour 13:341–343 [DOI] [PubMed]
  62. Muller MH, Latreille M, Tollon C. The origin and evolution of a recent agricultural weed: population genetic diversity of weedy populations of sunflower (Helianthus annuus L.) in Spain and France. Evol Appl. 2011;4:499–514. doi: 10.1111/j.1752-4571.2010.00163.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Navas ML. Trait-based approaches to unravelling the assembly of weed communities and their impact on agro-ecosystem functioning. Weed Res. 2012;52:479–488. doi: 10.1111/j.1365-3180.2012.00941.x. [DOI] [Google Scholar]
  64. Osborne JL, Clark SJ, Morris RJ, Williams IH, Riley JR, Smith AD, et al. A landscape-scale study of bumble bee foraging range and constancy, using harmonic radar. J Appl Ecol. 1999;36:519–533. doi: 10.1046/j.1365-2664.1999.00428.x. [DOI] [Google Scholar]
  65. Payseur BA, Cutter AD. Integrating patterns of polymorphism at SNPs and STRs. Trends Genet. 2006;22:424–429. doi: 10.1016/j.tig.2006.06.009. [DOI] [PubMed] [Google Scholar]
  66. Peakall R, Smouse PE. GenAlEx 6.5: genetic analysis in Excel. Population genetic software for teaching and research-an update. Bioinformatics. 2012;28:2537–2539. doi: 10.1093/bioinformatics/bts460. [DOI] [PMC free article] [PubMed] [Google Scholar]
  67. Peterman WE. ResistanceGA: an R package for the optimization of resistance surfaces using genetic algortihms. Meth Ecol Evol. 2018;9:1638–1647. doi: 10.1111/2041-210X.12984. [DOI] [Google Scholar]
  68. Peterman WE, Connette GM, Semlitsch RD, Eggert LS. Ecological resistance surfaces predict fine-scale genetic differentiation in a terrestrial woodland salamander. Mol Ecol. 2014;23:2402–2413. doi: 10.1111/mec.12747. [DOI] [PubMed] [Google Scholar]
  69. Pfeifer B, Wittelsbürger U, Ramos-Onsins SE, Lercher MJ. PopGenome: an efficient swiss army knife for population genomic analyses in R. Mol Biol Evol. 2014;31:1929–1936. doi: 10.1093/molbev/msu136. [DOI] [PMC free article] [PubMed] [Google Scholar]
  70. Pimentel D, Zuniga R, Morrison D. Update on the environmental and economic costs associated with alien-invasive species in the United States. Ecol Econ. 2005;52:273–288. doi: 10.1016/j.ecolecon.2004.10.002. [DOI] [Google Scholar]
  71. R Core Development Team (2016). R: a language and environment for statistical computing, 3.2.4. www.r-project.org
  72. Ricciardi A. Are modern biological invasions an unprecedented form of global change? Conserv Biol. 2007;21:329–336. doi: 10.1111/j.1523-1739.2006.00615.x. [DOI] [PubMed] [Google Scholar]
  73. Schmidt T, Arens P, Smulders MJM, Billeter R, Liira J, Augenstein I, et al. Effects of landscape structure on genetic diversity of Geum urbanum L. populations in agricultural landscapes. Flora Morphol Distrib. Funct Ecol Plants. 2009;204:549–559. doi: 10.1016/j.flora.2008.07.005. [DOI] [Google Scholar]
  74. Schulke B, Waser NM. Long-distance pollinator flights and pollen dispersal between populations of Delphinium nuttallianum. Oecologia. 2001;127:239–245. doi: 10.1007/s004420000586. [DOI] [PubMed] [Google Scholar]
  75. Sexton JP, Hangartner SB, Hoffmann AA. Genetic isolation by environment or distance: which pattern of gene flow is most common? Evolution. 2014;68:1–15. doi: 10.1111/evo.12258. [DOI] [PubMed] [Google Scholar]
  76. Shah VB, McRae BH (2008). Circuitscape: a tool for landscape ecology. In: Proceedings of the 7th Python in science conference, pp. 62–65.
  77. Siliceo-Cantero HH, García A, Reynolds RG, Pacheco G, Lister BC. Dimorphism and divergence in island and mainland Anoles. Biol J Linn Soc. 2016;118:852–872. doi: 10.1111/bij.12776. [DOI] [Google Scholar]
  78. Simberloff D. Invasive species: what everyone needs to know. Oxford: Oxford University Press; 2013. [Google Scholar]
  79. Slatkin M. Gene flow in natural populations. Annu Rev Ecol Syst. 1985;16:393–430. doi: 10.1146/annurev.es.16.110185.002141. [DOI] [Google Scholar]
  80. Spear SF, Balkenhol N, Fortin MJ, McRae BH, Scribner K. Use of resistance surfaces for landscape genetic studies: considerations for parameterization and analysis. Mol Ecol. 2010;19:3576–3591. doi: 10.1111/j.1365-294X.2010.04657.x. [DOI] [PubMed] [Google Scholar]
  81. Tiffin P, Rausher MD. Genetic constraints and selection acting on tolerance to herbivory in the common morning glory Ipomoea purpurea. Am Nat. 1999;154:700–716. doi: 10.1086/303271. [DOI] [PubMed] [Google Scholar]
  82. Trakhtenbrot A, Nathan R, Perry G, Richardson DM. The importance of long-distance dispersal in biodiversity conservation. Divers Distrib. 2005;11:173–181. doi: 10.1111/j.1366-9516.2005.00156.x. [DOI] [Google Scholar]
  83. Treier UA, Müller-Schärer H. Differential effects of historical migration, glaciations and human impact on the genetic structure and diversity of the mountain pasture weed Veratrum album L. J Biogeogr. 2011;38:1776–1791. doi: 10.1111/j.1365-2699.2011.02516.x. [DOI] [Google Scholar]
  84. Väli nbspUuml, Einarsson A, Waits L, Ellegren H. To what extent do microsatellite markers reflect genome-wide genetic diversity in natural populations? Mol Ecol. 2008;17:3808–3817. doi: 10.1111/j.1365-294X.2008.03876.x. [DOI] [PubMed] [Google Scholar]
  85. Wang IJ, Bradburd GS. Isolation by environment. Mol Ecol. 2014;23:5649–5662. doi: 10.1111/mec.12938. [DOI] [PubMed] [Google Scholar]
  86. Wang IJ, Savage WK, Shaffer HB. Landscape genetics and least-cost path analysis reveal unexpected dispersal routes in the California tiger salamander (Ambystoma californiense) Mol Ecol. 2009;18:1365–1374. doi: 10.1111/j.1365-294X.2009.04122.x. [DOI] [PubMed] [Google Scholar]
  87. Webster TM, Nichols RL. Changes in the prevalence of weed species in the major agronomic crops of the southern United States: 1994/1995 to 2008/2009. Weed Sci. 2012;60:145–157. doi: 10.1614/WS-D-11-00092.1. [DOI] [Google Scholar]
  88. Weckworth BV, Musiani M, Decesare NJ, Mcdevitt AD, Hebblewhite M, Mariani S. Preferred habitat and effective population size drive landscape genetic patterns in an endangered species. Proc R Soc B. 2013;280:1–9. doi: 10.1098/rspb.2013.1756. [DOI] [PMC free article] [PubMed] [Google Scholar]
  89. White DR, Harary F. The cohesiveness of blocks in social networks: node connectivity and conditional density. Sociol Methodol. 2001;31:305–359. doi: 10.1111/0081-1750.00098. [DOI] [Google Scholar]
  90. Will H, Tackenberg O. A mechanistic simulation model of seed dispersal by animals. J Ecol. 2008;96:1011–1022. doi: 10.1111/j.1365-2745.2007.01341.x. [DOI] [Google Scholar]
  91. Wilson GA, Rannala B. Bayesian inference of recent migration rates using multilocus genotypes. Genetics. 2003;163:1177–1191. doi: 10.1093/genetics/163.3.1177. [DOI] [PMC free article] [PubMed] [Google Scholar]
  92. Woolcock JL, Cousens R. A mathematical analysis of factors affecting the rate of spread of patches of annual weeds in an arable field. Weed Sci. 2000;48:27–34. doi: 10.1614/0043-1745(2000)048[0027:AMAOFA]2.0.CO;2. [DOI] [Google Scholar]
  93. Wright S. Evolution in Mendelian populations. Genetics. 1931;16:97–159. doi: 10.1093/genetics/16.2.97. [DOI] [PMC free article] [PubMed] [Google Scholar]
  94. Wright S. The genetical structure of populations. Ann Eugen. 1949;15:323–354. doi: 10.1111/j.1469-1809.1949.tb02451.x. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

41437_2018_106_MOESM1_ESM.docx (18.3KB, docx)

Supplemental material - titles/legends for supplemental figures and tables

Supplemental Figure 1 (7.1MB, pdf)
Supplemental Figure 2 (1.2MB, pdf)
Supplemental Figure 3 (1.3MB, pdf)
Supplemental Figure 4 (2.1MB, pdf)
Supplemental Figure 5 (419.6KB, pdf)
Supplemental Figure 6 (191.5KB, pdf)
Supplemental Figure 7 (2MB, pdf)
41437_2018_106_MOESM9_ESM.docx (24.7KB, docx)

Supplementary material - supplemental tables

Data Availability Statement

All data available from the Dryad Digital Repository: 10.5061/dryad.6rc405m.

Articles from Heredity are provided here courtesy of Nature Publishing Group

RESOURCES