OUTRIDER: A Statistical Method for Detecting Aberrantly Expressed Genes in RNA Sequencing Data

Abstract

RNA sequencing (RNA-seq) is gaining popularity as a complementary assay to genome sequencing for precisely identifying the molecular causes of rare disorders. A powerful approach is to identify aberrant gene expression levels as potential pathogenic events. However, existing methods for detecting aberrant read counts in RNA-seq data either lack assessments of statistical significance, so that establishing cutoffs is arbitrary, or rely on subjective manual corrections for confounders. Here, we describe OUTRIDER (Outlier in RNA-Seq Finder), an algorithm developed to address these issues. The algorithm uses an autoencoder to model read-count expectations according to the gene covariation resulting from technical, environmental, or common genetic variations. Given these expectations, the RNA-seq read counts are assumed to follow a negative binomial distribution with a gene-specific dispersion. Outliers are then identified as read counts that significantly deviate from this distribution. The model is automatically fitted to achieve the best recall of artificially corrupted data. Precision-recall analyses using simulated outlier read counts demonstrated the importance of controlling for covariation and significance-based thresholds. OUTRIDER is open source and includes functions for filtering out genes not expressed in a dataset, for identifying outlier samples with too many aberrantly expressed genes, and for detecting aberrant gene expression on the basis of false-discovery-rate-adjusted p values. Overall, OUTRIDER provides an end-to-end solution for identifying aberrantly expressed genes and is suitable for use by rare-disease diagnostic platforms.

Introduction

No clear pathogenic variant can be pinpointed for the majority of individuals suspected to suffer from a Mendelian disorder after undergoing whole-exome or whole-genome sequencing (WES or WGS, respectively).^{1, 2, 3} A possible reason is that the pathogenic variant is regulatory. Accurately identifying pathogenic regulatory variants is difficult. One difficulty is that any individual harbors a very large number of rare non-coding variants, about 60,000 compared with 475 protein-affecting rare variants per genome (with minor allele frequency [MAF] < 0.005).⁴ Another difficulty is that the interpretation of non-protein-coding regions of the genome remains challenging.⁵

Two recent studies have shown that using RNA sequencing (RNA-seq) to directly investigate gene expression defects in cells of affected individuals provides a complementary method to pinpoint pathogenic regulatory defects.^{6, 7} RNA-seq can help to reveal splicing defects, the mono-allelic expression of heterozygous loss-of-function variants, and expression outliers (i.e., genes aberrantly expressed outside their physiological range).^{6, 7} The two studies used different approaches to identify expression outliers. Cummings et al.⁶ computed Z scores on the log-transformed gene-length-normalized read counts by subtracting the mean count and dividing by the standard deviation. Expression outliers were identified as read counts with an absolute Z score greater than 3. Cummings et al. did not apply a formal statistical test for outlier detection and also explicitly note that their outlier analysis was underpowered to draw definitive conclusions.⁶ This study did not yield any convincing pathogenic expression-outlier candidates. In contrast, the study by Kremer et al.⁷ identified four out of six newly diagnosed individuals as expression outliers. Read-count outliers were identified as those with an absolute Z score greater than 3 and statistical significance according to DESeq2, a statistical test originally developed for differential expression analyses,⁸ which the authors applied by testing each sample against the rest of the cohort. DESeq2 is based on the negative binomial (NB) distribution, which can be used to model overdispersed count data.⁹ Altogether, the reason for the difference remains unclear because of the relatively small number of diagnosed individuals, the absence of ground truth, and the lack of a direct comparison between the two approaches based on the same data.

The two studies differed not only in whether a statistical test was applied but also in the way the data were controlled for confounders. Cummings et al.⁶ used RPKM (reads per kilobase per million mapped reads) expression values. These control for variations in sequencing depth but not for other sources of covariation among the read counts. Controlling for further sources of covariation is important because the identification of a gene as aberrantly expressed depends on the context, for example, the sex of the donor. Genes encoded on the Y chromosome are not present and thus not expressed in women. However, in men, loss of the expression of a Y-chromosome-encoded gene can be an aberrant expression event. Hence, not taking the sex of the donor into account would not allow for the detection of aberrantly silenced Y-chromosome-encoded genes in males. Although the sex of the donor is usually available and can be easily controlled for, other contexts for gene expression—such as the exact tissue of origin of the sample, the sample’s cell-type composition, the genetic background, and technical biases—might not be known a priori, causing similar but less intuitive variations. Kremer et al.⁷ controlled expression levels for sex, biopsy site as inferred from the HOX gene set, and common technical sources of variation, which were identified by visual inspection of a hierarchical clustering of the samples. In a study that identified expression outliers, although not for the diagnosis of rare diseases, Li et al.¹⁰ controlled for sex and the top three genotype principal components, as well as for hidden confounding effects estimated by the probabilistic estimation of expression residuals (PEER) method.¹¹ However, the algorithms controlling for covariations in RNA-seq read-count data used in the studies of Li et al.¹⁰ and Kremer et al.⁷ were neither assessed nor tuned to detect aberrantly expressed genes.

Here, we introduce OUTRIDER (Outlier in RNA-Seq Finder), an algorithm that provides a statistical test for outlier detection in RNA-seq samples while controlling for covariations among the gene read counts (Figure 1A). The modeling of covariation is performed by an autoencoder that controls for read-count variations caused by factors not known a priori. Its parameters are optimized automatically for recalling read counts corrupted in silico. Autoencoders were introduced to find low-dimensional representations of high-dimensional data.^{12, 13, 14} They have been shown to be useful for extracting meaningful biological features from RNA-seq data¹⁵ and imputing missing values in single-cell RNA-seq data.¹⁶ A subclass of autoencoders, the so-called denoising autoencoders, are used for reconstructing corrupted high-dimensional data by exploiting correlations in the data.¹⁷ In OUTRIDER, the autoencoder approach is used to control for the common covariation patterns among genes.

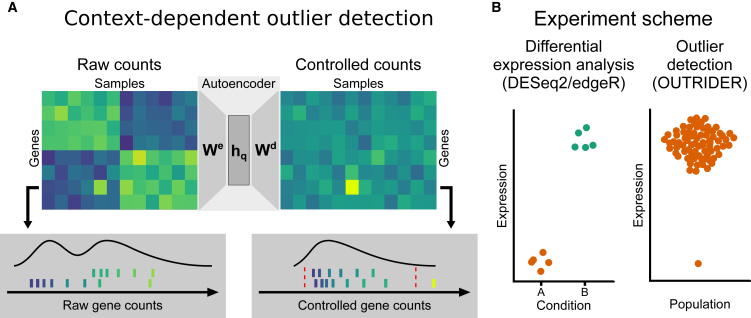
Figure 1.

OUTRIDER Overview

(A) Context-dependent outlier detection. The algorithm identifies gene expression outliers whose read counts are significantly aberrant given the covariations typically observed across genes in an RNA-seq dataset. This is illustrated by a read count (left panel, fifth column, second row from the bottom) that is exceptionally high in the context of correlated samples (left six samples) but not in absolute terms for this given gene. To capture commonly seen biological and technical contexts, an autoencoder models covariations in an unsupervised fashion and predicts read-count expectations. Comparing the earlier mentioned read count with these context-dependent expectations reveals that it is exceptionally high (right panel). The lower panels illustrate the distribution of read counts before and after controlling for covariations for the relevant gene. The red dotted lines depict significance cutoffs.

(B) Schema showing the differences in the experimental designs for differential expression analyses and outlier detection analyses; relevant analysis packages are mentioned.

Differential-expression algorithms, such as DESeq2⁸ and edgeR,¹⁸ have been conceived to compare small predefined groups of samples, typically treatment versus control, with a handful of replicates. To manage such small sample sizes, these approaches borrow information across genes to have robust estimates of the within-group variability. The setup for rare-disease diagnostics is different. In rare-disease diagnostics, replicates are typically not available for most individuals, and there is no typical experiment design of treatment versus control; rather, there are several tens of samples, where one sample is tested against all others. Also, one is not interested in detecting a subtle fold change between two controlled populations but rather in identifying an outlier within a large population (Figure 1B). We note that DESeq2 and edgeR also have procedures based on Cook’s distance and Pearson residuals^{8, 19} to mark or downweight outliers but with a different purpose than for rare-disease diagnostics. These methods aim to increase the robustness of the differential-expression analysis rather than assess the significance of the outlier data points. Here, we adopt a typical approach for outlier detection for the univariate case by modeling the distribution of the population and testing each data point to determine whether it significantly deviates from this distribution.²⁰

In this article, we describe the OUTRIDER algorithm, which combines an autoencoder and a statistical test for outlier detection, and delineate the added value of these two components against state-of-the-art alternatives by utilizing simulated data and two experimental datasets.

Material and Methods

Datasets

The RNA-seq read counts, in the following called counts, were downloaded from Data S1 published as part of the study by Kremer et al.⁷ for the rare-disease cohort. GTEx counts were obtained from the Genotype-Tissue Expression (GTEx) Portal (V6P counted with RNA-SeQC v.1.1.8).²¹ Counts for the Kremer et al. dataset were computed according to the UCSC Genome Browser build hg19²² with consideration of the full gene body. In contrast, GTEx is based on the Gencode v.19 annotation,²³ and the count of a gene is defined as the number of paired-end read pairs overlapping exons of that gene only. Samples with a low RNA integrity number (RIN < 5.7) were filtered out from the GTEx dataset. FPKM (fragments per kilobase per millions of reads) values were obtained with DESeq2,⁸ where the gene length was defined as the aggregated length of all the exons. We then filtered for expressed genes, defined as genes for which at least 5% of the samples had a FPKM value greater than 1 (Figure S1). Additionally, we discarded genes that had zero counts in more than 75% of the samples.

Statistical Model

We assume that the count $k_{ij}$ of gene $j=1,\dots ,p$in sample $i=1,\dots ,n$ follows a NB distribution with gene-specific dispersion parameter ${\text{θ}}_j$ and expected value $c_{ij}$:

$$P\left(k_{ij}\right)=\mathrm{N}\mathrm{B}\left(k_{ij}|{\mu }_{ij}=c_{ij},{\text{θ}}_j\right).$$ (Equation 1)

The used parameterization of the NB distribution can be found in the Supplemental Material and Methods. We limited the parameter range for ${\theta }_j$ to the interval [0.01, 1000]. The lower limit prevents convergence issues for genes with unusual high dispersion (${\theta }_j$ close to zero), and the upper limit is used to avoid overfitting. The expected count $c_{ij}$ is the product of the sample-specific size factor $s_i$ and the exponential of the factor$y_{ij}$:

$$c_{ij}=s_i·\exp \left(y_{ij}\right)$$ (Equation 2)

The size factors $s_i$ capture variations in sequencing depth; they are robustly estimated as the median of the ratios of the gene read counts to their geometric means as implemented in DESeq.²⁴ The factors $y_{ij}$ capture covariations across genes. They are modeled with an autoencoder of encoding dimension $1<q<\text{min}\left(p,n\right)$. Specifically,

$${\mathbf{y}}_i={\mathbf{h}}_i{\mathbf{W}}_d+\mathbf{b},$$ (Equation 3)

$${\mathbf{h}}_{\text{i}}={\stackrel{\sim }{\mathbf{x}}}_i{\mathbf{W}}_e,$$ (Equation 4)

where the$p\times q$ matrix ${\mathbf{W}}_e$ is the encoding matrix, the $q\times p$ matrix ${\mathbf{W}}_d$ is the decoding matrix, the q-vector ${\mathbf{h}}_{\text{i}}$ is the encoded representation, and the p-vector $\mathbf{b}$ is a bias term. Having a decoding matrix that is not the transpose of the encoding matrix, unlike for principal-component analysis (PCA), turned out to be important, most likely because the property that the matrix inverse equals the matrix transpose does not generalize to the NB loss function. The input vector to the autoencoder ${\stackrel{\sim }{\mathbf{x}}}_i$ is computed as follows:

$${\tilde{x}}_{ij}=x_{ij}–\overline{x_j}\text{,}\text{where}$$ (Equation 5)

$$x_{ij}=\text{log}\left(\frac{k_{ij}+1}{s_i}\right),$$ (Equation 6)

where we add 1 to prevent computing the logarithm of 0, we divide by the size factor to control for sequencing depth, and we center gene-wise by subtracting the mean $\overline{x_j}$. In the following, we call the combination of Equations 2–6 the autoencoder or, in short, $c_{ij}=AE\left(k_{ij}\right)$.

Fitting the Parameters

Fitting the autoencoder is implemented as an iterative three-step procedure in which the parameters ${\mathbf{W}}_e$ and ${\mathbf{W}}_d$ and the ${\theta }_j$ values are iteratively updated until convergence. First, the encoder and decoder matrices are initialized with PCA through the “pca()” function provided by the package pcaMethods,^{25, 26, 27} the bias vector is set to the mean of the log-transformed size-factor-normalized counts $\overline{x_j}=\underset{i}{\text{mean}}\left(\text{log}\left((k_{ij}+1)/s_i\right)\right)$, and the dispersion parameters are estimated by the method of moments, yet the dispersion parameters are restricted to the interval [0.01, 1000]. Before the iterative procedure starts, the gene-specific entries of the decoder matrix ${\mathbf{W}}_d$ and then the gene-specific dispersion parameters are fitted by maximum likelihood. The autoencoder is then fitted through repetition of the following three update steps: (1) the encoder matrix is updated, (2) the decoder matrix is updated per gene, and (3) the dispersion parameters are refitted per gene as detailed below. In each update step, the average negative log-likelihood is minimized with respect to the current parameters by the optimization method L-BFGS as implemented in “optim().”²⁸ For all three steps, detailed derivations of the used loss functions and the respective gradients can be found in the Supplemental Data.

Convergence Criteria for the Iterations of the Update Steps

The autoencoder is updated in an iterative fashion. The three update steps described above are repeated until the average negative log-likelihood of each step in one iteration does not differ more than the convergence threshold of 10⁻⁵ from the last step of the previous iteration or at most 15 iterations.

Fitting the Encoding Dimension

The optimal autoencoder dimension is obtained through evaluation of the performance of calling corrupted counts. To this end, we artificially introduced corrupted counts $k_{ij}^c$ randomly with a frequency of 10⁻² to the given count matrix. These corrupted counts are obtained as follows:

$$u_{ij}={\log }_2\left(\frac{k_{ij}}{s_i}+1\right),$$ (Equation 7)

$$k_{ij}^c=\text{round}\left(s_i{2}^{u_{ij}\pm e^z{\sigma }_{u_j}}\right),$$ (Equation 8)

where z, the amplitude of the corrupted count, is drawn from a normal distribution characterized by a mean of log(3) and a standard deviation of log(1.6). The sign of the shift is randomly selected. The optimal dimension is then selected as the dimension maximizing the area under the precision-recall curve for identifying corrupted counts.

p Value Computation

For every pair of gene j and sample i, we test the null hypothesis that the count $k_{ij}$ follows the distribution described by Equation 1. The algorithm computes two-sided p values by using the following equation:

$$P_{ij}=2·\min \left\{\frac{1}{2},\sum _{k=0}^{k_{ij}}NB\left(k_{ij}|{\mu }_{ij},{\text{θ}}_j\right),1-\sum _{k=0}^{k_{ij}-1}NB\left(k_{ij}|{\mu }_{ij},{\text{θ}}_j\right)\right\}.$$ (Equation 9)

The term 1/2 is included to handle cases when both other terms exceed 1/2, which is possible because of the discrete nature of the NB distribution.

Expression levels of different genes for the same sample are correlated because of biological confounding effects such as co-regulation, which cannot be entirely excluded even after controlling by the autoencoder. The computed p values can therefore be correlated. Multiple-testing correction was performed with the Benjamini-Yekutieli false-discovery rate (FDR) method, which holds under positive dependence.²⁹

Z Score Computation

Z scores $Z_{ij}$ are computed on a logarithmic scale as follows:

$$Z_{ij}=\frac{l_{ij}-{\mu }_j^l}{{\sigma }_j^l},$$ (Equation 10)

where $l_{ij}$ is the log-transformed controlled count calculated as $l_{ij}={\log }_2\left((k_{ij}+1)/(c_{ij}+1)\right)$, ${\sigma }_j^l$ is the standard deviation of $l_{ij}$ for gene j, and ${\mu }_j^l\text{ is }$the mean of $l_{ij}$ for gene j.

Benchmark by Injection of Outliers

To assess the sensitivity and specificity of alternative outlier detection methods, we injected artificial outliers with pre-specified amplitudes on the logarithmic scale (Z scores). This process was separate from the injection of corrupted data described earlier in Fitting the Encoding Dimension. We used the outlier injection scheme described in this section to independently assess OUTRIDER’s performance in comparison with that of other approaches.

We used this benchmark separately for both datasets: the GTEx skin tissue not exposed to the sun and the rare-disease cohort from Kremer et al.⁷ The counts were replaced with a probability of 10⁻⁴ by an outlier count $k_{ij}^o$, defined as follows:

$$k_{ij}^o=\text{round}\left(s_i{2}^{{\overline{u}}_j\pm e^z{\sigma }_{u_j}}\right),$$ (Equation 11)

where ${\overline{u}}_j$ is the mean of $u_{ij}$ for gene $j$ in the log space.

Alternative Control Methods

We benchmarked OUTRIDER against PEER³⁰ and PCA.^{25, 26, 27} Both were used instead of the autoencoder to model covariations. In the case of PCA, we obtained the matrix of expected counts by using the first q loadings as the ${\mathbf{W}}_e$ and ${\mathbf{W}}_d$ matrices, where $q$ is the encoding dimension inferred for the autoencoder. The bias term $\mathbf{b}$ was set to the gene means. In the case of PEER, we set the number of factors to one-fourth of the number of samples as suggested by Stegle et al.¹¹ We then subtracted the residuals from the log-transformed counts and multiplied the size factors to obtain $c_{ij}.$ For PEER, we used the provided residuals to compute Z scores to avoid numerical inaccuracies due to conversion to counts. For both PCA and PEER, we fitted a NB model with a per-gene adjustment $a_j$and a dispersion parameter ${\text{θ}}_j$on top of the obtained controlled counts (Equation 12) to obtain NB p values. We used the adjustment parameter to capture deviations between the estimated mean from the log-normal model and that from the NB model:

$$P\left(k_{ij}\right)=NB\left(k_{ij}|{\mu }_{ij}=a_j·c_{ij},{\text{θ}}_j\right).$$ (Equation 12)

Enrichment Analysis

We obtained rare variants (MAF < 0.05 within all 652 GTEx samples and in gnomAD³¹) from the GTEx WGS data (V7). We further filtered this set for those with predicted moderate or high impact according to the Variant Effect Predictor (VEP).³² To be comparable with Li et al., we only used the 441 individuals considered in their analysis for our enrichment analysis. As described in Li et. al.,¹⁰ we computed enrichments for rare variants found within outlier genes as the proportion of outliers having a rare variant over the proportion of non-outliers having a rare variant.

Implementation

OUTRIDER is implemented as an R package that is available through Bioconductor.

Results

We considered two RNA-seq datasets, which we refer to as the Kremer and GTEx datasets. The Kremer dataset contained 119 RNA-seq samples from skin fibroblasts of individuals with a suspected rare mitochondrial disorder.⁷ This dataset was analyzed in a previous study, where the systematic effects were controlled by manual inspection of sample correlation matrices.⁷ In this previous study, four genes were identified as aberrantly expressed out of six pathogenic genes detected by RNA-seq analysis and validated by functional assays.⁷ This dataset therefore served as our benchmark dataset for rare-disease applications. The GTEx dataset contained 250 RNA-seq samples obtained from the not-sun-exposed skin tissue in the GTEx project (V6P).²¹ Unless stated otherwise, we focused on these skin samples because the tissue was similar to the tissue of origin of the Kremer dataset. The donors of the GTEx samples did not suffer from any condition and were not under treatment. Nevertheless, aberrant gene expression in these samples has been reported.¹⁰

For both datasets, we filtered out genes not expressed across the whole dataset, resulting in 10,556 genes in the Kremer dataset and 17,065 genes in the GTEx dataset (Figures S1A and S1B). In the GTEx dataset, we additionally filtered out one sample because of a low RIN (<5.7), resulting in 249 samples. Both datasets exhibited a strong correlation structure with very distinct sample clusters (Figures S2A and S2E). These correlations could have arisen from biological variations such as the sex of the donor, the origin of the tissue, population structure, or hidden confounders such as poorly understood systematic technical variations.^{7, 10} Applying the autoencoder on the counts allowed covariations to be estimated and controlled for. The dimension of the autoencoder was fitted with a scheme in which a fraction of counts were artificially corrupted and fitted with OUTRIDER. Then the optimal dimension for the autoencoder was selected as the dimension maximizing the area under the precision-recall curve for identifying corrupted counts. We estimated the optimal encoding dimension to be 45 for the GTEx dataset and 21 for the Kremer dataset. Running the same assessment by using PCA instead of the autoencoder yielded 54 and 24 principal components, respectively. Encoding dimensions close to the estimated optimum yielded similar results. Moreover, using different corruption amplitudes had little impact on the optimal encoding dimension (Figure S3). After we controlled for covariation, clusters disappeared from both datasets (Figure S2).

Improving the Detection of Outliers by Using a NB Model

The OUTRIDER algorithm assumes that counts follow a NB distribution with a mean that is the expected value provided by the autoencoder. Assuming NB distributions with gene-specific dispersions, it detects expression outliers as significant deviations of the observed counts from these expected values. In contrast, PCA and PEER assume normal distribution and therefore require some transformation of the count data, typically the log-transformation.

To understand the differences between OUTRIDER, PCA, and PEER, we performed simulations of counts by assuming either (1) a simulation scheme corresponding to the assumptions of OUTRIDER or (2) a simulation scheme close to the assumptions of PCA and PEER. For both simulation schemes, the latent space was set to have ten dimensions. For the first simulation scheme, we drew counts from the NB distribution. For the second scheme, we drew values from a log-normal distribution and rounded them to the nearest integer to obtain counts. Means fitted by OUTRIDER were closer to the simulated means than means fitted by PCA or PEER throughout the entire range of counts on the basis of the NB simulation scheme (Figure S4A). In the log-normal case, all three methods were almost equal, but for low expression levels (simulated means lower than 30), OUTRIDER performed better than PCA or PEER on the log-normal simulated data. These simulation analyses emphasize the relevance of using a count distribution for fitting the expected counts, especially in the low count range.

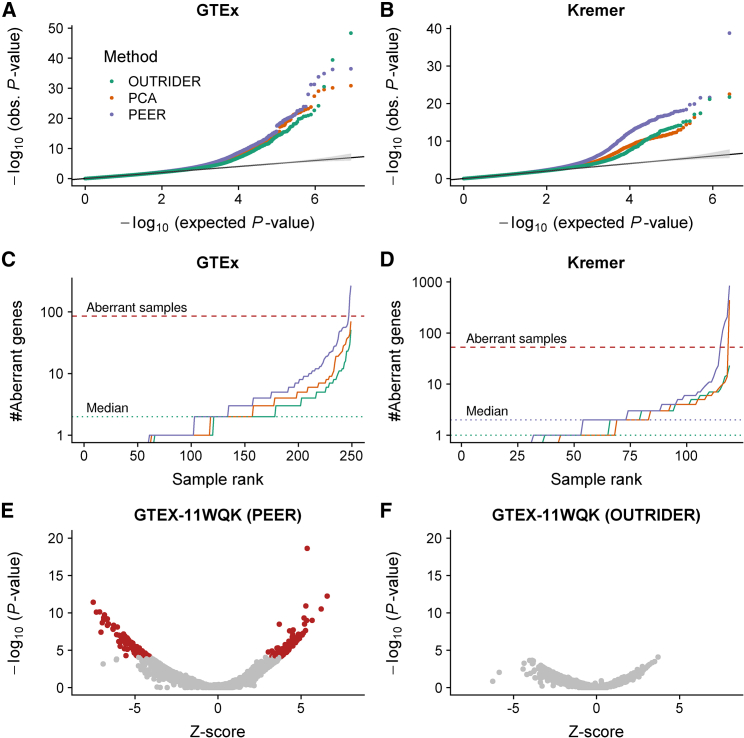
We then applied OUTRIDER on experimental data. Quantile-quantile plots for individual genes indicated that OUTRIDER reasonably modeled the count distribution (Figures 2 and S5) on the GTEx and Kremer datasets and that the resulting p values can be used for detecting outliers (Figures 2C and 2D). To untangle the contribution of the autoencoder from the p value computation, we substituted the autoencoder with either PCA or PEER to estimate the expected counts. Across all genes, the OUTRIDER p values deviated less from the expected uniform distribution than the NB p values computed on top of PCA or PEER (Figures 3A and 3B). These results show that, on experimental data, the distribution of the data is better captured when modeling the covariation with OUTRIDER than when using either PCA or PEER. Consistent with these observations, the distribution of the number of outlier counts per sample at a FDR less than 0.05 (Benjamini-Yekutelli method²⁹) was more even for OUTRIDER than for PCA and PEER for both datasets (Figures 3C and 3D). Moreover, samples with a high number of outliers according to OUTRIDER had similar numbers of outliers according to PCA and PEER. In contrast, in samples with a high number of outliers according to PCA and PEER, OUTRIDER did not find any or only a few outliers. To showcase this, we picked the most aberrant sample by PEER and compared it with the prediction by OUTRIDER in Figures 3E and 3F. In order to flag such aberrant samples, we introduced a cutoff (number of outliers > 0.5% of expressed genes). Accumulated over all GTEx tissues, we found 9, 18, and 214 out of 8,166 samples to be aberrant by using OUTRIDER, PCA, and PEER, respectively. Altogether, the smaller number of samples with an excessive number of outliers found by OUTRIDER further indicates that OUTRIDER captures the data distribution better than PCA and PEER.

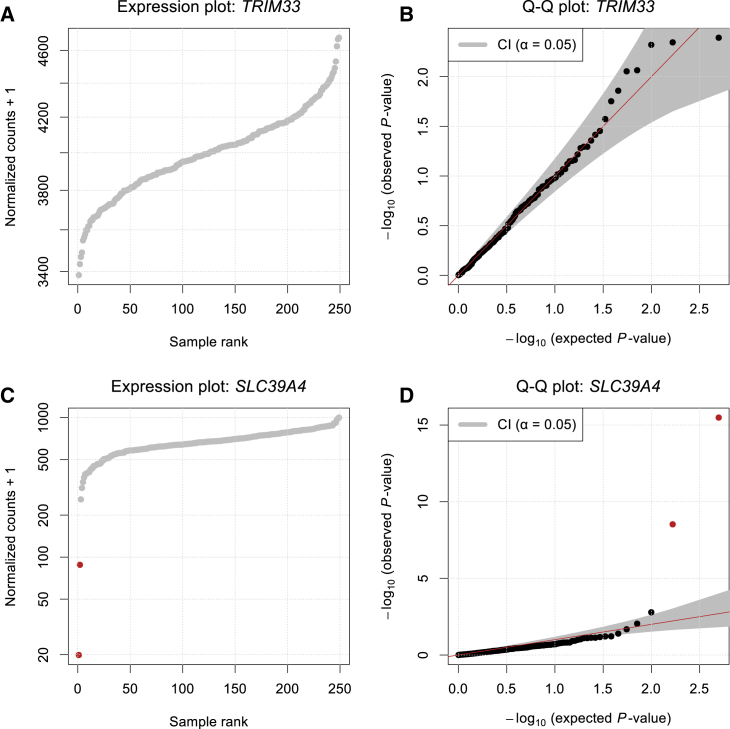
Figure 2.

Using the NB Distribution for Significance Assessment

Normalized RNA-seq read counts plotted against their rank (A and C) and quantile-quantile plots of observed p values against expected p values with 95% confidence bands (B and D); outliers are shown in red (FDR < 0.05). Shown are data for TRIM33 (MIM: 605769) with no detected expression outlier (A and B) and data for SLC39A4 (MIM: 607059) with two expression outliers (C and D).

Figure 3.

RNA-Seq Expression-Outlier Detection

(A and B) Quantile-quantile plots for the GTEx (A) and Kremer datasets (B). Observed p values are plotted against the expected p values for three different methods. The diagonal marks the expected distribution under the null hypothesis with 95% confidence bands (gray).

(C and D) Number of aberrant genes (FDR < 0.05) per sample for the data shown in (A) and (B) (C and D, respectively). The dashed line represents the abnormal sample cutoff (>0.5% aberrantly expressed genes).

(E and F) p values versus Z scores for a representative abnormal sample in PEER (E) and the same sample in OUTRIDER (F). Genes with significantly aberrant read counts are marked in red.

Recall Benchmark

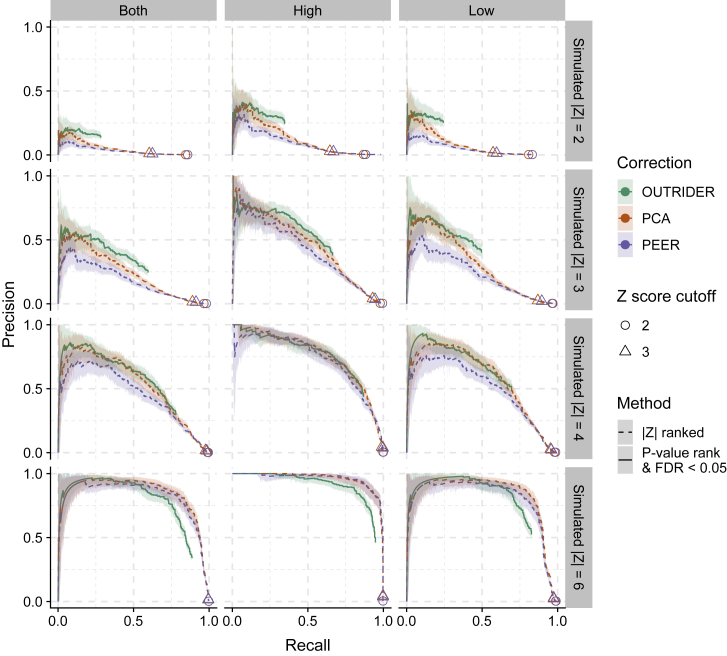
We then benchmarked OUTRIDER for recalling outliers. To this end, we injected simulated outliers into the GTEx and Kremer datasets and monitored the fraction of these simulated outliers that could be recalled. Simulated outliers were injected with a frequency of 10⁻⁴ into the count matrices, resulting in 381 injected outliers for the GTEx dataset and 113 injected outliers for the Kremer dataset. The injection of outliers was done according to three scenarios: (1) all underexpressed, (2) all overexpressed, and (3) 50% overexpressed and 50% underexpressed. Each scenario was repeated for four different simulated amplitudes (with Z score values of 2, 3, 4, and 6). We monitored the recall of injected read-count outliers and the precision, i.e., the number of injected outliers among the reported outliers, by using different detection methods. We note that the precision and the recall in this setup were underestimated because the original data also contained genuine outliers. The precision-recall curves showed that the OUTRIDER ranking outperformed ranking by Z score with PCA or PEER, except for simulated Z scores of 6 (Figure 4). Moreover, the two most commonly used Z score cutoffs^{6, 10} (|2| and |3|) recalled almost all the outliers (median = 97%) for both PCA and PEER but at the cost of a high FDR (precision < 0.02). The advantage of p values is that they provide a principled way to establish a cutoff that accounts for statistical significance and multiple testing. Combining either PCA or PEER to model the expected counts with the NB model to obtain p values and FDR estimates led to improved precision-recall curves over PCA and PEER with Z score ranking, particularly for the underexpressed simulations (Figures S6 and S7). This analysis delineates the importance of using a count distribution and a p-value-based strategy.

Figure 4.

Outlier-Detection Benchmark

The proportion of simulated outliers among reported outliers (precision) plotted against the proportion of reported simulated outliers among all simulated outliers (recall) for increasing p values up to FDR < 0.05 (OUTRIDER) or decreasing absolute Z scores (PCA and PEER). Plots are provided for four simulated amplitudes (by row with simulated absolute Z scores of 2, 3, 4, and 6 from top to bottom) and for three simulation scenarios (by column from left to right: aberrantly high and low counts, aberrantly high counts, and aberrantly low counts). The read counts were controlled for gene covariation with OUTRIDER (green), PCA (orange), or PEER (blue). The ranking of outliers was bootstrapped to yield 95% confidence bands.

Furthermore, we investigated the performance of an alternative strategy to detect outliers that can be easily implemented in DESeq2⁸ or edgeR.¹⁹ We controlled for known confounders as covariates and used Cook’s distance, as done in DESeq2,⁸ and the Pearson residuals, as done in edgeR,¹⁹ instead of the p value to score outliers (Supplemental Material and Methods). For the Kremer dataset, these known confounders were sex and the body site inferred from the HOX gene set.⁷ For the GTEx dataset, these were sex, age, and ischemic time. Both methods gave the same rankings because Pearson residual and Cook’s distance are monotonically related. However, both showed much poorer precision-recall curves than the PCA, PEER, and OUTRIDER alternatives on the Kremer and GTEx datasets (Figures S6 and S7).

At the FDR = 0.05 cutoff, the recall was limited between 0.3 for injected outliers with |Z| = 2 and 0.8 for injected outliers with |Z| = 6 (Figure 4). To investigate which type of outliers were not recovered, we stratified the precision-recall curves by mean expression levels of the gene. Figure S8 shows the results for the |Z| = 4 scenario with over- and underexpressed genes, which is representative of the other |Z| levels and scenarios. Here, we observed that in the lowest bin (mean count < 57; Figure S8B), the p value ranking outperformed the Z score ranking. This is due to the instability of Z scores for small counts. Nevertheless, we observed an increase in the precision for the Z score ranking with increasing mean count. Altogether, this underlines the importance of using p values instead of Z scores, particularly for genes with low expression levels.

Applying OUTRIDER to the Kremer dataset resulted in a recall of 61 outliers (9.9%) identified by Kremer et al. (Figure S9A) on the basis of the 48 previously undiagnosed samples.⁷ Additionally, OUTRIDER detected 85 new expression outliers, of which 54 were downregulated. OUTRIDER was able to recall all six pathogenic events (three expression outliers, one mono-allelic expression, and two splicing defects) validated by Kremer et al. Despite the fact that CLPP (MIM: 601119) and MCOLN1 (MIM: 605248) were only reported as having splice defects by Kremer et al., the resulting loss of expression was detected by OUTRIDER. On the Kremer dataset, PCA called 3.8 more outliers than OUTRIDER and missed two pathogenic events, and PEER called 7.8 times more outliers than OUTRIDER and missed one pathogenic event (Figure S9B). These results are consistent with the results from the simulations.

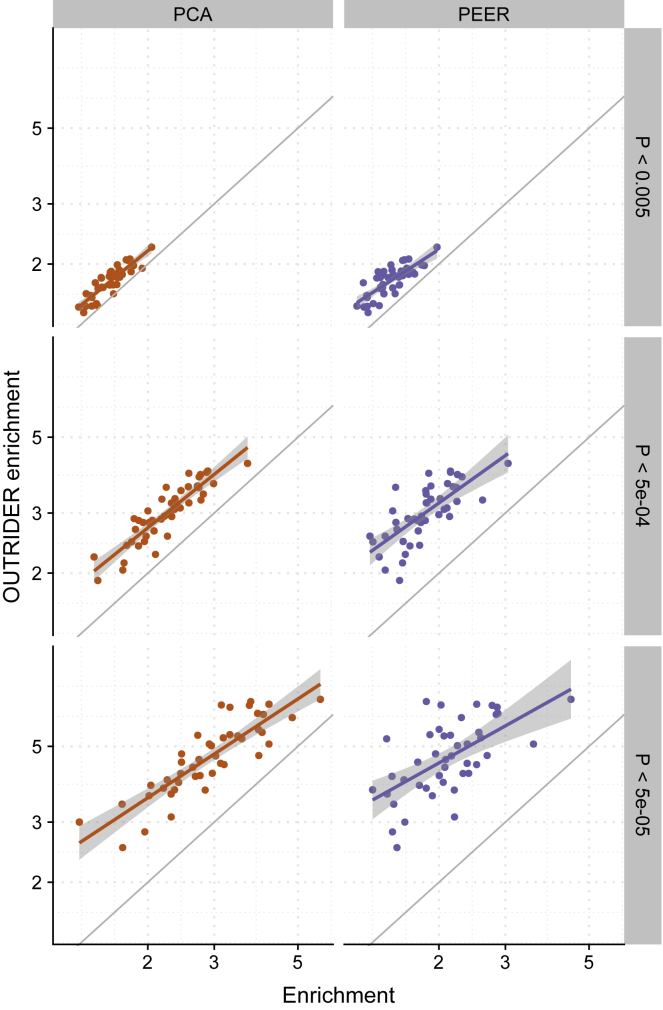
To further evaluate the performance of OUTRIDER on experimental data, we assessed the enrichment of rare variants among outliers, given that previous studies linked rare variants with aberrant gene expression.^{10, 33} We applied OUTRIDER, as well as PCA and PEER, on all GTEx tissues and computed enrichments of rare variants within expression outliers on the basis of different p value cutoffs (Figure 5). We considered variants with a MAF < 0.05 and a predicted moderate or high impact according to the VEP,³² which gave a manageable amount of variants to handle and covered the variants causing nonsense-mediated decay and transcript amplification. OUTRIDER showed higher enrichments than PCA and PEER across all tissues for three different nominal p value cutoffs (Figure 5). Furthermore, the highest enrichment was achieved with the highest cutoff regardless of the control method (Figure 5). We observed the same trend when we calculated the enrichment on the basis of Z score cutoffs (Figure S10). Overall, OUTRIDER had across all cutoffs the highest enrichment in comparison with the other approaches, including the original Z scores computed by Li et al. in a PEER-based approach.¹⁰ Only in the case of |Z| > 5 did OUTRIDER and PCA achieve similar enrichment scores.

Figure 5.

OUTRIDER SNP Enrichment

Enrichment of rare (MAF < 0.05) moderate- and high-impact variants (according to the VEP) computed on genes found to be aberrantly expressed by OUTRIDER is plotted against enrichments computed on genes found to be aberrantly expressed by PCA or PEER for all GTEx tissues with three different p value cutoffs.

Finally, we investigated the sensitivity of sample size. To this end, we used the Kremer dataset and the six known pathogenic events to estimate the required dataset to reach significance. We monitored the nominal p values of the pathogenic events after randomly removing samples from the dataset and keeping the samples containing these six pathogenic outliers (Figure S11). As expected, the p values slowly increased toward 1 as sample size decreased. Although OUTRIDER had overall lower p values than PCA and PEER, our approach needed 60 samples to recall the majority of the pathogenic events. PCA and PEER, which had similar p values, needed at least 80 samples to recover most of those events.

Discussion

We have introduced OUTRIDER, an end-to-end solution for identifying expression outliers within RNA-seq data, controlling for hidden confounders in an automated fashion, and providing estimates of statistical significance. OUTRIDER combines an autoencoder that allows for automatically controlling technical and biological variations among genes and a statistical test based on the NB distribution. OUTRIDER outperformed preceding methods in recalling simulated outliers and pathogenic outliers from a rare-disease cohort and yielded outliers with a higher enrichment of rare variants in a cohort of healthy donors. OUTRIDER has two advantages over preceding methods. First, it computes p values that can be adjusted to control the FDR. Z-score-based approaches lack p values, so the setting of cutoffs is arbitrary. Second, the model’s parameters are automatically fitted through optimization of the model’s ability to recall corrupted counts. OUTRIDER is implemented and made available as an R Bioconductor package. The package allows for a full analysis to be made with only a few lines of code and provides plotting functionality for visualizing the results. Furthermore, the package comes along with a comprehensive vignette guiding the user through a typical analysis.

We implemented OUTRIDER so that it is not restricted to the provided autoencoder, allowing the statistical test to be used with alternative methods modeling the expected counts. In particular, PCA and PEER can be substituted for the autoencoder. Alternatively, autoencoders with additional layers could be employed to capture nonlinear relationships. However, the analysis of correlations post-control did not suggest the need for a more complex autoencoder. This is consistent with the study of Way and Greene, who modeled covariations in RNA-seq samples by using a single-layer autoencoder.¹⁵ Independently of the way the counts are controlled, OUTRIDER offers functionality for finding the optimal encoding dimension by using a modeling scheme based on corrupted count data. An advantage of this hyperparameter optimization is that no manual intervention is needed.

Current standard methods used to control for covariations of RNA-seq data across individuals include PEER^{10, 34, 35} or PCA.³⁶ Both approaches assume the input data to be log-normal distributed, which is suboptimal for count data. To directly work on counts instead of transformed counts, we introduced OUTRIDER, which uses the NB distribution, a more suitable distribution for count data. On simulated counts, we observed better inference of the expected counts by using OUTRIDER than by using either PEER or PCA on log-transformed counts. This was especially true for genes with low expression and for underexpressed outliers. Altogether, this resulted in better rankings of outliers and a significantly improved enrichment of rare variants among expression outliers detected in RNA-seq read counts. This improved model for RNA-seq read counts could potentially boost studies that are distinct from outlier calling and rely on controlling for covariations. In particular, mapping of expression quantitative loci could be attempted but was not investigated in this study. Also, one could in principle extend OUTRIDER to include known confounding covariates, for instance, by adding them along with the latent factors before the decoder layer. However, the robustness and the practical added value of such a hybrid approach would have to be investigated.

In differential expression analyses, outlier detections are used for obtaining robust estimators of fold changes and within-group variance. Notably, DESeq2⁸ uses Cook’s distance to flag extreme observations, whereas edgeR¹⁹ uses Pearson residuals to downweight the impact of extreme observations on the model. This idea is distinct from our aim of assessing the significance of outliers. Nonetheless, these or similar robust estimators³⁷ could be incorporated into OUTRIDER to improve the estimation of expected counts. This would, however, come with the disadvantage of adding more parameters and a certain degree of circularity.

We have not addressed the handling of replicate samples because we do not expect them to be performed by default in diagnostic settings. The reason for this is that expression outliers are events that show strong effects; therefore, replicates are not essential for detecting these types of events. If a putative disease-causing event, such as an aberrantly expressed gene, is detected, follow-up experiments involving assays complementary to RNA-seq are preferred over replicates to establish the functional link of the event to the disease.^{1, 5} In contrast, if an RNA-seq sample is suspected to have a technical problem, a new library can be prepared, and the new data are substituted for the former. Neither of these situations results in replicate samples. When replicates are available, users can exclude the replicated samples from the fit to not lower the specificity. Afterward, they can combine the p values of replicate samples by using Fisher’s method of combining p values³⁸ by assuming independence of the read counts conditioned on the expected means predicted by the autoencoder. The same strategy could be applied for pseudo-replicate samples, such as affected individuals of the same family. More elaborated statistical tests have been designed to leverage family structures in normal population studies.^{34, 39} These methods are based on the normal distribution and log-transformed counts. Our comparison to PEER and PCA suggests that these methods could be improved by a count distribution such as the NB.

Another related issue is the modeling of multiple samples from the same individual. In analyzing GTEx samples, Li et al. have shown that some outliers are shared across multiple tissues for a given individual.¹⁰ If tissues are fitted jointly, it can be difficult to detect outliers shared across tissues because they might be modeled as expected covariation by the autoencoder and because the large number of outlier data points could lead to a poor fit of the NB distribution. In a rare-disease diagnostic setting, we do not expect a large number of tissues to be available per individual. To study the GTEx data, we suggest following the strategy of Li et al.,¹⁰ i.e., to fit a model per tissue and summarize results across tissues with a meta-analysis strategy. We have performed the tissue-wise p value computations with OUTRIDER and provide them on our website (Web Resources).

In general, the autoencoder controlling scheme and the count modeling approach benefit from additional sequencing data; the more data of unrelated individuals that can be combined, the better the estimation of the typical patterns within a population will be. This holds true when the overall data are equally distributed across population structures or sequencing protocols because each sample is assumed to be an independent representative of the whole population. This assumption was partially violated in this study because RNA-seq datasets such as GTEx comprise >85% individuals of European descent.²¹ Such overrepresentation of a given population in the dataset is disadvantageous in general, and additional samples from underrepresented groups would be especially beneficial. More testing is needed for assessing whether our strategy for controlling counts can control for different data sources, including data from multiple sequencing platforms or control datasets. The ability to control for different protocols would enable count data to be combined from multiple sources. This would allow studies with a few samples to merge their results with sources such as the publicly available GTEx dataset.²¹ Currently, the best practice is to use the same cell-handling and library-preparation protocol that reduces the analyzable dataset and therefore limits the statistical power. According to a power analysis, 50–60 samples were enough for OUTRIDER to recall most of the known pathogenic events, which are mainly a complete loss of expression. To allow for the detection of more subtle outliers, a larger cohort size is recommended.

The initial aim of developing OUTRIDER was to create a framework for detecting expression outliers for RNA-seq data in a rare-disease diagnostic setting. OUTRIDER will be useful for the identification of potentially disease-causing genes in individuals for whom current methods, such as WES and WGS, only provide variants of unknown significance. However, our approach is not restricted to such data or experiments. Our re-analysis of the tissues of the GTEx dataset¹⁰ indicates that OUTRIDER can provide a more accurate set of expression outliers than existing methods also for studying expression outliers in normal populations. In principle, OUTRIDER could model any count data derived from next-generation sequencing. Our approach could also be applied to data such as DNA accessibility from ATAC-seq reads. In this case, promotor regions or enhancers would be used as features instead of gene bodies. Finally, the methodology of OUTRIDER could be adapted to detect splicing outliers or outliers in proteomics or metabolomics.

Declaration of Interests

The authors declare no competing interests.

Published: November 29, 2018

Web Resources

• GTEx Portal, https://www.gtexportal.org/home

• OMIM, http://www.omim.org

• OUTRIDER, http://bioconductor.org/packages/OUTRIDER/

• OUTRIDER analysis pipeline, https://github.com/gagneurlab/OUTRIDER-analysis/

• OUTRIDER supplemental data, https://i12g-gagneurweb.in.tum.de/public/paper/OUTRIDER/