Abstract
In this paper, we develop a general Bayesian clinical trial design methodology, tailored for time-to-event trials with a cured fraction in scenarios where a previously completed clinical trial is available to inform the design and analysis of the new trial. Our methodology provides a conceptually appealing and computationally feasible framework that allows one to construct a fixed, maximally informative prior a priori while simultaneously identifying the minimum sample size required for the new trial so that the design has high power and reasonable type I error control from a Bayesian perspective. This strategy is particularly well suited for scenarios where adaptive borrowing approaches are not practical due to the nature of the trial, complexity of the model, or the source of the prior information. Control of a Bayesian type I error rate offers a sensible balance between wanting to use high-quality information in the design and analysis of future trials while still controlling type I errors in an equitable way. Moreover, sample size determination based on our Bayesian view of power can lead to a more adequately sized trial by virtue of taking into account all the uncertainty in the treatment effect. We demonstrate our methodology by designing a cancer clinical trial in high-risk melanoma.
Keywords: Bayesian type I error rate, clinical trial design, cure rate, power prior, sample size determination
1 ∣. INTRODUCTION
Survival models that accommodate a cured fraction in the studied population, known collectively as cure rate models, have become popular tools for analyzing data from oncology clinical trials. These models have been used for studying time-to-event data for various types of cancers, including breast cancer,1,2 leukemia,3 multiple myeloma,4 prostate cancer,5 and melanoma.6 When a survival curve plateaus in the right tail after an adequate follow-up period, cure rate models can be more advantageous than alternative models such as the Cox proportional hazards model or the piecewise exponential model. In this paper, we develop a general Bayesian clinical trial design methodology, tailored to the promotion time cure rate model,7-9 that is designed for a scenario in which a previously completed clinical trial (ie, a historical trial) is available to inform the design and analysis of the new one. The primary purpose of the proposed methodology is to provide a framework that allows one to construct a fixed, maximally informative prior a priori while simultaneously identifying the minimum sample size required for a new trial such that the design has high power and reasonable type I error control from a Bayesian perspective.
The Food and Drug Administration requires that all proposed trial designs demonstrate reasonable type I error control. Traditionally, frequentist type I error control (or supremum type I error control) has been the focus. This is currently the case for the Center for Drug Evaluation and Research but no longer for the Center for Devices and Radiological Health where fully Bayesian designs are more common.10 For a design to exhibit Frequentist type I error control, the type I error rate cannot exceed some prespecified level at the value of the parameter defining the boundary between the null and alternative hypotheses. For unbiased statistical tests, this ensures that the type I error rate is controlled for every possible null value of the parameter. The requirement to have frequentist type I error control is not an issue for Bayesian designs based on objective priors (ie, designs using noninformative priors that are designed to yield good frequentist operating characteristics). However, when one has informative prior information, if they wish to control the supremum type I error rate strictly (and the prior is viewed as data that are conditioned on for analysis), all prior information must be discarded. This property is provable for simple cases, and the results we present in this paper further illustrate this fact. Thus, while the authors would strongly agree that type I error control is an important operating characteristic for trial designs that make use of information arising external to the trial, we would also argue that in the presence of credible information regarding a treatment effect, compromises with respect to the traditional approach to type I error control are warranted.
In contrast to the traditional approach to controlling type I errors, the traditional approach to powering a trial (ie, controlling type II errors) is much less conservative. A common procedure is to select a plausible (though often optimistic) effect and then determine the sample size required to have some specified level of power to detect the non-null treatment effect. Even if the chosen parameter values are relatively likely based on historical data (eg, maximum a posteriori [MAP] estimates), there is often significant uncertainty in these values that goes unaccounted for in the design. Not acknowledging the plausibility of a small treatment effect during design can result in a study that is dramatically underpowered. A design approach that can naturally take into account all the uncertainty in the treatment effect for the determination of power is desirable.
To address the aforementioned challenges, we propose a trial design methodology based on Bayesian versions of type I error rate and power. These Bayesian operating characteristics are defined as weighted averages of the type I error rate and power associated with fixed parameter values with weights determined by prespecified sampling prior distributions over the null and alternative parameter spaces. We develop a framework for using one's belief about the treatment effect (determined based on the historical data, expert opinion, or both) to construct the needed sampling priors and compare designs based on several possible choices in the context of time-to-event trials with a cured fraction. Specifically, we develop “default” sampling priors that are constructed through conditioning the historical trial posterior distribution on either the null or alternative hypothesis, extensions to the default priors that allow removal of implausible effects by truncating the tails of the default priors, and sampling priors where the treatment effect distribution is elicited independently of the historical data. We note that the Center for Devices and Radiological Health will consider designs that control a Bayesian version of the type I error rate when the historical data are of high quality,11 although the design may still be required to control the supremum type I error rate at an acceptable level (eg, twice the nominal Bayesian type I error rate).
Our results demonstrate that when one permits control of a Bayesian type I error rate, a significant fraction of the prior information can be incorporated into the design and analysis of the new trial. However, borrowing the prior information is not free. When the historical data posterior distribution is highly informative, the size of the future trial must be large to justify borrowing a significant amount of the available information. This is the inherent compromise in the proposed methodology. Furthermore, when one designs a trial to have high Bayesian power, the sample size required will generally be larger than the sample size required for a similarly designed trial that is powered to detect the most likely treatment effect suggested by the historical data. Hence, our Bayesian design methodology is not simply a mechanism for reducing sample size in the new trial, but rather a procedure for using the information from the historical trial to inform all aspects of the new trial's design and analysis while assuring reasonable type I error control.
The trial design methodology we present in this paper is essentially a Bayesian sample size determination method. There is a large literature on Bayesian sample size determination. Much of it focuses on simple models including 1 and 2 sample normal or binomial models, linear regression models, and generalized linear models. Comparatively, little has been done with survival models for right-censored data. Notable exceptions are Ibrahim et al12 and Chen et al.13,14 Bayesian designs that control type I error in some sense have been recently considered in Ibrahim et al12 and Chen et al.13-15 The approach to type I error control considered by those authors is closely related to frequentist type I error control and the associated sampling priors can be viewed as limiting cases of the truncated priors that we develop in this paper. Bayesian analysis of univariate cure rate models has been considered in Chen et al,9,18,19 Ibrahim et al,16,17 and Tsodikov et al.20 For the proposed methodology, information from the historical trial is borrowed by way of the power prior.21 Although Bayesian analysis using cure rate models with the power prior has been previously investigated, the work to date has only focused on analysis with no attention being paid to clinical trial design. Frequentist trial design using cure rate models was considered in Bernardo and Ibrahim.22
The rest of this article is organized as follows: In Section 2, we develop a stratified promotion time cure rate model, discuss some properties, and derive the corresponding likelihood. In Section 3, we discuss the power prior and an asymptotic approximation to the marginal posterior distribution for the treatment effect that obviates the need for MCMC in design simulations. In Section 4, we formally define Bayesian versions of type I error and power and discuss the simulation process for determining an appropriate set of controllable characteristics for the new trial. In Section 5, we present a detailed example design using data from a previously published clinical trial. We close the paper with some discussion in Section 6.
2 ∣. THE PROMOTION TIME CURE RATE MODEL
We consider a flexible promotion time cure rate model where the promotion time distribution is allowed to vary over levels of a stratification variable. The unstratified version was proposed originally by Yakovlev et al,7 and a thorough treatment from the Bayesian perspective was first given in Chen et al.9 The model is typically motivated through a latent competing risks framework. Using notation similar to Ibrahim et al,17 we let Ni denote the number of “metastasis-competent” tumor cells for subject i that remain after initial treatment. We assume that Ni follows a Poisson distribution with parameter , where zi is a binary treatment indicator; xi = (xi1, …, xip is a p × 1 vector of baseline covariates that includes an intercept; γ is the treatment effect; and β = (β1, …, βp) is a p × 1 vector of regression coefficients corresponding to the covariates. Further, let Zij denote the random time for the jth metastasis-competent tumor cell to produce detectable disease in subject i. Hence, one can view Zij as the “promotion time” for the jth metastasis-competent tumor cell. Conditional on Ni, the Zij are assumed to be independent and identically distributed according to the cumulative distribution function F (z ∣ ψsi = 1 – S (z∣ ψsi), where si is the stratum to which subject i belongs and ψs represents the promotion time model parameters for stratum s. The time to detectable cancer relapse for subject i is given by Yi = min {Zij, 0 ≤ j ≤ Ni}, where Zi0 = ∞. Suppressing the notation for covariates, the marginal probability of survival past time y for subject i is given as follows:
| (1) |
The quantity in (1) is a marginal probability in the sense that it is not conditional on the latent number of metastasis-competent tumor cells or even whether or not the subject is cured. We note that Sp (∞ ∣ θi, ψsi) = P(Ni = 0 ∣ θi) = exp(−θi) > 0 and hence Sp (y ∣ θi, ψsi) is not a proper survival function. The form in (1) shows that the time to relapse is influenced by the initial number of metastasis-competent tumor cells as well as their rate of progression. The subdensity corresponding to (1) is given by
with corresponding subhazard given by
| (2) |
From (2), it is apparent that the promotion time formulation of the cure rate model leads to a proportional hazards structure for the subhazard. The probability of survival past time y conditional on subject i being uncured is given by
| (3) |
and the corresponding hazard is
| (4) |
Where
We note that S* (y ∣ θi, ψsi) is a proper survival function and, accordingly, h* (y ∣ θi, ψsi) is a proper hazard function. Unfortunately, (4) does not have a proportional hazards structure since P(Yi < ∞ ∣ Yi > y, θi, ψsi) depends on y. It is straight forward to show that h* (y ∣ θi, ψsi) is increasing in θi, which is desirable. This means that increasingly negative values of the regression parameters are associated with a greater cured fraction and lower hazard in the uncured population.
As pointed out in Chen et al,9 the promotion time cure rate model has a connection with the standard mixture cure rate model.23 It can be readily seen from (3) that
Thus, the promotion time cure rate model can be written as a standard mixture cure rate model with cured fraction exp(−θi) and survival function S* (y ∣ θi, ψsi). For the induced standard mixture cure rate model, the cured fraction and the survival function both depend on θi, which is an uncommon specification for that model. One can also see that any standard mixture cure rate model can be written as a promotion time cure rate model.
The promotion time cure rate model may be preferred over the standard mixture cure rate model for several reasons as noted in Chen et al.9 First, the model has the natural biological motivation described above. Second, the model has a proportional hazards structure leading to convenient interpretation of covariate effects on the subhazard. The standard mixture cure rate model does not have a proportional hazards structure when the cured fraction is modeled as a function of covariates using a logistic regression function. Third, the model can be efficiently sampled with a Gibbs sampler. Lastly, unlike the standard mixture cure rate model, the promotion time cure rate model yields a proper posterior distribution under a wide class of noninformative improper priors for the regression coefficients, including a uniform improper prior.
To complete the specification of the survival model in (1), we must specify a distribution for the promotion times. Common choices are the Weibull distribution (fully parametric) and piecewise exponential distribution (semiparametric). Analysis with each of these promotion time models is discussed in detail in Ibrahim et al17 for the case where a single promotion time model is shared by all subjects. For the design example in Section 4, we use a separate Weibull model for each level of the stratification variable. We note that our choice to allow stratification in the model for the promotion times is uncommon. However, the model selection results discussed in Section 4 suggest that this approach can lead to better fit compared with the more standard modeling framework.
Following Ibrahim et al,17 the “complete” data likelihood based on a Weibull model for the promotion times can be written as follows:
where ξ = {γ, β, ψs : s = 1, …, S} is the set of all parameters in the model; ψs = {λs, αs} is the set of Weibull promotion time model parameters for stratum s; and D = {(yi, νi, zi, xi, si) : i =1, …, n} is the observed data with νi representing whether an event occurred for subject i. In what follows, we will represent the collection of all promotion time model parameters by ψ to simplify exposition. Bayesian analysis of the promotion time cure rate model has been primarily performed using the complete data likelihood with the Ni being treated as missing data and therefore included in the Gibbs sampler with the parameters. This approach was proposed in Chen et al9 and described in full detail in Ibrahim et al.17 The benefit of such an approach is that the full conditionals for all parameters are log-concave (based on the priors discussed in Ibrahim et al17) and so the parameters can be easily sampled with rejection sampling or adaptive rejection sampling methods.24 The Ni have closed-form full conditionals for direct Poisson sampling. Alternatively, one can analytically sum out the latent Ni variables to obtain the “observed” data likelihood:
| (5) |
For MCMC analysis based on the observed data likelihood, the regression parameters still have log-concave full conditionals, and they can be sampled efficiently with the same techniques mentioned above. Unfortunately, the full conditionals for the parameters in the promotion time model will not necessarily have log-concave full conditionals, and so we recommend slice sampling 25 for those parameters. Even though slice sampling does not directly sample from the full conditionals, since the sampling procedure using the marginal likelihood does not condition on the Ni quantities, this approach is likely more efficient than the Gibbs sampler using the complete data likelihood. In our analyses, when MCMC was used, we fit the model using a slice sampler.
3 ∣. THE POWER PRIOR AND THE POSTERIOR DISTRIBUTION
The form of the power prior21,26 using the observed data likelihood formulation in (5) is as follows:
| (6) |
where 0 ≤ a0 ≤ 1 is a fixed scalar parameter; D0 = {(yj, νj, zj, xj, sj) : j = 1, …, n0} is the historical data; is the likelihood for the historical data; and π0(ξ) is an initial noninformative prior. When a0 = 0, the historical data are essentially discarded and the power prior reduces to the initial prior. In contrast, when a0 = 1, the power prior corresponds to the posterior distribution from an analysis of the historical data using the initial prior. For intermediate values of a0, the weight given to the historical data is diminished to some degree leading to a prior that is more informative than the initial prior but less informative than using the historical trial posterior as the prior for the new trial. The power prior provides a natural mechanism for transforming historical data into a subjective prior. One only needs to specify the initial prior π0(ξ) and elicit a value for a0 for the prior to be fully specified. In our approach, the value of a0 is determined a priori so that the design yields desirable Bayesian power while controlling the Bayesian type I error rate.
Aside from its simple construction, a second appealing characteristic of the power prior with fixed a0 is that analysis using it with a noninformative initial prior is closely related to weighted maximum likelihood analysis where historical trial subjects are given a weight of a0 and new trial subjects are given a weight of one. To see this connection, note that the logarithm of the posterior (ignoring the normalizing constant) is given by
which is approximately equal to the weighted log-likelihood based on the combined trials with wi = 1 for new trial subject i and w0,j = a0 for historical trial subject j. The only difference between the logarithm of the posterior distribution and the weighted log-likelihood is the term log π0(ξ), which has little influence since π0(ξ) is noninformative by construction.
When the sample sizes for the new and historical trials are reasonably large, the Bayesian central limit theorem assures us that
| (7) |
where is the weighted maximum likelihood estimator (MLE) from a joint analysis of both trials with weights described above and is the relevant diagonal element of the inverse of the observed information matrix for the weighted log-likelihood evaluated at the weighted MLE. One can then obtain weighted MLEs and perform approximate Bayesian inference by appealing to the asymptotic normal approximation in (7). This approach is appealing since, for many data models, off-the-shelf software is available for weighted maximum likelihood analysis. A slightly better approximation can be obtained by replacing the weighted MLEs with MAP estimates and using a normal approximation (ie, Laplace approximation) to the full posterior. The only drawback of this approach is that some custom programming will likely be required to obtain the MAP estimates through a Newton-Raphson–type procedure. In our experience, either technique is sufficient to allow accurate estimation of the Bayesian type I error rate and power when the initial prior is sufficiently noninformative. Note that the approximations just described result in an approximate multivariate normal posterior distribution for ξ. One must simply extract the appropriate mean and variance component to approximate the marginal posterior distribution for γ. It is important to note that the marginal posterior distribution for some of the nuisance parameters (eg, components of ψ) may not be approximately normal. This is not problematic since all that is needed during design is for the approximation in (7) to be accurate. In rare cases where it is of interest to evaluate inference on parameters other than γ when designing the new trial, a simulation-based design approach that uses MCMC to fit the model may be necessary.
Using the normal approximation in (7), the posterior probabilities needed for our analyses are trivial to compute. Consider the null and alternative hypotheses H0 : γ ≥ 0 and H1 : γ < 0, respectively. One can approximate the posterior probability P (γ < 0 ∣ D, D0, a0) as follows:
| (8) |
where Zi and Z2 are standard normal variables. For the case where and are weighted MLEs, the right-hand side of (8) is precisely 1 minus the 1-sided P value from a weighted maximum likelihood analysis of the combined trials.
4 ∣. A SIMULATION-BASED APPROACH TO BAYESIAN DESIGN OF A SUPERIORITY TRIAL
The null and alternative hypotheses for a superiority trial in the context of the cure rate model may be written as H0 : γ ≥ 0 and H1 : γ < 0, respectively. We will accept H1 if P (γ < 0 ∣ D, D0, a0) is at least as large as some critical value ϕ. During design, one examines various possible values for the number of subjects to be enrolled in the new trial (n), the duration of the new trial (T), a0, and ϕ in search of a set of values that provide sufficient Bayesian power while controlling the Bayesian type I error rate at no more than α(s). We refer to the set of values {n, T, a0, ϕ} as the key controllable trial characteristics.
In general, T should be at least as large as the duration of time it is expected to take for the survival curves to plateau. Thus, it is natural to fix T for design purposes based on the time when the survival curves approximately level off in the historical trial. This is the approach we suggest in practice and the approach taken in our example in Section 5. We further restrict the search space for the key controllable trial characteristics by fixing ϕ = 1 – α(s). This choice of ϕ is justified by the fact that the posterior probability P (γ < 0 ∣ D, D0, a0 = 0) (based on an analysis of the new trial data without incorporating historical data) will be asymptotically uniformly distributed when γ = 0 and the model is correct. In other words, the posterior probability of the alternative hypothesis has the same asymptotic behavior as a frequentist P value when there is a single test of a true null hypothesis. Accordingly, rejecting the null hypothesis when P (γ < 0 ∣ D, D0, a0 = 0) ≥ ϕ = 1 – α(s) will provide frequentist type I error control at level α(s) (asymptotically). A heuristic justification of these ideas follows directly from the relationship in (8) but more rigorous exposition on the connection between the so-called posterior probabilities of the half-space and frequentist P values can be found in Dudley and Haughton.27 In this light, one can view our design procedure as starting out with a size α(s) frequentist hypothesis test (based on taking a0 = 0) and then modifying the test by borrowing increasing amounts of information from the historical trial until it functions as a size α(s) hypothesis test with respect to the Bayesian type I error rate.
4.1 ∣. Formal definition of the Bayesian type I error rate and power
To formally define the Bayesian type I error rate and Bayesian power, we first introduce the concepts of sampling and fitting priors that were formalized in Wang and Gelfand 28 and extended in Chen et al15 to investigate Bayesian type I error and power. Let and be the null and alternative sampling priors and let π(f) (ξ) be the fitting prior. A sampling prior specifies a probability distribution for the model parameters conditional on a particular hypothesis being true. In the context of the cure rate model, the null sampling prior will give zero weight to values of ξ having a negative γ component and the alternative sampling prior will give zero weight to values of ξ having a nonnegative γ component. The sampling priors are referred to as such because they are used to sample parameter values in the simulation-based estimation procedure for the Bayesian type I error rate and power. This procedure is detailed in section 4.6. The fitting prior π(f) (ξ) is simply the prior used to analyze the data. In our case, π(f) (ξ) is the power prior given in (6).
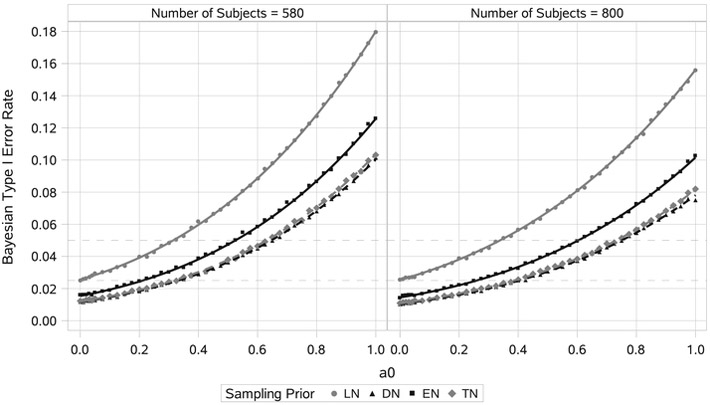
FIGURE 6.
Estimated Bayesian type I error rate curves and point estimates for sample sizes n = 580 and n = 800. Each point estimate was based on 100 000 simulated trials. Curves were estimated separately for each null sampling prior using least-squares regression based on cubic polynomials in both a0 and n with interactions (R2 > 0.999). DN, default null; EN, elicited null; LN, limiting-case truncated null; TN, truncated null
For a fixed value of ξ, define the null hypothesis rejection rate as
where 1 {P (γ < 0 ∣ D, D0, a0) ≥ ϕ} is an indicator that we accept H1 based on the posterior probability P (γ < 0 ∣ D, D0, a0) determined by the observed data D. For null values of ξ, the quantity r (ξ ∣ D0, a0) is the type I error rate, and for alternative values of ξ, it is the power. For “chosen” null and alternative sampling priors, the Bayesian type I error rate α(s) and Bayesian power 1 – β(s) are defined as
| (9) |
and
| (10) |
The expectation in (9) is with respect to the null sampling prior distribution for ξ and the expectation in (10) is with respect to the alternative sampling prior distribution for ξ. We note that Chen et al15 define the Bayesian type I error rate and power in terms of the null and alternative prior predictive distribution of the data, and , respectively. Our presentation here simply changes the order of integration to highlight the fact that the Bayesian type I error rate and Bayesian power are weighted averages of the quantities based on fixed values of ξ. Our recipe for simulation-based estimation of the Bayesian type I error rate and Bayesian power follows closely the presentation in Chen et al.15
4.2 ∣. Sampling prior elicitation
The Bayesian type I error rate and power become well defined upon specification of null and alternative sampling priors. Of course, there is no one “correct” choice for the sampling priors. The guiding principle for selection of these priors is that they should provide weights for null and alternative parameter values that are sensible to all stakeholders of the new trial. In sections 4.3 to 4.5, we introduce several possible choices for the sampling priors, and we compare properties of designs based on them in Section 5. Specifically, we develop “default” sampling priors that are constructed through conditioning the historical trial posterior distribution on either the null or alternative hypothesis, extensions to the default priors that remove implausible effects by truncating the tails of the default prior distributions (ie, “truncated” sampling priors), and sampling priors where the treatment effect distribution is elicited independently of the historical data (ie, “partially elicited” sampling priors).
Before delving into specifics regarding each type of sampling prior, it is important to understand how one might choose from among them for a given design problem. Figure 1 provides a flow diagram designed to guide practitioners in this effort. The first question that must be answered is whether it is plausible that the investigational therapy could be inferior to the control. In some cases, inferiority will be plausible, but in other cases, it may not be. If inferiority is simply not plausible, then perhaps the most appropriate null sampling prior would place all mass on null values of ξ associated with no treatment effect (ie, γ = 0). This null sampling prior can be viewed as a limiting-case truncated null (LN) sampling prior defined in section 4.4. If inferiority of the investigational therapy is plausible, then one can entertain a null sampling prior that spreads mass over the plausible subspace of null the parameter space. A natural way to construct such a null sampling prior is to simply condition the historical trial posterior distribution on the null hypothesis (eg, condition on γ ≥ 0). This method of construction results in a fully data-driven sampling prior. It is a reasonable strategy to the extent that one finds the tail of the null sampling prior distribution for the treatment effect plausible. Obviously, this determination cannot be made in general. If the tail is not plausible, it may be necessary to truncate it at the worst plausible treatment effect. As an alternative to constructing a data-driven null sampling prior, it may be possible to elicit the null sampling prior from expert opinion. This type of approach provides maximum flexibility for controlling the relative weight of null parameter values but requires an external source of knowledge that is separate from the historical data.
FIGURE 1.
Flow diagram for null sampling prior selection [Colour figure can be viewed at wileyonlinelibrary.com]
The process of choosing an acceptable alternative sampling prior will likely be less contentious than that of choosing a null sampling prior. The default alternative (DA) sampling prior seeks to let the historical data fully determine the relative weighting of alternative parameter values for power analysis. We presume that in most applications, the historical trial data will suggest that there is treatment efficacy, but the evidence will not be overwhelming (hence the desire to conduct another trial). In these cases, the DA prior will put significant mass on small treatment effects. If resources permit, sample size calculation based on power analysis using the DA sampling prior would make the most sense for design problems where any treatment effect would be clinically meaningful. A truncated alternative (TA) sampling prior would be preferred in cases where a minimal clinically meaningful treatment effect is known or when the default prior has a tail that is too optimistic regarding treatment efficacy. As with the null sampling prior case, one can always elicit an alternative sampling prior for the treatment effect parameter independently of the historical data.
4.3 ∣. Default sampling priors
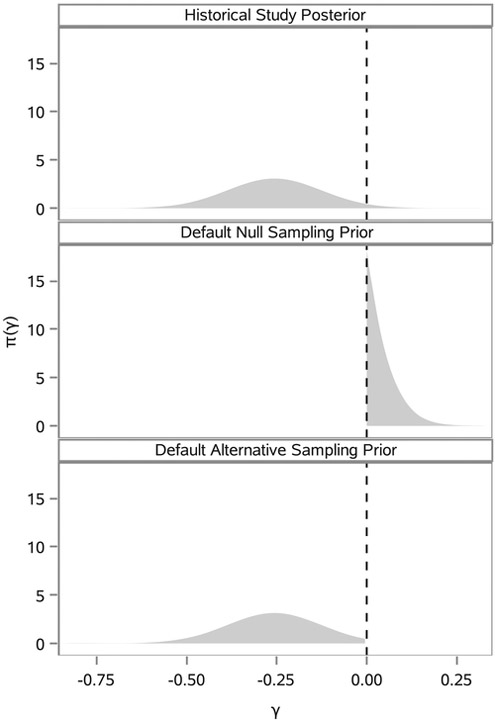
The default sampling priors arise naturally when the entirety of one’s knowledge about ξ comes by way of the historical data. After collecting that data, one’s belief about the parameters is determined by π (ξ ∣ D0) = π0 (ξ ∣ D0, a0 = 1) (ie, the power prior with no discounting). In light of this, reasonable choices for the null and alternative sampling priors are (the historical posterior given that H0 is true) and (the historical posterior given that H1 is true). Figure 2 illustrates the marginal posterior distribution for γ based on our analysis of the historical trial data used in the example application in Section 5 along with the corresponding default null (DN) and alternative marginal sampling priors for γ.
FIGURE 2.
π (γ ∣ D0) and corresponding default marginal sampling priors
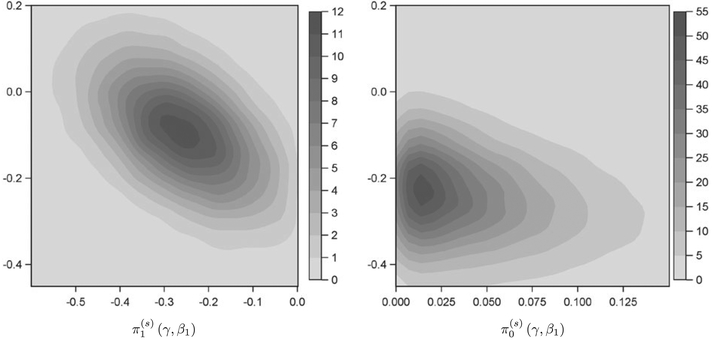
Conditioning on the null or alternative hypothesis induces changes in the joint distribution for ξ with the predominant change being to the distribution for the intercept parameter β1 in the model for the cured fraction. Figure 3 presents a kernel density estimate of the bivariate null and alternative sampling prior densities for the treatment effect parameter γ and the intercept parameter β1 in the model for the cured fraction based on our analysis of the historical trial data used in the example application in Section 5. It is clear that if one assumes there is a null effect (ie, γ ≥ 0), that implies larger negative values for β1 (ie, a higher cured fraction in the control arm). By defining the sampling priors as we have, we preserve the stochastic relationships between the treatment and nuisance parameters that are implied by the historical data under the assumption that a particular hypothesis is true. A standard alternative approach is to specify a point-mass (PM) alternative sampling prior with all parameters set to their posterior means. For the null sampling prior, the value of γ is simply set to zero with other parameters remaining unchanged. This approach is only sensible when γ is independent of the remaining parameters in ξ given D0. As Figure 3 shows, this is not the case.
FIGURE 3.
Bivariate kernel density estimate for default alternative and null sampling priors. The horizontal axis corresponds to the treatment effect parameter γ, and the vertical axis corresponds to the intercept parameter β1 in the model for the cured fraction. The vertical axes are presented on the same scale to facilitate qualitative comparison of β1 values
4.4 ∣. Truncating the default sampling priors
The default sampling priors previously described are sensible and automatic. However, there will be instances where it is desirable to modify the default priors. For example, researchers may deem it impossible for the investigational therapy to “decrease” the cured fraction by more than a certain amount relative to the control. In addition, researchers may want to compute power over a restricted alternative space that rules out implausibly large or clinically insignificant effect sizes. In this section, we introduce intuitive modifications to the default sampling priors that still preserve the stochastic relationships between the treatment and nuisance parameters that are implied by the historical data.
The truncated null (TN) sampling prior is defined as . As γ0,u → 0, less and less information can be borrowed from the historical data if the Bayesian type I error rate is to be controlled at level α(s). When γ0,u = 0 (ie, the limiting case), Bayesian type I error control is similar to frequentist type I error control in that no information can be borrowed if the Bayesian type I error rate is to be controlled at level α(s). The fundamental difference between frequentist and Bayesian type I error control is that the latter implicitly assumes the nuisance parameters in the cure rate model for the new trial are consistent with the posterior distribution from the historical trial after conditioning on the appropriate null event (ie, ≤ γ ≤ γ0,u). In other words, Bayesian type I error control is defined based on a specific null sampling prior distribution for the nuisance parameters, whereas frequentist type I error control is based on a constraint that must be satisfied for any value of the nuisance parameters.
The TA sampling prior is defined as . If “any” positive treatment effect would be clinically meaningful and resources permit, we recommend leaving γ1,u = 0 for power analysis. Otherwise, γ1,u can be set to the smallest clinically meaningful treatment effect. Secondary power analyses can be performed using more optimistic choices. If desired, one may choose a value for γ1,l to reflect skepticism regarding a large positive treatment effect.
4.5 ∣. Partially elicited sampling priors
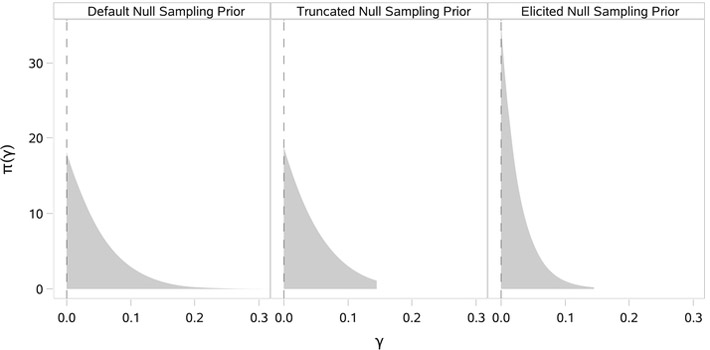
The TN sampling priors provide a mechanism for ruling out implausible treatment effects in the definition of the Bayesian type I error rate or power. However, this strategy only provides one avenue for customization of the sampling priors. Unfortunately, it does not provide a mechanism by which one can adjust the relative weighting of plausible treatment effects. In contrast, direct elicitation of a sampling prior distribution for the treatment effect parameter provides complete control. Focusing on elicitation of a null sampling prior for the treatment effect, one straightforward approach is to specify a worst-case treatment effect γ0,u and choose a parametric distribution with support restricted to [0, γ0,u] with rate of decay in the tail such that . This type of strategy was used to construct the elicited null (EN) sampling prior depicted in Figure 4, which is presented alongside a pair of default and TN sampling priors for comparison purposes. The EN sampling prior has exponential decay (λ = 35), shifting substantially more weight to smaller values of γ compared with either the default or TN sampling priors. Elicited alternative sampling priors for the treatment effect could be constructed using an analogous procedure.
FIGURE 4.
Default, truncated, and elicited null sampling priors for the treatment effect γ
In the case of partially elicited sampling priors for ξ, the key idea is that one will elicit a marginal distribution for the treatment effect parameter γ independently of the historical data. It is still important to construct a sampling prior distribution for the nuisance parameters that is realistic given the assumptions regarding the treatment effect. This historical data should be used for this purpose. An EN sampling prior for ξ is defined as , where is a sampling prior distribution over the null space for γ and π (β, ψ ∣ D0, γ) is the historical posterior distribution for the nuisance parameters β and ψ conditional on γ. An elicited alternative sampling prior could be analogously defined.
Drawing samples from the default and truncated sampling priors only requires basic rejection sampling. One simply needs to use MCMC to fit the cure rate model to the historical data using the initial prior and reject samples that are inconsistent with the supported parameter space associated with the sampling prior under consideration. Sampling from partially elicited sampling priors requires a 2-step procedure. First, one must draw samples from the elicited (marginal) sampling prior distribution for the treatment effect. In the case of the EN sampling prior described above, this is accomplished by direct sampling from an exponential distribution with rate parameter λ = 35 and rejecting any samples that are larger than 0.15. For each sampled value of γ, a corresponding value for β and ψ is obtained by using MCMC to draw a single sample from π (β, ψ ∣ D0, γ) (ie, by fitting the cure rate model to the historical data treating γ as fixed in the likelihood and initial prior).
4.6 ∣. Simulation-based estimation of the Bayesian type I error rate and power
In this section, we describe the simulation process that is used to estimate the Bayesian type I error rate and power. Let B be the number of simulation studies to be performed. To estimate the Bayesian type I error rate, we proceed as follows:
Sample ξ(b) from the null sampling prior (ξ).
- Given ξ(b), simulate the new trial data D(b). This can be done using the following steps (for each subject):
- Simulate xi, zi, and si based on the chosen distribution for the covariates, randomization fraction, and distribution for the stratification variable.
- Calculate and simulate Ni ~ Poisson (θi).
- Simulate Zij ~ F (z ∣ ξsi independently for j = 1, …, Ni, and calculate zi = min (Zij : j = 0, …, Ni) with Zi0 = T.
- Simulate the time to censorship, denoted as ci, according to the chosen distribution. If only administrative censoring is entertained, then set ci = T.
- iv. If Zi < ci, then set yi = zi and νi = 1; otherwise, set yi = ci and νi = 0.
Update the fitting prior π(f) (ξ) based on the likelihood for the simulated data to obtain the posterior distribution π(ξ∣D(b),D0, a0), and calculate the posterior probability of the alternative hypothesis P(γ < ∣ D(b), D0, a0).
- Compute the null hypothesis rejection indicator for simulated trial b:
- Approximate the Bayesian type I error rate with the empirical null hypothesis rejection rate:
Steps 1 to 4 are first repeated for b = 1, …, B to obtain the outcome for each simulated trial, and then step 5 combines the results to estimate the Bayesian type I error rate. The process for estimating Bayesian power is identical. One simply needs to use the alternative sampling prior in place of the null sampling prior in the algorithm above.
5 ∣. BAYESIAN DESIGN OF A SUPERIORITY TRIAL IN HIGH-RISK MELANOMA
The E1690 trial was conducted to assess the use of Interferon Alfa-2b (IFN) as an adjuvant therapy following surgery for deep primary or regionally metastatic melanoma. A detailed report on the trial was given in Kirkwood et al.6 Briefly, E1690 was a prospective, randomized, 3-arm clinical trial designed to evaluate the efficacy of high-dose IFN for 1 year and low-dose IFN for 2 years relative to observation (OBS) in high-risk melanoma patients using relapse-free survival (RFS) and overall survival endpoints. We restrict our attention to the high-dose IFN regimen and consider the design of a subsequent trial to further evaluate the efficacy of IFN using an RFS endpoint.
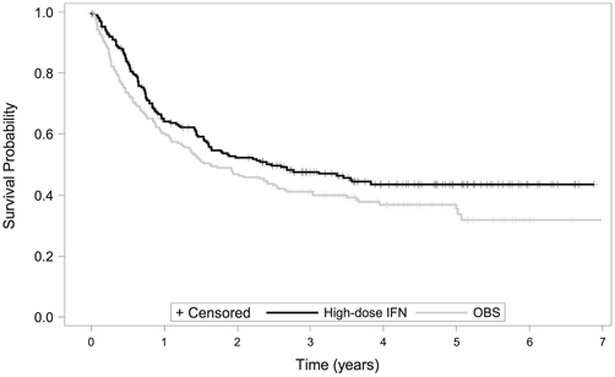
Patients enrolled in the E1690 trial had histologically proven American Joint Committee on Cancer stage IIB or stage III primary or recurrent regional nodal involvement from cutaneous melanoma without evidence of systemic metastatic disease (disease stages 1, T4cN0; 2, T1-4pN1cN0; 3, T1-4cN1; and 4, T1-4N1 recurrent). The randomization and primary analysis were stratified by disease stage and the number of positive nodes at lymphadenectomy. The primary analysis was based on a stratified log-rank test, and the 2-sided P value was .054. There were 215 subjects and 114 relapses observed in the high-dose IFN group and 211 subjects and 126 relapses observed in the OBS group. Among the set of subjects who did not experience relapse, the median observation time was over 4 years. Figure 5 presents the Kaplan-Meier estimator for the survival curves for the high-dose IFN and OBS groups. Note the clear plateau appearing at approximately 4 years. This suggests a cure rate model is appropriate for these data. Overall, the data from E1690 suggest a treatment benefit with respect to RFS, but the evidence is not overwhelming by traditional statistical criteria.
FIGURE 5.
Kaplan-Meier curves for the E1690 high-dose interferon Alfa-2b (IFN) and observation (OBS) groups
In the E1690 data, disease stage and the number of positive nodes at lymphadenectomy were highly predictive of RFS, and so we consider these characteristics for inclusion in the design model to help ensure exchangeability of subjects across the 2 trials. To formally choose the design model, we compared a variety of promotion time cure rate models that adjusted for these covariates in the model for the cured fraction and/or stratified by them in the model for the promotion times. Table 1 lists the 6 best fitting models according to the deviance information criterion.29 In addition to the 6 models shown in Table 1, a variety of other models were considered including models that adjusted for disease stage in the model for the cured fraction and models that stratified by treatment and/or the number of positive nodes at lymphadenectomy in the promotion time model. We selected the model having the best fit according to deviance information criterion for design. The design model had separate Weibull promotion time distributions for disease stages 1 to 2 and for disease stages 3 to 4. The model for the cured fraction included an intercept, a treatment indicator, an indicator for having 2 to 3 positive nodes, and an indicator for having ≥4 positive nodes. Table 2 presents the posterior mean, the posterior standard deviation, and 95% highest posterior density interval for all parameters based on an analysis of the E1690 data using independent normal priors on the regression parameters (mean zero and variance 105) and independent gamma priors on the promotion time model parameters (shape parameter and inverse scale parameter equal to 10−5). Summaries for the default sampling priors are also included for comparison. We note the highest posterior density interval for the treatment effect puts a nonnegligible amount of mass in both the null region and the alternative region although the evidence clearly favors treatment efficacy (about 97.5% of the mass is in the alternative region).
TABLE 1.
DIC for 6 best candidate design models
| Stratification variables | Cured fraction model covariates | Weibull DIC | Exponential DIC |
|---|---|---|---|
| Stages 1-2 and 3-4 | Treatment, 2-3 nodes, ≥4 nodes | 1011.317 | 1011.557 |
| Stages 1, 2, 3, and 4 | Treatment, 2-3 nodes, ≥4 nodes | 1014.234 | 1015.368 |
| Stages 1-2 and 3-4 | Treatment, ≥2 nodes | 1017.845 | 1017.530 |
Abbreviation: DIC, deviance information criterion.
TABLE 2.
Summaries for historical trial posterior and default sampling priors
| Posterior |
Default Alternative |
Default Null |
||||
|---|---|---|---|---|---|---|
| Parm | Mean (SD) | HPD | Mean (SD) | HPD | Mean (SD) | HPD |
| γ | −0.26 (0.13) | (−0.51, 0.00) | −0.26 (0.12) | (−0.49,−0.02) | 0.05 (0.04) | (0.00, 0.14) |
| β1 | −0.09 (0.12) | (−0.33, 0.14) | −0.09 (0.12) | (−0.33, 0.14) | −0.25 (0.11) | (−0.46,−0.04) |
| β2 | 0.23 (0.17) | (−0.11, 0.57) | 0.23 (0.17) | (−0.10, 0.57) | 0.21 (0.17) | (−0.13, 0.54) |
| γ3 | 0.77 (0.16) | (0.46, 1.08) | 0.77 (0.16) | (0.46, 1.08) | 0.77 (0.16) | (0.46, 1.08) |
| λ1 | 1.20 (0.13) | (0.94, 1.47) | 1.20 (0.13) | (0.94, 1.47) | 1.21 (0.13) | (0.96, 1.48) |
| α1 | 1.06 (0.07) | (0.92, 1.21) | 1.06 (0.07) | (0.92, 1.21) | 1.06 (0.07) | (0.92, 1.20) |
| λ2 | 0.48 (0.09) | (0.30, 0.65) | 0.48 (0.09) | (0.30, 0.65) | 0.49 (0.09) | (0.32, 0.66) |
| α2 | 0.67 (0.08) | (0.52, 0.82) | 0.67 (0.08) | (0.52, 0.82) | 0.67 (0.08) | (0.51, 0.82) |
Abbreviations: HPD, highest posterior density; SD, standard deviation.
Our primary purpose in this section is to compare and contrast designs based on different choices of sampling priors. To illustrate how the choice of null sampling prior impacts the amount of information that can be borrowed from the historical trial, we considered 4 possibilities: the DN sampling prior, the TN sampling prior that imposes the constraint that γ ≤ 0.15, a partially EN sampling prior that imposes the constraint that γ ≤ 0.15 but has more rapid tail decay, and the LN sampling prior that places all mass at γ = 0. For the DN, TN, and EN sampling priors, the marginal sampling prior distribution for the treatment effect is shown in Figure 4. The constraint that γ ≤ 0.15 corresponds to an assumption that the investigational therapy is unlikely to decrease the cured fraction in melanoma patients with ≤ 1 positive node at lymphadenectomy by more than 5% relative to the control regimen.
To illustrate how the choice of alternative sampling prior impacts power, we considered 3 possibilities: a PM alternative sampling prior with parameters set to the DA sampling prior means in Table 2, the TA sampling prior that imposes the constraint that −0.41 ≤ γ ≤ −0.14, and the DA sampling prior. For the TA sampling prior, the constraint that −0.41 ≤ γ corresponds to an assumption that the investigational therapy is unlikely to increase the cured fraction in melanoma patients having ≤1 positive node at lymphadenectomy by more than 15% relative to the control regimen. The constraint that γ ≤ −0.14 might be applied if an increase of less than 5% in the cured fraction for the same patients would not be clinically meaningful given other considerations (eg, toxicity).
For design simulations, we assumed uniform enrollment over a period of 3 years and a trial duration of T = 6.5 years measured from the time of enrollment of the first subject. The only censoring was administrative at the time of trial completion. To maintain a plausible relationship between cancer stage and number of positive nodes at lymphadenectomy, we simulated these characteristics by sampling linked pairs with replacement from the E1690 dataset. We also used 1:1 randomization. We considered designs that controlled the Bayesian type I error rate at 2.5% (α(s) = 0.025).
The first step in the design process is to find the largest value of a0 that results in Bayesian type I error control for each sample size being considered. To do this, we performed simulations studies using n ranging from 560 to 860 with a step size of 10 with each n being matched with an array of a0 values covering the interval [0-1]. For each combination of n and a0, we estimated the Bayesian type I error rate based on 100 000 simulated trials. Next, to interpolate and smooth type I error rates for values of n and a0, we performed multiple linear regression of the estimated type I error rates onto both n and a0 (considering degree-3 polynomials in both n and a0 with interactions). For the 4 null sampling priors we considered, the smallest R2 value was >0.999, indicating a near perfect fit in all cases. Figure 6 presents the estimated Bayesian type I error rate as a function of a0 for each null sampling prior for the sample sizes n = 560 and n = 860.
It is clear from Figure 6 that no information can be borrowed from the historical trial when the Bayesian type I error rate is defined using the LN sampling prior. As was noted in section 4.4, Bayesian type I error control using the LN sampling prior is closely related to frequentist type I error control. In contrast, we see that when the Bayesian type I error rate is defined using the DN sampling prior, one is able to borrow a meaningful amount of information from the historical trial without surpassing the 2.5% type I error rate threshold (a0 = 0.32 for n = 560, a0 = 0.42 for n = 860). Referring back to Figure 4, we note that the TN and DN sampling priors were quite similar with respect to the distribution for the treatment effect parameter. Given that fact, it is not surprising that the amount of borrowing they permit is also quite similar. This suggests that the TN sampling prior need only be considered when one wishes to truncate the DN sampling prior tails in such a way as to reallocate a substantial portion of the mass.
The proposed methodology is not designed to control the supremum I error rate at any specific level. However, we acknowledge that reasonable control of the supremum type I error rate (ie, when γ = 0) is a desirable property. Regulatory bodies will likely be interested in this even if other stakeholders are not. The worst-case performance of a design (with respect to type I errors) can be evaluated by identifying n and a0 pairs based on a Bayesian type I error rate defined using a chosen null sampling prior (eg, the DN sampling prior) and then evaluating the Bayesian type I error rate for those same pairs using the LN sampling prior, which places all mass on γ = 0. Figure 7 presents the estimated supremum Bayesian type I error rate when the amount of borrowing is determined using the DN and EN sampling priors as well as the case where no borrowing (NB) is performed (ie, a0 = 0). In our opinion, the supremum Bayesian type I error rate is quite reasonable for both the DN and EN sampling priors for this historical trial dataset. If so inclined, one could approach this design problem by directly limiting the supremum Bayesian type I error rate at some elevated level (eg, 5%). This latter strategy is precisely the approach one would take if they were unwilling to entertain inferiority of the investigational therapy (see Figure 1).
FIGURE 7.
Wost-case performance of designs with a0 determined using the default null (DN) and elicited null (EN) sampling priors compared with a design with no borrowing (ie, a0 = 0). For scatter plot points corresponding to n = 560 and n = 860, the identified values of a0 (above) and the estimated supremum Bayesian type I error rate (below) are annotated for reference
Having identified how much information can be borrowed from the historical trial for each sampling size under consideration based on the Bayesian type I error rate restriction, the second step in the design process is to identify the minimum sample size required to ensure adequate Bayesian power based on the chosen alternative sampling prior. Table 3 presents estimated Bayesian power for sample sizes ranging from 560 to 860 for several combinations of null and alternative sampling priors. Power analysis where the amount of borrowing was determined using the TN sampling prior is omitted because of similarity with power analysis where the amount of borrowing was determined using the DN sampling prior. For comparison sake, we also performed power analysis for a design with NB. The results in Table 3 are based on a similar interpolation and smoothing strategy as described above.
TABLE 3.
Bayesian power estimates for select sample sizes
| NB |
EN |
DN |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| n | DA | TA | PM | a0 | DA | TA | PM | a0 | DA | TA | PM |
| 560 | 0.62 | 0.66 | 0.68 | 0.21 | 0.67 | 0.72 | 0.75 | 0.32 | 0.69 | 0.75 | 0.79 |
| 570 | 0.62 | 0.67 | 0.69 | 0.21 | 0.67 | 0.73 | 0.76 | 0.33 | 0.70 | 0.76 | 0.79 |
| 580 | 0.62 | 0.67 | 0.70 | 0.21 | 0.68 | 0.73 | 0.76 | 0.33 | 0.70 | 0.76 | 0.80 |
| 590 | 0.63 | 0.68 | 0.70 | 0.21 | 0.68 | 0.74 | 0.77 | 0.33 | 0.71 | 0.77 | 0.81 |
| 600 | 0.63 | 0.69 | 0.71 | 0.22 | 0.68 | 0.74 | 0.78 | 0.34 | 0.71 | 0.77 | 0.81 |
| 610 | 0.64 | 0.69 | 0.72 | 0.22 | 0.69 | 0.75 | 0.78 | 0.34 | 0.72 | 0.78 | 0.82 |
| 620 | 0.64 | 0.70 | 0.72 | 0.22 | 0.69 | 0.75 | 0.79 | 0.34 | 0.72 | 0.78 | 0.82 |
| 630 | 0.65 | 0.70 | 0.73 | 0.22 | 0.70 | 0.76 | 0.80 | 0.35 | 0.72 | 0.79 | 0.83 |
| 640 | 0.65 | 0.71 | 0.74 | 0.22 | 0.70 | 0.76 | 0.80 | 0.35 | 0.73 | 0.79 | 0.84 |
| 650 | 0.65 | 0.71 | 0.74 | 0.23 | 0.70 | 0.77 | 0.81 | 0.35 | 0.73 | 0.80 | 0.84 |
| 660 | 0.66 | 0.72 | 0.75 | 0.23 | 0.71 | 0.77 | 0.81 | 0.36 | 0.73 | 0.80 | 0.85 |
| 670 | 0.66 | 0.72 | 0.76 | 0.23 | 0.71 | 0.78 | 0.82 | 0.36 | 0.74 | 0.81 | 0.85 |
| 680 | 0.66 | 0.73 | 0.76 | 0.23 | 0.71 | 0.78 | 0.83 | 0.36 | 0.74 | 0.81 | 0.86 |
| 690 | 0.67 | 0.73 | 0.77 | 0.24 | 0.72 | 0.79 | 0.83 | 0.37 | 0.74 | 0.82 | 0.86 |
| 700 | 0.67 | 0.74 | 0.77 | 0.24 | 0.72 | 0.79 | 0.84 | 0.37 | 0.75 | 0.82 | 0.87 |
| 710 | 0.68 | 0.74 | 0.78 | 0.24 | 0.72 | 0.79 | 0.84 | 0.37 | 0.75 | 0.82 | 0.87 |
| 720 | 0.68 | 0.74 | 0.79 | 0.24 | 0.73 | 0.80 | 0.85 | 0.38 | 0.75 | 0.83 | 0.87 |
| 730 | 0.68 | 0.75 | 0.79 | 0.24 | 0.73 | 0.80 | 0.85 | 0.38 | 0.76 | 0.83 | 0.88 |
| 740 | 0.69 | 0.75 | 0.80 | 0.25 | 0.73 | 0.81 | 0.86 | 0.38 | 0.76 | 0.83 | 0.88 |
| 750 | 0.69 | 0.76 | 0.80 | 0.25 | 0.74 | 0.81 | 0.86 | 0.39 | 0.76 | 0.84 | 0.89 |
| 760 | 0.69 | 0.76 | 0.81 | 0.25 | 0.74 | 0.81 | 0.86 | 0.39 | 0.77 | 0.84 | 0.89 |
| 770 | 0.70 | 0.77 | 0.81 | 0.25 | 0.74 | 0.82 | 0.87 | 0.39 | 0.77 | 0.85 | 0.90 |
| 780 | 0.70 | 0.77 | 0.82 | 0.25 | 0.75 | 0.82 | 0.87 | 0.40 | 0.77 | 0.85 | 0.90 |
| 790 | 0.70 | 0.77 | 0.82 | 0.26 | 0.75 | 0.83 | 0.88 | 0.40 | 0.77 | 0.85 | 0.90 |
| 800 | 0.71 | 0.78 | 0.83 | 0.26 | 0.75 | 0.83 | 0.88 | 0.40 | 0.78 | 0.85 | 0.91 |
| 810 | 0.71 | 0.78 | 0.83 | 0.26 | 0.76 | 0.83 | 0.88 | 0.41 | 0.78 | 0.86 | 0.91 |
| 820 | 0.71 | 0.78 | 0.84 | 0.26 | 0.76 | 0.84 | 0.89 | 0.41 | 0.78 | 0.86 | 0.91 |
| 830 | 0.71 | 0.79 | 0.84 | 0.27 | 0.76 | 0.84 | 0.89 | 0.41 | 0.78 | 0.86 | 0.92 |
| 840 | 0.72 | 0.79 | 0.84 | 0.27 | 0.76 | 0.84 | 0.89 | 0.42 | 0.79 | 0.87 | 0.92 |
| 850 | 0.72 | 0.79 | 0.85 | 0.27 | 0.77 | 0.84 | 0.90 | 0.42 | 0.79 | 0.87 | 0.92 |
| 860 | 0.72 | 0.80 | 0.85 | 0.27 | 0.77 | 0.85 | 0.90 | 0.42 | 0.79 | 0.87 | 0.92 |
Abbreviations: DA, default alternative; DN, default null; EN, elicited null; NB, no borrowing; PM, point mass; TA, truncated alternative.
A comparison of the power analyses associated with NB suffices to illustrate the conservative nature of the DA (or TA) sampling prior compared with the PM alternative sampling prior. The NB design that uses the PM alternative prior for power analysis is essentially equivalent to a traditional frequentist design that uses an optimistic effect size to compute power. For that design, we see that 70% Bayesian power is obtained with a sample size of 580. In contrast, 70% Bayesian power requires sample size of 620 for the TA sampling prior and a sample size of 770 for the DA sampling prior. Thus, performing a power analysis that acknowledges the full amount of uncertainty in the treatment effect (ie, using the DA sampling prior) or at least more uncertainty (ie, using the TA sampling prior) results in an appreciably larger sample size. Focusing on the power analysis based on the TA sampling prior, one can compare the implications of increasingly liberal Bayesian type I error control. When the type I error rate restriction is based on the EN sampling prior, a sample size of 720 (a0 = 0.24) is required to have 80% Bayesian power to detect a non-null treatment effect. When the type I error rate restriction is based on the DN sampling prior, the required sample size falls to 650 (a0 = 0.35).
6 ∣. DISCUSSION
In this paper, we have developed a framework for clinical trial design in the presence of historical data. The proposed methodology allows one to a priori determine a fixed, maximally informative prior while simultaneously identifying the minimum sample size required for a new trial subject to Bayesian type I error and power requirements. To develop a clinical trial design methodology that seeks to borrows information from a historical trial (or any other external source of information), one must decide on 2 key features of the design: (1) the operating characteristics to which the design must adhere in the presence of borrowing and (2) the mechanism through which the prior information will be borrowed. There is not 1 correct choice in either case. There are simply choices and their justifications. For our development, we settled on Bayesian type I error control and Bayesian power as the primary operating characteristics of interest because these constructs allow for the seamless incorporation of one's belief about the parameters through specification of null and alternative sampling priors. In particular, the authors find controlling the Bayesian type I error rate based on the DN sampling prior (for example) to be more appealing than simply allowing the supremum Bayesian type I error rate to be elevated by a specified amount, as the latter strategy makes essentially no use of the prior information in determining what null effects are plausible. In addition, Bayesian power is a natural companion criteria that is ideally suited for design problems in which historical data inform the treatment effect.
When exploring different mechanisms for borrowing the prior information, it became apparent to the authors that the pool of existing methodology (be it Bayesian or frequentist) is not well suited to address the challenges of the design problem we have considered. Existing approaches can be broadly categorized into 2 classes of methods: (1) meta-analytic methods that attempt to let the statistical model determine or at least influence the amount of information borrowed from the historical trial and (2) methods that use interim looks at the data and a statistic that measures prior-data conflict to determine whether the prior information should be used.
For the first class of methods, commonly applied statistical tools include hierarchical/random effects models and hierarchical priors. When the prior information consists of a single historical trial (or even just a few trials), these approaches are strongly influenced by the choice of hyperpriors (which must be informative). To ensure that designs based on these approaches have reasonable operating characteristics (whatever they may be), the hyperpriors must be tuned using large-scale simulation studies that are more computationally demanding than the approach we have proposed, especially for hierarchical priors. Unless the model being entertained is quite simple, the aforementioned challenges make these methods impractical for this design problem. The second class of methods are not well suited for time-to-event trials where inference is based on the cured fraction. This is because these trials are traditionally fixed length and require a relatively long follow-up period in order to accurately characterize the cured fraction. Thus, shortening the length of the trial by virtue of borrowing prior information is simply not feasible. Of course, fewer subjects could be enrolled initially in anticipation of borrowing a certain amount of prior information. However, in instances where less information is actually borrowed, enrolling and following up on more subjects would be necessary to maintain adequate power. This, of course, would greatly increase the length of the trial compared with a traditional trial, making this approach equally unappealing. Moreover, for both classes of methods, the authors are unaware of any general software that can be used to design clinical trials in the presence of historical data for advanced statistical models such as cure rate regression models. Rather than attempting to tune a complicated procedure that adjusts the amount of information borrowed from the historical trial one way or another in real-time, we find it operationally and conceptually much easier to simply discount the prior information a priori to the point at which one can live with the consequences of using it even if it is inconsistent with the truth. This type of strategy can be applied for virtually any design problem, included time-to-event trials with a cured fraction. The logistical complexity of implementing the trial, once designed, is no greater than that of running a traditional nonadaptive clinical trial.
Exploring designs that borrow information on a treatment effect parameter using a Bayesian type I error rate based on the DN sampling prior is still an active topic of research for the authors. While the E1690 trial provides an interesting example of a highly informative historical trial dataset, we are actively exploring the use of this methodology for datasets with a mild to moderate level of informativeness. Our results thus far suggest that this design strategy tends to strongly penalize highly informative datasets such that the resulting design is similar to cases where the historical data are less informative. A illustration of this property is provided in Appendix S1.
In this paper, we have made use of null sampling prior distributions for the entire parameter vector ξ but acknowledge that the key parameter of interest is the treatment effect γ. Having a plausible null sampling prior distribution for the nuisance parameters is helpful for estimating characteristics of the design that are of secondary importance (eg, the expected number of events or the expected time until a certain number of events have been accrued). The approach that we have taken makes the implicit assumption that, if in fact the null hypothesis is true, the nuisance parameters for the new trial model are no more inconsistent with the historical data than what is implied by conditioning on 0 ≤ γ ≤ γ0,u for the chosen value of γ0,u. Like any assumption, it may not hold. If the nuisance parameters in the new trial model are even more inconsistent with the historical data than what is implied by the conditioning event, borrowing information through the nuisance parameters may lead to inflation of type I error rates beyond what Bayesian type I error control is intended to permit. One straightforward protection that avoids any pitfalls related to null sampling prior misspecification is to only borrow information through the treatment effect parameter. That is to say, one can allow the nuisance parameters {β, ψ} to differ between the new trial and historical trial likelihoods, electing to use what is called a partial-borrowing power prior.12 This protection can be implemented with little reservation provided one is willing to sacrifice the ability to synthesize information on the nuisance parameters across trials. However, in the case where one desires to borrow information on all parameters, and when both the historical and new trials have approximately balanced sample size across treatment groups, the impact of null/alternative sampling prior misspecification for the nuisance parameters on type I error control/power is minimal (though such misspecification will obviously result in biased estimates of the nuisance parameters). We illustrate this robustness property with a simulation study focusing on the type I error rate under null sampling prior misspecification in Appendix S2.
The design framework we have proposed uses the historical data to define the sampling priors and in the fitting prior. This should not be misconstrued as a double use of the data. In actuality, there is only one use of the historical data and that is to define the sampling priors. Our use of the historical data in the fitting prior is superficial. It is simply one reasonable method for generating a size α(s) hypothesis test with respect to the Bayesian type I error rate. One could just as easily fix a0 = 0 in the power prior and modify the posterior probability critical value ϕ (making it smaller) until an appropriately sized test is obtained. In fact, these 2 approaches result in equivalent hypothesis tests in terms of type I error control and power. For example, the designs from Section 4 based on the DN and DA sampling priors with n = 560, 660, 760, and 860 (a0 = 0.325, 0.357, 0.391, and 0.422, respectively) can be obtained using a0 = 0 by taking ϕ = 0.95, 0.948, 0.945, and 0.943, respectively. Our approach uses a standard evidence threshold (ie, ϕ = 1 – α(s)) and effectively requires that the total amount of evidence in the combined dataset must exceed the standard threshold. The approach that modifies the critical value effectively requires a reduced level of evidence in the new trial alone. We chose to incorporate the historical data into a power prior because, by doing so, we are able to quantify the fraction of the prior information that is used in the design which is appealing.
All design computations were performed using the posterior approximation described in Section 3 on the Longleaf computing cluster at the University of North Carolina at Chapel Hill. The accuracy of the asymptotic posterior approximation is demonstrated via simulation in Appendix S3. Analyses were performed using SAS/STAT® software and R30 using underlying C++ code through Rcpp.31 Specifically, R was used to fit the cure rate model using MCMC to obtain samples from the null and alternative sampling priors and SAS was used for all other aspects of the design simulations.
Supplementary Material
ACKNOWLEDGMENTS
The authors wish to thank the editor, associate editor, and referees for helpful comments and suggestions, which have led to improvements of this article. This research was partially supported by National Institutes of Health grants #GM 70335 and P01CA142538.
Funding information
National Institutes of Health, Grant/Award Number: 70335 and P01CA142538
Footnotes
SOFTWARE AND DATA
A GitHub repository (https://github.com/psioda/bayes-design-hist-cure-rate) contains the SAS and R programs and other resources needed to reproduce the analyses presented in this paper. All files (SAS data sets, programs, logs, shell scripts, etc) used in that example are provided at https://figshare.com.
Additional supporting information may be found online in the Supporting Information section at the end of the article.
REFERENCES
- 1.Woods L, Rachet B, Lambert P, Coleman M. “Cure” from breast cancer among two populations of women followed for 23 years after diagnosis. Ann Oncol. 2009;20(8):1331–1336. [DOI] [PubMed] [Google Scholar]
- 2.Tsodikov A Semi-parametric models of long- and short-term survival: an application to the analysis of breast cancer survival in Utah by age and stage. Stat Med. 2002;21(6):895–920. [DOI] [PubMed] [Google Scholar]
- 3.Tsodikov A, Loeffler M, Yakovlev A. A cure model with time-changing risk factor: an application to the analysis of secondary leukaemia. A report from the international database on hodgkin's disease. Stat Med. 1998;17(1):27–40. [DOI] [PubMed] [Google Scholar]
- 4.Othus M, Barlogie B, LeBlanc ML, Crowley JJ. Cure models as a useful statistical tool for analyzing survival. Clin Cancer Res. 2012;18(14):3731–3736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zaider M, Zelefsky MJ, Hanin LG, Tsodikov A, Yakovlev A, Leibel SA. A survival model for fractionated radiotherapy with an application to prostate cancer. Phys Med Biol. 2745;46(10):2001. [DOI] [PubMed] [Google Scholar]
- 6.Kirkwood JM, Ibrahim JG, Sondak VK, et al. High-and low-dose interferon alfa-2b in high-risk melanoma: first analysis of intergroup trial e1690/s9111/c9190. J Clin Oncol. 2000;18(12):2444–2458. [DOI] [PubMed] [Google Scholar]
- 7.Yakovlev A, Asselain B, Bardou V, et al. A simple stochastic model of tumor recurrence and its application to data on premenopausal breast cancer. Biometrie et Analyse de Donnees Spatio-Temporelles. 1993;12:66–82. [Google Scholar]
- 8.Yakovlev A Threshold models of tumor recurrence. Math Comput Model. 1996;23(6):153–164. [Google Scholar]
- 9.Chen MH, Ibrahim JG, Sinha D. A new Bayesian model for survival data with a surviving fraction. J Am Stat Assoc. 1999;94(447):909–919. [Google Scholar]
- 10.Food and Drug Administration. Guidance for the Use of Bayesian Statistics in Medical Device Clinical Trials. 2010. Online, Accessed 27 January 2016 [Google Scholar]
- 11.Pennello G, Thompson L. Experience with reviewing Bayesian medical device trials. J Biopharm Stat. 2007;18(1):81–115. [DOI] [PubMed] [Google Scholar]
- 12.Ibrahim JG, Chen MH, Xia HA, Liu T. Bayesian meta-experimental design: evaluating cardiovascular risk in new antidiabetic therapies to treat type 2 diabetes. Biometrics. 2012;68(2):578–586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chen MH, Ibrahim JG, Xia AH, Liu T, Hennessey V. Bayesian sequential meta-analysis design in evaluating cardiovascular risk in a new antidiabetic drug development program. Stat Med. 2014;33(9):1600–1618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chen MH, Ibrahim JG, Zeng D, Hu K, Jia C. Bayesian design of superiority clinical trials for recurrent events data with applications to bleeding and transfusion events in myelodyplastic syndrome. Biometrics. 2014;70(4):1003–1013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chen MH, Ibrahim JG, Lam P, Yu A, Zhang Y. Bayesian design of noninferiority trials for medical devices using historical data. Biometrics. 2011;67(3):1163–1170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ibrahim JG, Chen MH, Sinha D. Bayesian semiparametric models for survival data with a cure fraction. Biometrics. 2001;57(2):383–388. [DOI] [PubMed] [Google Scholar]
- 17.Ibrahim JG, Chen MH, Sinha D. Bayesian Survival Analysis. New York: Springer Science & Business Media; 2001. ISBN 978-0387952772. [Google Scholar]
- 18.Chen MH, Harrington DP, Ibrahim JG. Bayesian cure rate models for malignant melanoma: a case-study of eastern cooperative oncology group trial e1690. J R Stat Soc Ser C (Appl Stat). 2002;51(2):135–150. [Google Scholar]
- 19.Chen MH, Ibrahim JG, Sinha D Bayesian inference for multivariate survival data with a cure fraction. JMultivar Anal. 2002;80(1):101–126. [Google Scholar]
- 20.Tsodikov A, Ibrahim J, Yakovlev A. Estimating cure rates from survival data: an alternative to two-component mixture models. J Am Stat Assoc. 2003;98(464):1063–1078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ibrahim JG, Chen MH. Power prior distributions for regression models. Stat Sci. 2000;15(1):46–60. [Google Scholar]
- 22.Bernardo P, Ibrahim JG. Group sequential designs for cure rate models with early stopping in favour of the null hypothesis. Stat Med. 2000;19(22):3023–3035. [DOI] [PubMed] [Google Scholar]
- 23.Berkson J, Gage RP. Survival curve for cancer patients following treatment. J Am Stat Assoc. 1952;47(259):501–515. [Google Scholar]
- 24.W R Gilks PW. Adaptive rejection sampling for Gibbs sampling. J R Stat Soc Ser C (Appl Stat). 1992;41(2):337–348. [Google Scholar]
- 25.Neal RM. Slice sampling. Ann Statist. 2003;31(3):705–767. [Google Scholar]
- 26.Ibrahim JG, Chen MH, Gwon Y, Chen F. The power prior: theory and applications. Stat Med. 2015;34(28):3724–3749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Dudley RM, Haughton D. Asymptotic normality with small relative errors of posterior probabilities of half-spaces. Ann Statist. 2002;30(5):1311–1344. [Google Scholar]
- 28.Wang F, Gelfand AE. A simulation-based approach to bayesian sample size determination for performance under a given model and for separating models. Stat Sci. 2002;17(2):193–208. [Google Scholar]
- 29.Spiegelhalter DJ, Best NG, Carlin BP, Van Der Linde A. Bayesian measures of model complexity and fit. J R Stat Soc Ser B (Stat Methodol). 2002;64(4):583–639. [Google Scholar]
- 30.Core Team RR: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; 2014. http://www.R-project.org/ [Google Scholar]
- 31.Eddelbuettel D Seamless R and C++ Integration with Rcpp. New York: Springer; 2013. ISBN 978-1461468677. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.