Drug-Drug Interaction Discovery: Kernel Learning from Heterogeneous Similarities

Abstract

We develop a pipeline to mine complex drug interactions by combining different similarities and interaction types (molecular, structural, phenotypic, genomic etc). Our goal is to learn an optimal kernel from these heterogeneous similarities in a supervised manner. We formulate an extensible framework that can easily integrate new interaction types into a rich model. The core of our pipeline features a novel kernel-learning approach that tunes the weights of the heterogeneous similarities, and fuses them into a Similarity-based Kernel for Identifying Drug-Drug interactions and Discovery, or SKID³. Experimental evaluation on the DrugBank database shows that SKID³ effectively combines similarities generated from chemical reaction pathways (which generally improve precision) and molecular and structural fingerprints (which generally improve recall) into a single kernel that gets the best of both worlds, and consequently demonstrates the best performance.

1. Introduction

Drug-drug interactions (DDIs) occur when multiple medications are co-administered and can potentially cause adverse effects on the patients. DDIs have emerged, around the world, as a major cause of hospital admissions, rehospitalizations, emergency room visits, and even death [1]. These numbers are even more stark among older adults, who are more likely to be prescribed multiple medications; the study by Becker et al. [1] identifies that the elderly have an increased risk factor of as much as 8.5 times over the general population. Consequently, DDIs contribute to increased hospital stays and increasing costs of health care, even though up to 50% of these adverse drug effects (ADEs) are preventable [2]. While regulatory agencies such as the U. S. Food and Drug Administration have rigorous approval processes for new drugs, controlled clinical trials do not always uncover all possible drug interactions. For example, the last stage of the FDA approval process involves a Phase III clinical trial, which typically enrolls 1000–5000 individuals, while the drug may be prescribed to millions of patients after approval. In addition to clinical trials, in vitro and in vivo experiments are also used to identify DDIs. However, these approaches are highly labor-intensive, costly and time-consuming. Another factor is that many known DDIs involve medications such as anti-inflammatories or anticoagulants, which are prescribed for common and chronic conditions. Other confounding factors that make studying DDIs a difficult challenge include dosage variations and demographic variability.

All of these challenges have led to a shift in research towards in silico approaches that leverage advances in AI and machine learning [3] for DDI discovery. These approaches for DDI can be viewed in one of two ways.

• The feature-based view, which roughly categorizes the approaches based on the type of DDI features used. These are either text-based (which involves the analysis of abstracts or EHRs) or structure-based (which involve the study of chemical, molecular and pharmacological properties). Our approach is structure-based.

• The algorithm-based view distinguishes between approaches as classification (which treat DDI discovery as a binary classification problem) and clustering (which assume that similar drugs may interact with a same drug). Our approach is a hybrid of both these paradigms.

In our prior work, we have performed ADE discovery and subgroup discovery from electronic health records (EHR) [4] and text-mining of medical journal abstracts [5]. These approaches address the problem of post-marketing surveillance, that is, they seek to exploit the new information available after a drug has been approved and has been prescribed to larger, more diverse populations. In this work, we address pre-trial discovery, that is, we reframe the problem as one of studying drug-drug interactions, rather than taking a single drug and finding adverse events associated with it. The primary motivation is to preemptively identify potential DDI and ADE risks during drug design. As we show in this work, our novel formulation incorporates elements of both classification and similarity based algorithms, which improves discovery as well as explainability. The result is a kernel that we call SKID³ (Similarity-based Kernel for Identifying Drug-Drug interactions and Discovery).

Our problem setting differs from current approaches in three significant ways, that motivated us to develop SKID³:

• A majority of current work focuses on drug-interaction discovery through information extraction, specifically through text mining. These approaches attempt to identify drug interactions from various unstructured text-based sources such as biomedical journals and semi-structured sources such as electronic health records.

  We approach the problem by looking at structured sources of information for insights into drug interactions. That is, we characterize drug similarities using different properties of drugs such as molecular structure and pharmacological interaction pathways. This allows us to pose the DDI discovery problem as a structure prediction [6] task.

• The approaches that do use structural information generally aim to extract explicit vector representations of properties such as 3-d structure, which allows the application of off-the-shelf machine-learning techniques such as support vector machines and kernel learning [7].

  We, instead, analyze structural similarities between drugs in ways that are natural and intuitive to their representation (such as random walks on chemical interaction pathways), rather than forcing an artificial and uninterpretable embedding in a vector space.

• Finally, many current approaches focus on a single type of interaction or similarity, whether it is discovered from text sources or from structural analysis. This is a significant drawback, as this analysis approach ignores the diverse pharmacological facets to drug-drug interaction to look at one (or a few) interaction types in isolation.

  We develop a general and extensible framework that admits heterogeneous characterizations arising from any source including text-based, molecular structure, pharmacological, phenotypic, genomic, therapeutic similarities. This allows us to exploit diverse characterizations of drug similarities from various perspectives, fusing them into one coherent, interpretable model.

We make the following contributions with our proposed solution to address the above limitations:

• We characterize molecular similarity between two drugs using a novel approach: knowledge-refined random walks to measure the reachability of one drug from another; reachability informs the intuition that drugs that are more reachable are more interactive. As far as we are aware, this is the first work on exploiting bias knowledge to characterize drug similarities for DDI discovery.

• We develop a novel framework that combines multiple similarity measures into unified kernel that exploits and fuses their potential. In addition to our novel reachability measure (described above), we also use four other measures that capture molecular and chemical similarities through SMILES strings and MACCS fingerprints.

• We formulate DDI as a kernel-learning problem that fuses heterogeneous similarity measures. Our formulation enables us to treat each similarity as a different view of drug interactions. By fusing similarities from different sources, our formulation aims to reconcile various (molecular, pharmacological etc.,) views into a single model. Further, our formulation incorporates terms to capture both individual as well as neighborhood interactions, leading to greater robustness.

• From a machine-learning standpoint, our formulation is general in that it admits a variety of regularization and loss functions. In this work, we show our approach for a specific formulation that attempts to simultaneously align the optimal kernel with the heterogeneous similarity measures as well as predict the drug-drug interactions.

• From an optimization standpoint, our formulation is a bilinear program, which is a non-convex optimization problem. We illustrate an alternating minimization approach for solving this problem; this approach identifies robust and relevant local solutions for DDI discovery and scales well with the underlying drug database size.

• Our empirical evaluation on a data set constructed from DrugBank uncovers previously known drug-drug interactions with high accuracy. Furthermore, a closer inspection of “false positives” and “false negatives” identified by SKID³ reveals that it has identified drug-drug interactions, missing from Drug-Bank, but existing in other independent sources. This clearly demonstrates the potential of our approach to perform DDI discovery. More specifically, it also offers us a path forward: DDI discovery via active learning with semi-supervised data, which is the real-world problem setting.

The rest of the paper is organized as follows: after reviewing related work in the next section, we define the problem of DDI prediction/discovery. We then present similarity measures and formulate kernel learning for DDI discovery. Next, we present our comprehensive experimental evaluation before concluding the paper by motivating interesting research directions.

2. Related Work

The interactions of a drug can be specified in two ways: (1) the drug has an adverse effect on the human body, called adverse drug events (ADEs), and (2) the drug interacts with another drug called drug-drug interactions (DDIs). Most recent research has focused on finding ADEs from text. Different approaches have been taken in order to identify and discover ADEs in the machine learning community, especially from the natural language processing (NLP) perspective. Chee et al. [8] make use of ensemble classifiers to extract ADEs, while Liu et al. [9] used transductive SVMs to extract ADEs from online health forums. Gurulingappa et al. [10] use NLP with support vector machines (SVMs) to extract ADEs from MEDLINE casereports. Karlsson et al. [11] and Page et al. [4] perform ADE information extraction from EHR data. More recently, Kang et al. [12] took a knowledge-based approach for extracting ADEs from bio-medical text, while Natarajan et al. [13] use Markov logic networks for the same problem.

The problem of DDI prediction and discovery has received far less attention, although similarity-based methods have proven to be very popular. The problem of DDI discovery is a pairwise classification task, which lends itself very well to kernel-based methods [7]. Kernels are naturally suited to representing pairwise similarities, and are constructed directly from the data vectors during pre-processing. Most similarity-based methods for DDI discovery/prediction also use text sources such as biomedical research literature as the underlying data source, and construct NLP-based kernels from these medical documents [14, 15]. Our work differs considerably from such approaches as we do not restrict ourselves to corpus-based NLP kernels for similarity, but rather focus on molecular and structural similarities. It should be noted, however, that our framework can easily support such NLP-based similarities as it is designed to work with heterogeneous similarity measures; this will be an interesting next step.

Fusing multiple kernels has also been studied as a viable approach for DDI discovery. Chowdhury and Lavelli [16] combined linguistic and NLP kernels for the DDIExtraction2011 challenge. While this work used multiple similarities (kernels), they were all constructed from the same data, making their approach homogeneous. The work of Cheng et al. [17] is closest to our heterogeneous approach; they consider four types of drug-drug similarities (phenotypic, therapeutic, structural and genomic). However, a significant difference from our approach is that they treat pairwise similarities directly as features for use with standard machine-learning models such as SVMs and k-nearest neighbor classifiers. This approach destroys the structural and neighborhood information inherent in drug-drug similarity matrices; this means that their model does not capture the true complexity of the DDI manifold. Our method differs from Cheng et al’s as we combine heterogeneous similarities jointly and (locally) optimally, rather than combining kernels into a single feature set.

It should also be noted that other multiple kernel approaches do not learn relative weights of similarities, that is, kernel combination is not a part of the learning process and is performed a priori using fixed weights. This is a significant difference, as our approach learns a kernel as well as relative weights between similarities to show which ones have the most influence on the final kernel. Molecular structure similarity analysis has been studied in the context of DDIs before, where Vilar et al [18] used SMILES code and MACCS fingerprints, with a matrix multiplication method thresholded by a Tanimoto coefficient cutoff to predict new DDIs. Similarity-based kernels were also used in the different task of drug-target interactions prediction [19]. The work of Tatonetti et al. [20], Thomas et al. [21] and Percha et al. [22] are also relevant, though they were applied to drug-target interaction prediction.

From a machine-learning standpoint, our work is closely related to multiple kernel learning, which combines the power of multiple kernels together to learn a linear or non-linear kernel combination. The work of Lanckriet et al. [23] optimizes over a linear combination of multiple kernels through semidefinite programming. In this seminal work, Lanckriet et al., test their method on two data sets and demonstrate that learning a combination of kernels is indeed better than learning single kernels for classification. Bach et al. [24] built upon this work and proposed more efficient algorithms for multiple kernel learning. Sonnenburg et al. [25] further generalized the formulation by posing the multiple kernel learning problem as an semi-infinite linear program that is easier to solve. In recent years, the multiple kernel learning has also been extended to multi-class problems [26] and localized kernels [27], where kernels are learned more precisely using the local information available. These and other methods are discussed by Gönen and Alpaydın [28]. These approaches all rely on the fact that multiple kernel learning can be equivalently cast in terms of the SVM dual; thus these approaches are used for individual classification of training examples. Our framework is considerably different, however, as we are interested in pairwise classification of training examples to identify interactions.

Our framework, instead, relies on kernel alignment, which serves to regularize a kernel learning problem. Specifically, we seek to learn a single kernel from multiple similarities by aligning the kernel with the labels [29] as well as local neighborhood [30]. At a high level, our approach seeks to perform manifold regularization [31] and alignment, to fuse information from various similarity measures into one kernel.

3. Drug-Drug Interactions

Before we define the DDI task, we give terse definitions of various entities involved when two or more drugs interact. The target or drug target is the protein modified by the drug in order to achieve the desired effect once the drug is administered to the body. Enzymes are catalysts that accelerate biological reactions, while transporters are proteins that help drugs reach the intended target [32], and also help in determining whether the drug will be absorbed, distributed or eliminated.

DDIs can be either synergistic (positive, and help increase the effect of the drugs) or antagonistic (negative, cause serious side effects). In this work, we do not differentiate between these two types of interactions. DDIs themselves can be inherently classified into two categories [33]:

• Pharmacokinetic: is the effect that a drug goes through when administered, for example, it is absorbed or metabolized. In case of DDIs, pharmacokinetic refers to the (synergystic or antagonistic) effect of one drug on the other drug’s absorption, distribution, metabolism and excretion when administered simultaneously or within a short time span of one another.

• Pharmacodynamic: is the effect that body goes through when a drug is administered. In case of DDIs, pharmacodynamic refers to the effect of one drug on another drug when they are operating on the same target or even different targets, but with similar behaviour towards the different targets i.e do they inhibit the tendency of the the target to act which can cause an unwanted interaction.

The pharmacokinetic category consists of metabolism interactions like enzyme inhibitors and substrates. Target, enzyme and transporter inhibitors are chemical molecules that bind to the target (or enzyme, or transporter resp.), and inhibit its activity. Enzyme/transporter substrates are molecules which react with the enzyme/transporter, and are converted into different molecules called products. The pharmacodynamic category, on the other hand, occurs due to the agonists and antagonists. An agonist binds to a target, and evokes a response, while an antagonist binds to the target and inhibits a response.

We build our approach based on these two categories with the motivation that if two drugs interact, then there should exist a “path of relationships” describing the molecular and structural properties of the drugs, especially when there is an interaction. Thus, we extract relations as shown in Table 1 from the DrugBank database, whose general schema is shown in figure 1. These relations ensure that we are in the domain of pharmacokinetic and pharmacodynamic categories of the DDIs. Another motivation for using these relations is that the effect of enzymes on DDIs, especially the cytochrome P450, have been well studied extensively in medical literature [34, 35]. Thus, the use of such relations becomes natural in DDI prediction, and can be considered a form of domain expertise.

Table 1.

Initial relations

Initial Relations
Enzyme(enzyme,drug)
Target(target,drug)
Transporter(transporter,drug)
EnzymeSubstrate(drug, enzyme)
EnzymeInhibitor(drug, enzyme)
EnzymeInducer(drug, enzyme)
TargetSubstrate(drug, target)
TargetAntagonist(drug, target)
TargetInducer(drug, target)
TargetInhibitor(drug, target)
TargetAgonist(drug, target)
TransporterSubstrate(drug, transporter)
TransporterInhibitor(drug, transporter)
TransporterInducer(drug, transporter)

Figure 1.

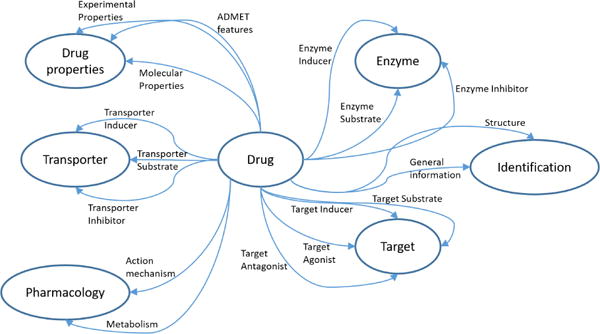
A general schema representation of the DrugBank database

4. Kernel Learning for Drug Drug Interactions

In classical multiple kernel learning [24, 23], kernels are typically constructed in two different ways. First, multiple kernels can be constructed from the same data source (homogeneous), or from different data sources (heterogeneous). These multiple kernels are then combined in a linear or non-linear fashion. A point to keep in mind in such a multiple-kernel learning setting is the assumption that we have the complete data vectors x_i from which we can construct multiple kernels. Our method diverges considerably from this representation since we never have an explicit representation or embedding of the drugs. Instead, we have several different similarity measures, from which we construct a single kernel for our prediction/discovery task.

4.0.1. Reachability

A key component describing drug-drug interactions is the charaterization of how two drugs react with each other. This is captured using a directed graph of known chemical reactions between drugs and enzymes, transporters etc. using ADMET (absorption, distribution, metabolism, excretion and toxicity) features. The idea of reachability follows from the intuition that two drugs are likely to interact with one another if one is reachable from the other via one or more paths in an ADMET knowledge graph.

While there exist numerous approaches in graph theory for reachability analysis on graphs [36, 37], our choice is guided by the fact that we operate on multi-relational, directed, relatively sparse graphs involving several thousands of entities/nodes representing drugs, enzymes, targets etc. An iterative search within such a large graph may be intractable. We are inspired by the success of randomized approaches in computational statistics and the seminal work on the path ranking algorithm (PRA, [38]). These approaches show that random walks on a knowledge graphs can be used to generate robust predictive models for relation extraction and reachability analysis. We adapt a similar approach to construct our reachability measure. The estimation of reachability between 2 drugs in a given drug pair proceeds as follows (Figure 2):

Figure 2.

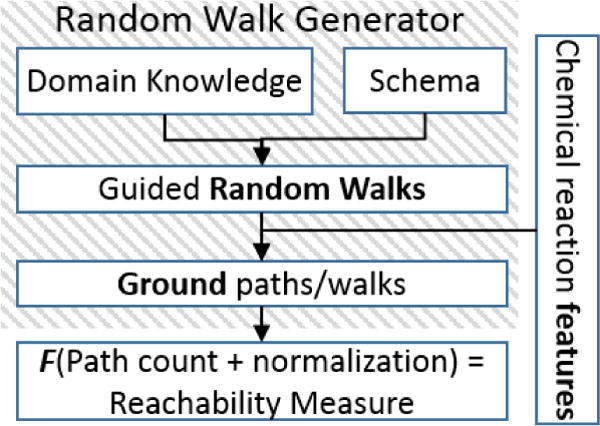
Reachability measure generation

(a) Preprocessing

A knowledge graph is constructed for known chemical reactions using ADMET features.

(b) Guided (Parameterized) Random Walk Generation

Parameterized random walks are sequences of relations with shared arguments, where the arguments are entity classes (not entity instances) starting and ending in the drug entity. Essentially, parameterized random walks are paths in the relational schema of chemical reactions (Figure 1). Similar to PRA [38], our random-walk generation allows for walking against the implicit direction of the relation. Thus, the relations prefixed with represent the inverse of a given relation. An example of a random walk through an ADMET graph looks like: TargetInhibitor(d0, t0)) ∧ _TargetInhibitor(t0, d1)) ∧ TransporterSubstrate(d1, t2)) ∧ _Transporter Inhibitor(t2, d3). We impose certain restrictions on the walks, including disallowing same relation types from following each other (a relation and its inverse are considered different types). We generate several random walks of varying length. Guidance is induced via refining the parameterized walks using domain knowledge [39] (Table 2) that indicate certain types of chemical reactions (or a series), which when present in the walks, increases the likelihood of an interaction between the two drugs at the start and end of the path.

Table 2.

Domain knowledge

Enzyme Inhibitor(drug, enzyme) ∧ _EnzymeInducer(enzyme, drug)

Enzyme Inhibitor(drug, enzyme) ∧ _TransporterInhibitor(transporter, drug)

Enzyme Inhibitor(drug, enzyme) ∧ _EnzymeInhibitor(enzyme, drug)

Enzyme Inhibitor(drug, enzyme) ∧ _EnzymeInhibitor(enzyme, drug) ∧ EnzymeInhibitor(drug, enzyme)

(c) Instantiation

Instantiation of a parameterized walk, $\mathbb{W}$, is the process of finding all possible paths, satisfying $\mathbb{W}$, that exist in the network of chemical reactions $\mathcal{G}$ between two drugs of a given pair〈d₁, d₂〉 (Figure 3). If we consider paths as subgraphs, and $\mathbb{W}$ a motif, then set of instances ${\mathrm{ℐ}}_{\langle }{ }_{{\mathbf{d}}_1,{\mathbf{d}}_2\rangle }=\left\{{\forall }_g\right|g\subseteq \mathcal{G},g|=\mathbb{W},{\mathbf{d}}_1\wedge {\mathbf{d}}_2\in g\}$. Searching for the set of instances is a combinatorially hard problem (#P-complete). We exploit the power of graph databases to compute this. The network of reactions is represented as an RDF¹ graph and the parameterized walks are posed as SPARQL queries [40]. Some example groundings for a couple of given random walks are shown in table 3 and table 4.

Figure 3.

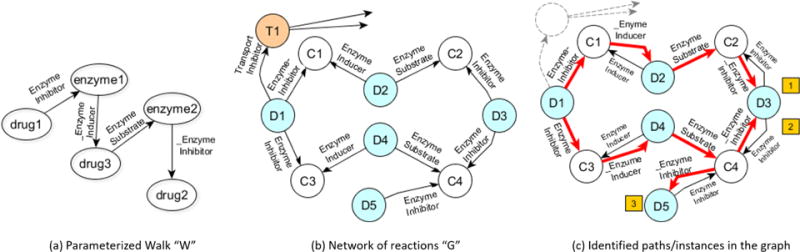
Instantiation process of a parameterized random walk $\mathbb{W}$ (left) is equivalent to sub-graph matching for a given motif. The graph $\mathcal{G}$ (middle) shows a part of the chemical reaction network (D_x, C_x & T_x indicate drugs, enzymes and transporters resp.). The rightmost figure shows how 3 different instances/paths (marked in red) have been identified that satisfy $\mathbb{W}$.

Table 3.

Few of the groundings generated for the random walk TargetAgonist (d0, e1) ∧ _TargetAgonist (e1, d1) ∧ EnzymeSubstrated1, e2)(∧ _EnzymeInhibitor (e2, d2)

Tramadol,Mu-type opioid receptor,Morphine,Cytochrome P450 2C8,Pravastatin

Morphine,Mu-type opioid receptor,Tramadol,Cytochrome P450 3A4,Tadalafil

Hydromorphone,Mu-type opioid receptor,Morphine,Cytochrome P450 2D6,Amlodipine

Methadone,Mu-type opioid receptor,Oxycodone,Cytochrome P450 3A4,Risperidone

Oxycodone,Mu-type opioid receptor,Hydromorphone,Cytochrome P450 2D6,Risperidone

Table 4.

Few of the groundings generated for the random walk TransporterSubstrate(d0, t1) ˄ Transporter(t1, d1) ˄ TargetInhibitor(d1, e1) ˄ Enzyme(e1, d2)

Pravastatin,Multidrug resistance protein 1,Acetaminophen,H synthase 1,Hydromorphone

Metoprolol,Multidrug resistance protein 1,Diclofenac,H synthase 2,Ibuprofen

Venlafaxine,Multidrug resistance protein 1,Acetylsalicylic acid,H synthase 1,Diphenhydramine

Cephalexin,Solute carrier family 22 member 6,Naproxen,H synthase 1,Zolpidem

Levothyroxine,Solute carrier organic anion transporter family member 1C1,Diclofenac,H synthase 1,Hydromorphone

(d) Measure/Score generation

The reachability measure is generated for every drug pair 〈d₁, d₂〉 by obtaining the cardinality (count) of the instance set ${\mathrm{ℐ}}_{\langle }{ }_{{\mathbf{d}}_1,{\mathbf{d}}_2\rangle }$.

4.0.2. Similarities based on SMILES and SMARTS strings

The simplified molecular-input line-entry system (SMILES) is a commonly-used specification for describing chemical and molecular structure using ASCII strings. The SMILES arbitrary target specification (SMARTS) is an extension of SMILES that is also commonly used for specifying molecular sub-structures precisely. We extract four similarity measures based on molecular and chemical properties of the drug (specified by SMILES and SMARTS strings) using the package rdkit². We compute four similarity measures from SMILES strings [41], which have been previously proven useful in various bio-computing tasks [42, 43, 44]:

• (S1) Molecular Feature Similarity (FS) compares the chemical properties of two drugs using 19 features extracted from their SMILES strings. These features include the number of valence electrons, number of aromatic rings and number of hydrogen donors and receptors, which are important for determining the reactiveness of a molecule. We use the Jaccard distance between all features as the similarity between two drugs.

• (S2) SMILES String Similarity (SS) is the similarity between the SMILES strings themselves, which is calculated using edit distance between the strings.

• (S3) Molecular Fingerprint (FP) similarity is computed between the fingerprints, which are bit-string representations of the molecular structure.

• (S4) Molecular ACCess System (MACCS) keys are a particular type of fingerprint generated from SMARTS strings. Similarities on MACCS are commonly used in the drug discovery domain, though they have been proven to be useful on the DDI domain as well [45].

4.1. Notation and Problem Description

Before describing our approach in detail, we formalize our notation. Given a drug database with N drugs, we are interested in discovering whether a pair of drugs d_i and d_j interact with each other. Recall that we do not distinguish between synergistic and antagonistic interactions. Let all possible drug pairs in the database be $\mathcal{P}=\{({\mathbf{d}}_i,{\mathbf{d}}_j)|1\le i,j\le N\}$, and we use the short-hand notation ij to denote the drug-drug pair (d_i, d_j). As mentioned previously, our problem setting is considerably different from the classical multiple kernel learning framework. We do not attempt to construct an explicit vector representation or embedding of a drug d_i. Instead, given N drugs, we construct M pairwise similarity matrices S_m, for m = 1, …, M. As described above, these similarities can be constructed using various drug properties that represent the potential for interactions such as molecular structure, pharmacological attributes etc. Since these “similarities” represent potential for interactions, they can also be constructed from natural language text extracted from such diverse sources as electronic health records [4] and journal abstracts [5].

Our approach seeks to combine different interaction measures and similarities, S_m, from various sources into one coherent kernel. Note that the only requirement on the similarity matrices is that $S_m\in {\mathbb{S}}^N$, the space of all N × N symmetric matrices. We do not assume positive semi-definiteness (psd³) of similarity measures; as we show below, it is possible to align a psd kernel with non-psd similarity matrices. Thus, any symmetric scoring function σ_m(d_i, d_j) can be used to generate a similarity matrix S_m. This allows our approach to be agnostic to multiple representations of a drug. For example, σ₁ can be string alignment similarity of the genomic strings of two drugs, while σ₂ can be the bag-of-words co-occurence count of the two drugs in a biomedical corpus. Broadly, any scoring function that measures similarity of a potential for interaction can be considered a candidate similarity measure.

The (i, j)-th element of S_m is denoted $s_m^{ij}$, and describes the interaction between d_i and d_j according to interaction measure S_m. The interaction label y_ij = +1 if the drugs d_i and d_j interact adversely with each other and y_ij = −1 otherwise. We denote the matrix of all drug-drug interactions as $Y\in {\mathbb{S}}^N$, the symmetric matrix whose (i, j)-th entry is the interaction label y_ij. Generally, we only know the true labels for a small subset of drug pairs, $\mathrm{ℒ}\subset \mathcal{P}$, and our goal is to learn a model on $\mathrm{ℒ}$ in order to discover drug-drug interactions in the remaining pairs $\mathcal{U}=\mathcal{P}\backslash \mathrm{ℒ}$. Our problem can be formulated as follows:

Given: For N drugs, M interaction similarities Sm, a small subset of known interactions yjj for pairs $ij\in \mathrm{ℒ}\subset \mathcal{P}$,

Learn: A kernel Z ⪰ 0, and interaction similarity combination weights αm ≥ 0, ${\displaystyle {\sum }_{m=1}^M{\alpha }_m=1}$,

Predict/Discover: Previously unknown pairwise drug-drug interactions ${\widehat{y}}_{ij}=\text{sign}(z_{ij})$, for pairs $ij\in \mathcal{U}=\mathcal{P}\backslash \mathrm{ℒ}$.

Our novel formulation addresses kernel learning at an element-wise, local and global level, enabling us to learn robust models for discovery of new drug-drug interactions.

4.2. Incorporating Neighborhood Information

We view each interaction/similarity measure as a graph that provides a different view of the neighborhood of a drug. That is, each similarity matrix S_m represents a fully-connected graph with $s_m^{ij}$ representing the edge weight between drugs d_i and d_j. Since each S_m measures similarities differently, the neighborhood of a drug ${\mathcal{N}}_m({\mathbf{d}}_i)$ with respect to different S_m will be different. In order to effectively incorporate this multi-view neighborhood information, we construct graph Laplacians L_m, m = 1, …, M, for each similarity. Laplacians are naturally locality-preserving [46, 47], that is, they preserve the neighborhood structure in the data. This allows us to learn a kernel that fuses neighborhood information ${\mathcal{N}}_m$ from multiple interaction types. Without loss of generality, we set the diagonal of S_m to zero: diag(S_m) = 0, reflecting that drugs do not interact with themselves. The Laplacian can be constructed as

$$L_m=(1+\delta )I_N-D^{-\frac{1}{2}}{S}_m{D}^{-\frac{1}{2}},$$ (1)

where I_N is an N × N identity matrix and D is a diagonal matrix with entries $d_{ii}={\displaystyle {\sum }_{j=1}^N{s}_{ij}^m}$ (the row sum of the similarity matrix S_m).

We formulate the following kernel learning problem:

$$\begin{array}{l}\begin{array}{cc}\underset{L,Z,\mathbf{\alpha }}{\text{minimize}}& \stackrel{\text{alignment}}{\overbrace{\langle L,Z\rangle +\langle L,Y\rangle }}+\stackrel{\text{regularization}}{\overbrace{{\lambda }_{1}r(\alpha )}}\\ & \underset{\text{loss}\text{functions}}{\underbrace{{\lambda }_2({\mathrm{\ell }}_1(Z,Y)+{\mathrm{\ell }}_2(L,Y)}}\end{array}\\ \text{subject}\text{to}L={\displaystyle \sum _{m=1}^M{\alpha }_m{L}_m,\mathbf{\alpha }\ge 0,\mathbf{e}\prime \mathbf{\alpha }}=1,Z\mathrm{\succcurlyeq }0.\end{array}$$ (2)

We highlight the various components of the formulation (2):

The variable $L={\displaystyle {\sum }_{m=1}^M{\alpha }_m{L}_m}$ is a convex combination of the Laplacians L_m arising from the various interaction similarities. The matrix variable L is introduced purely for convenience of notation and can easily be eliminated from the objective function of (2). We select a convex rather than a linear or conic combination in order to improve interpretability [28]. That is, positive α_m enable us to intuitively interpret the importance of one similarity relative to the others. The formulation attempts to identify a combination weights α as well as a kernel Z ⪰ 0, which ensures that Z is psd.

The alignment terms are inspired by the success of alignment-based regularization for kernel learning [29]. Hoi et al [30] observe that these alignment terms essentially perform manifold regularization [31], which has the effect of incorporating local neighborhood information encoded in the different Laplacians as well as the labels into learning α and Z. Specifically, 〈L, Y〉 encourages the weights on the Laplacians α to be consistent with the labels Y. The impact of labels is also propagated into Z by the 〈L, Z〉 term.

The entries of the learned kernel z_ij directly provide a unified interaction score and we predict drug interactions as

$${\widehat{y}}_{ij}=\text{sign}(z_{ij}).$$ (3)

While the unified kernel Z is positive semi-definite, it’s entries can still be negative, which is a fact that we exploit here. Enforcing positive semi-definiteness also naturally imposes symmetry on the learned kernel.

In order that the elements of Z capture interactions effectively into a score, we require a loss function that ensures that the interaction margin is maximized. We use the hinge loss to ensure that y_ijz_ij ≥ 1 holds. Intuitively, these constraints ensure that z_ij ≥ 1 when y_ij = +1 and z_ij ≤−1 when y_ij = −1. The interaction margin behaves very similarly to the margin in SVMs [7]. Thus, we select ℓ₁ to be the hinge loss in (2), which is applied to the drug pairs with known labels (indexed by) $ij\in \mathrm{ℒ}$:

$${\mathrm{\ell }}_1(Z,Y)={\displaystyle \sum _{ij\in \mathrm{ℒ}}\max (1-y_{ij}{z}_{ij},0).}$$ (4)

The loss function ℓ₁ ensures element-wise consistency between the learned kernel Z and the labels Y. In a similar vein, the loss function ℓ₂ aims to propagate this consistency into the combination weights α. To this end, we measure the element-wise deviation of the weighted Laplacian with the labels as well, through the Frobenius norm:

$${\mathrm{\ell }}_2(L,Y)=\frac{1}{2}{\Vert L-Y\Vert }_F^2.$$ (5)

Finally, we also add a regularization term over α, typically to ensure robustness in weight learning. In this work, we chose the classical L₂ regularizer, $r(\mathbf{\alpha })=\frac{1}{2}{\Vert \mathbf{\alpha }\Vert }_2^2$. Other norms can also be used, depending on what properties of α are desired. For instance, the L₁ regularizer, r (α) = ║α║₁ encourages sparsity, while the L_∞ regularizer, r(α) =║α║_∞ encourages the model to select the single best kernel. We use L₂ regularization here, and defer the exploration of the properties of the other regularizers to future work.

We formulate the following kernel learning problem:

$$\begin{array}{l}\begin{array}{cc}\underset{L,Z,\mathbf{\alpha }}{\text{minimize}}& \langle L,Z\rangle +\langle L,Y\rangle +\frac{{\lambda }_1}{2}{\Vert \mathbf{\alpha }\Vert }_2^2\\ & {\lambda }_2{\displaystyle \sum _{ij\in \mathrm{ℒ}}{\xi }_{ij}+\frac{{\lambda }_2}{2}{\Vert L-Y\Vert }_F^2}\end{array}\\ \begin{array}{cc}\text{subject}\text{to}& y_{ij}{z}_{ij}-1+{\xi }_{ij}\ge 0,{\xi }_{ij}\ge 0,\forall ij\in \mathrm{ℒ},\\ & L={\displaystyle \sum _{m=1}^M{\alpha }_m{L}_m,\mathbf{\alpha }\ge 0,\mathbf{e}\prime \mathbf{\alpha }}=1,Z\mathrm{\succcurlyeq }0\end{array}.\\ \end{array}$$ (6)

The slack variables ξ_ij ≥ 0 measure the hinge loss of the pairwise interaction fit between the labels and the entries of Z as shown in equation (4). These slack variables function in a manner very similar to the slack variables in SVMs: if the prediction z_ij and the label y_ij have the same sign, then the model correctly identifies the interaction for drugs d_i and d_j. In this case, we will have, y_ijz_ij > 0 and consequently, ξ_ij = 0. However, for misidentified interactions, ξ_ij = 1 − y_ijz_ij > 0. Thus, by minimizing ξ_ij, we are able to minimize the misclassification of drug-drug interactions. The formulation (6) is an instance of a bilinear program, owing to the terms $\langle L,Z\rangle ={\displaystyle {\sum }_{m=1}^M{\alpha }_m\langle L_m,Z_m\rangle }$

We solve (6) using alternating minimization [48]. At the t-th iteration, we fix the current estimate of the similarity weights ${\widehat{\alpha }}^t$ (note that when α are fixed, this also fixes L, owing to the equality constraint in eq. 6). This allows us to infer the new interactions scores ${\widehat{Z}}_{i,j}^{t+1}$ by solving the following sub-problem, which we denote SubProbE $(Z|{\widehat{\alpha }}^t)$. This can be interpreted as the expectation step of an EM procedure, where we identify the hidden variables, in this case, the drug-drug interactions Z. We can now fix $Z={\widehat{Z}}^{t+1}$ in (6), which gives us a sub-problem we denote SubProbM $(\mathbf{\alpha }|{\widehat{Z}}^{t+1})$. Again, this step can be considered equivalent to the maximization step of an EM procedure, where we estimate the parameters (here, α, which parameterize the influence of the various similarities on the final kernel). This procedure is summarized in Algorithm 1. Both sub-problems were solved using SDPT3 [49].

Algorithm 1.

Alternating Minimization for Learning SKID³

1:	${\widehat{\mathbf{\alpha }}}^0=1/m$ ⊳ Initialize weights uniformly
2:	${\widehat{Z}}^0=I_N$ ⊳ Initialize kernel to identity matrix
3:	for t ≤ tmax do
4:	${\widehat{Z}}^{t+1}\leftarrow \text{SubProbE(Z|}{\widehat{\mathbf{\alpha }}}^t)$ ⊳ Update Z
5:	${\widehat{\mathbf{\alpha }}}^{t+1}\leftarrow \text{SubProbE}(\mathbf{\alpha }\text{|}{\widehat{Z}}^{t+1})$ ⊳ Update α
6:	If $\frac{1}{N^2}{\Vert {\widehat{Z}}^{t+1}-{\widehat{Z}}^t\Vert }_F^2+\frac{1}{m}{\Vert {\widehat{\mathbf{\alpha }}}^{t+1}-{\mathbf{\alpha }}^t\Vert }_2^2\le {\tau }_{\text{tol}}$ then
7:	break ⊳ Converged to tolerance
8:	end if
9:	t ← t + 1
10:	end for

5. Experiments

In this section, we aim to answer the following questions, which address the effectiveness of our proposed approach:

• (Q1) How effective are the similarity measures on their own for the task of identifying drug-drug interactions?

• (Q2) Is kernel learning effective for the DDI task?

• (Q3) Is combining multiple similarity measures more advantageous than using a single similarity measure? How do the learned weights change with increasing database size?

• (Q4) Does our work motivate further clinical investigations?

• (Q5) How scalable is our method?

Our data set consists of 78 drugs obtained from DrugBank⁴. This gives rise to 3003 possible interactions⁵. All our reported results were obtained across five runs with a held-out test set of 603 drug pairs. Different methods were trained with increasing number of drug pairs ranging from 400 to 2400, chosen randomly for each run.

The results of our experiments are shown in Figure 5. Note that all the metrices shown in the results are averaged over 5 runs on a hold-out set. Figures 5(a)–5(d) show that a kernels learned from each individual similarity measure (described in Sec. 4.0.1 and 4.0.2) are able to perform reasonably well on the DDI prediction task, thereby answering Q1 affirmatively.

Figure 5.

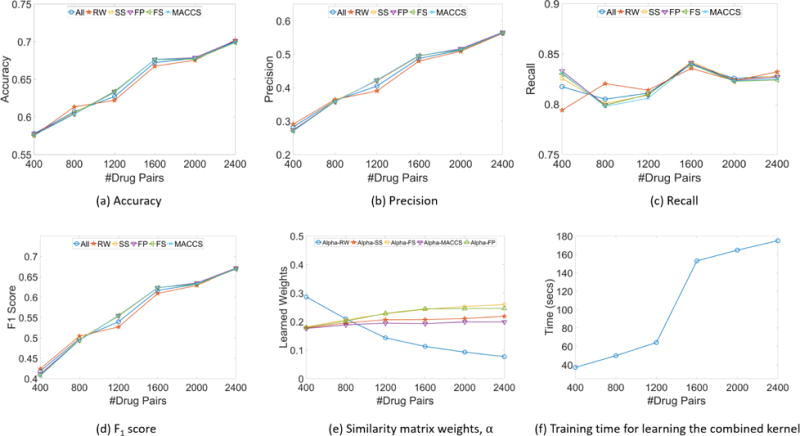
Experimental results, with kernels learned using All similarity measures ( SKID³), random-walk reachability (RW), SMILES string similarity (SS), molecular feature similarity (FS), molecular fingerprint similarity (FP) and MACCS fingerprint similarity (MACCS). (a)–(d) Classification performance of each kernel on a hold-out test set as the size of the training set increases; (e) Weights of each individual kernel in All, as training set size increases; (f) Training time for learning the combined kernel ( SKID³) that fuses all the similarity measures, as training set size increases.

We also learn a single kernel (Z ≡ SKID³) as well as the weights for the five similarity measures (α_m). It is evident that learning from multiple similarity measures provide a more stable learning curve that performs well. Our initial hypothesis was that the similarities generated from molecular structures (SS, FS, FP and MACCS) and chemical reaction pathways (RW) fused into a single kernel could combine the advantages of both. That is, our hypothesis was that similarity fusion should achieve the high precision of the molecular structures similarity as well as the high recall of the chemical reaction pathways similarity. The results clearly confirm this, thereby answering Q2 and Q3 affirmatively. Figure 5(e) shows the change of the learned weights as the number of training drug pairs increases. A key observation from Figure 5(e) is that the influence of the random walk (RW) similarity decreases, while the weight of the molecular structure similarities increases. This suggests that RW similarities are particularly effective in smaller databases, for targeted identification of interactions.

Q1–Q3 evaluate the performance of our approaches and confirm existing interactions as provided by DrugBank. Our goal with Q4 was to see if SKID³ is able to discover new interactions. In order to answer Q4, it is necessary that our analysis goes beyond ground truth that we are considering in constructing the model. Thus, we look closely at the false positives and false negatives, under the intuition that DrugBank (or any other database) is never fully complete or accurate.

In Table 5 we present a few drug pairs that are supposedly “incorrectly classified” by our method using the DrugBank ground truth⁶. Table 5 shows that the interactions discovered by our approach can be supported by independent sources or research. Specifically, according to the ground truth, 6 interactions were flagged as false positives. On the contrary, according to literature, these are likely true interactions. Thus, we answer Q4 affirmatively. This is a crucial observation in the task of drug surveillance: many sources of DDIs need to be carefully and continuously curated for updating this ground truth. This result highlights the fact that SKID³ can indeed not only classify DDIs, but can help in knowledge refinement as well as knowledge discovery. Validating this hypothesis more fully requires large-scale evaluation, which is an interesting direction for future research.

Table 5.

Table depicting example drug pairs where the prediction does not match the ground truth. However, we additionally cite sources (last column) that support our prediction.

Drug 1	Drug 2	DrugBank Ground Truth	Predicted Class	Independent Source
Amitriptyline	Tamsulosin	Not interacting	Interacting	Drugs.com [50]
Omeprazole	Metformin	Not interacting	Interacting	Nies et al. [51], rxlist.com [52]
Salbutamol	Clonidine	Not interacting	Interacting	Thoolen et al. [53]
Cephalexin	Diclofenac	Not interacting	Interacting	Ali et al. [54]
Amoxicillin	Metronidazole	Not interacting	Interacting	Pavicic et al. [55]
Amphetamine	Salbutamol	Not interacting	Interacting	DrugBank6
Cephalexin	Methadone	Interacting	Not interacting	Drugs.com [56]

Finally, Figure 5(f) shows the time taken by our method. The training time increases linearly with the number of drug pairs, showing the scalability of our method and answering Q5 affirmatively. This result has practical implications for scalable DDI discovery with full drug databases.

6. Conclusion and Future work

We consider the problem of drug-drug interaction discovery, and develop a framework to exploit deeper structures and drug features using kernel learning. Our extensible framework can fuse information from multiple views including chemical reaction pathways and molecular structure, which we have demonstrated here. Furthermore, our formulation can easily admit other types of interactions as similarities including phenotypic, pharmacological, genomic and text, to name a few.

Our evaluations on the DrugBank database established the superiority of our proposed approach, which is distinct from many current approaches that generally ignore drug properties and instead seek interactions through text mining of existing literature. Extending this work to include more features including other semantic similarity metrics is an interesting direction. Combining the results of learning from DrugBank with other NLP based extraction techniques is another direction. Finally, using other labeling techniques such as weak supervision or distant supervision can potentially lead to larger training sets and can make the discovery process more effective.

Figure 4.

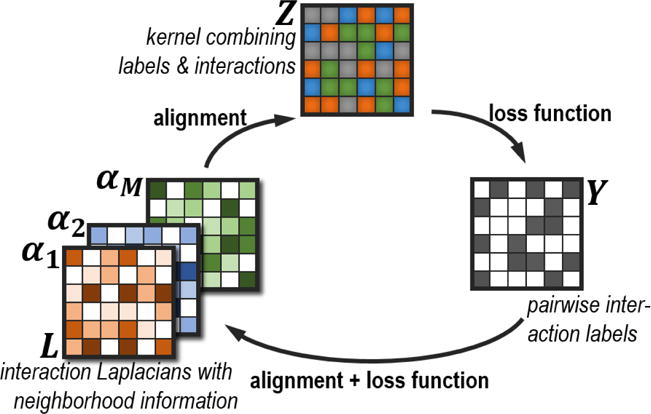
Our formulation aims to learn a positive semi-definite kernel Z and combination weights α_m for various similarity measures. These similarities represent interaction scores, which help determine how likely two drugs are to interact. The similarities can be constructed from diverse sources (such as molecular, structural, genomic, text). The similarity measures are expressed through Laplacians, which view the interactions as a neighborhood graph. In this manner, we can incorporate local information into the kernel. The loss functions ensure that the learned Z is element-wise consistent with the labels.