ATP Release by Red Blood Cells under Flow: Model and Simulations

Abstract

ATP is a major player as a signaling molecule in blood microcirculation. It is released by red blood cells (RBCs) when they are subjected to shear stresses large enough to induce a sufficient shape deformation. This prominent feature of chemical response to shear stress and RBC deformation constitutes an important link between vessel geometry, flow conditions, and the mechanical properties of RBCs, which are all contributing factors affecting the chemical signals in the process of vasomotor modulation of the precapillary vessel networks. Several in vitro experiments have reported on ATP release by RBCs due to mechanical stress. These studies have considered both intact RBCs as well as cells within which suspected pathways of ATP release have been inhibited. This has provided profound insights to help elucidate the basic governing key elements, yet how the ATP release process takes place in the (intermediate) microcirculation zone is not well understood. We propose here an analytical model of ATP release. The ATP concentration is coupled in a consistent way to RBC dynamics. The release of ATP, or the lack thereof, is assumed to depend on both the local shear stress and the shape change of the membrane. The full chemo-mechanical coupling problem is written in a lattice-Boltzmann formulation and solved numerically in different geometries (straight channels and bifurcations mimicking vessel networks) and under two kinds of imposed flows (shear and Poiseuille flows). Our model remarkably reproduces existing experimental results. It also pinpoints the major contribution of ATP release when cells traverse network bifurcations. This study may aid in further identifying the interplay between mechanical properties and chemical signaling processes involved in blood microcirculation.

Introduction

ATP is known not only as an energy carrier but also as a prominent signaling molecule in many physiological processes (1). A notable example is the case of blood flow, in which red blood cells (RBCs) have the ability to release ATP under several types of stimuli. Experimental evidence (1) supports the idea that ATP is capable of modulating vasomotor tone in the microcirculation via diffusion toward endothelial cells (ECs), which then in turn elicit a vasodilation reaction cascade of the smooth muscle of the arteriolar trees, without nerve-ending intervention. In vivo studies (2) confirmed that ATP release by RBCs due to shape deformation played a vital role in pulmonary vascular resistance modulation. In recent years, systematic in vitro experimental studies revealed that ATP release by RBCs is quite sensitive to low oxygen level, shear stress, and sufficiently high shape deformation (3, 4, 5, 6). This mechanical-dependent release is believed to play an important role in the microcirculation because, in these zones (e.g., in arterioles and capillaries), the shear stress is the highest, and shape deformations may become quite large. The actual ATP concentration level as well as its heterogeneities (e.g., its gradient) has most likely a potential role in a global and precise understanding of signaling pathway and related pathologies for “RBC to EC to smooth muscle.” Presently, this is a quite ambitious task that is beyond the objective of this study. Rather, here we shall concentrate on the first basic question, on how the geometry of networks, the flow properties, and RBC dynamics affect the ATP concentration in microcirculation.

Although direct access to high-resolution spatiotemporal ATP concentration patterns in microvessel networks is a formidable task, statistical analysis in in vitro studies provided some essential key elements. Along this line, Forsyth et al. (6) performed an in vitro study in which RBCs were subjected to various levels of shear stress for a long enough time period. ATP release was measured subsequently and compared with the amount of ATP obtained under static conditions. By varying the amplitude of the shear stress, two distinct ATP release pathways were hypothesized from previous experimental studies (3, 6, 7, 8, 9). One pathway is triggered by the amplitude of the shear stress, whereas the second pathway requires sufficiently large RBC shape deformation. Both pathways were shown to be shear stress dependent. More precisely, when the shear stress was nonzero but below a critical value (3 Pa in their experiment), most RBCs perform tumbling (flipping in a shape-preserving manner) with a very limited deformation. In this case, the release level of ATP was quite independent of the amplitude of the shear stress once the threshold value was crossed. Beyond a second critical value of shear stress, a large proportion of RBCs underwent tank-treading motion with large shape deformation. In this case, the total ATP amount showed a monotonic increase with shear stress. Other experimental studies of RBCs passing through a narrow channel (5) have also pointed to the fact that when the characteristic shear stress on the RBC increased from around 0.02 to 0.1 Pa, a release of ATP was observed with a time delay in the range of 20–70 ms.

The experimental evidence reporting on the link between membrane shear stress, shape deformation, and the level of ATP release has motivated theoretical studies in an attempt to explain the ATP release mechanism on a molecular level. In (10), the authors proposed a possible pathway in which the deformation creates cytoskeletal defects, from which actin molecules are freed. Subsequently, actin molecules aggregate on the cystic fibrosis transmembrane conductance regulator (CFTR), which causes its activation in favor of ATP release. Yet the CFTR is believed to modulate ATP release in an indirect manner in that it upregulates the so-called pannexin 1 hemichannel (Px1). Actually, Px1 is believed to be the main avenue for ATP release from the RBC membrane. It is directly sensitive to mechanical stress, as well as to cytoplasmic oxygen and calcium levels. Experiments have also reported on a presumable mechanism from Piezo1, a cation channel that responds to membrane shear stress by allowing calcium influx (11). An elevation of calcium level is known to facilitate Px1 activation for intracellular ATP release.

In vivo, RBCs are constantly exposed to flow in which they experience various levels of shear stress and deformation. Several numerical studies on RBC dynamics in the circulation reveal nontrivial steady or time-dependent shapes. In (12), a vesicle model (in which the membrane is made of a pure lipid bilayer) was employed to represent the RBC. A complex diagram of single-vesicle dynamics was reported later in (13, 14).

Despite the oversimplification of the vesicle two-dimensional (2D) model, several similar shapes were also found subsequently in more elaborate three-dimensional (3D) models, which included the membrane cytoskeleton (15, 16). This points to the fact that the simplified 2D vesicle problem captures several important RBC shapes and dynamics. The two main ingredients of this ATP release model are 1) the local shear stress and 2) the deformation amplitude. Both effects are present in two dimensions and three dimensions. We do not expect a qualitative difference between two and three dimensions because the two modes of motion (tumbling (TB) and tank treading (TT)) are exhibited in both two and three dimensions. However, we have to keep in mind that the 3D properties of RBC may become essential. For example, an RBC is endowed with a network of spectrins (cytoskeleton), and it may undergo large deformation as compared to a 2D model. These factors are expected to quantitatively shift the results. To cope with the complex problem of ATP release, we shall adopt here a 2D vesicle model and focus on the most important RBC dynamics related to ATP release, namely the local shear stress and local membrane deformation, leaving more advanced 3D simulations to the future.

Here, our major goal is to propose a model of ATP release and its coupling with membrane shear stress and shape deformation. The basic elements of the model of ATP release are guided by in vitro experimental data (5, 6) and inspired by the molecular mechanism involving RBC shape deformation (10). To the best of our knowledge, this is the first model of ATP release from RBCs under flow. As we will see, the model is inspired by existing in vitro shear experiments and will be validated by reproducing the experimentally observed features.

Once the model is established, we shall use a lattice-Boltzmann method to investigate it numerically under microcirculation conditions. A complex issue is the handling of the advection-diffusion problem on a moving and deformable boundary. The implementation of coupling the ATP release to the fluid flow will be mainly presented in the Supporting Materials and Methods. We propose an empirical ATP release model, which remarkably reproduces the essential ATP patterns reported experimentally under shear flow. This model will be analyzed in a systematic way for different scenarios in the microcirculation. More precisely, we consider a pipe flow with various steady or unsteady shapes of RBC, then the scenario of an RBC hitting a bifurcation, and finally the post-hitting lateral migration and its relation to ATP release. The ATP release is found to show a strong dependence on RBC dynamics. Finally, we present some general conclusions and future directions.

Methods

The model of RBC dynamics and coupling to the chemical problem

Under shear flow, both vesicles (in two and three dimensions) and RBCs exhibit the following two main modes: TT (the cell or vesicle acquires a given orientation while the membrane rotates around the center of mass) and TB (a quasi-solid-like flipping). For vesicles, TB occurs at high enough internal fluid viscosity with respect to the external one, whereas TT prevails at low enough internal viscosity (17). For RBCs (18, 19, 20, 21), the transition from TB to TT can be achieved by increasing shear stress. For low shear stress, RBCs exhibit TB, whereas for large shear stress, we have TT. Experiments reported (6) that the ATP release critically depends on the dynamical mode (TT or TB). Thus, it is sufficient to consider a 2D vesicle that is known to exhibit both TT and TB.

X(s) refers to the coordinate of the vesicle shape defined on a 2D space x = (x, y), with s ∈ [0, P), the curvilinear coordinate (local arc length), where P is the perimeter of the vesicle. Ω_in refers to the vesicle internal domain with a constant area A, whereas Ω_ex designates the “plasmic” domain. The reduced area is defined as τ = 4πA/P² to quantify the deflation of the vesicle. τ = 1 corresponds to a circle, whereas any other shape corresponds to τ < 1. R₀ = 3 μm is a characteristic radius of the vesicle, which is defined by $\pi R_0^2=A$. In the vesicle model, the Helfrich bending energy (22) is adopted to extract the membrane force:

$$\mathbf{H}\left(\mathbf{X}\left(s\right)\right)=\frac{\kappa }{2}\oint c^{2}ds+\oint \zeta ds.$$ (1)

κ is the bending rigidity modulus, c is the local curvature, s is the curvilinear coordinate, and ζ is a Lagrange multiplier, which enforces local membrane inextensibility. The force-per-unit length along the membrane can be obtained thanks to a functional differentiation f(s) = δH/δX(s).

The vesicle is immersed into an incompressible flow field u; thus, its shape evolution obeys the following:

$$\frac{\partial \mathbf{X}}{\partial t}=\int \delta \left(\mathbf{x}-\mathbf{X}\right)\mathbf{u}\left(\mathbf{x}\right)dxdy.$$ (2)

The fluid velocity u is defined on domain x ∈ [0, L] × [−W/2, W/2], where L is the domain length and W is the width. It satisfies the incompressible continuity condition $\mathit{\nabla }\cdot \mathbf{u}=0$, as well as the momentum conservation condition:

$$\rho \left(\frac{\partial \mathbf{u}}{\partial t}+\mathbf{u}\cdot \mathit{\nabla }\mathbf{u}\right)=-\mathit{\nabla }p+\mathit{\nabla }\cdot \left(\mu \mathit{\nabla }\mathbf{u}\right)+\mathbf{F}\left(\mathbf{x}\right).$$ (3)

Here, ρ is the fluid density, and $\mathbf{F}=\mathrm{\oint }\mathbf{f}\left(s\right)\cdot \delta \left(\mathbf{x}-\mathbf{X}\left(s\right)\right)ds$ is the force that the vesicle applies on the fluid. μ is the dynamic viscosity and takes two generally distinct values inside and outside the vesicle:

$$\mu \left(\mathbf{x}\right)=\{\begin{array}{cc}{\begin{array}{c}\mu \end{array}}_{in}& if\mathbf{x}\in {\mathit{\Omega }}_{in}\\ {\mu }_{ex}& if\mathbf{x}\in {\mathit{\Omega }}_{ex}\end{array}.$$ (4)

The viscosity contrast is defined as the ratio between internal and external viscosity λ = μ_in/μ_ex.

The capillary number is defined as $Ca={\mu }_{ex}{\dot{\gamma }}_w{R}_0^3/\kappa$ and represents the ratio between the applied shear force and the bending force. ${\dot{\gamma }}_w={\partial u_x/\partial y|}_{y=-W/2}$ is the shear rate at y = −W/2. For a linear shear flow, the shear rate is constant. However, this is not the case for a pipe flow, and this is why we have to specify the definition of what is meant by the typical shear rate.

The chemical problem can be described without reference to any specific molecule, albeit later we will focus specifically on ATP. The concentration, defined on domain Ω_ex, is denoted as a(t, x), and it obeys, in general, the diffusion-advection-reaction equation. In its full generality, the concentration evolution equation takes the following form:

$$\frac{\partial a}{\partial t}+\mathbf{u}\cdot \mathit{\nabla }a=\mathit{\nabla }\cdot \left(D\mathit{\nabla }a\right)+R,$$ (5)

where $D\simeq 2.36\times {10}^{-10}{m}^2/s$ is the ATP diffusion coefficient in plasma, with its value taken from (23). R is a reaction term. In what follows, we will set it to zero, because we will be exclusively interested in ATP release not involving reactions. The Peclet number is defined as $Pe={\dot{\gamma }}_w{R}_0^2/D$, which ranges approximately from 1.0 to 200 in our simulations.

On the vesicle membrane, if n denotes the normal vector toward Ω_ex, the boundary condition of ATP release is set as follows:

$$D\frac{\partial a}{\partial \mathbf{n}}=\psi \left(\mathbf{S}\left(s\right)\right).$$ (6)

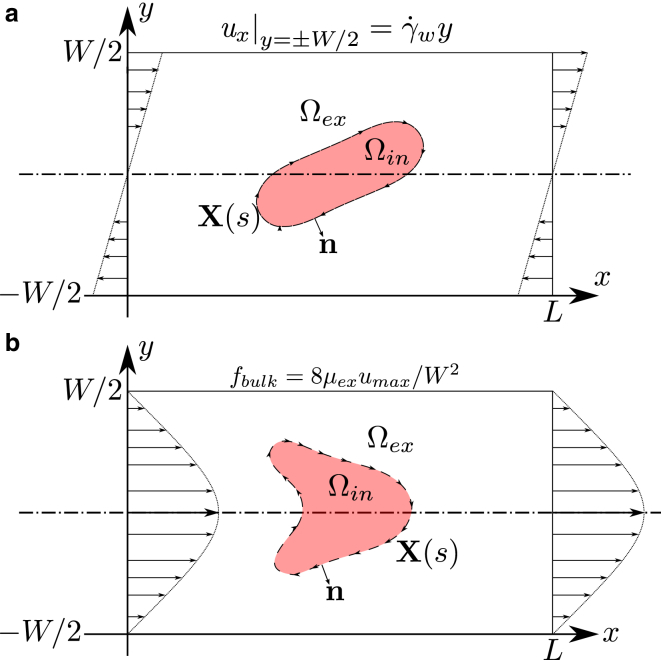
This equation yields the total ATP flux across the membrane, which is a priori an unknown function of the precise membrane state at a given point of the membrane. ψ(S(s)) is the ATP flux across the membrane, and it constitutes the main focus of the modeling. The vector S can be viewed as a collection of local states of the membrane. We will see later how ψ(S(s)) can be inferred after a close inspection of experimental facts. Finally, and for simplicity, we impose that the concentration obeys periodic boundary conditions along x and has zero flux across the bounding walls. Schematics of model configuration can be found in Fig. 1.

Figure 1.

A schematic view of the studied configuration: (a) shows the case of a linear shear flow obtained by imposing the velocity of the upper and lower walls; (b) shows a similar configuration but for a Poiseuille flow; the imposed flow is generated by a bulk force term f_bulk, which ensures a parabolic profile with maximal velocity u_max. In both configurations, the ATP concentration a is defined on Ω_ex, and a Neumann boundary condition is imposed on the moving boundary X(s). To view this figure in color, go online.

Lattice-Boltzmann model for fluid-membrane-solute coupling

An immersed-boundary-lattice-Boltzmann method is implemented based on an identical numerical algorithm from (24). By choosing a pseudo-Reynolds number of around 0.1, the method is well validated against the well-established boundary-integral method in the Stokes limit (for the boundary-integral method, see (25)). A similar lattice-Boltzmann scheme is used to solve the advection-diffusion equation (Eqs. 5 and 6). This advection-diffusion solver has been validated against known analytical benchmarks as well as against the Galilean invariance tests for static and moving boundaries. The code was developed under Compute Unified Device Architecture to benefit from graphics processing unit acceleration, allowing for the fluid-membrane-solute coupling simulation within an acceptable computational time. The numerical methodology is briefly introduced in Supporting Materials and Methods. The general numerical procedure for the boundary condition and the immersed-boundary method can be found in (19, 26, 27, 28).

A similar study, but with a static boundary, has been proposed regarding the drug delivery problem (29, 30). Problems related to diffusion-advection of a concentration field in a velocity field created by vesicles or capsules under flow have been treated recently (30, 31). In those studies, the vesicle/capsule membrane is fully transparent to the solute. That is, solute is advected passively by the flow. In our study, we will consider the problem of kinetics of ATP across the vesicle membrane. This requires implementation of an appropriate boundary condition on a curved and moving interface (i.e., a Neumann boundary condition for the ATP release).

ATP release modeling

The model of ATP release proposed has been inspired by in vitro experimental observations (6). Because this is essential information to our problem, we have felt it worthwhile to briefly recall the main experimental results.

Shear experiment

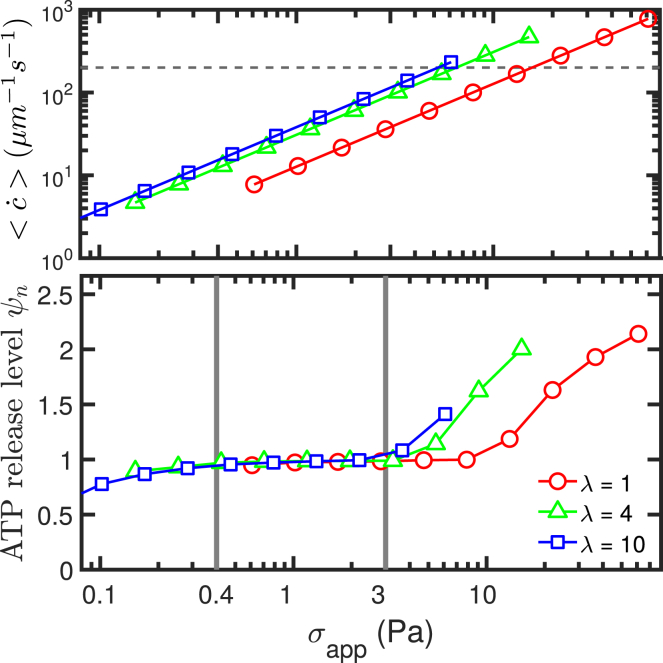
In the experimental study performed in (6), an RBC suspension was prepared at 1% hematocrit, implying negligible interaction among RBCs. Solutions were then mixed with dextran to create different viscosity contrasts λ by changing μ_ex, whereas μ_in = 0.012 Pa ⋅ s. The explored viscosity contrasts were λ = 1.6, 3.8, and 11.1. The RBC solutions were sheared in a cone-and-plate viscometer (shear rate ranges from 50 to 5000 s⁻¹) corresponding to different shear stresses mimicking physiological values in different blood vessels in vivo. After 30 s of exposure to the shear flow, the blood sample was mixed gently with bioluminescent luciferase/luciferin so that a photomultiplier could count the photon emission, which was proportional to the averaged value of the extracellular ATP concentration. Each data point of the experiment was averaged over five independent measurements. The apparent shear stress (defined as the product of the imposed shear rate and the effective viscosity of the suspension provided by the rheometer) and cell motion (TT or TB) were also recorded statistically thanks to several performed experiments.

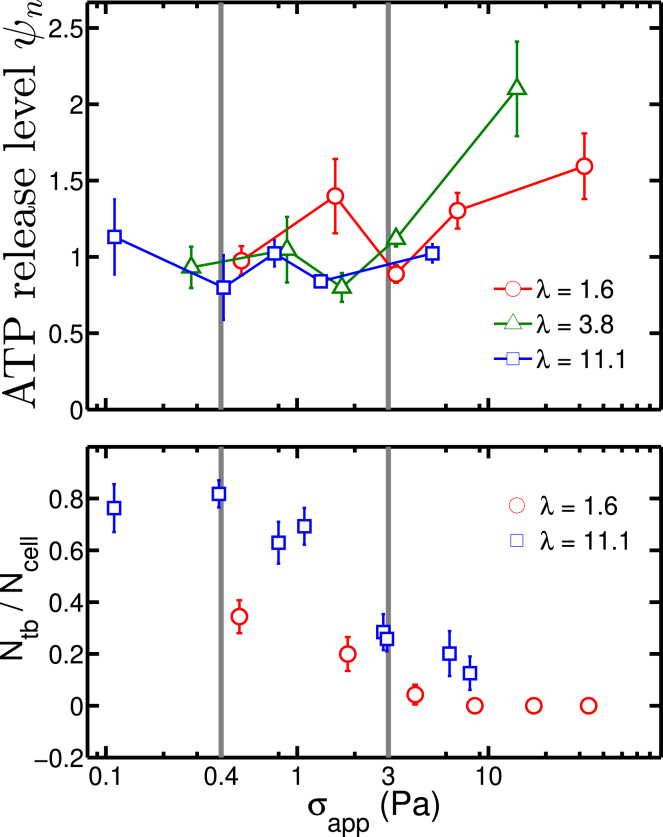
It was found that ATP release initiated at a critical shear stress σ_c ≤ 0.1 Pa (the lower limit of apparent shear stress in Fig. 2), and then the release level remained constant (a plateau regime). When the shear stress exceeded a value of about 3 Pa, the ATP release started to increase monotonically. In the first interval of shear stress (σ_c ≤ 0.1–3 Pa), most RBCs performed a TB motion. In this configuration, the cell underwent a solid-like motion with minimal shape deformation. This means that in this shear stress interval, once a critical shear stress is attained, the cell starts ATP release. Increasing the shear stress further does not increase the amount of ATP release. Beyond a shear stress of about 3 Pa, most of the cells performed a TT motion in which cell shape deformation becomes significant. A further increase of shear stress implies higher shape deformation and higher ATP release. In this regime (TT), the ATP release is attributed to shape deformation, whereas in the former regime (TB), a critical shear stress is needed for ATP release. This means that two main pathways can be identified: one related to a critical shear stress, and the other related to shape deformation.

Figure 2.

An adapted figure of ATP release level (upper panel) and tumbling (TB)/tank-treading (TT) motion data (lower panel) extracted from experimental study in (6). The data are categorized into three different zones: below 0.4 Pa is the range of shear thickening, in the middle range below 3 Pa is the range of shear thinning, and in the last zone beyond 3 Pa, the shear thinning stops, and a large portion of RBCs undergo TT motion. A detailed definition of ψ_n is given in Eq. 10. To view this figure in color, go online.

Other investigations focused on the molecular origin of ATP release support the idea that Px1 is the main avenue for shear-induced ATP release. This channel may also become activated because of a drop in oxygen content or in the presence of a high enough intracellular calcium concentration (8). It is assumed that this channel requires a critical shear stress for its activation. The increase of ATP release found in the TT regime is attributed to the CFTR. It is recognized that CFTR itself may not directly release ATP; rather, it upregulates Px1 so that a further increase of shear stress causes further deformation and thus amplifies the release. As described in the Introduction, CFTR activation requires the presence of actin; the latter is more likely to be freed when cell deformation is high enough (that is, in the TT regime).

Further support for the roles played by Px1 and CFTR are provided by data using specific inhibitors (6). Carbenoxolone and glibenclamide are used to inhibit the Px1 channels and CFTR, respectively. The study revealed that glibenclamide-treated RBCs no longer show increased ATP release with shear stress (TT regime). However, carbenoxolone-treated RBCs show a collapse of ATP release both in TT and TB regimes. In the TT regime, cell deformation is higher than in the TB one, but the collapse is similar in both regimes. This points to the fact that Px1 is a channel that is quite insensitive to cell deformation.

To summarize, the ATP release level is mainly affected by membrane shear stress σ_mem(t, s) and by deformation: once the membrane shear stress reaches a critical value, the Px1 becomes activated, and no further release takes place upon further increasing the shear stress. Once in the TT regime, CFTR enters into play to upregulate Px1, and because higher shear stress enhances cell deformation, an increasing upregulation of Px1 is expected with shear stress.

ATP release model

We have seen above that two mechanisms are possible, one associated with the level of shear stress and the other with the level of membrane deformation. A schematic representation of this model can be found in Fig. 3. Let us focus on the latter first. For this scenario, once the shear stress exceeds a value (inducing RBC TT regime), the ATP release level is amplified monotonically to induce CFTR activation. Because RBCs have no organelle or nucleus, we consider that cell reaction takes place at the RBC membrane. We quantify the deformation level by the local curvature. Once in the TT regime, the cytoskeletal material point will explore with time different cell membrane local curvatures. Let $\dot{c}\left(s\right)=\left|Dc\left(s\right)/Dt\right|$ denote the time derivative of local curvature quantifying the level of an instantaneous variation of deformation at a given point, where D/Dt is the time derivative on a fixed point on Lagrangian curvilinear coordinate s.

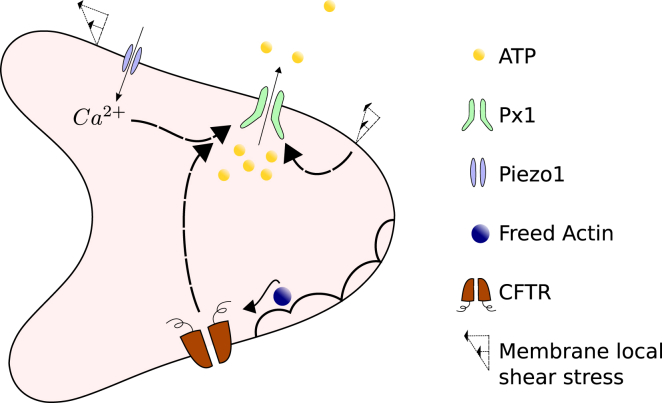
Figure 3.

Schematics of the ATP release pathway in RBC: Px1 is the main avenue for ATP release that can be activated by the local shear stress and Ca²⁺ ions; the Piezo1 cation channel can be activated by the local shear stress and trigger Ca²⁺ influx; actin is freed from deformation-induced cytoskeletal defects; CFTR is activated by freed actin and consequently upregulates Px1. To view this figure in color, go online.

The membrane local shear stress is given by σ_mem(s) = μ_ex|∂u_t(X(s))/∂n|, where t is the tangential vector. We can also define the apparent shear stress (for the sake of comparison with experiments) as ${\sigma }_{app}={\mu }_{ex}\left|\langle \partial u_x/\partial y\rangle \right|$, where the average is performed along the bounding wall in a shear experiment. The effective viscosity μ_eff of the suspension is given by ${\sigma }_{app}/{\dot{\gamma }}_w$, so that ${\mu }_{eff}{\dot{\gamma }}_w$ (used in experiments) coincides with the apparent stress.

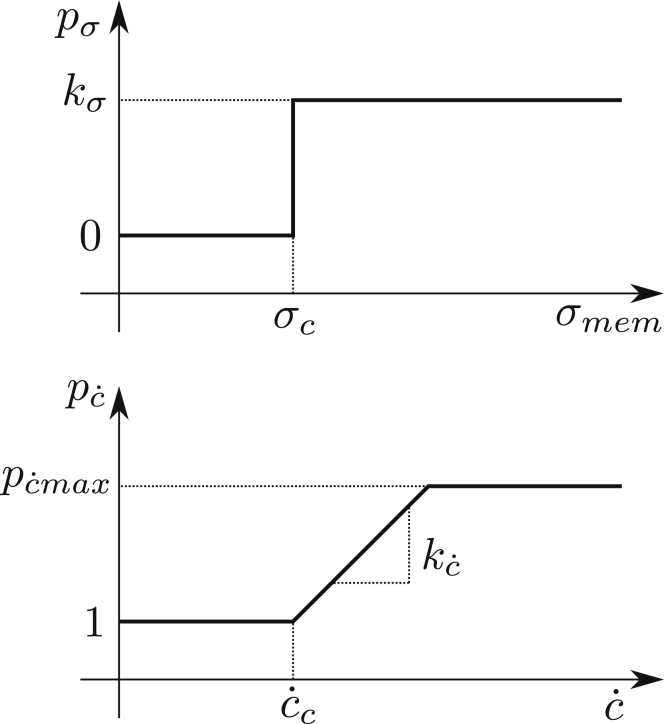
ATP release rate due to Px1 channels is modeled (Fig. 4, upper panel) as follows:

$$p_{\sigma }=k_{\sigma }\cdot H\left({\sigma }_{mem}-{\sigma }_c\right),$$ (7)

where H(x) is the Heaviside step function and k_σ is a phenomenological coefficient, which will be extracted from confrontation with experimental data on ATP release. The above equation expresses the fact that the channel is activated above a critical shear stress σ_c on the membrane. This effect does not depend on deformation. The deformation affects CFTR, which in turn upregulates Px1. The function expressing the fact that a curvature change will affect CFTR (Fig. 4, lower panel) is written as follows:

$$p_{\dot{c}}=min\left(1+k_{\dot{c}}\cdot \left(\dot{c}-{\dot{c}}_c\right)\cdot H\left(\dot{c}-{\dot{c}}_c\right),p_{\dot{c}max}\right).$$ (8)

Figure 4.

Schematics of contribution from shear stress (upper panel) and curvature change (lower panel) to ATP release.

Because CFTR affects the ATP release indirectly by upregulating Px1, $p_{\dot{c}}$ is understood as an amplification factor. The value of $p_{\dot{c}}$ is limited between 1 (no release because of deformation) and $p_{\dot{c}max}>1$. The existence of an upper limit, expressed by $p_{\dot{c}max}$, is based on the notion that there should exist a maximal amount of free actin and a limited level of activatable CFTR. The phenomenological parameter $p_{\dot{c}max}$ will be determined by comparison with experiments.

All together, we write the ATP release flux equation (Eq. 9) as a product between the two functions, namely

$$\psi =p_{\sigma }{p}_{\dot{c}}.$$ (9)

The product means 1) if the shear stress is below a critical value, there is no activation of Px1, and thus the flux vanishes; and 2) once the shear stress has exceeded a critical value, the Px1 pathway is activated, and even if no CFTR is present, ATP release takes place. If the curvature change is sufficiently large (beyond a critical value), CFTR is produced and amplifies the ATP release. We will see that these ingredients capture the essential experimental features.

We find it convenient to define a reference level of release, which we take to be the unity level and is defined as the total release when all points on the membrane have reached a shear stress σ₁ ≥ σ_c and a curvature change ${\dot{c}}_1\le {\dot{c}}_c$. We set ${\psi }_1={\int }_0^P\psi \left({\sigma }_1,{\dot{c}}_1\right)ds=k_{\sigma }P$. Thus, a normalized ATP release level can be quantified by the following ratio:

$${\psi }_n={\int }_0^P\psi \left(\sigma ,\dot{c}\right)ds/{\psi }_1,$$ (10)

which is an important indicator for the origin of release. Indeed, a value ψ_n > 1 means that the deformation of the cell contributes to ATP release.

For completeness, we would like to comment on some simplifying assumptions adopted here. In the upstream of the pathway (Fig. 3), the Piezo1 channel is activated by shear stress allowing calcium influx, which in turn indirectly activates Px1. This can be thought of as being absorbed into the value of k_σ as long as we are not interested in the details of calcium kinetics. In addition, the cytoskeletal defects leading to actin generation and CFTR activation are taken as simple and bounded linear functions of $\dot{c}$. The existence of a time delay for release mentioned in (5) is ignored. That is, we consider that all the reactions on the membrane take place on a much faster timescale than RBC deformation or shear stress change, despite the fact that they might have a comparable timescale when the blood flow is fast enough. Although the details of ATP renewal mechanism in RBCs are not well understood, bulk ATP generation occurs via a glycolysis process in the RBC cytoplasm, and under healthy conditions, blood sugar concentration has a quite stable value in plasma, around 5.0 mM. Thus, it is reasonable to assume that in the time interval of interest for ATP release, RBCs are saturated enough in ATP so that the release rate is not affected by the actual content of ATP.

Results and Discussion

ATP release under linear shear flow

Membrane shear stress and deformation behavior under flow

To test the model and to specify the range of parameters involved, we investigated the membrane shear stress and curvature change via numerical simulations. We refer to the experimental data in Fig. 2 (lower panel). It is found experimentally that the proportion of TB RBCs decreases as the apparent shear stress σ_app increases and the viscosity contrast λ decreases. The transition from TB to TT on increasing shear stress is attributed to the shear elasticity of the cytoskeleton, whereas the viscosity-contrast-dependent transition is due to hydrodynamic dissipation (18, 19, 20). Although the 2D vesicle model does not consider cytoskeleton, it can capture the viscosity-contrast-induced transition, which is the main reason for TT motion at a high σ_app regime. It will be seen below that if the ATP release is presented as a function of apparent shear stress itself, the behavior found in experiments and in simulations are very similar.

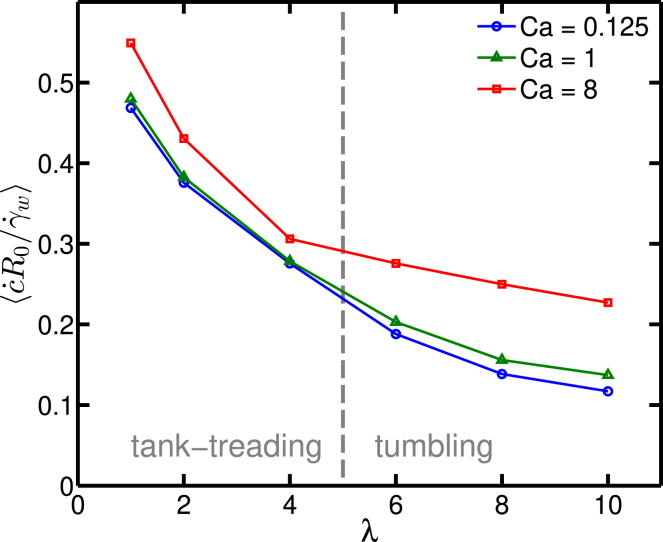
In the experiments, a dilute RBC suspension was considered (volume fraction of about 1%), so that the interaction among RBCs is negligible. It is thus sufficient to consider a single cell subject to a linear shear flow. We consider that a channel width of W = 12.5R₀ and length L = 25R₀ which results in a hematocrit 1.05% and a sufficiently weak confinement effect. We have explored the viscosity contrasts λ = [1, 2, 4, 6, 8, 10]. The reduced area is set to τ = 0.6 or 0.7, but no significant difference between these two values was detected in the results. We explored a wide range of capillary numbers Ca = [0.125, 1.0, 8.0]. Because the typical timescale for RBC deformation is in the range of 0.01 s (32), we have chosen our simulation time to be large enough as compared to that time. More precisely, the explored range goes from 0.5 to 10 s under different shear rates (recall that in the experiments of Forsyth et al. (6), the shear stress was applied during 30 s). During the full time interval of the simulation, we observed enough loops of repeatable periodic release pattern. The ATP release rate is then averaged over the simulation time after transients have decayed. The normalized mean curvature change (defined as $\langle \dot{c}{R}_0/{\dot{\gamma }}_w\rangle$) is shown in Fig. 5. A decrease in normalized curvature change is observed upon increasing λ, which implies a higher activation level of CFTR in TT situations than in TB cases. The inflection of the curve between λ = 4 and λ = 6 for Ca = 8 is attributed to the fact that when the capillary number is high, even if the cell shows TB, the distortion of the shape starts to play a role at that capillary number. Note that the capillary number in vivo and in the experiments of Forsyth et al. (6) remains smaller or comparable to unity. We have deliberately explored even higher values here to highlight the robustness of the results. Note that the values of the mean membrane shear stress $\langle {\sigma }_{mem}\rangle$ are very close to the apparent shear stress σ_app regardless of the values of the viscosity contrast λ and the capillary number Ca (see Fig. S2). Therefore, no real distinction will be made between these two quantities when representing the results (in fact, the experiments in (6) referred to σ_app).

Figure 5.

Curvature change versus viscosity contrast. To view this figure in color, go online.

Analysis of the ATP release from the model and confrontation with experiments

A systematic investigation has been conducted on different parameter values in Eqs. 7 and 8. By presenting the normalized ATP release ψ_n as a function of σ_app, we could compare the model behavior with the experimental data in Fig. 2 (upper panel). This investigation revealed that the proposed ATP release model provides qualitatively similar results to the experiments in that the value of σ_c is critical to the shape of plateau, ${\dot{c}}_c$ is sensitive to the position of inflection point (at 3 Pa in the experiments), and $k_{\dot{c}}$ and $p_{\dot{c}max}$ correspond to the slope and maximal value of ψ_n.

Although the ATP release criterion is linear, hidden nonlinearities are present because of the nonlinear shape dynamics of RBC. Thus, the fitting procedure is not an easy task. We have adopted a trial-and-error procedure to determine the parameter set in Table 1, which provides the most quantitatively comparable results to those reported by experiments (compare Figs. 2 and 6, upper panel). Note that because in Fig. 6 we only consider the normalized ATP release level, the value of k_σ is not needed at this level.

Table 1.

Parameters for ATP Release Model

Notation	Value	Origin
${\dot{c}}_c$	2 × 102μm−1 s−1	estimated
$k_{\dot{c}}$	6 × 10−3μms	estimated
$p_{\dot{c}max}$	2.5	estimated
σc	0.05 Pa	estimated
kσ	∼7 × 103 (nmol/L) ⋅ μm/s	estimated

Figure 6.

Mean curvature change (upper panel) and ATP release level (lower panel) versus apparent shear stress, with a reduced area τ = 0.7 and capillary number Ca = 1. The dashed line in the upper panel corresponds to the critical curvature change ${\dot{c}}_c$ beyond which ATP release due to deformation takes place. To view this figure in color, go online.

Smaller capillary numbers such as Ca = 0.125 and reduced area 0.6 or 0.7 provide almost identical results, as in Fig. 6. At larger values of Ca (Ca = 8), a deviation is observed (as testified by the behavior of the deformation amplitude in Fig. 5), especially at large enough λ. This is due to the fact that the membrane starts to develop buckling, even though the vesicle is tumbling. This enhances the effect of shape deformation and thus CFTR activation. For RBCs, buckling is quite rare; this is why we do not pay particular attention to this problem here.

Our results (Fig. 6) capture the plateau below 3 Pa seen in the experiments (Fig. 2, upper panel), which is associated mainly with the TB regime, as well as the increase of ATP release with shear stress associated mainly with the TT regime. This has allowed us to fix the model parameters. In addition, our results reproduce well the amplitude of variation of ATP release, from the small shear stress to the highest one.

Actually, at small enough apparent shear stress in Fig. 6 (below ∼0.3 Pa), the ATP release shows a small drop, whereas our model (Eq. 7) would have suggested that the ATP release, once it takes place, would follow the plateau level. In fact, our criterion is local (it senses the local stress), whereas Fig. 6 refers to an apparent stress. The local threshold can thus be significantly lower than the average one. In other words, for small apparent shear stress, it is possible that only few localized points on the membrane can release ATP (see Fig. 7).

Figure 7.

A snapshot showing the inhomogeneous ATP release along the membrane, with τ = 0.6, λ = 8, Ca = 1, ${\dot{\gamma }}_w=50{\mathrm{s}}^{-1}$, and Peclet number 1.91. In this situation, the magnitude of ${\sigma }_{mem}\approx {\dot{\gamma }}_w\cdot {\eta }_{ex}=0.075\text{Pa}$ is close enough to σ_c = 0.05 Pa, which leads to strong inhomogeneity of ATP flux along the membrane (not each membrane point reaches its threshold value at a given time). The contour map from white to red represents a relative local concentration, whereas the blue arrows represent the velocity field, and the black dot on the membrane is a virtual tracer particle. The unit for the color bar is nmol/L, but note that the concentration gradient in the normal direction along the membrane is more relevant because it is proportional to the ATP release rate. T, time. To view this figure in color, go online.

Hitherto, we have only described the normalized value of ATP release and not the absolute level of this release. To estimate the absolute value, we need to evaluate k_σ. Confrontation of our model with experiments (6) suggests the value given in Table 1. This is estimated by considering the RBC volume, surface area, and average ATP concentration in plasma (a₀ ≈ 1000 nmol/L; see (33)). The precise way for determining k_σ is explained in the Supporting Materials and Methods.

Note that the actual value of the critical shear stress σ_c still suffers from some uncertainties. Combining the outcomes from experiments in a linear shear flow (6) and in a Poiseuille flow experiment from (5) suggests that this value lies in the range 0.02–0.1 Pa. Further systematic experiments will be needed to acquire more statistics with the hope of better refining our estimates.

Finally, our model shows that in some shear rate ranges (${\dot{\gamma }}_w>2000\mathrm{Hz}$ in this study), an increase in internal viscosity, μ_in, triggers a decline in ATP release level. This is attributed to the fact that a hardened cell (due to an increase of internal viscosity) implies a smaller level of membrane deformation and thus a decline in ATP release. This suggests that pathologies leading to an increase in RBC rigidity may be associated with an impairment in ATP release (see Fig. S3).

ATP release in confined Poiseuille flow

To study how the ATP release happens in microcirculation, we start from long straight channels that mimic the precapillary arteriole. Vesicles, as well as RBCs under Poiseuille flow, have shown various shapes and dynamics (13, 14, 15, 16). Typical examples are parachute and slipper shapes. The observed shapes and dynamics depend, in particular, on flow conditions (capillary number, confinement, etc.). Because our study focuses here on a 2D vesicle, we shall refer to the phase diagram of shapes obtained in (13), in which besides the parachute and slipper shapes, a snaking motion is also revealed. We consider here also a single vesicle. In capillaries, the hematocrit is quite low (it can drop down to 5% (34, 35)) so that focusing on a single cell constitutes a reasonable assumption. The imposed flow is of Poiseuille type. We define the degree of confinement as Cn = 2R₀/W. We recall the general definition of the capillary number $Ca={\mu }_{ex}{\dot{\gamma }}_w{R}_0^3/\kappa$. The wall shear stress in a Poiseuille flow is given by ${\dot{\gamma }}_w=4u_{max}/W$, where u_max is the maximal velocity at the channel centerline. Assuming that an RBC has a characteristic radius around R₀ = 3 μm and bending modulus κ = 3 × 10⁻¹⁹ J, we can map the nondimensional pair (Ca, Cn) onto physical units (u_max, W) if need be. We have the following relations:

$$\begin{array}{c}{u}_{max}=\frac{\kappa }{2\mu R_0^2}\frac{Ca}{Cn}\\ W=\frac{2R_0}{Cn}\end{array}$$ (11)

We explored Ca = [5, 10, 15, 50, 90] and Cn = [0.15, 0.3, 0.45, 0.6, 0.75]; the length of the periodic simulation box is fixed at L = 53.3R₀, which is validated to be long enough to eliminate artifacts due to periodic boundary conditions. The resulting ATP release levels are shown in Fig. 8.

Figure 8.

ATP release levels for Poiseuille flow in long straight channels. To view this figure in color, go online.

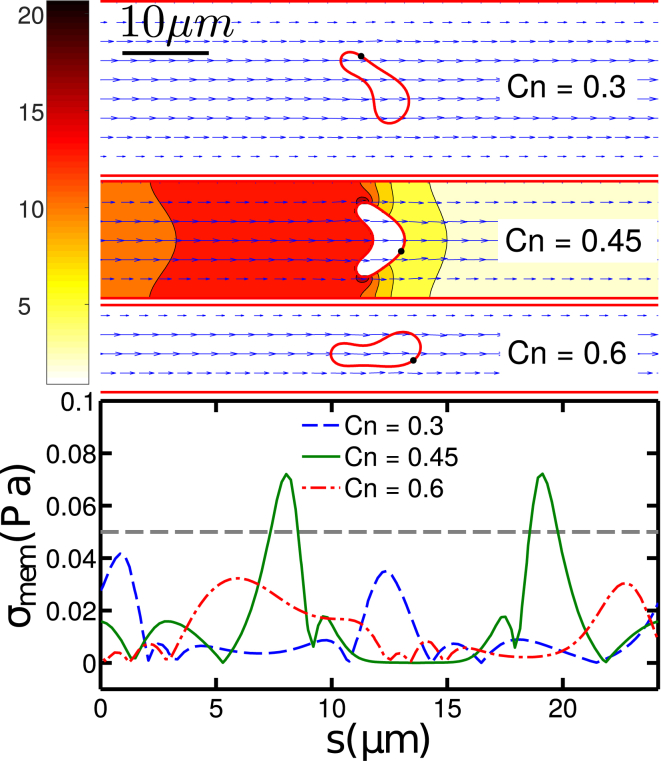
It is quite intuitive that the shear stress generally increases with both the confinement and the capillary number. For Ca > 15, the ATP release level increases monotonically by reducing the channel width for a fixed pressure drop. The subtle peak at Ca < 10 and Cn ≈ 0.45 in Fig. 8 is due to the slipper-parachute-slipper/snaking transition (13). Indeed, the parachute shape, which occurs for Cn = 0.45, has a larger cross section in the channel than the snake-like shape (Fig. 9, upper panel). This larger cross section implies a higher membrane shear stress σ_mem at two endpoints of the parachute (Fig. 9, lower panel)

Figure 9.

Plasmic ATP concentration (upper panel) and membrane shear stress distribution (lower panel) for Ca = 5 and Cn = [0.3, 0.45, 0.6]; corresponding Peclet numbers are Pe = [23.5, 10.5, 5.9], respectively. The unit for the color bar is nmol/L. Note that the ATP release rate is proportional to the concentration gradient in the normal direction to the membrane. When Cn = 0.45, the RBC assumes a parachute shape and has a nonzero ATP release at two lateral end points. The horizontal dashed line in (lower panel) indicates the critical membrane shear stress σ_c = 0.05 Pa. To view this figure in color, go online.

An important remark is in order. The curvature change (shape deformation) level of this single vesicle in the long straight channel never reaches the activation threshold of CFTR (the largest $\dot{c}$ is still one order of magnitude smaller than ${\dot{c}}_c$ (see Fig. S5)). This means that the ATP release effect due to deformation is weak in such a geometry, at least for a single cell. It must be kept in mind, however, that in vivo RBCs often meet bifurcations in the microcirculation where they experience large shape deformation. This naturally leads us to discuss the effect of bifurcations.

ATP release at and after a bifurcation

The microcirculation involves a complex vessel network. RBCs flowing in arteries enter arterioles and then capillaries. During their travel in the microcirculation, they experience a cascade of branching vessels. Many numerical studies have been performed in single or multiple bifurcations regarding more or less complex models of blood flow (36, 37, 38, 39, 40, 41). The arterioles are wrapped by smooth muscle cells and are well innervated, so in principle they are capable of controlling their pressure via vasomotion. The capillary vessels are not endowed with smooth muscle cells, so that their pressure gradient can only be passively affected thanks to arterioles located upstream. The presence of ATP as a signaling molecule may offer another alternative. If a sufficient amount of ATP is released from RBCs at downstream capillaries (because of their ample deformations), a reaction with purinergic receptors (a class of membrane receptors that mediates vascular reactivity, etc.) (42, 43) on the surface of ECs will lead to an intercellular calcium/eNOS (endothelial nitric oxide synthase) signal. This signal can be transmitted to neighboring ECs (in the form of waves) until reaching arterioles, ultimately giving rise to vasodilation in arterioles.

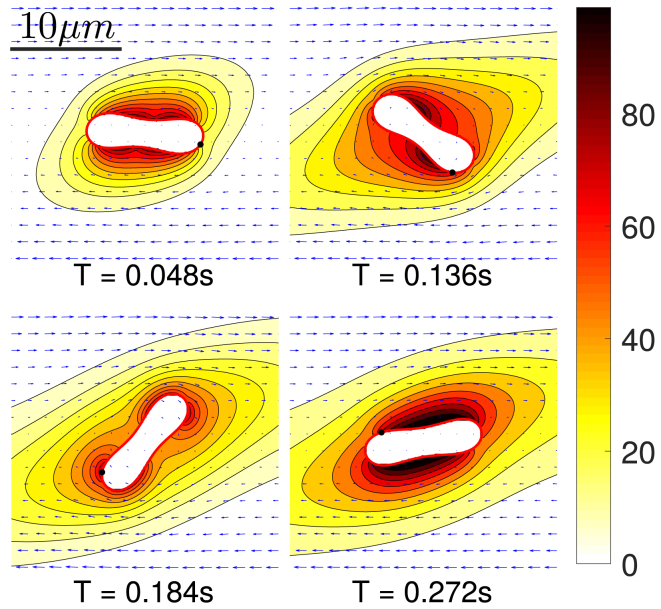
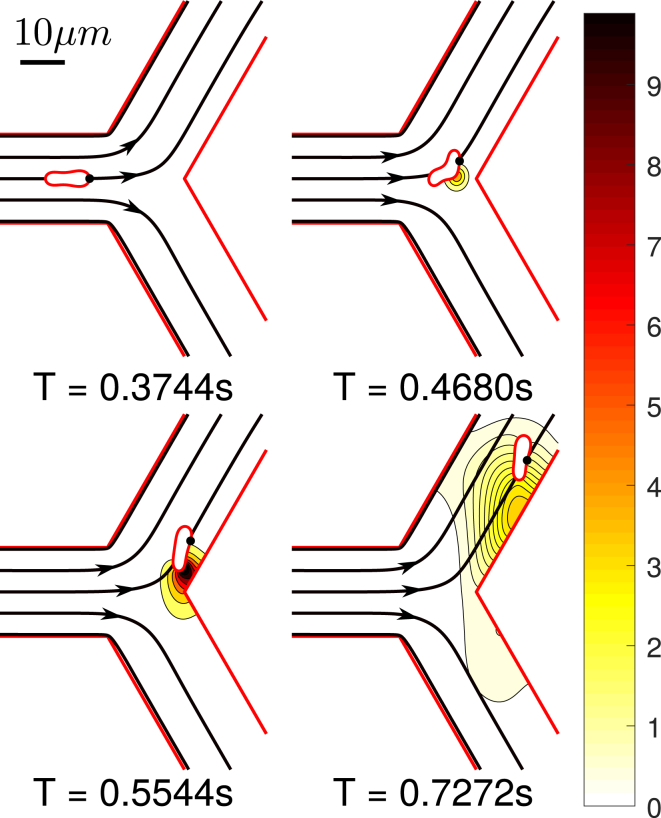
In precapillary and capillary networks, the topological complexity can significantly contribute to the ATP release. Indeed, an RBC frequently encounters bifurcations. At this point, the cell is strongly deformed (see Fig. 10) when entering a new vessel and scrapes initially along the vessel wall while progressively moving away from the vessel wall because of a well-documented wall-induced lift force (17, 44, 45, 46, 47, 48). Before the RBC hits a new bifurcation, it travels a length of about 100 μm in capillaries. This scenario is reproduced in our simulation (Fig. 10). Close to the wall, the cell has a larger membrane shear stress and higher deformation rate as compared to the centered cell in a channel. This means that after each branching, a higher ATP release will occur in RBCs. We measured the distance needed for an RBC to return to the daughter branch channel center and thus to the (low) level of release we obtained above for a straight channel. We find that this distance is typically comparable to or longer than the characteristic vessel branching length in the microcirculation. This implies that RBCs are likely to strongly enhance their ATP release in the microvasculature thanks to the cascade of bifurcations.

Figure 10.

Snapshots of bifurcation scenario with inlet (Ca, Cn) = (5, 0.3) and Pe = 1.06. The ATP release starts when the cell approaches bifurcation vertex and ends when it migrates close enough to the centerline. The unit for the color bar is nmol/L. Note that the ATP release rate is proportional to the concentration gradient in the normal direction to the membrane. Streamlines are shown with black arrows. One may notice that the RBC motion is highly correlated with its local streamline. At T = 0.4680 s, one may see that the RBC is largely deformed before hitting the vertex and this is due to the fact that the streamlines point towards the daughter branch. T, time. To view this figure in color, go online.

We have selected a demonstrative case to show the ATP release of a cell hitting a bifurcation. The geometry is composed of one straight vessel with (Ca, Cn) = (5, 0.3) as the inlet and two outlet vessels with (Ca, Cn) = (3.0, 0.3) and (Ca, Cn) = (2.0, 0.3). Their capillary numbers are preset to different values, rather than identical, to avoid perfect unrealistic symmetries that artificially lead to a high residence time at the bifurcation vertex before the cell selects one of the two daughter vessels. The cell is initially positioned at the centerline of the inlet with a relaxed biconcave shape. Fig. 10 shows snapshots of the cell position before, at, and after the bifurcation. Fig. 11 shows the lateral position and normalized ATP release situation during this process.

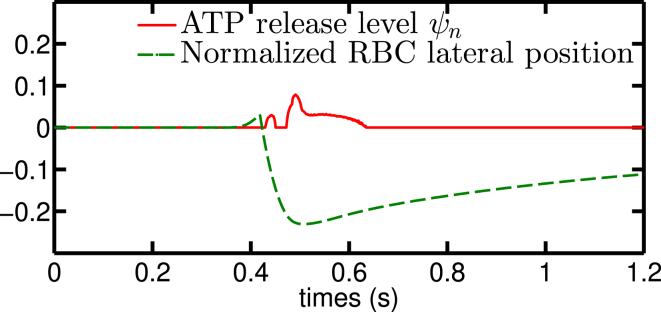
Figure 11.

A bifurcation configuration composed of inlet and outlet with parameters that do not release ATP shows a slight nonzero release level when the RBC “hits” the bifurcation point. The lateral off-center position correlates strongly with the release level. This implies that the edge-to-center migration affects the ATP release process. The lateral position is defined as the ratio between vessel diameter and the minimal distance of the centroid of RBC to the closest point on centerlines of all vessels, valued from −0.5 to 0.5. To view this figure in color, go online.

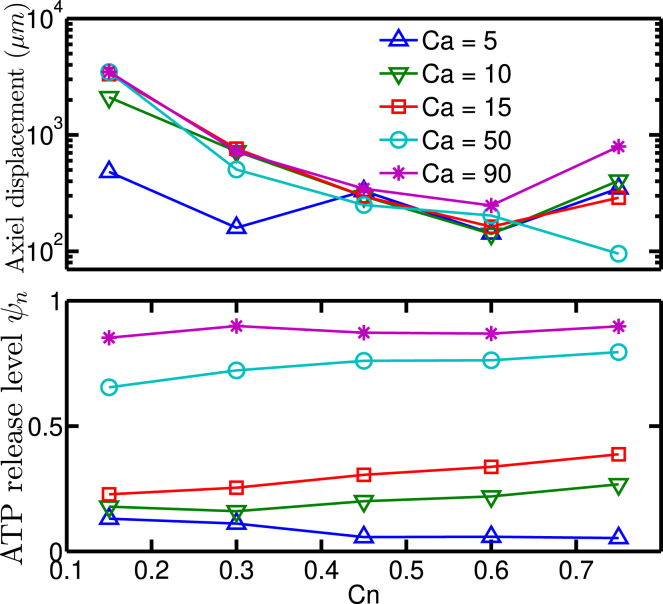
Once the cell hits the bifurcation, it deforms significantly close to the wall and begins to lift off until it reaches the centerline. We have analyzed the ATP release during liftoff. The lateral migration after a bifurcation is a robust feature. We have also investigated the effects of different bifurcation angles, initial positions, and capillary number (see Fig. S6). It is found that the overall features reported above are not significantly affected. We have found that it is sufficient to consider the case of a straight channel with the cell located initially in the vicinity of the wall. Because the timescale for shape response to stress is fast (as compared to the migration time), this is practically equivalent to following the cell from a bifurcation. We explored again the ranges Ca = [5, 10, 15, 50, 90] and Cn = [0.15, 0.3, 0.45, 0.6, 07]. It can be seen in Fig. 12 that during a typical liftoff (where the ATP release reaches approximately its basal level for a straight channel), the cell would have traveled about 100–1000 μm, which is comparable to the typical micro-vessel length of precapillary and capillary networks. The observed nonlinearity at Ca = 5 and Cn = 0.6 is mainly due to the transition between parachute-to-slipper or snaking evoked before. We clearly see that the ATP release level is dramatically different from that obtained for long straight channels when the confinement Cn is smaller than ∼0.5, which corresponds to 12 μm. This is a typical value for arterioles connecting capillaries. When Cn > 0.5, the normalized ATP release is, however, not affected much by this lateral migration.

Figure 12.

RBC axial displacement (upper panel) and normalized ATP release level (lower panel). The measurement is during the process of an RBC migration from the wall to the center, ending up with a steady shape and ATP release level. Comparing the lower panel presented here to Fig. 8 shows that for low confinement, the lifting process causes more ATP release than when the cell is in a steady centered shape. To view this figure in color, go online.

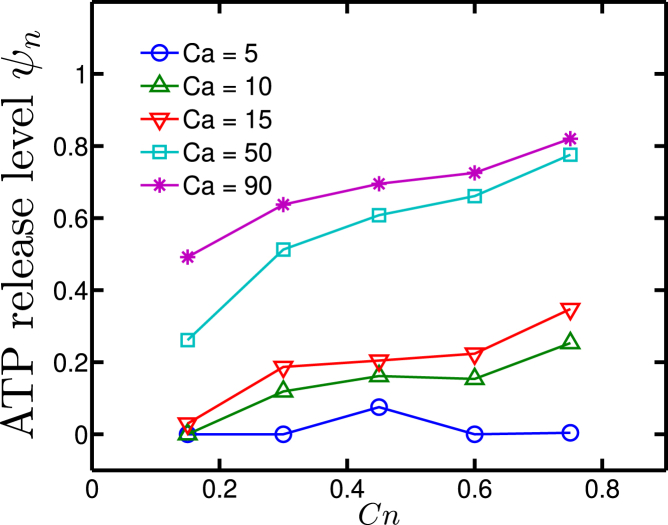
We also confirmed that the release is amplified by large curvature change when Ca ≥ 50 (Fig. 13). When an RBC is close to the wall, the membrane shear stress can be estimated as ${\sigma }_{mem}\sim {\sigma }_{wall}={\dot{\gamma }}_w{\mu }_{ex}=\kappa /R_0^{3}Ca$. This value is around 0.5 Pa, which is significantly below the value beyond which the deformation component of the ATP release takes place for the linear shear experiments (which is ∼3 Pa; see Fig. 6). A possible explanation is that the capillary number is high and that the presence of the wall induces strong distortion of the vesicle, making the local deformation high as compared to the linear shear flow, despite the fact that the apparent shear stresses are similar in both cases.

Figure 13.

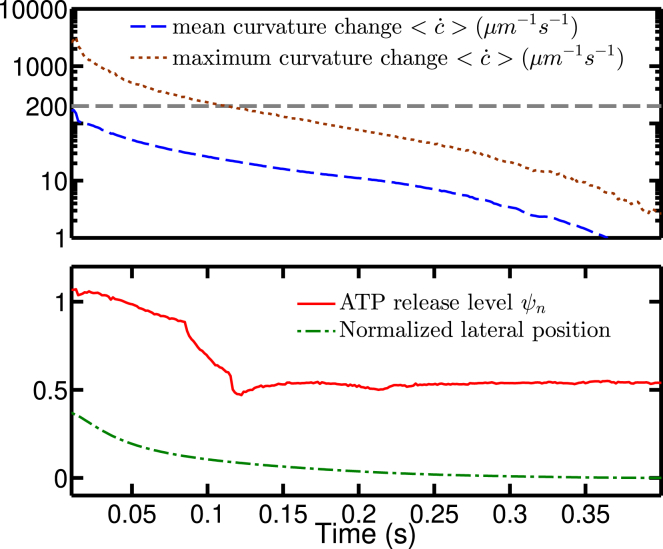
The upper panel shows the history of mean and maximal curvature change during the migration process at (Ca, Cn) = (50, 0.3). The horizontal gray dashed line corresponds to the value of the critical curvature change ${\dot{c}}_c=200\mu {\mathrm{m}}^{-1}{\mathrm{s}}^{-1}$; the lower panel shows the ATP release level and normalized lateral position history at (Ca, Cn) = (50, 0.3). To view this figure in color, go online.

To exemplify the effect of shape deformation close to the wall, Fig. 13 gives an example at (Ca, Cn) = (50, 0.3) where one finds that the deformation does affect ATP release level when the RBC is close enough to the wall. It also means that if a vessel network has a shorter characteristic length than usual, it may result in more ATP release per RBC.

Conclusions

In this work, we have proposed a model for ATP release from RBCs and have explored it numerically. We have addressed the question of how geometry and stress amplitude in precapillary networks affect the ATP release from RBCs. With the help of experimental data, numerical simulations, and assumptions on molecular mechanisms, we were able to fix the model and its parameter values that generate results that semiquantitatively match existing in vitro shear experiments. In this model, the mechanical properties are mainly represented by membrane shear stress and curvature change (as an indicator of deformation level). At the molecular level, the Px1 hemichannel is considered as a main player of ATP release thanks to its sensitivity to shear stress level. When the cell deforms significantly, another mechanism becomes possible, in which free actin is detached (because of high deformation) from cytoskeletal defects, which in turn activate the CFTR protein. The latter then upregulates Px1 to promote ATP release. Interestingly enough, despite the oversimplification of the model—using only a Heaviside step function (for shear stress sensing) and a bounded linear function (for deformation sensing)—the model remarkably captures the essential pattern of ATP release reported in in vitro shear experiments.

A lattice-Boltzmann-based numerical solver coupling vesicle dynamics and solute advection-diffusion with arbitrary moving boundary conditions has been developed. This solver is straightforwardly applicable to more detailed models in the future, including multicellular systems in complex geometry.

An estimate of the distance needed for an RBC after hitting a bifurcation before it returns back to its ATP release level of a steady shape in a long straight channel has been investigated. We found that this distance is hundreds of microns for confinements smaller than 0.3 (20 μm in diameter) and thousands of microns for a confinement of 0.15 (40 μm in diameter). This value is comparable or larger than the typical length of a blood vessel branch in precapillary arterioles or large capillaries, which implies that bifurcations boost the mechanically dependent ATP release in the microvasculature.

Author Contributions

H.Z. has developed the ATP model and the corresponding code and performed simulations. Z.S. has developed the code dealing with fluid flow. B.H. has participated in the model development. A.I.B. has contributed in designing the research plans. C.M. has designed the research topic and plans. All the authors have contributed to the article writing and interpretations.

Editor: Alexander Dunn.