Abstract
Purpose
Use Compressed Sensing (CS) for three dimensional (3D) biexponential spin-lattice relaxation time in the rotating frame (T1ρ) mapping of knee cartilage, reducing the total scan time and maintaining the quality of estimated biexponential T1ρ parameters (short and long relaxation times and corresponding fractions) comparable to fully-sampled scans.
Methods
Fully-sampled 3D-T1ρ-weighted datasets were retrospectively undersampled by factors 2–10. CS reconstruction using twelve different sparsifying transforms were compared for biexponential T1ρ-mapping of knee cartilage, including temporal and spatial wavelets and finite differences, dictionary from Principal Component Analysis (PCA), K-means Singular Value Decomposition (K-SVD), and exponential decay models, and also low rank and low rank plus sparse models. Synthetic phantom (n=6) and in vivo human knee cartilage datasets (n=7) were included in the experiments. Spatial filtering prior to biexponential T1ρ parameter estimation was also tested.
Results
Most CS methods performed satisfactorily for an acceleration factor (AF) of 2, with relative median normalized absolute deviation (MNAD) around 10%. Some sparsifying transforms, such as low rank with spatial finite difference (L+S SFD), spatiotemporal finite difference (STFD), and exponential dictionaries (EXP) significantly improved this performance, reaching MNAD below 15% with AF up to 10, when spatial filtering was used.
Conclusion
Accelerating biexponential 3D-T1ρ mapping of knee cartilage with CS is feasible. The best results were obtained by STFD, EXP and L+S SFD regularizers combined with spatial pre-filtering. These three CS methods performed satisfactorily on synthetic phantom as well as in vivo knee cartilage for AFs up to 10, with median error below 15%.
Keywords: T1ρ relaxation, biexponential model, compressed sensing, sparse reconstruction, low rank
INTRODUCTION
Osteoarthritis (OA) is the most common form of arthritis and a leading cause of chronic disability in the elderly population (1,2). Currently, OA affects more than 27 million people in the United States alone, generating high expenses to the healthcare system (3,4). OA is connected with the degradation of components of the extracellular matrix (ECM) of articular cartilage (5), mainly composed by proteoglycan (PG), collagen fibers and water (6). Early diagnosis of cartilage degeneration requires detection of changes in PG concentration and collagen integrity, preferably noninvasively and before morphological changes occur (7,8).
The spin–lattice relaxation rate in the rotating frame (R1ρ) has been shown to decrease linearly with the decreasing PG content of articular cartilage (9). Several researchers (10,11) have demonstrated that the spin–lattice relaxation time in the rotating frame (T1ρ) is more sensitive to proteoglycan content of the cartilage, while spin–spin relaxation time (T2) is more sensitive to collagen orientation and integrity of network and hydration. Most of the previous studies (7,8,11) have utilized the monoexponential models to characterize the T1ρ relaxation mapping of articular cartilage in the knee joint. However, the monoexponential estimation of T1ρ alone is not able to provide information on short and long components and their fractions.
Recent studies (12–14) have shown that T1ρ relaxation may have multiexponential components, following the hypothesis of multicompartmental structure. In (13), it was shown that biexponential models for T1ρ can bring more information about the ECM composition in human knee cartilage.
The quantitative 3D-T1ρ mapping usually requires the use of four or five T1ρ-weighted images with different spin-lock lengths (TSLs) to obtain the monoexponential T1ρ maps (15). However, biexponential analysis of cartilage typically requires a larger number of TSLs in order to maintain accuracy and the precision of biexponential T1ρ quantification (13), resulting in a long scan time. High spatial resolution is also needed in order to visualize the thin and curved cartilage and fine structures in the knee joint. As a result, in vivo application of biexponential 3D-T1ρ mapping techniques is still very limited.
An effective alternative is compressed sensing (CS) (16) to reduce the total scan time in quantitative T1ρ mapping. This fast magnetic resonance imaging (MRI) uses pseudo-random k-space undersampling (17) that generates (intentionally) noise-like artifacts in standard reconstruction. However, exploiting the compressibility, or sparsity, of magnetic resonance (MR) image representation in transformed domains, CS effectively removes these artifacts, recovering most of the original image (18). Moreover, CS can make use of multicoil, or parallel, imaging for further increases in speed (19). Recently, several CS methods have been applied to high-dimensional MR imaging such as dynamic imaging (20,21). Moreover, parametric relaxation mapping (22–25) is particularly suitable for CS due to increased compressibility in the parameter direction, which turns into higher accelerations.
Studies such as (25–29) and (30) have demonstrated that a reduction in acquisition time using CS is possible for monoexponential T1ρ mapping of cartilage, brain and intervertebral disc. Nevertheless, the feasibility of CS for biexponential T1ρ mapping has not been demonstrated yet.
In this paper, we extend our previous experiments of CS for monoexponential mapping (30) to biexponential mapping. The feasibility of using CS to accelerate biexponential 3D-T1ρ mapping is evaluated for knee cartilage by comparing twelve different types of sparsity promoting functions on synthetic phantoms (with and without noise) and in vivo knee cartilage datasets. Our main aim is to answer the question of what are the best regularization penalties and suitable acceleration factors for CS reconstruction with least components error when the final objective is to reduce image acquisition time of biexponential 3D-T1ρ mapping of human articular cartilage.
METHODS
MRI Data Acquisition and Standard Reconstruction
Seven in vivo human knee 3D-T1ρ-weighted datasets were acquired with 10 different TSLs using a modified 3D Cartesian turbo-Flash sequence (13). The MRI scans were performed using a 3T clinical MRI scanner (Prisma, Siemens Healthcare, Erlangen, Germany) with a 15-channel Tx/Rx knee coil (QED, Cleveland OH). The 3D-T1ρ acquisition parameters were: TR/TE=7.5ms/4ms, flip angle=8°, matrix size 256×128×64, longitudinal magnetization restoration delay=1020ms, 64 k-space lines captured per preparation pulse, spin-lock frequency=500Hz, slice thickness=2mm, field of view (FOV)=120mm×120mm, and receiver bandwidth=515 Hz/pixel.
The T1ρ-weighted scans of the knee were acquired in sagittal plane from seven healthy volunteers (age=29.6±7.5 years), with 10 TSLs including 2/4/6/8/10/15/25/35/45/55ms, and total acquisition time of 32 minutes. The T1ρ-protocol was repeated on three volunteers on the same day for repeatability evaluation. This study was approved by the institutional review board (IRB) and all the volunteers consented before scanning.
SENSE reconstruction (31,32) of the fully-sampled data was utilized as reference. The coil maps, required by SENSE, were estimated using ESPIRiT (33) from the central k-space area.
Synthetic Phantom
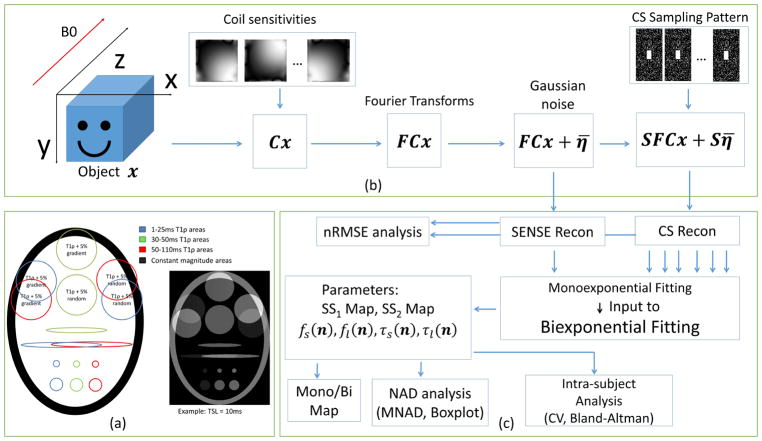
The utilized synthetic phantom is described in (30) and illustrated in Figure 1(a). It is composed of three T1ρ relaxation areas with times: 1–25ms (blue), 30–50ms (green) and 50–110ms (red). Two areas partially intersect, generating a biexponential model (13). Other areas are purely monoexponential. As described in (30), the magnitudes in some areas are randomly selected, generating intersection areas with 10% dispersion from 50/50 in the fractions of short and long components of the biexponential.
Figure 1.
(a) Synthetic phantom utilized in the experiments, composed of three areas with different T1ρ time ranges. The T1ρ relaxation times were randomly selected from the ranges 1–25ms, 30–50ms, and 50–110ms, intersections generate a biexponential signal. (b) MRI acquisition model used for CS reconstructions, including coil sensitivities C, Fourier transform F, and k-space undersampling pattern S using Poisson disk with fully-sampled central area, also additive white Gaussian noise η̄. (c) Diagram of the process, including reconstruction, fitting, mono/biexponential detection, reconstruction and fitting error analysis and intra-subject analysis.
The k-space dataset was created by multiplying the phantom images by coil sensitivities, 4-coils were utilized, followed by 2D Fourier transform. White Gaussian noise was added to the data in k-space for the noisy experiment, with its standard deviation set to 17% of the mean signal amplitude, resulting in an acquisition SNR of 15dB (5.62 in linear scale). The acquisition SNR is defined as SNR = 10 log ||FCx||2/||η||2, from the model: y = FCx + η with F and C described in equation [1] (not to be confused with image SNR, which is the visually observed noise in the reconstructed images and depends on the type of reconstruction).
Retrospective Undersampling
3D k-space data were retrospectively undersampled along the two-phase encoding dimensions (ky and kz) after applying 1D Fourier transform along the frequency encoding direction (kx). As shown in Figure 1(b), the ky-kz data were undersampled following a 2D Poisson disk random pattern (34). The acceleration factor (AF) is defined as the ratio of total k-space samples by the number of measured k-space samples. A central rectangular k-space area was not undersampled and also used for coil sensitivity map estimation (31×15 for AF=2, 21×9 for AF ≥ 4, on a 128×64 fully-sampled captured datasets, and 63×63 for AF=2, and 41×41 for AF ≥ 4, on a 256×256 fully-sampled synthetic dataset).
CS Reconstruction Algorithms
Following (30), twelve different regularization functions are compared for CS. All the compared regularization functions are found in the image reconstruction literature, even though not tested for this specific problem, and are good candidates for this problem, as detailed below. The regularization penalties, described in Table 1, use l1-norm with different sparsifying transforms, nuclear-norm (35,36) of the Casorati matrix representation of the image, i.e. low rank (LR) model, and the low rank plus sparse (L+S) model, where the nuclear-norm and the l1-norm are combined (37). In the Casorati matrix, each row contains the magnetization signal of one particular voxel over TSL.
Table 1.
Different compressed sensing methods, their corresponding equation problem and minimization algorithm, a brief description, average number of iterations to converge and the average processing time to converge.
| CS Method | Equation | Minimization algorithm | Transform/Dictionary | Avg. iterations | Avg. Time |
|---|---|---|---|---|---|
| TFD 1 | [1] | FISTA -FGP | Temporal finite difference of order 1 | 40 | 514 sec |
| TFD2 | [1] | FISTA -FGP | Temporal finite difference of order 2 | 60 | 684 sec |
| TFD3 | [1] | FISTA -FGP | Temporal finite difference of order 3 | 80 | 691sec |
| STFD | [1] | FISTA-FGP | Spatial and temporal finite difference, spatial order 1 and temporal order 2 | 120 | 1298 sec |
| WAV | [2] | FISTA | 3D Wavelet transform (2D+time) Daubechies 4, with 4 levels of decomposition. | 43 | 1005 sec |
| PCA | [2] | FISTA | Unitary transform from temporal PCA of fully-sampled data | 43 | 121 sec |
| KSVD | [2] | FISTA | Overcomplete temporal dictionary computed from fully-sampled data using KSVD | 400 | 249 sec |
| EXP | [2] | FISTA | Overcomplete temporal dictionary of exponentials with 100 relaxation times between 1 and 300 ms | 400 | 1290 sec |
| LR | [3] | Modified FISTA | Applied to a NyNz × Nt matrix formed with the reshaped NyNzNt × 1 vector. | 38 | 194 sec |
| L+S | [4] | Modified FISTA | Same as LR, plus identity for l1-norm | 80 | 218 sec |
| L+S SFD | [4] | Modified FISTA-FGP | Same as LR, plus spatial finite difference for l1-norm | 120 | 837 sec |
| L+S WAV | [4] | Modified FISTA | Same as LR, plus 2D spatial wavelet for l1-norm, also Daubechies 4, with 4 levels. | 55 | 1052 sec |
The l1-norm (16) regularized CS problems are posed as:
| [1] |
or
| [2] |
where x is a vector that represents the reconstructed image sequence, originally of size Ny × Nz × Nt, with Ny being the image size in the y-axis and Nz the size in the z-axis, Nt is the number of TSLs. y is a vector that represents the captured k-space, with original size of Ny × Nz × Nt × Nc, where Nc is the number of coils. The matrix C contains the coil sensitivities and F the Fourier transforms of each sensitivity-weighted image. The undersampling matrix S is a diagonal matrix, where the non-sampled k-space points have zeros in their diagonal positions; the respective elements in y are replaced by zeros as well. The squared l2-norm or Euclidean norm, , is the sum of the squared magnitudes, the l1-norm, ||u||1, is the sum of the magnitudes, and λ is the regularization parameter. The transform T and dictionary D in the regularization term are chosen as described in Table 1.
In Table 1, transform T contains the temporal finite differences (FD) of order 1, 2, and 3 for TFD1, TFD2, or TFD3. Those are temporal only high-order total variation (TV) (38–40). Also, T may contain the spatiotemporal FD (STFD) (40–42) set to order 1 spatially and order 2 temporally.
Fixed dictionary models for D are utilized for 3D wavelet transform (43), WAV in Table 1, or for overcomplete multiexponential dictionary D, EXP in Table 1 (44,45), with much more columns than rows. Learned dictionary models for D can be created using temporal principal component analysis (PCA) (46), using singular value decomposition (SVD) on the Casorati representation (23), or the K-SVD (47). In the case of the K-SVD, an overcomplete dictionary D is computed, instead of an orthogonal transform, as in PCA.
The LR reconstruction is defined as:
| [3] |
In [3], ||x||* represents the matrix nuclear-norm (35) where x is reshaped as a NyNz × Nt Casorati matrix, and the SVD is utilized at each iteration using the currently available reconstruction (48).
The L+S reconstruction (37) is given by:
| [4] |
where x is decomposed into a sparse part s and a low rank part l, recombined by x = l + s. The low rank part uses of the nuclear-norm ||l||*, while the sparse part uses of the l1-norm with a specific sparsifying transform T, as listed in Table 1 for L+S reconstructions. This is also an overcomplete description of the images to be reconstructed (49). The highly correlated temporal part is represented by the LR component, while the temporally varying part, usually sparse in some spatially transformed domain, is represented by the sparse part. In (50), a similar combination of low rank and wavelet sparsity was studied for T2 mapping.
Also following (30), and its supplemental material, the regularization parameters, λ or λl and λs, were adjusted in order to minimize ||x̂λ − xref||2 where x̂λ is the CS reconstruction and xref the fully-sampled data SENSE reconstruction. The CS reconstruction was performed using fast iterative shrinkage-thresholding algorithms (FISTA) (51) and its modification coupled with fast gradient projection (FGP) (52) as the proximal operator. For L+S problems, the same algorithm can be used for s and l vectors. A modified FISTA for nuclear-norm is in (53). All methods stopped when ||xi+1 − xi||2/||xi+1||2 < 10−5, or when i > 400, being i the iteration index. The methods K-SVD and EXP stopped by the maximum number of iterations, but their normalized update values, i.e. ||xi+1 − xi||2/||xi+1||2, were close to the stopping tolerance.
Exponential Models and Fitting Algorithms
The T1ρ relaxation is usually considered an exponential decay process. Typically, the model is described as:
| [5] |
where x(t,n) is one particular voxel at 3D position n over TSL time t, ā(n) is a complex-valued magnetization, and τ(n) is the T1ρ relaxation time at position n. However, magnitude-only models with positive real-valued a(n) and a constant component b, included due to residual noise, can also be considered, changing [5] to:
| [6] |
The biexponential model can be written as:
| [7] |
Where 0 ≤ fs (n) ≤ 1 and fl (n) = 1 − fs (n) are the fractions of short and long components at position n, respectively. Also, τs(n) and τl(n) are the T1ρ relaxation times of the short and long components, respectively.
The biexponential T1ρ parameters estimation, or simply fitting process, was done using non-linear least squares, using model [7], where the minimization was done using conjugate gradient Steihaug’s trust-region (CGSTR) algorithm (54). The CGSTR algorithm stopped at a maximum of 2000 iterations or normalized parameter update lower than 10−4. Biexponential estimation started with monoexponential fitting results, using model [6], classifying them as short (1–25ms) or long (25–300ms), depending on its estimated monoexponential T1ρ relaxation time. Similar to (12), F-test was utilized for detecting mono/biexponential voxels. We follow the F-test method from (55), voxels were assumed to have biexponential behavior if F-ratio>5.14 (p-value=0.05) related to monoexponential. This means the sum of the squares (SS) of the biexponential fitting process is reduced significantly compared to monoexponential fitting. Also, both fractions (fs (n) and fl (n)) need to be higher than 10% in order to be a valid biexponential in these experiments. Figure 1(c) illustrates the process. The choice of 10% comes from tests with synthetic experiments (noisy). Together with F-test, it achieved the most correct detection of mono and biexponential voxels. More information about this is found in the online supporting material, and also within Supporting Figures S8 and S9, and Supporting Table S2.
Spatial filtering, used as a denoising over the regions of interest (ROIs), prior to the parameter estimation is sometimes helpful (56) to improve the quality of the estimated parameters. In this paper, we compare the non-filtered results with standard linear filter of spatially averaging of a 3×3 square of voxels (57).
Analysis of the CS Reconstruction and Fitting
The performance of the CS methods was evaluated according to the quality of the reconstructed images and the quality of the estimated biexponential T1ρ parameters. Image reconstruction quality was assessed using normalized root mean squared error (nRMSE) against SENSE reconstruction of the fully-sampled data or the ground truth (for the synthetic phantom). The nRMSE is defined as:
| [6] |
The fitting process was applied only on each specific ROI. For in vivo knee cartilage, 5 ROIs were employed, following (13): medial femoral and tibial cartilages, lateral femoral and tibial cartilages and patellar cartilage. In those regions, the biexponential T1ρ parameters, including T1ρ times and fractions for short and long components, from CS reconstructions were compared against the parameters obtained from the reference reconstruction (and ground truth, when available).
The quality was assessed using normalized absolute deviation (NAD) of the parameters obtained in each voxel position n, given by:
| [7] |
where p(n) is one of the four biexponential parameters (fs (n), fl (n), τs (n), τl (n)). Voxels in which any of the fractions were lower than 10% were excluded from the evaluation. As observed here and in (13), small fractions had inaccurate estimated T1ρ parameters, even for fully-sampled images, leading to unrealistic NADs.
The errors in an ROI or sets of ROIs were quantized by the median of NADs (MNAD):
| [8] |
An MNAD of 0.1 corresponds to a median deviation of 10% on the estimated parameters compared to the reference, and it is more robust than the mean to measure the errors due to the instability of the non-linear least squares. Box plots are used for complete statistics about the NADs (median shows central tendency and quartiles shows the variability of the NADs).
Intra-subject repeatability is assessed using the coefficient of variation (CV), defined as CV=SD/M, being SD the standard deviation and M the mean of the median parameters of an ROI of two scans for the same volunteer. Bland-Altman plots were also used for selected methods.
RESULTS
Synthetic Phantom
The synthetic phantom results tell us how undersampling and noise affect the reconstruction quality and the biexponential fitting of the tested methods. This is only possible because the ground truth is available. It is important to state that fully-sampled SENSE reconstruction is not necessary the ground truth because it is corrupted by noise.
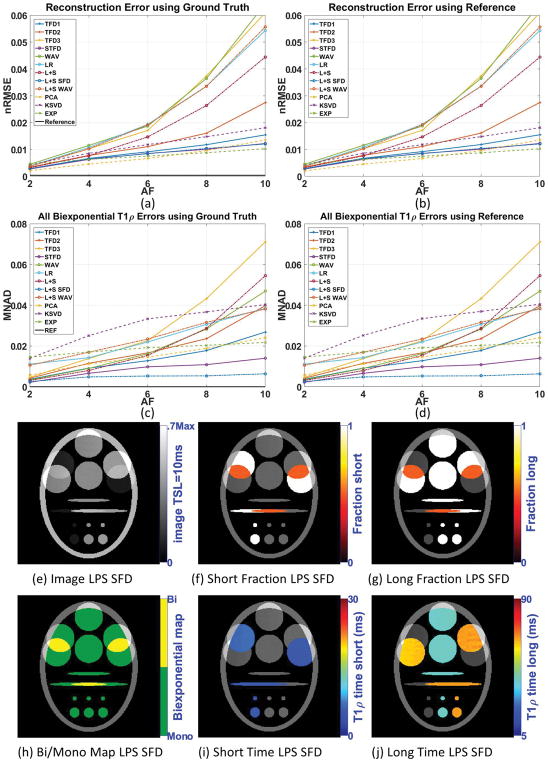
Figure 2(a) shows the reconstruction errors (nRMSE), and 2(c) shows the parameters error (MNAD) for the noiseless case when compared with the ground truth and 2(b) and 2(d) when comparing with the reference. When no specific biexponential parameter is mentioned, then all four parameters are being evaluated together. The Supporting Figure S1 provides individual MNAD for each parameter (fs (n), fl (n), τs (n), τl (n)). From Figure 2, we can infer that fully-sampled SENSE (coil combination of the fully-sampled data) is reliable to be used as reference when no noise is present, since its error is negligible. Comparing figures 2(a) and 2(c), as well as 2(b) and 2(d), it is observable that best reconstruction does not necessarily translate into best biexponential parameters. The MNAD for biexponential fitting is primarily affected by size of the reconstruction error, measured by nRMSE. However, the temporal shape of the reconstruction error is also important. One particular regularization function can, for example, reduce voxel magnitude for small TSL more than for large TSL, which will, consequently, affect the estimated relaxation parameters. More details on this, with an example, are included in the online supplemental information of this paper, with Supporting Figure S12. Some differences are also because nRMSE assesses the entire image, while MNAD assesses only a region of interest. A comparison of nRMSE at the entire image and only at ROI’s is included in the online supplemental information of this paper, with Supporting Figures S10 and S11.
Figure 2.
Results for synthetic phantom with no noise in the acquisition, including (a) reconstruction error (nRMSE) and (c) biexponential parameters error (MNAD) compared with ground truth, (b) reconstruction error (nRMSE) and (d) biexponential parameters error (MNAD) compared with reference for different acceleration factors (AF). Representative image and maps for L+S SFD using AF=6 are shown in (e)–(j).
In this experiment, methods L+S SFD and STFD were the best regarding biexponential parameters (providing good reconstruction quality too). Figures 2(e)–(j) show some visual results of L+S SFD.
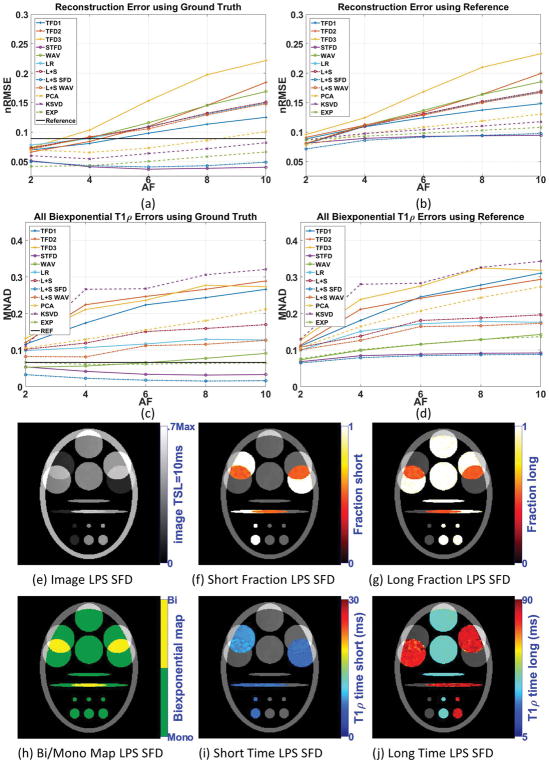
Figures 3(a) and 3(c) show the resulting reconstruction (nRMSE) and biexponential fitting errors (MNAD) for the synthetic noisy case when compared with ground truth, and 3(b) nRMSE and 3(d) MNAD when comparing with reference. Supporting Figure S2 details MNAD for each biexponential parameter. The results from Figure 3 show that fully-sampled SENSE reconstruction performed worse than some CS methods, such as L+S SFD, STFD, and EXP.
Figure 3.
Results for synthetic phantom with 15dB of noise in the acquisition, including (a) reconstruction error (nRMSE) and (c) biexponential parameters error (MNAD) compared with ground truth, (b) reconstruction error (nRMSE) and (d) biexponential parameters error (MNAD) compared with reference, for different acceleration factors. Representative image and maps for L+S SFD using AF=6 are shown in (e)–(j).
Comparing the results from Figure 2, with noiseless data, with the results from Figure 3, with noisy data, we can clearly observe that this level of noise can cause more errors in the fully-sampled reconstructed image (and its estimated relaxation parameters) than undersampling alone, with AF up to 10, in any noiseless CS reconstruction (and its estimated relaxation parameters).
Following the same observation of the noiseless case, good reconstruction not necessarily translates into good biexponential fitting. A clear example is the results with KSVD (compare figures 3(a) and 3(c)).
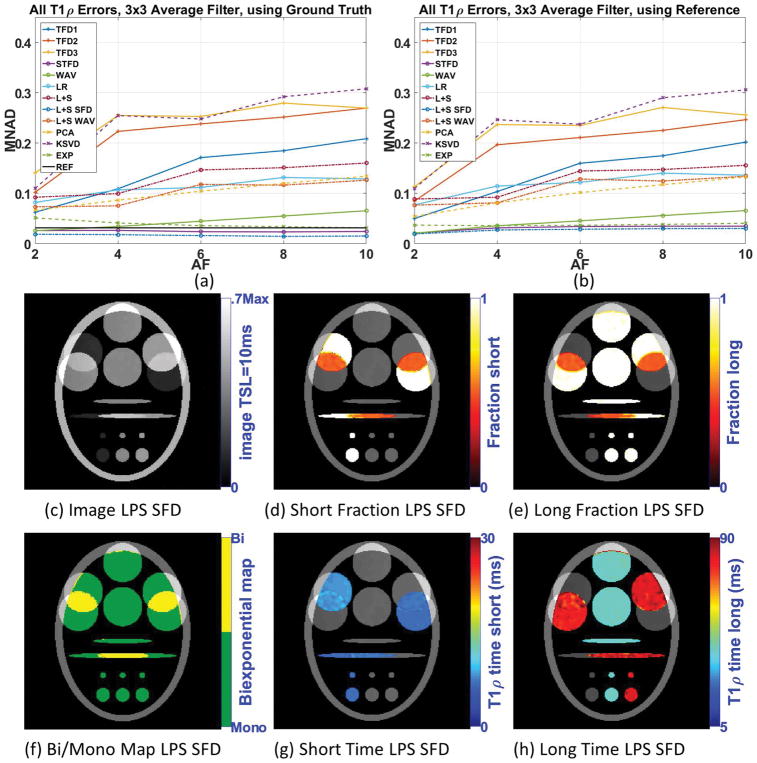
A common alternative to reduce noise and artifacts, improving the fitting results, is filtering prior to fitting. Figure 4(a) shows the biexponential fitting error (MNAD) after 3×3 averaging filter when compared with ground truth, and 4(b) when compared with reference. Supporting Figure S3 details the biexponential fitting error. Note that all methods have their MNAD reduced when filtering was utilized, including the reference. In general, the filtering reduces noise, but at the cost of reducing details of the biexponential maps (compare figures 3(e)–(j) and figures 4(c)–(h)). Another negative effect of filtering is the mixture of information of two different regions, especially at the boundaries. In Figure 4(j), for example, the filtering process artificially created biexponential voxels on the boundaries of regions with different monoexponential T1ρ values. Nevertheless, methods such as L+S SFD and STFD performed better than the reference in terms of fitting results with 3×3 averaging filter in the synthetic experiments.
Figure 4.
Results for synthetic phantom with 15dB of noise in the acquisition, including (a) parameters error (MNAD) compared with ground and (b) compared with the reference, when 3×3 averaging filter is utilized, for different acceleration factors. Representative image and maps for L+S SFD using AF=6 are shown in (c)–(h).
In Vivo Knee Cartilage Data
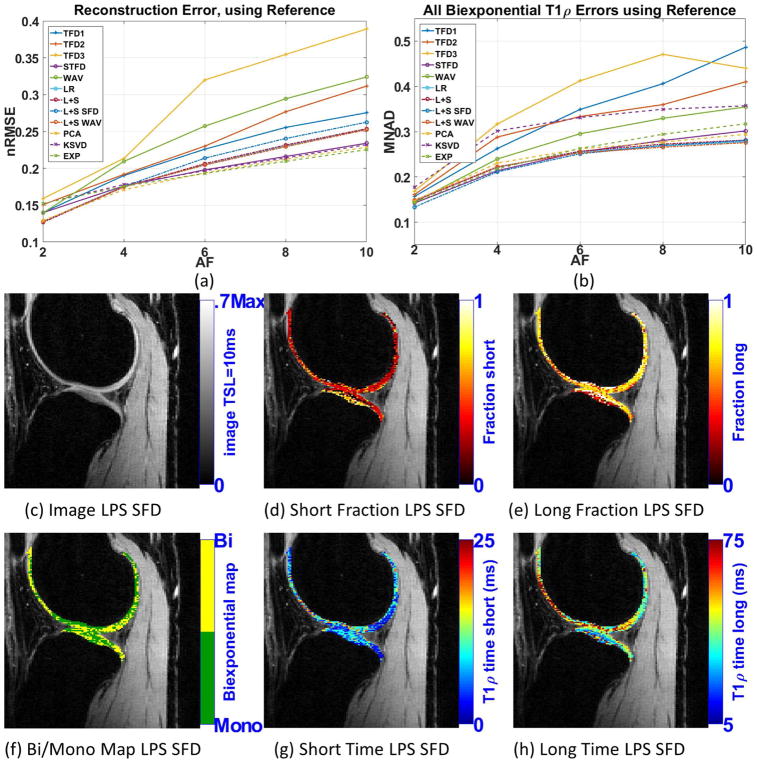
Our goal is to find suitable CS regularizations that perform well with in vivo knee cartilage. This region is challenging since it usually has small motion-related artifacts. Moreover, cartilage is curved and very thin. For this experiment, no ground truth is available. So, CS results were only compared with the reference (fully-sampled SENSE, possibly corrupted by noise and other artifacts).
Figure 5(a) shows the resulting reconstruction error (nRMSE) and 5(b) shows the resulting biexponential parameters error (MNAD). The detailed biexponential fitting errors are available in the Supporting Figure S4. Similar to the synthetic case, not all good CS reconstructions produced good biexponential parameters, KSVD is an example. Here, many CS methods had good results, with similar error levels, such as L+S SFD, STFD, L+S WAV, L+S, LR, PCA, and EXP. From synthetic noisy experiments, shown in figure 3(d), one can note that the best methods have similar MNAD when compared with the reference. Figures 5(c)–(h) show some visual results for L+S SFD at AF=4.
Figure 5.
Results for human knee cartilage, including (a) reconstruction error (nRMSE), and (b) parameters error (MNAD) compared with reference (SENSE), for different acceleration factors. Representative image and maps for L+S SFD using AF=4 are shown in (c)–(h).
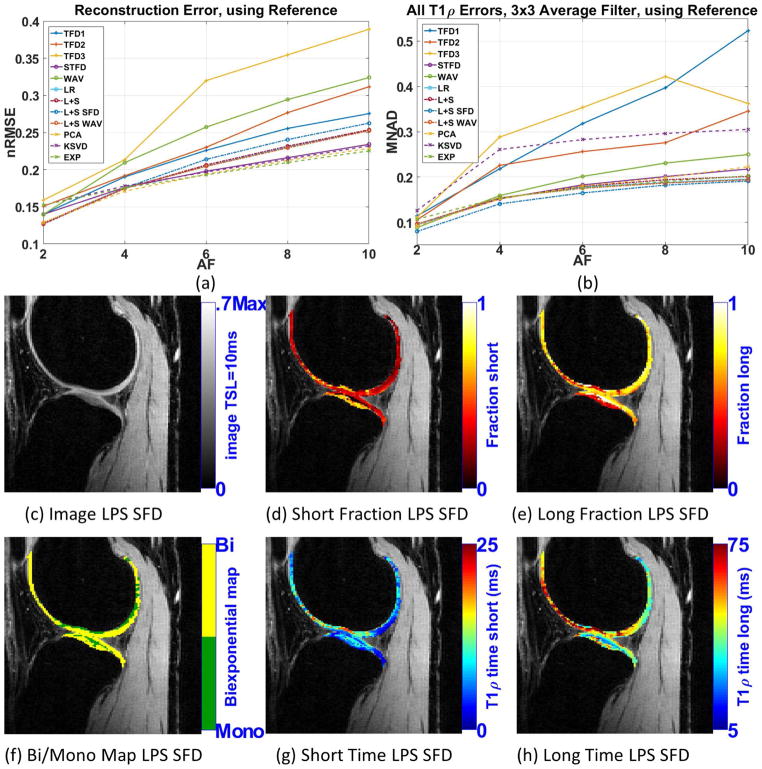
Figure 6(b) shows the MNAD for biexponential when 3×3 averaging filter is utilized. Supporting Figure S5 details this error for each parameter. As observed in the synthetic experiments, all the biexponential errors were reduced with pre-filtering. The use of pre-filtering gave some small advantage for L+S SFD, making it slightly better than the other methods: STFD, L+S WAV, L+S, LR, PCA, and EXP, which were all very good.
Figure 6.
Results for human knee cartilage, (a) reconstruction error (nRMSE), and (b) parameters error (MNAD) compared with reference (SENSE), for different acceleration factors, when 3×3 averaging filter is utilized. Representative image and maps for L+S SFD using AF=4 are shown in (c)–(h).
Figures 6(c)–(h) shows some visual results for L+S SFD at AF=4 when 3×3 averaging filter is used. We can clearly observe that biexponential maps look much less noisy than in figures 5(c)–(h), and perhaps more useful for further medical evaluation. Visual comparison with the reference can be seen in Supporting Figure S7.
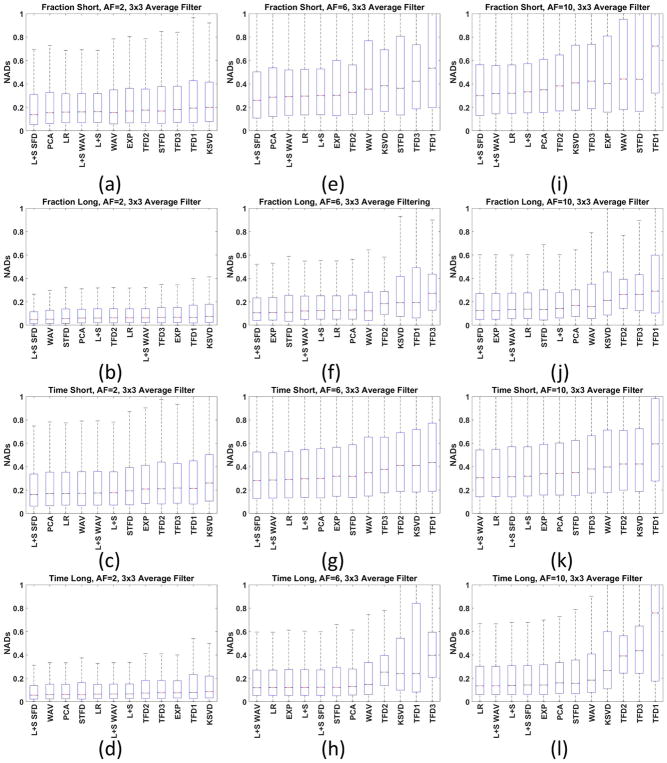
Figure 7 shows box plots for some specific AFs (2, 6 and 10) for the biexponential fitting results when filtering is utilized. The box plot shows much more information about the statistics of the NADs than only the median. Nevertheless, these results show that distributions of the NADs are very similar for all the best CS methods. It gives us support to exclude methods that did not perform satisfactorily: KSVD, TFD1, TFD2, and TFD3.
Figure 7.
Box plot of the NAD for all human knee cartilage datasets with 3×3 averaging filter for AF=2 (a) fraction-short, (b) fraction-long, (c) T1ρ-short, (d) T1ρ-long, (e)–(h) AF=6 and (i)–(l) AF=10. The box plot shows more information about the NADs than only the MNAD. The horizontal red bars represent the median of NAD (or NMAD), the blue box represent the central interquartile, where MAD values from percentile 25% to 75% are placed. The dashed dark lines represent the range of the data.
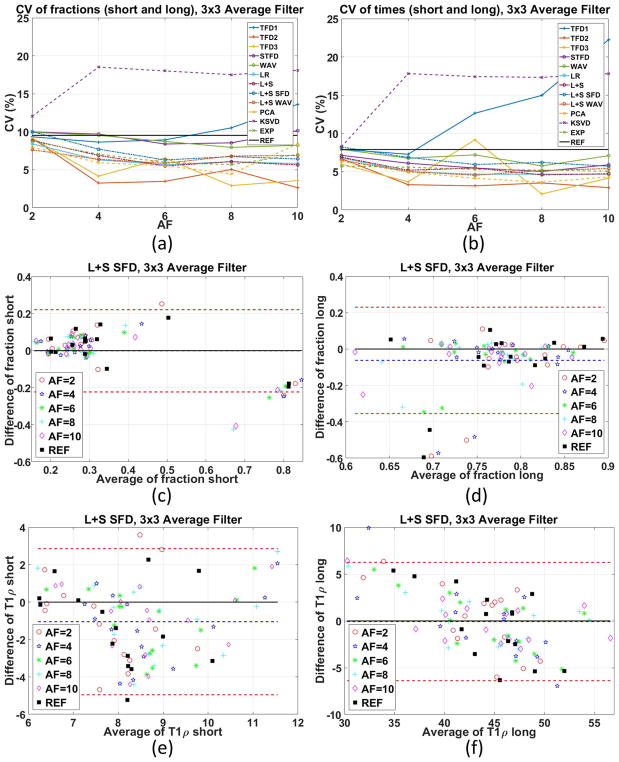
Figure 8 shows some intra-subject repeatability by the coefficient of variation and Bland-Altman plots for the method considered best so far, the L+S SFD, more details in Supporting Figure S6. Almost all CS methods achieved lower or similar CV than the reference, with some exceptions. This interesting result supports the use of CS for biexponential T1ρ mapping.
Figure 8.
Coefficient of variation (CV), shown in percentage, of the different methods and acceleration factors with 3×3 averaging filter for (a) fractions, (b) times, considering two repetitions with each of the three volunteers. Bland-Altman plots for the L+S SFD method with 3×3 averaging filter for (c) fraction-short, (d) fraction-long, (e) T1ρ-short, (f) T1ρ-long considered the best in the previous experiment.
Overall Classification
In order to have an overall quantification of the results, we compute MNAD for all the results with synthetic noisy and in vivo datasets together, all compared to the reference. The first score, in Table 2A, is simply the MNAD of all biexponential errors (NADs), among 3 noisy synthetic datasets and 7 in vivo datasets, when no-filter is utilized. The resulting number provides us a median (normalized) parameter error of a particular method for the desired AF. The second score, in Table 2B, the MNAD was obtained when 3×3 averaging pre-filter was utilized.
Table 2.
A) Ranking the methods using its MNAD up to certain acceleration factor, for synthetic and in vivo datasets. Values lower than 0.2 (error of 20%) are bold-marked. B) Ranking the methods by its MNAD, when 3×3 averaging pre-filter is utilized, up to certain acceleration factor, for synthetic and in vivo datasets. Values lower than 0.15 (error of 15%) are bold-marked.
| A. Median of normalized absolute deviation with no pre-filters | |||||||||
| AF 2 | AF4 | AF 6 | AF8 | AF 10 | |||||
| L+S SFD | 0.109 | STFD | 0.165 | STFD | 0.190 | L+S SFD | 0.207 | L+S SFD | 0.216 |
| STFD | 0.114 | L+S SFD | 0.166 | L+S SFD | 0.195 | STFD | 0.208 | STFD | 0.222 |
| WAV | 0.118 | EXP | 0.174 | EXP | 0.208 | L+S WAV | 0.231 | L+S WAV | 0.239 |
| EXP | 0.119 | WAV | 0.188 | L+S WAV | 0.222 | EXP | 0.234 | LR | 0.241 |
| LR | 0.131 | L+S WAV | 0.189 | LR | 0.226 | LR | 0.236 | L+S | 0.250 |
| L+S WAV | 0.132 | L+S | 0.192 | L+S | 0.228 | L+S | 0.241 | EXP | 0.251 |
| L+S | 0.133 | LR | 0.196 | WAV | 0.231 | WAV | 0.259 | WAV | 0.282 |
| PCA | 0.134 | PCA | 0.211 | PCA | 0.246 | PCA | 0.267 | PCA | 0.286 |
| TFD1 | 0.141 | TFD1 | 0.236 | TFD2 | 0.303 | TFD2 | 0.329 | KSVD | 0.352 |
| TFD2 | 0.143 | TFD2 | 0.262 | TFD1 | 0.315 | KSVD | 0.342 | TFD2 | 0.372 |
| TFD3 | 0.155 | TFD3 | 0.294 | KSVD | 0.316 | TFD1 | 0.364 | TFD3 | 0.403 |
| KSVD | 0.159 | KSVD | 0.295 | TFD3 | 0.370 | TFD3 | 0.428 | TFD1 | 0.428 |
| B. Median of normalized absolute deviation when 3×3 averaging pre-filter is utilized | |||||||||
| AF 2 | AF 4 | AF 6 | AF 8 | AF 10 | |||||
| L+S SFD | 0.056 | L+S SFD | 0.098 | L+S SFD | 0.114 | L+S SFD | 0.125 | L+S SFD | 0.131 |
| WAV | 0.062 | STFD | 0.103 | STFD | 0.123 | STFD | 0.136 | STFD | 0.147 |
| STFD | 0.065 | EXP | 0.111 | EXP | 0.127 | EXP | 0.137 | EXP | 0.148 |
| PCA | 0.078 | WAV | 0.113 | WAV | 0.145 | L+S WAV | 0.166 | L+S WAV | 0.172 |
| EXP | 0.079 | L+S WAV | 0.128 | PCA | 0.157 | WAV | 0.171 | LR | 0.173 |
| LR | 0.088 | PCA | 0.129 | L+S WAV | 0.159 | LR | 0.172 | L+S | 0.184 |
| L+S WAV | 0.090 | L+S | 0.130 | LR | 0.160 | PCA | 0.176 | WAV | 0.188 |
| L+S | 0.093 | LR | 0.140 | L+S | 0.165 | L+S | 0.177 | PCA | 0.198 |
| TFD1 | 0.094 | TFD1 | 0.179 | TFD2 | 0.241 | TFD2 | 0.260 | KSVD | 0.305 |
| TFD2 | 0.096 | TFD2 | 0.215 | TFD1 | 0.261 | KSVD | 0.295 | TFD2 | 0.317 |
| TFD3 | 0.111 | KSVD | 0.256 | KSVD | 0.268 | TFD1 | 0.317 | TFD3 | 0.340 |
| KSVD | 0.120 | TFD3 | 0.278 | TFD3 | 0.328 | TFD3 | 0.393 | TFD1 | 0.409 |
From Table 2A, one can notice that a median error below 20% (bold marked) is expected when using AFs up to 6 with the methods STFD and L+S SFD. According to Table 2B, one can expect an MNAD below 15% up to AF of 10 when 3×3 averaging pre-filter is utilized with the methods STFD, L+S SFD, and EXP. In the literature (58), 5% error is considered acceptable for reproducibility for the monoexponential case. There are no similar error bounds for biexponential models. According to our experiments, the best results are for L+S SFD, which achieved 5.6% error at AF=2.
DISCUSSION
Recommended CS Methods
For AF=2, almost all CS methods produced good results, with low MNAD (0.109~0.159 without filtering, 0.056~0.120 with 3×3 averaging filter). As AF increases, fewer methods can provide low MNAD. We marked in bold letters, in tables 2A, 2B some suggested methods for each AF.
Our experimental results indicated that the use of 3×3 averaging filter provided the lowest MNAD for almost all CS methods. However, no matter if pre-filter is used or not, we observed that the CS methods STFD, L+S SFD, and EXP appeared among the best methods most of the time. This indicates that these three are the most suitable CS methods for accelerating biexponential T1ρ mapping of the cartilage in the knee joint. This result is consistent with our previews experiments with monoexponential T1ρ mapping in (30). On the other hand, methods L+S WAV, L+S, LR, PCA, and WAV also produced satisfactory results and could be considered.
Performance of the Regularization Penalties for Biexponential Fitting
Biexponential fitting is much more difficult and unstable than monoexponential fitting. In this case, the temporal shape of the reconstructed signal is extremely important (see more about this in the online supporting material of this paper, in Supporting Figure S12). Thus, the choice of regularizing penalty is important, since it affects how the signal will look like. Since noise strongly perturbs the fitting process, imposing spatial smoothness through regularization and/or spatial filtering prior to fitting produce positive effects. In this sense, the simple temporal finite differences, such as TFD1, TFD2, TFD3 did not perform well and their results were unstable.
The KSVD disappointed in some sense, even though it provided excellent reconstruction results, this did not translate into appropriate biexponential mapping. PCA performed better in this sense.
The STFD and WAV are both spatiotemporal models, imposing spatiotemporal correlation. The STFD performed very well, standing among the best methods in many tests. On the other hand, WAV did perform moderately well.
The EXP, which utilize a fixed overcomplete exponential dictionary, produced good results. It does not generate spatial correlation, so it was clearly benefited from the use of spatial pre-filters.
Some interesting positive results came from the LR and L+S penalties (L+S WAV and L+S SFD included). They all provided considerable results, especially with in vivo knee cartilage data. Moreover, the combination of low rank plus sparsity in the spatial finite difference domain (L+S SFD) provided the best results. Supporting Table S1 shows general qualification regarding the performance of the regularization functions for different aspects of the reconstruction and fitting.
We clearly observed that pre-filtering reduced mapping error. In part, because it reduced noise in the reference and in CS reconstructions, resulting in stable fitting and low MNAD. Even though there are better denoising filters (56) than standard 3×3 averaging, it still does a good job of reducing the errors. The drawback of filtering is the reduction of fine details in the biexponential mapping and possibly mixture of different regions.
Comparison with Previous Studies
As far as we know, this is the first study on the use of CS to accelerate biexponential T1ρ mapping. In (13), reduced number of TSLs and GRAPPA (59) were tested for accelerated acquisition, up to AF=3. Most studies on accelerating general biexponential mapping apply to T2 relaxation, where optimal or reduced time samples is searched (60,61), but no precise error per AF is given.
CS has been successfully utilized for monoexponential T1ρ mapping. In (29) a combination of CS and autocalibration reconstruction (ARC) was utilized for knee cartilage T1ρ monoexponential mapping errors close to 5%, or lower, for AFs around 2. In (25), three specific CS-like methods: integrating PCA and dictionary learning (PANDA), focal underdetermined system solver with PCA (k-t FOCUSS-PCA) and model-based dictionary learning (MBDL) were compared to accelerate brain and spine T1ρ mapping up to AF of 4. T1ρ relaxation errors between 8.9% and 12% were reported. In (26), a combined reconstruction with locally adaptive iterative support detection (k-t LAISD) and joint image reconstruction and sensitivity estimation in SENSE (JSENSE) method was proposed for knee cartilage T1ρ mapping, with acceleration up to 3 and 3.5. In (27) blind compressed sensing (BCS) was applied to monoexponential T2 and T1ρ mapping of the brain.
Here, we provide a broad evaluation, using AF from 2, up to 10, comparing twelve CS methods, with and without pre-filtering, on 6 synthetic datasets and 7 in vivo human knee cartilage datasets for biexponential T1ρ mapping. These results complement our previous results in (30) for monoexponential T1ρ mapping. In order to keep all evaluations completely unbiased, we are not proposing or claiming any method of our own. All penalties appeared elsewhere in the literature for different applications, in the exact or similar form used here. The important novelty here is the evaluation of their performance for biexponential T1ρ mapping.
Limitations of This Study and Future Directions
In our tests, the regularization parameters were selected to minimize l2-norm of the difference between CS and the fully-sampled SENSE, essentially minimizing nRMSE. However, the ideal parameter would be the one that makes the reconstruction closer to the ground truth (unknown in practical cases). Therefore, how to choose the regularization parameter is still an open question. See more details on the criterion and procedure to choose the regularization parameters in the online supplemental information of (30).
In this study, we did not evaluate prospective undersampling. We hope to address this in the future, together with an automatic choice of the regularization parameter, when a fully sampled reference is not available.
It is also known that the ratio between short and long component/fraction affects the stability of the biexponential fitting (13,45). In the synthetic phantom study, the ratios are randomly dispersed by at most 10% around a 50/50 ratio and are free in real data sets. Performance of the methods with different components/fractions, especially for small fractions, and the stability of biexponential model will be addressed in future work.
The number of TSLs and their distribution are also relevant. Our choice was based on previous study (13) showing the best tradeoff between T1ρ quality and scan time, but different distributions are possible. The use of different AFs in each TSL should also be investigated in the future.
Model-based reconstructions are promising approaches for monoexponential relaxation (62,63). It is not clear yet if they can be successful with biexponential models due to the instability and non-unicity of this inverse problem.
CONCLUSION
This study shows that CS can accelerate biexponential T1ρ mapping of cartilage in the knee joint. Twelve different CS methods were compared, being the most indicated methods: L+S SFD, STFD, and EXP. In addition, the use of pre-filtering prior to T1ρ fitting is recommended at the expense of spatial smoothing. These best CS methods performed satisfactorily for AFs up to 10, with error below 15%. The use of CS is a good alternative to make clinical studies with the biexponential model a viable approach.
Supplementary Material
Supporting Table S1: Qualification of the methods according to their performance on different aspects.
Supporting Table S2: Some Fratio values based on the choice of the p-value for the problem of detecting mono or biexponential voxels.
Supporting Figure S1: Details of the biexponential parameter errors (MNAD) for synthetic phantom with no noise in the acquisition: (a) fraction-short error (c) fraction-long error (e) T1ρ-short error, (g) T1ρ-long error, compared with the ground truth; (b) fraction-short error (d) fraction-long error (f) T1ρ-short error, (h) T1ρ-long error, compared with the reference.
Supporting Figure S2: Details of the biexponential parameter errors (MNAD) for synthetic phantom with 15dB of noise in the acquisition: (a) fraction-short error (c) fraction-long error (e) T1ρ-short error, (g) T1ρ-long error, compared with the ground truth; (b) fraction-short error (d) fraction-long error (f) T1ρ-short error, (h) T1ρ-long error, compared with the reference.
Supporting Figure S3: Details of the biexponential parameter errors (MNAD) for synthetic phantom with 15dB of noise in the acquisition when 3×3 averaging filter is used: (a) fraction-short error (c) fraction-long error (e) T1ρ-short error, (g) T1ρ-long error, compared with the ground truth; (b) fraction-short error (d) fraction-long error (f) T1ρ-short error, (h) T1ρ-long error, compared with the reference.
Supporting Figure S4: Details of the biexponential parameter errors (MNAD) for in vivo human knee cartilage: (a) fraction-short error (c) fraction-long error (e) T1ρ-short error, (g) T1ρ-long error, compared with the reference.
Supporting Figure S5: Details of the biexponential parameter errors (MNAD) for in vivo human knee cartilage with 3×3 averaging filter: (a) fraction-short error (c) fraction-long error (e) T1ρ-short error, (g) T1ρ-long error, compared with the reference.
Supporting Figure S6: Details of the coefficient of variations (CV) for intra-subject in vivo human knee cartilage with 3×3 averaging filter: (a) fraction-short (b) fraction-long (c) T1ρ-short, (f) T1ρ-long.
Supporting Figure S7: Visual comparison of some results of the knee cartilage, with and without filtering, for reference and L+S SFD with AF=2 and AF=6.
Supporting Figure S8: Illustration of the monoexponential and biexponential fitting for the knee cartilage dataset (medial).
Supporting Figure S9: Number of wrongly classified voxels as biexponential or monoexponential according to the choices of αF, αs and αl for the utilized criterion.
Supporting Figure S10: Comparison of (a) nRMSE, (b) nRMSE for ROI only and (c) MNAD for the synthetic noisy phantom.
Supporting Figure S11: Comparison of (a) nRMSE for entire image, (b) nRMSE for ROI only and (c) MNAD with no filter and (d) MNAD with 3×3 averaging filter, for the in vivo knee cartilage.
Supporting Figure S12: (a) Ground truth, KSVD reconstruction and fitted biexponential curve, and (b) distribution of the reconstruction error over time.
Acknowledgments
This study was supported by NIH grants R01-AR060238, R01-AR067156, and R01-AR068966, and was performed under the rubric of the Center of Advanced Imaging Innovation and Research (CAI2R), a NIBIB Biomedical Technology Resource Center (NIH P41-EB017183).
References
- 1.Lawrence RC, Felson DT, Helmick CG, et al. Estimates of the prevalence of arthritis and other rheumatic conditions in the United States: Part II. Arthritis Rheum. 2008;58:26–35. doi: 10.1002/art.23176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Felson DT. Risk factors for osteoarthritis: understanding joint vulnerability. Clin Orthop Relat Res. 2004:S16–21. doi: 10.1097/01.blo.0000144971.12731.a2. [DOI] [PubMed] [Google Scholar]
- 3.Sun BH, Wu CW, Kalunian KC. New developments in osteoarthritis. Rheum Dis Clin North Am. 2007;33:135–148. doi: 10.1016/j.rdc.2006.12.003. [DOI] [PubMed] [Google Scholar]
- 4.Bitton R. The economic burden of osteoarthritis. Am J Manag Care. 2009;15:S230–S235. doi: 10.1002/art.1780290311. [DOI] [PubMed] [Google Scholar]
- 5.Borthakur A, Mellon E, Niyogi S, Witschey W, Kneeland JB, Reddy R. Sodium and T1ρ MRI for molecular and diagnostic imaging of articular cartilage. NMR Biomed. 2006;19:781–821. doi: 10.1002/nbm.1102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sophia Fox AJ, Bedi A, Rodeo SA. The Basic Science of Articular Cartilage: Structure, Composition, and Function. Sports Health. 2009;1:461–468. doi: 10.1177/1941738109350438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Regatte RR, Akella SVS, Lonner JH, Kneeland JB, Reddy R. T1ρ relaxation mapping in human osteoarthritis (OA) cartilage: Comparison of T1ρ with T2. J Magn Reson Imaging. 2006;23:547–553. doi: 10.1002/jmri.20536. [DOI] [PubMed] [Google Scholar]
- 8.Mlynárik V, Trattnig S, Huber M, Zembsch A, Imhof H. The role of relaxation times in monitoring proteoglycan depletion in articular cartilage. J Magn Reson Imaging. 1999;10:497–502. doi: 10.1002/(SICI)1522-2586(199910)10:4<497::AID-JMRI1>3.0.CO;2-T. [DOI] [PubMed] [Google Scholar]
- 9.Regatte RR, Akella SV, Borthakur A, Kneeland JB, Reddy R. Proteoglycan Depletion–Induced Changes in Transverse Relaxation Maps of Cartilage: Comparison of T2 and T1ρ. Acad Radiol. 2002;9:1388–1394. doi: 10.1016/S1076-6332(03)80666-9. [DOI] [PubMed] [Google Scholar]
- 10.Akella SVS, Reddy Regatte R, Gougoutas AJ, Borthakur A, Shapiro EM, Kneeland JB, Leigh JS, Reddy R. Proteoglycan-induced changes in T1ρ-relaxation of articular cartilage at 4T. Magn Reson Med. 2001;46:419–423. doi: 10.1002/mrm.1208. [DOI] [PubMed] [Google Scholar]
- 11.Nishioka H, Nakamura E, Hirose J, Okamoto N, Yamabe S, Mizuta H. MRI T1ρ and T2 mapping for the assessment of articular cartilage changes in patients with medial knee osteoarthritis after hemicallotasis osteotomy. Bone Jt Res. 2016;5:294–300. doi: 10.1302/2046-3758.57.BJR-2016-0057.R1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Yuan J, Zhao F, Chan Q, Wang Y-XJ. Observation of bi-exponential T1ρ relaxation of in-vivo rat muscles at 3T. Acta radiol. 2012;53:675–681. doi: 10.1258/ar.2012.120108. [DOI] [PubMed] [Google Scholar]
- 13.Sharafi A, Xia D, Chang G, Regatte RR. Biexponential T1ρ relaxation mapping of human knee cartilage in vivo at 3T. NMR Biomed. 2017;30:e3760. doi: 10.1002/nbm.3760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wang N, Xia Y. Dependencies of multi-component T2 and T1ρ relaxation on the anisotropy of collagen fibrils in bovine nasal cartilage. J Magn Reson. 2011;212:124–132. doi: 10.1016/j.jmr.2011.06.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Yuan J, Wang Y-XJ. T1rho MR imaging: Principle, technology, and application. In: Majumdar A, Ward RK, editors. MRI: Physics, Image Reconstruction, and Analysis. CRC Press; 2015. pp. 565–592. [Google Scholar]
- 16.Lustig M, Donoho DL, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007;58:1182–95. doi: 10.1002/mrm.21391. [DOI] [PubMed] [Google Scholar]
- 17.Candes EJ, Wakin MB. An Introduction to Compressive Sampling. IEEE Signal Process. Mag. 2008;25:21–30. [Google Scholar]
- 18.Lustig M, Donoho DL, Santos JM, Pauly JM. Compressed Sensing MRI. IEEE Signal Process. Mag. 2008;25:72–82. [Google Scholar]
- 19.Otazo R, Kim D, Axel L, Sodickson DK. Combination of compressed sensing and parallel imaging for highly accelerated first-pass cardiac perfusion MRI. Magn Reson Med. 2010;64:767–776. doi: 10.1002/mrm.22463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Feng L, Srichai MB, Lim RP, Harrison A, King W, Adluru G, Dibella EVR, Sodickson DK, Otazo R, Kim D. Highly accelerated real-time cardiac cine MRI using k-t SPARSE-SENSE. Magn Reson Med. 2013;70:64–74. doi: 10.1002/mrm.24440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Feng L, Grimm R, Block KT, Chandarana H, Kim S, Xu J, Axel L, Sodickson DK, Otazo R. Golden-angle radial sparse parallel MRI: Combination of compressed sensing, parallel imaging, and golden-angle radial sampling for fast and flexible dynamic volumetric MRI. Magn Reson Med. 2014;72:707–717. doi: 10.1002/mrm.24980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Huang C, Graff CG, Clarkson EW, Bilgin A, Altbach MI. T2 mapping from highly undersampled data by reconstruction of principal component coefficient maps using compressed sensing. Magn Reson Med. 2012;67:1355–1366. doi: 10.1002/mrm.23128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Doneva M, Börnert P, Eggers H, Stehning C, Sénégas J, Mertins A. Compressed sensing reconstruction for magnetic resonance parameter mapping. Magn Reson Med. 2010;64:1114–1120. doi: 10.1002/mrm.22483. [DOI] [PubMed] [Google Scholar]
- 24.Velikina JV, Alexander AL, Samsonov A. Accelerating MR parameter mapping using sparsity-promoting regularization in parametric dimension. Magn Reson Med. 2013;70:1263–1273. doi: 10.1002/mrm.24577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhu Y, Zhang Q, Liu Q, Wang Y-XJ, Liu X, Zheng H, Liang D, Yuan J. PANDA- T1ρ: Integrating principal component analysis and dictionary learning for fast T1ρ mapping. Magn Reson Med. 2015;73:263–272. doi: 10.1002/mrm.25130. [DOI] [PubMed] [Google Scholar]
- 26.Zhou Y, Pandit P, Pedoia V, Rivoire J, Wang Y, Liang D, Li X, Ying L. Accelerating t1ρ cartilage imaging using compressed sensing with iterative locally adapted support detection and JSENSE. Magn Reson Med [Internet] 2016;75:1617–1629. doi: 10.1002/mrm.25773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bhave S, Lingala SG, Johnson CP, Magnotta VA, Jacob M. Accelerated whole-brain multi-parameter mapping using blind compressed sensing. Magn Reson Med. 2016;75:1175–1186. doi: 10.1002/mrm.25722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Zhang T, Pauly JM, Levesque IR. Accelerating parameter mapping with a locally low rank constraint. Magn Reson Med [Internet] 2015;73:655–661. doi: 10.1002/mrm.25161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Pandit P, Rivoire J, King K, Li X. Accelerated T1ρ acquisition for knee cartilage quantification using compressed sensing and data-driven parallel imaging: A feasibility study. Magn Reson Med. 2016;75:1256–1261. doi: 10.1002/mrm.25702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zibetti MVW, Sharafi A, Otazo R, Regatte RR. Accelerating 3D-T1ρ mapping of cartilage using compressed sensing with different sparse and low rank models. Magn Reson Med. 2018 doi: 10.1002/mrm.27138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med. 1999;42:952–62. [PubMed] [Google Scholar]
- 32.Pruessmann KP, Weiger M, Börnert P, Boesiger P. Advances in sensitivity encoding with arbitrary k -space trajectories. Magn Reson Med. 2001;46:638–651. doi: 10.1002/mrm.1241. [DOI] [PubMed] [Google Scholar]
- 33.Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, Lustig M. ESPIRiT-an eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn Reson Med. 2014;71:990–1001. doi: 10.1002/mrm.24751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Lustig M, Alley M, Vasanawala S, Donoho DL, Pauly JM. L1 SPIR-iT: autocalibrating parallel imaging compressed sensing. Proc Intl Soc Mag Res Med. 2009;17:379. [Google Scholar]
- 35.Recht B, Fazel M, Parrilo PA. Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization. SIAM Rev. 2010;52:471–501. doi: 10.1137/070697835. [DOI] [Google Scholar]
- 36.Cai J-F, Candès EJ, Shen Z. A singular value thresholding algorithm for matrix completion. SIAM J Optim. 2010;20:1956–1982. doi: 10.1137/080738970. [DOI] [Google Scholar]
- 37.Otazo R, Candès E, Sodickson DK. Low-rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components. Magn Reson Med. 2015;73:1125–1136. doi: 10.1002/mrm.25240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Stefan W, Renaut RA, Gelb A. Improved total variation-type regularization using higher order edge detectors. SIAM J Imaging Sci. 2010;3:232–251. doi: 10.1137/080730251. [DOI] [Google Scholar]
- 39.Bredies K, Kunisch K, Pock T. Total generalized variation. SIAM J Imaging Sci. 2010;3:492–526. doi: 10.1137/090769521. [DOI] [Google Scholar]
- 40.Yue Hu, Ongie G, Ramani S, Jacob M. Generalized Higher Degree Total Variation (HDTV) Regularization. IEEE Trans Image Process. 2014;23:2423–2435. doi: 10.1109/TIP.2014.2315156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Le Montagner Y, Angelini E, Olivo-Marin J-C. Video reconstruction using compressed sensing measurements and 3d total variation regularization for bio-imaging applications. IEEE International Conference on Image Processing; IEEE; 2012. pp. 917–920. [DOI] [Google Scholar]
- 42.Knoll F, Bredies K, Pock T, Stollberger R. Second order total generalized variation (TGV) for MRI. Magn Reson Med [Internet] 2011;65:480–491. doi: 10.1002/mrm.22595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Wakin MB, Laska JN, Duarte MF, Baron D, Sarvotham S, Takhar D, Kelly KF, Baraniuk RG. Compressive imaging for video representation and coding. Picture Coding Symposium. 2006;1:13. [Google Scholar]
- 44.Whittall KP, MacKay AL. Quantitative interpretation of NMR relaxation data. J Magn Reson. 1989;84:134–152. doi: 10.1016/0022-2364(89)90011-5. [DOI] [Google Scholar]
- 45.Reiter DA, Lin P-C, Fishbein KW, Spencer RG. Multicomponent T2 relaxation analysis in cartilage. Magn Reson Med. 2009;61:803–809. doi: 10.1002/mrm.21926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Wold S, Esbensen K, Geladi P. Principal component analysis. Chemom Intell Lab Syst. 1987;2:37–52. doi: 10.1016/0169-7439(87)80084-9. [DOI] [Google Scholar]
- 47.Aharon M, Elad M, Bruckstein A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans Signal Process. 2006;54:4311–4322. doi: 10.1109/TSP.2006.881199. [DOI] [Google Scholar]
- 48.Chiew M, Smith SM, Koopmans PJ, Graedel NN, Blumensath T, Miller KL. k-t FASTER: Acceleration of functional MRI data acquisition using low rank constraints. Magn Reson Med. 2015;74:353–364. doi: 10.1002/mrm.25395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Candès EJ, Li X, Ma Y, Wright J. Robust principal component analysis? J ACM. 2011;58:1–37. doi: 10.1145/1970392.1970395. [DOI] [Google Scholar]
- 50.Peng X, Ying L, Liu Y, Yuan J, Liu X, Liang D. Accelerated exponential parameterization of T2 relaxation with model-driven low rank and sparsity priors (MORASA) Magn Reson Med. 2016;76:1865–1878. doi: 10.1002/mrm.26083. [DOI] [PubMed] [Google Scholar]
- 51.Beck A, Teboulle M. A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems. SIAM J Imaging Sci. 2009;2:183–202. doi: 10.1137/080716542. [DOI] [Google Scholar]
- 52.Beck A, Teboulle M. Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems. IEEE Trans Image Process. 2009;18:2419–2434. doi: 10.1109/TIP.2009.2028250. [DOI] [PubMed] [Google Scholar]
- 53.Toh KC, Yun S. An accelerated proximal gradient algorithm for nuclear norm regularized linear least squares problems. Pacific J Optim. 2010;6:615–640. [Google Scholar]
- 54.Steihaug T. The conjugate gradient method and trust regions in large scale optimization. SIAM J Numer Anal. 1983;20:626–637. doi: 10.1137/0720042. [DOI] [Google Scholar]
- 55.Motulsky H, Christopoulos A. Fitting Models to Biological Data Using Linear and Nonlinear Regression: A Practical Guide to Curve Fitting. New York: Oxford University Press; 2004. [Google Scholar]
- 56.Bustin A, Ferry P, Codreanu A, Beaumont M, Liu S, Burschka D, Felblinger J, Brau ACS, Menini A, Odille F. Impact of denoising on precision and accuracy of saturation-recovery-based myocardial T1 mapping. J Magn Reson Imaging. 2017 doi: 10.1002/jmri.25684. [DOI] [PubMed] [Google Scholar]
- 57.Bovik AC. In: Handbook of Image and Video Processing. 1. Bovik A, editor. San Diego, CA: Academic Press; 2000. [Google Scholar]
- 58.Li X, Benjamin Ma C, Link TM, Castillo D-D, Blumenkrantz G, Lozano J, Carballido-Gamio J, Ries M, Majumdar S. In vivo T1ρ and T2 mapping of articular cartilage in osteoarthritis of the knee using 3T MRI. Osteoarthr Cartil. 2007;15:789–797. doi: 10.1016/j.joca.2007.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA) Magn Reson Med. 2002;47:1202–1210. doi: 10.1002/mrm.10171. [DOI] [PubMed] [Google Scholar]
- 60.Shrager RI, Weiss GH, Spencer RGS. Optimal time spacings for T2 measurements: monoexponential and biexponential systems. NMR Biomed. 1998;11:297–305. doi: 10.1002/(SICI)1099-1492(199810)11:6<297::AID-NBM531>3.0.CO;2-A. [DOI] [PubMed] [Google Scholar]
- 61.Gilani N, Rosenkrantz AB, Malcolm P, Johnson G. Minimization of errors in biexponential T2 measurements of the prostate. J Magn Reson Imaging. 2015;42:1072–1077. doi: 10.1002/jmri.24870. [DOI] [PubMed] [Google Scholar]
- 62.Zhao B, Lam F, Liang Z-P. Model-based MR parameter mapping with sparsity constraints: parameter estimation and performance bounds. IEEE Trans Med Imaging. 2014;33:1832–1844. doi: 10.1109/TMI.2014.2322815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Wang X, Roeloffs V, Klosowski J, Tan Z, Voit D, Uecker M, Frahm J. Model-based T1 mapping with sparsity constraints using single-shot inversion-recovery radial FLASH. Magn Reson Med. 2017;0:1–11. doi: 10.1002/mrm.26726. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Table S1: Qualification of the methods according to their performance on different aspects.
Supporting Table S2: Some Fratio values based on the choice of the p-value for the problem of detecting mono or biexponential voxels.
Supporting Figure S1: Details of the biexponential parameter errors (MNAD) for synthetic phantom with no noise in the acquisition: (a) fraction-short error (c) fraction-long error (e) T1ρ-short error, (g) T1ρ-long error, compared with the ground truth; (b) fraction-short error (d) fraction-long error (f) T1ρ-short error, (h) T1ρ-long error, compared with the reference.
Supporting Figure S2: Details of the biexponential parameter errors (MNAD) for synthetic phantom with 15dB of noise in the acquisition: (a) fraction-short error (c) fraction-long error (e) T1ρ-short error, (g) T1ρ-long error, compared with the ground truth; (b) fraction-short error (d) fraction-long error (f) T1ρ-short error, (h) T1ρ-long error, compared with the reference.
Supporting Figure S3: Details of the biexponential parameter errors (MNAD) for synthetic phantom with 15dB of noise in the acquisition when 3×3 averaging filter is used: (a) fraction-short error (c) fraction-long error (e) T1ρ-short error, (g) T1ρ-long error, compared with the ground truth; (b) fraction-short error (d) fraction-long error (f) T1ρ-short error, (h) T1ρ-long error, compared with the reference.
Supporting Figure S4: Details of the biexponential parameter errors (MNAD) for in vivo human knee cartilage: (a) fraction-short error (c) fraction-long error (e) T1ρ-short error, (g) T1ρ-long error, compared with the reference.
Supporting Figure S5: Details of the biexponential parameter errors (MNAD) for in vivo human knee cartilage with 3×3 averaging filter: (a) fraction-short error (c) fraction-long error (e) T1ρ-short error, (g) T1ρ-long error, compared with the reference.
Supporting Figure S6: Details of the coefficient of variations (CV) for intra-subject in vivo human knee cartilage with 3×3 averaging filter: (a) fraction-short (b) fraction-long (c) T1ρ-short, (f) T1ρ-long.
Supporting Figure S7: Visual comparison of some results of the knee cartilage, with and without filtering, for reference and L+S SFD with AF=2 and AF=6.
Supporting Figure S8: Illustration of the monoexponential and biexponential fitting for the knee cartilage dataset (medial).
Supporting Figure S9: Number of wrongly classified voxels as biexponential or monoexponential according to the choices of αF, αs and αl for the utilized criterion.
Supporting Figure S10: Comparison of (a) nRMSE, (b) nRMSE for ROI only and (c) MNAD for the synthetic noisy phantom.
Supporting Figure S11: Comparison of (a) nRMSE for entire image, (b) nRMSE for ROI only and (c) MNAD with no filter and (d) MNAD with 3×3 averaging filter, for the in vivo knee cartilage.
Supporting Figure S12: (a) Ground truth, KSVD reconstruction and fitted biexponential curve, and (b) distribution of the reconstruction error over time.