Emergent elasticity in the neural code for space

Significance

We develop a theoretical model, grounded in known properties of neural dynamics and synaptic plasticity, that can fuse information gathered from the past history of velocity and sequence of encountered landmarks during exploratory behavior, to construct a self-consistent internal representation of space. Moreover, through model reduction techniques, we obtain conceptual insights into how consistent internal spatial representations naturally emerge through an elastic relaxation process in an effective spring–particle system. We verify several experimentally testable predictions of our model involving the spatial behavior of grid cells in the medial entorhinal cortex, as well as suggest additional experiments.

Abstract

Upon encountering a novel environment, an animal must construct a consistent environmental map, as well as an internal estimate of its position within that map, by combining information from two distinct sources: self-motion cues and sensory landmark cues. How do known aspects of neural circuit dynamics and synaptic plasticity conspire to accomplish this feat? Here we show analytically how a neural attractor model that combines path integration of self-motion cues with Hebbian plasticity in synaptic weights from landmark cells can self-organize a consistent map of space as the animal explores an environment. Intriguingly, the emergence of this map can be understood as an elastic relaxation process between landmark cells mediated by the attractor network. Moreover, our model makes several experimentally testable predictions, including (i) systematic path-dependent shifts in the firing fields of grid cells toward the most recently encountered landmark, even in a fully learned environment; (ii) systematic deformations in the firing fields of grid cells in irregular environments, akin to elastic deformations of solids forced into irregular containers; and (iii) the creation of topological defects in grid cell firing patterns through specific environmental manipulations. Taken together, our results conceptually link known aspects of neurons and synapses to an emergent solution of a fundamental computational problem in navigation, while providing a unified account of disparate experimental observations.

How might neural circuits learn to create a long-term map of a novel environment and use this map to infer where one is within the environment? This pair of problems is challenging because of their nested, chicken and egg nature. To localize where one is in an environment, one first needs a map of the environment. However, in a novel environment, no such map is yet available, so localization is not possible. Similarly, building a map of a novel environment from scratch can be difficult when one cannot even determine one’s own location in the environment. Thus, neural circuits must create a map over time, through exploration in a novel environment, without initially having access to any global estimate of position within the environment. This chicken and egg problem is known in the robotics literature as simultaneous localization and mapping (SLAM) (1).

Here we explore how known aspects of neural circuit dynamics and synaptic plasticity can conspire to self-organize, through exploration, a solution to the problem of creating a global, consistent map of a novel environment. In particular, neural circuits receive two fundamentally distinct sources of information about position: (i) signals indicating the speed and direction of the animal, which can be path integrated over time to update the animal’s internal estimate of position, and (ii) sensory cues from salient, fixed landmarks in the environment. To create a map of the environment, neural circuits must combine these two distinct information sources in a self-consistent fashion so that sensory cues and self-motion cues are always in coregister.

For example, consider the act of walking from landmark A to landmark B. Sensory perception of landmark A triggers a pattern of neural activity, and subsequent walking from A to B evolves this activity pattern, through path integration, to a final pattern. Conversely, sensory perception of landmark B itself triggers a neural activity pattern. Any circuit that maps space must obey a fundamental self-consistency condition: The neural activity pattern generated by perception of A, followed by path integration from A to B, must match the neural activity pattern triggered by perception of B alone. Only in this manner can neural activity patterns be in one to one correspondence with physical positions in space and become independent of the past trajectory used to reach any physical location.

In the following, we develop an analytic theory for how neuronal dynamics and synaptic plasticity can generate self-consistent neural maps of space upon exploration through a novel environment. Moreover, our analytic theory makes experimentally testable predictions about neural correlates of space. Indeed, many decades of recordings in multiple brain regions have revealed diverse neural correlates of spatial maps in the brain. In particular, the medial entorhinal cortex (MEC) contains neurons encoding for direction, velocity, and landmarks, as well as grid cells exhibiting striking firing patterns reflecting an animal’s spatial location (2–6). Moreover, the geometry of these firing patterns depends on the shape of the environment being explored (7–10). In particular, these grid firing patterns can be deformed in irregular environments (11, 12), in a manner evocative of deformations of solids forced into an irregular container, suggesting a mechanical model for these deformations (13–15). Also, these firing patterns are not simply driven by current sensory cues; there is evidence for path integration (16–18) in that firing patterns appear almost immediately (2), phase differences are preserved across environments (19), and firing patterns become noisier the longer an animal is away from a landmark (20, 21) and can shift, depending on which landmark the animal most recently encountered (22, 23).

Despite this wealth of experimental observations, no mechanistic circuit model currently explains how known aspects of neuronal dynamics and synaptic plasticity can conspire to learn, through exploration, a self-consistent internal map of a novel environment that both behaves like a deformable medium and also retains, at higher order, some knowledge of recently encountered landmarks. Here, we show how an attractor network that combines path integration of velocity with Hebbian learning (22, 24–26) of synaptic weights from landmark cells can self-organize to generate all of these outcomes. Intriguingly, a low-dimensional reduced model of the combined neuronal and synaptic dynamics provides analytical insight into how self-consistent maps of the environment can arise through an emergent, elastic relaxation process involving the synaptic weights of landmark cells.

Model Reduction of an Attractor Network Coupled to Sensorimotor Inputs

Our theoretical framework (SI Appendix, section II) assumes the existence of three interacting neural components: (i) an attractor network capable of realizing a manifold of stable neural activity patterns, (ii) a population of velocity-tuned cells that carry information about the animal’s motion, and (iii) a population of sensory-driven landmark cells that fire if and only if the animal is in a particular region of space. Our goal is to understand how these three populations can interact together and self-organize through synaptic plasticity, sculpted by experience, to create a self-consistent internal map of the environment. Here, we describe the neuronal and synaptic dynamics of each component in turn, as well as describe a model reduction approach to obtain a low-dimensional reduced description of the entire plastic circuit dynamics. Our low-dimensional description provides insight into how self-consistency of the neural map emerges naturally through an elastic relaxation process between landmarks.

A Manifold of Stable States from Attractor Network Dynamics.

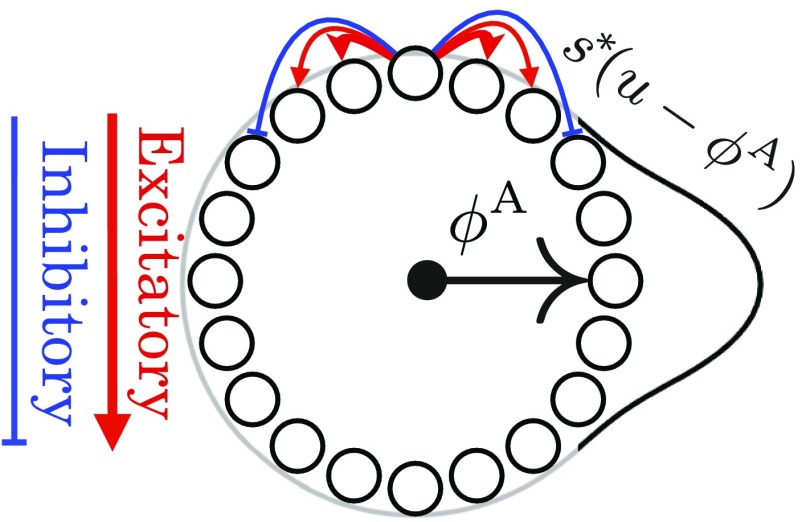
We first consider a 1D attractor network consisting of a large population of neurons whose connectivity is determined by their position on an abstract ring, as in Fig. 1. For analytical simplicity, we take a neural field approach (27), so that position on the ring of neurons is described by a continuous coordinate $u$, with the firing rate of a neuron at position $u$ given by $s\left(u\right)$. Each neuron interacts with neighboring neurons through a translation invariant connectivity, yielding the dynamics

$$\frac{ds\left(u\right)}{dt}=-\frac{s\left(u\right)}{{\tau }_m}+\mathcal{G}\left({\int }_{u\prime }\text{J}\left(u-u\prime \right)s\left(u\prime \right)\right).$$ [1]

Here $\text{J}\left(u-u\prime \right)$ defines the synaptic weight from a cell at position $u\prime$ to a cell at $u$, ${\tau }_m$ is a single-neuron time constant, and $\mathcal{G}$ is a nonlinearity. Many appropriate choices of $\mathcal{G}$ and $\text{J}$, corresponding for example to short-range excitation and long-range inhibition, will yield a family of stable, or steady-state, localized bump activity patterns $s^{\hspace{0.17em}*}\hspace{0.17em}\left(u-{\varphi }^{\text{A}}\right)$, parameterized by the position of their peak ${\varphi }^{\text{A}}$ (28, 29) (Fig. 1). This 1D family of stable bump activity patterns can itself be thought of as ring of stable firing patterns in the space of all possible firing patterns. Just as $u$ indexes a family of neurons on the neural sheet, the coordinate ${\varphi }^{\text{A}}$ indexes the different stable neural activity patterns, with a particular value of ${\varphi }^{\text{A}}$ corresponding to a stable bump on the neural ring centered at coordinate $u={\varphi }^{\text{A}}$. For simplicity we set units such that the coordinate $u$ along the neural ring and the coordinate ${\varphi }^{\text{A}}$ along the ring of stable attractor patterns are both angles, defined modulo $2\pi$. Thus, $u$ and ${\varphi }^{\text{A}}$ are phase variables denoting position along the neural ring and the ring of bump-attractor patterns, respectively.

Fig. 1.

Schematic of a ring attractor with short-range excitation (red arrows) and longer-range inhibition (blue arrows). This yields a 1D family of bump-attractor states $s*\left(u-{\varphi }^{\text{A}}\right)$, which are mapped onto a single periodic variable, or attractor phase, ${\varphi }^{\text{A}}$ representing the peak of the bump pattern.

Motions Along the Attractor Manifold Due to External Inputs.

So far, the attractor network described above has a ring of stable bump activity patterns parameterized by the periodic coordinate ${\varphi }^{\text{A}}$, but these neural activity patterns are as yet unanchored to physical space. We will eventually show how to anchor the coordinate ${\varphi }^{\text{A}}$ along the attractor manifold to the actual position of the animal in physical space. However, to appropriately form such an internal map of position, and thereby map the environment, the attractor state must be influenced by external inputs from both velocity- and landmark-sensitive cells in a self-consistent manner.

Path Integration Through Velocity-Conjunctive Attractor Cells.

Following refs. 28 and 29, we achieve path integration by coupling the attractor network to velocity-conjunctive attractor cells such that east (west) movement-selective cells form feedforward synapses onto the attractor ring that are shifted in the positive (negative) $u$ direction (Fig. 2 A and B). When these inputs are weak compared with the recurrent inputs determining the bump pattern (SI Appendix, section III), we can show analytically that this choice of connectivity leads to path integration:

$$d{\varphi }^{\text{A}}/dt=kv.$$ [2]

Here, $k$ is a constant of proportionality that relates animal velocity $v$ to the rate of phase advance in the attractor network ($k=2\pi$/field spacing). Thus, the connectivity of the velocity-conjunctive attractor cells in Fig. 2 A and B ensures that as the animal moves east (west) along a 1D track, the attractor phase moves clockwise (counterclockwise), at a speed proportional to velocity. Solving Eq. 2 allows us to recover path integration (Fig. 2C), where the resulting integrated attractor phase is only a function of current position $x\left(t\right)$:

$${\varphi }^{\text{A}}\left(t\right)={\varphi }^{\text{A}}\left(0\right)+k\left[x\left(t\right)-x\left(0\right)\right]\hspace{0.17em}.$$ [3]

The collection of neurons in the attractor traces out periodic firing patterns as a function of spatial position, all with the same period but different phases.

Fig. 2.

(A) A ring of east velocity selective cells has outgoing connections onto the attractor ring that are biased in the clockwise direction. Such cells also receive unbiased incoming connections from attractor network cells (not shown). Thus, these east velocity selective cells will fire conjunctively if the animal is moving east and the attractor bump is nearby on the ring. When these cells fire, the biased outgoing connections to the attractor network will then excite cells clockwise relative to the current attractor bump and inhibit cells active in the bump. Thus, the attractor bump will move in the clockwise direction. (B) Similarly, when the animal moves west, the firing of west-conjunctive cells with counterclockwise biased connections will cause the attractor pattern to move counterclockwise. (C) As the animal moves east, the phase of the attractor bump rotates clockwise at a rate proportional to the velocity (Eq. 2). The firing rate of an individual cell (shaded gray) then becomes a periodic function of position (Eq. 3). The firing rates of all other attractor cells are also periodic functions of position with the same period but different phases, yielding a module of 1D grid cells. (D) Schematic of a landmark cell correcting the attractor bump phase (Eq. 4). A single landmark cell can provide excitation that is centered at a certain location on the attractor network ring. When this landmark cell fires, its efferent synapses provide excess excitation to this location, thereby pulling the phase of the attractor bump toward the peak of the landmark cell’s efferent synaptic strength profile.

However, even though these 1D grid cell firing patterns are now a function of physical space, they still are not yet anchored to the environment. There is as yet no mechanism to set the phase of each cell relative to landmarks, and indeed these grid patterns rapidly decohere without anchoring to landmarks, as demonstrated experimentally (20, 30). Coupling the attractor network to landmark-sensitive cells can solve this problem.

Landmark Cells.

We model each landmark cell $i$ as a purely sensory-driven cell with a firing rate that depends on location through $s_i^{\text{L}}\left(t\right)={\text{H}}_i\left(x\left(t\right)\right)$. Here ${\text{H}}_i\left(x\right)$ is the firing field of the landmark cell. An example of a landmark cell could, for example, be an entorhinal border cell (4). Every landmark cell forms feedforward connections onto each cell in the attractor network at ring position $u$ with a synaptic strength ${\text{W}}_i\left(u\right)$.

Consider for example a single landmark cell whose synaptic strength $\text{W}\left(u\right)$ as a function of position $u$ on the neural ring consists of a single bump centered at a particular location $u={\varphi }^{\text{L}}$ (Fig. 2D). When the landmark inputs are weak relative to the recurrent inputs that determine the shape of the bump pattern, then the external landmark inputs will not change the shape of the attractor bump, but will cause it only to change its position. Intuitively, landmark cell firing should cause the attractor bump to move to the location ${\varphi }^{\text{L}}$ on the ring at which the landmark cell provides its peak synaptic strength. Thus, we expect the attractor phase ${\varphi }^{\text{A}}$ to move to and be pinned at the phase ${\varphi }^{\text{L}}$.

We confirm this intuition analytically in SI Appendix, section III.2 by deriving an effective dynamics obeyed by the attractor phase in response to landmark cell input:

$$d{\varphi }^{\text{A}}/dt=\omega \mathcal{F}\left({\varphi }^{\text{L}}-{\varphi }^{\text{A}}\right).$$ [4]

Here, $\mathcal{F}$ is a force law that determines how a landmark cell with peak synaptic strength at ${\varphi }^{\text{L}}$ causes the attractor phase ${\varphi }^{\text{A}}$ to move. We have also introduced a parameter $\omega$ that controls how strongly landmark cells influence the attractor phase. Generically, the force law $\mathcal{F}$ is positive (negative) when its argument is positive (negative). Thus, it acts as a restoring force: When each landmark cell fires, it causes the attractor phase ${\varphi }^{\text{A}}$ to flow toward the phase ${\varphi }^{\text{L}}$ corresponding to the location of the landmark cell’s peak outgoing synaptic strength. An attractor phase ${\varphi }^{\text{A}}$ that is smaller (larger) than the landmark cell synapses’ peak location ${\varphi }^{\text{L}}$ will increase (decrease) and settle down at ${\varphi }^{\text{L}}$ (Fig. 2D). In SI Appendix, section III.2, we show how to analytically compute the force law $\mathcal{F}\left({\varphi }^{\text{L}}-{\varphi }^{\text{A}}\right)$ governing the velocity of the bump peak; in general, the force law will have the same qualitative features as $\sin \left({\varphi }^{\text{L}}-{\varphi }^{\text{A}}\right)$. [See SI Appendix, section VI for attractor dynamics where $\mathcal{F}$ is exactly $\sin \left({\varphi }^{\text{L}}-{\varphi }^{\text{A}}\right)$.]

In summary, we have so far described path integration dynamics that enable the attractor phase to move in response to motion in Eq. 2 and pinning dynamics of a landmark cell that force the attractor phase to move to a particular phase ${\varphi }^{\text{L}}$ through Eq. 4. However, there is as yet no mechanism to enforce consistency between the attractor phases arrived at through path integration and the various attractor phases arrived at through pinning by landmark cells. We next introduce Hebbian plasticity of efferent landmark cell synapses during exploration while both path integration and landmark cells are active. This plasticity will self-organize each landmark cell’s pinning phase (i.e., the position of its peak synaptic strength profile onto the attractor network), to yield a self-consistent spatial map.

Hebbian Learning of Landmark Cell Synapses.

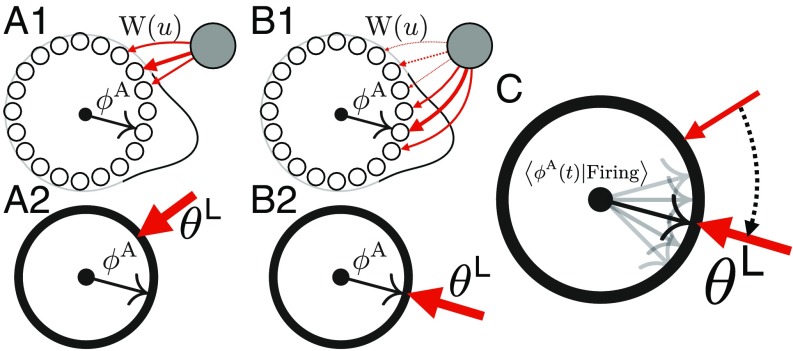
We assume that each synapse ${\text{W}}_i\left(u\right)$ from a landmark cell $i$ to an attractor cell at position $u$ undergoes Hebbian plasticity with some weight decay, thereby learning to reinforce attractor patterns that are active when the landmark cell fires. Moreover, we assume plasticity acts slowly, over a timescale $\text{T}$ that is much longer than the timescale $t$ over which exploration occurs. Hebbian learning then drives the synaptic strengths of each landmark cell $i$ toward the long-time average of attractor patterns $s\left(u\right)$ that occur conditioned on cell $i$ firing (Fig. 3 B2) through (SI Appendix, section III.5)

$$d{\text{W}}_i\left(u\right)/d\text{T}=⟨s\left(u\right)|i\text{Firing}⟩-{\text{W}}_i\left(u\right).$$ [5]

Fig. 3.

(A1) Before learning, the synaptic weights $\text{W}\left(u\right)$ from a landmark cell to the attractor network need not match the average firing rate of the network conditioned on the landmark cell firing. (A2) In the reduced model description, this prelearned state reflects a situation in which the average attractor phase ${\varphi }^{\text{A}}$ when the landmark cell fires does not match the peak position of the synaptic weights ${\theta }^{\text{L}}$. (B1) During learning, the old weights (dashed lines) will decay, while new weights (solid lines) will be formed at locations of peak firing. (B2) In the reduced model description this Hebbian learning plus decay will cause the peak synaptic weight position ${\theta }^{\text{L}}$ to match the average attractor phase ${\varphi }^{\text{A}}$ seen while the landmark cell is firing. (C) Schematic of Eq. 7, where the landmark pinning phase ${\theta }^{\text{L}}$ linearly approaches the average attractor state $⟨{\varphi }^{\text{A}}|\text{Firing}⟩$.

Combined Neural and Synaptic Dynamics During Navigation.

Because the learned synaptic weight profiles of each landmark cell tend to become localized, we can approximate the entire weight profile ${\text{W}}_i\left(u\right)$ of landmark cell $i$ by a single number ${\theta }_i^{\text{L}}$ that closely reflects the position on the ring at which the landmark cell $i$ provides its peak synaptic excitation (see SI Appendix, section III.6 for details). Also, because the attractor bump is close to this distribution when the landmark cell fires, we can derive simplified, linearized equations for the combined neural and synaptic dynamics valid after the initial steps of learning (SI Appendix, section IV):

$$d{\varphi }^{\text{A}}/dt=kv+{\sum }_i{\omega }_i{\text{H}}_i\left(x\left(t\right)\right)\left({\theta }_i^{\text{L}}-{\varphi }^{\text{A}}\right),$$ [6]

$$d{\theta }_i^{\text{L}}/d\text{T}=⟨{\varphi }^{\text{A}}\left(t\right)|i\hspace{0.17em}\text{Firing}⟩-{\theta }_i^{\text{L}}.$$ [7]

In essence Eqs. 6 and 7 constitute a significant model reduction of Eqs. 1 and 5. In this reduction, the entire pattern of neural activity of the attractor network is summarized by a single number ${\varphi }^{\text{A}}$, denoting a point, or phase, on the ring manifold of stable attractor states. Similarly, the entire pattern of synaptic weights ${\text{W}}_i\left(u\right)$ from landmark cell $i$ into the attractor network is summarized by a single number ${\theta }_i^{\text{L}}$, denoting the learned attractor network phase associated with the landmark cell’s synapses.

Intuitively, the reduced Eq. 6 describes both path integration and dynamics in which each landmark cell $i$ attempts to pin the attractor phase ${\varphi }^{\text{A}}$ to the landmark cell’s learned phase, ${\theta }_i^{\text{L}}$, each time the physical position $x\left(t\right)$ of the animal is within the landmark’s firing field ${\text{H}}_i$. In turn, synaptic plasticity described in Eq. 7 aligns the learned pinning phase ${\theta }_i^{\text{L}}$ of each landmark cell $i$ to the average of the attractor phases ${\varphi }^{\text{A}}$ that occur when the animal is in the firing field of the landmark cell (Fig. 3).

As we will see below, as an animal explores its environment, these coupled dynamics between attractor phase ${\varphi }^{\text{A}}$ and landmark pinning phases ${\theta }_i^{\text{L}}$ settle into a self-consistent steady state such that the attractor phase yields an internal estimate of the animal’s current position that is, to first order, largely independent of the history of the animal’s previous trajectory. Moreover, each landmark cell learns a pinning phase ${\theta }_i^{\text{L}}$, consistent with the location of its firing field in physical space.

Learning a Simple Environmental Geometry

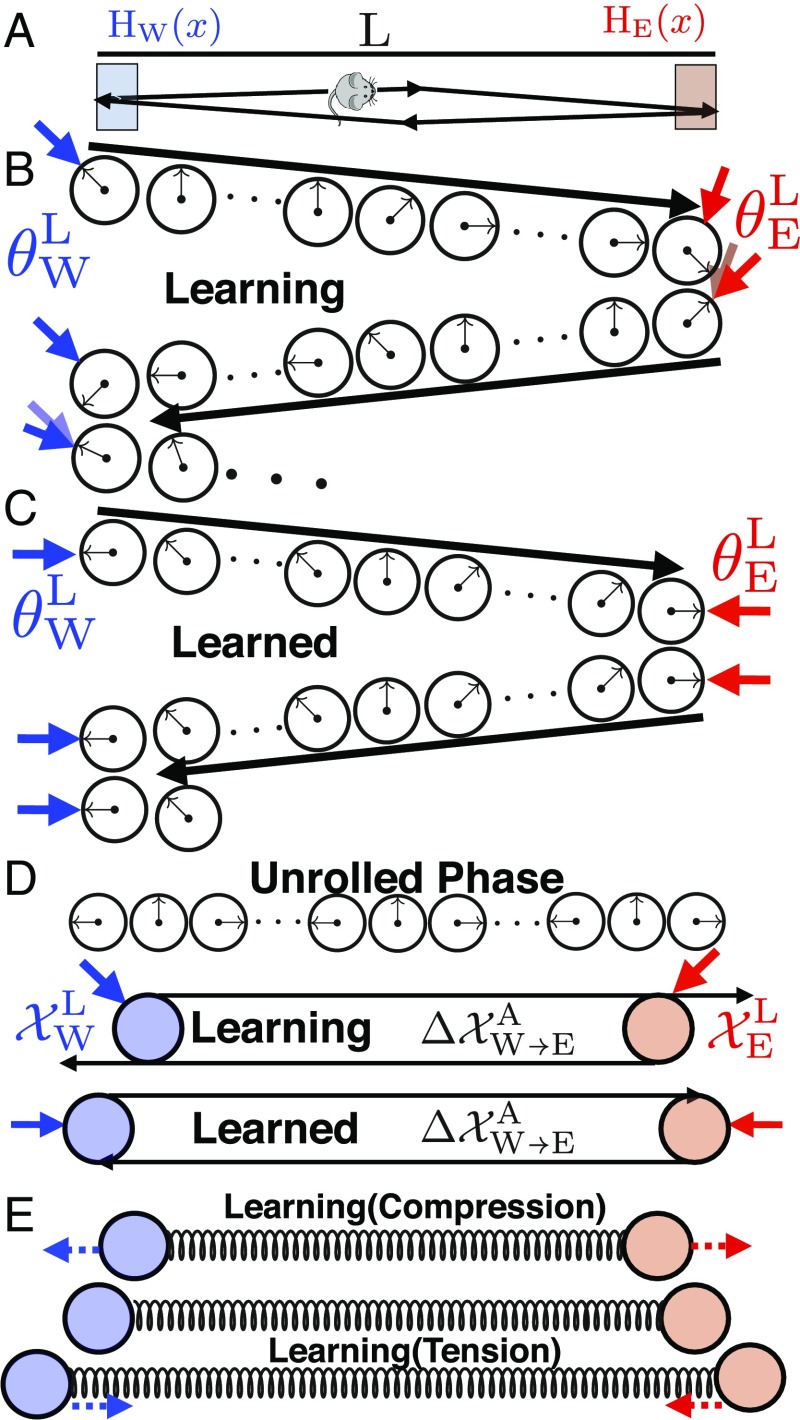
We now examine solutions to these equations to understand how neuronal dynamics and synaptic plasticity conspire to yield a consistent map of the environment. To build intuition, we first consider the dynamics of Eqs. 6 and 7 for the simple case of an animal moving back and forth between the walls of a 1D box of length $\text{L}$, at a constant speed $v_0=\text{L}/\tau$, yielding a total time of $2\tau$ to complete a full cycle (Fig. 4A). In this environment we assume two landmark cells with firing fields localized at the east (west) wall. Their pinning phases ${\theta }_{\text{E}}^{\text{L}}$ (${\theta }_{\text{W}}^{\text{L}}$) encode the peak position of their outgoing synaptic weights. How does circuit plasticity yield a consistent environmental representation through exploration?

Fig. 4.

(A) An animal moving between two landmarks at the edges of a 1D track. (B) A single cycle of exploration as the animal moves from the west to the east wall and back. When the animal encounters the west (east) wall, the attractor phase (black arrow) is pinned to the associated landmark pinning phase (blue/red arrow for west/east wall). As the animal moves from one wall to the other, the attractor phase advances from this pinned phase due to path integration. During learning, the pinning phase from any one wall, plus the phase advance due to path integration, will not equal the pinning phase of the other wall. However, plasticity will adjust the pinning phase of each wall to reduce this discrepancy (motion of red and blue arrows). During this inconsistent prelearned state, the attractor phase at any interior position will depend on path history. (C) After learning, the pinning phase from any one wall, plus the phase advance due to path integration, equals the pinning phase of the other wall, yielding a consistent internal representation of space in which the attractor phase assigned to any interior point becomes independent of path history. (D) We can “unroll” the attractor and landmark phases into linear position variables. Thus, landmark cell synapses can be thought of as points in physical space (blue and red circles). (D, Top) If the phase advance due to path integration exceeds the phase difference between the pinning phases of the landmarks, then the distance between the landmark cells in unrolled phase is closer than the physical distance between the firing fields of the landmarks. (D, Bottom) Plasticity then exerts an outward force pushing the two landmark cells farther apart until their separation in unrolled phase equals the physical distance between their firing fields. (E) In general, the changing positions in unrolled phase associated with landmark cell synapses due to synaptic plasticity can be described by a damped spring-like interaction as in Eqs. 8 and 9. If the separation between the two landmark cell synapses in unrolled phase is smaller (larger) than the physical separation between their firing fields, then the spring will be compressed (extended), yielding an outward (inward) force. This force will move the positions associated with landmark cell synapses until their separation in unrolled phase equals the rest length of the spring, which in turn equals the physical separation between landmark firing fields.

We build intuition in the limit $\omega \to \infty$, where landmark cells fully anchor the attractor state when the animal touches the edge. At $t=0$, the animal starts at the west wall at physical position $x\left(0\right)=-\text{L}/2$. Through Eq. 6, the west border cell pins the initial attractor phase so that ${\varphi }^{\text{A}}\left(0\right)={\theta }_{\text{W}}^{\text{L}}$. At $t=\tau$, the animal travels to the east wall at physical position $x\left(\tau \right)=+\text{L}/2$, and the attractor phase advances due to path integration to become ${\varphi }^{\text{A}}\left({\tau }^{-}\right)={\theta }_{\text{W}}^{\text{L}}+k\text{L}$. However, upon encountering the east wall, the east border cell pins the attractor phase to ${\theta }_{\text{E}}^{\text{L}}$.

Before any learning, there is no guarantee that the east border cell pinning phase ${\theta }_{\text{E}}^{\text{L}}$ equals the attractor phase ${\theta }_{\text{W}}^{\text{L}}+k\text{L}$, obtained by starting at the west wall and moving to the east wall; sensation and path integration might disagree (Fig. 4B). However, plasticity described in Eq. 7 will act to move ${\theta }_{\text{E}}^{\text{L}}$ closer to ${\theta }_{\text{W}}^{\text{L}}+k\text{L}$. Then as the animal returns to the left wall at time $t=2\tau$, path integration will retard the attractor phase ${\varphi }^{\text{A}}\left(2\tau \right)={\theta }_{\text{E}}^{\text{L}}-k\text{L}$, and an encounter with the west wall leads the west border cell to pin the attractor phase to ${\theta }_{\text{W}}^{\text{L}}$. Again, there is no guarantee that the west border cell pinning phase ${\theta }_{\text{W}}^{\text{L}}$ agrees with the attractor phase ${\theta }_{\text{E}}^{\text{L}}-k\text{L}$ obtained by starting at the east wall and traveling to the west wall, but circuit plasticity will change ${\theta }_{\text{W}}^{\text{L}}$ to reduce this discrepancy. Overall, plasticity over multiple cycles of exploration (Fig. 3 B2) yields the iterative dynamics

$${\theta }_{\text{E}}^{\text{L}}\to {\theta }_{\text{W}}^{\text{L}}+k\text{L},{\theta }_{\text{W}}^{\text{L}}\to {\theta }_{\text{E}}^{\text{L}}-k\text{L}.$$

Thus, the phase difference ${\theta }_{\text{E}}^{\text{L}}-{\theta }_{\text{W}}^{\text{L}}$ between the pinning phases of the two landmark cells will approach the phase advance $k\text{L}$ incurred by path integration between the two landmarks. Thus, learning can precisely coregister sensation and path integration so that these two information sources yield a consistent map of space (Fig. 4C). In particular, the attractor phase assigned by the composite circuit to any point in the interior of the environment now becomes independent of which direction the animal is traveling, in contrast to the case before learning (compare the assigned interior phases in Fig. 4B with those in Fig. 4C).

Learning as an Elastic Relaxation Between Landmarks

To gain further insight into the learning dynamics, it is useful to interpret the periodic attractor phase ${\varphi }^{\text{A}}\left(t\right)$ as an internal estimate of position through the “unrolled” coordinate variable ${\mathcal{X}}^{\text{A}}={\varphi }^{\text{A}}/k$. Likewise, we can replace the landmark phase ${\theta }_i^{\text{L}}$ with another linear variable ${{\mathcal{X}}^{\text{L}}}_i={\theta }_i^{\text{L}}/k$, denoting the internal representation of the position of landmark $i$ (Fig. 4D). This enables us to associate physical positions to landmark cells, or more precisely their pinning phases, although these assigned positions are defined only up to shifts of the grid period. By “unrolling” the learning rule of Eq. 7, we derive the learning and plasticity dynamics of unrolled phase for the landmark cells over the long timescale $\text{T}$ of exploration,

$$d{\mathcal{X}}_{\text{E}}^{\text{L}}/d\text{T}=-{\text{M}}_{\text{WE}}\left[{\mathcal{X}}_{\text{E}}^{\text{L}}-\left({\mathcal{X}}_{\text{W}}^{\text{L}}+\mathrm{\Delta }{\mathcal{X}}_{\text{W}\to \text{E}}^{\text{A}}\right)\right]$$ [8]

$$d{\mathcal{X}}_{\text{W}}^{\text{L}}/d\text{T}=-{\text{M}}_{\text{WE}}\left[{\mathcal{X}}_{\text{W}}^{\text{L}}-\left({\mathcal{X}}_{\text{E}}^{\text{L}}+\mathrm{\Delta }{\mathcal{X}}_{\text{E}\to \text{W}}^{\text{A}}\right)\right],$$ [9]

where $\mathrm{\Delta }{\mathcal{X}}_{\text{W}\to \text{E}}^{\text{A}}=-\mathrm{\Delta }{\mathcal{X}}_{\text{E}\to \text{W}}^{\text{A}}=\text{L}$ (SI Appendix, section V).

These dynamics for the two landmark cell synapses in unrolled phase are equivalent to those of two particles at physical positions ${\mathcal{X}}_{\text{W}}^{\text{L}}$ and ${\mathcal{X}}_{\text{E}}^{\text{L}}$, connected by an overdamped spring with rest length $\text{L}$ and spring constant ${\text{M}}_{\text{WE}}$ (Fig. 4E). If the separation ${\mathcal{X}}_{\text{E}}^{\text{L}}-{\mathcal{X}}_{\text{W}}^{\text{L}}$ between the particles is less (greater) than $\text{L}$, then the spring is compressed (extended), yielding a repulsive (attractive) force between the two particles. Learning stabilizes the two particle positions when their separation equals the spring rest length, so that ${\mathcal{X}}_{\text{E}}^{\text{L}}-{\mathcal{X}}_{\text{W}}^{\text{L}}=\text{L}$.

This condition in unrolled phase is equivalent to the fundamental consistency condition for a well-defined spatial map, namely that the phase advance due to path integration equals the phase difference between the pinning phases of landmark cells (Fig. 4C). However, the utility of the unrolled phase representation lies in revealing a compelling picture of how a spatially consistent map arises from the combined neuronal and synaptic dynamics, through simple, emergent first-order relaxational dynamics of landmark particles connected by damped springs. As we see below, this simple effective particle–spring description of synaptic plasticity in response to spatial exploration generalizes to arbitrary landmarks in arbitrary 2D environments.

We note that if the environment has not been fully learned or has been recently deformed, the internal representation of landmarks will lag behind the true geometry for a time, leading to “boundary-tethered” firing fields seen in refs. 22, 25, and 31. Additionally (SI Appendix, section V), we have solved the dynamics when the firing fields of the border cells have a finite extent ${\text{L}}_{\text{Wall}}$ and the landmark cells have a finite strength $\omega$, and we find the dynamics obey those of Eqs. 8 and 9, with a different rest length $\mathrm{\Delta }{\mathcal{X}}_{\text{W}\to \text{E}}^{\text{A}}=\text{L}-2\left({\text{L}}_{\text{Wall}}-v_0\tanh \left(\omega {\text{L}}_{\text{Wall}}/2v_0\right)\hspace{0.17em}/\omega \right)$.

Generalization to 2D Grid Cells

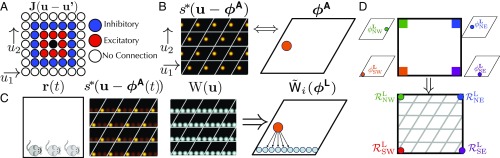
To make contact with experiments, we generalize all of the above to 2D space. Now grid cells live on a periodic 2D neural sheet, where each cell has position $\mathbf{u}=\left(u_1,u_2\right)$. The analogue of Eq. 1 is

$$\frac{ds\left(\mathbf{u}\right)}{dt}=-\frac{s\left(\mathbf{u}\right)}{{\tau }_m}+\mathcal{G}\left({\iint }_{\mathbf{u}\prime }\mathbf{\text{J}}\left(|\mathbf{u}-\mathbf{u}\prime |\right)s\left(\mathbf{u}\prime \right)\right),$$ [10]

where $\mathbf{\text{J}}$ includes short-range excitation and long-range inhibition (Fig. 5A). Attractor dynamics on this sheet can yield a 2D family of steady-state bump activity patterns $s^{\hspace{0.17em}*}\hspace{0.17em}\left(\mathbf{u}-{\mathit{\varphi }}^{\mathbf{\text{A}}}\right)$ with hexagonal symmetry (SI Appendix, section VII). The attractor state is now a 2D phase ${\mathit{\varphi }}^{\mathbf{\text{A}}}$ on the periodic rhombus (Fig. 5B). Velocity-conjunctive attractor cells yield a generalization of Eq. 2:

$$d{\mathit{\varphi }}^{\mathbf{\text{A}}}/dt=\mathbf{K}\hspace{0.17em}d\mathbf{\text{r}}/dt.$$ [11]

Here we have replaced $k$ in 1D with $\mathbf{K}$, a two-by-two matrix that translates 2D animal velocity into phase advance in the 2D attractor network. $\mathbf{K}$ determines both grid spacing and orientation.

Fig. 5.

(A) A 2D neural sheet with short-range excitation and long-range inhibition, analogous to Fig. 1. Each neuron on the continuous sheet now has coordinates $\mathbf{u}=\left(u_1,u_2\right)$. (B) A 2D analogue of a single attractor pattern on the neural sheet, with high firing rates in red (compare with Fig. 1). The set of all unique stable attractor patterns is now indexed not by a single phase variable as in 1D, but by a 2D phase variable ${\mathit{\varphi }}^{\mathbf{\text{A}}}$ ranging over a rhombus or unit cell. Copies of the unit cell are shown via white lines. (C) The landmark cell Hebbian weights will be a combination of 2D attractor states (Eq. 13). As the animal travels along the south wall, the average firing rates will form a “streak” across the neural sheet. This leads the Hebbian weights on the neural sheet to form the same streak; this learned state can be represented as a distribution over the periodic rhombus. Analogously, there is a force law, where the state of an attractor network ${\mathit{\varphi }}^{\mathbf{\text{A}}}$ will be pulled toward this distribution ${\tilde{\text{W}}}_i\left({\mathit{\varphi }}^{\mathbf{\text{L}}}\right)$ (Eq. 15). (D) Similar to Fig. 4D, we can unroll the 2D attractor phase into a 2D position variable, thereby associating landmark pinning phases to points in physical space. Given landmarks in all four corners, the landmark pinning phases correspond to different points on the phase rhombus, but through unrolling this rhombus, each one can be associated to a physical corner of the environment.

We again assume the effect of landmark cells on the attractor network is strong enough to affect the position of the bump pattern, but not strong enough to change its shape. Then learned Hebbian synaptic weights ${\text{W}}_i\left(\mathbf{u}\right)$ of landmark cell $i$ onto the attractor network can be expressed as a weighted superposition of attractor bump patterns with weighting coefficients ${\tilde{\text{W}}}_i\left({\mathit{\varphi }}^{\mathbf{\text{L}}}\right)$:

$${\text{W}}_i\left(\mathbf{u}\right)={\iint }_{{\mathit{\varphi }}^{\mathbf{\text{L}}}}{\tilde{\text{W}}}_i\left({\mathit{\varphi }}^{\mathbf{\text{L}}}\right)s^{\hspace{0.17em}*}\hspace{0.17em}\left(\mathbf{u}-{\mathit{\varphi }}^{\mathbf{\text{L}}}\right).$$ [12]

The learning dynamics are then (see SI Appendix, section XI1 for a proof)

$$d{\tilde{\text{W}}}_i\left({\mathit{\varphi }}^{\mathbf{\text{L}}}\right)/d\text{T}=\text{Pr}\left({\mathit{\varphi }}^{\mathbf{\text{A}}}\left(t\right)={\mathit{\varphi }}^{\mathbf{\text{L}}}|i\hspace{0.17em}\text{Firing}\right)-{\tilde{\text{W}}}_i\left({\mathit{\varphi }}^{\mathbf{\text{L}}}\right),$$ [13]

where ${\tilde{\text{W}}}_i\left({\mathit{\varphi }}^{\mathbf{\text{L}}}\right)$ is a distribution over the periodic rhombus (Fig. 5C). Also, each landmark cell $i$ will affect the attractor phase through

$$d{\mathit{\varphi }}^{\mathbf{\text{A}}}/dt={\omega }_i{\text{H}}_i\left(\mathbf{\text{r}}\left(t\right)\right)\underset{{\mathit{\varphi }}^{\mathbf{\text{L}}}}{\iint }{\tilde{\text{W}}}_i\left({\mathit{\varphi }}^{\mathbf{\text{L}}}\right)\hspace{0.17em}\mathit{ℱ}\left({\mathit{\varphi }}^{\mathbf{\text{L}}}-{\mathit{\varphi }}^{\mathbf{\text{A}}}\right),$$ [14]

where $\mathit{ℱ}$ is a 2D force law that pulls ${\mathit{\varphi }}^{\mathbf{\text{A}}}$ toward ${\mathit{\varphi }}^{\mathbf{\text{L}}}$. In general, a landmark cell $i$ will pull the attractor state ${\mathit{\varphi }}^{\mathbf{\text{A}}}$ on the rhombus toward the center of mass of the cell’s synaptic weights ${\tilde{\text{W}}}_i\left({\mathit{\varphi }}^{\mathbf{\text{L}}}\right)$ when viewed as a density over the rhombus (Fig. 5C).

Combined 2D Neural and Synaptic Dynamics During Exploration

By combining the effects of path integration in Eq. 11 with landmark cells in Eq. 14, we obtain the full dynamics of the 2D attractor phase driven by both animal velocity and landmark encounters:

$$\begin{array}{ccc}\hfill d{\mathit{\varphi }}^{\mathbf{\text{A}}}/dt& =\hfill & \mathbf{K}\hspace{0.17em}d\mathbf{\text{r}}/dt\hfill \\ \hfill & \hfill & +\hspace{0.17em}{\sum }_i{\omega }_i{\text{H}}_i\left(\mathbf{\text{r}}\left(t\right)\right){\iint }_{{\mathit{\varphi }}^{\mathbf{\text{L}}}}{\tilde{\text{W}}}_i\left({\mathit{\varphi }}^{\mathbf{\text{L}}}\right)\hspace{0.17em}\mathit{ℱ}\left({\mathit{\varphi }}^{\mathbf{\text{L}}}-{\mathit{\varphi }}^{\mathbf{\text{A}}}\right).\hfill \end{array}$$ [15]

Now in an analogy to Fig. 4D, we can unroll the attractor phase ${\mathit{\varphi }}^{\mathbf{\text{A}}}\left(t\right)$ into a 2D linear variable ${\mathcal{R}}^{\mathbf{\text{A}}}\left(t\right)={\mathbf{K}}^{-1}{\mathit{\varphi }}^{\mathbf{\text{A}}}\left(t\right)$, reflecting an internal estimate of the animal’s physical position (up to the grid period). Furthermore, by linearizing the force law, we can simplify Eq. 15 by summarizing ${\tilde{\text{W}}}_i\left({\mathit{\varphi }}^{\mathbf{\text{L}}}\right)$ by its mean phase and then unrolling it to obtain another $2\text{D}$ position variable ${\mathcal{R}}_i^{\mathbf{\text{L}}}$ reflecting an internal estimate of the center of mass of landmark firing-field $i$ (Fig. 5D and SI Appendix, section VII.4.D). In analogy to Eqs. 6 and 7 this yields dynamics for the 2D internal position and landmark estimates given a 2D animal trajectory $\mathbf{\text{r}}\left(t\right)$:

$$d{\mathcal{R}}^{\mathbf{\text{A}}}/dt=d\mathbf{\text{r}}/dt+{\sum }_i{\omega }_i\hspace{0.17em}{\text{H}}_i\left(\mathbf{\text{r}}\left(t\right)\right)\left({\mathcal{R}}_i^{\mathbf{\text{L}}}-{\mathcal{R}}^{\mathbf{\text{A}}}\right),$$ [16]

$$d{\mathcal{R}}_i^{\mathbf{\text{L}}}/d\text{T}=⟨{\mathcal{R}}^{\mathbf{\text{A}}}\left(t\right)|\text{Cell}\hspace{0.17em}i\hspace{0.17em}\text{Firing}⟩-{\mathcal{R}}_i^{\mathbf{\text{L}}}.$$ [17]

Spatial Consistency Through Emergent Elasticity

We showed in Eqs. 8 and 9 and Fig. 4 D and E that the emergence of spatial consistency between path integration and landmarks through Hebbian learning dynamics, during exploration of a simple 1D environment, could be understood as the outcome of an elastic relaxation process between landmark cell synapses, viewed as particles in physical space connected by damped springs. Remarkably, this result generalizes far beyond this simple environment. As long as the exploration dynamics are time reversible [time reversible means that for any $\mathbf{\text{r}}\left(t\right)$, the reverse path $\mathbf{\text{r}}\left(-t\right)$ is equally likely], the learning dynamics of any set of landmark cells in any 2D geometry yield this particle–spring interpretation:

$$d{\mathcal{R}}_i^{\mathbf{\text{L}}}/d\text{T}=-{\sum }_j{\text{M}}_{ij}\left({\mathcal{R}}_i^{\mathbf{\text{L}}}-\left[{\mathcal{R}}_j^{\mathbf{\text{L}}}+\mathrm{\Delta }{\mathcal{R}}_{j\to i}^{\mathbf{\text{A}}}\right]\right).$$ [18]

The spring constant ${\text{M}}_{ij}$ is related to the frequency with which the animal moves between each pair of landmark firing fields $i,j$, while the rest displacement $\mathrm{\Delta }{\mathcal{R}}_{j\to i}^{\mathbf{\text{A}}}$ is the average change in unrolled attractor phase as the animal moves from firing-field $j$ to firing-field $i$, roughly related to the distance between the landmark firing fields. Precise expressions for the spring constants and rest lengths are derived from the statistics of exploration in SI Appendix, section VIII.

Overall, this elastic relaxation process converges toward an internal map where all pairs of landmark cell synapses, viewed as particles in unrolled phase, or physical space, become separated by the physical distance between their firing fields. This convergence ensures a consistent internal environmental map of external space in which velocity-based path integration of attractor phase starting at the pinning phase of landmark $i$ and ending at landmark $j$ will yield an integrated phase consistent with the pinning phase of landmark $j$ itself. These relaxation dynamics explain path-dependent shifts in firing patterns observed in recently deformed environments (22). Also, the experimental observation in ref. 10 that, in multicompartment environments, consistent maps within compartments form before consistent maps between compartments is also explained by these relaxation dynamics. In essence, the longest-lived learning mode of the relaxation dynamics corresponds to differences in maps between compartments.

Furthermore, as we explain in the next three sections, these relaxation dynamics yield several experimental predictions: (i) systematic path-dependent shifts in fully learned 2D environments, (ii) mechanical deformations in complex environments, and (iii) the prediction of creation of topological defects in grid cell firing patterns through specific environmental manipulations.

Path Dependence in 2D Environments

We saw above that exploration in a simple 1D geometry led to a consistent internal map in which the attractor network phase was mapped onto the current physical position alone, independent of path history (Fig. 4C). This consistency arises through the elastic relaxation process in Eqs. 8 and 9, which makes the distance between the landmark cells in unrolled phase ${\mathcal{X}}_{\text{E}}^{\text{L}}-{\mathcal{X}}_{\text{W}}^{\text{L}}$ equal to the physical distance between their firing fields $\text{L}$, just like two particles connected by a spring with rest length $\text{L}$ (Fig. 4E). This situation will generalize to 2D if there are only two landmarks, namely a west and an east border cell (Fig. 6 A1). However, it becomes more complex with the addition of a third landmark cell, for example a south border cell (Fig. 6 A2).

Fig. 6.

(A1) For two landmark cells, the rest length $\mathrm{\Delta }{\mathcal{R}}_{\text{W}\to \text{E}}^{\mathbf{\text{A}}}$ of the spring connecting them equals the physical width $\text{L}$ of the environment, and so the two landmark particles learn unrolled pinning phases ${\mathcal{R}}_{\text{E}}^{\mathbf{\text{L}}}$ and ${\mathcal{R}}_{\text{W}}^{\mathbf{\text{L}}}$ obeying the spatial consistency condition ${\left({\mathcal{R}}_{\text{E}}^{\mathbf{\text{L}}}-{\mathcal{R}}_{\text{W}}^{\mathbf{\text{L}}}\right)}_{\text{Eq}}=\mathrm{\Delta }{\mathcal{R}}_{\text{W}\to \text{E}}^{\mathbf{\text{A}}}=\text{L}\widehat{\mathbf{x}}$ as in Fig. 4C. Blue and red arrows represent animal trajectories between the west and east walls, having path integration distance $\mathrm{\Delta }{\mathcal{R}}_{\text{W}\to \text{E}}^{\mathbf{\text{A}}},\hspace{0.17em}\mathrm{\Delta }{\mathcal{R}}_{\text{E}\to \text{W}}^{\mathbf{\text{A}}}$. (A2) The addition of a southern landmark cell will cause a pinning effect which pulls ${\mathcal{R}}_{\text{W}}^{\mathbf{\text{L}}},{\mathcal{R}}_{\text{E}}^{\mathbf{\text{L}}}$ closer together. The animal can travel from the east and west landmark fields to the southern landmark field with little path integration (blue/black and black/red arrow pairs), yielding $\mathrm{\Delta }{\mathcal{R}}_{\text{W}\to \text{S}}^{\mathbf{\text{A}}}\approx 0$, $\mathrm{\Delta }{\mathcal{R}}_{\text{S}\to \text{E}}^{\mathbf{\text{A}}}\approx 0$. (B) If the attractor phase is advanced on a west to east trajectory (blue) relative to an east to west trajectory (red), then any particular grid cell (in this case the shaded gray cell) will fire earlier (later) on a west to east (east to west) trajectory. Thus, grid fields computed from trajectories leaving the west (east) border will shift west (east). (C1) When landmark pinning phases are pulled together closer than the path integration distance between them, then the attractor phase will shift away from whichever wall the animal last encountered. Therefore it will phase advance on west to east trajectories relative to east to west trajectories, as in Fig. 4B and in B. (C2) Thus simulations of Eqs. 13 and 15 lead to grid cell firing patterns shifted toward whichever wall the animal last encountered.

In this case, east and west landmark particles will be connected by a spring of rest length $\mathrm{\Delta }{\mathcal{R}}_{\text{E}\to \text{W}}^{\mathbf{\text{A}}}=\text{L}\widehat{\mathbf{x}}$, as before, but they will each also be connected to the south landmark particle with springs. Intuitively, as the animal travels from the east or west walls to the south walls, the landmark pinning phases of each of these three border cells will be attracted toward each other. (More complex, nonoverlapping distributions yield the same deformations.) The combined three-particle elastic system will settle into an equilibrium configuration in which the difference in unrolled phase between east and west landmarks will be less than the physical separation $\text{L}$ or equivalently the rest length $\mathrm{\Delta }{\mathcal{R}}_{\text{E}\to \text{W}}^{\mathbf{\text{A}}}$ of the spring connecting them. This in turn implies that the attractor phase assigned to any physical position in the interior will be relatively phase advanced (retarded) if the mouse is on a trajectory leaving the west (east) wall. This path dependence in the attractor phase is entirely analogous to that seen in Fig. 4B. However, the reason is completely different. In Fig. 4B, the landmark particles are not separated by the rest length of the spring connecting them because the environment is not fully learned and so the particles are out of equilibrium, whereas in Fig. 6 A2, the particles are not separated by the rest length, even in a fully learned environment, because additional springs from the south landmark create excess compression (See SI Appendix, section IX for details).

This theory makes a striking experimentally testable prediction, namely that even in a fully learned 2D environment, grid cell firing fields, when computed on subsets of mouse trajectories conditioned on leaving a particular border, will be shifted toward that border (Fig. 6B). This shift occurs because at any given position, the attractor phase depends on the most recently encountered landmark. In particular, on a west to east (east to west) trajectory, the attractor phase will be advanced (retarded) relative to an east to west (west to east) trajectory. Thus, on a west to east trajectory, the advanced phase will cause grid cells to fire earlier, yielding west-shifted grid cell firing fields as a function of position. Similarly on an east to west trajectory, grid fields will be east shifted. In summary, the theory predicts grid cell firing patterns conditioned on trajectories leaving the west (east) border will be shifted west (east). While we have derived this prediction qualitatively using the conceptual mass–spring picture in Fig. 6 A2, we confirm this intuition through direct numerical simulations of the full circuit dynamics in Eqs. 13 and 15 (Fig. 6 C2). Under reasonable parameters, our simulations can yield path-dependent shifts of up to $\sim$2 cm toward the wall the animal last touched (SI Appendix, section XII).

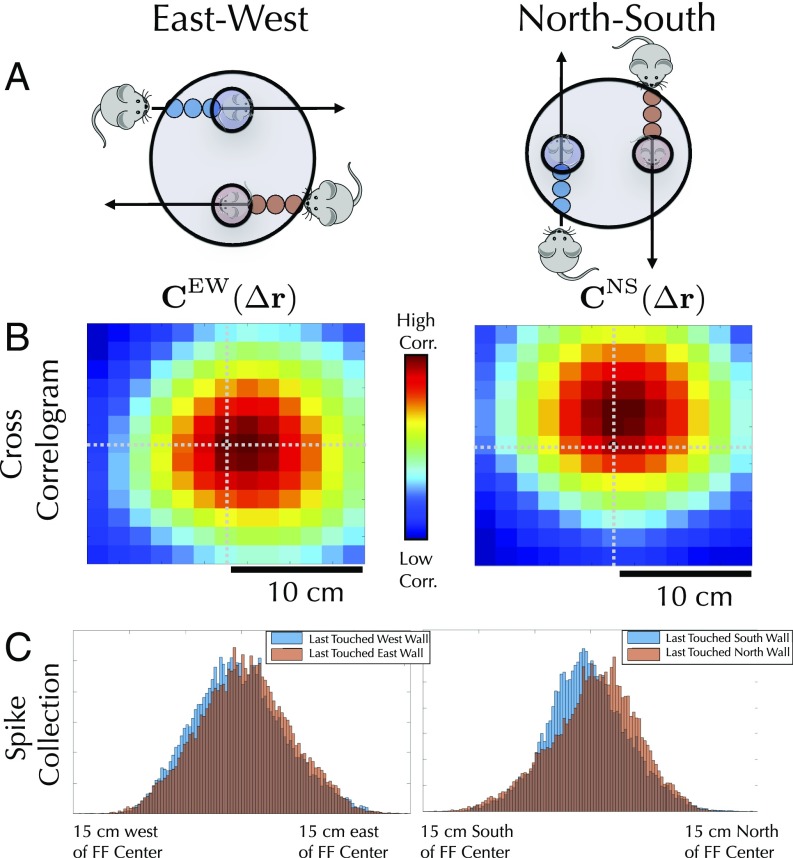
We searched for such subtle shifts in a population of 143 grid cells from 14 different mice that had been exploring a familiar, well-learned, 1-m open field (SI Appendix, section XII.2), using two separate analyses, based on cross-correlations and spike shifts with respect to field centers.

Cross-Correlations.

One method for detecting a systematic firing-field shift across many grid fields is to cross-correlate firing-rate maps conditioned on trajectories leaving two different borders (SI Appendix, section IX.1.A). For example, for each cell, we can ask how much and in what direction we must shift its west border-conditioned firing field to match, or correlate as much as possible with, the same cell’s east-conditioned firing field. In particular, for each cell, we can compute the correlation coefficient between a spatially shifted west-conditioned field and an unshifted east-conditioned field and plot the average correlation coefficient as a function of this spatial shift. The theory predicts that we will have to shift the west-conditioned firing field eastward to match the east-conditioned firing field (Fig. 7A). This prediction is confirmed by a peak in the cross-correlation as a function of spatial shift when the spatial shift is positive or directed east (Fig. 7B). A similar logic holds for north and south.

Fig. 7.

(A) Our theory predicts that grid cell firing patterns will be shifted toward whichever wall the animal last encountered, even in a fully learned environment. In B, Left (B, Right) this shift is detected by computing the cross-correlation between west (south) conditioned firing fields, shifted by a spatial offset $\mathrm{\Delta }\mathbf{r}$, and the unshifted east (north) conditioned firing field. The cross-correlation peaks when the spatial shift is positive in the x direction (positive in the y direction), as predicted by theory. Cross-correlations are averaged over all grid cells. (C) This effect can also be seen by comparing histograms of spike positions around firing-field centers for different path conditions.

Overall, this analysis shows that grid patterns are shifted toward the most recently encountered wall, both for the north–south (NS) walls (3 cm, $P=1.5\cdot 10^{-5}$, binomial test; $P=1.5\cdot 10^{-5}$, sign-flip test) and the east–west (EW) walls (1.5 cm, $P=10^{-7}$, binomial test; $P=10^{-7}$, sign-flip test), matching the sign and magnitude seen in simulations.

Firing-Field Centers.

These results can be corroborated by computing shifts in spikes relative to firing-field centers, when conditioning spikes on the path history (SI Appendix, section IX.1.B). For each firing-field center, we calculate the average spike position within that firing field conditioned on the animal having last touched a particular wall. For each cell, we calculate the average shift across all firing fields and examine how the shifts depend on which wall the animal last touched. Again, the patterns are shifted toward whichever wall the animal last touched (Fig. 7C) for both the NS walls (0.5 cm, $P=10^{-5}$, binomial test; $P=10^{-5}$, sign-flip test) and the EW walls (0.5 cm, $P=3\cdot 10^{-4}$, binomial test; $P=2\cdot 10^{-2}$, sign-flip test). The discrepancy in the estimated magnitude of the shift between the methods of analysis is likely due to poorly defined firing fields; a method based on firing-field centers will give a lower signal-to-noise ratio, and thus a lower shift magnitude, than the cross-correlogram method.

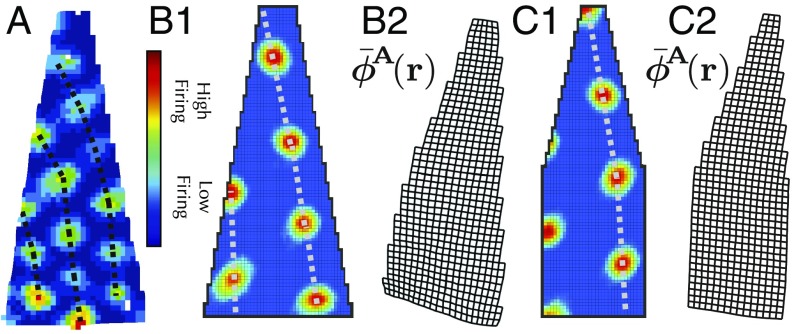
Mechanical Deformations in Complex Environments

Another experimental observation that can be reproduced by our theory is the distortion (11) of grid cell patterns seen in an irregular environment (Fig. 8A). Landmark cells with firing fields distributed across an entire wall will pull the attractor phase to its associated landmark pinning phase regardless of where along the wall the animal is. The presence of a diagonal wall then causes the average attractor phase as a function of position to curve toward the wall, yielding spatial grid cell patterns that curve away from the wall (Fig. 8 B1, B2, C1, and C2). Previous theoretical accounts of this grid cell deformation have relied on purely phenomenological models that treated individual grid cell firing fields as particles with mostly repulsive interactions (15), without a clear mechanistic basis underlying this interaction. Our model instead provides a clear mechanistic basis for such deformations, grounded in the interaction between attractor-based path integration and plastic landmark cells. Such dynamics yield an emergent elasticity where the particles are landmark cell synapses rather than individual firing-field centers.

Fig. 8.

(A) Experimental data of grid cell firing patterns deformed, curving away from a wall in an irregular geometry. (B1) A full simulation of Eq. 15. Eq. 13 also yields grid firing patterns bent away from the wall. (B2) Visualization of the average attractor state as a function of position ${\mathit{\varphi }}^{\mathbf{\text{A}}}\left(\mathbf{\text{r}}\right)$ (periodicity removed for visualization purposes). The reversal between the bending of the internal attractor phase and the bending of firing-rate maps is similar to the reversal seen in Fig. 6B. (C1 and C2) Same as B1 and B2, but for a slightly different geometry.

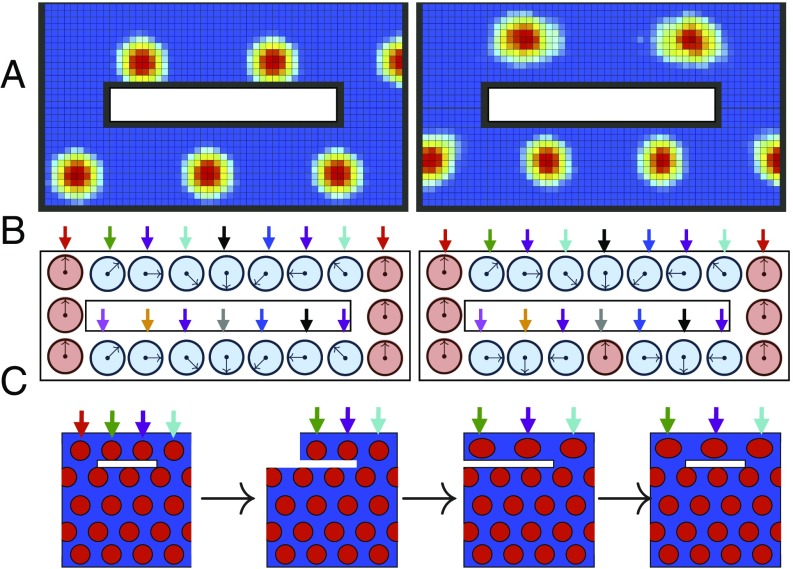
Topological Defects in Grid Fields: A Prediction

While the dynamics of the linearized Eqs. 16 and 17 will always flow to the same relative landmark representations ${\mathcal{R}}_i^{\mathbf{\text{L}}}$, this is not the case for the full dynamics of Eqs. 13 and 15, which can learn multiple different stable landmark cell synaptic configurations. One striking example of this is the ability of the learning dynamics to generate “topological defects,” where the number of firing fields traversed is not the same for two different paths (Fig. 9 A and B and SI Appendix, section XII). An environmental geometry capable of supporting these defects will yield a set of firing patterns that depends not only on the final geometry, but also on the history of how this geometry was created (Fig. 9C).

Fig. 9.

(A) Two steady-state grid cell patterns emerging from the same cue-rich environment. In the first firing pattern, the combination of landmark pinning and path integration yields a phase advance of four firing fields in traveling from west to east along either corridor. The second pattern has a topological defect: Traveling from the west to the east through the north corridor yields a phase increase of $\sim 1.5$ firing fields; traveling east to west through the south corridor yields a phase decrease of $\sim 2.5$ firing fields. This second pattern is stable nonetheless. (B) Schematic of 1D underlying attractor state as a function of space. The two patterns in A correspond to two different landmark pinning-phase patterns learned by the many landmarks. Both landmark pinning patterns are stable under Eqs. 13 and 15. In the first pattern, the combination of landmark pinning and path integration yields the same phase advance in both the north and south corridors. The second pattern has a topological defect: The phase advance in the north corridor is one full rotation less than the phase advance through the south corridor. This is possible because many landmark cues (colored arrows) can yield many landmark cells with multiple stable synaptic configurations or pinning phases under Eqs. 13 and 15. (C) Schematic of proposed “deformation schedule” that could yield a topological defect in grid cell firing patterns. By separating/truncating the northern corridor, stretching it (along with spatial cues, denoted by colored arrows), and then reconnecting it, it may be possible to introduce one of these defects. Even though the initial geometry is identical to the final geometry, the deformation schedule has led to a firing pattern which is three fields wide in the north and four fields wide in the south.

Discussion

Overall, we have provided a theoretical framework for exploring how sensory cues and path integration may work together to create a consistent internal representation of space. Our framework is grounded in biologically plausible mechanisms involving attractor-based path integration of velocity and Hebbian plasticity of landmark cells. Moreover, systematic model reduction of these combined neural and synaptic dynamics yields a simple and intuitive emergent elasticity model in which landmark cell synapses act like particles sitting in physical space connected by damped springs whose rest length is equal to the physical distance between landmark firing fields. This simple emergent elasticity model not only provides a conceptual explanation of how neuronal dynamics and synaptic plasticity can conspire to self-organize a consistent map of space in which sensory cues and path integration are in register, but also provides predictions involving small shifts in firing fields even in fully learned environments, potential topological defects in grid cells, and grid cell mechanical deformation when borders are irregular. Furthermore, a special case of this model can explain sudden grid cell remapping events in altered virtual reality environments as the disagreement between landmarks and path integration is gradually increased; the model remaps due to sudden phase transitions in its dynamics (32).

This work opens up many interesting avenues. For example, further explorations of the nonlinear regime of our model may yield interesting experimental signatures that distinguish different modes of interaction between attractors, path integrators, and landmark cells. Incorporating heterogeneity of neural representations observed in MEC (33) into our framework is another intriguing direction. Also, as the reliability of sensory and velocity cues changes, it is interesting to ask what higher-order mechanisms may differentially regulate the effect of landmarks and velocity on the internal representation of space. More generally, our theory provides a unified framework for understanding how systematic variations in environmental geometry and the statistics of environmental exploration interact to precisely sculpt neural representations of space.