Abstract
Summary
SPUTNIK is an R package consisting of a series of tools to filter mass spectrometry imaging peaks characterized by a noisy or unlikely spatial distribution. SPUTNIK can produce mass spectrometry imaging datasets characterized by a smaller but more informative set of peaks, reduce the complexity of subsequent multi-variate analysis and increase the interpretability of the statistical results.
Availability and implementation
SPUTNIK is freely available online from CRAN repository and at https://github.com/paoloinglese/SPUTNIK. The package is distributed under the GNU General Public License version 3 and is accompanied by example files and data.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Over the last few years, mass spectrometry imaging (MSI or IMS) has demonstrated great potential in discovering and elucidating chemical processes in a wide variety of research contexts. MSI has been used to determine possible cancer biomarkers (Franck et al., 2009), and recent technologies are capable of detecting molecular signals at the cellular level (Kompauer et al., 2017). The properties of such data type, such as high ion dimensionality and the presence of noise fluctuations in the spectral profiles, make the pre-processing phase and the extraction of informative features for the subsequent statistical analysis extremely important.
Software packages, such as MALDIquant (Gibb and Strimmer, 2012) can filter peaks based on the presence of signals in a minimum fraction of samples, but unfortunately these filters do not to take into account the information contained in the spatial localization of the signals as addressed in recent work (Alexandrov and Bartels, 2013; Fonville et al., 2012; Palmer et al., 2017).
SPUTNIK (SPatially aUTomatic deNoising for Ims toolKit) provides a series of filters which aim select meaningful and informative peaks, based on the plausibility of their spatial distributions, given the information about the signal source (Supplementary Material S1, Table S1). It provides an estimation of split peaks, a correlation-based filter, a pixel count based filter and a series of tests based on complete spatial randomness. Each class of filters is designed to remove uninformative peaks based on specific assumptions. An example of the effects of each filter (with the default parameters) on the final dimensionality of two example datasets (MALDI-MSI and DESI-MSI) is shown in Supplementary Material S1, Figure S1. SPUTNIK is freely distributed as an R package written using S4 object-oriented programming.
Two example workflows showing how to apply SPUTNIK to both MALDI-MSI and DESI-MSI datasets are provided together with the package (Supplementary Materials S2 and S3). The original imzML and the associated optical image files for the MALDI-MSI dataset are available at https://www.ebi.ac.uk/pride/archive/projects/PXD001283/.
An example of the application of the SPUTNIK pipeline to MALDI-MSI from mouse urinary bladder specimen (Rompp et al., 2010) is shown in Figure 1 (see complete workflow in Supplementary Material S2). The sum of the matched peaks intensities (pre-processed using MALDIquant) was used as a reference for determining the tissue specimen location and ROI detection. The ROI quality was visually evaluated comparing its morphology with an external tissue image (e.g. optical image of H&E stained tissue). The dataset was filtered using a correlation-based filter (reference = binary ROI calculated by k-means, measure = Spearman’s correlation, threshold = 0); followed by a count pixels filter with a minimum number of connected pixels equal to 4. Finally, a complete spatial randomness filter was applied using the Kolmogorov-Smirnov test with the total ion count image as a covariate; Bonferroni corrected P-values (α = 0.001) were used to select the peaks. The pipeline was capable of reducing the dimensionality from 1175 peaks to 204 peaks. Visualization of the filtered dataset and analyses based on the reduced number of peaks result in images with enhanced contrast (Fig. 1B and C). This also provided improved clustering results, with an enhanced contrast due to the removal of signals associated with noise. A complete workflow of the application of SPUTNIK on the example DESI-MSI dataset is available in Supplementary Material S3.
Fig. 1.
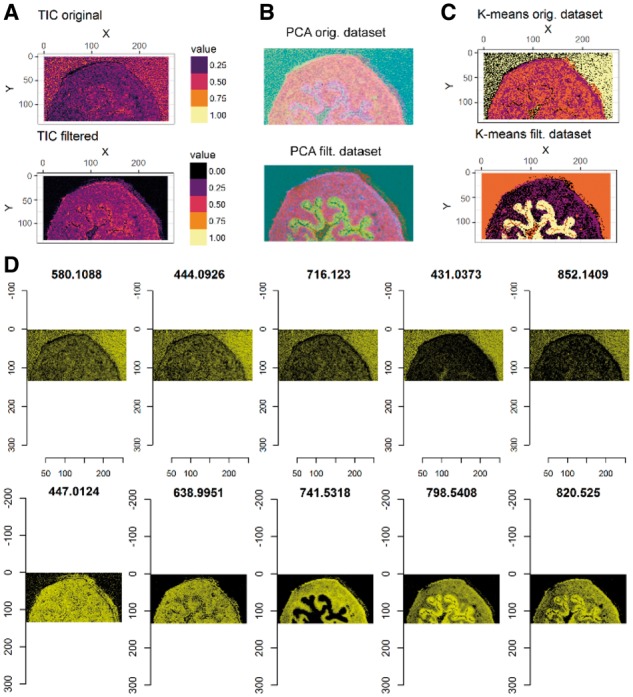
A comparison between the original and the filtered MALDI-MSI dataset (Rompp et al., 2010): (A) total ion count (TIC) images, (B) RGB images of the three first principal components scores scaled in [0, 1] and (C) results of k-means clustering with four clusters applied to the PCA scores responsible for 95% of the total variance. The heatmaps (D) show the intensities of five filtered (top row) and five selected peaks (bottom row) with the five largest average intensities (Supplementary Material S1, Fig. S6). The images of the filtered peaks show that they are mainly localized outside of the tissue region. All the results confirm that the filters reduce the effect of signal noise and allow a clear identification of tissue sub-structures
2 Algorithms details
2.1 Split peak estimation
Random peak shifting can generate false multiple peaks during the peak-matching procedure. These peaks signals, which represent the same ion source, are assigned to multiple m/z values. In order to identify the occurrence of this issue, we hypothesized that split peaks are randomly assigned to contiguous m/z values within the limits of instrumental error. Additional conditions to assign multiple peaks to the same m/z value are: (i) their peak intensity signals are localized in small or non-overlapping spatial regions, (ii) at least one of the peaks signal images shows a sufficient level of ‘spatial regularity’, (iii) the combined signal, generated by merging the intensities of the candidate split peaks, is associated with an image with a spatial regularity at least as high as the images associated with the original peaks. Spatial regularity measures available are: (i) ratio of scattered pixels (defined as the number of Otsu’s thresholded (Otsu, 1975) disconnected signal pixels divided by the total number of signal pixels), (ii) spatial chaos (Palmer et al., 2017), (iii) Gini index (Hurley and Rickard, 2009). An example of simulated split peak merging from the DESI-MSI sample is shown in Supplementary Material S1, Figure S2. Based on its purpose, the split peak tool should always be applied before any other filtering tool.
2.2 Reference similarity filter
Often, signals derived from non-informative peaks (e.g. matrix or solvent related peaks) are characterized by an unrelated spatial distribution compared to the geometrical shape of the expected signal source (e.g. a tissue section). In order to identify and remove these peaks, we designed a filter based on the similarity between the peak intensity images and a reference image. Available measures to estimate the similarity between the peak and the reference signal distributions are: Pearson’s correlation, Spearman’s correlation, structural similarity index measure (Wang et al., 2004) and normalized mutual information. Two options are available for calculating the reference signal, a continuous measure among ‘sum’, ‘median’, ‘mean’ or ‘first principal component scores’ of the entire set of peak intensities, and a binary mask, representing the region of interest (ROI), calculated either applying Otsu’s thresholding to the reference signal seen as an image, or applying k-means clustering with two clusters on the entire dataset. Additionally, external reference and ROI images can be used, after opportunely resizing and registering them with the MS image. The command ‘msImage’ allows to easily convert arbitrary images represented as pixel intensity matrices into MS images compatible with SPUTNIK (an example of the filter applied using the ROI generated by the H&E optical image registered with the sum of the ion intensities in the 800–900 m/z range is shown in Supplementary Material S1, Fig. S3). By default, a similarity threshold equal to 0 guarantees that ions also localized in small regionswithin the ROI are not filtered. Scaled first three principal components scores image of the filtered peaks data confirm that the filter successfully removes the ions localized outside of the tissue in the DESI-MSI and MALDI-MSI examples (Supplementary Material S1, Fig. S4). When off-tissue regions are available, the user should run the reference similarity filter before all the other filters. In this way, the dataset dimensionality can be significantly reduced, increasing the global contrast between tissue and off-tissue regions.
2.3 Pixel count based filter
The Poisson spatially distributed signals (due to shot-like noise) are characterized by a more scattered spatial distribution than the real signal. Meaningful clusters of pixels should be larger than the expected smallest spatial sub-regions. Under this assumption, we designed a filter that takes into account the number of connected pixels where the peak intensity is higher than the background level. Using a binary ROI mask, calculated similarly to that described in the ‘Reference similarity filter’ section or generated externally (e.g. binarization of the registered optical image of the H&E stained tissue), the connected signal sub-regions are detected from Otsu’s thresholded binary peak image within the ROI. Subsequently, the filter selects those peaks characterized by connected regions larger than the provided number of pixels, which are user-defined based on the expected smallest meaningful image sub-regions. Different levels of ‘aggressiveness’ take into account the clusters size which is also outside of the ROI. When off-tissue regions are not present, pixel count based filter can be used with an ROI consisting of a matrix of all ones (Supplementary Material S1, Fig. S5).
2.4 Complete spatial randomness filter
A further filter is based on the rejection of the null hypothesis of a peak signal following a complete spatial random distribution. The assumption behind these statistical tests is that a non-informative peak signal is spatially distributed as a homogeneous spatial Poisson process (Maimon and Rokach, 2010). The tests use Otsu’s thresholded binary pixels associated with the peak signal to define a two-dimensional point pattern process; two tests are currently available: (i) Clark Evans test (Clark and Evans, 1954), (ii) Kolmogorov-Smirnov test against a covariate distribution (Berman, 1986), calculated with the same methods used to extract the reference image. The tests are based on the already available spatstat R package (Baddeley and Turner, 2005). This represents the least aggressive filter, since it does not take into account of the connectivity between pixels and the tissue spatial distribution, but only tests whether ion intensities reflect the overall contrast between the tissue and off-tissue regions. Similarly to the count pixel filter, this filter should be used when off-tissue regions are not available (Supplementary Material S1, Fig. S5).
More details about the algorithms are available in Supplementary Material S1.
3 Conclusions
SPUTNIK provides a collection of flexible filters for the detection of peaks associated with non-realistic spatial distributions, given the prior information about the signal source localization.
Two tutorials, distributed with the package, show how to apply the filtering pipeline to MALDI-MSI and DESI-MSI datasets.
Supplementary Material
Acknowledgements
We would like to thank Dr. Luisa Doria for providing the ovarian cancer DESI MSI dataset included in the package. The ovarian sample was approved by the institutional review board at Imperial College Healthcare National Health Service Trust (Tissue Bank sub-collection number GYN/HG/12/060).
Funding
This work was supported by Cancer Research UK Grand Challenge Program (Project title: ‘A Complete Cartography Through Multiscale Molecular Imaging’). The Department of Surgery and Cancer is funded by grants and infrastructure support by the National Institute for Health Research (NIHR) Imperial Biomedical Research Centre (BRC). GC is supported by the National Institute for Health Research (NIHR) Imperial Biomedical Research Centre (BRC). The views expressed in this publication are those of the author(s) and not necessarily those of the NHS, the National Institute for Health Research or the Department of Health.
Conflict of Interest: none declared.
References
- Alexandrov T., Bartels A. (2013) Testing for presence of known and unknown molecules in imaging mass spectrometry. Bioinformatics ,29, 2335–2342. [DOI] [PubMed] [Google Scholar]
- Baddeley A., Turner R. (2005) Spatstat: an R package for analyzing spatial point patterns. J. Stat. Soft. ,12, 1–42. [Google Scholar]
- Berman M. (1986) Testing for spatial association between a point process and another stochastic-process. J. R. Stat. Soc. C Appl. ,35, 54–62. [Google Scholar]
- Clark P.J., Evans F.C. (1954) Distance to nearest neighbor as a measure of spatial relationships in populations. Ecology ,35, 445–453. [Google Scholar]
- Fonville J.M., et al. (2012) Robust data processing and normalization strategy for MALDI mass spectrometric imaging. Anal. Chem. ,84, 1310–1319. [DOI] [PubMed] [Google Scholar]
- Franck J., et al. (2009) MALDI imaging mass spectrometry: state of the art technology in clinical proteomics. Mol. Cell Proteomics ,8, 2023–2033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gibb S., Strimmer K. (2012) MALDIquant: a versatile R package for the analysis of mass spectrometry data. Bioinformatics ,28, 2270–2271. [DOI] [PubMed] [Google Scholar]
- Hurley N., Rickard S. (2009) Comparing measures of sparsity. IEEE Trans. Inf. Theory ,55, 4723–4741. [Google Scholar]
- Kompauer M., et al. (2017) Atmospheric pressure MALDI mass spectrometry imaging of tissues and cells at 1.4-mum lateral resolution. Nat Methods ,14, 90–96. [DOI] [PubMed] [Google Scholar]
- Maimon O., Rokach L. (2010) Introduction to knowledge discovery and data mining. In: Maimon O., Rokach L., (eds), Data Mining and Knowledge Discovery Handbook. Springer, Boston, MA: 1–15. [Google Scholar]
- Otsu N. (1975) A threshold selection method from gray-level histograms. Automatica, 9, 62– 27. [Google Scholar]
- Palmer A., et al. (2017) FDR-controlled metabolite annotation for high-resolution imaging mass spectrometry. Nat. Methods ,14, 57–60. [DOI] [PubMed] [Google Scholar]
- Rompp A., et al. (2010) Histology by mass spectrometry: label-free tissue characterization obtained from high-accuracy bioanalytical imaging. Angew. Chem. Int. Ed. Engl. ,49, 3834–3838. [DOI] [PubMed] [Google Scholar]
- Wang Z., et al. (2004) Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. ,13, 600–612. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


