A Polymer Model for the Quantitative Reconstruction of Chromosome Architecture from HiC and GAM Data

Abstract

It is widely believed that the folding of the chromosome in the nucleus has a major effect on genetic expression. For example, coregulated genes in several species have been shown to colocalize in space despite being far away on the DNA sequence. In this manuscript, we present a new, to our knowledge, method to model the three-dimensional structure of the chromosome in live cells based on DNA-DNA interactions measured in high-throughput chromosome conformation capture experiments and genome architecture mapping. Our approach incorporates a polymer model and directly uses the contact probabilities measured in high-throughput chromosome conformation capture experiments and genome architecture mapping experiments rather than estimates of average distances between genomic loci. Specifically, we model the chromosome as a Gaussian polymer with harmonic interactions and extract the coupling coefficients best reproducing the experimental contact probabilities. In contrast to existing methods, we give an exact expression of the contact probabilities at thermodynamic equilibrium. The Gaussian effective model reconstructed with our method reproduces experimental contacts with high accuracy. We also show how Brownian dynamics simulations of our reconstructed Gaussian effective model can be used to study chromatin organization and possibly give some clue about its dynamics.

Introduction

Although the chromosome has been classically seen as the carrier of the genetic information, there has been increasing evidence that its folding is a determinant of genetic regulation (1, 2). In particular, coexpressed genes were found to be more often in contact than unrelated genes (3, 4, 5), and the epigenetic state of the chromatin was shown to be related to its folding (6). The advent of chromosome conformation capture (3C) experiments has provided unprecedented insights on chromosome architecture in live cells (7), and the combination of 3C techniques with high-throughput sequencing methods (high-throughput chromosome conformation capture experiments; Hi-C) has enabled the measurement of contacts between thousands of loci on the chromosome. Extensive Hi-C data have now been generated for several eukaryotic cells including human (8, 9), yeast (10), and fly (11) but also bacteria (12, 13, 14). In eukaryotes, the patterns observed in contact matrices generated from Hi-C experiments have revealed a high-level organization in sub-megabasepair topologically associated domains (15, 16). This organization displays significant changes throughout the cell cycle (17) but also during cell differentiation (18) and in the context of cell pluripotency (19) or cell senescence (20). More recently, the genome architecture mapping (GAM) technique was developed, representing an alternative way to measure interactions between chromosomal loci (21). Its application to mouse embryonic stem cells confirmed that actively transcribed genes sometimes separated by large genomic distances were more often in contact. Based on these experimental findings, several studies have suggested that chromosome architecture and genetic expression are intimately connected (22, 23, 24, 25, 26, 27, 28).

Several methods have been proposed to reconstruct the chromosome folding from Hi-C data (see Supporting Materials and Methods, Section 2 for a short review). A first class of models aimed at reconstructing chromosome configurations such that the distances d_ij between chromosomal loci take prescribed values, inferred from the Hi-C contact probabilities c_ij (10, 12, 29, 30, 31). Those studies generally assumed that these average distances would scale like d_ij ∼ 1/c_ij. Yet a scaling analysis tells us that $d_{ij}\sim c_{ij}^{-\gamma }$, with γ = 0.3 for a self-avoiding chain (see Supporting Materials and Methods, Section 3). Another class of models aimed at finding an ensemble of chromosome configurations that reproduces the experimental contact probabilities, $c_{ij}^{exp}$ (32, 33). Yet, most of these methods did not incorporate a realistic polymer model of the chromosome. Thus, the configurations obtained may violate topological constraints imposed by the chain structure of the chromosome.

Here, we model the chromosome as a Gaussian polymer and introduce harmonic interactions to constrain its folding (see Fig. 1). The rigidity of these interactions will be determined by the cross-linking frequency between pairs of genomic loci obtained from the Hi-C protocol. This defines our Gaussian effective model (GEM). The inverse problem to solve consists in finding the effective couplings such that the contact probabilities of the model, c_ij, reproduce the contact probabilities obtained from a Hi-C experiment, $c_{ij}^{exp}$, similarly to previous studies (34, 35, 36). Yet, in those methods, the contact probabilities of the model could only be computed through Monte Carlo or Brownian dynamics (BD) simulations. In contrast, we provide an exact relation between the contact probabilities and the harmonic couplings of our model. Based on this relation, we propose a minimization scheme to find a physical GEM with contact probabilities as close as possible to the experimental ones. We then apply our method to Hi-C and GAM data, thus demonstrating that experimental contact probability matrices can be quantitatively reproduced by our effective polymer model.

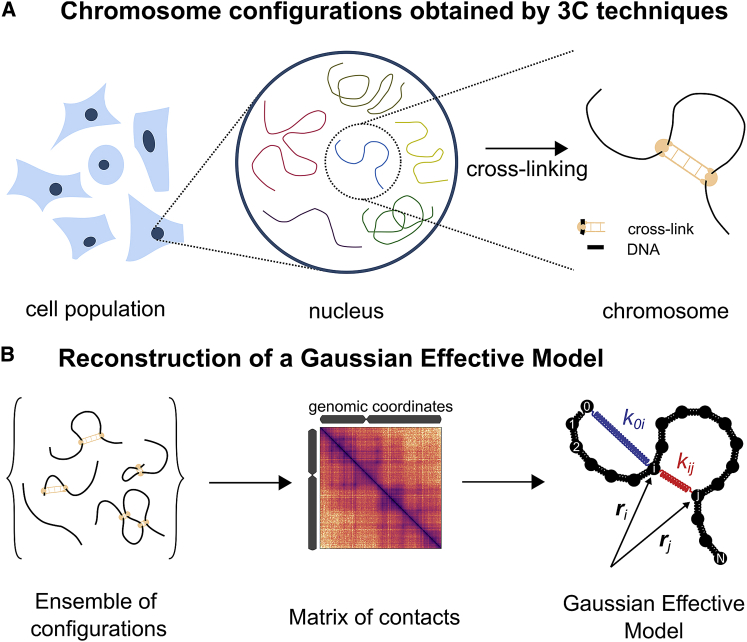
Figure 1.

(A) Configurations adopted by a chromosome in a cell population are retrieved using 3C techniques. (B) We use the count matrix generated by the Hi-C protocol, containing information on the ensemble of chromosome configurations, to reconstruct a GEM. Harmonic interactions with elastic coefficients k_ij are added on top of a Gaussian polymer model and adjusted to reproduce the experimental contacts. To see this figure in color, go online.

We suggest that our reconstructed GEM can be used to study chromatin organization. Typically, coarse-grained models of the chromosome are simulated by BD (37, 38). Because of the complexity of the DNA-DNA and DNA-protein interactions, practical implementations generally require some dimensional reduction or arbitrary choices for unknown parameters such as binding energies or protein binding sites. In contrast, BD simulations of the reconstructed GEM offer a simple alternative that reproduces faithfully the contacts observed in Hi-C or GAM experiments.

Methods

GEM

We model the chromosome as a beads-on-string polymer comprising N + 1 monomers with coordinates {r_i}_{i = 0...N}, each monomer corresponding to a genomic bin with size b, which, depending on the resolution, may represent from 5 kbp to 1 Mbp. Despite some controversy (39), euchromatin is generally regarded as a fiber of diameter 30 nm and persistence length l_p = 60 nm ≈ 6 kbp (40). Thus, we choose to neglect the bending rigidity of the chromosome and consider the Gaussian chain potential for the chromosome backbone:

$$\beta U_0\left[\left\{{\mathbf{r}}_i\right\}\right]=\frac{3}{2b^2}\sum _{i=1}^N{\left({\mathbf{r}}_i-{\mathbf{r}}_{i-1}\right)}^2,$$ (1)

where β = (k_BT)⁻¹ is the inverse temperature.

The Hi-C protocol uses a cross-linking agent to induce proximity ligations between DNA fragments that are close to each other in the nucleus (Fig. 1 A). The matrix of contacts generated subsequently encodes information on the ensemble of configurations adopted by the chromosome (Fig. 1 B). We represent the underlying interactions that constrain its folding as harmonic springs with rigidity 3k_ij/b², leading to the interaction potential

$$\beta U_I\left[\left\{{\mathbf{r}}_i\right\}\right]=\frac{3}{2b^2}\sum _{0\le i<j\le N}{k}_{ij}{\left({\mathbf{r}}_i-{\mathbf{r}}_j\right)}^2.$$ (2)

The probability of a particular configuration at equilibrium is given by a Boltzmann weight. Namely, if we denote the total energy as U = U₀ + U_I, we have

$$\text{Pr}\left(\left\{{\mathbf{r}}_i\right\}\right)=\frac{1}{Z}{e}^{-\beta U\left[\left\{{\mathbf{r}}_i\right\}\right]}.$$ (3)

Actually, the total energy is quadratic in the r_i variables and may be written

$$\begin{array}{cc}\beta U\left[\left\{{\mathbf{r}}_i\right\}\right]& =\frac{3}{2b^2}\sum _{i,j}{\sigma }_{ij}^{-1}{\mathbf{r}}_i·{\mathbf{r}}_j\end{array}.$$ (4)

As a result, the probability distribution in Eq. 3 is Gaussian, hence the name GEM. The GEM is completely determined by its covariance matrix $\text{Σ}={\left[{\sigma }_{ij}\right]}_{i,j=1\dots N}$ or equivalently its two-point correlation functions. In particular, we have $\langle {\mathbf{r}}_i\cdot {\mathbf{r}}_j\rangle ={\sigma }_{ij}{b}^2$ and $\langle {\mathbf{r}}_i^2\rangle ={\sigma }_{ii}$, where the brackets denote an average taken over the Gaussian distribution in Eq. 3. Its inverse is expressed as

$${\Sigma }^{-1}=T+W,$$ (5)

where T is a tridiagonal matrix enforcing the chain structure from Eq. 1 and W is a matrix of reduced couplings enforcing the interactions from Eq. 2. The matrix W has the structure of a Kirchhoff (or valency-adjacency) matrix as defined in graph theory (41). These matrices read as follows:

$$\begin{array}{c}T=\left(\begin{array}{ccccc}2& -1& \dots & 0& 0\\ -1& 2& \dots & 0& 0\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& \dots & 2& -1\\ 0& 0& \dots & -1& 1\end{array}\right),\\ W=\left(\begin{array}{ccccc}\sum _{\begin{array}{c}j=0\\ j\ne 1\end{array}}{k}_{1j}& -k_{12}& \dots & -k_{1N-1}& -k_{1N}\\ -k_{21}& \sum _{\begin{array}{c}j=0\\ j\ne 2\end{array}}{k}_{2j}& \dots & -k_{2N-1}& -k_{2N}\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ -k_{N-11}& -k_{N-12}& \dots & \sum _{\begin{array}{c}j=0\\ j\ne N-1\end{array}}{k}_{N-1j}& -k_{N-1N}\\ -k_{N1}& -k_{N2}& \dots & -k_{NN-1}& \sum _{\begin{array}{c}j=0\\ j\ne N\end{array}}{k}_{Nj}\end{array}\right)\end{array}.$$ (6)

As an essential feature of the GEM, the pair distances have Gaussian distributions:

$$\text{Pr}\left({\mathbf{r}}_{ij}=\mathbf{r}\right)={\left(\frac{2\pi \langle r_{ij}^2\rangle }{3}\right)}^{-3/2}\text{exp}\left(-\frac{3}{2}\frac{r^2}{\langle r_{ij}^2\rangle }\right),$$ (7)

where the mean-square distance $\langle r_{ij}^2\rangle$ is related to the covariance matrix through the classical identities $\langle r_{ij}^2\rangle =\langle {\mathbf{r}}_i^2\rangle +\langle {\mathbf{r}}_j^2\rangle -2\langle {\mathbf{r}}_i\cdot {\mathbf{r}}_j\rangle$.

We now formally express the contact probability between monomers i and j as

$$\begin{array}{ccc}{c}_{ij}& =& \langle \mu \left(r_{ij}\right)\rangle ,\\ & =& \int {\text{d}}^3\mathbf{r}\mu \left(r\right)\langle \delta \left({\mathbf{r}}_{ij}-\mathbf{r}\right)\rangle .\end{array}$$ (8)

In Eq. 8, μ(r_ij) is the probability that a cross-link is formed between monomers i and j that are separated by a distance r_ij. The cross-linking agent used in Hi-C experiments, namely formaldehyde, is known to polymerize in solution, resulting in cross-links of variable lengths (42). Therefore, in this work, we have considered a Gaussian form factor

$${\mu }_{\xi }\left(r\right)=\text{exp}\left(-\frac{3}{2}\frac{r^2}{{\xi }^2}\right),$$ (9)

where the threshold ξ represents the typical distance under which two monomers can be cross-linked. With this definition, we can compute the thermodynamic average in Eq. 8 and obtain (see Supporting Materials and Methods, Section 5) the following:

$$c_{ij}={\left(1+\frac{\langle r_{ij}^2\rangle }{{\xi }^2}\right)}^{-3/2}.$$ (10)

We have thus expressed explicitly the contact probability between monomers i and j as a function of their mean-square distance. As might be expected, the contact probability c_ij is a decreasing function of $\langle r_{ij}^2\rangle$. Similar expressions can be obtained for other choices of form factors (see Supporting Materials and Methods, Section 5).

In summary, Eqs. 5 and 10 define a unique correspondence between the coupling matrix [k_ij]_{i, j = 0...N} and the contact probability matrix [c_ij]_{i, j = 0...N}. The only free parameter is the threshold ξ. We can therefore reconstruct the GEM reproducing a given contact probability matrix. For example, we have successfully applied this method to contact probabilities obtained by sampling configurations of a predefined GEM through BD simulations (see Supporting Materials and Methods, Section 5). We note that our model does not take into account excluded volume effects.

Reconstruction of an admissible GEM

We realized that the presence of noise in the contact probabilities could lead to an unstable GEM having a covariance matrix with negative eigenvalues and therefore a nonfinite free energy (see Supporting Materials and Methods, Section 6). To solve this issue, we reasoned that although a GEM is unstable, there may exist a stable GEM with very close contact probabilities. We therefore introduce the least-square estimator (LSE) between some experimental contact probability matrix and the one of a candidate (stable) GEM:

$$\text{LSE}=\frac{1}{{\left(N+1\right)}^2}\sum _{i,j}{\left(c_{ij}-c_{ij}^{exp}\right)}^2.$$ (11)

In Eq. 11, the LSE is a function of the k_ij variables because the c_ij are computed from the coupling matrix using the GEM mapping introduced above. Our goal is then to minimize the LSE under the constraint that the GEM is stable. A rigorous enforcement of this principle would be to ensure that its covariance matrix Σ has strictly positive eigenvalues, which is difficult to implement in practice. Instead, we consider the more restrictive condition

$$k_{ij}\ge 0,$$ (12)

which is a sufficient condition of stability of the GEM.

Implementation

We use a steepest descent algorithm with projection to minimize Eq. 11 under the constraint in Eq. 12 (see Supporting Materials and Methods, Section 7). We thus obtain the positive couplings $k_{ij}^{\ast }$, minimizing the LSE. As seen earlier, computing the c_ij as a function of the k_ij relies on the choice of a threshold ξ. Therefore, we repeat the above minimization procedure for several values of ξ and choose the one with the smallest LSE. In fine, the reconstructed couplings $k_{ij}^{opt}$ define the best physically admissible GEM with contact probabilities $c_{ij}^{opt}$, reproducing the experimental values of the contact probabilities.

Results

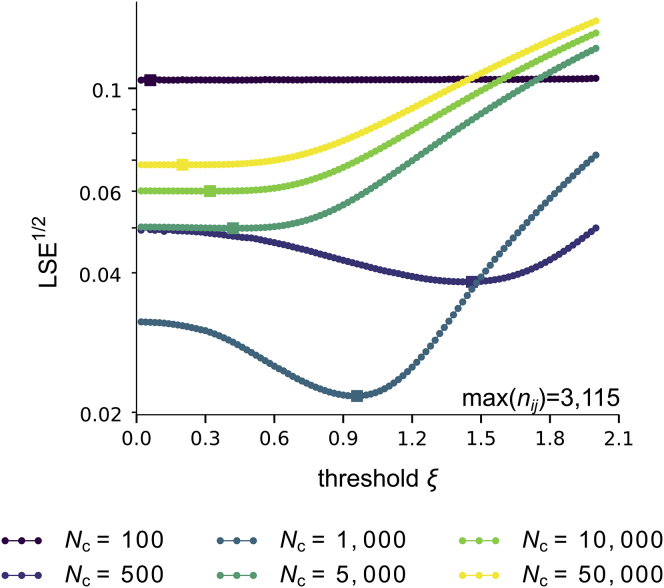
We have applied our reconstruction method to Hi-C data generated from human lymphoblastoid cells (type GM12878) (9). For a given chromosome, these data come under the form of count matrices, in which each entry n_ij corresponds to the number of contacts detected between bins i and j on the chromosome. To compute the contact probability matrix, we applied a global normalization factor N_c to the Hi-C count matrices, c_ij = n_ij/N_c (see Supporting Materials and Methods, Section 4). One may picture N_c as the number of cells in the experimental sample. Because this normalization is not known, we adjusted both free parameters ξ and N_c when applying our reconstruction method so as to minimize the LSE between experimental and GEM contact probabilities. For data of chromosome 8 at a bin resolution of 5 kbp, the best reconstructed GEM was obtained for N_c = 10³ and ξ = 0.96 (see Fig. 2).

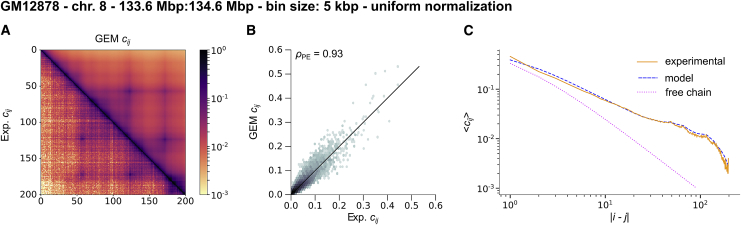
Figure 2.

Application of the GEM reconstruction method to Hi-C data from (9) for chromosome 8 at bin resolution 5 kbp. The best GEM is obtained for values of ξ and N_c that minimize the LSE between experimental and GEM contact probabilities. The maximal number of contacts detected among (i, j) bin pairs is denoted as max(n_ij). To see this figure in color, go online.

The typical discrepancy between experimental and GEM contact probabilities was small, LSE^1/2 = 0.022, suggesting that this chromosome region can be well represented by a GEM. Much of the structure found in the experimental contact probability matrix was indeed well captured in the reconstructed model (Fig. 3 A). This agreement was also readily seen when considering the average contact probability $\langle c_{ij}\rangle$ at a given contour length (Fig. 3 C).

Figure 3.

Best reconstructed GEM for Hi-C data of human chromosome 8 at 5 kbp resolution (9). (A) A comparison between experimental (lower left) and GEM (upper right) contact probabilities. (B) A comparison of experimental and GEM contact probabilities (two-dimensional (2D) histogram). We give the Pearson correlation coefficient. (C) A comparison of the average contact probability as a function of the contour length. To see this figure in color, go online.

Other methods, more sophisticated than the one used above, have been proposed to estimate contact probabilities from Hi-C count matrices (9, 43, 44, 45). For completeness, we have also applied our reconstruction procedure to contact probabilities generated from the same Hi-C data but using the matrix balancing normalization, which produces a stochastic matrix of contact probabilities (see Supporting Materials and Methods, Section 4). In this case, the only free parameter to adjust was the threshold ξ. We found that the reconstructed GEM also reproduced well the experimental contact probabilities (see Fig. S11). Yet, the LSE was larger than for the previous normalization. A possible explanation for this increased value may be that a stochastic contact probability matrix is a poor representation of a cross-linked polymer.

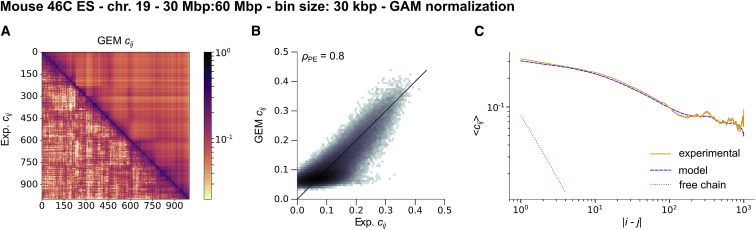
To demonstrate that the effectiveness of our method is not limited to Hi-C data only, we have also applied our reconstruction procedure to GAM experimental data of mouse embryonic stem cells (21). Briefly, with this technique, slices of cell nuclei are obtained by making cryosections, and their DNA content is sequenced. The main output is an array of cosegregation frequencies, representing the probability for two genomic bins to be present in the same slice. We developed a normalization scheme to convert these cosegregation frequencies into contact probabilities (see Supporting Materials and Methods, Section 4). This does not introduce additional parameters, so when applying our reconstruction procedure, we only had to adjust the threshold ξ. For example, we applied our method to GAM data generated from mouse embryonic stems cells for chromosome 19 with a bin resolution of 30 kbp (Fig. 4). Again, the reconstructed model well reproduced the experimental contact probabilities, with a typical discrepancy LSE^1/2 = 0.032. Although this value is slightly greater than in the Hi-C case presented above, the size of the corresponding polymer is larger, with N = 1000. Therefore, the quantitative agreement between experiment and reconstructed model remains very good. Note that the optimal threshold of the reconstruction was quite small, ξ^opt = 0.48. Yet it appears that the precise value of the threshold is not critical. Indeed, below $\xi \underset{˜}{<}1.0$, the relative variations of the LSE became very small (see Fig. S17). Hence, the threshold may actually be seen as a regularization parameter for the reconstructed contact probability matrix.

Figure 4.

Best reconstructed GEM for GAM data of mouse chromosome 19 at 30 kbp resolution (21). (A) A comparison between experimental (lower left) and GEM (upper right) contact probabilities. (B) A comparison of experimental and GEM contact probabilities (2D histogram). We give the Pearson correlation coefficient. (C) A comparison of the average contact probability as a function of the contour length. To see this figure in color, go online.

We have applied our reconstruction procedure to various chromosomes and bin resolutions from either Hi-C or GAM data sets (see Table S1 together with Figs. S1–S25). Overall, the contact probabilities of the reconstructed GEMs quantitatively reproduced the experimental ones. We found in general that the typical distance between experimental and reconstructed model contact probabilities was LSE^1/2 ∼ 0.01–0.05. Thus, we conclude that our method allows us to represent to a quantifiable accuracy the ensemble of configurations adopted by the chromosome.

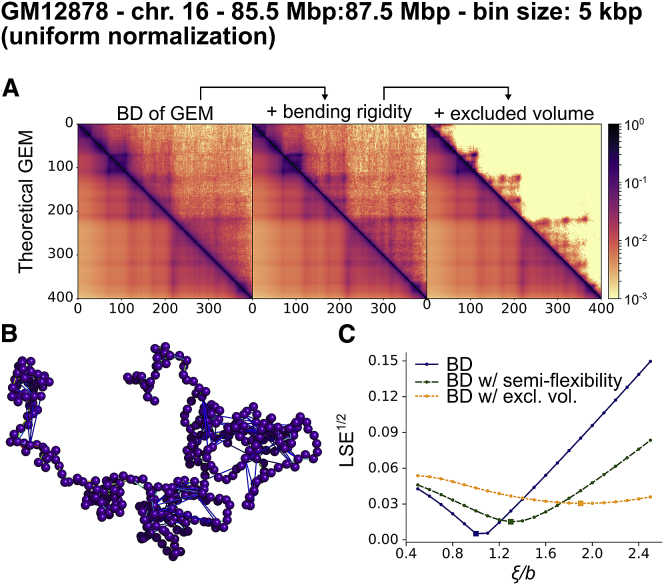
To illustrate possible applications of our method to study chromosome organization, we used the reconstructed coupling matrices to perform BD simulations of the chromosome (see Supporting Materials and Methods, Section 8). To do so, we replaced the Gaussian chain potential in Eq. 1 with a finitely-extensible non-linear elastic bond potential, we took into account the polymer bending rigidity, and we introduced excluded volume interactions. We then performed BD simulations and used the sampled configurations to compute the equilibrium contact probabilities, which we compared to the ones of the GEM (see Fig. 5 A; Figs. S26 and S27). In the presence of excluded volume and semiflexibility, the obtained contact probabilities were not as close to the GEM ones. Yet, the essential structure of the contact probability matrix remained. In Fig. 5 B, we show a typical configuration for human chromosome 16.

Figure 5.

BD of the reconstructed GEM for Hi-C data of human chromosome 16 (9) (5 kbp resolution). (A) Contact probability matrices obtained through BD simulation of 1) the GEM, 2) the GEM with bending rigidity, and 3) the GEM with bending rigidity and with excluded volume. The contact probabilities were computed from BD trajectories and are compared with the theoretical values for the GEM. (B) A snapshot of a configuration obtained by BD of the reconstructed GEM with bending rigidity and excluded volume. The couplings are represented by tie lines, from weak couplings (in blue) to strong couplings (in red). (C) LSE as a function of the threshold ξ between contact probabilities computed from the BD trajectory and the theoretical values. To see this figure in color, go online.

Discussion

In this article, we have proposed a polymer model constrained by Hi-C or GAM experimental measurements to represent the chromosome. We modeled the DNA as a flexible polymer (because the resolution is much larger than the persistence length of the DNA), with harmonic interactions between chromosomal loci encoding the contact frequency in Hi-C and GAM experiments. The spring constants are chosen so as to best reproduce the experimentally measured contact probabilities. We computed the explicit mapping defined in Eqs. 5 and 10, which relates the harmonic couplings to the contact probabilities between monomers. We then used this property to reconstruct a physically admissible GEM of the chromosome by minimizing the distance between experimental and model contact probabilities. We applied this method to many chromosomes and data sets. Overall, the quantitative agreement obtained suggested that the GEM offers a good representation of the chromosome. To illustrate potential applications of our method, we then used the reconstructed GEM to perform BD simulations of the chromosome. Although it is not a substitute for first-principles molecular dynamics simulations, this approach is valuable because the trajectories simulated by BD reproduce the experimental contact probabilities.

Models for cross-linked polymer

Properties of cross-linked polymers have been extensively studied (46, 47, 48). However, in those studies, the rigidities of the harmonic interactions were uniform (i.e., k_ij = k in Eq. 4). A similar model was also reintroduced to account for the particular scaling of the radius of gyration of the chromosome in the interphase nucleus, in which the k_ij were distributed as Bernoulli variables and hence defined random loops (49, 50). Recently, another model with quadratic interactions was proposed to obtain polymer states with arbitrary fractal dimension (51), in which the harmonic couplings followed a power law of the contour distances. Yet, these studies did not attempt to compute Hi-C contact probabilities or to predict chromatin conformations. Our model also presents some similarities with the Gaussian elastic network model used in the context of protein folding (52, 53).

Do the reconstructed couplings represent biological interactions?

Hi-C data are often generated from a population of cells. Thus, if a pair of chromosomal loci has a number of contacts that is statistically significant, it means that specific interactions should favor their colocalization. Therefore, the couplings k_ij can be seen as defining coarse-grained potentials representing the superimposition of many microscopical interactions, such as the bridging by divalent proteins, and used as effective interactions in coarse-grained models of the chromosome. Yet, the mean pair potentials $e_{ij}=3/2k_{ij}\langle r_{ij}^2\rangle$, expressed in k_BT, provide a more physical interpretation of the reconstructed interactions. Eventually, the effective model obtained can give clues about where the major constraints that determine the folding of the chromosome are applied.

Fractal globule scaling of the contact probabilities

It is believed that the so-called fractal globule model (or crumpled polymer) provides a more realistic framework to describe the chromosome than classical polymer models (54, 55). In short, the presence of excluded volume and confinement results in high energy barriers from one configuration to the other, leading to a behavior different from an ideal polymer. In particular, the fractal globule was shown to reproduce the scaling for the mean contact probability as a function of the contour length, c_ij ∝ |i − j|⁻¹, observed in Hi-C experiments (8). We note that although our GEM does not incorporate excluded volume, it reproduces the experimental scaling because the couplings are reconstructed from the experimental contacts.

Robustness of the method

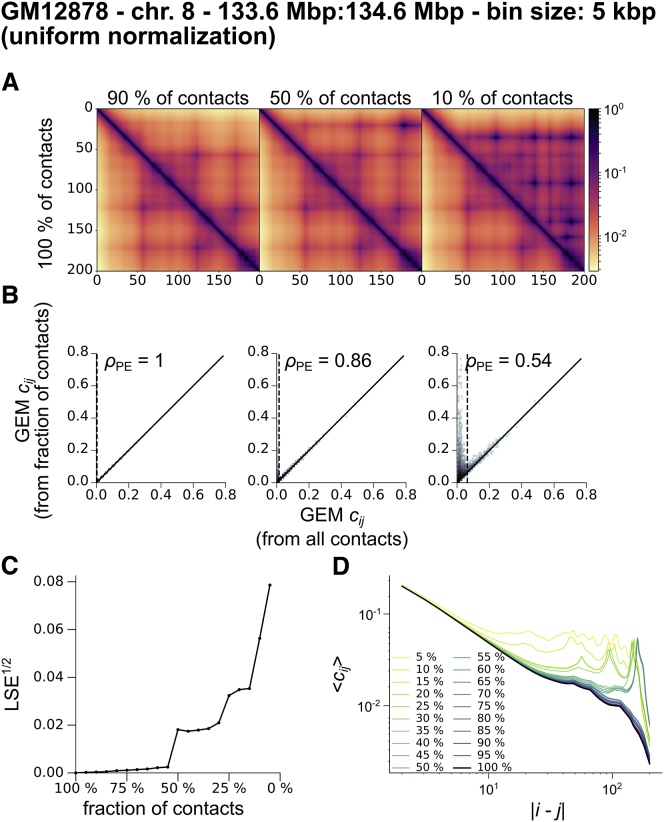
To investigate the robustness of the reconstructed GEM, we repeated the minimization procedure but considered only a subset of the experimental contacts in the sum from Eq. 11. Specifically, we retained only the top fraction of the experimental contact probabilities. In Fig. 6 A, we compared the contact probabilities of the original reconstructed GEM for human chromosome 8 with the contact probabilities of the GEMs reconstructed by considering only the top 90, 50, and 10%. Starting from 50%, we noticed that some artifacts appear in the reconstructed GEM for long-range contacts. These are located in regions that are sparse in contacts in the experimental contact probability matrix. As a result, very few significant contacts are retained in those regions for the minimization procedure. In fact, contacts below the thresholding quantile, which were discarded from the reconstruction, tend to be overestimated in the newly reconstructed GEM (Fig. 6 B). This suggests that regions of the contact probability matrix that contain little meaningful information (significant contacts in our case) will be poorly reconstructed. Overall, Fig. 6 C shows that the distance to the original reconstructed GEM increases as the fraction of contacts retained shrinks, and Fig. 6 D illustrates that long-range contacts are indeed the first to suffer from reconstruction artifacts. The same analysis for other data sets is given in Figs. S28 and S29.

Figure 6.

Robustness of GEM reconstruction for Hi-C data of human chromosome 8 (9) (5 kbp resolution). For all GEM reconstructions, we used a threshold ξ = 1 and a normalization factor N_c = 10³. (A) A comparison of the contact probabilities of the reconstructed GEM with those of a GEM obtained by performing the minimization only on the top 90, 50, and 10% experimental contacts. (B) 2D histograms corresponding to the matrices shown in (A). We give the Pearson correlation coefficients. The thresholding quantiles are represented by vertical dashed lines. (C) A comparison of the GEMs reconstructed from a decreasing fraction of the experimental contacts with the original GEM. LSE^1/2 is the Euclidean distance between contact probabilities divided by (N + 1). (D) Average contact probability as a function of the contour length for GEMs reconstructed from a decreasing fraction of the experimental contacts. To see this figure in color, go online.

Future improvements

A first improvement to our model would be to explicitly include semiflexibility in the polymer structure. This can be done by adding harmonic interactions extending to second-nearest neighbors in Eq. 1. However, this refinement might appear superfluous as long as we consider bin resolutions beyond ∼5 kbp. A second improvement would be to extend the method to several chromosomes by adjusting the matrix T, which defines the chain structure.

The code used to perform the reconstruction of a GEM by minimization is available at https://github.com/gletreut/gem_reconstruction. Other data and code involved in this study are available upon request.

Author Contributions

F.K. and H.O. designed the research. G.L.T. and H.O. performed the research. G.L.T. wrote the code and analyzed the data. All authors contributed to the writing of the article.

Editor: Tamar Schlick.

Supporting Citations

References (56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66) appear in the Supporting Material.

Supporting Material

Data S1. LAMMPS Configuration Files

The LAMMPS configuration files used to perform the BD simulations in Fig. 5 are provided.