Noninvasive diagnostic imaging using machine-learning analysis of nanoresolution images of cell surfaces: Detection of bladder cancer

Significance

New noninvasive and accurate diagnostic tests of cancer are important. Here we describe such a test, which is applied to the detection of bladder cancer, one of the most common cancers and cause of cancer-related deaths. This method can also be applied for the detection of other cancers, in which cells or body fluid are available for analysis without the need for invasive biopsy, e.g., upper urinary tract, urethra, colorectal and other gastrointestinal, cervical, aerodigestive cancers, etc. Furthermore, the described approach can be extended to detect cell abnormalities beyond cancer as well as to monitor cell reaction to various drugs (nanopharmacology). Thus, this approach may suggest a whole new direction of diagnostic imaging.

Abstract

We report an approach in diagnostic imaging based on nanoscale-resolution scanning of surfaces of cells collected from body fluids using a recent modality of atomic force microscopy (AFM), subresonance tapping, and machine-leaning analysis. The surface parameters, which are typically used in engineering to describe surfaces, are used to classify cells. The method is applied to the detection of bladder cancer, which is one of the most common human malignancies and the most expensive cancer to treat. The frequent visual examinations of bladder (cytoscopy) required for follow-up are not only uncomfortable for the patient but a serious cost for the health care system. Our method addresses an unmet need in noninvasive and accurate detection of bladder cancer, which may eliminate unnecessary and expensive cystoscopies. The method, which evaluates cells collected from urine, shows 94% diagnostic accuracy when examining five cells per patient’s urine sample. It is a statistically significant improvement (P < 0.05) in diagnostic accuracy compared with the currently used clinical standard, cystoscopy, as verified on 43 control and 25 bladder cancer patients.

New noninvasive diagnostic methods are in high demand in medicine. When applied for cancer detection, such methods are key in the progression to defeating this disease (1). Here we present a method of diagnostic imaging, which is based on nanoscale-resolution imaging of physical properties of surfaces of cells collected from body fluids. Collected cells are imaged using a recent modality of atomic force microscopy (AFM), subresonance tapping (2, 3), and the obtained images are analyzed using machine-learning methods. The method is applied to the detection of bladder cancer, using cells collected from urine.

Bladder cancer is one of the most common cancers and causes of cancer-related deaths both in the United States (with estimated 81,190 new cases and 17,240 deaths only in 2018, with >500,000 survivors) and globally (4). The 5-y survival rate drops from 95% for patients with cancer detected at its early stage to 10% for those at the metastasis stage (5). The gold standard for diagnosis includes cystoscopy, biopsy, and tumor resection for pathology examination. Because of a high (50–80%) recurrence rate, frequent costly and invasive cystoscopy examinations (e.g., every 3–6 mo) are required to monitor patients for recurrence and/or progression to a more advanced stage. The requirement for frequent cystoscopy makes bladder cancer the most expensive cancer per patient to diagnose, monitor, and treat. It is recognized as a major health issue by global authorities incurring significant burden in the healthcare systems (6). In addition, cystoscopy has still limited accuracy for the detection of low-grade tumors (sensitivity, 61%) (7) although this grade of tumor is the most frequent; moreover, sensitivity for carcinoma in situ can be also low (8). It also has a limited ability to detect occult microscopic cancer and tumors in atypical locations such as the upper urinary tract and prostatic urethra. A low-cost, accurate, effective, and noninvasive test will greatly expand participation of patients in screening and early detection evaluation programs because it will decrease the patient discomfort and potential postprocedural complications, while it can assist in improving diagnosis, monitoring, and surveillance, acting as adjunctive to cystoscopy and/or eliminating unnecessary cystoscopies.

At present, there are no such clinically accepted methods that are noninvasive, accurate, and sufficiently simple. Urinalysis [search for the blood in urine (9)] and voided urine cytology [VUC, visual cytologic examination of cellular material present in the urine by means of optical microscopy (10)], is one of the current standards-of-care noninvasive examination of cells in urine used to assist with cancer diagnosis and surveillance, has low sensitivity, and high interobserver variations (11, 12). Although specificity (accuracy of no-cancer detection) of VUC is high (>90%), the sensitivity is low (20–80%) (13, 14), in particular, for the detection of low-grade cancer (20–25%) (15, 16). Methods based on noninvasive analysis of chemical biomarkers show promise but still are either not sufficiently accurate or repeatable to be adopted for widespread use (15) and are not currently recommended for diagnosis. Physical fluorescent, Raman, infrared, partial-wave optical, and various cell mechanics testing methods are still under development (17–19).

AFM was previously used to differentiate between cancer and normal cells and tissues (19–21). However, it is hard to work with living cells and tissues in clinical environment. Moreover, there is still too much uncertainty in the measuring cell mechanics (22). Another method to image fixed cells with high resolution to detect cancer cells was suggested in ref. 23. But, it was developed for cell lines in vitro (not suitable for clinical use) and was very slow.

Here we report an approach to detect cancer using imaging of cells extracted from body fluids, in this case urine. When using cells extracted from urine (in a manner similar to VUC method), and then fixed and imaged with AFM, one may expect the detection of bladder cancer using the method of ref. 23 to identify malignant cervical epithelial cells in vitro. However, a straightforward use of that method does not work because, for example, not all cells extracted from cancer patients are malignant. Furthermore, the method developed here includes machine-learning analysis. The machine-learning methods (part of aka artificial intelligence) have already demonstrated their efficiency in recognition of different objects and patterns in medical applications (24, 25). In contrast to the previous analyses, we applied such methods not to each image directly but to the sets of surface parameters (e.g., roughness, directionality, fractal properties, etc.) derived for each image. The considered parameters are used in engineering to describe material surfaces (see the complete parameters list in SI Appendix, Materials and Methods). The use of the parameters instead of images substantially decreases the dimension of the data space, and therefore allows avoiding the problem of big data analysis, the need for a large size of the training set.

The presented method is mainly based on the use of AFM Ringing imaging mode (2, 3). Although it is possible to do the imaging using standard subresonance tapping (for example, PeakForce QNM), Ringing mode is substantially faster (5–20×) and less prone to possible artifacts. The described method demonstrates statistically significant improvement (P < 0.05) in diagnosing bladder cancer even in comparison with the currently used clinically used standard, cystoscopy.

Methods

Urine samples were collected at the Dartmouth-Hitchcock Medical Center and Cleveland Clinic as part of an IRB-approved protocol. All of the human subjects gave informed consent. The samples were studied with AFM under the appropriate IRB at Tufts University. We analyzed urine samples from 43 individuals without evidence of bladder cancer and 25 cancer patients with pathologically confirmed bladder cancer (14 low grade and 11 high grade). Cells were collected in similar manner to VUC (10), then specially fixed, washed with water, freeze-dried on a glass slide, and imaged using subresonant tapping AFM modalities [PeakForce and Ringing mode (3)]. Details of samples collection, preparation, imaging, and analyzing the images are described in SI Appendix.

Results

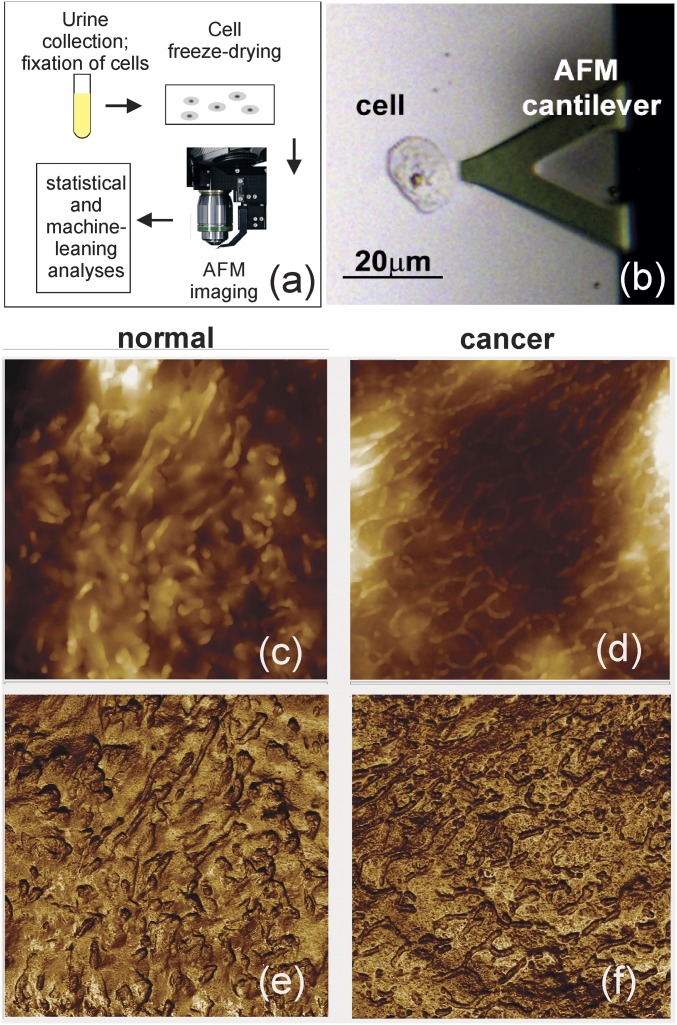
Fig. 1 shows examples of cell surfaces imaged with the subresonant tapping AFM modalities (PeakForce and Ringing mode). Cells to image were randomly chosen with the help of an optical microscope build-in the AFM, Fig. 1B. On average, six cells per patient were imaged. Subresonant tapping modes allow for simultaneous imaging of multiple physical properties of cell surface. We chose only the two most robust channels, sample height and adhesion between the AFM probe and sample, i.e., the channels that provide images quantitatively independent of the variation of laboratory conditions. (Although there are more robust channels in Ringing mode, these are not used here because to date we have insufficient statistics obtained solely with this mode as it was introduced very recently.) Both the height and adhesion channels are well controlled and thus robust (repeatable when using different AFMs, probes, temperature, humidity). Fig. 1 C–F shows an example of typical AFM images of cells collected from noncancer and cancer patients. One can see a surface covered with microvilli and microridges, which is common for epithelial cells.

Fig. 1.

The described detection method. (A) The method schematic. (B) Optical location of a cell with AFM cantilever. (C–F) AFM images (10 × 10-μm²) of (C and D) height and (E and F) adhesion of the cell surface. Examples of cell images taken from noncancer (C and E) and cancer (D and F) subjects are shown. The images were obtained using subresonance tapping mode.

Approximately 25 mL of urine was collected on each patient, a similar amount to that collected for VUC to obtain adequate cellularity (26). Nevertheless, 18 out of 43 healthy controls and 1 low-grade cancer sample showed no cells in their urine samples. Such a large number of samples with no cells could be explained by the fact that many objects, which would be identified as cells with just optical microscopy, were not cells, as was clearly seen only with AFM. Such cell-like objects showed distinctive layered structures never observed on cells (SI Appendix, Fig. S1) and therefore can easily be excluded. When analyzing the data, we considered both cases, taking these no-cell cases into account and ignoring them. The classification results did not change noticeably, independently of inclusion of samples with no cells into the analysis, in particular, when multiple cells are used for classification (SI Appendix, Tables S4 and S6).

To check that the results are independent of specific machine-learning algorithm, we evaluated three different machine-learning methods: Random Forest (27), Extremely Randomized Forest (28), and Gradient Boosting Trees (29). These methods were chosen as they are the least prone to overtraining (overfitting), which is a common problem of machine-learning methods (30). The first two methods are bootstrap unsupervised, and the last is a supervised method of building trees (see SI Appendix, Materials and Methods, item 10 for more detail).

Many machine-learning methods can be subject to artifacts of training, for example, be overtrained to give higher accuracy for a specific subset at the expense of accuracy on a more general subset. To avoid it, the training and testing (validation) are done on two independent cohorts. Specifically, we split the entire dataset into the training and testing subsets (cohorts). The decision trees are built using only the data from the training subset. Then the accuracy of the diagnosis is found using only the testing subset. The splitting was done by keeping the data from the same individuals in just one of the other subsets to avoid artificial overtraining due to the correlation between different cells of the same individual. Note that such an approach is essentially similar to blind testing. We observed that ignoring this rule results in artificially high detection accuracy.

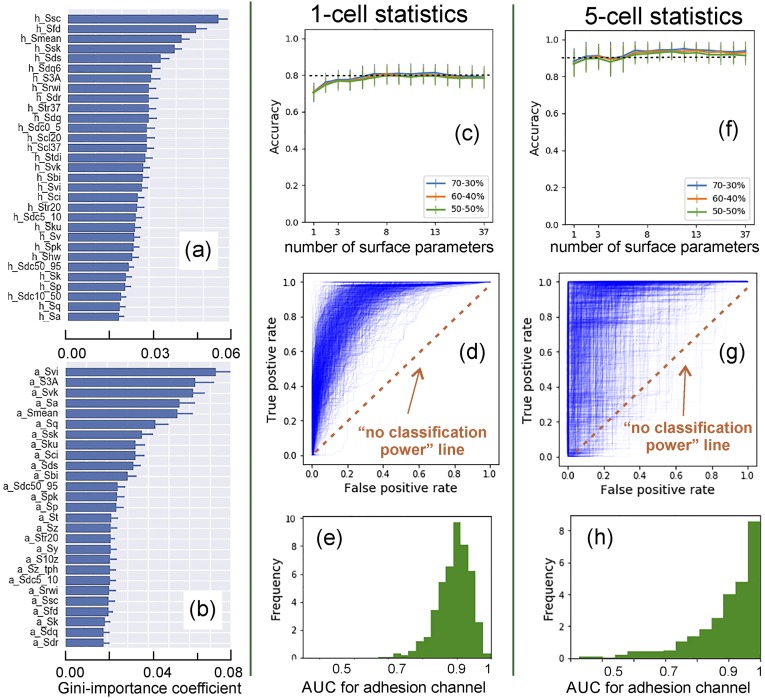
To verify that our results do not depend on the way we do splitting for training and testing, we repeated the above procedure doing the random split multiple times. Specifically, the obtained dataset [the sets of surface parameters (input) and diagnoses (output)] were randomly split to have S% of the total data for training and 100-S% for testing. We considered S = 50, 60, and 70%. Generating the random splits 1,000 times for each S, one can derive a full statistical analysis of the machine-learning methods, which includes the confusion matrix (accuracy, sensitivity, and specificity), receiver operating characteristic (ROC) curves (true-positive versus false-positive rates), and the distributions of the area under the ROC curve. The algorithm is presented in detail in SI Appendix, Materials and Methods. One can see a quite narrow distribution of area under the ROC curve (AUC), i.e., virtually independent of a particular split and the split percentage (Fig. 2).

Fig. 2.

An example of Random Forest method for the case of one and five cell analyses. One thousand randomly chosen split for training and testing datasets were used. The most important parameters for segregation between noncancer and cancer patients are identified (using Gini index) for (A) height, (B) adhesion; the averaged value and one SD of the parameters are shown (see SI Appendix, Materials and Methods for the description of image parameters). The dependence of accuracy of cancer detection on the number of surface parameters and percentage split between training and testing sets (70–30%, 60–40%, 50–50%; average and one SD) are presented for (C) one-cell and (F) five-cell analysis. (D and G) One thousand ROC curves, (E and H) Statistical distributions of AUC for (D and E) one-cell, and (G and H) five-cell analysis. One can see high repeatability (robustness) of the classification accuracy of the method. The average accuracy of cancer detection is 80% (for one-cell) and 90+% (five-cell analysis). The results of accuracy and ROC are obtained using the adhesion channel.

Fig. 2 demonstrates the strategy described above for an example of the Random Forest model. First, we built the ranking of the surface parameters by their segregation power (“importance” with respect to Gini-index measure) for the cell images obtained in height and adhesion channels. Fig. 2 A and B shows an example of the ranking for the best surface parameters. (The ranking of all parameters for this and two other models are presented in SI Appendix, Fig. S7.) It is calculation intensive and not optimal to consider all parameters for classification. To reduce dimensionality of the parameter space, we kept N_p best parameters for each channel (height and adhesion), which were identified by (i) their highest segregation power and (ii) low interparameter correlation (to exclude the parameters that were correlated with the others, see SI Appendix, Supplementary test, section 1 for detail). By changing the degree of allowable correlation while keeping the parameters with the highest segregation power, we can find the behavior of one of the key statistical parameters, accuracy (defined as the ratio of the total number of correct assessments to the total number of all assessments).

The accuracy and ROC results in Fig. 2 are shown for the adhesion channel only. The height channel produced almost no useful information (Table 1), which is in agreement with the previous study of the fractal dimension (23) and linked to lower resolution of the images collected in the height channel. It is sufficient to keep the number of the surface parameters 8–10 to obtain high accuracy, Fig. 2C. Hereafter, we considered 10 top parameters. Interestingly, the accuracy decreased by taking into account more surface parameters. This is presumably because the parameters with lower segregation power bring more noise than signal. Fig. 2C demonstrates ∼80% accuracy in identification of both cancer and noncancer patients based on the analysis of just one single cell. This result is statistically robust (small SD) and independent of the percent split between training and testing sets (70/30, 60/40, 50/50 are shown in Fig. 2C).

Table 1.

Statistics of diagnosis of cancer for an individual by considering N cells and requesting that M cells out of the considered N ($M\le N$) were classified as collected from a cancer patient to put diagnosis of cancer

No. of cells	Data	Random forest			Extremely randomized forest			Gradient boosting trees
		AUC/accuracy	Sens/spec		AUC/accuracy	Sens/spec		AUC/accuracy	Sens/spec
N = 1	Height	75/73	50/84	76/69	77/74	53/84	77/70	74/73	46/86	75/68
M = 1	Adh.	88/83	68/90	84/77	88/83	69/90	85/78	87/82	69/89	84/77
N = 3	Height	75/82	36/95	75/68	78/82	42/94	77/69	73/81	34/96	73/66
M = 2	Adh.	91/90	73/96	87/80	90/90	72/96	87/80	89/90	69/96	85/78
N = 5	Height	69/86	34/97	72/61	70/86	39/96	76/64	68/86	36/97	70/61
M = 2	Adh.	91/94	81/98	91/82	90/94	78/97	89/80	91/94	78/98	88/80

Sensitivity and specificity, averaged AUC, and accuracy were calculated for 1,000 random splits of the entire data onto training and versification sets (70% training and 30% verification split) for all three methods. The accuracy is found for the smallest error of classification. Sensitivity and specificity are given for that case (the left column of Sens/spec part of the table); the right column of Sens/Spec part is another example demonstrating higher sensitivity (the threshold to separate cancer from noncancer cases was chosen to keep the difference between sensitivity and specificity <5%).

Another important statistical characteristic is the ROC curve (curves that show sensitivity and specificity defined for different thresholds separating cancer and noncancer cases). The classification accuracy is higher when the AUC curves are closer to 1. Such curves and histograms of the AUC are shown in Fig. 2 D and E. Each ROC curve was calculated for a specific random split between training and testing subsets (generated as explained before). The variations of these curves are rather narrow, which means that the prediction accuracies do not depend on a specific choice of training versus testing sets.

To validate our method and demonstrate the absence of any overtraining artifacts, we also use the following additional approach. We use the same algorithms and the same dataset as described above but with artificially randomized diagnosis (50/50% cancer and normal). If our approach lacks artifacts of training, one should see generating of diagnostic algorithms with no classification power, i.e., close to 50% accuracy (or the AUC is 0.5). One can see that the accuracy of the method indeed dropped to ubiquitous 53 ± 10% (the result of 1,000 random choices of diagnosis sets, SI Appendix, Fig. S6), thereby confirming the absence of classification artifacts, i.e., the described classification shown in Fig. 2 is factual. To amplify, these results demonstrate the robustness of the models and the absence of overfitting, which is a common problem for many machine-learning methods dealing with multiple parameters.

So far, the presented cancer classification was described for single cells. Obviously, the diagnosis based on just one cell cannot be robust because of the possibility of sampling error. Furthermore, not all cells collected from urine are derived from the bladder (urothelial cells). It is known that a number of cells collected in VUC can be exfoliated from elsewhere in the urinary tract (26, 31). Albeit possible, it would be highly speculative to expect that field carcinogenesis is expanded to the entire urine tract. To overcome these pitfalls, we consider more than one cell to establish diagnosis. Simple probabilistic reasoning shows that such an approach can result in very high accuracy (see SI Appendix, Materials and Methods, section 2, for detail).

There are multiple ways to extend the algorithm of cancer/no-cancer diagnosis to the case of using N cells. Here we use the following algorithm: if at least M cells out of N ($M\le N$) are identified as cells coming from a cancer patient, then the patient is diagnosed with cancer. Fig. 2 F–H shows the statistical analysis similar to that described in the case of 1 cell (N = M = 1) but for an example of N = 5, M = 2. One can see a similar robustness and 94 ± 1% for the accuracy of identification of both cancer and noncancer individuals. The randomization test described above shows 50 ± 22% for the AUCs (the result of 1,000 random choices of diagnosis sets). The higher SD compared with N = M = 1 case (±10%) is explained by a higher tolerance of the error in the described N, M method to both presence or absence of cancer cells; see the previous paragraph.

Table 1 shows examples of the statistical results for several best cases of detection of cancer and no-cancer patients for all three machine-learning methods and both channels (see SI Appendix, Tables S2 and S3 for the statistics of all N, M for $N\le 5$). This table also shows sensitivity (accuracy of detection of cancer) and specificity (accuracy of diagnosis of the absence of cancer). In contrast with the accuracy, sensitivity and specificity are interconnected, and cannot be maximized separately. Here we present two examples of sensitivity/specificity pairs defined for the different points on the ROC curves. One example shows higher specificity while the other one higher sensitivity.

Discussion

Here we present a method of diagnostic imaging exemplified by the detection of bladder cancer. The method is based on the utilization of unique information, physical nanoscale images of the surface of cells extracted from body fluids, urine in the case of bladder cancer. Other techniques that could provide similar information are unknown. Current biomarker methods are not cell-based. The spectroscopic optical methods (Raman, partial wave, infrared, fluorescent) are based on the properties of the entire cell, not its surface. The described method is likely to synergistically enhance the cancer detection when combined with the other methods because our imaging method uses physical properties of the cell surface.

The presented method demonstrates an accuracy of 94% (examples of sensitivity/specificity pairs are 81/98% and 91/82%; see Table 1 for detail). Using the most general statistical classification parameter, the AUC, one can statistically compare our method (AUC = 0.92 ± 0.09) with the invasive, currently used clinical standard, cystoscopy (AUC = 0.77, ref. 32; it is also in agreement with ref. 33). Using one-way ANOVA, one can see that improvement is statistically significant with the P value < 0.05 even with the present number of tested individuals. Comparing to the clinically used VUC, our method demonstrates higher sensitivity, whereas the specificity is comparable to the best reported results (sensitivity/specificity 20–80/>90% of VUC versus, e.g., 81/98% of our method). Furthermore, it is expected that our method will be free of subjective judgment, i.e., such as inter- and intraobserver variability, which is a serious problem of the VUC method (12, 13). The accuracy of our method is already better than that of currently used noninvasive methods such as biochemical evaluation of the urine (NMP22, sensitivity/specificity 40–74/74–99%, BTA, 66–70/65–75%) or cellular analysis (FISH, 67–87/72–96%) (14, 15, 34) immunocytochemistry (77–91/68–83%), etc. (34).

Our method has the potential for seamless incorporation into existing clinical practice as it uses the cells collected from urine in a manner similar to VUC. Being one of the oldest noninvasive methods, VUC has several fundamental limitations: a relatively low resolution of optical examination, the need in subjective evaluation of cell images, a small number of cells available from urine of normal and cancer patients with low-grade tumors. Our method overcomes these limitations with the help of high-resolution AFM and computer-supported machine-learning methods of data analysis to improve the accuracy of detection of bladder cancer and to make a determination that is independent of subjective judgment. Furthermore, our method requires only a small number of randomly chosen cells to do the AFM imaging and analysis. This is a substantial departure from traditional VUC, in which a large number of cells must be screened to find only a few cells that may look malignant. Our approach is based on the premises of field carcinogenesis, which has been established as a common event in many malignancies, in particular, in bladder cancer, in which both genetic and exogenous milieu risk factors lead not only to a localized tumor but may affect the entire organ area (35–37). In such an approach, the majority of cells collected from a cancer patient should carry a degree of the physical signature of cancer. Our results provide evidence that the described method is sufficiently sensitive to detect this cancer signature.

Fundamentally, the observed cancer signature presumably comes from the specific cellular glycocalyx and extracellular matrix of malignant cells (20, 38), glycosaccharides, and glycoproteins of the pericellular glycocalyx. The images show the nonspecific adhesion between the AFM probe and the cell surface, which is covered with glycocalyx. This is principally different compared with the previously used AFM methods to segregate cancer cells, which were based on the observed difference in the elastic properties of cells (19), not on the imaging the adhesive properties of cell surface. Furthermore, the previous works were based on the point indentation, in which one number (the modulus value) was assigned to the entire cell. The imaging of the adhesion between the AFM probe and cell surface is key to identify cancer in our method. The most important parameters (Fig. 2B) to segregate between cancer and normal cases describe the distribution of the adhesion over the cell surface, rather than the overall value of the adhesion. The mechanisms controlling for self-assembly of particular spatial distribution of glycocalyx on cells are currently unknown.

It should be noted that despite the 30-y old history of AFM, this is the only microscopy that has not been used for the medical purposes as of yet. As we have shown, the accuracy of our AFM method is higher than that of currently used clinical standard, cytoscopy, and the currently used noninvasive methods such as VUC and biochemical evaluation. Thus, our method may result in a possible first clinical application of AFM. Clearly, additional larger cohorts of patients will need to be tested to confirm our results before this method can be introduced into clinical practice. When introduced, it will help facilitate screening, reduce overdiagnosis [currently a substantial problem (39)], and consequently, the number of unnecessary and costly medical procedures. We anticipate that the use of the described AFM modality can also be applied to improve the detection, diagnosis, and follow-up for other tumor types in which cytology is used to aid in diagnosis and surveillance (e.g., upper urinary tract, urethra, colorectal and other gastrointestinal, cervical, aerodigestive cancers, etc.), including cancer grades. The described approach can be extended to detect other cancers and other none-malignant cell abnormalities as well as to the detection of cell reaction to various drugs (“nanopharmacology”). Therefore, we expect the described method may be a new direction of biomedical imaging.