Whole-Brain Neuronal Activity Displays Crackling Noise Dynamics

Summary

Previous studies suggest that the brain operates at a critical point in which phases of order and disorder coexist, producing emergent patterned dynamics at all scales and optimizing several brain functions. Here, we combined light-sheet microscopy with GCaMP zebrafish larvae to study whole-brain dynamics in vivo at near single-cell resolution. We show that spontaneous activity propagates in the brain’s three-dimensional space, generating scale-invariant neuronal avalanches with time courses and recurrence times that exhibit statistical self-similarity at different magnitude, temporal, and frequency scales. This suggests that the nervous system operates close to a non-equilibrium phase transition, where a large repertoire of spatial, temporal, and interactive modes can be supported. Finally, we show that gap junctions contribute to the maintenance of criticality and that, during interactions with the environment (sensory inputs and self-generated behaviors), the system is transiently displaced to a more ordered regime, conceivably to limit the potential sensory representations and motor outcomes.

Highlights

• •Zebrafish whole-brain activity displays scale-invariant neuronal avalanches
• •These scale-invariant avalanches are suggestive of critical phenomena
• •Sensory inputs and self-generated behaviors deviate the dynamics from criticality
• •Blocking gap junctions disrupts criticality and deteriorates sensory processing

Ponce-Alvarez et al. show that zebrafish larvae generate spontaneous neuronal avalanches across the entire brain. These collective cascading events exhibit scale invariance, typical of critical phenomena (e.g., earthquakes, paper crumpling). The brain’s critical dynamics are modulated during interactions with the environment.

Introduction

Recent studies have shown that neuronal populations display collective activity patterns that are characterized by sequences of activations called “neuronal avalanches” (Beggs and Plenz, 2003, Mazzoni et al., 2007, Pasquale et al., 2008, Friedman et al., 2012, Hahn et al., 2010, Hahn et al., 2017, Shriki et al., 2013, Tagliazucchi et al., 2012, Priesemann et al., 2014). It has been proposed that the statistics of neuronal avalanches are signatures of criticality, a particular operating regime between phases of order and disorder in which several brain functions could be optimized, such as input sensitivity and dynamic range (Shew and Plenz, 2013). Indeed, previous reports show that the sizes and durations of neuronal avalanches are scale invariant (i.e., they follow power-law statistics with power exponents that depend on each other, which are typical features of systems at criticality). Another signature of criticality is the presence of scaling relations. For instance, Friedman et al. (2012) have shown that the dynamics of long-duration avalanches are similar to those of short-duration avalanches when they are properly rescaled. These previous studies suggest signs of criticality in spiking activity and local field potentials (LFPs) of neural cultures in vitro (Beggs and Plenz, 2003, Mazzoni et al., 2007, Pasquale et al., 2008, Friedman et al., 2012), LFP signals in vivo (Hahn et al., 2010), field potentials and fMRI blood-oxygen-level-dependent (BOLD) signals in vivo (Shriki et al., 2013, Tagliazucchi et al., 2012), voltage imaging in vivo (Scott et al., 2014), and 10–100 single-unit or multi-unit spiking and calcium-imaging activity in vivo (Priesemann et al., 2014, Bellay et al., 2015, Hahn et al., 2017, Seshadri et al., 2018). Despite these advances, criticality in the brain remains an open question, since mesoscopic measurements (from LFPs to BOLD signals) might distort the dynamics, and spiking data from a limited number of neurons are prone to subsampling effects (Priesemann et al., 2014) that are known to strongly bias the characterization of collective behavior, even in the case of scale-free networks (Levina and Priesemann, 2017, Stumpf et al., 2005). Therefore, to study criticality in the nervous system, it is necessary to monitor whole-brain dynamics with single-cell resolution. Moreover, how criticality is affected when the organism interacts with the environment remains elusive, and the functional connectivity mechanisms that promote a critical state are unknown.

Here, we addressed these open questions by studying the statistics of the zebrafish whole-brain dynamics and by interpreting them within the framework of criticality. Specifically, we used transgenic zebrafish larvae expressing genetically encoded calcium indicators (GCaMP5 or GCaMP6f) in combination with selective-plane illumination microscopy (SPIM) to monitor whole-brain dynamics with near single-neuron resolution in an intact, behaving vertebrate (Ahrens et al., 2013, Panier et al., 2013, Romano et al., 2017). Using this approach, we were able to study the collective dynamics of neuronal activity and its propagation across the whole brain, in three-dimensional space and time, in the form of neuronal avalanches, and at a wide range of scales. Analyzing the spatiotemporal activity patterns in 3D space is important because scale-invariant behaviors observed at criticality do not depend on the microscopic details of the system. Instead, they often depend on the dimension of the system and the type of phase transition. Thus, a system at criticality has universal properties that can be explained by simple mathematical models (Sethna et al., 2001). We were particularly interested in comparing the statistics of neuronal avalanches with those of critical three-dimensional systems that operate close to a non-equilibrium disorder-induced phase transition, for which the associated dynamics produce avalanches at all scales, or “crackling noise” (Sethna et al., 2001). Crackling noise arises in heterogeneous systems under external drive when the heterogeneity of the system’s elements (quenched disorder) is strong enough to compete with the interactions between them.

Here, we detected neuronal avalanches propagating in the brain during periods of both spontaneous and visually induced activity. We analyzed the spatial statistics of the activity patterns (their number, sizes, scaling properties, and correlation functions) and the spatiotemporal dynamics of the neuronal avalanches (sizes, durations, scaling properties, and spectral content) and compared these statistics during spontaneous activity, during the presentation of visual stimuli, during self-generated motor behaviors, and in pharmacologically perturbed conditions. Our results suggest that whole-brain dynamics fluctuate close to the critical point of a non-equilibrium disorder-induced phase transition, from which it can be displaced by interactions with the environment (sensory inputs and behavioral outputs). In addition, we found that gap junctions might be involved in maintaining a critical regime in the vertebrate nervous system.

Results

To study the spatiotemporal activity patterns emerging from whole-brain dynamics, we analyzed the neuronal activity from six zebrafish larvae (6–8 days post-fertilization [dpf]) recorded using SPIM (see STAR Methods and Figures S1A–S1C). In our study, morphological images were segmented into regions of interest (ROIs) corresponding to putative single neurons and neuropil regions, from which fluorescence fluctuations were extracted. Larvae were head restricted to simultaneously monitor neuronal activity and spontaneous tail movements. The six datasets were composed of $N$ = 41,115–89,349 selected ROIs recorded during long recordings of 1–2 hr composed of Q segments that each included a period of spontaneous activity (20 min) and a shorter period (4 min) of visual stimulation (Q ranges between 3 and 9, see Table S1 and Figure S1D). Visual stimulation was composed of gratings moving in different directions. Whole-brain activity was characterized by the activation of groups of ROIs that could span large parts of the brain (see Video S1). We aimed to describe the statistics of these events. For this, the activity of each putative neuron was binarized by imposing an activity threshold. Then, we identified clusters of co-active and spatially contiguous ROIs and quantified their number, size, and evolution over time (see STAR Methods).

Video S1. Whole-Brain Neuronal Activity, Related to Figures 1 and 2

The first row displays the relative increase in fluorescence (ΔF/F) in the hexagonal ROIs in five different coronal sections. The second row shows the corresponding binarized activity used to compute the clusters. The last row depicts the time course of the percentage of active ROIs in the entire volumetric recording.

Percolation Transition of the Spatial Clusters of Co-active and Contiguous ROIs

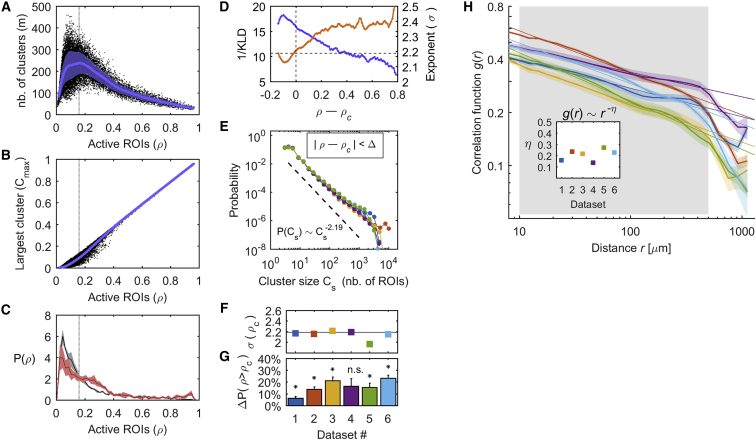
First, we characterized the spatial patterns of collective neuronal activity by calculating the number of clusters and their sizes (number of activations; see STAR Methods). We studied the cluster statistics within the framework of percolation theory. Percolation describes the behavior of clusters in a graph and how the cluster sizes change with the number of active units, going from small clusters to the emergence of a large cluster beyond a critical level of activity. Throughout this study, we analyzed the spontaneous and the visually evoked activity together, unless specified otherwise. For each time t, we computed the proportion of active ROIs $\left(\rho \right)$, the number of clusters (m), and the size of the i-th cluster ($C_s\left(i\right)$, $1\le i\le m$). First, we calculated the relation between ρ and m and found that the number of clusters peaked when $\sim$ 15% of the ROIs were active, a value that we denoted as ρ_c (Figures 1A, S2A, and S2B; Table S1). Interestingly, the variability of m was also maximized at this level of activation. Thus, there exists a fraction of active ROIs, ρ_c, for which the largest diversity of clusters was observed. Second, we calculated the relationship between ρ and the normalized size of the largest cluster (i.e., C_max = max(C_s)/C_all, where C_all is the size of the largest cluster obtained when all recorded ROIs are hypothetically active, i.e., above the activity threshold), which ranges between 91.40% and 99.74% of the ROIs for the different datasets. We found that C_max grows with ρ and spans a broad range of scales, from few ROIs to almost the entire brain, as it can be essentially as large as $\sim 1$ (Figures 1B and S2C). Third, we found that the level of network activation was different during the spontaneous and stimulus-evoked activity: the distribution of ρ, denoted as $P\left(\rho \right)$, showed that most often, the level of spontaneous activation was below p_c, and 10.52%–44.93% of the time, p was larger than ρ_c (Figures 1C and S2F). The activation level during the stimulus-evoked activity exceeded the value ρ_c significantly more often than in the spontaneous activity in 5 of the 6 datasets (17.82%–60.29% of the time, p < 0.01, paired t test comparing $P\left(\rho >{\rho }_c\right)$ during spontaneous and visual stimulation periods; see Figure 1G).

Figure 1.

Statistics of the Clusters of Co-active and Contiguous ROIs

(A) Number of clusters (m) as a function of the proportion of active ROIs (ρ). Blue line, mean of m; blue area, its standard deviation.

(B) Normalized size of the largest cluster (C_max) as a function of ρ (blue trace: average C_max).

(C) Distribution of ρ (black, spontaneous activity; red, stimulus-evoked activity) calculated for each of the Q spontaneous and evoked segments (solid line, mean distribution; shaded area, SEM). Note that the stimulus-evoked distribution is skewed to the right.

(D) We calculated the cluster size distribution for the set of clusters that appeared with ρ comprised within small intervals (ρ – Δ; ρ + Δ). Using the Kullback-Leibler divergence (KLD), we calculated the goodness of fit of the power law (blue) and, using MLE, we estimated the power exponent (orange) as a function of ρ. (A)–(D) show results for dataset 1. Note that, for ρ = ρ_c, the goodness of fit is close to its maximum and the corresponding power exponent is equal to one predicted in the case of 3D percolation, equal to 2.19 (dashed horizontal line).

(E) Size distribution P(C_s) of clusters that appeared with ρ between ρ_c – Δ and ρ_c + Δ. Each color represents a dataset. Error bars are smaller than the symbols’ size. Black line, power-law distribution predicted in 3D percolation.

(F) Power exponents σ(ρ_c) estimated using MLE.

(G) Difference between the proportion of time that ρ > ρ_c during the stimulus-evoked activity and the proportion of time that ρ > ρ_c during the spontaneous activity (^∗p < 0.01, paired t test). Error bars, SEM across the Q spontaneous-evoked segments. See also Figure S2.

(H) Correlation function g(r): average correlation between pairs of cells as a function of the Euclidean distance r, for each dataset (calculated for each of the Q segments and then averaged; colored areas, SEM). The straight lines represent power-law fits using least squares for r falling between 50 μm and 500 μm (gray area). Note that for distances longer than 500 μm, r approximates the size of the larva in one of its 3 dimensions.

Inset: estimated power-law exponent (estimation errors are smaller than the symbols’ size).

The above behaviors are signatures of the existence of a percolation critical point (ρ_c). Percolation theory shows that, close to the critical probability, the distribution of cluster sizes follows a power law with an exponent that depends only on the dimensions of the system (it does not depend on the details of the physical system). To test this, we computed the distribution of cluster sizes $C_s$, noted $P\left(C_s\right)$, and approximated it by a power law, which appears as a straight line in a log-log plot, such that $P\left(C_s\right)\sim C_s^{-\sigma }$ (Figures 1D–1F). We used a maximum likelihood estimation (MLE) method to assess the power law that best fitted the size distribution of the set of clusters that appeared with ρ comprised within small intervals (ρ – Δ; ρ + Δ), with Δ = 0.02. In the interval between ρ_c – Δ and ρ_c + Δ, $P\left(C_s\right)$ was well approximated by a power law (Kolmogorov-Smirnov [KS] test, ks < 0.05) with log-likelihood ratio (LLR) tests supporting the power law when compared to an alternative heavy-tailed distribution such as the lognormal (see STAR Methods and Table S1). Moreover, the power law goodness of fit (calculated using the inverse of the Kullback-Leibler divergence) was close to its maximum for all datasets in the interval between ρ_c – Δ and ρ_c + Δ (Figures 1D and S2D). The corresponding power law exponent σ(ρ_c) was between 1.97 and 2.22 for the different datasets, with an average of 2.15 ± 0.04 (Figures 1E, 1F, and S2E; Table S1). The values of σ(ρ_c) were close to the theoretical exponent of a 3D percolation process close to the critical point, equal to 2.19 (Jan and Stauffer, 1998).

The Correlation between ROIs Decays as a Power Law of the Distance

The previous results (Figures 1B and 1E) show that ROIs can form activity clusters of practically all sizes. This suggests the presence of long-range functional correlations between ROIs. We tested this hypothesis by studying the correlations between pairs of cells as a function of the Euclidean distance $r$ between them (i.e., the correlation function $g\left(r\right)$). Specifically, for each dataset, we calculated Pearson’s pairwise correlations and the Euclidean distance between all possible pairs among 40,000 randomly selected ROIs. We found that $g\left(r\right)$ decays approximately as a power law (i.e., $g\left(r\right)\sim r^{-\eta }$ with a least-squares exponent $\eta$ equal to 0.22 ± 0.02 on average) for $r$ between 50 μm and 500 μm (Figure 1H). These power-law exponents were preserved during spontaneous and stimulus-evoked activity (p = 0.18, paired t test; correlation coefficient = 0.65). Long-range power-law correlations are a hallmark of complex systems at criticality, which are characterized by non-trivial emergent collective spatiotemporal dynamics (Expert et al., 2011). Consequently, we next characterized how patterned activity propagates when including the time dimension.

The Temporal Dynamics of the Clusters Show Neuronal Avalanches Suggestive of Critical Behavior

We observed that, once a cluster was initiated, it could grow, collide with other clusters, or terminate. We tracked the clusters across time using the following procedure, which is a usual definition of avalanches in sand-pile models, Ising models, and analyses of fMRI recordings (Tagliazucchi et al., 2012): a new avalanche was initiated at time t₀ if a cluster i was composed of ROIs that were not active at time t₀ – 1; if at time t₀ + 1, at least one of the ROIs of the cluster i pertained to a cluster, then the avalanche was continued until this condition no longer held (see STAR Methods and Figure S3).

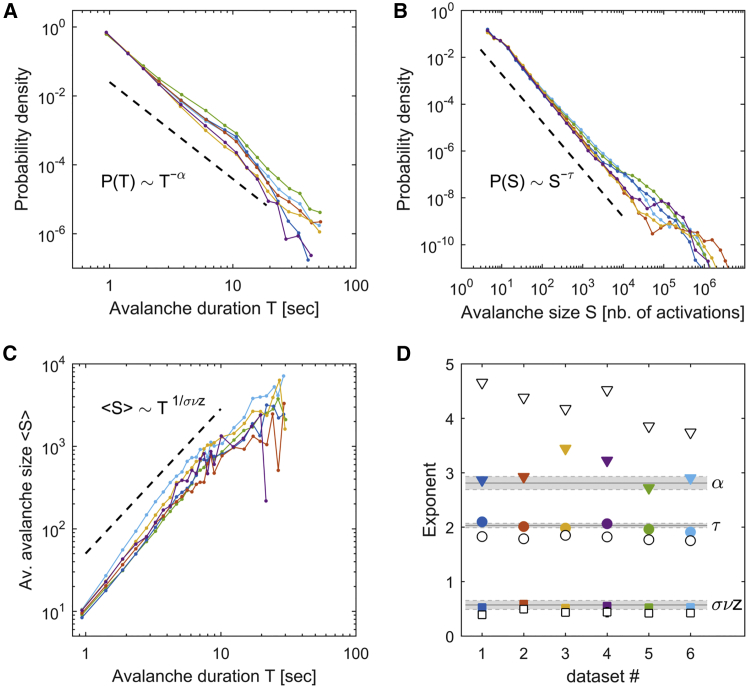
The total number of detected avalanches, $n_{av}$, ranged between 2.39 × 10⁵ and 7.94 × 10⁵ for the different datasets. An avalanche was described by its duration $T$ (the time it lasted) and its size $S$ (the number of neuronal activations during the avalanche). Using KS statistics and LLR tests to compare candidate heavy-tailed distributions, we found that avalanche durations and sizes were both well approximated by truncated power-law distributions (i.e., $P\left(T\right)\sim T^{-\alpha }$ and $P\left(S\right)\sim S^{-\tau }$) for all datasets (Figures 2A and 2B, and Table S2 for details). Thus, avalanches spanned a broad range of scales. The averaged MLE power-law exponents, $\alpha$ and $\tau$, were equal to 3.01 ± 0.11 and 2.01 ± 0.03, respectively. In contrast, shuffled data that preserved the spatial correlations but randomized the temporal structure (time-shuffled data, see STAR Methods) led to significantly different exponents ($\alpha$ = 4.22 ± 0.15 and $\tau$ = 1.80 ± 0.02; p < 0.001, two-sample t test; Figure 2D). Notably, the power laws observed in the data (but not in the shuffled data) are typical of critical systems that operate close to a non-equilibrium disorder-induced phase transition, producing avalanches at all scales, a phenomenon known as crackling noise (Sethna et al., 2001). The universal critical exponents for the avalanche durations and sizes of such systems are known to be equal to 2.81 ± 0.11 and 2.03 ± 0.03, respectively, as obtained by numerical simulations of the random field Ising model (RFIM) in three dimensions, which is the paradigmatic theoretical model of disorder-induced critical dynamics (Perković et al., 1995, Sethna et al., 2001; see also STAR Methods). Thus, the observed scaling exponents of the neuronal avalanches are suggestive of non-equilibrium critical behavior.

Figure 2.

Neuronal Avalanches Show Critical Statistics

(A) Distribution of avalanche durations $T$ (in s).

(B) Distribution of avalanche sizes $S$ (i.e., cumulative sum of the number of activated ROIs).

(C) Relation between $S$ and $T$, for each dataset. In (A), (B), and (C), each color corresponds to a dataset and the black dashed line indicates the power law expected in the case of critical behavior. The validity of the power-law fitting was evaluated using Kolmogorov-Smirnov statistics and log-likelihood ratio tests; see Table S2 for more details.

(D) Measured exponents for each dataset (colored filled symbols) and the corresponding time-shuffled data (open symbols). Triangles, $\alpha$ exponent; circles, $\tau$ exponent; squares, $\sigma \nu z$ exponent. Error bars (estimation errors) are smaller than the size of the symbols. The gray horizontal lines and the gray shaded areas indicate the expected critical exponents and their uncertainty, respectively, in 3D random field Ising models.

See Table S2 for more details. See also Figures S3 and S4.

Criticality theory also predicts that the average size $\langle S\rangle \left(T\right)$ of avalanches of duration $T$ is given by the scaling relation (Perković et al., 1995, Sethna et al., 2001, Friedman et al., 2012). This relation was confirmed in the data for durations shorter than the power-law cutoffs (Figures 2C; see also Table S2). Moreover, using least squares to estimate the exponent, we found that for all datasets, the value of the exponent $\sigma \nu z$ was consistent with that expected for criticality in three dimensions, equal to 0.57 ± 0.09 (Perković et al., 1995) (Figure 2D; see also Table S2), while time-shuffled datasets displayed significantly different exponents: on average, $\sigma \nu z$ = 0.54 ± 0.01 for the original data and $\sigma \nu z$ = 0.43 ± 0.02 for the shuffled data (p < 0.001, two-sample t test). Furthermore, the critical exponents $\alpha$, $\tau$, and $\sigma \nu z$ must obey $\left(\tau -1\right)/\left(\alpha -1\right)=\sigma \nu z$ (Perković et al., 1995, Sethna et al., 2001, Friedman et al., 2012). This relation is consistent with the exponents we measured. Indeed, the obtained values of $q=\left(\tau -1\right)/\left[\sigma \nu z\left(\alpha -1\right)\right]$ fluctuate around $\sim 1$ ($q$ ranges between 0.79 and 1.13 and $q=$ 0.94 ± 0.05 on average), and when the analyses were performed using the avalanche durations and sizes of all datasets, we found exponent values that were strongly consistent with the theory ($\alpha$ = 2.90 ± 0.01, $\tau$ = 1.99 ± 0.01, and $\sigma \nu z$ = 0.54 ± 0.02, see Figures S4A–S4C). In contrast, time-shuffled data largely deviated from this relationship ($q$ ranges between 0.47 and 0.65, $q=$ 0.58 ± 0.03 on average). Finally, we tested whether the exponents depend on the size of the clusters composing the neuronal avalanches and on the temporal resolution of the data (dt = 0.47 s). For this, active ROIs were assigned to the same cluster when their distance, in 3D space, was shorter than a given value (Figures S4D–S4F). We found that avalanche exponents were close to the theoretically predicted ones, for all larvae, for clusters defined within spheres of a radius up to $\sim$30 μm; longer radii led to different and inconsistent exponents. The size of the clustering neighborhood used in the present study lies below this threshold. We also note that the exponents were consistent for time bins shorter or equal to 1.41 s (Figures S4G–S4I).

Universal Scaling Functions as Signs of Criticality

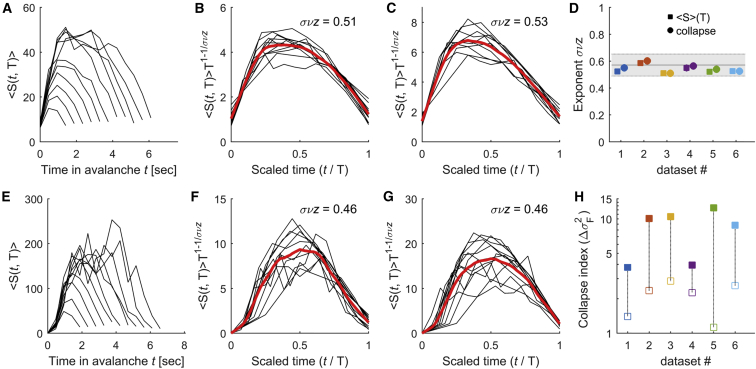
Besides scale invariance and power exponent relations, a further signature of criticality is the existence of universal scaling functions that capture the systems’ dynamics at different scales. We studied two aspects of the avalanche dynamics: the temporal profile of the avalanches and the time intervals between avalanches. Let $S\left(t,T\right)$ be the number of activations at time t in an avalanche of duration $T$. Close to criticality, the average avalanche profile, $\langle S\left(t,T\right)\rangle$, is expected to be similar across temporal scales (Perković et al., 1995, Sethna et al., 2001, Friedman et al., 2012). Specifically, the relation between the normalized time $t/T$ and the scaled avalanche profile follows a single form that does not depend on the temporal scale, . This invariance across scales is known as “shape collapse.” To estimate the scaling parameter $a$, we used the method of Marshall et al. (2016), which produces the best possible collapse of the data (see STAR Methods). Note that close to criticality, the scaling parameter $a$ and the exponent $\sigma \nu z$ are related: $a=\sigma \nu z^{-1}-1$. This is the consequence of the relationship and $\langle S\rangle \left(T\right)$ being equal to the integral of between $t=0$ and $t=T$. Thus, data collapse is a different, more precise method both to assess criticality and to estimate the exponent $\sigma \nu z$. The empirical avalanche profiles showed that avalanches built up and terminated in a stereotypical way for a wide range of durations (Figure 3A) such that the average time-course of short avalanches resembled that of longer avalanches. We found that empirical avalanche profiles could indeed be collapsed (scaling reduces the variance by an amount of $\Delta {\sigma }_F^2$ = 3.78 – 12.52), with a scaling parameter $\sigma \nu z$ ranging between 0.47 and 0.58 for the different datasets with an average of 0.55 ± 0.02 (Figures 3B and 3C; see also Table S2). Note that the exponent values were consistent with the values of $\sigma \nu z$ estimated through the relationship between $\langle S\rangle$ and $T$ (Figure 3D). In contrast, in time-shuffled datasets, the temporal profiles of avalanches did not collapse (Figures 3E–3H).

Figure 3.

Universal Scaling Functions: Avalanche Profiles

(A) Averaged temporal profile, $\langle S\left(t,T\right)\rangle$, of avalanches of durations $T$, where $T$ = 2.82 – 7.99 s (data from dataset 3).

(B) Scaled avalanche profiles as a function of the scaled time t/T. Red line, averaged scaled avalanche profile; σνz, best scaling parameter (data from dataset 3).

(C) Same as (B) but for dataset 6.

(D) Estimated σνz exponents using scaling collapse (circles) and the relation $\langle S\rangle \left(T\right)$ (squares). Each color represents a different dataset. Estimation errors are smaller than the size of the symbols. Note the similarity between the exponents calculated with the two different methods. The gray area indicates the theoretically expected critical exponent and its uncertainty. See Table S2 for more details.

(E–G) Same as (A)–(C), respectively, but for the corresponding time-shuffled datasets, for which collapse was substantially reduced.

(H) Amount of collapse $\left(\Delta {\sigma }_F^2\right)$ for the original datasets (filled symbols) and the shuffled datasets (open symbols).

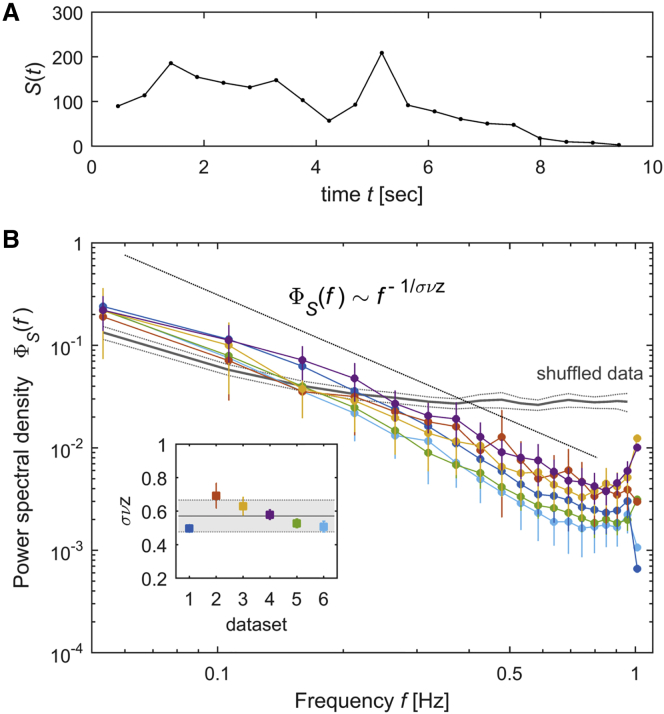
Criticality theory predicts that the frequency content of the dynamics within the avalanches scales as ${\text{Φ}}_S\left(f\right)\sim f^{-1/\sigma \nu z}$, with the same critical exponent as in the scaling relation and as in the shape collapse of avalanche profiles (Kuntz and Sethna, 2000, Travesset et al., 2002). Therefore, we next investigated the time courses of neuronal avalanches in the frequency domain (see STAR Methods). We found that the power spectral density (PSD) of the time courses of the avalanches, ${\text{Φ}}_S\left(f\right)$, decayed with the frequency $f$ approximately as a power law (Figures 4A and 4B). Using least squares, we estimated the power-law decay exponent of ${\text{Φ}}_S\left(f\right)$ and found that, indeed, the values of $\sigma \nu z$ were close to those obtained through the relation $\langle S\rangle \left(T\right)$ and the shape collapse analysis, and they were consistent with the theoretical values ($\sigma \nu z$ ranges between 0.50 and 0.69 for the different datasets and $\sigma \nu z$ = 0.57 ± 0.04 on average). For time-shuffled datasets, the PSD became more uniform across frequencies and largely deviated from the predicted power law ($\sigma \nu z$ ranges between 3.30 and 4.45 for the different shuffled datasets and $\sigma \nu z$ = 3.76 ± 0.23 on average). Hence, the exponent $\sigma \nu z$ was consistently close to its theoretically predicted critical value using different approaches (scaling relation between avalanche size and duration, avalanche shape collapse, and PSD of avalanche profiles), constituting consistent evidence suggesting that neuronal avalanche dynamics were critical.

Figure 4.

Universal Scaling Functions: Power Spectrum of Avalanche Time Courses

(A) Temporal profile S(t) of an example avalanche of duration 9.4 s.

(B) We calculated the power spectral density (PSD) of the time courses of neuronal avalanches. Each color represents a different dataset. Error bars indicate SEM. The PSD of avalanche time courses, ${\text{Φ}}_S\left(f\right)$, decays approximately as a power law of the frequency $f$ with an exponent equal to $1/\sigma \nu z$ (black line). In contrast, the PSD of time-shuffled data was uniform across frequencies and largely deviated from the predicted power law (the gray solid line is the mean PSD across shuffled datasets, and the thin gray lines depict SEM).

Inset: exponent $\sigma \nu z$ estimated using least-squares for each dataset. Error bars indicate the exponent estimation error. The values of $\sigma \nu z$ estimated using this analysis are close to the expected critical exponent (0.57) indicated by the solid black line; the gray shaded area indicates the uncertainty of the critical exponent.

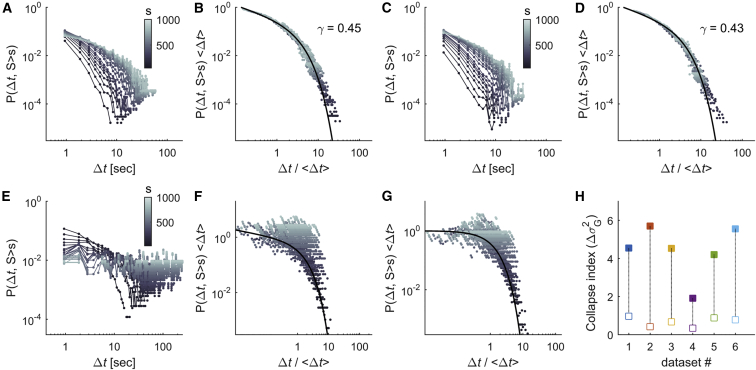
Avalanche dynamics can also be characterized by the time between the avalanches, called the recurrence time interval. We studied the conditional distributions $P\left(\Delta t,S>s\right)$ of time intervals $\Delta t$ between consecutive avalanches of size larger than a given threshold s. As expected, large avalanches were separated by longer intervals (Figures 5A and 5C), so that the mean interval $\langle \Delta t\rangle$ increased with threshold s. For each minimum size s, it is possible to express the time in units of the mean interval, such that $\Delta t$ becomes $\Delta t/\langle \Delta t\rangle$, which implies that the conditional distribution is changed to $P\left(\Delta t,S>s\right)\langle \Delta t\rangle$. Notably, in these rescaled axes, the distributions collapsed onto a single curve, or scaling function, independent of the threshold s (Figures 5B and 5D). This suggests that the occurrence of avalanches can be described by a self-similar process (i.e., a process showing the same statistical properties at different scales or magnitudes). As in previous studies, the scaling function can be approximated by a single gamma distribution with one single shape parameter $\gamma$ ranging between 0.20 and 0.51 (Corral, 2007) (see STAR Methods; see also Table S2). In the gamma distribution assumption, the scaling function decays approximately as a power law with exponent $1-\gamma$ for $\Delta t<\langle \Delta t\rangle$; for $\Delta t>\langle \Delta t\rangle$ the decay is exponential. A gamma point process with $\gamma =$ 1 is equivalent to a Poisson process, while if $\gamma$ < 1, as in the present data, the process is more irregular and more burst-like than a Poisson process. Consistent with previous findings, these scaling features are similar to those reported for the recurrence time distributions of critical phenomena such as earthquakes and rock fractures (Corral, 2007, Davidsen et al., 2007). In contrast, shuffled datasets in which we randomly permuted the avalanche sizes, while keeping the sequence of avalanches onsets, did not collapse (Figures 5E–5H). Hence, correlations between avalanche times and sizes are necessary for the process to be self-similar.

Figure 5.

Universal Scaling Functions: Recurrence Time Intervals

(A) Recurrence time distributions $P\left(\Delta t,S>s\right)$. The distributions of time intervals $\Delta t$ between consecutive avalanches of sizes larger than a given threshold s were calculated for different values of s (gray color code; data from dataset 2).

(B) Rescaled recurrence time distributions as a function of the rescaled time $\Delta t/\langle \Delta t\rangle$. The black curve indicates the gamma distribution onto which the scaled recurrence time distributions collapsed (γ: shape parameter of the gamma distribution; data from dataset 2).

(C and D) Same as (A) and (B), respectively, but for dataset 3. See Table S2 for more details.

(E–G) Same as (A), (B), and (D), respectively, but for the corresponding shuffled datasets. Note the absence of collapse for the shuffled data.

(H) Amount of collapse $\left(\Delta {\sigma }_G^2\right)$ for the original datasets (filled symbols) and the shuffled datasets (open symbols).

Propagation of Neuronal Avalanches in the Brain

Our data allowed us to analyze the spatial and temporal statistics of neuronal avalanches and to provide insights into which mechanisms contribute to their initiation. For this, we examined how avalanches propagated throughout the brain. We tracked the averaged location of an avalanche by calculating its center of mass (CM) and followed its temporal evolution by computing the averaged velocity of the CM, noted $\overrightarrow{V}$ (see STAR Methods). We next examined the distribution of $\overrightarrow{V_{xy}}$ (i.e., the projection of $\overrightarrow{V}$ into the coronal section [x-y plane] of the brain) (Figures 6A and 6B). We found that the direction of propagation $\left(\theta \right)$ of avalanches was constrained by the brain’s anatomy: avalanches preferentially traveled parallel to the caudo-rostral axis, as shown by the anisotropy of the direction of propagation (Figure 6C). When pooling all datasets, the average propagation velocity of the CMs in 3D space (i.e., $\langle \Vert \overrightarrow{V}\Vert \rangle$, was 389 ± 23 μm/s) and the average distance traveled by the avalanches’ CMs was $\langle D\rangle$ = 261 ± 23 μm (Figures 6D and 6E).

Figure 6.

Propagation of Neuronal Avalanches

(A and B) Probability distribution of the projection of the velocity vector into the coronal (x-y) plane of the brain, ${\overrightarrow{V}}_{xy}$, for two representative datasets (A, dataset 1; B, dataset 2). The probability density is shown in color scale.

(C) Probability distribution of the direction of propagation in the coronal (x-y) plane, $\theta$, for each dataset.

(D) Left: distribution of velocity magnitude. Right: differences in median velocities $\Delta V$ of the avalanches during periods of spontaneous and the stimulus-driven activity. ^∗p < 0.001, two-sided Wilcoxon rank-sum test.

(E) Left: probability distribution of the distance traveled by the neuronal avalanches. Right: differences in median distances $\Delta D$ of the avalanches during periods of spontaneous and the stimulus-driven activity (p > 0.05, two-sided Wilcoxon rank-sum test).

(F) Locations of the initial centers of mass (i.e., $\overrightarrow{CM}\left(t=1\right)$), of neuronal avalanches projected on the coronal (x-y) plane of the brain (for dataset 1). Each green dot corresponds to an avalanche. Note that the vast majority of the initiation sites occurred in the neuronal somata rather than in the neuropil (dense white regions).

(G) Probability distribution of the number of simultaneous avalanches, $N_s$, normalized by its mean $\langle N_s\rangle$, for each dataset (solid lines). The narrow distributions are the expected Poisson distributions given $\langle N_s\rangle$.

(H) Probability distribution of detecting two simultaneous avalanches with CMs separated by a distance d, for each dataset. Points indicate distance bins for which the probability of simultaneous avalanches is significantly (p < 0.01) higher than chance (i.e., randomized data; see STAR Methods).

See also Figure S5.

Interestingly, propagating avalanches during periods of visual stimulation were significantly faster than those during the spontaneous activity period (p < 0.001, two-sided Wilcoxon rank-sum test) for all datasets, with differences in median velocity $\Delta V$ ranging between 3 and 19 μm/s (Figure 6D, right). In contrast, the median distances traveled by the avalanches were not significantly different between spontaneous and visually induced activity (p > 0.05, two-sided Wilcoxon rank-sum test, Figure 6E, right).

Furthermore, our analysis allowed us to study the correlation between neuronal avalanches that occurred quite evenly in different locations of the brain (Figure 6F). We were interested in the interaction between parallel avalanches that occurred simultaneously at different spatial locations. Indeed, the distribution of the number of concomitant avalanches $N_s$ largely deviated from a Poisson distribution (i.e., the expected distribution if simultaneous avalanches occurred by chance), indicating the presence of correlations (Figure 6G). We calculated the probability distribution of observing two avalanches that initiated simultaneously with CMs separated by a distance d and compared it to the expected distribution when the times of avalanche initiation were randomized (see STAR Methods). Overall, pairs of avalanches with CMs less than 150 μm apart tended to occur in the same time frame with a probability that was $\sim$8% greater than expected by chance (Figure 6H). These results suggest that neuronal avalanches are initiated through a local mechanism with weak short-range spatial correlations due to local connectivity.

Our results suggest that criticality is an emergent phenomenon of whole-brain dynamics. To examine whether criticality also emerges at the level of local networks, we analyzed neuronal avalanches in two distinct anatomical brain regions with different functions (the optic tectum involved in sensory processing and integration and the rhombomere 7 region containing the reticulospinal circuit implicated in the generation of motor patterns; see Figure S5). Both regions displayed avalanches with durations and sizes distributions showing power-law statistics with power exponents close to the corresponding critical values. Nevertheless, while durations and average sizes of the avalanches in the optic tectum showed the expected scaling relation (, with $\sigma \nu z\approx$ 0.57), reticulospinal avalanches deviated from it. This means that for a given duration $T$, the average size of the avalanches was larger than that predicted by criticality theory. Thus, in contrast to the optic tectum, avalanches in the reticulospinal circuit were faster than expected in a critical system.

Sensory Stimulation and Self-Generated Behaviors Deviate Brain Dynamics to an Ordered Regime

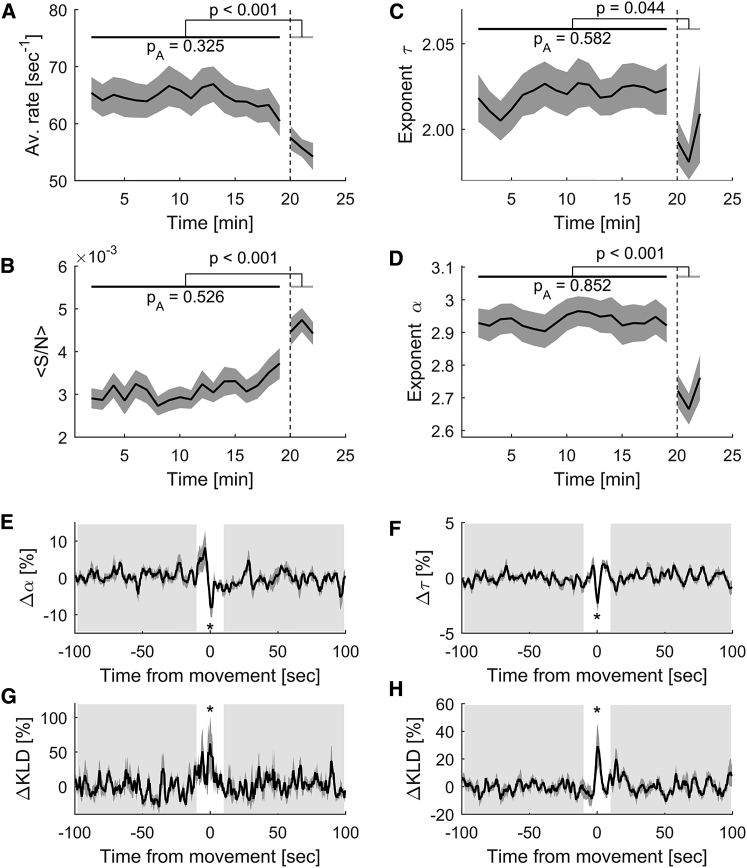
Our previous results (Figures 1G and 6D) show that sensory drive affects the propagation of neuronal activity in the larva’s brain. To further test whether sensory stimulation affects criticality in the brain, we studied how visual stimuli affect the statistics of the neuronal avalanches. For this, we compared several avalanche properties during periods of spontaneous activity with those during periods in which visual stimulation was presented to the larvae. Using sliding windows of 120.32 s, shifted in steps of 60.16 s, we calculated the rate of avalanche initiation, the average avalanche size and duration, and the exponents $\alpha$ and $\tau$. Notably, during periods of spontaneous activity, the statistical properties of neuronal avalanches remained constant (p values ranged between 0.33 and 0.85; one-way repeated-measures [RM] ANOVA tests comparing the values of each statistical property in the different time windows during periods of spontaneous activity), with size and duration exponents close to those predicted by theory in critical systems (Figures 7A–7D). However, during the visual stimulation periods, the avalanche characteristics significantly changed (p < 0.05, two-sided Wilcoxon rank-sum tests) and we observed: a decrease in the avalanche initiation rate (64.77 ± 0.72 versus 55.78 ± 1.16 avalanches per second, Figure 7A), an increase in the average size of the avalanches ($\langle S/N\rangle$ = 0.307% ± 0.007% versus$\langle S/N\rangle$ = 0.454% ± 0.016%, Figure 7B), an increase in the average duration of the avalanches ($\langle T\rangle$ = 1.37 ± 0.005 s versus $\langle T\rangle$ = 1.445 ± 0.012 s), and a decrease in the duration and size power exponents ($\tau$ = 2.02 ± 0.01 versus $\tau$ = 2.00 ± 0.01, $\alpha$ = 2.94 ± 0.02 versus $\alpha$ = 2.71 ± 0.03, Figures 7C and 7D). Recently, it has been proposed that stimulus-induced changes in neuronal avalanches can be fully explained by changes in the rate of activity events (Yu et al., 2017). Here, we showed that the differences between spontaneous and stimulus-induced activity patterns cannot be explained by differences in the rate of calcium events alone but rather by changes in their correlation structure (Figures S6A–S6E). Together, our results suggest that, at rest, the nervous system of the larva constantly functions in a critical regime rather than fluctuating between phases of order and disorder. In contrast, visual stimulation affects the characteristics of the avalanches, slightly shifting the dynamics of the nervous system away from criticality, toward a regime where neuronal avalanches are more ordered (i.e., faster, larger, and longer).

Figure 7.

Sensory Stimulation and Self-Generated Behavior Transiently Deviate the Brain’s Dynamical State from Criticality

(A–D) The average rate of avalanche initiation (A), the average avalanche size (B), and the average power exponents of the distribution of avalanche sizes (C) and durations (D) were calculated for avalanches included within sliding time windows, for all spontaneous and evoked segments and all datasets. Shaded areas indicate SEM. We compared the values during periods of spontaneous activity (black horizontal line) and during periods of visual stimulation (gray horizontal line) using a two-sided Wilcoxon rank-sum test (p, p value). We also compared the values measured in all windows during spontaneous activity using a RM-ANOVA; p_A indicates the resulting p value (high p values suggest that avalanche properties were constant during periods of spontaneous activity).

(E and F) Averaged exponents describing the distributions of durations (E) and sizes (F) of spontaneous neuronal avalanches around self-generated tail movement onsets. Exponents were normalized by the corresponding averaged values during the reference periods (from –100 to –10 s and from +10 to +100 s, shaded areas; with respect to movement onsets, white areas).

(G and H) Averaged changes of the Kullback-Leibler divergence (KLD) between the distributions of durations (G) and sizes (H) of spontaneous avalanches and theoretical power laws (relative to reference periods).

In (E)–(H), ^∗p < 0.001, two-sample t test comparing values at movement onset and values in the absence of movements.

See also Figures S6 and S7.

These results show that sensory inputs affect the dynamical regime of neuronal avalanches. We further asked how the statistics of spontaneous avalanches are influenced by the generation of spontaneous (self-generated) behavioral outputs. The head-restrained configuration of our recordings allowed us to monitor both spontaneous neuronal activity and self-generated tail movements (see STAR Methods). During spontaneous activity, larvae produced isolated and sporadic tail movements, called swimming bouts (with occurrence frequency equal to 0.051 ± 0.033 Hz), which occurred irregularly in time (coefficient of variation equal to 1.72 ± 0.26) and had short-term serial correlations in terms of movement laterality (consecutive bouts within less than 10 s had a significantly higher probability to be toward similar directions than for longer intervals; 0.74 ± 0.09 versus 0.61 ± 0.13, p < 0.001, Mann-Whitney test). We observed that, with respect to periods of spontaneous activity, neuronal avalanches during tail movements had larger sizes, and their distribution across different brain regions was biased toward hindbrain motor areas (Figure S7). We calculated the avalanche statistics around the onsets of detected tail movement events, t_on, and compared them to those in the absence of movements (Figures 7E and 7F). Specifically, we collected the durations and sizes of neuronal avalanches initiated at each time frame within t_on ± 100 s. We observed a significant (p < 0.001, two-sample t test) decrease in the exponent values describing the distribution of the sizes and the durations of avalanches around t_on, with respect to the values in the absence of movements (from –100 to –10 s and from +10 to +100 s, with respect to movement onsets). The decreases in exponent values were accompanied by deviations from power-law statistics (Figures 7G and 7H). These differences were not fully explained by differences in the rate of calcium events but rather by changes in their correlation structure (Figures S6F–S6J). Hence, these results suggest that, during the emergence of self-generated behaviors, brain dynamics transiently deviate from criticality.

Disrupting Electrical Coupling Deviates the Brain Activity from Criticality

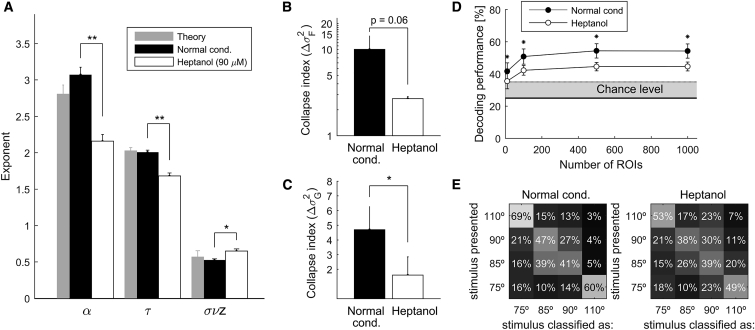
To get insights into the physiological mechanisms contributing to stabilization of the brain’s activity on the critical regime, we characterized the statistical properties of neuronal avalanches when zebrafish larvae were exposed to a low concentration of heptanol, a gap junction blocker (see STAR Methods) (Saint-Amant and Drapeau, 2000, Muto and Kawakami, 2011, Warp et al., 2012). We first quantified the freely swimming behavior of a cohort of larvae with and without exposure to 90 μM heptanol. At this concentration of heptanol, the locomotor activity of the larvae could not be distinguished from that of the controls (see STAR Methods and Figures S8A–S8D). However, when analyzing the spontaneous avalanches, we found that larvae exposed to heptanol displayed substantially fewer avalanches than the original datasets ($\sim$1 versus $\sim$30 avalanches per frame), with ($\alpha$, $\tau$, $\sigma \nu z$) exponents that significantly deviated from the critical values observed in normal conditions (Figure 8A; Table S2). Moreover, larvae exposed to heptanol displayed neuronal avalanches for which neither the temporal profiles nor the recurrence-time distributions collapsed, showing no evidence of self-similarity (Figures 8B and 8C).

Figure 8.

Gap Junctions Play a Role in Maintaining Criticality in the Nervous System

(A) Average distribution exponents (α, τ, σνz) of spontaneous neuronal avalanches displayed by larvae in normal experimental conditions (datasets 1–6; black bars) and by larvae exposed to heptanol (90 μM) (datasets 7 and 8; white bars). For comparison, the gray bars indicate the critical exponents of 3D random field Ising theoretical models.

(B and C) Profile (B) and recurrence-time (C) collapse indices of neuronal avalanches calculated in normal conditions (black bars) and under heptanol exposure (white bars). In (A)–(C), p indicates the p value of two-sample t tests; ^∗p < 0.05, ^∗∗p < 0.01. Error bars, SEM.

(D) Decoding of visual stimuli at one optical plane of the optic tectum (n = 14 larvae, 8 in normal conditions and 6 after expsure to heptanol at 90 μM). Stimuli consisted of single light spots randomly presented at 4 possible closely spaced azimuth locations in the visual field (75°, 85°, 90°, and 110°). A maximum likelihood decoder was used to classify the stimuli location based on the activity of n ROIs. For n > 100, the classification performance was significantly higher than chance (i.e., 25%) for larvae in normal conditions. However, the decoding efficiency was significantly lower for larvae exposed to heptanol. ^∗p < 0.001, two-sample t test.

(E) Decoding confusion matrices averaged across larvae in normal conditions (left) and across larvae exposed to heptanol (right), for n = 1,000. The off-diagonal matrix elements represent the probability of erroneously classifying one stimulus as a different one. The diagonal corresponds to correct classifications. Notice that, as expected, the decoder confused nearby stimuli.

See also Figure S8.

Furthermore, to investigate the role of the brain critical dynamics in the processing of sensory information, we performed experiments in which visual stimuli were projected on a screen at different locations in the field of view of the larva (see STAR Methods). The visual stimuli consisted of single light spot randomly presented at four possible closely spaced azimuth locations in the visual field (75°, 85°, 90°, 110°, with 0° defined as the head-tail longitudinal axis of the larva, facing the larva’s head). The visually induced calcium responses, recorded at one optical plane of the optic tectum, were used to classify the spatial location of the stimuli, by means of a maximum likelihood decoder (MLD; see STAR Methods and Figures S8E–S8G). We found that exposure to heptanol led to a significant decrease in the decoder’s average classification performance with respect to larvae in normal conditions (for a population of 1,000 ROIs, the average classification performance was: 54.3% ± 4.5% versus 44.7% ± 2.8%, p < 0.001, two-sample t test; the chance level was 25%; see Figures 8D and 8E). Altogether, these results suggest that pharmacological perturbation of electrical synapses deviates the brain’s dynamical state from criticality, stressing the role of gap junctions in maintaining the dynamics of the brain at criticality, and that criticality may enhance sensory processing.

Discussion

Criticality is a regime at the border between phases of order and disorder, producing the maximal diversity of possible emergent patterned dynamics. It has been suggested that neuronal circuits and many other biological networks, such as gene regulatory networks, operate at criticality to optimize information processing and to accomplish tradeoffs between stability and responsiveness and between robustness and evolvability (Torres-Sosa et al., 2012). Here, we monitored whole-brain dynamics with near single-neuron resolution in the intact, behaving zebrafish larvae and interpreted the observed collective statistics in the framework of criticality. Our results are consistent with critical phenomena associated with phase transitions. As in models of disorder-induced phase transitions in three dimensions (Seppälä et al., 2002), our results show that the spatial statistics of clusters of co-active contiguous ROIs, as measured by their size distribution, reached the theoretical values close to the percolation point ρ_c, at which maximal diversity of spatial patterns was observed. Spatial patterns were organized as emergent scale-invariant spatial correlations, producing a large repertoire of modes of interactions, allowing for short-range and long-range functional connectivity. Moreover, the temporal evolution of the spatial clusters (neuronal avalanches) presented scale-invariant distributions, with power-law exponent values and exponent relations predicted in critical phenomena that exhibit crackling dynamics, as observed in earthquakes, Barkhausen noise in ferromagnets, paper crumpling, rock fractures, and many others (Perković et al., 1995, Sethna et al., 2001). Furthermore, neuronal avalanche evolution and recurrence in time can be described by single universal scaling functions across many size and timescales, as predicted in critical phenomena (Perković et al., 1995, Sethna et al., 2001, Corral, 2007), and as observed in cortical cultures (Friedman et al., 2012, Lombardi et al., 2014). Here, we also found that power spectra of avalanche time courses decayed with a $1/f^{1/\sigma \nu z}$ power law with an exponent close to the scaling exponent relating the avalanche size to its duration, as expected in crackling dynamics (Kuntz and Sethna, 2000, Travesset et al., 2002). These findings are all signatures of self-similarity and scale invariance of brain activity, with functional consequences in terms of an enhanced repertoire of spatial, temporal, and interactive modes, which are essential to adapt, process, and represent complex environments (Chialvo, 2010, Hidalgo et al., 2015). In other words, a critical nervous system could encode complex and ever-changing environmental conditions into a large diversity of distinct collective neuronal patterns that span multiple temporal and spatial scales, both locally (segregation) and across specialized brain regions (integration) (Sporns, 2013).

Close to phase transitions, complex systems show properties that are independent of the system’s details and can thus be captured by simple models. The RFIM is the archetypal model of interconnected binary units presenting a non-equilibrium disorder-induced phase transition and producing avalanche dynamics at all scales (Perković et al., 1995, Sethna et al., 2001, Sethna et al., 2005). When this system interacts with the environment through an external force H, avalanches arise as a competition between an ordering force, due to interactions, and a disordering force, due to heterogeneity. In models of neural networks, heterogeneity and interactions can be described by the variance of excitabilities of the neurons (Δ) and synaptic couplings of strength J, respectively (Hernández-Navarro et al., 2017). When $\Delta \sim J$, the balance between order and disorder is achieved and avalanches of all scales are observed. In this case, if H is fixed and equal to a critical value H_c, avalanche distributions have exponents equal to $\left(\alpha ,\tau ,\sigma \nu z\right)\approx$ (3/2, 2, 1/2). However, if H(t) varies over time, the predicted exponents become $\left(\alpha ,\tau ,\sigma \nu z\right)\approx$ (2.03, 2.81, 0.57), as observed in our study. The avalanche statistics observed here can thus be interpreted as produced by a critical system exposed to time-varying inputs, as expected for the nervous system of an intact, non-anesthetized, non-paralyzed organism.

Systems at criticality are assumed to reach optimal computation capabilities (under specific definitions of optimality), in terms of stimulus discriminability, information transmission, and state repertoire (Shew and Plenz, 2013). Moreover, it is suggested that brain diseases shift the nervous system away from criticality—as during epileptic seizures (Meisel et al., 2012, Hobbs et al., 2010). For these reasons, it has been argued that healthy neural systems are poised at a critical point, especially during rest (Massobrio et al., 2015). It is believed that this dynamical regime stabilizes without fine-tuning through self-organization, implemented by synaptic plasticity and by excitation/inhibition (E/I) balance (Levina et al., 2007, Magnasco et al., 2009, Bellay et al., 2015), and evolutionarily selected to adapt to complex environments (Hidalgo et al., 2015). Consistent with these views, we found that larvae exposed to a low concentration of heptanol, a gap junction blocker (Saint-Amant and Drapeau, 2000, Muto and Kawakami, 2011, Warp et al., 2012), displayed neuronal avalanches with altered exponents and showed no evidence of self-similarity, presumably deviating the brain from a critical point. This suggests the involvement of gap junctions in maintaining criticality in the zebrafish brain, either due to gap-junction-specific synaptic properties or by affecting neuronal excitability and the E/I balance (Lewis and Rinzel, 2000, Traub et al., 2001, Memelli et al., 2012). Most probably, gap junctions are only a part of a functioning system that could settle at criticality due to a combination of multiple factors (synaptic plasticity, homeostasis, etc.) that tend to balance the amount of order and disorder in the system. Moreover, when decoding the tectal responses to visual stimuli, we found that the neuronal activity of larvae exposed to heptanol led to a decrease in classification performance. This suggests that deviation from critical dynamics is accompanied by a degradation of information processing, thus suggesting a functional and computational relevant role of criticality in the nervous system.

Furthermore, our results suggest that sensory stimulation and self-generated behaviors transiently change the critical dynamics, which are otherwise constantly observed during periods of spontaneous activity. Collective activity during stimulus-elicited activity was more ordered, with faster, larger, and longer avalanches. This is consistent with recent findings using LFPs in an ex vivo preparation (Shew et al., 2015) and previous functional imaging studies in humans (He, 2011), and it has functional relevance in terms of enhanced stimulus detection (Clawson et al., 2017). Furthermore, we observed that spontaneous self-generated behaviors were accompanied by transient deflections of the avalanche exponents, slightly displacing the system away from the critical behavior. Overall, our study suggests that crackling noise dynamics might be the default mode of the healthy nervous system, a suitable regime for internal representations and exploration of the spontaneous state repertoire, which can be seen as the prior expectations of potential sensory inputs and behavioral outputs (Berkes et al., 2011). However, when the animal interacts with the environment, the nervous system transiently imbalances the amounts of order and disorder to limit the potential sensory responses to comply with the expectations about the detected stimulus and to restrict motor outcomes to select coherent behaviors (e.g., efficient foraging strategies). The latter is supported by the observation that consecutive movements are more likely to have a similar laterality if they were chained within less than 10 s than for longer inter-bout intervals.

Our analysis allowed the study of the spatiotemporal distribution of simultaneous neuronal avalanches at different locations of the brain. We showed that the locations at which avalanches began, or “epicenters,” were evenly distributed across the neuronal somata regions of the brain. We found that pairs of avalanches were slightly correlated for short and moderate distances ($\sim$150 μm), suggesting that avalanche initiation is a locally driven process with moderate correlations due to local connectivity. Ignition of avalanches might occur due to a local imbalance of the E/I ratio, where activity nucleates and spreads (Orlandi et al., 2013). Furthermore, by studying the statistics of neuronal avalanches in different brain regions, we found that, while criticality was observed at the whole-brain level, the dynamics of single anatomical brain regions can be suggestive of critical behavior (e.g., optic tectum) or slightly deviate from it (e.g., reticulospinal circuit). Interestingly, the avalanches in the reticulospinal circuit were faster than those predicted by crackling noise dynamics and those observed in the optic tectum. We speculate that this difference may reflect the discrepancy in the connectivity architectures of the local circuits adapted for their functional role, with a recurrent network in the optic tectum to serve integration and processing of the sensory information, and a feedforward architecture in the reticulospinal network producing large volleys of activity to rapidly trigger motor movements.

In conclusion, whole-brain spontaneous neuronal activity displays cascading events, exhibiting scale-invariant and order-disorder balance properties that can be interpreted within the framework of criticality. These events initiate locally and spread to large portions of the brain, as needed for integrated communication among segregated specialized brain regions. Moreover, our results support the view that the vertebrate nervous system can rebalance the amounts of order and disorder depending on the interactions with the environment (e.g., strong oncoming sensory inputs and emergent spontaneous behavioral outputs) to rapidly return to a preferred state where levels of order and disorder are balanced enabling the largest possible dynamical repertoire.

STAR★Methods

Key Resources Table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Experimental Models: Organisms/Strains
Tg(elavl3:GCaMP5G)	Boulanger-Weill et al., 2017	RRID: ZFIN_DB-ALT-161209-7
Tg(elavl3:GCaMP6f)	Wolf et al., 2017	RRID: ZFIN_ZDB-ALT-180201-1
Software and Algorithms
HCImageLive 4.3 (Image acquisition)	This paper	https://hcimage.com/hcimage-overview/hcimage-live/
MATLAB scripts (Data Analysis, stimulus control, scanner and piezo control)	This paper	https://www.mathworks.com/products/matlab.html
NCC MATLAB Toolbox	Marshall et al., 2016	http://www.nicholastimme.com/software.html
Python package Powerlaw	Alstott et al., 2014	https://github.com/jeffalstott/powerlaw

Contact for Reagent and Resource Sharing

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Germán Sumbre (sumbre@biologie.ens.fr)

Experimental Model and Subject Details

Zebrafish larvae were raised in 0.5x E3 embryo medium and kept under a 14/10 hr on/off light cycle. After 5 days-post-fertilization (dpf), larvae were fed with paramecia. Calcium imaging experiments were performed using 6-8 dpf Tg(huC:GCaMP5)^ens102Tg (Boulanger-Weill et al., 2017) or Tg(huC:GCaMP6f) zebrafish larvae (datasets 1–6, see Table S1). Tg(huC:GCaMP6f)^a12200Tg was provided by DGC. Hildebrand (Harvard, USA) (Wolf et al., 2017). Both transgenic lines are in Nacre background (mitfa−/−). Note that zebrafish sex differentiation begins only between 21 and 23 dpf (Uchida et al., 2002). For imaging purposes, the larvae were placed dorsal-side up on a coverslip platform (5mm high, 5 mm wide) and head-fixed in 2% low-melting agarose (Invitrogen, USA) in E3 embryo medium. Once jellified, the agarose around the tail was removed, letting it free to move. No paralyzer agents or anesthetics were used. All protocols used in this study were approved by Le Comité d’Éthique pour l’Expérimentation Animale Charles Darwin (038393.03).

Method Details

Selective-plane illumination microscopy

We used selective-plane illumination microscopy (SPIM) to record the neuronal activity at near cellular resolution across the brain (Figure S1). Optical sectioning was achieved by the generation of a micrometer-thick light sheet to excite GCaMP from the side of the larva. The GCaMP emission was collected by a camera whose optical axis was orthogonal to the excitation plane (a 488 nm laser, Phoxx 480-200, Omicron). The laser beam was first filtered by a 488 cleanup filter (XX.F488 Omicron) and coupled to a single-mode fiber optic. The beam was expanded using a telescope (f = 50 mm, LA1131-A, and f = 150 mm, LA1433-A, Thorlabs) and projected onto two orthogonal galvanometric mirrors (HP 6215H Cambridge technology) to scan the laser beam, whose angular displacement were converted into position displacement by a scan lens (f = 75 mm AC508-075-A-ML, Thorlabs). The laser beam was then refocused by a tube lens (f = 180 mm, U-TLUIR, Olympus) and focused on the pupil of a low-NA (0.16) 5x objective lens (UPlan SAPO 4x, NA = 0.16, Olympus) facing the specimen chamber. The arrangement yielded a 1mm-wide illumination sheet and a beam waist of 3.2 μm (1/e2). The emitted fluorescence light was collected by a high-NA water-dipping objective (N16XLWD-PF, 16x, NA = 0.8, Nikon) mounted vertically on a piezo translation stage (PI PZ222E). A tube lens (f = 180mm U-TR30IR, Olympus), a notch filter (NF03-488, to filter the laser’s excitation light), a band-pass filter (FF01 525/50 Semrock) and a low-pass filter (FF01 680 SP25 Semrock, to filter the IR light) were used to create an image of the GCaMP emitted fluorescence on a sCMOS sensor (Orca Flash 4.0, Hamamatsu). The volumetric brain recordings were obtained by sequentially recording the fluorescence in 40 coronal sections spaced by 5 μm. For this purpose, the light sheet was scanned vertically in the dorso-ventral direction in synchrony with the objective of the emission path. The camera was triggered to acquire an image every T_exposure = 10 ms. Once the 40 coronal sections were recorded, the position of the light sheet and the objective of the emission path was reset to their initial dorsal position (T_reset = 70 ms). This resulted in a volumetric acquisition time of 0.47 s (i.e., 40 × T_exposure + T_reset) or a rate of 2.1 Hz.

Spontaneous and visual stimulation periods

The experiment was composed of Q consecutive segments of 20 min of spontaneous activity and 4 min of visual stimulation (Figure S1D). Q was different for different datasets and ranges between 3–9 (see Table S1). Each visual stimulation period contained 8 sub-episodes during which a moving grating was presented below the larva for 10 s. The inter-stimulus interval was equal to 20 s. The stimuli were projected on a screen (#216 White Diffusion, Rosco Cinegel) placed 5 mm below the larva and covering a field of view of 35 × 25 mm (148°, 136°), using a pico-projector (PK320, Optoma). To avoid interference with the GCaMP5 and GCaMP6f emission signal (peaking at 547 nm and filtered using a band-pass filter, FF01-520/70 Semrock), only the projector’s red (620 nm) LED was used, and a band-pass filter (629/56, FF01629/56, Semrock) was placed in the projector’s lens. To focus the stimulus on the screen we used a Plano-Convex lens (f = 125 mm, LA1986-B Thorlabs). Gratings had a spatial period of 10 mm, with maximal contrast, and they moved orthogonally to the stripes with velocity equal to 1 cm/s. During each visual stimulation period, the orientations of the 8 consecutive gratings were equal to 0°,60°,180°, −60°,0°,60°,180°, and −60°, respectively, relative to the larva. In the cases in which larvae were exposed to heptanol, the experiment did not include visual stimulation periods and was composed of 70.5 min of spontaneous activity.

Monitoring motor behavior

A small hole in the stimulus projecting screen allowed imaging of the locomotor behavior of the larva (e.g., tail movements), using a small microscope (DZ 1/L.75-5, The Imaging Source) connected to a fast infrared camera (Hxg20nir, Baumer). The larva was illuminated using an IR LED (NG50L 810nm, BDlaser). To separate between the IR light and the projected visual stimuli, we used a dichroic mirror (FM201, Thorlabs). From the binarized image of the larva, we extracted the tail curvature using the method described in (Jouary and Sumbre, 2016).

In order to compute the similarity between successive tail movements, we additionally recorded the behavior of 25 head-restrained Nacre larvae during 3 h while a homogeneous non-patterned illumination was projected below the larvae. The directionality of a tail movement was computed as the sign of the average of the cubed value of the tail curvature for movement classified as Asymmetrical Scoots, Routine Turn or C Bends (Jouary and Sumbre, 2016).

Heptanol experiments

To study the role of gap junctions on spontaneous activity patterns, the neuronal activity from two 7-dpf zebrafish GCaMP5 larvae were exposed to 90 μM heptanol. The heptanol was added to the bath for a duration of 3 hours and washed out just before the experiments (datasets 7 and 8). The concentration of heptanol used here was $\sim 1$0 times lower than previously used in zebrafish to block gap junctions (Saint-Amant and Drapeau, 2000, Muto and Kawakami, 2011, Warp et al., 2012), and did not significantly affected the larva’s behavior under free-swimming conditions. This was tested by comparing the trajectory of 15 freely swimming GCaMP5 larvae at 7 dpf with 15 other larvae exposed to 90 μM of heptanol for 3 hours prior to the recordings. The larvae were placed in a custom-made Plexiglas 30 well plate (15 mm diameter x 5 mm height) filled with embryo medium at room temperature and let habituate for 10 min before the experiment. Homogeneous illumination from below was provided by an electroluminescent panel (MiniNeon, France). Spontaneous behavior was monitored with an Imaging Source DMK 21BF04 camera at 30 Hz for 20 min. We located the position of each larva as the centroid of the background-subtracted images (custom-made code, MATLAB). Figure S8A displays the swimming trajectories and averaged speeds of the control and the heptanol groups.

We additionally tested whether heptanol affects the information processing of sensory stimuli, we ran experiments using 14 larvae at 6 dpf, among them 6 larvae were exposed to 90 μM of heptanol for 3 hours prior to the recordings. The heptanol was then washed out and the larva was introduced in the SPIM recording chamber filled with embryo medium. The chamber was 3D-printed using resin (FormLabs FLGPBK04), and measures 45 mm (l) x 35 mm (w) x 35 mm (h). The larva was restrained in low-melting agarose and placed dorsal-side up at 8 mm from the side of the excitation objective. For experiments in which the tail movement was monitored, we removed the agarose around the tail. Stimuli consisted of single light spot of 4 deg. displayed at four possible closely spaced locations in the visual field (75°, 85°, 90°, 110°, with 0° defined as the longitudinal head-tail axis of the larva, facing the larva’s head), which were randomly presented for a duration of 1 s each, at an inter-stimulus interval of 10 s, on a screen (#216 White Diffusion, Rosco Cinegel) placed on the side of the camber opposite to the excitation objective. The stimuli were generated using MATLAB and Psychtoolbox (Pelli, 1997, Brainard, 1997), and projected using a pico-projector (PK320, Optoma). To avoid interference with the GCaMP emission signal, only the projector’s red (620 nm) LED was used, and a BLP01-561 Semrock long-pass filter was placed in the front of the projector.

Random Field Ising Model

We interpreted our data in the framework of crackling noise dynamics. The Random Field Ising Model (RFIM) is a canonical model to study non-equilibrium disorder-induced phase transitions that produce crackling dynamics (Perković et al., 1995, Sethna et al., 2001, Sethna et al., 2005). The RFIM was introduced to describe a simplified three-dimensional ferromagnetic system. The model is defined on a cubic lattice of magnetic spins $s_i$ with $s_i$ = ± 1 (pointing up or down). Neighboring spins interact through ferromagnetic couplings $J$. Quenched disorder (representing impurity, defects, inhomogeneities, etc.) is modeled by imposing a random field $h_i$ at each spin, taken from a normal distribution with standard deviation $\Delta$, i.e.,

$$P\left(h\right)=\frac{1}{\Delta \sqrt{2\pi }}{e}^{-\frac{h^2}{2{\Delta }^2}}$$

The parameter $\Delta$ controls the amount of (quenched) disorder of the system. An external driving magnetic field $H\left(t\right)$ is applied to the system. The Hamiltonian of the system is given by:

$$\mathcal{H}=-\sum _{i,j}{J}_{ij}{s}_i{s}_j-\sum _i\left(H+h_i\right)s_i.$$

The force $F_i=\left(H+s_i+{\sum }_j{J}_{ij}{s}_j\right)$ exerted on the spin i makes the spin flip either because of the external field (initiation of a new avalanche), or due to the influence of the neighboring spins (propagating an existing avalanche).

Here, we briefly review the scaling properties of the RFIM. If the disorder $\Delta$ is large (i.e., $\Delta \gg J$) then the spins flip independently, producing small avalanches. If the disorder is small (i.e., $\Delta \ll J$) large avalanches are observed that can span the entire system. When $\Delta \sim J$ the balance between order and disorder is achieved and avalanches of all scales are observed. This last case represents a disorder-induced phase transition, achieved at a critical value ${\Delta }_c$ of the disorder.

At the critical point the expected behavior of the system would yield the following scaling relations. The distribution of avalanche sizes measured at a field $H$, or in a small range of fields centered around $H$ at the critical quenched disorder ${\Delta }_c$ scales as:

$$P\left(S,H\right)\sim S^{-\tau },$$

with $\tau =$ 3/2 for $H=H_c$ (in mean-field; for simulations one gets: $\tau \approx$ 1.6). However, the avalanche-size distribution integrated over the field $H$, scales as:

$$P\left(S\right)\sim S^{-\left(\tau +\sigma \beta \delta \right)},$$

with $\tau +\sigma \beta \delta \approx$ 2.03 at the critical quenched disorder ${\Delta }_c$. Note that when analyzing empirical data, it is not possible to know a priori if the distribution is integrated or not. Thus, the observed exponent $\tau$ can be “$\tau$” or ” $\tau +\sigma \beta \delta$ “. Therefore, we simply write $P\left(S\right)\sim S^{-\tau }$.

Similarly, the distribution of avalanche durations $T$ at the critical quenched disorder ${\Delta }_c$ scales as:

$$P\left(T\right)\sim T^{-\alpha },$$

with $\alpha =$ 2 for $H=H_c$ and $\alpha \approx$ 2.81 for the avalanche-duration distribution integrated over the field $H$. The avalanche duration scales with average avalanche size as: . The exponent $\sigma \nu z$ satisfies the following relation: $\sigma \nu z=\left(\tau -1\right)/\left(\alpha -1\right)$. Thus, in the integrated case, we obtain $\sigma \nu z\approx$ 0.57.

Quantification and Statistical Analysis

Image segmentation and GCaMP signal extraction

The first step consisted in compensating for possible drifts in the horizontal plane. For this purpose, each frame was registered according to the maximal cross-correlation with a reference frame. The reference frame was the average of a 10 s. The registered stacks were then manually inspected to evaluate the drift in the ventro-dorsal plane, a drift that could not be compensated. Experiments with such drifts were discarded. Movement artifacts were detected according to large deviations in the maximum of the cross-correlation between successive frames. All frames with large deviations were discarded, they mostly occurred during large tail movements. Individual regions of interest (ROIs) were defined, in each plane, as hexagons of side lengths equal to 6.3 μm, corresponding to an area roughly equal to a neuron’s soma of the zebrafish larva. The advantage of using a hexagonal grid was to maximize the area of the brain covered by the ROIs. The neuropil and neuronal somata were not dissociated in the analysis. We selected the hexagonal ROIs that showed coherent activity among the pixels composing them. For this, we calculated the average correlation $\left(c_{pix}\right)$ between the fluctuations of fluorescence intensity $\Delta F/F$ of the pixels composing a ROI and the average fluorescence of the ROI. We selected ROIs with $c_{pix}$ > 0.25, for datasets 1–5, and $c_{pix}$ > 0.20, for datasets 6–8. To avoid taking into account ROIs with baselines difficult to estimate, we excluded ROIs with extreme fluorescence intensity variance (> 90th percentile of the distribution of signal variances). The hexagonal ROIs that passed these selection criteria were associated to putative single neurons. The number of selected ROIs for further analyses ranged between N = 41,115–89,349 (see Table S1).

Activity clusters and neuronal avalanches

We were interested on the clusters of co-active and contiguous ROIs. For this, we first binarized the activity of each of the cells by thresholding the fluctuations of fluorescence intensity $\Delta F/F$ with a threshold equal to $3{\sigma }_{noise}$, where ${\sigma }_{noise}$ is the standard deviation of the baseline fluctuations of the cell (Romano et al., 2017). Above this threshold the activity was set to 1, otherwise it was set to 0. Next, at each time step t, we detected the connected components, i.e., clusters formed by contiguous co-activated ROIs, on the three-dimensional spatial distribution of the active cells. This was done using the MATLAB function bwconncomp. The algorithm finds the connected components in a co-activated nearest neighbors graph: two ROIs i and j of the 3D matrix are connected if they are both active and j is in the neighborhood of i. The neighborhood of a ROI i is composed of the 20 ROIs that surround it (6 within the same plane and 7 in each of the two planes above and below it). A cluster is composed of at least 3 co-active, contiguous ROIs. At each time frame t, we obtained $m$ clusters that we noted $C_{i,t}$, where $i\in \left\{1,\dots ,m\right\}$, with associated sizes (number of ROIs) noted $C_s\left(i\right)$.

Neuronal avalanches describe the spatiotemporal evolution of the activity clusters. A new avalanche was initiated at time t₀ by the activation of a cluster $\left(C_{i,t_0}\right)$ of ROIs that were not active at the preceding time frame, i.e., $C_{i,t_0}\cap C_{j,t_0-1}=\varnothing$. If at least one ROI of the cluster $C_{i,t_0}$ continued to be part of a cluster at time t₀ + 1, i.e., $C_{i,t_0}\cap C_{j,t_0+1}\ne \varnothing$, then the avalanche was continued, and so on, until this condition no longer held (Figure S3). The size of the avalanche was given by the number of activations during the avalanche.

The definition of avalanches used here is that used in studies of sand-pile, Ising models, and in a recent fMRI study (Tagliazucchi et al., 2012), but it is different from that used in most of previous studies on neuronal avalanches (Beggs and Plenz, 2003, Mazzoni et al., 2007, Pasquale et al., 2008, Friedman et al., 2012, Hahn et al., 2010, Hahn et al., 2017, Shriki et al., 2013, Priesemann et al., 2014). In those studies, avalanches were defined as consecutive time bins with at least one active site (among tens to hundreds of signals). In the present study, this standard definition is not practical since at each time frame the probability that at least one among the $N$ recorded ROIs ($N>$ 40,000) is active is extremely high, leading to one single avalanche that never terminates. Thus, a spatial constraint needs to be included. Ideally, one would like to concentrate on cascade patterns produced by synaptically coupled neurons, but unfortunately, we do not have this connectivity information. Thus, we focused on nearby ROIs which we assumed are putative neurons that are likely to be connected. The size of the clusters used to analyze the avalanches was chosen within a range in which the statistics of the neuronal avalanches were consistent. We observed that for clusters of a radius below $\sim$30 μm, the avalanches showed consistent exponents for the power-law distributions for the size, the duration and their relationship, that matched those from theory. Above 30 μm, the exponents were inconsistent and deviated from the theoretical ones (Figures S4D–S4F). The definition of the size of the clustering neighborhood used in the present study lies below this threshold. We also note that the exponents were consistent for time bins shorter or equal to 1.41 s (Figures S4G–S4I). Notice that since nearby neurons share common tuning properties, spatially compact avalanches are likely to transmit functionally relevant information (Romano et al., 2015), making the avalanche definition biologically meaningful. Zebrafish larvae connectome will allow us in the future, to exactly define avalanches and test dynamic models that produce the observed statistics (Hildebrand et al., 2017).

Power-law fitting

We used maximum likelihood estimation (MLE) to fit truncated power laws to the data as described in Marshall et al. (2016). The cutoffs used to truncate the data are indicated in Tables S1 and S2. This method estimates the power-law exponent. The estimation error of the exponent was calculated using bootstrap re-sampling (1,000 re-samplings). To evaluate the fit between the empirical data and the MLE fit we used Kolmogorov-Smirnov (KS) statistics.

Clauset et al. (2009) proposed to evaluate the significance of power-law fits using synthetic power-law surrogates to derive a distribution of KS values. These are then compared to the KS statistic of the empirical distribution: the p value of rejecting the power-law fit is given by the proportion of sample distributions with KS-statistics larger than the KS statistic between the original distribution and the model distribution. In our data, we found that this method systematically rejects the power-law hypothesis (p < 0.05). However, it is known that, due to its dependence on sample size, this method is not informative in the large sample size regime (Clauset et al., 2009, Klaus et al., 2011, Alstott et al., 2014, Marshall et al., 2016), as in our case where the number of observed avalanches per experiment is > 100,000. Indeed, because any empirical data rarely follows an idealized mathematical relationship in the large sample regime, even small deviations from a perfect power law (due to noise) would lead to the rejection of the power-law hypothesis. For this reason, we tested the power-law hypothesis by asking whether the power law is the best descriptor of the data compared to an alternative heavy-tailed distribution, i.e., the lognormal distribution. For this, we calculated the log-likelihood ratio (LLR) between the two candidate distributions, as follows:

The lognormal distribution follows the density function: $P\left(x\right)=1/\left(x\sigma \sqrt{2\pi }\right)\exp \left[-1/2{\left(\log \left(x-\mu \right)/\sigma \right)}^2\right]$, with dispersion parameter $\sigma >$ 0 and location parameter $\mu >$ 0. For a given data $x=\left(x_1,\dots ,x_n\right)$, the LLR between the power-law and the lognormal was given by $LLR\left(x\right)=L{L}_{PL}\left(x\right)-L{L}_{LN}\left(x\right)$, where $L{L}_{PL}$ and $L{L}_{LN}$ are the log-likelihoods of the power law and the lognormal, respectively. LLR is positive if the likelihood of the power law model for a given empirical dataset is larger than the likelihood of the exponential model, and it is negative otherwise. To test whether the LLR is significantly different from zero, the p value for the LLR test is given by: $p=erfc\left(\left|LLR/\sqrt{2n{\kappa }^2}\right|\right)$, where $erfc$ is the complementary error function, ${\kappa }^2=1/n{{\sum }_{i=1}^n\left[\left(L{L}_{PL}\left(x_i\right)-L{L}_{PL}\left(x\right)/n\right)-\left(L{L}_{LN}\left(x_i\right)-L{L}_{LN}\left(x\right)/n\right)\right]}^2$, and $\left|LLR\right|/\sqrt{2n{\kappa }^2}$ is the normalized log-likelihood ratio (Klaus et al., 2011, Alstott et al., 2014). See Tables S1 and S2.

Scaling shape collapse

We evaluated the similarity of average avalanche profiles, $\langle S\left(t,T\right)\rangle$, across different temporal scales. For this, we used the method of Marshall et al. (2016) to automatically find the scaling parameter $a$ that produces the best possible collapse given by: . The method estimates the scaling parameter $a$ that minimizes the variance ${\sigma }_F^2$ across the avalanche profiles in the normalized time $\left(t/T\right)$. The amount of collapse, $\Delta {\sigma }_F^2$, was quantified by comparing the variance across avalanche profiles in the normalized time with and without scaling, i.e., $\Delta {\sigma }_F^2={\sigma }_F^2\left(0\right)/{\sigma }_F^2\left(a\right)$, where $a$ is the estimated scaling parameter.

We estimated the curve onto which the scaled inter-avalanche time intervals conditional distributions collapse using a gamma distribution, as in previous studies on earthquake temporal occurrence (Corral, 2007). The gamma distribution is given by:

$$G_{\gamma }\left(\theta \right)=\frac{\gamma }{\text{Γ}\left(\gamma \right)}{\left(\gamma \theta \right)}^{\gamma -1}{e}^{-\gamma \theta },$$

where $\gamma$ is the shape parameter, $\theta$ represents the normalized time interval , and $\text{Γ}$ is the Euler gamma function. The shape parameter was estimated using least-squares. As for avalanche profiles, we quantified the amount of collapse $\Delta {\sigma }_G^2$ by comparing the variance across recurrence time log-distributions in the normalized time with and without scaling ($\Delta {\sigma }_G^2$ is equal to the variance of divided by the variance of ) (see Table S2).

Kullback-Leibler divergence

We quantified how well a given empirical distribution can be described by a power law, $PL\left(x\right)=K{x}^a$, where the constant $K$ is chosen so that the integral of $PL$ equals 1, and where the power-law exponent $a$ was estimated from the empirical distribution using MLE. We calculated the Kullback-Leibler divergence (KLD) between the empirical distribution and $PL$. The KLD is a measure of dissimilarity between the empirical distribution and the theoretical power law; thus, the inverse of KLD can be used as a measure of goodness-of-fit of the power-law model. Let $P_{\text{emp}}\left(x\right)$ be the empirical distribution constructed using a histogram of B bins that partition the data into $\left\{x_1,x_2,\dots ,x_B\right\}$. The KLD between $P_{\text{emp}}\left(x\right)$ and $PL\left(x\right)$ is given by:

$$KLD=\sum _{k=1}^B{P}_{\text{emp}}\left(x_k\right)\log \frac{P_{\text{emp}}\left(x_k\right)}{PL\left(x_k\right)}.$$

Power spectrum of avalanche time courses

We calculated the power spectral density (PSD) of the neuronal avalanche time-course $S\left(t\right)$ using the fast Fourier transform. The PSD of an avalanche of duration $T$ is given as $2{\left|\tilde{S}\left(f\right)\right|}^2/T,$ where $\tilde{S}\left(f\right)$ is the Fourier transform of $S\left(t\right)$ and $f$ is the frequency. We restricted the analysis to avalanches of duration $T$ comprised between 3.76 s (8 time points) and 18.8 s (40 time points). The choice of the upper limit of $T$ is determined by the upper cutoff used in the other avalanche analyses, and the lower limit of $T$ was chosen to get enough time points. To estimate the PSD from avalanche time courses of different durations, we interpolated the PSD to the same spectral resolution. Specifically, we calculated the average PSD across all avalanches of duration $T$, denoted by ${\text{Φ}}_S\left(f,T\right)$. We then linearly interpolated it to a fixed spectral resolution given by $f\in \left[1/T_{\text{max}},2/T_{\text{max}},\dots ,1/\left(2dt\right)-1/T_{\text{max}}\right]$, where $T_{max}=$ 18.8 s and $dt$ is the temporal resolution of the data ($dt=$ 0.47 s). Finally, we averaged the interpolated PSDs across all durations.

Surrogate datasets

For each dataset, the data could be represented as an N × L binary matrix, where N is the number of cells and L is the number of time frames. Our neuronal avalanche analysis describes the spatiotemporal statistics of the data. We compared these statistics to several types of surrogate/shuffled data. The first type of surrogate, called time-shuffled data, was designed to probe the sensitivity to the temporal organization of the ensemble activity. It was obtained by randomizing the time indices of the N-dimensional activity vectors, thus destroying the temporal organization of the data while preserving the spatial correlations. This control is important since Ca²⁺ transients last significantly longer than the voltage fluctuations that produced them, thus, fundamentally limiting the temporal resolution of neural activity as measured through Ca²⁺ signals. The second type of re-sampling was specifically designed to assess whether the collapse of the conditional recurrence time interval distributions $\text{P}\left(\text{Δ}t,S>s\right)$ artifactually arises due to thresholding. Specifically, this surrogate dataset randomizes the neuronal avalanche sizes while keeping the sequence of starting/ending times fixed, thus destroying the correlation between avalanche sizes and recurrence times. Due to the large amount of data and the computational cost of our analyses, the data was re-sampled once for the two first types of surrogates. A third surrogate was used to compare the distribution of observing two avalanches that initiated simultaneously with centers of mass separated by a distance d to the expected distribution when the times of avalanche initiation were randomized. In this case, randomization was repeated 20 times for each of the Q data segments composing each dataset.

Center of mass of a neuronal avalanche

The center of mass (CM) of a given neuronal avalanche of duration $T$ was given by the average location of the distribution of active ROIs composing the avalanche at each time t. Let $n$ be the number of ROIs participating in the avalanche at time t and ${\overrightarrow{x}}_i$ the 3D spatial coordinates of the i-th ROI. The CM is given as: $\overrightarrow{CM}\left(t\right)=1/n{\sum }_{i=1}^n{\overrightarrow{x}}_i$, for $1\le t\le T$. We followed the temporal evolution of the avalanche by calculating its averaged velocity of the CM, $\overrightarrow{V}$, given by the averaged time derivative of the CM: $\overrightarrow{V}={\sum }_{t=1}^{T-1}\left[\overrightarrow{CM}\left(t+1\right)-\overrightarrow{CM}\left(t\right)\right]/\left(T-1\right)$. To get reliable estimates of $\overrightarrow{V}$, only avalanches of duration $T\ge$ 2.35 s were used. It is important to note that the velocity of the center of mass should not be confounded with transmission velocity, nor with front propagation ($V$ = 0 for an avalanche that grows in a perfect isotropic way). We instead used it here to describe global tendencies of propagation and to compare spontaneous versus stimulus-driven activity (see Figure 6).

Maximum likelihood decoder

We used a maximum likelihood decoder (MLD, see Figures S8E–S8G) to classify the location of visual stimuli presented to larvae from the fluorescence signals $\Delta F/F$ in the optic tectum (Avitan et al., 2016). For this purpose, we compared the decoding efficiency between larvae in normal conditions (n = 8) with respect to larvae exposed to 90 μM heptanol (n = 6, see STAR Methods). Specifically, we presented to the larvae a set of four light spots projected at different spatial locations (75°, 85°, 90°, 110°). Each stimulus lasted 1 s and was presented for $n_{stim}$ = 40 repetitions. The inter-stimulus interval was equal to 10 s. As a measure of neuronal response, we used the mean fluorescence signal during the stimulus presentation for each ROI. The number of ROIs ranged between 1766–2490 for the different larvae. The MLD chooses the stimulus that is statistically most likely to have elicited an observed response of $n$ signals, i.e., $\overrightarrow{r}=\left[r_1,r_2,\dots ,r_n\right]$. It uses a leave-one and cross-validation procedure. For this, the probability distribution of the response of each ROI to each stimulus type j was computed, i.e., $P\left(r_i\text{|}j\right)$, using $n_{stim}-1$ observations of the stimulus. The remaining observation, $r_{i,test}$, was used for testing. To obtain continuous conditional probability estimates, the histograms $P\left(r_i\text{|}j\right)$ were smoothed using a normal kernel function. With the simplifying assumption that the responses of the ROIs were statistically independent from each other, the learned conditional probability of the population response is given by the product over all individual conditional probabilities:

$$P\left(\overrightarrow{r}\text{|}j\right)=\prod _{i=1}^{n}P\left(r_i\text{|}j\right).$$

Decoding the population response consisted of searching for the stimulus $\left(s_{ML}\right)$ which maximized the probability of the testing response: $s_{ML}=\underset{j\in \left\{1,2,\mathrm{3,4}\right\}}{\text{argmax}}P\left({\overrightarrow{r}}_{test}\text{|}j\right).$ This procedure was repeated, each time leaving one response vector out and using the remaining population response vectors to learn the conditional probabilities. The performance was defined as the proportion of population response vectors that were correctly classified. To assess statistical significance of the classification performance we calculated the probability of getting correct classifications by chance, which is given by the binomial distribution: $P\left(k\right)=\left(\begin{array}{c}m\\ k\end{array}\right)p^k{\left(1-p\right)}^{m-k}$, where p is the probability of getting a correct classification by chance (p = 1/4) and m is the number of tests. Significant decoding was reached when the decoding performance exceeded the 95th percentile of $P\left(k\right)$. The classification performance was computed using the fluorescence signals of 10 randomly chosen ensembles of $n$ ROIs and then averaged over ensembles and larvae.

Statistical tests and software

The significance of power-law fits was evaluated using Kolmogorov-Smirnov (KS) statistics between the empirical data and the MLE fit and by log-likelihood ratio (LLR) tests between the power-law distribution and the log-normal distribution. When using one-way repeated-measures (rm) ANOVA, where the ANOVA’s sphericity assumption was not met (using the Mauchly test), p values were corrected using the Huynh-Feldt estimates of sphericity. No statistical methods were used to determine sample sizes in advance, but sample sizes are similar to those reported in other studies in the field.

Data was analyzed with custom routines written in MATLAB. Power-law and scaling shape collapse analyses were performed using the NCC MATLAB Toolbox described in Marshall et al. (2016) and available at: www.nicholastimme.com/software.html. LLR tests were performed using the Python package Powerlaw, described in Alstott et al. (2014), and available at: https://github.com/jeffalstott/powerlaw. The Orca Flash 4.0 sCMOS camera (Hamamatsu) was controlled using HCImageLive 4.3 (Hamamatsu). The scanner and the piezo were controlled using custom-made routines in MATLAB.

Data and Software Availability

Custom written MATLAB code will be made available by the authors upon request.

Published: November 15, 2018