Development of a Statistical Model for Discrimination of Rupture Status in Posterior Communicating Artery Aneurysms

Abstract

Background

Intracranial aneurysms at the posterior communicating artery (PCOM) are known to have high rupture rates compared to other locations. We developed and internally validated a statistical model discriminating between ruptured and unruptured PCOM aneurysms based on hemodynamic and geometric parameters, angio-architectures, and patient age with the objective of its future use for aneurysm risk assessment.

Methods

A total of 289 PCOM aneurysms in 272 patients modeled with image-based computational fluid dynamics (CFD) were used to construct statistical models using logistic group lasso regression. These models were evaluated with respect to discrimination power and goodness of fit using ten-fold nested cross-validation and a split-sample approach to mimic external validation.

Results

The final model retained maximum and minimum wall shear stress (WSS), mean parent artery WSS, maximum and minimum oscillatory shear index, shear concentration index, and aneurysm peak flow velocity; along with aneurysm height and width, bulge location, non-sphericity index, mean Gaussian curvature, angio-architecture type, and patient age. The corresponding area under the curve (AUC) was 0.8359. When omitting data from each of the three largest contributing hospitals in turn, and applying the corresponding model on the left-out data, the AUCs were 0.7507, 0.7081 and 0.5842, respectively.

Conclusions

Statistical models based on a combination of patient age, angio-architecture, hemodynamics and geometric characteristics can discriminate between ruptured and unruptured PCOM aneurysms with an AUC of 84%. It is important to include data from different hospitals to create models of aneurysm rupture that are valid across hospital populations.

Introduction

The posterior communicating artery (PCOM) is a common site for aneurysm development. Aneurysms at this location account for approximately 25% of all intracranial aneurysms [14]. They have a larger rupture risk than aneurysms at other locations [23] such as the middle cerebral artery (MCA) or other segments of the internal carotid artery (ICA) [7, 33]. As such, clinicians often need to decide whether or not to treat PCOM aneurysms, but reliable aneurysm-specific parameters to guide and support these decisions are lacking.

Previously published prediction models for aneurysm rupture include the PHASES score [15] and a score developed in Japanese cohorts [30]. Furthermore, a multivariate logistic regression model for discrimination between ruptured and unruptured aneurysms based on hemodynamic and morphological parameters has been presented [35]. The three models were developed from data of aneurysms at different locations. Furthermore, both the PHASES and the Japanese score do not include hemodynamic and morphological information (besides aneurysm size). The multivariate model is based on a comparatively small sample size and has not been validated so far.

In a previous study, we found that hostile hemodynamic conditions characterized by strong and concentrated inflow jets, concentrated regions of elevated wall shear stress (WSS), oscillatory WSS, and complex unstable flow patterns were associated with rupture of PCOM aneurysms; and that such conditions were more commonly found in bifurcation-type angio-architectures [8]. In the current paper we extend that prior work by creating and evaluating models that discriminate between PCOM aneurysm rupture status based on numerous demographic, anatomical, geometrical and hemodynamic features. Once validated in the future with prospective longitudinal data, these models could potentially be used to improve current risk assessment of PCOM aneurysms.

Methods

Patient and Image Data

All aneurysms at the posterior communicating artery (PCOM) from our database of image-based cerebral aneurysm models, included in a previous publication [8], were analyzed. Our database includes patient and image data of patients who underwent cerebral angiography. The cohort’s characteristics are summarized in Tab. 1. There were 300 patients from 6 different hospitals harboring 322 PCOM aneurysms with known rupture status. After exclusion of fusiform aneurysms, infundibula, and one further case because it was the only case in one of our angio-architecture groups (see Statistical Modeling sub-section), the sample size was reduced to 289 aneurysms in 272 patients. The overall prevalence of ruptured aneurysms for the 289 aneurysms was 49% (142 ruptured and 147 unruptured). Of the 272 patients, 17 had two PCOM aneurysms (2 ipsilateral, 15 bilateral, see Fig. 1 in the Online Suppl. Material for the ipsilateral cases). The majority of aneurysms in our database came from three contributing hospitals: 1) Mayo Clinic (mayo), 2) Mt. Sinai Medical Center (sinai), 3) Inova Fairfax Hospital (inova). At these three hospitals, there were 40 PCOM aneurysms out of a total of 256 aneurysms from all locations (16%, mayo), 77 out of 417 (18%, sinai), and 198 out of 1298 (15%, inova). The prevalence of rupture status at the time of presentation of PCOM aneurysms for these hospitals were 41% (mayo), 51% (sinai), and 52% (inova). Unfortunately, patient gender and age information were not available for the mayo cases.

Tab. 1.

Cohort Characteristics.

Whole cohort (cases with known rupture status and location; fusiform aneurysms excluded)	Number of patients	1265
	Number of aneurysms (ruptured/unruptured)	1931 (558/1373)
	Patient age (mean ± sd) (of 1065 patients with known age)	56.21 (13.82)
	Patients with multiple aneurysms	358
	Gender ratio (of 1076 patients with known gender)	810 F, 266 M
	Number of patients with SAH	558
	Distribution by location	ACA: 65 (3.37%)
		ACOM: 278 (14.40%)
		BA: 136 (7.04%)
		ICA: 741 (38.37%)
		MCA: 354 (18.33%)
		PCOM: 312 (16.16%)
		VA: 45 (2.33%)
Cohort used for this study	Number of patients	272
	Number of PCOM aneurysms (ruptured/unruptured)	289 (142/147)
	Patient age (mean ± sd) (of 232 patients with known age)	59.09 ± 14.26
	Patients with multiple PCOM aneurysms	17
	Gender ratio (of 234 patients with known gender)	193 F, 41 M
	Number of patients with SAH	161

ACA=Anterior cerebral artery, ACOM=anterior communicating artery, BA=basilar artery, ICA=internal carotid artery, MCA=middle cerebral artery, PCOM=posterior communicating artery, VA=vertebral artery

Hemodynamic Modeling

Patient-specific computational fluid dynamics (CFD) models were constructed from 3D angiographic images [5]. The trunk of the ICA down to the cavernous segment was included in order to appropriately describe the inflow into the aneurysm. Arteries were cut perpendicularly to their axes for subsequent inlet and outlet definition. The vessels were modeled by unstructured grids with a maximum element size of 0.2 mm.

For the CFD simulations, pulsatile flow conditions derived from phase-contrast MR measurements in healthy subjects [13] were scaled with a power-law of the inlet vessel area [6] and applied as inflow boundary conditions at the proximal ICA using the Womersley solution [29]. Outflow boundary conditions were set as pressure and flow outlets, consistent with Murray’s law. Blood was modeled as a Newtonian fluid with a density of 1.0 g/cm³ and a viscosity of 0.04 poise. Vessel walls were approximated as rigid. The 3D incompressible Navier-Stokes equations were numerically solved with an in-house finite element solver [24]. Two cardiac cycles with a heart rate of 60 beats per minute were computed with 100 time steps per cardiac cycle. For the hemodynamic characterization, results from the second cycle were used.

Post-Processing

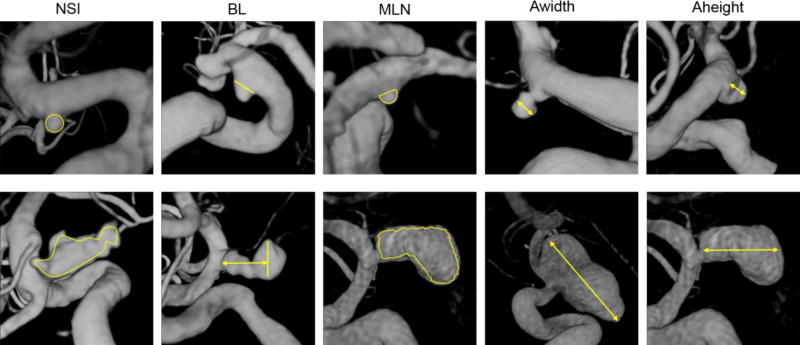
In a post-processing step, hemodynamic and morphological variables previously used to compare hemodynamic conditions in ruptured and unruptured PCOM aneurysms were automatically calculated from the computed flow field and the 3D geometrical model of the aneurysm [4, 20, 25, 26]. A total of 22 hemodynamic and 25 geometrical parameters were computed (see Tab. 2 and 3 in the Online Suppl. Material as well as Fig. 1 for an illustration of selected shape parameters).

Fig. 1.

Illustration of selected shape parameters (NSI-non-sphericity index, BL-bulge location, MLN-mean surface curvature, Awidth-aneurysm width, Aheight-aneurysm height). Top panel: Aneurysms with low values of respective variable. Bottom panel: Aneurysms with high values of respective variable. For the definition of all shape parameters see the Online Suppl. Material and the references therein

Statistical Modeling

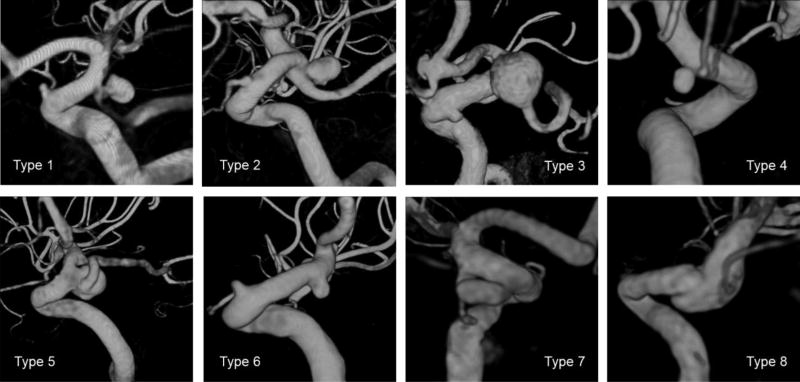
Prediction models were fitted to the data using logistic group lasso regression [22]. This approach of regularized regression results in models where, depending on the magnitude of a tuning parameter, certain regression coefficients are set to exactly zero. Hence, only variables with a non-zero coefficient are retained in the final model. Since the penalty term of the lasso regression penalizes more complex models (models including more variables), lasso regression can also be used for model fitting in situations where the sample size is comparably small relative to the number of variables [3]. Ten-fold cross-validation was used to select the aforementioned tuning parameter. In this step, the data were split in training and validation sets for each of the ten folds, and the optimization parameter achieving on average the highest area under the curve (AUC) of the receiver operating characteristic (ROC) curve in the validation set was selected for the final model. All 22 hemodynamic and 25 morphological parameters as well as patient age were used for model fitting. Additionally, patient gender and previously defined angio-architecture classes [8] were included as categorical variables and coded by dummy variables with a sum-to-zero constraint (see Tab. 1 in the Online Suppl. Material and Fig. 2 for an illustration of the types of angio-architectures). The columns of the feature matrix of the continuous parameters were centered and standardized to unit-norm. The sub-feature matrix for the dummy variables for the angio-architectures was standardized using a singular value decomposition [27].

As only one aneurysm belonged to angio-architecture type 8, this case was excluded for model fitting. Since gender and age were missing from the mayo data, the sample size was reduced to 245 aneurysms for training a “complete model” including all variables. For this reason, a second model was created omitting these two variables but using the entire sample of 289 aneurysms.

Statistical Model Evaluation

The model’s performance was evaluated as previously described [10]. Briefly, its discrimination for rupture status at presentation and goodness of fit were assessed. Each model’s discrimination was measured by the AUC of the ROC curve. An “optimal threshold” for classification was selected as the probability corresponding to the point on the ROC curve with the smallest distance to (0,1). Based on this threshold the model’s accuracy was evaluated. The goodness of fit was visually estimated by means of calibration plots [28]. As part of the visualization, observed outcomes were regressed on the predicted probability using the loess algorithm with a span parameter of 0.75 [1].

First, the model was internally validated by 160 repetitions of ten-fold nested cross-validation [31]. For each repetition, the process of model fitting was performed in part of the data (training set) and evaluated on the left-out data (validation set). Based on the evaluation of the fitted models in each of the cross-validation samples, the optimism in the AUC was estimated and subtracted from the AUC for the final model [28]. Moreover, it was noted for how many of the cross-validation samples each of the variables was retained in the fitted models. The relative frequency of retention in the cross-validation models can be seen as an indicator for the importance of a variable.

Secondly, for the model excluding patient information, a split-sample approach was used to mimic external validation. Aneurysms of patients from one of the three hospitals with the largest numbers of data were excluded for model fitting and subsequently used for model evaluation.

All statistical analysis was performed with scripts written in the R language.

Results

Complete Model

The results from the evaluation and validation of the fitted models are summarized in Tab. 2.

Tab. 2.

Summary of the results for models fitted for subsamples based on hospitals.

Model	Variables	Hosp. excluded	Sample Size	AUC	AUC nested CV	AUC of left- out data	Ssize left-out
1	Hem, morph, gender, age, angioarch	mayo (missing data)	245	0.8359	0.7547	-	-
2	Hem, morph, angioarch	-	289	0.7920	0.7297	-	-
2a	Hem, morph, angioarch	mayo	250	0.7679	0.6936	0.5842	39
2b	Hem, morph, angioarch	sinai	217	0.7928	0.7361	0.7081	72
2c	Hem, morph, angioarch	inova	118	0.7933	-	0.7507	168

Hem = hemodynamic variables, morph = morphological variables, angioarch = angioarchitectures. The column "AUC nested CV" refers to the AUC of the model after subtracting the estimated optimism by nested cross-validation. The sample size (Ssize) of the left-out data used for evaluation of the models by the split-sample approach is given in the last column

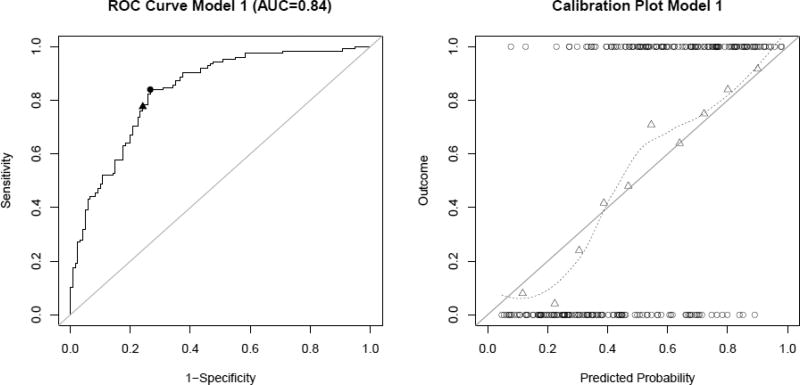
The best discrimination was achieved for the complete model (model 1) including patient information (gender and age) in addition to hemodynamic, morphological parameters, as well as angio-architecture (AUC=0.8359, after correction for optimism AUC=0.7547). Based on the ROC, the “optimal threshold” for classification of an aneurysm as ruptured or unruptured was 0.46. For this threshold, the sensitivity was 0.84, the specificity 0.73, positive predictive value (PPV) 0.77, negative predictive value (NPV) 0.81, and the misclassification error 0.21. If all aneurysms having a predicted probability greater than the “default threshold” of 0.5 are classified as ruptured, the specificity increases to 0.76, but the TPR is reduced to 0.78 and the misclassification error increases to 0.23. The PPV remains the same and the NPV decreases to 0.76. Both thresholds are indicated in Fig. 3. The calibration plot for this model (Fig. 3, right) shows a reasonable fit to the data, although the fitted line deviates slightly from the 45° straight line corresponding to perfect goodness of fit.

Fig. 3.

ROC curve (left) and calibration plot (right) for model 1 (complete model). The circle and triangle on the ROC curve indicate the value corresponding to a classification threshold of 0.46 and 0.5, respectively. The circles at the top and the bottom of the calibration plot show the observed data. Observed outcome grouped by deciles is depicted as triangles and represented by the loess smoother with the dashed line. For a perfectly calibrated fit, all triangles and the loess smoother would lie on the 45°-line

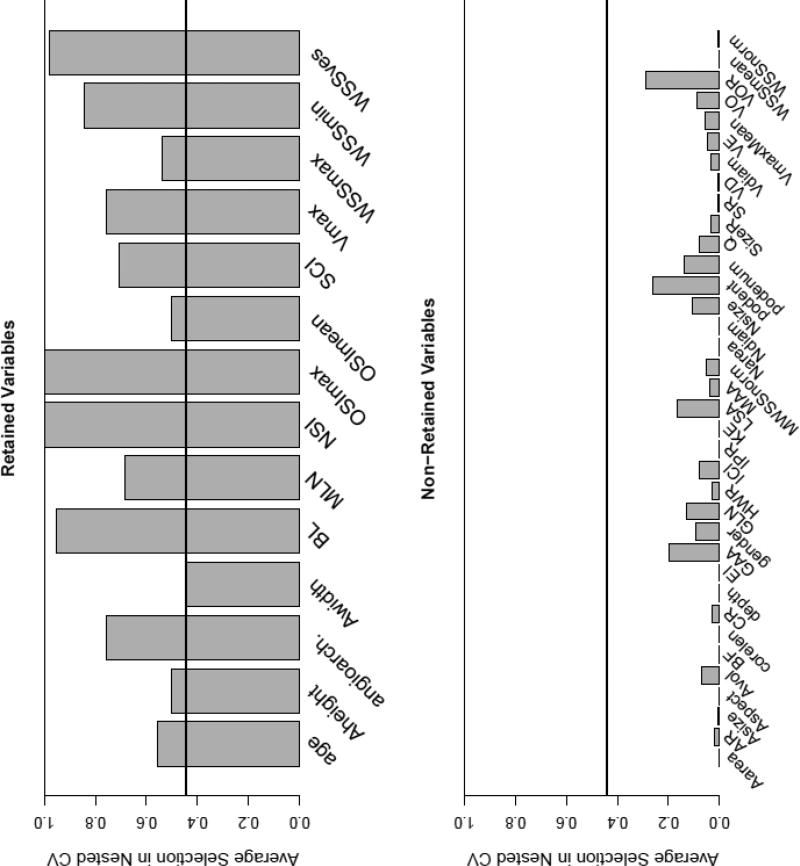
The final model retained the following variables (variables having non-zero coefficients): maximum and minimum wall shear stress (WSS), shear concentration index (SCI), maximum and mean oscillatory shear index (OSI), WSS in the parent vessel (WSSves), peak velocity (Vmax), aneurysm height, width, bulge location (BL), non-sphericity index (NSI) and the mean aneurysm surface curvature (MLN). The coefficients for these variables are listed Tab. 4 in the Online Suppl. Material. The relative frequencies of variable retention in the cross-validation samples are presented in Fig. 4. The minimum frequency of all variables having non-zero coefficients in the final model was higher than the maximum frequency of all variables with coefficients of zero (0.44 vs. 0.29, indicated by the black horizontal line in Figure 4). Among the variables retained in the model, OSImax and NSI had the highest frequency of selection during nested cross-validation (in 100% of the models).

Fig. 4.

Relative frequency of inclusion of variables in samples from nested cross-validation for variables retained in the final model (top) and variables that dropped out in the process of model fitting (bottom). The definitions of the variables can be found in Tab. 2 and 3 in the Online Suppl. Material

Model Excluding Gender and Age

The model excluding gender and age (model 2) achieved an AUC of 0.7920 (Tab. 2). For the “optimal threshold” of 0.47, the TPR, FPR and misclassification error were 0.76, 0.30, and 0.27, respectively. The coefficients for this model are listed in Supplementary Tab. 4, and the calibration plot in Supplementary Fig. 2 (top left). In contrast to model 1 that includes gender and age for model fitting, the aneurysm neck size (Nsize), the POD entropy describing temporal flow stability (podent), and the volume-to-ostium ratio (VOR) had non-zero coefficients, whereas WSSmax, OSImean, and aneurysm height were not retained in model 2.

Effects of Patient Population

To evaluate the effects of different hospital populations, three models excluding gender and age (model 2a, 2b and 2c) were fitted by omitting data from each of the three hospitals in turn (see Tab. 2). The sample sizes for each of these models were 250, 217 and 118, respectively. The coefficients for these models are listed in Tab. 4 in the Online Suppl. Material. Variables that were included in all fitted models (including model 1 and 2) were OSImax and NSI.

The model built after omitting the mayo data (model 2a) had an AUC of 0.7679 but when applied to the mayo data that had been left out, the AUC was only 0.5842 indicating reduced discrimination on this external population. In contrast, the models omitting sinai (model 2b) and inova (model 2c) data had AUCs of 0.7928 and 0.7933, respectively; when applying these models to the left out data, the AUCs were 0.7081 and 0.7507, respectively.

The calibration plots for these models when evaluated in the left-out data are presented in Supplementary Fig. 2. These plots indicate a suboptimal fit of model 2a, while reasonably good fits for models 2b and 2c.

Discussion

The results of this study suggest that statistical models based on a combination of patient information, angio-architecture, hemodynamics and geometric characteristics can discriminate between ruptured and unruptured PCOM aneurysms with an AUC of 84%.

Effects of Patient’s Age and Gender

In our study, younger age associated with higher rupture risk, consistent with previous studies of PCOM aneurysms [37]. The general association of age and rupture is not clear in the literature. Older age is assigned higher risk in the PHASES score [15], and was associated with higher risk of aneurysm growth in a recent study [2]. However, other studies suggested higher risk for younger patients in anterior communicating aneurysms [21], middle cerebral artery aneurysms [32], and in general [18].

It is known that females have a higher incidence of aneurysms both in general and particularly in those located at the PCOM [16]. The association between gender and risk of aneurysm rupture, however, is not clear in the literature [18, 34]. Our results indicate that considering gender does not improve the discrimination of ruptured and unruptured PCOM aneurysms. Hence, other than gender-related mechanisms seem to be important for aneurysm rupture at this location.

Effects of Angio-Architectures

Angio-architectures types 1–3 and 5 (true PCOM aneurysms and aneurysms involving the PCOM origin or bifurcation) associated with higher rupture risk, while types 4,6 and 7 (resembling sidewall aneurysms) associated with lower probability of rupture. The frequency of inclusion of angio-architectures in the nested cross validation samples was 0.76, indicating that angio-architectures are important for discrimination. To verify this finding, a model was fitted excluding angio-architectures. This model resulted in a reduction of the AUC to 0.8263.

Effects of Geometry

Holding all other variables fixed, a higher probability of being ruptured was associated with larger bulge location and more elongated shape (less spherical), in agreement with previous studies [11, 19]. In our sample, a higher rupture risk was also associated with smaller aneurysm height and width, in contrast to previous studies suggesting increased rupture risk with increasing PCOM aneurysm size [12, 17]. However, in a previously performed univariate analysis in our data, ruptured PCOM aneurysms were significantly larger compared to unruptured aneurysms, which is consistent with the literature and current clinical knowledge. This finding demonstrates a difficulty when interpreting the association of a variable with rupture in a multivariate model since the corresponding regression coefficient quantifies the change of risk when all other variables are kept constant. In contrast to the model constructed from aneurysms at several locations by Xiang et al. [35], size ratio was not retained in our final model.

Effects of Hemodynamics

The probability of rupture increased with the mean WSS in the parent vessel and with higher aneurysm peak velocity and maximum WSS and OSI, as well as with lower minimum WSS and mean OSI, suggesting that focalized elevations of WSS and OSI surrounded by lower values may constitute hostile hemodynamic environments that predispose aneurysms to rupture. Lower normalized WSS (WSSnorm) associated with rupture in two previous studies of PCOM aneurysms [12, 36] and in one study including several locations [35]. However, as a result of the modeling fitting process, WSSnorm was not retained in our final model. In the model of Xiang et al. [35], higher mean OSI was associated with higher rupture probability, but in our model, mean OSI was included only in 50% of the nested cross-validation samples and with a negative association. In contrast, maximum OSI was retained in all models with a positive association, suggesting that this is an important parameter. In one previous multivariate model of PCOM aneurysms based on hemodynamics and morphology [19], the rupture probability increased with the area under low shear (LSA) and inflow angle; while another study found significant differences in LSA between ruptured and unruptured PCOM aneurysms [36]. In our study, inflow angle was not considered, and LSA was not retained in the final model.

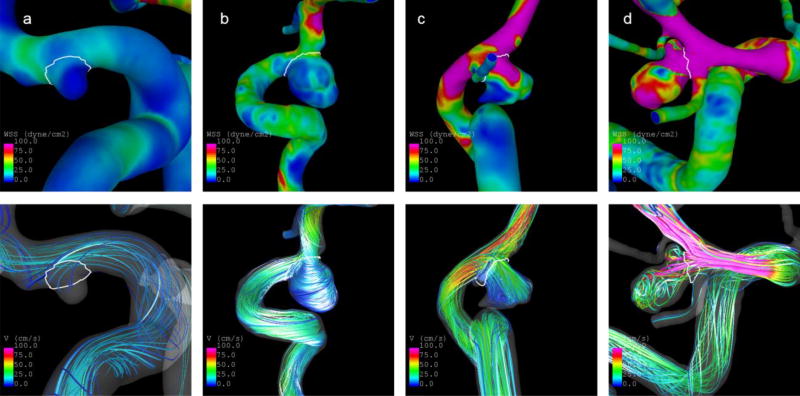
Fig. 5 illustrates the above discussed finings with four cases. The two unruptured aneurysms at the left have low predicted rupture probabilities (4.7% and 10.8%, respectively, based on Model 1). Both of them have an angio-architecture of the lower-risk type 6, a more regular shape, which is also indicated by a low NSI, and are exposed to lower and more regular flow conditions characterized particularly by a lower maximum OSI (see Tab. 3). In contrast, the two ruptured aneurysms at the right have predicted probabilities of 86.4% and 97.7%, respectively. They have a type 2 angio-architecture, which is associated with a higher rupture risk. Moreover, they are more complex in shape and exposed to higher flow conditions.

Fig. 5.

Illustration of cases with low (a–b) and high (c–d) predicted probabilities of being ruptured based on Model 1. Top panel: WSS distribution at half of the cardiac cycle. Bottom panel: Blood flow velocities at half of the cardiac cycle. The predicted probabilities and selected aneurysm characteristics are shown in Tab. 3

Tab. 3.

Characteristics of illustrated cases in Fig. 5.

Case	Prob.	Angio-Type	NSI	OSImax	WSSves [dyne/cm2]	Asize [cm]	Patient age [years]
a	0.0473	6	0.1659	0.0317	12.5408	0.3559	57
b	0.1083	6	0.1795	0.2159	34.2509	1.0198	81
c	0.8636	2	0.2707	0.3497	77.2606	0.7472	31
d	0.9778	2	0.2737	0.3431	148.0400	0.6548	42

Prob=Probability of being ruptured based on Model 1

Model Evaluation

Before applying a prediction model in clinical practice, internal and external validation of the model are essential. In this study, models were internally validated using nested cross-validation and a split-sample approach to mimic external validation. The results from the cross-validation suggested that the retention of variables for the fitted models is reasonably stable with respect to small changes in the data.

The results of the split-sample approach showed that the discrimination power of the models was reduced when applied to the left-out data, especially for the mayo data. This suggests that differences in the hospital populations may affect the performance of the models when applied to a different population, and that in particular, the mayo population may be different from the inova and sinai populations. In fact, the overall rupture prevalence (including all locations) of our inova and sinai datasets is 31% which is significantly different (p=0.002, Chi-squared test) from 21% for the mayo dataset. When restricted to PCOM aneurysms, the rupture prevalence were 52% for inova, 51% for sinai, and 41% for mayo. However, these differences were not statistically significant, most likely due to the small sample size of the mayo PCOM dataset. These differences may reflect the different admission and referral practice patterns at different hospitals. These findings indicate that it is important to include data from different hospitals to create generic statistical models of aneurysm rupture that are valid across populations.

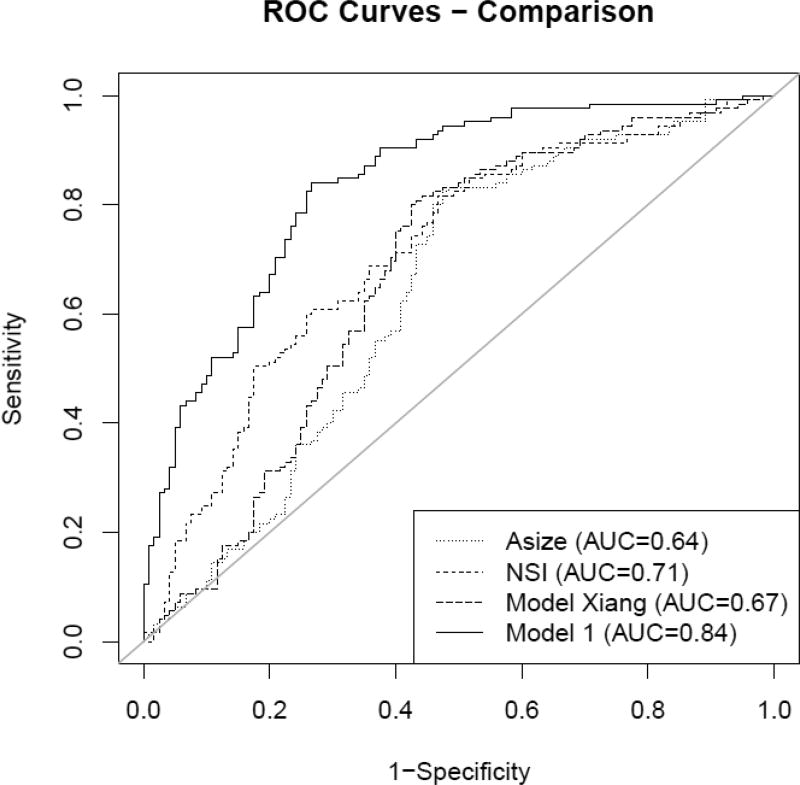
Compared to a previously developed model by Xiang et al. [35] as well as univariate models only using aneurysm size or NSI, the model’s discrimination was remarkably higher (see Fig. 6). This result indicates that applying the model could have additional value over using only aneurysm size, NSI for quantifying shape complexity, or the model reported in [35] when deciding on treatment of an unruptured aneurysm.

Fig. 6.

Comparison of ROC curves for the presented model, a model reported by Xiang et al. [35] and univariate models for aneurysm size and NSI

Furthermore, when applying a recently developed model for aneurysms at various locations [10] to the PCOM cohort here, the AUC was with 0.79 lower than the AUC of the final Model 1. This finding suggests that having a location-specific model including information that is specific to this location, like angio-architectures, could potentially improve rupture risk assessment compared to a more general model.

In this regard, this study aimed at developing a statistical model for discriminating rupture status in PCOM aneurysms. Aneurysms of the anterior communicating artery (ACOM) have a comparable prevalence and risk of rupture [15], indicating a potential for a similar study in those aneurysms. This study focused on PCOM aneurysms motivated by our previous findings [8]. Furthermore, the different types of angio-architectures are more clearly defined for these aneurysms. Future work could include the development of a statistical model for ACOM aneurysms as well.

Clinical Considerations

The presented “probability models” were developed and validated using cross-sectional data. They thus discriminate between ruptured and non-ruptured aneurysms at the time of presentation to the hospital. In contrast, for the training of a predictive model, longitudinal data would be necessary. Nowadays, these data are, however, difficult to obtain and always inherently biased since high-risk aneurysms get treated so that follow-up data of these cases are not available. Therefore, based on the implicit assumption that rupture-prone aneurysms resemble aneurysms that have already ruptured, the presented model can be used as a “surrogate” for a predictive model. Aneurysms classified as “unruptured” or “low-risk” with our model should be observed during follow up to identify possible changes that could increase the predicted rupture risk. To assess the performance of our model in terms of rupture prediction, its validation in prospective longitudinal data is planned in the future.

Besides a thorough external evaluation of the presented model, it is important to provide clinicians with means for applying the model in a clinical setting. Therefore, a web-based tool that allows clinicians the application of the model to new cases will be developed. In addition to providing clinicians purely with the predicted rupture probabilities for a new case, this interface will include visualizations of the specified input parameters for facilitating their interpretation and to illustrate the computed results. After a prior evaluation with clinicians, such a tool could eventually enable the application of the presented model in a clinical setting.

To enable other groups the validation of the proposed model, the Transparent Reporting of a multivariable prediction model for Individual Prognosis Or Diagnosis (TRIPOD) [9] was followed for this publication.

Besides addressing the “standard CFD assumptions”, the current study could be enhanced in several ways. Patient characteristics other than age and gender (e.g. hypertension, smoking, family history, etc.) were not studied due to lack of data for some cases. No validation with the split-sample approach was possible for the complete model due to lack of patient information (age) in the mayo data.

This study is based on data of aneurysms that were assessed by 3D cerebral angiography. Consequently, aneurysms that were only imaged by means of MR angiography or CT angiography as well as undiagnosed aneurysms and aneurysms with fatal ruptures are inherently excluded from our dataset, resulting in a selection bias.

Future multi-center studies with larger and more comprehensive samples from multiple hospitals and populations should be conducted to evaluate and further improve the predictive models, which in turn should be tested on longitudinal datasets.

Conclusions

Statistical models of PCOM aneurysm rupture based on aneurysm hemodynamics, morphology, angio-architecture and patient age, can discriminate between ruptured and unruptured PCOM aneurysms with an AUC of 84%. It is important to include data from different hospitals to create such models of aneurysm rupture that are valid across different hospital populations. Future work will include the external validation of the developed models.

Fig. 2.

Illustration of defined angio-architectures. Type1=True PCOM, Type2=At ICA-PCOM bifurcation, Type3=PCOM from fundus, Type4=PCOM proximal/detached, Type5=PCOM proximal/attached, Type6=No PCOM visible in 3DRA, Type7=PCOM distal/detached, Type8=PCOM distal/attached