Abstract
Preference-based decisions are essential for survival, for instance when deciding what we should (not) eat. Despite their importance, preference-based decisions are surprisingly variable and can appear irrational in ways that have defied mechanistic explanations. Here we propose that subjective valuation results from an inference process that accounts for the structure of values in the environment and that maximizes information in value representations in line with demands imposed by limited coding resources. A model of this inference process explains the variability in both subjective value reports and preference-based choices, and predicts a new preference illusion that we validate with empirical data. Interestingly, the same model explains the level of confidence associated with these reports. Our results imply that preference-based decisions reflect information-maximizing transmission and statistically optimal decoding of subjective values by a limited-capacity system. These findings provide a unified account of how humans perceive and valuate the environment to optimally guide behavior.
Introduction
At any given moment, organisms receive much more sensory and interoceptive information than they can physically process. These capacity limitations are thought to have biased brain evolution towards information-processing strategies that are maximally efficient for the control of behavior, an idea known as efficient coding1,2. Such efficient-coding strategies can be observed in sensory systems where the precision with which neural representations encode different states of an environmental variable (e.g., different orientations) is proportional to the frequency with which this state is actually encountered3,4. This strategy ensures that the information encoded is as great as possible given the dynamic range of the physical system used to represent it5. However, these representations not only need to be efficiently encoded but also need to be decoded and interpreted so that the resulting percepts provide maximally accurate information about the state of the world and the organism. Bayesian statistics imply that optimal perceptual processes would have to combine the representation of the environmental information (i.e., the likelihood of a state) with an a-priori expectation of these states6–8. While efficient coding and Bayesian decoding theories may appear related, they have only recently been combined in a unified theoretical framework that can account for various low-level perceptual biases4,9. But whether similar encoding and decoding strategies also operate in other domains than low-level perceptual systems remains an open question.
In the domain of preference-based decisions, it is commonly assumed that organisms rely on strategies that maximize the utility of the chosen option, based on stable and accurate representations of preferences that are not systematically affected by processing-resource constraints. However, empirically-observed choice behavior often deviates from the predictions of rational choice theory10. Purely descriptive theories of such anomalies have been offered, postulating either competition between parallel action-selection processes based on simple heuristics10 or some type of arbitrary external noise that has no clear psychological or neural basis11–13. While such theories can account for some observed effects of choice variability, biases, or confidence in isolation11–15, a common framework linking these different aspects of behavior is largely missing. Moreover, these models sometimes contain assumptions about value representations that appear implausible given the constraints imposed by the limited-capacity nature of biological systems.
In order to account for these limitations, recent work has sought to find shared principles in the mechanisms underlying subjective valuation and sensory perception11–13,16–21. Theories from this line of research have suggested that subjective value representations may resemble percepts in that they are derived by inference processes that exploit prior information about the relevant distribution of value stimuli in the environment16,17,19,21. Moreover, related lines of work suggest that neural reward circuits can flexibly adapt to different value contexts in the evironment22–25, possibly consistent with the notion that neural resources are allocated efficiently to the encoding of subjective values. However, it is unknown whether efficient coding and Bayesian decoding principles are indeed used jointly to generate preference-representations, and it is unclear whether this information-processing scheme can explain the variability, biases, and confidence in value-based decisions in humans. This lack of knowledge may reflect that the distribution of subjective values in the natural environment is not easily measurable (in contrast to corresponding distributions of sensory signals26), since it depends on the long-term experience of each specific organism with the objects in its environment25.
Here we propose a way to test whether preference-based decisions are indeed guided by a value representation scheme that combines both efficient coding and Bayesian-decoding principles. We achieve this by introducing a novel approach for studying subjective valuation that takes account of the important fact that neither decision makers nor experimenters have direct access to the “true” stimulus values underlying all value-related behaviors (e.g., ratings and choices). We demonstrate with modelling and behavioral experiments that choice variability, biases, and confidence in human preference-based decisions can all be explained by a single value-inference process. This process maximizes information transmission by optimally allocating limited resources to value representations, based on prior knowledge about the distribution of object values in the individual environment. Our approach accounts comprehensively for several aspects of value judgements and value-based choices and proposes that humans may make value-based choices optimally given resource constraints.
Results
Efficient coding of subjective value
In studies of perceptual decisions, experimenters usually have complete knowledge of any experimental stimulus value v (for instance, the angular orientation of displayed Gabor patches). This is different in experiments studying value-based choices, since experimenters have no direct access to the “true” value v of the presented object to an observer (Fig. 1a). Here we assume that this “true” value v has been shaped by each observer’s personal history of experiences with this type of object and is therefore entirely subjective. A common strategy adopted by experimenters is thus to first derive an estimate of this subjective value - based on empirical choices or subjective reports (Fig. 1a) - that is subsequently used as input to a decision model11,12,14,15,27–29. However, we will show that this strategy is suboptimal because the value estimates are likely to be as inaccurate and biased as the subsequent choices. This is because the observer herself does not have direct access to the “true” value v – after all, she does not have perfect memory of all her lifetime experiences. Thus, the observer needs to derive an estimate of the object’s value v every time this is necessary, for instance when having to rate this value or when choosing between this object and another one. Any noise and bias resulting from encoding/decoding processes used to infer this value estimate should thus affect any type of behavior in similar ways. Given these limitations, we elaborate a new approach that yields more precise estimates of subjective values for the study of preference-based decisions, based on the principles of efficient coding and Bayesian decoding.
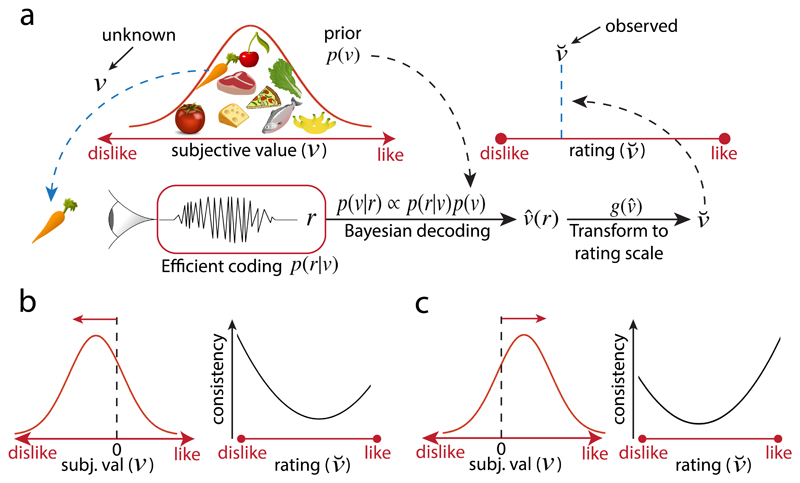
Figure 1. Simplified schema of the value inference model.
a) Observers infer the true value v of a food item by Bayesian inference constrained by efficient coding. The perceived food item with value value v elicits an internal response r. The corresponding likelihood function p(r|v) is constrained by the prior belief p(v) via efficient coding. In this example, the prior p(v) matches the distribution of subjective values v of supermarket products. The prior is combined with the likelihood to generate a posterior distribution p(v|r) via Bayes rule, to generate a subjective value estimate This estimate is subsequently mapped to the bounded rating scale imposed by the experimenter, resulting in an observed rating Crucially, unlike for experiments of perception, the experimenter has no access to the “true” stimulus value v that the participant uses to generate a rating. b,c) Choice consistency predictions as a function of the rating scale position (right plots in each panel) for two different priors (depicted on left of each panel). Prior distributions with higher density over low subjective values lead to higher choice consistency for low-valued goods (panel b); on the other hand, prior distributions with higher density over high subjective values lead to higher choice consistency for higher valued goods (panel c).
We model valuation as a probabilistic inference process incorporating both encoding and decoding (Fig. 1a; see Methods for full details). Presentation of an object with “true” stimulus value v elicits an internal noisy response r (encoding) that is used by the observer to generate a subjective value estimate (decoding) that is reported behaviorally (Fig. 1a). In experimental settings, such behavioral reports typically have to be given on physically bounded rating scales11,12,14,15,27 that can differ across different settings. To account for this step, we assume that the individual’s internal subjective scale for is physically unbounded but can be flexibly mapped via a function to any bounded scale in line with experimental demands (Methods).
Inspired by previous work in the perceptual domain9, we assume that encoding of subjective values is efficient in the sense that the mutual information between the stimulus values v and the internal response r is maximized. This results in optimal use of the underlying neuronal scale given the expected/learned natural distribution of values in the given environment, i.e., the prior p(v). Different from work in the perceptual domain and standard approaches in neuroeconomic studies, we suppose that the experimenter has no knowledge about the specific stimulus value v0 that generated the reported rating scale value However, if the experimenter obtains several value ratings for a given good (and if she repeats this for the full distribution of goods in a given context or environment), then it is possible to infer the stimulus value v0 that is most likely to have generated the observed rating distribution for that good (Methods and Supplementary Fig. 1). Moreover, if individuals employ this encoding approach, then inferred values v based on the rating data should predict subsequent choice behavior in a multi-choice task. For instance, in a two-alternative choice task, the optimal strategy is to choose good 1 over good 2 if where the value estimates are the Bayesian posterior means of each good, respectively (see Methods).
One can also make predictions of choice discriminability between two objects based on their position in the rating scale (Fig. 1b,c). If the prior distribution has higher density over low subjective values, then predicted discriminability resembles a u-shaped function, but with higher choice accuracy for lower-valued goods (Fig. 1b). On the other hand, if the prior distribution has higher density over high subjective values, then higher choice accuracy should be observed for higher-valued goods (Fig. 1c). Interestingly, the latter prediction would be diametrically opposite to predictions based on Weber’s law8, which generally assumes that higher value magnitudes should lead to poorer discrimination. Our efficient coding theory implies that Weber’s Law should hold in the case of a particular kind of prior distribution that may be realistic for some sensory magnitudes, but not for the distribution of values for consumption goods assumed here.
Subjective value rating and choice behavior
In a first behavioral experiment (Experiment 1), we presented a set of food items to n=38 study participants and asked them to indicate on a continuous rating scale their preference to consume the presented item (Fig 2a; Methods). Crucially, the participants were familiar with the food products and had seen all of them before the ratings took place, ensuring that they could effectively use the full range of the rating scale. The products (M=64 goods) were a representative sample of products typically encountered in the two biggest supermarket chains in Switzerland. Nevertheless, we ensured prior to testing that participants were indeed familiar with all products (Methods).
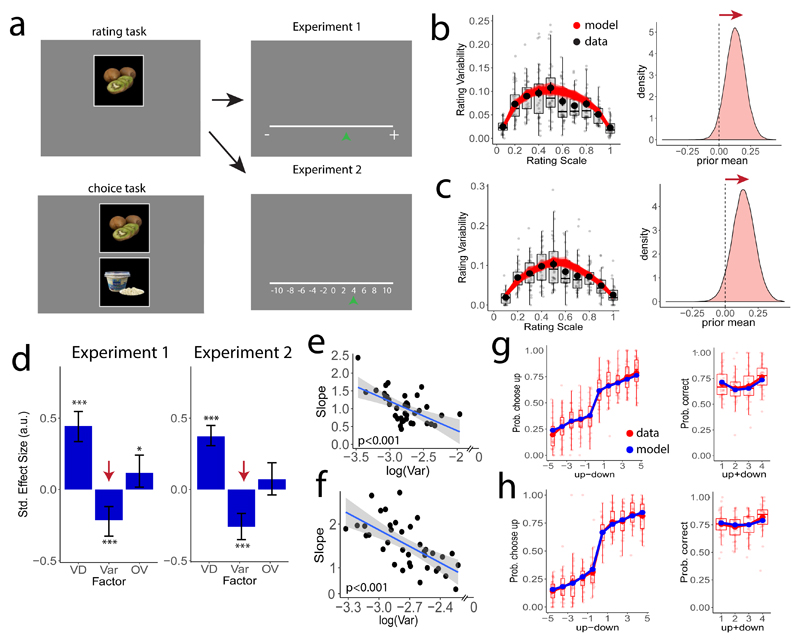
Figure 2. Paradigm and results for Experiments 1 and 2.
a) Example display from the preference rating phase (two rounds) during which the participants rated their preference to eat the displayed food item using a continuous scale (Experiment 1, n=38) or a discrete scale with numerical cues (Experiment 2, n=37). The lower-left panel shows an example display from the decision-making task requiring participants to choose which of the two items (upper or lower) they preferred to consume after the experiment. (b) Left panels show rating variability plotted as a function of each item’s mean rating across both rounds for experiment 1 (black dots show the mean across participants; dot error bars represent the s.e.m. across participants). Based on our model fits, we simulated 500 experiments in which we draw N=2 ratings for each good and plot the simulated rating variability as a function of the mean rating (semi-transparent red lines). Right panels show that posterior estimates of the expected value of the prior are shifted towards higher rating values (the zero position maps to the center of the rating scale). c) Same as panel b but for experiment 2. d) Standardized estimates from multiple logistic regression show that the higher the value difference VD between the mean ratings, the more consistent the choices. Crucially, the higher the variability in the ratings of the alternatives, the less consistent the decisions. Total value of the two ratings of each good had no reliable influence on choices across the two experiments. Error bars in this panel represent the 95% highest-density interval of the posterior estimates. (*) P<0.05; (***) P<0.001. e,f) The trial-to-trial effect shown in panel d was also reflected across participants, as the general level of variability in the rating task correlated negatively with the slope of a logistic regression (Experiment 1: panel e, βrobust = -0.77±0.20, P<0.001; Experiment 2: panel f, βrobust = -1.2±0.25, P<0.001). g,h) Observed data (red dots) match the model predictions (blue dots), plotted as a function of the two items’ absolute value difference ( in 10-tiles, left panels) and overall value ( in quartiles, right panels) (panel g: Experiment 1; panel h: Experiment 2). Lower and upper boxplot hinges correspond to the 25th and 75th percentile and each semitransparent dot represents the data of one participant.
We then asked participants to rate the same items a second time, but crucially, they had been unaware that this second rating phase was going to take place, thus allowing a clean estimation of variability in the decoded values (Methods, Fig. 2b). We tested whether this variability actually reflected the value coding/decoding operations rather than just random noise or an artifact of the bounded rating scale. To this end, the same participants underwent a series of incentive-compatible choices in which they selected from pairs of the previously-rated food items the one item they preferred to eat. We defined a consistent choice as a trial in which the subject chose the item they had assigned a higher average rating across the two previous ratings. Choice consistency was affected by the value difference between the two items’ prior ratings: The higher the value difference, the more consistent the choices (multiple logistic regression, βRandEffects=0.44±0.05, P<0.001; Fig. 2d). This concurs with the long-held notion that stronger evidence leads to more consistent choices11,12. Importantly, choice consistency also depended on the variability in the value ratings: The higher this variability for the items on a given trial, the less consistent the decision (βRandEffects = -0.21±0.05, P<0.001; Fig. 2d). Extending this trial-to-trial effect of rating variability, we observed that each participant’s average level of variability in the rating task was negatively correlated with the slope of the logistic regression of her individual choices on the items’ mean value difference (βrobust = -0.77±0.20, P<0.001; Fig. 2e). In other words, the higher the variability in the initial value ratings, the less consistent the subsequent choices between the rated items, both compared across trials and across participants. This already suggests that properties of the value coding/decoding operations can somehow affect preference-based choices, but it does not characterize by what mechanisms they may influence the observed decisions. In the next sections, we will address this question by formal tests of the theoretical framework outlined in our model specification.
In Experiment 1, the rating scale was continuous and without numerical cues (Fig. 2a). One may wonder whether rating variability might represent imprecisions in the participants’ assignment of the decoded subjective values to this rating line. We therefore conducted a second experiment (Experiment 2, n=37) in which the rating scale was divided into discrete steps with explicitly assigned numerical values (Fig. 2a; Methods). The variability in ratings across this scale clearly resembled the shape observed in Experiment 1 (Fig. 2c) and had a similar significant impact on choice behavior (βRandEffects = -0.25±0.05, P<0.001; Fig. 2d). Again, each participant’s level of variability in the rating task correlated negatively with the slope of the regression of choice consistency on value difference between the goods (βrobust = -1.2±0.25, P<0.001; Fig. 2f). Thus, the influence of rating variability on subsequent choices does not depend on specifics of the rating procedure but may reflect characteristics of the noisy coding/decoding operations used by the observer to estimate the subjective value.
Testing the efficient coding hypothesis
We now investigate to what extent the observed rating variability in Experiments 1 and 2 can be explained by the efficient coding model. We started by inferring the values v(1,⋯,M) of each good m that maximized the likelihood of the observed set of ratings for each participant (Methods). In Experiments 1 and 2, the rating data set consisted of M=64 and M=61 goods respectively, with N=2 ratings for each good. The fitted model successfully captured the empirically-observed rating variability (Fig 2b-c) and the distribution of subjective value estimates (Supplementary Fig. 2). We compared the quality of these efficient-coding model fits with those of a simple flexible model that assumes constant Gaussian noise over the rating scale with no prior distribution constraints on the values v(1,⋯,M). For both Experiments 1 and 2, the efficient coding model explained the rating distribution better than the alternative model (Supplementary Fig. 3).
Exploration of the rating data revealed that the distribution of ratings was highly variable across participants (Supplementary Figs. 4,5), perhaps indicating that each individual holds different priors over values due to different long-term experience. The inferred prior distributions for both experiments based on our model revealed that the expected value of the prior across the population was shifted towards higher values (Fig. 2b,c). Choice discriminability should therefore resemble the shape predicted in Figure 1c. If the subjective values of the products are derived using efficient-coding principles, then using the framework described above should allow us to predict each individual’s preference-based decisions. It is important to emphasize that for these prediction analyses, we fixed for each participant the parameters of the prior distribution p(v) and the stimulus values v(1,⋯,M) to the specific values obtained when fitting the model to the separate rating data. Using these out-of-sample parameters and values, and only adjusting the encoder and external noise, our model did a good job at predicting the choice data (Fig. 2g,h) as suggested by both the qualitative predictions and leave-one-out cross-validation metrics (Methods and Supplementary Note 1). To determine which aspects of the operations formalized in the efficient-coding model are most relevant for explaining behavior, we compared the predictive power of our model to that of alternative models (Supplementary Note 1). For both experiments, the efficient coding model predicted the data best, as suggested by both the qualitative predictions and leave-one-out cross-validation metrics (Supplementary Note 1).
It may be argued that the specific pattern of observed choices in our experiments could also be captured by a model that does not contain efficient coding but instead fits the full shape of the likelihood function to the observed data, as done e.g. in in previous work on perceptual discrimination26. However, it is important to emphasize that our approach does not require us to fit arbitrary shapes of likelihood functions, as these shapes naturally arise from the efficient-coding formalized in our model, which only requires fit of one free parameter: Noise in the efficient-coding space (for a detailed discussion of this topic see Supplementary Note 2). Thus, the explanatory power of our model does not reflect the general flexibility of Bayesian inference per se but specifically relates to the efficient coding of values embedded in the Bayesian inference process.
The results presented so far suggest that subjective-value representations guiding human preference-based decisions are inferred and employed optimally using both efficient coding and Bayesian decoding. However, it remains unclear whether internal noise due to efficient coding is the main factor explaining fluctuations and potential biases in subjective value estimations. We investigate this issue in the following section.
Illusions of subjective value
The theory used here predicts in general that for a stimulus with value v0 near the peak of the prior, the subjective value estimate (and the resulting rating ) should be biased away from the prior, with the strength of this bias determined by the degree of noise in the internal representations used for inference9. We thus investigated whether a conceptually similar type of bias emerges during subjective value estimation, reflecting an expectation-induced preference illusion and further supporting efficient coding of subjective value.
The estimation of this valuation bias necessarily requires knowledge of the exact stimulus value v0 that serves as input on any given trial, which is difficult in our case since the experimenter does not have direct access to v0 (Fig. 1a). In order to cope with this problem, we first derived predictions of the estimation bias for different levels of internal noise σ in the value representations. We assumed that this noise varies with the stimulus presentation times, based on theoretical frameworks postulating that value estimates are constructed using samples from memories/emotions associated with the physical features of the objects30. This suggests that a reduction in visual stimulation time should reduce the number of samples that can be drawn and should therefore increase the noise in the internal value representations31. To make this intuition explicit, we formulated a mathematical proof confirming that the number of discrete samples (e.g., memories) that can be drawn over time is inversely proportional to the level of encoding noise in a capacity-limited system (Supplementary Note 3). Crucially, this proof provides a normative foundation for the theoretical frameworks30–32 motivating our approach and confirms the validity of the assumptions underlying our simulations and experimental strategy.
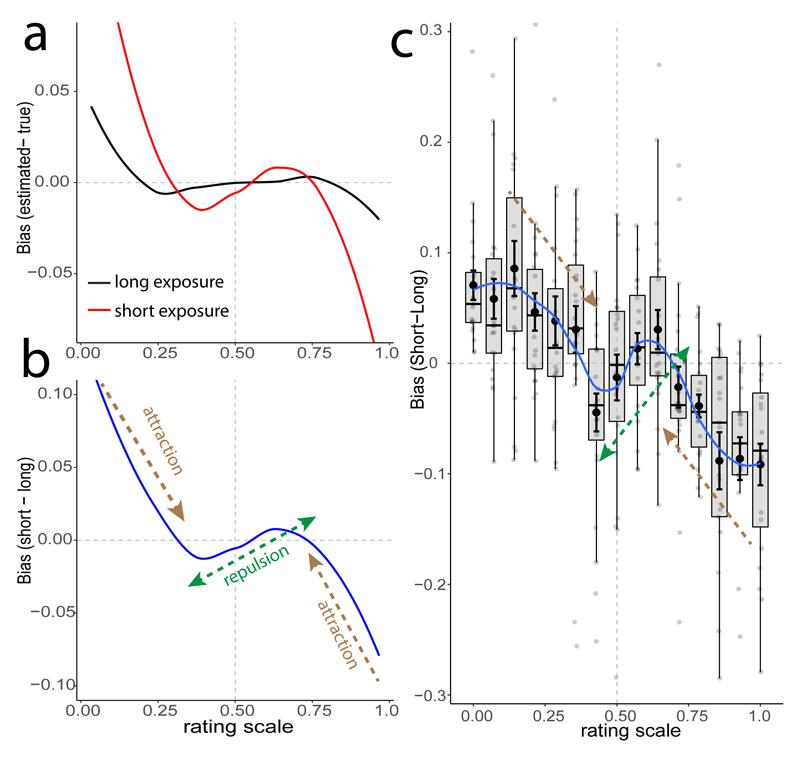
In order to derive initial qualitative predictions for the value estimation bias for different presentation times – and therefore levels of encoding noise – we performed model simulations using the prior p(v) obtained in Experiments 1 and 2, with the consequence that its peak was slightly shifted to the right of the rating scale (Fig 2b,c). We selected two levels of encoding noise σ based on the noise levels observed in Experiment 1 (see Supplementary Note 4 for a detailed discussion of the relation between encoding noise and the specific bias pattern). The simulations predicted biases for long exposure times (low σ, black line in Figure 3a) and short exposure times (high σ, red line in Fig. 3a) that are markedly different once the value estimates have been mapped onto the bounded rating scale via Crucially, the difference between these two predictions (high and low σ) is independent of v0:
| (1) |
Figure 3b shows that simulated rating trials with short exposure time (i.e., high σ) have stronger repulsive (“anti-Bayesian”) biases near the center of the prior (intersection point to the right of the center of the rating scale), but also stronger attraction biases when v0 is further away from the peak of the prior. For values close to the prior, this prediction agrees with previous work showing repulsive noise-related biases in perceptual tasks9; however, as v0 moves away from the prior, our simulations predict the opposite tendency (attraction) that would also be expected based on classical Bayesian frameworks.
Figure 3. Illusion of preference (Experiment 3).
a) Model-predicted biases for two degrees of internal measurement noise (σ) during subjective-value estimations: high (red, generated by short valuation exposure) and low (black, generated by long valuation exposure). b) Model-predicted differences of the biases for high and low σ across the value rating scale. c) Difference of the empirical estimates between low and high exposure times (n=24, mean data are black dots with s.e.m. across participants, blue line interpolates these data for visualization). Note the qualitative and quantitative overlap with the model prediction in panel b. This suggests that human valuation exhibits complex illusions of subjective preference, as predicted by the Bayesian and efficient coding hypothesis (see also Supplementary Fig. 7). Lower and upper boxplot hinges correspond to the 25th and 75th percentile and each semitransparent dot represents the data of one participant.
We devised a behavioral paradigm (Experiment 3) to investigate whether these model-predicted biases are in fact observed for subjective value estimations. Healthy individuals (n=24) rated goods with similar procedures as in Experiment 1. However, for the first round of ratings, a randomly determined half of the goods for each participant were presented for a duration of 900 ms and the other half for a duration of 2600 ms. Participants did not know whether a given item was going to be presented for the short or long duration. In the second round of ratings, the presentation durations were inverted for each good, but participants did not know that this second round was going to take place (see methods for further details). Thus, participants were not able to predict the presentation times of individual items and could not develop differential information sampling strategies for items with long vs short presentation times. On each trial, the rating scale was presented just after the image had disappeared from the screen (see Figure 1a), and participants were instructed to then provide their rating as fast as possible (mean RTs of 1.53±0.45 and 1.39±0.4 for low and high exposure times, respectively, see Supplementary Fig. 6). Thus, the effective sampling time (time from the onset of stimulus presentation until response) was 1.53±0.4 s longer for long exposure times (βRandEffects=1.4±0.08, P<0.001; Supplementary Fig. 6), supporting our assumption that participants could draw a higher number of samples (and therefore reduce internal noise in the value representations) for images with long exposure times. We computed the difference in the ratings between short and long durations and plotted this difference as a function of the rating of the long duration (Fig. 3c). The results of this analysis match the non-intuitive quantitative predictions of the efficient coding model (Fig. 3b), in showing systematic repulsion for the four data points near the peak of the prior and attraction for the other values that are further away from the prior (Supplementary Fig. 7). Note that the repulsion effect that is both predicted and observed at the center of the scale here is not confined to always be at this location - its location and extent over the rating scale depends on the interaction of the three key parameters of our model: The prior location, prior shape, and level of encoding noise (Supplementary Note 4).
Control analyses confirmed that our results are not caused by systematic temporal order effects (no difference in value ratings between the first and second rounds for each of the exposure times; paired t-tests, all P>0.18). We also compared the accuracy of our model’s predictions to that of control models in which we factorially varied all possible sources of noise that could in principle have affected the ratings (pre-encoding noise, efficient-coding noise, post-encoding noise, and lapses). Models without efficient coding lead to very different predictions that are not supported by our empirical data (Supplementary Fig. 8). In order to test this quantitatively, we performed a factorial model comparison to quantify the strength of empirical support given by our data for the presence of each noise source (Supplementary Fig. 9 and Supplementary Table 1). This revealed that the only noise source reliably accounting for the variation in subjective value estimation due to time pressure is internal noise in efficient coding (Bayes Factor > 100; see Supplementary Fig. 9). This strongly suggests that the biases in subjective value estimates observed in Experiment 3 originate in the efficient-coding operations formalized in our model.
Confidence in subjective valuation
It has been suggested that the perceived confidence in subjective value reports reflects a second-order judgement (the confidence rating) about a first-order judgment (the subjective value rating)15. However, two important issues have remained unaddressed. First, previous work has not explicitly defined a generative model of the encoding and decoding of value representations; second-order statements about these ratings would therefore be subject to the same problems curtailing the validity of the ratings themselves. Second, previous work has remained agnostic about both the information structure of values in the environment and capacity limitations. We therefore tested whether the reported confidence in subjective value estimations can be predicted based on the encoding/decoding process proposed here.
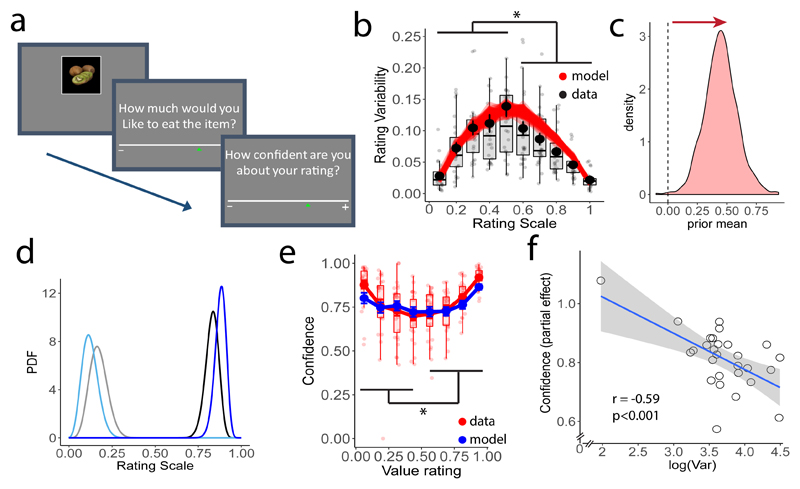
We conducted a new experiment (Experiment 4) in which participants provided value ratings as in experiment 1, but they now also gave a confidence rating after each value rating (Fig. 4a). We inferred the subjective values v(1,⋯,M) exactly as for Experiments 1 and 2. Once again we found a shift of the expected prior (i.e., its mean) towards higher values alongside higher rating variability for higher than low-rated items (hierarchical linear regression of rating variability for each item vs. mean rated value: βRandEffects= -0.18±0.04, P<0.001). Based on these results, we derived three qualitative predictions for the confidence ratings based on the definitions of confidence formulated above. First, confidence should be higher for rating values near the extremes of the rating scale (Fig. 4d), reflecting the transformation from the subjective space to the bounded scale. This prediction is in line with previous work15. Second, given the shift of the prior density towards higher subjective values (Fig. 4c), the efficient coding framework predicts that the second-order judgement of the posterior probability perceived in the rating scale should decrease for item values towards the right side of the rating scale; confidence reports should therefore be higher for items with higher subjective value (Fig. 4d). Third, because lower levels of variability in the rating estimates generate narrower posterior distributions, the average variability of each participant’s ratings should be negatively related to her general level of confidence.
Figure 4. Confidence (Experiment 4).
a) Participants (n=28) provided value ratings as in experiments 1 and 2, but also rated their confidence in the value ratings. b) Rating variability plotted as a function of each item’s mean rating across both rounds (solid black dots) was higher for low-rated items (β= -0.18±0.04, P<0.001). c) Posterior estimates of the expected value of the prior are shifted towards higher rating values (the zero position maps to the center of the rating scale). d) Posterior densities were constructed for four symmetric subjective values v (different colors) in the unbounded subjective scale. Group of densities on the left (light colors) and right side (dark colors) reflect low and high subjective values, respectively. Given the expected value of the prior (panel c), the efficient-coding model predicts lower levels of confidence for low-rated goods (relatively wide posteriors; light colors) than for high-rated goods (relatively narrower posteriors; dark colors). e) Empirical confidence ratings (solid red dots) match the predictions (blue dots) of the best-fitting confidence model (red; see also Supplementary Table 2) across different value ratings (x-axis). Confidence was higher for higher model-predicted subjective values (βRandEffects=0.22±0.070, P=0.002). f) Confidence relates to value-rating variability (shown is the partial correlation after controlling for rating value). As predicted by the model, these two metrics are negatively correlated (r = -0.59, p<0.001). Dots represent the data of single participants, the blue line represents the identified correlation line, and the shaded area the 95% confidence interval of this line. In all other plots, error bars around data points represent s.e.m. across participants. Lower and upper boxplot hinges correspond to the 25th and 75th percentile and each semitransparent dot represents the data of one participant.
The data (see Figure 4e,f) confirm all three predictions. First, confidence increases for values closer to the extremes of the rating scale (quadratic effect βRandEffects=0.41±0.03, P<0.001). Second, confidence was higher for higher model-predicted subjective values vm (βRandEffects=0.22±0.070, P=0.002). This runs counter to previous suggestions15 that confidence ratings should be symmetric with respect to the center of the rating scale: Both our model and empirical data reveal that this is not necessarily the case, as the confidence ratings depend on the prior distribution (Supplementary Table 2). Third, across participants, the higher the variability in the subjective value estimations, the less confident the participants are (βrobust = -0.59, P<0.0011). Crucially, this regression analysis controls for the mean value ratings for each participant (Fig. 4f), thereby confirming our model predictions that confidence relates to rating variability independently of how valuable the participants rated the items. Finally, to test these model predictions more quantitatively for the observed data using our framework, we implemented 11 different proposed models of how confidence may be derived15,33–35 from the posterior distributions of rating values given by our framework (see full details of the model specifications in Supplementary Table 2). Crucially, we fixed both the parameters of the prior distribution and values v(1,⋯,M) for each participant to the values obtained by fitting the model to her prior rating data. We found that a model based on the statistical definition of confidence (i.e., the probability that the rating is correct33,34) provided the best fit to the empirical confidence reports (Fig 4e, Supplementary Table 2). These results confirm that our efficient-coding model can capture the value inference processes that underlie not only subjective value estimates but also the reported confidence in these estimates.
Discussion
Our work demonstrates that variability, biases, and confidence in preference-based choices are all consistent with information-maximizing transmission and statistically optimal decoding of values by a limited-capacity system. This suggests that principles governing the encoding and interpretation of low-level sensory signals are also relevant when humans report and choose based on subjective preferences. More specifically, our results support theoretical proposals according to which, just as in the case of sensory systems, subjective value systems optimize the use of limited resources for processing value information and exploit environmental regularities in order to guide preference-based decisions16,17,19. Thus, our findings provide a fundamental step toward a unified account of how humans perceive and valuate the environment in order to optimally guide behavior.
Our work introduces a new framework that may serve to improve the modelling and prediction of preference-based decision making, and more generally any cognitive process that involves fully subjective value estimations (such as pain36 and health37 perception, to mention only two examples). We demonstrate that the common practice of using value ratings as inputs to decision models11,12,14,15,27–29 is suboptimal, since these reports should be just as variable and biased as the choices that the experimenter wants to model. This is not a trivial issue, as both ratings and choices can be subject to complex non-linearities due to the encoding/decoding strategies implemented by the valuation system. Our model provides a solution to this problem, since it makes it possible to employ a single set of ratings to determine both the observer’s subjective values and their underlying prior distribution, while simultaneously accounting for capacity limitations. These parameters and values can then be used to predict fully independent preference-based decisions with higher accuracy than existing standard approaches in the literature. This procedure differs from traditional economic approaches that derive preferences directly from observed choices38 and that ignore the processes involved in estimating subjective values (and the associated sources of variability). Our results show that this ignorance is not warranted; a detailed understanding of these processes should be a critical aspect to consider in theories of decision making and economic behavior39.
In our model specification, variability in subjective value estimates and choices emerges from both internal noise in the coding of value and unspecific (external) noise in the decision process. This perspective is fundamentally different from standard approaches where preference variability is solely attributed to unspecified noise in the decision process (e.g., noise added to deterministic value functions13 through the application of a softmax function or diffusion noise in sequential sampling models11–13). Based on our empirical and modelling work, we argue that positing unspecified sources of noise in the decision process may be insufficient, given that accounting for noise involved in the coding of value appears to be crucial for deriving more accurate predictions of economic decisions21. Even though some characteristics of the models used for this purpose (e.g., encoding rules and loss function of the Bayesian encoder) may be refined by future research on both perception40 and subjective valuation23, our findings clearly illustrate the general utility of this approach.
In some respects, our model of the coding of value resembles the one posited by decision-by-sampling theory41. That theory proposes that estimated subjective values directly reflect samples drawn from an internal noisy representation of value, but unlike in our approach, no optimal Bayesian decoding is assumed. As a consequence, decision-by-sampling theory cannot account for our finding that biases in valuation are changed by time pressure, since drawing fewer samples should lead to value estimates that are noisier, but not different on average. This contrasts with the predictions of the framework presented here, which we show to be fully congruent with the empirically observed biases under time pressure.
Our results support the idea that reported confidence in subjective value estimations is well captured by a statistical measure of confidence33,34. While a recently proposed framework15 provides an elegant model of confidence judgments for individual value estimates, it does not provide a precise account of what information should actually be encoded but focuses only on what may be decoded. Additionally, that framework does not account for the effects of capacity limitations in information processing and the distribution of object values in the environment. Our work provides a more comprehensive characterization, by demonstrating that the same efficient coding framework that accounts for biases and variability in subjective value estimates and choices also accounts for the reported confidence in these value estimates. In general, we hope that these results may motivate researchers to further develop explicit process models of metacognition42.
While our work highlights similarities between perceptual and value inference, it has remained agnostic as to how the internal response used for this purpose is derived from low- and high-level sensory signals. Understanding such feature extraction will be important for characterizing how the internal value response may be constructed, e.g. by sampling from memory30,43 and emotion systems44. While we formally demonstrate that the precision of encoded subjective values in capacity-limited systems may relate to the number of discrete samples that can be drawn (e.g., from memory or emotion systems), we have so far only focused on the encoding and readout of simple one-dimensional subjective values associated with an object. However, the framework used here could be parsimoniously extended to incorporate a whole range of lower-level sensory signals and to encompass more complex hierarchical structures. Despite this interesting challenge to further understanding the construction of preferences10, it is remarkable that a simple normative specification inspired by fundamental principles of low-level sensory perception can capture important aspects of preference-based decisions.
Bayesian models have often been criticized for allowing an arbitrary choice of prior and likelihood functions, as a consequence of which it is suggested that their predictions are vacuous45. However, in this study we have shown that by fully constraining the decision model to the distribution of object values – while taking account of capacity constraints – it is possible to accurately capture preference-based choice behavior using a parsimonious model. In line with previous work on low-level sensory perception4,9, our results demonstrate that the above-mentioned critique is not always valid. This should motivate researchers to pursue the identification of optimal solutions to computational problems posed by the environment – in both perception and subjective valuation – without ignoring the fact that biological systems are by definition limited in their capacity to process information.
Taken together, our findings suggest that resource-constrained models inspired by models of perception3,9,16 may have far-reaching implications not only in neuroscience, but also in psychology16,46–48 and economics19,21,48–50. Such models offer the prospect of explanations for seemingly irrational aspects of choice behavior, grounded in the need to represent the world with only finite precision. Recent work suggests that features of economic decisions such as risk aversion21 and preference reversals19 can be understood as further examples of biases resulting from optimal Bayesian inference from imprecise internal representations of value. This supports our emphasis on the desirability of developing models of decision making that account simultaneously for the goals of the organism, its environment, and its biological constraints.
Methods
Participants
The study tested healthy young volunteers (total n=127, age 19-37 years, 55 females: n=38 in experiment 1, 17 females; n=37 new participants in experiment 2 (replication of results obtained in experiment 1), 14 females; n=24 new participants in experiment 3, 11 females; and n=28 new participants in experiment 4, 13 females). Participants were randomly assigned to each experiment. No data was excluded from the analyses. Sample size was determined based on previous studies using similar stimuli and tasks11,51. Participants were instructed about all aspects of the experiment and gave written informed consent. None of the participants suffered from any neurological or psychological disorder or took medication that interfered with participation in our study. Participants received monetary compensation for their participation in the experiment, in addition to receiving one food item in the decision-making task (see below). The experiments conformed to the Declaration of Helsinki and the experimental protocol was approved by the Ethics Committee of the Canton of Zurich.
For all experiments, participants were asked not to eat or drink anything for 3 hours before the start of the experiment. After the experiment, participants were required to stay in the room with the experimenter while eating the food item that they had chosen in a randomly selected trial of the decision-making task (see below). All experiments took place between 9am and 5pm. Our experiments did not include different conditions determined a priori by the experimenter, since the participants themselves sorted trials into conditions as a direct consequence of their ratings and choices given during the experiment. Blinding was therefore neither necessary nor possible.
Value rating task
Experiments 1 and 2 consisted of three main phases: (1) rating phase 1, (2) rating phase 2, and (3) the decision-making task. In rating phase 1, we asked the participants to provide subjective preference ratings for a set of 64 food items using an on-screen slider scale (Figure 2a). All of the food items were in stock in our lab and participants were notified about this. Importantly, participants saw all food products before the ratings so that they could effectively use the full range of the rating scale. Moreover, participants knew that all products were randomly drawn from the two biggest supermarkets in Switzerland. Based on pilot measurements and previous studies11,51 in our lab, we selected food items that varied all the way from items that most participants would find unappealing (e.g., raw broccoli) to items that most participants would find highly appetitive (e.g., ice cream). This was important as our model should capture the full range of subjective values that humans typically assign to food items on a daily basis. During the ratings, participants indicated “how much they wanted to eat the presented food item at the end of the experiment”. The slider scale was continuous in experiment 1 with no numbers displayed (Fig. 2a), whereas the rating scale in experiment 2 was divided in 20 steps of equal size with numbers displayed under each step (Fig. 2a). This was done to ensure that the effects observed in Experiment 1 did not reflect the absence of reference points in the middle of the rating scale. Participants were informed that the rightmost endpoint would indicate items that they would most love to eat, whereas the leftmost endpoint would indicate items that they would most hate to eat. The initial location of the slider was randomized for each item to reduce anchoring effects.
Rating phase 2 was identical to rating phase 1 and took place immediately after phase 1. The order of the items’ presentation was randomized. Crucially, participants were not informed before the rating phase 1 that a second rating phase and a decision-making task would take place. This was important as it prevented participants from actively memorizing the location of the rating in the slider in the first phase, thus providing us with a clean measure of the variability in the value estimates.
In Experiment 3, participants provided value ratings as in Experiment 1, but for the first round of ratings, half of the goods were presented with a duration of 900 ms and the second half with a duration of 2600 ms. For the second round of ratings, the presentation durations were inverted for each good. The exposure time (900 ms or 2600 ms) was pseudo-randomly selected for each good in the first round of ratings, and participants did not know in advance for how long they were going to see each specific food item. The rating scale appeared only once the image disappeared from the screen (see Figure 1a), and the participants were instructed to provide their rating as fast as possible (mean RTs 1.53±0.45 and 1.39±0.4 for low and high exposure times, respectively). Crucially, participants were not informed in advance about the details of the time manipulations.
In Experiment 4, participants provided value ratings as in experiment 1, but indicated after each rating their confidence in their first-order rating (Fig. 4a). Following procedures of previous work15, we informed participants that the leftmost side of the rating scale means “Not at all” confident and the rightmost side means “Totally” confident.
Choice task
For Experiments 1 and 2, immediately after the two rating phases, an algorithm selected a balanced set of decision trials divided into four value difference levels on the rating scale (rating difference ~5%, ~10%, ~15% and ~20% of the length of the rating scale), as defined by the average rating across phases 1 and 2 provided by each participant. Decision-making trials started with central presentation of a fixation cross for 1-2 seconds. Immediately after this, two food items were displayed simultaneously, one in the upper and one in the lower hemifield (Fig. 2a). The food items were presented until response and participants had up to four seconds to make a choice. Participants were instructed to choose which of the two items (upper or lower) they preferred to consume at the end of the experiment. To make these choices, participants pressed one of two buttons on a standard keyboard with their right-index finger (upper item) or their right thumb (lower item). In Experiments 1 and 2, we defined a consistent choice as a trial in which the subject chose the item with a higher mean rating from the prior rating phase. Each experimental session comprised a maximum of 240 trials (this depended on the rating distribution of each participant) divided into 6 runs of 40 trials each. The trials were fully balanced across rating-difference levels (~5%, ~10%, ~15% and ~20% of the length of the rating scale) and location of consistent response option (Up or Down).
Model
We assume that the presentation of an object with stimulus value v elicits an internal noisy response r (encoding) that the observer uses to generate a subjective value estimate – the decoded stimulus value. At the encoding stage, a function F(v) maps the stimulus space to a new space where the Fisher information is uniform over the entire real line. This requires the definition
| (2) |
| (3) |
where p(χ) is an improper prior distribution, so that F(v) → ∞ as v → ∞, and F(v) → –∞ as v → –∞. We assume that conditional on the value v, an internal noisy (neural) response is generated
| (4) |
with δ ~ N(0,σ2), where σ measures the degree of noise in the internal representation that is constant over all possible values F(v). We also note that the prior distribution for possible values of F(v) is uniform on the real line. The posterior mean estimate of F(v) (the estimator that minimizes mean squared error) is then given by
| (5) |
with ϵ1 ~ N(0,σ2). Here E[.] means the expectation over possible values of ϵ1. This estimator is a deterministic function that maps each measurement r to an estimated subjective value ; this deterministic mapping therefore cannot account for trial-to-trial fluctuation in the value estimates. The variability in the value estimates arises because of the variability in the measurement r on each trial. Accounting for this variability, it follows that for any true stimulus, v0, the mean estimate should be given by
| (6) |
with ϵ2 ~ N(0,σ2). E[.] now means the expectation over possible values of (ϵ1 + ϵ2) ~ N(0,2σ2).
In the small-noise limit, we can take a second-order Taylor expansion:
| (7) |
where , and the derivatives of are evaluated at . Taking the expected value over possible realizations of ϵ1 we obtain
| (8) |
Conditional on a particular stimulus value v0, this is a random variable with expected value
| (9) |
and variance
| (10) |
If we approximate this distribution by a normal distribution with the mean and variance just calculated above, we would obtain a probability density for given by
| (11) |
where θ is a set of parameters of the prior distribution (see below). This expression is the likelihood of a given subjective value estimate conditioned on a true stimulus value v0. If one wants to write the joint likelihood of a pair of values occurring when v0 is drawn from the prior, one obtains
| (12) |
In addition to internal noise in the coding of value σ, we also account for late noise in the decision stage (i.e., post-decoding noise), which may capture any unspecific forms of downstream noise occurring during the response process that are unrelated to valuation per se. We assume this late noise to be normally distributed; therefore, it can be easily added to our model as follows (see Supplementary Note 1 for further discussion on the different sources of noise)
| (13) |
The last part of the model defines the probability distribution in the space of the bounded rating scale. Without loss of generality, we assume that this scale is bounded from 0 to 1, with a monotonic mapping of subjective preference values that preserves preference ordering. Transforming the unbounded internal scale to this bounded physical scale requires a mapping that preserves monotonicity. A convenient and relatively simple function allowing this transformation is the logistic function: which provides a one-to-one mapping of the estimate from the subjective to the physical scale on any given trial. The implied joint probability density on the rating scale is thus given by
| (14) |
Here the inverse mapping of the subjective to the unbounded scale is given by
| (15) |
and its first derivative is
| (16) |
Recall that we are assuming here that the decision maker maximizes mutual information between the input stimulus and the noisy measurement, therefore F(v) is defined as the cumulative density function (CDF) of the prior distribution p(v). Here we assume that the prior follows a logistic distribution
| (17) |
where μ and s represent the mean and scale, respectively. The advantage of using this distribution is that its CDF and both the first and the second derivative of the quantile function have closed-form solutions; however, any similar prior distribution could be used without greatly affecting the quantitative predictions presented here. are given by:
| (18) |
| (19) |
| (20) |
Thus, for any experimental data set consisting of M goods and N value ratings for each good, we can find the set of parameters of the prior, the internal valuation noise σ, external noise σext, and the “true” stimulus values v(1,⋯,M) that maximize the likelihood of the observed set of ratings (under the constraint that v(1,⋯,M) is distributed following p(v)).
In order to compute choice consistency predictions that an experimenter would obtain when performing such analysis in the rating scale (Fig. 1b,c), we first computed for a fine-grained sequence of subjective values v0 their corresponding expected value and variance perceived in the rating scale (if we assume that the experimenter can obtain a large number of ratings for each good) via
| (21) |
and
| (22) |
where the subscript () reflects the expected value () and variance () at position in the rating scale. We then looked for expected values closer to the values [0.1,0.11,0.12, … 0.89,0.9] and used their corresponding variance to approximate the level of choice consistency as follows:
| (23) |
with δ = 0.05 (note that different values of δ move the accuracy curve up or down but does not affect the general u-shaped curve obtained in our predictions; see Fig. 1b,c).
Behavioral analyses and statistics
Preference-rating variability in Experiments 1 (n=38), 2 (n=37) and 4 (n=28) was computed as the standard deviation (SD) for each item across the rating phases 1 and 2. To visualize this effect, we plotted the SD as a function of the mean rating (Figs. 2b,c; 4b). To investigate the influence of both VD and rating variability on the consistency of choices (Fig. 2d), we performed a hierarchical logistic mixed-effects regression of choices (defining consistent=1, inconsistent=0) on three main regressors of interest, namely: value difference (VD), summed-variability (Var, defined as the sum of the two SDs of the two food items presented in each trial), and the summed-value (OV, defined as the sum of mean rating values of the two food items presented in each trial). All regressors of interest were included in the same model. Similarly, all the population-level regressions described for Experiment 4 were based on a hierarchical linear mixed-effects regression approach. All mixed-effects regressions in this study had varying subject-specific constants and slopes (i.e., random-effects analysis). Posterior inference of the parameters in the hierarchical models was performed via the Gibbs sampler using the Markov Chain Monte Carlo (MCMC) technique implemented in JAGS52, assuming flat priors for both the mean and the noise of the estimates. For each model a total of 10,000 samples were drawn from an initial burn-in step and subsequently a total of new 10,000 samples were drawn with three chains (each chain was derived based on a different random number generator engine, and each with a different seed). We applied a thinning of 10 to this final sample, thus resulting in a final set of 1,000 samples for each parameter. We conducted Gelman–Rubin tests53 for each parameter to confirm convergence of the chains. All latent variables in our Bayesian models had , which suggests that all three chains converged to a target posterior distribution. We checked via visual inspection that the posterior population level distributions of the final MCMC chains converged to our assumed parametrizations. The “p-values” reported for these regressions are not frequentist p-values but instead directly quantify the probability of the reported effect differing from zero. They were computed using the posterior population distributions estimated for each parameter and represent the portion of the cumulative density functions that lies above/below 0 (depending on the direction of the effect). The regressions across participants reported for Experiments 1,2 and 4 were computed using robust linear regressions using the rlm function54 implemented in the statistical computing software R55.
In order to fit the efficient coding model to the rating data in Experiments 1, 2 and 4, we found the stimulus values v(1,⋯,M), parameters of the prior θ, encoding noise σ and external noise σext that maximized the likelihood function (Eq. 14) of the observed set of ratings for each participant under the constraint that v(1,⋯,M) is distributed following p(v;θ) (Supplementary Fig. 1). Alternatively, defining , one can find the values estimates in the efficient space under the constraint that these are uniformly distributed. Using either approach, we found nearly identical results for the fitted parameters, which is expected for correct model specification. Posterior inference of the parameters for this model can be conveniently performed via the Gibbs sampler.
We used the stimulus values v(1,⋯,M) and prior parameters θ fitted to the rating in order to predict choices in the two-alternative choice task in Experiments 1 and 2. Following our modelling specification, over many trials the probability that an agent chooses an alternative with stimulus value v1 over a second alternative with stimulus value v2 is given by:
| (24) |
where Φ() is the CDF of the standard normal distribution and the expressions for E[.] and Var[.] are given in Eqs. 9 and 10 (see above). In other words, the input values of the choice model are fully constrained by the efficient coding model based on the fits to the rating data and therefore the choice model has only two free parameters, namely the resource noise of the encoder σ and the external noise σext. Fits to the choice data were performed via the Gibbs sampler using a hierarchical Bayesian model assuming flat priors for both noise terms. When evaluating different models, we are interested in our model’s predictive accuracy for unobserved data, thus it is important to choose a metric for model comparison that considers this predictive aspect. Therefore, in order to perform model comparison, we used a method for approximating leave-one-out cross-validation (LOO) that uses samples from the full posterior56. The smaller the LOO the better the fit. We found that in Experiments 1 and 2, the best model was the efficient-coding model. Crucially, this finding is fully replicated when using a different Bayesian metric such as the wAIC56. Description of the different choice models tested here is presented in Supplementary Note 1.
Supplementary Material
Acknowledgements
R.P. thanks Xue-Xin Wei and Alan Stocker for inspiring discussions. We thank Silvia Maier for providing us with the set of food images and Cornelia Schnyder for research assistance. This work was supported by a grant of the Swiss National Science Foundation (grant IZK0Z1_173607) and an ERC starting grant (ENTRAINER) to R.P; by a grant of the U.S. National Science Foundation to M.W.; and by grants of the Swiss National Science Foundation (grants 105314_152891 and 100019L_173248) and an ERC consolidator grant (BRAINCODES) to C.C.R.
Footnotes
Author contributions
R.P and C.C.R. designed the study. R.P. collected and analyzed the data. All authors interpreted the results and wrote the manuscript.
Competing Interests Statement
The authors declare no competing financial interests
Reporting Summary.
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data availability
The data that support the findings of this study and the analysis code are available from the corresponding author upon request.
Code availability
Code to infer subjective values and prior parameters based on rating data is provided in the Supplementary Software file.
References
- 1.Barlow HB. Possible principles underlying the transformations of sensory messages. 1961 [Google Scholar]
- 2.Attneave F. Some informational aspects of visual perception. Psychol Rev. 1954;61:183. doi: 10.1037/h0054663. [DOI] [PubMed] [Google Scholar]
- 3.Ganguli D, Simoncelli EP. Efficient sensory encoding and Bayesian inference with heterogeneous neural populations. Neural Comput. 2014;26:2103–2134. doi: 10.1162/NECO_a_00638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wei X-X, Stocker AA. Lawful relation between perceptual bias and discriminability. Proc Natl Acad Sci U S A. 2017;114:10244–10249. doi: 10.1073/pnas.1619153114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Laughlin S. A Simple Coding Procedure Enhances a Neuron’s Information Capacity. Zeitschrift für Naturforsch C. 1981;36:910–912. [PubMed] [Google Scholar]
- 6.Stocker AA, Simoncelli EP. Noise characteristics and prior expectations in human visual speed perception. Nat Neurosci. 2006;9:578–85. doi: 10.1038/nn1669. [DOI] [PubMed] [Google Scholar]
- 7.Kording KP, Wolpert DM. Bayesian integration in sensorimotor learning. Nature. 2004;427:244–247. doi: 10.1038/nature02169. [DOI] [PubMed] [Google Scholar]
- 8.Petzschner FH, Glasauer S, Stephan KE. A Bayesian perspective on magnitude estimation. Trends Cogn Sci. 2015;19:285–293. doi: 10.1016/j.tics.2015.03.002. [DOI] [PubMed] [Google Scholar]
- 9.Wei X-X, Stocker AA. A Bayesian observer model constrained by efficient coding can explain’anti-Bayesian’percepts. Nat Neurosci. 2015;18:1509–1517. doi: 10.1038/nn.4105. [DOI] [PubMed] [Google Scholar]
- 10.Lichtenstein S, Slovic P. The construction of preference. Cambridge University Press; 2006. [Google Scholar]
- 11.Polanía R, Krajbich I, Grueschow M, Ruff CC. Neural oscillations and synchronization differentially support evidence accumulation in perceptual and value-based decision-making. Neuron. 2014;82:709–720. doi: 10.1016/j.neuron.2014.03.014. [DOI] [PubMed] [Google Scholar]
- 12.Krajbich I, Armel C, Rangel A. Visual fixations and the computation and comparison of value in simple choice. Nat Neurosci. 2010;13:1292–1298. doi: 10.1038/nn.2635. [DOI] [PubMed] [Google Scholar]
- 13.Hunt LT, et al. Mechanisms underlying cortical activity during value-guided choice. Nat Neurosci. 2012;15:470–6. doi: 10.1038/nn.3017. S1–3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.De Martino B, Fleming SM, Garrett N, Dolan RJ. Confidence in value-based choice. Nat Neurosci. 2013;16:105–10. doi: 10.1038/nn.3279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lebreton M, Abitbol R, Daunizeau J, Pessiglione M. Automatic integration of confidence in the brain valuation signal. Nat Neurosci. 2015;18:1159–1167. doi: 10.1038/nn.4064. [DOI] [PubMed] [Google Scholar]
- 16.Summerfield C, Tsetsos K. Do humans make good decisions? Trends Cogn Sci. 2014;19:27–34. doi: 10.1016/j.tics.2014.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Louie K, Glimcher PW. Efficient coding and the neural representation of value. Ann N Y Acad Sci. 2012;1251:13–32. doi: 10.1111/j.1749-6632.2012.06496.x. [DOI] [PubMed] [Google Scholar]
- 18.Glimscher PW, Camerer C, Fehr E, Poldrack A. Neuroeconomics: Decision Making and the Brain. Elsevier; 2008. [Google Scholar]
- 19.Woodford M. Prospect Theory as Efficient Perceptual Distortion. Am Econ Rev. 2012;102:41–46. [Google Scholar]
- 20.Summerfield C, Tsetsos K. Building Bridges between Perceptual and Economic Decision-Making: Neural and Computational Mechanisms. Front Neurosci. 2012;6:70. doi: 10.3389/fnins.2012.00070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Khaw MW, Li Z, Woodford M. Risk Aversion as a Perceptual Bias. Work Pap. 2017 [Google Scholar]
- 22.Padoa-Schioppa C. Range-Adapting Representation of Economic Value in the Orbitofrontal Cortex. J Neurosci. 2009;29:14004–14014. doi: 10.1523/JNEUROSCI.3751-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Rustichini A, Conen KE, Cai X, Padoa-Schioppa C. Optimal coding and neuronal adaptation in economic decisions. Nat Commun. 2017;8 doi: 10.1038/s41467-017-01373-y. 1208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Cox KM, Kable JW. BOLD subjective value signals exhibit robust range adaptation. J Neurosci. 2014;34:16533–43. doi: 10.1523/JNEUROSCI.3927-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Khaw MW, Glimcher PW, Louie K. Normalized value coding explains dynamic adaptation in the human valuation process. Proc Natl Acad Sci U S A. 2017;114:12696–12701. doi: 10.1073/pnas.1715293114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Girshick AR, Landy MS, Simoncelli EP. Cardinal rules: visual orientation perception reflects knowledge of environmental statistics. Nat Neurosci. 2011;14:926–932. doi: 10.1038/nn.2831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Louie K, Khaw MW, Glimcher PW. Normalization is a general neural mechanism for context-dependent decision making. Proc Natl Acad Sci U S A. 2013;110:6139–44. doi: 10.1073/pnas.1217854110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Grueschow M, Polania R, Hare TA, Ruff CC. Automatic versus Choice-Dependent Value Representations in the Human Brain. Neuron. 2015;85:874–85. doi: 10.1016/j.neuron.2014.12.054. [DOI] [PubMed] [Google Scholar]
- 29.Hare TA, Schultz W, Camerer CF, O’Doherty JP, Rangel A. Transformation of stimulus value signals into motor commands during simple choice. Proc Natl Acad Sci U S A. 2011;108:18120–18125. doi: 10.1073/pnas.1109322108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Shadlen MNN, Shohamy D. Decision Making and Sequential Sampling from Memory. Neuron. 2016;90:927–939. doi: 10.1016/j.neuron.2016.04.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Milosavljevic M, Malmaud J, Huth A, Koch C, Rangel A. The drift diffusion model can account for value-based choice response times under high and low time pressure. Judgement Decis Mak. 2010;5:437–449. [Google Scholar]
- 32.Gluth S, Sommer T, Rieskamp J, Büchel C. Effective Connectivity between Hippocampus and Ventromedial Prefrontal Cortex Controls Preferential Choices from Memory. Neuron. 2015;86:1078–1090. doi: 10.1016/j.neuron.2015.04.023. [DOI] [PubMed] [Google Scholar]
- 33.Pouget A, Drugowitsch J, Kepecs A. Confidence and certainty: distinct probabilistic quantities for different goals. Nat Neurosci. 2016;19:366–374. doi: 10.1038/nn.4240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Sanders JI, Hangya B, Kepecs A. Signatures of a Statistical Computation in the Human Sense of Confidence. Neuron. 2016;90:499–506. doi: 10.1016/j.neuron.2016.03.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.van den Berg R, Yoo AH, Ma WJ. Fechner’s law in metacognition: A quantitative model of visual working memory confidence. Psychol Rev. 2017;124:197–214. doi: 10.1037/rev0000060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wiech K. Deconstructing the sensation of pain: The influence of cognitive processes on pain perception. Science (80-. ) 2016;354:584–587. doi: 10.1126/science.aaf8934. [DOI] [PubMed] [Google Scholar]
- 37.Hare TA, Camerer CF, Rangel A. Self-control in decision-making involves modulation of the vmPFC valuation system. Science (80-. ) 2009;324:646–648. doi: 10.1126/science.1168450. [DOI] [PubMed] [Google Scholar]
- 38.Sen AK. Choice Functions and Revealed Preference. Rev Econ Stud. 1971;38:307. [Google Scholar]
- 39.Bernheim BD, Rangel A. Beyond Revealed Preference: Choice-Theoretic Foundations for Behavioral Welfare Economics. Q J Econ. 2009;124:51–104. [Google Scholar]
- 40.Sims CR. Rate–distortion theory and human perception. Cognition. 2016;152:181–198. doi: 10.1016/j.cognition.2016.03.020. [DOI] [PubMed] [Google Scholar]
- 41.Stewart N, Chater N, Brown GDA. Decision by sampling. Cogn Psychol. 2006;53:1–26. doi: 10.1016/j.cogpsych.2005.10.003. [DOI] [PubMed] [Google Scholar]
- 42.Fleming SM, Daw ND. Self-evaluation of decision-making: A general Bayesian framework for metacognitive computation. Psychol Rev. 2017;124:91–114. doi: 10.1037/rev0000045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Weber EU, Johnson EJ. Mindful judgment and decision making. Annu Rev Psychol. 2009;60:53–85. doi: 10.1146/annurev.psych.60.110707.163633. [DOI] [PubMed] [Google Scholar]
- 44.Baxter MG, Murray EA. The amygdala and reward. Nat Rev Neurosci. 2002;3:563–573. doi: 10.1038/nrn875. [DOI] [PubMed] [Google Scholar]
- 45.Bowers JS, Davis CJ. Bayesian just-so stories in psychology and neuroscience. Psychol Bull. 2012;138:389–414. doi: 10.1037/a0026450. [DOI] [PubMed] [Google Scholar]
- 46.Griffiths TL, Lieder F, Goodman ND. Rational Use of Cognitive Resources: Levels of Analysis Between the Computational and the Algorithmic. Top Cogn Sci. 2015;7:217–229. doi: 10.1111/tops.12142. [DOI] [PubMed] [Google Scholar]
- 47.Sims CR. Efficient coding explains the universal law of generalization in human perception. Science. 2018;360:652–656. doi: 10.1126/science.aaq1118. [DOI] [PubMed] [Google Scholar]
- 48.Li V, Michael E, Balaguer J, Herce Castañón S, Summerfield C. Gain control explains the effect of distraction in human perceptual, cognitive, and economic decision making. Proc Natl Acad Sci U S A. 2018;115:E8825–E8834. doi: 10.1073/pnas.1805224115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Landry P, Webb R. Pairwise Normalization: A Neuroeconomic Theory of Multi-Attribute Choice. SSRN Electron J. 2017 doi: 10.2139/ssrn.2963863. [DOI] [Google Scholar]
- 50.Robson AJ. The Biological Basis of Economic Behavior. J Econ Lit. 2001;39:11–33. [Google Scholar]
- 51.Polanía R, Moisa M, Opitz A, Grueschow M, Ruff CC. The precision of value-based choices depends causally on fronto-parietal phase coupling. Nat Commun. 2015;6 doi: 10.1038/ncomms9090. 8090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Plummer M, et al. JAGS: A program for analysis of Bayesian graphical models using Gibbs sampling. Proceedings of the 3rd International Workshop on Distributed Statistical Computing (DSC 2003); March 20–22; 2003. [Google Scholar]
- 53.Gelman A, et al. Bayesian Data Analysis. Third Edition. Vol. 2013 CRC Press; 2013. [Google Scholar]
- 54.Venables WN, Ripley BD. Modern Applied Statistics with S. Springer; 2002. [Google Scholar]
- 55.R Core Team. R: A Language and Environment for Statistical Computing. 2017.
- 56.Vehtari A, Gelman A, Gabry J. Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC. Stat Comput. 2016:1–20. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.