Computational protein structure refinement: Almost there, yet still so far to go

Abstract

Protein structures are essential in modern biology yet experimental methods are far from being able to catch up with the rapid increase in available genomic data. Computational protein structure prediction methods aim to fill the gap while the role of protein structure refinement is to take approximate initial template-based models and bring them closer to the true native structure. Current methods for computational structure refinement rely on molecular dynamics simulations, related sampling methods, or iterative structure optimization protocols. The best methods are able to achieve moderate degrees of refinement but consistent refinement that can reach near-experimental accuracy remains elusive. Key issues revolve around the accuracy of the energy function, the inability to reliably rank multiple models, and the use of restraints that keep sampling close to the native state but also limit the degree of possible refinement. A different aspect is the question of what exactly the target of high-resolution refinement should be as experimental structures are affected by experimental conditions and different biological questions require varying levels of accuracy. While improvement of the global protein structure is a difficult problem, high-resolution refinement methods that improves local structural quality such as favorable stereochemistry and the avoidance of atomic clashes are much more successful.

Graphical Abstract

Protein structure refinement to improve a template-based model (green) towards the native structure (red) continues to be a challenging computational problem.

Introduction

When the first protein structures were solved via X-ray crystallography^{1, 2}, it became instantly clear that detailed structural information at the atomistic level is the key to a full mechanistic understanding of biological processes. The sequence-structure-function paradigm is now an essential feature of modern molecular and cellular biology³. Accurate protein structures are necessary as starting points for rational drug design⁴, protein engineering applications⁵, and to understand functional implications of mutations associated with genomic variations within populations⁶. We have reached an age where structural information is available for most types of proteins⁷. Nevertheless, the number of known genes continues to greatly outnumber the number of available protein structures by orders of magnitude as experimental protein structure determination remains a slow and tedious process. This has motivated computational efforts to predict protein structures soon after the first protein structures became available^{8, 9}. Since early on, ab initio methods have aimed at structure prediction via physics-motivated models with the idea that, starting from extended chains, the native structure could be found via sampling or optimization as the lowest (free) energy state^{10, 11}. To overcome computational limitations, these approaches have often invoked simplified models of proteins such as polymers decorated with patterns of polar and hydrophobic side chains^12–14. While much has been learned at the fundamental level about protein structures and the folding process¹³, pure ab initio methods that do not use any information from known structures largely fail to accurately and reliably predict the structures of all but very small proteins^{15, 16}. This remains true today even as more sophisticated models can be sampled extensively on today’s computers. In contrast, using knowledge from known structures to predict new structures, has always been a far more successful strategy^17–20. Homology modelling, which assumes that similar amino acid sequences lead to similar structures, is the standard method for predicting protein structures²¹. Furthermore, advanced methods that assemble models based on structural fragments taken from known structures are often able to generate useful models for sequences where homologous proteins with known structures cannot be found^22–24.

Predicted structural models generated with today’s methods can be impressively accurate^{25, 26}, but they still often do not reach experimental accuracy (considered to be <1Å root mean square deviation (RMSD) for all heavy atoms). The reliance on structural templates inherently limits the ability to capture subtle variations in protein structures as a result of minor differences in amino acid sequence. Template-based modelling is also problematic when interaction partners such as other proteins, nucleic acids or ligands, perturb the structure and when templates that include such interactions are not available. This has created the need for structure refinement methods to improve initial models towards experimental accuracy^27–36. Structure refinement methods are widely used already to derive atomistic structures from nuclear magnetic resonance (NMR) restraints^{37, 38} and during crystallographic structure determination^39–41 either de novo or via molecular replacement. The use of lower-resolution data, such as from electron microscopy (EM)⁴², small-angle X-ray scattering (SAXS)^{43, 44}, or cross-linking information⁴⁵ can also be very effective in guiding structure refinement when combined with template-based modelling. In the absence of experimental data, structure refinement is tasked with improving initial template-based models using just computation. As template-based models often come within 2–5 Å Cα RMSD from an experimentally determined native structure⁴⁶, the goal of structure refinement is a seemingly moderate degree of improvement in accuracy by just a few Å. While an accurate overall fold of the native structure, based on the backbone Cα atoms, is often the main target of structure prediction, high-resolution refinement also comes with the expectation of generating accurate side chain orientations⁴⁷ and a high stereochemical quality that is comparable to experimental structures^48–50.

Template-based models already incorporate knowledge from existing structures. Therefore, structure refinement has to rely on alternative strategies⁵¹. A common idea is to use atomistic force fields in conjunction with energy minimization or more extensive sampling methods, in particular molecular dynamics (MD) simulations⁵². The resolution of atomistic force fields matches the target resolution of structure refinement. The hope is that conformational sampling can reach the native state as the state with the lowest free energy with no or few kinetic barriers since the initial model is already very close to the correct structure. Other strategies involve the targeted optimization of certain aspects of a given model^53–55. Such an approach would be especially effective when there is knowledge about which parts of a given structure are least accurate and would benefit most from refinement. Highly successful structure refinement has been documented in anecdotal cases for a while^{28, 34, 36, 52, 56–60}, but broadly useful strategies for structure refinement have only recently begun to emerge^61–66. What seemed to be a relatively straightforward task, turned out to be exceedingly challenging. The objective of this review is to present the current state of the art and outline the significant challenges that remain.

The goal of structure refinement: How close is close enough?

Template-based models often correctly capture the overall fold of a given protein structure. On the other hand, effective atomic coordinate precisions as high as 0.2 Å provided by most crystal structures⁶⁷ are not needed, for example, to determine which residues to mutate in biochemistry experiments that investigate a proposed biochemical mechanism. Therefore, it has to be established first what level of accuracy is necessary to obviate experimental structures before discussing how to reach such accuracy.

Mechanistic analyses

A primary use of high-resolution structures is to provide mechanistic insight that may require 1 Å resolution or better, especially when reaction mechanisms involving quantum mechanics would be applied⁶⁸. Mechanistic analyses likely also require the accurate modelling of side chains and cofactors such as ions or ligands. However, as such questions are often focused on certain parts of a given structure, an accuracy better than 1 Å RMSD for all heavy atoms may not be needed across an entire structure for a model to be useful. Fortunately, the functionally most important regions of a given protein are also typically most conserved among homologues with the same function. Therefore, initial template-based models may already be highly accurate at mechanistic key sites and refinement methods may not need to improve those regions by much in order to reach experimental accuracy.

Prediction of binding partners

Protein structures serve as the starting point for a variety of further computational analyses. An important application is the identification of potential binding partners, such as proteins, ligands, and potential drug molecules^{69, 70}. This type of analysis may be important for functional predictions but also during rational drug design applications. Previous studies have shown that homology models are often inferior to experimental structures for reliably predicting protein-protein interfaces⁷¹ and for generating docked conformations with small-molecule ligands^{72, 73}. The docking of small molecules is expected to require high structural accuracy near the binding site and preferable models of holo structures since docking to apo structures may not be successful if, for example, binding sites are occluded⁷⁴. Protein-protein interactions are sensitive to shape complementary over larger parts of a given protein surface. This may necessitate the accurate modelling of dynamic regions on the surface such as loops as they can alter the overall shape substantially if modelled incorrectly, even if such parts may otherwise not be functionally important^75–77.

Biological relevance of experimental reference structures

The ultimate goal of structural prediction is to generate high-resolution models of proteins in their biologically most relevant conformation. In contrast, much of the assessment of structure prediction methods is driven by comparisons against experimental reference structures from X-ray crystallography or NMR, e.g. in the context of the biannual Critical Assesment of protein Structure Prediction (CASP) competitions²⁵. Crystal structures may or may not exactly correspond to the biologically most relevant due to crystal contacts⁷⁸ and other peculiarities of the artificial crystal environment that could have a significant effect on protein structures⁷⁹. While it may be possible to consider the crystal environment during computational structure refinement, focusing refinement methods too much on exactly reproducing X-ray structures distracts from capturing what is biologically most relevant. Another related concern is that although crystallography has promoted a largely static view of structural biology, in reality, protein structures exhibit significant dynamics, especially at physiological temperatures⁸⁰. Therefore, the most accurate representation of protein structures would be an ensemble spanning the native state with, for example, alternate conformations for flexible loops⁸¹. Computational refinement methods could in principle deliver such ensembles and comparisons could be made against crystallographic B-factors or NMR-derived ensembles. But a broader validation of how accurate computer-generated ensembles are could bemore challenging.

Structure refinement via minimization and molecular dynamics simulations

The use of force-field based energy minimization or MD simulation has long been a popular strategy for structure refinement following homology model generation^82–90. The immediate benefit of force-field based refinement is the resolution of atomic clashes, deviations from standard bonding geometries, and other gross pathologies that may have been introduced as a result of using coarse-grained representations⁹¹ or the combination of templates from multiple structures⁹² during homology modeling. Distorted bond geometries and unfavorable atomic interactions correspond to high-energy states with atomistic force fields that can be quickly relieved when subjected to short optimization^{55, 83, 91, 93–95}. On the other hand, the use of longer MD simulations for protein structure refinement (see Fig. 1, left side) has appeared as an obvious choice to achieve more extensive refinement without requiring any further knowledge or assumptions^{86, 96}. Confidence in the ability of MD simulations to deliver on the promise of being able to refine approximate models stems from ample evidence that modern atomistic simulations typically maintain native conformations in close correspondence with experimental data^{97, 98} while also being able to fold peptides and small proteins via MD simulations given sufficient sampling^{16, 99–103}. This suggests that MD simulations should in principle be able to accomplish refinement by sampling conformations on a downhill energy landscape towards the native state, at least to within the 1–3 A Cα RMSD deviations that are typically seen in MD simulations that are started from experimental structures¹⁰⁴. The two main challenges in MD-based structure refinement are the accuracy of the model to ensure that the native state is indeed at the global minimum¹⁰⁵ and the amount of conformational sampling that is needed to reach the native state from an initial model³². Refinement may be further complicated by a lack of a clear downhill funnel from near-native conformations to the native basin as a result of roughness in the energy landscape and/or force field inaccuracies when atomistic models are applied^{87, 106}. Another challenge is the selection of a refined model from the conformational ensemble generated in MD simulations where the last conformation in a given run may not necessarily be the most native-like structure⁶². All of these issues are discussed in more detail in the following.

Figure 1:

Typical refinement protocols via MD-based sampling (left) and iterative structure optimization (right). Grey colors indicate optional elements. KB: Knowledge-based.

Force fields and solvation models

An accurate energy description is essential to distinguish the native state from similar, but less accurate initial models that may have been generated by template-based modeling. The first choice may be atomistic force fields that have improved significantly in accuracy over the last decade^{97, 98, 100, 107–111}. Backbone torsion potentials, a key ingredient to correctly reproduce secondary structure propensities, have been fine-tuned to balance ab initio data with experimental data on small peptides and torsional distributions in structures from the Protein Data Bank (PDB)^{97, 107, 109}. Other improvements have focused on side chain rotamer sampling and a better balance of solvation and salt-bridge interactions of charged and polar residues^{107, 112, 113}. Most recently, the attention has shifted to the sampling of disordered regions as most available force fields have a tendency to over-stabilize ordered and compact states^{107, 114–117}. While the sampling of disordered peptides is less relevant in the context of structure refinement, which generally targets well-folded proteins, a better balance between folded and disordered states may benefit the sampling of more dynamic regions such as longer loops that are part of many folded proteins. The most recent sets of force fields perform very well when folding model peptides and smaller proteins and there is evidence that force field improvements translate into better accuracy during structure refinement^{61, 87, 107, 118, 119}. In addition to physics-based force fields, statistical potentials have also been used in MD- or minimization-based refinement methods^{56, 83, 120}. Other efforts aim at specifically training potentials to deepen the energy of protein native states^{87, 119} and/or to penalize excursions to non-native states⁸⁸.

As the inclusion of solvent is generally important in modeling biological systems, it is also key for successful refinement¹²¹. Atomistic force fields are typically meant to be combined with explicit water to account for solvation effects. However, the high cost of explicit solvent and requirements for extensive sampling demand significant computational resources. Therefore, implicit solvent methods have been used as a more efficient alternative in MD simulations^122–125. Generalized Born models are especially attractive and have led to success in protein folding and refinement^{34, 35, 94, 120, 121, 126–136}, but even simpler models such as a distant-dependent dielectric can be applicable during refinement⁸⁵. However, implicit solvent models may have artifacts such as an overstabilization of salt-bridges and secondary structure elements that may require specially optimized force fields to be effective^{133, 137–140}.

Coarse-grained models offer advantages over fully atomistic force fields^{141, 142} by reducing computational costs, and providing smoother energy landscapes that are helpful in navigating the transition from a slightly incorrect but already well-folded initial model to the native state. Although very coarse models, such as Cα-based protein models are problematic when applied to high-resolution structure refinement, moderately coarse-grained models such as UNRES^{143, 144} or PRIMO^{145, 146} can be suitable alternatives to the more expensive all-atom standard force field treatments during refinement⁸⁵.

Conformational sampling strategies

In addition to the accuracy of the energy function, conformational sampling is essential to overcome the kinetic barriers during the transition from an initial model to the native state during refinement. Initial attempts at MD-based structure refinement quickly established that sub-nanosecond time scales are not sufficient⁵². Instead, much longer time scales on the order of 100 ns or beyond may be required to achieve any significant refinement at all³⁶. Furthermore, it has been found that unrestrained sampling that is started from an initial template-based model often deviates quickly and sometimes quite significantly away from the native state rather than towards it^{58, 82}. Even simulations on 100 μs time scales, when unrestrained, generally do not come back towards the native state³². Force field issues have been suggested as an obvious culprit³². Another argument is that the initial template-based models are overly compact so that the only way to refine further would be to first expand the structure away from the native state⁹². More generally, the idea is that homology models may not lie exactly on the folding funnel exhibiting and local defects such as mispacked side chains or incorrect secondary structures may only be resolvable on low free energy paths via partial unfolding and eventual refolding¹⁴⁷. Since unfolding and refolding may take a very long time, this has led to a general practice of applying weak restraints with respect to a given initial model during refinement so that large structural drifts are prevented while still allowing some refinement towards the native state^{32, 34, 56, 61, 62, 89, 90, 95}. Restraints are commonly implemented based on Cα RMSD but may alternatively encode pairwise distances within a given reference structure¹²⁶. The application of restraints can be effective when the initial model is close to the native state, but this practice opposes larger conformational arrangements that are needed to refine models that are further away from the native state. In some refinement protocols, restraints are applied based on selected fragments rather than the entire structure¹⁰⁶ or are limited to regions deemed least reliable^{59, 60}, either based on previous knowledge^{59, 60} or quality assessment criteria⁹⁵. There are also methods that combine multiple, possibly conflicting sets of restraints based on homologs^{89, 90} or other knowledge to maintain the conformational sampling close to the native state¹⁴⁸.

MD simulations are often combined with enhanced sampling methods such as replica exchange (REXMD)¹⁴⁹ or other related techniques¹⁵⁰. In protein folding simulations, enhanced sampling techniques can accelerate in silico folding by several orders of magnitude^151–156. Consequently, some of these methods have also been used in the context of refinement^{37, 58, 59, 120, 127, 128, 147, 157}. Other strategies for navigating the high-dimensional space of atomistic models during refinement include normal mode (NMA) based sampling^{31, 41, 158}, torsional dynamics^{58, 84, 126, 159}, or multi-scale methods where coarse-grained and atomistic models are mixed^{85, 132, 160–165}. Other methods sample conformations either via the direct replacement of fragments from a library, often via Monte Carlo (MC) sampling,^{53, 158, 166} or by guiding MD sampling by constraints from such fragments¹⁰⁶. Thus, traditional force field based methods are effectively combined with knowledge-based (KB) approaches. In all cases, the general idea is to focus sampling on lower-resolution space to more efficiently overcome the major barriers during refinement. However, refinement either via directly enhancing sampling of atomistic models or by confining sampling to lower-resolution space has so far not quite provided the breakthrough one would hope for. The reason is probably that the accelerated sampling does not prevent structures drifting away from the native state if restraints are not applied¹⁵⁷. On the other hand, the use of restraints largely cancels the advantage of enhanced sampling so that the effective performance becomes similar to what can be achieved with regular MD simulations.

Selecting refined structures from MD ensembles

MD simulations generate trajectories that follow the free energy landscape for a given system according to the force field used in the simulation. In the ideal case where the native structure indeed corresponds to the free energy minimum and the sampling is long enough to reach full convergence, the largest population of structures in the ensemble generated by MD would be expected to correspond to the native state. However, it is not guaranteed that any snapshot, and in particular the final structure from a long MD run, corresponds to the native state as there may be excursions to non-native states with energies similar to the native state. In practical scenarios, where sampling is more limited and/or the native state is only a metastable state with a given force field, there may be larger excursions for much of a given trajectory. Therefore, simply taking the final structure from an MD run is rarely the best choice for obtaining improved structures. One common approach to overcome this challenge is to treat the structural ensemble as a set of decoys and apply clustering and/or scoring methods to find the most native-like structures^{35, 94, 105, 126, 167–172}. The generation of decoys followed by scoring is a widely applied strategy in structure prediction. However, during refinement, where the generated models are very similar to each other and to the native state, the limited accuracy and noise in typical scoring functions may cause high false positive rates^{35, 170, 173, 174}. As a consequence, it is often very difficult to identify the most refined models, or even distinguish refined models from models that have become worse in snapshots from MD simulations^{31, 62}. An interesting alternative to traditional scoring is to use the stability in MD simulations as a scoring function¹¹⁸. In a similar spirit, one may also score based on the distance by which models deviate from an initial model during refinement⁶² as structures that remain closer to an initial model generally appear to be closer to the native state.

A different strategy to selecting one or few structures is to consider larger subsets of conformations from an MD-generated ensemble and obtain a refined model via conformational averaging of those conformations^{61, 62, 66, 158}. The subset may be determined via scoring as well but applying scoring functions as a filter is more robust than selecting one or few structures. In addition, the conformational averaging further reduces sensitivity to noise in the scoring function¹⁷⁵. Conformational averaging of a structural ensemble generated via MD is also conceptually more consistent with how MD ensembles should be compared to experimental structures since experiments implicitly involve extensive ensemble- and time-averaging¹⁷⁶. Indeed, subset averaging of MD simulations has contributed to the most robust success in structure refinement to date^{62, 175}.

Structure refinement via structure optimization

While MD-based refinement typically relies on a physics-based force field to move an initial model towards the native state, an alternative approach is the targeted optimization of specific aspects of a given structure (see Fig. 1, right side), often via iterative protocols. In particular, the hydrogen bond network that is key for secondary structure formation may be examined and re-optimized^{55, 93, 106} or structural elements of a given model such as secondary structure elements or loops may be resampled extensively to find better conformations^{28, 58, 95, 118}. The resampling of structural fragments using a fragment library as already mentioned above in the context of MD simulations^{106, 158, 166} would also fall into this category as such methods have the potential to re-optimize larger sections at once. While most optimization protocols involve conventional sampling or minimization using a suitable energy function, an alternative approach is the use of a constraint-based geometric technique where parts of a structure are iteratively pulled open and reannealed to mimic chaperon-induced unfolding and refolding¹⁴⁷. As in the application of restraints, selective refinement could target only certain parts of a structure based on quality assessment criteria to determine which parts are most likely in need of refinement. Targeted optimization often involves the generation of decoys followed by subsequent scoring which would be subject to same challenges and uncertainties as the scoring of snapshots generated via full MD simulations¹¹⁸.

Certain structure quality criteria can be targeted via optimization without requiring knowledge of the native structure. An example is the MolProbity score¹⁷⁷ that combines various stereochemical quality criteria such as the avoidance of atomic clashes, bond, angle, and torsion distributions consistent with statistics from known structures, favorable hydrogen bond patterns and other generic features of protein structures. Most optimization protocols focus at least in part on structure quality by improving side chain orientations, hydrogen bonding, and/or general stereochemical accuracy^{49, 83, 178}. Clashes and major bond distortions are easily removed with standard force fields whereas hydrogen bonding geometries of donors and acceptors in close proximity can be optimized with KB functions^{106, 179}. Since the local structure quality and overall accuracy of the fold, measured based on Cα coordinates, are only weakly correlated in typical template-based models⁴⁹, the local quality can often be improved without altering the Cα coordinates⁴⁹ and therefore quality optimization can be employed as a final step for example after MD-based refinement that would focus more on improving the overall fold⁴⁹.

Performance of refinement methods

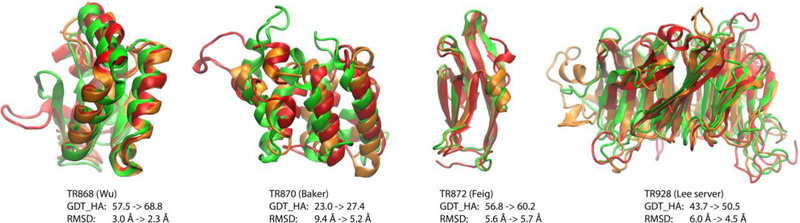
Until recently, successful structure refinement without the use of experimental data was limited to selected cases while overall consistency was lacking. Up until CASP8, the overall most consistent structure refinement method was essentially not to attempt refinement at all⁶⁵. In CASP9, refinement methods started to eke out, on average, very slight improvements⁶⁴. Beginning with CASP10, MD-based refinement became successful as a result of force field improvements, extensive sampling, and the application of ensemble averaging^{46, 63}. The current state of the art is that almost any model can now be refined by a modest amount (on average by 1–3 units of the Global Distance Test (GDT) score¹⁸⁷), with very few models becoming worse while some models may become significantly better (up to 10 GDT units; see the example for TR872 in Fig. 2). GDT captures the number of residues where Cα coordinates can be superimposed within four different RMSD cutoffs (1, 2, 4, 8 Å for GDT_TS and 0.5, 1, 2, 4 Å for GDT_HA) and essentially reflects how much of a given structure is accurate to within a few Å while being insensitive to incorrectly modeled parts. Improvements in GDT scores are consistent with the refinement of structural regions that are already fairly good in the initial model. In terms of RMSD, reliable refinement methods rarely exceed improvements by more than 1 Å. Since the overall RMSD is more sensitive to parts of a model that deviate significantly from the native structure, this suggests that consistent refinement of those regions is more difficult. The most successful refinement protocols (see Table 1) largely use MD or MC-type sampling methods and/or energy minimization with a combination of atomistic force fields and/or KB scoring terms, but alternative methods focusing on structure optimization can also perform similarly well. The use of restraints during the MD simulations is common but it limits more significant refinement, especially in more dynamic regions such as loops. Less conservative approaches that sample more aggressively and do not use restraints continue to result in remarkable successes (see for example the best predictions for the TR868 and TR870 CASP12 targets from the Wu and Baker groups in Fig. 2)^{29, 158}. As these methods also generate many deteriorated models for other targets, a lack of consistency hinders practical applications, though. In particular, it remains difficult, despite much effort, to discriminate successful from unsuccessful cases¹⁵⁸. Therefore, less conservative methods are only useful in cases where high failure rates can be tolerated, for example to improve success with molecular replacement during crystallographic refinement^{64, 188}.

Figure 2:

Examples of successful protein structure refinement based on CASP12 targets (from CASP12 web site: http://www.predictioncenter.org/casp12/index.cgi). Experimental, initial, and refined structures are shown in red, green, and orange, respectively. RMSD values refer to Cα atom deviations. The GDT_HA score is explained in the text.

Table 1:

Selected Refinement Protocols and Web Services

Name Reference	Method	Selection	Web server
KoBaMIN Chopra et al.83	Minimization w/ KB force field	Minimized structure	http://csb.stanford.edu/kobamin/
Carlsen & Røgen88	Optimization with iteratively refined KB potential	Minimized structure	N/A
3DRefineCheng et al.55, 180	H-Bond Optimization Minimization w/physics & KB force field (MESHI178)	Minimized structure	http://sysbio.rnet.missouri.edu/3Drefine/
Anton Shaw et al.32	Very long MD (100 μs)	Force field/Cluster size	N/A
PREFMD Feig et al.61, 62, 66	MD (μs scale) with restraints	Averaging over subset based on DFIRE181, RW+182, iRMSD62	http://feig.bch.msu.edu/web/services/prefmd
Schröder et al.89, 90	MD (ns scale) with restraints from coupled homologs	Final structure	N/A
Wu et al.29	(REX)MD (μs scale) with optimized force field	Best RMSD	N/A
Honig & Mark120	REXMD	Scoring with RAPDF183/DFIRE181	N/A
Olson & Lee157	REXMD	Scoring with force field, GOAP184, dDFIRE185	N/A
GNEIMO Vaidehi et al.58, 84	Torsional space REXMD	Force field	N/A
FG-MD Zhang et al.106	Fragment-guided MD	KB scoring function	http://zhanglab.ccmb.med.umich.edu/FG-MD/
GalaxyRefine Seok et al.47, 186	Sidechain repacking Iterative MD (ps scale)	Final structure	http://galaxy.seoklab.org/refine
TIGRESS Floudas et al.126	Constraint based sampling (torsion MD, Rosetta24, MD)	Selection based on machine learning	http://atlas.princeton.edu/refinement
Kosztin et al.118	Targeted optimization (RosettaRelax24) and MD	MD-based stability	N/A
ROSETTA Baker et al.158	Iterative relaxation MD-based sampling NMA-based sampling Fragment rebuilding	Clustering and averaging Scoring with GOAP184	N/A
FRODA Ozkan et al.147	Selective unfolding with geometric method, refolding with REXMD	Clustering and scoring with DFIRE181	N/A
Skolnick et al.87	REXMC (A-TASSER119) with optimized force field	Force field energy	N/A
locPREFMD Feig et al.49	Iterative optimization targeting local geometry	MolProbity117 score	http://feig.bch.msu.edu/web/services/locprefmd

Closer inspection of Fig. 2 reveals a general trend that refinement is most successful in regions where only minor rearrangements are necessary. Correct reorientations of helices appear to be especially successful. On the other hand, larger structural errors remain largely uncorrected or structures may even become worse in those areas after refinement. In other words, the most problematic parts of a given model that would benefit most from refinement remain also the hardest parts to improve. How to improve those parts of an initial model will be the main challenge going forward towards achieving near-experimental accuracy.

Structure refinement via MD can incur significant computational costs as the best current protocols apply sampling from tens of nanoseconds to microsecond scales. Although very long MD simulations do not necessarily lead to better refinement³², even moderate-length MD simulations require significant resources. This has limited broad adoption of MD-based refinement as part of standard structure prediction pipelines. Although refinement web servers have become available, they tend to offer only a limited amount of refinement^{55, 83, 180, 186}. It will require additional efforts and resources to focus on optimizing computational efficiency for MD-based methods so that more significant refinement via web-based services can benefit the broader community.

Related to the development of computationally efficient refinement protocols is the question of how to tell when sufficient refinement has been achieved. In principle, successful refinement methods should continue refinement until the native structure is reached and at that point there should be no further structural changes. However, the lack of structural variation during continued application of a given refinement protocol could also simply reflect being stuck in a non-native metastable state. How to distinguish those two is so far an unresolved problem.

The practical utility of refinement methods would benefit from knowledge about what kind of initial models are most likely to improve upon refinement. One question is how refinement success depends on the initial model, both in terms of distance from the native structure and how it was generated. Analysis from recent rounds of CASP suggests that models that are closer to the native structure may be generally more amenable to refinement^{46, 63, 66}. This may be useful information since the quality of initial models can be assessed with some degree of certainty¹⁸⁹. Another question is how the method used for initial model generation affects refinement. Analysis based on CASP results has offered some insights⁶⁶, but as prediction methods used in CASP often involve convoluted pipelines and may include refinement already as part of their modeling protocol, it is difficult to arrive at clear conclusions.

While the refinement of the overall protein fold remains a significant challenge, at least the improvement of the local stereochemical quality has turned out to be more straightforward^{49, 83, 106}. Generally, the optimization of force field and/or KB terms with iterative protocols that target a reduction in quality scores such as MolProbity¹⁷⁷ are sufficient and perform well. For example, the locPREFMD method is able to improve MolProbity scores for almost any starting structure to values below 1–1.5, which is comparable to experimental structures. Although locPREFMD uses MD simulations as part of the protocol, simulations are short and the resulting stereochemical refinement can be completed on moderate resources within minutes⁴⁹.

Conclusions

Computational protein structure refinement aims at turning approximate initial models, which can be generated today for many genes where no experimental structures exist, into structures with accuracy and quality that is comparable to experimental structures. While that remains a significant challenge, recent successes, especially with protocols based on MD simulations that can deliver modest but consistent refinement, are beginning to point in the right direction. Such MD-based methods may become part of standard prediction pipelines to improve template-based models. Moreover, methods that target local structural quality have become available to apply finishing touches to generate models that satisfy most quality criteria expected from experimental structures. However, as the overall degree of refinement with the best methods still remains modest on average, the refinement problem is far from solved.

Going forward, it appears that the ever-recurring issues of force field and scoring function accuracy on one side and sampling insufficiency on the other side still need to be fully addressed. Current force fields are much improved, but they are far from perfect and the most successful refinement protocols combine standard atomistic force fields with KB functions in some form or fashion. One underappreciated aspect involves polarization effects that are difficult to capture with fixed charge force fields and that have limited for example the accurate description of hydrogen bonding^{179, 190}. It will, therefore, be interesting to see how much can be gained with polarizable force fields¹⁹¹ in the context of structure refinement. However, sampling is probably still the more significant challenge. Having to use restraints to obtain consistent refinement is a major impediment towards more significant refinement and the key to developing more effective refinement methods will be how to prevent initial models from deviating too far from initial models while still allowing refinement by several Å RMSD. One idea to overcome this conundrum may be the simultaneous use of multiple restraints^{148, 192} and/or adaptive restraints^{15, 89, 90} to limit sampling while still being able to reach the native state. Another successful path may be to continue to explore strategies that explicitly follow an unfolding/refolding scheme¹⁴⁷ as that more likely mimics what nature would do to reach the native state from misfolded states via chaperones¹⁹³.

As refinement methods become better at reaching experimental accuracy, the exact reproduction of experimental conditions will become increasingly important. Current methods generally do not fully consider ionization equilibria of titratable amino acid side chains, the potential effect of ligands and ions, and the structural constraints imposed by crystal packing for structures solved by crystallography. There is a danger, however, to overemphasize single structures under very specific, possibly artificial conditions, whereas the ultimate goal should be to produce structural ensembles that are representative of the biological context including the crowded conditions of the cellular environment^{194, 195}.

Finally, another underdeveloped direction is the prediction and refinement of membrane protein structures^196–198. It may be that similar strategies as for soluble proteins will be successful but limited assessment, during CASP for example, has effectively discouraged efforts by the community to date. As a consequence, it is much less clear, for example, how well scoring functions work for membrane protein structures^{199, 200} and how the sampling challenges present for soluble proteins translate to membrane proteins²⁰¹.