Self-organized shape dynamics of active surfaces

Significance

Morphogenesis, the emergence of shape and form in biological systems, is a process that is fundamentally mechanochemical: Shape changes of material are driven by active mechanical forces that are generated by chemical processes, which in turn can be affected by the deformations and flows that occur. We provide a framework that integrates these interactions between the geometry of deforming materials and active processes in them by introducing the shape dynamics of self-organized active surfaces. We show that the tight coupling between surface mechanics and active processes gives rise to the spontaneous formation of nontrivial shapes, shape oscillations, and directed peristaltic motion. Our simple yet general description lays the foundation to explore the regulatory role of shape in morphogenetic processes.

Abstract

Mechanochemical processes in thin biological structures, such as the cellular cortex or epithelial sheets, play a key role during the morphogenesis of cells and tissues. In particular, they are responsible for the dynamical organization of active stresses that lead to flows and deformations of the material. Consequently, advective transport redistributes force-generating molecules and thereby contributes to a complex mechanochemical feedback loop. It has been shown in fixed geometries that this mechanism enables patterning, but the interplay of these processes with shape changes of the material remains to be explored. In this work, we study the fully self-organized shape dynamics using the theory of active fluids on deforming surfaces and develop a numerical approach to solve the corresponding force and torque balance equations. We describe the spontaneous generation of nontrivial surface shapes, shape oscillations, and directed surface flows that resemble peristaltic waves from self-organized, mechanochemical processes on the deforming surface. Our approach provides opportunities to explore the dynamics of self-organized active surfaces and can help to understand the role of shape as an integral element of the mechanochemical organization of morphogenetic processes.

Morphogenesis is the generation of patterns and shapes by dynamic processes. In the biological context, cells and tissues are shaped during developmental processes that give rise to organisms starting from a fertilized egg. Biological morphogenesis is fundamentally mechanochemical; i.e., it relies on an interplay between chemical signals and active mechanics (1–3). Active mechanical processes in cells are generated in the cytoskeleton, a gel-like network of protein filaments. Motor proteins, such as myosin, interact with cytoskeletal filaments and generate movement and forces driven by the hydrolysis of ATP (4), thus making the cytoskeleton an active material. The capacity of living matter to generate spontaneous motion, flows, and material deformations as a result of molecular force-generating processes can be captured by the theory of active matter (5, 6).

The cellular actomyosin cortex is a thin layer of an active material near the cell membrane, which governs cell mechanics and cell shape changes. For example, during cell division a contractile ring forms in the cell cortex that drives cortical flows and constricts the cell to create two daughter cells (7–10). Active cortical contractions also play a role in tissue shape changes (11, 12). For example, during gastrulation it has been suggested that contraction of the apical cell cortex drives the invagination of a 2D cell layer, called the epithelium (13). These examples show that active mechanical processes on surfaces play a key role in driving morphogenesis.

The emergent character of morphogenetic processes naturally arises from a feedback loop in which chemically regulated active stresses induce material flows and deformations that in turn affect the chemical regulators (14). This raises the fundamental question of how active stresses are dynamically organized during shape changes of cells and tissues. In the absence of shape changes, it has already been demonstrated that advection of regulators of active stress gives rise to mechanochemical self-organization and patterning (14–16). The general process of morphogenesis introduces additional feedback via changes of the underlying geometry that enables the generation of shapes by self-organizing processes. Here, we present a general framework to describe the dynamics of shapes that arise from the self-organization of mechanochemical processes on an active surface and develop a numerical technique to capture the corresponding shape changes of surfaces with axial symmetry.

Our formulation can be seen as a generalization of previous work, in which shapes are determined from a minimization of energy functionals (17–19) or from a deformations dynamic that is guided by phenomenological rules (20–22). Here, we derive the deformation dynamics and the steady states from the general force and torque balance on curved surfaces. This allows including constitutive relations that are associated with energy functionals of the surface shape (23), as well as constitutive relations that describe active elastic or viscous materials (24, 25). In particular, we consider in this work an active thin film description, which has been extensively applied as a generic model to account for the dynamic behavior of the cellular cortex and tissue layers (7, 16, 26, 27). In our description, active stresses in the material can depend on the concentration of a stress-regulating molecular species that is dynamically changing in response to flows on and deformations of the surface. We study this system on surfaces with spherical and tubular geometries, which represent a broad class of biological structures including the cellular cortex (7, 9, 17, 24, 26, 27) and various types of biological tissue (12, 16, 19, 28).

To solve the resulting equations and the shape dynamics numerically, we use an integral representation of the deforming surface and develop a dynamic coordinate transformation. We show that a mechanochemical instability of a spherical active surface leads to spontaneous polarization and the formation of deformed stationary shapes. We point out that surface deformations, even in the absence of this instability, lead to an accumulation of stress regulators in regions of high curvature due to geometric effects. Furthermore, we show that the self-organization of active stress regulators can spontaneously constrict tubular surfaces and can lead to mechanochemical shape oscillations. Finally, we describe the emergent formation of directed flows on tubular surfaces with bending rigidity that resemble a peristaltic wave resulting from the coupling between self-organized active stresses and surface geometry.

Geometry and Mechanics of Self-Organized Active Surfaces

We consider a time-dependent surface $\mathrm{\Gamma }\subset {\mathbb{R}}^3$ that is represented by a parameterization $\mathbf{X}\left(s^1,s^2,t\right)\in {\mathbb{R}}^3$. The parameters $\left(s^1,s^2\right)$ and $t$ denote the surface coordinates and time, respectively. Basis vectors in the tangent space of $\mathrm{\Gamma }$ are given by ${\mathbf{e}}_i={\partial }_i\mathbf{X}$ (Fig. 1A), where ${\partial }_i=\partial /\partial s^i$ denote partial derivatives with respect to the surface coordinates. The metric tensor is defined by $g_{ij}={\mathbf{e}}_i\cdot {\mathbf{e}}_j$ and $g^{ij}{g}_{jk}={\delta }_k^i$, where we use the Einstein summation convention. With the surface normal $\mathbf{n}={\mathbf{e}}_1\times {\mathbf{e}}_2/|{\mathbf{e}}_1\times {\mathbf{e}}_2|$, vector fields on the surface can be decomposed into tangential and normal parts $\mathbf{a}={\mathbf{a}}_{\parallel }+{\mathbf{a}}_{\perp }$, where ${\mathbf{a}}_{\parallel }=a^i{\mathbf{e}}_i$ and ${\mathbf{a}}_{\perp }=a_n\mathbf{n}$. The surface shape is characterized by the curvature tensor $C_{ij}=-\mathbf{n}\cdot {\partial }_i{\partial }_j\mathbf{X}$. The mean curvature $H$ of the surface is defined by $2H=g^{ij}{C}_{ij}=C_{\hspace{0.17em}k}^k$.

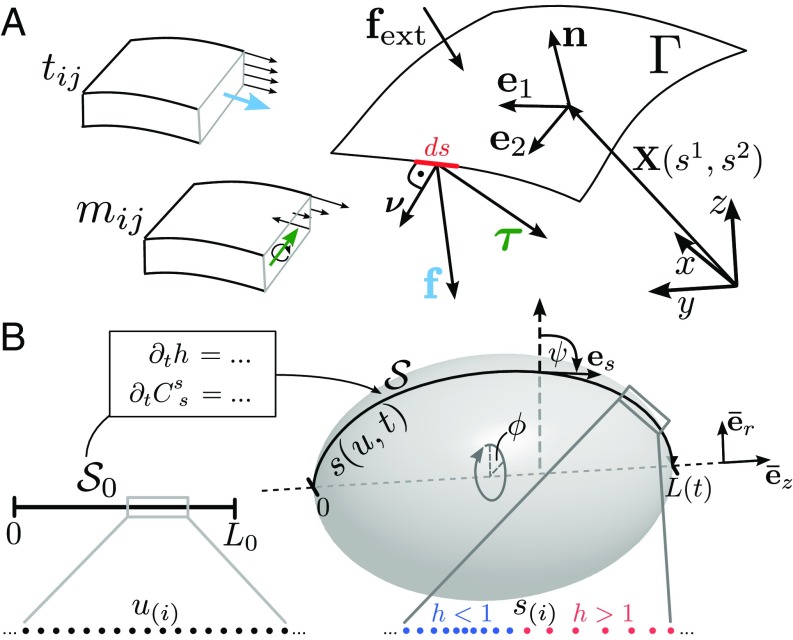
Fig. 1.

Description of curved surfaces. (A) Parameterization $\mathbf{X}\left(s^1,s^2\right)$ of a curved surface $\mathrm{\Gamma }$ embedded in ${\mathbb{R}}^3$. The tension tensor $t_{ij}$ and moment tensor $m_{ij}$ are used to describe forces $\mathbf{f}$ and torques $\mathit{\tau }$ in the surface acting on a line element $ds$. (B) Representation of an axisymmetric, deforming surface with arc-length parameterization map $s\left(u,t\right):{\mathcal{S}}_0\to \mathcal{S}$. Shown is a schematic set of collocation points $u_{\left(i\right)}$ used for the numerical discretization, mapped onto the inhomogeneous grid $s_{\left(i\right)}$ in physical space via the coordinate transformation $h$. The meridional curvature $C_{\hspace{0.17em}s}^s$ encodes the shape of axisymmetric surfaces. The vectors $\left({\overline{\mathbf{e}}}_r,{\overline{\mathbf{e}}}_{\varphi },{\overline{\mathbf{e}}}_z\right)$ denote the normalized standard basis in cylindrical coordinates, $\psi$ is the tangent angle, and ${\mathbf{e}}_s={\partial }_s\mathbf{X}\left(\varphi ,s,t\right)$.

Force and Torque Balance Equations of Curved Surfaces.

To describe deformations of $\mathrm{\Gamma }$ as a result of mechanical stresses within and onto the surface, surface configurations should obey force and torque balance equations that we briefly introduce in the following. Consider a line element of length $ds$ across the surface with in-plane normal $\mathit{\nu }={\nu }^i{\mathbf{e}}_i$ (Fig. 1A). The forces acting on this line element can be written as $\mathbf{f}=ds{\nu }_i{\mathbf{t}}^i$ (23). This defines the in-plane tension tensor $t_{ij}$ and the out-of-plane shear tension $t_n^i$ by ${\mathbf{t}}^i=t^{ij}{\mathbf{e}}_j+t_n^i\mathbf{n}$. Torques $\mathit{\tau }=ds{\nu }_i{\mathbf{m}}^i$ acting on the line element can be treated in the same way. Additionally, external forces ${\mathbf{f}}^{\text{ext}}=f^{\text{ext},i}{\mathbf{e}}_i+f_n^{\text{ext}}\mathbf{n}$ may act on the surface. With these definitions, the force and torque balance equations read (23–25)

$${\nabla }_i{t}_{\hspace{0.17em}j}^i+C_{ij}{t}_n^i=-f_j^{\text{ext}}$$ [1]

$${\nabla }_i{t}_n^i-C_{ij}{t}^{ij}=-f_n^{\text{ext}}$$ [2]

$${\nabla }_i{m}^{ij}+C_i^{\hspace{0.17em}j}{m}_n^i={ϵ}_i^{\hspace{0.17em}j}{t}_n^i$$ [3]

$${\nabla }_i{m}_n^i-C_{ij}{m}^{ij}=-{ϵ}_{ij}{t}^{ij},$$ [4]

where ${\nabla }_i$ denotes the covariant derivative and ${ϵ}_{ij}$ denotes the covariant Levi–Civita tensor (SI Appendix). Eqs. 1 and 2 describe the force balance in the directions tangential and normal to the surface, respectively, and we have omitted inertial effects. Eq. 3 determines how bending moments in the surface are balanced by out-of-plane shear tension $t_n^i$, and Eq. 4 determines their coupling to the antisymmetric part of the tension tensor $t_{ij}$. Constitutive relations of the material provide expressions for the tension and moment tensors $t_{ij},m_{ij},m_n^i$ (25), which are introduced in Constitutive Relations of Active Fluid Surfaces.

Constitutive Relations of Active Fluid Surfaces.

To define the active thin film description studied in this work, we first introduce the equilibrium properties of the surface. We consider here a surface with constant surface tension $\gamma$ and bending rigidity $\kappa$, described by the Helfrich free energy (29)

$$F_H=\int dA\left[\gamma +\kappa {\left(C_{\hspace{0.17em}k}^k\right)}^2\right].$$ [5]

Bending rigidity has been implicated as a key element in determining cell and tissue shapes (3, 19, 21). The tension and moment tensors of a surface described by Eq. 5 read (23)

$$t_{ij}^H=\gamma g_{ij}+\kappa C_{\hspace{0.17em}k}^k\left(C_{\hspace{0.17em}k}^k{g}_{ij}-2C_{ij}\right)$$ [6]

$$m_{ij}^H=2\kappa C_{\hspace{0.17em}k}^k{ϵ}_{ij}.$$ [7]

Spontaneous curvature and Gaussian bending rigidity lead to additional terms in Eqs. 5–7, which we do not consider here for simplicity (25). Note that the normal force balance Eq. 2 yields for $t_{ij}=t_{ij}^H$ and $m_{ij}=m_{ij}^H$ the well-known shape equation of membranes (23).

To characterize flows and deformations of the thin film, we use the symmetric part of the in-plane strain rate tensor ${\mathbf{e}}_i\cdot {\partial }_j\mathbf{v}$, which reads (25)

$$v_{ij}=\frac{1}{2}\left({\nabla }_i{v}_j+{\nabla }_j{v}_i\right)+C_{ij}{v}_n.$$ [8]

The component ${\mathbf{v}}_{\parallel }=v^i{\mathbf{e}}_i$ denotes the in-plane flows, ${\mathbf{v}}_{\perp }=v_n\mathbf{n}$ describes deformations of the surface, and $\mathbf{v}={\mathbf{v}}_{\parallel }+{\mathbf{v}}_{\perp }$ is the flow velocity of surface elements. The deformation velocity $v_n$ contributes to strains that are generated when deforming curved surface regions, such that curvature becomes a natural element of the constitutive equations of a deforming surface. The deviatoric tension of the isotropic active thin film is given by (25, 27)

$$t_{ij}^d=2{\eta }_s\left(v_{ij}-\frac{1}{2}{v}_{\hspace{0.17em}k}^k{g}_{ij}\right)+{\eta }_b{v}_{\hspace{0.17em}k}^k{g}_{ij}+{\xi }_a{g}_{ij}.$$ [9]

Here, ${\eta }_s$ and ${\eta }_b$ are the shear and bulk viscosities. The viscous limit is justified whenever the turnover time scales of the substructures that constitute the surface are smaller than the time scales of deformations and in-plane flows (8, 30, 31). An effective in-plane compressibility can for example arise from surface height changes (8, 32) or from an exchange of surface material with the environment, which we do not explicitly take into account. The last term with ${\xi }_a\ge 0$ describes an isotropic, contractile active tension in the surface. The constitutive relations can be obtained using

$$t_{ij}=t_{ij}^H+t_{ij}^d$$ [10]

$$m_{ij}=m_{ij}^H,$$ [11]

with the contributions to the tension and moment tensors given by Eqs. 6, 7, and 9. Additionally, we consider $m_n^i=0$ and note that $t_n^i$ can be computed using the moment balance Eq. 3. Furthermore, we assume that the volume enclosed by the surface is conserved, which defines a pressure $p$ that enters the normal force balance Eq. 2 as $f_n^{\text{ext}}=p$ (SI Appendix).

Chemical Regulation of Active Tension.

We consider an active tension amplitude of the form ${\xi }_a=\xi f\left(c\right)$, where $\xi$ is the contractility and $c$ is a concentration field that regulates the strength of the local active tension. Following previous works (7, 14, 15), this regulation is represented by a saturating Hill function

$$f\left(c\right)=\frac{c^m}{c_0^m+c^m}.$$ [12]

The concentration field $c$ is changing over time due to advective transport, reactions, and diffusion and therefore plays a crucial role for the self-organization of morphogenetic processes. These processes are captured by the dynamic equation for the concentration field (25, 33)

$${\partial }_{t}c=-{\nabla }_i\left(c{v}^i\right)-2H{v}_{n}c+D{\mathrm{\Delta }}_{\mathrm{\Gamma }}c-k\left(c-c_0\right).$$ [13]

The first term on the right-hand side describes advection due to in-plane flows. The second term describes dilution and accumulation due to local surface expansion ($H{v}_n>0$) or compression ($H{v}_n<0$), respectively, that occurs during deformations of surface regions with nonvanishing mean curvature $H$. Isotropic in-plane diffusion with diffusion constant $D$ is incorporated using the Laplace–Beltrami operator ${\mathrm{\Delta }}_{\mathrm{\Gamma }}c=g^{ij}{\nabla }_i{\nabla }_{j}c$. The last term describes the turnover with a rate $k$ and preferred concentration of the stress regulator $c_0$.

Dynamic Representation of Deforming Axisymmetric Surfaces

For a given deformation velocity $v_n$, the dynamics of the surface $\mathrm{\Gamma }$ represented by the Lagrangian parameterization $\mathbf{X}\left(s^1,s^2,t\right)$ obeys

$$\frac{d\mathbf{X}}{dt}=v_n\mathbf{n},$$ [14]

where $\frac{d}{dt}$ denotes the total time derivative. In the following, we consider deformations of axisymmetric surfaces and develop a framework to numerically solve Eq. 14 for a given deformation velocity $v_n$.

An arbitrary axisymmetric surface can be represented explicitly using an arc-length parameterization

$$\mathbf{X}\left(\varphi ,s,t\right)=r\left(s,t\right)\hspace{0.17em}{\overline{\mathbf{e}}}_r\left(\varphi \right)+z\left(s,t\right){\overline{\mathbf{e}}}_z,$$ [15]

where $\left({\overline{\mathbf{e}}}_r,{\overline{\mathbf{e}}}_{\varphi },{\overline{\mathbf{e}}}_z\right)$ is the normalized standard basis ${\overline{\mathbf{e}}}_{\alpha }\cdot {\overline{\mathbf{e}}}_{\beta }={\delta }_{\alpha \beta }$ with $\alpha ,\beta \in \left\{r,\varphi ,z\right\}$ in cylindrical coordinates, $\varphi =s^1\in \left[\mathrm{0,2}\pi \right]$ is the azimuthal angle, and $s=s^2\in \left[0,L\left(t\right)\right]$ is the arc-length parameter of the meridional outline (Fig. 1B). In the following, we use $\varphi$ and $s$ explicitly as tensor indexes. The nonvanishing components of the curvature tensor are the azimuthal curvature $C_{\hspace{0.17em}\varphi }^{\varphi }\left(s,t\right)=\sin \psi /r$ and the meridional curvature

$$C_{\hspace{0.17em}s}^s\left(s,t\right)={\partial }_s\psi ,$$ [16]

where $\psi \left(s,t\right)$ is the tangent angle defined by $\left({\partial }_{s}r,{\partial }_{s}z\right)=\left(\cos \psi ,\sin \psi \right)$. This definition implies that the full shape information about $\mathrm{\Gamma }$ is encoded in the meridional curvature $C_{\hspace{0.17em}s}^s$, together with a point $\mathbf{X}\left(t\right){|}_{s=0}$. Indeed, for given $C_{\hspace{0.17em}s}^s$, we can compute the tangent angle from Eq. 16 as

$$\psi \left(s,t\right)=\psi \left(t\right){|}_{s=0}+\underset{0}{\overset{s}{\int }}{C}_{\hspace{0.17em}s}^s\left(s\prime ,t\right)ds\prime$$ [17]

and reconstruct $\mathrm{\Gamma }$, parameterized as in Eq. 15, via

$$r\left(s,t\right)=r\left(t\right){|}_{s=0}+{\int }_0^s\cos \left[\psi \left(s\prime ,t\right)\right]ds\prime$$ [18]

$$z\left(s,t\right)=z\left(t\right){|}_{s=0}+{\int }_0^s\sin \left[\psi \left(s\prime ,t\right)\right]ds\prime .$$ [19]

Consequently, the shape of the surface $\mathrm{\Gamma }$ during deformations, and therefore the solution to Eq. 14, can be found by determining the time evolution of the meridional curvature $C_{\hspace{0.17em}s}^s$ and of the values of $\psi$, $r$, and $z$ at $s=0$.

An arc-length parameterization $s\in \mathcal{S}\left(t\right)≔\left[0,L\left(t\right)\right]$ simplifies the parametric form of covariant equations and the shape reconstruction via Eqs. 17–19. However, the time dependence of the domain $\mathcal{S}$ makes it difficult to evaluate the total time derivative in the equation of the shape dynamics, Eq. 14, and renders the arc-length parameterization impractical for the numerical treatment of differential equations on a deforming surface. We therefore introduce additionally a Eulerian parameterization of $\mathrm{\Gamma }$ given by

$${\mathbf{X}}_e\left(\varphi ,u,t\right)=r\left(u,t\right)\hspace{0.17em}{\overline{\mathbf{e}}}_r\left(\varphi \right)+z\left(u,t\right){\overline{\mathbf{e}}}_z,$$ [20]

where $u$ is a parameter on an interval ${\mathcal{S}}_0=\left[0,L_0\right]$ that remains fixed during surface deformations. For convenience, we chose here $L_0=L{|}_{t=0}$, such that ${\mathcal{S}}_0=\mathcal{S}{|}_{t=0}$. The azimuthal angle $\varphi$ is defined as in Eq. 15. Note that $\mathbf{X}$ and ${\mathbf{X}}_e$ represent the same surface $\mathrm{\Gamma }$, but for the Eulerian parameterization, the shape dynamics Eq. 14 can be written as

$$\frac{\partial {\mathbf{X}}_e}{\partial t}=v_n\mathbf{n}.$$ [21]

The surface coordinates $s$ and $u$ are then related by a time-dependent coordinate transformation $h\left(u,t\right)$ that is defined by

$$s\left(u,t\right)={\int }_0^{u}h\left(u\prime ,t\right)du\prime .$$ [22]

To obtain a dynamic equation for $h\left(u,t\right)$, we first note that we have $g_{ss}=h^{-2}{g}_{uu}=1$ and thus $g_{uu}=h^2$. Furthermore, it follows from Eq. 21 and the definition of the metric tensor that for an Eulerian parameterization (SI Appendix) ${\partial }_t{g}_{ij}=2C_{ij}{v}_n$, which implies

$${\partial }_{t}h\left(u,t\right)=h{C}_{\hspace{0.17em}s}^s{v}_n.$$ [23]

Here, we have used $C_{uu}=h^2{C}_{\hspace{0.17em}s}^s$. For our choice ${\mathcal{S}}_0=\mathcal{S}{|}_{t=0}$ of the fixed interval where $u$ is defined, $h$ is uniquely determined as the solution of Eq. 23 with initial condition $h\left(u\right)=1$.

To reconstruct the deforming surface via Eqs. 17–19 as a function of time, we need the meridional curvature $C_{\hspace{0.17em}s}^s$ that obeys (SI Appendix)

$${\partial }_t{C}_{\hspace{0.17em}s}^s\left(u,t\right)=-{\left(C_{\hspace{0.17em}s}^s\right)}^2{v}_n-\frac{1}{h}{\partial }_u\left(\frac{1}{h}{\partial }_u{v}_n\right).$$ [24]

The first term captures curvature changes due to stretching of the meridional outline, and the second term describes the outline’s bending that occurs in the case of an inhomogeneous deformation velocity $v_n$. Altogether, Eqs. 17–19 and 22–24 provide a framework to solve Eq. 14 for a given deformation velocity $v_n$ on axisymmetric surfaces.

Self-Organization of Active Surface Deformations

We now combine the dynamics of surfaces with the physics of an active fluid film. For a given surface shape and distribution of active tension, the instantaneous deformation velocity $v_n$ and the meridional in-plane flow $v_s={\mathbf{e}}_s\cdot {\mathbf{v}}_{\parallel }$ can be obtained by solving hydrodynamic equations of the active fluid surface. The hydrodynamic equations result from combining the force and torque balance Eqs. 1–4 with the constitutive relations Eqs. 10 and 11 (SI Appendix). Note that these equations determine the velocities up to a constant velocity vector because the system is Galilei invariant. The dynamics of the shape together with dynamics of the stress regulator are then obtained by solving Eqs. 13 and 14, using at all times the instantaneously determined velocity fields. This combination of geometry and active hydrodynamics captures the mechanochemical feedback mediated by the chemical regulator, where the latter organizes active stress patterns and depends itself on material flows and on changes of the geometry.

We now study self-organized surface deformations of axisymmetric spherical and tubular surfaces. To characterize the strength of the mechanochemical feedback, we introduce a dimensionless contractility parameter

$$\alpha =\frac{\xi }{\gamma }{c}_0{\partial }_{c}f\left(c_0\right).$$ [25]

In the following, we first perform a linear stability analysis of homogeneous states to determine parameter regimes where the surface is unstable. We then study the full nonlinear surface dynamics using the framework introduced in the preceding sections and detailed further in SI Appendix.

Self-Organized Shape Dynamics of Spherical Surfaces.

We first consider axisymmetric surfaces of spherical topology and analyze the linear stability of the homogeneous steady state with $c=c_0$ and $\mathbf{v}=0$ on a sphere with radius $R=R_0$. We expand small perturbations of this state as $\delta c={\sum }_{l=0}^{\infty }\delta c_l{Y}_l$, $\delta R={\sum }_{l=0}^{\infty }\delta R_l{Y}_l$, and $\delta {\mathbf{v}}_{\parallel }={\sum }_{l=0}^{\infty }\left(\delta v_l^{\left(1\right)}{\mathbf{\Psi }}_l+\delta v_l^{\left(2\right)}{\mathbf{\Phi }}_l\right)$. Here, $Y_l$, ${\mathbf{\Psi }}_l$, and ${\mathbf{\Phi }}_l$ denote axisymmetric scalar and vector spherical harmonics (34). Expanding the force balance Eqs. 1–4 and the dynamic Eq. 13 for the concentration field to linear order (SI Appendix), we find that for increasing contractility parameter $\alpha$ the mode $l=1$ has the largest growth rate and is the first mode that becomes unstable at $\alpha ={\alpha }_s^{*}$, where

$${\alpha }_s^{*}=\frac{{\eta }_b}{\gamma }\left(\frac{2D}{R_0^2}+k\right).$$ [26]

This instability is independent of the bending rigidity $\kappa$.

The growing mode $l=1$ characterizes a polar asymmetry. Using a randomly perturbed concentration field as initial condition in our numerical approach, we find that for $\alpha >{\alpha }_s^{*}$ the instability leads to the spontaneous formation of a single patch of the stress regulator and an asymmetric surface shape (Fig. 2B and Movie S1). In the final steady state the advective influx of stress regulator into the contractile region is balanced by a diffusive outflux away from it. The resulting inhomogeneous tension across the surface leads to an oblate shape with broken mirror symmetry with respect to the $z$ axis and thus spatially varying curvature (Fig. 2B, Right).

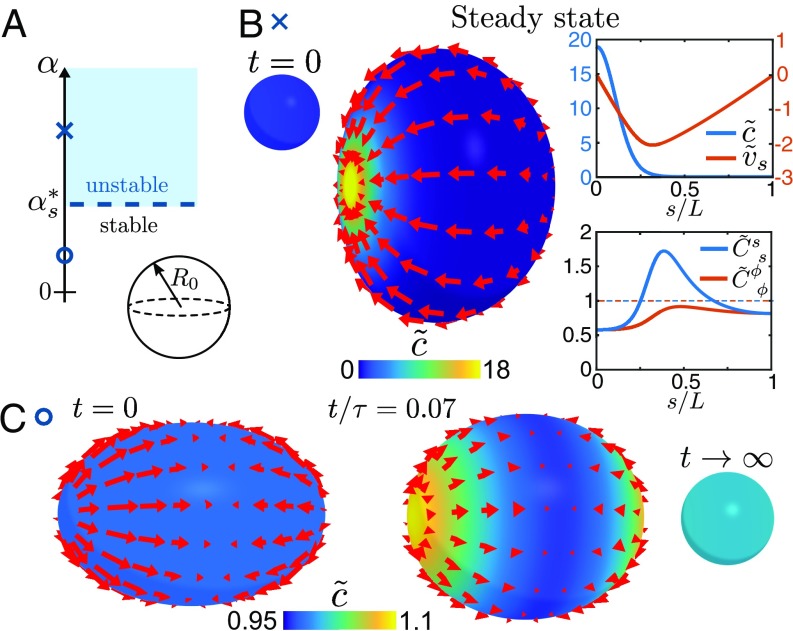
Fig. 2.

Shape dynamics of spherical surfaces with concentration-dependent active tension. (A) Schematic stability diagram of the system. The critical contractility ${\alpha }_s^{*}$ is independent of the bending rigidity $\kappa$. (B) Mechanochemically unstable surface with $\alpha >{\alpha }_s^{*}$ and $\kappa =0$. (Left) After a small concentration perturbation on a sphere ($t=0$, not to scale), a deformed steady-state shape emerges with a localized patch of stress regulator (Movie S1). Red arrows denote the in-plane flow field ${\mathbf{v}}_{\parallel }$. (Right) Profiles of the concentration $\tilde{c}=c/c_0$, in-plane flow ${\tilde{v}}_s=v_s\tau /R_0$ ($v_s={\mathbf{e}}_s\cdot \mathbf{v}$, $\tau ={\eta }_b/\gamma$), and principle curvatures ${\tilde{C}}_{\hspace{0.17em}s}^s=R_0{C}_{\hspace{0.17em}s}^s$, ${\tilde{C}}_{\hspace{0.17em}\varphi }^{\varphi }=R_0{C}_{\hspace{0.17em}\varphi }^{\varphi }$ of the steady-state surface. In the steady state, the diffusive outflux away from the contractile patch is balanced by an advective influx. The resulting tension across the surface is inhomogeneous, which leads to a deformed steady-state shape. (C) Relaxation dynamics of a mechanochemically stable surface with $\alpha <{\alpha }_s^{*}$ and $\kappa =0$, starting with a spheroidal shape with eccentricity 0.75 (Movie S2). Inhomogeneities in the initial mean curvature ($t=0$) lead to transient inhomogeneities in the concentration field ($t/\tau =0.07$) due to a deformation-induced local expansion and compression of the surface, before the stable steady state of a sphere is reached ($t\to \infty$, not to scale). Surface flows in B and C are shown in the reference frame where the pole velocities satisfy $\mathbf{v}\left(s=0\right)=-\mathbf{v}\left(s=L\right)$ (SI Appendix). The parameters used in these simulations are given in SI Appendix.

For $\alpha <{\alpha }_s^{*}$ the homogeneous concentration on the sphere represents a stable solution. This is revealed by the relaxation of a deformed sphere toward this stable steady state. Such a relaxation is depicted in Fig. 2C, where we use a spheroidal surface with a homogeneous concentration as initial condition. During the relaxation process, we observe the transient formation of concentration maxima at the poles (Movie S2). These maxima appear as a consequence of the large mean curvature $H$ at those locations, which leads to a locally increased surface compression during deformations (Eq. 13).

Self-Organized Shape Dynamics of Tubular Surfaces.

We now study the self-organization of an active surface with a tubular geometry. We analyze the linear stability of the homogeneous steady state with $c=c_0$ and $\mathbf{v}=0$ on a cylinder with radius $r_0$ and length $L_0$ and consider periodic boundary conditions. We expand small axisymmetric perturbations of this state as $\delta c={\sum }_{n=-\infty }^{\infty }\delta c^{\left(n\right)}\exp \left(i{k}_{n}z\right)$, $\delta r={\sum }_{n=-\infty }^{\infty }\delta r^{\left(n\right)}\exp \left(i{k}_{n}z\right)$, and $\delta {\mathbf{v}}_{\parallel }={\overline{\mathbf{e}}}_z{\sum }_{n=-\infty }^{\infty }\delta v_z^{\left(n\right)}\exp \left(i{k}_{n}z\right)$ with $k_n=2\pi n/L_0$. From the corresponding expansion of the force balance Eqs. 1–4 and the dynamic Eq. 13 for the concentration field to linear order, we derive the stability diagram as a function of the contractility parameter $\alpha$ and the aspect ratio $L_0/r_0$ (Fig. 3A and SI Appendix). For $\kappa =0$ the cylinder surface is unstable in the blue-shaded region. For $\alpha <{\alpha }_c^{*}$ with

$${\alpha }_c^{*}=\frac{{\eta }_b}{\gamma }\left(\frac{D}{r_0^2}+k\right),$$ [27]

the instability occurs when the aspect ratio $L_0/r_0$ increases beyond a critical value that equals $2\pi$ and does not depend on $\alpha$. This instability corresponds to the Plateau–Rayleigh instability and is not driven by the self-organization of the stress regulator. The case $\alpha =0$ and $\kappa =0$ exactly represents the classical Plateau–Rayleigh scenario (35). For $\alpha >{\alpha }_c^{*}$ instabilities are driven by the mechanochemical self-organization of the fluid surface. In this regime the aspect ratio $L_0/r_0$ at which the cylinder surface becomes unstable is smaller than $2\pi$ and decreases for increasing contractility parameter $\alpha$. The linear stability analysis reveals furthermore a region where eigenvalues are complex (dark blue-shaded area in Fig. 3A), which indicates oscillatory behavior at the instability. These characteristics of the stability diagram remain qualitatively unchanged when the bending rigidity $\kappa$ is finite. The instability line for $\kappa =0.25\gamma r_0^2$ is shown as a red dashed line in Fig. 3A. The red-shaded region indicates complex eigenvalues. Note that the value of ${\alpha }_c^{*}$ in general depends on $\kappa$ (SI Appendix).

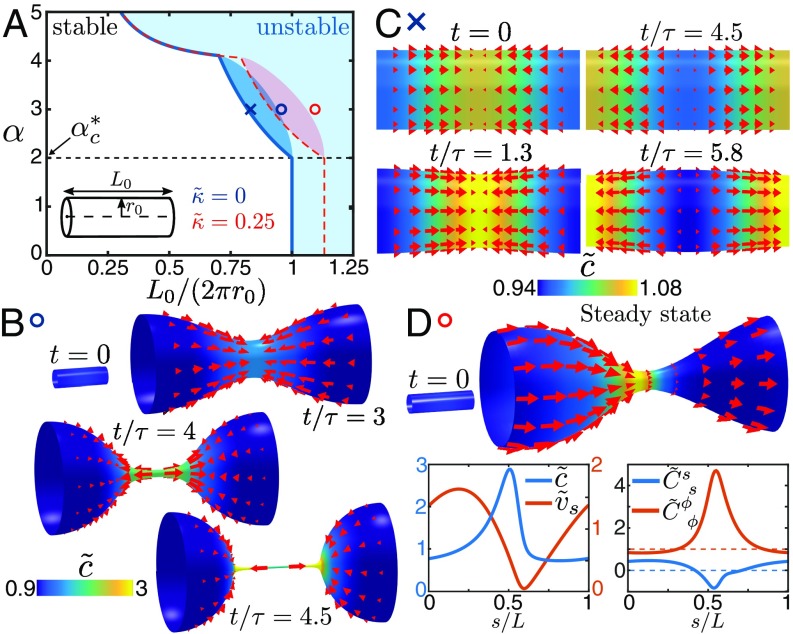
Fig. 3.

Shape dynamics of tubular active fluid surfaces with concentration-dependent active tension. (A) Representative stability diagram of the system. Stable and unstable regions are separated by the blue curve for $\kappa =0$ and the red dashed line for $\tilde{\kappa }=0.25$, where $\tilde{\kappa }=\kappa /\left(\gamma r_0^2\right)$. For $\kappa =0$ the dark blue-shaded region indicates parameter regimes where eigenvalues of the Jacobian are complex. The critical contractility ${\alpha }_c^{*}$ (Eq. 27) is described in the main text. (B) Concentration $\tilde{c}=c/c_0$ and in-plane flow ${\mathbf{v}}_{\parallel }$ (red arrows) during the spontaneous formation of a contractile ring (Movie S3) for parameters indicated with a blue circle in the stability diagram ($\tau ={\eta }_b/\gamma$, $t=0$ not to scale). This mechanism can constrict surfaces with aspect ratios below the Rayleigh threshold of $2\pi$. (C) Concentration and in-plane flow over one oscillation period for parameters indicated with a blue cross in the stability diagram (Movie S4). Oscillations result from the interplay between geometric stability of cylinder surfaces with $L_0/r_0<2\pi$ and the mechanochemical instability of the active fluid film. Surface flows in B and C are shown in the reference frame where ${\int }_0^L{v}_{s}ds=0$ (SI Appendix). (D) Steady state of directed surface flows relative to a constricted shape ($t=0$ not to scale). Shown are concentration (color code as in B), in-plane flow ${\tilde{v}}_s=v_s\tau /r_0$ ($v_s={\mathbf{e}}_s\cdot \mathbf{v}$), and principle curvatures ${\tilde{C}}_{\hspace{0.17em}s}^s=r_0{C}_{\hspace{0.17em}s}^s$, ${\tilde{C}}_{\hspace{0.17em}\varphi }^{\varphi }=r_0{C}_{\hspace{0.17em}\varphi }^{\varphi }$. The surface flow is shown in the reference frame where the constriction does not move (SI Appendix). In the reference frame where ${\int }_0^L{v}_{s}ds=0$, this steady state resembles peristaltic motion (Movie S5). The parameters used in these simulations are given in SI Appendix.

We also study the surface dynamics beyond the linear regime, using our numerical approach. For $\kappa =0$, $\alpha >{\alpha }_c^{*}$, and aspect ratios $L_0/r_0$ inside the unstable region of the stability diagram (blue circle in Fig. 3A), the cylinder surface constricts and generates a thin cylindrical neck region with decreasing radius (Fig. 3B and Movie S3). The numerical analysis indicates that this radius vanishes at finite time. The concentration of the stress regulator increases along the tubular neck. For parameters that correspond to complex eigenvalues in the linear stability diagram (blue cross in Fig. 3A), the cylinder constricts and expands periodically (Fig. 3C and Movie S4) with increasing amplitude until the neck radius vanishes. For $\alpha <{\alpha }_c^{*}$ and $L_0/\left(2\pi r_0\right)>1$, the instability also leads to a tubular neck with vanishing radius, however, not driven by contractility but by surface tension $\gamma$ due to the Plateau–Rayleigh character of the instability in this parameter regime. In this case, the concentration of stress regulator increases in the neck predominantly because of a local reduction of surface area.

For $\kappa >0$, an unstable cylinder surface constricts and reaches at long times a finite neck radius for all values of the contractility parameter $\alpha$. For $\alpha >{\alpha }_c^{*}$ a high concentration of stress regulator additionally builds up in the neck region. The concentration pattern and surface flows that emerge at long times spontaneously break the mirror symmetry with respect to the $z$ axis (Fig. 3D and Movie S5). As a consequence, average flows directed along the $z$ axis occur in a reference frame, where the constriction does not move. This corresponds to a peristaltic contraction wave that propagates in a reference frame where the average flow vanishes. Our numerical results reveal that such propagating solutions emerge in all parameter regimes for which the cylinder surface is linearly unstable and $\alpha >{\alpha }_c^{*}$. For $\alpha <{\alpha }_c^{*}$ no propagating solutions occur. To test whether the stabilization of a finite neck radius is sufficient for directed flows to occur via spontaneous symmetry breaking, we chose $\kappa =0$ and consider an external force ${\mathbf{f}}^{\text{ext}}=F_0\left(r_0/r-1\right){\overline{\mathbf{e}}}_r$ that also stabilizes small neck radii. In this setting, we again find the formation of directed flows relative to the constricted shape. This shows that the spontaneous symmetry breaking for $\alpha >{\alpha }_c^{*}$ is an intrinsic property of the self-organized active fluid film and its tight coupling to the surface geometry.

Discussion

We have introduced a simple but general model for the mechanochemical self-organization of surface geometry. Active stresses in the surface are regulated by a diffusible and advected molecular species. Gradients of active stress induce surface flows and shape changes, which in turn influence the distribution of the stress regulator. As a consequence, shape changes, shape oscillations, and spontaneous surface flows can be generated via mechanochemical instabilities. In contrast to mechanochemical instabilities that have been discussed in fixed geometries (14–16), the phenomena described in the present paper give rise to shape changes and depend themselves crucially on the shape changes that occur.

To solve the dynamic equations for the shape, the flows, and the concentration fields, we have developed a numerical approach based on an integral representation of axisymmetric surfaces. We use a time-dependent coordinate transformation, which allows us to obtain the shape dynamics in an implicit surface representation. The explicit coordinates of surface points can be calculated independently.

Using our approach, we have identified a mechanochemical shape instability of a sphere that leads to concentration and flow patterns with a polar asymmetry and an accordingly asymmetric oblate shape. For periodic cylinder surfaces, we find contractility-induced instabilities beyond a critical value ${\alpha }_c^{*}$ together with the Plateau–Rayleigh instability for contractility parameters smaller than ${\alpha }_c^{*}$. Near the point that separates these two regimes, we find that the instability is oscillatory. This could result from a competition between a weak contractile instability and the stability of the cylinder with respect to the Plateau–Rayleigh criterion in this parameter region. On tubular surfaces with stabilized neck radii, we have described the spontaneous formation of directed surface flows. In a reference frame of vanishing average surface flows, this corresponds to a propagating surface constriction that resembles the dynamics of a peristaltic wave (Movie S5).

Our framework provides a basis to explore a large variety of systems that involve the mechanochemical self-organization of deforming active surfaces. Here, we have focused on simple cases, where the active material is embedded in an environment with a homogeneous pressure. The latter exerts a force per area normal to the surface with position-independent magnitude. In many real situations, the surrounding medium has material properties that can give rise to more complex patterns of external forces, including tangential shear forces acting on the surface. Furthermore, it will be interesting to consider active surface material properties with different constitutive relations, such as viscoelastic systems and materials that are anisotropic or chiral. Biological examples of such materials are given by epithelial tissues with planar polarity (1) and by anisotropic cytoskeletal systems (30). Furthermore, the minimal model of a single stress regulator chosen here could be extended to more complex chemical schemes that involve several species and interactions between them. These extended models could represent, for example, the actin dynamics present in the cell cortex and its biochemical regulators (3) or the behavior of sets of morphogens spreading in epithelial tissues (11). Finally, we note that many biological processes, such as the migration of cells or invagination events in tissues (13, 27), lead to shapes that are not axisymmetric. A generalization of our approach to nonaxisymmetric surfaces therefore provides an important challenge.