Reading the (functional) writing on the (structural) wall: multimodal fusion of brain structural and function via a deep neural network based translation approach reveals novel impairments in schizophrenia

Abstract

This work presents a novel approach using a deep neural network for finding linkage/association between multimodal brain imaging data, such as structural MRI (sMRI) and functional MRI (fMRI). Motivated by the machine translation domain, we consider two different imaging views of the same brain like two different languages conveying some common facts that enables finding linkages between two modalities. The proposed translation based fusion model contains a computing layer that learns “alignments” (or links) between dynamic connectivity features from fMRI data and static gray matter patterns from sMRI data. The approach is evaluated on a multi-site dataset consisting of eye-closed resting state imaging data collected from 298 subjects (age- and gender matched 154 healthy controls and 144 patients with schizophrenia). We used dynamic functional connectivity (dFNC) states as the functional features and ICA-based sources from gray matter densities as the structural features. The dFNC states characterized by weakly correlated intrinsic connectivity networks (ICNs) were found to have stronger association with putamen and insular gray matter pattern, while the dFNC states of profuse strongly correlated ICNs exhibited stronger links with the gray matter pattern in precuneus, posterior cingulate cortex (PCC), and temporal cortex. Further investigation with the estimated link strength (or alignment score) showed significant group differences between healthy controls and patients with schizophrenia in several key regions including temporal lobe, and linked these to connectivity states showing less occupancy in healthy controls. Moreover, this novel approach revealed significant correlation between a cognitive score (attention/vigilance) and the function/structure alignment score that was not detected when data modalities were considered separately.

1. Introduction

Multiple types of brain data from the same individual using various imaging techniques, such as structural MRI (sMRI), functional MRI (fMRI), EEG, and MEG have created enormous opportunities to investigate the structure and function of the brain as well as its disorders in a more comprehensive manner. A combination of two or more types of data for joint analysis is called multimodal fusion. Despite challenges to consider when combining data, research in multimodal fusion is rapidly growing due to its added value for basic, clinical, and cognitive neuroscience. Each imaging technique essentially provides a different view of brain structure or function. For example, BOLD fMRI measures the hemodynamic response related to the neural activity in the brain dynamically; sMRI provides information about the tissue type of the brain [gray matter (GM), white matter (WM), and cerebrospinal fluid (CSF)]. Diffusion MRI (dMRI) likewise can provide information on structural connectivity among brain networks. A general motivation for multimodal fusion is to take advantages of cross-modal information, thereby potentially revealing important variations that may only partially be detected by a single modality. More importantly, data fusion approaches can help avoid incorrect conclusions resulting from unimodal methods and help compensate for imperfect imaging studies (Calhoun and Sui, 2016).

The use of multimodal data fusion is especially useful in finding relationship of brain pathologies in psychosis as substantial pathophyisological questions can only be answered from cross-modal information (Schultz et al., 2012). Among different brain disorders, schizophrenia is the most widely studied psychosis and has served as a test bed for various fusion approaches (Sui et al., 2012b). Nowadays, schizophrenia, which is characterized by lack of integration between thought, emotion, and behavior, is considered to be a brain-based disease due to increasing evidence that both structural and functional brain alteration are found in the patients (Fusar-Poli et al., 2011). To further resolve complex neuropathological puzzle of schizophrenia, multimodal imaging represents a promising strategy in psychosis research. Although approaches to study data fusion are rapidly growing, the number of studies is still limited and further efforts are needed to consolidate findings so far, and to extend the scope of other pathophysiological features contributing to schizophrenia. To this end, we developed a novel machine learning approach for investigating neuronal mechanisms that may underlie structure-function alterations in the patients with schizophrenia.

With regard to the different approaches for brain imaging data fusion, a number of psychosis-related fusion studies have been published. A widely adopted method is spatial overlap that qualitatively describes the pattern of brain alterations from different modalities indicating information of brain pathologies (Skudlarski et al., 2010; Camchong et al., 2011; Jacobson et al., 2010). A central assumption in this approach, motivated from systems neuroscience, is that the structure of the brain can predict and/or is related to functional connectivity. For example, Salgado-Pineda et al. found aberrant spatial overlaps in the schizophrenic patients regarding both parameters (GM volume decrease and neuronal hypoactivation) in three regions, including thalamus, anterior cingulate cortex, and inferior parietal in an attentional processing cognitive task (Salgado-Pineda et al., 2004).

Recently, data-driven approaches that are more informative and fuse the full data sets from different MRI modalities are receiving much attention as they make fewer assumptions about specific relationship among data sets (Michael et al., 2011; Calhoun et al., 2006; Sui et al., 2012a; Calhoun and Adali, 2009). These methods typically extract features from each imaging type and search for variations in structure-function links in the feature space which simplifies the fusion strategy but enables one to study the full joint information among modalities. Fusion in such a feature space has been used to identify indirect or direct associations to be inferred on putative structure-function relationships (Schultz et al., 2012).

Motivated by the merits of data-driven fusion approaches and the recent development of deep neural network based machine learning methods (Hinton et al., 2006; Bengio, 2009; Arel et al., 2010), we leverage both by bringing them into the multimodal fusion framework for brain imaging research. A limitation with most of the existing multimodal fusion methods is that they capture only linear relationship between different modalities (Calhoun et al., 2006; Correa et al., 2008), while the different types of data do likely interact nonlinearly and this information has the potential to provide rich information. Recent work on deep learning for unimodal brain imaging has shown that deep belief networks (DBNs) can uncover potential hidden relationship and thus facilitate discovery (Plis et al., 2014; Brosch et al., 2013; Kim et al., 2015). We hypothesize that gray matter variations might interact with the brain functional dynamics in an intricate way, and such relationships are buried in the data. In this work, we, therefore, utilize the ability of high level representation of deep models for potential discovery of brain structure-function links. We also expect that the estimated link strength (learned from data) would possibly show group differences between healthy controls and patients, thereby presenting a new framework for multimodal fusion in the psychosis research.

The proposed novel multimodal fusion approach extends the idea of machine translation (in natural language processing) for finding links between brain structure and function. Our view point is that sMRI and fMRI are different views/measurements of the same brain, and we take an analogy that different languages convey common concepts or facts in different ways. The key ingredient of this novel approach is an “attention” (not to be confused with the cognitive term attention) module that learns an alignment between features of two different modalities similar to the deep machine translation model (Bahdanau et al., 2014). In our context, alignments are associations/links between time varying fMRI and static sMRI features. Unlike the case in (Bahdanau et al., 2014) where the input and output are ordered sequences, one of the imaging modailities (sMRI) gives us an unordered set of features. Therefore, we modify the model’s attention mechanism to investigate brain structure-functional relationships. We also examine the learned alignments for group differences between healthy controls (HCs) and patients with SZ, as well as their relationships with cognitive scores, thereby exhibiting potential advantages of the proposed method.

Our method advances existing methods in two distinct ways. First, to our best knowledge, this is the first study on deep multimodal learning in neuroimaging. Second, existing multimodal approaches consider functional aspect of imaging data in a static manner, while functional dynamics may convey important neuronal mechanisms of psychosis (Damaraju et al., 2014). In contrast, our fusion approach combines sMRI features and dynamic functional connectivity features to find variations across presumably hidden associations between brain structure and function.

2. Materials and Methods

We first briefly describe about data collection and preprocessing, and then the translation-based fusion model is explained in this section.

2.1. Participants

In this work, we perform analysis on two modalities of data, T1-weighted structural images and T2*-weighted functional images. The resting state fMRI data were collected from 154 healthy controls (110 males, 44 females; mean age 37) and 144 schizophrenic patients (110 males, 34 females; mean age 38) during eye closed condition at seven different scanning sites. A total of 162 volumes of echo planar imaging BOLD fMRI data were collected with a TR of 2 s on 3T scanners. For the same subjects, T1-weighted structural images were collected as well. Full details on the participants and data collection can be found in (Keator et al., 2016) and a summary of demographics are provided in (Damaraju et al., 2014).

2.2. Data collection

MR images were collected on a 3-Tesla Siemens Trio scanner at six sites and on a 3T General Electric Discovery MR750 scanner at one site. High-resolution T1-weighted structural images were acquired with a turbo-flash sequence (TE = 2.94 ms, TR = 2.3 s, flip angle = 9°, number of excitations = 1, slice thickness = 1.2 mm, field of view = 256 mm, resolution = 256 × 256) resulting in 0.86 × 0.86 × 1.2 mm³ voxels. T2*-weighted functional images were acquired using a gradient-echo EPI sequence (TR/TE 2s/30ms, flip angle 77 degrees, 32 slices collected sequentially from superior to inferior, 3.4 × 3.4 × 4 mm³ with 1 mm gap, 162 frames, 5:38 min). Participants were instructed to keep their eyes closed during the scan.

2.3. Data preprocessing

Structural data: T1-weighted images were normalized to MNI space, resliced to 2 × 2 × 2 mm, and segmented into gray, white, and CSF images using the unified segmentation methods of SPM5 (Ashburner and Friston, 2005). Data quality was checked by correlations against the segmented templates; if the subject’s segmented gray matter data did not correlate at 0.9 or higher with the template across all voxels, it was removed from consideration. Gray matter segmentations were finally smoothed by a Gaussian filter of 10 mm Full Width Half Maximum (FWHM). We analyzed gray matter density (GMD) with independent component analysis (ICA) to extract features as relationships among GMD regions, which is called source-based morphometry (SBM) (Xu et al., 2009). The ICA was performed using the group ICA of fMRI (GIFT) toolbox¹ and 50 components were estimated. After analyzing stability of the components and visual inspection, 23 components were selected, and hereafter they are referred to as structural components.

Functional data: We used resting state fMRI data and performed rigid body motion correction using the INRIAlign (Freire and Mangin, 2001) toolbox in SPM to correct for subject head motion followed by slice-timing correction to account for timing differences in slice acquisition. Then the fMRI data were despiked using AFNI’s 3dDespike algorithm to mitigate the impact of outliers. The fMRI data were subsequently warped to a Montreal Neurological Institute (MNI) template and resampled to 3 mm³ isotropic voxels. Instead of Gaussian smoothing, we smoothed the data to 6 mm full width at half maximum (FWHM) using AFNI’s BlurToFWHM algorithm which performs smoothing by a conservative finite difference approximation to the diffusion equation. This approach has been shown to reduce scanner specific variability in smoothness providing “smoothness equivalence” to data across sites (Friedman et al., 2008). Each voxel time course was variance normalized prior to performing group independent component analysis. These processed data were then decomposed into components using spatial group independent component analysis (GICA) implemented in the GIFT toolbox (Calhoun et al., 2001). Each component can be regarded as temporally coherent intrinsic connectivity networks (ICN), and 47 such networks were selected as in (Damaraju et al., 2014). For feature representation, pairwise correlation between ICN time courses were computed yielding a correlation matrix of size 47 × 47. In order to capture dynamics, correlation was estimated using a sliding window approach with a window size of 22 TR (44 s) in steps of 1 TR (2 s) [see Damaraju et al. (2014) for details]. We refer to this windowed correlation matrix as dynamic functional network connectivity (dFNC). However, in order to reduce the total time steps for our translation model, we took average of every 4 consecutive correlation matrices. Finally, a discrete sequence of dFNC states were obtained using k-means clustering algorithm on the dFNC matrices, with a setting of k = 5 using the elbow criterion.

2.4. Translation-based multimodal fusion model

Machine translation models that produce sentences in one language from another are common in the natural language processing discipline. Essentially, different languages convey common concept or fact in different ways with their own constructs. We can consider sMRI and fMRI as two different views of the same brain, and take an approach from the machine translation discipline to deal with multimodal neuroimaging data.

A recently proposed neural machine translation model has shown state-of-the-art performance with its novel attention mechanism (Bahdanau et al., 2014). The main feature of the attention module is to learn alignment between phrases of two different languages for improving translation performance. We exploit this idea of attention mechanism to learn alignment (linkage) between dFNC states and brain structural components. However, unlike the sequence to sequence matching in the language translation, input in our case is an unordered set of sMRI component loadings and output are temporally ordered dFNC states. To tackle this problem, we propose a simple modification in the attention network in our translation model. Figure 1 depicts the different parts of our translation model in the context of neuroimaging. The model stacks several neural-network layers (six layers in total) which we describe below.

Figure 1:

A translation model for learning alignment between functional dFNC states and structural components. The attention network module is a feed forward network (input: 23, hidden: 50, output: 23) with a 50% dropout (Srivastava et al., 2014) in the hidden layer. The sequence predictor module has a recurrent layer (consisting of 50 gated recurrent units) and a feedforward network (input: {50+23 = 73}, hidden: 50, output: 5) with a 50% dropout in the hidden layer. The recurrent layer uses the dFNC correlation matrix as an embedding in the real vector space for the dFNC states.

As shown in Fig. 1, two main parts of our translation-based fusion model are: (1) sequence predictor and (2) attention network. The input-output setting of the model is as follows. Input is an unordered set of structural component loadings of a subject, x = {x₁,…, x_j,… x_J}, and the output is a temporally ordered dFNC state sequence, y = {y1,…, y_i,…y_T}, of the same subject estimated from the preprocessing step described in Section 2.3. The central theme of the model is that information for predicting a sequence y from the corresponding loading coefficients x may spread through out the structural components, which can be selectively retrieved as the sequence predictor predicts a dFNC state at each time step. This is achieved by training both sequence predictor and attention network jointly from the multimodal data. Further details of the model are described below.

Sequence predictor

The sequence predictor is a probabilistic model that predicts one dFNC state of a sequence at each time step, where we define each conditional probability as

$$p(y_i\mid y_1,\dots ,y_{i-1},\mathbf{x})=h({\mathbf{s}}_i,{\mathbf{c}}_i),$$ (1)

where s_i is the current hidden state of a unidirectional recurrent layer and c_i (more details will be provided shortly) is the current selective focus over structural components, referred to as context hereafter. A few points about the probability model of Eq. (1) are noteworthy. First, it embodies a fusion implicitly as the probability is conditioned on previous output history (from one modality) and the input (from the other modality). Second, the time index i indicates dynamic property of one of data modalities. Finally, right hand side of Eq. (1) captures the aspect of deep learning, i.e., the predictor works with latent representations of input and output as opposed to the direct input-output, which are learned from the data.

We realize Eq. (1) by a feedforward neural network (NN) [a single hidden layer with softmax output] stacking it on a recurrent layer. At each time point, the recurrent layer computes the current hidden state s_i which is a function of past state, previous output from the feedforward NN, and the current context, i.e.,

$${\mathbf{s}}_i=g({\mathbf{s}}_{i-1},y_{i-1},{\mathbf{c}}_i).$$

The recurrent layer helps finding a learnable smooth trajectory in a latent representational space. We use gated recurrent units (GRUs) in the recurrent layer as they work well for sequence representation (Chung et al., 2014). Each output dFNC state y_i indicates one of the centroids of five clusters (see Section 2.3). Since the centroids are 47 × 47 matrices lying in rather a low dimensional subspace, we reduce the dimension into 4, i.e., y_i ∈ R⁴, using principal component analysis (PCA). The remaining term, current context c_i, is described in the next subsection.

Attention network

For our study, attention network is the most important part as it enables learning association(s) between functional dynamics and structural features. Just before the sequence predictor predicts i-th dFNC state, the attention network first computes an alignment score (indicating strength of association) as to how well the structural component x_j matches with dFNC state y_i. This score is based on recurrent state s_i–1 and evaluated for all structural components, i.e., for j = 1, 2,…, J, in each time step i. We use a feedforward neural network (NN) with a single hidden layer for the attention module as described below.

$${\mathbf{e}}_i={\mathbf{V}}^{⊺}\tanh \left({\mathbf{W}}_s{\mathbf{s}}_{i-1}+{\mathbf{W}}_x^{⊺}\mathbf{x}\right)$$ (2)

$${\alpha }_{\mathit{ij}}=\frac{\text{exp}(e_{\mathit{ij}})}{\sum _{j=1}^J\text{exp}(e_{\mathit{ij}})},\text{for}j=1,2,\dots ,J$$ (3)

Here V, W_s and W_x are the parameters of a feedforward NN, and e_i is a vector of length J containing unnormalized alignments. Then the normalized alignments are computed according to Eq. (3) to provide a probabilistic interpretation. The attention network modulates the structural components with its learned alignments and computes a context vector c_i at i-th time step as

$${\mathbf{c}}_i={\alpha }_i•\mathbf{x}$$ (4)

where ● indicates element wise multiplication. In other words, the context vector serves as the currently focused structural components with their soft alignments. In effect, each alignment α_ij reflects the importance of structural component x_j with respect to previous hidden state s_i–1 in deciding next state s_i and generating dFNC state y_i by the sequence predictor.

Our interest with the translation-based fusion model described above is to examine brain structure-function relationship in terms of the alignments, α_ij, for i-th dFNC state and j-th structural components. Note that these alignments are learned from the data, thus taking representational advantage of deep learning (Bengio, 2009). Since similar models have been proved to be able to find meaningful associations in machine translation (e.g., alignment between phrases of two languages (Bahdanau et al., 2014)) and image caption generation (e.g., association between phrases in text and regions in image (Xu et al., 2015)), we rely on our method for finding associations between fMRI and sMRI features faithfully.

Both the sequence predictor and attention network are trained jointly using a gradient based optimization algorithm called rmsprop (Tieleman and Hinton, 2012) with respect to a negative log-likelihood based cost function,

$$-\log (p(\mathbf{y}\mid \mathbf{x}))-\lambda \sum {\alpha }_{\mathit{ij}}^2.$$

In order to avoid the overfitting problem, we use L₂ regularization on alignments and a 50% dropout (Srivastava et al., 2014) in the hidden layers of feedforward NNs (see Fig. 1). No dropout was adopted in the recurrent layer and inputs.

There are some architectural choices and hyper parameters for our model shown in Fig. 1. Based on the lowest negative log-likelihood on a hold out subset of data over several configurations, we selected number of the hidden neurons in both feedforward NNs as 50, the number of recurrent units in the recurrent layer as 50; and set the learning rate and the coefficient of L₂ norm as 0.01 and 0.5, respectively. The model with this configuration was trained using a gradient descent algorithm (Tieleman and Hinton, 2012) over entire data, and then the alignments were extracted from the model. We took 100 runs with different random neural-network weight initializations of the model, and the alignments were averaged over 100 runs for subsequent analysis.

3. Results

Here, we present our results in terms of learned alignments between dFNC states and ICA-based structural components. The dFNC states and structural components were computed following the processing of fMRI and sMRI data, respectively, as described in Section 2.3. In effect, the dFNC states capture dynamics of fMRI in terms of changes in functional connectivity among various gray matter areas of brain, while the structural components represent patterns of GMD covariation among subjects. Consequently, the alignments learned by our model give an account of possible associations between different states of functional connectivity and brain GMD patterns.

The dFNC states and structural components

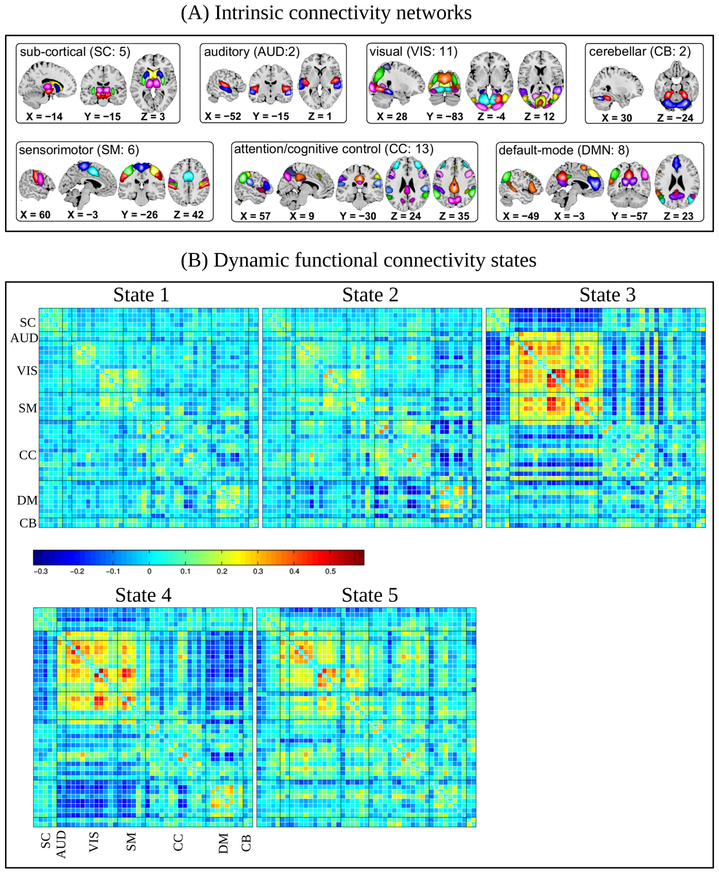
Following previous study (Damaraju et al., 2014) on dFNC, a total of 47 ICNs were identified with GICA and arranged into groups based on their anatomical and presumed functional properties. As shown in Fig. 2(A), the ICNs were grouped into subcortical (SC), auditory (AUD), visual (VIS), somatomotor (SM), cognitive control (CC), default-mode network (DMN), and cerebellar (CB) networks covering majority of subcortical and cortical gray matter. The time courses associated with 47 ICNs were windowed first and then functional connectivity was measured as temporal correlation among ICNs within the window. We clustered the resulting dFNC correlation matrices for all subjects using k-means algorithm with the elbow criterion and obtained five clusters as shown in Fig. 2(B). Each subject, therefore, stays in one of the five transient states at any given time point. All the states exhibits modular organization in the functional connectivity patterns within sensory systems and default mode regions, which is consistent with prior literature (Allen et al., 2012). There are also noticeable differences among the transient states. For example, States 1 and 2 are sparsely connected, i.e., the most ICNs have weaker correlation among them indicating less synchronicity across majority of subcortical and cortical gray matter areas. State 2, however, differs from State 1 in terms of higher positive correlation among regions of DMN and more negative correlation between DMN and other cortical regions. States 3, 4, and 5 show relatively high to moderate correlations/anticorrelation among many ICNs. In particular, we can see very strong positive correlation among the ICNs of various sensory and motor systems in these three states. The ICNs within the DMN of State 4 have higher positive correlation, while the state exhibits strong anticorrelation between DMN and sensory ICNs. State 3 characterizes a unique aspect of functional connectivity pattern comprising increased subcortical connectivity, very strong anticorrelation between subcortical and sensory/motor systems, and a breakdown of default-mode connectivity which might be related to a transient state of drowsiness (Allen et al., 2012).

Figure 2:

(A) Intrinsic connectivity networks (a total of 47) arranged into groups: subcortial (SC), auditory (AUD), visual (VIS), somatomotor (SM), cognition control (CC), default mode (DM), and cerebellar (CB). An associated number in each group indicates the number of ICNs included the group. (B) The dFNC states as the centroids resulting from cluster analysis of dFNC correlation matrices. States 1 and 2 have low correlation among 47 ICNs, while 3, 4, and 5 have high to moderate correlation.

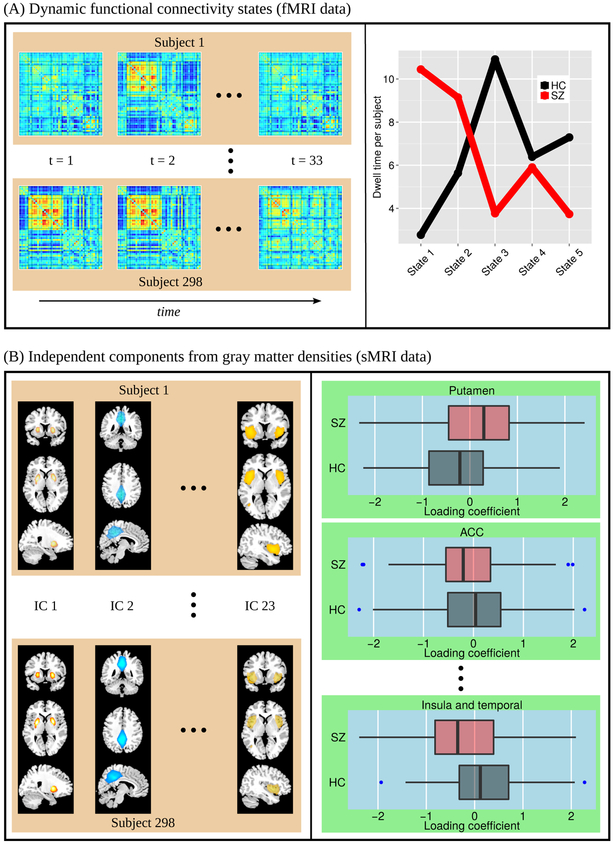
According to Allen et al. (2012), dFNC states depicts connectivity patterns that are quasi-stable, i.e., they reoccur over time and are present in numerous subjects. Left panel of Fig. 3(A) displays an example of how each subject dwells and make transition between states over time. It should be mentioned that a single subject may or may not dwell all of the five subjects during his/her entire scan time. Moreover, some states were transitioned to more by the HC group, while some others were more dwelled by the patients. To summarize dFNC states over HC and patient group, the state occupancy rates are shown in the right panel of Fig. 3(A) in terms of average dwelling time per subject. It can be observed that patients with SZ spent more time than the HCs in states 1 and 2, wherein most ICNs exhibited weaker functional connectivity. On the other hand, HCs made more transitions than patients in states 3, 4, and 5 that represented high to moderate correlations among many of the ICNs.

Figure 3:

sMRI and dynamic fMRI features used as input and output of the translation model. (A) Dynamic functional connectivity (dFNC) features as dFNC state sequence. Left panel shows examples of time sequences of dFNC states transitioned by each subject. Right panel shows group-average dwell time per subject for each of the five transient states. (B) Loading coefficients as sMRI features (left panel: each subject has a set of 23 values for the corresponding loading coefficients and right panel: box-plot of loading coefficients between HCs and patients with SZ.

Features from other modality, i.e., structural MRI, were computed from gray matter densities (GMD) using ICA decomposition into sources and their associated weights (loading coefficients) in the subjects. The sources represent maximally independent spatial components (maps). Each component captures gray matter covariation within a source, but independent of other sources. This type of analysis is also known as source based morphometry (SBM) (Xu et al., 2009). A total of 23 structural components were selected with SBM analysis. Some of the components are shown in the left panel of Fig. 3(B) (all of 23 components are mentioned and shown in the next section). We used a set of 23 loading coefficient values for each subject as sMRI feature values in our translation model. The right panel of Fig. 3(B) displays a box-plot of loading coefficients between two groups, HCs and patients with SZ, showing that some components have higher mean values in their weights for the HCs and some components have lower than the patients.

The sMRI features (loading coefficients) and fMRI features (dFNC state sequence) described above are set as the input and output of our translation model (see Fig. 1), respectively, with a goal that the attention module would learn alignments (strength of associations) between sMRI and fMRI features. The alignment results are described in the next section.

Alignments between dFNC states and structural components

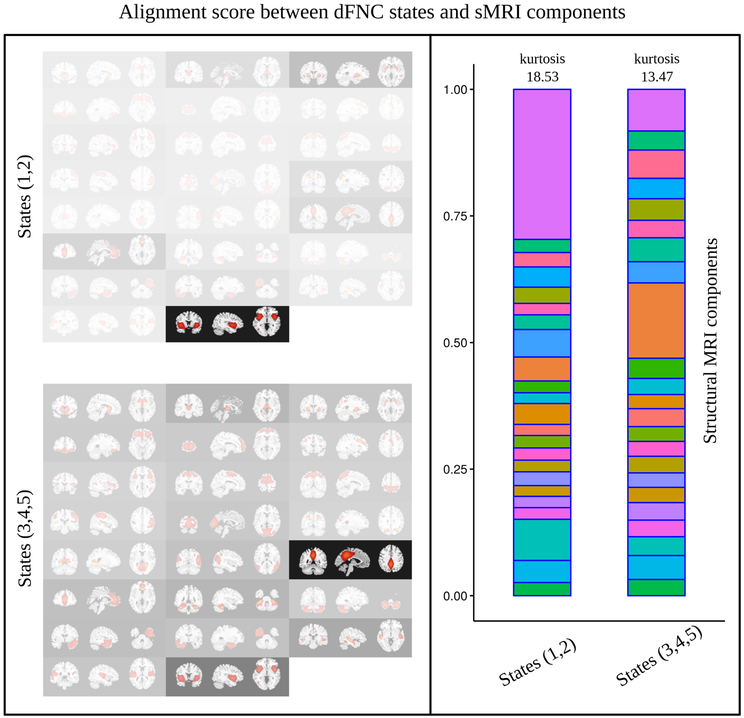
To illustrate how the attention network selectively finds associations between dFNC states and structural components, the learned alignment scores (as described in (Eq. 4)) are depicted in Fig. 4 by overlaying transparency masks over the structural components. The higher the alignment score the higher the transparency. Alignments in the left top panel are averaged over states 1 and 2 where patients with SZ made more transitions, while the left bottom panel shows an average over states 3, 4, and 5, wherein HCs were more engaged. Note that the alignments were first averaged over all subjects, and then were summarized for the states. A distinction can be observed between the associations of dFNC patterns and structural components. For example, precuneus, posterior cingulate cortex (PCC), and several temporal gyri were more strongly associated with the dFNC states (3,4, and 5) consisting of many strongly correlated ICNs, compared to the states (1 and 2) having mostly weakly correlated ICNs. On the contrary, the strengths of association with insula (and part of temporal gyri) and putamen were found to be higher for the dFNC states 1 and 2. Another distinction can be seen in the right panel of Fig. 4 which depicts that alignments are more uniformly spread out for the dFNC states 3,4, and 5 than those of states 1 and 2 across. Alignment scores for individual states are shown in Fig. 3. In effect, each dFNC state has alignment scores across all 23 structural components and they sum to 1.00 [Eq. (3)]. If equal focus or attention was given to every structural component, the alignment score would be 1/23 = 0.043. Besides, the alignment scores vary across subjects for each dFNC state - structural component pair. Therefore, we show the mean alignments (thresholded at 0.056) across all subjects including HC and SZ in Fig. 5(A). States 1 and 2 where ICNs were sparsely connected had some similarity in their alignments, for example, both showed stronger associations with putamen and insula. On the other hand, state 3, 4, and 5 showed their associations with some of the structural components in the saliency and default mode networks [precuneus, PCC, and anterior cingulate cortex (ACC)], and in temporal cortex, in addition to the insula. In other words, the alignments for states 3,4, and 5 were more spread out than those for states 1 and 2, in addition to their regional differences across the brain.

Figure 4:

Left panel: alignment scores between dFNC states and structural components depicted as over-layed transparency masks. The higher the alignment score higher the transparency. Top diagram shows alignments averaged over dFNC states 1 and 2 (wherein patients with SZ made more transitions). Bottom diagram presents alignments averaged over dFNC states 3, 4, and 5 (wherein the HCs made more transitions). Right panel: Same alignment scores (of left panel) shown as stacked plots. In each stack, alignment scores sum to 1.0 over 23 structural components (colors are provided to match each structural component in both of the stacks as a visual aid. From bottom to top: caudate, thalamus, putamen, orbitofrontal, medial frontal, middle frontal, inferior frontal, SMA, superior parietal, right post central, cuneus and visual, middle occipital, calcarine, middle temporal and occipital, precuneus and posterior cingulate cortex, anterior cingulate cortex, upper cerebellum, lower cerebellum, right inferior temporal, left inferior temporal, middle temporal, superior temporal, and insula and temporal, respectively.

Figure 5:

Alignments learned by the translation-based fusion model. (A) Mean alignments across all subjects (both HC and SZ) thresholded at 0.057. (B) Group differences in alignments. The significances (FDR corrected) of Kolmogorov-Smirnov tests are provided as asterisks (‘****’: p < 10⁻⁴; ‘***’: p < 10⁻³); ‘**’: p < 10⁻²; ‘*’: p < 0.05; and ‘ns’: p > 0.05.

The group differences in alignments are shown in Fig. 5(B) and Fig. 6. It should be mentioned here that no discriminating information of HC and SZ was given during the training of the model. To measure the significance, Kolomogorov-Smirnov tests were performed and the p-values are provided in each plot of Fig. 5(B). Mean alignments of states 1 and 2 with putamen were significantly higher for the patients with SZ. Healthy controls showed more alignments than SZ in case of states 3 and 5 with middle temporal gyri which is involved in various cognitive tasks. States 2, 3, and 5 also showed higher associations with precuneus and PCC for the healthy controls. Interestingly, most of the states exhibited significantly higher alignments with insula for the patients with SZ.

Figure 6:

Group differences in learned alignments between fMRI and SMRI features. A red connection indicates higher mean for patients, black denotes higher mean for HCs. Significance of group differences are displayed as width of connections; the higher the significance, the wider the connecting lines between dFNC sates and structural components.

Relationships between alignments and meta-data

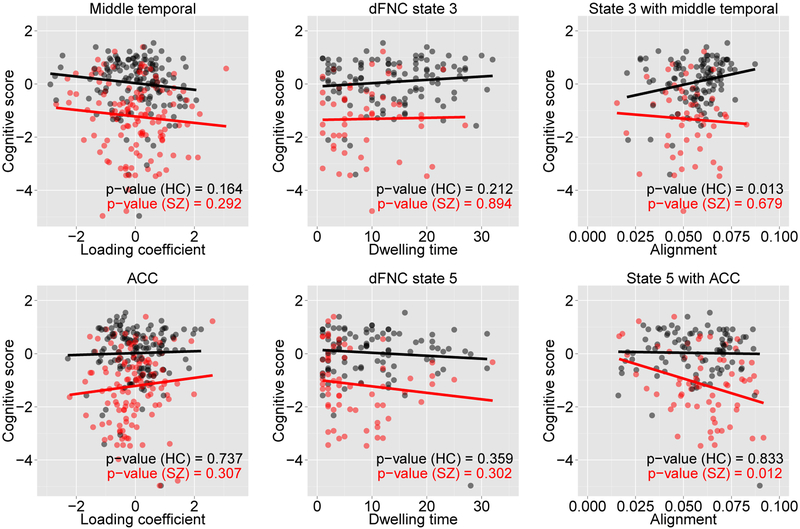
We examined the learned alignment scores to study their group-wise relationship with a cognitive score (attention/vigilance). This domain score was taken from (van Erp et al., 2015), which was based on the d-prime across blocks continuous performance test (CPT) z-scores (Vermeiren and Cleeremans, 2012). It measures how well a respondent discriminates between non-targets from targets. Figure 7 shows a linear regression fit between attention and vigilance score and alignments along with the p-values of significance test. Also shown are the relationships when each of the structural and functional features were considered individually. The alignments of state 3 with middle temporal gyri revealed a strong positive correlation for the HC group, and those of state 5 with ACC showed a strong negative correlation for the patients with SZ. No such relationship, however, could be found when individual modality of data were examined. This clearly shows a benefit of taking multimodal approach because individual modality might capture only partial views.

Figure 7:

Linear regression fit for attention and vigilance score with alignments [top panel: alignments of state 3 with middle temporal gyri and bottom panel: alignments of state 5 with ACC]. Each plot is annotated with the significance level (p-value). Relationships with individual modality, structure and dFNC, are also shown in the left two plots of top and bottom panels.

4. Discussion

This study has proposed a novel method of multimodal fusion for neuroimaging data with a particular goal of finding association between brain structure and functional dynamics. The key idea is that to some extent information about dynamic fMRI features are spread over gray matter structural patterns, which can be selectively extracted using state-of-the-art machine learning techniques. To this end, we leverage the recent advancement of attention mechanism in deep learning to find (possibly nonlinear) alignments/associations between brain structure and function.

The dFNC patterns capture changing functional connectivity as the time proceeds. An analysis on the patterns by k-means clustering resulted in two major types of patterns. Among five clusters (states), states 1 and 2 account for weaker connectivity within majority of ICNs and demonstrates no strong connectivity between subgroups (SC, AUD, VIS, SM, CC, DM, and CB). These are also the states wherein the patients with SZ made significantly more transitions than the HCs, suggesting a dysconnectivity in the SZ (Damaraju et al., 2014). Our translation-based multimodal fusion approach adds more information revealing possible linkage of these states (1 and 2) with some of the brain structures. In particular, these states have stronger associations with insula and putamen. Insula has been shown to have strong connection with aberrant activities in default mode and central executive networks in schizophrenic patients (Manoliu et al., 2014). It also shows more of gray matter volume loss in practically any other brain region in the patients with SZ. Parts of it along to circuits are concerned with distinguishing between stimuli coming from inside and outside the body, which gives it an obvious potential role in schizophrenia. Our findings of stronger associations between states 1(2) and insula are consistent with this finding as the states were significantly dwelled by the patients with SZ. On the other hand, states 3, 4, and 5 speaks for high to moderate correlations among the several ICNs, including regions in AUD, VIS, and SM. Interestingly, the HCs made more transitions in these states. With regard to their associations with the brain structures, significantly more alignments are revealed with the GMDs in precuneus, PCC, and temporal cortex. Furthermore, comparing alignment distributions across structural components, states 3, 4, and 5 seem to be more evenly spread out than the states 1 and 2. This is expected because many ICNs showed stronger functional connectivity in states 3, 4, and 5. These distinctive new findings suggest potential advantages of our novel multimodal approach in the psychosis research.

Besides finding associations between brain structure and functional dynamics, we examined learned alignments for their possible relationships to cognitive scores (van Erp et al., 2015). A strong positive correlation between attention and vigilance score and alignment of state 3 with middle temporal gyri, for the HCs, was revealed only when multimodal fusion was adopted. Neither of unimodal features indicated such relationship. Likewise, a strong negative correlation for the patients with SZ was found between their cognitive scores and alignments of state 5 with ACC, while unimodal features failed to provide such information. The positive correlation in the HCs and negative correlation in the patients suggest distinct structural-functional mechanisms, thereby demonstrate an interplay between deficits and dysfunction in the patients. The observed relationships are consistent and extends previous reports on structural-functional abnormalities in patients with SZ. Using a data-driven multimodal fusion approach, Michael (Michael et al., 2011) showed significantly differing structure-function association in the ACC and temporal regions. Koch et al. (Koch et al., 2013) investigate white matter connectivity and cortical thickness for aberrant structure-function association in the schizophrenic patients. Their study suggests a complex disruption of gray and white matter integrity within cingulo-temporal network which is hypothesized to have a major psychopathological relevance in schizophrenia.

The method proposed in this paper employs advanced machine learning technique in the multimodal fusion framework. It is highly suitable when one of (or both) the modalities has (have) dynamics in its (their) features. A limitation of our present study is that we worked with somewhat distilled data for the functional dynamics (i.e., dFNC states). However, in principle, the deep learning approach has a potential for learning dynamic features from the fMRI data, and thus can offer a favorable framework for multimodal fusion in the brain imaging research. We plan to explore this in future work.