Leveraging Polygenic Functional Enrichment to Improve GWAS Power

Abstract

Functional genomics data has the potential to increase GWAS power by identifying SNPs that have a higher prior probability of association. Here, we introduce a method that leverages polygenic functional enrichment to incorporate coding, conserved, regulatory, and LD-related genomic annotations into association analyses. We show via simulations with real genotypes that the method, functionally informed novel discovery of risk loci (FINDOR), correctly controls the false-positive rate at null loci and attains a 9%–38% increase in the number of independent associations detected at causal loci, depending on trait polygenicity and sample size. We applied FINDOR to 27 independent complex traits and diseases from the interim UK Biobank release (average N = 130K). Averaged across traits, we attained a 13% increase in genome-wide significant loci detected (including a 20% increase for disease traits) compared to unweighted raw p values that do not use functional data. We replicated the additional loci in independent UK Biobank and non-UK Biobank data, yielding a highly statistically significant replication slope (0.66–0.69) in each case. Finally, we applied FINDOR to the full UK Biobank release (average N = 416K), attaining smaller relative improvements (consistent with simulations) but larger absolute improvements, detecting an additional 583 GWAS loci. In conclusion, leveraging functional enrichment using our method robustly increases GWAS power.

Introduction

Genome-wide association studies (GWASs) are the prevailing approach for identifying risk loci for common diseases and complex traits.^{1, 2} In this study design, millions of single-nucleotide polymorphisms (SNPs) are assayed in a large collection of individuals and marginally tested for association to a trait under investigation. To safeguard against false positive associations, practitioners must impose stringent p value thresholds, which can limit power. Consequently, only a small fraction of total SNP-heritability is explained by SNPs that are significant at genome-wide thresholds (e.g., p ≤ 5 × 10⁻⁸).^{3, 4} For a fixed GWAS sample size, power to detect significant associations is determined by the effect size, minor allele frequency (MAF), and levels of linkage disequilibrium (LD) at causal and non-causal variants. These three parameters interact in non-trivial ways in the context of complex traits; for example, it has been reported that after adjusting for MAF, SNPs with lower levels of LD have larger causal effects.^{5, 6, 7, 8} These observations motivate the development of new strategies that leverage polygenic signal to improve GWAS power.

Emerging functional genomics data have revealed that certain categories of variants are enriched for disease heritability.^{7, 9, 10, 11, 12, 13, 14, 15, 16, 17} Thus, incorporating functional information into association analyses has the potential to increase GWAS power.^{18, 19, 20, 21, 22, 23, 24, 25, 26} However, previous integrative methods for GWAS hypothesis testing either assume sparse genetic architectures when estimating functional enrichment,^{22, 25} require knowledge or approximation of the true effect size distribution,^{18, 19, 20} or do not produce p values for each SNP as output.^{22, 23, 24, 26} In addition, general-purpose methodologies for association testing that can integrate prior information^{27, 28, 29} have not been thoroughly evaluated in the context of GWAS leveraging functional genomics data.

In this work, we propose an approach that uses polygenic modeling to weight SNPs according to how well they tag functional categories that are enriched for heritability. Our procedure takes as input summary association statistics along with pre-specified functional annotations (which can be overlapping and/or continuous valued) and outputs well-calibrated p values. We utilize a broad set of 75 coding, conserved, regulatory, and LD-related annotations that have previously been shown to be enriched for disease heritability.^{7, 14} We incorporate the weights computed by our method using the weighted-Bonferroni procedure described by Roeder et al.,¹⁸ a theoretically sound approach that ensures proper null calibration and can improve power when employed with informative weights. Through extensive simulations and analysis of UK Biobank phenotypes,^{30, 31, 32} we demonstrate that our approach reproducibly identifies additional GWAS loci while controlling false positives.

Material and Methods

Overview of FINDOR Method

We build upon previous works^{7, 14, 18, 21, 28, 33} to develop an integrative GWAS framework for functionally informed novel discovery of risk loci (FINDOR). Our approach involves two steps. First, we use stratified LD score regression¹⁴ to compute the expected ${\chi }^2$ statistic of each SNP based on the functional annotations that it tags; we make use of a broad set of coding, conserved, and regulatory annotations¹⁴ as well LD-dependent annotations⁷ (conditional on MAF, variants with lower LD have larger causal effect sizes). Second, we stratify SNPs into bins of expected ${\chi }^2$ and estimate the proportion of null $\left({\hat{\pi }}_0\right)$ and alternative $\left({\hat{\pi }}_1\right)$ SNPs within each bin using the Storey ${\pi }_0$ estimator to obtain bin-specific weights.^{21, 28, 33} We limit the number of bins to 100 and normalize the weights to have mean 1, ensuring proper null calibration¹⁸ (see Details of FINDOR Method below). We then divide the observed p values within each bin by these weights to produce re-weighted p values for each SNP. Bins with larger values of ${\hat{\pi }}_1$ will have larger weights, leading to more significant p values. We have released open-source software implementing the method (see Web Resources).

Details of FINDOR Method

The aim of our method is to re-weight SNPs according to how well they tag heritability enriched categories. This is accomplished in two steps. First, we estimate a function that predicts the ${\chi }^2$ statistic (i.e., tagged variance) at each SNP using a comprehensive assortment of functional annotations which include coding, conserved, and regulatory annotations,¹⁴ as well as LD-dependent annotations.⁷ The stratified LD score regression^{7, 14} framework is a natural choice for this task. In stratified LD score regression, the association statistic at SNP j measured (or imputed) in N_j individuals is expressed in terms of its tagging of studied annotations. Specifically,

$$\text{E}\left({\chi }_j^2\right)=N_j\sum _C{\tau }_C\ell \left(j,C\right)+N_j\alpha +1,$$ (Equation 1)

where α represents confounding biases,³⁴ ${\tau }_C$ is the effect size on per-SNP heritability of annotation C, and $\ell \left(j,C\right)$ is the LD score that indicates the degree to which SNP j tags annotation C:

$$\ell \left(j,C\right)=\sum _{k}C\left(k\right)r_{k,j}^2.$$ (Equation 2)

Here, C(k) is the value of annotation C at SNP k and $r_{k,j}^2$ signifies the squared Pearson correlation coefficient between SNPs k and j^{7, 14} (computed from 503 European individuals of the 1000 Genomes (V3) reference panel³⁵). In a typical analysis, the quantity of interest is an estimate of ${\tau }_C$ $\left(\widehat{{\tau }_C}\right)$, which can be interpreted as the strength of enrichment (or depletion) of heritability within annotation C. These values are obtained through a multivariate (weighted) regression of the observed ${\chi }^2$ statistics at HapMap3 SNPs against the corresponding values of $\ell \left(j,C\right)$. In this work, we use $\widehat{{\tau }_C}$ to predict the expected ${\chi }^2$ statistic at all GWAS SNPs. For a given SNP j, we have:

$$\widehat{{\chi }_j^2}=N_j\sum _C\widehat{{\tau }_C}\ell \left(j,C\right)+N_j\hat{\alpha }+1.$$

The $\widehat{{\tau }_C}$ parameters can either be global estimates that are learned from the entire GWAS dataset (restricted to HapMap3 SNPs) or chromosome-specific estimates that are learned from the remaining off-chromosome data (e.g., $\widehat{{\tau }_C}$ for chromosome 1 is learned from chromosomes 2 through 22). Empirically, we find that using the entire genome does not introduce false positives (see Figure 1).

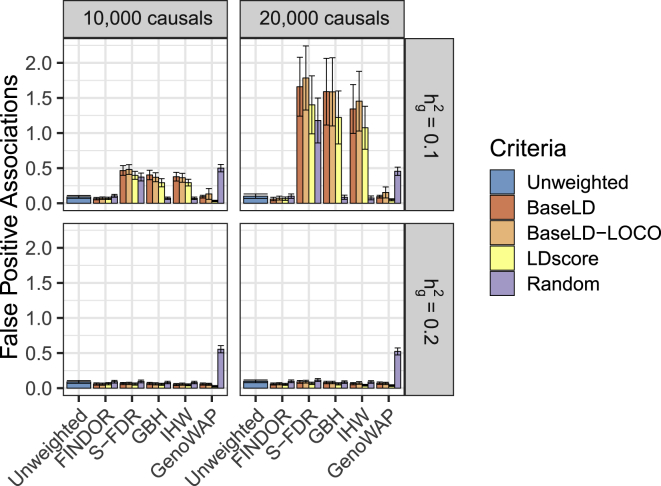
Figure 1.

FINDOR Is Well Calibrated in Simulations of Null Loci

We report the average number of independent, genome-wide significant (p < 5 × 10⁻⁸) associations on null chromosomes. Results are averaged across 1,000 simulations. Error bars represent 95% confidence intervals. Numerical results are reported in Table S3.

Second, we stratify SNPs based on their expected ${\chi }^2$ into B distinct, evenly sized bins. In practice, to ensure a sufficiently coarse partitioning of the data, we set B = 100. For densely imputed data such as the UK Biobank, this results in each bin b containing $\approx 100$K SNPs. We then estimate the proportion of null $\left({\hat{\pi }}_{0,b}\right)$ and alternate $\left({\hat{\pi }}_{1,b}\right)$ SNPs by fitting a cubic spline to the histogram of p values as proposed by Storey and Tibshirani.³³ Following Hu et al.,²⁸ we weight each p value by dividing the nominal p value by the ratio of ${\hat{\pi }}_{1,b}$ to ${\hat{\pi }}_{0,b}$. Intuitively, bins with higher proportion of true alternates will have their p value weighted downward (i.e., made more significant). However, unlike Hu et al.,²⁸ we normalize these weights to have mean 1:

$${\hat{w}}_b=\frac{\frac{{\hat{\pi }}_{1,b}}{{\hat{\pi }}_{0,b}}}{\frac{1}{B}{\sum }_{b=1}^B\frac{{\hat{\pi }}_{1,b}}{{\hat{\pi }}_{0,b}}}.$$ (Equation 3)

Applying these weights while imposing a global p value threshold of 5 × 10⁻⁸ yields the well-known “weighted-Bonferroni” procedure first described in Genovese et al.³⁶ With independently derived weights that average to 1, this procedure guarantees control of type I error (see Appendix of Genovese et al.³⁶). However, the weights $\left({\hat{w}}_b\right)$ used in our approach are data dependent. Theory developed by Roeder et al.¹⁸ demonstrated that a weighting scheme with weights that average to 1 preserves control of type I error with high probability if the number of weights learned (e.g., 100) is significantly less than number of hypothesis test performed (e.g., 1 million), making the normalization step in Equation 3 critical.

S-FDR, GBH, IHW, and GenoWAP Methods

We adapted three previously proposed FDR-based methodologies that leverage prior information to serve as comparators to our approach: stratified false discovery rate (S-FDR),²⁷ grouped Benjamani Hochberg (GBH),²⁸ and independent hypothesis weighting (IHW).²⁹ Because these are FDR-controlling procedures, we calibrate the expected level of FDR control required to match the more traditional criteria for genome-wide significance (p ≤ 5 × 10⁻⁸). We refer to this level of genome-wide FDR control as q_GW, which we estimate as the maximum q-value³³ among SNPs with p values ≤ 5 × 10⁻⁸. We implemented S-FDR by binning SNPs according to various criteria used in this study. We then computed q-values for each bin and rejected any SNP within the bin whose q-value was less than q_GW. This stratified FDR strategy is similar to Schork et al.²¹ GBH and IHW were implemented in the IHW (v.1.1.3) and IHWpaper (v.1.0.2) packages,²⁹ which we ran using the default setting and specified the level of FDR control to be q_GW. GBH takes as input group labels that were identical to the groupings used with FINDOR and S-FDR, while IHW handled raw measurements of the auxiliary information (e.g., each SNP had its own unique value of predicted tagged variance under baselineLD annotation model).

For completeness, we also adapted GenoWAP,²³ a Bayesian approach for prioritizing GWAS results that combines association strength with functional data to produce a posterior probability for each SNP. GenoWAP makes use of functional scores (prior probabilities) produced by the GenoCanyon annotation model³⁷ (and its extensions^{17, 38}), which lie between 0 and 1. (On the other hand, the expected ${\chi }^2$ statistics computed using the baseline-LD model do not represent prior probabilities and do not lie between 0 and 1.) GenoWAP includes a key hyperparameter, the threshold for the GenoCanyon functional score that distinguishes functional from non-functional SNPs. Although this hyperparameter is typically set to 0.1 for the GenoCanyon functional model, it remains unclear what is an appropriate value for a different annotation model (e.g., the baseline-LD model). To address these complexities, we first downloaded GenoCanyon functional scores (v.1.0.3; see Web Resources) and determined that 39% of the SNPs in our SNP set have GenoCanyon functional score greater than 0.1. We then categorized the top 39% of SNPs as “functional” using the various criteria explored in our study (baseLD, baseLD-LOCO, LDscore, and random, see below). To ensure a fair comparison to our approach, we ranked SNPs based on the resulting posterior probability and counted the number of independent GWAS loci in the top K SNPs, where K was the total number of genome-wide significant SNPs reported by FINDOR for the corresponding functional criteria.

Functional Annotations

We employed the 75 functional annotations of the baselineLD model, which were previously demonstrated to be enriched for heritability across a wide variety of complex traits⁷ (see Table S1). For clarity, we provide a brief description of the model’s contents below. This model is an extension of the 53 annotation baseline model developed by Finucane et al.¹⁴ Briefly, the initial baseline model consisted of 24 main annotations to which 500 bp flanking windows were added to create secondary annotations. These include histone modifications H3K4me1, H3K4me3, H3K4ac, H3K9ac, and H3K27ac that span multiple cell types; genic elements describing coding, 3′ UTR, 5′ UTR, promoter, and intronic regions; combined chromeHMM and Segway segmentations (7 states); digital genomic footprint and transcription factor binding sites; DNase hypersensitivity I sites; super enhancers and FANTOM5 enhancers; and sites conserved across mammals (see Finucane et al.¹⁴ and references therein). The baseline model was augmented in Gazal et al.⁷ by adding four more binary annotations based on super-enhancers and typical enhancers, as well as two conserved annotations based on GERP++ scores. The baselineLD model was then created by adding ten common MAF bin annotations and six LD-related annotations (predicted allele age, LLD-AFR, recombination rate, nucleotide diversity, background selection statistic, and CpG content).

Simulations

Simulations were based on real imputed genotypes of British ancestry individuals from the UK Biobank interim release. We removed poorly imputed SNPs whose INFO score was less than 0.6, a standard threshold on a quality control metric that measures the statistical information of an imputed SNP’s allele frequency.³⁹ We then filtered out rare variants whose minor allele count was less than five in European individuals of the 1000 Genomes and additionally excluded the MHC region on chromosome 6. This resulted in 9.6M SNPs for analysis. We randomly subsampled n individuals from this dataset (in our main simulations, n = 100K) and simulated continuous phenotypes under a polygenic model with normally distributed causal effect sizes and a specified number of causal variants. All causal variants were placed on odd chromosomes (the median MAF of causals variants was equal to 0.09 on average). Genotypes were standardized so that each causal variant explained an equal proportion of the phenotypic variance. We simulated different values of SNP-heritability $\left(h_g^2\right)$ and number of causal variants, choosing relatively small values of SNP-heritability ($h_g^2=0.1$ and 0.2) in our main simulations to match the estimated SNP-heritability values for real traits (see Table 1). We also performed auxiliary simulations at $h_g^2=0.5$. To induce functional enrichment, we altered the prior probability that a SNP was selected to be causal, setting this to be proportional to $\text{Var}\left({\beta }_j\right)=\sum _{C}C\left(j\right){\tau }_C$. Empirically estimated enrichment parameters (τs) were obtained from a meta-analysis of the 31 traits reported by Gazal et al.⁷ (see Table S1). This allowed our simulations to more closely reflect the complex, multi-faceted genetic architectures observed in real data. We note that functional enrichment was estimated without knowledge of the true functional enrichment used to simulate phenotypes. To obtain the baselineLD leave-one-chromosome-out (baseLD-LOCO) criteria, we estimated chromosome-specific τs using off-chromosome data. To evaluate how our method performed with only a subset of SNPs, we simulated traits using the full set of UK Biobank SNPs and then down-sampled to HapMap3 SNPs. Finally, we used PLINK v.1.9⁴⁰ to compute association statistics for each SNP. The primary metric of interest in both real and simulated data was the number of independent GWAS loci (at a level of p < 5 × 10⁻⁸) that the various methodologies identified. We conservatively define independent loci using PLINK’s LD-clumping algorithm with a 5 Mb window and an r² threshold of 0.01. When defining independent GWAS loci for FDR-based methods, we transformed FDR values back to p values, such that FDR-significant SNPs had their p values set below the threshold used for LD-clumping. Reference LD for this procedure was based on the same 113K British ancestry individuals for both simulations and real data analysis. To avoid over-counting loci where allelic heterogeneity was likely present in real data, we collapsed independent signals that were within 100 kb of one another into a single locus.

Table 1.

FINDOR Increases Power across 27 UK Biobank Traits

Class	Trait	N	${\mathit{h}}_{\mathit{g}}^{\mathbf{2}}$	145K			459K
				Unweighted	FINDOR	%Improve	Unweighted	FINDOR	%Improve
Anthropometric	balding type I	68K/208K	0.21	96	100	4.2%	334	346	3.6%
	body mass index	145K/458K	0.28	117	132	12.8%	908	950	4.6%
	heel T score	141K/446K	0.33	300	308	2.7%	1,130	1149	1.7%
	height	145K/458K	0.64	674	690	2.4%	2,395	2402	0.3%
	waist-hip ratio	145K/458K	0.17	98	104	6.1%	460	506	10.0%
Blood Cell	eosinophil count	140K/440K	0.21	187	200	7.0%	699	731	4.6%
	mean corpular hemoglobin	141K/443K	0.22	237	248	4.6%	765	791	3.4%
	red blood cell (RBC) count	141K/445K	0.25	192	206	7.3%	840	885	5.4%
	RBC distribution width	141K/445K	0.20	198	212	7.1%	652	674	3.4%
	white blood cell count	131K/444K	0.21	148	165	11.5%	713	750	5.2%
Disease	auto immune traits	145K/459K	0.04	14	18	28.6%	75	86	14.7%
	cardiovascular diseases	145K/459K	0.12	38	49	28.9%	285	314	10.2%
	eczema	145K/459K	0.08	35	46	31.4%	181	198	9.4%
	hypothyroidism	145K/459K	0.05	27	30	11.1%	139	153	10.1%
	respiratory diseases	145K/459K	0.06	24	29	20.8%	104	109	4.8%
	type 2 diabetes	145K/459K	0.05	14	14	0.0%	76	86	13.2%
Other	age at menarche	75K/242K	0.25	52	56	7.7%	318	338	6.3%
	age at menopause	44K/143K	0.11	18	18	0.0%	85	91	7.1%
	FEV1-FVC ratio	124K/370K	0.27	174	185	6.3%	684	714	4.4%
	forced vital capacity (FVC)	124K/372K	0.23	90	99	10.0%	544	565	3.9%
	hair color	143K/452K	0.14	140	143	2.1%	428	436	1.9%
	morning person	130K/410K	0.11	14	14	0.0%	156	165	5.8%
	neuroticism	124K/372K	0.11	11	16	45.5%	128	149	16.4%
	smoking status	145K/458K	0.10	18	24	33.3%	154	178	15.6%
	sunburn occasion	109K/344K	0.07	23	25	8.7%	78	82	5.1%
	systolic blood pressure	134K/422K	0.22	98	106	8.2%	666	703	5.6%
	years of education	144K/455K	0.14	17	24	41.2%	286	315	10.1%
	overall	145K/459K	NA	3,054	3,261	6.8%	13,283	13866	4.4%
	average per-trait	130K/409K	0.18	113	120	13%	491	513	6.9%

For each trait, we report the number of independent, genome-wide significant loci identified by the unweighted approach and by FINDOR in the 145K and 459K UK Biobank releases. Complete results are reported in Table S7.

UK Biobank Dataset

While our simulations are intended to explore the potential of the method, analyses of real traits are necessary to determine the value of the method, as simulation assumptions may not always be reflective of real traits. Thus, we chose to analyze data from the UK Biobank, a large-scale prospective cohort study with a deep catalog of phenotypic and genetic information.^{30, 31} We used BOLT-LMM^{32, 41} to compute mixed model association statistics. A key advantage of this approach is that it allowed us to retain related individuals in this dataset, thereby maximizing power and data usage.³² We performed basic QC on each trait following standard GWAS practices (see Loh et al.³² for details). For each phenotype, we generated three sets of summary statistics based on individuals’ self-reported European ancestry. The first set of summary statistics consisted of 145K individuals from the interim UK Biobank release.^{30, 41} This served as our “discovery” dataset and had mean sample size of $\approx 130K$ across 27 independent traits (see below). We then created two additional sets of summary statistics derived from the full UK Biobank release.³¹ Our “replication” dataset consisted of 314K individuals in the final release that were not present in the interim release (mean sample size = 283K). This dataset was used to verify findings in the discovery sample. Our “full” dataset was the entire compendium of 459K individuals (average n = 416K). While we computed summary statistics at 20 million SNPs which passed filtering and QC thresholds (see Loh et al.³²), to ensure compatibility with simulations, we ran association analyses restricting to the same set of well-imputed $\approx$ 9.6M biallelic SNPs which, upon intersection, resulted in 9.6M SNPs for the interim release and 8.9M in the full release.

To avoid over-representation of certain phenotypic classes in our real data analysis, we constructed a set of 27 (roughly) independent and heritable traits, retaining only traits that exhibited a phenotypic correlation r² < 0.1. We made this choice for two reasons. First, this prevents classes of phenotypes with many correlated traits from dominating our overall results. Second, including correlated traits might lead to double-counting of pleiotropic loci, which could inflate the total number of GWAS loci that we report. To ensure adequate power to estimate functional enrichment, we also required that the traits have a heritability Z-score > 6 in the 145K dataset to be included in our analysis.¹⁴ An overview of the phenotypes analyzed in this work can be found in Table 1.

Independent Non-UK Biobank Data

To confirm the robustness of our findings, we sought to replicate them in non-UK Biobank GWASs. We were able to obtain publicly available GWAS summary statistics for nine GWAS traits that were part of the 27 trait analysis (see Table S2). As SNP coverage was not uniform, we intersected the datasets and examined only significant findings that were present in both GWASs. When per-SNP sample sizes were unavailable, we used the max n obtained from the corresponding publication (see Table S2). External GWAS alleles were polarized to the UK Biobank and standardized effect sizes were compared $\left(Z/\sqrt{N}\right)$.

Replication Analysis

We carried out replication analysis in independent UK Biobank (27 traits; 3,307 loci) and non-UK Biobank (9 traits; 446 loci) data. To ensure compatibility across all traits and datasets, standardized effect sizes were computed by dividing Z-scores by the square root of the study sample size. To quantify replication, we computed the replication slope, defined as the slope resulting from a regression of the standardized effect sizes in the replication data versus the discovery data. We restricted our analysis to lead SNPs at independent, genome-wide significant loci (lead SNP together with all of its LD partners [r² > 0.01] within 5 Mb) in the discovery data that were also present in the replication data. We defined three class of loci: those that were genome-wide significant using only the unweighted approach, using only FINDOR p values (i.e., new discoveries), or using both methods (i.e., genome-wide significant with raw p values and genome-wide significant after re-weighting). Since different SNPs at the same GWAS locus overlap different annotations, it is possible that they fall within different bins (and thus receive different weights). This could potentially lead to different lead SNPs at the same GWAS locus for the FINDOR-based p values and unweighted p values. We therefore designated a locus as genome-wide significant using both methods if the lead SNP discovered by unweighted p values had an r² > 0.01 with the lead SNP discovered by FINDOR. Finally, for each of these three classes, we estimated replication slopes and standard errors by regressing standardized effect sizes of lead SNPs in replication data versus discovery data, across multiple traits.

Results

Simulations Assessing Calibration and Power

We assessed calibration and power via simulations using real genotypes from the UK Biobank interim release³⁰ (n = 100K subsampled British-ancestry samples, M = 9.6M well-imputed SNPs; see Material and Methods). We simulated polygenic traits with 10,000 or 20,000 causal variants and SNP-heritability $\left(h_g^2\right)$ equal to 0.1 or 0.2. All causal variants were placed on odd chromosomes, with functional enrichment based on a meta-analysis of 31 traits using the baselineLD model described in Gazal et al.⁷ (Table S1; see Web Resources), and even chromosomes served as null data. Weights were computed by running stratified LD score regression¹⁴ on association statistics computed from simulated phenotypes, without knowledge of the true functional enrichment parameters used to generate the phenotypes. We compared FINDOR to three other methods that can incorporate auxiliary information for each SNP: stratified false discovery rate (S-FDR),²⁷ grouped Benjamini Hochberg (GBH),²⁸ and independent hypothesis weighting (IHW).²⁹ For completeness, we also compared to GenoWAP,²³ a Bayesian integrative method for prioritizing GWAS results that produces posterior probabilities for each SNP. For each of the five methods, we considered four different criteria for stratifying SNPs into bins: predicted ${\chi }^2$ statistics under the baselineLD model (baseLD); predicted ${\chi }^2$ statistic under the baselineLD model trained using off-chromosome data via a leave-one-chromosome-out approach (baseLD-LOCO); total LD score of a SNP (LDscore), motivated by a previous study reporting that simple LD information can be used to improve GWAS power;¹⁹ and randomly chosen bins (random). We also considered unweighted raw p values (unweighted), a natural benchmark. For both null (even) and causal (odd) chromosomes, the primary metric was the number of independent genome-wide significant associations identified. Throughout this work, we define an independent association as a SNP that exceeds a significance threshold (e.g., 5 × 10⁻⁸), together with all linked SNPs that have an r² > 0.01 within 5 Mb. We performed 1,000 simulations and averaged results across simulations. Further details of the simulation framework are provided in the Material and Methods section.

We first assessed calibration on null chromosomes. We determined that FINDOR was well calibrated, producing a similar number of false-positive (independent, genome-wide significant) associations at null loci as the unweighted approach (see Figure 1 and Table S3). This remains true whether we infer functional enrichment and compute expected ${\chi }^2$ statistics using all GWAS data (baseLD) or using off-chromosome data (baseLD-LOCO), motivating the use of the baseLD stratification criteria in the remainder of this work. Similarly, FINDOR was well calibrated at less stringent significance thresholds (see Table S4) and in scenarios with high GWAS power ($h_g^2=0.5$, see Figure S1). Although FINDOR makes multiple passes over the data, which in principle could overfit the data and produce false positives, this does not occur in practice, likely due to the small number of global parameters estimated (hundred) relative to the large number of hypothesis tests performed (millions). Furthermore, when we restricted GWAS data to 1.2 million HapMap 3 SNPs, our approach produced similar findings (Figure S2), such that we can recommend the use of 100 bins for a wide range of SNP densities.

On the other hand, S-FDR, GBH, and IHW each exhibited moderate to severe increases in false-positive associations, particularly at parameter settings with lower power, i.e., higher polygenicity and lower SNP-heritability. For example, at a polygenicity of 20,000 causal variants and $h_g^2=0.1$, we observe an average (SE) of 0.10 (0.02) false positives per simulated GWAS using raw unweighted p values and 0.06 (0.01) using FINDOR with baseLD criteria, while S-FDR, GBH, and IHW with baseLD yield 1.6 (0.2), 1.6 (0.2), and 1.3 (0.2) false positives, respectively (see Figure 1 and Table S3). This inflation is exacerbated at smaller sample sizes (see Figure S3). We hypothesize that this may be due to the fact that the theoretical guarantees provided by these procedures are unlikely to be valid when the auxiliary information incorporates the dependence structure between hypothesis tests; this limitation was previously noted by Ignatiadis et al.²⁹ and clearly affects both baseLD and LDscore stratifying criteria. Furthermore, while GBH and IHW were consistently well-calibrated under random stratification (see Figure 1, purple bars), S-FDR was not, perhaps because S-FDR requires additional adjustments for the number of strata used.⁴² In contrast, GenoWAP remained well calibrated under baseLD stratification but was susceptible to false positives under random stratification, suggesting that the method is not robust to mis-specification of the prior. While our simulations were directly based on the baselineLD model, it cannot guarantee that the true genetic architecture of real traits would be perfectly captured by this model, thus meriting caution in applying GenoWAP with baseLD to real traits.

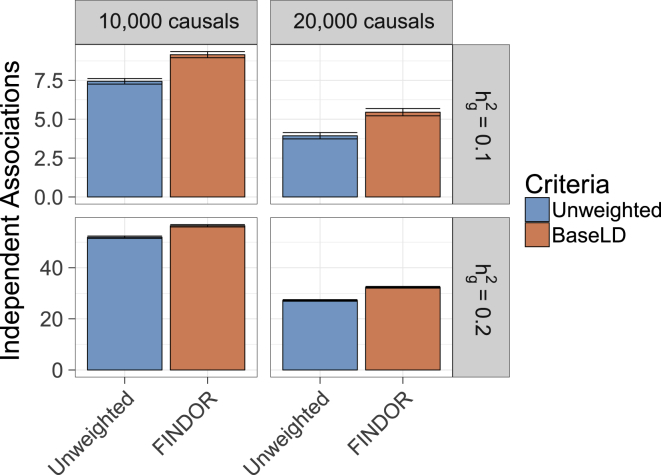
We next evaluated power to detect true associations on causal chromosomes. We primarily focused on the unweighted and FINDOR methods, as the other methods were susceptible to false positives at parameter settings with lower power (see Figure 1). Compared to the unweighted method, FINDOR attained an 8.6%–38% increase in the number of true (independent, genome-wide significant) associations, depending on polygenicity (10,000 or 20,000 causal variants) and SNP-heritability (0.1 or 0.2) (see Figure 2 and Table S5). The relative improvement was smaller at lower polygenicity and larger SNP-heritability, each of which correspond to higher absolute power. Our method has a fixed budget of weights that it can allocate, and we hypothesize that when absolute power is high it is more likely to allocate weights to SNPs that are already genome-wide significant, explaining the smaller relative improvement. In addition, the enrichment estimates provided by stratified LD score regression are expected to be less precise at lower polygenicity. However, the smaller relative improvement still translated into a larger absolute improvement in settings with higher absolute power. For completeness, we also report the power of IHW, GBH, S-FDR, and GenoWAP methods in Figure S4; these methods were generally at least as well-powered as FINDOR (though susceptible to false positives at parameter settings with lower power; see Figure 1). We also report the power of four hybrid methods that first run FINDOR to compute the number of SNPs rejected at p = 5 × 10⁻⁸ and then run each other method (GBH, IHW, S-FDR, GenoWAP) to output the same number of SNPs as FINDOR rejects (FINDOR-GBH, FINDOR-IHW, FINDOR-S-FDR, FINDOR-GenoWAP); the true positive rate for each hybrid method was similar to FINDOR, although slightly lower for FINDOR-GenoWAP (Figure S5). We do not recommend the use of the hybrid methods (see Discussion).

Figure 2.

FINDOR Increases Power in Simulations of Causal Loci

We report the average number of independent, genome-wide significant (p < 5 × 10⁻⁸) associations on causal chromosomes. Results are averaged across 1,000 simulations. Error bars represent 95% confidence intervals. Numerical results are reported in Table S4.

Application to 27 UK Biobank Traits

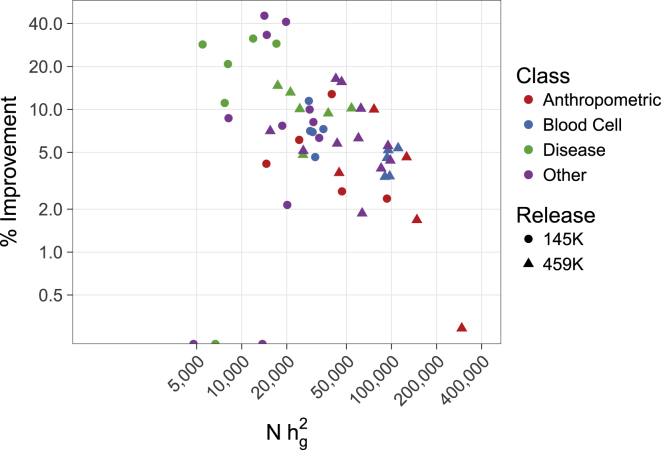
We applied FINDOR to the interim UK Biobank release,³⁰ which includes N = 145K European-ancestry samples and M = 9.6M well-imputed SNPs. We analyzed 27 independent, highly heritable traits (average N = 130K; see Table 1 and Material and Methods). We computed summary association statistics using BOLT-LMM v.2.1⁴¹ (unweighted approach). We applied FINDOR to these summary statistics and compared the number of independent, genome-wide significant associations identified by FINDOR versus the unweighted approach. In total, FINDOR identified 207 more associations (see Tables 1, S6, and S7), a statistically significant improvement (block-jacknife SE = 20.4, p < 1 × 10⁻²⁰). This corresponds to an average per-trait improvement of 13% (SE = 2.5%) and an aggregate improvement of 6.8%; FINDOR identified more associations than the unweighted approach for 24 out of 27 traits, and the same number of associations for the remaining 3 traits. The aggregate improvement was lower than the average per-trait improvement because the relative improvement was smaller for traits with higher power (i.e., more associations) (see Figure 3), consistent with simulations. In particular, disease traits exhibited a larger improvement (20% average per-trait, 22% aggregate, see Table S8), consistent with smaller effective sample size (i.e., smaller value of sample size ^∗ observed-scale SNP-heritability) due to the relatively small number of disease cases. Qualitatively similar results were obtained at a more stringent p value threshold of 5 × 10⁻⁹ (see Table S9). We note that, compared to the 13% average per-trait improvement of FINDOR with the baselineLD model,⁷ FINDOR with the baseline model¹⁴ (which excludes LD-related annotations) attained only a 7.1% average per-trait improvement and 4.3% aggregate improvement (72 fewer GWAS hits; jackknife SE on difference = 13.3, p = 6.3 × 10⁻⁸, see Table S6). This indicates that the LD-related annotations of the baselineLD model contain valuable information for increasing association power; in particular, these annotations avoid the phenomenon of strong LD between in-annotation and out-annotation SNPs that may limit the potential of coding, conserved, and regulatory annotations to increase association power despite their strong enrichments for trait heritability.

Figure 3.

Relative Improvement of FINDOR in Real UK Biobank Phenotypes Decreases as a Function of Absolute Power

We plot the relative improvement in the number of independent GWAS loci identified by FINDOR compared to unweighted p values versus sample size times observed-scale SNP-heritability, using log scales. The three circles at the bottom of plot correspond to traits where the number of loci was identical for FINDOR compared to unweighted p values (0% improvement). Numerical results are reported in Tables 1, S6, S7, and S15.

Next, we carried out a UK Biobank-based replication analysis for the 27 traits using non-overlapping samples in the full UK Biobank release. Starting with the 459K European-ancestry samples, we excluded the 145K samples that were present in the interim release and computed summary statistics using BOLT-LMM v.2.3, a highly computationally efficient implementation for very large datasets.³² This produced a well-powered replication dataset (average N = 283K). We evaluated strength of replication by computing the replication slope, defined as the slope of a regression of estimated standardized effect sizes in replication data versus discovery data, restricting to lead SNPs at genome-wide significant loci from the discovery data (we excluded lead SNPs that were not present in the replication data). We computed replication slopes for three classes of loci: those that were genome-wide significant (1) using only the unweighted approach, (2) using only FINDOR p values, or (3) using both methods. The 49 loci that were significant only using the unweighted approach produced a replication slope of 0.57 (SE = 0.043). The 230 loci that were significant using only FINDOR (i.e., discoveries) produced a slightly stronger replication slope of 0.66 (SE = 0.018); the difference was not statistically significant based on the small number of data points, particularly for unweighted only. We note that the loci evaluated for these two classes were all distinct, suggesting that the standard errors on the replication slopes are not miscalibrated due to double-counting of pleiotropic loci. As expected, the 2,766 loci that were significant using both methods produced the strongest replication slope of 0.91 (SE = 0.003), as this class of loci included the most significant associations (see Figure 4 and Table S10). For completeness, we also applied IHW, GBH, S-FDR, and GenoWAP to the interim UK Biobank release and carried out a similar replication analysis using non-overlapping samples from the full UK Biobank release. We determined that the replication slopes of these methods were comparable to FINDOR overall (see Table S11). However, consistent with simulation results (Figure 1), the replication slopes were severely attenuated for traits with lower power (see Table S12), such that we cannot recommend these methods for broad use.

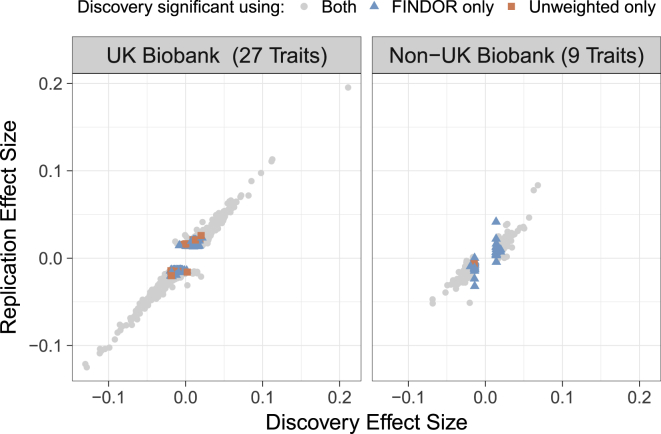
Figure 4.

Additional Loci Identified by FINDOR Replicate in Independent Samples

We plot the standardized effect sizes $\left(Z/\sqrt{N}\right)$ in the UK Biobank replication sample (average n = 283K, left panel) and non-UK Biobank replications sample (average n = 158K, right panel) versus the UK Biobank discovery sample (average n = 132K). For additional loci identified by FINDOR (blue triangles), the replication slope was positive and highly significant in both cases (UK Biobank = 0.66, Non-UK Biobank = 0.69). Numerical results are reported in Tables S10 and S13.

We also performed a separate replication analysis for nine traits for which summary statistics from independent, non-UK Biobank GWAS were available (see Material and Methods, Table S2). In this analysis, the 31 loci that were significant only using FINDOR (i.e., discoveries) produced a replication slope of 0.69 (SE = 0.11) in non-UK Biobank data, which did not differ significantly from the replication slope for the 411 loci that were significant using both methods (0.67, SE = 0.012, see Figure 4 and Table S13). Only a single locus was significant only using unweighted p values in this analysis, so we do not report a replication slope for this class. Compared to FINDOR, the IHW, GBH, S-FDR, and GenoWAP methods yield slightly deflated, though not significantly different, replication slopes in independent non-UK Biobank data (see Table S14). Overall, these results confirm that the additional loci identified by FINDOR robustly replicate in independent samples.

Finally, we applied FINDOR to the 27 traits using the full set of 459K European-ancestry samples (average N = 416K), analyzing summary statistics computed using BOLT-LMM v.2.3.³² The unweighted approach identified 13,283 independent genome-wide significant associations in this data. FINDOR identified 583 more associations (see Table S15, jackknife SE = 40.6, p < 1 × 10⁻²⁰), corresponding to an average per-trait improvement of 6.9% (SE = 0.66%) and an aggregate improvement of 4.1% (see Table 1); FINDOR identified more associations than the unweighted approach for all 27 traits. Once again, the relative improvements decreased as a function of sample size times observed-scale SNP-heritability (see Figure 3, Table 1), with larger relative improvements for disease traits (10% average per-trait, 10% aggregate) and smaller relative improvements in the 459K release versus the 145K release, consistent with simulations. We further characterized unweighted-only and FINDOR-only loci by contrasting their overlap with molecular QTL 95% causal sets.⁴³ This annotation class is not directly included in the baselineLD model and thus provides an independent assessment of whether new GWAS loci uncovered by our approach are more amenable to biological interpretation. The lead SNPs at FINDOR-only loci had substantial overlap with molecular QTL 95% causal sets (and substantially larger molecular QTL causal posterior probabilities on average), compared to unweighted-only loci (see Table S16). This arises because molecular QTL annotations have non-trivial correlations to the baseline LD model (average $\left|r\right|\approx 0.05$, see Hormozdiari et al.⁴³) and implies that loci identified by FINDOR not only are more numerous but may potentially provide deeper mechanistic insights. Overall, these results indicate that FINDOR can provide a substantial increase in power, particularly for studies with smaller effective sample sizes, such as studies of disease traits.

Discussion

We have introduced a p value weighting approach that leverages polygenic functional enrichment to improve association power. We demonstrated in simulations that our FINDOR framework is properly calibrated under the null and improves power to detect causal loci. We reproducibly identified hundreds of new loci across a broad set of UK Biobank traits, with increased prospects for biological interpretation (see Table S16). We achieved this by using a multi-faceted functional enrichment model that includes coding, conserved, regulatory, and LD-related annotations.^{7, 14}

Previous studies have leveraged functional enrichment to achieve 3%–5% increases in association power.^{22, 25} First, Pickrell²² reported a 5.0% increase in power (average n = 57K for 18 traits) using fgwas, a hierarchical Bayesian model in which genomic blocks are re-weighted based on relevant functional data. We were unable to compare FINDOR to fgwas, both because fgwas outputs regional posterior probabilities of association (for genomic blocks spanning thousands of SNPs) instead of per-SNP p values, and because the current fgwas software implementation (v.0.3.6) does not support continuous annotations. Second, Sveinbjornsson et al.²⁵ employed a p value weighting scheme with weights that were estimated across hundreds of GWASs based on a sparse functional enrichment model consisting of five variant effect predictor (VEP) annotations.⁴⁴ The authors reported a 2.7% overall increase in power (p < 1 × 10⁻⁸ median $N_{eff}=4/\left(1/N_{case}+1/N_{control}\right)=6$K for 123 binary traits, median n = 23K for 96 quantitative traits), and a 13.7% increase in the number of “unsettled” associations (1 × 10⁻¹⁰ < p < 1 × 10⁻⁸), a metric that yields much larger relative improvements. Despite the similarity between the methods, we were unable to compare FINDOR to the method of Sveinbjornsson et al.,²⁵ because this method aggregates functional enrichment estimates across hundreds of GWASs while our method is applied in a trait-specific manner. (However, it could potentially be fruitful to incorporate VEP annotations and/or weights from Sveinbjornsson et al.,²⁵ which more finely dissects coding variants, into our functional model; indeed, our initial efforts to incorporate weights for sub-categories of coding variants from Sveinbjornsson et al.²⁵ increased the FINDOR improvement from 7% to 12% overall; see Table S17.) Thus, we focused our comparisons on previous methods that could incorporate information from our polygenic functional enrichment model and produce p value thresholds for hypothesis testing: stratified FDR (S-FDR),²⁷ grouped Benjamini Hochberg (GBH),²⁸ and independent hypothesis weighting (IHW).²⁹

Stratifying SNPs based on predicted (tagged) variance was previously proposed by Schork et al.²¹ (incorporating ten functional annotations), which made a key contribution to the literature by highlighting the potential of this approach. The study demonstrated that this criteria improved replication rates and also reported that it increased power when applying S-FDR.²⁷ However, S-FDR did not achieve proper null calibration in our simulations, even under random stratification (Figure 1), perhaps because S-FDR requires additional adjustments for the number of strata used.⁴² Furthermore, S-FDR, GBH, and IHW were all unable to correctly control false positives when LD-dependent stratification criteria (LDscore or baseLD) were employed, particularly at parameter settings with lower power (Figure 1); as noted above, theoretical guarantees about false positives are unlikely to be valid when the stratification criteria incorporate the dependence structure between hypothesis tests.²⁹ (In contrast, the GenoWAP method was susceptible to false positives under random stratification.) Interestingly, the loci identified by IHW, GBH, S-FDR, and GenoWAP attained overall replication slopes similar to FINDOR in our analyses of UK Biobank traits, which are generally well powered (see Table S11); however, consistent with our simulations, the replication slopes for IHW, GBH, S-FDR, and GenoWAP were severely attenuated for UK Biobank traits with lower power (Table S12), such that we cannot recommend these methods for broad use. We also do not recommend the use of hybrid methods that first run FINDOR to compute the number of SNPs rejected at p = 5 × 10⁻⁸ and then run each other method (GBH, IHW, S-FDR, GenoWAP) to output the same number of SNPs as FINDOR rejects (FINDOR-GBH, FINDOR-IHW, FINDOR-S-FDR, FINDOR-GenoWAP) (Figure S5; the true positive rate for each hybrid method was similar to FINDOR, although slightly lower for FINDOR-GenoWAP), due to the considerable complexity of these methods.

Our approach bears some similarity to the multi-threshold association tests proposed by Eskin¹⁹ and Darnell et al.²⁰ which use knowledge of the true effect size distribution to solve a convex optimization problem to determine appropriate thresholds. Given knowledge of the true effect size distribution, this approach is theoretically optimal;^{18, 19} however, this information is rarely available in practice and must be fixed a priori or approximated from the data.^{18, 19, 20} Finally, although we employ a fundamentally different weighting strategy, our method draws on insights from Roeder et al.,¹⁸ which established the theoretical basis for data-driven p value weighting.

We conclude with several limitations of our work. First, previous studies have demonstrated that complex traits often exhibit cell-type-specific functional enrichments,^{10, 11, 12, 13, 14, 15, 16, 17, 22, 45, 46} which we did not incorporate in this study. Incorporating cell-type-specific functional enrichments may further increase power, although care will be required to avoid overfitting since identifying critical cell types requires extensive model selection. Second, our modeling of MAF-dependent architectures is limited; while our baselineLD functional model includes MAF-bin annotations for common SNPs (MAF > 5%), it does not model MAF-dependent architectures for rare and low-frequency variants. A possible future direction would be to incorporate MAF-dependent annotations, e.g., via the widely used “α model.”^{5, 47, 48} Third, we cannot formally rule out the possibility that there could exist simulation settings in which FINDOR would fail to control type I error. However, FINDOR controlled type I error in all of our simulations, including a range of realistic genetic architectures and stratification criteria; in particular, FINDOR controlled type I error when the prior was mis-specified via random stratification. Fourth, we anticipate that GWASs will grow larger and more powerful in the years ahead, but the relative improvement of our method decreases as a function of absolute power. However, we anticipate that our method will continue to produce large relative improvements for disease phenotypes (as in Table 1), for which the ongoing challenge of recruiting disease case subjects will continue to limit effective sample size. Fifth, our UK Biobank replication of loci from the interim UK Biobank release could in principle be inflated by relatedness within the UK Biobank; however, our non-UK Biobank replication produced a concordant replication slope, suggesting that this effect is limited. Sixth, replication slopes may be attenuated due to winner’s curse,⁴⁹ but we did not correct for winner’s curse when estimating replication slopes. However, attenuation due to winner’s curse would not impact the comparison between replication slopes of GWAS loci identified only using unweighted p values versus GWAS loci identified only using FINDOR p values. Seventh, we evaluated our method using only European-ancestry samples. Although our previous work has provided evidence that functional enrichment is consistent across populations,^{16, 50} generalizing our results to non-European samples is currently an open question, as it is unclear whether functional enrichments inferred in large European samples should be incorporated. Despite these limitations, we anticipate that FINDOR will be a valuable and practical tool for leveraging polygenic functional enrichment to improve GWAS power.

Declaration of Interests

The authors declare no competing interests.

Published: December 27, 2018

Web Resources

• BOLT-LMM association statistics (459K), http://data.broadinstitute.org/alkesgroup/UKBB/

• BOLT-LMM v2.3 software, http://data.broadinstitute.org/alkesgroup/BOLT-LMM/

• FINDOR software, https://github.com/gkichaev

• GenoCanyon Annotations, http://genocanyon.med.yale.edu/GenoCanyon_Downloads.html

• LDscore regression software, https://github.com/bulik/ldsc

• LDscores for baselineLD model: https://data.broadinstitute.org/alkesgroup/LDSCORE/

• UK Biobank, http://www.ukbiobank.ac.uk/

Supplemental Data

Table S7. List of Independent, Genome-wide Significant Loci for All 27 traits in 145K and 460K UK Biobank Releases

We report independent, genome-wide significant loci for both Unweighted and FINDOR.