Effects of multiple transmission pathways on Zika dynamics

Abstract

Although the Zika virus is transmitted to humans primarily through the bite of infected female Aedes aegypti mosquitoes, it can also be sexually and vertically transmitted within both populations. In this study, we develop a new mathematical model of the Zika virus which incorporates sexual transmission in humans and mosquitos, vertical transmission in mosquitos, and mosquito to human transmission through bites. Analysis of this deterministic model shows that the secondary transmission routes of Zika increase the basic reproductive number ($R_0$) of the virus by 5%, shift the peak time of an outbreak to occur 10% sooner, increase the initial growth of an epidemic, and have important consequences for control strategies and estimates of $R_0$. Furthermore, sensitivity analysis show that the basic reproductive number is most sensitive to the mosquito biting rate and transmission probability parameters and reveal that the dynamics of juvenile mosquito stages greatly impact the peak time of an outbreak. These discoveries deepen our understanding of the complex transmission routes of ZIKV and the consequences that they may hold for public health officials.

1. Introduction

Zika is a vector-borne disease transmitted to humans primarily through the bite of infected female Aedes aegypti mosquitoes. The Zika virus (ZIKV) was first found in Uganda in 1947 and has since spread sporadically to regions in Africa and Asia (Gao et al., 2016). However, since 2015, Zika has been reported in over 50 countries in the Americas including the United States and has been associated with serious clinical implications such as Guillain-Barré syndrome and increased microcephaly in newborns (Gao et al., 2016). To date, there have been approximately 200,000 confirmed cases of Zika and approximately 2600 confirmed congenital syndrome cases associated with ZIKV infection (P. A. H. O., & W. H. Organization, 2015-2017).

Transmission of Zika within human and mosquito populations is quite complex. Although ZIKV is primarily transmitted to humans through the bite of infected Aedes mosquitoes, recent reports have confirmed sexual and perinatal transmission among humans (Hamel et al., 2016). In addition to these transmission routes, the virus can spread vertically from a female mosquito to her offspring (Thangamani, Huang, Hart, Guzman, & Tesh, 2016) and has the potential to spread sexually in Aedes mosquitoes. While sexual transmission of ZIKV within mosquito populations is not yet confirmed (in part because of the lack of studies investigating transmission of ZIKV within mosquitoes), this transmission route is highly probable given evidence of sexual transmission of the Dengue virus (DENV), a closely related flavivirus, in Aedes mosquitoes (Leon, 1987).

Since little is known about Zika, mathematical models are essential to understanding the transmission dynamics of the disease, deriving key epidemiological quantities, and informing the creation of disease control strategies (Manore and Hyman). Most of the early mathematical models of Zika were employed to estimate the basic reproductive number, $R_0$, of the virus (the number of secondary infections that a single infected individual can make in a completely susceptible population). By examining the 2013/2014 Zika outbreak in French Polynesia through a simple compartmental model which incorporates only human-vector transmission, $R_0$ was found to range between 2.6 and 4.8 (Kucharski et al., 2016). This range for $R_0$ is consistent with other estimates (Gao et al., 2016; Towers et al., 2016).

As evidence of sexual transmission of ZIKV emerged, researchers began to investigate the impact of this additional transmission pathway on the spread of the disease. In (Gao et al., 2016), authors present one of the first mathematical models to examine the combined effects of direct (sexual) and indirect (vector to human) modes of ZIKV transmission in the human population. Their deterministic model utilized data from several South American countries and showed that sexual transmission contributes very little to $R_0$ (3%) but has the potential to increase the risk of infection and epidemic size of an outbreak. To further explore the contribution of sexual and vector transmission of Zika, an age-and-sex structured model was developed in (Maxian, Neufeld, Talis, Childs, & Blackwood, 2017). Analysis of the model revealed that human-mosquito interaction parameters have a more significant impact on $R_0$ than do sexual transmission parameters which contribute less than $5\text{\%}$ to the reproductive number. However, sexual transmission was shown to strongly contribute to an outbreak in regions where mosquito populations are sparse. In addition to the two transmission mechanisms studied in the previous models, the effect of migration on disease spread was investigated in (Baca-Carrasco & Velasco-Hernández, 2016). As with other studies, it was shown that sexual transmission alone cannot drive the spread of Zika but that this transmission pathway and migration can increase the magnitude and duration of outbreaks.

Researchers in (Bewick, Fagan, Calabrese, & Agusto, 2016) are among the first to develop and analyze a mathematical model of Zika which incorporates vertical transmission of the virus in humans (in addition to transmission of the disease through mosquito bites). Sensitivity analysis of the model showed that mosquito demographic parameters and human-mosquito transmission parameters play critical roles in the diffusion of Zika. The authors also investigated the effects of varying levels of control techniques on Zika and found that personal protection strategies were more effective at controlling the spread of disease than delayed conception or mosquito-reduction.

Although incorporating the additional transmission mechanisms of ZIKV into mathematical models adds to their complexity, these epidemiological details can impact the initial growth rate of an outbreak and estimates of the basic reproductive number (Lloyd, 2001, 2009; Nowak et al., 1997; Wearing, Rohani, & Keeling, 2005). In a general exploration of the sensitivity of parameter estimates to model structure, Lloyd (Lloyd, 2009) shows that models with algebraically identical $R_0$ expressions can have drastically different initial growth rates due to variations in the biological assumptions of the models (e.g. SIR versus SEIR classes and exponential versus gamma distribution of infectious and latent periods). The sensitivity of the initial growth rate of an outbreak to the model structure can lead to inaccurate estimates of the basic reproductive number of a disease. As detailed in the within-host study of viral dynamics in (Nowak et al., 1997) and the disease management context of (Wearing et al., 2005), this results in unrealistic predictions of the effectiveness of control measures needed to curtail the spread of a pathogen.

While individually, some of the transmission mechanisms of the ZIKV are unlikely, in combination they can affect the persistence of Zika. The different components can increase the size and duration of outbreaks, result in peak infections occurring sooner in Zika outbreak history, and allow the virus to circulate at low levels until favorable environmental conditions cause an outbreak. In contrast to previous studies which focus on at most two transmission pathways of the ZIKV, we introduce a new mathematical model which incorporates (1) sexual and (2) vertical ZIKV transmission within mosquito populations as well as (3) sexual transmission in humans and (4) vector to human transmission. We omit vertical ZIKV transmission in humans both to simplify our model and because the infectious period of Zika (at most two weeks (Shutt, Manore, Pankavich, Porter, & Del Valle, 2017)) is too short for an infant class to contribute to further sexual or vertical transmission of the disease. By analyzing the simultaneous ZIKV transmission cycles in humans and vectors, something which no other model has done, we aim to answer the following research question: what is the relative contribution of the individual and combined transmission mechanisms (1–4) on the spread of Zika? Quantifying the effects of these transmission pathways will not only contribute to a better understanding of the overall population dynamics of Zika but may also aid in the formation of control strategies.

In the following sections, we formulate a mathematical model incorporating transmission modes 1–4 and compare it with a simplified vector transmission model to determine the combined effects of secondary transmission pathways on the spread of Zika. We derive and numerically approximate the basic reproductive numbers of both models which are used to determine whether an epidemic will occur ($R_0>1$ implies sustained disease spread within a population). We also analyze the sensitivity of the basic reproductive number, peak time, and final epidemic size to variations in parameter values. In addition, we explore how differential timing of control measures (based on the proportion of people infected in each model) may affect the outcome of an outbreak. Lastly, we investigate how secondary transmission pathways impact estimates of Zika's $R_0$.

2. Model formation

The deterministic mathematical model discussed in this paper utilizes a system of nonlinear ordinary differential equations to capture the overall trends in Zika dynamics and estimate the likely contribution of each transmission route. In the model, we consider two populations: humans and mosquitoes. Humans are compartmentalized into susceptible, exposed, symptomatic, asymptomatic, and recovered, classes ($S_h$, $E_h$, $I_h$, $A_h$, $R_h$) with the total number of humans denoted by $N_h$. In the vector population, we consider susceptible, exposed, and infectious female mosquitoes ($S_{vf}$, $E_{vf}$, $I_{vf}$), infectious male mosquitoes ($I_{vm}$), and susceptible and infected juvenile mosquitoes ($S_e$, $I_e$). The total number of adult female, adult male, and juvenile mosquitoes is given by $N_{vf}$, $N_{vm}$, and $N_e$ respectively. We also include demographics for the mosquito population and not the human population because the lifespan of the mosquito is much shorter than that of a human. A complete list of the state variables used in this model is shown in Table 1.

Table 1.

Epidemiological Classes.

State Variable	Description
$S_h$	Susceptible Humans
$E_h$	Exposed Humans
$I_h$	Symptomatic Infected Humans
$A_h$	Asymptomatic Infected Humans
$R_h$	Recovered Humans
$N_h$	Total Number of Humans
$S_{vf}$	Susceptible Adult Female Mosquitoes
$E_{vf}$	Exposed Adult Female Mosquitoes
$I_{vf}$	Infectious Adult Female Mosquitoes
$I_{vm}$	Infectious Adult Male Mosquitoes
$S_e$	Susceptible Juvenile Mosquitoes
$I_e$	Infectious Juvenile Mosquitoes
$N_e$	Total Number of Juvenile Mosquitoes
$N_{vm}$	Total Number of Adult Male Mosquitoes
$N_{vf}$	Total Number of Adult Female Mosquitoes

Susceptible humans become exposed to ZIKV after it is transmitted to them through the bite of an infectious female mosquito or through sexual contact with an infected person. This infected person could be symptomatic or asymptomatic since the sexual transmission of ZIKV from both classes has been documented (Fréour et al., 2016; Gao et al., 2016). After a person is infected with ZIKV, he or she incubates the virus at rate δ before becoming infectious. Infectious humans recover at rate γ and are assumed to have lifelong immunity following recovery. This assumption is based on evidence from other flaviviruses, such as DENV, and the presence of ZIKV neutralizing antibodies in human and animal sera (Dawes et al., 2016; Fagbami, 1979; Dudley et al., 2016). We neglect ZIKV induced mortality in this model because symptoms of Zika (rash, fever, conjunctivitis, and muscle and joint pain) are mild and rarely result in death (Paixão, Barreto, da Glória Teixeira, da ConceiçãoCosta, & Rodrigues, 2016).

Susceptible adult female mosquitoes become exposed to ZIKV after feeding on an infected person. We assume that asymptomatic humans can transmit ZIKV to mosquitoes, as is the case in (Duong et al., 2015). During exposure to ZIKV, mosquitoes undergo an incubation period of 7–10 days before becoming infectious (Hamel et al., 2016). Once a mosquito is infectious, we assume that it does not clear the virus.

The life cycle of Aedes mosquitoes consists of four successive stages: egg, larva, pupa, and adult. In this model, we begin our observation of the mosquito population following the hatching of eggs (at rate r) and combine the two aquatic stages (larva and pupa) into the juvenile mosquito compartments $S_e$ and $I_e.$ The growth of the juvenile vector population is limited by the carrying capacity K of the breeding site. These juvenile vectors mature at a rate ${\gamma }_e$ into either susceptible or infectious adult mosquitoes. We assume that those infected juvenile mosquitoes that mature into infectious male mosquitoes can transmit ZIKV to female vectors through sexual contact. This assumption is based on experimental studies which show evidence of venereal transmission of viruses from male to female Aedes mosquitoes (Thangamani et al., 2016; Thompson & Beaty, 1978). We do not include sexual transmission from female to male mosquitoes since female mosquitoes are not shown to transmit DENV through sexual contact. Finally, since male mosquitoes do not feed on humans, we assume that they can only become carriers of ZIKV through vertical transmission from their mother.

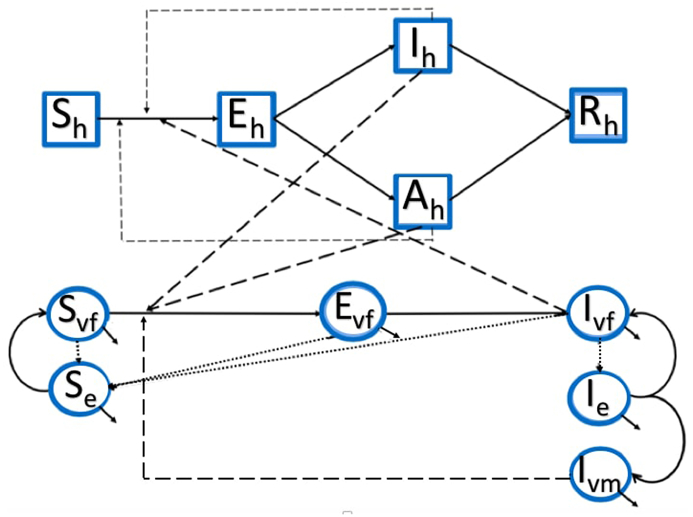
A flowchart of ZIKV transmission is illustrated in Fig. 1. The system of equations that will hence forth be referred to as the full model is given by (1) and the parameter values are shown in Table 2.

$$\begin{array}{l}{\dot{S}}_h=-b{\beta }_{vh}\frac{I_{vf}{S}_h}{N_h}-a\frac{S_h}{N_h}\left({\beta }_a{A}_h+{\beta }_I{I}_h\right)\\ {\dot{E}}_h=b{\beta }_{vh}\frac{I_{vf}{S}_h}{N_h}+a\frac{S_h}{N_h}\left({\beta }_a{A}_h+{\beta }_I{I}_h\right)-\delta E_h\\ {\dot{I}}_h=\varphi \delta E_h-\gamma I_h\\ {\dot{A}}_h=\left(1-\varphi \right)\delta E_h-\gamma A_h\\ {\dot{R}}_h=\gamma \left(I_h+A_h\right)\\ {\dot{S}}_{vf}=\alpha {\gamma }_e{S}_e-b\frac{S_{vf}}{N_h}\left({\beta }_{hs}{I}_h+{\beta }_{ha}{A}_h\right)-s{\beta }_{mf}\frac{I_{vm}{S}_{vf}}{N_{vm}}-\mu S_{vf}\\ {\dot{E}}_{vf}=b\frac{S_{vf}}{N_h}\left({\beta }_{hs}{I}_h+{\beta }_{ha}{A}_h\right)+s{\beta }_{mf}\frac{I_{vm}{S}_{vf}}{N_{vm}}-\left({\delta }_v+\mu \right)E_{vf}\\ {\dot{I}}_{vf}={\delta }_v{E}_{vf}-\mu I_{vf}+{\gamma }_e\alpha I_e\\ {\dot{I}}_{vm}={\gamma }_e{I}_e\left(1-\alpha \right)-\mu I_{vm}\\ {\dot{S}}_e=r\left(1-\frac{N_e}{K}\right)\left(N_{vf}-q{I}_{vf}\right)-\left({\gamma }_e+{\mu }_e\right)S_e\\ {\dot{I}}_e=rq\left(1-\frac{N_e}{K}\right)I_{vf}-\left({\gamma }_e+{\mu }_e\right)I_e\end{array}$$ (1)

Fig. 1.

ZIKV Transmission Model Schematic: The solid lines in this flow chart represent movement between different state variables. Thin dashed lines represent disease transmission between different classes of the same population, thick dashed lines represent disease transmission across different populations, and dotted lines represent birth in the mosquito population.

Table 2.

Model Parameters and Values.

Symbol	Description (Units)	Value (Range)	Source
b	Mosquito biting rate (days−1)	0.50 ($0.33-1$)	Manore, Hickmann, Xu, Wearing, and Hyman (2014)
ϕ	Proportion of symptomatic infections (Dimensionless)	0.20	Dawes et al. (2016)
a	Sexual contact rate between humans (days−1)	0.14 ($0.01-0.20$)	Maxian et al. (2017)
q	Vertical transmission probability in mosquitoes (Dimensionless)	0.01	Ciota, Bialosuknia, Ehrbar, and Kramer (2017)
${\beta }_{vh}$	Transmission probability, mosquito to human (Dimensionless)	0.30 ($0.10-0.75$)	Manore et al. (2014)
${\beta }_{hs}$	Transmission probability symptomatic human to mosquito (Dimensionless)	0.30 ($0.10-0.75$, baseline)	Manore et al. (2014)
${\beta }_{ha}$	Transmission probability asymptomatic human to mosquito (Dimensionless)	${\beta }_{hs}/2$	Assumed
${\beta }_a$	Transmission probability- asymptomatic humans to susceptible humans (Dimensionless)	${\beta }_I/2$	Assumed
${\beta }_I$	Transmission probability- symptomatic humans to susceptible humans (Dimensionless)	0.35 ($0-1$)	Assumed
δ	Incubation rate in humans (days−1)	0.2 ($0.14-0.50$)	Gao et al. (2016)
γ	Recovery rate (days−1)	0.14 ($0.07-0.30$)	Shutt et al. (2017)
${\gamma }_e$	Maturation rate- mosquitoes (days−1)	0.06 ($0.06-0.20$)	Yang, Macoris, Galvani, Andrighetti, and Wanderley (2009)
μ	Natural mortality rate of adult female mosquitoes (days−1)	0.07 ($0.03-0.09$)	Yang et al. (2009)
${\mu }_e$	Natural mortality rate of juvenile mosquitoes (days−1)	0.07 ($0.03-0.47$)	Yang et al. (2009)
${\delta }_v$	Incubation rate in mosquitoes (days−1)	0.10 ($0.06-0.22$)	Shutt et al. (2017)
α	Proportion of female juvenile mosquitoes (Dimensionless)	0.5	Esteva and Yang (2005)
${\beta }_{mf}$	Transmission probability-infected male vectors to susceptible female vectors (Dimensionless)	0.45 ($0.15-0.65$)	Leon (1987)
r	Egg hatching rate (days−1)	0.40 ($0.13-1$)	Byttebier, De Majo, and Fischer (2014)
K	Carrying capacity (total number of juvenile mosquitoes)	$\mathrm{4,413,320}$	Assumed
s	Mosquito sexual contact rate (days−1)	1	Esteva and Yang (2005)
$N_h$	Total number of humans	$\mathrm{76,182}$	Shutt et al. (2017)

3. Parameter estimates

The parameter values used in this model were retrieved from previously published literary sources as shown in Table 2. However, due to the scarcity of available data on the transmission dynamics of ZIKV, some of the values, namely b, ${\beta }_{vh}$, ${\beta }_{hs}$, and ${\beta }_{mf}$, are based on DENV studies since DENV and ZIKV are of the same genus and are both spread by Aedes aegypti mosquitoes. Since no studies were found investigating sexual transmission of ZIKV in Aedes aegypti mosquitoes, the ${\beta }_{mf}$ parameter was retrieved from a study on Aedes albopictus and is an average of the transmission probability of DENV in this species across various days after female mosquito blood meals (Leon, 1987). Lastly, since clinical studies suggest that the viral load of asymptomatically infected ZIKV patients is approximately half of the viral load of symptomatic patients, we assume that the transmission probability of asymptomatic people is half of the transmission probability of symptomatic people (Aubry, Richard, Green, Broult, & Musso, 2016; Musso & Gubler, 2016). The initial susceptible human population ($\mathrm{76,182}$ people) in our work represents the calculated at-risk population for Zika in El Salvador that is presented in Shutt et al. (2017). Assuming that at demographic equilibrium there are 6 adult female mosquitoes per person (a ratio within the range of values found in literature (Focks, Sackett, Bailey, & Dame, 1981; Ritchie, Montgomery, & Hoffmann, 2013; Williams, Johnson, Ball, & Ritchie, 2013)), the carrying capacity, K, was derived through back calculation of the equilibrium value of adult female mosquitoes, $N_{vf}^{\text{*}}=K\left(\frac{\alpha {\gamma }_e}{\mu }-\frac{{\mu }_e+{\gamma }_e}{r}\right)$.

4. Results

To understand the contribution of additional transmission pathways (1–3) on the spread of Zika, we compare the basic reproductive numbers and key epidemiological quantities of dynamical system (1) with those of a vector-only transmission model (2) which incorporates disease transmission in the human and vector populations solely through mosquito bites.

$$\begin{array}{l}{\dot{S}}_h=-b{\beta }_{vh}\frac{I_{vf}{S}_h}{N_h}\\ {\dot{E}}_h=b{\beta }_{vh}\frac{I_{vf}{S}_h}{N_h}-\delta E_h\\ {\dot{I}}_h=\varphi \delta E_h-\gamma I_h\\ {\dot{A}}_h=\left(1-\varphi \right)\delta E_h-\gamma A_h\\ {\dot{R}}_h=\gamma \left(I_h+A_h\right)\\ {\dot{S}}_{vf}=\alpha {\gamma }_e{S}_e-b\frac{S_{vf}}{N_h}\left({\beta }_{hs}{I}_h+{\beta }_{ha}{A}_h\right)-\mu S_{vf}\\ {\dot{E}}_{vf}=b\frac{S_{vf}}{N_h}\left({\beta }_{hs}{I}_h+{\beta }_{ha}{A}_h\right)-\left({\delta }_v+\mu \right)E_{vf}\\ {\dot{I}}_{vf}={\delta }_v{E}_{vf}-\mu I_{vf}\\ {\dot{S}}_e=r\left(1-\frac{S_e}{K}\right)N_{vf}-\left({\gamma }_e+{\mu }_e\right)S_e\end{array}$$ (2)

4.1. Disease-free equilibria

The disease-free equilibrium is the point where no disease is present within the population. For system (1), this occurs when $I_h=I_{vf}=I_e=0$. Setting all of the differential equations in (1) equal to zero, we find an infinite line of non-isolated disease-free equilibria of the form $[S_h^{\text{*}},\mathrm{0,0,0},R_h^{\text{*}},S_{vf}^{\text{*}},\mathrm{0,0,0},S_e^{\text{*}},0]$, where $S_h^{\text{*}}$ and $R_h^{\text{*}}$ are free variables such that $S_h^{\text{*}}+R_h^{\text{*}}=N_h$, $S_{vf}^{\text{*}}=\frac{\alpha {\gamma }_e{S}_e^{\text{*}}}{\mu }$, and $S_e^{\text{*}}=K\left(1-\frac{\mu \left({\mu }_e+{\gamma }_e\right)}{\alpha r{\gamma }_e}\right)$. The value of $S_e^{\text{*}}$ is only biologically feasible (i.e. greater than zero) when $r>\frac{\mu \left({\mu }_e+{\gamma }_e\right)}{\alpha {\gamma }_e}$.

Similarly, we find non-isolated disease-free equilibria for system (2) of the form $[S_h^{\text{**}},\mathrm{0,0,0},R_h^{\text{**}},S_{vf}^{\text{**}},\mathrm{0,0},S_e^{\text{**}}]$, where $S_h^{\text{**}}$ and $R_h^{\text{**}}$ are free variables such that $S_h^{\text{**}}+R_h^{\text{**}}=N_h$, $S_{vf}^{\text{**}}=S_{vf}^{\text{*}}$, and $S_e^{\text{**}}=S_e^{\text{*}}$. The authors note that an endemic equilibrium exists for system (1) and involves the transmission of ZIKV solely within the mosquito population. Due to the focus of the current study on the contribution of Zika transmission pathways to the spread of the disease within the human population, we omit detailed computation of the endemic equilibrium.

$$X=\left(\begin{array}{c}{S}_h\\ S_{vf}\\ S_e\\ R_h\end{array}\right),Y=\left(\begin{array}{c}{E}_h\\ E_{vf}\end{array}\right),Z=\left(\begin{array}{c}{I}_h\\ A_h\\ I_{vf}\\ I_{vm}\\ I_e.\end{array}\right)$$

4.2. Basic reproductive number

The next-generation operator method proposed by Diekmann, Heesterbeek, and Metz (1990) was used to derive the basic reproductive numbers of system (1) and (2), denoted $R_{0f}$ and $R_{0v}$ respectively.

To obtain $R_{0f}$, we begin by separating the state variables into uninfected (X), noninfectious infected (Y), and infectious (Z) classes;

After substituting the equilibrium values of the Y classes into the differential equations for the Z classes, we generate the Jacobian matrix

$$A=\left(\frac{\partial }{\partial Z}\right)\left(\frac{dZ}{dt}\right).$$

Evaluating A at the disease-free equilibrium for system (1), we obtain $A=M-D$, with

$$M=\left(\begin{array}{ccccc}\frac{\varphi a{\beta }_I{S}_h^{\text{*}}}{N_h}& \frac{\varphi a{\beta }_a{S}_h^{\text{*}}}{N_h}& \frac{\varphi b{\beta }_{vh}{S}_h^{\text{*}}}{N_h}& 0& 0\\ \frac{\left(1-\varphi \right)a{\beta }_I{S}_h^{\text{*}}}{N_h}& \frac{\left(1-\varphi \right)a{\beta }_a{S}_h^{\text{*}}}{N_h}& \frac{\left(1-\varphi \right)b{\beta }_{vh}{S}_h^{\text{*}}}{N_h}& 0& 0\\ \frac{{\delta }_{v}b{\beta }_{hs}{S}_{vf}^{\text{*}}}{\left({\delta }_v+\mu \right)N_h}& \frac{{\delta }_{v}b{\beta }_{ha}{S}_{vf}^{\text{*}}}{\left({\delta }_v+\mu \right)N_h}& 0& \frac{{\delta }_{v}s{\beta }_{mf}{S}_{vf}^{\text{*}}}{\left({\delta }_v+\mu \right)N_{vm}^{\text{*}}}& {\gamma }_e\alpha \\ 0& 0& 0& 0& {\gamma }_e\left(1-\alpha \right)\\ 0& 0& qr\left(1-\frac{N_e^{\text{*}}}{K}\right)& 0& 0\end{array}\right)$$

and

$$D=\left(\begin{array}{ccccc}\gamma & 0& 0& 0& 0\\ 0& \gamma & 0& 0& 0\\ 0& 0& \mu & 0& 0\\ 0& 0& 0& \mu & 0\\ 0& 0& 0& 0& {\gamma }_e+{\mu }_e\end{array}\right),$$

where $N_{vm}^{\text{*}}=K\left(1-\alpha \right)\left(\frac{{\gamma }_e}{\mu }-\frac{{\mu }_e+{\gamma }_e}{\alpha r}\right)$, and $N_e^{\text{*}}=K\left(1-\frac{\mu \left({\mu }_e+{\gamma }_e\right)}{\alpha r{\gamma }_e}\right)$.

Since $S_h^{\text{*}}$ can take on any value at the disease-free equilibrium, we take $S_h^{\text{*}}=N_h$ and calculate $R_{0f}$, which is the dominant eigenvalue of $M{D}^{-1}$. Due to the complexity of the analytic expression for $R_{0f}$ we estimate it using parameter values in Table 2 and obtain $R_{0f}\approx 2.32$.

Similarly, $R_{0v}$ is calculated as the dominant eigenvalue of the next generation matrix $M_v{D}_v^{-1}$, where

$$M_v=\left(\begin{array}{ccc}0& 0& \frac{\varphi b{\beta }_{vh}{S}_h^{\text{**}}}{N_h}\\ 0& 0& \frac{\left(1-\varphi \right)b{\beta }_{vh}{S}_h^{\text{**}}}{N_h}\\ \frac{{\delta }_{v}b{\beta }_{hs}{S}_{vf}^{\text{**}}}{\left({\delta }_v+\mu \right)N_h}& \frac{{\delta }_{v}b{\beta }_{ha}{S}_{vf}^{\text{**}}}{\left({\delta }_v+\mu \right)N_h}& 0\end{array}\right)$$

and

$$D_v=\left(\begin{array}{ccc}\gamma & 0& 0\\ 0& \gamma & 0\\ 0& 0& \mu \end{array}\right).$$

Taking $S_h^{\text{**}}=N_h$, we have

$$M_v{D}_v^{-1}=\left(\begin{array}{ccc}0& 0& e\\ 0& 0& f\\ c& d& 0\end{array}\right)$$

where $e=\frac{\varphi b{\beta }_{vh}}{\mu },f=\frac{\left(1-\varphi \right)b{\beta }_{vh}}{\mu },c=\frac{{\delta }_{v}b{\beta }_{hs}{S}_{vf}^{\text{**}}}{\left({\delta }_v+\mu \right)\gamma N_h}$, and $d=\frac{{\delta }_{v}b{\beta }_{ha}{S}_{vf}^{\text{**}}}{\left({\delta }_v+\mu \right)\gamma N_h}$. The simpler matrix structure in this scenario leads to the analytic expression $R_{0v}=\sqrt{ec+fd}$ where the first term under the radical contains parameters involved in disease transmission between symptomatic humans and mosquitos and the second term involves transmission between asymptomatic humans and mosquitos.

Using parameter values in Table 2, we obtain $R_{0v}\approx 2.21$. Hence, the secondary transmission pathways increase the basic reproductive number by an estimated $5\text{\%}$.

4.3. Visualizing ZIKV dynamics

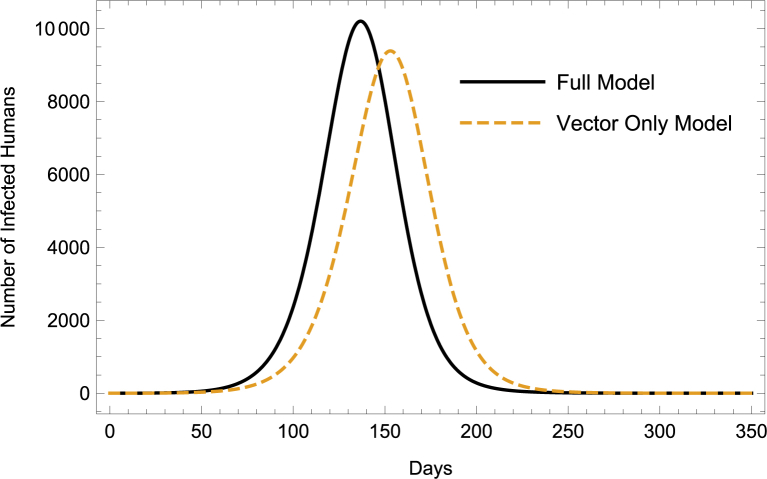
To visualize the difference between the dynamics of the vector-only model and full model, we generate numerical simulations in Mathematica using the baseline parameter values. Assuming that there are 6 adult female mosquitoes per person and about seven juvenile mosquitoes per adult female mosquito (values within previously reported ranges (Focks et al., 1981; Ritchie et al., 2013; Williams et al., 2013)), we estimate the initial susceptible adult female and juvenile mosquito populations to be $\mathrm{457,092}$ and $\mathrm{3,199,644}$ respectively. The initial susceptible adult male mosquito population for system (1) is the same as the initial susceptible adult female mosquito population. Starting with only one infected individual (or mosquito) in each infected class, we observe through Fig. 2 and Table 3 that the full model predicts an outbreak occurring (and ending) approximately two weeks sooner than the vector-only model with more infections during the first half of the epidemic.

Fig. 2.

ZIKV Dynamics: Full Model vs. Vector-Only Model.

Table 3.

Comparison of ZIKV Dynamics, *-Proportion of At-Risk Population Infected.

	Vector-Only Model	Full Model
Duration	312 days	300 days
Final Size*	.99	.99
Peak Time	153 days	137 days
Peak Size*	.12	.13

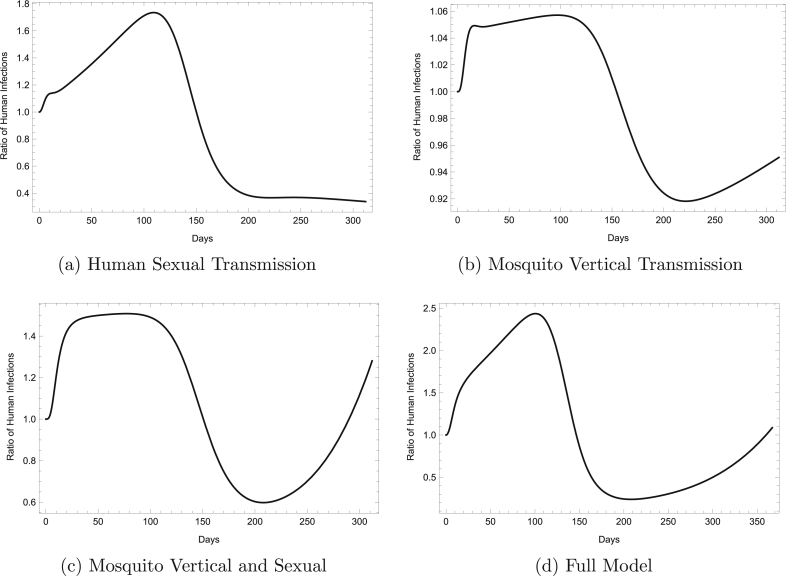
In order to track the effect of additional transmission pathways on the course of a Zika outbreak, we graph the ratio of infected humans in a set of models that each include one or more secondary transmission pathways (in addition to transmission via mosquito bites) to infected humans in the vector-only model. The set of models considered includes a human sexual transmission model, mosquito vertical transmission model, mosquito vertical and sexual transmission model, and full model. The human sexual transmission, mosquito vertical transmission, and mosquito vertical and sexual transmission models were derived by simply deleting terms or equations in the full model that did not correspond to the additional transmission route(s) under investigation.

As expected, the fastest growth in infected humans is seen with the full model, where about 2.5 times as many people are infected with ZIKV at the peak of the epidemic than in the vector-only model. At the point when the epidemic is growing fastest, the human sexual transmission model predicts almost 1.8 times as many Zika cases. Through Fig. 3, we see that sexual transmission in the mosquito population greatly impacts the initial growth of an outbreak and results in up to 1.5 times as many Zika infections at the epidemic's peak than model (2). This is approximately 42% higher than the ratio of Zika cases observed at the peak of an epidemic when modeling only vertical transmission in the mosquito population.

Fig. 3.

The Ratio of Human Infections Over Time. The figures show the ratio of Zika cases in models including secondary transmission pathways a, b, c, or d to Zika cases in the vector-only model over the time course of an outbreak.

4.4. Sensitivity analysis

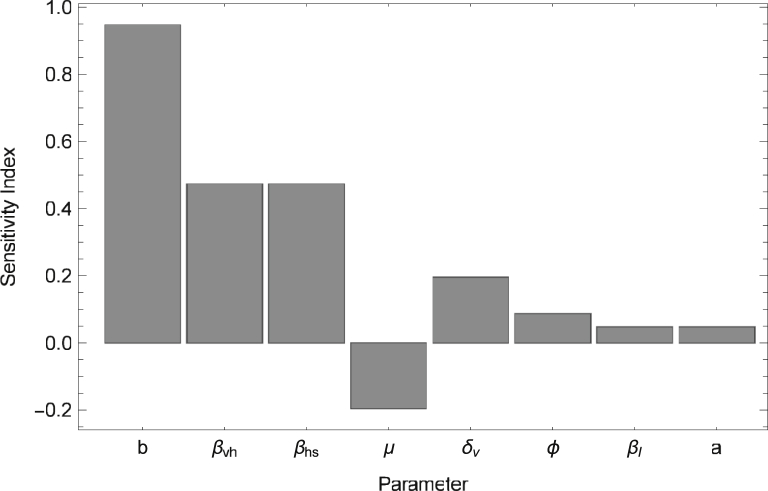
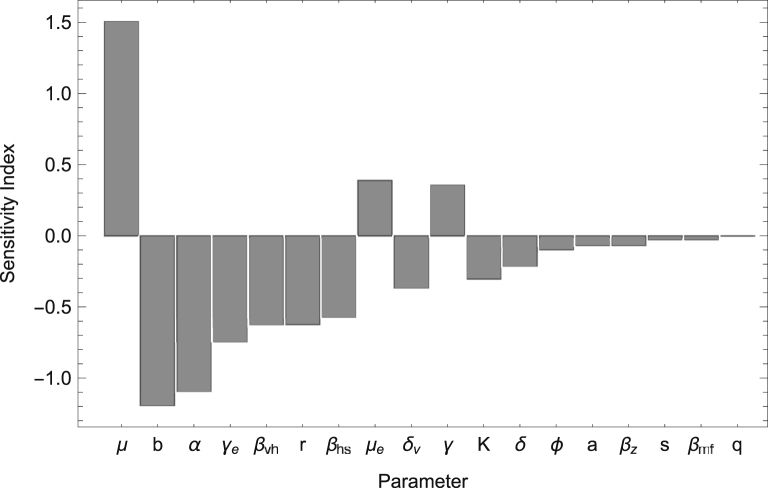
Since the additional transmission pathways of ZIKV resulted in an increase in the basic reproductive number and decrease in the peak time (the time of the maximum number of infected humans) of a Zika outbreak, we conduct a sensitivity analysis to determine how variations in individual parameter values impact $R_{0f}$ and the peak time. In particular, we calculate the normalized sensitivity index, which as described in Arriola and Hyman (2009) is given by $\frac{\partial u}{\partial p}\frac{p}{u}$, where u represents the output variable and p represents the specific parameter under investigation. No simple analytic expression exists for either $R_{0f}$ or the peak time (the expression for $R_{0f}$ is complex and not easily manipulated); thus we compute the normalized sensitivity index numerically using $\frac{\text{Δ}u}{\text{Δ}p}\frac{p}{u}$. In Fig. 4, Fig. 5, the sensitivity indices are calculated by increasing each parameter by $0.1\text{\%}$ (a small amount used to approximate the derivative), while keeping other parameters at the baseline values found in Table 2. We note that one can choose to increase the parameters by other values; however, the ordering of the parameters based on decreasing magnitude of sensitivity indices (as shown in Fig. 4, Fig. 5) will be preserved.

Fig. 4.

Sensitivity Analysis for$R_{0f}$: Sensitivity Indices are listed in order of decreasing magnitude. Parameters not shown (i.e. ${\gamma }_e,r,q,s,{\beta }_{mf},K,\alpha ,{\mu }_e,\delta ,\gamma$) have indices $<0.003$.

Fig. 5.

Sensitivity Analysis for Peak Time: Sensitivity Indices are listed in order of decreasing magnitude.

The results of the sensitivity analysis in Fig. 4, Fig. 5 reveal that $R_{0f}$ is most sensitive to parameter values involved in the vector to human transmission of ZIKV such as the biting rate (b), transmission probabilities (${\beta }_{vh}$, ${\beta }_{hs}$), and the mortality rate of adult female mosquitos (μ). The peak time is also greatly impacted by the mortality rate of adult female mosquitos (μ) and the biting rate (b), and is highly sensitive to parameters that impact juvenile mosquito stages such as the proportion of female juvenile mosquitoes (α) and maturation rate (${\gamma }_e$). These results indicate that methods which decrease b, ${\beta }_{vh}$, and ${\beta }_{hs}$, and increase μ would be most beneficial at reducing $R_{0f}$ while methods which decrease b, α, and ${\gamma }_e$, and increase μ may significantly delay the peak time of an outbreak. Although not shown here, a sensitivity analysis was also performed for the final epidemic size and yielded indices of magnitude less than 0.1 for all parameters except for μ which had a sensitivity index of $-0.13$.

4.5. Consequences for implementing control measures

Assuming that public health officials utilize predictive modeling tools to determine the timing and intensity of control strategies, the variation in the magnitude of infected individuals between the vector-only and full models (as seen in Fig. 3) may impact the outcome of such strategies. Here, we examine how differences in the type of model used to describe the spread of Zika impact the final size of an epidemic and estimates of the basic reproductive number of the virus.

As a result of the various aspects of vector-borne diseases (i.e. seasonality, type of vector, and location) there is no universal threshold that is used to determine when vector control methods should begin. Instead, public health officials must make decisions to implement control measures based on when they predict that the prevalence of a disease will be high enough to warrant them. In the case of Zika, their prediction will vary depending on whether the secondary transmission routes of the pathogen are taken into account.

To illustrate this, we assume that due to certain factors (i.e. limited resources), it would be more economical to implement Zika control measures when approximately $5\text{\%}$ of the population is infected with the virus. In this scenario, we consider the possibility that public health workers rely on model predictions instead of case reports for the number of Zika infected individuals present over time. This is because reported cases may not be a good indicator of the actual number of Zika infections in a population due to low reporting rates, a large asymptomatic class associated with ZIKV, and misdiagnosis of Zika (since it is clinically similar to diseases like Chikungunya and Dengue).

If the secondary transmission pathways of ZIKV are neglected, the vector-only transmission model (2) predicts that the $5\text{\%}$ threshold will be reached 123 days after the first ZIKV infection. However, if the additional transmission mechanisms of ZIKV (1–4) are considered, model (1) predicts that controls should begin 108 days after ZIKV introduction. Using model (1), which provides a more holistic view of Zika transmission than the vector-only model, we explore how this difference in the implementation of control measures may affect the final size of a ZIKV outbreak.

Since there are currently no vaccines for ZIKV, control methods focus on vector reduction through larvicides and adulticides and prevention of mosquito bites through the use of repellents. To stimulate the effect of applying each of the three control measures mentioned above, we vary the parameters ${\mu }_e,\mu ,$ and b. This is because the use of larvicides and adulticides will increase the juvenile and adult mosquito mortality rates, while using repellents will reduce mosquito biting rate. Presumably, an effective control measure will decrease the basic reproductive numbers, $R_{0f}$ and $R_{0v}$ below one. Observing the change in $R_{0f}$ and $R_{0v}$ as each of the control parameter values is varied, we find that larvicides and adulticides must reduce the average juvenile and adult mosquito lifetimes below 9 and 11 days respectively and that repellents must prevent a mosquito from biting for at least 5 days. With this, we choose our control parameters to be ${\mu }_{ec}=0.107$ days⁻¹, ${\mu }_c=0.089$ days⁻¹, and $b_c=0.180$ days⁻¹ and observe the effects of enacting each control individually and in combination. As adulticides are typically the last resort in integrated vector control strategies (W. H. Organization, S.P. for Research, and T. in Tropical Diseases, 2009), the only double control scenario that we employ is the use of repellents and larvicides.

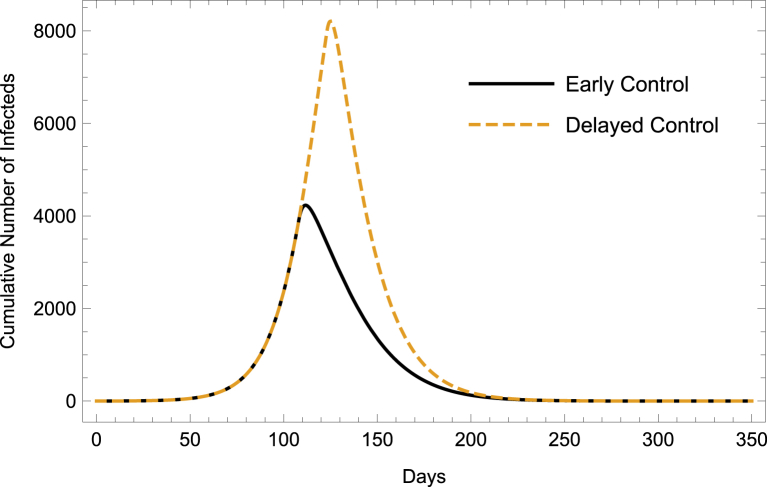
When we consider a continuous application of larvicides, adulticides, and repellents from the time that controls are initiated to the end of the epidemic, we find that a slight delay in the application of control measures (initiation at day 123 versus day 108) results in up to $28\text{\%}$ more people infected with Zika in the full model (depending on the type of control that is used (Fig. 6, Table 4)).

Fig. 6.

Cumulative Infections Under Continuous Application of Larvicides, Adulticides, & Repellents. Early control refers to initiation of the combined control measures at day 108 while delayed control refers to initiation at day 123.

Table 4.

Proportion of At-Risk Population Infected with Continuous Application of Controls, L-larvicide, A-adulticide, R-repellent.

Initiation of Control Measures (days)	Control Type
	L	A	R	L & R	L, A, & R
108	0.99	0.93	0.53	0.48	0.38
123	0.99	0.96	0.75	0.73	0.66

Since control measures are typically administered in discrete intervals rather than continuously over an entire outbreak period, we considered a separate scenario where larvicides and adulticides are applied at specific times, namely every two days for ten days and thereafter once a week as suggested by the World Health Organization in (W. H. Organization, S.P. for Research, and T. in Tropical Diseases, 2009). In this case, delayed application of control measures resulted in a similar percent increase ($25\text{\%}$, full results not shown) in the number of people infected with Zika in the full model.

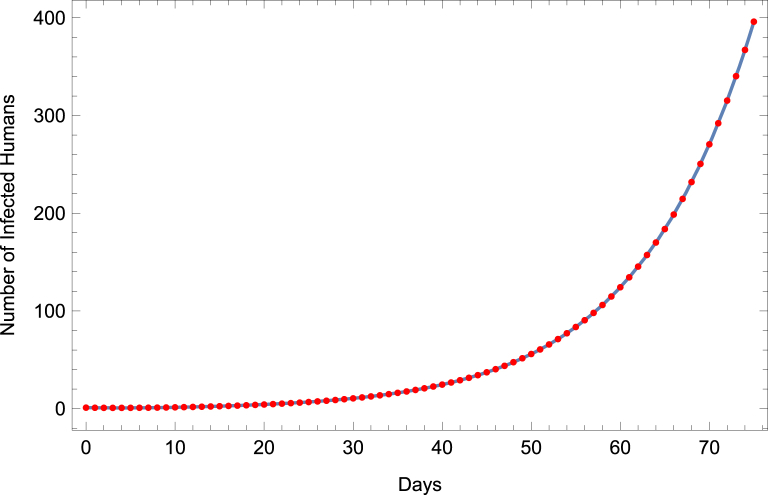
Another way that public health officials may utilize mathematical models is to estimate the basic reproductive number of a disease through incidence data. These estimates play a crucial role in the formation of control strategies and may vary between different models, as described in (Lloyd, 2001, 2009; Nowak et al., 1997; Wearing et al., 2005). To examine how differences in model structure affect $R_0$ estimates, we fit initial Zika incidence data to models (1) and (2) separately, and in each case estimate transmission parameters. ${\beta }_{vh}$, ${\beta }_{hs}$, and ${\beta }_{ha}$. Using Mathematica's build-in function FindFit, with the other parameters fixed at baseline values, we fit the respective models to time-series data for the number of ZIKV infected individuals (both symptomatic and asymptomatic) generated by the full model. We then use the best-fit transmission parameter values to estimate $R_0$. For illustrative purposes, we assume that public health officials fit the vector-only model to incidence data from the first 75 days of an outbreak. The results of the data fitting can be seen in Fig. 7. Although the curve aligns quite well with the data points, we find that the fitted model estimates $R_0$ to be approximately 3 (with ${\beta }_{vh}\approx 0.35$, ${\beta }_{hs}\approx 0.48$, and ${\beta }_{ha}\approx 0.1$). This is $30\text{\%}$ higher than that $R_0$ value obtained from the full model.

Fig. 7.

Fitting Vector-Only Model to Zika Incidence Data. Vector-only model is fit to ZIKV incidence data produced by full model (dots).

5. Discussion & conclusion

Mathematical models are useful in predicting disease dynamics and estimating key parameters that can be used to combat the spread of a disease. While it is common for researchers to simplify these models in order to better analyze them, the simplifications often overlook certain biological components of a disease which may dramatically influence its spread. In this paper, we illustrate the impact of such simplifications in the context of Zika virus dynamics.

We examine a new mathematical model which incorporates multiple transmission avenues of the unique Zika arbovirus and compare it with a model that only incorporates the transmission of the virus through direct human and mosquito contacts. Since many researchers agree that the transmission of Zika through mosquito bites drives the spread of this disease (Gao et al., 2016; Towers et al., 2016), it may be easy to overlook (or even dismiss) the secondary transmission routes. However, we have shown that these additional pathways not only increase the basic reproductive number of Zika and shift the outbreak to occur sooner than expected, but they also have important consequences for Zika control strategies.

When reflecting on the different ways that public health authorities may use Zika models to inform control efforts, our results show that if only the human-mosquito contacts are considered, authorities run the risk of enacting controls too late and overestimating the basic reproductive number. Delaying the implementation of control strategies based on using the vector-only model, inevitably results in more people infected at the end of an outbreak than if the full model were used. The overestimation of $R_0$ that is associated with fitting model (2) to initial Zika incidence data from the full model is reminiscent of the work in (Lloyd, 2001, 2009; Nowak et al., 1997; Wearing et al., 2005) where differences in model assumptions (e.g. the inclusion of latent periods and distribution of latent and infectious periods) result in strikingly different estimates of $R_0$ obtained from the initial growth rate of a disease or pathogen. While use of simpler models in (Lloyd, 2001, 2009; Nowak et al., 1997; Wearing et al., 2005) to estimate the basic reproductive number consistently resulted in underestimations, using our simplified vector-only model to estimate $R_0$ from initial growth results in an overestimate. This is because secondary transmission pathways increase the initial growth of an epidemic much more than they increase $R_0$. The overestimation of $R_0$ may lead to aggressive control efforts, which although not be as detrimental to the overall health of the public as grossly underestimating this quantity, will result in wasted resources. Hence, we recommend that public health officials take into consideration the additional transmission pathways of Zika when enacting controls and estimating crucial disease parameters.

While the mathematical model considered in this study is unique in its combination of multiple ZIKV transmission pathways, some of its results resemble those of previous studies. For one, the numerical approximations of $R_{0v}$ and $R_{0f}$ in section 4.2 are comparable with other estimates of $R_0$ for Zika (Gao et al., 2016; Maxian et al., 2017). In addition, since the basic reproductive number for Zika increased by only $5\text{\%}$ between the vector-only (1) and full models (2), our study supports the notion that vector transmission is primarily responsible for the spread of ZIKV as described in Towers et al. (2016) and Maxian et al. (2017) and Gao et al. (2016). The percent increase in $R_0$ that is described in section 4.2 is comparable to the percent increase in $R_0$ for studies that consider only sexual transmission (Gao et al., 2016; Maxian et al., 2017). Thus, our analysis suggests that ZIKV transmission within mosquito populations does not contribute substantially to the initial spread of the disease.

The few studies that describe sensitivity analysis as it pertains to Zika modeling have focused on the effects of parameter values on $R_0$ (e.g. (Bewick et al., 2016; Maxian et al., 2017)), however the present study is distinct in that it also analyzes the sensitivity of other important epidemiological quantities such as the final size and peak time. Sensitivity analysis for these latter output variables has not been discussed elsewhere. Similar to (Bewick et al., 2016; Maxian et al., 2017), our results show that Zika's basic reproductive number is most sensitive to the mosquito biting rate and transmission probability parameters (a fact which supports vector-to-human transmission as a driving force in the beginning of an outbreak). Therefore, in order to reduce the possibility of a ZIKV epidemic, public health campaigns should emphasize measures which lower the biting rate and probability of transmission of the virus between humans and mosquitos.

Although we agree that $R_0$ is a vital epidemiological quantity, we note that this value describes the transmissibility of disease within a completely susceptible population and only tells whether or not a disease will spread. Given that a disease will spread, public health officials may look to other epidemiological quantities, such as the final epidemic size and peak time to determine the intensity of an outbreak and inform control strategies. Hence understanding how the final epidemic size and peak time are affected by parameter values would be of great interest. We find that of the three output variables ($R_{0f}$, final epidemic size, and peak time), the final epidemic size is least sensitive to changes in parameter values (all except one of the sensitivity indices $<0.1$) and the peak time is most sensitive to variations in parameters (the magnitude of seven of its sensitivity indices were $>0.5$ with two of the seven indices having magnitude $>1$). These results are supported by the numerical simulations in section 4.3. In addition, the peak time is shown to be most sensitive to the death rate of adult female mosquitos, a parameter which plays a crucial role in accelerating the demographic renewal of mosquitoes and reducing the duration of infection within the vector population.

It is in the sensitivity analysis for the peak time that we see the importance of parameters such as α, ${\gamma }_e$, and r which affect the dynamics of the juvenile mosquito stages. With regards to the peak time, these parameters have sensitivity indices with magnitude $>0.6$. This suggests that in order to delay the peak time of a foreboding ZIKV outbreak and potentially provide public health officials with more time to mobilize their resources and gather information on the nature of the outbreak, attention should be paid to the juvenile mosquito stages and if possible to developing methods that retard mosquito maturation.

When considering the effectiveness of ZIKV control measures, our study shows (as does (Bewick et al., 2016)) that combined personal protection and mosquito reduction strategies are the most effective at limiting the transmission of ZIKV and that individually, personal protection is more effective than vector reduction. The effect of differential timing of control measures based on the additional transmission pathways of ZIKV is unique to this study. To our knowledge, no other studies address how the timing of control measures impact the outcome of ZIKV outbreaks. Our investigation of this effect shows that although the transmission routes result in a slight qualitative change in ZIKV dynamics, neglecting them when predicting the initiation of control measures may have a profound impact on final size of epidemics. This discovery deepens our understanding of the complex transmission routes of ZIKV and the consequences that they may hold for public health officials.

In the future, the initiation and duration of controls that were implemented in the current model can be adapted to vector control strategies of particular cities to predict how their strategies affect disease outcomes in the face of Zika's additional transmission pathways. Furthermore, we would like to fit the full model to actual Zika incidence data of a specific region to obtain better estimates of parameter values. Lastly, due to the discrete nature of epidemiological data, it may also be beneficial to formulate a discrete time model that incorporates the additional transmission pathways of Zika and compare its predicted disease dynamics and effects of control with the results found in this paper.

6. Coding

To increase the transparency and reproducibility of our work, we encourage requests for the codes used to build this model and obtain the figures in this article to be sent to the corresponding author Omomayowa Olawoyin at omomayowa.olawoyin@mavs.uta.edu.

Handling Editor: J. Wu