Neurite imaging reveals microstructural variations in human cerebral cortical gray matter

Abstract

We present distinct patterns of neurite distribution in the human cerebral cortex using diffusion magnetic resonance imaging (MRI). We analyzed both high-resolution structural (T1w and T2w images) and diffusion MRI data in 505 subjects from the Human Connectome Project. Neurite distributions were evaluated using the neurite orientation dispersion and density imaging (NODDI) model, optimized for gray matter, and mapped onto the cortical surface using a method weighted towards the cortical mid-thickness to reduce partial volume effects. The estimated neurite density was high in both somatosensory and motor areas, early visual and auditory areas, and middle temporal area (MT), showing a strikingly similar distribution to myelin maps estimated from the T1w/T2w ratio. The estimated neurite orientation dispersion was particularly high in early sensory areas, which are known for dense tangential fibers and are classified as granular cortex by classical anatomists. Spatial gradients of these cortical neurite properties revealed transitions that colocalize with some areal boundaries in a recent multi-modal parcellation of the human cerebral cortex, providing mutually supportive evidence. Our findings indicate that analyzing the cortical gray matter neurite morphology using diffusion MRI and NODDI provides valuable information regarding cortical microstructure that is related to but complementary to myeloarchitecture.

1. Introduction

Classical anatomists subdivided the postmortem human brain into many distinct cortical areas to provide an anatomical framework for analyzing specific brain functions (Brodmann, 1909; Hopf, 1955, 1956; Hopf and Vitzthum, 1957; Vogt and Vogt, 1919a, 1919b; von Economo and Koskinas, 1925). Particularly, myeloarchitectonics focused on layer-specific distribution of myelinated axons and their intra-cortical wiring arrangements (Braak, 1980; Nieuwenhuys, 2013) and enabled anatomists to parcellate the whole cerebral cortex into as many as 200 candidate areas (see reviews by Nieuwenhuys, 2013; Nieuwenhuys et al., 2015; Nieuwenhuys and Broere, 2017). Recent non-invasive magnetic resonance imaging (MRI) methods have enabled mapping of contrast related to myelin content over all of the cerebral neocortex (Eickhoff et al., 2005; Salat et al., 2009; Sigalovsky et al., 2006). This technique relied mostly on the T1-weighted (T1w) contrast, which was shown to be correlated with myelin content (Bock et al., 2009, 2013) and partly on T2-star weighted contrast co-localized with iron (Fukunaga et al., 2010). This approach was later augmented by Glasser and Van Essen (Glasser and Van Essen, 2011) using the T1w/T2-weighted (T2w) ratio. Combined with improvements in data acquisition and analysis by the Human Connectome Project (HCP), this enabled high-quality individual subject myelin mapping (Glasser et al., 2013; Glasser et al., 2014), which contributed substantially to a recent in-vivo parcellation of the human cerebral cortex (Glasser et al., 2016). Although the T1-based MRI contrast provides information regarding the myelin content within voxels, it does not reflect morphological features such as the geometrical arrangement of myelinated axons in the cortex.

Diffusion MRI (dMRI) provides unique insights into brain microstructure and geometry of fiber tract orientations (Johansen-Berg and Behrens, 2013). Fiber orientations can be assessed using diffusion tensor imaging (DTI) (Basser et al., 1994) which models diffusion as a Gaussian distribution to estimate quantitative parameters such as mean diffusivity (MD) and fractional anisotropy (FA), thereby providing a popular means to investigate tissue microstructure (Bennett et al., 2009; Bodini et al., 2009) (for review, Johansen-Berg and Behrens, 2013). However, the parameter estimates of the DTI model do not relate to specific features within tissue microstructure and are consequently sensitive to multiple structural compartments concurrently (Pierpaoli et al., 1996). Several models have been proposed that attribute diffusion signal b-value dependence to a set of compartments representing different environments of water (Assaf et al., 2008; Assaf and Basser, 2005; Behrens and Johansen-Berg, 2005; Clark and Le Bihan, 2000; Genc et al., 2017).

Among these diffusion models is Neurite Orientation Dispersion and Density Imaging (NODDI) (Zhang et al., 2012), an approach to interpreting in vivo dMRI by linking the dMRI signal to estimates of neuroanatomical microarchitecture. The NODDI model assumes three microstructural environments for water diffusion (intra-cellular, extra-cellular and cerebrospinal fluid [CSF] compartments). The intra-cellular compartment is assumed to be infinitely anisotropic for diffusion motion, an extreme version of the diffusion presumed to occur in neurites (a collective term referring to both dendrites and axons). This compartmentalization enables quantitative measures such as neurite density index (NDI) and orientation dispersion index (ODI) and aims to reduce the limitations of the DTI model. For example, in parts of the centrum semiovale where FA is low, ODI and NDI show high values, reflecting the crossing of many axons (Zhang et al., 2012). Some studies have reported white matter changes of NODDI related to aging (Billiet et al., 2015; Chang et al., 2015; Eaton-Rosen et al., 2015; Genc et al., 2017; Kodiweera et al., 2016; Kunz et al., 2014) and neurologic disorders (Adluru et al., 2014; Billiet et al., 2014; Timmers et al., 2015). Other studies reported NODDI changes in cortical gray matter in focal cortical dysplasia (Winston et al., 2014), aging (Nazeri et al., 2015) and schizophrenia (Nazeri et al., 2016). However, the distributions of NODDI measures in cortical gray matter have not previously been investigated in detail. Previous efforts to resolve cortical architecture using high-resolution DTI (Aggarwal et al., 2015; McNab et al., 2013) covered only limited portions of the cortex and did not characterize neurite morphology.

In the present study, we investigated the distribution of neurite properties across the human cerebral cortex by applying the NODDI model to high-resolution HCP data (Sotiropoulos et al., 2013). The imaging data were preprocessed with the HCP pipelines, and the cortical surfaces were reconstructed based on T1w and T2w images (Glasser et al., 2013). Using high-resolution dMRI data, statistical aspects of cortical neurite properties were assessed using NODDI (Zhang et al., 2012) with optimization for intrinsic diffusivity of the cortical gray matter tissue followed by mapping from the cortical grey matter ribbon to the surface. We also compared the NODDI results with cortical maps of conventional DTI to better understand the relationships between these measures. We discuss how these cortical maps of neurite properties relate to previously reported maps of myeloarchitecture and cytoarchitecture and the significance of neurite morphology mapping for a better understanding of cortical myelomicrostructure.

2. Materials and Methods

Surface maps of NODDI and DTI measures, myelin contrast and cortical thickness were generated using the publicly available HCP dataset. The data were analyzed using the HCP pipelines (https://github.com/Washington-University/Pipelines), Connectome Workbench (https://github.com/Washington-University/workbench), FreeSurfer 5.3 (https://surfer.nmr.mgh.harvard.edu/), Functional Magnetic Resonance Imaging of the Brain Software Library (FSL) 5.09 (www.fmrib.ox.ac.uk/fsl) and MATLAB (http://www.mathworks.com/). Data analyses were performed at RIKEN, and ths use of HCP data in this study was approved by the institutional ethical committee (KOBE-IRB-16–24).

2.1. Subjects and HCP data preprocessing

Analyses were based on high-resolution structural images (0.7-mm isotropic T1w and T2w images) and dMRI images (1.25-mm isotropic resolution) obtained from 505 healthy subjects (age, 22–35 years) in the publicly available HCP dataset (Van Essen et al., 2013). The dMRI image included 270 volumes with 90 volumes for each of three shells of b-values (b =1000, 2000 and 3000 s/mm²) in addition to 18 non-diffusion-weighted (b=0 s/mm²) volumes. We used preprocessed data using methods detailed previously (Glasser et al., 2013). In brief, the structural images were preprocessed (corrected for gradient nonlinearity, readout, and bias field; aligned to AC-PC “native” space and averaged when multiple runs were available; then registered to MNI 152 space using FSL’s FNIRT). The native space images were used to generate individual white and pial surfaces (Glasser et al., 2013) using the Freesurfer and HCP pipelines. In the PostFreeSurfer pipeline, the individual subject’s native-mesh surfaces were registered using a multimodal surface matching (MSM) algorithm (Robinson et al., 2014) with MSMSulc to the Conte69 folding-based template (Van Essen et al., 2012). Cortical myelin content was estimated by dividing the T1w image by the T2w image, mapping onto the cortical surface and correcting for the bias field (Glasser et al., 2013, 2014; Glasser and Van Essen, 2011) and cortical thickness was calculated in FreeSurfer using white and pial surfaces. Subsequently, these surfaces were non-linearly registered across subjects using MSMAll surface registration, which was based on the multi-modal areal features, such as myelin maps, resting state network maps, and resting state visuotopic maps (Glasser et al., 2016; Robinson et al., 2014).

Diffusion MRI data was also preprocessed using the HCP pipelines. In brief, corrections for gradient distortion, static-field (B₀) distortion and eddy current distortion, and cross modal registration were performed (Glasser et al., 2013, Sotiropoulos et al., 2013). The intensity was normalized by the mean of volumes with b=0 s/mm² (b0 volumes) and the B₀-inhomogeneity distortion was corrected using two opposing phase encoded images and FSL’s Topup (Andersson et al., 2003). The eddy current induced field inhomogeneities, and the head motion for each image volume was corrected using FSL’s Eddy (version 5.0.9, before the HCP’s recent recomputation that included outlier detection) (Andersson et al., 2012), followed by correction for the gradient nonlinearity. Diffusion data were registered to the structural T1w AC-PC space using the b0 volume and the white surface using the BBR cost function in FSL and FreeSurfer’s BBRegister. The diffusion gradient vectors were rotated based on the rotational information of the b0 to T1w transformation matrix.

2.2. NODDI and DTI calculation

The NODDI method models brain microarchitecture using three compartments: (1) intracellular (restricted diffusion, bounded by the membrane of neurites and myelin sheaths), (2) extracellular (anisotropic hindered diffusion, outside of neurites and potentially including glial cells), and (3) CSF compartments (isotropic diffusion) (Zhang et al., 2012). The normalized signal of dMRI (A) is thus written as:

$$A=\left(1-v_{iso}\right)\{v_{ic}{A}_{ic}+\left(1-v_{ic}\right)A_{ec})\}+v_{iso}{A}_{iso}$$ (1)

where A_ic and ν_ic are the normalized signal and volume fraction of the intra-cellular compartment (neurite density index, NDI); A_ec is the normalized signal of the extracellular compartment; A_iso and ν_iso are the normalized signal and volume fraction, respectively, of the CSF compartment. Each compartment is described by different diffusion distributions: infinitely anisotropic with Watson distribution¹, anisotropic Gaussian distribution, and isotropic distributions, respectively. The additional NODDI parameters are:

• d_∥: intrinsic free diffusivity

• K: concentration parameter of Watson distribution

• μ: mean orientation of Watson distribution

• d_iso: isotropic diffusivity

where the original NODDI model, designed for analyses of the white matter, assumes the diffusivity (d_∥ =1.7 × 10⁻³ mm²/s) and in CSF (d_iso=3.0 × 10⁻³ mm²/s). Because we investigated gray matter properties, we sought to estimate the value of d_∥ using the following procedure introduced by Guerrero et al. (2016). Briefly, for an empirically chosen range of d_∥ from 0.6 to 2.5 and a step size of 0.1, the NODDI model was fitted to a set of the cortical voxel data chosen from the middle axial slice of the segmented cortical ribbon volume generated with the HCP pipeline (ribbon.nii.gz). The quality of fit of the model was assessed using a maximum likelihood function, and the value of d_∥ with best fit to the data was selected for each voxel (Fig. S1A). Subsequently, the optimal value of d_∥ (d*_∥) was determined for each subject using maximum likelihood estimation with log-normal distribution (Fig. S1B). The calculated cross-subject mean (s.e.m.) of the d*_∥ was 1.1 (0.1) × 10⁻³ mm²/s.

The NODDI model was fitted using the optimized value of d*_∥ and Accelerated Microstructure Imaging via Convex Optimization (AMICO) (Daducci et al., 2015), which re-formulates the original NODDI model as a linear system and shortens the calculation time. We used default values of regularization (λ=0.001 and γ=0.5) for AMICO. All diffusion data (b=0, 1000, 2000, and 3000 s/mm²) were used to evaluate NODDI parameter estimates in the AC-PC aligned structural space. The validity of using an optimized value of d*_∥, and the assumption of equality of intra-cellular and extra-cellular parallel diffusivity are discussed in section 4.5.

Because several studies have addressed cortical diffusion properties using high-resolution DTI (Aggarwal et al., 2015; McNab et al., 2013), we also calculated MD and FA with conventional DTI using DTIFIT in FSL. All diffusion data were used to be consistent with NODDI, and DTI was fitted using least squares on the log-transformed signals. We also fitted DTI using the diffusion data using only b=1000 s/mm² (108 volumes) to be in line with typical DTI experiments (Johansen-Berg and Behrens, 2013) and simulation study for optimization (Alexander and Barker, 2005). The inverted MD was calculated with the following formula: inversed MD=1/MD. Subsequently, these DTI measures were mapped onto the cortical surface similar to NODDI (see section 2.4) to compare the neurite and diffusion properties.

2.3. Surface mapping

The parameters of NODDI (v_ic, K and d_iso) and DTI (FA and MD) were mapped onto the cortical surface using an algorithm weighted towards the cortical mid-thickness (Glasser and Van Essen, 2011). For each mid-thickness surface vertex on the native mesh, the algorithm identified cortical ribbon voxels within a cylinder orthogonal to the local surface. The voxels were excluded if the value exceeded ±1SD of all values within the cortical ribbon, to remove voxels with substantial partial volume in the CSF or white matter. For the remaining voxels their values were weighted using a Gaussian function (FWHM= ~4 mm, σ=5/3 mm) along the axis normal to the surface, and the resulting value was assigned to the vertex. The surface maps were subsequently resampled based on MSMAll surface registration (Glasser et al., 2016; Robinson et al., 2014) and onto the 32k group average surface mesh. Finally, the orientation dispersion index (ODI) was calculated using the surface metric of K and the following equation (Zhang et al., 2012):

$$ODI=\frac{2}{\mathrm{\pi }}\arctan (1/K)$$ (2)

To evaluate the correspondence between NODDI surface maps and the HCP multimodal parcellation, we estimated the local gradient maxima (‘ridges’) of group-average NDI and ODI maps using the method described previously (Glasser et al., 2016), and borders were created from these gradients using the border optimization function in Connectome Workbench.

Although the NODDI model inherently takes care of the partial volume effects (PVE) in each compartment, the surface mapping algorithm may include residual PVE (despite the steps outlined above) in regions where the cortex is very thin, as the gray matter values may be contaminated with white matter and/or CSF values. Therefore, when a significant correlation was found between the estimated neurite measure and cortical thickness, we further investigated whether the correlation might be induced by the PVE. This was performed in all subjects by mapping the measure of the ODI at the border of the white and gray matter (Fig. S2D) and CSF value (F_iso) onto the surface (Fig. S2E) and correlating the averaged surface value with cortical thickness.

2.4. Statistical analysis

Surface maps (NDI, ODI, MD, FA, myelin and cortical thickness) were averaged across subjects, cortex parcellation was performed using HCP’s multi-modal parcellation version 1.0 (HCP_MMP1.0 210P MPM version; Glasser et al., 2016). The mean value for each of the 180 parcels/hemisphere was calculated. Associations between neurite (NDI, ODI) and other cortical properties (MD, FA, myelin and cortical thickness) were investigated using Pearson correlation analysis on their average maps. We also calculated the correlation matrix in each subject and estimated the mean of correlation coefficient using Fisher Z transformation.

We also assessed subject variability and reproducibility for cortical mapping of NODDI and other metrics. We identified HCP retest data in 32 of 505 subjects. Subject variability was calculated based on the standard deviation of the subject’s variable of cortical metrics. The subject variable was obtained by averaging the test and retest data. Reproducibility was assessed with the coefficient of repeatability and proportional bias (Bland and Altman, 1986; Bland, 2005).

Because the quality of NODDI parameter estimates seemed to depend on the image quality and preprocessing, we estimated practical quality by temporal signal-to-noise ratio (tSNR) of preprocessed b=0 volumes, and surface parcels with tSNR<17 were removed from the analysis. The cutoff was defined somewhat arbitrarily, but as shown in section 3.5, all regions with mean tSNR<17 were located near air-filled sinuses, where signals usually suffer from B₀ field inhomogeneity, and showed artifactually high values in the estimated values in NDI and ODI.

3. Results

3.1. Cortical distribution of NDI and similarity to myelin map

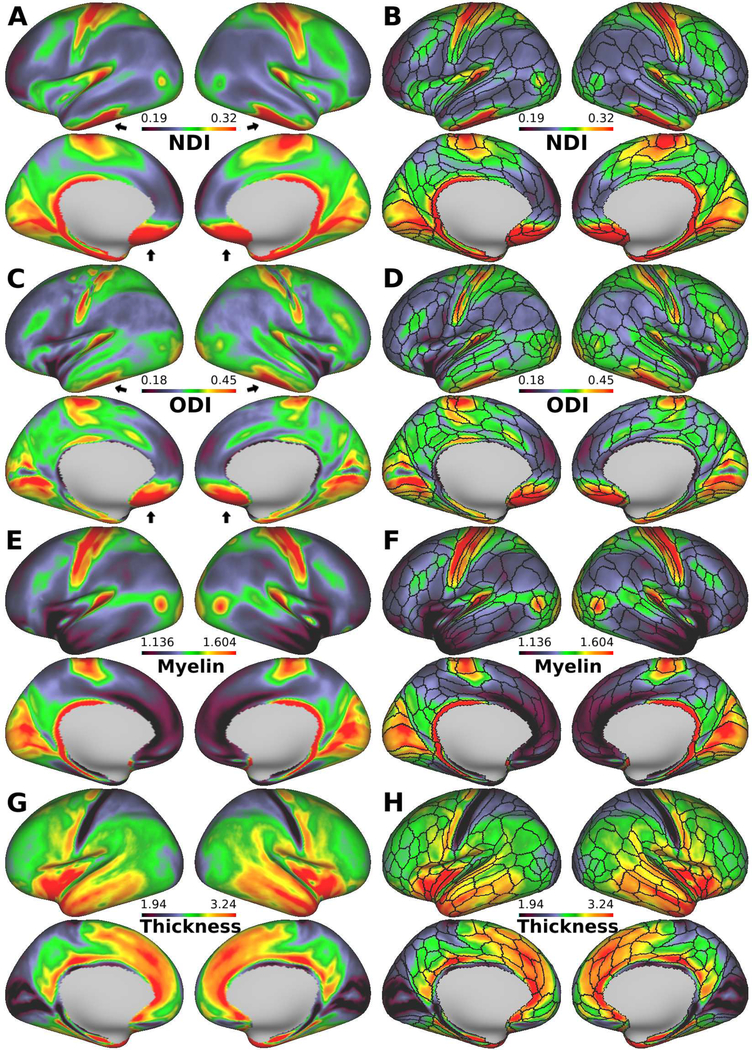
Figure. 1A–D shows the lateral and medial views of the inflated group average surface maps of NDI and ODI for 505 subjects, with the HCP_MMP1.0 parcel boundaries overlaid in panels B and D. Cortical neurite density index (NDI, Fig. 1A,B) showed high values in early motor and somatosensory areas in the central sulcus, early auditory areas in the Sylvian fissure, early visual areas in the occipital lobe, retrosplenial complex, middle temporal (MT and MST) areas, and areas LIPv and 47m in the intraparietal and orbitofrontal cortices, respectively. In contrast, values were generally low in many other regions, including those associated with higher cognitive functions.

Figure 1.

Diffusion MRI derived neurite properties, myelin, and cortical thickness maps of 505-subject average cerebral cortex. (A) Neurite density index (NDI), (C) orientation dispersion index (ODI), (E) myelin and (G) cortical thickness. (B, D, F and H) The imaging modalities superimpose with the boundaries of the Human Connectome Project (HCP) multi-modal parcellations, 210P MPM (black lines) (Glasser et al, 2016). NDI is relatively uniform within most of the parcels, and transitions in neurite properties often occur near parcel boundaries, whereas ODI is heterogenous in some parcellations, such as motor, somatosensory, and primary visual (see also Fig. 3). The black arrows (anterior and middle cranial fossa) indicate artifacts regions where the NDI and ODI values are overestimated because of low signal-to-noise ratio. Data at https://balsa.wustl.edu/Xvw6

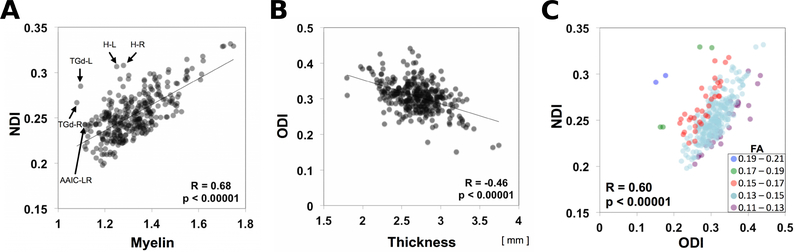
We found a striking similarity in the NDI maps compared with the myelin maps obtained using the T1w/T2w ratio (Fig. 1E, F). This was evident when the cross-subject mean values in each parcel were analyzed in detail. A strong positive correlation was found between NDI and estimated myelin content (R=0.68, p<0.00001, df=329) (Fig. 2A, Table S1). However, this trend has clear exceptions, including lightly myelinated regions, such as the anterior insular cortex (anterior agranular insula complex [AAIC]), anterior cingulate cortex, temporal polar cortex (area TG dorsal [TGd]) and hippocampus, that have moderate values in the NDI maps but low values in the myelin maps (Fig 2A). In contrast, the correlation between NDI and cortical thickness was negative and weaker, but still significant (R=−0.18, p=0.001, df=329) (Fig. S3C, Table S1).

Figure 2.

Correlation between neurite orientation dispersion and density imaging (NODDI) and cortical architectural properties for each of the HCP_MMP1.0 areas. (A) Neurite density index (NDI) plotted against myelin. (B) Orientation dispersion index (ODI) plotted against cortical thickness. (C) NDI plotted against ODI classified by the value of FA. Each data point represents 505-subject mean values for each of the 300-parcels, where SNR exceeded 17. Abbreviations: H-L: left hippocampus; H-R: right hippocampus; TGd-L: left area TG dorsal; TGd-R: right area TG dorsal; AAIC-LR: left and right anterior agranular insula complex. Data at https://balsa.wustl.edu/8MKx

Sharp transitions in the cortical NDI map frequently agreed with boundaries in the HCP_MMP1.0 cortical parcellation. When the NDI map was overlaid with HCP parcel boundaries made from the multi-modal MRI analysis (Glasser et al., 2016) (Fig. 1B), many of the borders in the NDI contrast corresponded with existing area borders in the HCP parcellation. The correspondence of the cortical NDI contrast and HCP parcellation was evident when the transitions in the NDI map were highlighted using surface gradients, and the borders of NDI map were estimated from the gradient (Fig. S4A,C).

3.2. Cortical distribution of ODI and moderate negative correlation with thickness

The orientation dispersion index (ODI) was particularly high in the early sensory cortical areas early somatosensory, auditory and visual cortices, and relatively low in the frontal, parietal, and temporal cortices (Fig. 1C,D). Although the ODI and NDI maps were strongly correlated (R=0.60, p<0.00001, df=329) (Fig. 2C, Table S1), clear differences were observed, particularly in the primary motor cortex, where values are low to moderate for ODI, but high for NDI (see also section 3.3).

Cortical thickness (Fig. 1G, H) was inversely correlated with the ODI map (more so than with the NDI map). A correlation analysis across cortical parcellations showed a strong negative correlation between ODI and cortical thickness (R=−0.46, p<0.00001, df=329) (Fig. 2B, Table S1). All of the early sensory areas showed high ODI and thin cortex. Lateral and medial aspects of the frontal cortex showed low ODI and relatively thick cortex, whereas the superior parietal cortex showed high ODI and was thin. The correlation between ODI and myelin was highly significant but not as strong as for NDI (R=0.62, p<0.00001, df=329) (Fig. S3A, Table S1). Transitions in ODI also corresponded in many regions with areal boundaries in the HCP_MMP1.0 parcellation (Fig. 1D). The borders in the ODI map estimated from its gradient map support this observation (Fig. S4B,D).

3.3. Cortical NDI and ODI are positively correlated but different in some regions.

The previously noted similarities between the NDI and ODI maps (Fig. 1A,C) and positive correlation between NDI and ODI (R=0.60, p<0.00001, df=329) (Fig. 2C, Table S1) were consistent with previous observations (Zhang et al., 2012). The positive correlation is even more evident when points on the scatterplot were divided into five subgroups based on the mean FA range of each parcel (Fig. 2C), a visualization shown in Fig. 10 of Zhang et al. (2012). They showed more clearly that a particular value of tissue FA can be achieved by different combinations of NDI and ODI; e.g., two regions can have the same FA if the one with larger NDI value also has the larger ODI.

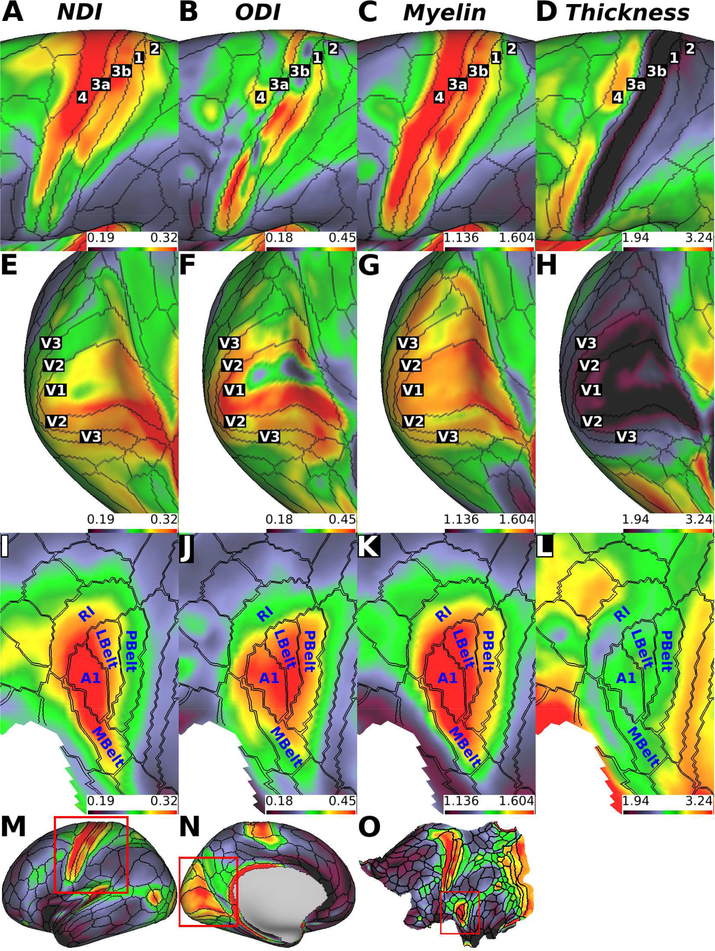
The expanded surface views in Fig. 3 reveal additional noteworthy relationships among these measures for somatomotor, auditory, and visual cortex. Fig. 3A and B, shows that area 4 and the early somatosensory cortex (area 3a, 3b, 1 and 2) all have high NDI values (area 4=0.315, area 3a=0.297, area 3b=0.303, area 1=0.276, area 2=0.264), whereas ODI values are more variable but are lower in area 4 on average than in the somatosensory areas (area 4=0.343, area 3a=0.372, area 3b=0.335, area 1=0.367, area 2=0.337) (Fig. 3A,B).

Figure 3.

Zoomed views of 505-subject neurite density (NDI), orientation dispersion (ODI), myelin, and thickness maps in exemplar early sensory cortices. (A, B, C and D) Motor somatosensory cortex, (E, F, G, H) visual cortex, and (I, J, K and L) auditory cortex. (M, N, O) Full-hemisphere views showing myelin maps with boxes outlining expanded regions in A - L. Abbreviations: 1: area 1; 2: area 2; 3a: area 3a; 3b: area 3b; 4: area 4; A1: primary auditory cortex; LBelt: lateral belt complex; MBelt: medial belt complex; PBelt: parabelt complex; RI: retro insular cortex; V1; primary visual cortex; V2: secondary visual area; V3: third visual area. Data at https://balsa.wustl.edu/K3xg

Within the early visual cortex, areas V1, V2, and V3 have comparably high NDI and ODI values on average (Fig. 3E, F). However, area V1 showed internal heterogeneity, wherein ODI was lower near the fundus of the calcarine relative to the banks and lips of the calcarine, and it was inversely correlated with cortical thickness. In contrast, in early auditory areas, including primary auditory area (A1), medial belt complex (MBelt), lateral belt complex (LBelt), parabelt complex (PBelt) and retro-insular cortex (RI) showed NDI and ODI distributions that were more uniform within each parcel (Fig. 3I, J). Area A1, MBlet, LBelt and PBelt had higher ODI, relative to area RI (Fig. 3J). Notably, ODI in the auditory cortex was less correlated with cortical thickness than that in the somatosensory and visual areas.

Although the NDI contrast was aligned with many HCP parcellation boundaries as described in section 3.1, the correspondence between the ODI map and parcel boundaries was not as strong. Specifically, ODI was heterogeneous within several motor, somatosensory, and primary visual areas (Fig. 3B, F). Whether ODI is sensitive to within-area organization (e.g. somatotopy) or whether these reflect artifactual fluctuations remains to be determined.

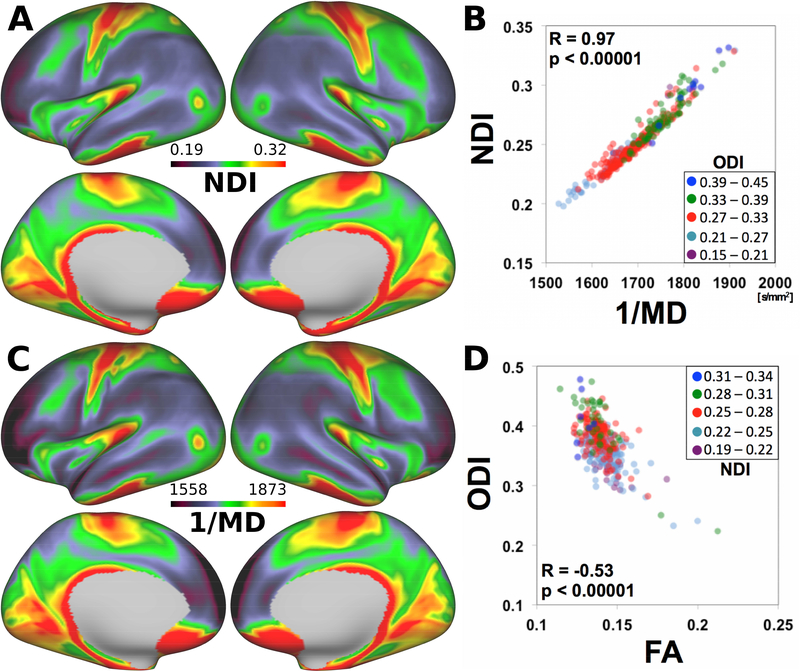
3.4. Comparison of NODDI and DTI - cortical NDI is strikingly similar to inverse MD

We also compared the surface maps of NODDI measures with those of DTI (Fig. 4). When DTI was fitted to all the diffusion data, the average surface maps of the DTI measures, FA, and MD, are shown in Figure S5 A–D. The NDI map (Fig. 4A) was strongly negatively correlated with the MD map and thus highly correlated with the inverse MD map (Fig. 4C); with R=0.97 p<0.00001, df=329 (Fig. 4C, Table S1). These findings indicated that NDI in the NODDI model strongly coupled with MD in the DTI model (see Discussion). A plot of ODI versus FA (Fig. 4D) revealed a moderate negative correlation (R=–0.53, p<0.00001, df=329). The relationship between ODI and FA depended modestly on the values of NDI (colored symbols in Fig. 4D), which was consistent with a previous report (Zhang et al., 2012).

Figure 4.

Comparison of NODDI and DTI for cortical mapping. (A) NDI and (B) inverse MD (1/MD) show a similar spatial distribution across the cortical mantle. (C) 1/MD plotted against NDI exhibits a strong positive linear relationship. (D) The relationship between orientation dispersion index (ODI) and fractional anisotropy (FA) depends on NDI. Each data point represents 505-subject mean values for each of the 331 parcels, where SNR was >17. DTI data were based on the fitting using all the diffusion data, including b=1000,2000, and 3000 s/mm². See also Fig. S5 for conventional DTI data calculated upon diffusion data <1000 s/mm² and Table S1 for correlation with NODDI data. Data at https://balsa.wustl.edu/DjLn

When diffusion data with b=1000 s/mm² was used for fitting in line with conventional DTI, the cortical surface map of MD inverse was less similar to the NODDI NDI than that based on all the diffusion data (Fig. S5. E–H). The correlation of the mean values in parcels between NDI and inverse MD was not so high (R=0.32, p<0.00001) as found for DTI that used all the diffusion data (Table S1).

3.5. SNR, single subject maps, reproducibility and potential partial volume effect

Neurite density and ODI values were artifactually high in the orbitofrontal and inferior temporal cortices, where SNR is <17 (Figure 1A,C and S6). Thus, we removed these cortical areas (29 in the two hemispheres) from the correlation analyses presented above.

The NDI and ODI maps in an exemplar individual subject (Fig. S7) had a similar spatial pattern similar to the group average maps (Fig. 1), and they also showed similar correlation patterns between modalities. In fact, all but two of the correlations found in the average maps were also confirmed to be significant at p<0.001 in the mean correlation in each subject (12 of 15 vs 14 of 15; Table S1). We also addressed the subject variability and reproducibility of the NODDI data. The maps of coefficient of repeatability (Fig. S8G,H) and inter-subject variability (Fig. S8A,B) for NODDI parameters have similar patterns. Most of the cortical metrics were measured on a ratio scale (i.e., the higher their between- and within-subject means were, the higher their variabilities were). In addition, the cortical metrics showed no significant proportional bias on Bland-Altman plots (data not shown). Therefore, the cortical metrics could be analyzed via conventional statistics using generalized linear models.

One potential confound in the current study is the partial volume effects (PVE) from the CSF and white matter, which might influence ODI estimates, a concern particularly in areas where the cortex was thin with respect to dMRI voxel size. We found that ODI decreased with cortical thickness (Fig. 2B), and PVE might contribute to this relationship. To investigate the impact of white matter PVE contaminating the cortical ODI estimate, we analyzed ODI values of the white matter surface and found they were not significantly correlated with thickness (Fig. S2D). The fraction of CSF in the NODDI model (F_iso) was also mapped on the surface, but there was again not a significant correlation with thickness (Fig. S2E). Although this provided no evidence that the PVE from the white matter and CSF contributed to the negative correlation between cortical ODI and thickness (Fig. 2B and S2A), some PVE contribution nonetheless remained possible. However, we hypothesized that laminar differences in neurite properties also contribute significantly as well (see section 4.2).

4. Discussion

Our findings provide evidence for distinct patterns of neurite properties in the human cerebral neocortex. We found that cortical NDI was high in sensorimotor, early visual and auditory and MT areas, closely resembling myelin maps. Cortical ODI was particularly high in early sensory cortices (somatosensory, visual, and auditory) and relatively low not only in regions associated with higher cognitive functions, but also in the primary motor cortex, and the pattern is inversely correlated with cortical thickness. Thus, the distribution of estimated cortical neurite properties is closely associated not only with myelin content, but also with cortical thickness, which was closely related to cortical microstructural features such as cytoarchitecture (spatial arrangement of neuronal cell bodies, cell types in layers and columns) and myeloarchitecture (laminar distribution of myelinated fibers) (Zilles and Amunts, 2012).

4.1. Cortical neurite density may reflect densities of cortical myelinated axons

Our finding that NDI correlates with cortical myelin agrees with earlier experimental evidence, suggesting that myelinated axons restrict diffusion of water molecules more strongly than non-myelinated axons (Beaulieu, 2009). Furthermore, when a diffusion-based neurite model was applied to high-quality data in ex-vivo rodent brain obtained at 16.4T, cortical NDI was strongly correlated with the optical staining intensity of myelinated axons but less with non-myelinated axons and dendrites, such as the stratum radiatum of the hippocampus (Jespersen et al., 2010). Recent NODDI studies also showed that low NDI occurs in regions with non-myelinated axons of newborn brain white matter (Eaton-Rosen et al., 2015; Kunz et al., 2014). An association between NDI and myelin is supported by histological evidence, indicating that (1) axon density is strongly correlated with myelin content (R=0.81) (Schmierer et al., 2007) and (2) cortical neuron density co-varies with myelin content (Collins et al., 2010; Glasser et al., 2014; Glasser and Van Essen, 2011). A recent study that directly compared NDI and histology in spinal cord also supports this: NDI is sensitive not only to neuronal elements but also to myelin density (Grussu et al., 2017). Since myelin water has much shorter T2 than typical choices of TE in diffusion MRI experiments (Wu et al., 2006), diffusion signals contain negligible contributions from myelin water, thus providing no sensitivity to myelin. Altogether, the strongest contributor to variation of NDI across the cortex is likely to be the density of myelinated axons and not myelin itself. However, NDI may also be sensitive to unmyelinated fibers known to be present in limbic areas (Nieuwenhuys, 1996) as suggested by the modestly low NDI (Fig. 1A) versus extremely low myelin content (Fig. 1C) in the anterior cingulate and insular cortices.

4.2. Cortical neurite orientation dispersion reflects the heterogeneity of neurite fiber orientations

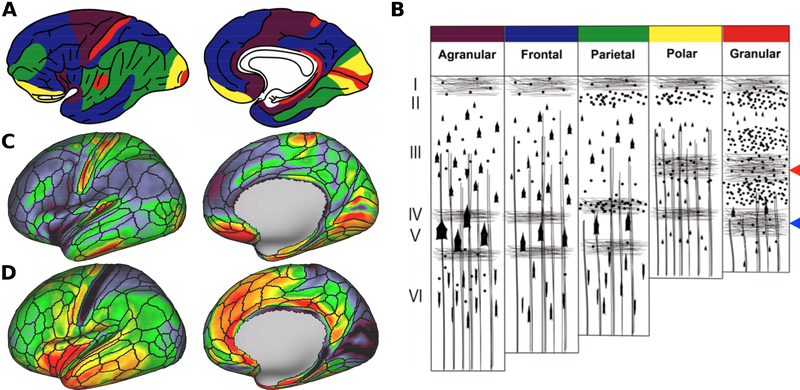
We considered whether cortical neurite ODI captures a cortical geometric aspect of myeloarchitecture, particularly related to heterogeneity of neurite fiber orientations. Previous study in post mortem tissues showed that ODI is specific and sensitive to the neurite orientation dispersion in histology (Grussu et al., 2017). Axons in most cortical regions are aligned preferentially along radial or tangential axes and less commonly in oblique orientation (Zilles et al., 2015), thus heterogeneity in cortical fiber orientation may be associated with the proportion of tangential fibers relative to the radial. Cortical tangential fibers are found in layers 1, 4, and 5, particularly, those in layers 4 and 5B (see Fig. 5 below), known as the outer and inner bands of Baillarger (Baillarger, 1840), are dense but seen in variable degrees in all of cortical regions, and thus have been a main factor that defines myeloarchitectonic parcellation of the cortex (Braak, 1980; Nieuwenhuys, 2013). Previous high-resolution dMRI studies revealed anisotropic diffusion throughout the human neocortex, which was predominantly in a radial orientation (McNab et al., 2009), whereas dominant tangential diffusion orientation was suggested in the primary somatosensory and auditory areas (McNab et al., 2013). Primary motor cortex lacks any Baillarger band despite high myelin content; it has strong radial diffusion orientation in DTI particularly in the mid-cortical layers (Aggarwal et al., 2015; McNab et al., 2013). Our NODDI analysis suggests that the heterogeneity of fiber orientation is actually higher in primary sensory areas, including somatosensory, auditory, and visual areas, known for their strong Baillarger bands. This is partly supported by ex-vivo high resolution MRI study using explicit fiber modelling to show multiple components of fiber orientations in the outer Baillarger band (stria of Gennari) of area V1 (Kleinnijenhuis et al., 2013).

Figure 5.

Comparison between von Economo – Koskinas atlas (von Economo and Koskinas, 1925) and neurite orientation dispersion and density imaging (NODDI). (A) Cortical distribution of von Economo’s five main cytoarchitectonic types. Color codes are deciphered in the (B) cytoarchitecture type scheme superimposed with tangential and radial myelinated axons. (Braak, 1980; Nieuwenhuys, 2013; Triarhou, 2009; von Economo and Koskinas., 1925). The outer and inner stripes of Baillarger are indicated by the red and blue arrowheads, respectively. (C) Orientation dispersion index (ODI) map exhibits relative high values in granular and polar cortices. (D) Cortical thickness map shows relatively low values in granular and polar cortices. Data at https://balsa.wustl.edu/vpmD

4.3. Cortical neurite properties resemble microscopic findings and cortical classifications

The cortical distribution of neurite orientation estimates and cortical thickness estimates resemble seminal classifications based on cortical microscopic features (Fig. 5). Based on cytoarchitectural features of cell density, size of cell bodies, and thickness of cortical layers (Triarhou, 2009; von Economo and Koskinas, 1925), five distinct cortical types have been proposed: agranular, frontal, parietal, polar, and granular (Fig. 5A, B). The granular cortex is located in the primary sensory areas, and characterized by a thin cortex and highly developed granular layers (layers 2 and 4) with many densely packed small neurons, such as small pyramidal neurons and stellate neurons. Moreover, the granular cortex has prominent tangential myelinated fiber bands of Baillarger (Fig. 5B) (Baillarger, 1840). The agranular cortex is relatively thick and lacks clear granular layers and has more large pyramidal cells (Triarhou, 2009; von Economo and Koskinas, 1925) (Fig. 5B). The other three types (frontal, parietal, and polar) represent intermediates between the agranular and granular cortices.

In agreement with this classification, we found that ODI is relatively high in early sensory areas (somatosensory, visual, and auditory), areas also known as granular cortex (Triarhou, 2009; von Economo and Koskinas, 1925) (Fig. 5A,C). Conversely, in the agranular cortex, radial efferent axons of large pyramidal cells are distinctly present instead of the inner band of Baillarger in layer 5 (Braak, 1980) (Fig. 5B). Again, we found that ODI was relatively low in primary motor cortex, anterior insular area and anterior cingulate area, classified as agranular cortex (von Economo and Koskinas, 1925) (Fig. 5A,C). Taken together, our finding supports the notion that cortical fiber organization is closely associated with cytoarchitecture of the cortex (Nieuwenhuys, 2013; Zilles and Amunts, 2012).

The contrast of NDI and ODI is also consistent with recent in vivo cortical parcellation of the human brain (Glasser et al., 2016), which is based on multi-modal MRI data, including structural and functional, but not diffusion MRI. We found that many of the gradients in the NDI and ODI maps were well correspondent to borders in the HCP parcellation made from multi-modal MRI information (Glasser et al., 2016) (Fig. S4A,B). The HCP parcellation was made using the multi-modal cortical information for myelin, thickness, task, and resting-state fMRI, but not using those of dMRI data (Glasser et al., 2016). Therefore, our results indicate that the cortical neurite properties from dMRI also had similar information regarding the cortical functional segregation, mutually supporting the validity of our cortical mapping.

4.4. Association between NDI in NODDI and MD in DTI

When we compared the NODDI measures with DTI, an unexpectedly strong negative correlation was found between NDI and MD when diffusion tensor was fitted to all the diffusion data (Fig. 4C). Previous neuroanatomical studies revealed that MD was negatively correlated with axon density (R=−0.66) in post-mortem human brain white matter (Mottershead et al., 2003; Schmierer et al., 2007), supporting our finding of a negative correlation between MD and NDI (Fig. 4C). In addition, an association between NDI and MD was predicted from the relationship of the underlying diffusion models. Recently, Edwards et al. (2017) and Lampinen et al. (2017) independently solved the equation of NODDI and DTI models and derived a mathematical formula for the relationship between NDI and MD in conditions that the CSF compartment (v_iso) was negligible. The NDI (v_ic) was expressed by a simple function of MD as follows:

$$v_{ic}=1-\sqrt{\frac{1}{2}\left(\frac{3MD}{d_{//}}-1\right)}$$ (2)

where MD is mean diffusivity, and d_∥ is a constant for intrinsic diffusivity assumed in the NODDI (Edwards et al., 2017; Lampinen et al., 2017). Our data suggest that the estimated CSF compartment was small (<10%) in cortical gray matter, and ODI varies over a limited range of values (Fig. 4C); these are conditions close to those assumed by Edwards et al. (2017) and Lampinen et al. (2017). Hence, our finding of a strong negative correlation between MD and NDI may largely reflect predictions based on diffusion and neurite models.

Note that the equation (2) is eligible only if high b-value data were used for both models of NODDI and DTI. There was not a strong correlation between NDI and conventional MD (R= −0.32), with the latter being obtained by fitting tensor model to the diffusion data with b=1000 s/mm² as in a conventional method (Johansen-Berg and Behrens, 2013). We presume there are two reasons for this, which relate to amount and type of diffusion weight of obtained data. First, the total amount of diffusion data collected with b=1000 s/mm² is relatively small compared to that of the data collected with b=1000, 2000, and 3000 s/mm², so the results may be contaminated by fitting noise in the former.

Second the CSF signal may not be as negligible in the low b-value data such as those in b=1000 s/mm² compared to higher b-value data, thus violating the validity of equation (2). The intra-axonal compartment is thought to be contributed by slow diffusion, which can be probed by using higher b-values, making measurements more sensitive to smaller water displacements (Assaf and Cohen, 2009). In fact, recent studies suggest that high b-value DWI is more sensitive to the status of myelin sheets and intra-axonal water (Assaf and Cohen, 2009; Bashat et al., 2005; Cohen and Assaf, 2002; Hagmann et al., 2010). Supporting our notion, a correlation of MD calculated using diffusion data with b=3000 s/mm² was much higher than those only using b=1000 s/mm² data (data not shown). Since the detailed investigations are beyond the scope of the current study, we address DTI and its b-value dependency of equation (2) in a future study.

4.5. Optimization and validity of NODDI in the gray matter

NODDI was well validated by histology and ex-vivo MRI: ODI is highly sensitive and specific to neurite orientation dispersion, while NDI is sensitive to neuronal elements and to the local amount of myelin(Grussu et al., 2017). This was based on findings in post mortem tissues with very high-resolution MRI. Despite we also applied NODDI to high-resolution in vivo MRI data, there may be several concerns particularly associated with assumptions in the NODDI model. In the current study, we estimated the optimized value of intra-cellular diffusivity for gray matter areas (1.1 × 10⁻³ mm²/s) and used it as an assumed value when calculating NODDI parameters. The NODDI also has its basis on the tortuosity model (Szafer et al., 1995), which assumes equality of the intracellular and extracellular axial diffusivity. The model is concerned with potential bias in the white matter where neurites are densely packed (Jelescu et al., 2016, 2015; Lampinen et al., 2017) and is likely more valid in tissues where neurites are sparser, similar to the gray matter (Fieremans et al., 2008; Novikov and Fieremans, 2012). However, a recent study applied a general framework for estimating orientational and microstructural parameters and revealed that while the intra-cellular axial diffusivity in the gray matter was close to our data, the extracellular axial diffusivity was much higher than this value and variable across areas (Novikov et al., 2016). Although this approach appears promising for more generalized estimation of neurite distribution, we feel it needs to be evaluated for stability and robustness of fitting before practical application, which we consider outside the scope of the current study.

5. Conclusions

We examined cortical neurite properties using the HCP dMRI data and NODDI in human cortex in vivo. NDI was high in the sensorimotor strip, early visual and auditory areas, and area MT, and was highly correlated with myelin maps estimated from T1w/T2w images. ODI was particularly high in the early sensory cortices, known for dense tangential fibers and classified as granular cortex by von Economo and Koskinas. Because diffusion signals are considered insensitive to myelin water itself, our findings suggest that cortical NODDI provides valuable information about the microarchitecture of myelinated neurites, which is closely related to, but complementary to myeloarchitecture.

Our findings have several implications for the future application of cortical neurite mapping. Tangential myelinated fibers are thought to mainly comprise axonal collaterals leaving descending (radially oriented) axons from the pyramidal cells (Braitenberg, 1962, 1974), and hence related to local intra-cortical connections. Radial and tangential fibers in the cortex originate from different developmental processes (Callaway and Katz, 1990; Marín-Padilla, 1992), and they differ in plasticity after injury (Van der Loos and Woolsey, 1973) and aging (Scheibel et al., 1975). Therefore, assessment of tangential cortical fibers with the cortical NODDI may be potentially useful to such processes in relation to the neurocognitive behaviors of living human subjects.