A practical Bayesian adaptive design incorporating data from historical controls

Abstract

In this paper, we develop the fixed-borrowing adaptive design, a Bayesian adaptive design which facilitates information borrowing from a historical trial using subject-level control data while assuring a reasonable upper bound on the maximum type I error rate and lower bound on the minimum power. First, one constructs an informative power prior from the historical data to be used for design and analysis of the new trial. At an interim analysis opportunity, one evaluates the degree of prior-data conflict. If there is too much conflict between the new trial data and the historical control data, the prior information is discarded and the study proceeds to the final analysis opportunity at which time a noninformative prior is used for analysis. Otherwise, the trial is stopped early and the informative power prior is used for analysis. Simulation studies are used to calibrate the early stopping rule. The proposed design methodology seam-lessly accommodates covariates in the statistical model, which the authors argue is necessary to justify borrowing information from historical controls. Implementation of the proposed methodology is straightforward for many common data models, including linear regression models, generalized linear regression models, and proportional hazards models. We demonstrate the methodology to design a cardiovascular outcomes trial for a hypothetical new therapy for treatment of type 2 diabetes mellitus and borrow information from the SAVOR trial, one of the earliest cardiovascular outcomes trials designed to assess cardiovascular risk in antidiabetic therapies.

1 |. INTRODUCTION

The Prescription Drug User Fee Act VI describes activities that the US Food and Drug Administration (FDA) will undertake to facilitate the advancement of complex adaptive, Bayesian, and other novel clinical trial designs,¹ the goals of which are echoed by the 21st Century Cures Act,² which was signed into law in December of 2016. Such novel designs may provide promising approaches to investigate the efficacy and/or safety of therapeutic products in a variety of settings ranging from products intended to treat rare diseases to products intended to treat conditions that afflict a large portion of the US population. One possible pathway for innovation is through the development of methods that incorporate evidence from sources external to a randomized controlled trial (eg, expert opinion or data from earlier trials). Defining the scope of what constitutes potentially valid evidence and defining when and where such evidence can be incorporated into the design and analysis of future randomized controlled clinical trials (RCTs) will undoubtedly be a challenge. However, it would seem that one obvious source of such evidence would be information for control subjects from previously conducted (or ongoing) clinical trials and observational studies in the same disease population as in a future trial. In this paper, we develop and evaluate the fixed-borrowing adaptive design that incorporates subject-level control data from a previously completed clinical trial in the design and analysis of a new trial.

In the case of trials assessing rare outcomes, borrowing information from sources external to an RCT may be particularly useful due to the substantial cost of conducting well-powered trials in such settings. For example, for all new therapeutic agents intended for the treatment of type 2 diabetes mellitus (T2DM), cardiovascular outcomes trials (CVOTs) are effectively required to demonstrate that the investigational product does not result in an unacceptable increase in the risk of major adverse cardiovascular events (MACEs).³ Even in trials enriched for high risk T2DM patients, these events are rare. For example, in three such trials, the annualized event rate for MACEs was as low as 2% to 3%.^4–6 It has been noted that the pool of completed CVOTs could be a valuable source of information to be used in the design and analysis of future CVOTs.⁷ While our methodological development was motivated by the FDA Guidance for evaluating cardiovascular risk of oral products intended to treat T2DM, the methodology we develop in this paper is more generally applicable in any therapeutic area where control subject data are available from a previously completed clinical trial. Henceforth, we refer to such subjects as historical controls and the source trial as a historical trial, but note that, in many applications, the data will have been collected in the recent past and collection may even be ongoing.

The fixed-borrowing adaptive design makes use of the simplest form of the power prior.⁸ In this case, the power prior is a fixed prior. That is, the informativeness of the prior (ie, the amount of information borrowed from the historical trial) is fixed a priori and not dynamically adjusted through the statistical model as is the case with hierarchical priors (eg, normalized power priors⁹). For our approach, the amount of information borrowed would be agreed to by the trial sponsor and pertinent regulatory body during the planning stages of the new trial. At a preplanned interim analysis opportunity, one evaluates the extent of prior-data conflict based on a simple statistic derived from the weighted log-likelihoods for the new and historical trial data. If the conflict is too great, the new trial continues to the preplanned final analysis opportunity where the data are analyzed with a noninformative prior (ie, no borrowing). Otherwise, the trial is stopped early and the data are analyzed with an informative power prior. In addition to agreeing upon the amount of information to be borrowed, the trial sponsor and regulatory stakeholders must come to an agreement on how conservatively they will evaluate prior-data conflict at the interim analysis opportunity.

There is a growing body of work devoted to the use of data from historical trials in the design and analysis of new trials. Much of the work has focused on model-based methods that use the new and historical data to estimate the degree of heterogeneity between the different sources to dynamically adjust how much information is borrowed. These methods include, eg, power priors where the borrowing parameter is treated as a random variable,^8–11 commensurate priors,¹² and robust meta-analytic-predictive priors.¹³ Each of these methods is challenging to implement when the control group distribution is not indexed by a single scalar parameter (ie, when there are covariates) and/or the data are non-normal. In contrast, a simple power prior with a fixed borrowing parameter seamlessly accommodates covariates in the statistical model and can be constructed easily for many common data models, including linear regression models, generalized linear regression models, and proportional hazards models. Moreover, we argue that in many cases (such as the application we present in this paper) it is necessary to use statistical models that adjust for one or more covariates to justify borrowing information on control subjects (ie, to ensure approximate exchangeability of subjects across trials) and that the assumption of exchangeability of trial parameters (which motivates the use of hierarchical models and/or hierarchical priors) is simply not tenable. We discuss these points in much greater detail in Section 2 through the lens of designing a CVOT for risk assessment in the T2DM therapeutic area.

Essentially all of the meta-analytic priors aforementioned contain hyperparameters, which, in part, control the degree of information borrowing. In most (if not all) cases, these hyperparameters are not elicited according to any sort of a priori belief; they are mechanical constructs to be manipulated to obtain a design having good properties. When evaluating the performance of an analysis prior that is based on historical data, most authors evaluate the performance of the prior with respect to type I error control. This is appropriate since reasonable type I error control is of great importance to regulators. However, just as borrowing information from historical controls can inflate the type I error rate when the information provided by the historical data is inconsistent with the true model for the new trial data, so too can it degrade power to detect a clinically meaningful effect size. It would seem desirable to have a procedure for borrowing the prior information that provides precise control of the type I error rate and statistical power. For our method, we deal with this problem directly by setting bounds on the maximum type I error rate and minimum power for a chosen effect size and letting these bounds determine the trial’s early stopping rule (ie, when the prior information must be discarded).

The rest of this paper is organized as follows. In Section 2, we motivate the proposed methodology in the context of designing a CVOT. We discuss the large degree of heterogeneity in a set of already completed CVOTs, how that heterogeneity guided our strategy for borrowing information, justification for and challenges with covariate selection to ensure exchangeability of subjects across trials, and our perspective for viewing the prior information which motivated the idea of bounding the type I error rate and power. In Section 3, we provide a detailed development of the fixed-borrowing adaptive design, including a discussion of the power prior, a procedure for accurate posterior analysis without Markov chain Monte Carlo (MCMC) methods, and the simulation-based procedure for determining the early stopping rule for the trial. In Section 4, we apply the methodology to design a future CVOT that borrows information from the SAVOR trial, one of the first completed CVOTs designed to assess risk in the T2DM therapeutic area. We close this paper with some discussion in Section 5.

2 |. MOTIVATING DISCUSSION

2.1 |. A comparison of several completed trials

For our motivational discussion here and the example application of the methodology in Section 4, we focus on the design of large safety CVOTs in the T2DM therapeutic area. In December of 2008, the FDA issued a guidance for industry effectively establishing a two-stage framework for the assessment of cardiovascular risk in all new therapeutic agents intended for the treatment of T2DM.³ In the second stage, a randomized controlled trial is generally conducted to demonstrate that the treatment causes no more than a 30% increase in risk for MACE. In practice, the hazard ratio estimated from a Cox proportional hazards model¹⁴ is used as the basis for cardiovascular risk assessment and so stage two can equivalently be characterized as having to rule out a hazard ratio of 1.3. This quantity is commonly referred to as the stage two risk margin.

Even though the CVOTs that have been completed to date are homogeneous in that they each enrolled subjects diagnosed with T2DM, they are quite heterogeneous in many other important aspects of the recruited patient populations. There are differences in basic demographic characteristics (eg, age criteria), in the required level of glycemic control (ie, ranges for hemoglobin A1c (HbA1c)), and in definitions of qualifying cardiovascular disease history. To illustrate this, we briefly compared inclusion/exclusion criteria for three completed CVOTs, ie, the SAVOR,^6,15 EXAMINE,^16,17 and TECOS^18,19 trials. These were multicenter randomized double-blind placebo-controlled trials designed to evaluate the effects of saxagliptin, alogliptin, and sitagliptin, respectively, compared with placebo (all administered on top of standard of care). The primary analysis in each trial was based on the incidence of MACE. The SAVOR trial serves as the source of historical control data in our example application in Section 4.

The target population for the SAVOR trial was enriched to include subjects that were at comparatively high risk for cardiovascular events. Enrolled subjects were required to be at least 40 years of age and to have had a recent HbA1c value of at least 6.5% but also less than 12.0%. In addition to age and glycemic control criteria, subjects enrolled in the SAVOR trial were required to have a history of cardiovascular disease or to present with multiple risk factors that included renal failure. The set of qualifying events defining a history of cardiovascular disease were ischemic heart disease, peripheral arterial disease (PAD), and/or ischemic stroke. Acceptable risk factors for cardiovascular disease included dyslipidemia, hypertension, and being a smoker at enrollment. Subjects were excluded from the SAVOR trial if they had an acute cardiovascular event in the two-month period before enrollment, if they were severely obese (BMI>50), if they had severe dyslipidemia, and/or if they had severe hypertension.

In the EXAMINE trial, subjects were required to be at least 18 years of age. Those subjects not being treated with insulin at enrollment were required to have an HbA1c value of at least 6.5% but also less than 11.0%. Subjects being treated with insulin at enrollment were required to have had a recent HbA1c value of at least 7.0% but also less than 11.0%. Unlike the SAVOR trial, the EXAMINE trial enrolled only those subjects who presented with acute coronary syndrome (acute myocardial infarction or unstable angina requiring hospitalization) between 15 and 90 days prior to enrollment. Subjects were excluded from the EXAMINE trial if they had one of several hemodynamically unstable cardiovascular disorders (NYHA class 4 heart failure, refractory angina, uncontrolled arrhythmia, critical valvular heart disease, or severe hypertension). Due to the requirement that enrolled subjects have acute coronary syndrome, the target population in the EXAMINE trial had fundamentally higher cardiovascular risk than the population targeted by SAVOR (at least in the period immediately following enrollment).

The TECOS trial did not specifically target subjects who had acute coronary events (although it appears these subjects were not specifically excluded either). Like the SAVOR trial, the TECOS trial enrolled subjects with chronic conditions that are associated with increased cardiovascular risk. The TECOS subjects were required to have a history of cardiovascular disease defined as having coronary artery disease, ischemic cerebrovascular disease (eg, ischemic stroke), or PAD. These criteria would suggest the target population for TECOS was at least qualitatively similar to SAVOR with respect to cardiovascular disease. However, unlike in the SAVOR trial, TECOS subjects were required to be at least 50 years old and to have had a recent HbA1c value of at least 6.5% but also less than 8.0%, resulting in a target population that was somewhat older but had better glycemic control compared with the SAVOR and EXAMINE trials. Moreover, the TECOS trial excluded subjects with renal failure.

Currently, no two completed CVOTs are highly similar in terms of their recruited patient populations. As a result, the assumption of exchangeability of trials (or trial parameters) that is often made to justify the use of hierarchical models for information borrowing across multiple historical trials is not tenable. For this reason, we develop the proposed methodology as a means to borrow information from a single historical trial that was selected and used, as much as possible, as a blueprint for the design of the new one (apart from differences in the investigational treatment). By this we mean that, on paper, the historical trial and the new trial should be as similar as possible. In the context of CVOTs, basic inclusion and exclusion criteria related to age, level of glycemic control, cardiovascular disease history, and other known prognostic factors for MACE should be nearly identical. Moreover, the standard of care used to treat control subjects in the new trial should be consistent with the standard of care at the time when the historical trial was conducted.

2.2 |. Covariate selection

Regardless of protocol design, it is unreasonable to assume that subjects in the historical and new trials are all exchangeable. That is, one cannot justify performing the primary analysis using a very simple model (ie, no covariate adjustment) as commonly done in RCTs. It is necessary to adjust for a reasonable set of prognostic factors to help better ensure exchangeability of subjects across trials. In our experience, there will often be many characteristics (ie, potential covariates) that are associated with a given outcome, but only a few that are captured in clinical databases with the level of clarity and consistency that makes them well-defined across trials.

For example, consider the MACE endpoint that is commonly used for CVOTs. In such trials, history of percutaneous coronary intervention (PCI) is commonly collected in medical history, but incidence information alone provides an incomplete picture of a subject’s cardiovascular risk. Knowing whether the procedure was elective or performed to resolve an acute life-threatening event would be valuable, as would knowing the date that the procedure was performed. Presumably, procedures from the distant past may not be relevant. The true relationship between a subject’s history of PCI and their underlying cardiovascular risk is likely too complicated to be useful in the statistical analysis. In contrast, characteristics like age at enrollment, duration of diabetes, baseline HbA1c, and estimated glomerular filtration rate provide clear and concrete information about the overall health of the subject and about cardiovascular risk at the time of trial enrollment (even if these characteristics represent surrogates for true underlying risk factors that are not clearly captured in the available data). We suggest one focus on adjusting for the latter type of characteristics in the statistical model and rely on the similarity of the protocol designs to adequately address the former. This approach is admittedly imperfect, and it speaks to the need to evaluate the extent of prior-data conflict to determine if information borrowing from the historical trial seems reasonable once some data are collected in the new trial. Our proposed approach for evaluating prior-data conflict is described in detail in Section 3.6.

2.3 |. Perspectives for viewing the prior information

Throughout this paper, we assume a common model applies to the data from both trials (eg, the Cox model with piecewise constant baseline hazard), but we entertain the prospect that the parameters may differ. There are two perspectives that are generally considered when evaluating the impact of borrowing prior information for a Bayesian design. The first perspective, which stems from the assumption that subjects are exchangeable across trials, is to view the historical data that forms the prior as part of the random process. The exchangeability of subjects across trials implies that the new and historical trial subjects can be viewed as two random samples from the same model.²⁰ In light of that fact, one might consider the type I error rate and power averaged over the generative processes for both data sets. From that perspective, when exchangeability holds, it should be clear that borrowing any amount of information from the historical data will not inflate the type I error rate and that borrowing information will generally increase power or allow sample size reduction. When the exchangeability assumption is not met, borrowing the prior information will impact the design’s type I error rate and power, but neither of these operating characteristics can be easily evaluated from this perspective since the parameters in both models are unknown. Moreover, the idea of averaging over the generative process for the historical trial data seems somewhat unnatural since those data are already observed at the time the new trial is being designed. For these reasons, we view this perspective as an interesting philosophical justification for why a Bayesian, convinced the exchangeability assumption is met, might not focus on the type I error rate as an operating characteristic of interest for trial design in this setting. However, for reasons described in Sections 2.1 and 2.2, there will always be reason to be at least somewhat skeptical of the exchangeability assumption.

As an alternative to the first perspective, one can view the historical data that forms the prior as nonrandom (ie, data that is conditioned upon in the analysis). In this setting, the prior simply reflects the current state of knowledge, which may or may not be consistent with the truth. Being consistent with the truth is an imprecise phrase that can be interpreted as the prior mean or mode being a good approximation of the true parameter value for the new trial model. From this perspective, even though exchangeability is a guiding principle for the design, whether or not the subjects in the two trials are actually exchangeable is of little importance when it comes to evaluating the impact of borrowing the prior information on the type I error rate and power. All that truly matters is whether or not the prior information is consistent with the truth. When it is not, borrowing the prior information may inflate the type I error rate and/or degrade the power. Adopting this second perspective should not be misconstrued as disregarding the principle of exchangeability. That principle is still fundamental to the design through its governance of how one selects the historical trial and designs and implements the protocol for the new trial. It is as important as any other aspect of the methodology presented in this paper.

3 |. THE FIXED-BORROWING ADAPTIVE DESIGN

3.1 |. Preliminaries

Let θ = (γ,ψ) be the collection of all parameters in the combined model for the new trial subjects and historical controls. Here, γ is the treatment effect parameter for the new trial and ψ is a vector of nuisance parameters common to the data models for the new trial and historical controls. Our method is designed for the case where the historical data inform ψ but not γ. In the context of a linear regression model for a continuous endpoint, ψ will contain a mean parameter for the control group and effects for important covariates and/or prognostic factors for the outcome of interest. In the context of a Cox model for a time-to-event endpoint, ψ will contain baseline hazard parameters and effects for covariates that are adjusted for in the hazard ratio regression model. The aforementioned covariate effects should be included in the model to justify the assumption of exchangeability of subjects across trials.

We write D_j and $\mathcal{L}(\mathit{\theta }|{\mathbf{D}}_j)$ to represent the new trial data and corresponding likelihood at the time of the jth preplanned analysis opportunity. When referencing the new trial data for general developments that are unrelated to the actual analysis timing, we will simply write D. For the proposed design, there are two preplanned opportunities to test the one-sided interval hypotheses H₀ : γ ≥ γ ₀ versus H₁ : γ < γ ₀. We refer to these opportunities as the interim or first analysis opportunity (j = 1) and the final or second analysis opportunity (j = 2). We are careful to use the term opportunity here because the actual hypothesis test will be performed only once, the timing of which being based on the degree of prior-data conflict observed at the first analysis opportunity and a prespecified threshold for the acceptable level of conflict. When the statistic measuring prior-data conflict is smaller than the prespecified threshold, the trial is stopped at the first opportunity and an informative power prior is used for the analysis. Otherwise, the trial continues to the second opportunity at which time the new trial data are analyzed without incorporating the historical control data.

3.2 |. The power prior

The power prior may be written as follows:

$${\pi }_0(\mathit{\theta }|{\mathbf{D}}_0,a_0)\propto {[\mathcal{L}(\mathit{\psi }|{\mathbf{D}}_0)]}^{a_0}{\pi }_0(\mathit{\theta }),$$ (1)

where 0 ≤ a₀ ≤ 1 is a fixed scalar parameter, D₀ are the historical control data, $\mathcal{L}(\mathit{\psi }|{\mathbf{D}}_0)$ is the likelihood for ψ given the historical control data, and π₀(θ) is an initial (noninformative) prior for all parameters. In most cases one will specify π₀(θ) = π₀(γ) × π₀(ψ) (ie, independent initial priors for γ and ψ). In many cases one or both of these initial priors can be improper and the resulting power prior will still be proper (assuming a₀ > 0), but this will need to be verified on a case-by-case basis. For a complete review of the power prior and its generalizations see the work of Ibrahim et al.²¹

When a₀ = 0, the historical data are essentially discarded and the power prior reduces to the initial prior. In contrast, when a₀ = 1, the power prior corresponds to the posterior distribution from an analysis of the historical data using the initial prior. For intermediate values of a₀, the information in the historical data is discounted to some degree leading to a prior that is more informative than the initial prior but less informative than using the historical trial posterior as the prior for the new trial. Our approach requires that stakeholders agree on a value of a₀ a priori, which we denote by $a_0^{*}$. If the new trial stops at the first opportunity, the analysis is performed using the power prior obtained by taking $a_0=a_0^{*}$. If sufficient prior-data conflict is observed at the first analysis opportunity, the trial is continued to the final opportunity, and the analysis is performed using the power prior with a₀ = 0 (ie, the initial prior).

3.3 |. The hypothesis test decision rule

We consider the one-sided null and alternative hypotheses H₀ : γ ≥ γ ₀ versus H₁ : γ < γ ₀ and reject H₀ if the posterior probability of the alternative hypothesis P(γ < γ ₀ |D,D₀, a₀) is at least as large as some prespecified critical value ϕ. To decrease the search space for the number of study characteristics that are manipulated in design simulations, we recommend fixing ϕ = 1 − α, where α is the targeted one-sided type I error rate for the design. This approach is motivated by the fact that the posterior probability P(γ < γ ₀ |D,D₀, a₀ = 0) is asymptotically equivalent to a frequentist p-value when γ = γ ₀ and when there is a single analysis based on a fixed sample size. In other words, ϕ = 1 − α is the asymptotically correct choice to control the supremum type I error rate at level α when there is no borrowing from the historical data (as will be the case if the hypothesis is tested at the final analysis opportunity).

3.4 |. Approximate posterior calculations without MCMC

Our method bases inference on the posterior probability P(γ < γ ₀ | D,D₀, a₀). Computation of that quantity via MCMC is straightforward but prohibitively slow for large scale simulation studies unless the sample size is small or the model sufficiently simple. To avoid this general problem, we propose an asymptotic approximation for P(γ < γ ₀ | D,D₀, a₀) that is easily implementable using standard software, fast to compute, and accurate for large sample sizes. The approximation exploits a connection between Bayesian analysis with the power prior and maximum likelihood analysis using case weights (also known as weighted maximum likelihood analysis).

Assume the data for the new and historical trials are independent samples of size n and n₀, respectively. Let ℓ (θ | D_i) and ℓ(ψ | D_0,j) denote the log-likelihoods for subjects i and j from the new and historical trials, respectively. The logarithm of the posterior (ignoring the normalizing constant) is given as follows:

$$\log \pi (\mathit{\theta }|\mathbf{D},{\mathbf{D}}_0,a_0)=\sum _{i=1}^n{w}_i\cdot \mathcal{l}(\gamma ,\mathit{\psi }|{\mathbf{D}}_i)+\sum _{j=1}^{n_0}{w}_{0,j}\cdot \mathcal{l}(\mathit{\psi }|{\mathbf{D}}_{0,j})+\log {\pi }_0(\mathit{\theta }),$$

where w_i is equal to 1.0 and w_0,j = a₀. Thus, apart from the normalizing constant (which does not depend on the parameters) and the logarithm of the initial prior (which is flat relative to the likelihood of the historical data), the log posterior distribution is equal to the weighted log-likelihood. The Bayesian central limit theorem²² assures us that, when the sample size for the combined trials is reasonably large,

$$\pi (\gamma |\mathbf{D},{\mathbf{D}}_0,a_0)\stackrel{.}{\propto }\text{Normal}(\gamma |\widehat{\gamma },{\sigma }_{\widehat{\gamma }}^2),$$

where $\widehat{\gamma }$ is the weighted maximum likelihood estimator from a joint analysis of both trials with aforementioned weights described and ${\sigma }_{\widehat{\gamma }}^2$ is the relevant diagonal element of the inverse of the observed information matrix for the weighted log-likelihood evaluated at the weighted maximum likelihood estimator. Using this connection, we can approximate relevant posterior probabilities for Bayesian analyses using results that are readily obtainable from standard software for weighted maximum likelihood analysis. We have the following:

$$P\left(\gamma <{\gamma }_0|\mathbf{D},{\mathbf{D}}_0,a_0\right)\approx P\left(Z\le \frac{{\gamma }_0-\widehat{\gamma }}{{\sigma }_{\gamma }}|\mathbf{D},{\mathbf{D}}_0,a_0\right)=1-\mathrm{\Phi }\left(\frac{\widehat{\gamma }-{\gamma }_0}{{\sigma }_{\widehat{\gamma }}}\right),$$ (2)

where Z is a standard normal random variable. Note that the right-hand side of the equality in (2) is one minus the one-sided p-value that arises from weighted maximum likelihood analysis of the combined studies. We have found the approximation error of this approach is quite small in many cases. In practice, we recommend using the asymptotic approximation for any large scale simulation to identify an appropriate set of design characteristics (ie, sample size and value of a₀) and then running a small scale confirmatory simulation using MCMC to ensure the operating characteristics are still acceptable in cases where exact Bayesian inference is desired.

3.5 |. Selecting the interim analysis timing and randomization strategy

During design, one must select the sample sizes n₁ and n₂ at which the two preplanned analysis opportunities will occur. The randomization strategy (eg, balanced or unbalanced) must also be specified. In the case of trials having time-to-event endpoints, we note that the effective sample size is typically the number of observed events and not the number of subjects enrolled. This is the case for our example application in Section 4. For this section, our use of the term sample size is intended to be general.

In most cases, it is straightforward to identify a reasonable choice for n₂. This is because the sample size n₂ is only relevant to the final analysis opportunity at which a noninformative prior will be used to analyze the new trial data. In the case of performing a single test of a one-sided null hypothesis using a fixed sample size, Bayesian analysis with a noninformative prior and frequentist analysis align, and so in many cases standard formulae are available for computing the sample size required to obtain a desired level of power. For example, when designing a CVOT to rule out the stage two risk margin (ie, to rule out a hazard ratio of 1.3) and to ensure 90% power under the assumption of no treatment effect on CV risk, one would need approximately n₂ = 612 events based on a frequentist analysis of the Cox proportional hazards model (assuming balanced randomization and a significance level of α = 0.025). A Bayesian analysis for the same n₂ that uses a noninformative prior yields virtually identical power.

The optimal choice for n₁ is less obvious. If the interim analysis opportunity occurs early, a relatively large fraction of the total sample size will need to come from the historical trial, and the constraints we impose on the type I error rate and power will make it necessary to discard the prior information with relatively high probability and continue the new trial to the final analysis opportunity, even when the new trial nuisance parameters are equal to their respective historical trial posterior means (ie, the prior information is perfectly consistent with the truth). On the other hand, if the new trial does stop early, there can be a considerable reduction in total sample size and/or duration of the trial. If the interim analysis opportunity is late, a relatively small fraction of the total sample size will come from the historical trial. In this case, the new trial will have a higher probability of early stoppage, but the efficiency gain from doing so will be less. In the application presented in Section 4, we explore this tradeoff by comparing designs that attempt to borrow different fractions of the total sample size from a historical trial.

Based on the proposed adaptive design framework, arguments can be made for using balanced or unbalanced randomization in the new trial. If 50% of the desired control group sample size is to be borrowed from the historical trial, then it would seem appealing to randomize two new trial subjects to receive investigational treatment for everyone randomized to control (ie, 2:1 randomization). This would result in approximately balanced sample size in the two groups at the interim analysis opportunity. In this case, 1:1 randomization would lead to a larger effective sample size in the control group at the interim analysis opportunity, which would be suboptimal for power. In contrast, balanced randomization in the new trial would be preferred in instances where the new trial proceeds to the final analysis opportunity (since there will be no borrowing in this case). In practice, the constraints imposed on the type I error rate and power lead to continuing the new trial to the final analysis opportunity a significant portion of the time, and so we advocate using balanced randomization as a general rule. Our simulation studies did not suggest one randomization strategy to be superior to the other under the aforementioned constraints on the type I error rate and power.

3.6 |. Evaluation of prior-data conflict

For our design approach, one uses the interim analysis opportunity to assess the degree of prior-data conflict to determine whether or not it appears reasonable to borrow the prior information once some data have been collected in the new trial. To assess prior-data conflict, we propose using a simple likelihood ratio statistic W, which is given as follows:

$$W=\log \left(\mathcal{L}\left({\widehat{\mathit{\theta }}}_1|{\mathbf{D}}_1\right)\mathcal{L}{\left({\widehat{\mathit{\psi }}}_0|{\mathbf{D}}_0\right)}^{a_0}\right)-\log \left(\mathcal{L}(\widehat{\mathit{\theta }}|{\mathbf{D}}_1)\mathcal{L}{(\widehat{\mathit{\psi }}|{\mathbf{D}}_0)}^{a_0}\right),$$ (3)

where $\widehat{\mathit{\theta }}=(\widehat{\gamma },\widehat{\mathit{\psi }})=\mathrm{argmax}\mathcal{L}(\mathit{\theta }|{\mathbf{D}}_1)\mathcal{L}{(\mathit{\psi }|{\mathbf{D}}_0)}^{a_0}$, ${\widehat{\mathit{\theta }}}_1=({\widehat{\gamma }}_1,{\widehat{\mathit{\psi }}}_1)=\mathrm{argmax}\mathcal{L}(\mathbf{\theta }|{\mathbf{D}}_1)$, and ${\widehat{\mathit{\psi }}}_0=\mathrm{argmax}\mathcal{L}{(\mathit{\psi }|{\mathbf{D}}_0)}^{a_0}$. Aside from being the maximum likelihood estimate, $\widehat{\mathit{\theta }}$ is approximately equal to the posterior mode from an analysis of the new trial data using the power prior and assuming a common set of nuisance parameters, and ${\widehat{\mathit{\theta }}}_1$ and ${\widehat{\mathit{\psi }}}_0$ are approximately equal to the posterior modes when one assumes the nuisance parameters are different between the two trials (ie, subjects are not exchangeable). Focusing on the case where the nuisance parameters differ, W can be viewed as the logarithm of the ratio of the mode density value to the density value associated with restricting ${\widehat{\mathit{\psi }}}_1={\widehat{\mathit{\psi }}}_0=\widehat{\mathit{\psi }}$ (the mode value based on assumed exchangeability).

When W ≤ w₀ for prespecified constant w₀, then the study is stopped at the interim analysis opportunity, and the data is analyzed using the power prior based on the predetermined value of a₀. If the inequality does not hold, the trial continues to the final analysis opportunity and the data are analyzed using the initial prior (ie, a₀ = 0). The W statistic takes its boundary value of zero when the mode of the historical data likelihood is the same as the mode of the new trial likelihood (with respect to the nuisance parameters). This case corresponds to perfect agreement between the two data sets. As the modes of the two likelihoods separate, the corresponding values of W will become large, suggesting that the prior information is not consistent with the truth and that it should potentially be discarded.

Of course, there will always be some prior-data conflict simply due to random error. That is to say, W > 0 with probability one. The fundamental question is how large w₀ should be. We would argue that there is not a single correct answer to that question. Before a meaningful determination can be made, one must appreciate the consequences of borrowing the prior information when it is inconsistent with the truth. In this case, borrowing the prior information will lead to systematic bias in estimates of the treatment effect, potentially inflating the type I error rate and/or degrading the power. Thus, the question of how much prior-data conflict is tolerable might equivalently be phrased as a question of how much of an impact on the type I error rate and power one is willing to permit by borrowing prior information that is inconsistent with the truth. For our design methodology, we automate the determination of w₀ by specifying tolerability bounds on the maximum type I error rate and minimum power and letting those bounds induce the correct choice for w₀.

3.7 |. Simulation-based calibration of the stopping rule

Identification of an acceptable choice for w₀ requires a large scale simulation study over an array of possible nuisance parameter values for the new trial. This array should include the case where the nuisance parameter values in the new trial are equal to their respective historical data posterior means (ie, ψ = E [ψ | D₀]) and cases where the nuisance parameters values in the new trial are increasingly different from their respective historical data posterior means. Using simulated data sets corresponding to each possible value of the nuisance parameters, one evaluates the maximum type I error rate and minimum power based on different possible choices for w₀ until an acceptable value is identified.

Let θ₀₁, …, θ_0M represent the collection of null parameter values considered and let θ₁₁, … ,θ_1M represent the corresponding alternative parameter values. We assume θ_0m = θ_1m apart from the value of γ, which will be fixed at γ₀ for null parameter values and at some chosen value γ₁ for alternative parameter values. Let δ_e be the maximum tolerable elevation in the type I error rate and δ_p be the maximum tolerable reduction in power. Let B represent the number of simulation studies to be performed for a given parameter value. For hypothesis h = 0, 1, parameter value m = 1, … , M, and simulation study b = 1, … , B, one does the following.

1. Simulate the new trial data sets ${\mathbf{D}}_{hm,1}^{(b)}$ and ${\mathbf{D}}_{hm,2}^{(b)}$ corresponding to the interim and final analysis opportunities.

2. Compute the posterior probability of the alternative hypothesis at the interim analysis opportunity using the power prior $p_{hm,1}^{(b)}=P(\gamma <{\gamma }_0|{\mathbf{D}}_{hm,1}^{(b)},{\mathbf{D}}_0,a_0)$ and at the final analysis opportunity using the initial prior $p_{hm,2}^{(b)}=P(\gamma <{\gamma }_0|{\mathbf{D}}_{hm,2}^{(b)})$.

3. Compute the likelihood ratio statistic $w_{hm,1}^{(b)}$ in (3) based on observed data ${\mathbf{D}}_{hm,1}^{(b)}$ at the interim analysis opportunity.

4. Construct indicator variables for whether or not the null hypothesis should be rejected based on the data at the time of the interim and final analysis opportunities. Specifically, we construct $r_{hm,j}^{(b)}=1\{p_{hm,j}^{(b)}\ge \varphi \}$ for j = 1, 2.

Once the set of simulation results $\{(r_{hm,1}^{(b)},r_{hm,2}^{(b)},w_{hm,1}^{(b)}):h=0,1;m=1,\dots ,M;b=1,\dots ,B\}$ are obtained, one can then determine an appropriate value for w₀ using the following procedure.

1. Initialize w₀ = 0. This choice of w₀ does not permit early stoppage.

2. For each h = 0, 1 and m = 1, … , M, compute the empirical null hypothesis rejection rate

   $${\widehat{r}}_{hm}=\frac{1}{B}\sum _{b=1}^B\left[r_{hm,1}^{(b)}\cdot 1\left(w_{hm,1}^{(b)}\le w_0\right)+r_{hm,2}^{(b)}\cdot 1\left(w_{hm,1}^{(b)}>w_0\right)\right].$$ (4)

3. Compute the maximum type I error rate over the array of null parameter values ${\widehat{r}}_0=\max \left\{{\widehat{r}}_{0m}:m=1,\dots M\right\}$ and minimum power over the array of alternative parameter values ${\widehat{r}}_1=\min \left\{{\widehat{r}}_{1m}:m=1,\dots M\right\}$.

4. Let α and 1 − β be the desired type I error rate and power, respectively. If ${\widehat{r}}_0\le \alpha +{\delta }_e$ and ${\widehat{r}}_1\ge 1-\beta -{\delta }_p$, then one increments w₀ by some small amount and repeats steps 2 and 3. Otherwise, one terminates the search and selects the value of w₀ from the previous iteration.

The aforementioned procedure will identify the largest possible value for w₀ that is acceptable under the constraints placed on the type I error rate and power. In Appendix A of the Supporting Information section, we provide a recipe for the data simulation process used in the application in Section 4. In Appendix B of the Supporting Information section, we provide specific guidance on how to choose θ₀₁, … , θ_0M and θ₁₁, … , θ_1M.

4 |. DESIGNING A CVOT

In this section, we provide an in-depth application of the fixed-borrowing adaptive design to design a CVOT for a hypothetical treatment for T2DM. We use one of the earliest CVOTs conducted in this therapeutic area, the SAVOR trial, as the historical trial selected for borrowing. As noted in Section 2, the SAVOR trial was a multicenter randomized double-blind placebo-controlled trial designed to evaluate the effect of saxagliptin compared with placebo (both administered on top of standard of care) on the incidence of MACE. The rationale for the SAVOR trial was discussed in the work of Scirica et al,¹⁵ and the study results were discussed in another work of the aforementioned authors.⁶

We included the following characteristics in the proportional hazards model: age at enrollment, gender, history of myocardial infarction, history of stroke, logarithm of the duration of diabetes, logarithm of the baseline HBA1c, and baseline estimated glomerular filtration rate. Each of these characteristics had strong association with the MACE endpoint in the SAVOR trial, and it was felt that these characteristics could be consistently measured across trials. Data for many other medical history characteristics (eg, history of PCI, history of PAD, and history of hypertension) were available and could be evaluated for potential inclusion in the model. However, as discussed in Section 2, most medical history provides imprecise information about underlying cardiovascular risk. Our decision to include a particular characteristic in the model reflected a balance between statistical significance of the characteristic based on analysis of the SAVOR data and clarity of the information provided by the characteristic. In the chosen model, we stratified by age due to a potential violation of the proportional hazards assumption. The number of levels for the stratification factor and the number of baseline hazard components within each stratification level were chosen using a model selection procedure based on the Bayesian information criterion. We used data for n₀ = 8142 control subjects that participated in the SAVOR trial and had complete data for each of the characteristics that were included in the model. Of those subjects, ν₀ = 601 experienced a MACE event. Table 1 presents posterior summaries based on 100 000 MCMC samples from a Bayesian analysis using an independent normal prior on each hazard ratio regression parameter (mean zero and variance 10⁵) and an independent noninformative gamma prior for each baseline hazard parameter (shape and inverse scale parameters equal to 10⁻⁵).

TABLE 1.

Posterior summaries for SAVOR control subjects

Parameter	Characteristic	Mean	SD	HPD
β1	Male	0.3860	0.0935	(0.2008, 0.5664)
β2	History of Stroke	0.6465	0.1040	(0.4465, 0.8530)
β3	History of MI	0.4798	0.0839	(0.3167, 0.6453)
β4	log[Duration of Diabetes (yrs)]	0.0823	0.0425	(0.0007, 0.1667)
β5	log[HbA1c (%)]	1.4804	0.2452	(1.0082, 1.9651)
β6	eGFR (mL/min/1.73m2)	−0.0141	0.0020	(−0.0181,−0.0101)
λ1,1 : [0,∞)	Age ≤ 65	0.0164	0.0017	(0.0131, 0.0198)
λ2,1 : [0,∞)	65 < Age ≤ 75	0.0164	0.0017	(0.0131, 0.0198)
λ3,1 : [0, 1.04)	Age > 75	0.0223	0.0038	(0.0151, 0.0300)
λ3,2 : [1.04,∞)		0.0361	0.0054	(0.0259, 0.0468)

Note: The time axis partition is denoted alongside baseline hazard parameters. Abbreviations: eGFR, estimated glomerular filtration rate; HbA1c, hemoglobin A1c; SD, standard deviation; HPD, Highest Posterior Density Interval.

For our simulations to determine w₀, we set the new trial hazard ratio regression parameters equal to their respective historical posterior means from Table 1. For the baseline hazard parameters, we considered perturbations of the posterior means ranging from a 45% decrease to a 45% increase with a step size of 1%, uniformly perturbing all baseline hazard parameters by the same amount at a given time. For each possible value of the new trial parameters, we simulated 100 000 hypothetical trials. To mimic a realistic covariate distribution, we sampled entire covariate vectors (including stratum) from the SAVOR controls, with replacement. Enrollment for 5000 subjects was simulated to be linearly increasing over a three-year period and no dropout was assumed. For reasons discussed in Section 3.5, balanced randomization was used.

Note that, for our design simulations to determine w₀, we did not consider perturbations to the posterior means of all nuisances parameters (eg, we did not consider perturbations to baseline hazard parameter posterior means and hazard ratio regression parameter posterior means). Such an approach is not computationally feasible unless the number of nuisance parameters is quite small. More importantly, considering a broader discrete subspace of the overall parameter space to explore for determination of w₀ is unnecessary. In general, it is sufficient to consider perturbations to the overall model intercept while leaving other nuisance parameters fixed at their respective historical posterior means. In the context of the proportional hazards model with piecewise constant baseline hazard, uniformly perturbing the baseline hazard parameters is equivalent to perturbing the overall model intercept. In Appendix B of the Supporting Information section, we provide a detailed discussion regarding why focusing on the proposed discrete subspace of the overall parameter space is appropriate for ensuring bounded control of the type I error rate and power over the entire parameter space.

In this section, to distinguish the number of enrolled subjects at each analysis opportunity from the number of accrued events, we represent the number of events at the interim and final analysis opportunities by ν₁ and ν₂ instead of n₁ and n₂. We considered designs that had interim analysis opportunities at ν₁ = 536, ν₁ = 459, ν₁ = 383, and ν₁ = 306 events corresponding to a 12.5%, 25.0%, 37.5%, and 50.0% reduction in the number of events required for the interim analysis opportunity compared with the number of events required for a nonadaptive trial that accrues 612 events. We also evaluated the impact of different choices for a₀ for a given value of ν₁. The total number of events for a given analysis is a combination of the events accrued in the new trial plus the events borrowed from the historical trial. One needs to borrow a sufficient number of events from the historical trial so that the interim analysis, if performed, is well powered. The quantity a₀ determines the fraction of events borrowed from the historical trial. We refer to the quantity ν₁ + a₀ · ν₀ as the effective number of events at the interim analysis opportunity. In general, the value of a₀ should be chosen so that the effective number of events at the interim analysis is at least as large as ν₂ = 612. We evaluated choices for a₀ that yielded an effective number of events equal to 612 (no additional events), 765 (153 additional events), and 918 (306 additional events). For example, for ν₁ = 536, ν₀ = 601, and ν₁ + a₀ · ν₀ = 765, one would need a₀ = 0.381.

We considered three sets of tolerability bounds for the type I error rate and power, ie, (δ_e, δ_p) = (0.025, 0.05),(0.050, 0.10), and (0.075, 0.15). Table 2 presents the values for $e^{w_0}$ that were determined using the procedure described in Section 3.7 for each combination of design inputs (ie, δ_e, δ_p, ν₁, and a₀). Note that, since the critical value w₀ is a function of the chosen value for the borrowing parameter a₀ and number of events ν₁, the values of $e^{w_0}$ are only directly comparable when holding both fixed. As shown in Table 2, more liberal bounds on the maximum type I error rate and minimum power permit use of the historical trial data in the presence of greater prior-data conflict.

TABLE 2.

Identified values of $e^{w_0}$ for each combination of design inputs

Additional		Reduction in Number of Events
Events	(𝛿e,𝛿p)	12.5%	25.0%	37.5%	50.0%
0	(0.025, 0.050)	2.7	3.3	3.9	4.5
	(0.050, 0.100)	5.5	5.8	6.4	7.4
	(0.075, 0.150)	13.5	9.5	10.0	11.0
153	(0.025, 0.050)	4.3	5.2	6.0	6.4
	(0.050, 0.100)	7.4	8.6	10.5	11.0
	(0.075, 0.150)	11.6	13.5	15.6	17.3
306	(0.025, 0.050)	5.5	6.4	7.4	7.8
	(0.050, 0.100)	9.5	10.5	12.8	14.2
	(0.075, 0.150)	14.2	16.4	20.1	23.3

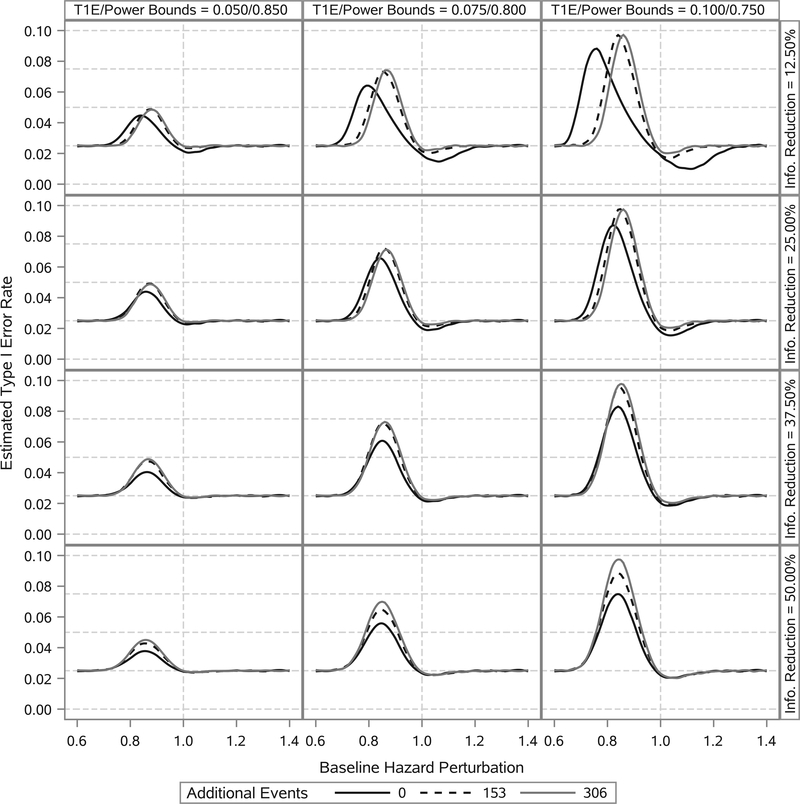
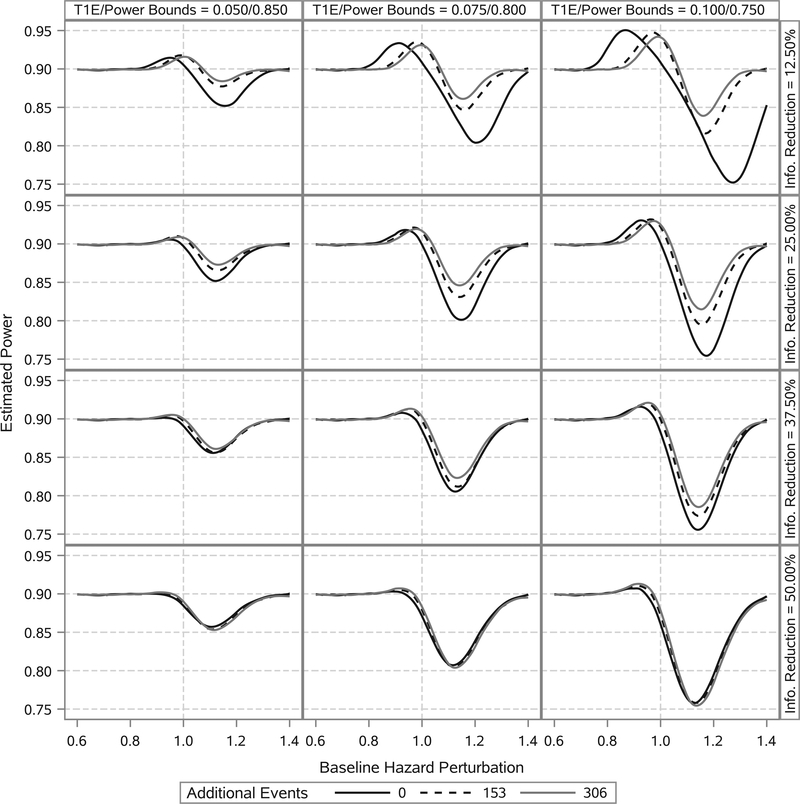
Figures 1 and 2 present the estimated type I error rate and power curves, respectively, as functions of the baseline hazard perturbation. It is apparent that, if the true new trial baseline hazard parameters are uniformly lower than their historical trial posterior means, the type I error rate is inflated to some degree. In contrast, if the true new trial baseline hazard parameters are uniformly higher than their historical trial posterior means, the power is reduced to some degree. The worst-case scenarios occur when the new trial baseline hazard parameters are moderately different from their historical trial posterior means. This is because when the discrepancy is too great, the trial essentially never stops at the interim analysis opportunity due to its adaptive nature. The degree of perturbation in the baseline hazard that results in the worst-case type I error rate and power is clearly a function of the amount of information borrowed, with less borrowing corresponding to more extreme perturbations of the baseline hazard. Interestingly, if the true new trial nuisance parameters are equal to their historical trial posterior means (ie, the prior information is perfectly consistent with the truth), the type I error rate is less than or equal to 2.5% and the power is approximately equal to 90% even when the effective number of events for the interim analysis opportunity is 612. Lastly, one can see that when ν₁ is approximately 50% of ν₂ there is essentially no power benefit to borrowing additional events from the historical trial beyond that which results in an effective number of events equal to 612.

FIGURE 1.

Estimated type I error rate as a function of baseline hazard perturbation. Columns correspond to different bounds on the type I error rate (T1E) and power. Rows correspond to different levels of reduction in the total number of events required for the interim analysis opportunity. Curves within a panel correspond to the number of additional events borrowed from the historical trial beyond that required to have an effective number of events equal to 612. Curves are estimated using LOESS methods based on 91 point estimates. Estimates correspond to baseline hazard perturbations ranging from a 45% reduction to a 45% increase. Each point estimate was computed using 100 000 simulation studies

FIGURE 2.

Estimated power as a function of baseline hazard perturbation. Columns correspond to different bounds on the type I error rate (T1E) and power. Rows correspond to different levels of reduction in the total number of events required for the interim analysis opportunity. Curves within a panel correspond to the number of additional events borrowed from the historical trial beyond that required to have an effective number of events equal to 612. Curves are estimated using LOESS methods based on 91 point estimates. Estimates correspond to baseline hazard perturbations ranging from a 45% reduction to a 45% increase. Each point estimate was computed using 100 000 simulation studies

Figure 3 presents the estimated probability of early stoppage as a function of the baseline hazard perturbation. One can see that if the new trial baseline hazard parameters are at least 40% lower or at least 40% higher than their historical trial posterior means, the new trial has a very small probability of early stoppage for each combination of design inputs we considered. In some cases, there is a relatively high probability of early stoppage over a range of baseline hazard perturbations (eg, the top right panel of Figure 3). As a general rule, using a more informative power prior necessitates that one be more conservative with respect to evaluating prior data conflict. For the case where the required number of events at the interim analysis opportunity is reduced by 50%, the probability of early stoppage is only 0.52 based on the most liberal bounds on the type I error rate and power even when the prior information is perfectly consistent with the truth.

FIGURE 3.

Estimated probability of early stoppage as a function of baseline hazard perturbation. Columns correspond to different bounds on the type I error rate (T1E) and power. Rows correspond to different levels of reduction in the total number of events required for the interim analysis opportunity. Curves within a panel correspond to the number of additional events borrowed from the historical trial beyond that required to have an effective number of events equal to 612. Curves are estimated using LOESS methods based on 91 point estimates. Estimates correspond to baseline hazard perturbations ranging from a 45% reduction to a 45% increase. Each point estimate was computed using 100 000 simulation studies. The maximum probability of early stoppage is annotated in the top left corner of each panel

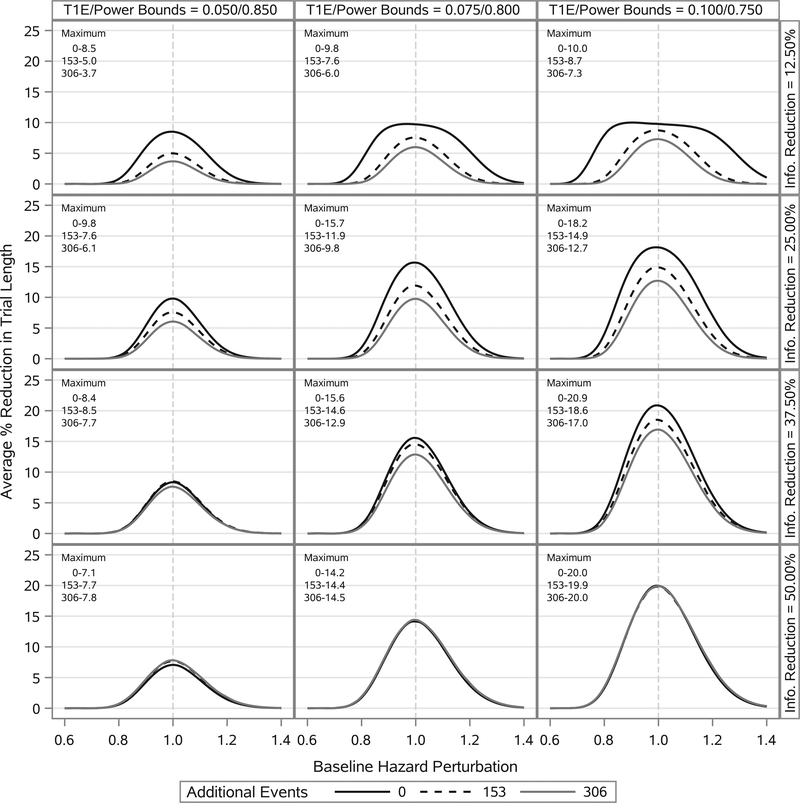
The probability of early stoppage alone does not characterize the overall utility of the design. For the design to be useful, when the new trial stops early there should be a marked reduction in the length of the trial compared with a trial that only stops at 612 events. The average length of time to reach the final analysis opportunity (ie, the length of a trial with no borrowing) was 3.82 years when the new trial nuisance parameters equaled their respective historical data posterior means. Under the same conditions, the average length of time to the interim analysis opportunity was 3.46 years (a 9.4% decrease) for a 12.5% event reduction, 3.10 years (a 18.8% decrease) for a 25.0% event reduction, 2.75 years (a 28.0% decrease) for a 37.5% event reduction, and 2.39 years (a 37.4% decrease) for a 50.0% event reduction. Figure 4 presents the average percent reduction in overall trial length (unconditional on early stoppage) as a function of baseline hazard perturbation. The greatest reductions in trial length come when a sizable fraction of the total information is borrowed from the historical trial (eg, 50.0% of the required events). However, even when a small fraction of the total information comes from the historical trial (eg, 12.5% of the required events), one sees a meaningful reduction in trial length (eg, 10%) over a wide range of perturbations in the baseline hazard. Overall, in situations where the prior is consistent with the truth, the adaptive design will have a meaningful probability of early stoppage resulting in a trial that is appreciably shorter in duration than a traditional trial with no borrowing.

FIGURE 4.

Estimated average percent reduction in trial length (unconditional on early stoppage) as a function of baseline hazard perturbation. Columns correspond to different bounds on the type I error rate (T1E) and power. Rows correspond to different levels of reduction in the total number of events required for the interim analysis opportunity. Curves within a panel correspond to the number of additional events borrowed from the historical trial beyond that required to have an effective number of events equal to 612. Curves are estimated using LOESS methods based on 91 point estimates. Estimates correspond to baseline hazard perturbations ranging from a 45% reduction to a 45% increase. Each point estimate was computed using 100 000 simulation studies. The maximum percent reduction is annotated in the top left corner of each panel

5 |. DISCUSSION

In this paper, we have developed the fixed-borrowing adaptive design for use when designing a future trial with an aim to borrow information on historical control subjects from a previously conducted trial. Our choice to develop the design from the Bayesian perspective is a matter of preference. One could just as easily develop the design from a frequentist perspective if so inclined. This is achieved by viewing the historical data likelihood as nothing more than a carefully chosen penalty and a₀ as a tool for controlling the strength of the penalty. Regardless of philosophical perspective, the core principle of the method is paradigm-free, ie, to provide a framework for borrowing prior information from a carefully selected historical data set and to mitigate the undesirable consequences of borrowing the prior information when it is inconsistent with the truth.

In order to gain efficiency (eg, reduction in trial length or required sample size), a tradeoff must be made. The tradeoff is that one must be willing to allow for the possibility of an inflated type I error rate or decreased power subject to the user-specified bounds. Although our approach focuses on bounding the maximum type I error rate, it is important to appreciate that the actual (unknowable) type I error rate for the design is not likely to be near the bound if the historical data are to be believed. Moreover, the actual type I error rate for the design will only equal the bound if the true nuisance parameters in the generative model for the new trial are equal to the worst-case values. For example, consider the design from Section 4 that is based on a 50.0% event reduction, which borrows no excess events (ie, effective number of events equal to 612 at the interim analysis opportunity), and that uses the most liberal type I error rate and power bounds (ie, bottom right panel of Figure 1). The actual type I error rate for the design reaches its maximum value when the baseline hazard in the new trial is 16% less (uniformly) compared with the historical posterior mean. In this case, the actual type I error rate is approximately 7.5% (which is less than the user-specified bound only because the power bound criteria was more stringent in this case). It should be noted that such values for the nuisance parameters in the new trial are unlikely given the historical information. In fact, computing a ratio of historical posterior density values reveals that the posterior mean value for the nuisance parameters is more than 3000 times more likely than the worst-case value. For these reasons, we caution users of this method against interpreting the type I error and power bounds as though they represent the actual operating characteristics of the design. Liberal bounds for the maximum type I error rate and minimum power (eg, a 10% maximum type I error rate and 75% minimum power) are reasonable when the historical data are viewed as highly pertinent and such bounds are necessary to achieve marked gains in efficiency over standard designs.

During development of the fixed-borrowing adaptive design, we considered a variety of choices for the stopping rule before ultimately deciding on using a simple likelihood ratio statistic. For example, we considered using the Bayes factor and a prior-predictive p-value for the marginal likelihood²³ of the new trial. When type I error and power constraints are imposed on the design, the choice of statistic to use as the basis of the stopping rule is not that important (aside from the requirement that it provide a reasonable metric for measuring prior-data conflict). The critical value to which the statistic is compared (ie, w₀) must be calibrated through simulation to achieve the desired properties. In light of this information, we elected to use the simple likelihood ratio statistic due to its interpretability as a measure of prior-data conflict and its computational simplicity for the large scale simulation studies that are critical to precisely characterizing the properties of the design.

The fixed-borrowing adaptive design permits either borrowing a predetermined amount of information or borrowing no information. The beauty of this approach is its simplicity. A similar approach could be used for many data types and models (assuming one could write down the likelihood). We also considered the use of hierarchical priors such as the joint and normalized power priors. These priors model a₀ as a random variable and assigns it a proper prior distribution. The virtue of this approach is that one can examine a posterior functional (eg, E [a₀ D₁,D₀]) and determine if enough information is being borrowed to warrant stopping the trial at any time. This approach seems appealing owing to its apparent turnkey nature. However, controlling the appropriateness of information borrowing requires careful specification of the prior for a₀. For example, one cannot simply specify a uniform prior for a₀. In fact, the prior for a₀ must be calibrated through simulation to achieve desired properties in the design. Such simulations are particularly burdensome when a₀ is modeled as a random variable because doing so leads to a much more computationally demanding model fitting step (ie, MCMC is unavoidable). Our evaluations of competing approaches based on meta-analytic priors suggested that a dynamic borrowing approach offered no gains over the fixed borrowing approach, leading us to favor the simpler approach based on a fixed power prior.

In the proposed application, we utilized the fixed-borrowing adaptive design to borrow information through subject-level data from a historical trial. We acknowledge that this proposal is somewhat forward-thinking as it would require a level of data sharing that is currently uncommon. However, it is the authors’ hope that the availability of methods like the fixed-borrowing adaptive design will help motivate such collaboration. In the meantime, one can easily use the proposed adaptive design framework based on summary historical data extracted from publications. In such applications, since covariate adjustment to help ensure exchangeability of subjects across trials is essentially impossible, ensuring the design appropriately mitigates the undesirable consequences of borrowing the prior information when it is inconsistent with the truth should be of paramount concern.