Plasmon Rulers as a Probe for Real-Time Microsecond Conformational Dynamics of Single Molecules

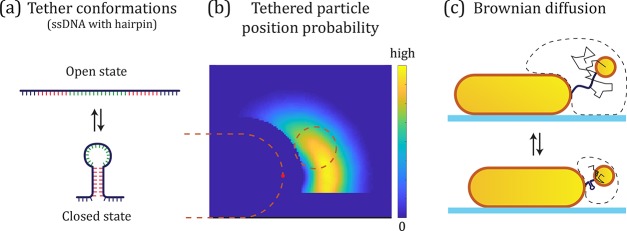
Abstract

Biopolymers such as DNA, RNA, and proteins exploit conformational changes to modulate their function. Although state-of-the-art single-molecule approaches enable identification of conformational states, the transition path and metastable intermediates often remain elusive because they occur on microsecond time scales. Here we introduce a method to probe conformational dynamics with microsecond integration times based on a heterodimer of plasmonic particles. By combining Brownian dynamics and electromagnetic simulations, we find that integration times of 1 μs can be routinely achieved, providing the capability to identify short-lived intermediates and transition paths at the single-molecule level in real-time. Importantly, plasmon rulers require no specialized equipment but can be probed on existing fluorescence microscopes equipped with a fast camera. The approach combines the advantages of fluorescent probes (zero-force, parallelization) and mechanical probes such as optical tweezers (continuous microsecond integration times). They offer a unique opportunity to study conformational dynamics and compare measurements to full-atom simulations, where computational demands limit the simulation time.

Introduction

Biopolymers like DNA, RNA, and proteins form the basic machinery of life.¹ After expression, these biopolymers fold into a three-dimensional structure on submillisecond time scales,² and some undergo conformational changes in their folded form in response to temperature, pH, ionic strength, or ligand binding.³⁻⁵ Mechanistic understanding of protein folding and conformational dynamics is key to understanding molecular function and has great potential impact in molecular biophysics, biochemistry, and medicine. As such, the characterization and understanding of protein folding is an active area of research.

All-atom simulations have predicted the mechanism and speed at which selected proteins change conformation.⁶ These simulations predict that the lifetime of a conformational state is typically seconds or longer, but the transition between two conformations involves barrier crossing that occurs on microsecond time scales. Real-time measurements of these transition path times are crucial because they contain information about the folding mechanism itself and its event-to-event heterogeneity. Importantly, such real-time microsecond measurements will enable a direct comparison with full-atom simulations, where the total simulation time is often limited because of computational demands.

Conformational landscapes of individual biopolymers have been studied using single-molecule fluorescence techniques⁷⁻⁹ and using mechanical probes such as optical and magnetic tweezers,¹⁰⁻¹² tethered particle motion,¹³⁻¹⁵ and atomic force microscopy.¹⁶ Recent single-molecule fluorescence measurements achieved microsecond times by a photon-by-photon analysis of the fluorescence trajectories and reported an estimate of the transition path time (< 20 μs) for a small protein.^17,18 However, averaging over several hundred single-molecule trajectories was required to overcome the limited brightness and photostability of the fluorophores.

Recently, real-time measurements with microsecond integration times were presented that resolved force-induced unfolding of a bacteriorhodopsin by atomic force microscopy¹⁹ and folding of a DNA hairpin in optical tweezers.¹⁰ In contrast to fluorescence measurements, these methods do not operate under naturally occurring zero-force conditions and require micron-sized or larger force probes that are attached to the biomolecule using long compliant tethers. These factors complicate the interpretation of experiments and are a topic of current research.^19,20 There is clearly a need for a single-molecule method to probe conformational dynamics with a (real-time) microsecond temporal resolution under zero-force conditions.

Here, we propose such a method based on a dimer of metal nanoparticles (a plasmon ruler) (see Figure 1a). A conformational change of the tether molecule will modulate the interparticle distance and shifts the plasmon resonance of the dimer.^21,22 Recent work by Ye et al. demonstrates the ability of plasmon rulers to measure the conformational dynamics of a protein with 30 ms time resolution.²³ We numerically explore the limits of different plasmon rulers by a combination of Brownian dynamics simulations and electromagnetic modeling to show that a time-resolution of 1 μs can be routinely achieved with commercially available particles. The temporal resolution is mainly determined by the size of the tether particle, enabling multiplexed measurements by varying the size and shape of the primary particle. This new application of plasmon rulers combines the advantages of fluorescent probes (zero-force conditions, wide-field imaging) and force-based methods (continuous microsecond integration times), paving the way to unravel the folding process and its heterogeneity in real-time.

Figure 1.

Plasmon rulers for the measurement of biopolymer conformational dynamics and folding. (a) Schematic representation of the canonical nanoruler geometry and the heterodimer geometry. Both systems are formed by a surface immobilized primary particle that is linked to a tether particle via a biomolecule. (b) Numerical simulation of the evanescent field around a gold nanosphere and nanorod resonantly excited at the (longitudinal) plasmon resonance. The evanescent field rapidly decays from the surface of the particle, inducing distance-dependent coupling between the particles. (c) Comparison of the scattering spectrum of the nanoruler in the proximal and distal state. A change in the interparticle separation leads to a change in the plasmon coupling and concomitant plasmon shift. If the scattered intensity is recorded at a single wavelength (black vertical line), a change in the distance between the particle leads to a change in the scattered light intensity. Bottom: distance-dependent signal expected for the plasmonic nanoruler (red line, plotted is the plasmon shift for a 20 × 70 nm² nanorod with a Ø 18 nm tether particle) compared to a commonly used FRET pair (blue line, plotted is the FRET efficiency for a Cy5–Cy3 FRET pair).

So far, plasmon rulers have been used on millisecond-to-second time scales to measure DNA stiffness,²⁴ drug response in cells,²⁵ and the kinetics of enzyme-induced bending and cleavage of DNA.²⁶ These reports indicated that plasmon rulers reveal interparticle distances with subnanometer resolution,²⁷ while providing a photostable optical signal. However, their applicability to study microsecond processes in real-time remains unknown because thermal fluctuations of the interparticle distance introduce signal fluctuations at these short time scales. Here we explicitly simulate these thermal fluctuations using Brownian dynamics simulations of the plasmon-ruler; subsequent electromagnetic modeling extracts the optical signal and noise as a function of particle shape and size.

We compare two geometries, namely, the canonical plasmon ruler formed by a dimer of spherical gold nanoparticles and a heterodimer with a gold nanorod as primary particle²⁸ (see Figure 1a). The primary particle in the canonical dimer is a 50 nm diameter gold nanosphere, whereas the heterodimer is constructed around a 20 × 70 nm² gold nanorod. These particle sizes were chosen because they exhibit a similar but large scattering cross section that enables the use of very small tether particles. The enhanced electric fields around the particles are shown in Figure 1b for excitation resonant with the plasmon. The fields around the nanorod are significantly stronger than the sphere, mainly because its longitudinal plasmon resonance occurs in the near-infrared, away from the interband absorption of gold.

The evanescent field rapidly decays from the surface of the particle, inducing distance-dependent coupling between the particles. In that sense, a plasmon ruler shares similarities with Förster resonance energy transfer (FRET), where distance dependent dipolar coupling between two fluorophores is exploited.²⁹ In Figure 1c, we show the normalized plasmon shift for the heterodimer as a function of particle-separation, calculated using the boundary element method (BEM).^30,31 We compare this distance-dependent plasmon shift to the distance-dependent FRET efficiency of the commonly employed FRET pair Cy3–Cy5. It shows that the plasmon ruler is sensitive to distance changes over a significantly larger range than a typical FRET pair. This sensitivity range can be further tuned by modifying the size of the primary particle, which modifies the decay length of the near-field.³²

Results

We first investigate the conformational changes of a two-state (open and closed) ssDNA tether of 50 nucleotides that can form a hairpin structure as shown in Figure 2a. Later, we extend this to an arbitrary number of states. In solution-phase experiments the small tethered sphere will diffuse through the enhanced field and cause time-dependent shifts of the plasmon resonance due to a fluctuating interparticle distance. The change in the conformation of the tether leads to a change in the confinement of the tethered sphere. Typically, for a shorter tether, the time-averaged interparticle distance is reduced leading to a red-shift of the plasmon resonance of the dimer. As shown in Figure 1c, we propose to probe these plasmon shifts using a light source with a wavelength on the red wing of the plasmon so that shifts of the plasmon resonance are translated to changes in the scattered intensity.³³ This makes the proposed experimental method directly compatible with any existing fluorescence microscope, with the main difference that we detect elastic scattering instead of the Stokes-shifted emission.

Figure 2.

(a) ssDNA molecule with a sequence that can form a DNA hairpin structure. (b) The position distribution described by the calculated potential E of the tether particle, here plotted for the heterodimer in the open conformation. The dashed lines indicate the size of the particles used in the simulation. (c) The probability P gets more confined as the hairpin closes, leading a decrease in the average interparticle distance. This results in stronger plasmonic coupling between the particles and a red-shift of the plasmon as illustrated in Figure 1c.

The detectability of a conformational change is then quantified by the signal-to-noise ratio (SNR). The number of detected photons N(t) exhibits a mean and standard deviation: μ_N ± σ_N. If the state of the system in Figure 2 changes between open and closed, or vice versa, this is observed as a change in the signal intensity:

1

with a compound deviation:

2

We define the SNR as the ratio between the change in the mean intensity Δμ_N and the compound noise σ_tot:

3

To determine the SNR with which we can probe conformational dynamics we then need to find μ_N,open and μ_N,closed, as well as their standard deviations σ_open and σ_closed. We used a numerical approach to simulate the optical signal generated by the dimer. The approach consists of three steps: (1) we calculate the Brownian motion trajectory of the particle attached via a tether with a certain contour and persistence length. (2) The scattering spectrum corresponding to each position of the tether particle is calculated using the boundary element method (BEM). (3) The resulting time-dependent optical signal is calculated using specific experimental parameters such as probe wavelength, integration time, and collection efficiency of the setup. We shortly describe each step below, and elaborate descriptions can be found in the Supporting Information.

In the first step, we determine the configuration space (i.e., the position distribution) of the tether particle using a Monte Carlo simulation method.³⁴ Herein the tether was attached to the side of the primary particle, and a Kratky–Porod chain was built segment by segment. The open state of the tether was modeled as 50 nucleotides ssDNA linked to the particles via a polyethylene glycol linker, i.e. PEG–ssDNA–PEG with the appropriate segment and persistence length for each component. The PEG components are neutral in charge and have a total contour length of 10 nm. In the closed state, we assumed that the stem (in red in Figure 2a) is far more rigid than the single-stranded portions of the strand, so that the particle-dynamics is determined by the 7 nucleotide single-stranded part (in blue in Figure 2a).^35,36 This means that the effective contour length of the DNA changes from 31.5 to 4.4 nm upon state switching. The design of the hairpin is based on systems studied using FRET with a few extra nucleotides to act as a spacer between the hairpin and the plasmon ruler.³⁷

From the position distribution for the open and closed states, we determined an effective potential E that describes the confinement experienced by the particle due to the tether and the nearby interfaces. This potential is plotted for the open conformation in Figure 2b, where we find a probability distribution with sharp boundaries dictated by the particle surface and underlying substrate. At physiological ionic strength the Debye length is <1 nm, indicating that electrostatic interactions between the PEGylated particles and between a PEGylated particle and the ssDNA are effectively shielded. The maximum excursion of the tether particle is therefore determined by the contour length of the tether. The Brownian motion trajectory of the tether particle (sketched in Figure 2c) within this potential E was simulated using Brownian dynamics simulations, yielding the tether particle’s position over time.³⁸

In the second step, we perform electromagnetic simulations to account for the fact that the scattering cross-section of the dimer depends on the position of the tether particle relative to the primary particle. Using BEM simulations,³¹ we calculated the dimer’s scattering cross-section for a linearly polarized probe for a grid of coordinates covering the 3D position of the tether particle. The Brownian motion trajectories obtained in step (1) were then used to obtain the scattering cross-section of the nanoruler as a function of time σ_scat(t,λ_probe). We then calculate the detected number of photons N(t) by taking into account the incoming photon flux, the collection efficiency of the setup (η_det = 0.05), the integration time, and shot noise. The absorption and scattering cross sections are determined for each geometry separately. The photon flux of the illumination light was chosen to limit the temperature-rise on the surface of the nanoruler to 2 K (see Supporting Note 6). This minimizes thermal effects on the biomolecule and leads to negligible changes in the diffusion coefficient of the particles. The result of this step is the detected optical signal including all relevant noise sources. Experimental observation of the angular orientation of gold nanoparticles at microsecond integration times have been demonstrated, where similar photon fluxes were employed.³⁹

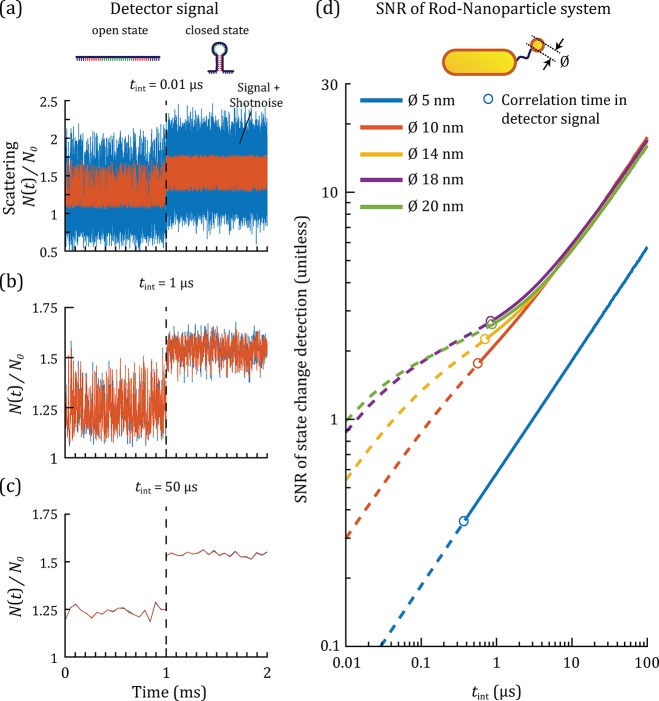
Representative calculated timetraces for three different integration times are shown in Figure 3a–c for a tether particle size of 20 nm. The timetraces show the signals in the open and closed state, with an instantaneous transition at t = 1 ms. These simulations reveal three regimes: (1) for short integration times (Figure 3a), shot noise is the predominant contribution to the SNR. (2) For intermediate integration times (Figure 3b), the shot noise is similar in magnitude to the fluctuations induced by the Brownian motion of the tether particle (Brownian noise). (3) For longer integration times (Figure 3c), the Brownian noise is dominant over shot noise and gets averaged out leading to an increase in SNR with integration time.

Figure 3.

(a–c) Normalized detector signal N(t)/N₀ for a heterodimer (20 × 70 nm² rod, sphere Ø 20 nm) as a function of time for three different integration times t_int (a) 0.01 μs–in the shot noise limited regime, (b) 1 μs–in the intermediate regime, (c) 50 μs–in the Brownian noise limited regime. The signal due to the Brownian motion and plasmonic coupling is shown in red, and the signal with shot noise added is shown in blue. The first millisecond shows the signal of the system in the open state, the second millisecond in the closed state. (d) The SNR of the detection of a state change between the open and closed state as a function of the integration time for particle diameters of 5, 10, 14, 18, and 20 nm. The time needed by the tether particle to explore the available space in the open state, τ_p, is shown as open circles (see text for more details).

These three regimes are also recognized in Figure 3d, where we show the SNR as a function of t_int for different tether particle sizes. For the 5 nm tether particle, shot noise is dominant across all t_int because the plasmon shift is small upon interparticle distance changes, leading to the expected scaling of the SNR as 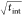. The plasmon shift increases with tether particle size, and for tether particles larger than 10 nm a transition between the shot noise limited regime and regime limited by Brownian noise is observed for integration times between 0.2 and 2 μs. With larger tether particle sizes (14, 18, 20 nm in diameter), shot noise becomes less significant and the transition to the shot noise dominated regime occurs at shorter t_int.

The characteristic time at which the tether particle explores all tether configurations defines the ultimate temporal resolution of the plasmon ruler. We will refer to this time as the characteristic time of the plasmon ruler, τ_p. We quantify τ_p by considering the autocorrelation function of the detector signal, which was fitted with a single exponential decay to yield the characteristic correlation time τ_p (see Supporting Note 7). Two major contributions determine τ_p: the diffusion constant of the particle and the length of the molecular tether. The open circles in Figure 3d show the SNR at an integration time equal to τ_p of the open state. Note that τ_p in the closed state is shorter, but the longer correlation time determines the shortest accessible time scales. We find a clear trade-off between the SNR and τ_p because the smaller tether-particles diffuse faster but generate a smaller plasmon shift upon conformational changes. Crucially, the heterodimer enables the observation of conformational changes of ssDNA hairpins with SNR ∼ 3 with continuous submicrosecond integration times.

We now consider the potential for wavelength-multiplexed measurements. A clear move toward multiplexed studies is currently observed for FRET based sensors, for example to study multiple and correlated molecular events in life cell studies.⁴⁰ To construct plasmon rulers with different center wavelengths, we exploit the fact that the plasmon wavelength of the ruler is largely determined by the size, shape, and material of the primary particle.⁴¹ We demonstrate the ability to multiplex by considering a dimer of two spherical particles, whose plasmon wavelength occurs around 580 nm. The primary particle of diameter 50 nm is bound to the substrate and a tether particle (diameter 10–50 nm) is bound via the state switching tether. A diameter of 50 nm for the primary particle yields a scattering cross-section that is close to the 20 × 70 nm² rod when both are excited on the red wing of their plasmon resonance.

The temporal response of this canonical sphere–sphere dimer is remarkably similar to the heterodimer, and we again observe a crossover from a shot noise limited regime to a Brownian noise limited regime on time scales of ∼1 μs (see Supporting Note 8). Surprisingly, the SNR of the sphere–sphere dimer is similar to the heterodimer, despite the larger primary particle and broader plasmon resonance.⁴² The similarity in SNR is caused by a smaller absorption cross section of the sphere–sphere dimer allowing for a higher excitation power before the surface temperature increase exceeds 2 K. The SNR does not increase continuously with the tether particle diameter but has an optimum at 18 nm for the heterodimer. This reflects the fact that larger particles become substantially larger than the near-field, contributing increasingly less to the plasmon shift. Additionally, a larger particle will have a lower diffusion coefficient, which reduces the SNR for shorter integration times because the Brownian motion is averaged less by integration of the signal, leading to the effective detection of more Brownian noise. A direct comparison of the correlation time τ_p for the two geometries is shown in Figure 4, where we find that τ_p is mainly determined by the diameter of the tether particle in the investigated size-regime. This implies that robust sensors with a well-defined temporal resolution can be constructed as long as the diameter of the tether particle is well controlled. Current synthesis protocols for gold spheres result in a size distribution with a coefficient of variation of no more than 10%, yielding the required control over τ_p.

Figure 4.

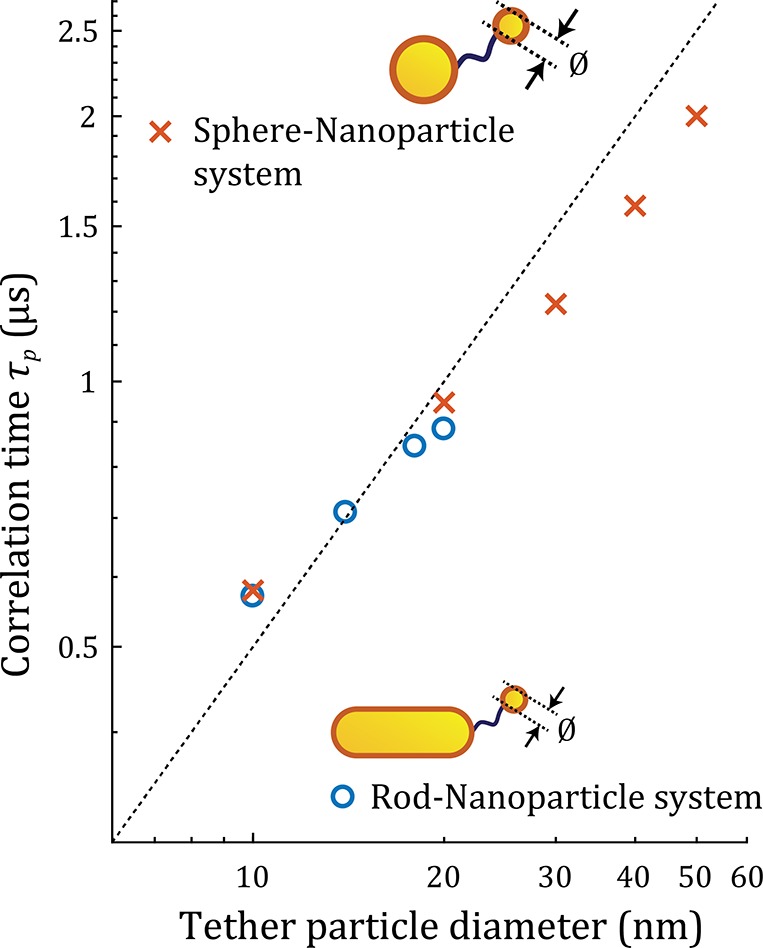
Correlation time τ_p for the heterodimer and sphere–sphere dimer as a function of the diameter of the tether particle. The corresponding SNRs for t_int = τ_p are around 2 for all tether particle diameters (see Figure S4). The dashed line indicates a linear guide to the eye (slope of 50 ns/nm).

Our simulations assume that the tether particle is attached on the tip of the primary particle. Attachment to the side of the nanorod would lead to a factor 5 smaller plasmon shift (see Figure S1) and thus factor 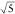lower SNR ratio in the shot noise limited regime. Tip-specific functionalization is thus preferred and can be achieved using site-specific functionalization protocols reported in literature.⁴³⁻⁴⁶ In addition, pioneering work by Mirkin and Alivisatos allows for the synthesis and purification of monovalent constructs.^47,48 For the heterodimer, the optimum signal-to-noise ratio is then achieved by employing a linearly polarized excitation field along the nanorod-axis (see Figure 1b). For the sphere–sphere dimer, the orientation of the dimer’s dipole moment is modulated by the position of the tether particle, so in this case circularly polarized light results in maximum signal-to-noise ratio.

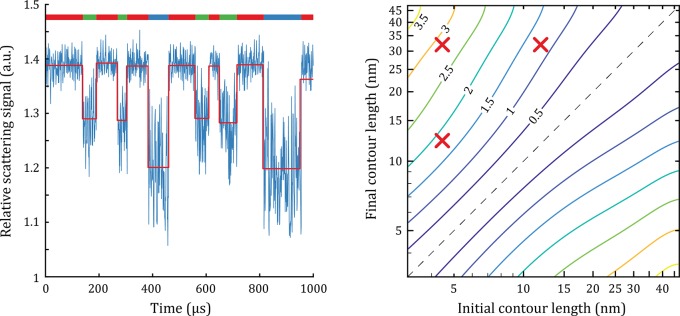
Up to now we considered a two-state switching tether with a fixed initial and final contour length. However, many biomolecules exhibit short-lived intermediates in their folding trajectory with microsecond lifetimes; prime examples are metastable intermediates of small folding proteins,⁴⁹ partially open intermediates associated with membrane transporters,⁵⁰ and pseudoknots in oligonucleotides.⁵¹ Such metastable states have typical lifetimes of some tens of microseconds but cannot be detected directly. In Figure 5a, we show a simulated timetrace of an oligonucleotide that exchanges between three conformations on microsecond time scales. Extraction of the underlying states using change-point analysis illustrates the capability of the plasmon ruler to reliably detect short-lived intermediate conformations. This also allows us to generalize our results to an arbitrary conformational change by considering a change in contour length from l_init to l_fin. We focus on the heterodimer and numerically evaluate its capability to resolve these transitions for an 18 nm diameter tether particle at t_int = 1 μs. We plot the results in Figure 5, where contour lines indicate the SNR achievable for a certain

4

Figure 5.

(a) Timetrace of a three-state DNA hairpin representing a system with an intermediate metastable state, simulated for t_int = 1 μs and η_det = 5%. The red line presents the analysis of the timetrace using a change point step finding algorithm.⁵² The dimer consists of a nanorod of 20 × 70 nm² and a tether particle with a diameter of 18 nm. The colored bar at the top of the graph represents the state of the system. The contour lengths of the three states are, respectively, 50 nt for the open state (31.5 nm, blue), 20 nt for the intermediate state (12.5 nm, green), and 7 nt for the closed state (4.4 nm, red). The states have a random lifetime between 30 and 150 us. (b) The calculated SNR for an arbitrary change in the contour length of a ssDNA tether for t_int = 1 μs. The SNR is shown as a contour plot with the initial and final contour length of the ssDNA tether on the x-axis and y-axis. Note that under all conditions the Brownian motion of the tether particle is the limiting factor; the shot noise is negligible. The red crosses correspond to the DNA contour length change occurring between the open, intermediate, and closed state of the hairpin. The dashed line indicates zero change in contour length.

As expected, larger values for Δl lead to a higher SNR for detection of the state-change, reaching SNR > 3.5 for Δl = 40 nm. We find that a certain Δl can be resolved with higher SNR for shorter l_init. This is explained by three effects: (i) at shorter l_init the relative change in contour length is larger; (ii) because of the increased effect of molecular coiling at larger tether lengths, the time-averaged particle-separation scales sublinearly with contour length; and (iii) the plasmon shift for a certain value of Δl is larger if it occurs closer to the nanorod surface because the gradient in the near-field is higher (Figure 1c).

The required SNR to extract a state change depends on the lifetimes of the intermediate states and the used analytical method. For example, detection of a state-change by simple thresholding requires a SNR ∼ 2, while hidden Markov modeling can analyze state changes at lower SNR.⁵³⁻⁵⁵ At SNR = 1, discrete contour length changes of 3 nm → 5.5 nm → 9 nm → 15 nm → 35 nm are detectable and directly relevant to the folding of aptamers, DNA hairpins, and polypeptides, for example. This implies that under optimized conditions, up to five individual states can be distinguished, providing the opportunity to investigate multistate folding.

Discussion and Conclusions

Our numerical simulations show that plasmonic nanorulers are a promising platform to study the conformational dynamics of molecules in real-time at microsecond time scales. Because of the brightness and photostability of the plasmon resonance, the temporal resolution is not limited by shot noise but rather by the diffusion of the tether particle that introduces fluctuations of the optical signal. The use of a large primary particle allows for the use of a very small tether particle, thus minimizing interference of the molecular dynamics. The ultimate temporal resolution is approximately 3 orders of magnitude higher than state-of-the-art single-molecule FRET because of a higher photon budget and approximately ∼10 times higher than recent force-based methods owing to the nanometer-sized tether particles.¹⁰ Surprisingly, we observe a very similar response between both types of dimers because of the compensating effect of the ratio between the absorption and scattering cross-section. In our simulation results, the most optimal system for the observation of molecular dynamics with an integration time of 1 μs is a nanorod with dimensions 20 × 70 nm² with a tether particle of Ø 18 nm.

One of the strengths of single-molecule FRET is the ability to probe many constructs simultaneously in the field of view of the microscope to acquire statistics. Plasmon rulers are equally well probed in parallel by imaging the scattered signal on a camera,³³ where access to microsecond time scales is warranted by an intensified CCD camera or by commercially available high-speed CMOS cameras. This makes the experimental implementation of plasmon rulers straightforward because the microscope required is already available in nearly any research laboratory. Plasmonic nanorulers therefore overcome important hurdles in existing techniques and combine the advantages of single-molecule FRET (zero-force conditions, parallelization) and force-based methods (continuous microsecond integration times), paving the way to start unraveling the folding process and its heterogeneity in real-time.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.8b03860.

• Additional details, methods, figures, and tables regarding the simulation, system parameters, particle heating calculations, signal autocorrelation, and SNR of the sphere–sphere nanoruler (PDF)

Author Contributions

E.V. and P.Z. initiated the research. E.V. developed and performed the tethered particle and Brownian dynamics simulation, M.H. performed the BEM simulations. All authors interpreted and discussed the results. The manuscript text was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.