ncdDetect2: improved models of the site-specific mutation rate in cancer and driver detection with robust significance evaluation

Abstract

Motivation

Understanding the mutational processes that act during cancer development is a key topic of cancer biology. Nevertheless, much remains to be learned, as a complex interplay of processes with dependencies on a range of genomic features creates highly heterogeneous cancer genomes. Accurate driver detection relies on unbiased models of the mutation rate that also capture rate variation from uncharacterized sources.

Results

Here, we analyse patterns of observed-to-expected mutation counts across 505 whole cancer genomes, and find that genomic features missing from our mutation-rate model likely operate on a megabase length scale. We extend our site-specific model of the mutation rate to include the additional variance from these sources, which leads to robust significance evaluation of candidate cancer drivers. We thus present ncdDetect v.2, with greatly improved cancer driver detection specificity. Finally, we show that ranking candidates by their posterior mean value of their effect sizes offers an equivalent and more computationally efficient alternative to ranking by their P-values.

Availability and implementation

ncdDetect v.2 is implemented as an R-package and is freely available at http://github.com/TobiasMadsen/ncdDetect2

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

A key challenge in cancer genomics is to understand and characterize the mutational processes that shape cancer genomes (Pon and Marra, 2015). Most mutations are neutral and do not affect cellular functions. However, a small number of driver mutations give the cell growth advantages. As different cancers experience shared selection pressures, they often accumulate in the same cancer genes or regulatory elements across patients, thereby leading to a local excess of mutations. Cancer drivers can therefore be detected by a significant excess of observed mutations compared to that expected from the mutation rate. In this regard, accurate modeling of the background mutation rate is essential for driver detection.

We previously built a detailed model of the position-specific mutation rate in cancer by including the main genomic features known to correlate with mutation rate, such as replication timing, expression levels and position-specific sequence context (Bertl et al., 2018). However, we do not know all relevant genomic features that affect and explain mutation rate variation, and, more generally, we still lack a full understanding of the complex and heterogeneous mutation processes in cancer genomes (Lawrence et al., 2013). Missing some of the explanatory genomic features when modeling the mutation rate leads to a higher variation in the observed mutation counts than predicted. This phenomenon, known as overdispersion, has been observed in previous attempts to model the mutation rate (Lochovsky et al., 2015; Martincorena et al., 2017). Failing to include overdispersion may result in an inflated number of false positives, as the background model then underestimates the probability of extreme events. Incorporating overdispersion captures the true variance of the mutation rate better and ensures robust predictions with good specificity. In contrast with previous models using the regional mutation load (Lochovsky et al., 2015; Martincorena et al., 2017), we here introduce overdispersion in a site-specific framework.

The present work extends the original ncdDetect method (v.1) (Juul et al., 2017).The ncdDetect method seeks to identify genomic regions subject to recurrent positive selection across samples of large cancer cohorts. First, a background model for the neutral mutation rate is learned for each sample and genomic position. Next, ncdDetect scans through a set of predefined regions and identify regions harbouring a significant amount of mutations or a surprisingly large predicted functional impact. The set of regions can contain any element type of interest, e.g. promoter regions, enhancers, 3′ or 5′ UTRs. While the method can also be applied to protein-coding sequences, methods leveraging the distinction between synonymous and non-synonymous mutations are expected to perform better. Various site-specific scores indicating the functional impact of a mutation can be applied, e.g. CADD, LINSIGHT or phyloP (Huang et al., 2017; Kircher et al., 2014; Pollard et al., 2010). ncdDetect can also operate with simple 0–1 scores, to simply evaluate the mutational burden.

The novel contributions of this work are threefold: First, we analyse the observed-to-expected mutation load, evaluate the levels of overdispersion for different region types, and characterize the length scale of remaining genomic features that affect mutation rate but are not included in the mutation-rate model. Since multiple additional genomic features are likely relevant to the mutation rate in cancer genomes, this characterization of length scale is the product of not one, but several genomic features. In longer terms, the goal should be to identify and incorporate all of these genomic features in the mutation-rate model in order to reduce the degree of overdispersion. In terms of cancer driver detection, this will improve the detection power while still controlling the false positive rate. As for now, we reduce the amount of overdispersion in the mutation-rate model by adding a measure of local genomic mutation rate.

Second, we introduce overdispersion in the ncdDetect cancer driver detection method (Juul et al., 2017). Overdispersion of mutation count statistics has been observed and modeled in cancer genomics previously. Generally, including overdispersion leads to higher specificity. For instance, one study found that the number of mutations in a regulatory element was better described by a beta-binomial model than a binomial model, i.e. by including a beta-distributed prior of the regional mutation rate to capture rate uncertainty and overdispersion in counts (Lochovsky et al., 2015). In another study (Martincorena et al., 2017; Nik-Zainal et al., 2016), overdispersion was captured by modeling the expected number of mutations in a gene using a negative-binomial model, i.e. a Poisson distribution with a gamma distributed rate. Where these models consider the mutation load regionally and thus lend themselves naturally to classic models for overdispersed count data, we build a novel framework to capture overdispersion in a site-specific model. We improve the efficiency of the P-value evaluation by using a highly accurate saddle-point approximation (Madsen et al., 2017).

Third, we explore alternative approaches to prioritizing findings: It is conventional to rank and prioritize findings according to their P-value. Evaluating the P-value allows the use of multiple testing procedures to estimate the number of findings (Benjamini and Hochberg, 1995) and rudimentary model control by checking for inflation or deflation of P-values. However, ranking by P-values favours long elements with small effect sizes at the expense of shorter elements with large effect sizes, which are often of higher biological relevance (Henderson and Newton, 2016). Empirical Bayes procedures are often used to remedy this problem (Love et al., 2014; Smyth, 2004). In a Bayesian setting, the overdispersion parameter is directly related to the variance of a prior distribution on the effect size. We demonstrate a correspondence between including overdispersion and Bayesian shrinkage towards the prior, and thereby offer ranking of candidates by the posterior mean effect size as a computationally fast alternative to P-value evaluation. This approach has great promise as datasets become bigger and computation loads consequently increase.

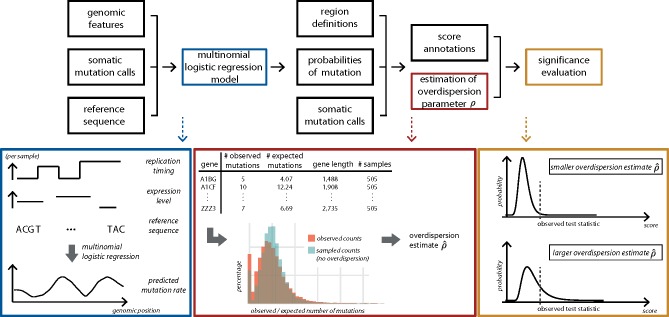
The methodological improvements are implemented in ncdDetect v.2 as an R-package, which is accompanied by a tutorial available at github.com. A graphical overview of ncdDetect v.2 is presented in Figure 1.

Fig. 1.

Overview of ncdDetect v.2. For each sample, the genomic features replication timing, expression level and reference sequence are used as explanatory variables to predict the sample- and position specific probabilities of mutation in a multinomial logistic regression model (blue box). For a specific genomic region type, the observed and expected number of mutations are collected for each specific candidate element (red box; illustrated for protein-coding genes). This information is applied to estimate the overdispersion parameter ρ as explained in Section 2.4. The estimated amount of overdispersion is accounted for in the significance evaluation of each candidate element, as explained in Section 2.2. The larger the overdispersion estimate, the harder it will be for a genomic candidate element to reach significance (yellow box)

2 Materials and methods

We previously developed the method ncdDetect for detection of non-coding cancer driver elements (Juul et al., 2017). With this method, we compare observed mutation counts to the background mutation rate, which is based on various genomic features, and estimated for each sample and genomic position. The genomic features included in the background model of the mutation rate are replication timing, tissue-specific gene expression level, trinucleotides (the nucleotide under consideration and its left and right flanking bases), and genomic segment [3′ and 5′ untranslated regions (UTRs), splice sites, promoter elements and protein-coding genes]. The position-specificity of the method provides great flexibility in terms of modeling the mutation rate in cancer at any genomic resolution without having to average features with varying values within specified regions. The setup further allows us to assign different scores to each mutation at each position. In the present analysis, we use CADD and LINSIGHT scores. Including measures of functional impact improves the ability of ncdDetect to reveal recurrent positive selection across cancer genomes.

The background model used in ncdDetect relies on multinomial logistic regression to predict position-specific mutation probabilities (Bertl et al., 2018). The position-specific setup leaves, however, no room for estimating overdispersion, as overdispersion in this model does not change the position-specific predictions and cannot capture regional dependencies (Fig. 2A).

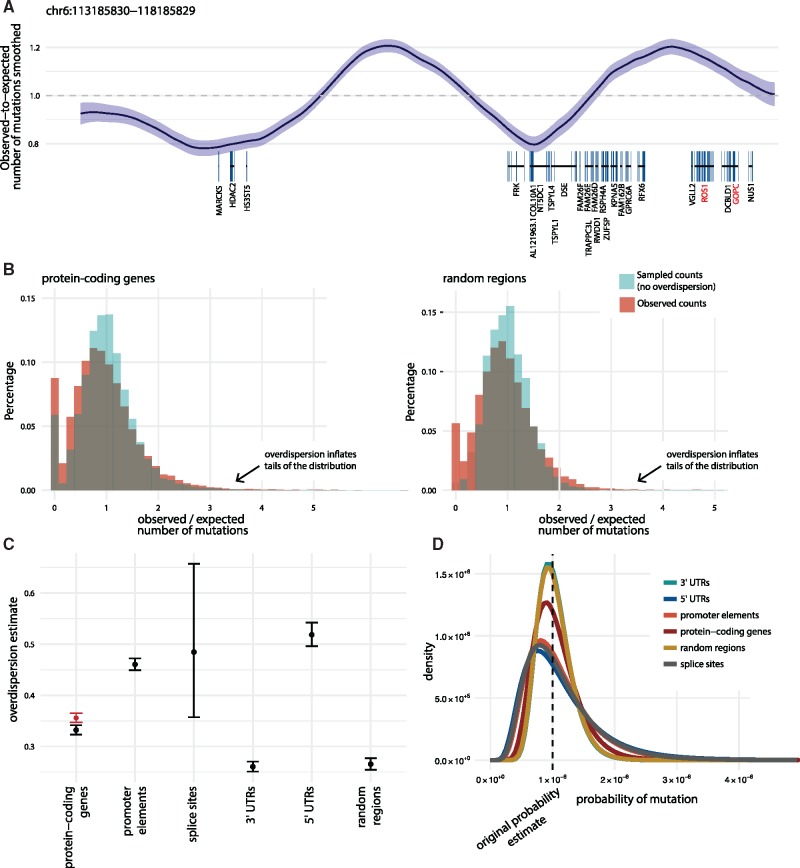
Fig. 2.

Illustration and estimation of overdispersion. (A) The smoothed ratio between the observed and expected number of mutations on representative 5 Mb genomic section (chr6: 113 185 830–118 185 829). Mutation counts are considered in bins of size 1 kb. Bottom: Protein-coding genes with COSMIC CGC genes highlighted (red). In regions where the mutation rate is underestimated (observed-to-expected ratio > 1), ncdDetect v.1 is likely to call false positive cancer drivers. (B) Observed-to-expected number of mutations shown for protein-coding genes as well as 10 000 randomly sampled regions, all of length equal to the median length of protein-coding genes (1300 bps). The ratio between observed and expected mutation counts are shown (red histograms). For each region of a given region type, a set of mutations were sampled directly from the background model. The ratio between the sampled and expected counts are similarly depicted (blue histograms). The overlaid histograms illustrate the two main sources of variation in the observed-to-expected ratio; namely sampling variance and overdispersion. Similar plots for the remaining region types are shown in Supplementary Figure S1. The observed and expected number of mutations for a given region type are used for overdispersion estimation. (C) The estimated overdispersion parameters, including 95% confidence limits, calculated for each considered region type. For protein-coding genes, results are shown both including (red) and excluding (black) known drivers. (D) A typical position with a predicted mutation probability of 10⁻⁶ is considered. The densities show the variation around this point estimate given by the overdispersion estimate for the different region types. The densities are obtained as logit transforms of normal variables, whose variances are determined by the amount of overdispersion. The resulting distribution is known as a logit-normal (Supplementary Section S5)

We thus estimate the amount of overdispersion in a region-based setting: For each region, we imagine drawing a random effect representing a scaling of the expected mutation rate to what it would have been, had all relevant genomic features been included. Henceforth, we will refer to the standard deviation of this random effect as overdispersion. We use an empirical prior as the distribution of the random effect, which we marginalize out by numerical integration in the significance evaluation of a candidate cancer driver element. In the following we first describe the model used in ncdDetect and then show how to include overdispersion in a position-specific setup.

2.1 ncdDetect v.1

Let $X_1,\dots ,X_N$ be a sequence of independent random variables with discrete outcomes in a state space enumerated by the integers $\{1,\dots ,4\}$. The first outcome for each of the random variables ${\left\{X_n\right\}}_{n=1}^N$ corresponds to no mutation. Furthermore let $s_n:\{1,\dots ,4\}\to ℝ,\hspace{0.17em}n=1,\dots ,N$ be a sequence of mappings from the state space to arbitrary real numbers. Typically $s_n(1)=0$ and $s_n(k)>0$ for k = 2, 3, 4. Next, define $S_n=s_n(X_n)$ and $S={\sum }_{n=1}^N{S}_n$. Denote the mutation probabilities by, $p_{nk}=p(X_n=k)$. We call this model the weighted Poisson-bionomial model.

To evaluate the probability of $P(S>t)$, consider the set

$$A_t=\{\mathit{k}=(k_1,\dots ,k_N)|\sum _{n=1}^N{s}_n(k_n)>t\}.$$

We can compute the tail probability of S as,

$$P(S>t)=\sum _{\mathit{k}\in A_t}\prod _{n=1}^N{p}_{n{k}_n}.$$ (1)

2.2 Including overdispersion

To introduce overdispersion we relax the assumption that the variables $X_1,\dots ,X_N$ are independent and replace it with a conditional independence assumption: We assume that the variables $X_1,\dots ,X_N$ are conditionally independent given an additional parameter γ distributed according to a normal distribution, $\gamma \sim \mathcal{N}(0,{\rho }^2)$. As γ increases or decreases the probability of no mutation changes accordingly.

If no mutation has a score of 0 and mutations have positive scores, smaller values of γ will lead to a higher probability of large values of S and vice versa. Thus the larger the variance ${\rho }^2$, the larger the variance of S.

We now describe how the mutation probabilities change with γ. Let $v_{nk}=\text{log}\hspace{0.17em}{\widehat{p}}_{nk}$, for $n=1,\dots ,N,\hspace{0.17em}k=1,\dots ,4$, where ${\widehat{p}}_{nk}$ are the predicted mutation probabilities. Let $p_{nk}(\gamma )=p(X_n=k|\gamma )$. Define a set of probability vectors

$$\begin{array}{cc}{p}_{n1}(\gamma )& =\frac{\hspace{0.17em}\text{exp}\hspace{0.17em}(v_{n1}+\gamma )}{\hspace{0.17em}\text{exp}\hspace{0.17em}(v_{n1}+\gamma )+{\sum }_{k=2}^4\hspace{0.17em}\text{exp}\hspace{0.17em}(v_{nk})}\\ p_{nk}(\gamma )& =\frac{\hspace{0.17em}\text{exp}\hspace{0.17em}(v_{nk})}{\hspace{0.17em}\text{exp}\hspace{0.17em}(v_{n1}+\gamma )+{\sum }_{k=2}^4\hspace{0.17em}\text{exp}\hspace{0.17em}(v_{nk})}, \text{for} k>1.\end{array}$$

The probability vectors $p_n$ follow a logit-normal distribution [Atchison 1980]. Note that when γ = 0, $p_{nk}(\gamma )={\widehat{p}}_{nk}$. Intuitively, for $\gamma <0$ the probability of the first outcome decreases for all variables $X_1,\dots ,X_N$, whereas for $\gamma >0$ the probability of the first outcome increases for all variables. We call the unconditional distribution of S an overdispersed weighted Poisson binomial distribution.

To evaluate the probability of $P(S>t)$, note that conditional on γ we have a weighted Poisson binomial distribution and we can compute $P(S>t|\hspace{0.17em}\gamma )$ as

$$P(S>t|\hspace{0.17em}\gamma )=\sum _{\mathit{k}\in A_t}\prod _{n=1}^N{p}_{n{k}_n}(\gamma ).$$ (2)

Next the unconditional $P(S>t)$ can be computed by integrating over γ,

$$P(S>t)=\int P(S>t|\hspace{0.17em}\gamma )d\gamma .$$ (3)

2.3 Computation

As described in Juul et al. (2017), the integrand in Eq. (1) can be evaluated using a dynamic programming algorithm known as convolution. However as a novel improvement we use saddlepoint approximation to greatly reduce the computational complexity (Madsen et al., 2017).

To employ saddlepoint approximation we need to compute the cumulant generating function of the conditional distribution of S given γ:

$$\kappa (\theta )=\text{log}\hspace{0.17em}\mathbb{E}[e^{\theta S}|\hspace{0.17em}\gamma ].$$

This can be computed in linear time using

$$\begin{array}{cc}\hspace{0.17em}\text{log}\hspace{0.17em}\mathbb{E}[e^{\theta S}|\hspace{0.17em}\gamma ]& =\text{log}\hspace{0.17em}\prod _{n=1}^N\mathbb{E}[e^{\theta S_n}|\hspace{0.17em}\gamma ]\\ & =\sum _{n=1}^N\hspace{0.17em}\text{log}\hspace{0.17em}\sum _{k=1}^4{p}_{nk}(\gamma )\hspace{0.17em}\text{exp}\hspace{0.17em}(\theta s_n(k)).\end{array}$$ (4)

In a similar fashion, $k\prime (\theta )$ and ${\kappa }^{″}(\theta )$ can be computed in linear time as well. To evaluate Eq. (3) in full we do numerical integration using the trapezoid rule using a fixed number of points evenly spaced in the interval $[-3\rho ;3\rho ]$.

2.4 Estimating ρ

To estimate the parameter ${\rho }^2$ in the overdispersed weighted Poisson binomial distribution, we approximate the total number of events in a region by a betabinomial distribution. As the logistic-normal distribution is well-approximated by a beta distribution this is a reasonable approximation. Let X_i denote the number of mutations in region i, we model this by a betabinomial model

$$\begin{array}{cc}{X}_i& \sim \text{Binomial} (N·L,p_i)\\ p_i& \sim \text{Beta} ({\alpha }_i,{\beta }_i)\end{array}$$

where L is the length of the region and N is the number of samples. α_i and β_i are chosen such that the mean of p_i is equal to the predicted mean and the coefficient of variation is equal to the overdispersion parameter.

$$\frac{\mathbb{S}\mathbb{D}[p_i]}{\mathbb{E}[p_i]}=\sqrt{\frac{{\beta }_i}{{\alpha }_i({\alpha }_i+{\beta }_i+1)}}=\rho .$$

Since the predicted mutation probabilities and ρ completely determines α_i and β_i, we can estimate ρ with regular maximum likelihood methods.

2.5 Computing the autocorrelation of genomic features

To compute the autocorrelation of the observed-to-expected mutation rate, we randomly select 200 regions, 5 Mb each, across the genome. For each region, s, and bin, i, let x_si denote the observed-to-expected mutation ratio. We calculate the empirical autocovariance at lag k using a pooled version of the method described in Box et al. (2015):

$$c_k=\frac{1}{S}\frac{1}{N-k}\sum _{s=1}^S\sum _{i=1}^{N-k}(x_{si}-{\overline{x}}_s)(x_{s,i+k}-{\overline{x}}_s).$$

The empirical autocorrelation at lag k is then

$$R_k=\frac{c_k}{c_0}.$$

The same strategy is used to compute the autocorrelation of other genomic features.

2.6 Posterior mean ranking

Taking a Bayesian viewpoint, the overdispersion parameter can be seen as the standard deviation in a prior distribution of the effect sizes, γ_i. The background model gives rise to an expected score e_i and corresponding variance v_i for each element under consideration. The observed effect size is the ratio between the observed score o_i and the expected score e_i,

$${\widehat{\gamma }}_i=\frac{o_i}{e_i}-1\sim N({\gamma }_i,v_i/e_i^2).$$

We estimate a normal prior distribution of γ with mean 0 and a variance, ${\sigma }^2$ learned using the method described in Section 2.4. The posterior mean (PM) is then given by

$$E[{\gamma }_i|{\widehat{\gamma }}_i,v_i,e_i,\sigma ]=\frac{{\sigma }^2{\widehat{\gamma }}_i}{{\sigma }^2+v_i/e_i^2}.$$

2.7 Local mutation rate

The position- and sample-specific mutation probabilities obtained from the background model are adjusted by the local mutation rate in the n = 10 000 bases flanking either side of a given region of interest. The procedure is as follows:

Let X_i denote the number of mutations observed in the flanks of region i. Let p_i be the number of expected mutations in the flanks of region i per base pair per sample.

We then assume that

$$X_i\sim \text{Binomial}(2·n,\text{logit}(\text{logistic}(p_i)+{\gamma }_i))$$

where

$${\gamma }_i\sim N(0,{\sigma }^2).$$

We estimate σ as described in Section 2.4.

The posterior is then given by

$$p({\gamma }_i|x_i)\propto p(x_i|{\gamma }_i)p({\gamma }_i).$$

The MAP estimate ${\gamma }_i^{\text{MAP}}$ of γ_i can be found for each region and cancer type using numerical optimization, e.g. BFGS [Fletcher, Roger (1987)]. Next each predicted probability of mutation in region i is adjusted by a factor ${\gamma }_i^{\text{MAP}}$.

2.8 Scoring schemes

With ncdDetect, position- and sample-specific mutation probabilities are combined with a score to indicate functional impact in the significance evaluation of a candidate driver element. In the present analyses, we apply phyloP-, CADD- and LINSIGHT scores (Huang et al., 2017; Kircher et al., 2014; Pollard et al., 2010).

PhyloP, a position-specific score of evolutionary conservation, is used as a proxy for functional impact, as described in Juul et al. (2017). Combined Annotation-Dependent Depletion (CADD) scores annotate each genomic nucleotide with a score according to its deleteriousness, and pre-computed values were downloaded from http://cadd.gs.washington.edu. We applied their PHRED-like scaled scores. LINSIGHT is a method to predict if a mutation is likely to have a deleterious fitness consequence at a given non-coding genomic position. Pre-computed values for all genomic positions, except those that fall in protein-coding regions, were obtained from http://compgen.cshl.edu/yihuang/LINSIGHT/. Both CADD- and LINSIGHT scores were scaled and rounded to integers for the analyses with ncdDetect, as was also the case with phyloP scores (Juul et al., 2017).

3 Results

3.1 Overdispersion estimates vary between region types

We started by analysing the variation in the mutation rate across different types of regions. More specifically, we analysed the degree of regional variation unaccounted for (i.e. overdispersion) by our position- and sample-specific mutation-rate model. We first considered the pattern of overdispersion along the genome. Illustrating the difference between the observed and predicted mutation counts showed segments with elevated or decreased mutation rates (Fig. 2A).

In our significance evaluation with ncdDetect, we aim to correct for this overdispersion using an empirical Bayes approach: First we compute the ratio between the observed and expected mutation load for each considered region type [5′ and 3′ untranslated regions (UTRs), protein-coding genes, splice sites and promoter elements], as well as a set of randomly sampled genomic regions. As the vast majority of regions are expected to be neutral, the two main sources of variation in this ratio are overdispersion and sampling variance (Fig. 2B, Supplementary Fig. S1). Using a beta-binomial model, we estimate overdispersion for each region type (Fig. 2C, Table 1). We observe differences between the obtained estimates for different region types; 3′ UTR regions are found to have the least amount of overdispersion, while 5′ UTRs have the most. As it is harder to disentangle sampling variance from overdispersion in region types mainly composed of small regions (e.g. splice sites), the overdispersion estimates obtained for such regions tend to have wider confidence intervals. Specifically for protein-coding genes, we removed putative cancer drivers of the COSMIC Cancer Gene Census (CGC) (Forbes et al., 2015) before estimation to avoid that the increased rate of true drivers inflated the overdispersion estimate.

Table 1.

Number of regions, median length and overdispersion estimate for each of the considered region types

Region type	Number of regions	Median region length (bps)	Overdispersion estimate*
Protein-coding genes	19 256	1302	0.332 [0.323; 0.341]
Promoter elements	19 157	848	0.460 [0.449; 0.472]
Splice sites	17 867	32	0.485 [0.357; 0.657]
3′ UTRs	18 481	1022	0.260 [0.251; 0.270]
5′ UTRs	18 220	260	0.518 [0.496; 0.542]
Randomly sampled regions	10 000	1300	0.266 [0.255; 0.277]

Note: Besides the five region types defined in Juul et al. (2017), we also estimate the magnitude of overdispersion for 10 000 randomly sampled regions, each of size 1300 bps.

^*95% confidence limits in brackets.

The uncertainty of the predicted mutation rate for a given position is determined by the overdispersion estimate and reflected in the amount of variation in the rate density (Fig. 2D). The effect of overdispersion can be thought of as a random factor that scales the mutation rate. The estimated level of overdispersion (σ) approximately corresponds to the standard deviation of the size of the factor. There will thus be about 95% chance that the overdispersed mutation rates fall within a factor $1\pm 2\sigma$ from the original rate prediction.

Concretely, the overdispersion estimation for protein-coding genes is 0.332 (Table 1). With a mutation probability of 1e−6, this translates into a 95% probability of the true mutation probability being in the interval [0.52e−6, 1.92e−6] (Fig. 2D). When the random overdispersion factor is high, it can thus explain a moderate increase in the mutation rate. For protein-coding genes, a 53% (1.64 SD) elevation in the mutation rate will thus never be nominally significant.

3.2 Length scale of regions with biased mutation rates

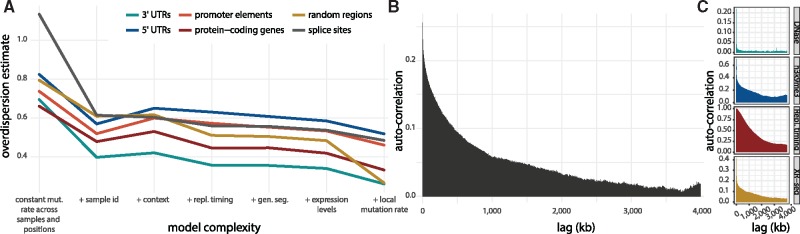
The neutral background mutation rate is predicted by the statistical mutation-rate model relying on a number of genomic features known to correlate with the mutation rate in cancer (Bertl et al., 2018). As described above, if explanatory genomic features are left out, some of the variation in the observed counts will not be captured by the mutation-rate model. This residual variation can be accounted for by overdispersion. Indeed, we observe a tendency for a decrease in overdispersion when more genomic features are added to the background mutation-rate model (Fig. 3A).

Fig. 3.

Overdispersion as an effect of missing genomic features in the background mutation model. (A) Overdispersion estimates on the basis of background models of increasing complexity. The simplest model with a constant mutation rate across all samples and positions results in the highest overdispersion estimate across all region types. For increasingly complex models, the overdispersion estimate has a decreasing trend. In the model furthest to the right, a correction for local mutation rate is performed, as described in Section 2.7. (B) The autocorrelation between observed-to-expected mutation rate in 1 kb windows, based on approximately 1 Gb scattered across the genome. The autocorrelation decreases slowly over approximately a few megabases, suggesting that genomic features that vary slowly across the genome are missing. (C) Auto-correlation functions for DNase hypersensitivity, h3k9me3 histone modification, replication timing and nucleotide excision repair (XR-seq) for comparison

Based on the mutation-rate model, we analyse the scale of the autocorrelation in observed-to-expected mutation ratios, to characterize the length scale of segments with a unidirectional bias in their rates (Fig. 3B). This helps define the length of regions where we overestimate or underestimate the mutation rate and, in longer terms, may help characterize and potentially identify the genomic features missing from the model. The autocorrelation slowly decreases with distance on a megabase scale, which suggests that missing genomic features have relatively long periods. To relate this length scale to known genomic features, we compare with the autocorrelation functions of DNase hypersensitivity (Thurman et al., 2012); the histone modification h3k9me3 (ENCODE Project Consortium and others, 2012); replication timing (Chen et al., 2010); and XR-seq data that measures the activity of nucleotide excision repair (Hu et al., 2015) (Fig. 3C). DNase hypersensitivity shows the fastest decay rate, while replication timing displays the slowest decay rate. Of these, replication timing is included in the model. The similarity between the auto-correlation function of a feature and that of the observed-to-expected mutation ratio can be quantified using an auto-correlation distance. Although our list of features is far from exhaustive, XR-seq has an auto-correlation function most resembling that of the observed-to-expected mutation ratio (Supplementary Section S2 and Fig. S6). The unaccounted for genomic features will increase the overdispersion estimates. To instead explicitly capture the bias from these sources, we locally normalize our mutation rate predictions by the local bias between the observed and predicted mutation rates. We evaluate the local bias in windows within the length scales learned from the autocorrelation analyses described above. This leads to decreased overdispersion estimates and improved driver discovery power.

3.3 Ranking by the posterior mean is computationally advantageous

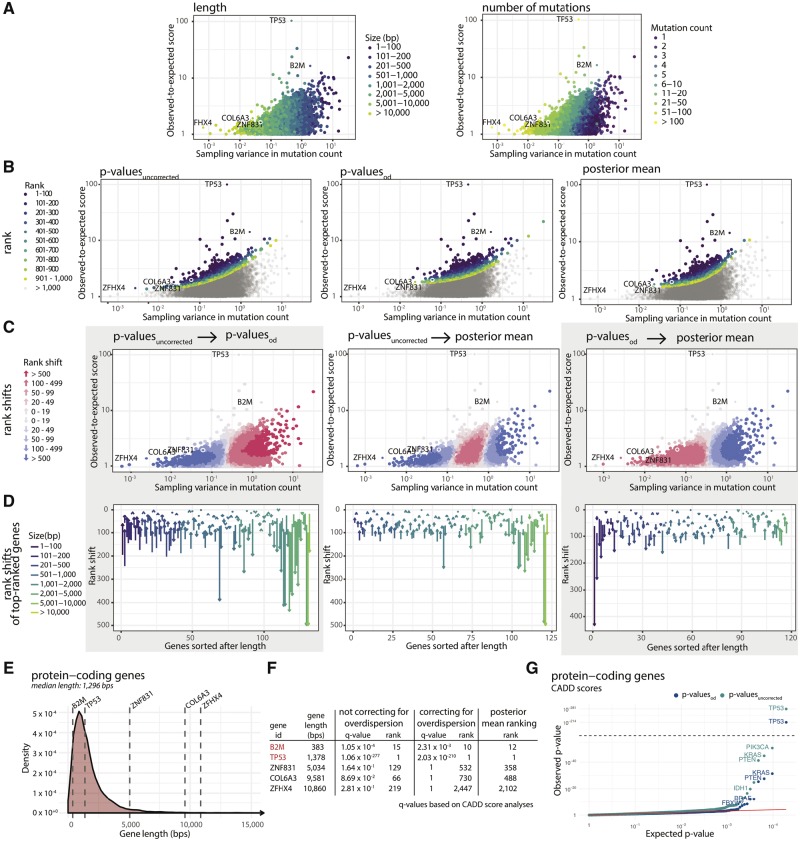
Besides from ranking elements according to their P-value, we here also rank elements according to their posterior mean (PM) estimate of the effect size. Ranking according to PM estimates as well as overdispersion-corrected P-values (henceforth referred to as $P{-\text{values}}_{\text{od}}$) put larger emphasis on effect size compared to ranking according to P-values obtained without correcting for overdispersion ($P{-\text{values}}_{\text{uncorrected}}$) (Fig. 4A–B).

Fig. 4.

Comparison of ranking methods. (A) We define the effect size as the ratio between the observed and expected score of functional impact, here CADD score. The effect size is plotted against the sampling variance of the effect size under the null-model. A high sampling variance means the outcome is uncertain and an extreme effect size is needed to achieve significance. The sampling variance decreases with region length and effect size increases with the number of mutations. (B) Points colored according to their rank under each of the three different ranking methods. Compared to $P{-\text{values}}_{\text{uncorrected}},\hspace{0.17em}P{-\text{values}}_{\text{od}}$ and posterior mean (PM) both put more emphasis on effect size compared to sampling variance. (C) Pairwise comparison of ranking methods. The shift in rank for all elements having a positive effect size. $P{-\text{values}}_{\text{od}}$ generally give higher ranks to short genes with moderate to large effect size. PM has a similar effect, but it does not give higher ranks to the shortest of genes. (D) Pairwise comparison of ranking methods for top-ranked genes. The shift in rank for all elements ranked in top-100 for either of two methods. Long genes are generally ranked much lower using $P{-\text{values}}_{\text{od}}$ and PM compared to $P{-\text{values}}_{\text{uncorrected}}$. (E) The lengths of five selected genes are highlighted in a density plot showing the length distribution of all protein-coding genes. (F) Re-ranking of individual elements of representative lengths when ranking according to $P{-\text{values}}_{\text{od}}$ and PM. The three long protein-coding genes ZFHX4, ZNF831 and COL6A3 all become less significant when taking overdispersion into account and are down-ranked by PM. The known short COSMIC CGC gene B2M is up-ranked with both overdispersion and posterior mean. G: CADD score-based QQplots of P-values for protein-coding genes obtained with and without overdispersion. QQplots for the remaining region types are shown in Supplementary Figure S2

PM ranking has the advantage of having a straightforward interpretation: Had the scores been 0–1 scores, e.g. indicating whether a mutation has occurred or not, PM will translate directly into an estimate of the relative increase/decrease of the mutation rate. One should maintain this mental picture when scores represent functional impact. Another advantage of PM is that is very fast to compute, as there is no need to evaluate or approximate the full null distribution for significance evaluation.

As expected, the ranking of elements changes when taking overdispersion into account ($P{-\text{values}}_{\text{od}}$) or ranking elements by PM. A modest increase in mutation rate can be explained by the random effect. This generally means that long genes with small effect sizes become less significant and are ranked lower (Fig. 4C–D). Similarly, short genes are ranked higher. Examples of long protein-coding genes that become less significant when accounting for overdispersion are ZFHX4 [10 860 base pairs (bps)], ZNF831 (5034 bps) and COL6A3 (9581 bps). None of these genes have substantial reported cancer driver potential. On the other hand, the rather short COSMIC CGC gene B2M is ranked higher when accounting for overdispersion (Fig. 4E–F).

Overall, there is a striking difference between the distribution of P-values obtained with and without the use of overdispersion: The QQplots of $P{-\text{values}}_{\text{uncorrected}}$ exhibit a substantial amount of inflation, which is effectively remedied by incorporating overdispersion in the significance evaluation of a candidate element (Fig. 4G, Supplementary Fig. S2).

Ranking elements by their posterior mean estimate of effect size is a simple alternative to the computationally expensive calculation of P-values. Calculation of the PM-ranks only requires an observed and expected score for each candidate element, as well as an overdispersion estimate. We have shown that the ranking of elements according to PM is similar to what is obtained with $P{-\text{values}}_{\text{od}}$. However, by ranking elements using P-values, it is straightforward to divide the final list into significant and non-significant elements. Using PM, such a differentiation is less clear.

One possible way to combine PM and P-value ranking is to use PM to make a preliminary ranking of the genes. Next the Benjamini-Hochberg step-up procedure can be applied to a set of top genes, where the P-value is computed. This limits the number of genes where the more time-consuming P-value computation is needed. As the PM ranking does not correspond perfectly to the P-value ranking and a P-value is not computed for every gene, this approach is conservative in that at least as many genes would have been called had we computed the P-value for all genes (Supplementary Section S3).

3.4 Modeling overdispersion improves driver detection specificity

We applied ncdDetect with overdispersion to the annotated protein-coding genes, splice sites, promoter elements and 5′ and 3′ UTRs defined in Juul et al. (2017) (Supplementary Tables S1–S3). We used a dataset consisting of 505 whole genomes, distributed across 14 different tumour types (Fredriksson et al., 2014). In the original version of ncdDetect, we used phyloP to signify mutational impact (Pollard et al., 2010). Here, we compare performance using both phyloP, LINSIGHT and CADD scores (Huang et al., 2017; Kircher et al., 2014). To establish significance, we first compute the overdispersion parameter for each type of score. Next for each region and each type of score, the observed score is computed and the significance is approximated using the method described in Section 2.3.

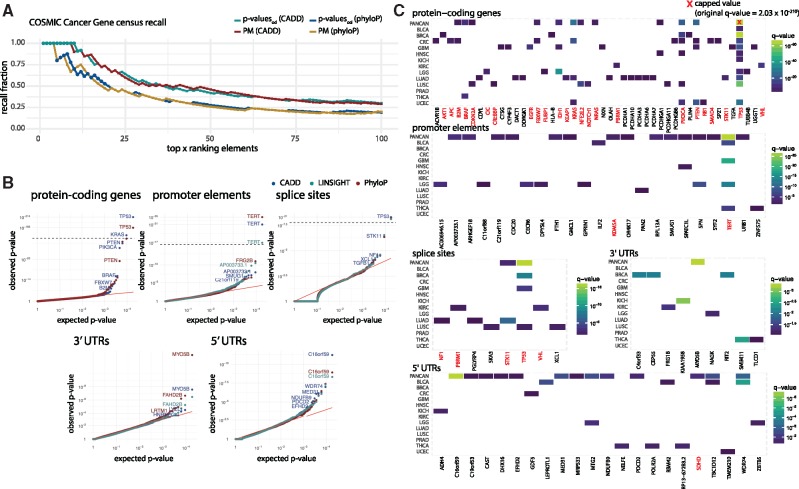
When comparing the fraction of COSMIC CGC genes among the top ranked candidates, the performance is similar whether elements are ranked according to $P{-\text{values}}_{\text{od}}$ or PM. Further, CADD-score based P-values have a COSMIC CGC recall rate superior to that of phyloP-score based P-values (Fig. 5A). As LINSIGHT scores are only available for non-coding genomic regions, we are not able to evaluate the performance of these on protein-coding genes. With CADD scores we identify 12 significant protein-coding genes, of which 11 are known COSMIC CGC cancer driver genes. With phyloP scores we identify 19 significant protein-coding genes, of which 10 are COSMIC CGC genes. The distribution of P-values does not change substantially between scoring schemes (Fig. 5B). Because of the superior performance of CADD scores on protein-coding genes, the following results are based on them. Since many of the mutations observed in melanoma samples are likely caused by mutational processes not captured by the background model, melanoma-specific results are not considered in the results section (Sabarinathan et al., 2016). These are instead included in Supplementary Figure S3. All P-values are corrected for multiple testing, and a false discovery rate of 0.1 is applied (Benjamini and Hochberg, 1995).

Fig. 5.

Performance of ncdDetect v.2 after correcting for overdispersion. (A) A comparison of the fraction of COSMIC CGC genes among top-ranked candidates. Results shown are obtained by ranking elements according to $P{-\text{values}}_{\text{od}}$ as well as PM, using both CADD and phyloP scores. For P-value based results, filled points denote significant elements (q < 0.10), while crosses denote insignificant elements (q $\ge$ 0.10). For PM-based results, there are no filled points due to the inability to determine significance in this setting. (B) QQplots of $P{-\text{values}}_{\text{od}}$ for each considered region type obtained with phyloP, CADD or LINSIGHT scores. Note that LINSIGHT scores are not available for protein-coding genes. (C) Cancer driver candidates identified with ncdDetect v.2 using CADD scores, after accounting for overdispersion. All elements with a colored tile have a q-value less than 0.10. Melanoma-specific results are shown in Supplementary Figure S3

Forty-six different protein-coding genes are significant in at least one specific cancer type (Fig. 5C). Of these 46 genes, 24 (52%) are COSMIC CGC genes. Among the analysed promoter elements, TERT is ranked the highest (q = $1.32\times {10}^{-27}$, PANCAN analysis). In total, we detect 15 significant promoter elements in the PANCAN analyses, of which seven (AP003733.1, ARHGEF18, CDC20, FTH1, RPL13A, SMUG1 and TERT) overlap with promoters identified in other non-coding cancer driver studies (Melton et al., 2015; Weinhold et al., 2014). Two of the ten significant promoter elements (TERT and KDM5A) are associated to COSMIC CGC genes. In the analyses of splice sites, we find two significant potential cancer drivers in the PANCAN set of samples, TP53 (q = $4.12\times {10}^{-17}$, PANCAN analysis) and STK11 (q = $3.73\times {10}^{-3}$, PANCAN analysis), both of which are COSMIC CGC genes and previously reported (Juul et al., 2017; Lee et al., 2010; Mularoni et al., 2016). Among the analysed 3′ UTRs, we find one significant hit in the PANCAN analyses, namely MYO5B (q = $4.94\times {10}^{-3}$, PANCAN analysis). With respect to 5′ UTRs, we detect 13 potential cancer driver candidates in the PANCAN analyses, of which five (DHX16, SDHD, WDR74, C16orf59 and MED31) have previously been reported in cancer driver detection studies (Weinhold et al., 2014), and of which one (SDHD) is a COSMIC CGC gene (Fig. 5C).

Naturally, cancer driver candidates need to be validated biologically or clinically to determine their true ability to drive cancer, however, such analyses are outside the scope of this work.

When comparing these results to those obtained with ncdDetect v.1, we see that modeling overdispersion improves the driver detection specificity. An application of ncdDetect on simulated data shows that the number of false positives detected increases with the amount of overdispersion. As the amount of overdispersion decreases, the ability of ncdDetect to recall true positives improves (Supplementary Section S6).

3.5 Comparison to existing driver detection tools

Benchmark studies of ncdDetect against other driver detection methods are crucial to determine its usability and performance. However, benchmark analyses of non-coding cancer driver detection methods are challenged by a limited amount of published systematic non-coding cancer driver screens. Besides from the recurrently mutated promoter region of the TERT gene (Horn et al., 2013; Huang et al., 2013), neither putative lists of true-positive non-coding cancer driver elements, nor bona fide sets of true-negatives exist. Because of this, the results of ncdDetect on protein-coding genes are taken as proxy of its performance. Here, we apply the COSMIC CGC (Forbes et al., 2015) as a true-positive set of protein-coding cancer driver genes. However, non-coding driver detection methods do not exploit our understanding of translation and splicing, as it does not generalize to non-coding regulatory regions. Methods tailored for protein-coding genes are therefore better powered in these regions and are generally expected to outperform non-coding driver detection methods. For promoter elements, the results were compared to previously described candidates in the literature.

The published ExInAtor PANCAN results on protein-coding genes, using the same 505 whole genome cancer samples as those analysed here, show three significant genes (q < 0.10), of which one is a COSMIC CGC gene. In contrast, ncdDetect finds 11 out of 12 significant genes in the COSMIC CGC set, as described above. ncdDetect further has a higher COSMIC CGC recall rate compared to ExInAtor (Supplementary Fig. S4). Top-50 candidates for ncdDetect and ExInAtor for all cancer-specific cohorts are presented in Supplementary Table S5.

For promoter elements, LARVA and ncdDetect both call the three candidates TERT, AP003733.1 and RPL13A significant (q < 0.10) (Supplementary Table S6). Several of the candidates solely detected by ncdDetect have previously been reported by other non-coding cancer driver screens (Supplementary Fig. S5) (Melton et al., 2015; Weinhold et al., 2014).

We further applied ncdDetect to 560 breast cancer samples (Nik-Zainal et al., 2016) (Supplementary Table S4). Across these samples, we call two promoter elements significant (q < 0.10) (ZNF143 and CCDC107). ZNF143 was recently reported to contribute to the development of breast cancer (Paek et al., 2017), and both of these promoter elements were detected to harbour a significant number of mutations in another recently published breast cancer driver screen (Rheinbay et al., 2017). Regarding splice sites, we call two elements significant (TP53 and CBFB), both detected in the original study of these data (Nik-Zainal et al., 2016). We call three 5′ UTR regions significant (TBC1D12, LEPROTL1 and AC006455.1). Notably, the promoters of both TBC1D12 and LEPROTL1 were recently detected in a driver screen of breast cancer samples (Rheinbay et al., 2017). In the analysis of protein-coding genes, we call 17 genes significant, of which 12 are known COSMIC CGC genes (TP53, PIK3CA, PTEN, AKT1, CBFB, MAP2K4, GATA3, RB1, SF3B1, CDH1, MAP3K1 and FOXA1) and five are not (DAZAP1, LRRC2, DLL4, GIGYF2 and LAMA2). The analysis of these 560 breast cancer samples emphasizes that ncdDetect is able to call elements with a relatively high degree of specificity, but also that the sensitivity is lower than that reported in the original analysis of these data (93 significant genes of which 78 are COSMIC CGC genes). However, the discrepancy may be explained by their use of a driver discovery method tailored for protein-coding regions, which thus accounts for the impact of missense, nonsense and splice-site mutations.

4 Discussion

It is not possible to identify and include all relevant genomic features when modeling the mutation rate in cancer genomes. Consequently, the observed variation cannot be captured by regression models unless they include overdispersion in some form. Here, we capture as much of the mutation rate variation as practically possible in the background mutation rate model, and then account for the unavoidable remaining amount of overdispersion. We have estimated the amount of overdispersion arising from our position-specific model of the mutation rate in cancer genomes. As a first step towards characterizing genomic features missing from the background model, we analysed the autocorrelation structure of the observed-to-expected mutation pattern. We found that the autocorrelation declined slowly, suggesting that at least some of the missing genomic features operate on a rather long length scale of a few megabases.

Not accounting for overdispersion has previously led to a substantial amount of false positives in cancer driver detection analyses (Juul et al., 2017; Lawrence et al., 2013; Lochovsky et al., 2015), and, indeed, we observe this trend in the simulation study of the effects of overdispersion (Supplementary Section S6). By adjusting for overdispersion in the significance evaluation of candidate cancer driver elements, we here obtained great specificity improvements of our driver detection results compared to those obtained with ncdDetect v.1. Using CADD scores, 12 protein-coding genes were called significant by ncdDetect, of which 11 were known COSMIC CGC cancer driver genes.

Overdispersion captures the amount of deviation between the predicted and the actual mutation rate in a region. These deviations can be on a sample, cancer-type or pan-cancer level. Deviations that are specific to a sample will cancel out when accumulating the mutation load across many samples, contrastingly deviations shared among all cancers will remain even as we accumulate many samples. Thus we observe that the estimated overdispersion decreases as we include more samples, but does not asymptote to zero (Supplementary Section S4).

It is an interesting line of study whether a fraction of the sample or cancer type-specific deviations may be caused by mutational processes or potentially even selection pressures. Despite the complex sample level properties of the actual mutation rate, the distributional assumptions of the mutation load accumulated across samples remain valid.

We furthermore found that ranking elements by the posterior mean of their effect sizes performed similarly to ranking elements according to their overdispersion-corrected P-values. While this alternative ranking scheme is less computationally costly than computing P-values, it does not define an explicit significance threshold. To overcome this, posterior mean ranking could be coupled with calculating P-values for top-ranked elements. PM ranking can be used to find top genes for which the P-value is computed. The Benjamini-Hochberg step-up procedure for controlling the false discovery rate can be applied to this subset of genes for which the P-value is known. We show that this approach is conservative, i.e. the genes that are called significant would also have been declared significant had we computed all the P-values.

Our efforts to model the background mutation rate more accurately, has led to higher specificity in our cancer driver detection results. Still our method will continue to benefit from a more accurate model of the mutation rate. This will lead to an improved trade-off between the sensitivity and specificity of the results, as more variation is accounted for directly by the mutation rate model rather than by overdispersion. For example, it could prove beneficial to add additional genomic features describing mutational processes that act in specific regions in relation to melanoma (Sabarinathan et al., 2016). While we consider such efforts to be outside the scope of this study, it is a worthy long-term goal to further understand the mutational processes in cancer and identify additional genomic features to include as explanatory variables in the background model.