Linking spherical mean diffusion weighted signal with intra-axonal volume fraction

Abstract

Diffusion MRI has been widely used to assess brain tissue microstructure. However, the conventional diffusion tensor imaging (DTI) is inadequate for characterizing fiber direction or fiber density in voxels with crossing fibers in brain white matter. The constrained spherical deconvolution (CSD) technique has been proposed to measure the complex fiber orientation distribution (FOD) using a single high b-value (b ≥ 3000 s/mm²) to derive the intra-axonal volume fraction (V_in) from the calculated FOD. Recently, the spherical mean technique (SMT) was developed to fit V_in directly from a multi-compartment model with multi-shell b-values. Although different numbers of b-values are needed in the two techniques, both methods have been suggested to be related to the spherical mean diffusion weighted signal $(\overline{\mathrm{S}})$. The current study compared the two techniques on the same high-quality Human Connectome Project diffusion data and investigated the relation between $\overline{\mathrm{S}}$ and V_in systematically. At high b-values (b ≥ 3000 s/mm²), $\overline{\mathrm{S}}$ is linearly related to V_in, and $\overline{\mathrm{S}}$ provides similar contrast with V_in in white matter. At low b-values (b ~ 1000 s/mm²), the linear relation between $\overline{\mathrm{S}}$ and V_in is sensitive to the variations of intrinsic diffusivity. These results demonstrate that $\overline{\mathrm{S}}$ measured with the typical b-value of 1000 s/mm² is not an indicator of V_in, and previous DTI studies acquired with b = 1000 s/mm² cannot be re-analyzed to provide V_in-weighted contrast.

Introduction

Diffusion MRI is a valuable tool to study brain tissue microstructure (e.g. fiber direction, fiber density and fiber size) non-invasively. The conventional diffusion tensor image (DTI) model has been widely used to provide quantitative measurements of diffusivity, fractional anisotropy (FA), and direction for water diffusion in white matter [1,2]. The value of FA is strongly affected by radial diffusivity (RD) perpendicular to the main fiber direction which, in turn, is dominated by water diffusion in the extra-axonal space. For example, demyelination and axon loss in white matter injuries result in increased RD and decreased FA [3]. Thus, a higher value of FA is linked with higher fiber density, and FA has been used as a biomarker of white matter integrity [4]. However, the conventional DTI model cannot describe situations with fiber crossings and orientation dispersion appropriately, which are common in brain white matter [5,6]. For this reason, the interpretation of FA as white matter integrity has been questioned [7]. Moreover, it was recently observed that the crossing fiber problem cannot be solved by simply increasing spatial resolution [6].

A number of methods have been proposed to better describe the diffusion weighted signals and estimate fiber orientations from high angular resolution diffusion imaging. These methods include ball-stick model [8–10], Q-ball imaging [11], diffusion spectrum imaging [12], and spherical deconvolution [13,14] among others. Typically, the fiber orientation distribution (FOD) or the orientation density function (ODF) is derived to model the distribution of axonal fiber orientations in each voxel. Numerical simulations suggested that FOD amplitude computed using spherical deconvolution would be proportional to the intra-axonal volume occupied by fibers along the corresponding fiber orientation [15]. The term apparent fiber density (AFD), as a measure of FOD amplitude, was proposed to be an indicator of intra-axonal volume fraction of axons in a given direction [15]. The total AFD (AFD_total), which is the integral of FOD over all directions, is in turn proportional to the intra-axonal volume fraction of all axons within a voxel (V_in) [15–17]. Note that the surface integral of FOD is also linearly related to the spherical mean diffusion weighted signal averaged over all gradient directions $(\overline{\mathrm{S}})$ [14], which means the intra-axonal volume fraction can be linked with the spherical mean diffusion weighted signal ( V_in ⇔AFD_total ⇔FOD⇔ $\overline{\mathrm{S}}$ ) [15]. Recent analytical work derived that ${\text{V}}_{\text{in}}=2\cdot \sqrt{\frac{b\lambda }{\pi }}\cdot \frac{\overline{\mathrm{S}}}{{\text{S}}_0}$ if the diffusion weighting b-value is sufficiently large, where λ is the intrinsic diffusivity and S₀ is the signal for b = 0 [18].

Another diffusion-based approach to estimate V_in is multi-compartment modeling. Various methods have been developed to estimate V_in and/or axon diameter [19–26]. Briefly, the diffusion signals are expressed analytically to be from a simplified two- or three-compartment model covering intra- and extra-axonal spaces, and then the measured signals are fit to the analytical model with different degrees of diffusion weighting (diffusion time, b-value, and gradient direction). A single fiber direction or a fixed fiber orientation distribution is usually assumed for simplicity. The more complex the orientation distribution the more parameters in the model [26]. Instead of fitting the raw signal at each gradient direction, the spherical mean technique (SMT) was proposed to focus on the direction-averaged diffusion weighted signal, which is independent of the fiber orientation distribution [27]. Hence, the SMT-based V_in estimation is not affected by the crossing fiber problem [28]. More recently, the rotationally invariant framework was generalized to the higher-order spherical harmonics [29–31].

Given the substantial advantage of $\overline{\text{S}}$ in estimating white matter intra-axonal volume fraction, in the current study we used high-quality Human Connectome Project diffusion data to investigate systematically the effect of b-value on the relation between $\overline{\text{S}}$ and V_in, at both low and high b-values. In addition, CSD-based AFD_total and SMT-based V_in were estimated and compared on the same data. Only white matter was considered in the current study.

Materials and methods

Theory

Following the widely used two-compartment model of intra- and extra-axonal spaces, the diffusion weighted signals of white matter can be expressed as

$$S(b,\theta ,\phi )=S_0\cdot \left[V_{in}\cdot S_n^{in}+\left(1-V_{in}\right)\cdot S_n^{ex}\right]$$ (1)

where θ and φ are the polar angle and azimuthal angle of gradient direction in spherical coordinates, and ${\mathrm{S}}_{\mathrm{n}}^{\text{in}}$ and ${\text{S}}_{\text{n}}^{\text{ex}}$ are the normalized signal attenuations per volume from the intra- and extra-axonal spaces, respectively. Note that T₂ difference between intra- and extra-axonal spaces is not considered, and thus, V_in is T₂-weighted intra-axonal volume fraction. Since the myelin contribution is completely ignored, the term intra-axonal water fraction may be a better terminology [32].

Axons are modeled as cylinders with axial diffusivity equal to the intrinsic diffusivity $({\lambda }_{\Vert }^{\text{in}}=\lambda )$. Due to the small axon size (~ 1 μm) in brain white matter [33] and relatively long diffusion time on human scanner [34], the intra-axonal radial diffusivity is reasonably assumed to be 0 $\left({\lambda }_{\perp }^{\text{in}}=0\right)$. To minimize the number of unknown parameters in the system, the extra-axonal water diffusion is modeled as a rotationally symmetric tensor [28] with axial diffusivity ${\lambda }_{\Vert }^{\text{ex}}=\lambda$ and radial diffusivity ${\lambda }_{\perp }^{\text{ex}}=\left(1-{\text{V}}_{\text{in}}\right)\cdot \lambda$, which is based on the first-order tortuosity approximation for a system of randomly placed parallel cylinders [35]. As demonstrated previously [14,27–29,31], the spherical mean diffusion weighted signal is independent of the complex fiber orientation distribution, and it can be expressed as

$$\begin{gathered} \overline{S}(b)=S_0\cdot [V_{in}\cdot {\overline{S}}_n^{in}+\left(1-V_{in}\right)\cdot {\overline{S}}_n^{ex}] \\ {\overline{S}}_n^{in}=\frac{\sqrt{\pi }\cdot \mathrm{erf}(\sqrt{b\lambda })}{2\sqrt{b\lambda }} \\ {\overline{S}}_n^{ex}=\frac{\sqrt{\pi }\cdot \mathrm{erf}\left(\sqrt{b\lambda V_{in}}\right)}{2\sqrt{b\lambda V_{in}}}\cdot \exp \left(-b\lambda \left(1-V_{in}\right)\right) \end{gathered}$$ (2)

where erf is the error function. The contribution of the extra-axonal water to the total mean signal can be neglected with sufficiently large b-values. In that case, Eq. (2) can be simplified to [18]

$$\overline{S}(b)=S_0\cdot V_{in}\cdot \frac{\sqrt{\pi }}{2\sqrt{b\lambda }}$$ (3)

According to Eq. (2), SMT-based V_in and λ can be fit directly from the spherical mean signal decay as a function of b-value. And according to Eq. (3), if λ is known or assumed to be constant, V_in or V_in-weighted contrast can be derived from the normalized mean signal $\left({\overline{\text{S}}}_{{}_{\text{n}}}=\overline{\text{S}}/{\text{S}}_0\right)$ at a single high b-value.

CSD-based AFD_total is computed from spherical deconvolution [13,14], where the diffusion weighted signals are expressed as the convolution of fiber FOD (P(θ, φ)) and the single fiber response function (R(b, θ)).

$$S(b,\theta ,\phi )=P(\theta ,\phi )\otimes R(b,\theta )$$ (4)

$$S(b,\theta ,\phi )=\sum _{l=0}^{\infty }\sum _{m=-l}^l{s}_{lm}{Y}_{lm}(\theta ,\phi )\text{and}P(\theta ,\phi )=\sum _{l=0}^{\infty }\sum _{m=-l}^l{p}_{lm}{Y}_{lm}(\theta ,\phi )$$ (5)

$$R(b,\theta )=S_0\cdot e^{-b\lambda {\cos }^2\theta }$$ (6)

$$AF{D}_{total}={\int }_0^{2\pi }{\int }_0^{\pi }P(\theta ,\phi )\sin \theta d\theta d\phi =\sqrt{4\pi }\cdot p_{00}=\frac{\overline{S}(b)}{S_0}\cdot \frac{2\sqrt{b\lambda }}{\sqrt{\pi }\cdot \mathrm{erf}(\sqrt{b\lambda })}$$ (7)

Details of the last equality in Eq. (7) can be found elsewhere [14]. It is evident from Eqs. (2) and (7) that AFD_total is equivalent to ${\overline{\text{S}}}_{{}_{\text{n}}}/{\overline{\text{S}}}_{{}_{\text{n}}}^{{}_{\text{in}}}$. Furthermore, AFD_total is equal to V_in when the diffusion weighting b-value is sufficiently large. Practically, AFD_total or the fiber FOD can be estimated from either single-shell single-tissue constrained spherical deconvolution (SSST-CSD) [15,36] or multi-shell multi-tissue constrained spherical deconvolution (MSMT-CSD) [37,38]. To differentiate the two situations, AFD_total computed from SS-CSD will be referred to as ${\text{AFD}}_{\text{total}}^{\text{ss}}$, and ${\text{AFD}}_{\text{total}}^{\text{ms}}$ for MSMT-CSD.

Data acquisition

High-quality data from 35 healthy adults, referred to as the MGH-USC Adult Diffusion Dataset of the Human Connectome Project (HCP), were downloaded from ConnectomeDB (http://db.humanconnectome.org). Data were acquired on a 3T CONNECTOM scanner with a custom-made 64-channel head coil. The scanner maximum gradient strength is 300 mT/m. T₁-weighted images were acquired with a Multi-Echo Magnetization Prepared Rapid Acquisition Gradient Echo (MEMPRAGE) sequence at 1mm isotropic resolution. Diffusion data were acquired with 4 different b-values (i.e., 4 shells): 1000 s/mm² (64 directions), 3000 s/mm² (64 directions), 5000 s/mm² (128 directions), and 10,000 s/mm² (256 directions). One non-diffusion weighted b = 0 image was collected for every 13 diffusion weighted images. Other diffusion imaging parameters were: repetition time (TR) = 8800 ms, echo time (TE) = 57 ms, gradient duration (δ) = 12.9 ms, gradient separation (Δ) = 21.8 ms, image resolution = 1.5×1.5×1.5 mm³, parallel imaging acceleration factor = 3, and multiband factor = 1. The signal-to-noise ratio (SNR) was about 18.5 for white matter in b=0 image, which was calculated from the first 21 b = 0 images using a maximum-likelihood approach [39]. Images with b = 10,000 s/mm² were not used in the current study due to the low SNRs in these images. Among the 35 subjects in the dataset, there were slight residual parallel imaging aliasing artifacts on b = 0 images in most subjects. Thus, seven subjects with minimal residual aliasing artifacts were selected for current study.

Data analysis

As downloaded, the data were preprocessed with corrections for gradient nonlinearity distortions, head motion, and eddy current artifacts [40]. In addition, we corrected for spatial intensity inhomogeneity artifacts [41,42] with MRtrix [43]. Subsequently, the bias field corrected 21 b = 0, 64 b = 1000 s/mm², 64 b = 3000 s/mm², and 128 b = 5000 s/mm² images were used for the following data analyses. DTI: FA, RD and axial diffusivity (AD) were estimated using iteratively reweighted linear least squares estimator in MRtrix. DTI was performed with b ≤ 1000 s/mm². $\underset{\_}{{\text{AFD}}_{\text{total}}^{\text{ms}}}$: T₁-weighted image was linearly co-registered to the corresponding b = 0 image and then segmented to gray matter, white matter, and cerebrospinal fluid using FSL [41,42]. The response functions for the three tissue types were estimated based on distinct b-value dependence for each tissue type [37]. Note that the experimentally estimated response function may depart from Eq. (6). Multi-component FODs were calculated using MSMT-CSD [37], and ${\text{AFD}}_{\text{total}}^{\text{ms}}$ was estimated by the FOD of the white matter-like component. Track Density Imaging (TDI): anatomically-constrained tractography (ACT) [44] was performed with the FOD of the white matter-like component generating 100 million streamlines, which were subsequently filtered to 10 million using the spherical-deconvolution informed filtering of tractograms (SIFT) method [45]. SIFT reduces the number of streamlines, but provides more biologically meaningful results consistent with the underlying FOD [16]. The TDI map [46] was calculated as the number of streamlines after SIFT in each voxel. $\underset{\_}{{\text{AFD}}_{\text{total}}^{\text{ss}}}:{\text{AFD}}_{\text{total}}^{\text{ss}}$ was estimated with b = 5000 s/mm² only. The response function was computed using the iterative single fiber selection algorithm [47]. SSST-CSD was used for FOD estimation [36], and ${\text{AFD}}_{\text{total}}^{\text{ss}}$ was calculated from the l = 0 term of the FOD following Eq. (7). The analysis of DTI, ${\text{AFD}}_{\text{total}}^{\text{ms}}$, TDI after SIFT, and ${\text{AFD}}_{\text{total}}^{\text{ss}}$ were carried out in MRtrix. SMT: V_in and λ were fit using the SMT software with default settings (https://ekaden.github.io). All other analyses (e.g. Pearson correlation, linear fitting, and statistics) were performed in MATLAB (Mathworks, Natick, MA, USA). Statistical results are given as mean ± standard deviation (n = 7) where applicable.

Results

Figure 1 shows the numerically calculated values of ${\overline{\text{S}}}_{{}_{\text{n}}}$ and ${\overline{\text{S}}}_{{}_{\text{n}}}/{\overline{\text{S}}}_{{}_{\text{n}}}^{{}_{\text{in}}}$ as a function of V_in based on Eq. (2) for water diffusion at typical λ and b-values (1 ≤ λ ≤ 3 μm²/ms and 1000 ≤ b ≤ 5000 s/mm²). It is evident that ${\overline{\text{S}}}_{{}_{\text{n}}}$ can be well described as a linear function of V_in. The solid line represents the linear fitting at each b-value. The slope of ${\overline{\text{S}}}_{{}_{\text{n}}}/{\overline{\text{S}}}_{{}_{\text{n}}}^{{}_{\text{in}}}$ vs. V_in is close to 1 and the intercept is close to 0 when bλ ≥ 5, suggesting that the extra-axonal contribution can be neglected when bλ ≥ 5. At low b-value of 1000 s/mm², ${\overline{\text{S}}}_{{}_{\text{n}}}/{\overline{\text{S}}}_{{}_{\text{n}}}^{{}_{\text{in}}}$ or ${\overline{\text{S}}}_{{}_{\text{n}}}$ is still linearly correlated with V_in.

Figure 1.

Numerical values of ${\overline{\text{S}}}_{{}_{\text{n}}}$ and ${\overline{\text{S}}}_{{}_{\text{n}}}/{\overline{\text{S}}}_{{}_{\text{n}}}^{{}_{\text{in}}}$ as a function of V_in based on Eq. (2). The markers represent the calculated values, and the solid lines represent the corresponding linear fittings. The dashed line is identity line (y = x).

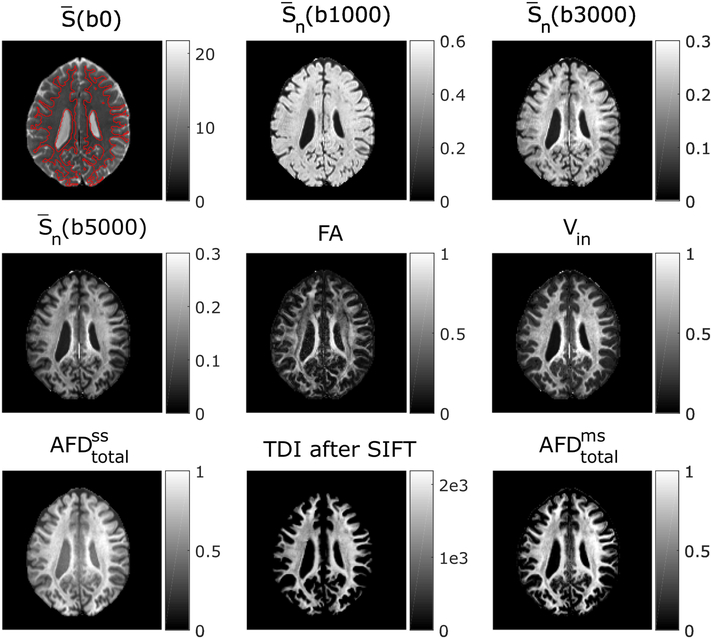
Figure 2 shows the various maps acquired from a representative subject. The white matter was segmented from T₁-weighted MEMPRAGE image and overlaid on b = 0 image. The threshold was set to 0.9 for white matter partial volume. With the increase of b-value, gray matter signal decays faster [48] and ${\overline{\text{S}}}_{{}_{\text{n}}}$ shows better gray matter-white matter contrast. V_in, ${\text{AFD}}_{\text{total}}^{\text{ss}},$ and ${\text{AFD}}_{\text{total}}^{\text{ms}}$ have more homogeneous contrasts in white matter than FA.

Figure 2.

Various maps acquired from a representative subject. The white matter region is outlined in red on b = 0 image.

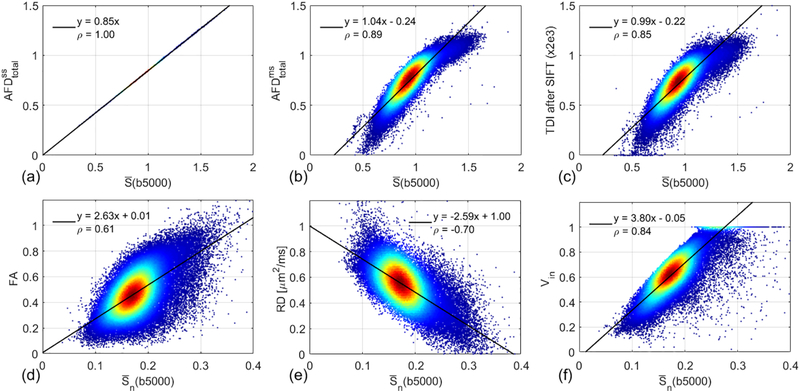
Based on Eq. (3) and Figure 1, the mean signal at b = 5000 s/mm² is linearly related to the intra-axonal volume fraction, and thus, can be regarded as a reasonable indicator of V_in. Figure 3 shows the correlations between diffusion metrics and the mean signal at b = 5000 s/mm². Note that FA, RD, and V_in were derived from the normalized signal attenuations (S_n), which were insensitive to the effects of T₂ variations and RF inhomogeneity. However, ${\text{AFD}}_{\text{total}}^{\text{ss}}$, ${\text{AFD}}_{\text{total}}^{\text{ms}}$, and TDI after SIFT were based on the raw diffusion weighted signals without voxel-wise b = 0 normalization following previous CSD-based studies [15,37,45]. Thus, ${\text{AFD}}_{\text{total}}^{\text{ss}},{\text{AFD}}_{\text{total}}^{\text{ms}}$, and TDI after SIFT were compared with $\overline{\text{S}}(\text{b}5000)$, while FA, RD, and V_in were compared with ${\overline{\text{S}}}_{{}_{\text{n}}}(\text{b}5000)$. The density scatter plot is from all the white matter voxels of the same subject shown in Figure 2. Red denotes higher density of points, and blue denotes lower density. The solid line indicates the result of linear least squares fitting. Pearson’s linear correlation coefficient (ρ) is also provided for each subplot. The statistical results of ρ for all seven subjects are summarized in Table 1. Consistent with Eq. (7), the correlation coefficient between ${\text{AFD}}_{\text{total}}^{\text{ss}}$ and $\overline{\text{S}}(\text{b}5000)$ is 1, which means that ${\text{AFD}}_{\text{total}}^{\text{ss}}$ and $\overline{\text{S}}(\text{b}5000)$ provide the same contrast. At high b-value of 5000 s/mm², the contrast is the intra-axonal volume fraction. ${\text{AFD}}_{\text{total}}^{\text{ms}}$ was calculated with multi-shell b-values, here 1000, 3000 and 5000 s/mm², and the correlation coefficient between ${\text{AFD}}_{\text{total}}^{\text{ms}}$ and $\overline{\text{S}}(\text{b}5000)$ is slightly less than 1 (ρ = 0.91 ± 0.02). The correlation between TDI after SIFT and $\overline{\text{S}}(\text{b}5000)$ is also high (ρ = 0.86 ± 0.02). As expected, FA has a weak correlation with ${\overline{\text{S}}}_{{}_{\mathrm{n}}}(\text{b}5000)$ (ρ = 0.65 ± 0.03). RD shows a negative correlation with ${\overline{\text{S}}}_{{}_{\mathrm{n}}}(\text{b}5000)$ (ρ = −0.70 ± 0.02). The correlation coefficient between V_in and ${\overline{\text{S}}}_{{}_{\mathrm{n}}}(\text{b}5000)$ is high (ρ = 0.85 ± 0.03).

Figure 3.

Density scatter plots and Pearson correlations between diffusion metrics and the mean signal at b = 5000 s/mm² using all the white matter voxels of the same subject shown in Figure 2. Red denotes higher density of points, and blue denotes lower density. The solid line indicates the result of linear least squares fitting.

Table 1.

Summary of Pearson’s linear correlation coefficients shown in Figure 3.

ρ	${\mathbf{AFD}}_{\mathbf{total}}^{\mathbf{ss}}$	${\mathbf{AFD}}_{\mathbf{total}}^{\mathbf{ms}}$	TDI after SIFT	FA	RD	Vin
$\overline{\mathrm{S}}$(b5000)	1.00 ± 0.00	0.91 ± 0.02	0.86 ± 0.02	−−−−−	−−−−−	−−−−−
${\overline{\mathrm{S}}}_{\mathrm{n}}$(b5000)	−−−−−	−−−−−	−−−−−	0.65 ± 0.03	−0.70 ± 0.02	0.85 ± 0.03

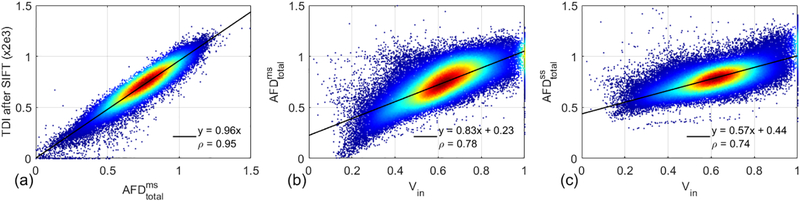
Figure 4 (a) and Table 2 show the strong correlation between TDI after SIFT and ${\text{AFD}}_{\text{total}}^{\text{ms}}$ (ρ = 0.95 ± 0.01). The correlations between AFD_total and V_in are shown in Figure 4 (b-c) and Table 2. The correlation coefficient between ${\text{AFD}}_{\text{total}}^{\text{ss}}$ and V_in (ρ = 0.69 ± 0.08) is slightly lower than that between ${\text{AFD}}_{\text{total}}^{\text{ms}}$ and V_in (ρ = 0.74 ± 0.05).

Figure 4.

Density scatter plots and Pearson correlations between TDI after SIFT and ${\text{AFD}}_{\text{total}}^{\text{ms}}$ (a), ${\text{AFD}}_{\text{total}}^{\text{ms}}$ and V_in (b), ${\mathrm{AFD}}_{\text{total}}^{\text{ss}}$ and V_in (c) using all the white matter voxels of the same subject shown in Figure 2. Red denotes higher density of points, and blue denotes lower density. The solid line indicates the result of linear least squares fitting.

Table 2.

Summary of Pearson’s linear correlation coefficients shown in Figure 4.

ρ	${\mathbf{AFD}}_{\mathbf{total}}^{\mathbf{ms}}$	${\mathbf{AFD}}_{\mathbf{total}}^{\mathbf{ss}}$
TDI after SIFT	0.95 ± 0.01	−−−−−
Vin	0.74 ± 0.05	0.69 ± 0.08

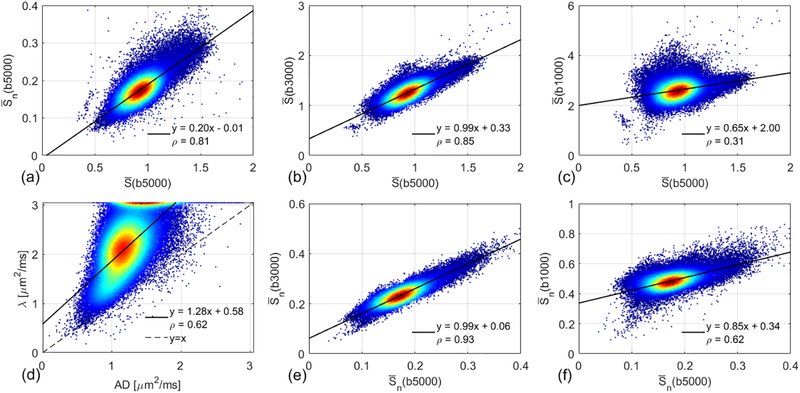
Figure 5 and Table 3 show the correlations between the mean signals at different b-values. The correlation coefficient between $\overline{\text{S}}(\text{b}5000)$ and ${\overline{\text{S}}}_{{}_{\mathrm{n}}}(\text{b}5000)$ is less than 1 (ρ = 0.78 ± 0.04), due to the varied S₀ over the white matter regions. The correlation coefficient between ${\overline{\text{S}}}_{{}_{\mathrm{n}}}(\text{b3}000)$ and ${\overline{\text{S}}}_{{}_{\mathrm{n}}}(\text{b}5000)$ (ρ = 0.93 ± 0.01) is higher than that between $\overline{\text{S}}(\text{b}3000)$ and $\overline{\text{S}}(\text{b}5000)$ (ρ = 0.85 ± 0.02). The correlation between ${\overline{\text{S}}}_{{}_{\mathrm{n}}}(\text{b}1000)$ and ${\overline{\text{S}}}_{{}_{\mathrm{n}}}(\text{b}5000)$ is weak (ρ = 0.57 ± 0.09), and there is little correlation between $\overline{\text{S}}(\text{b}1000)$ and $\overline{\text{S}}(\text{b5}000)$ (ρ = 0.29 ± 0.07). As expected, the fitted λ is larger than AD.

Figure 5.

Density scatter plots and Pearson correlations between the mean signals at different b-values using all the white matter voxels of the same subject shown in Figure 2. Red denotes higher density of points, and blue denotes lower density. The solid line indicates the result of linear least squares fitting. The dashed line in (d) is identity line (y = x).

Table 3.

Summary of Pearson’s linear correlation coefficients shown in Figure 5.

ρ	${\overline{\mathbf{S}}}_{\mathbf{n}}$(b5000)	$\overline{\mathbf{S}}$(b3000)	$\overline{\mathbf{S}}$(b1000)	λ	${\overline{\mathbf{S}}}_{\mathbf{n}}$(b3000)	${\overline{\mathbf{S}}}_{\mathbf{n}}$(b1000)
$\overline{\mathrm{S}}$(b5000)	0.78 ± 0.04	0.85 ± 0.02	0.29 ± 0.07	−−−−−	−−−−−	−−−−−
${\overline{\mathrm{S}}}_{\mathrm{n}}$ (b5000)	−−−−−	−−−−−	−−−−−	−−−−−	0.93 ± 0.01	0.57 ± 0.09
AD	−−−−−	−−−−−	−−−−−	0.62 ± 0.04	−−−−−	−−−−−

Discussion

The CSD-based AFD_total technique was proposed to estimate the complex FOD using spherical deconvolution and calculate the intra-axonal volume fraction from the estimated FOD [15]. The SMT-based V_in technique was developed to model the spherical mean diffusion weighted signals independent of the confounding FOD and fit the intra-axonal volume fraction directly [28]. Both techniques are related to the spherical mean diffusion weighted signal, and the intra-axonal volume fraction (V_in) is linked with the spherical mean diffusion weighted signal $(\overline{\text{S}})$ directly [18]. The current study compared the two techniques and investigated the relation between V_in and $\overline{\text{S}}$ systematically at different b-values. At high b-values (b ≥ 3000 s/mm²), $\overline{\text{S}}$ is linearly related to V_in, and $\overline{\text{S}}$ provides similar contrast with V_in in white matter. However, at low b-values (b ~ 1000 s/mm²), the linear relation between $\overline{\text{S}}$ and V_in is sensitive to the variations of λ, and $\overline{\text{S}}$ cannot be used as an indicator of V_in.

To the best of our knowledge, our work is the first to compare CSD-based AFD_total and SMT-based V_in. CSD is mainly for fiber tractography and SMT is one of the tissue modeling methods. As mentioned in a recent AFD_total study [16], the comparison of the tissue modeling methods and the CSD-based methods for measuring V_in remains to be determined. However, without a gold standard, the direct comparison of CSD and SMT may not provide any clear information. Based on previous analytical works, we can link the two methods mathematically. Both methods suggest that the spherical mean signal measured at a high b-value (b ≥ 3000 s/mm²) can be regarded as a reasonable indicator of white matter V_in. Then CSD-based AFD_total and SMT-based V_in were compared indirectly through the spherical mean signal. Our study may help better interpret AFD_total results at different b-values, and it can assist with protocol optimization for future SMT-based studies.

Data

Data analyses were performed on the high-quality MGH-USC Adult Diffusion Dataset of the Human Connectome Project. The high resolution, high b-value diffusion data are beyond what can be obtained on current clinical scanners. It should be noted that slight residual parallel imaging aliasing artifacts existed on b = 0 images of most subjects. They were noticeable on the ${\overline{\text{S}}}_{{}_{\text{n}}}(\text{b}1000)$ images. Seven subjects with minimal residual aliasing artifacts were selected for current study. Susceptibility induced image distortions were not considered as they were not significant in most of the brain. The existing susceptibility distortions affected the accuracy of the anatomically-constrained whole brain tractography since it relied on the undistorted T₁-weighted structural image for tissue segmentation. All the tractography-based connectivity studies would then be compromised. However, it is not expected to affect the voxel-wise correlation between TDI after SIFT and ${\text{AFD}}_{\text{total}}^{\text{ms}}$, because the voxel-wise values of TDI after SIFT were mainly dominated by local FODs rather than tractography [45]. Images with b = 10,000 s/mm² were excluded in this study due to the significant Rician bias associated with low-SNR magnitude data [49]. As demonstrated recently, complex diffusion data could be used to extract real-valued diffusion data without Rican bias [50].

AFD_total

In the original AFD work [15], the authors employed computer simulations to support the use of AFD as a quantitative measure of V_in. By combining two spherical deconvolution techniques [13,14], we describe AFD_total mathematically as a function of the spherical mean signal, which is in turn related to V_in. Based on Eq. (7), AFD_total could be derived from diffusion measurements with a single b-value. λ is assumed constant in the model, and then, ${\text{AFD}}_{\text{total}}^{\text{ss}}$ is linearly related to $\overline{\text{S}}$. At high b-values, ${\text{AFD}}_{\text{total}}^{\text{ss}}$ is equivalent to V_in. ${\text{AFD}}_{\text{total}}^{\text{ms}}$ is based on the linear least squares fitting of diffusion measurements with multi-shell b-values [37]. ${\text{AFD}}_{\text{total}}^{\text{ms}}$ cannot be linked with a specific $\overline{\text{S}}$, but it is highly correlated with $\overline{\mathrm{S}}(\mathrm{b}5000)$ as shown in Figure 3. Another difference between ${\text{AFD}}_{\text{total}}^{\text{ms}}$ and ${\text{AFD}}_{\text{total}}^{\text{ss}}$ is that ${\text{AFD}}_{\text{total}}^{\text{ms}}$ is based on a multi-tissue model which is less sensitive to partial volume effects at gray matter/white matter interface [38]. Fiber tractography is usually biased by tracking algorithms and seeding options. SIFT was developed to reduce the number of streamlines and improve biological plausibility [45]. Consistent with previous results [16,45], TDI after SIFT is highly correlated with AFD_total. It was also observed that AFD_total had smaller intra- and inter-subject variations than TDI after SIFT [16]. AFD_total is recommended for voxel-wise quantification of total tract density (i.e. without tract orientation information) and AFD for tract density along a specific direction [15,16].

SMT-based V_in

There are two unknown variables (V_in and λ) in Eq. (2), which means a minimum of two b-values may be sufficient to extract the intra-axonal volume fraction accurately. The b-value dependence has been investigated previously and the results suggested far separated b-values for better performance [28]. The current study highlights the importance of acquiring both low and high b-values. With only high b-values, Eq. (2) simplifies to Eq. (3) making it impossible to estimate V_in and λ independently. At low b-values, $\overline{\text{S}}$ is sensitive to λ variation, but poorly correlated with V_in. The maximal b-value used in typical multi-shell protocols is 3000 s/mm², however, it is unclear whether b = 3000 s/mm² is sufficient for SMT model. Our simulation and experiment results (Figure 1 and Figure 5) suggest that b = 3000 s/mm² is indeed sufficient for SMT-based studies in human brain white matter. The quantification of SMT-based V_in is based on a simplified two-compartment model with assumptions of ${\lambda }_{\Vert }^{\text{ex}}=\lambda$ and ${\lambda }_{\perp }^{\text{ex}}=\left(1-{\text{V}}_{\text{in}}\right)\cdot \lambda$. Furthermore, the T₂ difference is not considered. Recent studies [29–31] have proposed to expand the rotationally invariant framework and acquire more comprehensive diffusion and/or relaxation dataset to fit those extra variables (${\lambda }_{\Vert }^{\text{ex}},{\lambda }_{\perp }^{\text{ex}},T_2^{in}$, and $T_2^{ex}$). Future work will be needed to further validate the accuracy.

B = 0 normalization

The voxel-wise b = 0 normalization is able to remove the effects of T₂ spatial variations and RF inhomogeneity. As shown in Figure 5, the correlation between ${\overline{\text{S}}}_{{}_{\text{n}}}(\text{b}3000)$ and ${\overline{\text{S}}}_{{}_{\text{n}}}(\text{b5}000)$ is higher than that between $\overline{\text{S}}(\text{b}3000)$ and $\overline{\text{S}}(\text{b}5000)$. But b = 0 normalization cannot remove the T₂ difference between intra- and extra-axonal spaces. In addition, the normalized diffusion weighted signal may be affected by partial volume effects, especially at low image resolutions [51]. Thus, the SMT-based V_in is T₂-weighted intra-axonal volume fraction. In white matter voxels with cerebral spinal fluid (CSF) partial volume, the fitted V_in will be lower than the real axonal volume fraction due to the long T₂ of CSF. For this reason, previous CSD-based studies were based on the raw diffusion weighted signals without voxel-wise b = 0 normalization. At high b-values, CSF signal decays to 0 and the measured diffusion weighted signal is completely from the white matter intra-axonal space. However, it becomes challenging to perform global normalization across subjects [15]. Following previous studies, the current study used the raw diffusion signals for CSD-based measures, and the normalized signals for DTI and SMT.

Conclusion

The CSD-based AFD_total technique and the SMT-based V_in technique were compared on the same MGH-USC Human Connectome Project diffusion data for estimating intra-axonal volume fraction. Both techniques are essentially based on the spherical mean diffusion weighted signal. The relation between $\overline{\text{S}}$ and V_in was investigated at both low and high b-values. At high b-values (b ≥ 3000 s/mm²), $\overline{\text{S}}$ is linearly related to V_in. At low b-values (b ~ 1000 s/mm²), $\overline{\text{S}}$ may be significantly affected by the variations of λ, which makes $\overline{\text{S}}$ an unreliable indicator of V_in. These results demonstrate that $\overline{\text{S}}$ measured with the typical b-value of 1000 s/mm² is not an indicator of V_in, and previous DTI studies acquired with b = 1000 s/mm² cannot be re-analyzed to provide V_in-weighted contrast.