Extreme Biophysics: Enzymes Under Pressure

Abstract

A critical question about piezophilic (pressure-loving) microbes is how their constituent molecules maintain function under high pressure. Here, factors are examined that may lead to the increased activity under pressure in dihydrofolate reductase from the piezophilic Moritella profunda compared to the homologous enzyme from the mesophilic Escherichia coli. Molecular dynamics simulations are performed at various temperatures and pressures to examine how pressure affects the flexibility of the enzymes from these two microbes, since both stability and flexibility are necessary for enzyme activity. The results suggest that collective motions on the 10 ns timescale are responsible for the flexibility necessary for “corresponding states” activity at the growth conditions of the parent organism. In addition, the results suggest that while the lower stability of many enzymes from deep-sea microbes may be an adaptation for greater flexibility at low temperatures, high pressure may enhance their adaptation to low temperatures.

GRAPHICAL ABSTRACT

Determining adaptations of enzymes for extreme pressure and temperature is important for understanding structure-function relationships in enzymes and may help in defining the “limits of life”. Atomistic simulations of dihydrofolate reductase from a mesophile and a “piezophile” identify collective motions as responsible for the flexibility necessary for “corresponding states” enzyme activity. In addition, the adaptions for low temperature and high pressure environment of deep-sea microbes are identified as greater flexibility and lower density.

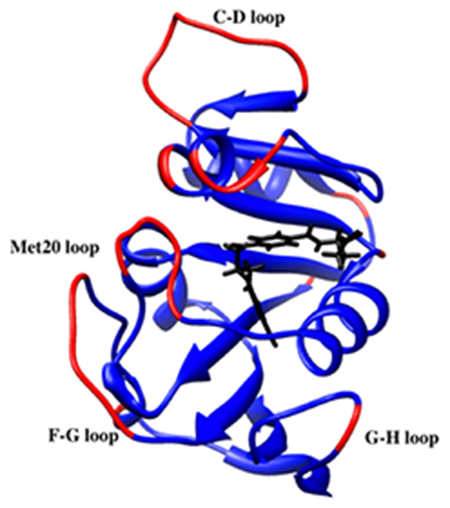
Introduction

The discoveries of “extremophilic” microbes and even higher organisms that thrive under extremes of temperature, pressure, salinity, pH, etc. raise many questions including the nature of adaptations in their constituent molecules to function under conditions where their counterparts in mesophiles fail.^1,2 Fundamentally, determining the adaptations of enzymes for extreme conditions can lead to a greater understanding of enzyme structure-function relationships. Practically, understanding these adaptations can be used in biotechnology so that enzymes can be bioengineered to function under specific conditions.³ In addition, determining the limiting conditions where enzyme activity can be maintained could be one of the factors in defining the “limits of life”, which could guide the search for life in extreme environments such as beneath the oceanic and continental surface or even extraterrestrially.

Of extreme conditions, the effects of high pressure have been relatively unexplored, both because of the difficulty in producing high pressure in the lab and because of the difficulty in collecting samples of “piezophiles”, which are microbes adapted for high pressure environments. Thus, the development of high-pressure instrumentation for biophysical measurements^4–9 means that experiments can now be performed at high pressure. Molecular studies are also going beyond in vitro to in vivo; for instance, incoherent neutron scattering under high pressure has been used to investigate molecular motions in deep-sea microbes.¹⁰ In addition, concerted efforts are being made to sample additional microbes from the deepest ocean and far beneath the continental surface at pressures beyond 1 kbar.¹¹

For proteins, the effects of pressure are thought to be compression and denaturation.¹² Pressure denaturation, though seemingly contrary to volume reduction necessary to lower the free energy, apparently occurs since water can pack more tightly against polypeptide than polypeptide against polypeptide so that more open solvated states become favorable.^13,14 However, so far, the activity of relatively few enzymes has been studied under pressure. One of the most studied experimentally for both structure and activity under pressure is dihydrofolate reductase (DHFR). Multiple crystal structures of DHFR from mesophiles, including the recently deposited structures of Escherichia coli (Ec) DHFR at pressures up to 7.5 kbar¹⁵ can be found in the Protein Data Bank (PDB).¹⁶ Structures of EcDHFR at 1 bar bound with different combinations of the co-factor NADP+/NADPH, substrate dihydrofolate (DHF), product tetrahydrofolate (THF), and substrate or product analogs have contributed to a detailed structural picture of the molecular mechanism of DHFR.¹⁷ Based on crystal structures¹⁸ and NMR experiments¹⁹, conformational changes between “occluded”, “closed”, and “open” conformations of the nicotinamide binding site involving the Met20 loop have been implicated in the catalytic activity. In particular, transient open conformations appear important for nicotinamide to enter its binding pocket. Interestingly, although only the occluded conformation is seen in THF-bound DHFR by NMR at 1 bar, a high-pressure ¹⁵N/¹H two-dimensional NMR study has demonstrated the appearance of a second conformation as pressure is increased up to 2 kbar.²⁰

A thorough experimental comparison has also been made of the pressure dependence of the activity and stability of DHFR from a moderate piezophile and a mesophile,²¹ specifically, from Moritella profunda (Mp), with a P_G, or optimal growth pressure, of 220 bar at 6 °C,²² and E. coli, with a T_G, or optimal growth temperature, of 37 °C at 1 bar. At 25 °C, MpDHFR showed maximum enzyme activity at 500 bar while EcDHFR showed monotonic inactivation by pressure above 1 bar (Fig. 1a), which suggests pressure adaptations of MpDHFR although structural differences are not apparent between the three crystal structures of MpDHFR and those of EcDHFR. The initial increase in activity of MpDHFR is associated with a change in activation volume of −8.6 mL mol⁻¹ while the decrease is associated with a change of 8.6 mL mol⁻¹, and the monotonic decrease in EcDHFR with a change of 7.5 mL mol⁻¹. This suggests that the decrease may be due to the same effect, although the molecular nature of either the increase or the decrease is not clear. For instance, the abovementioned pressure effect on the Met20 loop might play a role in the activity changes, although others have suggested that Met20 loop motion is important for the catalytic cycle in E. coli but not in M. profunda.^23,24 In addition, enzyme activity does not always increase with pressure for DHFR from deep-sea bacteria, although the activity measurements were made at 25 °C and not T_G of the organism.²⁵ Another interesting observation is that the unfolding pressure (P_u) at 25 °C is 2.7 kbar with a volume change of −77 mL mol⁻¹ for EcDHFR but only 0.7 kbar with a volume change of −44 mL mol⁻¹ for MpDHFR (both measurements were for the apo-enzyme, which is less stable than the folate bound form), indicating MpDHFR is actually more sensitive to pressure denaturation²¹ (Fig. 1b). The marginal stability of enzymes from piezophiles has been noted for DHFR from other piezophiles as well as other enzymes, and is actually more general than the initial increase in enzyme activity with pressure.²⁵

Figure 1.

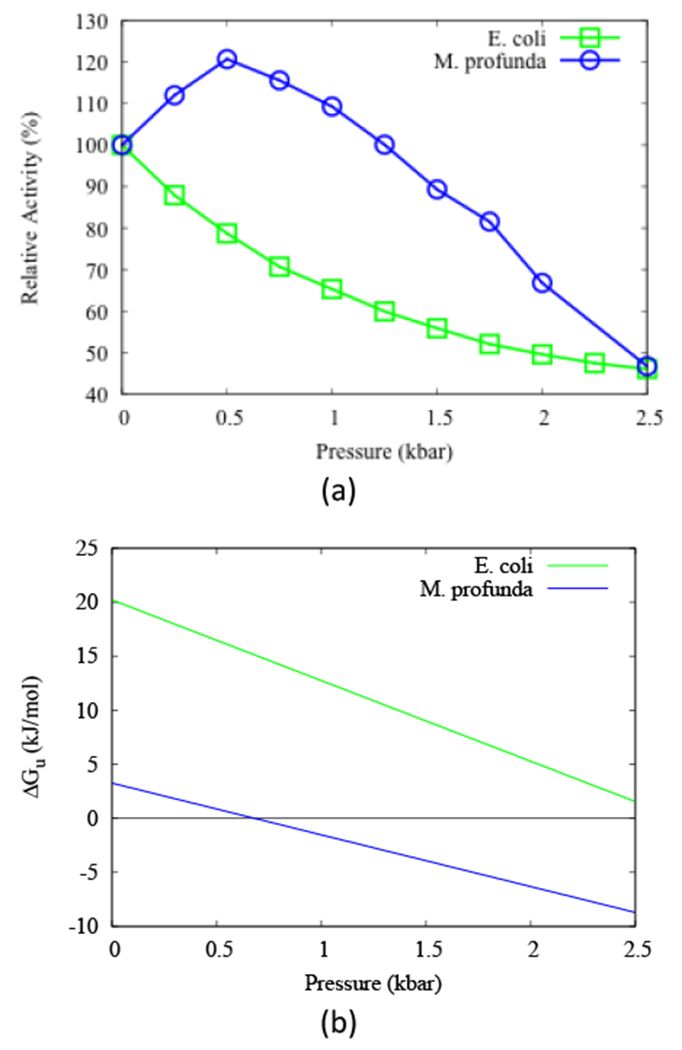
(a) The relative activity of DHFR and (b) free energy of unfolding of apo-DHFR as functions of pressure at 298 K from E. coli (green) and M. profunda (blue). Reproduced from ref. ²¹

Since extremophiles actually thrive under extreme conditions, many studies have focused on their enzyme function under those conditions since enzyme activity is a requirement for growth. Studies indicate that homologous enzymes from psychrophiles (cold-loving), mesophiles, and thermophiles (hot-loving) appear to have maximum activity near the respective T_G of the microbes,²⁷ consistent with the idea that enzyme activity is similar at “corresponding states” – namely, the T_G of the microbes.²⁶ In addition, since protein stability and flexibility are necessary to maintain enzyme activity, and since more interactions promote stability while fewer interactions promote flexibility, the need to maintain the balance between stability and flexibility has been noted.²⁷ For instance, enzymes from thermophiles apparently need more stabilizing interactions so that they do not become too flexible and unfold at the high T_G of their organism. Thus, high stability appears to the evolutionary driving force for thermophiles. On the other hand, enzymes from psychrophiles apparently have fewer stabilizing interactions so that they are flexible enough for activity at the low T_G of their organism, which also reduces their stability both to heat- and cold-unfolding. Thus, flexibility appears to be the evolutionary driving force for psychrophiles, which can be accomplished by lowering the stability as long as their cold-unfolding temperature is lower than the organism’s T_G. Therefore, the initial increase in activity with temperature was attributed to the increase in flexibility with temperature and the subsequent decrease in activity was attributed to destabilization of the protein as it approaches its unfolding transition. Of course, the “flexibility” and “stability” may be more or less localized to the active site depending on the size of the enzyme, but are more likely to apply to the whole protein if the enzyme is small.

However, as yet the corresponding states hypothesis has not been examined for enzymes from piezophiles compared to mesophiles at their respective P_G. If compression is important, enzymes from piezophiles may need to maintain flexibility similar to psychrophiles. Thus, the adaptation may be lower stability, resulting in a low P_u compared to mesophilic homologs as long as it is higher than P_G of the organism. On the other hand, since pressure tends to favor open conformations that can lead to unfolding, enzymes from piezophiles may need to be more stable and thus less flexible than mesophilic homologs. In addition, understanding the effects of pressure is further complicated by the fact that most “piezophilic” enzymes have been isolated from piezophiles that live in cold ocean environments, so the effects of P_G and T_G are difficult to separate. In fact, M. profunda is considered a psychropiezophile, since it was isolated at 2 °C.²²

Moreover, while both protein stability and flexibility have been identified as essential for active enzymes, the question of the nature of this flexibility still remains. For instance, the flexibility could be only in the large conformational changes necessary for activity with adaptations localized to a few regions such as the active site region and hinges for global motion. On the other hand, the flexibility could be a global property of the entire protein such as the atomic fluctuations that give rise to the deformability of a protein, which then influences the large conformation changes. The latter would imply more general adaptations such as a lower limit to the overall stability. So far, while there are many clues from studies of enzymes from thermophiles and psychrophiles, there is still debate over the nature of this flexibility²⁷ and is likely to involve contributions of both local and global properties.

Understanding the nature of flexibility for enzyme function is essential not only for basic knowledge, but has many important implications. The most obvious are for bioengineering enzymes, in which a “materials science” approach of developing an understanding of the contribution of global properties such as the limiting values of stability and flexibility necessary for enzyme activity could provide design criteria. This is of particular importance because, as noted above, flexibility and stability are coupled since a very flexible protein may not be stable enough and a very stable protein may not be flexible enough. However, before a general understanding can be made of the coupling, the roots of the “flexibility” and ways to measure it must be determined in the same manner that stability can be measured as a free energy difference between the folded and unfolded state, or in terms of unfolding temperatures or pressures.

Here, a comparison is made of effects of pressure and temperature on MpDHFR and EcDHFR. The nature of the flexibility under different conditions is examined in the context of the corresponding states hypothesis. The focus is on global properties of the protein such as the molecular volume and the average root mean-square fluctuations (RMSF) of atomic positions. In particular, the RMSF are studied to determine the timescale of the motions involved in the flexibility. Molecular dynamics simulations of the DHFR-THF binary complex, as in the high-pressure NMR studies,²⁰ from both M. profunda and E. coli are performed at all possible combinations of the optimal T_G and P_G (GTP) of both organisms as well as at standard temperature and pressure (STP).

Methods

Molecular dynamics (MD) simulations and other coordinate manipulations were performed using the molecular mechanics package CHARMM version 37b2.²⁸ The set-up was performed in CHARMMing²⁹ and summarized briefly here; default protocols were used except as noted. The starting coordinates for the proteins used in the simulations were obtained for EcDHFR (PDB ID: 1RX2¹⁸) and MpDHFR (PDB ID: 2ZZA³⁰) from the PDB with hydrogen positions generated by HBUILD.

The CHARMM36 all-atom nonpolarizable potential energy parameter set^31,32 was used for the proteins. However, water was modeled by TIP4P-Ew³³ because of the importance of understanding changes in the properties of water under pressure. Additionally, a force field for THF was generated using the CHARMM Generalized Force Field server.³⁴ A CGenFF was first generated for THF using the coordinates ZINC13513942 from the ZINC server.³⁵ Since the substrate is modeled with folate in the crystallographic structures 1RX2 and 2ZZA, the carbon coordinates within the pteridine rings were modified to yield a chair conformation of the ring with single bonds rather than the planar conformation with double bonds present for folate. Subsequently, the original CGenFF was used with CHARMM to generate hydrogens on the THF coordinates generated from the modified crystallographic folate substrates, and this new molecule was then used to generate a final CGenFF.

The simulations utilized the leapfrog Verlet algorithm with a time step of 0.001 ps and were maintained in the NPT ensemble with the Nose-Hoover algorithm^36,37 for the thermostat and barostat. Periodic boundary conditions and the particle mesh Ewald (PME) summation algorithm with a k-space grid spacing of about 0.49 ų⁸ were used. Each protein was first solvated in a rhombic dodecahedral simulation box of equilibrated TIP4P-Ew with a distance between faces of 70.9021 Å. The smallest distance from a protein atom to a side of the box for either protein is ~11.5 Å. The proteins were then neutralized in 0.15 M KCl, which resulted in 7420 and 7414 water molecules, 27 and 26 K⁺, and 14 and 15 Cl⁻ for EcDHFR and MpDHFR, respectively. The C-terminal lysine was missing in the crystal structure of MpDHFR and so was not included in the simulations; however, it was not close to either the THF or NADPH binding sites. Subsequently, the system was minimized with 100 steps of steepest descent and 100 steps of adopted basis Newton Raphson minimization³⁹, with the protein backbone atoms restrained with a harmonic spring constant of 100 kcal mol⁻¹ Å⁻². Next, the system was heated at 1 bar starting at 200 K below the final temperature, in increments of 5 K every 2.5 ps with velocities assigned according to a Gaussian distribution at every increment, and then pressurized if necessary in increments of 20 bar every 2 ps. Finally, the system was equilibrated and simulated using identical methods at all temperatures and pressures, with the first 4 ns designated as equilibration, and the subsequent 50 ns designated as production run.

Apparent Molecular Volume

The molecular volume 〈V_m〉 of the protein is examined in two ways. First, a measure of the spatial extent of the protein is

$$\langle V_{\mathrm{app}}\rangle =\langle V_{\mathrm{MD}}\rangle -N_{\mathrm{W}}\langle V_{\mathrm{H}2\mathrm{O}}\rangle$$ (1)

where 〈V_MD〉 is the average volume of the simulation box, N_w is the number of water molecules in the simulation, and 〈V_H2O〉 is the average molecular volume of a water molecule from a simulation of the pure solvent. The 〈V_app〉 per heavy atom, 〈V_app〉/N_HA, where N_HA is the number of heavy atoms in the protein, is thus a measure of the average volume available to a heavy atom.

RMS Fluctuations

The average fluctuations for the entire protein are examined at various time scales. First, the trajectory of length T is divided evenly into subsets of length τ. The average deviations in the coordinates of each atom i from a mean structure averaged over the time τ for each subset $j{\langle {\delta }_{\tau }{x}_i^2\rangle }_j,{\langle {\delta }_{\tau }{y}_i^2\rangle }_j,{\langle {\delta }_{\tau }{z}_i^2\rangle }_j$ are first averaged over the entire trajectory. The second moments of the fluctuations of atom i on a timescale τ were defined as

$$m_{2x,i}(\tau )=\frac{\tau }{T}\sum _{j=1}^{T/\tau }{\langle {\delta }_{\tau }{x}_i^2\rangle }_j$$ (2)

and similarly in the y and z directions. Next, the mean square fluctuations per residue or for the entire protein are defined as an average overall N_HA

$${\sigma }^2(\tau )=\frac{1}{N_{\mathrm{HA}}}\sum _{i=1}^{N_{\mathrm{HA}}}\left[{\mathrm{m}}_{2x,i}(\tau )+{\mathrm{m}}_{2y,i}(\tau )+{\mathrm{m}}_{2z,i}(\tau )\right]$$ (3)

where N_HA is all backbone heavy atoms of the residue or all heavy atoms in the protein, as denoted in the results.

Anharmonicity

The excess kurtosis of the fluctuations, a measure of anharmonicity, of atom i on a timescale τ in the principal X-axis direction was also defined as

$$\mathrm{k}{\text{'}}_{4X,i}(\tau )=\frac{\tau }{T}{\sum _{j=1}^{T/\tau }\left(\frac{\langle {\delta }_{\tau }{X}_i^4\rangle }{{\langle {\delta }_{\tau }{X}_i^2\rangle }^2}\right)}_j-3$$ (4)

since the deviation from harmonicity is most important along the direction of the largest fluctuations. Next, the excess kurtosis per residue or for the entire protein is defined as an average of over all relevant N_HA as above,

$${\gamma }_2(\tau )=\frac{1}{N_{\mathrm{HA}}}\sum _{i=1}^{N_{\mathrm{HA}}}\mathrm{k}{\text{'}}_{4X,i}(\tau )$$ (5)

γ₂ serves as a measure of the anharmonicity,⁴⁰ although not a unique determinant of the underlying potential surface. For instance, γ₂ is zero if the fluctuations follow a Gaussian distribution, indicating a harmonic well and negative if there are fewer very large fluctuations than a Gaussian, which may indicate that the sampling time is insufficient to explore the larger fluctuations. In addition, γ₂ is positive if there are more very large fluctuations than in a Gaussian, which might be due to an incomplete transition to another state, and γ₂ is negative if there is a double well, since this results in both more intermediate fluctuations and fewer very large fluctuations. Thus, there are two possible reasons for negative contributions, and both positive and negative γ₂ can be indicative of an alternative conformation.

Results

The crystal structures of EcDHFR and MpDHFR do not show obvious structural differences (Fig. S1); domain assignments are also shown Fig. S1 with the associated residue numbers given in Table S1. There are slight differences in the types of interactions (Table 1), since EcDHFR has slightly more hydrogen bonds and ion pairs, indicating it may be slightly more stabilized by polar and ionic interactions, while MpDHFR has slightly more buried nonpolar atoms, indicating it might be slightly more stabilized by hydrophobic interactions. The stabilization of MpDHFR by hydrophobic interactions rather than polar or ionic interactions is consistent with its lower stability in Fig. 1b. The MD simulations of EcDHFR and MpDHFR were performed at various combinations of T_G and P_G of the organisms (i.e., T_G = 310 K and P_G = 1 bar for E. coli and T_G = 279 K and P_G = 220 bar for M. profunda ²²) as well as at STP. The simulations under all of the conditions showed relatively small root mean-square deviations (RMSD) from the starting crystal structures (Table S2).

Table 1.

Comparison of structural features in crystal structures of DHFR with THF built-in.

	MpDHFR	EcDHFR
Number of backbone hydrogen bonds[a]	101	106
Number of hydrogen bonds[a]	131	142
Number of negative residues/number of residues	22/162	26/159
Number of positive residues/number of residues	14/162	15/159
Number of ion pairs[b]	4	7
Number of polar atoms[c]/number of atoms	474/2588	469/2542
Exposed surface area (Å2)	4072	3904
Number of apolar atoms[d]/number of atoms	836/2588	831/2542
Exposed surface area (Å2)	1295	1451

^[a]Amide N to carbonyl O less than 2.4 Å.

^[b]Carboxylic O to amino N less than 4.0 Å.

^[c]N and O atoms, probe radius=1.4 Å.

^[d]C and S atoms, probe radius=1.4 Å.

The RMSF averaged over all heavy atoms (Eqn. 3) were examined on different timescales at different temperatures and pressures (Fig. S2). They increase with increasing τ as different kinds of motions are explored. The short timescale RMSF up to ~100 ps of both MpDHFR and EcDHFR are very similar at a given temperature, regardless of organism or pressure, and they also increase with temperature as expected (shown for 10 ps as lower lines in Fig. 2). These fluctuations are determined by motions such as bond or bond angle vibrations and hindered rotations about a dihedral angle minimum so that each atom can be considered to be fluctuating in its own potential well. However, the long timescale RMSF above ~1 ns, while continuing to increase with temperature, begin to show marked differences in the simulations. They are generally larger at higher pressures (shown for 10 ns as upper lines in Fig. 2), which is consistent with increasing pressure leading to increasing populations of more open conformations that eventually lead to high pressure unfolding. The one exception is for EcDHFR at 280 K and 1 bar, which is larger than at 280 K and 220bar although within the error bars. The RMSF are apparently large due to an anomalous separation of the G-H loop during this simulation. In addition, the long timescale RMSF are larger for MpDHFR at a given temperature and pressure than EcDHFR, which is also consistent with the experimental lower stability of MpDHFR (Fig. 1b) and indicates flexibility may be an evolutionary driving force. As might be expected based on studies of psychrophiles versus mesophiles at STP, the RMSF at STP are greater for MpDHFR compared to EcDHFR.^27,41,42 These fluctuations are influenced by collective motions of groups of atoms in addition to local fluctuations of each atom. The net result is that the long timescale RMSF for MpDHFR at the GTP of M. profunda appear similar as those for EcDHFR at the GTP of E. coli, which suggests that they are an indicator of “corresponding states” flexibility.

Figure 2.

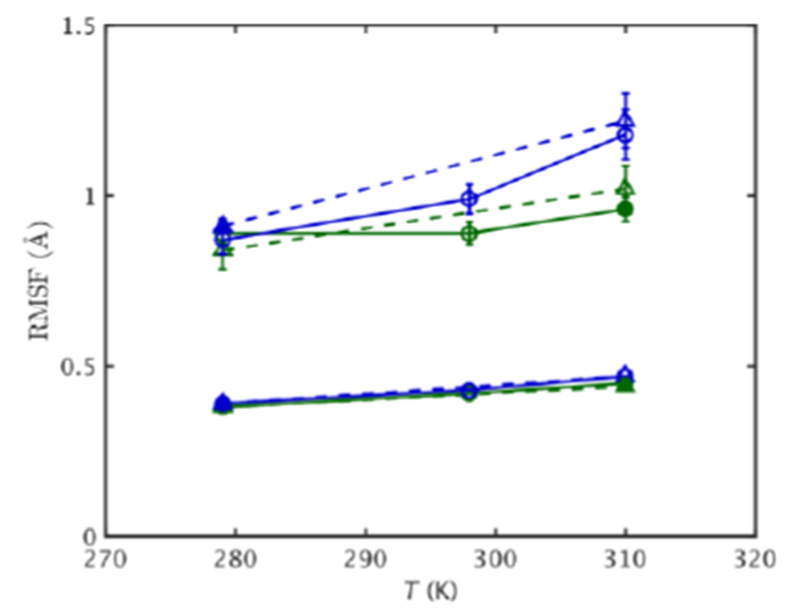
RMSF vs. T for EcDHFR (green) and MpDHFR (blue) at 1 bar (solid line) and 220 bar (dashed line), with filled symbol indicating GTP for that organism. Lower/upper set of lines are for fluctuations on a τ = 0.01/10.00 ns time scale. Standard errors using block averaging over 0.01/10 ns intervals are shown.

The molecular volume was also examined as a function of temperature (Fig. 3). 〈V_app〉/N_HA (Eqn. 1) serves as a measure of the average volume each atom can move in (see Methods). 〈V_app〉/N_HA is somewhat larger at higher pressure, especially at lower temperatures, which is consistent with larger RMSF at higher pressure. In addition, 〈V_app〉/N_HA for MpDHFR is slightly larger than for EcDHFR at a given state point, which is also consistent with the larger RMSF in MpDHFR at a given state point.

Figure 3.

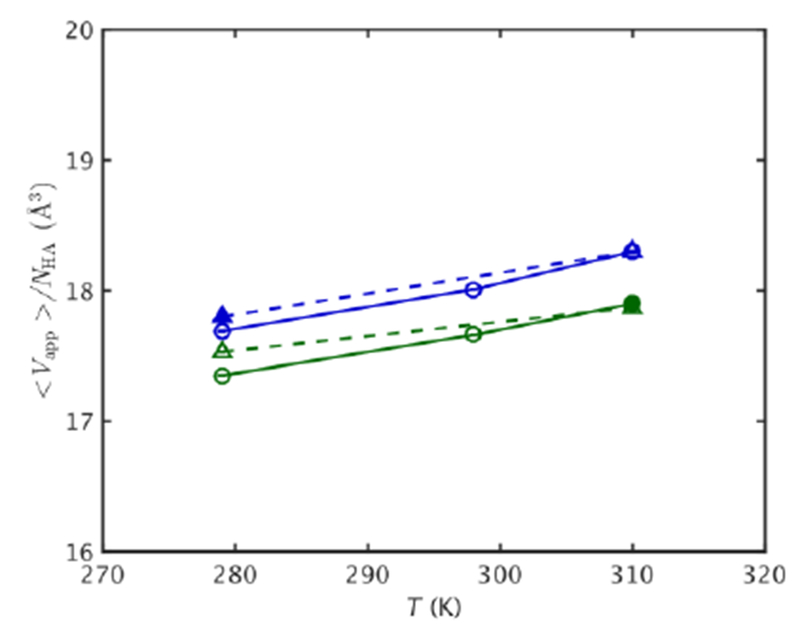
〈V_app〉/N_HA vs. T for EcDHFR (green) and MpDHFR (blue) at 1 bar (solid line) and 220 bar (dashed line), with filled symbol indicating GTP for that organism. Standard errors using block averaging over 10 ns intervals are shown.

The average 10 ns timescale RMSF for the backbone per residue as a function of distance of the residue from the geometric center along with linear least-squares fit lines with slope m, intercept b, and correlation coefficient R (Fig. 4) illustrates the effects of pressure and temperature on fluctuations as a function of how buried the residue is. Comparing the RMSF of MpDHFR at its GTP with when it is at T_G of E. coli (Fig. 4a), the main effect of low temperatures is to decrease fluctuations as indicated by the decrease in slope, and lower stability appears to be an adaptation to increase fluctuations at low temperatures. However, comparing the RMSF of MpDHFR at its GTP with when it is at P_G of E. coli (Fig. 4b), the main effect of increased pressure seems to be to increase the fluctuations as indicated by the larger slope, so pressure appears to partially counteract the effects of low temperature. In addition, pressure at 220 bar seems to affect the outer loops more so that the RMSF are larger further from the geometric center consistent with 〈V_app〉/N_HA (Fig. 3). Thus, the net effects of the increased flexibility due to the low stability adaptation for temperature and the increased flexibility due directly to the increased pressure result in the overall similar RMSF as a function of distance from the geometric center for EcDHFR and MpDHFR at the GTP of their respective organisms seen in Fig. 2 (Fig. 4c). In addition, the RMSF are similar in similar regions for EcDHFR and MpDHFR. In particular, the RMSF per residue are large near Met20 for both EcDHFR and MpDHFR at the GTP of their respective organisms (Fig. 5). Although transitions to the open state were not observed in the short 50 ns simulations, large fluctuations of the Met20 loop are consistent with the transient open conformation of the Met20 loop for binding of nicotinamide¹⁷ as well as NMR results of EcDHFR showing increasing populations of a second conformation of the Met20 loop with increasing pressure.²⁰ This is discussed further in the Discussion section.

Figure 4.

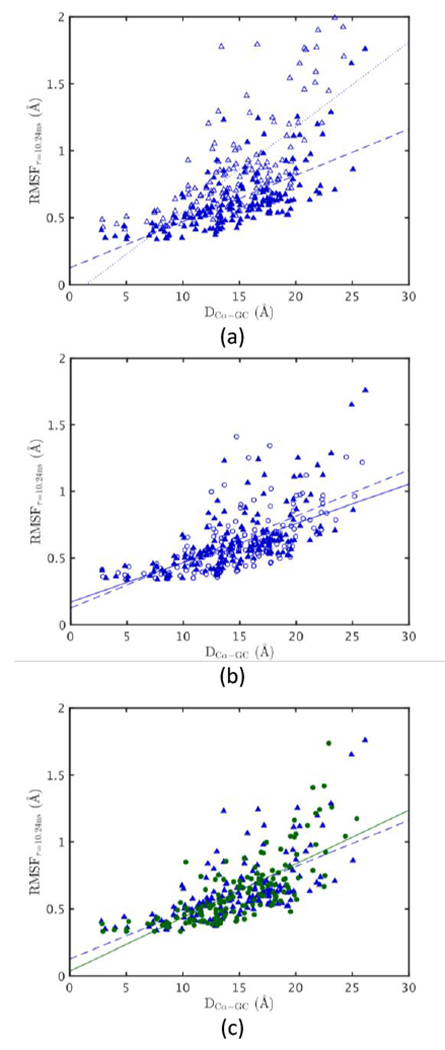
RMSF per residue vs. distance from geometric center (GC). MpDHFR at P_G = 220 bar and T_G = 280 K (blue ▴) with fit (blue dashed, m = 0.034, b = 0.126 Å, R = 0.66) and (a) MpDHFR at P_G = 220 bar and T = 310 K (blue ▵) with fit (blue dotted, m = 0.063, b = −0.089 Å, R = 0.71), (b) MpDHFR at P = 1 bar and T_G = 280 K (blue 엯) with fit (blue line, m = 0.029, b = 0.170 Å, R = 0.62), and (c) EcDHFR at P_G = 1 bar and T_G = 310 K (green ●) with fit (green line, m = 0.040, b = 0.036 Å, R=0.75).

Figure 5.

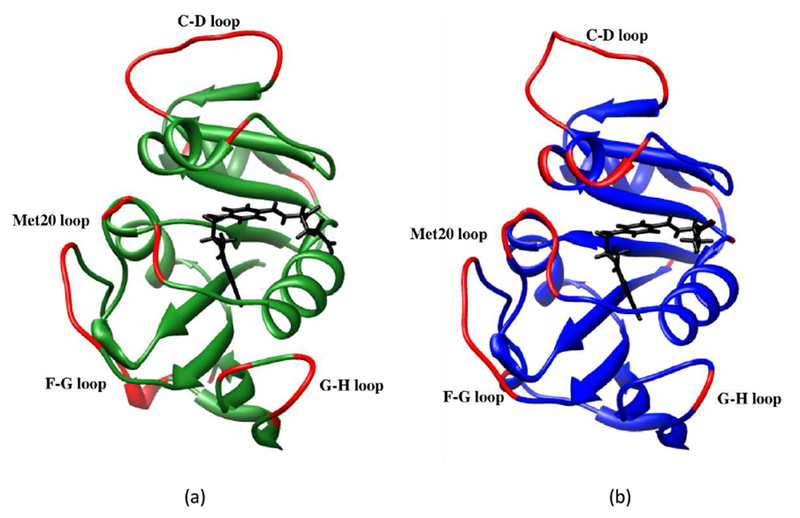
Residues in a) EcDHFR and b) MpDHFR with tetrahydrofolate in black and with RMSF > 0.75 Å at GTP of the respective organisms in red.

To examine the origin of similar long timescale RMSF at the corresponding states, the excess kurtosis of the fluctuations along the major principal axis direction of the fluctuations averaged over all atoms, γ₂, (Eqn. 5) was also examined on different time scales at different temperatures and pressures (Fig. S3). The short time scale γ₂ of both MpDHFR and EcDHFR are very similar at a given temperature, regardless of organism or pressure (shown for 10 ps as lower lines in Fig. 6), and increase from −0.5 to −0.1 as τ increases to 100 ps. The slightly negative values appear to be due to insufficient sampling of large fluctuations due to the short periods averaged over. Above τ = ~1 ns, γ₂ continues to increase above 0 as the fluctuations become somewhat anharmonic (Fig. S3) and marked differences between the simulations appear as seen in the RMSF. Interestingly, the long timescale γ₂ decreases with pressure and is smaller for MpDHFR than EcDHFR at a given temperature (shown for 10 ns as upper lines in Fig. 6). By examining the RMSF per residue (Fig. S4, S5) and the absolute value of γ₂ per residue (Figure S6, S7), it appears that the inner core of both proteins are relatively harmonic, and that the slightly smaller values of the average over the protein with increased pressure and in MpDHFR relative to EcDHFR are due to more double wells (which have γ₂ < 0) rather than being more harmonic. Thus, γ₂ indicates that the corresponding states flexibility is associated with fluctuations that are large enough to cause transitions of collective motions between different conformations; i.e., so that the RMSF are no longer completely within a single harmonic well for a given atom.

Figure 6.

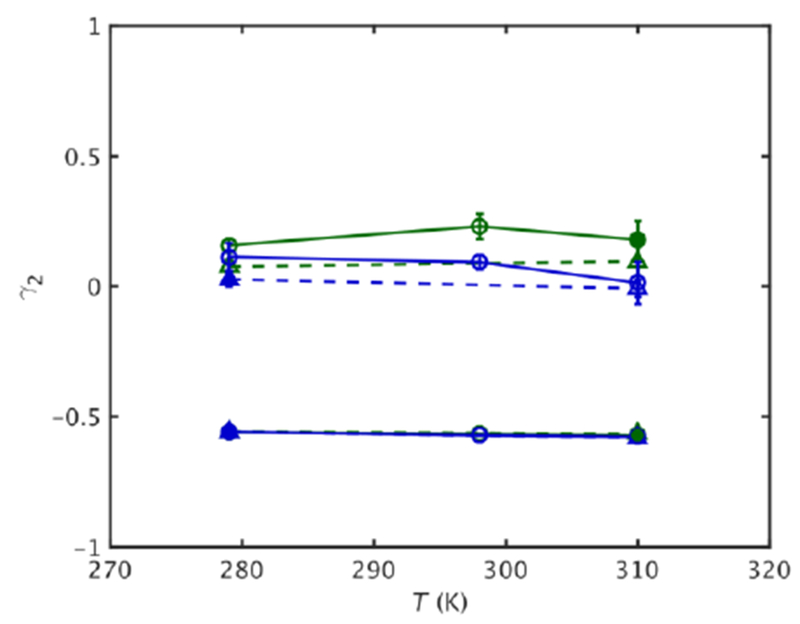
Kurtosis vs. T for EcDHFR (green) and MpDHFR (blue) at 1 bar (solid line) and 220 bar (dashed line), with filled symbol indicating GTP for that organism. Lower/upper set of lines are for fluctuations on a τ = 0.01/10.00 ns time scale. Standard errors as in Fig. 2 are shown.

Discussions

The simulation results here must be considered in light of two viewpoints, that of biochemical/biophysical experiments of the molecule and of what happens in the microbe itself. For instance, considering the environmental effects that may appear in typical biochemical/biophysical experiments and simulations of a specific enzyme, the experimental dynamical properties of liquid water are important. The self-diffusion coefficient of water D_W has been noted to increase slightly with pressure before decreasing with pressure; for instance, the increase occurs up to ~800 bar at ~298 K,⁴³ which is reproduced by the TIP4P-Ew model ⁴⁴ used here. These fluctuations may be transmitted to the protein,⁴⁵ or may reflect a more general phenomenon of pressure on condensed phases. In addition, considering the environment of the enzyme in a microbe, not only are the properties of water important, but also the effects of the intracellular milieu including co-solutes and crowding. In particular, the effects on enzymes of “piezolytes”, which are small molecules that are upregulated in response to pressure by microbes,^46–48 may be important and are amenable to biophysical experiments. The nature of these effects requires further exploration, both experimentally and computationally.

Given the above caveats about the microbial intracellular environment, the results here suggest the following picture of the effects of pressure and the adaptations that MpDHFR has made for high-pressure environments (Fig. 7), although it is not necessarily unique nor is it generalizable. Considering motion on a ~10 ns timescale, atoms in loop regions of EcDHFR generally have motion within one well with occasional excursions towards a second well. For example, an atom in the Met20 loop of THF bound DHFR should oscillate mainly in the well corresponding to the occluded conformation as seen in the simulations. However, to make transitions to the open conformation as needed for binding of nicotinamide¹⁷, the fluctuations of the Met20 loop are expected to be larger than a more buried region of the protein. In addition, the lower stability of MpDHFR would lead to larger fluctuations. Thus, at 310 K and 1 bar (i.e., the growth conditions of E. coli, left side of Fig. 7), the effective well for an atom would presumably have a smaller force constant k as well as a smaller barrier to transitions for MpDHFR than for EcDHFR so the RMSF would be larger for MpDHFR. At 310 K and 220 bar (middle of Fig. 7), the higher pressure would favor the more open conformation and thus its effective well would be lower so that both MpDHFR and EcDHFR might have increased RMSF because of a greater population of the open conformation than at 1 bar. There seems to be little change in the force constants of a given well at this pressure, although neutron scattering experiments indicate that the force constants increased with pressures above 500 bar.⁴⁹ Also, at 310 K, the greater preference for open conformations along with lowered barriers in MpDHFR especially if multiple atoms are involved would tend to destabilize the protein, as indicated in experiment. However, at 280 K and 220 bar (i.e., the growth conditions of M. profunda, right side of Fig. 7), the kinetic energy is less so barrier crossings into the open conformation would be fewer so the relative population of the open conformation might be smaller depending on timescales. Thus, the relative populations of the closed and open conformations of MpDHFR at the GTP of M. profunda might be more like EcDHFR at the GTP of E. coli, which shows how the long timescale RMSF of a DHFR at the growth conditions of organism from which it comes can give rise to the corresponding states flexibility.

Figure 7.

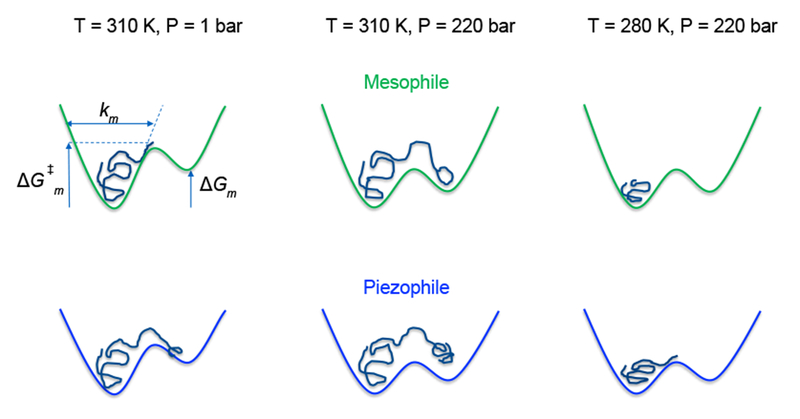
Schematics of an “average” atom in the mesophilic (m) EcDHFR and in the psychropiezophilic (p) MpDHFR. The force constant k_i, free energy difference between wells ΔG_i, and transition barrier ΔG^‡_i, i = m or p, are indicated for the mesophile at standard T, P. Left well corresponds to the more favored conformation and right well corresponds to a more open conformation with lower probability.

For experimental verification of this picture, the results here indicate that the most relevant timescale might be best explored by NMR experiments. While the RMSF from a simulation are most directly related to the temperature factors from crystallographic determinations of structure, these also include effects of lattice vibrations, crystal disorder, and nearest neighbors. In addition, neutron scattering data also appears to be restricted to the sub-nanosecond timescale,^49,50 while the relevant motions appear to be above the nanosecond timescale. Thus, a computational (and experimental) challenge may be in bridging timescales between different experimental measures.

In addition, Fig. 7 suggests a possible reason for the observed changes in enzyme activity with pressure (Fig. 1b). For MpDHFR, the activity may initially increase with pressure because open conformations tend to be favored by pressure and a more open conformation (or a certain population of this conformation) might be needed for good activity, for instance, the open conformation of the Met20 loop. Since the relative populations of closed and open conformations may not be the same in DHFR from different deep-sea microbes and also may be temperature dependent, this may explain why the initial increase is not always seen. In addition, the activity at higher pressures might be reduced due to partial unfolding or distortion of the active site. On the other hand, for EcDHFR, the decrease in activity above 1 bar may be due to excessive populations of open conformations or disruptions of the active site that do not lead to unfolding because of the greater stability of EcDHFR.

Overall, the results lead to a general picture of the evolutionary adaptations in enzymes for cold deep-sea environments. The results indicate that the lower stability, which gives rise to greater flexibility, of MpDHFR compared to EcDHFR may be an adaptation for low temperature. However, high pressure may actually enhance the adaptation to low temperatures by increasing flexibility because stability is limited in how much it can be lowered by having fewer or weaker interactions. Thus, at moderately high pressures below ~500 bar, pressure might actually aid in adaptation to low temperatures by increasing the flexibility of outer loops, which are often involved in binding. More subtly, the lower density that is a result of lower stability might also enhance ability of water to penetrate the outer loops, and so lower density could be considered an adaptation to these pressures. In addition, at high pressures above ~500 bar, the lower overall density of MpDHFR may also aid in adaptation to high pressure by protecting against compressive effects noted in the neutron scattering experiments.^49,50 Finally, specific adaptations to high pressure might also play a minor role, such as altering the ratio of open and closed conformations to a more optimal balance. Thus, the low stability of enzymes might help psychrophilic bacteria to adapt to a wide variety of pressures, which is consistent with the observation that Shewanella and other bacteria found in cold deep-sea environments have low enzyme stability and a range of P_G from 1 bar to 6.5 kbar.⁵¹ Further study of these enzymes would help define the role of adaptations to temperature and pressure.

Conclusions

The atomic fluctuations of the mesophile EcDHFR and the psychropiezophile MpDHFR have been investigated in molecular dynamics simulations. While longer simulations and better force fields are warranted, the main conclusion is that flexibility needed for the corresponding states of activity of these two enzymes appears to have its roots in fluctuations on the 1 to 10 ns timescale, where collective motions appear. In addition, pressures near 200 bar seem to affect the enzymes mainly by making other conformations more accessible, leading to larger fluctuations, perhaps affecting the exterior more than the interior of the protein. The lower stability of MpDHFR apparently leads to larger fluctuations than in EcDHFR, so lower stability may be an adaptation mainly for temperature. However, high pressure may actually enhance adaptation to low temperatures by increasing flexibility by shifting conformational equilibria. In addition, the lower protein density of MpDHFR, a presumable consequence of its lower stability, may enhance adaptation to high pressure by favoring water penetration and protecting against its compressive effects. In other words, temperature affects the fluctuations of all atoms, while pressure appears to affect the exterior more than the interior. Overall, this indicates that both temperature and pressure of organism must be considered determining corresponding states activity. In addition, this implies that enzymes from microbes near deep-sea hydrothermal vents may have very different adaptations for pressure.