Skip to main content
PMC home page
Molecular Biology of the Cell logoLink to Molecular Biology of the Cell
. 2019 Jan 1;30(1):160–168. doi: 10.1091/mbc.E18-01-0018

Geometric instability catalyzes mitochondrial fission

Ehsan Irajizad a, Rajesh Ramachandran b, Ashutosh Agrawal a,*
Editor: Patricía Bassereauc
PMCID: PMC6337907  PMID: 30379601

Abstract

The mitochondrial membrane undergoes extreme remodeling during fission. While a few membrane-squeezing proteins are recognized as the key drivers of fission, there is a growing body of evidence that strongly suggests that conical lipids play a critical role in regulating mitochondrial morphology and fission. However, the mechanisms by which proteins and lipids cooperate to execute fission have not been quantitatively investigated. Here, we computationally model the squeezing of the largely tubular mitochondrion and show that proteins and conical lipids can act synergistically to trigger buckling instability and achieve extreme constriction. More remarkably, the study reveals that the conical lipids can act with different fission proteins to induce hierarchical instabilities and create increasingly narrow and stable constrictions. We reason that this geometric plasticity imparts significant robustness to the fission reaction by arresting the elastic tendency of the membrane to rebound during protein polymerization and depolymerization cycles. Our in vitro study validates protein–lipid cooperativity in constricting membrane tubules. Overall, our work presents a general mechanism for achieving drastic topological remodeling in cellular membranes.

INTRODUCTION

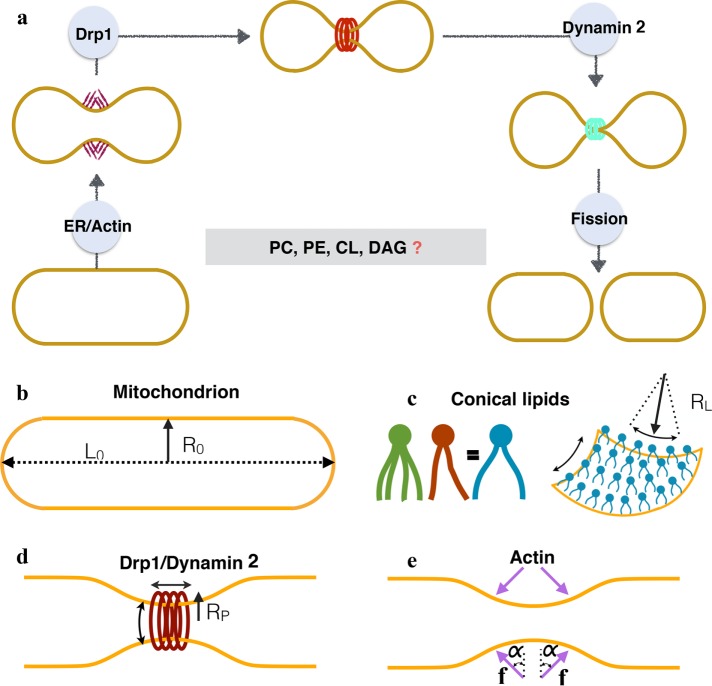
Mitochondria are dynamic organelles that form intricate networks and undergo continuous structural remodeling via the opposing processes of fission and fusion (Labbé et al., 2014; Kraus and Ryan, 2017; Ramachandran, 2018). While balanced mitochondrial dynamics is essential for cellular homeostasis, disruption in such dynamics is linked to various cancers, cardiac dysfunction, and neurogenerative disorders including Alzheimer's, Parkinson's, and Huntington's diseases (Youle and van der Bliek, 2012; Itoh et al., 2013; Labbé et al., 2014). Pioneering experimental studies have provided insights into the molecular machinery of one such key process, mitochondrial fission (Figure 1A). According to the current working model, the fission event is a three-step process (Lee et al., 2016; McBride and Frost, 2016; Lu et al., 2018): in the first step, actin–myosin cytoskeletal networks apply forces at endoplasmic reticulum (ER)-mitochondria contact sites to initiate mitochondrial constriction; in the next step, GTP-regulated dynamin-related protein 1 (Drp1) polymerization enhances the constriction, and in the final step, dynamin 2 facilitates complete membrane fission to create two daughter mitochondria (Figure 1).

FIGURE 1:

FIGURE 1:

Open in a new tab

(a) Current working model of mitochondrial fission in mammalian cells. The initial squeezing by actin/ER forces is followed by an increased constriction by a protein Drp1, which is subsequently brought to fission by a protein dynamin 2. While the list of fission proteins has expanded in the recent past, there is also a growing body of evidence that suggests the role of conical lipids in mitochondrial fission (key conical lipids shown in the box). How these lipids collaborate with fission proteins and catalyze fission reaction remains unresolved. In this study we use computational modeling and in vitro experiments to investigate this core puzzle. (b) The basic setup and the key players of membrane remodeling. We simulate an idealized mitochondria in the form of a hollow spherocylinder (a cylinder capped by two hemispheres) made of a lipid bilayer. The geometry is defined by two parameters: the radius R0 and the total length L0. (c) Conical lipids such as PE, CL, and DAG generate spherical curvatures (same in all the directions; see Supplemental Figure S1). Here we suppress the biochemical differences between such lipids and model the effect of a generic cone-shaped lipid with a preferred radius of curvature RL. (d) Drp1 and dynamin 2 are assumed to form a cylindrical coat and generate unequal curvatures in the circumferential and longitudinal directions. The preferred radius of curvature in the circumferential direction RP controls the squeezing capabilities of these proteins. (e) Actin and ER are assumed to apply compressive forces (f) onto the spherocylinder. Because the exact orientation of these forces is not known, we simulate forces at different angles (α).

While the fission proteins play an inarguably critical role, a growing body of evidence reveals that conical lipids, present in abundance in mitochondria (Figure 1), regulate mitochondrial morphology and fission. For example, two conical lipids, phosphatidylethanolamine (PE) and cardiolipin (CL) have been found to be essential for mitochondrial function and cell viability (Gohil et al., 2005; Schlame and Ren, 2009). A moderate reduction in the PE concentration has been shown to cause a significant alteration in mitochondrial functions and morphology (Steenbergen et al., 2005; Chan and McQuibban, 2012; Joshi et al., 2012; Tasseva et al., 2013; Van Der Veen et al., 2014). Recently, CL has been shown to promote Drp1 self-assembly and stimulate Drp1 GTPase activity (Macdonald et al., 2014). CL degradation to PA, on the other hand, has been shown to restrict Drp1 activity in fission (Adachi et al., 2016). Interestingly, while CL facilitates Drp1 polymerization, Drp1 also promotes local CL clustering and nonbilayer phase transition (Stepanyants et al., 2015). Another conical lipid that has been implicated in fission is diacylglycerol (DAG; Choi et al., 2006; Huang et al., 2011). DAG is predicted to localize at fission sites and also regulate actin dynamics (Frohman, 2015). Furthermore, DAG has been shown to promote fission in peroxisomes, which also requires Drp1 activity (Guo et al., 2007; Frohman, 2015).

While these experimental studies strongly suggest a potential role for conical lipids in mitochondrial dynamics, they do not reveal their precise roles in the fission process (Figure 1). How do these lipids act in concert with the fission machinery during the fission reaction? Do these lipids actively contribute to constriction, or do they only assist in promoting the assembly of the fission proteins? How are the superconstrictions, observed during in vivo and in vitro studies (Stepanyants et al., 2015; Lee et al., 2016), stabilized through dynamic protein polymerization and depoly­merization cycles?

The lack of experimental techniques to image membrane dynamics at the length and time scales relevant for mitochondrial fission makes it difficult to parse the roles of proteins and lipids. Therefore, to address the above issues, we resort to computational modeling and investigate this fission puzzle. We employ membrane physics and differential geometry to investigate the shape evolution of an idealized tubular mitochondrion leading to “membrane necking” in the presence of the established membrane remodeling effects of fission proteins and of conical shaped lipids (Figure 1, b–e). The study reveals that proteins and lipids can act synergistically to trigger buckling instability to generate extreme constriction. More remarkably, the study shows that the conical lipids can collaborate with multiple fission protein partners to trigger hierarchical instabilities that lead to stepwise constriction of the tubular structure. These sequential instabilities, in addition to promoting constriction, stabilize constricted geometries by arresting the elastic tendency to revert to the undeformed geometry during protein cycles. Data from in vitro studies (previously published and new) validate the core modeling proposal and show that conical lipids are critical to achieving and maintaining superconstrictions in membrane tubules. Because the estimated lipid concentrations required for inducing instability are well within the physiologically known concentrations in mitochondria, our findings may be of relevance to mitochondrial fission events in living cells. Furthermore, because curvature-inducing proteins and lipids are ubiquitous in cells, the proposed mechanisms might be at play in other topological remodeling events in cellular membranes.

RESULTS

Actin–lipid cooperativity

We follow the chronological sequence of protein activity revealed by the experimental studies. First, we model the constriction due to actin filaments and conical lipids. We increase the magnitude of the actin force in the center of the spherocylinder (Figure 2b-1, magenta domain) and the lipid concentration in the adjacent domains (Figure 2b-2, blue domains). This local increase in the lipid concentration could be a consequence of curvature-mediated lipid dynamics, as has been revealed in several experimental and theoretical studies (Mukhopadhyay et al., 2008; Kamal et al., 2009; Renner and Weibel, 2011; Sakuma et al., 2011; Koldsø et al., 2014; Boyd et al., 2017). The results here are presented for α = 45°. The results for the radial force are presented in the Supplemental Material (Supplemental Figure S4).

FIGURE 2:

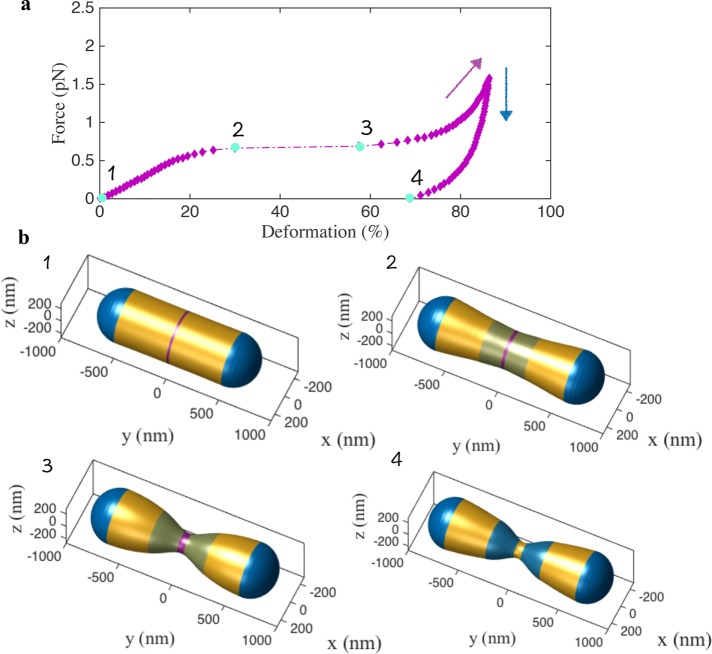
FIGURE 2:

Open in a new tab

Predicted role of actin–lipid cooperativity during membrane constriction. (a) The force-deformation curve shows a linear response in the initial phase but then undergoes a drastic snap-through transition around 30% deformation (from stage 2 to stage 3), indicating a classic buckling instability. The actin force domain is shown in magenta and the domains with higher lipid concentrations are shown in blue. After instability, the force deformation proceeds along a nonlinear curve with increasing stiffness (magenta arrow). Upon unloading (decreasing the actin force), the shape takes a new path (blue arrow), maintaining 68% deformation upon complete removal of the actin force (stage 4). This shows that the lipids arrest the constricted state preventing the spherocylinder from reverting to the undeformed configuration, thereby inducing a geometric plasticity. (b) The computed shapes at stages 1, 2, 3, and 4 during the force-deformation response shown in a.

The force-deformation response and the shape evolution are shown in Figure 2 (Supplemental Movie S1). The force-deformation curve (Figure 2a) presents the first key result that reveals a classic buckling instability. The constriction increases linearly up to ∼30% (Figure 2b-2), at which point it undergoes a rapid snap-through transition reaching nearly ∼58% constriction (Figure 2b-3). A further increase in the force and lipid concentration resumes constriction along a smooth curve (magenta arrow) with increasing slope indicating strain hardening. If we reduce the applied actin force, to simulate the cyclic nature of actin polymerization and depolymerization (Li et al., 2015; Moore et al., 2016), the geometry evolves along a curve different from the loading curve (blue arrow). Despite a complete removal of the actin force, there is a nearly ∼68% residual constriction in the spherocylinder (Figure 2b-4). This geometric plasticity arises from lipid localization and is critical to arrest the elastic tendency of the spherocylinder to expand back to its undeformed geometry and stabilizes the constricted geometry. In the absence of lipid aggregation, the spherocylinder reverts to the original undeformed shape upon actin depolymerization (Supplemental Figure S5). The details of the geometries in Figure 2 and the prescribed lipid curvatures are presented in Supplemental Figure S6.

Movie S1.

Download video file (243.9KB, mov)
Open in a new tab

Movie S1.

Drp1–lipid cooperativity

Next, we investigate the constriction induced by Drp1 and its synergy with the conical lipids. We continue from the ∼68% constricted geometry (diameter ∼160 nm) obtained in Figure 2 after actin depolymerization and gradually increase the circumferential curvature, stiffness, and the Drp1-coated area in the center of the spherocylinder to simulate Drp1-mediated squeezing (Figure 3b). As before, increased constriction is accompanied by an increase in lipid concentration in the adjacent (blue) domains. Because Drp1 polymerization is known to sequester CL (Stepanyants et al., 2015), we prescribe CL-induced curvature underneath the Drp1 coat. We simulate the polymerization phase until the geometry achieves ∼80% constriction reaching a diameter ∼94 nm, a value in the established range for Drp1 (Francy et al., 2015). We then split the Drp1 coat and move them apart. This splitting and moving apart of the Drp1 coat has been recently revealed in an in vivo study (Lee et al., 2016).

FIGURE 3:

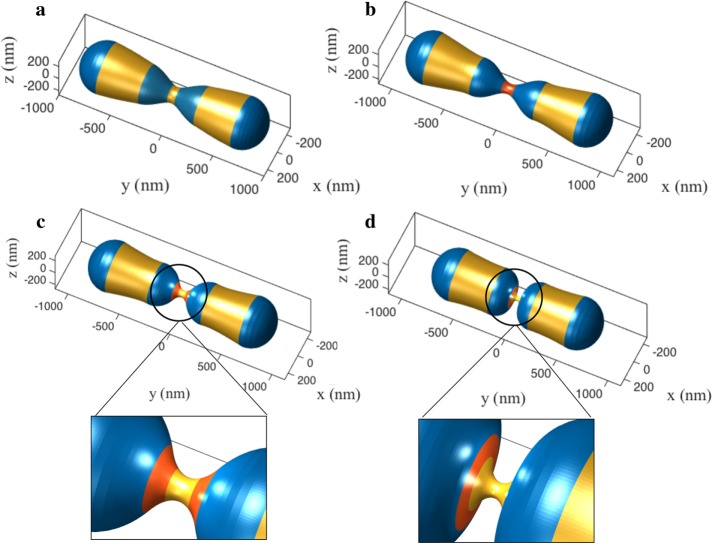
FIGURE 3:

Open in a new tab

Predicted role of Drp1-lipid cooperativity during the constriction process. (a) The deformation response due to Drp1 and lipid generated curvatures from the 68% constricted state obtained in Figure 2b-4. (b) During the first phase, the curvature and stiffness of the Drp1 coat and the lipid localization is increased, causing the constriction to undergo a monotonic increase. (c) In the second phase, the coat is split and the two domains are moved apart. (d) Upon reaching a critical separation, the shape undergoes a second buckling instability, which yields a highly constricted state. The insets show the zoomed-in view of the constrictions. The red domain indicates the Drp1-coated region, and the adjacent blue domains show the regions of lipid localization.

The deformation response shown in Figure 3 (Supplemental Movie S2) presents our second key finding. Drp1 polymerization, as per expectations, leads to a more constricted and elongated neck (Figure 3b). In contrast, the structure first expands mildly upon splitting and increased separation between the two Drp1 domains (Figure 3c). But at a critical separation, the system undergoes an unexpected second instability that significantly enhances the constriction leading to an extreme necking (Figure 3d; diameter ∼32 nm). This superconstricted geometry is a consequence of lipid enrichment in the blue domain, which has a natural propensity to close the tubule to form hemispherical geometry as on the poles. These results again reinforce the core notion that conical lipids can cooperatively act with another fission protein to induce instability and generate stable superconstrictions.

Movie S2.

Download video file (158.5KB, mov)
Open in a new tab

Movie S2.

Effect of dynamin 2

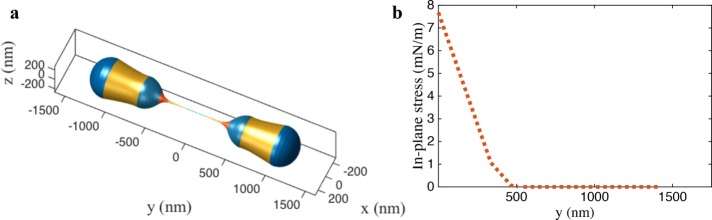
Finally, we model the effect of the dynamin 2 on mitochondrion squeezing. We assume that dynamin 2 constricts the tubule further, in a manner similar to Drp1. We start from the buckled geometry in Figure 3d. An increase in the cylindrical curvature brings the spherocylinder to the fission state with a tubule diameter ∼5 nm (Figure 4a and Supplemental Movie S3). Notably, the decrease in the radius results in a dramatic increase in the in-plane stress in the membrane to ∼8 mN/m (Figure 4b). For a membrane with a stretch modulus of 250 mN/m and an area extensibility of 3% (Rawicz et al., 2000), the rupture tension is nearly 7.5 mN/m. Thus, the squeezing by dynamin 2 brings the geometry very close to the rupture point, potentially resulting in the culmination of the fission reaction. It is important to note that the constriction of 5 nm diameter can also be reached in the absence of dynamin 2 with a higher lipid concentration. However, the in-plane stress remains nearly negligible despite the desired constriction (Supplemental Figure S7). This drastic increase in the stress in the presence of dynamin 2 suggests that a possible role of the final fission protein could be to accentuate the membrane stress to trigger the final dissociation of a mitochondrion into two daughter mitochondria.

FIGURE 4:

FIGURE 4:

Open in a new tab

Simulation of the final stage leading to membrane fission. (a) Dynamin 2–induced squeezing from the postbuckling shape presented in Figure 3. (b) Increased squeezing leads to extreme tubulation with near-rupture in-plane stress in the membrane.

Movie S3.

Download video file (296.6KB, mov)
Open in a new tab

Movie S3.

In vitro validation of protein–lipid cooperativity

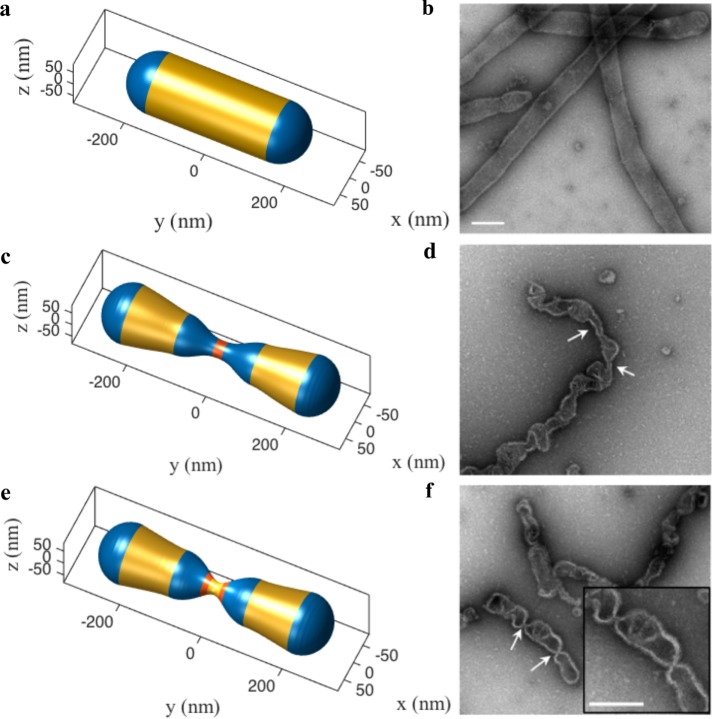
We now compare the numerically computed shapes with the shapes observed in in vitro experiments previously published by Ramachandran and coworkers (Stepanyants et al., 2015) to test the validity of the modeling predictions (Figure 5). The procedure is described in detail elsewhere (Stepanyants et al., 2015); briefly, liposomes composed of 35% PE, 25% CL, and 40% PC were preincubated with soluble Drp1 to allow for the formation of helical Drp1-decorated membrane spherocylinders. GTP hydrolysis was later initiated by the addition of GTP to these membranes tubules, and samples were obtained and negatively stained at defined time points for electron microscopy (EM) visualization. Because the in vitro setup lacks actin and dynamin 2 proteins, we subjected the membrane tubule (150 nm in diameter to match experimental geometry) to squeezing effect from Drp1 proteins and conical lipids only.

FIGURE 5:

FIGURE 5:

Open in a new tab

In vitro validation of protein–lipid cooperativity during membrane squeezing. We simulate the constriction of a 150-nm-radius spherocylinder in the presence of the squeezing effect of Drp1 and conical lipids to compare to in vitro results presented in Stepanyants et al. (2015). As before, the spherocylinder undergoes extreme necking via buckling instability triggered jointly by curvatures from Drp1 and conical lipids. (a) The simulated geometry of an undeformed spherocylinder. (b) EM micrograph of the undeformed tubules (Stepanyants et al., 2015). (c) An intermediate simulated shape (Drp1 domain in red and high lipid concentration domain in blue). (d) EM micrograph of constricted tubules (Stepanyants et al., 2015). It is important to note that both c and d show similar local undulations and constrictions. (e) The postbuckling shape obtained by splitting of the Drp1 coat. (f) EM micrograph of tubules with highly constricted necks (Stepanyants et al., 2015). The narrow necks and the geometry of the neighboring domains show excellent agreement. Scale bar, 200 nm.

Figure 5a shows the initial geometry and Figure 5, c and e, shows the geometries before and after the splitting of the Drp1 coat, respectively. As before, Figure 5e shows the extreme constriction upon reaching a critical separation between the split Drp1 domains leading to a stable superconstriction. The computed shapes in Figure 5, a, c, and e, show excellent agreement with in vitro shapes (Figure 5, b, d, and f). Not only are the superconstricted geometries in Figure 5, e and f, in excellent agreement, the irregular geometries with local bumps in Figure 5, c and d, show good resemblance.

Our computational predictions validate previous EM observations of Drp1-induced local membrane constrictions in mixed lipid bilayers containing conical lipids (Stepanyants et al., 2015), and strongly suggest that proteins and lipids act synergistically to create superconstrictions conducive for fission. It was also previously noted that in the absence of PE, no membrane constrictions were observed despite the presence of CL to bind Drp1 (Stepanyants et al., 2015). Guided by these combined predictions, we further investigated the role of conical lipids experimentally in membrane squeezing and stabilization. Consistent with our numerical assessment, under identical experimental conditions as earlier, but with a reduced concentration of PE (22.5%) in the membrane, no superconstrictions were observed despite the presence of a Drp1 helical coat enwrapping the tubulated membrane (Figure 6). The observed experimental shape, in fact, closely resembles the computed shape in the absence of lipid localization (Figure 6b). The formation of Drp1-dependent membrane necks at 35% PE, but not at 22.5% PE, further strongly suggests that adequate spherical curvature from conical lipids is essential for extreme membrane remodeling.

FIGURE 6:

FIGURE 6:

Open in a new tab

Experimental validation of the obligatory role of conical lipids in inducing necking. (a) EM micrograph showing an absence of necking in Drp1 polymer enwrapped membrane tubules with a lower concentration of PE lipids. PE concentration was reduced from 35% (results shown in Figure 5) to 22.5%. The concentrations of Drp1 and CL lipids were left unchanged (compared with experimental studies shown in Figure 5). (b) A simulated geometry with the split Drp1 coat in the absence of lipid localization. The experimental and computed shapes show good qualitative agreement.

DISCUSSION

In this study, we have systematically investigated the mechanics of protein–lipid-mediated squeezing in a dividing mitochondria-like spherocylinder. Our study reveals three key findings. First, conical lipids can act synergistically with fission proteins to trigger buckling instabilities. Second, buckling instabilities promote extreme necking and stabilize the constrictions by arresting the elastic tendency of the spherocylinder to revert to the undeformed geometry during protein polymerization and depolymerization cycles. Third, conical lipids can collaborate with different fission proteins to trigger hierarchical instabilities and step-by-step constriction (Figure 7). The presence of partial constriction and no necking in in vitro experiments with reduced concentrations of conical lipids corroborates the synergistic role of proteins and lipids in generating membrane constrictions.

FIGURE 7:

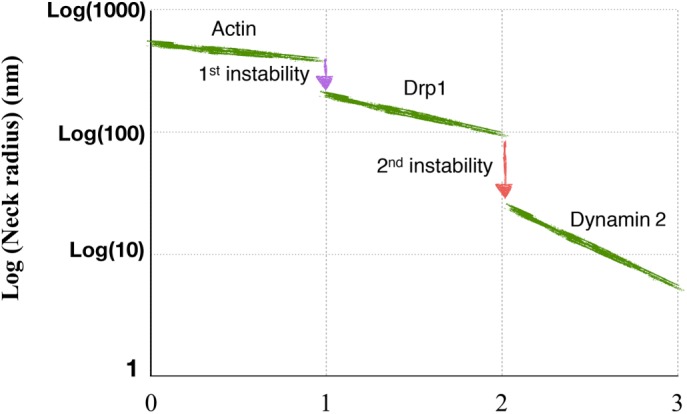
FIGURE 7:

Open in a new tab

Schematic summarizing the proposed shape transition pathway during the protein–lipid mediated fission of mitchondria. The study reveals that the conical lipids act synergistically with fission proteins to trigger hierarchical instabilities and generate step-by-step constrictions.

Are estimated lipid concentrations physiologically relevant?

To answer this critical question, we compute the changes in concentrations of conical lipids to achieve instabilities presented in Figures 2 and 3. While the modeling predictions are unable to distinguish between the lipid species required for instability and constriction, the in vitro finding that no constrictions are observed with a lower PE concentration (and regular CL concentration) suggests two possibilities: 1) PE is the key lipid contributing to fission, and 2) CL is the key lipid contributing to fission and PE concentration regulates CL sorting. The first scenario is discussed below, and the second scenario is presented in the Supplemental Material. We use the spontaneous curvature of PE lipids of 1/3 nm−1 (Zimmerberg and Kozlov, 2006) to get the estimates of lipid concentration and compare the variation in lipid concentration between the initial state (Figure 2b-1) and the state just at the onset of instabilities in the actin–lipid (Figure 2b-2) and Drp1–lipid (Figure 3c) squeezing phases. We emphasize again that the lipid concentrations discussed here are the concentration differences between the inner and the outer leaflets of the membrane and not their absolute concentrations in the leaflets.

For the initial geometry, we require 1.2 and 0.6% PE concentrations in the spherical cap and the cylindrical domains, respectively (Figure 8a). For the states just before instabilities in the actin–lipid and Drp1–lipid constriction phases, the concentration in the spherical domains remain unchanged but the concentration in the cylindrical domains reduces to 0.5 and 0.19%, respectively, and the concentration in the regions adjacent to the protein domain (blue domains next to the red domain) increases to 0.80 and 1.56%, respectively (Figure 8, b and c). This suggests that in comparison to the initial concentration of 0.6%, only 0.20 and 0.96% change in concentrations are required to trigger instabilities and achieve extreme necking. The analysis for CL lipids shows a similar qualitative behavior and the instability is achieved at lower values of lipid sorting (Supplemental Figure S8).

FIGURE 8:

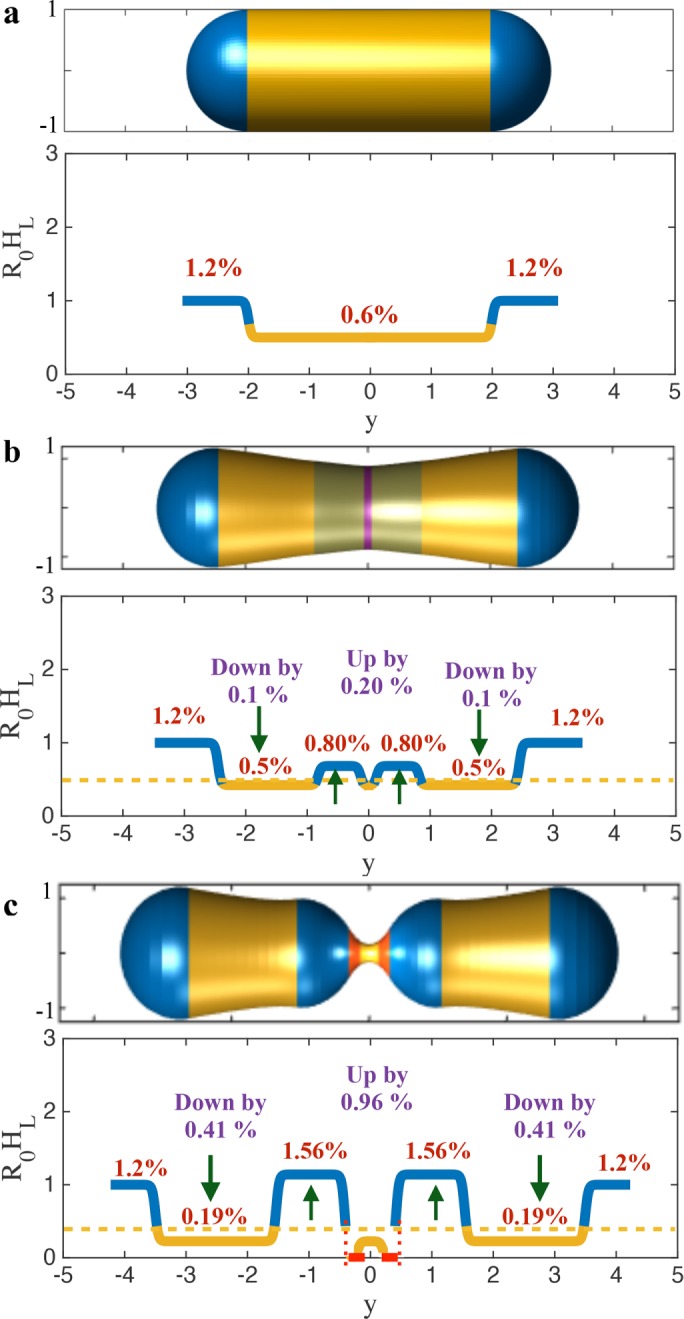
FIGURE 8:

Open in a new tab

Lipid requirements for the predicted geometric instabilities. (a) The initial geometry and the required PE concentrations.  For a tubule radius of 250 nm and PE lipid radius of curvature of 3 nm (Zimmerberg and Kozlov, 2006), the required (asymmetric) concentration is 1.2% in the hemispherical domain and 0.6% in the cylindrical domain. (b) The geometry before actin–lipid induced instability and the required PE concentrations. Only 0.20% change in the PE concentration is required in the domain adjacent to actin to trigger the instability. This increase is accompanied by a concomitant decrease in the PE concentration by 0.1% in the cylindrical domain. (c) The geometry before Drp1–lipid induced instability and the required PE concentrations. Only 0.96% change in the PE concentration is required in the domain adjacent to Drp1 to trigger the instability. This increase is accompanied by a concomitant decrease in the PE concentration by 0.41% in the cylindrical domain. These small changes in the areal concentration are sufficient to achieve extreme necking. It is important to note that the required PE lipids into the central blue domains can come from the nearby yellow domains and are not required to come from the blue domains at the poles. Thus, local rearrangement by ∼1.5% adjacent to the protein domain is enough to generate necking conducive for fission.

These numbers show that the interleaflet concentration difference required for achieving instability is minimal. Although we do not explicitly model the dynamics of lipids and their lipid distribution, the sorting of conical lipids has been revealed in both the experimental and the modeling studies. For example, coarse-grained molecular dynamics studies have revealed membrane-curvature–dependent lipid clustering (Koldsø et al., 2014; Boyd et al., 2017).

In addition, experimental studies have shown cardiolipin localization in high curvature domains of bacterial spheroplasts (Renner and Weibel, 2011) and strong asymmetric distribution of conical 1,2-dihexanoyl-sn-glycero-3-phosphocholine (DHPC) lipids (Sakuma et al., 2011). Furthermore, what our calculations suggest is that even if the curvature-based lipid sorting is weak, as was revealed in Kamal et al. (2009), lipids could still actively contribute to mitochondrial shape transitions. In fact, it is remarkable that the experimental study predicts a 4% asymmetry in 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine (DOPE) concentration in a vesicle of 100 nm radius (Kamal et al., 2009), which nearly coincides with the required asymmetric PE concentration to trigger instability in a similarly sized spherocylinder investigated in our in vitro study (data shown in Supplemental Figure S9).

Is the proposed mechanism robust?

We consider three extensions of the simulations presented earlier in the Results section. First, because mitochondria exhibit diverse shapes, we simulate the squeezing of a spherocylinder with varied aspect ratios (L0/2R0). The shape transitions for aspect ratios of 1.5 and 4 are shown in Supplemental Figures S10, S11, S12, and S13, respectively. These results again show the proposed sequential instabilities and the superconstriction as predicted for the case of a perfect spherocylinder. Second, we model a local increase in the concentration of conical lipids near the protein domain without any change of lipid concentration in the cylindrical domain. Such a scenario can potentially occur in two cases: 1) conical lipids are recruited from the ER at the constriction sites as proposed in the literature (Osman et al., 2011; Mesmin, 2016), and 2) proteins and membrane curvature either catalyze flipping of lipids between the leaflets or cluster lipids due to direct electrostatic interactions to give rise to an increased lipid asymmetry. The corresponding shape transitions during the actin–lipid and Drp1–lipid phases are shown in Supplemental Figures S14 and S15. As seen in Figures 2 and 3, the spherocylinder still undergoes sequential instabilities during the step-by-step constriction process. Third, we test the impact of the sizes of the protein-active area (actin and Drp1) and the lipid domains (adjacent blue domains) on shape transition. The results for the cases with 50% increase and 25% decrease in the domain sizes are shown in Supplemental Figures S16, S17, S18, and S19. Despite significant changes in sizes, the spheroyclinder undergoes similar instability-based constrictions. These results collectively suggest that the proposed mechanism is robust and is independent of the shape of the spherocylinder, the cause of lipid localization and variations in protein/lipid domain sizes.

Proposed mechanism requirement, rationale, and evidence

Our study reveals that an important requirement for the onset of instability is the aggregation of conical lipids in the inner leaflet adjacent to the protein-active domain. Thus, sequestration of CL underneath Drp1 coat observed in the experiments is not capable of triggering instability. This is a key prediction made by the computational model. The instability is a result of energetics, where the system prefers to undergo a large deformation in order to reach an energetically optimal state. This is driven by the conical lipids in the inner leaflet in the blue domains, which want the spherocylinder to close up. It is also important to note that the superconstricted shape is ideal for the conical lipid clusters and is a natural shape for the formation of daughter mitochondria.

As far as direct evidence is concerned, it is extremely difficult to identify an instability during a constriction process either in vitro or in vivo. To track instability, a continuous high-resolution time-dependent observation has to be made. However, remarkably, the study by Moore et al. (2016) shows constricted shapes of mitochondria in postactin phase in DRP1-deficient cells. This suggests that these constricted shapes are potentially stabilized via buckling instabilities mediated by lipids. The constricted tubules should otherwise rebound back to their original shapes due to the high elastic energy stored in the superconstricted domain. In addition, the in vitro results of Stepanyants et al. (2015) also clearly show constricted tubules after Drp1 depolymerization. Because there is no active force acting on the tubules in this phase, instability-­induced equilibrium shape is likely the explanation for the observed geometries.

General principles for membrane fission

Going beyond mitochondrial fission, the findings of this study reveal some general physical principles that may contribute to our understanding of membrane fission at-large. A significant number of fundamental studies have provided mechanistic insights into the constriction-fission mystery (see the recent review article Frolov et al., 2015, and the references therein). Although several of these studies have recognized the role of lipid properties in membrane fission (Huttner and Zimmerberg, 2001; Kozlov, 2001; Chernomordik and Kozlov, 2003; Allain et al., 2004; Roux et al., 2005; Frolov et al., 2011), the active role of spatially segregated conical lipids in inducing buckling instability to drive extreme membrane constriction has not been demonstrated before. In this regard, this work reveals three key principles. First, it is critical to invoke the correct sequence of curvatures. The protein-mediated squeezing has to precede the lipid localization in order to achieve constriction. The reverse sequence would lead to radial expansion of the membrane tubule. Second, it is favorable to have spatial segregation in the protein and lipid domains. This avoids “curvature conflict” in the same region, allowing proteins and lipids to impose their complementary curvatures more strongly. Third, disintegration of the protein coat is vital for triggering instability. After proteins supply the initial energy (by squeezing the membrane tubule) and prime the system (by modulating lipid distribution), they hinder the snap-through transition of the membrane due to their stiffening effect. Thus, it is desirable that coat-forming proteins either move apart or leave, allowing the lipids to undergo instability-driven extreme remodeling. These features are a consequence of the interplay between geometry and elasticity, and hence are of a generic nature.

Limitations

As is true for all models, our mathematical framework has some limitations. First, the analytical work presented in this study is based on an idealized mitochondrion that is modeled as a spherocylindrical shell. Similar modeling idealizations restricted to axisymmetric shapes have been routinely and successfully used in the literature before to gain mechanistic insights into the membrane physics literature (please see Kozlovsky and Kozlov, 2003, for example). However, it would be valuable to investigate the mechanics of more realistic nonaxisymmetric shapes in a larger phase space. Such generalization is likely to lead to quantitative changes in the predictions altering the numerical values of actin forces and lipid curvatures required to trigger shape transitions. Second, the model does not explicitly account for the physical forces that may arise from the architectural remodeling of the inner membrane during mitochondrial fission. The recent study from Higgs labs shows that the inner membrane undergoes fission even before Drp1 is recruited to the mitochondria (Chakrabarti et al., 2018). Thus, our predictions should be valuable to understand the subsequent constriction of the outer membrane. However, even if the inner membrane were to apply some internal resistance, the effect would lead to some internal pressure that would oppose constriction. This again, would only lead to quantitative changes in the predictions. Third, our model does not explicitly account for protein–lipid dynamics and membrane fission. As a result, we prescribe force and curvature fields and stop at a shape with a highly constricted neck, which should serve as a precursor to fission. Although the assumptions invoked to bypass these limitations have been well established and employed in several studies (cited in the text), computational models to investigate the dynamics of specific proteins and lipids of interest in the future would provide additional insights. In particular, a stochastic analysis of lipid–protein dynamics would be insightful to understand the interplay between protein kinetics and lipid dynamics giving more in-depth knowledge of energetic barriers in undergoing instabilities and shape transitions. Fourth, in this work, we have prescribed the aggregation of conical lipids at fission sites, and predicted its consequence on the squeezing transition. Although we have analyzed and presented a two-step process, it awaits rigorous in vivo validation. It is possible that the proposed curvature-based lipid aggregation mechanism is triggered only beyond a certain threshold curvature during the squeezing process. In such a scenario, if the actin-induced squeezing does not exceed the threshold curvature, lipid cooperativity and the induced first buckling during the actin phase might not be observed. However, due to the substantially greater curvature at mitochondrial fission sites in the Drp1 phase, we expect the second instability to occur with much higher probability.

In summary, our study reveals a hierarchical instability-based mechanism of membrane squeezing triggered jointly by proteins and conical lipids. Despite various complexities, our findings might be of value to understanding mitochondrial fission in vivo. The in vitro studies lend support to our modeling predictions. We hope that our work will stimulate more biophysical studies to explore the role of conical lipids and their interactions with mitochondrial proteins during shape transformations observed in apoptosis and mitochondria-associated diseases. In a general context, our work might give new insights into other topological events during cellular transport and remodeling of cellular organelles driven by curvature-inducing proteins and lipids (McMahon and Gallop, 2005; Zimmerberg and Kozlov, 2006).

MATERIALs AND METHODS

We resort to continuum-scale modeling as it possesses the unique ability to quantify the roles of proteins and lipids without getting overwhelmed with the molecular details. The continuum approach has been successfully used to study actin-induced mitochondrial constriction (Manor et al., 2015) and the intricate architecture of the mitochondrial inner membrane and endoplasmic reticulum (Frey et al., 2002; Renken et al., 2002; Ponnuswamy et al., 2005; Terasaki et al., 2013). We model a mitochondrion as a hollow spherocylinder (a cylinder capped with hemispheres at the two ends; see Figure 1b) made of lipid membrane, which undergoes shape transition in the presence of known shape remodeling effects of fission proteins and conical lipids. This assumption is supported by the recent study from Higgs labs that reveals that the inner membrane undergoes fission even before Drp1 is recruited to the mitochondria (Chakrabarti et al., 2018).

A lipid membrane is treated as a 2D elastic fluid surface. The strain energy for such a surface depends on the local curvatures of the surface. In regions where the membrane possesses isotropic properties, strain energy depends on the two curvature invariants: the mean curvature (H) and the Gaussian curvature (K) (Canham, 1970; Helfrich, 1973; Jenkins, 1977; Lipowsky, 1991; Steigmann, 1999). 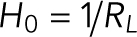Because conical lipids such as CL, PE, and DAG generate spherical curvatures (Figure 1c) that remain invariant in all the directions, the strain energy in CL/PE-rich domains is given by the well-known Helfrich–Canham energy Inline graphic, where Inline graphic is the spontaneous curvature imposed by the lipids and 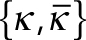Inline graphic are the bending moduli. A detailed explanation for why conical lipids will generate spherical curvatures as opposed to cylindrical curvatures is provided in the Supplemental Material (Supplemental Figure S1). In the current model, the spontaneous curvature generated by lipids is assumed to be proportional to the difference in their concentrations between the two leaflets (Supplemental Figure S2). Therefore, hereafter we refer to this asymmetric distribution of the conical lipids as lipid concentration. Also, the conical lipids are treated alike (Figure 1c) as the differences in the architecture of individual lipid species will only manifest as different prescribed values of the spontaneous curvature (H0). In regions where membranes lose isotropy and interact with proteins that form ring-like structures and generate cylindrical curvatures, the strain energy depends on an additional curvature invariant, called the curvature deviator (D; Kralj-Iglicˇ et al., 1999; Fošnaric et al., 2005; Walani et al., 2014). Because the contractile actin ring and Drp1 would generate distinct curvatures in the circumferential and the longitudinal directions (Figure 1d), the strain energy in the protein-rich domain is given by 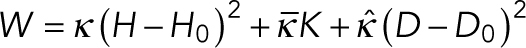Inline graphic, where 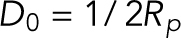Inline graphic is the spontaneous curvature and 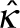Inline graphic is the bending moduli associated with the curvature deviator. The squeezing effect of actin and actomyosin is explicitly modeled via a force f acting on the membrane (Figure 2d; Walani et al., 2015). Because the orientation of the force at the ER contact sites is not known, we simulate two potential orientations (defined by α; Figure 1e).

One of the key features of our mathematical framework is that it allows spontaneous curvatures and bending moduli to depend on the surface coordinates, thus allowing seamless modeling of membrane heterogeneity, a feature critical to assessing the nuances of extreme localized remodeling. Because lipid membranes can undergo only 2–3% areal dilation before rupture, we impose areal incompressibility. We construct the system free energy and minimize it to obtain the Euler–Lagrange equations. We simplify the equations for the axisymmetric setting (Supplemental Figure S3) and compute the shape evolution of the idealized spherocylindrical mitochondrion. The simulations are quasistatic and deterministic in nature. The initial spherocylindrical geometry is obtained by prescribing two distinct conical lipid concentrations in the hemispherical and cylindrical domains. Here, we assume that a higher areal density of conical lipids leads to higher effective spontaneous curvatures. Further details of the model are presented in the Supplemental Material.

Supplementary Material

Click here for additional data file. (6.6MB, pdf)

Acknowledgments

This work was supported by National Science Foundation Grants no. CMMI 1437330 and no. CMMI 1562043 (to A.A.) and by National Institutes of Health Grant no. R01 GM-121583 (to R.R). R.R. acknowledges the Jason Mears lab (Case Western Reserve University) for assistance with EM.

Abbreviations used:

CL

cardiolipin

DAG

diacylglycerol

DHPC

1,2-dihexanoyl- sn-glycero-3-phosphocholine

DOPE

1,2-dioleoyl- sn-glycero-3-phosphoethanolamine

Drp1

dynamin-related protein 1

EM

electron microscopy

ER

endoplasmic reticulum

GTP

guanosine triphosphate

PC

phosphocholine

PE

phosphatidylethanolamine

Footnotes

This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E18-01-0018) on October 31, 2018.

REFERENCES

  1. Adachi Y, Itoh K, Yamada T, Cerveny KL, Suzuki TL, Macdonald P, Frohman MA, Ramachandran R, Iijima M, Sesaki H. (2016). Coincident phosphatidic acid interaction Restrains Drp1 in mitochondrial division. Mol Cell , 1034–1043. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Allain J-M, Storm C, Roux A, Amar MB, Joanny J-F. (2004). Fission of a multiphase membrane tube. Phys Rev Lett , 158104. [DOI] [PubMed] [Google Scholar]
  3. Boyd KJ, Alder NN, May ER. (2017). Buckling under pressure: curvature-based lipid segregation and stability modulation in cardiolipin-containing bilayers. Langmuir , 6937–6946. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Canham PB. (1970). The minimum energy of bending as a possible explanation of the biconcave shape of the human red blood cell. J Theor Biol , 61–81. [DOI] [PubMed] [Google Scholar]
  5. Chakrabarti R, Ji W-K, Stan RV, de Juan Sanz J, Ryan TA, Higgs HN. (2018). INF2-mediated actin polymerization at the ER stimulates mitochondrial calcium uptake, inner membrane constriction, and division. J Cell Biol , 251–268. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Chan EYL, McQuibban GA. (2012). Phosphatidylserine decarboxylase 1 (Psd1) promotes mitochondrial fusion by regulating the biophysical properties of the mitochondrial membrane and alternative topogenesis of mitochondrial genome maintenance protein 1 (Mgm1). J Biol Chem , 40131–4039. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Chernomordik LV, Kozlov MM. (2003). Protein-lipid interplay in fusion and fission of biological membranes. Annu Rev Biochem , 175–207. [DOI] [PubMed] [Google Scholar]
  8. Choi S-Y, Huang P, Jenkins GM, Chan DC, Schiller J, Frohman MA. (2006). A common lipid links Mfn-mediated mitochondrial fusion and SNARE-regulated exocytosis. Nat Cell Biol , 1255. [DOI] [PubMed] [Google Scholar]
  9. Fošnaric M, Bohinc K, Gauger DR, Iglic A, Kralj-Iglic V, May S. (2005). The Influence of anisotropic membrane inclusions on curvature elastic properties of lipid membranes. J Chem Inf Model , 1652–1661. [DOI] [PubMed] [Google Scholar]
  10. Francy CA, Alvarez FJD, Zhou L, Ramachandran R, Mears JA. (2015). The mechanoenzymatic core of dynamin-related protein 1 comprises the minimal machinery required for membrane constriction. J Biol Chem , 11692–11703. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Frey TG, Renken CW, Perkins GA. (2002). Insight into mitochondrial structure and function from electron tomography. Biochim Biophys Acta , 196–203. [DOI] [PubMed] [Google Scholar]
  12. Frohman MA. (2015). Role of mitochondrial lipids in guiding fission and fusion. J Mol Med , 263–269. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Frolov VA, Escalada A, Akimov SA, Shnyrova AV. (2015). Geometry of membrane fission. Chem Phys Lipids , 129–140. [DOI] [PubMed] [Google Scholar]
  14. Frolov VA, Shnyrova AV, Zimmerberg J. (2011). Lipid polymorphisms and membrane shape. Cold Spring Harb Perspect Biol , a004747. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Gohil VM, Thompson MN, Greenberg ML. (2005). Synthetic lethal interaction of the mitochondrial phosphatidylethanolamine and cardiolipin biosynthetic pathways in Saccharomyces cerevisiae. J Biol Chem , 35410–35416. [DOI] [PubMed] [Google Scholar]
  16. Guo T, Gregg C, Boukh-Viner T, Kyryakov P, Goldberg A, Bourque S, Banu F, Haile S, Milijevic S, San KH, et al (2007). A signal from inside the peroxisome initiates its division by promoting the remodeling of the peroxisomal membrane. J Cell Biol , 289–303. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Helfrich W. (1973). Elastic properties of lipid bilayers: theory and possible experiments. Z Naturforsch C , 693–703. [DOI] [PubMed] [Google Scholar]
  18. Huang H, Gao Q, Peng X, Choi S-Y, Sarma K, Ren H, Morris AJ, Frohman MA. (2011). PiRNA-associated germline nuage formation and spermatogenesis require MitoPLD profusogenic mitochondrial-surface lipid signaling. Dev Cell , 376–387. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Huttner WB, Zimmerberg J. (2001). Implications of lipid microdomains for membrane curvature, budding and fission: commentary. Curr Opin Cell Biol , 478–484. [DOI] [PubMed] [Google Scholar]
  20. Itoh K, Nakamura K, Iijima M, Sesaki H. (2013). Mitochondrial dynamics in neurodegeneration. Trends Cell Biol , 64–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Jenkins JT. (1977). The equations of mechanical equilibrium of a model membrane. SIAM J Appl Math , 755–764. [Google Scholar]
  22. Joshi AS, Thompson MN, Fei N, Hüttemann M, Greenberg ML. (2012). Cardiolipin and mitochondrial phosphatidylethanolamine have overlapping functions in mitochondrial fusion in Saccharomyces cerevisiae. J Biol Chem , 17589–17597. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Kamal MM, Mills D, Grzybek M, Howard J. (2009). Measurement of the membrane curvature preference of phospholipids reveals only weak coupling between lipid shape and leaflet curvature. Proc Natl Acad Sci USA , 22245–22250. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Koldsø H, Shorthouse D, Hélie J, Sansom MSP. (2014). Lipid clustering correlates with membrane curvature as revealed by molecular simulations of complex lipid bilayers. PLoS Comput Biol , e1003911. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Kozlov MM. (2001). Fission of biological membranes: interplay between dynamin and lipids. Traffic , 51–65. [DOI] [PubMed] [Google Scholar]
  26. Kozlovsky Y, Kozlov MM. (2003). Membrane fission: model for intermediate structures. Biophys J , 85–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Kralj-Iglicˇ V, Heinrich V, Svetina S, Žekš B. (1999). Free energy of closed membrane with anisotropic inclusions. Eur Phys J B , 5–8. [Google Scholar]
  28. Kraus F, Ryan MT. (2017). The constriction and scission machineries involved in mitochondrial fission. J Cell Sci , 2953–2960. [DOI] [PubMed] [Google Scholar]
  29. Labbé K, Murley A, Nunnari J. (2014). Determinants and functions of mitochondrial behavior. Annu Rev Cell Dev Biol , 357–391. [DOI] [PubMed] [Google Scholar]
  30. Lee JE, Westrate LM, Wu H, Page C, Voeltz GK. (2016). Multiple dynamin family members collaborate to drive mitochondrial division. Nature , 139–143. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Li S, Xu S, Roelofs BA, Boyman L, Lederer WJ, Sesaki H, Karbowski M. (2015). Transient assembly of F-actin on the outer mitochondrial membrane contributes to mitochondrial fission. J Cell Biol , 109–123. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Lipowsky R. (1991). The conformation of membranes. Nature , 475–481. [DOI] [PubMed] [Google Scholar]
  33. Lu B, Kennedy B, Clinton RW, Wang EJ, McHugh D, Stepanyants N, Macdonald PJ, Mears JA, Qi X, Ramachandran R. (2018). Steric interference fromi disordered regions controls dynamin-related protein 1 self-assembly during mitochondrial fission. Sci Rep , 10879. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Macdonald PJ, Stepanyants N, Mehrotra N, Mears JA, Qi X, Sesaki H, Ramachandran R. (2014). A dimeric equilibrium intermediate nucleates Drp1 reassembly on mitochondrial membranes for fission. Mol Biol Cell , 1905–1915. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Manor U, Bartholomew S, Golani G, Christenson E, Kozlov M, Higgs H, Spudich J, Lippincott-Schwartz J. (2015). A mitochondria-anchored isoform of the actin-nucleating spire protein regulates mitochondrial division. Elife , e08828. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. McBride HM, Frost A. (2016). Cell biology: double agents for mitochondrial division. Nature , 43. [DOI] [PubMed] [Google Scholar]
  37. McMahon HT, Gallop JL. (2005). Membrane curvature and mechanisms of dynamic cell membrane remodelling. Nature , 590–596. [DOI] [PubMed] [Google Scholar]
  38. Mesmin B. (2016). Mitochondrial lipid transport and biosynthesis: a complex balance. J Cell Biol , 9–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Moore AS, Wong YC, Simpson CL, Holzbaur ELF. (2016). Dynamic actin cycling through mitochondrial subpopulations locally regulates the fission-fusion balance within mitochondrial networks. Nat Commun , 12886. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Mukhopadhyay R, Huang KC, Wingreen NS. (2008). Lipid localization in bacterial cells through curvature-mediated microphase separation. Biophys J , 1034–1049. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Osman C, Voelker DR, Langer T. (2011). Making heads or tails of phospholipids in mitochondria. J Cell Biol , 7–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Ponnuswamy A, Nulton J, Mahaffy JM, Salamon P, Frey TG, Baljon ARC. (2005). Modeling tubular shapes in the inner mitochondrial membrane. Phys Biol , 73. [DOI] [PubMed] [Google Scholar]
  43. Ramachandran R. (2018). Mitochondrial dynamics: the dynamin superfamily and execution by collusion. Semin Cell Dev Biol , 201–212. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Rawicz W, Olbrich KC, McIntosh T, Needham D, Evans E. (2000). Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys J , 328–339. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Renken C, Siragusa G, Perkins G, Washington L, Nulton J, Salamon P, Frey TG. (2002). A thermodynamic model describing the nature of the crista junction: a structural motif in the mitochondrion. J Struct Biol , 137–144. [DOI] [PubMed] [Google Scholar]
  46. Renner LD, Weibel DB. (2011). Cardiolipin microdomains localize to negatively curved regions of Escherichia coli membranes. Proc Natl Acad Sci USA , 6264–6269. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Roux A, Cuvelier D, Nassoy P, Prost J, Bassereau P, Goud B. (2005). Role of curvature and phase transition in lipid sorting and fission of membrane tubules. EMBO J , 1537–1545. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Sakuma Y, Urakami N, Taniguchi T, Imai M. (2011). Asymmetric distribution of cone-shaped lipids in a highly curved bilayer revealed by a small angle neutron scattering technique. J Phys: Condens Matter , 284104. [DOI] [PubMed] [Google Scholar]
  49. Schlame M, Ren M. (2009). The role of cardiolipin in the structural organization of mitochondrial membranes. Biochim Biophys Acta , 2080–2083. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Steenbergen R, Nanowski TS, Beigneux A, Kulinski A, Young SG, Vance JE. (2005). Disruption of the phosphatidylserine decarboxylase gene in mice causes embryonic lethality and mitochondrial defects. J Biol Chem , 40032–40040. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Steigmann DJ. (1999). Fluid films with curvature elasticity. Arch Ration Mech Anal , 127–152. [Google Scholar]
  52. Stepanyants N, Macdonald PJ, Francy CA, Mears JA, Qi X, Ramachandran R. (2015). Cardiolipin's propensity for phase transition and its reorganization by dynamin-related protein 1 form a basis for mitochondrial membrane fission. Mol Biol Cell , 3104–3116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Tasseva G, Bai HD, Davidescu M, Haromy A, Michelakis E, Vance JE. (2013). Phosphatidylethanolamine deficiency in mammalian mitochondria impairs oxidative phosphorylation and alters mitochondrial morphology. J Biol Chem , 4158–4173. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Terasaki M, Shemesh T, Kasthuri N, Klemm RW, Schalek R, Hayworth KJ, Hand AR, Yankova M, Huber G, Lichtman JW, et al (2013). Stacked endoplasmic reticulum sheets are connected by helicoidal membrane motifs. Cell , 285–296. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. van der Veen JN, Lingrell S, da Silva RP, Jacobs RL, Vance DE. (2014). The concentration of phosphatidylethanolamine in mitochondria can modulate ATP production and glucose metabolism in mice. Diabetes , 2620–2630. [DOI] [PubMed] [Google Scholar]
  56. Walani N, Torres J, Agrawal A. (2014). Anisotropic spontaneous curvatures in lipid membranes. Phys Rev E , 62715. [DOI] [PubMed] [Google Scholar]
  57. Walani N, Torres J, Agrawal A. (2015). Endocytic proteins drive vesicle growth via instability in high membrane tension environment. Proc Natl Acad Sci USA , E1423–E1432. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Youle RJ, van der Bliek AM. (2012). Mitochondrial fission, fusion, and stress. Science , 1062–1065. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Zimmerberg J, Kozlov MM. (2006). How proteins produce cellular membrane curvature. Nat Rev Mol Cell Biol , 9–19. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Click here for additional data file. (6.6MB, pdf)

Articles from Molecular Biology of the Cell are provided here courtesy of American Society for Cell Biology

RESOURCES