Nonlinear Distributional Mapping (NoDiM) for harmonization across amyloid-PET radiotracers

Abstract

Introduction:

There is a growing need in clinical research domains for direct comparability between amyloid-beta (Aβ) Positron Emission Tomography (PET) measures obtained via different radiotracers and processing methodologies. Previous efforts to provide a common measurement scale fail to account for non-linearities between measurement scales that can arise from these differences. We introduce a new application of distribution mapping, based on well established statistical orthodoxy, that we call Nonlinear Distribution Mapping (NoDiM). NoDiM uses cumulative distribution functions to derive mappings between Aβ-PET measurements from different tracers and processing streams that align data based on their location in their respective distributions.

Methods:

Utilizing large datasets of Florbetapir (FBP) from the Alzheimer’s Disease Neuroimaging Initiative (n=349 female(%) = 53) and Pittsburgh Compound B (PiB) from the Harvard Aging Brain Study (n= 305 female(%) = 59.3) and the Australian Imaging, Biomarker & Lifestyle Flagship Study of Ageing (n=184 female(%)=53.3), we fit explicit mathematical models of a mixture of two normal distributions, with parameter estimates from Gaussian Mixture Models, to each tracer’s empirical data. We demonstrate the accuracy of these fits, and then show the ability of NoDiM to transform FBP measurements into PiB-like units.

Results:

A mixture of two normal distributions fit both the FBP and PiB empirical data and provides a strong basis for derivation of a transfer function. Transforming Aβ-PET data with NoDiM results in FBP and PiB distributions that are closely aligned throughout their entire range, while a linear transformation does not. Additionally the NoDiM transform better matches true positive and false positive profiles across tracers.

Discussion:

The NoDiM transformation provides a useful alternative to the linear mapping advocated in the Centiloid project, and provides improved correspondence between measurements from different tracers across the range of observed values. This improved alignment enables disparate measures to be merged on to continuous scale, and better enables the use of uniform thresholds across tracers.

1. INTRODUCTION

Positron emission tomography (PET) based molecular imaging of Alzheimer’s disease (AD) pathology is a vital tool for AD research, diagnosis, and clinical trials (Johnson et al., 2016; Klunk et al., 2004; Sperling et al., 2014a). PET imaging of the fibrillar β-amyloid (Aβ) protein is one of the primary screening and outcome measurements in primary and secondary prevention trials for AD (Sperling et al., 2014b), however difficulties in applying prior research due to issues of translation, comparison, and communication of Aβ-PET values (Klunk et al., 2015; Landau et al., 2013) remains a challenge. For instance, differences in scanning equipment (Joshi et al., 2009), processing methodology (Su et al., 2018), and radiotracer (Landau et al., 2014; Maass et al., 2017) create variations in the distribution of measured values. These issues are potentially magnified by the wide variety of Aβ-PET tracers in use (Johnson et al., 2013). Currently, three F-18 based Aβ-PET ligands are FDA approved and are widely used in clinical trials: florbetapir (FBP) (Clark et al., 2011); flutemetamol (Vandenberghe et al., 2010); and florbetaben (Rowe et al., 2008). C-11 Pittsburgh Compound B (PiB) (Klunk et al., 2004), is the current gold standard for Aβ-PET radiotracers. These ligands exhibit differences in dynamic range, measurement noise, off-target binding, and non-specific binding. As such, typical values of Aβ-PET positive values can range from 0.8 (Brendel et al., 2015) to 2.5 (Jack et al., 2013) standardized uptake value ratio (SUVr) depending on the processing methodology, target region, reference region, and ligand (Landau et al., 2015; Villemagne et al., 2014), which makes it problematic to discern the exact level of Aβ burden that a particular value is referring to.

To address these issues, the Centiloid project(Klunk et al., 2015) developed a standardized scale to facilitate the uniform reporting of Aβ-PET measures and allow the merging of large publicly available datasets such as the Australian Imaging, Biomarker & Lifestyle Flagship Study of Ageing (AIBL) and Alzheimer’s Disease Neuroimaging Initiative (ADNI). The Centiloid project established an arbitrary reference scale based on a reference PiB dataset, a prescribed processing methodology, and a linear transform that established 0 and 100 as the respective “typical” values of negative controls versus AD patients in the reference dataset (http://www.gaain.org/centiloid-project). Centiloid measures can thus be interpreted as an approximate percent signal of a typical AD patient from the reference sample, though it is important to note that the measurement range is not bounded by 0 and 100 but rather anchored at these two fixed points. Other Aβ-PET measures (with different processing, reference regions, etc.) are then mapped to this reference scale via linear transforms derived from comparisons of the same source data from different processing pipelines. For other tracers, paired sample datasets of individuals with both PiB and another tracer are used to derive linear fits that map the other tracer to PiB like units, and then the Centiloid transform is applied. In this way the 0 and 100 points of the scale remain invariant and always refer to the original PiB reference dataset.

The Centiloid mapping is based entirely on linear transforms, which are not appropriate in all cases. In particular when measurement variability is not scaled uniformly across the range of values it is a strong indication that measurements from two tracers or scales cannot be mapped onto one another with a single uniform slope. This phenomena can be particularly noticeable when comparing the ratio of variances of low amyloid groups across measurement scales to high amyloid groups across measurement scales. For instance a method may result in a larger range of high values while having little effect on the variability of low amyloid values, implying the need for two slopes to model low and high amyloid relations or some true non-linear function. These types of scaling differences can arise from spatial normalization approaches, atlas based regional definitions, tissue probabilities, and partial volume correction (Greve et al., 2016). In addition, when mapping between tracers, differences in dynamic range (Landau et al., 2013), non-specific binding, and off-target binding (Tolboom et al., 2009) create non-trivial differences in measurement scaling. The result of applying a linear transform in these situations can result in systematic under or over estimation of Aβ signal, particularly in the lower ranges of PET signal, as the linear transforms are biased to the larger measurement variance in the high Aβ group. This mismatch in low and intermediate ranges can create incongruencies between measurements across the range and notably in boundaries between low and high distributions where thresholds are commonly placed. In short the centiloid scale with chained linear transforms only guarantees a common range for Aβ measurements based on two fixed points at 0 and 100. However, as these fixed points are based on the means of the AD and control groups, it does not guarantee common upper or lower bounds beyond those points or that the actual measurement scales are comparable as one moves away from them.

Su et al. (Su et al., 2018) demonstrated this by applying a range of analytical approaches to a PiB-PET dataset. They found that different processing and analytical schemes produced different group means and variances after mapping data to the centiloid scale. They also report the thresholds, derived independently on data from different analytical approaches varied from 5.7 to 11.9 Centiloids (CL) and the “reliable worsening” threshold (Jack et al., 2017) varied from −2 to 11 CL. The implication is that even when dealing with the same dataset, conversion to centiloids can only engender similarity of measurement and not direct comparability. These deviations are likely to worsen across datasets, across sites, and across tracers, and impair the ability of researchers to meaningfully communicate and interpret values in the literature.

To address the issue of creating a common scale and to provide a uniform framework for cross-tracer mapping in general, we developed and here introduce the Nonlinear Distributional Mapping (NoDiM) method. NoDiM derives mappings between tracers from the distributional properties of the measurements using well established statistical orthodoxy. In particular NoDiM uses a mapping that equates values at equal points of probability (i.e. rank) to recover a transform that maps between measures so as to make the cumulative and probability distribution functions equivalent. We recently applied this method to combine FBP and PiB Aβ-PET data across three large, well characterized cohorts including ADNI, AIBL, and the Harvard Aging Brain Study (HABS) (Buckley et al., 2018).

In this report, we present a detailed exposition of the NoDiM method for translating measurements from separate but related Aβ-PET measurements onto a common scale. We used datasets that are highly comparable to each other to demonstrate its efficacy, though in order to maintain this comparability between cohorts, this initial methodological exposition excludes symptomatic subjects. Our approach creates a distribution based mapping, using an assumption of approximate rank ordering, which implicitly accounts for any non-linear associations in scale, variance, and dynamic range that may occur. Importantly this method does not require paired sample datasets, though there is a need for larger datasets. For the purposes of the present report, we will focus on translation between PiB and FBP, although the methods we present are applicable to any set of comparable tracers, including between tracers for other molecular pathologies such as tau.

2. METHODS & RESULTS

2.1. Empirical data: PiB and FBP datasets

For testing cross-tracer mapping, we used Aβ-PET data from three large longitudinal aging and AD cohorts: ADNI, AIBL, and HABS. For the purposes of this study we will only describe the participants from the cohorts that fulfilled criteria relating to their Aβ-PET scan. We accessed raw imaging data for ADNI and AIBL directly from LONI (http://loni.usc.edu/). AIBL and ADNI data collection methodology has been previously reported (Aisen et al., 2010; Ellis et al., 2009). For HABS, the data acquisition parameters are described below (Dagley et al., 2017).

The combined number of participants in our study was 838 clinically-normal older adults (ADNI: 349, AIBL: 184, HABS: 305), with an age range of 55–94 years (Female (%) = 55.4; Clinical Dementia Rating score = 0). This restriction to clinically normal older adults was undertaken to ensure comparability between the samples, as HABS, which comprises the majority of the PIB sample, contains only asymptomatic subjects at baseline. ADNI includes a subjective cognitive decline group, which was included as clinically-normal in the current study.

We conducted the procedures for this study under the ethical guidelines stipulated by the Partners Human Research Committee, which is the Institutional Review Board for the Massachusetts General Hospital and Brigham and Women’s Hospital.

2.2. Cohort demographics

Clinically-normal ADNI participants were significantly older than AIBL and HABS participants (p<0.001; see Table 1), and AIBL participants were significantly less educated than ADNI and HABS participants (p<0.001). AIBL participants also showed slightly higher proportions of apolipoprotein ε4 (APOE 4) carrier status (p=0.03) due to their recruitment strategy (Ellis et al., 2009).

Table 1.

Demographic information for ADNI, AIBL and HABS cohorts

	n	Whole Group	Across Cohorts
Study	838		ADNI (n=349)	AIBL (n=184)	HABS(n=305)
Age	838	73.2(6.8)	74.7 (6.6)*	72.5 (6.7)	73.3 (6.9)	<0.001
Sex F	838	55.4%	53%	53.3%	59.3%	0.216
Education	838	15.55(2.94)	16.4(2.64)	13.5(2.30)*	15.8(3.01)	<0.001
APOEε4 Carrier	783	29.8%	26.9%	37.5%*	28%	0.03
High Aβ (%)	838	29.7%	28.1%	34.8%	28.5%	0.23

2.3. Scan Acquisition

Aβ-PET images from ADNI were acquired using FBP-PET, while HABS and AIBL used PiB-PET; details of the acquisition protocols and preprocessing have been previously published (Dagley et al., 2017; Landau et al., 2012; Rowe et al., 2010). Each study used the following scan and acquisition parameters: For ADNI, FBP images were acquired using 20 minute continuous image acquisition beginning 50 minutes post injection; For AIBL, PiB-PET images were acquired using a 30 minute acquisition starting 40 minutes post injection. From this 30-minute acquisition, summed 50–70 minute SUVr images were created and processed; and for HABS, PiB-PET images were acquired with a 60-minute dynamic acquisition starting directly post injection. For this study, HABS PiB-PET measures were computed as SUVrs for the 40–60 minute post injection window.

Note that AIBL and HABS use different post injection PiB acquisition windows, so the distributions may be slightly shifted between the two cohorts. A minor linear adjustment (PiB5070 = PiB4060 * 1.036 – 0.177), details of which are contained in supplemental B, was performed on the HABS PiB data after conducting a separate analysis on the GAAIN Centiloid PiB dataset (http://www.gaain.org/centiloid-project). All analyses were conducted with and without this adjustment, with patterns of findings unaffected.

2.4. Image Processing

All Aβ-PET images were realigned, summed, and spatially normalized to standard template space using SPM12’s unified segmentation method (SPM12 (r7219): http://www.fil.ion.ucl.ac.uk/spm/). Region of interest measurements were made using a customized probabilistic template space atlas from 270 clinically normal elderly subjects from the HABS study based on Freesurfer segmentations. All 270 subjects underwent Freesurfer processing on their T1-weighted MPRAGE data including generation of the FS-GTM atlas (Greve et al., 2016). The native space FS-GTM atlas for each subject was normalized to template space via the SPM12 unified segmentation/normalization tool derived from the subjects T1-MPRAGE image. We then computed a group level template space atlas by assigning each template space voxel to the label that most frequently occurred across the 270 subjects. This template space atlas, based largely on the Desikan-Kiliany atlas (Desikan et al., 2013; Fischl et al., 2002), and described in detail in Greve, et al. (Greve et al., 2016), was then used to define both target and reference regions in template space for both FBP and PiB. As target region, we used the so called FLR (Frontal-Lateral-Retrosplenial)(Buckley et al., 2017; Mormino et al., 2014a; Schultz et al., 2017) which contains: inferior temporal, middle temporal, superior temporal, banks of superior temporal sulcus, transverse temporal, supramarginal, inferior parietal, superior parietal, insula, lateral orbitofrontal, pars orbitalis, pars triangularis, pars opercularis, caudal middle frontal, rostral middle frontal, superior frontal, medial orbitofrontal, rostral anterior cingulate, caudal anterior cingulate, posterior cingulate, precuneus, and isthmus cingulate. The global Aβ value for each subject was then expressed as a standardized uptake value ratio (SUVr), using whole cerebellum as the reference region, consistent with previous work on ADNI FBP data (Landau et al., 2012). Note that this processing stream differs from the standard centiloid approach which uses T1 weighted MRIs and SPM8’s “Normalize” method for non-linear warping(Klunk et al., 2015), and a data driven target region defined using group differences between AD and control subjects.

In order to illustrate the NoDiM approach we will first explore the theories salient to this method, followed by their application in the aforementioned three well characterised cohorts.

2.5. Distribution Based Theory

If we make two assumptions: 1) that rank ordering between two measurement scales is approximately preserved, and 2) that the sample distributions comprising the two measurement scales are equivalent, we can derive a mapping between the two measurement scales where they are equated based on values of equal rank. The rank-based mapping can be elegantly captured both conceptually and mathematically by the cumulative distribution function (CDF), which describes the probability of observing a value less than any given x. The first derivative of the CDF provides the probability density function which corresponds to the more familiar shape of the distribution (Smirnov, 1948). To create a mapping between two measurement scales we must 1) derive estimates of CDFs for each measurement distribution; resample each CDF with respect to the probability values in y such that for a prescribed set of probability values we estimate the corresponding value y’; 3) plot the y’ values against each other to derive the mapping of A to B and B to A; and finally 4) use spline interpolation to derive the corresponding value in A for any value of B, and vice versa. Values from either scale can then be transformed to the opposite scale free from any directional bias, which can otherwise be introduced when using error minimization derived fits.

2.6. Potential Approaches

To apply distributional mapping to real empirical Aβ-PET data we have two primary options for derivation of the CDF. We can 1) compute non-parametric Empirical CDFs (ECDF) for each tracer to derive the transformation function, or 2) devise CDFs based on assumed parametric distributions. The ECDF approach is dependent on having or creating comparable samples or using methods that account for sampling weights and the overall similarity of the two sample populations. If the proportions of true positive and true negative differ between the samples or if the true positives represent different areas of the true positive distribution, the resultant mapping will be biased. The parametric approach requires one to make assumptions about the shape of the distribution but allows for 1) easier dissemination of parameters for a reference scale and mappings; and 2) provides a method to explicitly match true positive and true negative rates between samples. As Gaussian mixture models (GMM) have previously been used to fit mixtures of two normal distributions to empirical Aβ-PET data for the purpose of deriving thresholds (Mormino et al., 2014b), the GMM offers a promising framework for an explicit model of the Aβ-PET distributions, as well as a method to estimate distribution parameters

2.7. Explicit CDF derivation with a two-component Gaussian mixture model.

Using the assumption that Aβ-PET distributions can be characterised as the mixture of two normal distributions, we can obtain the mean, standard deviation, and mixing proportions for each of the two normals from a two component GMM. These five parameters can be used to construct two normal distributions which are combined by weighting the cumulative probabilities of each distribution by the desired mixture proportion. Applying a GMM to both the clinically normal FBP ADNI dataset and the PiB HABs datasets we obtained the parameters needed to construct an explicit CDF for each distribution. Parameter estimates (10,000 bootstrapped samples to obtain parameter variance estimates) for FBP were [µ₁ = 0.9528(0.0075) ₁ = 0.069(0.0060) µ₂ = 1.216(0.0249) σ₂ = 0.1938(0.0127) Mix = 63/37(0.04728)], and for PiB were [µ₁ = 0.9465(0.00388) σ₁ = 0.056(0.0032) µ₂ = 1.3865(0.025) σ₂ = 0.2567(0.013) Mix = 66.5/33.5]. As expected the proportional mixing was different between the FBP and PiB samples.

To test the accuracy of the distribution fits, we used a two sample Kolmogorov–Smirnov (KS) test to compare 10,000 randomly selected samples from the empirical data with 10,000 randomly generated samples based on the GMM parameters. The results showed that the distributions were not significantly different (p > 0.05) in 95% of cases in accordance with the expected rate based on chance, and provides confidence that the explicit mathematical distribution achieves statistical parity with the empirical data. Other alternative and perhaps better mathematical descriptions of the data are possible and would be compatible with the NoDiM method.

2.8. Mathematical Transfer Function Estimation

Given good fits of the GMM models to the empirical data, and estimates of the μ and σ parameters for both tracers, we next create a mapping of FBP into PiB-like units. A key challenge lies in the proportional mixing, i.e. the proportion of true negatives and true positives as conditioned by the overlap between those distributions. Given the distribution estimates, we can precisely match the mixing proportions of the FBP and PiB distributions, however it is important to note that the mapping is sensitive to the selection of the mixing proportion. This sensitivity of the derived mapping to the mixing proportion is due to how the relatively few observations in the intermediate region between mixtures are mapped to each other. The upper left panel of Figure 2 Panel A demonstrates how the mixing proportion parameter affects the transfer function and also demonstrates a greater band of uncertainty when mapping FBP to PiB units than for PiB onto FBP units, which is reflective of the dynamic range of the two tracers. Supplement C explores the minimal impact seen when this mixing parameter is estimated incorrectly.

FIGURE 2.

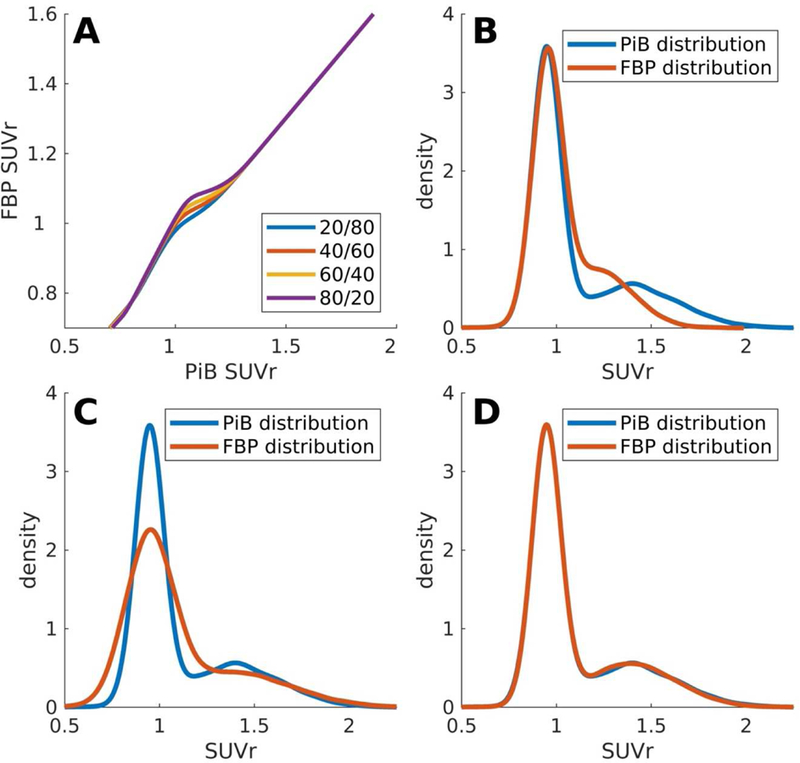
Distributional Transformation: Panel A shows the uncertainty in transforming Aβ-PET data with unknown distributional proportions. With low/high burden proportions creating an uncertainty envelope in the mid range. (Panel B) Raw Aβ-PET values from PiB and FBP show significant differences in their distributions. (Panel C) After linear scaling distributional differences remain. (Panel D) After NoDiM transformation Aβ-PET distributions can be aligned closely, maximizing the probability of transformed burdens aligning.

For the purposes of demonstrating the transformation we used a mixing proportion of 65/35 to approximately match the empirical samples. For a more general purpose, we would advise that researchers either use a GMM to estimate the mixing proportion for their sample (given a sufficiently large sample size) or use previously derived rates of Aβ positivity across different cohorts based on age, APOEε4 carriage, and clinical diagnosis. Figure 2 also demonstrates the transformation of FBP data to PiB like units on a simulated dataset of 10,000 samples created using the distribution parameter estimates from the empirical data using a 65/35 mixture of low and high Aβ. The upper right panel of Figure 2 demonstrates the higher range of PiB relative to FBP, the lower left panel shows the distribution after transformation using a linear mapping. The linear mapping was created by fitting between the upper and lower μs extracted from the empirical GMMs, thus creating maximal alignment between the modes of each distribution. There is a marked discrepancy in the distribution of Aβ values post linear transformation. The lower right panel shows the distributions after mapping with NoDiM.

When comparing NoDiM transformed FBP to the PiB distribution we found no significant difference, KS-stat = 0.008, p=0.92, whereas the linearly transformed FBP values were significantly different (KS-stat = 0.12, p<0.001) than the PiB distribution.

Using the same simulated dataset with known origin of values from low and high distributions we also compare sensitivity and specificity between tracers after mapping FBP to PiB-like units.

Figure 3 demonstrates better correspondence between the sensitivity and specificity profiles of NoDiM mapped FBP to PiB as compared to linearly transformed FBP data. The receiver operator characteristic curves, however, as expected, show identical area under the curve for both linear and NoDiM mapped data, which accords with the maintenance of rank order for both transforms. Notably, panel C highlights the fundamental and inescapable discrepancies in SNR and dynamic range between the measurements for each tracer. The fundamental characteristics of the measurements cannot be altered through transformation. It also highlights other potential avenues for cross-tracer mapping where values are mapped onto one another via correspondence of signal detection parameters.

FIGURE 3.

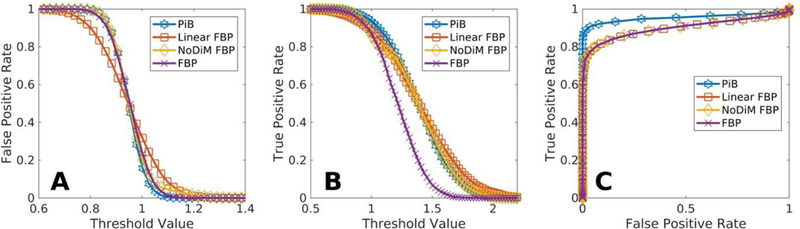
Proportion Harmonization: NoDiM transformed FBP values show sensitivity (panel B) and specificity (panel A) profiles that are more parsimonious with PiB than is possible with linearly transformed data. The resulting Receiver Operator Characteristic curve (panel C) demonstrates the inescapable reality of pairing radiotracers with different SNRs, no transformation can change the measurement characteristics.

2.9. Validation of NoDiM mapping with empirical data

As a final step we perform NoDiM mapping on the empirical datasets, mapping FBP to PiB like units using both a linear transform and the NoDiM transform. As with the simulated data, the NoDiM transform produces much greater similarity in the shape and overlap of the distributions than a linear transform. A two sample KS-test for the linear transform was significant (KS-stat=0.15, p<0.001) whereas the same test for NoDiM transform was not significantly different (KS-stat=0.06, p=0.54).

It is also important to note that, although the mapping itself it symmetrical, the direction of the mapping (e.g. FBP→PiB vs PiB→FBP) has consequences for how thresholds are applied and interpreted. For the FBP and PiB datasets used here, the Aβ thresholds derived from the GMM were incidentally found to be identical at 1.08 SUVr. This alignment holds no special meaning and is entirely happenstance. It is idiosyncratic to the specific pipeline used for this work and the GMM probability estimates derived from them. Different processing pipelines yield thresholds that differ from each other and from the 1.08 value used here. For PiB, based on the parameter estimations from those same GMMs, a value of 1.08 corresponds to the 99th percentile of the low Aβ distribution, and the 12th percentile of the high Aβ distribution, whereas for FBP a value of 1.08 is at the 97th percentile of the low distribution, and the 24th percentile of the high Aβ distribution. This means that at the point where there is 50/50 chance of the observation coming from either low or high distributions, PiB has lower false negative rate and a higher true positive rate than FBP.

If we map the FBP threshold to PiB units using NoDiM our threshold moves from 1.08 to 1.157, whereas if we map PiB to FBP units using NoDiM the threshold changes from 1.08 to 1.062. That is the FBP to PiB mapping results in a more conservative threshold and PiB to FBP mapping results in a more liberal threshold. Referring back to the simulated FBP dataset, using the 1.08 threshold value we find that among the values categorized as high there are 2,671 true positives and 193 false positives, resulting in a percent of true positives (PTP = true positives / (true+false positives)) of 93%. Using the PiB threshold mapped to FBP units with NoDiM we find a sample of 2,775 true positives and 331 false positives (PTP = 89%). If we were to use a linear mapping to project the PiB threshold into FBP units we would get a sample of 2,909 true positives and 771 false positives (PTP = 79%). This demonstrates a substantial change in the high Aβ sample. Figure 5 demonstrates how the proportion of true positives in the “high” sample changes for a given threshold for simulated PiB data as compared to simulated FBP data mapped with either the linear or NoDiM transform. The result is that the NoDiM transform more closely follows the PiB function, particularly at lower thresholds. At the threshold for which PiB has 90% true positives, the linear transformed FBP would result in a 65% PTP, while the NoDim transformed FBP would have an 80% PTP. Again it should be noted that while NoDiM improves the correspondence it does not make the tracers fully equivalent, as the inherent dynamic range and noise properties of the data remain fundamental to each measurement.

FIGURE 5.

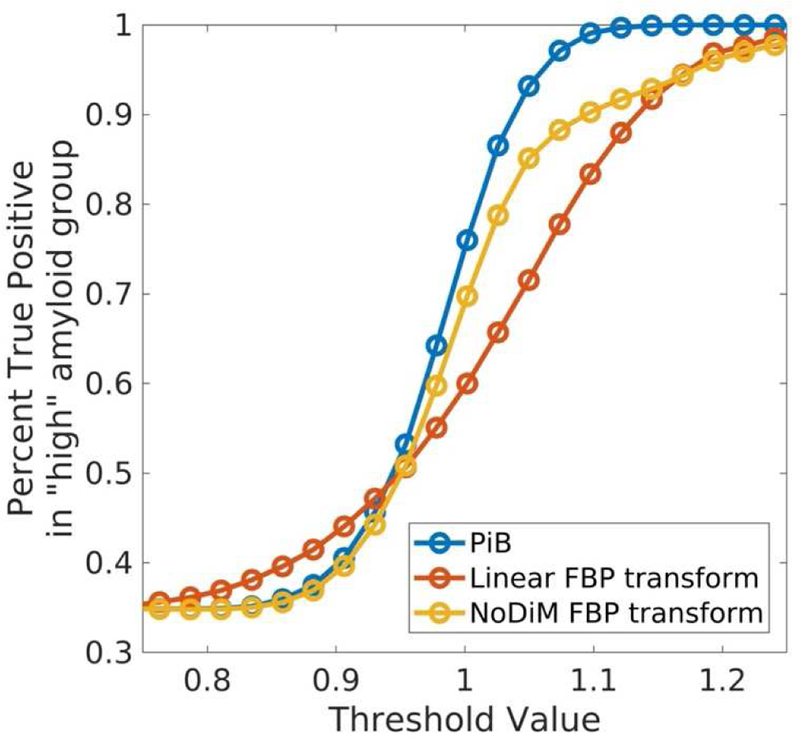
Threshold Proportional Matching: The percentage of true positives (true positives / (true+false positives)) for a given threshold more closely mirrors PiB when transforming values using NoDiM as opposed to a linear mapping.

3. DISCUSSION

We introduced NoDiM, a new application of distribution equating, based on well established statistical orthodoxy, for mapping Aβ-PET measurements onto a common scale. NoDiM is applicable to multiple Aβ-PET tracers, and could also accommodate other imaging modalities, such as mapping between tau-PET tracers, and can also be used to harmonize data from different analytical approaches. NoDiM provides an alternative to the current linear mapping approach, that allows better correspondence between measurement value and rank, and provides better variance matching within high and low Aβ groups. This maximises the probability that a given value will correspond to the same Aβ burden across tracers and processing methods.

While the NoDiM method will produce a transformation that makes measurements from different tracers more directly comparable than a linear transform, it nevertheless remains a fundamental truth that different tracers exhibit different measurement properties. While we can maximize the direct one-to-one comparability, no method can ever make measurements equivalent unless the binding signal and noise properties of the tracers themselves are equivalent. It is a fundamental truth that some tracers are better than others and have inherently better SNR and Sensitivity/Specificity profiles. Whether using linear or nonlinear transforms, there will always be some degree of discrepancy in the measurements, and that discrepancy is likely to be greatest in low and intermediate ranges between the low and high distributions. Researchers must make informed choices about whether to use a higher threshold for combined PiB/FBP data in order to minimize false positives, use a lower value to minimize the false negatives, or implement separate thresholds for different tracers. Alternatively, a new GMM can be run on merged data to derive a new 50% threshold for the combined dataset. Even when using a consistent approach to dichotomize different datasets, the threshold values should not be considered as fully equivalent.

The NoDiM approach lends itself to straightforward implementation. We have written and included (supplemental A) a short matlab script to perform the mapping based on µ and σ values for the low and high distributions of a reference scale, µ and σ values for the source scale, and an additional parameter for the expected mixing proportions. Given reference values one need only add the five parameters for the source scale to map data to the reference scale, and if the reference scale is provided in Centiloid values, then the NoDiM transform will automatically scale from native to Centiloid values. It is also important to note that the NoDiM transform is not necessarily non-linear. In cases where the relationship between tracers and measurement variance is linear (e.g. Navidea and PiB (Rowe et al., 2013)), NoDiM will return a linear transformation. Importantly we have demonstrated that a mixture of two normal distributions provides an excellent fit to both ADNI FBP data and HABS/AIBL PiB data.

Another important aspect to consider is that the specifics of the data processing have direct consequences for the mapping. That is, methods that provide better separation between low and high Aβ distributions will result in more consistent and more comparable mapping across tracers. Due to this, and given the focus in this report on clinically normal elderly we do not recommend that the parameter estimates reported here be used as reference values. The upper distribution parameter estimates will change slightly through the inclusion of the full disease spectrum in the samples, as these areas of the scales are more fully populated. We believe that more accurate pipelines should be employed (e.g. structural MRI based pipelines), and more representative samples that include impaired and clinically demented individuals should be used to establish population level parameter estimates for the reference scale.

Future work should also focus on alternative mathematical models for Aβ distributions, as well as empirically defined CDFs which would be ideal for mapping between different processing pipelines, as large samples can be used and samples will by definition be matched as the same data would be used for multiple measurements.

As we move toward big data approaches to gauge the effects of AD pathology on cognitive and functional outcomes, it becomes critical to have Aβ burden metrics that are comparable, and can be entered into pooled statistical analyses or translated between studies. Defining appropriate cut off values of Aβ-PET retention, regardless of the tracer used, is vital to informing preclinical AD trials on inclusion criteria (Sperling et al., 2014b), as misalignment of these cut-offs (Su et al., 2018) could easily result in inappropriately targeted populations, excess screening costs, and reduced statistical power. This is particularly important if recruitment arises from a variety of clinics or large registry platforms that utilize a variety of Aβ-PET radiotracers (Grill, 2017), or when observational studies that use PiB inform a clinical trial that, for feasibility reasons, is using a different tracer. Further, we have demonstrated the use of this method in a recent study which harmonized data across AIBL, ADNI and HABS to examine sex effects on the relationship between Aβ burden and cognitive decline (Buckley et al., 2018).

While the linear Centiloid transform will result in measures that can be approximately interpreted as proportional values relative to typical AD cases and will not alter the statistical properties of the measures, the transform will not properly align measures of approximately equal distributional probability, e.g. a Centiloid value of 19 will have different meanings depending on the method and tracer used to derive it (Su et al., 2018). The linear transform will only align values at the fixed points of 0 and 100, and does not ensure similar measurement bounds (range of values below 0 and above 100) or that values other than 0 and 100 are comparable.

NoDiM mapping will provide a common scale across measurements that is explicitly aligned based on location in the population distribution, but will do so at the cost of distorting the measurement scale by selectively compressing or stretching certain ranges of values to produce statistical alignment. This means that the NoDiM approach can hide the differential quality of different tracers and measurements, though we argue that this is necessary for the proper alignment of scales and for pooling data across tracers. However, there will be situations where there is inadequate comparability of measures and failure to meet criteria of comparable rank ordering, where no mapping, linear or otherwise is advisable. It is incumbent upon researchers attempting to align measures to investigate and provide sufficient evidence that any mapping between disparate measures is motivated. For the case of Aβ PET tracers, prior reports with paired sample datasets of individuals with both PiB and an F18 tracers have shown this assumption to be reasonably well justified for FBP (Landau et al., 2013, Navitsky, 2016), NAV4694 (Rowe et al., 2016), Florbetaben (Rowe et al., 2017), and Flutemetamol (Battle et al., 2016).

4. CONCLUSIONS

In conclusion, the NoDiM approach allows for more direct comparability between Aβ radiotracers that demonstrate differences in variance, dynamic range, noise, and frank nonlinearities. NoDiM facilitates direct comparisons of measurements obtained with different methods and tracers, allows for more harmonious definitions of Aβ positivity, and better aligns ranges of meaningful Aβ-PET signal. These features make NoDiM a useful alternative to linear Centiloid mapping, while incorporating the ability to maintain parity with the standard Centiloid scale as defined by Klunk and colleagues (Klunk et al., 2015). As the NoDiM approach is based on well-established parameter estimation orthodoxy, it is also extensible to other radioligands, and can accommodate a wide range of data processing and measurement approaches, and is ideal for translating findings across studies, and for merging large datasets of disparate Aβ tracers.

FIGURE 1.

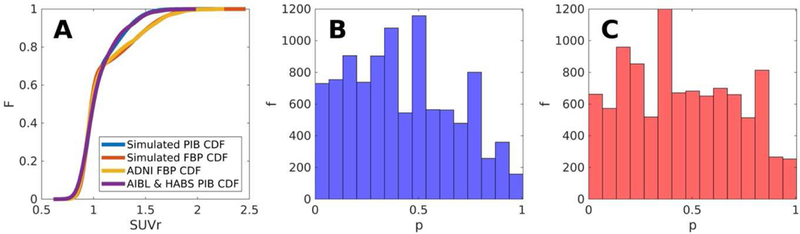
Synthetic CDF testing: The explicit CDFs (Panel A) constructed from GMM parameter estimates provide distributional approximations that mirror the empirical data from which they’re modelled. KS-test p values in panels (Panel B) and (Panel C) from 10,000 bootstraps provide confidence that synthetic and empirical data approach parity.

FIGURE 4.

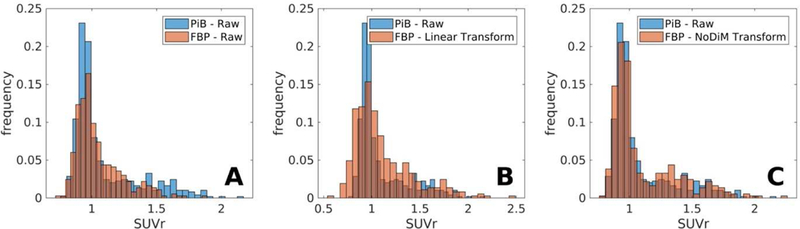
Empirical Histogram Harmonization: Empirical PiB and raw (Panel A), linearly transformed (Panel B), and NoDiM transformed (Panel C) FBP histograms highlight the distributional differences pre and post transformation.

Abbreviations

PET

Positron emission tomography

AD

Alzheimer’s disease

Aβ

β-amyloid

NoDiM

Nonlinear Distribution Mapping

CDF

cumulative distribution function

PiB

Pittsburgh Compound B

FBP

Florbetapir

SUVr

standardized uptake value ratio

AIBL

the Australian Imaging, Biomarker & Lifestyle Flagship Study of Ageing

ADNI

Alzheimer’s Disease Neuroimaging Initiative

HABS

Harvard Aging Brain Study

GMM

Gaussian mixture models

KS

Kolmogorov–Smirnov

APOEε4

apolipoprotein ε4

PTP

Percent True Positive