Active Tension Network model suggests an exotic mechanical state realized in epithelial tissues

Abstract

Mechanical interactions play a crucial role in epithelial morphogenesis, yet understanding the complex mechanisms through which stress and deformation affect cell behavior remains an open problem. Here we formulate and analyze the Active Tension Network (ATN) model, which assumes that the mechanical balance of cells within a tissue is dominated by cortical tension and introduces tension-dependent active remodeling of the cortex. We find that ATNs exhibit unusual mechanical properties. Specifically, an ATN behaves as a fluid at short times, but at long times supports external tension like a solid. Furthermore, an ATN has an extensively degenerate equilibrium mechanical state associated with a discrete conformal - “isogonal” - deformation of cells. The ATN model predicts a constraint on equilibrium cell geometries, which we demonstrate to approximately hold in certain epithelial tissues. We further show that isogonal modes are observed in the fruit y embryo, accounting for the striking variability of apical areas of ventral cells and helping understand the early phase of gastrulation. Living matter realizes new and exotic mechanical states, the study of which helps to understand biological phenomena.

Mechanics of growth and cellular rearrangement defines the shape of developing tissues, thereby playing a central role to morphogenesis. It has become a subject of intense study aiming to identify specific mechanical processes involved in cell and tissue-wide dynamics[1–4], uncover the regulatory mechanisms [5], and identify if and how the mechanical state of the tissue feeds back onto the larger developmental program [6–8].

An epithelial tissue is a monolayer of apico-basally polarized cells that are tightly connected to their lateral neighbors. Viewed from their apical sides, cells form an approximately polygonal tiling of the plane. Each cell has a cortical cytoskeleton consisting of actin-myosin fibers [9, 10] localized along its perimeter just below the apical surface [11]. A cell’s cortical cytoskeleton is linked to those of the neighboring cells via cadherin-mediated adherens junctions [12], resulting in a mechanical network that ensures the integrity of the epithelial layer. The equilibrium geometry of cells is determined by the balance of cytoskeletal and adhesive forces [5] within the tissue. Unlike passive materials, cells actively regulate these forces through mechano-transduction and internal remodeling [13, 14], resulting in an intrinsically dynamic relation between stress and strain, and controllable plasticity, that can drive rearrangement of cells. Elucidating the manner in which cellular activity manifests itself in the collective properties of the tissue is critical to advancing our understanding of morphogenesis.

In this study we formulate a phenomenological model of an epithelial tissue as a two dimensional Active Tension Network (ATN), which in addition to cytoskeletal elasticity describes cytoskeletal re-modelling through myosin activity and dynamic recruitment of myosin to the cytoskeleton, thus capturing the plastic and adaptive response of cells to external stress. We shall explore static and dynamic properties of the ATN model, validate some of its predictions by comparing with live imaging data, and identify new directions of further study.

Formulation of the Active Tension Net Model

Epithelial monolayers can be approximately represented by two-dimensional polygonal tilings, parameterized by a set of vertex coordinates {r_i} and are often described by Vertex Models [2, 15] which assume that the geometry of cells minimizes mechanical energy defined in terms of cell edge lengths (r_ij = |r_i − r_j|) and cell areas (A_α). We shall introduce a generalized class of vertex models by adding internal variables to capture active adaptation of the cytoskeleton. We begin by defining mechanical energy in its differential form [16]

$$\mathit{\text{dE}}[\{{\mathit{r}}_i\}]=\sum _{<i,j>}{T}_{\mathit{\text{ij}}}{\mathit{\text{ dr}}}_{\mathit{\text{ij}}}+\sum _{\alpha }{p}_{\alpha }{\mathit{\text{dA}}}_{\alpha }$$ (1)

where tension, T_ij, defines the change in mechanical energy in response to a change of edge length (dr_ij) and the 2D ‘apical pressure’, p_α, defines the response to a change in cortical area (dA_α). Tension Nets correspond to the situation where pressure differentials between neighboring cells are negligible so that mechanical balance is dominated by cortical tension. In this limit p_α ≈ p₀ with p₀ controlling the total area of cells, and preventing the collapse of the network under the action of tension.

Vertex dynamics is relaxational and is given by

$$\nu \frac{d}{\mathit{\text{dt}}}{\mathit{r}}_i=-{\partial }_{{\mathit{r}}_i}E=\sum _{{\{j\}}_i}{T}_{\mathit{\text{ij}}}{\hat{\mathit{r}}}_{\mathit{\text{ji}}}=\sum _{{\{j\}}_i}{\mathit{T}}_{\mathit{\text{ij}}}$$ (2)

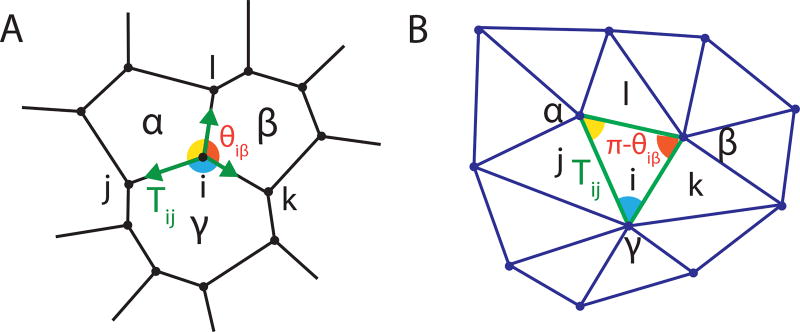
where {j}_i denotes the set of all vertices connected to vertex i, r̂_ji is a unit vector in the direction from r_i to r_j, and ν represents the effective friction (e.g. [21]) which determines the timescale of mechanical relaxation. Mechanical equilibrium of a Tension Net is reached when tensions balance, which geometrically means that for each vertex i, the three corresponding tension vectors T_ij, T_ik, T_il form a triangle. Since adjacent vertices share an edge, global tension balance implies that the set of T_ij’s defines a triangulation as shown in Fig. 1a,b [17, 18].

FIG. 1.

Force balance in a tension net defines a triangulation of the “tension plane”. (A) 2D array of cells represented by a polygonal tiling. In mechanical equilibrium tensions balance at each vertex. (B) Equilibrated tensions form a triangulation, with triangle angles supplementary to the angles at the corresponding vertex.

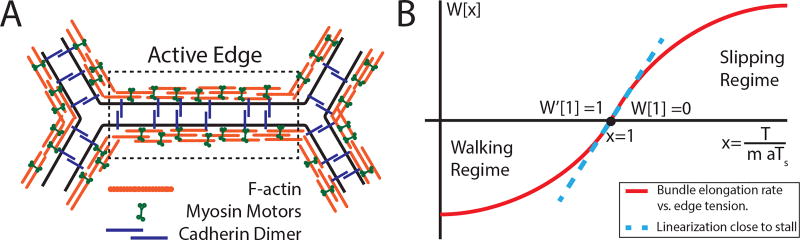
Microscopically, each edge in this network represents the mechanically coupled actomyosin bundles of neighboring cells, connected to each other via adherens junctions along the cell-cell interface, as shown schematically in Fig. 2a. Vertices serve as physical barriers to the lateral movement of cadherin clusters and contracting actomyosin bundles [19, 20]. The coupled actomyosin bundles along the cell edge form a natural mechanical unit - an “active edge” in Fig 2a - which carries tension. Edge tension, T_ij, depends on the edge length r_ij as well as on the intrinsic variables representing the local state of the actomyosin bundle and cadherin-mediated adhesion between cells. Specifically, we assume a simple elastic form, T_ij = K(r_ij − ℓ_ij), parameterizing the internal state of each interface by an intrinsic “rest length” ℓ_ij of the underlying actomyosin filament, itself a dynamical variable governed by

$${\ell }_{\mathit{\text{ij}}}^{-1}\frac{d}{\mathit{\text{dt}}}{\ell }_{\mathit{\text{ij}}}={\tau }_{\ell }^{-1}W\left(\frac{T_{\mathit{\text{ij}}}}{m_{\mathit{\text{ij}}}{\mathit{\text{aT}}}_s}\right)$$ (3)

The generic features of the “walking kernel” W(x), illustrated in Fig. 2b, are based on single-molecule experiments [22, 23]: myosins can walk, contracting the actin bundle, unless the load per myosin, T_ij/am_ij, reaches the “stall force” level T_s, above which the filament elongates as motors slip backwards [24]. Here m_ij is the average myosin line-density along the edge and a is the length scale over which motors share mechanical load.

FIG. 2.

Role of myosin motors in the ATN model. (A) Schematic of the basic active element of a tension network: actomyosin cables on apposing interfaces are cross-linked by cadherin dimers; (B) Dependence of the actomyosin bundle contraction rate on mechanical load: the “walking kernel” W(x), see Eq. (3), changes sign from contraction to elongation when mechanical load per myosin T/am exceed the stall load T_s.

Eqs. (2, 3) define the dynamics of a Tension Net with a specified myosin distribution on interfaces. The fixed point of these equations is reached when i) tensions balance at all vertices and ii) all edges are at their stall tension, set by the local myosin (linear) density (T_ij = aT_sm_ij). Global tension balance requires the set of T_ij’s to form a triangulation and therefore edge tensions, and hence myosin levels, cannot be prescribed independently. How can mechanical equilibrium be achieved? At this point we recall that myosin distribution within tissues is not fixed and is known to respond to mechanical cues [8, 25], although the exact form of this mechanical feedback is not fully understood. Here we propose a particular form of mechanical feedback on myosin, that will ensure convergence to a balanced state. The latter is achieved if myosin recruitment depends on the internal strain rate of each filament:

$$m_{\mathit{\text{ij}}}^{-1}\frac{d}{\mathit{\text{dt}}}{m}_{\mathit{\text{ij}}}=\alpha {\ell }_{\mathit{\text{ij}}}^{-1}\frac{d{\ell }_{\mathit{\text{ij}}}}{\mathit{\text{dt}}}$$ (4)

with α parameterizing the rate of myosin recruitment, which we assume to be slow relative to both mechanical relaxation and actomyosin contractility. This form of mechanical feedback recruits myosin to overloaded slipping bundles and reduces myosin on underloaded contracting bundles until the stall condition is reached, bringing the system to equilibrium. The “Dynamic Recruitment” hypothesis, defined by Eq (4), is dictated by the requirement of ATN stability and should be regarded as a prediction of the model to be tested by future experiments.

Equilibrium Manifold of a Tension Net

The ‘duality’ between an equilibrium tension net and the corresponding triangulation of the tension plane (see Fig. 1ab) implies the existence of certain constraints on cell geometry. Let θ_iβ be the angle at vertex i belonging to cell β; its complement π − θ_iβ is the corresponding angle of the dual triangle in the tension plane (Fig. 1ab). By applying the law of sines to the triangles surrounding dual vertex α one discovers the following constraint, true for every cell:

$${\chi }_{\alpha }=\prod _{i\in {𝒱}_{\alpha }}\frac{\text{sin }{\theta }_{i\gamma }}{\text{sin }{\theta }_{i\beta }}=1$$ (5)

The product is taken over the set 𝒱_α of vertices i that belong to cell α, while β and γ label other cells adjacent to i in clockwise order (Fig. 1a, see the SI for a full derivation). An array with all χ_α = 1 is geometrically compatible with tension-balance. Since χ_α can be readily measured, the compatibility constraint allows one to quantitatively assess whether a given cell array is consistent with a balanced tension net.

The geometry of the dual triangulation also constrains possible sets of balanced tensions. A triangulation is specified by the positions of its c (the number of polygonal cells in the array) vertices, and hence has 2c independent degrees of freedom. This number is smaller than the number of edges e = 3c (assuming all vertices in the cell array are three-fold), which means that T_ij’s can’t be prescribed independently: the balanced set satisfies c constraints.

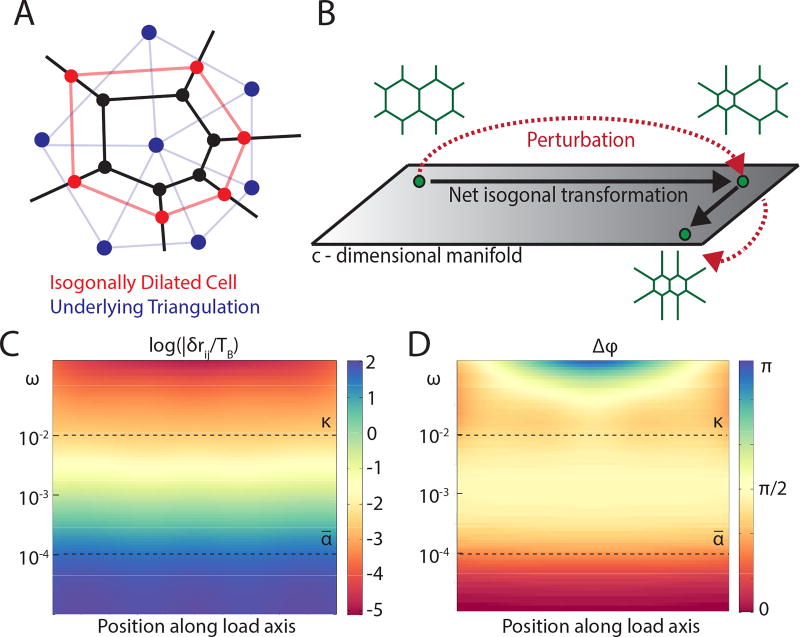
The above counting argument further implies that the map between cell geometry and tension triangulation is highly degenerate. The number of degrees of freedom of a compatible cell array is given by 2υ − c = 3c (υ being the number of vertices of the cell array), which is c degrees of freedom larger than that of the dual triangulation. Hence, a given set of balanced tensions corresponds to a manifold of nets with one degree of freedom per cell. Specifically, as long as none of the vertex angles are perturbed, we can freely “inflate” or “deflate” cells, as illustrated in Fig. 3a, with no cost of energy and thus without disturbing mechanical equilibrium and the underlying tension triangulation. Quite generally such angle preserving - hereafter referred to as “isogonal” deformations have the form

$$\delta {\mathit{r}}_i=S_{\alpha \beta \gamma }^{-1}[{\mathit{T}}_{\mathit{\text{ij}}}{\mathrm{\Theta }}_{\beta }+{\mathit{T}}_{\mathit{\text{ik}}}{\mathrm{\Theta }}_{\alpha }+{\mathit{T}}_{\mathit{\text{il}}}{\mathrm{\Theta }}_{\gamma }]$$ (6)

where δr_i denotes the displacement of vertex i shared by cells α, β, γ and S_αβγ (Fig. 1ab) is the area of the vertex’s dual triangle. {Θ_α} parameterize the c-dimensional manifold of equilibrim states. Tensions {T_ij, T_ik, T_il} capture the implicit geometric constraints within tension nets central to the structure of the isogonal modes: note for example that δr_i = 0 for Θ_α = Θ_β = Θ_γ. The compatibility condition (see Eq. 5) satisfied by equilibrium tension nets is essential for allowing such isogonal modes to exist. Because they do not invoke a restoring force, isogonal deformations are easily excitable “soft modes” and are expected to dominate observed fluctuations of tension nets close to mechanical equilibrium. We note that isogonal modes can be thought of as a discrete manifestation of the conformal symmetry that appears in 2D continuum elasticity in the limit of a vanishing bulk modulus (see SI for details). Isogonal modes also generalize the isoperimetric “breathing modes” of a hexagonal lattice [26].

FIG. 3.

Mechanical properties of an ATN. (A) Cartoon of an isogonal ‘breathing mode’ of a cell in a tension net. (B) Because ATN equilibrium is a manifold rather than a point, after a transient perturbation the system does not necessarily return to the same state, resulting in an ‘isogonal’ transformation. (C) Amplitude and (D) phase of the longitudinal strain (as a function of position) in response to periodic uniaxial forcing T_B cosωt applied at the boundaries (κ = 10⁻² and ᾱ = 10⁻⁴). As the frequency ω decreases below ᾱ the phase shifts from π/2 to 0 indicating crossover from viscous fluid behavior to an elastic solid. This contrasts with the conventional Maxwellian viscoelasticity crossover towards elasticity with ω increasing above κ (see SI for details).

Dynamical properties of Active Tension Nets

Let us consider the dynamics of small perturbations around a mechanical equilibrium state, which can be described by linearizing Eqs. (2–4). While detailed calculations are carried out in the SI, the key features can be understood from a vastly simpler analysis of a 1D “Active Tension Chain” model which has the form

$$\frac{d}{\mathit{\text{dt}}}\delta T_n=D{\nabla }^2\delta T_n-\kappa (\delta T_n-\delta m_n)$$ (7)

$$\frac{d}{\mathit{\text{dt}}}\delta m_n=\overline{\alpha }(\delta T_n-\delta m_n)$$ (8)

where δT_n and δm_n are deviations from the equilibrium state and n is an integer indexing edges along the chain (note that we have rescaled δm_n with T_sa to give it the units of tension). ∇²δT_n = δT_n+1 + δT_n−1 − 2δT_n is the discrete Laplacian in 1D and {D, κ, ᾱ} are parameters derived (in the SI) by linearization of Eqs. (2–4). Eq. 7 is recognized as the Maxwell model of viscoelasticity forced by myosin perturbations δm_n. A static local forcing δm₀ (in Eq. 7) would generate a persistent flow (i.e. non-zero rate of strain) and exponentially localized perturbations of tension with “screening length” $\lambda =\sqrt{D/\kappa }$. At long times myosin recruitment, Eq. 8, (with ᾱ ≪ κ) ensures that the chain converges towards mechanical equilibrium δm_n = δT_n = T_B where T_B is external tension at the boundaries. Relaxation towards this equilibrium is governed by $\frac{d}{\mathit{\text{dt}}}\delta m_n\approx \overline{\alpha }{\kappa }^{-1}D{\nabla }^2\delta T_n$ and $\frac{d}{\mathit{\text{dt}}}\delta r_n\approx \overline{\alpha }{\kappa }^{-1}D{\nabla }^2\delta T_n$ where $\frac{d}{\mathit{\text{dt}}}\delta r_n$ is the deformation rate of edge n. Hence despite the ATN’s viscoelastic response and floppy modes at short times, the long time behavior is effectively elastic with K_eff ~ ᾱκ⁻¹D. An analogous crossover from fluid-like response at intermediate times to solid-like behavior at long times occurs in the fully two-dimensional ATN (see Fig. 3cd).

ATN predictions and the Ventral Furrow (VF) formation in Drosophila embryo

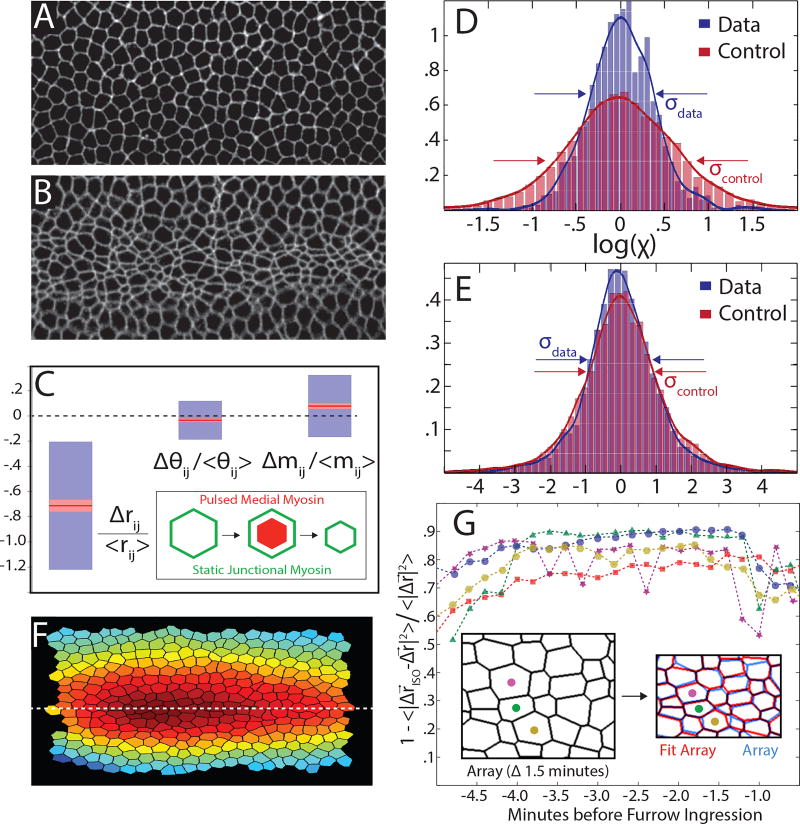
One of the striking predictions of the ATN model is the existence of the isogonal soft modes that allow easy variability of cell area. Extreme variability of apical cell area has been observed at the beginning of the gastrulation process in Drosophila, when cells along the ventral midline of the embryo constrict their apical surfaces, initiating the formation of a furrow that subsequently internalizes the future mesoderm [27], as shown in Fig. 4ab. This apical constriction was shown to be driven by pulsed contractions of the medial actomyosin network (located near the apical cell surface) that pull on the cortical cytoskeleton. The process has been described as a “ratchet” [28]: medial myosin pulses cause transient constrictions subsequently stabilized by the retracted cytoskeletal cortex.

FIG. 4.

Experimental tests of ATN model predictions. (A–B) Ventral view of Drosophila embryo (imaged using Spider-GFP marking cell membranes) at the beginning of VF formation (A) and 4 minutes later (B). Note the variability of apical cell area in (B). (C) The measured changes in edge length Δr_ij, edge orientation angle Δθ_ij and relative myosin level Δm_ij during VF formation: red lines denote the means (with pink haloes giving 95% confidence intervals on the mean given by the t-test) and blue boxes denote one standard deviation. Edge length shrinks by ~ 75% while relative changes in cortical myosin and edge orientation are considerably smaller. (D–E) Test of compatibility (Eq.5) compares the PDF of the measured log χ’s (blue) with the control distribution (red) defined by permuting angles. Embryonic mesoderm (D) exhibits a strong tendency towards compatibility (log χ ≈ 0) while epithelium of the third instar imaginal wing disc (E), does not. (F) Spatial profile of the isogonal mode amplitude, {Θ_α} describes increasing anisotropic compression of cells towards ventral midline. (G) Fraction of measured deformation (Δr) captured by isogonal deformation (Δr_iso) obtained via least squares minimization of Eq.6. Each color represents an independent measurement with 200 cells. Inset: a graphical comparison for a sample fit.

Here, we propose an alternative interpretation of the phenomenon in terms of the ATN model. If we assume that the cortical myosin concentrations are relatively static over the timescale of medial myosin pulsing, the ATN model predicts that any transient perturbation of mechanical balance due to medial myosin contractions would leave behind an isogonal deformation of the cell array, as it returns to mechanical balance dominated by cortical tensions that remain unchanged. Hence we predict that cell deformation during the early stages of ventral furrow formation should be well described by motion along an isogonal manifold.

The proposed model is predicated on the applicability of the tension net hypothesis that underlies the ATN model. While it is not yet possible to measure all internal tensions in a living tissue, Eqn. 5 provides us with a quantitative assay of the validity of the balanced tension net approximation in the ventral furrow using apical geometry alone. Exact satisfaction of the constraint log χ = 0 is not anticipated owing to the errors associated with the acquisition and analyses of imaging data, as well as due to cell array fluctuations that result in deviations from tension balance. Yet even if tension-balance is only approximate, we expect that the empirical log χ distribution would be closer to zero than the “control distribution” computed for a random cell array (see the SI for details). Fig. 4d presents the result of such an analysis for the VF. Based on ~ 5000 cells, we find a statistically significant (Kolmogorov-Smirnov [29] p < 10⁻⁹) accumulation of log χ near zero with respect to the null – consistent with an approximate tension balance within the tissue. This finding is non-trivial, as results of the same analysis for Drosphila larval wing imaginal disc [30], Fig. 4e, yielded no statistically significant tendency towards log χ ≈ 0. See the SI for further discussion of the statistical test and the analysis of other tissues.

We further quantified the early VF formation process using time-lapse imaging of fluorescently-labelled myosin and cell membranes (see Methods). Relative levels of cortical myosin (excluding an overall magnitude increase [28] that does not affect local tension balance) and edge orientations do not change significantly over the course of VF formation, despite large changes in edge lengths (Fig. 4c). This finding, together with the approximate “compatibility” of embryonic mesoderm (Fig. 4d), lend strong support to the validity of the assumptions underlying the ATN model interpretation of the VF formation process in terms of isogonal deformations driven by transient medial myosin pulses.

Analyzing five movies of VF formation (as in Fig 4ab) we found that isogonal deformations Δr^iso, found by least squares analysis of Eq. 6, consistently account for ~85% of the measured vertex displacements, Fig. 4g (see SI for more details). The spatial profile of {Θ_α}, integrated over the course of VF dynamics is approximately parabolic (see Fig. 4f), giving rise to isogonal, but anisotropic, constriction of cells with the long axis of cells oriented along the anterior-posterior direction [27]. Thus, the mesoderm during VF formation indeed appears to behave as a transiently perturbed ATN, owing along the isogonal manifold comprised of the degenerate set of its (mechanical) equilibrium states (see Fig. 3b). The ATN model provides a reduced set of degrees of freedom that accurately describe the dynamics of VF formation.

Finally we discuss the phenotypes of twist and snail mutants [28]. snail embryos fail to coalesce medial myosin structures and do not initiate pulsed contraction of cells [28]: hence snail embryos simply lack the transient perturbations necessary to induce isogonal “flow” along the equilibrium manifold. Conversely, twist embryos exhibit pulsed apical contraction of cells but are unable to fully stabilize the constricted state [28]. These mutants also appear to have reduced tension in the cortical cytoskeleton and exhibit strongly curved cell-cell interfaces. The latter fact suggests relatively large differences in pressures between adjacent cells, in which case contribution of pressure to local force balance cannot be neglected. Pressure variation lifts the degeneracy of the ATN mechanical equilibrium manifold so that isogonal deformations experience a restoring force, thus limiting the response to transient perturbations (see the SI for an extended discussion).

“Dynamic Recruitment” hypothesis

The ATN model presented in this study describes epithelial tissue dynamics in terms of three processes: i) fast relaxation towards mechanical equilibrium dominated by cortical tension, ii) myosin driven rearrangements of the cortex on an intermediate time scale, and iii) on the slowest timescale, Dynamic Recruitment (or reduction) of myosin that is driven by the internal rate of strain in the cortex, Eq. (4). The first two alone would result in a viscoelastic fluid behavior (driven by myosin generated internal forces). The unusual behavior arises from the assumed Dynamic Recruitment of myosin, which dramatically changes the asymptotic behavior so that while being able to flow at short times, ATNs, like solids, can support external stress at long times. While the presented measurements suggest the validity of tension-balance in describing the mechanical equilibrium of an epithelial tissue, new experiments will be needed to test the Dynamic Recruitment hypothesis, which was introduced to explain how myosin levels at different interfaces can be coordinated to attain tension balance across a tissue.

Materials and Methods

The following fly stocks where used for ventral furrow live recordings: Spider-GFP [32], sqh-GFP;membrane-mCherry [31]. Embryos where dechoreonated following standard protocols, and mounted in Matek Dishes for imaging. Images where acquired on a Leica SP8 confocal, with a 40x/N.A. 1.1 objective water immersion objective. See SI for details on image analysis and numerical simulation of ATN dynamics.

The data that support the figures and other findings of this study, as well as the MATLAB code used to perform simulations of ATN dynamics, are available from the corresponding author upon request.