Abstract
Modern imaging techniques allow the monitoring of circadian rhythms of single cells. Coupling between these single cellular circadian oscillators can generate coherent periodic signals on the tissue level that subsequently orchestrate physiological outputs. The strength of coupling in such systems of oscillators is often unclear. In particular, effects on coupling strength by varying cell densities, by knockouts, and by inhibitor applications are debated.
In this study we suggest to quantify coupling strength via analyzing period, phase, and amplitude distributions in ensembles of individual circadian oscillators. Network simulations show that period and phase distributions become narrower with increasing coupling strength. Moreover, amplitudes can increase due to resonance effects.
Our theoretical predictions are confirmed by studying recently published experimental data from PERIOD2 expression in slices of suprachiasmatic nuclei during and after the application of tetrodotoxin (TTX). Upon analyzing the corresponding period, phase, and amplitude distributions, we can show that treatment with TTX can be associated with a reduced coupling strength in the system of coupled oscillators.
We suggest that our approach is also applicable to quantify coupling in fibroblast cultures, hepatocyte networks, and for social synchronization of rodents, flies, and bees.
Keywords: Circadian Clock, Oscillator, Coupling, Synchronization, Suprachiasmatic Nucleus
1. Introduction
Networks of coupled oscillators are ubiquitous in living nature and physical systems [1, 2]. Therein, even weak coupling can lead to a synchronization or pattern formation [3, 4]. Often oscillator networks constitute incoherent states, i.e., oscillators have independent periods and random phases, or synchronized states due to overcritical coupling strength [5].
In chronobiology, dispersed fibroblasts represent an incoherent state [6] whereas the suprachiasmatic nucleus (SCN) exhibits complete synchronization in wild type animals under standard conditions [7]. The observation of frequency locking in the synchronized state allows a binary classification associated with undercritical and overcritical coupling.
There are, however, chronobiological questions requiring a more detailed quantification of coupling strength: Do increasing cell densities strengthen coupling between fibroblasts even if no global synchronization is achieved [8]? Do inhibitors of neuronal communication weaken coupling within the SCN despite persisting synchronization [9]? Is there a dependence of coupling strength on the number of cohabitating animals in systems with social synchronization [10]?
In all these cases, modern recording techniques allow to monitor rhythms of individual oscillators. In this work, we suggest to study the corresponding distributions of periods, phases, and amplitudes to quantify coupling strength beyond a binary classification into incoherent and coherent states. It will be shown that period distributions are helpful indicators in case of undercritical coupling, whereas narrowing of phase distribution and amplitude expansions can serve as markers of coupling strength in synchronized states.
We describe our concept in the context of circadian systems which constitute networks of coupled oscillators on different levels. Gene-regulatory feedback loops generate oscillations in almost every cell. Synchronization of these noisy oscillations can lead to precise self-sustained circadian rhythms on the organismic level.
In mammals, synchronized neurons in the suprachiasmatic nucleus (SCN) orchestrate physiological rhythms of the whole body with an astonishingly high precision. The network of SCN neurons illustrates that single cell oscillations can be quite different from network oscillations. Synchrony, precision and large amplitudes arise as emergent properties due to coupling [11–14].
There is also evidence that other cell types such as fibroblasts or hepatocytes can be coupled. It has been shown, for example, that cell densities of fibroblast cultures affect rhythmicity [8, 15]. In many cases, however, the coupling strength is not sufficient to allow synchronization.
Moreover, there are reports on social synchronization of circadian rhythmicity in weakly interacting mice [10], hamsters [16], flies [17] and bees [18]. Here tactile contacts, pheromones and common environmental factors are discussed as coupling mechanisms [19].
In all these examples of coupled circadian oscillators the type and strength of coupling is debated. Close to the synchronization threshold the Kuramoto theory provides a sophisticated framework to quantify synchronization [20]. For example, the synchronization index R, which is tantamount to the global phase coherence, is widely used to characterize the onset of synchronization, see e.g. [21].
The situation is less clear for overcritical coupling as found in the SCN or undercritical coupling as in dispersed fibroblasts. In these cases, wide ranges of coupling strength lead to practically the same phenotype – complete synchronization or desynchronization, respectively.
Here we analyze ensembles of coupled oscillators systematically in order to extract features that are associated with increasing coupling strength. These features are based on distributions of periods, phases and amplitudes. We show that narrowing of period-and phase distributions as well as amplitude expansion are related to an increasing coupling strength. Although an explicit calculation of coupling strength from ensembles of oscillators is currently impossible, a quantitative comparison between situations where putative coupling mechanisms are differentially manipulated can be done. In case of SCN networks, for example, the effects of GABA inhibitors could be tested and in fibroblasts, cultures of low and high cell densities can be compared.
As a first step, we analyze simulated networks in order to test the following hypotheses:
For undercritical coupling (desynchronized oscillators) the period distribution becomes narrower with increasing coupling strength. It is known from engineering that frequencies can approach each other due to coupling (frequency pulling) [22]. Furthermore, upon increasing coupling, some of the oscillators might constitute frequency-locked clusters.
For overcritical coupling (complete synchronization) the phase distribution becomes narrower with increasing coupling strength. Even in case of complete frequency locking, phases of individual oscillators differ due to varying intrinsic frequencies or amplitudes. On a population level, these different phases are termed “chronotypes”. It is plausible that for strong synchronizing signals the phase dispersion shrinks.
Coupling can induce amplitude expansion (“resonances”). Whereas rigid limit cycles can be described successfully as phase oscillators [23], amplitudes of weak oscillators near the Hopf bifurcation can be amplified by synchronizing agents. This implies, that an observation of resonant behavior provides also information on the underlying oscillator type.
After studying simulated networks we will analyze data from brain slices representing the network of SCN neurons. We exploit local fits with amplitude phase models to quantify period-, phase-and amplitude distributions for 3 different situations: (i) synchronized SCN mouse explants, (ii) application of TTX to reduce spike-associated coupling, and (iii) washout of TTX to restore coupling. It is reasonable to assume that these situations represent strong, weak and medium coupling, respectively [7, 24–29].
2. Analysis of Coupled Amplitude Phase Oscillators
2.1. Model Equations
In complex systems of coupled oscillators, the emergent behavior at the network level is influenced by both, the properties of the individual oscillators as well as the coupling topology and strength between the oscillatory units. At an abstract level, the oscillatory entities can be of diverse nature. In case of “social synchronization”, each oscillatory unit describes the dynamics at the level of the organism. In case of the SCN or fibroblast cultures, the oscillatory units correspond to cell autonomous circadian clocks. The intrinsic dynamical properties of the single oscillators can be conveniently parameterized by means of the generic phase-amplitude model
| (1) |
| (2) |
which is considered being the simplest description of a stable limit cycle in a two-dimensional plane and is commonly termed Poincaré oscillator [3]. Equation (1) determines the dynamical evolution of the radial coordinate ri(t), i.e., the time-dependent distance from the origin, while Equation (2) determines the change of the angular coordinate θi(t), see Figure S1 for an illustration. The parameters , , and denote the free running period, amplitude, and amplitude relaxation rate of oscillator i, respectively.
What kind of emergent network properties, not inherent to the isolated oscillatory units, arise due to mutual coupling and how do these properties depend on the coupling strength? In order to test this, we consider an ensemble of N = 1000 mutually coupled Poincaré oscillators and quantify the emergent properties upon mutual coupling by numerical simulations. For the sake of simplicity, we assume that all oscillators interact with each other through a mean-field, as proposed in previously published models of the SCN network [30, 31]. This kind of coupling tacitly implies a relatively fast diffusion of coupling agents (e.g. neuropeptides in case of SCN neurons) compared to the ~24h time scale of circadian free running periods and an equally weighted contribution of each oscillator to the mean field. The network dynamics in the presence of coupling can then be given by
| (3) |
| (4) |
where we have rewritten Equations (1)–(2) in Cartesian coordinates and made, without loss of generality, the assumption that the mean field additively couples solely to the x-coordinate, see Equation (3). Parameter K denotes the strength of the coupling between the mean field and the single oscillatory units.
To get an intuition about the impact of increasing coupling strength, we investigate the dynamics of system (3)-(4) for three representative values of K, as illustrated in Figure 1. In the corresponding simulations, we assume that all individual oscillators have an identical amplitude Ai = 1 and an amplitude relaxation rate of as suggested by [32–34]. The intrinsic free-running periods τi are chosen from a normal distribution with mean μτ= 24h and a standard deviation of as suggested by experiments with dispersed, i.e., presumably uncoupled, SCN neurons [35–38].
Figure 1: Temporal order formation upon coupling.
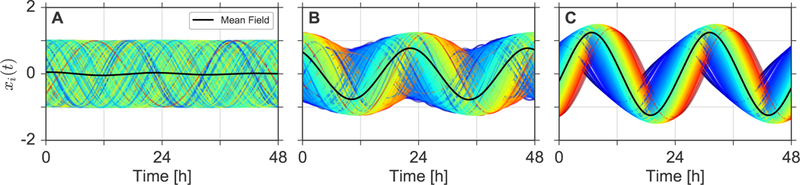
Steady state dynamics, i.e. after decay of transients, are plotted for a total length of two days and three different coupling strengths K = 0.04 (A), K = 0.07 (B), and K = 0.1 (C). Numerical solutions are color-coded with respect to their intrinsic free-running periods τi. Blue colors indicate short intrinsic periods while red colors indicate long intrinsic periods, leading to early and late phases in case of synchronization, respectively.
In case of K = 0.04, depicted in Figure 1A, no particular order can be observed and all oscillators seem to run at or close to their own intrinsic frequency. In oscillator theory, such (macro-)state is commonly referred to as the incoherent state [21]. If we subsequently increase the coupling, e.g., to K = 0.07, order emerges: a huge fraction of the oscillators appears to run at the same pace, thereby leading to a dramatic increase of the mean-field oscillation amplitude. In this partially-synchronized or mixed state, a cluster of synchronized oscillators co-exists together with a non-synchronized set of oscillators. Finally, large enough coupling, e.g., K = 0.1, leads to the emergence of a fully-synchronized state, where all oscillators are locked to the mean-field, see Figure 1C. As expected from previous analysis [39], an increasing modulation of the individual oscillators amplitude can be observed with increasing coupling strength K, i.e., the oscillators show a resonance effect. Additionally, it can be noticed that, within the synchronized cluster, oscillators with smaller free running periods τi tend to phase-lead with respect to oscillators having larger values of τi. This situation is analogous to the occurrence of chronotypes, i.e., the phase-of-entrainment of an organism with respect to an external Zeitgeber. If synchronized to an external stimulus, the phase is analogously correlated with its internal free-running period [40–43].
2.2. Emergent network properties are fingerprints of coupling
The examples of Section 2.1 show that certain dynamical properties such as amplitudes and periods of the individual oscillators are subject to change if the mutual coupling between the oscillators is varied. To study changes in amplitudes, phase organization, and periods in more detail, we investigate the oscillatory properties of every single oscillator for all three coupling strength K = 0.04, K = 0.07, and K = 0.1 numerically. To this end, instantaneous phases and amplitudes are determined by means of a Hilbert transformation (HT) as described in Section5.2 in further detail. An average period is estimated for each oscillator by fitting a straight line to the (unwrapped) phase θiHT(t) and defining the inverse slope of this line times 2θ as . By this means, a single, time-independent value for the average period of each oscillator in the coupled state is determined, even if the dynamics shows non-periodic behavior such as beating, see Supplementary Figure S2 for an example analysis.
A direct comparison of the intrinsic free-running periods T in the uncoupled state and the corresponding average periods in the coupled state reveals a typical dependency between the size of the synchronized cluster and the coupling strength K. In case of small coupling strengths K, the average period of a given oscillator is barely affected by the mean field coupling as one can see in Figure 2 for K = 0.04 (blue dots), i.e., no frequency locking occurs. Above a certain critical coupling strength, a set of oscillators whose free-running periods are close to the mean of the ensemble period, starts to form a frequency- or period-locked cluster, where all oscillators share a common oscillation period, i.e., they form a frequency plateau in the -diagram, see Figure 2 for K = 0.07 (green dots). Due to the non-vanishing oscillation amplitude of the mean field in such case (remember Figure 1B), even oscillators that are not locked to the synchronized cluster experience a change of their average period towards the period of the synchronized cluster, a phenomenon that is commonly known as frequency pulling [22]. For high coupling strengths K, the ensemble forms a giant synchronized cluster, where all oscillators tick at a common pace, see Figure 2 for K = 0.1 (red dots). As a consequence, the variance in the distribution of the average individual oscillator periods decreases with increasing coupling, see Figure 3A.
Figure 2: Increasing coupling leads to the formation of frequency plateaus.
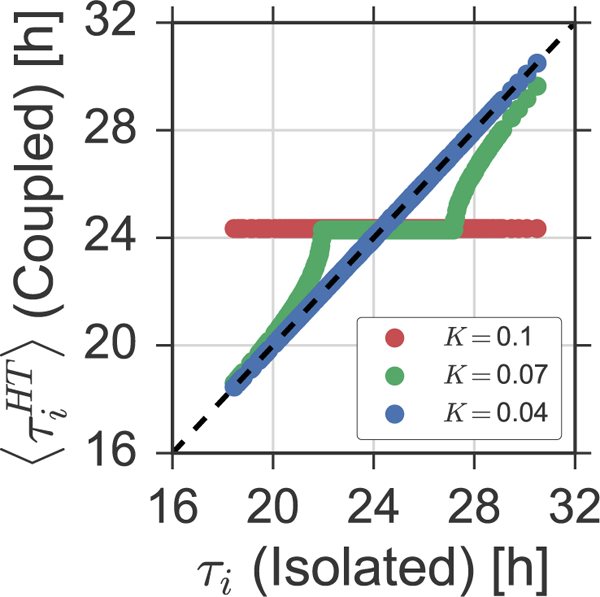
Average periods , determined by means of a Hilbert transform as described in Section 5.2, are plotted against their corresponding free-running periods τi for three different coupling strength, namely K = 0.04 (blue dots), K = 0.07 (green dots), and K = 0.1 (red dots).
Figure 3: Distributions of oscillator properties.
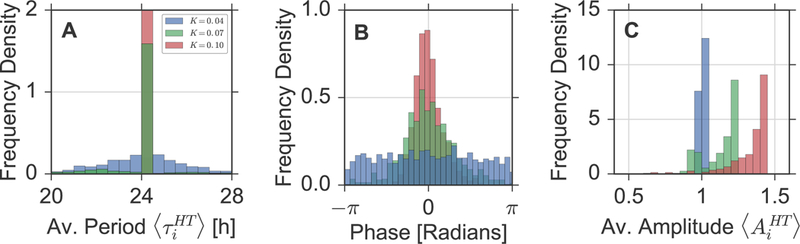
Histograms of the periods (A), phases (B) and amplitudes (C) of the individual oscillators for three different coupling strengths. Color coding represents the coupling strength, i.e K = 0.04 (blue), K = 0.07 (green), and K = 0.1 (red). Phase distributions are plotted for a time at the mid-point of the integration interval to reduce edge effects of the Hilbert transform [1]. All phase distributions have been centered such that the mean of the corresponding distribution lies at point zero.
As already noted in Section 2.1, we can observe a re-organization of the oscillation phases with varying coupling strength. While (instantaneous) oscillator phases are equally distributed across their whole co-domain in case of small coupling strength such as K = 0.04, the variance of their distribution successively decreases with increasing K, compare Figure 3B. Moreover, we find an increase of the mean value in the distribution of average amplitudes upon increasing coupling due to resonance effects, see Figure 3C.
Finally, in Figure 4, we systematically explore the above described findings for a broader range of coupling strength K. Based on synchronization properties, we can divide the dynamics into three different regimes. In case of undercritical coupling strength K, which approximately lies in the range of the oscillators do not synchronize to each other and the standard deviation in the distribution of periods is constantly close to the value of the free-running periods στ = 2h, see Figure 4A. In this incoherent state, phases spread all over the unit circle due to variations in the intrinsic periods, which leads to high values of the (circular) variance in the phase distribution and hence, a constantly low value of the classical order parameter R, see Figure 4B. After reaching a critical coupling strength , the fraction of synchronized oscillators increases, leading to a decreasing variance in the period and phase distribution and an increasing global phase coherence R, see Figure 4 A and B. For over-critical coupling strength , all oscillators form a fully synchronized cluster such that the variance in the distribution of periods drops to zero, see Figure 4A. The variance in the phase distribution and the order parameter R are close to zero and one, respectively, and slowly saturate to these values for a further increase in K, see Figure 4B. Overall, it can be noticed that the evolution of the global phase coherence R for increasing K closely resembles the behavior as known from the phase oscillator description in the paradigmatic Kuramoto model [20], see Supplementary Text 1.1 and Supplementary Figure S3 for further details.
Figure 4: Dependence of emergent network properties on the coupling strength K.
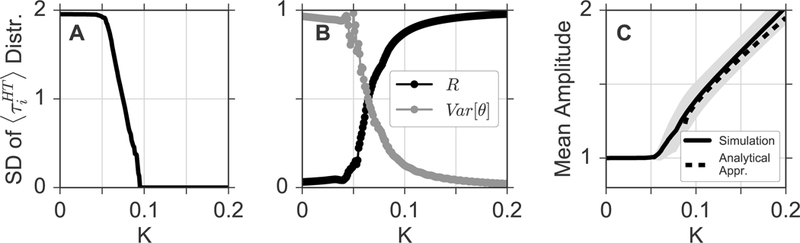
A) Standard deviations (SD) of the period distribution of individual oscillators in dependence of the coupling strength K. B) Circular variance (gray) of the phase distribution and global phase coherence R(t) in dependence of K. Variances are estimated by fitting a von Mises distribution to the phase values. C) Mean value (bold line) and standard deviation (gray shaded area) of the amplitude distribution in dependence of K. The dashed black line denotes the analytical approximation of the mean value as given by Equation 5.
Similar to the oscillation period, the amplitude of the oscillators experiences no change in the regime of under-critical coupling, see Figure 4C. As soon as the coupling exceeds the threshold , synchronization with the mean field leads to an amplitude expansion with increasing K. From symmetry considerations, we can estimate the resonance effect on amplitudes as
| (5) |
in case of over-critical coupling, see Supplementary Text 1.2 for a detailed derivation. Here, denotes the mean of the distribution of individual oscillator amplitudes for non-vanishing coupling K, while A and 7 are the intrinsic amplitude and radial relaxation rate of the oscillators. Finally, Δw equals where τ and σT are the mean and standard deviation of the intrinsic free-running periods. A comparison of the numerical results (Figure 4C, bold line) and the analytical approximation (Figure 4C, dashed line) reveals a good agreement in the investigated ranges of coupling strength K.
2.3. Dependence on Single Cell Properties
From Equation (5) it becomes clear that the amplitude not only increases with increasing coupling strength K but also depends on the intrinsic properties of the individual single-cell oscillators, i.e., the radial relaxation rate as well as the spread of the free-running periods στ. Such dependence on intrinsic oscillator parameters can also be observed with respect to other emergent network properties.
The critical coupling strength Kc increases with an increasing spread στ of the free-running period distribution, see Supplementary Figure S5A, similar to what can be observed in the Kuramoto model, compare Supplementary Text 1.1 and Figure S3 B. Contrarily, στ has little effect on the amplitude expansion for high coupling strength since Equation 5. converges to for , see also Supplementary Figure S5 B.
For fixed values of Ai = A and στ = 2h, an increasing radial relaxation rate leads to a mild increase in the critical coupling strength Kc, see Supplementary Figure S6 A, while having a dramatic effect on the amplitude expansion, see Supplementary Figure S6 B. Along these lines, rigid oscillators (e.g. for ) exhibit almost no variations in amplitude upon coupling, while non-rigid oscillators (e.g for ) exhibit a considerable increase in amplitude, see Supplementary Figure S6 B. This is tantamount to what has been observed in theoretical entrainment studies for non-rigid and rigid oscillators, see e.g. [39].
Finally, as can be also deduced from Equation (5), we can observe that an increasing intrinsic amplitude Ai = A of the individual oscillators has virtually no effect on the critical coupling strength Kc, see Supplementary Figure S7 A. Furthermore, an increasing intrinsic oscillator amplitude proportionally increases the oscillation amplitude at the network level, while having little effect on the amplitude expansion upon coupling, compare Supplementary Figure S7 B.
3. Experimental Data from Suprachiasmatic Nuclei
Studying simulated networks of mean-field coupled oscillators resulted in the following theoretical predictions: increasing coupling can lead to frequency locking, a narrowing period distribution, a decreasing variance of the phase distribution and an increasing amplitude due to resonance effects. We will use these predictions to interpret data from slices of SCN tissue ex vivo. It has been shown that, even though single SCN neurons are able to generate circadian rhythms, the remarkable precision of the SCN as a tissue crucially depends on heterogeneous inter-cellular couplings [11]. Here, we focus on previously published data from PER2::LUC recordings in five coronal SCN slices of neonatal to seven-day-old mice, where spike-associated couplings have been altered by pharmacological treatments with tetrodotoxin (TTX) [44]. Therein, after 4 days of bioluminescence recordings following the slice preparations, 2.5μM TTX was applied and remained in the medium for 6 days. Subsequently, TTX was washed out from the culture medium and recordings were maintained for at least 8 more days, see [29, 44] for details. In [44], single SCN neurons were automatically identified and tracked in the two dimensional bioluminescence timelapse recordings. Ensemble average bioluminescence intensities (black line) and standard deviations (gray shaded area) for each time point of the recordings of one SCN slice are plotted in Figure 5A. Time series data that corresponds to the other SCN slice preparations are plotted in Supplementary Figure S8. As already noted in [29, 44], application of TTX leads to a reduction in synchrony and a reduced amplitude of the SCN cells that can be partially reversed by washing out TTX. Here, we estimate oscillation properties of these single cell time series separately under all three conditions, i.e., before TTX application, during TTX application, and after washing TTX from the medium. To this end, we fit a (stochastic) generic amplitude-phase model with three parameters to the data by means of an autocorrelation function approach as described previously [32, 34], see Section 5.3 for further details. In Figure 5 (B)-(D), a representative fit under each condition is shown. By this method, we determine for each neuronal cell its free-running period, amplitude, radial relaxation rate and fluctuation or noise strength.
Figure 5: Fitting oscillator models to experimental data.
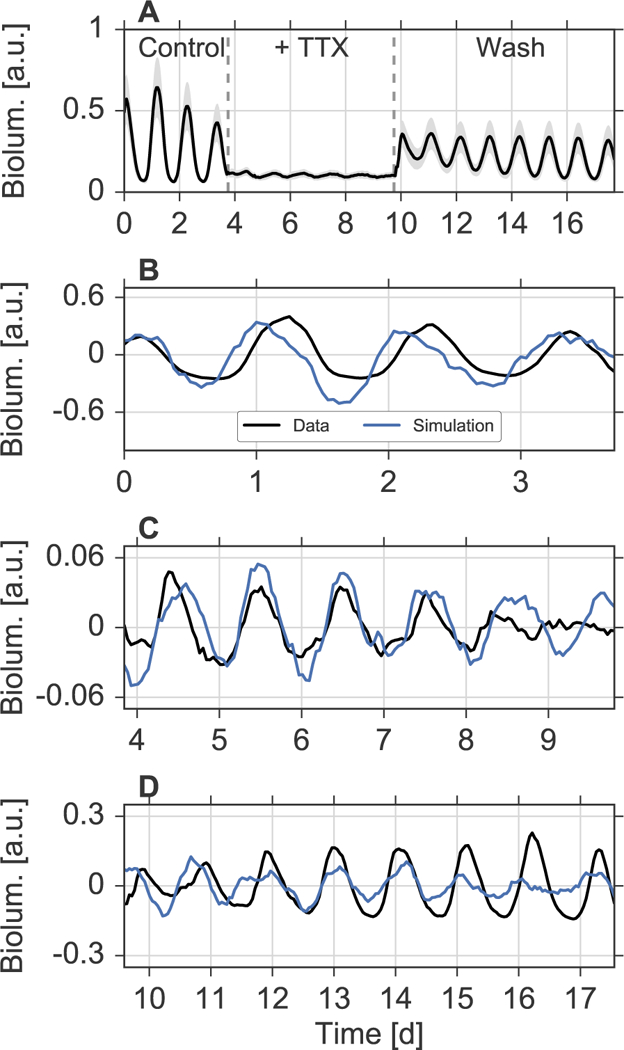
A) Ensemble averages (black line) and standard deviations (gray shaded area) of bioluminescence time-series from automatically identified and tracked neurons in coronal slices of the SCN as described in [44]. B-D) Fits to time series from representative cells under all three conditions, namely, before applying TTX (B), during the application of TTX (C), and after washing TTX from the culture medium (D). Black curves denote the original data, detrended by means of a Hodrick-Prescott filter as described in Section 5.3. Blue curves denote simulations of the stochastic ordinary differential Equations (6)–(7) for the parameters, obtained by fits to the corresponding experimental time series as described in Section 5.3. Initial conditions have been selected such that the stochastic dynamics resemble the experimental time series.
Interestingly, we can rediscover the characteristic patterns of different coupling regimes, as known from our simulation studies, when comparing period, phase, and amplitude distributions under all three experimental conditions, see Figure 6 for example distributions from the first SCN slice. Before application of TTX, the distribution of the single cell periods has a mean of and an empirical standard deviation of (Figure 6A, red). During the application of TTX, the ensemble mean of the period drops to a value of , accompanied by a broadening of its distribution to (Figure 6A, blue), lying close to the value that was previously published for distributions of dispersed SCN neurons [11, 35, 37]. Finally, washing out TTX from the medium partially reverses this effect: the distributions mean rises to a value of while its empirical standard deviation decreases to , lying close to the value before application of the neurotoxin (Figure 6A, green). Similarly, representative phase distributions show a narrow, broad, and intermediate spread before applying, during the application, and after washing out TTX, respectively, see Figure 6B. Lastly, the single cell oscillations in bioluminescence intensities experience, on average, an approximately 12-fold decline in their amplitudes during application of TTX which is again partly recovered by the washing procedure, see Figure 6C.
Figure 6: Emergent properties in SCN slice data.
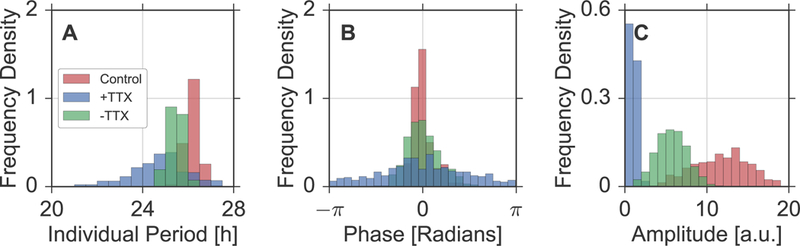
Period (A), phase (B), and amplitude distributions under three experimental conditions, i.e., before applying TTX (red bars), during the application of TTX (blue bars), and after washing out TTX from the medium (green bars). Periods and amplitudes of single neuronal biolouminscence time series are determined by means of oscillator fits as described in Section 5.3. Phases have been obtained at times t1 = 54 h (Control), t2 = 180 h (+TTX), t3 = 365 h (−TTX) by means of an analytic signal approach, equivalent to what has been used in case of simulated time series, see Section 5.2.
In summary, we observe an increase of the empirical standard deviation in the distributions of single cell periods and phases as well as a decreasing mean of the amplitude distribution upon application of TTX compared to the control condition or after washing out TTX. In analogy to our simulation results, it is therefore plausible to assume that the application of TTX corresponds to a dynamical regime with relatively weak inter-cellular couplings compared to the other conditions. Note, that application of TTX might affect also single cell oscillators. Such additional effects of TTX could contribute to the period and amplitude changes.
Quite similar results were obtained in the four other SCN slice preparations as shown in Supplementary Figures S9-S12. A summary of the statistical properties in the distributions of periods, phases, and amplitudes across all five SCN slice preparations can be found in Supplementary Tables S1-S3, respectively.
4. Summary and Discussion
The circadian clock can be regarded as a system of coupled oscillators on the levels of cells, peripheral organs, and organisms. In many cases, for example for the wildtype SCN, the individual oscillators are perfectly synchronized. In case of undercritical coupling (e.g. for dispersed fibroblasts) no synchronization is observed. For varying conditions (cell densities [8], population size [19], knockouts [45], developmental stages [34], inhibitor applications [14]) changes of coupling strength can be expected. However, as long as no transitions between coherent and incoherent states are induced, no obvious qualitative changes occur.
Here, we emphasize to quantify coupling strength by analyzing distributions of periods, phases, and amplitudes. Network simulations show that for undercritical coupling, period distributions become narrower due to partial synchronization and frequency pulling. For overcritical coupling, phase distributions are informative since large coupling induces narrow phase distributions. This effect resembles reduced spreads of chronotypes for strong Zeitgebers [42, 46]. Furthermore, amplitudes might increase with coupling due to resonance effects. We provide an analytical calculation for the amplitude expansion that agrees well with our numerical simulations.
We confirmed the theoretical predictions from oscillator theory using data from recent experiments with SCN slices [44]. The wildtype SCNs exhibit larger amplitudes and narrow period and phase distributions compared to data with TTX treatment.
There are numerous applications of coupling strength quantifications in SCN preparations. For example, it has been suggested that coupling is changing in early development [9]. Moreover, the relative strength of coupling via gap junctions and coupling factors such as VIP, GABA and AVP is discussed [14]. Our study encourages closer inspections of the corresponding period, phase, and amplitude distributions in forthcoming studies.
Circadian clocks have been found in virtually all mammalian tissues [47]. Thus, the quantification of coupling between cells in peripheral organs has been raised [39, 48]. There are indications that hepatocytes are coupled, leading to a rather strong liver clock [48, 49]. In dispersed fibroblasts, mathematical modeling predicts coupling even though no full synchronization is achieved [50]. Indeed, Noguchi et al.[8] have shown that increasing cell densities improve rhythmicity accompanied by increasing amplitudes. According to our concept, these observations indicate coupling.
In plant circadian systems, early studies suggested weak inter-cellular couplings of cell-autonomous clocks [51] but recent data show that circadian coupling allows synchrony among shoot apex clocks as quantified by phase variances [52]. Furthermore, the statistical analysis of individual periods and phases indicates coupling in social groups of rodents [10, 16] and honeybees [18].
In this paper, we suggested analyzing distributions of periods, phases and amplitudes as markers of coupling strength. There are also alternative methods to quantify coupling. For example, monitoring relaxation to equilibria provides information on coupling strength. In the SCN, local perturbations might be induced by optogenetic tools [53]. In flies, short light pulses induced transient desynchrony and the relaxation of the neuronal network revealed the kinetics of retuning [54].
Another strategy is to study the kinetics of SCN plasticity upon different protocols of light-dark cycles. Regional phase differences within the SCN network can be induced by very long photoperiods, e.g. 20 h of light and 4 h of darkness [28], or by entrain-ment with unnaturally short and long Zeitgeber periods such as 22 h or 26 h [55]. The relaxation dynamics of the induced phase differences can be exploited to explore coupling mechanisms.
Mathematically, a network of N uncoupled oscillators with different individual frequencies represents an N-dimensional torus [56]. Contrarily, complete synchronization constitutes a 1-dimensional limit cycle in phase space. Thus the attractor dimension [57] could be regarded as a measure of coupling strength. However, estimations of attractor dimensions require long, stationary time-series rarely available in chronobiology. Still, the observation of multiple period clusters [9], of ”relative coordination [58], and of splitting [59, 60] point to loss of synchrony due to reduced coupling.
Our simulations were based on amplitude-phase oscillators with global coupling. For more local coupling schemes, complex spatio-temporal patterns of periods, phases, and amplitudes can be expected. In such situations measures of spatial-coherence such as mutual information [44] or Morans I (Schmal et al.,submitted) can complement the analysis of overall distributions discussed in this paper.
Our approach assumes that periods, phases, and amplitudes can be measured for individual oscillators. In many cases, only overall signals are available for tissue slices or cell cultures [61]. In such cases only indirect cues provide information on coupling strength. It has been shown theoretically and experimentally [39] that coupling can establish strong oscillators [62], i.e., robust oscillations with limited sensitivity to perturbations and narrow entrainment ranges. Indeed, in vertebrates with strongly coupled pacemaker cells the entrainment ranges are much narrower than in invertebrates [63]. A narrow entrainment range implies also a high sensitivity of the entrainment phase with respect to period variations [43, 64], known also for human chronotypes [42, 65].
Mathematical modeling can provide connections between coupling strength and observed global characteristics such as phase response curves and entrainment ranges which, in turn, can be used to define strong and weak oscillators. In mammals, a hierarchy of strong oscillators due to coupling (SCN) and weak oscillators (fibroblasts, lung tissue, etc.) allow appropriate orchestration of circadian rhythms.
5. Materials and Methods
5.1. Numerical Simulations
Numerical solutions of Equations (3)–(4), have been obtained for a total integration time of 400 × 24 h at Δt = 0.25 h time steps by using the odeint function of SCIentificPYthon. Initial conditions of the N = 1000 oscillators have been chosen to be equally distributed among the unit circle, i.e., the radial component was set to while has been drawn from uniformly distributed random numbers between [0,2π[. The initial condition was chosen once and has then been fixed throughout all simulations.
5.2. Analysis of Simulated Time Series
The instantaneous phase θ(t) and amplitude A(t) of an oscillatory time series s(t) is estimated by means of an analytic signal approach as described in more detail in, e.g., [1]. The analytic signal is defined as , where denotes the Hilbert transform. Along these lines, the instantaneous phase and amplitude is defined by , and , respectively, where and denotes the real and imaginary part of z(t). Throughout this paper, Hilbert transformations of discrete time-series are performed numerically by the SCIentificPYthon function hilbert.
A further analysis of the instantaneous phases and amplitudes was restricted to a time interval between to ignore transient dynamics of the system and to minimize edge effects during the numerical estimation of the Hilbert transform [1]. Based on the definition of the instantaneous frequency of oscillator i, we calculate the time-averaged period (as found in Figures 2 and 3A) in the interval , where is the slope of a linear fit to the (unwrapped) instantaneous phase θi(t) in the interval . The average amplitude of an oscillator i, as depicted in Figure 3C, is simply determined by the time average of its instantaneous amplitude Ai(t) over the time interval .
5.3. Analysis of Experimental Time Series
Previously published data from PER2::LUC recordings in coronal SCN slices, as published in [44], are analyzed in Section 3. First, time series corresponding to bioluminescence recordings of single SCN neurons are detrended by means of a Hodrick-Prescott filter. To this end, we use the hpfilter function of the statsmodels Python module and choose a smoothing parameter of , where Δt is the experimental sampling rate of the time series, as suggested in [66]. Second, we fit the stochastic model
| (6) |
| (7) |
of a linear damped oscillator by means of an autocorrelation approach as described in [32]. Here, γ and denote the radial relaxation rate and the intrinsic free-running period of the oscillator, respectively, while for are independent, delta-correlated white noise terms with zero mean, i.e., and . In essence, the autocorrelation function
| (8) |
which can be analytically obtained from Equations (6)–(7), is fitted to the numerically obtained autocorrelation function of the experimental time series of interests. By this means, we can estimate the oscillator parameters , and the noise strength D for a given experimental time series. The amplitude of the resulting oscillations as plotted in Figure 6C can be obtained via , see [32] for details.
Simulations of the stochastic ordinary differential Equations (6)–(7), as depicted in Figure 5 B-D, have been obtained by means of Euler’s method for stochastic equations using XPP-AUTO [67, 68].
Supplementary Material
Acknowledgements
The authors gratefully thank Dr. Bharath Anantha-subramaniam and Dr. Grigory Bordyugov for stimulating discussions as well as Dr. Daniel Granados-Fuentes and Thomas Wang for experimental support.
Funding
This work has been supported by the Deutsche Forschungsgemeinschaft [grant number BO 3612/2–1] to CS, the Bundesministerium für Bildung und Forschung [grant number 01GQ1503] to HH, and the National Institute of Neurological Disorders and Stroke [grant number 095367–01] to EH. CS acknowledges support from the Joachim Herz Stiftung.
Footnotes
Competing Interests
We have no competing interests.
References
- [1].Pikovsky Arkady, Rosenblum Michael, and Kurths Jürgen. Synchronization: A Universal Concept in Nonlinear Sciences. Cambridge University Press, 2001. [Google Scholar]
- [2].Strogatz Steven H.. SYNC: The Emerging Science of Spontenous Order. Hyperion, New York, 2003. [Google Scholar]
- [3].Glass Leon and Mackey Michael C.. From Clocks to Chaos: The Rhythms of Life. Princeton University Press, 1988. [Google Scholar]
- [4].Winfree Arthur T.. The Geometry of Biological Time. Springer-Verlag, 1990. [Google Scholar]
- [5].Kuramoto Yoshiki. Chemical Oscillations, Waves, and Turbulence. Dover Publications, Inc., Mineola, New York, 2003. [Google Scholar]
- [6].Nagoshi Emi, Saini Camille, Bauer Christoph, Laroche Thierry, Naef Felix, and Schibler Ueli. Circadian Gene Expression in Individual Fibroblasts: Cell-Autonomous and Self-Sustained Oscillators Pass Time to Daughter Cells. Cell, 119 (5):693–705, 2004. [DOI] [PubMed] [Google Scholar]
- [7].Yamaguchi Shun, Isejima Hiromi, Matsuo Takuya, Okura Ryusuke, Yagita Kazuhiro, Kobayashi Masaki, and Okamura Hitoshi. Synchronization of Cellular Clocks in the Suprachiasmatic Nucleus. Science, 302(5649):1408–1412, 2003. [DOI] [PubMed] [Google Scholar]
- [8].Noguchi Takako, Wang Lexie L., and Welsh David K.. Fibroblast PER2 Circadian Rhythmicity Depends on Cell Density. Journal of Biological Rhythms, 28(3):183–192, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Ono Daisuke, Honma Sato, and Honma Ken-ichi. Differential roles of AVP and VIP signaling in the postnatal changes of neural networks for coherent circadian rhythms in the SCN. Science Advances, 2(9):e1600960, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Paul Matthew J., Indic Premananda, and Schwartz William J.. Social synchronization of circadian rhythmicity in female mice depends on the number of cohabiting animals. Biology Letters, 11(6):20150204, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Herzog Erik D., Aton Sara J., Numano Rika, Sakaki Yoshiyuki, and Tei Hajime. Temporal Precision in the Mammalian Circadian System: A Reliable Clock from Less Reliable Neurons. Journal of Biological Rhythms, 19(1):35–46, 2004. [DOI] [PubMed] [Google Scholar]
- [12].Welsh David K., Takahashi Joseph S., and Kay Steve A.. Suprachiasmatic Nucleus: Cell Autonomy and Network Properties. Annual Review of Physiology, 72(1):551–577, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Mohawk Jennifer A. and Takahashi Joseph S.. Cell autonomy and synchrony of suprachiasmatic nucleus circadian oscillators. Trends in Neurosciences, 34(7):349–358, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Herzog Erik D., Hermanstyne Tracey, Smyllie Nicola J., and Hastings Michael H.. Regulating the Suprachiasmatic Nucleus (SCN) Circadian Clockwork: Interplay between Cell-Autonomous and Circuit-Level Mechanisms. Cold Spring Harbor Perspectives in Biology, 9(1):a027706, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].John S O’Neill and Michael H. Hastings. Increased Coherence of Circadian Rhythms in Mature Fibroblast Cultures. Journal of Biological Rhythms, 23(6):483–488, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Paul Matthew J., Indic Premananda, and Schwartz William J.. Social forces can impact the circadian clocks of cohabiting hamsters. Proceedings of the Royal Society of London B: Biological Sciences, 281(1779):20132535, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Levine Joel D., Funes Pablo, Dowse Harold B., and Hall Jeffrey C.. Resetting the Circadian Clock by Social Experience in Drosophila melanogaster. Science, 298(5600):2010–2012, 2002. [DOI] [PubMed] [Google Scholar]
- [18].Fuchikawa Taro, Ada Eban-Rothschild Moshe Nagari, Shemesh Yair, and Bloch Guy. Potent social synchronization can override photic entrainment of circadian rhythms. Nature Communications, 7:11662, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Bloch Guy, Herzog Erik D., Levine Joel D., and Schwartz William J.. Socially synchronized circadian oscillators. Proceedings of the Royal Society of London B: Biological Sciences, 280(1765): 20130035, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Kuramoto Yoshiki. Self-entrainment of a population of coupled non-linear oscillators. In Prof Huzihiro Araki, editor, International Symposium on Mathematical Problems in Theoretical Physics, number 39 in Lecture Notes in Physics, pages 420–422. Springer Berlin; Heidelberg, 1975. [Google Scholar]
- [21].Strogatz Steven H.. From Kuramoto to Crawford: exploring the onset of synchronization in populations of coupled oscillators. Physica D: Nonlinear Phenomena, 143(1–4):1–20, 2000. [Google Scholar]
- [22].Wiener Norbert. Cybernetics: or Control and Communication in the Animal and the Machine, 2nd Edition The M.I.T. Press, 1961. [Google Scholar]
- [23].Ashwin Peter, Coombes Stephen, and Nicks Rachel. Mathematical Frameworks for Oscillatory Network Dynamics in Neuroscience. The Journal of Mathematical Neuroscience, 6(1), 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Baba Kenkichi, Ono Daisuke, Honma Sato, and Honma Ken-ichi. A TTX-sensitive local circuit is involved in the expression of PK2 and BDNF circadian rhythms in the mouse suprachiasmatic nucleus. European Journal of Neuroscience, 27 (4):909–916, 2008. [DOI] [PubMed] [Google Scholar]
- [25].Webb Alexis B., Angelo Nikhil, Huettner James E., and Herzog Erik D.. Intrinsic, nondeter-ministic circadian rhythm generation in identified mammalian neurons. PNAS, 106(38):16493–16498, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Enoki Ryosuke, Kuroda Shigeru, Ono Daisuke, Hasan Mazahir T., Ueda Tetsuo, Honma Sato, and Honma Ken-ichi. Topological specificity and hierarchical network of the circadian calcium rhythm in the suprachiasmatic nucleus. PNAS, 109(52):21498–21503, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Webb Alexis B., Taylor Stephanie R., Thoroughman Kurt A., Doyle Francis J., and Herzog Erik D.. Weakly Circadian Cells Improve Resynchrony. PLoS Comput Biol, 8(11):e1002787, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Evans JenniferA., Leise TanyaL., Castanon-Cervantes Oscar, and Davidson AlecJ.. Dynamic Interactions Mediated by Nonredundant Signaling Mechanisms Couple Circadian Clock Neurons. Neuron, 80(4):973–983, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Taylor Stephanie R., Wang Thomas J., Daniel Granados-Fuentes, and Erik D. Herzog. Resynchronization Dynamics Reveal that the Ventral Entrains the Dorsal Suprachiasmatic Nucleus. Journal of Biological Rhythms, page 0748730416680904, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Gonze Didier, Bernard Samuel, Waltermann Christian, Kramer Achim, and Herzel Hanspeter. Spontaneous Synchronization of Coupled Circadian Oscillators. Biophysical Journal, 89(1):120–129, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Locke James CW, Westermark Pl O., Kramer Achim, and Herzel Hanspeter. Global parameter search reveals design principles of the mammalian circadian clock. BMC Systems Biology, 2(1):22, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Westermark Pal O., Welsh David K., Okamura Hitoshi, and Herzel Hanspeter. Quantification of Circadian Rhythms in Single Cells. PLoS Comput Biol, 5(11):e1000580, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Ramkisoensing Ashna, Gu Changgui, van Engeldorp Gastelaars Heleen M.D., Michel Stephan, Deboer Tom, Rohling Jos H.T., and Meijer Johanna H.. Enhanced Phase Resetting in the Synchronized Suprachiasmatic Nucleus Network. Journal of Biological Rhythms, 29(1): 4–15, 2014. [DOI] [PubMed] [Google Scholar]
- [34].Tokuda IsaoT, Ono Daisuke, subramaniam Bharath Anantha, Honma Sato, Honma Ken-Ichi, and Herzel Hanspeter. Coupling Controls the Synchrony of Clock Cells in Development and Knockouts. Biophysical Journal, 109(10):2159–2170, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Welsh David K., Logothetis Diomedes E., Meister Markus, and Reppert Steven M.. Individual neurons dissociated from rat suprachiasmatic nucleus express independently phased circadian firing rhythms. Neuron, 14(4):697–706, 1995. [DOI] [PubMed] [Google Scholar]
- [36].Liu Chen, Weaver David R., Strogatz Steven H., and Reppert Steven M.. Cellular Construction of a Circadian Clock: Period Determination in the Suprachiasmatic Nuclei. Cell, 91:855–860, 1997. [DOI] [PubMed] [Google Scholar]
- [37].Honma Sato, Shirakawa Tetsuo, Kat-suno Yumiko, Namihira Masakazu, and Honma Ken-ichi. Circadian periods of single suprachiasmatic neurons in rats. Neuroscience Letters, 250(3):157–160, 1998. [DOI] [PubMed] [Google Scholar]
- [38].Honma Sato, Nakamura Wataru, Tetsuo Shi-rakawa, and Ken-ichi Honma. Diversity in the circadian periods of single neurons of the rat suprachiasmatic nucleus depends on nuclear structure and intrinsic period. Neuroscience Letters, 358(3):173–176, 2004. [DOI] [PubMed] [Google Scholar]
- [39].Abraham Ute, Adrian E Granada, Pal O Westermark, Markus Heine, Achim Kramer, and Hanspeter Herzel. Coupling governs entrainment range of circadian clocks. Mol Syst Biol, 6, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Aschoff Jürgen and Wever Rütger. Circadian period and phase-angle difference in chaffinches (Fringilla coelebs L.). Comparative Biochemistry and Physiology, 18(2):397–404, 1966. [DOI] [PubMed] [Google Scholar]
- [41].Pittendrigh Colin S. and Daan Serge. A functional analysis of circadian pacemakers in nocturnal rodents: IV. Entrainment: Pacemaker as clock. Journal of comparative physiology, 106(3): 291–331, 1976. [Google Scholar]
- [42].Granada Adrin E., Bordyugov Grigory, Kramer Achim, and Herzel Hanspeter. Human Chrono-types from a Theoretical Perspective. PLoS ONE, 8(3):e59464, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Schmal Christoph, Myung Jihwan, Herzel Hanspeter, and Bordyugov Grigory. A theoretical study on seasonality. Frontiers in Neurology, page 94, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Abel John H., Meeker Kirsten, Granados-Fuentes Daniel, Peter C. St John, Wang Thomas J., Bales Benjamin B., Doyle Francis J., Herzog Erik D., and Petzold Linda R.. Functional network inference of the suprachiasmatic nucleus. PNAS, 113(16):4512–4517, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Ono Daisuke, Honma Sato, and Honma Ken-ichi. Cryptochromes are critical for the development of coherent circadian rhythms in the mouse suprachiasmatic nucleus. Nature Communications, 4:1666, 2013. [DOI] [PubMed] [Google Scholar]
- [46].Roenneberg Till, Anna Wirz-Justice, and Martha Merrow. Life between Clocks: Daily Temporal Patterns of Human Chronotypes. Journal of Biological Rhythms, 18(1):80–90, 2003. [DOI] [PubMed] [Google Scholar]
- [47].Dibner Charna, Schibler Ueli, and Albrecht Urs. The mammalian circadian timing system: organization and coordination of central and peripheral clocks. Annual Review of Physiology, 72: 517–549, 2010. [DOI] [PubMed] [Google Scholar]
- [48].Guenthner Casey J., Luitje Martha E., Pyle Lorna A., Molyneux Penny C., Yu Jimmy K., Li Alexander S., Leise Tanya L., and Harrington Mary E.. Circadian Rhythms of PER2::LUC in Individual Primary Mouse Hepatocytes and Cultures. PLoS ONE, 9:e87573, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Saini Camille, Liani Andr, Curie Thomas, Gos Pascal, Kreppel Florian, Emmenegger Yann, Bonacina Luigi, Wolf Jean-Pierre, Poget Yves-Alain, Franken Paul, and Schibler Ueli. Realtime recording of circadian liver gene expression in freely moving mice reveals the phase-setting behavior of hepatocyte clocks. Genes & Development, 27(13):1526–1536, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Rougemont Jacques and Naef Felix. Dynamical signatures of cellular fluctuations and oscillator stability in peripheral circadian clocks. Molecular Systems Biology, 3(1), 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Thain Simon C., Hall Anthony, and Millar Andrew J.. Functional independence of circadian clocks that regulate plant gene expression. Current Biology, 10(16):951–956, 2000. [DOI] [PubMed] [Google Scholar]
- [52].Takahashi Nozomu, Hirata Yoshito, Aihara Kazuyuki, and Mas Paloma. A Hierarchical Multioscillator Network Orchestrates the Arabidopsis Circadian System. Cell, 163(1):148–159, 2015. [DOI] [PubMed] [Google Scholar]
- [53].Jones Jeff R., Tackenberg Michael C., and McMahon Douglas G.. Manipulating circadian clock neuron firing rate resets molecular circadian rhythms and behavior. Nature Neuroscience, 18 (3):373–375, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Roberts Logan, Leise Tanya L., Noguchi Takako, Galschiodt Alexis M., Houl Jerry H., Welsh David K., and Holmes Todd C.. Light Evokes Rapid Circadian Network Oscillator Desynchrony Followed by Gradual Phase Retuning of Synchrony. Current Biology, 25(7):858–867, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Azzi Abdelhalim, Evans Jennifer A., Leise Tanya, Myung Jihwan, Takumi Toru, Davidson Alec J., and Brown Steven A.. Network Dynamics Mediate Circadian Clock Plasticity. Neuron, 0(0), 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Grebogi Celso, Ott Edward, and Yorke James A.. Attractors on an N-torus: Quasiperiodicity versus chaos. Physica D: Nonlinear Phenomena, 15(3):354–373, 1985. [Google Scholar]
- [57].Doyne Farmer J, Ott Edward, and Yorke James A. The dimension of chaotic attractors. Physica D: Nonlinear Phenomena, 7(1):153–180, 1983. [Google Scholar]
- [58].Holst Erich v. Die relative Koordination. Ergebnisse der Physiologie, biologischen Chemie und experimentellen Pharmakologie, 42(1):228–306, 1939. [Google Scholar]
- [59].Gwinner Eberhard. Testosterone Induces “Splitting” of Circadian Locomotor Activity Rhythms in Birds. Science, 185(4145):72–74, 1974. [DOI] [PubMed] [Google Scholar]
- [60].de la Iglesia Horacio O, Meyer Jennifer, Carpino Alan, and Schwartz William J. Antiphase Oscillation of the Left and Right Suprachiasmatic Nuclei. Science, 290(5492):799–801, 2000. [DOI] [PubMed] [Google Scholar]
- [61].Maier Bert, Wendt Sabrina, Vanselow Jens T., Wallach Thomas, Reischl Silke, Oehmke Stefanie, Schlosser Andreas, and Kramer Achim. A large-scale functional RNAi screen reveals a role for CK2 in the mammalian circadian clock. Genes & Development, 23(6): 708–718, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Bordyugov Grigory, Abraham Ute, Granada Adrian, Rose Pia, Imkeller Katharina, Kramer Achim, and Herzel Hanspeter. Tuning the phase of circadian entrainment. Journal of The Royal Society Interface, 12(108):20150282, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [63].Aschoff Jürgen and Pohl Hermann. Phase relations between a circadian rhythm and its zeitgeber within the range of entrainment. Die Naturwissenschaften, 65(2):80–84, 1978. [DOI] [PubMed] [Google Scholar]
- [64].Hoffmann Klaus. Zum Einfluß der Zeit-geberstüarke auf die Phasenlage der synchronisierten circadianen Periodik. Zeitschrift fur vergleichende Physiologie, 62(1):93–110, 1969. [Google Scholar]
- [65].Wright Kenneth P., Gronfier Claude, Duffy Jeanne F., and Czeisler Charles A.. Intrinsic period and light intensity determine the phase relationship between melatonin and sleep in humans. Journal of Biological Rhythms, 20(2):168–177, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66].Peter C John St. and Doyle Francis J Quantifying Stochastic Noise in Cultured Circadian Reporter Cells. PLoS Computational Biology, 11(11), 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [67].Ermentrout Bard. Simulating, Analyzing, and Animating Dynamical Systems: A Guide to XP-PAUT for Researchers and Students. SIAM; 2002, Philadelphia, USA, 2002. [Google Scholar]
- [68].Schmal Christoph, Leloup Jean-Christophe, and Gonze Didier. Modeling and Simulating the Arabidopsis thaliana Circadian Clock Using XPP-AUTO In Staiger Dorothee, editor, Plant Circadian Networks, number 1158 in Methods in Molecular Biology, pages 337–358. Springer; New York, 2014. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


