Geometric Approximation: A New Computational Approach To Characterize Protein Dynamics from NMR Adiabatic Relaxation Dispersion Experiments

Abstract

A new computational strategy is reported that provides a fast approximation of numerical solutions of differential equations in general. The method is demonstrated with the analysis of NMR adiabatic relaxation dispersion experiments to reveal biomolecular dynamics. When an analytical solution to the theoretical equations describing a physical process is not available, the new approach can significantly accelerate the computational speed of the conventional numerical integration up to 10⁵ times. NMR adiabatic relaxation dispersion experiments enhanced with optimized proton-decoupled pulse sequences, although extremely powerful, have previously been refractory to quantitative analysis. Both simulations and experimental validation demonstrate detectable “slow” (microsecond to millisecond) conformational exchange rates from 10² to 10⁵ s⁻¹. This greatly expanded time-scale range enables the characterization of a wide array of conformational fluctuations for individual residues, which correlate with biomolecular function and were previously inaccessible. Moreover, the new computational method can be potentially generalized for analysis of new types of relaxation dispersion experiments to characterize the various dynamics of biomolecular systems.

Graphical Abstract

■. INTRODUCTION

Macromolecules in solution intrinsically undergo conformational dynamics representing interconversions between thermodynamically linked states on the energy landscape. Such protein dynamics have been shown to play crucial roles in various protein functions, such as ligand binding, catalysis, and allostery.^1–3 A recent study⁴ illustrated how internal motions are critical to ligand-induced opening and functional dimerization in cIAP1. In some cases, entropically driven conformational dynamics can directly regulate protein function. For example, a mutation affecting only the conformational dynamics in dihydrofolate reductase (DHFR) can “knock out” enzyme activity.⁵ Similarly, the biological function of the catabolite activator protein (CAP) is primarily driven by conformational dynamics even when a mutant form of the protein adopts an inactive conformation.⁶ Furthermore, the low-population (higher-energy) conformation may be the functional conformation, and the dynamic exchange between the two conformations is essential to biological function.⁷ This situation is likely to occur more frequently in biology than is generally appreciated, where it can become a form of triggerable regulation. Thus, it becomes increasingly important to understand the roles of conformational dynamics and interconversion rates associated with protein functions.

NMR spectroscopy is one of the few biophysical techniques that can characterize the conformational dynamics of biomolecules in aqueous solution at atomic resolution.⁸ Hence, it provides a link to map dynamical information onto the burgeoning structural information to form a more complete picture of biological function and identify hot spots with the potential for novel therapeutic interventions. Biological function and allostery occur across the microsecond to millisecond time scale, and NMR relaxation dispersion experiments have the ability to interrogate these processes (slow dynamics). For example, conventional rotating-frame relaxation (R_1ρ) experiments are used to probe conformational exchange on the microsecond time scale (10³−10⁴ s⁻¹),⁹ while Carr−Purcell−Meiboom−Gill (CPMG) experiments are sensitive to conformational exchange on the millisecond time scale (10²−10³ s⁻¹).¹⁰ In order to quantitatively extract dynamic parameters from these experimental data, several approximate analytic solutions have been derived for different types of relaxation dispersion experiments using sophisticated specific analytic approaches.^11–14 However, analytical solutions may not be available (or feasible) for newer, more complex experiments. Here we introduce a new computational approach, a geometric approximation method, as a general tool to provide solutions for relaxation dispersion experiments. It is subsequently applied to a sophisticated variant of the traditional R_1ρ and CPMG experiments, Heteronuclear Adiabatic Relaxation Dispersion (HARD),¹⁵ which yields rich information on conformational dynamics across an extremely wide range of time scales.

Classical Model.

The classical model for exchange between two sites,¹⁶ expressed by the Bloch−McConnell equation, has been used for many decades to describe the evolution of the bulk magnetization of a nuclear spin ensemble under chemical exchange in NMR spectroscopy. The Bloch−McConnell equation assuming a two-site exchange model is given by eq 1:

$$\underset{\frac{\text{d}}{\text{d}t}\left[\begin{array}{c}{N}_{\text{a}x}\\ N_{\text{b}x}\\ N_{\text{a}y}\\ N_{\text{b}y}\\ N_{\text{a}z}\\ N_{\text{b}z}\end{array}\right]=\left[\begin{array}{cccccc}-k_{\text{a}}-R_2& k_{\text{b}}& -{\delta }_{\text{a}}& 0& {\omega }_1& 0\\ k_{\text{a}}& -k_{\text{b}}-R_2& 0& -{\delta }_{\text{b}}& 0& {\omega }_1\\ {\delta }_{\text{a}}& 0& -k_{\text{a}}-R_2& k_{\text{b}}& 0& 0\\ 0& {\delta }_{\text{b}}& k_{\text{a}}& -k_{\text{b}}-R_2& 0& 0\\ -{\omega }_1& 0& 0& 0& -k_{\text{a}}-R_1& k_{\text{b}}\\ 0& -{\omega }_1& 0& 0& k_{\text{a}}& -k_{\text{b}}-R_1\end{array}\right]\left[\begin{array}{c}{N}_{\text{a}x}\\ N_{\text{b}x}\\ N_{\text{a}y}\\ N_{\text{b}y}\\ N_{\text{a}z}\\ N_{\text{b}z}\end{array}\right]+R_1\left[\begin{array}{c}0\\ 0\\ 0\\ 0\\ N_{\text{a0}}\\ N_{\text{b0}}\end{array}\right]}{\text{A}\underset{k_{\text{b}}}{\overset{k_{\text{a}}}{\rightleftarrows }}\text{B}}$$ (1)

The forward and reverse reaction rates (k_a and k_b), the resonance offsets of states A and B with respect to the radiofrequency (RF) pulse (δ_a and δ_b), the amplitude of the RF pulse (ω₁), and the longitudinal and transverse relaxation rates (R₁ and R₂) enable a complete description of the system. In principle, analysis of relaxation behavior in the context of this mathematical formalism would permit extraction of the exchange/reaction rates, chemical shifts/offsets, and populations either by numerical integration or via derivation of analytical solutions of the equation as a function of these variables (the conventional approach). However, numerical integration is extremely inefficient (vide infra) and approximate analytic solutions are available only for CPMG and R_1ρ experiments.^11–14 Each approximate analytic solution was derived using a complicated and widely different approach for each experimental scheme. For example, the general solution for the CPMG experiment was derived by treating the recursion relations as coupled difference equations,¹² while the solution for the R_1ρ experiment was derived by approximating the largest eigenvalue of the evolution matrix of the average density operator.¹⁴ Consideration of other relaxation experiments requires either derivation of new analytical solutions or an alternative approach.

Adiabatic R_1ρ and R_2ρ experiments measure longitudinal and transverse relaxation in an effective field by replacing conventional continuous-wave (CW) pulses with different (a series of) adiabatic pulses (herein we utilize hyperbolic secant (HS)-based pulses, denoted as HSn).^15,17 These experiments exhibit distinct relaxation dispersion profiles (R_ex) as a function of the exchange rate (k_ex) for microsecond to millisecond dynamics.¹⁸ The combination of adiabatic R_1ρ and R_2ρ has been shown to have many advantages over the conventional R_1ρ and CPMG experiments.¹⁵ However, several stringent assumptions have to date limited its application to a few special biological samples:^15,18 (i) the dynamics must be in the NMR-defined fast-exchange regime (where the exchange rate is much larger than the difference between the chemical shifts of the two states: k_ex ≫ Δω); (ii) a reference residue with no conformational exchange and the same intrinsic autorelaxation rates is required for data analysis; and (iii) the cross-correlation relaxation channels^19,20 are assumed to have no effect on the ¹⁵N relaxation rates during the adiabatic spin-lock periods. Assumptions (i) and (ii) result from the lack of general solutions to the equations describing the adiabatic relaxation rates, and assumption (iii) addresses the need for an optimized proton-decoupling scheme. Herein we demonstrate that the combination of adiabatic R_1ρ, adiabatic R_2ρ, and R₁ experiments can be interpreted by means of a novel geometric approximation method to yield accurate dynamic parameters (overcoming (i) and (ii)) and that effective proton-decoupling can be achieved (overcoming (iii)), providing a powerful set of tools to probe spin dynamics across a wide range of time scales.

■. MATERIALS AND METHODS

NMR Experiments.

All of the experimental tests were performed with ¹⁵N,²H-labeled biological samples using Bruker Avance spectrometers equipped with a helium-temperature TCI cryoprobe at 800 MHz and a nitrogen-temperature TCI Prodigy probe at 600 MHz. The composite adiabatic pulses were 16 ms long (comprising four 4 ms hyperbolic secants; HS1, HS2, HS4, HS6, HS8) and have been described previously.^15,18 Experiments were performed with a 1 mM sample of the mutant ubiquitin Ub14²¹ in 50 mM Tris buffer (pH 7.2) containing 10% D₂O. Further experiments were performed with 0.5 mM samples of the ubiquitin-conjugating enzymes UbcH5b²² (17 kDa, τ_c = 11 ns at 15 °C) and Ube2g2²³ (18 kDa, τ_c = 13 ns at 15 °C) in 50 mM Tris buffer (pH 7.2) containing 2 mM DTT and 10% D₂O.

In the case of Ub14, all of the experiments were carried out with a 3 s recycle delay, four or eight scans, 256 complex points in the ¹⁵N dimension, and 2048 complex points in the ¹H dimension for adiabatic R_1ρ or R_2ρ experiments, respectively. Data were processed in NMRpipe^24a using 64 points of linear prediction in the indirect dimension and subsequently analyzed using Sparky.^24b The total relaxation delays were 0, 16, 32, 48, and 64 ms (N = 0, 1, 2, 3, and 4) for both the adiabatic R_1ρ and R_2ρ experiments, and the ¹H π-pulse decoupling utilized γB₁ = 22 kHz. The adiabatic R_1ρ and R_2ρ rates were determined by fitting the data points with monoexponential decays, and only the initial decays were used for data fitting. The R₁ experiments were acquired and the data processed in the same way as in the adiabatic experiments. The relaxation delays for the R₁ experiments were 0.01, 0.05, 0.1, 0.2, 0.4, and 0.5 s.

In the case of the ubiquitin-conjugating enzymes (UbcH5b and Ube2g2), the experiments were carried out with a 3 s recycle delay, eight or 16 scans, 200 complex points in the ¹⁵N dimension, and 2048 complex points in the ¹H dimension for adiabatic R_1ρ or R_2ρ experiments, respectively. Data were processed without linear prediction in NMRpipe and subsequently analyzed using Sparky. The total relaxation delays were 0, 16, 32, and 48 ms (N = 0, 1, 2, and for the adiabatic R_1ρ experiments and 0, 16, and 32 ms (N = 0, 1, and 2) for the adiabatic R_2ρ experiments, and the ¹H π-pulse decoupling utilized γB₁ = 22 kHz. The R₁ experiments were acquired and the data processed in the same way as in the adiabatic experiments. The relaxation delays for the R₁ experiments were 0.01, 0.05, 0.2, 0.4, 0.6, and 0.8 s.

Geometric Approximation.

On the basis of the following theorem, the solution surface of any type (or any form) of differential equations can be built from a library of solution points as long as the solution is continuous and can be computed numerically.

Mathematically, it can be readily proven that any real continuous function for which the defined domain is closed and bounded (a compact subset) in Euclidean space can be uniformly approximated by a finite number of polynomial functions defined in the uniform grid with any given maximal order or with any given grid spacing. (This theorem can be derived from basic concepts in topology, the unique uniform structures of compact sets, and the polynomial approximation.²⁵)

In order to demonstrate this principle, the first step is to generate libraries of solution points as cornerstones on which to build the solution surfaces. In this work, 10 different libraries were computed (comprising R_1ρ and R_2ρ experiments, each using five different adiabatic pulses); each library is six-dimensional, based on the independent parameters. The computation of the library is rather time-consuming but must be done only once using a multiprocessor cluster. The library then serves as a basis set for analyzing the relaxation behavior of any molecule within the boundaries of the library. In order to shrink the size of the library, we assume that the adiabatic R_1ρ and R₂ρ rates are linear functions with respect to the intrinsic R₁ and R₂ autorelaxation rates, as shown in eq 2:

$$R_{x\rho }=f\left(\text{offset},k_{\text{ex}},\Delta \omega ,p_{\text{a}}\right)\times R_1+g\left(\text{offset, }{k}_{\text{ex}},\Delta \omega ,p_{\text{a}}\right)\times R_2+h\left(\text{offset, }{k}_{\text{ex}},\Delta \omega ,p_{\text{a}}\right)$$ (2)

where R_xρ is either the R_1ρ or R_2ρ relaxation rate for a given adiabatic pulse (HSn), R₁ and R₂ are the intrinsic autorelaxation rates, f(…) and g(…) are the slopes of R_xρ with respect to R₁ and R₂, respectively, for given dynamic parameters offset, k_ex, Δω, p_a), and h(…) is the relaxation rate due to chemical exchange (the so-called R_ex). Each six-dimensional solution surface is then decomposed into three four-dimensional surfaces ( f(…), g(…), and h(…)). The grid spacing can be first estimated by analyzing a one-dimensional projection with respect to a given parameter. The final grid spacing can be fine-tuned by constructing and analyzing the lower-dimensional solution surfaces or the partial solution surfaces to ensure that all of the features accurately represented. The calculated library is saved in a separate file for future data analyses.

The second step is to approximate intermediate points on the solution surfaces on the basis of the finite solution points in the library. (This step is performed only when the search algorithm is analyzing data with a given library.) The strategy is to estimate the adiabatic R_1ρ or R_2ρ relaxation rate for given dynamic parameters on the basis of the nearby solution points in the library using the polynomial approximation. The coefficients in the polynomial functions are first determined using the nearby solution points in the library, and then the approximated relaxation rates can be calculated using these locally defined polynomial functions. This is demonstrated in eqs 3 for the two-dimensional case with the second-order polynomial approximation:

$$\begin{gathered} R\left(x,y\right)=a{x}^2+bx+c{y}^2+dy+exy+f \\ a=0.5\cdot \left[R\left(1,0\right)+R\left(-1,0\right)\right]-R\left(0,0\right) \\ b=0.5\cdot \left[R\left(1,0\right)-R\left(-1,0\right)\right] \\ c=0.5\cdot \left[R\left(0,1\right)+R\left(0,-1\right)\right]-R\left(0,0\right) \\ d=0.5\cdot \left[R\left(0,1\right)-R\left(0,-1\right)\right] \\ e=R\left(1,1\right)-R\left(1,0\right)-R\left(0,1\right)+R\left(0,0\right) \\ f=R\left(0,0\right) \end{gathered}$$ (3)

In this two-dimensional example, with the assumption that the domain values in the library closest to the given dynamic parameters (x, y) are at the origin (0, 0), the coefficients a, b, c, d, e, and f can be determined from all of the nearby solution points, where “1” means increasing one unit in a given dimension and “−1” means decreasing one unit in a given dimension. The relaxation rate R(x, y) can then be calculated using this locally defined second-order polynomial function. The same idea can be applied to higher-dimensional solution surfaces.

The detailed implementation of the geometric approximation is shown in the Supporting Information.

■. RESULTS

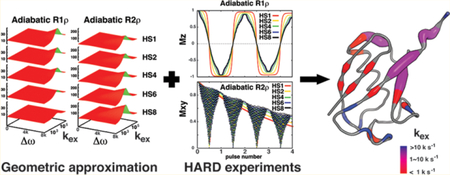
In order to utilize the rich information hidden in the adiabatic R_1ρ and R_2ρ experiments, analytic solutions for the relaxation rates during the adiabatic spin-lock pulses, which can be described by the time-dependent Bloch−McConnell equation, would be required. Previously, the approximate solution for the sadiabatic R_1ρ experiment had been proposed as the time average of the Trott−Palmer equation^14,26 (the approximate solution for the R_1ρ experiment). However, no approximate solution for the adiabatic R_2ρ experiment has been derived for all exchange time regimes. In the context of developing our numerical analysis, we found that there are two separate effects of adiabatic pulses on the relaxation dispersion profile of the adiabatic R²ρ experiment and that both effects need to be considered in deriving any approximate analytic solution. One effect is caused by the time-average spin-lock field, and the other is generated by the frequency of the refocusing adiabatic pulses (Figure S1). It is a daunting task to develop an analytic tool to provide a solution by characterizing these two effects at the same time.

Instead of developing a specific mathematical tool for a given experiment, we demonstrate a powerful and general approach using a geometric approximation method to provide solutions for relaxation of the bulk magnetization, which can be utilized to analyze both conventional experiments and the sophisticated adiabatic spin-lock periods. This method begins with the construction of solution surfaces defined on closed and bounded domains in Euclidean space on the basis of a library of solution points. Topologically, the continuous surfaces can be interpolated between the finite solution points in the library with polynomial functions (see Materials and Methods and the Supporting Information). The library represents six-dimensional computation of the relaxation behavior according to the Bloch−McConnell equation as a function of variables defining the dynamics in the system. The computation is performed with a moderate to coarse grid that depends on the smoothness of the surfaces and the given maximal order of the polynomial approximation. The resulting solution surfaces for the decay of the total magnetization (A + B) exhibit high accuracy, with an average deviation of less than 0.1% from the results of conventional numerical integration (Table 1). Combining the solution surfaces with Monte Carlo sampling²⁷ to search for solutions that match the experimental relaxation behavior (Figure 1) makes it possible to extract information on spin dynamics across a wide range of long (microsecond to millisecond) time scales in the absence of H−X coupling (see the Supporting Information). In simulated tests, the algorithm provided accurate dynamic parameters (k_ex , Δω, and p_a ) when no error was present (Figure 2). In the presence of up to 5% random errors, the extracted k_ex values were more resistant to errors than the other extracted dynamic parameters ( ω and p_a) (Figure 3). Moreover, the more precise the fit to the k_ex values (i.e., the smaller the standard deviation), the more accurate the fit results are (i.e., the better the coefficient of determination is) (Figure 3a,d,g). In practice, the use of the geometric approximation method in analyzing relaxation data can be up to 300 000-fold faster than the use of conventional numerical integration (see the Supporting Information). The speed increase does not consider the time spent in constructing solution surfaces based on the libraries, but this approach does circumvent the task of finding analytic solutions for a potentially unsolvable problem. Comparison of previous studies using the time average of the Trott−Palmer equation^14,26 to the geometric approximation showed that the analytic procedure yields a less accurate solution for the adiabatic R_1ρ experiment (Table 1) and that its performance in computational speed for analysis is 3 orders of magnitude less than that of our new approach. The new approach enables complete data analysis (adiabatic R_1ρ and adiabatic R_2ρ) without the need for supercomputing systems to repeatedly perform numerical integration and enables the practical examination of a wide range of microsecond to millisecond dynamics for many biological systems. Additionally, the wide range of dynamic time scales cannot be detected by the well-known CPMG experiments under the same conditions that are amenable for the HARD experiments (Figures 2, 3, and S2).²⁸

Table 1.

Deviation of the Approximate Solution Surfaces and the Approximate Analytic Solution from the Numerical Solutions^a

	time average of the Trott− Palmer equation	geometric approximation
	adiabatic R1ρ	adiabatic R1ρ	adiabatic R2ρb
average error	0.9%	0.05%	0.06%
standard	0.6%	0.04%	0.1%
deviation
largest error	12.4%	0.6%	3.2%

^aThe library for each solution surface is composed of 4 million solution points with an offset range of (−10 to 10) × 10³ s⁻¹, a Δω range of (−8 to 8) × 10³ s⁻¹, a k_ex range of (0.1 to 1000) × 10³ s⁻¹, and a p_a range of 55% to 100%. To compare the approximate solutions with the numerical ones, 10 000 random points were chosen. Errors are expressed as percentages of the deviations from the numerical solutions.

^bOnly experimentally accessible relaxation rates for adiabatic R_2ρ (<500 s⁻¹) were used for statistical analysis, and there is no approximate analytic solution for adiabatic R_2ρ that can be defined in all exchange regimes for the comparison.

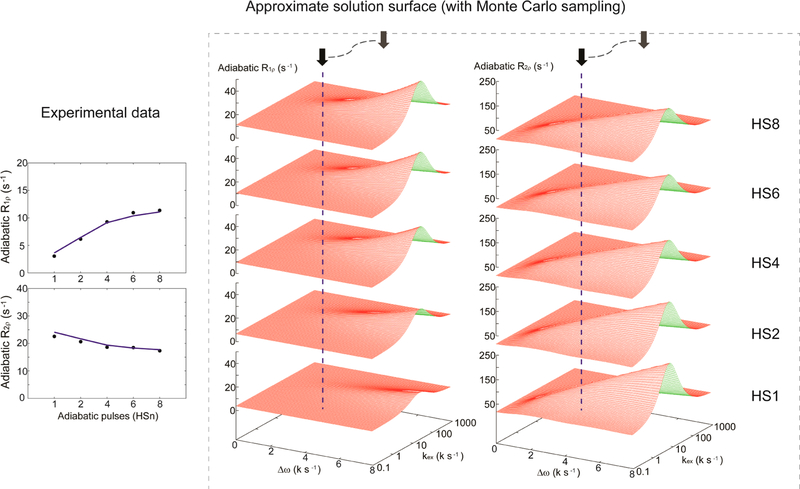
Figure 1.

Experimental data points (left) are used to match solutions within the approximate solution surfaces during the Monte Carlo search (right). The algorithm can rapidly approximate any solution point on the surfaces on the basis of a precomputed library within realistic boundary constraints. Massive Monte Carlo sampling combined with geometric interpolations is used to minimize the difference between the experimental data and approximate solutions to extract the desired dynamic parameters.

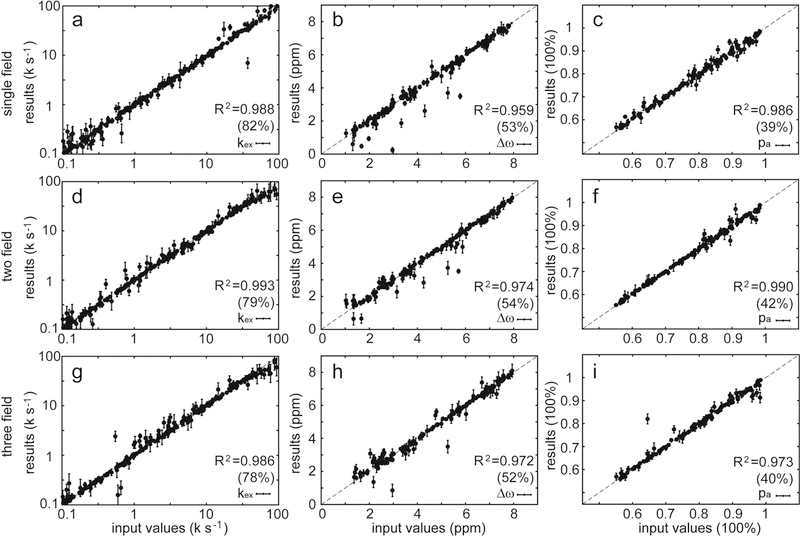
Figure 2.

Data analysis of adiabatic R_1ρ, adiabatic R_2ρ, and R₁ at single (18.8 T), two (14.1 and 18.8 T), or three (14.1, 16.5, and 18.8 T) magnetic fields using the geometric approximation. At these three magnetic fields, 300 relaxation data sets were simulated using the Bloch−McConnell equation with random input dynamic parameters. The fit results are plotted against the input values, and those with large standard deviations (SD of k_ex > 10^0.2, SD of Δω > 0.4 ppm, SD of p_a > 2.5%) during Monte Carlo sampling are not shown. The coefficient of determination (R²) was calculated for each dynamic parameter. The numbers in parentheses are the percentages of data that remained after the results with large standard deviations were filtered out.

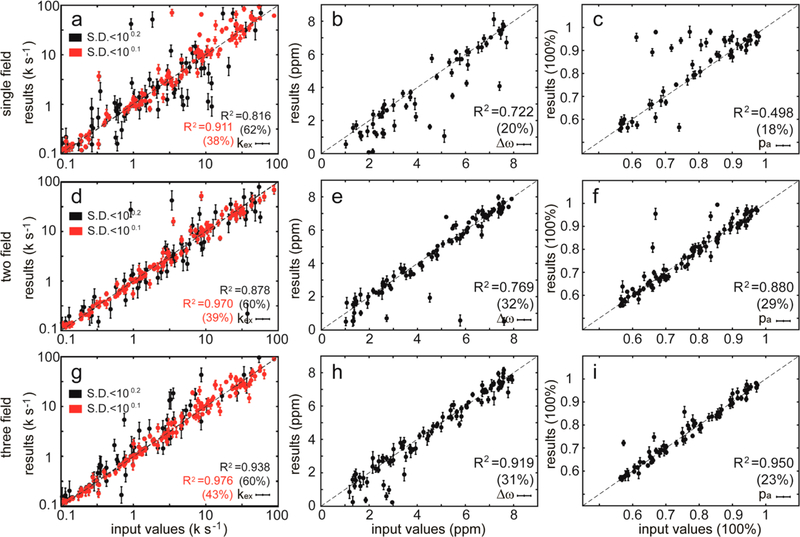
Figure 3.

Effects of random errors on the fit results for adiabatic relaxation dispersion experiments. Up to 5% random errors were introduced into the simulated data in Figure 2 before data analysis. The fit results are plotted against the input values, and those with large standard deviations (SD of k_ex > 10^0.2, SD of Δω > 0.4 ppm, SD of p_a > 2.5%) during Monte Carlo sampling are not shown. The red data points are those with smaller standard deviations (SD of k_ex < 10^0.1). The coefficient of determination (R²) was calculated for each dynamic parameter. The numbers in parentheses are the percentages of data that remained after the results with large standard deviations were filtered out.

The validity of the Bloch−McConnell equation in describing the evolution of the bulk magnetization depends on two assumptions: (1) the system is in the limit of weak RF field and (2) the system is an isolated single-spin system. The first assumption is automatically satisfied in solution-state NMR spectroscopy because of the fast tumbling of the molecules in solution, according to Abragam’s theory.²⁹ However, for the general application to two-spin systems (e.g., ¹⁵N−¹H^N), the second assumption holds only under the application of complete proton decoupling. The original HARD experiment did not include proton decoupling, and the analysis relied on normalizing the complex relaxation behavior utilizing a reference amino acid residue within the molecular system, which complicated a generalized data analysis.^15,18 To determine the most efficient proton-decoupling scheme, we examined both simulated and experimental effects of proton coupling. We utilized an expanded density matrix (32 × 32) approach combining the classical model¹⁶ (Bloch−McConnell equation, eq 1) and the quantum-mechanical model^20,29 (Abragam’s operator formalism, eq 4) to calculate the evolution of the magnetization during the adiabatic spin-lock periods and different decoupling schemes incorporated into the HARD experiment (see the Supporting Information).

Quantum-Mechanical Model.

The quantum-mechanical model can be expressed using Abragam’s operator formalism according to eq 4:

$$\frac{\text{d}{\sigma }^{*}}{\text{d}t}=-\frac{1}{2}\sum _{q,p,p^{\prime }}{J}_{p,p^{\prime }}^{\left(q\right)}\left({\omega }_q\right)\cdot \left[A_{p^{\prime }}^{\left(-q\right)},\left[A_p^{\left(q\right)},{\sigma }^{*}\right]\right]$$ (4)

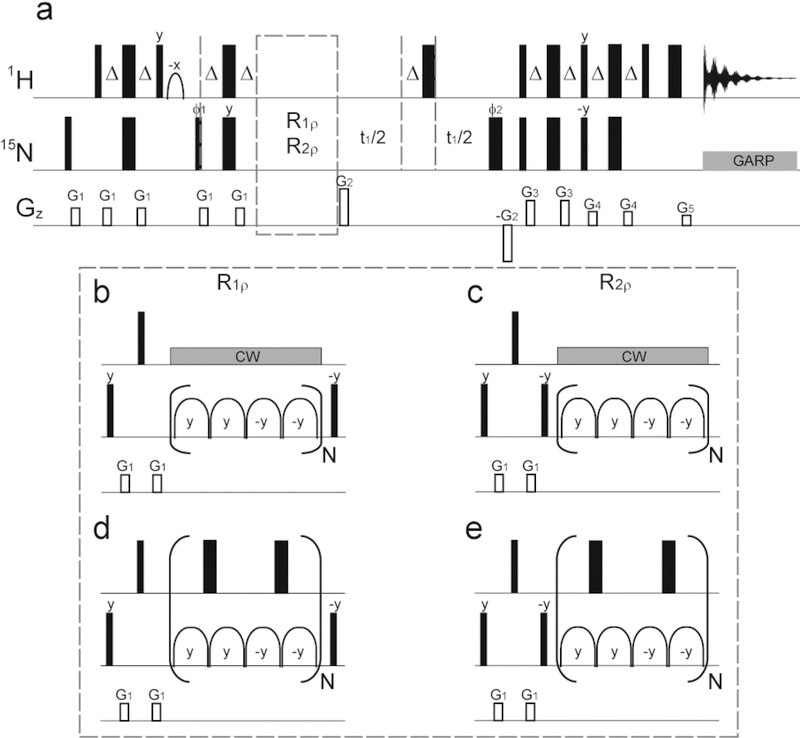
where σ* is the density matrix in the rotating frame for the two-spin system, J(ω) is the spectral density function, and $A_q^p$ is any operator contributing either dipole−dipole or chemical shift anisotropy interactions. Simulations of adiabatic R_1ρ and R_2ρ experiments indicated that proton coupling has only a moderate effect for small biomolecules (τ_c = 5 ns) but rather dramatic effects for larger biomolecules or complexes (τ_c = 30 ns) (Figure S3). Hence, it is essential to incorporate a decoupling scheme, which is resistant to off-resonance effects, for the accurate measurement of adiabatic R_1ρ and R_2ρ rates. The original HARD pulse sequence was modified to examine two modes of proton decoupling (Figure 4), either continuous-wave (CW) decoupling or π-pulse decoupling. CW decoupling can potentially introduce artificial relaxation dispersion and exhibits well-known off-resonance effects (Figures S4−S7). Computational and experimental evaluations demonstrated that incorporation of an appropriate π-pulse scheme effectively eliminates coupling effects, including off-resonance effects, and yields accurate relaxation dispersion data (Figures S6 and S7). The combination of this proton-decoupled HARD sequence with the geometric approximation method to analyze the relaxation data forms the basis of the acronym for the approach: geoHARD (geometric approximation on Heteronuclear Adiabatic Relaxation Dispersion).

Figure 4.

(a) Pulse sequences for the measurement of ¹⁵N adiabatic relaxation dispersion experiments. The sequences were modified from the original ones proposed by Mangia et al.¹⁵ Adiabatic hyperbolic secant pulses were used for the ¹⁵N spin-lock periods. (b, d) R_1ρ experiments and (c, e) R_2ρ experiments are included with a purge element and different proton-decoupling schemes. During ¹⁵N spin-lock periods, the offset of the proton decoupling was placed in the center of the amide proton region. The phases were ϕ₁ = x, −x, x, −x; ϕ₂ = x, x, y, y; and ϕ_rec = x, −x, x, −x. The gradient magnitudes for G₁−G₅ were 16.5, 44, 19.8, 13.2, and 8.9 G/cm, respectively, with a fixed length of 1 ms.

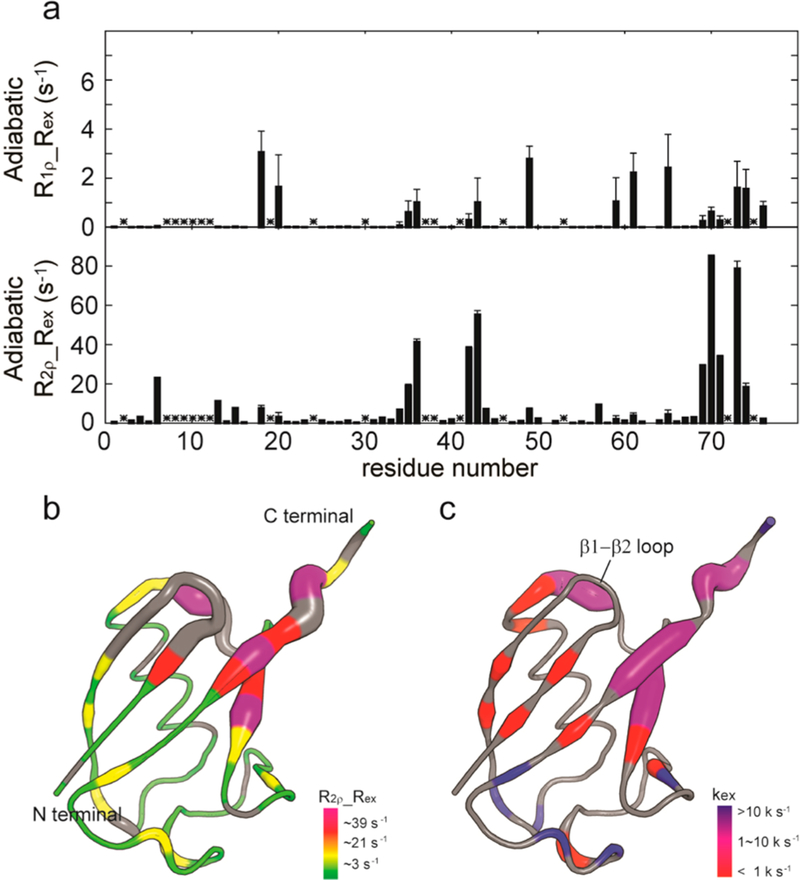
In order to experimentally validate geoHARD, we first tested the approach using Ub14, a phage-display-selected ubiquitin mutant (∼8 kDa).²¹ Ubiquitin is well-known for its roles in proteasome-mediated protein degradation and cellular signaling. Several studies have shown that the internal conformational dynamics in Ub has dramatic effects on its interaction with other binding partners.^21,30 Ub14 is a selected multiresidue mutant and was used to illustrate that increased conformational dynamics is correlated with stronger affinity for USP14 deubiquitinase.²¹ The conformational dynamics of this mutant has been well-characterized by conventional CPMG and R_1ρ methods in a previous study,²¹ and a synchronized motion (1600−2000 s⁻¹) of the mutant protein has been proposed on the basis of simultaneous analysis of CPMG data for several residues;²¹ hence, it was an excellent candidate to validate the geoHARD approach. Adiabatic R_1ρ, adiabatic R_2ρ, and R₁ experiments were measured at two magnetic fields (corresponding to ¹H frequencies of 600 and 800 MHz) and 25 °C (see the Supporting Information), and the data were then analyzed by the geometric approximation method (Figures S8−S10). The microsecond to millisecond dynamics in Ub14, probed by the apparent R_ex in the adiabatic R_2ρ experiments (Figure 5a), covers the complete range of microsecond to millisecond dynamics detected by the conventional relaxation dispersion experiments reported previously.²¹ Moreover, by mapping the apparent R_ex and k_ex onto the structures, we are able to categorize the residues exhibiting different ranges of k_ex values, spanning from 10² s ⁻¹ to 10⁵ s⁻¹ (Figure 5b,c and Table S1). Instead of fitting all of the relaxation data to get a single k_ex value by assuming that all of the motions are synchronized, we can dissect the heterogeneous distribution of microsecond to millisecond conformational dynamics in the whole protein. We are able not only to detect motions (residues at the C-terminal core opening) with a range of k_ex values similar or identical to the proposed synchronized motion but also to find those with completely different k_ex ranges (Figure 5c and Table S1). In fact, by combining our experimental data (Figure 5c) and the cluster analysis in the previous study,²¹ we can further support that the breathing at the C-terminal core opening is important in the binding of ubiquitin to USP14 deubiquitinase. Therefore, these data provide a new window into the correlation of structure and motion with biological function that requires more exploration.

Figure 5.

Dynamic parameters of amide groups in Ub14 characterized by geoHARD. (a) Plot of apparent R_ex values against the primary sequence. Unassigned residues are marked with asterisks. (b) Ribbon representation of the structure (1UBQ), wherein the diameter of the ribbon/sausage is directly proportional to the apparent R_ex derived from the adiabatic R_2ρ experiment. The larger the sausage, the larger is the value of R_ex. Colors: purple, >39 s⁻¹; red, 21−39 s⁻¹; yellow, 3−21 s⁻¹; green, <3 s⁻¹; missing data are shown in gray. (c) Mapping of k_ex (SD < 10^0.5 and R_ex > 2 s⁻¹) onto the ribbon structure. The k_ex values are classified into three groups: blue, >10000 s⁻¹; purple, 1000−10000 s⁻¹; red, <1000 s⁻¹.

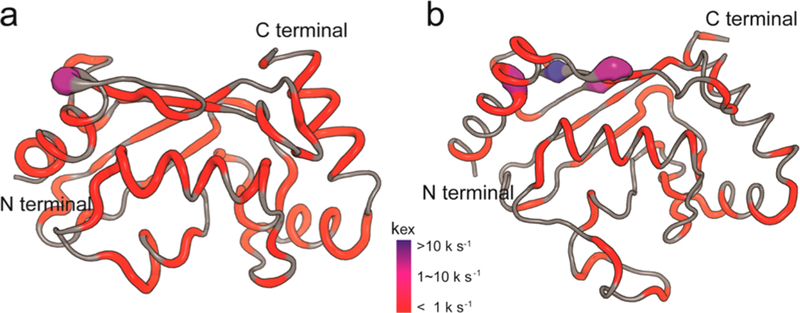
In a second application, we used geoHARD to detect the microsecond to millisecond conformational dynamics of two different ubiquitin-conjugating enzymes (UbcH5b and Ube2g2) (Figure 6). In the case of UbcH5b at 15 °C (Figure 6a), there is exchange distributed around the molecule that has not been previously accessible in a routine fashion.²² This can now be examined. It is reasonable to expect that such observations will be much more prevalent in biological molecules than has been previously recognized because of the experimental limitations that our new method alleviates. It is interesting that a high rate is observed on the “back side”, where ubiquitin has been shown to interact with UbcH5b,³¹ and is in the region where other E2 proteins have been shown to interact with allosteric effector domains from cognate E3 proteins.^23,32,33 In the case of Ube2g2 at 15 °C (Figure 6b), the presence of dynamics is quite revealing in areas that have been demonstrated to play roles in the dynamic allostery arising from interactions between this E2 and its cognate E3, gp78. In particular, rapid dynamics occurs at the “back side” binding site of the allosteric effector domain, G2BR, in the N-terminal α-helix and in the extended loop adjacent to the active site, which is also key to the allosteric enhancement of binding to the RING domain of gp78.^23,32 These data are consistent with molecular dynamics studies on apo-Ube2g2 (data to be published). The above results again demonstrate the potential impact of this new technique to increase our understanding of biomolecular systems.

Figure 6.

Dynamic parameters of amide groups in (a) UbcH5b and (b) Ube2g2 characterized by geoHARD. Values of k_ex (SD < 10^0.5 and R_ex > 2 s⁻¹) have been mapped onto the ribbon structures (UbcH5b, 1W4U; Ube2g2, 2KLY) and are classified into three groups: blue, >10000 s⁻¹; purple, 1000−10000 s⁻¹; red, <1000 s⁻¹.

■. DISCUSSION AND CONCLUSIONS

The geometric approximation method is a general strategy to provide specific solutions of differential equations provided that certain assumptions are satisfied (see Materials and Methods). Compared with conventional numerical integration analysis, this new approach allows us to significantly shorten the computational time for each sampling step as well as to massively sample through the complete multidimensional solution surfaces (see the Supporting Information). The current pure statistical Monte Carlo sampling of the solution surfaces may not be the most efficient way to find the solution, and a better sampling scheme may be incorporated to improve the efficiency and precision of the sampling in the future. However, accurate solutions are accessible without concern for the efficiency of convergence in the numerical integration approach once the library is computed. For example, numerical integration to calculate the adiabatic R_2ρ relaxation rates converges much slower than that for adiabatic R_1ρ relaxation rates (see the Supporting Information); however, the computational analysis times using the geometric approximation with precomputed libraries are the same for R_1ρ and R_2ρ. Extraction of accurate solutions for each experimental data set via the geometric approximation method is rapid for any molecular system and requires minimal computational power. Here we successfully applied this new approach to determine adiabatic relaxation rates, described by the time-dependent Bloch− McConnell equation, and we are able to extract rich information from the sophisticated experiments to improve our understanding of protein dynamics. This suggests that the present computational technique may be applied to benefit other disciplines in the future as well as to allow the design and analysis of new relaxation dispersion experiments to reveal important functional motions in biological systems.

We have utilized the geoHARD method to demonstrate the facile ability to detect and quantify conformational dynamics across a broad range of time scales while avoiding an assumption of synchronized motion. Of particular interest is the ability to characterize a heterogeneous distribution of conformational dynamics across a wide range of time scales (10²−10⁵ s⁻¹) that may imply important biological processes, including binding, allostery, and enzymatic turnover. Compared with conventional methods, geoHARD has many advantages. CPMG methods (10² ∼ 10³ s⁻¹) are rendered insensitive and error-prone by the constant time period and the large transverse relaxation in the laboratory frame, and the off-resonance effect due to imperfect π pulses can generate additional complications. In the case of R_1ρ experiments (10³−10⁴ s ⁻¹), accurate calibration of the offsets and power levels of CW pulses is extremely important because of the high sensitivity of relaxation dispersion to these two factors. Conversely, HARD experiments are generally more sensitive and contain smaller experimental errors in real applications, and the relaxation dispersion is, in general, offset-independent. The HARD experiments with the optimized proton-decoupling scheme are designed for protein samples with high deuteration levels and without ¹³C labeling. Although the π-pulse decoupling can efficiently remove the cross-correlation, the spin-flip mechanism resulting from incomplete deuteration in large molecules can potentially affect its decoupling efficiency. For additional ¹³C labeling, although theoretically the same π-pulse decoupling scheme can be used to remove the effects of the carbon coupling, this has not yet been examined and may suffer from bandwidth considerations. Thus, a high level of deuteration without ¹³C labeling is recommended when geoHARD is used. With the ability to accurately and rapidly analyze the data using the geometric approximation, the broader time scale probed by geoHARD will be powerful in examining allosteric effects and correlating with long molecular dynamics trajectories. The distribution of heterogeneous conformational dynamics in biomolecules, as revealed by this powerful tool, can help not only to increase our understanding of the tunable functions of proteins but also to accelerate the design of better modulators.