Modeling the health effects of time-varying complex environmental mixtures: Mean field variational Bayes for lagged kernel machine regression

Abstract

There is substantial interest in assessing how exposure to environmental mixtures, such as chemical mixtures, affect child health. Researchers are also interested in identifying critical time windows of susceptibility to these complex mixtures. A recently developed method, called lagged kernel machine regression (LKMR), simultaneously accounts for these research questions by estimating effects of time-varying mixture exposures, and identifying their critical exposure windows. However, LKMR inference using Markov chain Monte Carlo methods (MCMC-LKMR) is computationally burdensome and time intensive for large datasets, limiting its applicability. Therefore, we develop a mean field variational Bayesian inference procedure for lagged kernel machine regression (MFVB-LKMR). The procedure achieves computational efficiency and reasonable accuracy as compared with the corresponding MCMC estimation method. Updating parameters using MFVB may only take minutes, while the equivalent MCMC method may take many hours or several days. We apply MFVB-LKMR to PROGRESS, a prospective cohort study in Mexico. Results from a subset of PROGRESS using MFVB-LKMR provide evidence of significant positive association between second trimester cobalt levels and z-scored birthweight. This positive association is heightened by cesium exposure. MFVB-LKMR is a promising approach for computationally efficient analysis of environmental health datasets, to identify critical windows of exposure to complex mixtures.

1 | INTRODUCTION

There is growing interest from environmental health institutes and regulatory agencies to quantify and assess the health impacts of exposure to multi-pollutant mixtures (Carlin et al., 2013; Billionnet et al., 2012). Multi-pollutant mixtures can be used to describe an array of environmental exposures; in this article, we focus on exposures to heavy metal mixtures, which may include manganese, arsenic and lead, among others. While the effects of a single metal exposure, such as lead, on child development has been well researched, less is known about the joint effects of co-exposure to mixtures of heavy metals (Bellinger, 2008; Claus Henn et al., 2014). Furthermore, it is hypothesized that there may be certain time windows of susceptibility in pregnancy and early life, also called critical exposure windows, during which vulnerability to metal mixture exposures is increased. As there are many sequential developmental processes in fetal life and early childhood (Stiles and Jernigan, 2010), the health effects of heavy metal mixture exposures can be highly-dependent on exposure timing. In practice, understanding which chemical exposures to mitigate as well as when to intervene provides two important pieces of scientific knowledge. First, this knowledge can help inform the most health-protective interventions. Second, knowledge of the particular chemical and critical windows of exposure can help inform the biologic mechanism by which exposure is affecting health. In many cases, developmental processes occur sequentially, rather than concurrently. Hence, we observe a specificity of exposure timing on health effects, as exposures might affect a process that is operating at a specific life phase. Thus, when a person is exposed to a toxic chemical can be as important as the dose itself and can inform how exposures affect health.

Two primary objectives of mixtures research are (1) to quantify the health effects of exposure to complex metal mixtures, and (2) to identify time windows of susceptibility to the mixture exposures. It is well known that developmental processes occur in a time dependent manner and that dose response curves to individual chemicals vary based on the timing of exposure. To fit this biological framework, mixtures analysis needs to be able to address the role of critical windows. To date, the two objectives of mixtures research have mainly been studied separately, however, leaving a gap in the statistical literature for methods that link these two issues together. Methods to study the exposure-response relationship for complex mixtures include Bayesian kernel machine regression (Bobb et al., 2015), weighted quantile sum regression (Gennings et al., 2013), random forest and cluster analysis (Billionnet et al., 2012). While these methods accommodate a variety of exposure-response relationships, they do not account for potential time-varying exposures to complex mixtures which are a property of critical windows. There have also been recently developed methods to analyze time windows of susceptibility to exposures, including single pollutant distributed lag models, which have been used to describe the effect of a single chemical exposure (Hsu et al., 2015; Warren et al., 2012, 2013; Darrow et al., 2011). However, these methods do not account for interactions, effect modification between two chemicals at a time window, complex mixtures or interactions between chemical exposures measured at different times. One exception is the work of Bello et al. (2017), who extended the distributed lag framework to account for mixtures, but the method only quantifies the magnitude, not directionality, of the mixture effects, and also cannot identify the directionality of individual mixture components.

In the case of more complex exposure-response relationships, as is hypothesized to occur in complex mixtures data, many of the existing methods do not encompass all the desirable qualities of a flexible method, such as accounting for non-linear and non-additive exposure-response functions, accounting for potential time-varying exposures to complex mixtures and accounting for interactions. These are important to account for, as prior environmental health research has found evidence of nonlinear, or inverted-u relationships between single metal exposures and health outcomes (Claus Henn et al., 2010a), as well as evidence of interactions among metal mixtures (Claus Henn et al., 2014). Accordingly, Liu (2016); Liu et al. (2017) proposed a method that simultaneously estimates the complex exposure-response relationship between mixtures and health outcomes, and identifies critical windows. They termed the model lagged kernel machine regression (LKMR). The authors sought to model the exposure-response random effects for the exposures measured at a single time window, while controlling for exposures at all other time windows. This challenge of modeling random effects models has arisen in different fields of the statistics literature. Often, basis functions are used to specify random effects models, as occurs in spatial statistics (Gelfand and Schileip, 2016; Higdon, 1998, 2002; Calder, 2008), functional data analysis (Delicado et al., 2010), time series (Du and Zhang, 2008), and mixed modeling (Scheipl et al., 2015). In the LKMR model, the authors used a kernel function (further detailed in Section 3) to specify the random effects model. Kernel functions and basis functions are closely related; an unknown exposure response function can be either represented under the primal representation through basis functions, or under the dual representation through a kernel function.

Under LKMR, the non-linear and non-additive effects of time-varying mixture exposures are estimated while allowing for the effects to vary smoothly over time, similar to a distributed lag model. They used a novel Bayesian penalization scheme that combines the group and fused lasso (Kyung et al., 2010; Yuan and Lin, 2006; Park and Casella, 2008; Huang et al., 2012) within a Bayesian kernel machine regression framework (Bobb et al., 2015). Because there is often correlation among metal mixtures exposures within a given time window, as well as auto-correlation across time windows, the LKMR model uses the group and fused lasso penalties to account for these dependencies, respectively. The group lasso penalty regularizes the exposure-respone function at each time window, and provides a framework for incorporating the kernel matrix, while the fused lasso penalty shrinks the exposure-response functions of neighboring time windows towards each other. The authors described a Markov chain Monte Carlo (MCMC) algorithm using Gibbs sampling for LKMR, and focus on an environmental health data application with small sample size (N = 84). Specifically, they applied the method to describe how exposures to metal mixtures, captured in teeth biomarker, during pregnancy and early life are associated with neurodevelopment. However, due to the complexity of the LKMR model, computational time for updating parameters in the MCMC algorithm dramatically increased with the number of subjects or time points studied. As many iterations in the MCMC algorithm are needed to ensure that the chain converges to the target posterior distribution for the parameters of interest, this can be computationally burdensome.

In this article, we propose an approximation method for the LKMR model, in order to reduce computation time and allow for the analysis of larger datasets. The approximation method uses the mean field variational approximation method for Bayesian inference, or MFVB for short. Variational approximations are useful when standard sampling-based approaches to posterior approximation are impractical or infeasible. The central idea behind variational Bayes is that the posterior densities of interest are approximated by other densities for which inference is more tractable. Variational Bayes, shorthand for variational approximate Bayesian inference, is a computationally efficient alternative to MCMC (Ormerod and Wand, 2010). Unlike MCMC, variational Bayes is a deterministic technique. While MCMC tends to converge slowly, variational Bayes provides a fast approximation to the true posterior. converge slowly, variational Bayes provides a fast approximation to the true posterior.

In this article, we demonstrate the utility of MFVB for LKMR to study health effects associated with exposure to time-varying mixtures, and illustrate the method by applying it to a children’s environmental health study. Taking advantage of the computational efficiency of MFVB-LKMR, we apply it to analyze a larger set of data (N = 391), to describe how exposures to metal mixtures during pregnancy are associated with birth weight. We apply the method to the Programming Research in Obesity, Growth, Environment and Social Stressors (PROGRESS) study, an ongoing, prospective pre-birth cohort study in Mexico City. For this analysis, we focus on exposures during three critical peri-natal time windows: second trimester of pregnancy, third trimester of pregnancy, and birth. Metal mixtures are measured in time-varying maternal blood samples which represent exposures during the second and third trimesters of pregnancy. They are also measured in cord blood samples collected within 12 hours of delivery, which represent exposures near the time of birth. The data contains measurements of exposures to multiple metals, including arsenic (As), cadium (Cd), cobalt (Co), chromium (Cr), cesium (Cs), copper (Cu), manganese (Mn), antimony (Sb), and selenium (Se). The outcome of interest is birthweight z-scores, calculated according to the international infant growth charts developed by Fenton et al. (2013).

The article is developed as follows. In Section 2, we briefly review MFVB, while in Section 3, we review kernel machine regression. In Section 4, we detail the LKMR model and the corresponding MFVB algorithm. In Section 5, we describe the simulation study to evaluate the performance of the MFVB algorithm. In Section 6, we apply the method to data from PROGRESS. Finally, in Section 7, we provide the discussion and conclusion.

2 | REVIEW OF MEAN FIELD VARIATIONAL BAYES

In this section, we provide a summary of MFVB; for a detailed review, see Ormerod and Wand (2010). Suppose we use a Bayesian paradigm to conduct inference on the continuous parameter vector θ ∈ Θ corresponding to an observed data vector y. The posterior distribution p(θ|y) ≡ p(y, θ)/p(y) is used for Bayesian inference, where p(y) is known as the marginal likelihood. It can be shown that the logarithm of the marginal likelihood is bound by:

$$\log p(\mathbf{y})={\displaystyle \int q(\mathit{\theta })\log \left\{\frac{p(\mathbf{y},\mathit{\theta })}{q(\mathit{\theta })}\right\}d\mathit{\theta }+}{\displaystyle \int q(\mathit{\theta })\log \left\{\frac{q(\mathit{\theta })}{p(\mathit{\theta }\mathbf{y})}\right\}d\mathit{\theta }.}$$ (1)

There is an inequality:

$${\displaystyle \int q(\mathit{\theta })\log \left\{\frac{p(\mathbf{y},\mathit{\theta })}{q(\mathit{\theta })}\right\}d\mathit{\theta }+}{\displaystyle \int q(\mathit{\theta })\log \left\{\frac{q(\mathit{\theta })}{p(\mathit{\theta }|\mathbf{y})}\right\}d\mathit{\theta }\ge }{\displaystyle \int q(\mathit{\theta })\log \left\{\frac{p(\mathbf{y},\mathit{\theta })}{q(\mathit{\theta })}\right\}d\mathit{\theta },}$$ (2)

which holds because the the second term of (2),

$${\displaystyle \int q(\mathit{\theta })\log \left\{\frac{q(\mathit{\theta })}{p(\mathit{\theta }|\mathbf{y})}\right\}d\mathit{\theta }\ge 0}$$ (3)

is the Kullback-Leibler divergence between density q and p(·|y) and is greater or equal to zero for all densities q, and equal to zero if and only if q(θ) = p(θ|y) almost everywhere. Therefore, the q-dependent lower bound on the marginal likelihood is defined as $\underset{\_}{p}(\mathbf{y};q)$, where

$$\underset{\_}{p}(\mathbf{y};q)=\exp {\displaystyle \int q(\mathit{\theta })\log \left\{\frac{p(\mathbf{y},\mathit{\theta })}{q(\mathit{\theta })}\right\}d\mathit{\theta }.}$$ (4)

In variational approximation, we approximate the posterior density p(θ |y) using a q(θ). We seek to minimize the Kullback-Liebler divergence between q(θ) and p(θ |y), by maximizing $\underset{\_}{p}(\mathbf{y};q)$, so that q(θ) is a good approximation for p(θ |y). A common restriction for q(θ) is the product density restriction (Ormerod and Wand, 2010). Approximate Bayesian inference under product density restrictions is also called mean field variational Bayes (MFVB). In this article, we use MFVB to implement the LKMR model. There is a link between Gibbs sampling, which is used in the MCMC implementation of LKMR, and MFVB. Specifically, when Gibbs sampling is applicable, as in the case with LKMR, tractable solutions for MFVB also exist (Ormerod and Wand, 2010). However, we note that other options for the restriction of q(θ) also exist, such as semi-parametric mean field variational Bayes (Rohde and Wand, 2016), the restriction that q(θ) belongs to a parametric family of density functions (Ormerod and Wand, 2010), and tangent transform variational approximations (Jordan et al., 1999).

Under MFVB, we assume that q(θ) can be factored into ${\displaystyle {\prod }_{i=1}^M{q}_i({\theta }_i)}$ for some partition {θ₁, …, θ_M} of θ. By maximizing the log $\underset{\_}{p}(\mathbf{y};q)$ over each of the q₁,...q_M, we obtain the optimal densities:

$$q_i^{\ast }({\theta }_i)\propto \exp [E_{-{\theta }_i}\log p(\mathbf{y},\mathit{\theta })],i=1,\dots ,M,$$ (5)

where $E_{-{\theta }_i}$ indicates expectation with respect to the density ${\displaystyle {\prod }_{j\ne i}{q}_j({\theta }_j)}$. Using iteration, we can update each $q_i^{\ast }(\cdot )$ for i = 1,..., M. This MFVB algorithm allows us to obtain parameter updates, and then perform Bayesian inference.

3 | REVIEW OF KERNEL MACHINE REGRESSION METHODS

The kernel machine regression framework is used to estimate the effect of a complex environmental mixture when exposure is measured at a single time point. Kernel machine regression (KMR) is defined as follows: For each subject i = 1, …, N, M components of the exposure mixture z_i = (z_1i,..., z_Mi)^⊤ are associated with the continuous, normally distributed health outcome (y_i) through an unknown exposure response function, h(·), while controlling for C relevant covariates x_i = (x_1i,..., x_Ci)^⊤. The KMR model is

$$y_i=h(z_{1i},\dots ,z_{Mi})+{\mathbf{x}}_i^{\mathit{\top }}\beta +{\epsilon }_i,$$ (6)

where β denotes covariate effects, and ${\epsilon }_i\stackrel{\mathit{iid}}{~}N\left(0,{\sigma }^2\right)$.

The unknown exposure response function, h (·), is of particular interest, as it captures the unknown effect of a complex environmental mixture. h (·) can be specified in one of two ways. One possibility is to specify it using basis functions. However, explicit basis functions may be difficult to specify when the mixture is comprised of a large number of components with potentially complex interactions. Therefore, we use a kernel machine formulation to represent h (·), which does not require explicit basis functions to be specified. Mercer’s theorem (Cristianini and Shawe-Taylor, 2000) shows that under regularity conditions, the kernel function K (·,·) implicitly specifies a unique function space, H_k, spanned by a set of orthogonal basis functions. Therefore, a kernel function can represent any function h (·) ∈ H_k. Intuitively, kernels capture the similarity between exposure profiles z_i and z_j for any two subjects i, j. The specific kernel choice can be used to control the complexity and form of the unknown exposure-response function. For example, if a Gaussian kernel is used, the similarity is quantified through the Euclidean distance, and if a polynomial kernel is used, the similarity is quantified using the inner product. In our analyses, we use a kernel representation for h (·) as the exposure-response relationship may be complex, including potential nonlinear and non-additive associations.

The connection between kernel machine methods and linear mixed models was made by Liu et al. (2007), who developed least-squares kernel machine semi-parametric regression. They show that (6) can be alternatively expressed as the mixed model

$$y_i~N(h_i+{\mathbf{x}}_i^{\mathit{\top }}\mathit{\beta },{\sigma }^2)$$ (7)

$$\mathit{h}={(h_1,\dots ,h_n)}^{\mathit{\top }}~Gp[\mathbf{0},\tau \mathbf{K}(\cdot ,\cdot )],$$ (8)

where GP denotes Gaussian Process and K is a kernel matrix with i, j^th element K (z_i, z_j). h = (h₁,.., h_n)^⊤ represents the subject-specific random effects, each capturing the contribution of the exposure mixture z_i = (z_1i,..., z_Mi)^⊤ for subject i to the outcome mean for that subject.

4 | MEAN FIELD VARIATIONAL BAYES FOR LAGGED KERNEL MACHINE RE-GRESSION

4.1 | Review of lagged kernel machine regression

Next, we review lagged kernel machine regression (LKMR) for estimating the effects of a complex mixture when exposures are measured at multiple time points, with the additional objective of identifying critical windows of exposure. For each subject i = 1, …, N exposed to multi-pollutant mixtures z_{i t} = (z_1i,_t,..., z_Mi,_t)^⊤ at time intervals t = 1,..., ⊤, we use the LKMR model to relate the health outcome to the clinical covariates and time-varying exposure measurements

$$y_i={\beta }_0+{\displaystyle \sum _t{h}_t(z_{1i,t},\dots ,z_{Mi,t})+{\mathbf{x}}_i^{\mathit{\top }}\mathit{\beta }+{\epsilon }_i.}$$ (9)

The function h_t (z_i,_t) represents the time-specific effects of exposure mixtures, while controlling for exposure at the other time windows. The LKMR model can also be represented through mixed models, such that

$$y_i={\beta }_0+{\displaystyle \sum _t{h}_{i,t}+{\mathbf{x}}_i^{\mathit{\top }}\mathit{\beta }+{\mathit{\epsilon }}_i.}$$ (10)

h_t = (h_1,t, …, h_n,_t)^⊤ represents the subject- and time-specific effects of the mixture on the outcome, for the exposure z_1,t,..., z_n,_t measured at time t, controlling for exposures at all other time points.

Liu (2016); Liu et al. (2017) details the LKMR model, which can be represented as a hierarchical model. For brevity, we present a brief description of the hierarchical model here, with a primary focus on the MFVB approximation. LKMR uses regularization to account for collinearity of mixture components within and across multiple time points using a Bayesian grouped, fused lasso (Kyung et al., 2010; Yuan and Lin, 2006; Park and Casella, 2008; Tibshirani and Saunders, 2005), while allowing for the possibility of non-linear and non-additive effects of individual exposures. Through a Bayesian kernel machine framework, where the kernel distance functions are incorporated within the group lasso implementation, the model allows for specification of the unknown exposure-response relationship. The conditional prior of $\mathit{h}={({\mathit{h}}_1^{\mathit{\top }},\dots ,{\mathit{h}}_T^T)}^{\mathit{\top }}$ is

$$\pi (\mathit{h}|{\lambda }_1,{\lambda }_2)\propto \exp \left(-{\lambda }_1{\displaystyle \sum _{t=1}^{\mathit{\top }}{\Vert {\mathit{h}}_t\Vert }_{{\mathbf{G}}_t}-{\lambda }_2{\displaystyle \sum _{t=1}^{\mathit{\top }-1}{\left|{\mathit{h}}_{t+1}-{\mathit{h}}_t\right|}_1}}\right),$$ (11)

where ${\Vert {\mathit{h}}_t\Vert }_{{\mathbf{G}}_t}={({\mathit{h}}_{\mathbf{t}}^{\mathit{\top }}{\mathbf{G}}_{\mathbf{t}}{\mathit{h}}_{\mathbf{t}})}^{1/2}$ and ${\mathbf{G}}_t={\mathbf{K}}_t^{-1}$, where K_t denotes the kernel matrix for time t with i,j element K_t (z_i,_t, z_j,_t). The model applies broadly to many different choices of a kernel function. The model allows for interactions within each time point, but not for interactions across time points. The form for modeling the interactions is specified via the kernel function. A common choice for the kernel function is the quadratic kernel used in Liu et al. (2017), which is defined as K (z, z′) = (z^⊤ z′ + 1)². The quadratic kernel allows for both linear and nonlinear interactions among mixture components at every time window.

We specify the LKMR model using a hierarchical formulation by introducing latent parameters ${\mathit{\tau }}^{\mathbf{2}}=({\tau }_1^2,\dots ,{\tau }_{\mathit{\top }}^2)$ and ${\mathit{\omega }}^{\mathbf{2}}=({\omega }_1^2,\dots ,{\omega }_{\mathit{\top }-1}^2)$ which account for the group and fused lasso penalizations, respectively.

$$\mathbf{y}|\mathit{h},\mathbf{X},\mathit{\beta },{\sigma }^2~N_n\left(\mathbf{X}\mathit{\beta }+{\displaystyle \sum _t{\mathit{h}}_t,{\sigma }^2{\mathit{I}}_n}\right)$$ (12)

$$\mathit{h}|{\tau }_1^2,\dots ,{\tau }_{\mathit{\top }}^2,{\omega }_1^2,\dots ,{\omega }_{\mathit{\top }-1}^2~N_{n\mathit{\top }}\left(\mathbf{0},{\sum }_h\right)$$ (13)

$${\tau }_1^2,\dots ,{\tau }_{\mathit{\top }}^2,~\text{Gamma}\left(\frac{n+1}{2},\frac{{{\lambda }_1}^2}{2}\right)$$ (14)

$${\omega }_1^2,\dots ,{\omega }_{\mathit{\top }-1}^2~\text{Gamma}\left(1,\frac{{{\lambda }_2}^2}{2}\right)$$ (15)

where ${\tau }_1^2,\dots ,{\tau }_{\mathit{\top }}^2,{\omega }_1^2,\dots ,{\omega }_{\mathit{\top }-1}^2$, σ² are mutually independent.

The form of ${\sum }_h^{-1}$ is presented in the Supplementary Materials. ${\sum }_h^{-1}$ is parameterized by ${\mathit{\tau }}^2\left({\tau }_1^2,\dots ,{\tau }_{\mathit{\top }}^2\right),{\mathit{\omega }}^{\mathbf{2}}=\left({\omega }_1^2,\dots ,{\omega }_{\mathit{\top }-1}^2\right)$, and the parameters in K_t. There are diagonal blocks of size n × n, which arise due to the kernel structure placed on each h_t and involve the group lasso parameters ${\tau }_t^2$. Meanwhile, the off-diagonals involve ${\omega }_t^2$, which correspond to fused lasso and shrink the time-point-specific effects of the mixture toward each other. Figure 1 depicts the directed acyclic graph (DAG) of the Bayesian statistical model.

FIGURE 1.

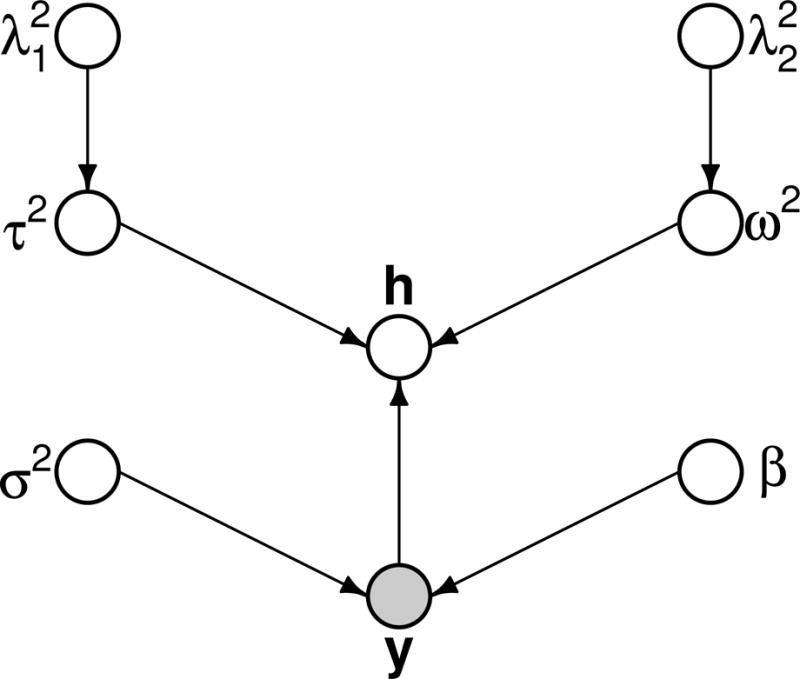
Distributed acyclic graph representation of Bayesian hierarchical model

4.2 | Markov Chain Monte Carlo approach

It can be shown via standard algebraic manipulations that the full conditional distributions for this model are given by the following, from which Gibbs sampling can be readily implemented:

$$\mathit{h}|\text{rest}~N\left\{{(\frac{1}{{\sigma }^2}{\mathit{W}}^{\mathit{\top }}\mathit{W}+{\sum }_h^{-1})}^{-1}\frac{1}{{\sigma }^2}{\mathit{W}}^{\mathit{\top }}(\mathbf{Y}-\mathbf{X}\mathit{\beta }),{(\frac{1}{{\sigma }^2}{\mathit{W}}^{\mathit{\top }}\mathit{W}+{\sum }_h^{-1})}^{-1}\right\}$$ (16)

$${\sigma }^2|\text{rest}~\text{Inverse}\text{Gamma}\left\{\frac{n}{2}+a,\frac{{(\mathbf{Y}-\mathit{W}\mathit{h}-\mathbf{X}\mathit{\beta })}^{\mathit{\top }}(\mathbf{Y}-\mathit{W}\mathit{h}-\mathbf{X}\mathit{\beta })}{2}+\gamma \right\}$$ (17)

$$\mathit{\beta }|\text{rest}~N\left\{{({\mathbf{X}}^{\mathit{\top }}\mathbf{X})}^{-1}{\mathbf{X}}^{\mathit{\top }}(\mathbf{Y}-\mathit{W}h),{\sigma }^2{({\mathbf{X}}^{\mathit{\top }}\mathbf{X})}^{-1}\right\}$$ (18)

$$\frac{1}{{\tau }_t^2}|\text{rest}~\text{Inverse}\text{Gamma}\left\{\sqrt{\frac{{\lambda }_1^2}{{\Vert \mathit{h}\Vert }_{G_t}^2}},{\lambda }_1^2\right\}$$ (19)

$$\frac{1}{{\omega }_t^2}|\text{rest}~\text{Inverse}\text{Gamma}\left\{\sqrt{\frac{{\lambda }_2^2}{{\displaystyle {\sum }_{n=1}^N{(h_{t+1,n}-h_{t,n})}^2}}},{\lambda }_2^2\right\}$$ (20)

$${\lambda }_1^2|\text{rest}~\text{Gamma}\left\{\frac{\mathit{\top }(n+1)}{2}+r_1,{\displaystyle \sum _{t=1}^{\mathit{\top }}\frac{{\tau }_t^2}{2}}+{\delta }_1\right\}$$ (21)

$${\lambda }_2^2|\text{rest}~\text{Gamma}\left\{\mathit{\top }-1+r_2,{\displaystyle \sum _{t=1}^{\mathit{\top }-1}\frac{{\omega }_t^2}{2}}+{\delta }_2\right\}$$ (22)

4.3 | Mean field variational Bayes approach

We now consider a MFVB approximation based on the following factorization for approximation of the joint posterior density function:

$$p(\mathit{\beta },{\sigma }^2,\mathit{h},{\mathit{\omega }}^2,{\mathit{\tau }}^2,{\lambda }_1^2,{\lambda }_2^2|\mathbf{Y})\approx q(\mathit{\beta })q({\sigma }^2)q(\mathit{h})q({\mathit{\omega }}^2)q({\mathit{\tau }}^2)q({\lambda }_1^2)q({\lambda }_2^2)$$ (23)

This leads to the following forms of the optimal q-densities:

$$q^{\ast }(\mathit{\beta })~N\left\{{({\mathbf{X}}^{\mathit{\top }}\mathbf{X})}^{-1}{\mathbf{X}}^{\mathit{\top }}(\mathbf{Y}-{\mathit{W}}_{{\mu }_{q(h)}}),{({\mu }_{q(\frac{1}{{\sigma }^2})}{\mathbf{X}}^{\mathit{\top }}\mathbf{X})}^{-1}\right\}$$ (24)

$$q^{\ast }({\sigma }^2)~\text{Inverse}\text{Gamma}\left\{\frac{n}{2}+a,\frac{{(\mathbf{Y}-{\mathbf{X}}_{{\mu }_{q(\mathit{\beta })}}-{\mathit{W}}_{{\mu }_{q(\mathit{h})}})}^{\mathit{\top }}(\mathbf{Y}-{\mathbf{X}}_{{\mu }_{q(\mathit{\beta })}}-{\mathit{W}}_{{\mu }_{q(\mathit{h})}})}{2}+\gamma \right\}$$ (25)

$$q^{\ast }(\mathit{h})~N\{{\{{\mu }_{q(\frac{1}{{\sigma }^2})}{\mathit{W}}^{\mathit{\top }}\mathit{W}+{\mu }_{q({\sum }_{{\tau }^2,{\omega }^2}^{-1})}\}}^{-1}{\mu }_{q(\frac{1}{{\sigma }^2})}{\mathit{W}}^{\mathit{\top }}(\mathbf{Y}-{\mathbf{X}}_{{\mu }_{q(\mathit{\beta })}}),$$ (26)

$${\left\{{\mu }_{q(\frac{1}{{\sigma }^2})}{\mathit{W}}^{\mathit{\top }}\mathit{W}+{\mu }_{q({\sum }_{{\tau }^2,{\omega }^2}^{-1})}\right\}}^{-1}\}$$

$$q^{\ast }(\frac{1}{{\tau }_t^2})~\text{Inverse}\text{Gaussian}\left\{{\left\{\frac{{\mu }_{q({\lambda }_1^2)}}{{\mu }_{q({\Vert {\mathit{h}}_t\Vert }_{G_t}^2)}}\right\}}^{1/2},{\mu }_{q({\lambda }_1^2)}\right\}$$ (27)

$$q^{\ast }(\frac{1}{{\omega }_t^2})~\text{Inverse}\text{Gaussian}\left\{{\left\{\frac{{\mu }_{q({\lambda }_2^2)}}{{\mu }_{q\left({{\displaystyle {\sum }_{n=1}^N\left(h_{t+1}{,}_n-h_{t,n}\right)}}^2\right)}}\right\}}^{1/2},{\mu }_{q({\lambda }_2^2)}\right\}$$ (28)

$$q^{\ast }({\mu }_{q({\lambda }_1^2)})~\text{Gamma}\left\{\frac{\mathit{\top }(n+1)}{2}+r_1,{\displaystyle \sum _{t=1}^{\mathit{\top }}\frac{{\mu }_{q({\tau }_t^2)}}{2}}+{\delta }_1\right\}$$ (29)

$$q^{\ast }({\mu }_{q({\lambda }_2^2)})~\text{Gamma}\left\{\mathit{\top }-1+r_2,{\displaystyle \sum _{t=1}^{\mathit{\top }-1}\frac{{\mu }_{q({\omega }_t^2)}}{2}}+{\delta }_2\right\}$$ (30)

where the parameters β, σ², h, ω², τ², ${\lambda }_1^2$, ${\lambda }_2^2$are updated according to the iterative algorithm in Algorithm 1. First, we initialized each of the optimal q-density parameters estimates μ_q (), and updated each of the parameters successively using the current estimates of the other parameters. The algorithm is iterated until the increase in $\log \{\underset{\_}{p}(\mathbf{y};q)\}$ is negligible. The form of $\log \{\underset{\_}{p}(\mathbf{y};q)\}$ can be found in the Supplementary Materials. The final updated parameter estimates μ_q () are used in the optimal q-densities (24) – (30) to obtain the posterior mean and variance estimates for each parameter.

4.4 | Prediction at new exposure profiles

An important aim of environmental health studies is the characterization of the exposure-response surface, particularly for prediction of health effects for unobserved exposure profiles at a given time point. Liu et al. (2017) provides details of this prediction approach; here, we summarize the approach and its adaptation to the variational Bayes context. In order to predict the exposure-response relationship for P new unobserved profiles of metal mixture exposures at time t, denoted by ${\mathbf{z}}_{1,t}^{\mathit{new}},\dots ,{\mathbf{z}}_{P,t}^{\mathit{new}}$ where each ${\mathbf{z}}_{P,t}^{\mathit{new}}={({\mathbf{z}}_{1P,t}^{\mathit{new}},\dots ,{\mathbf{z}}_{MP,t}^{\mathit{new}})}^{\mathit{\top }}$ for t = 1,..., ⊤ and p = 1,.., P, we first model the observed exposure data from n subjects measured at ⊤ time points. Next, we use the model to predict the exposure-response surface for P new time-varying mixture exposure profiles, which correspond to ${\mathit{h}}_t^{\mathit{new}}={(h_{1,t}^{\mathit{new}},\dots ,h_{P,t}^{\mathit{new}})}^{\mathit{\top }}$, given the observed data.

Liu et al. (2017) shows that we can define $\stackrel{\sim }{\mathit{h}}$ as a reordered h vector with time t, the time point of interest, at the end of the vector such that $\stackrel{\sim }{\mathit{h}}={\left({\mathit{h}}_1^{\mathit{\top }},\dots ,{\mathit{h}}_{t-1}^{\mathit{\top }},\dots ,{\mathit{h}}_{t+1}^{\mathit{\top }},\dots ,{\mathit{h}}_{\mathit{\top }}^{\mathit{\top }},{\mathit{h}}_t^{\mathit{\top }}\right)}^{\mathit{\top }}$, so that the covariance matrix of h can be easily defined. ${\sum ^{\sim }}_h$ denotes the corresponding reordered covariance matrix. The joint distribution of observed and new exposure profiles is

$$\left(\begin{array}{l}\stackrel{\sim }{\mathit{h}}\hfill \\ {\mathit{h}}_t^{\mathit{new}}\hfill \end{array}\right)~N\left[\mathbf{0},{\sum ^{\sim }}_h=\left(\begin{array}{ll}{\sum ^{\sim }}_{11}\hfill & {\sum ^{\sim }}_{12}\hfill \\ {\sum ^{\sim }}_{12}^{\mathit{\top }}\hfill & {\sum ^{\sim }}_{22}\hfill \end{array}\right)\right].$$ (31)

The conditional posterior distribution of ${\mathit{h}}_t^{\mathit{new}}$ is

$${\mathit{h}}_{\mathbf{t}}^{\mathbf{n}\mathbf{e}\mathbf{w}}|\mathit{\beta },{\mathit{\omega }}^{\mathbf{2}},{\mathit{\tau }}^{\mathbf{2}},{\sigma }^2~N_{n_{\mathit{new}}}\{{\sum ^{\sim }}_{12}^{\mathit{\top }}{\sum ^{\sim }}_{11}^{\mathit{\top }}{\left\{\frac{1}{{\sigma }^2}{\mathit{W}}^{\mathit{\top }}\mathit{W}+{\sum ^{\sim }}_{11}^{-1}\right\}}^{-1}\frac{1}{{\sigma }^2}{\mathit{W}}^{\mathit{\top }}(\mathbf{Y}-\mathbf{X}\mathit{\beta }),$$ (32)

$${\sum ^{\sim }}_{12}^{\mathit{\top }}{\sum ^{\sim }}_{11}^{-1}{\left\{\frac{1}{{\sigma }^2}{\mathit{W}}^{\mathit{\top }}\mathit{W}+{\sum ^{\sim }}_{11}^{-1}\right\}}^{-1}{\sum ^{\sim }}_{11}^{-1}{\sum ^{\sim }}_{12}+{\sum ^{\sim }}_{22}-{\sum ^{\sim }}_{12}^{\mathit{\top }}{\sum ^{\sim }}_{11}^{-1}{\sum ^{\sim }}_{12}\}.$$

The posterior mean and variance of ${\mathit{h}}_t^{\mathit{new}}$ can be approximated based on the estimated posterior mean of the other parameters, such as β, τ², ω², σ², ${\lambda }_1^2$ and ${\lambda }_2^2$, to reduce computation time.

5 | SIMULATION STUDY

In order to evaluate the performance of the proposed MFVB inference procedure, we conducted a simulation study for estimating health effects associated with time-varying mixture exposures. We compared the results of MFVB approximation to that of Bayesian MCMC for LKMR. We considered a three-toxicant scenario, where two toxicants exert a gradual, non-additive and non-linear effect over four time windows, and the other toxicant exerts a null effect at all four time windows, which are representative of pregnancy and early life. We used the following model: $y_i={\mathbf{x}}_i^{\mathit{\top }}\mathit{\beta }+{\sum }_t{h}_t\left({\mathbf{z}}_{i,t}\right)+e_i$ where z_i,_t =(z_1i,_t, z_2i,_t, z_3i,_t)^⊤, e_i ∼ N (0, 1), x_i = (x_1i, x_2i)^⊤ and x_1i ∼ N (10, 1) and x_2i ∼ Bernoulli(0.5). We simulated auto-correlation within toxicant exposures for metal m = 1, 2, 3 across time, and correlation among toxicants, using the Kronecker product for the exposure correlation matrix. Three choices for auto-correlation (AR-1) within toxicants were considered: high (0.8), medium (0.5) and low (0.2). The form of the exposure-response function, h_t (z_i,_t), was assumed to be proportional to a constant at all time points and was simulated as quadratic with two-way interactions. We assumed there is no effect of exposure to the mixture at time t = 1, and a gradual increase in the effect over time, by defining h_t (z) = α_t h(z), where α = (α₁, α₂, α₃, α₄) = (0, 0.5, 0.8, 1.0) and $h(\mathbf{z})=z_1^2-z_2^2+0.5z_1{z}_2+z_1+z_2$.

The results of the simulation are presented in Table 1. MFVB denotes the variational Bayes approximation to LKMR, while MCMC denotes the full MCMC algorithm for LKMR. For both procedures, we used the quadratic kernel function, such that K (z, z′) = (z^⊤z′ + 1)². Under the MCMC procedure, for each simulation we first burn in the sampler for 10,000 iterations and then run the Gibbs sampler for 10,000 iterations. The trace plots and marginal density plots of the different parameters can be found in the Supplementary Materials, Supplementary Figures S2a – S2c. Under the MFVB procedure, for each simulation the updates were run using the stopping criterion of a negligible change in $\log \{\underset{\_}{p}(\mathbf{y};q)\}$ Specifically, the iterations were stopped when change in $\log \{\underset{\_}{p}(\mathbf{y};q)\}<10\mathrm{e}-6$. We used R 3.3.2 to run the simulations, on the Odyssey high performance computing cluster supported by the FAS Division of Science, Research Computing Group at Harvard University. We evaluated the performance of the model to predict the exposure-response function by regressing the predicted $\widehat{\mathit{h}}$ on h at each time point. We present the intercept, slope and R² of the regressions over 100 simulations, each with a dataset of 300 subjects. The method is indicated to perform well when the regression shows an intercept close to zero, and slope and R² are close to one. We also present the root mean squared error (RMSE). Notably, the RMSE is generally smaller under MFVB as compared with MCMC. The reduction is most apparent in situations of high autocorrelation among mixture components, where there is up to 13% reduction in RMSE. We also see that the intercept, slope and R² tend to be very similar under MFVB and MCMC inference, indicating that the MFVB procedure is providing an accurate approximation to MCMC.

TABLE 1.

Simulation results, regression of $\widehat{\mathit{h}}$ on h for MFVB vs. MCMC

AR-1	Method	Time window	Intercept	Slope	R2	RMSE
0.8	MFVB	1	0.02	N/A	N/A	0.24
		2	0.00	0.89	0.97	0.23
		3	0.00	0.97	0.99	0.22
		4	−0.01	0.99	0.99	0.22
	MCMC	1	0.05	N/A	N/A	0.26
		2	0.01	0.91	0.96	0.26
		3	−0.02	0.98	0.99	0.24
		4	−0.04	1.00	0.99	0.22
0.5	MFVB	1	0.01	N/A	N/A	0.20
		2	0.00	0.92	0.97	0.25
		3	0.00	0.97	0.99	0.27
		4	0.01	0.99	0.99	0.22
	MCMC	1	0.06	N/A	N/A	0.23
		2	0.02	0.93	0.96	0.25
		3	−0.02	0.97	0.98	0.27
		4	−0.04	1.00	0.99	0.23
0.2	MFVB	1	0.04	N/A	N/A	0.22
		2	0.00	0.92	0.97	0.24
		3	−0.01	0.96	0.99	0.22
		4	−0.01	0.98	0.99	0.24
	MCMC	1	0.06	N/A	N/A	0.24
		2	0.01	0.93	0.97	0.24
		3	−0.02	0.96	0.99	0.22
		4	−0.04	0.98	0.99	0.23

Performance of estimated h_t (z_i,_t) across 100 simulated datasets, each with N = 300. RMSE denotes the root mean squared error of the $\widehat{\mathit{h}}$ as compared to h. Coverage denotes the proportion of times that the true h falls within in the 95% posterior credible interval of each time point. At time window 1, there is no effect; thus, slope and R² are not applicable to the regression of $\widehat{\mathit{h}}$ on h.

We next conduct a simulation to study the effect of varying sample sizes on estimated 95% posterior credible interval width and coverage, shown in Figure 2. Under MFVB, the 95% posterior credible interval is defined as the posterior mean +/− 1.96 times the square root of the posterior variance. Under MCMC, the 95% interval is quantile-based, calculated using the 0.025 and 0.975 quantiles of the poterior distribution. The coverage is defined as the proportion of times the true h_i,_t is contained in the 95% posterior credible interval. The same three-toxicant scenario was considered as in Table 1 with high AR-1, but for sample sizes of N = 100, 200, 300, 400, 500, and 800. Because of the computational infeasibility of applying the MCMC procedure to larger datasets, the simulations timed out on the computing cluster and were not recorded for sample sizes of N = 400, 500 and 800. The h contains the aggregated information for h₁, h₂, h₃, h₄. We note that for h, the estimated 95% posterior credible interval width is about half as small under MFVB as under MCMC. The interval width is also shorter for β and σ². As sample sizes increase, the interval widths estimated under both MFVB and MCMC shrink. Coverage is high for h across the range of sample sizes under MFVB. It ranges from 96% for N = 100, to 99% for N = 800. We note that the coverage of σ² increases substantially under MFVB for increasing sample sizes, changing from 49% for N = 100 to 87% for N = 800. Coverage of β under MFVB remains relatively constant, from 91% for N = 100 to 90% for N = 800.

FIGURE 2.

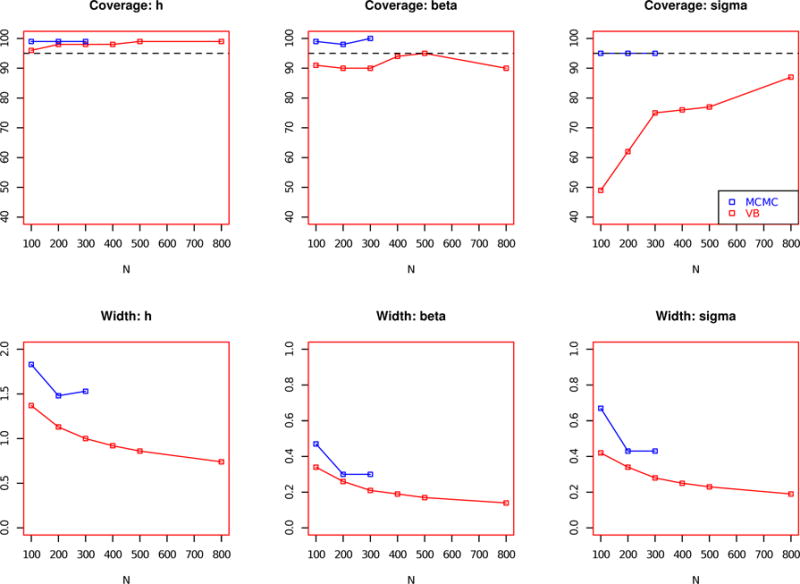
Coverage and posterior credible interval width of key parameters, using mean field variational approximation method for Bayesian inference and Markov chain Monte Carlo (MCMC). Performance estimated across 100 simulated data sets for key parameters h, βσ2 across a range of sample sizes (N = 100, 200, 300, 400, 500, 800). Width denotes the length of the 95% posterior credible interval. Coverage denotes the proportion of times that the true parameter falls within the 95% posterior credible interval. The dotted horizontal line marks 95%

Because we note that σ² is estimated to be smaller under VB than under MCMC, we expanded the simulation study of N=300 to explore this impact on the ensuing inference. In particular, we create plots which are also used in the Application section to understand the relative importance of each time-varying mixture component, as well as the interaction between two mixture components across time windows, comparing inference under MFVB-LKMR and MCMC-LKMR. The details regarding these plots can be found in Supplementary Materials Part C. We note that in each of these plots, the confidence bars or confidence bands are slightly narrower for VB than for MCMC. However, under this simulating example, we see that this slight narrowing does not lead to a change in inference on the estimated exposure-response relationship across the two estimation methods.

Lastly, Table 2 records the average computation time for MFVB and MCMC methods under the simulations in Figure 2. In general, the MFVB procedure is much faster than MCMC estimation. For example, for a sample size of N = 300, only 11 minutes is required under MFVB, whereas 3.5 days is required under MCMC.

TABLE 2.

Time in minutes for MFVB and MCMC applied to varying sample sizes in the simulation case

Method	N = 100	N = 200	N = 300
MFVB	0.17	1.8	10.8
MCMC	175	1409	4990

6 | APPLICATION

We applied the MFVB procedure for LKMR to study the association between birthweight and time-varying metal mixture exposures in the Programming Research in Obesity, Growth, Environment and Social Stressors (PROGRESS) study conducted in Mexico City. The primary outcome was birthweight z-scores, calculated according to the international infant growth charts developed by Fenton et al. (2013). Exposures to nine metals were measured in the mother’s blood at the second and third trimesters of pregnancy as well as birth. These metals included arsenic (As), cadium (Cd), cobalt (Co), chromium (Cr), cesium (Cs), copper (Cu), manganese (Mn), antimony (Sb), and selenium (Se). We controlled for socioeconomic status (3 categories: low, middle, high), mother’s hemoglobin during the second trimester of pregnancy, mother’s educational level (< high school, high school, > high school), child gender and mother’s IQ score from the Wechsler Abbreviated Scale of Intelligence (WASI). The largest auto-correlations were seen for time-varying exposures to manganese and cadmium, at 0.50 and 0.53, respectively. In our analysis, we logged, then centered and scaled metal exposure levels. We also centered and scaled the confounder variables. We considered all subjects with complete data, resulting in a sample size of N = 391.

As a primary analysis, we considered a linear regression model that simultaneously regressed birthweight on con-founders and metal exposures at all time points. Several metals were identified as significant at the α = 0.05 level. Third trimester manganese was positively associated with birthweight (p = 0.02), and third trimester antimony was also positively associated with birthweight (p = 0.01). Cesium at birth was negatively associated with birthweight (p = 0.04), and selenium at birth was positively associated with birthweight (p = 0.004). As the linear model suggested evidence of a potential exposure-response relationship across multiple time windows, we further explored this through the MFVB inference procedure for LKMR.

Next, we applied the MFVB inference procedure to analyze the effects of time-varying exposures of heavy metals during pregnancy on birthweight. Previous literature (Claus Henn et al., 2010b; Zota et al., 2009) has shown an inverted-u relationship between some metals, such as manganese, and neurodevelopment. Thus, K_t, the kernel matrix in our analysis, was chosen to be a quadratic kernel such that K (z, z′) = (1 + z^⊤z′)². A primary question of analysis is quantifying the effect of individual metal exposures on birthweight. Accordingly, we used the MFVB procedure to estimate the relative importance of each metal at the three time points, as shown in Figure 3. Relative importance is quantified by the difference in the estimated exposure-response function between a high level (75th percentile) and a low level (25th percentile) exposure for a single metal, holding all other metals constant at their median exposure levels. Figure 3 provides evidence that second trimester cobalt may be positively associated with birth weight, whereas second trimester copper may be negatively associated with birth weight. In addition, third trimester manganese is positively associated with birth weight. Lastly, copper and antimony at birth may be negatively associated with birth weight. Positive associations between manganese and birthweight have been seen in Zota et al. (2009), and are consistent with manganese’s role as an essential nutrient required for bone growth and development. As cobalt is an essential trace element that is part of the vitamin B12 complex and other cobalamins (Lindsay and Kerr, 2011), a higher exposure to cobalt may be indicative of healthy dietary habits which could lead to a higher birthweight.

FIGURE 3.

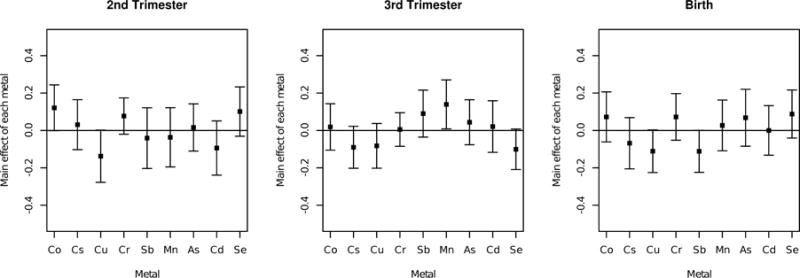
Mean field variational approximation method for Bayesian inference procedure for lagged kernel machine regression estimated relative importance of each metal at three critical windows for Programming Research in Obesity, Growth, Environment and Social Stressors data. Plot of the relative importance of each metal, as quantified by the difference in the estimated exposure–response function at the 75th percentile versus the 25th percentile of a given metal exposure while holding all other metal exposures constant at their median values

There is little known about the effect of co-exposure between cobalt and other metals on birthweight. Therefore, we focus on cobalt in this analysis, and identify a significant interaction between cobalt and cesium at a critical window of exposure. Because the exposure-response surface is nine-dimensional, due to the nine metal co-exposures studied at each time window, we use heat maps and cross-sectional plots to reduce dimensionality and graphically depict the exposure-response relationship. One way of visualizing the exposure-response surface between cobalt and cesium is through a heat map, depicted in Figure 4. The posterior mean of the exposure-response surface for cobalt and cesium is plotted across a range of exposures, while holding the other seven metals at their median exposures. We note that it is important to carefully interpret the potential interactions, particularly in areas of fewer observations. Therefore, we plot the exposure-response function only within a small region (within a 0.5 Euclidean distance) of an observed data point. At each time window, the shape of the exposure-response surface is suggestive of an interaction effect between the two metals. For example, we see that for exposures at the third trimester of pregnancy, high cobalt/high cesium and low cobalt/low cesium are associated with larger birthweights, while high cobalt/low cesium and low cobalt/high cesium are associated with smaller birthweights.

FIGURE 4.

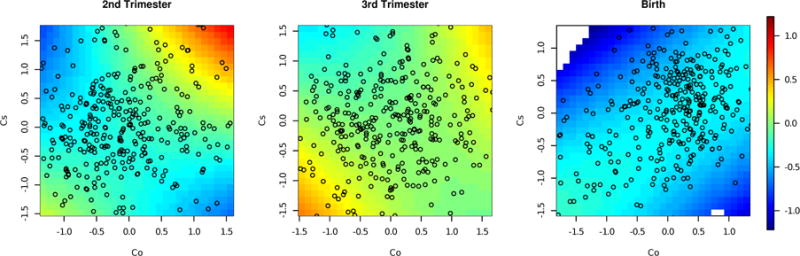
Mean field variational approximation method for Bayesian inference procedure for lagged kernel machine regression estimated time-specific Co–Cs exposure response functions applied to Programming Research in Obesity, Growth, Environment and Social Stressors data. Plot of the estimated posterior mean of the exposure–response surface for Co and Cs, at the median of As, Cd, Cr, Cu, Mn, Sb, and Se

In order to better quantify the time-varying interactions between cobalt and cesium and show estimates of the posterior uncertainty of the exposure-response function, we present plots of a cross-section of the exposure-response surface in Figure 5. Here, the cross-section of the exposure-response surface is plotted for cobalt, at low (25th percentile) and high (75th percentile) cesium exposures, while holding the other seven metals at their median exposure values. We see evidence suggestive of a positive interaction between cobalt and cesium at the second and third trimesters. At the second trimester, the top graph (low cesium) suggests a null effect of cobalt exposure on birthweight, while the bottom graph (high cesium) suggests a positive linear effect of cobalt exposure on birthweight. Thus, there appears to be effect modification for cobalt based on the level of cesium co-exposure. At the third trimester, a similar effect is seen. Here, cobalt exposure in the presence of high cesium levels is found to be positively associated with birthweight. Because the cross-sectional plots have graphically suggested an interaction between cobalt and cesium co-exposure in the presence of the seven other metals, we next quantify the estimated interaction effect at the three critical windows. First, we estimated the exposure-response effect for high (75th percentile) versus low (25th percentile) cobalt exposures, at high cesium levels and median levels of the seven other metals. Next, we estimated the exposure-response effect for high versus low cobalt exposures, at low cesium levels and median levels of the seven other metals. The difference between these two estimated exposure-response effects quantifies the cobalt-cesium interaction, which is depicted in Figure 6. We see that there is a significantly positive interaction between cobalt and cesium at the second trimester of pregnancy.

FIGURE 5.

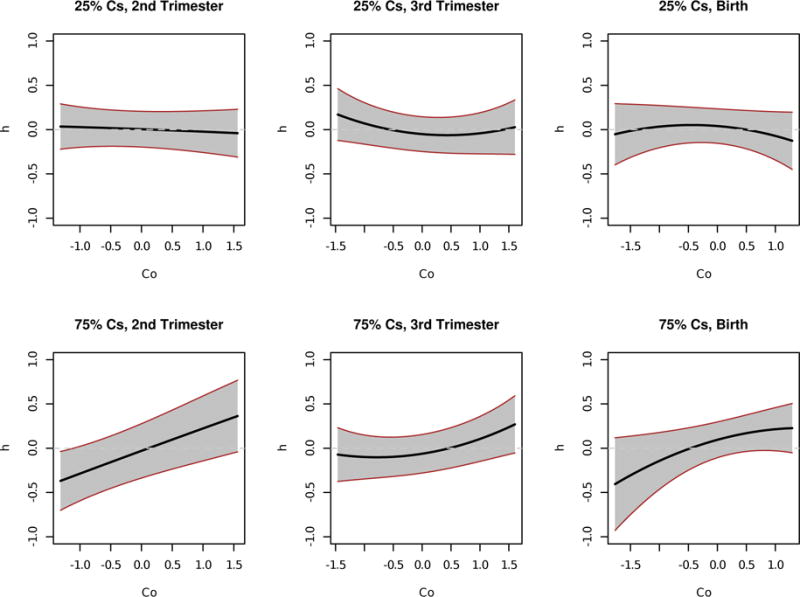
Mean field variational approximation method for Bayesian inference procedure for lagged kernel machine regression estimated time-specific exposure–response functions for Co at low and high Cs levels applied to Programming Research in Obesity, Growth, Environment and Social Stressors data. Plot of the cross-section of the estimated exposure–response surface for Co, at the 25th (top panel) and 75th (bottom panel) of Cs exposure, holding As, Cd, Cr, Cu, Mn, Sb, and Se constant at median exposures

FIGURE 6.

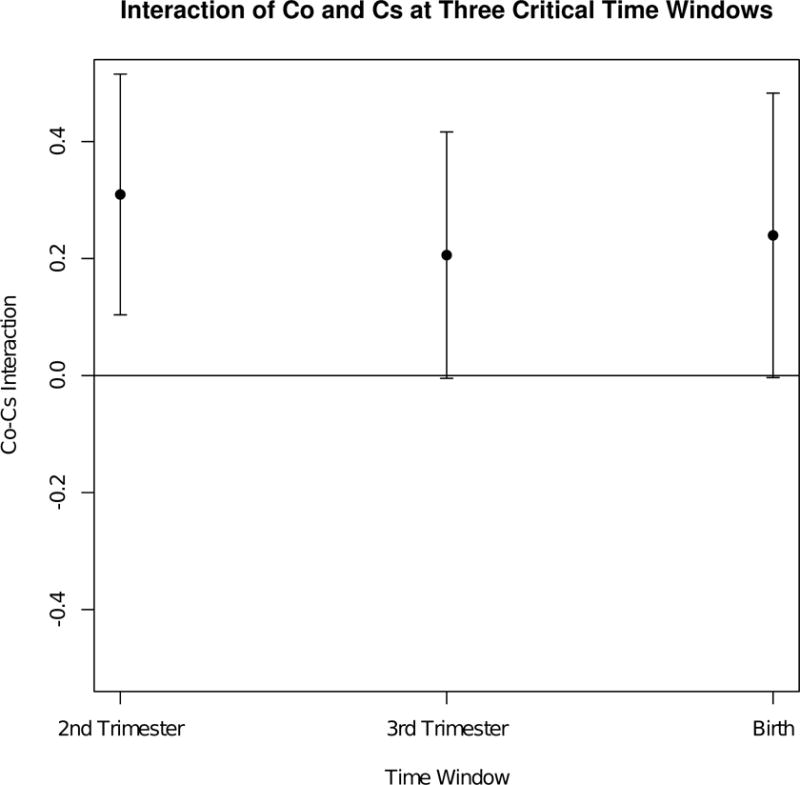
Mean field variational approximation method for Bayesian inference procedure for lagged kernel machine regression estimated Co–Cs interaction at three critical windows for Programming Research in Obesity, Growth, Environment and Social Stressors data. Plot of the estimated interaction effect between Co and Cs, holding As, Cd, Cr, Cu, Mn, Sb, and Se constant at median exposures. First, we estimated the exposure–response effect for high (75th percentile) versus low (25th percentile) cobalt exposures, at high cesium levels and median levels of the seven other metals. Next, we estimated the exposure–response effect for high versus low cobalt exposures, at low cesium levels and median levels of the seven other metals. The difference between these two estimated exposure–response effects quantifies the cobalt–cesium interaction

7 | DISCUSSION AND CONCLUSION

In this article, we have developed a MFVB inference procedure for the LKMR model, which allows for computationally efficient analysis of environmental health datasets to study complex mixtures. In recent years, there has been growing interest in the concept of the exposome, i.e. the totality of human exposures over a lifetime (Stigone et al., 2017; Buck Louis et al., 2017). This interest, in turn, led to the rapid growth of research into statistical methods to address complex mixtures (Herring, 2010; Park et al., 2014; Braun et al., 2016; Gennings et al., 2013; Bobb et al., 2015). In parallel, the growing recognition of the role of critical windows in toxicology has led to new methods to address finding critical windows (Wright, 2017). These issues converge biologically, as complex mixtures likely have time-specific critical windows. However, addressing both issues simultaneously is computationally challenging, as mixture datasets are large and are repeatedly measured. A key contribution of the article is the dramatic decrease in computational time required for MFVB as compared with MCMC, while also maintaining accuracy in estimation of the exposure-response relationship. We applied the MFVB algorithm to analyze a prospective cohort study of children’s environmental health in Mexico City, where we found evidence of interaction and effect modification for exposure to a pair of heavy metals. Specifically, we identified a possible positive interaction between cobalt and cesium at the second trimester of pregnancy. Cobalt is part of the vitamin B12 complex and other cobalamins (Lindsay and Kerr, 2011), which may account for its positive association with birthweight. In small quantities, cobalt is an essential element, and is naturally present in food (Caserta et al., 2013). Meanwile, the literature on cesium chronic toxicity and metabolism is sparse (Melniknov and Zanoni, 2010), but it is not an essential nutrient like cobalt. Our results suggest that in the presence of high cesium levels, the positive effect of cobalt on birthweight is more pronounced. As the literature on metal mixture exposures is sparse, these detected potential effects could serve as a starting point for future environmental health studies.

We note that because of the computational efficiency of the algorithm, we were able to analyze a prospective cohort study of moderate size (N =391) with ease. Simulations demonstrated that inference using MFVB-LKMR took minutes, while inference using MCMC-LKMR took hours or days. We showed that depending on the sample size, MCMC-LKMR may not be computationally feasible for larger sample sizes (e.g. larger than a few hundred participants when multiple time windows are studied). Furthermore, it may be untenable in a real-world application to run the MCMC-LKMR algorithm for even a moderate sample size, due to the frequent desire to run multiple secondary and sensitivity analyses.

Notably, we showed that MFVB inference maintains high accuracy for the key parameter of interest, h, which quantifies the unknown exposure-response relationship. Under varying simulation scenarios, MFVB estimates h well, often with smaller RMSE than using MCMC estimation. Posterior credible interval coverage is consistently 96-99% for h under MFVB for a range of sample sizes.

We also demonstrated that the coverage of the variance parameter, σ², varies significantly across the range of sample sizes. For small datasets, coverage can be poor, but increases considerably for larger sample sizes, reaching 87% under N = 800. When sample sizes are small, one could easily use MCMC estimation; thus, the coverage would not be a concern. However, MFVB inference was specifically created for large sample sizes, when it would be nearly impossible to conduct analysis under MCMC without a significant time burden. In the situation of large sample sizes, the coverage of σ² is much higher, albeit still smaller than than of MCMC. Thus, MCMC and MFVB are complementary approaches. For smaller datasets, the full MCMC is applicable as it has more accuracy than MFVB, whereas for larger datasets, MFVB is feasible and sufficiently accurate while MCMC is infeasible.

We also note that the width of the posterior credible intervals for β, σ², h are smaller under MFVB inference than under MCMC estimation. It is known that due to the form of the Kullback-Leibler divergence used in the variational Bayes framework (Bishop, 2006; Rue et al., 2009; Wang and Titterington, 2005), the procedure can underestimate the posterior variance. While this may be a contributing factor to the reduced coverage of the σ² parameter, in which interval widths may have been too short to properly capture the truth, this factor does not seem to hinder our analyses, as h is estimated well. If one was interested in adjusting for the sometimes underestimated posterior variance estimates, a grid-based method proposed by Ormerod (2011) could be used. However, in situations where the number of parameters estimated exceeds the sample size, as is in the case described in this article, the approach of calculation over the grid values can render the grid-based method computationally infeasible.

There may be alternative modeling approaches to the MFVB implementation of LKMR described here. For example, the computational MCMC challenges may be overcome by using a parallel Gibbs sampler to accelerate Gibbs sampling. This has been proposed by several authors such as Doshi-Velez et al. (2009) using the Indian Buffet Process, and Gonzalez et al. (2011) using the Chromatic sampler and the Splash sampler. Furthermore, mean field variational Bayes may also be parallelized, as proposed by Tran et al. (2016). However, because of the connection between MFVB and Gibbs sampling for LKMR, the method proposed here performs well for reduced computation time while maintaining reasonable accuracy.

Given the connection between the mixed-model representation of a kernel machine regression and spatial mixed models, a referee raised the interesting question of how the regularized estimation of the time-varying exposure-response associations impact estimation of the fixed regression coefficients β in the model. In the spatial statistics literature, Hodges and Reich (2010) have demonstrated that spatial confounding can occur, in which a random effect, or a spatially correlated error term, could alter the estimated fixed effects. They proposed restricted spatial regression to deal with spatial confounding, and others have explored the use of Bayesian group lasso to improve predictive ability for the spatial generalized linear mixed model by accounting for the collinearity between regression coefficients and spatial random effects (Hefley et al., 2017). In this work, estimation of these regression coefficient estimates were not of primary interest, but future work should explore the potential for such biases in the multivariate exposure setting and the utility of similar restricted spatial regression strategies in this setting.

In conclusion, we note that the complexity of the LKMR Bayesian model, coupled with the computational burden of estimation using MCMC, warrants and necessitates the variational Bayes approach. Furthermore, the high accuracy and similar coverage of key parameters between MCMC and MFVB illustrates the usefulness of the variational Bayes approach.

Additional information and supporting material for this article is available online at the journal’s website.

ALGORITHM 1.

MFVB algorithm for lagged kernel machine regression.

Initialize: ${\mu }_{q(1/{\sigma }^2)}>0$, ${\mu }_{q(\beta )}=1$, ${\mu }_{q(1/{\tau }^2)}=1$, ${\mu }_{q(1/{\omega }^2)}=1$.

Cycle:

${{\displaystyle {\sum }_{q(h)}\leftarrow \left\{{\mu }_{q(1/{\sigma }^2)}{W}^{\mathit{\top }}W+{\mu }_{q({\sum }_{{\tau }^2,{\omega }^2}^{-1})}\right\}}}^{-1}$

${\mu }_{q(h)}\leftarrow {\mu }_{q(1/{\sigma }^2)}{\displaystyle {\sum }_{q(h)}{W}^{\mathit{\top }}}(Y-X{\mu }_{q(\beta )})$

${\mu }_{q(\beta )}\leftarrow {(X^{\mathit{\top }}X)}^{-1}{X}^{\mathit{\top }}(Y-W{\mu }_{q(h)})$

${\mu }_{q(1/{\sigma }^2)}\leftarrow \frac{n+2a}{{(Y-X{\mu }_{q(\beta )}-W{\mu }_{q(h)})}^{\mathit{\top }}(Y-X{\mu }_{q(\beta )}-W{\mu }_{q(h)})+2\gamma }$

${\mu }_{q(1/{\tau }_t^2)}\leftarrow {\left\{\frac{{\mu }_{q({\lambda }_1^2)}}{{\mu }_{q({\Vert h_t\Vert }_{G_t}^2}}\right\}}^{1/2}$

${\mu }_{q(1/{\omega }_t^2)}\leftarrow {\left\{\frac{{\mu }_{q({\lambda }_2^2)}}{{\mu }_{q({\displaystyle {\sum }_{n=1}^N{(h_{t+1,n}-h_{t,n})}^2)}}}\right\}}^{1/2}$

${\mu }_{q({\lambda }_1^2)}\leftarrow \frac{\mathit{\top }(n+1)+2r_1}{{\displaystyle {\sum }_{t=1}^{\mathit{\top }}{\mu }_{q({\tau }_t^2)}+2{\delta }_1}}$

${\mu }_{q({\lambda }_2^2)}\leftarrow \frac{\mathit{\top }-1+r_2}{\frac{1}{2}{\displaystyle {\sum }_{t=1}^{\mathit{\top }-1}{\mu }_{q({\omega }_t^2)}+{\delta }_2}}$

until the increase in $\log \{\underset{\_}{p}(\mathbf{y};q)\}$ is negligible.