Quantile Regression in the Secondary Analysis of Case-Control Data

Abstract

Case-control design is widely used in epidemiology and other fields to identify factors associated with a disease. Data collected from existing case-control studies can also provide a cost-effective way to investigate the association of risk factors with secondary outcomes. When the secondary outcome is a continuous random variable, most of the existing methods focus on the statistical inference on the mean of the secondary outcome. In this paper, we propose a quantile-based approach to facilitating a comprehensive investigation of covariates’ effects on multiple quantiles of the secondary outcome. We construct a new family of estimating equations combining observed and pseudo outcomes, which lead to consistent estimation of conditional quantiles using case-control data. Simulations are conducted to evaluate the performance of our proposed approach, and a case-control study on genetic association with asthma is used to demonstrate the method.

1 Introduction

Case-control design is widely used in epidemiology and other fields as a cost-effective alternative to prospective cohort designs. It samples “cases” from a specific disease population and “controls” from those free of the disease. By comparing the distribution of exposures/predictors between cases and controls, one could identify factors that associate with the disease risk. Besides the primary disease status (D) and exposures of interest (X), case-control studies often collect additional variables (Y), which can be important biomarkers and characterizations of the disease or anthropometric parameters of the subjects. Hence, data are available to analyze the associations between the exposures and these secondary outcomes and can facilitate our understanding on the mechanism relevant to the secondary outcomes. The analyses on these secondary outcomes using existing case-control data are known as “secondary analyses” in the literature (Kraft, 2007; Richardson et al, 2007).

Due to the case-control sampling scheme, the selected subjects are no longer representative of the general population. Ignoring the data structure in secondary analyses would lead to biased inference on the association between the covariates of interest and the secondary outcomes. Naive approaches include analyzing among controls only or stratifying the association by disease status, but they do not directly address the question about the association at the population level. A few proposals have been made to estimate the population association while utilizing the case-control sample. Among them, the Inverse Probability Weighting (IPW) is a popular approach, which weights each observation by the reciprocal of its selection probability (Jiang, Scott and Wild, 2006; Richardson et al., 2007; Monsees, Tamimi and Kraft, 2009;). The IPW method usually performs well when the selection probability only depends on the disease status, but may suffer both bias and inflated variance due to the difficulty of correctly estimating the selection probability that may relate to the covariates or certain auxiliary variables. Other common approaches are likelihood-based methods, including Roeder, Carroll and Lindsay (1996), Lee, McMurchy and Scott (1997), Jiang, Scott and Wild (2006), and Lin and Zeng (2009). These methods estimate covariate effects on the mean of secondary outcome, which is only one measure of the central tendency of the outcome, and often require parametric distributional assumption on the secondary outcome.

In many applications, the vulnerable or high risk group to certain disease often consists of subjects with high or low values for their quantitative traits. For example, people with high body mass index (BMI) are predisposed to diabetes, cancers and many other disorders (Hjartaker, Langseth, and Weiderpass, 2008). Therefore, instead of examining risk factors for the mean of BMI, it is practically meaningful to investigate the risk factors for the upper quantiles of BMI, which are directly associated with high risk for many disease. Many studies also observe that covariate effect often varies across quantile levels. For example, Yang et al. (2012) found that an important genotype FTO is not only associated with the mean of BMI (Frayling et al, 2007) but also with the variance, suggesting that the FTO genotype influences the entire distribution of BMI and impacts differently at various quantiles. Hence, examining covariate’s effects at multiple quantiles provides a comprehensive view of association between the exposures and the outcome. For these reasons, quantile-based analyses have great potential to deepen and expand the existing knowledge from traditional secondary analysis.

In this paper, we propose to extend quantile regression (Koenker and Bassett, 1979) techniques to estimate the conditional quantiles of the secondary outcomes in case-control studies. The rest of the paper is organized as follows. Section 2 describes the proposed methods, where we first introduce the ideas of constructing estimating equations using both observed and pseudo outcomes, and then present two estimation algorithms to solve the equations. Large sample properties of the resulting estimators are also presented in Section 2. Section 3 includes simulation studies to illustrate the finite sample performance of the proposed methods with comparison to existing methods. In Section 4, we apply the proposed methods to a case-control asthma study and compared our methods to the least squares-based mean regression. We conclude with discussions in Section 5.

2 Proposed Methods

2.1 Notation and settings

Suppose we have a case-control sample, which consists of n₁ cases randomly selected from a disease population (D = 1), and n₂ healthy controls randomly selected from a disease-free population (D = 0). Potential risk factors for disease are denoted by X and measured from each enrolled subject. The primary goal of collecting the case-control sample is to identify the risk factors that are associated with the disease D. In addition to (D, X), certain subject characteristics or biomarkers of the disease, which we call “secondary outcomes” and denote as Y, are also measured on each subject. Denoting Q_Y (τ|X) as the τth conditional quantile of Y given X, we assume that in the general population, Q_Y (τ|X) is a linear function of X,

$$Q_Y(\mathrm{\tau }|\mathbf{X})={\mathbf{X}}^{\top }{\mathit{\beta }}_{0,\mathrm{\tau }},$$ (1)

where the coefficients β_0,τ denote the true effects of covariates X on the τth quantile of Y and are of primary interest in secondary analyses.

We denote the observed data by {x_i, y_i, d_i}_i=1,…,n where n = n₁ + n₂ is the total sample size; d_i = 1, i = 1, …, n₁ for the cases and d_i = 0, i = n₁ + 1, …, n for the controls. When both X and Y are related to the disease D, the association between X and Y often differs between the cases and controls. Consequently, direct regression of y_i against x_i using a case-control sample yields biased estimation for β_0,τ. In the next section, we propose an estimating equation based approach for secondary quantile analyses.

2.2 Proposed estimating equations

Let ψ_τ(X, Y, β) = [τ – I{Y ≤ X^⊤β}] X be the original set of quantile regression estimating functions. For any randomly drawn (Y, X) from the general population, the following equations hold at the true β_0,τ,

$$E_Y\left[{\mathrm{\psi }}_{\mathrm{\tau }}(\mathbf{X},Y,{\mathit{\beta }}_{0,\mathrm{\tau }})|\mathbf{X}\right]=0.$$

Conditioning on the disease status D, we expand the above equations to

$$\begin{array}{c}{E}_Y\left[{\mathrm{\psi }}_{\mathrm{\tau }}(\mathbf{X},Y,{\mathit{\beta }}_{0,\mathrm{\tau }})|\mathbf{X}\right]=E_Y\left[{\mathrm{\psi }}_{\mathrm{\tau }}(\mathbf{X},Y,{\mathit{\beta }}_{0,\mathrm{\tau }})|\mathbf{X},D=0\right]P(D=0|\mathbf{X})\\ +E_Y\left[{\mathrm{\psi }}_{\mathrm{\tau }}(\mathbf{X},Y,{\mathit{\beta }}_{0,\mathrm{\tau }})|\mathbf{X},D=1\right]P(D=1|\mathbf{X})=0,\end{array}$$ (2)

which will be the basis for constructing the proposed estimating equations. We now introduce a pseudo observation ỹ as the outcome under alternative disease status. Specifically, for i = 1, …, n₁, we define ỹ_i as the pseudo outcome of subject i if selected as a control, and for i = n₁ + 1, …, n, we define ỹ_i as the pseudo outcome of subject i if selected as a case. If we were able to observe those counter-factual outcomes, we could construct unbiased estimation equations for (2) with

$${\mathcal{S}}_{n,\mathrm{\tau }}(\mathit{\beta })={\displaystyle \sum _{i=1}^n{\mathrm{\psi }}_{\mathrm{\tau }}({\mathbf{x}}_i,y_i,\mathit{\beta })p(d_i|{\mathbf{x}}_i)+{\mathrm{\psi }}_{\mathrm{\tau }}({\mathbf{x}}_i,{\stackrel{\sim }{y}}_i,\mathit{\beta })p(1-d_i|{\mathbf{x}}_i)=0,}$$ (3)

where p(d_i | x_i) is the probability of being the observed disease status given x_i, and p(1 − | x_i) is the probability of being counter-factual disease status. One can show that, for each summand of (3), its conditional expectation given (x_i, d_i) is zero at the true β_0,τ and thus constitutes an unbiased estimating equation. Note that the disease risk may relate to Y or other auxiliary variables Z, and p(D|X) in (3) denotes the conditional probability given X, i.e. p(D|X) = ∫_y,z p(D|X, y, z) d F_{(y, z)} (y, z).

Because those pseudo outcomes are unobserved in reality, we propose two approaches to circumventing this difficulty. We first propose a model-based simulation approach to generating the pseudo counter-factual outcomes, and assemble the estimating equations accordingly. In the second approach, we replace ψ_τ (x_i, ỹ_i, β) by its conditional expectation, which is then estimated by a kernel smoothing technique.

2.3 Approach A: simulating pseudo counter-factual outcomes

To simulate the pseudo outcomes for a cases or control, we will model the conditional quantile process among its counterpart samples. Since quantile regression does not assume any parametric distribution in Y, we need expand the main model (1) to the entire quantile process in order to simulate counter-factual outcomes. This joint modeling approach has been explored in recent work, including Wei and Carroll (2009), Wei, Ma and Carroll (2012), and Wei and Yang (2014), to approximate the conditional quantile function without assuming a parametric likelihood. Specifically, we assume that the linear quantile model holds for any quantile level τ ∈ (0, 1). Under this assumption, we define β₀(τ | d)_d=0,1 as the quantile coefficient functions given disease status D = d such that

$${\mathit{\beta }}_0(\mathrm{\tau }|d)=\arg \underset{\mathit{\beta }}{\min }{E}_Y[\parallel {\mathrm{\psi }}_{\mathrm{\tau }}(Y,\mathbf{X},\mathit{\beta })\parallel |\mathbf{X},D=d]$$ (4)

for any τ ∈ (0, 1). Therefore, x^⊤β₀(τ | 0) defines the conditional quantile function of y given x among controls, and x^⊤β₀(τ | 1) defines that among disease population.

In what follows, we outline an estimation algorithm to estimate β₀(τ | d) from the data, and simulate counter-factual outcomes accordingly. Let $0<{\mathrm{\tau }}_1<{\mathrm{\tau }}_2<\cdots <{\mathrm{\tau }}_{k_n}<1$ be a set of k_n evenly spaced quantile levels.

1. We denote $\widehat{\beta }({\mathrm{\tau }}_k|d)$, d = 1/0 as the estimated quantile coefficients for β₀(τ_k | d), in (4) within cases and controls, respectively.

2. To approximate the coefficient process β₀(τ | d), we define $\widehat{\beta }(\mathrm{\tau }|d)$ be a piecewise linear functions on [0,1] that concatenates the estimates $\widehat{\beta }({\mathrm{\tau }}_k|d)$ for $0<{\mathrm{\tau }}_k<{\mathrm{\tau }}_2<\cdots <{\mathrm{\tau }}_{k_n}<1$ and is subject to the constraint of $\widehat{{\beta }^{\prime }}(0|d)=\widehat{{\beta }^{\prime }}(1|d)=0$.

3. For the ith subject, i = 1, …, n, we simulate its pseudo outcome ỹ_i by $\widehat{{\stackrel{\sim }{y}}_i}={\mathbf{x}}_i^{\top }\widehat{\beta }(u_i|1-d_i)$, where u_i is a random draw from Uniform (0, 1) distribution.

The simulated ${\widehat{\stackrel{\sim }{y}}}_i$’s follows the model-estimated conditional distribution of Y given x_i and d_i. Under certain mild conditions as outlined in Wei and Carroll (2009), $\widehat{\beta }(\mathrm{\tau }|1)$ and $\widehat{\beta }(\mathrm{\tau }|0)$ uniformly converge to the underlying true ones over the interval [1/(k_n + 1), k_n/(k_n + 1)] as n₁ and n₂ go to the infinity. Hence, with a reasonably large sample sizes, the simulated ${\widehat{\stackrel{\sim }{y}}}_i$ approximates the counter-factual outcome ${\stackrel{\sim }{y}}_i$ well.

With the simulated be ${\widehat{\stackrel{\sim }{y}}}_i$’s we construct the sampling estimating equations as

$${\displaystyle \sum _{i=1}^n{\mathrm{\psi }}_{\mathrm{\tau }}}({\mathbf{x}}_i,y_i,\mathit{\beta })p(d_i|{\mathbf{x}}_i)+{\mathrm{\psi }}_{\mathrm{\tau }}({\mathbf{x}}_i,{\widehat{\stackrel{\sim }{y}}}_i,\mathit{\beta })p(1-d_i|{\mathbf{x}}_i)=0.$$ (5)

Simulating pseudo outcomes is subject to sampling uncertainty, and brings extra variability into parameter estimation. To further stabilize the variance, we suggest to repeat the above simulation procedures m time, and use their average as final estimation. Let ${\widehat{\beta }}_{n,\mathrm{\tau }}^{(\ell )}$ as the estimated coefficients from the ℓ-th replicate using (5), we then use the average of ${\widehat{\beta }}_{n,\mathrm{\tau }}^{(\ell )}$ as the final estimate of the coefficients. i.e.

$${\widehat{\beta }}_{n,\mathrm{\tau }}=m^{-1}{\displaystyle \sum _{\ell =1}^m{\widehat{\beta }}_{n,\mathrm{\tau }}^{(\ell )}}.$$

Similar to the multiple imputation technique that is commonly used to handle missing data, the variance of ${\widehat{\beta }}_{n,\mathrm{\tau }}$ is fairly stable with a small number of m between 5 and 10. We will demonstrate the effect of different m in the section of simulations. In the rest of paper, we call ${\widehat{\mathit{\beta }}}_{n,\mathrm{\tau }}$ the SICO estimate since it uses SImulated Counter-factual Outcomes.

2.4 Approach B: estimating ψ_τ (x_i, ỹ_i, β) by its conditional expectation

Another way to circumvent the difficulty of unobserved counter-factual outcomes is to replace ψ_τ(x_i, ỹ_i, β) by its conditional expectation ${\stackrel{\sim }{\mathrm{\psi }}}_{\mathrm{\tau }}({\mathbf{x}}_i,\mathit{\beta })=E_{{\stackrel{\sim }{y}}_i}[{\mathrm{\psi }}_{\mathrm{\tau }}({\mathbf{x}}_i,{\stackrel{\sim }{y}}_i,\mathit{\beta })|{\mathbf{x}}_i]$. We reconstruct the estimating equations by

$$S_{n,\mathrm{\tau }}(\mathit{\beta })={\displaystyle \sum _{i=1}^n\left\{{\mathrm{\psi }}_{\mathrm{\tau }}({\mathbf{x}}_i,y_i,\mathit{\beta })p(d_i|{\mathbf{x}}_i)+{\tilde{\mathrm{\psi }}}_{\mathrm{\tau }}({\mathbf{x}}_i,\mathit{\beta })p(1-d_i|{\mathbf{x}}_i)\right\}=0},$$ (6)

where ${\tilde{\mathrm{\psi }}}_{\mathrm{\tau }}({\mathbf{x}}_i,\mathit{\beta })$ is estimated from the control sample if d_i = 1 and from the case sample if d_i = 0. In a simple scenario where we have sufficient number of cases and controls given each value of x_i, we could estimate the expectation terms by

$${\widehat{\tilde{\mathrm{\psi }}}}_{\mathrm{\tau }}({\mathbf{x}}_i,\mathit{\beta })=\frac{{\displaystyle {\sum }_{j=n_1+1}^{n_1+n_2}I({\mathbf{x}}_j={\mathbf{x}}_i){\mathrm{\psi }}_{\mathrm{\tau }}({\mathbf{x}}_j,y_j,\mathit{\beta })}}{{\displaystyle {\sum }_{j=n_1+1}^{n_1+n_2}I({\mathbf{x}}_j={\mathbf{x}}_i)}},i=1,\dots ,n_1;$$ (7)

$${\widehat{\tilde{\mathrm{\psi }}}}_{\mathrm{\tau }}({\mathbf{x}}_i,\mathit{\beta })=\frac{{\displaystyle {\sum }_{j=1}^{n_1}I({\mathbf{x}}_j={\mathbf{x}}_i){\mathrm{\psi }}_{\mathrm{\tau }}({\mathbf{x}}_j,y_j,\mathit{\beta })}}{{\displaystyle {\sum }_{j=1}^{n_1}I({\mathbf{x}}_j={\mathbf{x}}_i)}},i=n_1+1,\dots ,n$$ (8)

where I(·) is an indicator function. These are essentially the sample means of the estimating function with the same x_i but alternative diseases status. Following the law of large numbers, both estimates converge to the true expectations with $\sqrt{n}$ rate. Such applications can be found in single loci analysis in genetic studies (Kraft, 2007). In more general scenarios, especially when X includes continuous variables, the indicator function no longer produces valid estimates, since we may have very few observations at a given value of X. We propose to replace it by some suitable kernel function K_h(·) with bandwidth h, and approximate the expectation by

$${\widehat{\tilde{\mathrm{\psi }}}}_{\mathrm{\tau }}({\mathbf{x}}_i,\mathit{\beta })=\frac{{\displaystyle {\sum }_{j=n_1+1}^{n_1+n_2}{K}_h(\Vert {\mathbf{x}}_j-{\mathbf{x}}_i\Vert ){\mathrm{\psi }}_{\mathrm{\tau }}({\mathbf{x}}_j,y_j,\mathit{\beta })}}{{\displaystyle {\sum }_{j=n_1+1}^{n_1+n_2}{K}_h(\Vert {\mathbf{x}}_j-{\mathbf{x}}_i\Vert )}},i=1,\dots ,n_1;$$ (9)

$${\widehat{\tilde{\mathrm{\psi }}}}_{\mathrm{\tau }}({\mathbf{x}}_i,\mathit{\beta })=\frac{{\displaystyle {\sum }_{j=1}^{n_1}{K}_h(\Vert {\mathbf{x}}_j-{\mathbf{x}}_i\Vert ){\mathrm{\psi }}_{\mathrm{\tau }}({\mathbf{x}}_j,y_j,\mathit{\beta })}}{{\displaystyle {\sum }_{j=1}^{n_1}{K}_h(\Vert {\mathbf{x}}_j-{\mathbf{x}}_i\Vert )}},i=n_1+1,\dots ,n$$ (10)

With the estimated ${\tilde{\mathrm{\psi }}}_{\mathrm{\tau }}({\mathbf{x}}_i,\mathit{\beta })$, we can assemble the working estimating equations

$${\widehat{S}}_{n,\mathrm{\tau }}(\mathit{\beta })={\displaystyle \sum _{i=1}^n{\mathrm{\psi }}_{\mathrm{\tau }}}({\mathbf{x}}_i,y_i,\mathit{\beta })p(d_i|{\mathbf{x}}_i)+{\widehat{\tilde{\mathrm{\psi }}}}_{\mathrm{\tau }}({\mathbf{x}}_i,\mathit{\beta })p(1-d_i|{\mathbf{x}}_i)=0.$$ (11)

Note that the estimates in (7) – (10) are linear functions of the original quantile regression estimating functions. Hence one could reorganize the estimating functions (11) as

$${\widehat{S}}_{n,\mathrm{\tau }}(\mathit{\beta })={\displaystyle \sum _{i=1}^{n_1}{w}_i{\mathrm{\psi }}_{\mathrm{\tau }}}({\mathbf{x}}_i,y_i,\mathit{\beta })+{\displaystyle \sum _{j=n_1+1}^n{w}_j{\mathrm{\psi }}_{\mathrm{\tau }}({\mathbf{x}}_j,y_j,\mathit{\beta })}$$

where $w_i=p(d_i=1|{\mathbf{x}}_i)+{\displaystyle {\sum }_{j=n_1+1}^{n_1+n_2}\frac{K_h(\Vert {\mathbf{x}}_j-{\mathbf{x}}_i\Vert )p(d_j=1|{\mathbf{x}}_j)}{{\displaystyle {\sum }_{i=1}^{n_1}{K}_h({\mathbf{x}}_j={\mathbf{x}}_i)}}}$ and $w_i=p(d_i=0|{\mathbf{x}}_j)+{\displaystyle {\sum }_{i=1}^{n_1}\frac{K_h(\Vert {\mathbf{x}}_j-{\mathbf{x}}_i\Vert )p(d_i=0|x_i)}{{\displaystyle {\sum }_{j=n_1+1}^n{K}_h(\Vert {\mathbf{x}}_j-{\mathbf{x}}_i\Vert )}}}$. Since the weights w_i are not functions of β, solving the working estimating equations is equivalent to a weighted quantile regression and is computationally straightforward. We denote the resulting estimator as ${\tilde{\mathit{\beta }}}_{n,\mathrm{\tau }}$.

Finally, to choose an optimal bandwidth or a kernel function in (9), we propose to use K-fold cross-validation. Specifically, we randomly partition the data into K subsets and denote ${\widehat{\beta }}^{(-\ell )}(h)$ as the estimated quantile coefficients using bandwidth h without the the ℓth subset of data, ℓ = 1, …, K. The optimal bandwidth is defined as

$$h^{\mathit{opt}}=\arg \underset{h}{\min }{\displaystyle \sum _{\ell =1}^K\left[{\displaystyle \sum _{i\in C_{\ell }}{w}_i{\rho }_{\mathrm{\tau }}\{{\mathbf{x}}_i,y_i,{\widehat{\beta }}^{(-\ell )}(h)\}+{\displaystyle \sum _{j\in {\mathrm{\Gamma }}_{\ell }}{w}_j{\rho }_{\mathrm{\tau }}\{{\mathbf{x}}_j,y_j,{\widehat{\beta }}^{(-\ell )}(h)\}}}\right]},$$

where C_ℓ is the index set for the ℓ-th case subset, Γ_ℓ is the index set for the ℓ-th control subset, and ρ_τ(x, y, β) = (y − x^⊤ β)(τ − I {y − x^⊤ β < 0}) is the quantile regression objective function. Essentially, we choose the bandwidth that minimizes the weighted cross-validated quantile regression loss functions. In Supplementary Material, we present additional numerical studies to investigate the impacts by the choice of bandwidth and the proposed CV-based bandwidth selection.

We call ${\stackrel{\sim }{\mathit{\beta }}}_{n,\mathrm{\tau }}$ in Approach B as the KS estimates, since the kernel smoothing technique is used to approximate the estimating function. When the dimension of x increases or when covariate space is sparse, the kernel smoothing in the approach B could be difficult due to the curse of dimensionality. Approach A avoids the smoothing, and hence is readily applicable for any dimension of x. However, it makes a stronger assumption that linear quantile model holds for the entire quantile process. This assumption could be relaxed by using more general models such as semiparametric partly linear models.

2.5 Sample estimation of p(d_i | x_i)

In both approaches, we need to estimate the conditional disease probability p(d_i | x_i) and assume a logistic model

$$P(D=1|\mathbf{X})=\exp ({\gamma }_0+{\mathbf{X}}^{\top }{\mathbf{\gamma }}_1)/\{1+\exp ({\gamma }_0+{\mathbf{X}}^{\top }{\mathbf{\gamma }}_1)\}.$$ (12)

Note that model (12) is a working model to approximate the distribution of disease given X and may differ from the true disease model because the secondary outcome Y may also affect disease risk. In our simulation study in later section, we generate the data from logit {P(D = 1|X, Y)} = γ₀ + X^⊤γ₁ + Y γ₁. When disease prevalence low, which is one of the main reasons to employ a case-control design, P(D = 1|X, Y) = exp(γ₀ +X^⊤γ₁ + Y γ₁)/{1+exp(γ₀ +X^⊤γ₁ + Y γ₁ ≈ exp{γ₀ + X^⊤γ₁ + Y γ₁}. Consequently, the logistic model also holds for P(D = 1|X) if Y follows an exponential family distribution.

Further note that the intercept γ₀ cannot be consistently estimated directly from the case-control data, and needs to be re-calibrated to yield valid estimation of p(d_i | x_i) (Prentice and Pyke, 1979). Assuming that the overall disease prevalence in the general population, denoted by P₀, is known, we can estimate γ₀ by solving the following equation

$$P_0={\displaystyle {\int }_{\mathrm{x}}\exp ({\gamma }_0+{\mathbf{X}}^{\top }{\widehat{\mathbf{\gamma }}}_1)/\{1+\exp ({\gamma }_0+{\mathbf{X}}^{\top }{\widehat{\mathbf{\gamma }}}_1)}d{F}_{\mathrm{x}},$$ (13)

where F_x is the joint distribution of X, and ${\widehat{\gamma }}_1$ is the estimated slope from the case-control sample. When the covariate X is of high dimension, the joint distribution F_x is difficult to obtain. In this case, we propose to approximate γ₀ by solving its sample version:

$${\widehat{\gamma }}_0=\arg \underset{\gamma 0}{\min }{(P_0-n^{-1}{\displaystyle \sum _{i=1}^n}\exp ({\gamma }_0+{\mathbf{x}}_i^{\top }{\widehat{\mathbf{\gamma }}}_1)/\{1+\exp ({\gamma }_0+{\mathbf{x}}_i^{\top }{\widehat{\mathbf{\gamma }}}_1))}^2$$ (14)

Both (13) and (14) are univariate optimization. Therefore, obtaining ${\widehat{\gamma }}_0$ from either equation is computationally easy. The estimate of the conditional disease probability p(d_i | x_i) can be written as $\widehat{p}(d_i|{\mathbf{x}}_i)=\exp ({\widehat{\gamma }}_0+{\mathbf{x}}_i^{\top }{\widehat{\mathbf{\gamma }}}_1)/\{1+\exp ({\widehat{\gamma }}_0+{\mathbf{x}}_i^{\top }{\widehat{\mathbf{\gamma }}}_1)\}$.

2.6 Large sample properties of the proposed estimators

In this section, we establish the large sample properties of the proposed SICO estimator ${\widehat{\mathit{\beta }}}_{n,\mathrm{\tau }}$ and KS estimator ${\tilde{\mathit{\beta }}}_{n,\mathrm{\tau }}$. We first make the following assumptions.

Assumption 1

There exists a compact set Θ ⊂ R^p such that the true coefficient β_0,τ ∈ Θ is the unique solution to the estimating equations (2).

Assumption 2

The covariate x has bounded support $\mathcal{X}$, and there exists a consistent estimator of p(d_i | x_i) such that ${\max }_i|\widehat{p}(d_i|{\mathbf{x}}_i)-p(d_i|{\mathbf{x}}_i)|=o_p(1)$.

Assumption 1 is the identifiability condition, and commonly assumed in Z- and M- estimations. If p(d_i | x_i) truly follows a logistic model, Assumption 2 is satisfied readily. These assumptions lead to the estimation consistency. Recall that x^⊤β₀(τ | 0) is the conditional quantile function of y given x among controls, and x^⊤β₀(τ | 1) is that among disease population. We define a quantile density functional $h(\mathrm{\tau };\mathbf{x}|d)=1/\{{\mathbf{x}}^{\top }{{\mathit{\beta }}^{\prime }}_0(\mathrm{\tau }|d)\}$, and introduce smoothness condition on β₀(τ | d).

Assumption 3

The true coefficient functions β₀(τ | d) are smooth functions on (0, 1), and for d = 0, 1 and any x,

1. 0 < h(τ; x | d) < ∞, and lim_τ→0 h(τ; x | d) = lim_τ→1 h(τ; x | d) = 0;

2. there exist constants M and ν₁, ν₂ > −1 such that the first derivative of h(·) is bounded in a sense that

$$\underset{x}{\sup }|h^{\prime }(\mathrm{\tau };\mathbf{x}|d)|<M{\mathrm{\tau }}^{v_1}{(1-\mathrm{\tau })}^{v_2}.$$ (15)

Assumption 3 is used to achieve the uniform convergency of the estimated quantile coefficient process $\widehat{\beta }(\mathrm{\tau }|1)$ and $\widehat{\beta }(\mathrm{\tau }|0)$. Similar assumptions were used in Wei and Carroll (2009) and Wei, Ma and Carroll (2011). Condition 3(i) basically assumes that the conditional density f (y | x, d) is continuous, bounded away from zero and infinity, and diminishes to zero as τ goes to 0 and 1, while Condition 3(ii) is on the tail behavior of f (y | x, d), since h^′(τ; x | d) determines how smooth the density function diminishes as the quantile level goes to zero and one. The smaller ν₁ and ν₂, the heavier the tails of the condition distribution of y given x. Condition (15) covers a wide range of distributions, such as exponential, Gaussian and the student-t distributions. Assumptions 1–3 together ensure the consistency of ${\widehat{\mathit{\beta }}}_{n,\mathrm{\tau }}$. In what follows, we state the assumptions for the asymptotic normality.

We define the following matrixes.

$$G_n=n^{-1}{\displaystyle \sum _{i=1}^n\left[f_{y_i}({\mathbf{x}}_i^{\top }{\mathit{\beta }}_{0,\mathrm{\tau }})p(d_i|{\mathbf{x}}_i)+f_{{\stackrel{\sim }{y}}_i}({\mathbf{x}}_i^{\top }{\mathit{\beta }}_{0,\mathrm{\tau }})p(1-d_i|{\mathbf{x}}_i)\right]{\mathbf{x}}_i{\mathbf{x}}_i^{\top }},$$

where $f_{y_i}({\mathbf{x}}_i^{\top }{\mathit{\beta }}_{0,\mathrm{\tau }})$ is the density of y_i evaluated at ${\mathbf{x}}_i^{\top }{\mathit{\beta }}_{0,\mathrm{\tau }}$, and $f_{{\stackrel{\sim }{y}}_i}({\mathbf{x}}_i^{\top }{\mathit{\beta }}_{0,\mathrm{\tau }})$ is the density of counter-factual ỹ_i at ${\mathbf{x}}_i^{\top }{\mathit{\beta }}_{0,\mathrm{\tau }}$.

$$\begin{array}{c}{V}_{n,1}=n^{-1}{\displaystyle \sum _{i=1}^n\mathrm{var}\left\{{\mathrm{\psi }}_{\mathrm{\tau }}(y_i,{\mathbf{x}}_i,{\mathit{\beta }}_{0,\mathrm{\tau }})p(d_i|{\mathbf{x}}_i)\right\}}\\ V_{n,2}=n^{-1}{\displaystyle \sum _{i=1}^n\mathrm{var}\left\{{\mathrm{\psi }}_{\mathrm{\tau }}({\widehat{\stackrel{\sim }{y}}}_i^{(\ell )},{\mathbf{x}}_i,{\mathit{\beta }}_{0,\mathrm{\tau }})p(1-d_i|{\mathbf{x}}_i)\right\}}\\ U_{n,1}=n^{-1}{\displaystyle \sum _{i=1}^n\mathrm{cov}\left\{{\mathrm{\psi }}_{\mathrm{\tau }}(y_i,{\mathbf{x}}_i,{\mathit{\beta }}_{0,\mathrm{\tau }})p(d_i|{\mathbf{x}}_i),{\mathrm{\psi }}_{\mathrm{\tau }}({\widehat{\stackrel{\sim }{y}}}_i^{(\ell )},{\mathbf{x}}_i,{\mathit{\beta }}_{0,\mathrm{\tau }})p(1-d_i|{\mathbf{x}}_i)\right\}}\\ U_{n,2}=n^{-1}{\displaystyle \sum _{i=1}^n{\mathrm{cov}}_{\ell \ne {\ell }^{\prime }}\left\{{\mathrm{\psi }}_{\mathrm{\tau }}({\widehat{\stackrel{\sim }{y}}}_i^{(\ell )},{\mathbf{x}}_i,{\mathit{\beta }}_{0,\mathrm{\tau }})p(1-d_i|{\mathbf{x}}_i),{\mathrm{\psi }}_{\mathrm{\tau }}({\widehat{\stackrel{\sim }{y}}}_i^{(\ell )},{\mathbf{x}}_i,{\mathit{\beta }}_{0,\mathrm{\tau }})p(1-d_i|{\mathbf{x}}_i)\right\}}\end{array}$$

We then assume that.

Assumption 4

There exists a positive definite matrix G₀, such that G_n → G₀ in probability as n goes to infinity.

Assumption 5

There exists non-negative definite matrixes V₁, V₂, U₁ and U₂, such that lim_n→∞ V_n,1 = V₁, lim_n→∞ V_n,2 = V₂, lim_n→∞ U_n,1 = U₁, lim_n→∞ U_n,2 = U₂.

Theorem 2.1

Under Assumptions 1–5, for k_n → ∞ and k_n/n→0, we have

$$\sqrt{n}({\widehat{\mathit{\beta }}}_{n,\mathrm{\tau }}-{\mathit{\beta }}_{n,\mathrm{\tau }})\to N(0,G_0^{-1}{\sum }_0{G}_0^{-1}),$$

where Σ₀ = V₁ + m⁻¹ V₂ + 2U₁ + {(m − 1)/m}U₂

To establish the asymptotic propertiess for KS estimates ${\stackrel{\sim }{\mathit{\beta }}}_{n,\mathrm{\tau }}$, Assumptions 3 and 5 need to be modified into the following assumptions.

Assumption 3*

The conditional density of the outcome Y given (X, D) is absolutely continuous with bounded second derivative.

Assumption 5*

Let V_n = n⁻¹ var{S_n,τ(β_0,τ)}. We assume that there exists a nonnegative definite matrix V₀ such that lim_n→∞ V_n = V₀.

Theorem 2.2

When h = o(n^−1/5), n → ∞, and nh → ∞, the following statements hold under Assumptions 1, 2, 3*, 4 and 5*,

$$\sqrt{n}({\widehat{\mathit{\beta }}}_{n,\mathrm{\tau }}-{\mathit{\beta }}_{n,\mathrm{\tau }})\to N(0,G_0^{-1}{V}_0{D}_0^{-1}).$$

We here establish the theoretical properties for the proposed estimators but note that the asymptotic variances are difficult to estimate by any analytically tractable form. For our simulations and the real study application, we thus use the bootstrapping method to obtain the variance-covariance matrix of our proposed estimators.

3 Simulation Studies

3.1 Finite sample performance

In this section, we present several numerical studies to investigate the finite sample performance of the proposed estimation method with comparison to comparable existing methods. We consider the following base model with different distributions of (y_i, x_i, z_i)

$$y_i=1+0.12x_i+0.1z_i+(1+0.02x_i)e_i.$$ (16)

Under this heteroscedastic model, the covariate z has constant effect at all the quantile levels with coefficient 0.1, while the covariate effect of x is stronger on the upper quantiles than the lower ones. Specifically, the true x coefficient at the τth quantile is $0.12+0.02{\mathrm{Q}}_{e_i}(\mathrm{\tau })$. We consider the following distributions of (y_i, x_i, z_i).

• Model 1: x_i = u_i,1 + u_i,2 where u_i,1 and u_i,2 are i.i.d. Bernoulli random variables with p = 0.3. z_i ~ N(0, 1), and e_i ~ N(0, 1)

• Model 2: x_i = u_i,1 + u_i,2 where u_i,1 and u_i,2 are i.i.d. Bernoulli random variables with p = 0.3. z_i ~ N(0, 1), and $e_i\sim {\chi }_1^2/\sqrt{2}$

• Model 3: x_i ~ N(0, 1), z_i ~ N(0, 1), and e_i ~ N(0, 1)

• Model 4: x_i ~ N(0, 1), z_i ~ N(0, 1), and $e_i\sim {\chi }_1^2/\sqrt{2}$

Models (1) and (2) mimic data collected from a genetic study, where the covariate x_i is a single SNP with MAF 0.3. The outcome follows a normal distribution in Model (1) and a skewed chi-square distribution in Model (2). We scale e_i in Model (2) so that it has the same error variance as in Model (1) to standardize the signal-to-noise ratio. Models (3) and (4) consider continuous x_i with normal and skewed error distributions, respectively.

In all the models above, we also assume that the conditional disease probability

$$P(D=1|X,Z,Y)=\frac{\exp \{{\gamma }_0+\ln (1.2)X+\ln (1.2)Z+\ln (2)Y\}}{1+\exp \{{\gamma }_0+\ln (1.2)X+\ln (1.2)Z+\ln (2)Y\}},$$ (17)

and select γ₀ to make the overall disease prevalence approximately 5%. Under this setting, the odds ratio of Y for the disease is 2. Since the secondary trait Y is often biomaker for the disease, we expect strong association between Y and D, and relatively weaker associations between (X, Z) and Y. Similar settings were considered in Lin and Zeng (2009), except that they only considered a homoscedastic model, where the association between Y and X is constant across all the quantiles. When the disease prevalence is low, P(D = 1|X, Z) approximately follows a linear logistic model as well.

From each model above, we first simulate 500 cases and 500 controls to mimic a small case-control study, and then increase 2000 cases and 2000 controls for large case-control study. With each random sample, we estimate the quantile coefficients respectively at quantile levels 0.5, and 0.9 using the proposed SICO and KS estimators. For the SICO estimator, we simulate pseudo outcomes from the data with replicates m = 1, 10 and 100. In the KS estimation, we use a kernel function K_h((x₁, z₁)^⊤, (x₂, z₂)^⊤) = I(x₁ = x₂) exp {−(z₁ − z₂)²/h} for Models (1) and (2), where h is the bandwidth, and used standard Normal kernel function K_h((x₁, z₁)^⊤, (x₂, z₂)^⊤) = exp{−‖(x₁, z₁)^⊤ − (x₂, z₂)^⊤‖²/h} for Models (3) and (4). The bandwidths h is selected by the 5 fold cross-validation as in Section 2.3.2. When estimating p(D|X), we use the equation (14) with the disease prevalence of 5%. In order to show the impact from estimating p(D|X), we also recalculate the SICO and KS estimators using true p(D|X). Finally, we compare our estimates to the following approaches (1) unadjusted quantile regression (QR) using controls only; (2) unadjusted QR using cases only; (3) unadjusted QR using combined case control sample, (4) IPW approach using weights equal to 1/0.05 for all the cases, and weights 1/(1 − 0.05) for all the controls.

Tables 1 and 2 summarize the relative bias, standard errors, and mean square errors of the estimated x coefficients from various approaches. Very similar results for Models (1) and (3) can be found in Supplementary Materials. According to the tables, the estimated quantile coefficients from the three unadjusted quantile regression approaches are seriously biased in all the models. Hence, without appropriate adjustment, it is easy to miss the important factors. Both KS and SICO estimators produce fairly accurate estimates in all the models and at all the quantile levels with all the relative biases being controlled within 5%. We also compared the proposed estimates using the estimated p(D|X) to the ones using the true probabilities (results are not presented in the table), we found the differences between the two estimates are small. In these simulated data, we sample cases and controls solely depends on the disease status. As expected, the IPW also performs well in correcting the bias. The mean square errors of the SICO estimates (m >= 10) are slightly smaller than the IPW ones in all the four models. Overall, it suggests that the proposed estimating equation approach works well in performing unbiased secondary quantile analyses in case-control studies.

Table 1.

Relative bias (RB), standard error (SE) and mean squared error (MSE) of the estimated quantile coefficients under Model (2) at quantile levels of 0.5 and 0.9. In Model (2), x_i = u_i,1 + u_i,2 where u_i,1 and u_i,2 are iid bernoulli random variables with p = 0.3, z_i ~ N(0, 1), and $e_i\sim {\chi }_1^2/\sqrt{2}$ “‘QR_controls” stands for unadjusted quantile regression using controls only. “QR_cases” stands for unadjusted quantile regression using cases only. “QR_controls” are unadjusted quantile regression using both case and control samples. IPW is the estimates using inverse probability weighting; “KS” is the KS estimates using kernel smoothing. SICO(m) is the SICO estimates with m replicate.

n	Methods	τ = 0.5			τ = 0.9
		RB (%)	SE	MSE × n	RB (%)	SE	MSE × n
2000	QR_controls	−1.7	0.025	1.3	−22.3	0.102	23.2
	QR_cases	−28.8	0.086	17.4	−111.9	0.184	130.0
	QR_case-control	39.1	0.035	7.3	50.6	0.141	52.6
	IP	2.0	0.025	1.3	0.2	0.099	19.6
	KS	2.2	0.026	1.4	−0.9	0.100	19.8
	SICO (m=1)	2.7	0.028	1.6	0.0	0.108	23.1
	SICO (m=10)	2.0	0.026	1.3	0.2	0.098	19.3
	SICO (m=100)	2.1	0.025	1.3	0.5	0.096	18.5
500	QR_controls	−2.5	0.048	1.2	−19.0	0.197	19.8
	QR_cases	−34.7	0.184	17.9	−102.2	0.372	82.1
	QR_case-control	36.6	0.072	3.7	57.9	0.291	46.6
	IPW	1.3	0.049	1.2	4.3	0.201	20.2
	KS	2.6	0.051	1.3	5.0	0.204	20.7
	SICO (m=1)	2.2	0.054	1.5	8.0	0.224	25.1
	SICO (m=10)	1.5	0.048	1.2	3.5	0.198	19.5
	SICO (m=100)	1.6	0.048	1.1	2.8	0.194	18.9

Table 2.

Relative bias (RB), standard error (SE) and mean squared error (MSE) of the estimated quantile coefficients under Model (4) at quantile levels of 0.5, and 0.9. In Model (4), x_i ~ N(0, 1), z_i ~ N(0, 1), and $e_i\sim {\chi }_1^2/\sqrt{2}$. “QR_controls” stands for unadjusted quantile regression using controls only. “QR_cases” stands for unadjusted quantile regression using cases only. “QR_controls” are unadjusted quantile regression using both case and control samples. IPW is the estimates using inverse probability weighting; “KS” is the KS estimates using kernel smoothing. SICO(m) is the SICO estimates with m replicate.

n	Methods	τ = 0.5			τ = 0.9
		RB (%)	SE	MSE × n	RB (%)	SE	MSE × n
2000	QR_controls	1.7	0.017	0.6	−26.7	0.072	14.0
	QR_cases	6.9	0.069	14.4	−127.5	0.126	113.2
	QR_case-control	2.5	0.025	7.3	51.4	0.101	33.4
	IPW	2.5	0.025	1.3	0.5	0.096	18.5
	KS	2.0	0.020	0.8	−1.6	0.077	11.9
	SICO (m=1)	1.9	0.019	0.8	−3.4	0.079	12.4
	SICO (m=10)	1.8	0.018	0.6	−3.1	0.073	10.7
	SICO (m=100)	1.7	0.017	0.6	−3.1	0.071	10.0
500	QR_controls	−5.5	0.036	0.7	−27.2	0.146	11.6
	QR_cases	−36.0	0.140	10.9	−114.3	0.259	49.8
	QR_case-control	41.9	0.052	2.8	59.0	0.210	26.4
	IPW	−1.4	0.036	0.7	−0.1	0.150	11.2
	KS	−1.2	0.039	0.7	0.0	0.165	13.6
	SICO (m=1)	−1.1	0.039	0.8	−3.1	0.157	12.4
	SICO (m=10)	−1.2	0.035	0.6	−1.6	0.144	10.4
	SICO (m=100)	−1.4	0.035	0.6	−1.5	0.143	10.3

3.2 Further comparison between IPW and SICO estimates under various sampling schemes

The inverse probability weighting (IPW) technique has been widely used in secondary analysis of case-control data due to its simplicity. The validation of IPW estimates however relies on a correct specification of the selection probabilities, which are often unknown with few exceptions. In a simple scenario when the sampling only depends on the disease status, we have a representative random disease sample and a representative random control sample. In such case, the selection probability is homogeneous for all the cases and for all the controls, and IPW works well. However, when the sampling is related to the covariates or some auxiliary variables, the IPW estimates are either biased, or have low efficiency. The proposed estimates solving the estimating equations (5) are unbiased as long as y_i’s is a random sample given (d_i, x_i), hence the resulting estimates are less affected by sampling schemes. In this section, we compared the proposed and IPW estimates under the same Models (2)–(3), but two different sampling schemes. In the first sampling scheme, we over sample the cases with large X values from the disease population. In Model (2) where X is discrete and model error follows Chi-square distribution, we sample half cases with X = 2 and the rest from X = 0, 1; In Model (3) where X is continuous and model error follows Normal distribution, we over sample the extreme X values such that 40% case sample have X larger than 5. In the second sampling scheme, we assume there exists an auxiliary variable W ~ N(0, 1) that is independent of Y and X. In both case and control samples, positive W is oversampled with the selection probability 9 times that of the negative W.

Table 3 displays the relative biases, standard errors and mean square errors of the resulting SICO and IPW estimates from 500 Monte-Carlo samples. When the cases with X = 2 are over-sampled in Model (2), both IPW and proposed SICO estimates work well. When the extreme X values are over-sampled in Model (3), however, IPW estimates start to be biased. Although less severe than the IPW estimates, SICO estimates are also slightly biased in this case. The bias comes from recalibrating γ₀ following (14). When the sample distribution of X is seriously biased from that in population, the sample equation (14) with overall prevalence P₀ does not produce unbiased γ₀ estimation. Once one replaces the overall prevalence P₀ by the expected sample prevalence, the SICO estimate is no longer biased. Another way to alleviate bias is to consider profile estimation similarly as in Lin and Zeng (2009). In the second sampling scheme where positive W was over sampled, IPW estimates suffered from inflated variance and bias especially in Model (2) at quantile level 0.9. The SICO estimates are unaffected in both models.

Table 3.

Relative bias (RB), standard error (SE) and mean squared error (MSE) of the IPW and SICO estimation under Models (2) and (3) with two sampling schemes. IPW is the estimates using inverse probability weighting; and SICO(m) is the SICO estimates with m replicate.

Sampling	Estimation	τ = 0.5			τ = 0.9
		RB (%)	SE	MSE × n	RB (%)	SE	MSE × n
Model 2: Discrete X and Chi-square error
Oversample X = 2	IPW	1.5	0.025	1.3	0.5	0.097	18.9
	SICO (m=10)	1.2	0.025	1.3	−2.1	0.097	18.8
Oversample W > 0	IPW	−18.6	0.147	44.3	−106.0	0.312	251.0
	SICO (m=10)	−0.8	0.026	1.3	−1.0	0.102	20.7
Model 3: Continuous X and Normal error
Oversample X > 5	IPW	16.7	0.029	2.4	18.1	0.035	3.9
	SICO (m=10)	11.8	0.028	2.0	12.8	0.035	3.2
Oversample W > 0	IPW	10.0	0.039	3.4	3.7	0.053	5.6
	SICO (m=10)	−0.4	0.031	1.9	−2.8	0.038	2.9

3.3 When the estimated P(D|X) is biased

The proposed estimates require a consistently estimated P(D|X). In this section, we investigate the robustness of the proposed methods when the estimated P(D|X) is biased. We consider two possible reasons that could lead to the bias. One, the disease prevalence P₀ was not correctly estimated. Second, the logistic model for P(D|X) is misspecified.

We first simulate data from Model (1) in Section 3.1 and re-estimate the parameter in (16) with different disease prevalences, ranging from P₀/2 to 2P₀, where P₀ is the true prevalence. The mean relative bias and standard errors of the resulting estimates from 500 Monte-Carlo replicates are listed in Table (4). We find the estimation bias does increase slowly as the prevalence deviates from the true one, but the differences are small even when doubling P₀.

Table 4.

Relative biases (RB), standard errors (SE) and mean squared error (MSE) of the estimated quantile coefficients with disease misspecification under Model (1) at quantile levels 0.1, 0.5 and 0.9. P₀ is the true disease prevalence.

	WrongPrev	τ = 0.5			τ = 0.9
		RB (%)	SE	MSE × n	RB (%)	SE	MSE × n
KS	P0/2	−9.1	0.043	4.0	−7.9	0.059	7.2
	P0/1.5	−7.8	0.043	3.9	−6.4	0.059	7.0
	P0/1.2	−6.3	0.043	3.8	−4.4	0.058	6.7
	P0	−4.7	0.042	3.6	−2.0	0.056	6.3
	1.2P0	−3.7	0.042	3.5	−1.1	0.055	6.1
	1.5P0	−1.1	0.041	3.4	1.2	0.055	6.0
	2P0	3.4	0.040	3.3	5.2	0.052	5.5
SICO (T=10)	P0/2	−8.7	0.043	3.9	−7.5	0.058	6.9
	P0/1.5	−7.2	0.043	3.8	−5.9	0.057	6.6
	P0/1.2	−5.9	0.042	3.7	−4.2	0.056	6.4
	P0	−4.5	0.042	3.6	−2.7	0.056	6.2
	1.2P0	−2.9	0.042	3.5	−0.9	0.055	6.0
	1.5P0	−0.4	0.041	3.4	1.7	0.054	5.7
	2P0	3.4	0.040	3.3	5.8	0.052	5.4

We then consider two scenarios where the logistic model for P(D|X) is misspecified. First, we assume that the true P(D|X) follows a Probit model

$$P(d_i=1|x_i,z_i,y_i)=\mathrm{\Phi }\{-3.21+\ln (1.2)x_i+\ln (1.2)z_i+\ln (2)y_i\},$$

where Φ(·) denotes the cumulative distribution function (CDF) of the standard normal distribution. In second senerio, we use the same disease model (17) as in the earlier simulation, but disease prevalence is high, P(D|X) no longer follows a linear logistic model. Hence, we repeat the Model (2) with 10%, 20% and 30% disease prevalence rates. The results are displayed in Table (5). In all the cases, the relative biases from the SICO estimates are smaller than 4%, which indicates its robustness against the deviation from the logistic model P(D|X). The KS estimates relatively more sensitive to the bias under Model (2) with higher disease prevalence.

Table 5.

Relative biases (RB), standard errors (SE) and mean square errors (MSE*N) of the estimated quantile coefficients at quantile levels 0.1, 0.5 and 0.9 when the P(D|X) is mis-specified.

Link	Methods	τ = 0.5			τ = 0.9
		RB (%)	SE	MSE × 103	RB (%)	SE	MSE × 103
		Probit	KS	1.2%	0.047	2.2	3.9%	0.056	3.2
	SICO (m=10)	−2.6%	0.044	1.9	−2.1%	0.052	2.7
Model (2)	KS	1.5%	0.025	0.6	8.8%	0.095	9.2
(P0 = 0.1)	SICO (m=10)	−0.1%	0.024	0.6	−2.3%	0.089	8.0
Model (2)	KS	2.6%	0.022	0.5	8.5%	0.089	8.1
(P0 = 0.2)	SICO (m=10)	0.2%	0.021	0.4	−3.6%	0.081	6.6
Model (2)	KS	3.1%	0.020	0.4	12.3%	0.086	7.7
(P0 = 0.3)	SICO (m=10)	0.2%	0.019	0.4	−1.9%	0.079	6.2

4 Application to A Case-Control Genetic Association Study of Asthma

In this section, we apply our methods to study the association between the Thymic stromal lymphopoietin (TSLP) gene and asthma in a study from the New York University Bellevue Asthma Registry (Liu et al., 2011). The study consisted of 387 asthmatics and 212 healthy controls, and measured 10 tag SNPs in the TSLP gene. The secondary phenotype we considered was forced expiatory volume in one second (FEV₁), an important quantitative measure of lung function. We modeled the quantiles of FEV₁ by

$$Q_{{\mathrm{FEV}}_1}(\mathrm{\tau })={\beta }_{0,\mathrm{\tau }}+{\beta }_{2,\mathrm{\tau }}X+{\beta }_{3,\mathrm{\tau }}Z,$$ (18)

where X is the minor allele count for each of the 10 TSLP SNPs, and Z is a continuous variable derived as the first principal component score from 213 ancestry informative markers (AIMs) to adjust for population stratification. To evaluate effects of the TSLP gene variants on various levels of FEV₁, we estimated the model at quantile levels of 0.15, 0.25, 0.5, 0.75 and 0.85, respectively. Three approaches were used to estimated the quantile coefficients: the proposed KS and SICO methods, and the IPW approach. Similar to the simulation studies, we use a Gaussian kernel and select the bandwidth using 5-fold cross-validation for the KS estimates. When estimating the probability p(D|X), we calculated the overall asthma prevalence 9.1% based on 6 birth cohort studies. For comparison, we also applied the maximum likelihood method in Lin and Zeng (2009) to examine the association of mean FEV₁ with the TSLP SNPs. The resulting estimated quantile coefficients and mean regression coefficients are summarized in Table 6. All the p-values in Table 6 were calculated using bootstrap, i.e. we bootstrap cases and controls separately, and re-apply the entire estimating procedure to the bootstrap case-control sample.

Table 6.

Estimated allelic effects in the mean regression and quantile regression at quantile levels of 0.15, 0.25, 0.5, 0.75, and 0.85. The quantile coefficients are estimated using KS, SICO and IPW approaches.

SNPs	mean		MethodS	τ = 0.15		τ = 0.25		τ = 0.5		τ = 0.75		τ = 0.85
	Est.	P-value		Est.	P-value	Est.	P-value	Est.	P-value	Est.	P-value	Est.	P-value
rs2289276	0.6	0.593	KS	1.6	0.437	2.0	0.175	−0.2	0.900	0.5	0.797	1.1	0.496
			SICO(m=10)	1.1	0.157	1.8	0.007	0.0	0.999	−0.5	0.449	0.0	0.980
			IPW	2.0	0.257	1.5	0.292	−0.5	0.680	−0.3	0.877	0.3	0.865
rs1898671	0.2	0.920	KS	−2.3	0.235	−1.1	0.597	−1.2	0.585	0.7	0.740	1.6	0.391
			SICO(m=10)	−2.7	0.000	−2.2	0.003	−1.8	0.010	−0.4	0.550	1.0	0.161
			IPW	−3.1	0.176	−2.1	0.307	−0.7	0.776	0.6	0.800	1.5	0.473
rs11466741	−0.6	0.585	KS	0.1	0.950	2.4	0.144	0.2	0.884	1.7	0.318	1.2	0.373
			SICO(m=10)	0.8	0.235	2.2	0.000	0.6	0.277	1.5	0.010	1.1	0.033
			IPW	2.0	0.269	2.6	0.084	0.1	0.973	2.0	0.242	1.1	0.386
rs11466743	−8.1	0.009	KS	−17.4	0.066	−3.4	0.775	−1.4	0.824	−6.7	0.155	−7.3	0.313
			SICO(m=10)	−17.2	0.003	−6.7	0.015	−1.9	0.307	−7.5	0.000	−6.9	0.001
			IPW	−18.4	0.103	−3.9	0.733	−2.5	0.638	−6.8	0.216	−7.4	0.319
rs2289277	0.6	0.544	KS	2.5	0.198	2.5	0.039	−0.3	0.862	0.7	0.545	−0.2	0.891
			SICO(m=10)	3.0	0.000	2.6	0.000	0.2	0.797	0.5	0.309	−0.1	0.886
			IPW	3.4	0.105	2.1	0.075	−0.5	0.800	0.2	0.872	−0.5	0.637
rs2289278	3.5	0.041	KS	0.3	0.888	−1.5	0.610	6.0	0.078	2.1	0.349	0.1	0.951
			SICO(m=10)	0.5	0.691	−1.9	0.140	5.8	0.000	1.4	0.125	−0.8	0.336
			IPW	−1.2	0.641	−1.6	0.633	6.0	0.028	1.0	0.631	−0.6	0.780
rs11241090	−4.8	0.042	KS	−2.1	0.816	2.2	0.699	−1.4	0.658	−6.3	0.061	−7.1	0.147
			SICO(m=10)	−3.7	0.189	−0.3	0.900	−0.7	0.671	−5.9	0.000	−2.5	0.145
			IPW	−3.5	0.678	2.0	0.696	−2.5	0.486	−7.0	0.099	−7.2	0.222
rs10035870	−1.1	0.659	KS	−1.2	0.706	0.2	0.971	3.2	0.545	6.4	0.271	7.4	0.108
			SICO(m=10)	0.9	0.472	1.5	0.234	2.8	0.063	5.6	0.000	7.6	0.000
			IPW	−2.2	0.606	0.2	0.966	2.2	0.688	5.7	0.319	7.3	0.150
rs11466749	1.4	0.368	KS	2.5	0.226	2.3	0.246	−0.7	0.809	−1.7	0.438	−2.4	0.210
			SICO(m=10)	2.3	0.010	1.5	0.114	−0.8	0.455	−1.3	0.151	−2.5	0.003
			IPW	2.5	0.345	2.0	0.304	−0.9	0.775	−1.8	0.451	−3.0	0.197
rs11466750	−1.0	0.457	KS	0.9	0.673	0.6	0.733	0.4	0.853	−2.1	0.313	−2.4	0.218
			SICO(m=10)	0.5	0.424	0.5	0.510	0.2	0.801	−2.3	0.008	−1.9	0.003
			IPW	0.4	0.827	1.8	0.323	−1.1	0.592	−2.5	0.204	−1.6	0.406

The estimated quantile coefficients from the three approaches are comparable. However, due to the small sample size in this particular example, the bootstrap standard errors of the KS estimates and IPW estimates are much bigger than the ones from SICO estimates. Consequently, the SICO estimates are more powerful to detect the quantile associations with small sample sizes. In the following discussion, we focus on comparing the quantile based inference using SICO method to the mean regression in Lin and Zeng (2009).

From the mean coefficients output in Table 6, we observed that SNPs rs11466743, rs2289278 and rs11241090 had significant associations with mean FEV₁, with p-values of 0.009, 0.041 and 0.042, respectively. The results from quantile regressions also indicated significant association with these SNPs, and these associations remain significant even after a conservative Bonferroni correction for estimating different quantile levels and the number of SNPs. Moreover, the quantile analysis presented a more comprehensive picture on the effects of these two SNPs and suggested that the SNPs have different impact on the distribution of FEV₁. For example, having a G allele of SNP rs11241090 decreases the mean of FEV₁ value by 4.8. Based on the quantile analysis, however, this SNP has no effect on the median and lower quantiles (0.15th and 0.25-th quantiles) of FEV₁, but significantly decreases the upper 0.75th quantile of FEV₁ by 5.9. In addition, low FEV₁ indicates poor lung function and thus it is important to know the TSLP effects on the lower quartile of FEV₁. Specifically, our proposed method showed that SNPs rs2289276, rs11466741, and rs2289277 have significant association with the lower quartiles of FEV₁; however, the mean regression did not indicate significant association, illustrating the potential for the new approach to discover new associations.

Moreover, to see how genetic variants impact the distribution of FEV₁, we estimate the quantile coefficients on a fine grid of quantile levels. In Figures 1(a) and 1(b), we plotted the estimated conditional distribution functions with different genotypes at SNPs rs11466743 and rs2289277, respectively. Specifically, the solid curve in Figure 1(a) is the estimated quantile function for the patients whose genotype at rs11466743 is GG, and the dashed line is that of those whose genotype is AG/AA at rs11466743. In Figure 1(b), the solid curve is the estimated quantile function with genotype GG at rs2289277, the dashed line is that of genotype CG, and the dotted line is for genotype CC. Both SNP were found to have significant impact on the distribution of FEV₁. Based on Figure 1(a), rs11466743 has strong negative effect on both lower and upper quantiles of FEV₁, and thus subjects with the mutation allele of rs11466743 tend to have lower FEV₁ in general. In contrast, SNP rs2289277 only has strong impact on the lower quantiles, but makes little difference at the upper quantiles of FEV₁. As indicated in Figure 1(b), the subjects with genotype GG in rs2289277 are more likely to have a very low FEV₁ compared to those with genotype CC, however, they also have equal chance to have strong lung function. For example, for the subjects with rs2289277 genotype CC, the probability of FEV₁ being lower than 80, which indicates poor lung function, is nearly zero. However, for the subjects with genotype GG, this probability is nearly 20%. However, the probabilities of FEV₁ > 90 is 0.5 for all the genotypes, and the probabilities of FEV₁ > 100 are about 0.8 for all the genotypes.

Figure 1.

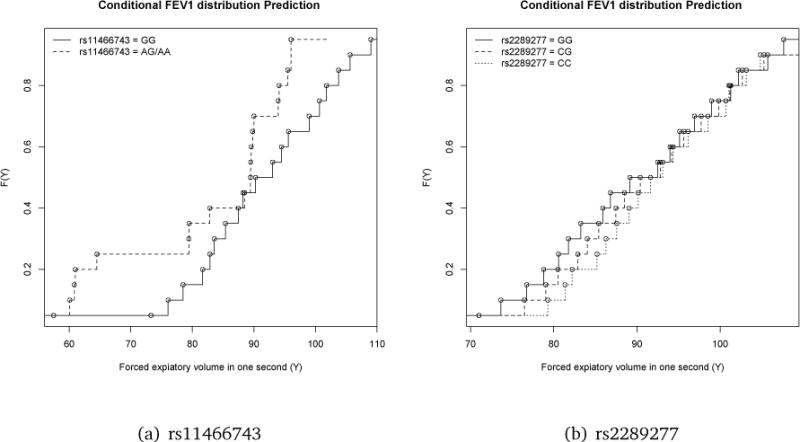
The estimated distribution functions of FEV₁ associated with SNP rs11466743 and rs2289277.

In the original case-control asthma study, we found that the SNP rs1898671 was associated with the asthma disease risk. When examining the association with the FEV₁ level, we identified different associated SNPs. Asthma is an immune disorder, and induces airway inflammation with the manifestation of poor lung function. But between disease relapses lung function may be normal or sub-normal. In addition, the reduction of spirometry measures may be caused by different disease mechanism than asthma.

5 Discussion

Quantile regression is a valuable tool to analyze secondary outcomes in existing case-control studies. It provides a comprehensive picture of the association between exposures and the secondary outcomes, and has a great potential to reveal the undiscovered pathways of disease processes. To our best knowledge, it is the first attempt to conduct secondary quantile analysis. We propose a new family of estimating equations for consistent conditional quantile estimation using case-control sample. The construction of estimating equations combines observed and counter-factual outcomes, which is a novel approach in quantile regression and also in secondary analyses. As shown in the simulation study, the proposed approaches are less affected by the sampling schemes than the IPW methods. These ideas can also be extended to construct estimating equations for other regressions, such as mean regression and generalized linear models.

The kernel smoothing technique works well with a small number of covariates. When covariates are of high dimension, or have sparse structure, it often encounters computational difficulty or bias. One natural solution is to incorporate penalty terms into the estimating functions, and select the covariates accordingly for a parsimonious model. Many penalization methods can be extended to the proposed model setting, such as the Lasso (Tibshirani, 1996), the smoothly clipped absolute deviation (SCAD) (Fan and Li, 2001), and the adaptive Lasso (Zhang and Lu, 2007). However, the theories and performance of resulting estimates need further investigation since the estimation equation involves kernel smoothing approximations. Another option is to reduce the model dimension using a propensity score approach (Rosenbaum and Rubin, 1984). Suppose X is the primary exposure of interest, and Z is a vector of controlling covariates. The propensity score is defined as a linear combination of Z^⊤θ such that X ⊥ Z conditional on Z^⊤θ. This way, one only needs to model Y against X and the propensity score Z^⊤θ to control for Z. Consequently, the model is reduced to a parsimonious two-covariate model.

The SICO estimates using simulated counter-factual outcomes from stratified conditional quantile process are easy to implement, and can be used for any dimension of model. However, one needs to assume that linear quantile models holds for the entire quantile process. This assumption could be relaxed by adopting more general semiparametric or nonparametric quantile models.