Ab initio thermodynamics of liquid and solid water

Significance

A central goal of computational physics and chemistry is to predict material properties by using first-principles methods based on the fundamental laws of quantum mechanics. However, the high computational costs of these methods typically prevent rigorous predictions of macroscopic quantities at finite temperatures, such as heat capacity, density, and chemical potential. Here, we enable such predictions by marrying advanced free-energy methods with data-driven machine-learning interatomic potentials. We show that, for the ubiquitous and technologically essential system of water, a first-principles thermodynamic description not only leads to excellent agreement with experiments, but also reveals the crucial role of nuclear quantum fluctuations in modulating the thermodynamic stabilities of different phases of water.

Abstract

Thermodynamic properties of liquid water as well as hexagonal (Ih) and cubic (Ic) ice are predicted based on density functional theory at the hybrid-functional level, rigorously taking into account quantum nuclear motion, anharmonic fluctuations, and proton disorder. This is made possible by combining advanced free-energy methods and state-of-the-art machine-learning techniques. The ab initio description leads to structural properties in excellent agreement with experiments and reliable estimates of the melting points of light and heavy water. We observe that nuclear-quantum effects contribute a crucial $0.2\hspace{0.17em}\mathrm{m}\mathrm{e}\mathrm{V}/{\mathrm{H}}_2\mathrm{O}$ to the stability of ice Ih, making it more stable than ice Ic. Our computational approach is general and transferable, providing a comprehensive framework for quantitative predictions of ab initio thermodynamic properties using machine-learning potentials as an intermediate step.

Liquid water and ice are ubiquitous on Earth, and their thermodynamic properties have important consequences in the climate system (1), the ocean, biological cells (2), refrigeration, and transportation systems. The solid phase that is stable at ambient pressure is ice Ih, whose hexagonal crystal structure is reflected in the sixfold symmetry of snowflakes. The cubic form, Ic, is a metastable ice phase whose relative stability with respect to ice Ih plays a central role in ice cloud formation in the Earth’s atmosphere (3–5) but is extremely difficult to measure experimentally (1).

Despite the simple chemical formula, ${\mathrm{H}}_2$O, theoretical predictions of the thermodynamic properties of liquid water and ice are extremely challenging. This is because of (i) the shortcomings of common water models including conventional force fields (6) and (semi-)local density functional theory (DFT) approaches (7–9), (ii) proton disorder in ice, and (iii) the importance of nuclear quantum effects (NQEs) (10). In particular, calculating the chemical potential difference $\mathrm{\Delta }{\mu }^{\text{Ih}\to \text{Ic}}={\mu }^{\text{Ic}}-{\mu }^{\text{Ih}}$ between Ic and Ih, which characterizes the relative stability, is extremely challenging because the zero-point configurational entropies (11), proton disorder (12), and harmonic vibrational energies of ice Ih and Ic (13) differ by <1 $\mathrm{m}\mathrm{e}\mathrm{V}/{\mathrm{H}}_2\mathrm{O}$, so that anharmonic quantum nuclear fluctuations play a decisive role.

Water and ice have been described with varying success by invoking approximations of differing severity, including simple electrostatic dipole models for the energetics of proton ordering (14), force-field-based path-integral molecular dynamics (PIMD) studies (15–18), first-principles quasiharmonic (QHA) (17, 19), and vibrational self-consistent field (VSCF) (13, 20) studies which provide an approximate upper bound for $\mathrm{\Delta }{\mu }^{\text{Ih}\to \text{Ic}}$. These have greatly advanced our understanding of the nature of liquid water and ice, but also highlight the harsh trade-offs between the accuracy of the description of the potential energy surface (PES) governing nuclear motion and the associated cost of sampling relevant atomistic configurations.

In this study, we make theoretical predictions of thermodynamic properties of ice and liquid water at a hybrid DFT level of theory, taking into account NQEs, proton disorder, and anharmonicity. This is made possible by exploiting advances in machine-learning (ML) techniques to avoid the prohibitively large computational expenses otherwise incurred by extensively sampling phase space by using first-principles methods. In particular, we use sophisticated thermodynamic integration (TI) techniques to accurately and rigorously compute the chemical potential difference between ice Ic and Ih and between ice Ih and liquid water.

First-Principles Thermodynamics

As the underlying electronic structure description, we use the hybrid revPBE0 (21–23) functional with a Grimme D3 dispersion correction (24, 25), which has been demonstrated to accurately predict the structure, dynamics, and spectroscopy of liquid water in molecular dynamics (MD) and PIMD simulations (26). revPBE0-D3 predicts a difference in lattice energy between the most stable proton-ordered forms of ice Ic and Ih of $U^{\mathrm{I}\mathrm{c}}-U^{\mathrm{I}\mathrm{h}}=-0.3\hspace{0.17em}\mathrm{m}\mathrm{e}\mathrm{V}/{\mathrm{H}}_2\mathrm{O}$ (see SI Appendix for further details), which is consistent with diffusion Monte Carlo predictions of $U^{\mathrm{I}\mathrm{c}}-U^{\mathrm{I}\mathrm{h}}=-0.4\pm 2.9\hspace{0.17em}\mathrm{m}\mathrm{e}\mathrm{V}/{\mathrm{H}}_2\mathrm{O}$ (12) and two different random-phase approximation predictions of $-0.2\hspace{0.17em}\mathrm{m}\mathrm{e}\mathrm{V}/{\mathrm{H}}_2\mathrm{O}$ and $0.7\hspace{0.17em}\mathrm{m}\mathrm{e}\mathrm{V}/{\mathrm{H}}_2\mathrm{O}$ (27).

Since thorough sampling of the phase space of water at the revPBE0-D3 level of theory is prohibitively expensive, we sample the phase space using a surrogate ML PES, $U_{\text{ML}}$. We then exploit the fact that the Gibbs free energy of the surrogate systems, $G_{\text{ML}}$, can be promoted to the revPBE0-D3 level of theory by using free-energy perturbation

$$\begin{array}{ccc}\hfill G\left(p,T\right)-G_{\mathrm{M}\mathrm{L}}\left(p,T\right)=-k_{\mathrm{B}}T\ln {⟨\hspace{0.17em}\exp \hspace{0.17em}\left[-\frac{U-U_{\text{ML}}}{k_{\mathrm{B}}T}\right]⟩}_{p,T,{\mathcal{H}}_{\text{ML}}},& \hfill & \hfill \\ \hfill & \hfill & \hfill \end{array}$$ [1]

where ${⟨\dots ⟩}_{p,T,{\mathcal{H}}_{\text{ML}}}$ denotes the ensemble average for the system sampled at temperature $T$ and pressure $p$ using the surrogate Hamiltonian ${\mathcal{H}}_{\text{ML}}$. Evaluation of Eq. 1 is rendered particularly affordable and robust by the high fidelity of our surrogate ML PES, which substantially exceeds that obtained from empirical force fields or local DFT calculations, which were previously used as implicit surrogates (28, 29). Eq. 1 is the central formula of our approach: It not only enables accurate and efficient free-energy estimation at the ab initio level by delegating phase-space sampling to cheap surrogate models, but also provides a general way for benchmarking and calibrating the ML potentials.

Neural Network Potential for Water

We constructed a flexible and fully dissociable neural network (NN) potential for bulk liquid water and ice following the framework of Behler and Parrinello (30–32) using the RuNNer code (33), which was trained on the basis of revPBE0-D3 energies and forces for 1,593 diverse reference structures of 64 molecules of liquid water computed by using the CP2K package (34). Further details regarding the DFT calculations, comparison with the energies computed by using VASP (35), and the training and validation of the NN potential can be found in SI Appendix. We have released this NN potential along with its training set (SI Appendix, Datasets S1 and S2).

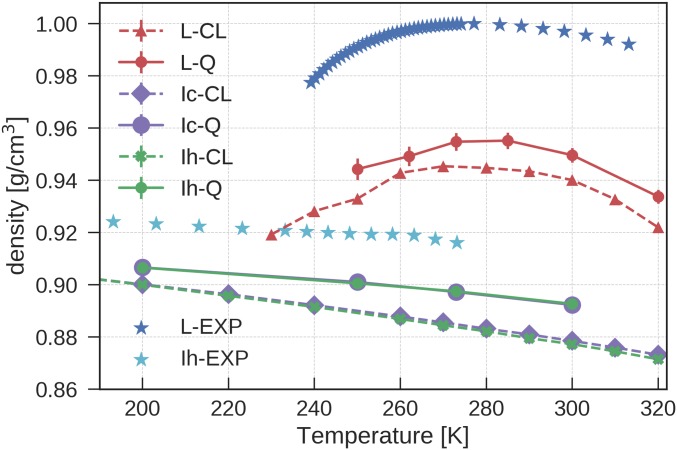
The revPBE0-D3-based NN potential describes the density (Fig. 1) and structural properties of water (Fig. 2) in very good agreement with experiments. Fig. 1 shows density isobars computed for ice Ic, ice Ih, and liquid water considering both the case of classical and quantum-mechanical nuclei. Fig. 1 highlights that (i) the predicted densities of liquid water and ice Ih and Ic agree with experiment to within 3%; (ii) the predicted thermal expansion coefficients show excellent agreement with experimental data; and (iii) the temperature of maximum density for liquid water matches the experimental value of $3.98\hspace{0.17em}°$C. It also shows that NQEs lead to an increase of $\sim$1% in the density of the three phases of water. This anomalous increase for the ice Ih phase has been observed in previous QHA calculations by using a number of different DFT functionals (17). Experimentally, the suppression of NQEs can be partially achieved by deuteration, and it has been observed that the molar volume of ${\mathrm{D}}_2$O is 0.4% (40) larger compared with ${\mathrm{H}}_2$O for liquid water at the ambient temperature and $\sim$0.3% larger for hexagonal ice at 250 K (41).

Fig. 1.

Classical (CL) and quantum (Q) density isobars for ice Ic, ice Ih, and liquid water (L) at $P=1$ bar computed via (PI)MD simulations using the NN potential. The predicted densities of ice Ic and Ih almost overlap both at the quantum and the classical level. The experimental results for undercooled water are taken from ref. 36.

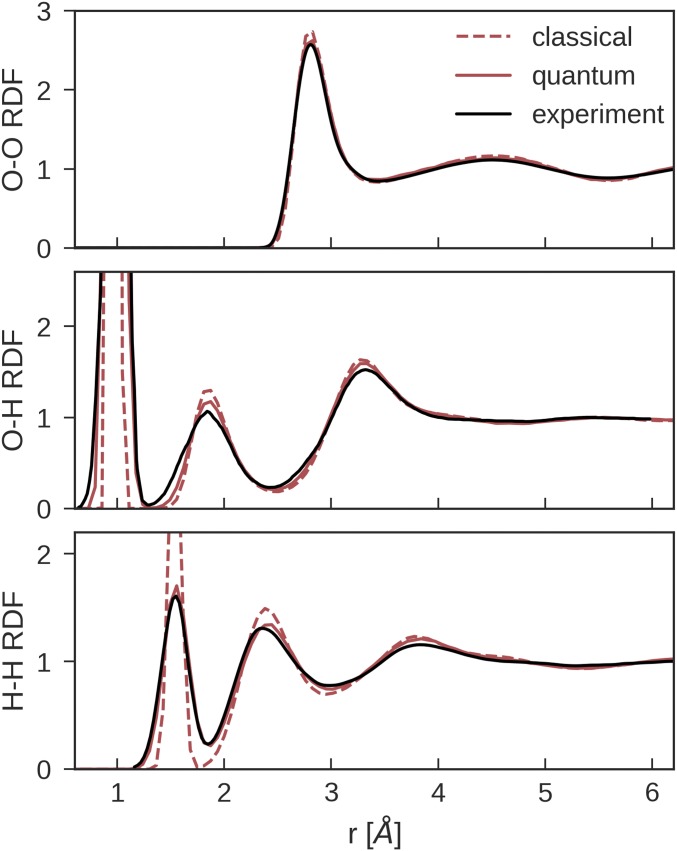
Fig. 2.

Oxygen–oxygen, oxygen–hydrogen, and hydrogen–hydrogen RDFs at 300 K and experimental density computed via (PI)MD simulations in the constant number of particles, volume, and temperature (NVT) ensemble using the NN potential. The experimental O–O RDF was obtained from ref. 37, and the experimental O–H and H–H RDFs were taken from refs. 38 and 39.

Fig. 2, Top, shows that NQEs have a slight destructuring effect on the oxygen–oxygen (O–O) radial distribution function (RDF), bringing it in excellent agreement with experiments from X-ray diffraction measurements (37), as also seen in the ab initio (PI)MD calculations with revPBE0-D3 (26). This destructuring has been observed in simulations using other DFT functionals (42) as well as empirical water models (43, 44) and was rationalized as a result of competing quantum effects (16, 45). Fig. 2, Middle and Bottom, further shows that NQEs cause a significant broadening of the oxygen–hydrogen (O–H) and hydrogen–hydrogen (H–H) RDFs, especially around their respective first peaks, which plays a predominant role in ensuring the match between the simulations and experiment. It is worth noting that the agreement between the NN and the experimental RDFs in Fig. 2 is significantly better compared with most benchmarked empirical water models and DFT functionals (46, 47).

Promoting ML Potential to DFT

Despite the excellent performance of the NN potential, the fitting strategy, the finite cutoff radii applied to the description of atomic environments, and possible “holes” in the training set (48) inevitably lead to small residual errors compared with the underlying first-principles reference. To assess their significance, we have trained a collection of NN potentials using different training sets and/or initial random seeds, which demonstrates that predictions of the chemical potential difference between ice Ic and Ih from two different NN potentials can be as large as $1\hspace{0.17em}\mathrm{m}\mathrm{e}\mathrm{V}/{\mathrm{H}}_2\mathrm{O}$ (SI Appendix, Fig. S4 for further detail). Promoting the results to the DFT level eliminates these residual errors and any dependence on the specific NN potential used. This allows us to achieve submillielectronvolt accuracy in free energies (as required to resolve the greater stability of ice Ih compared with Ic) and to make unbiased properties predictions at the reference ab initio level of theory in general.

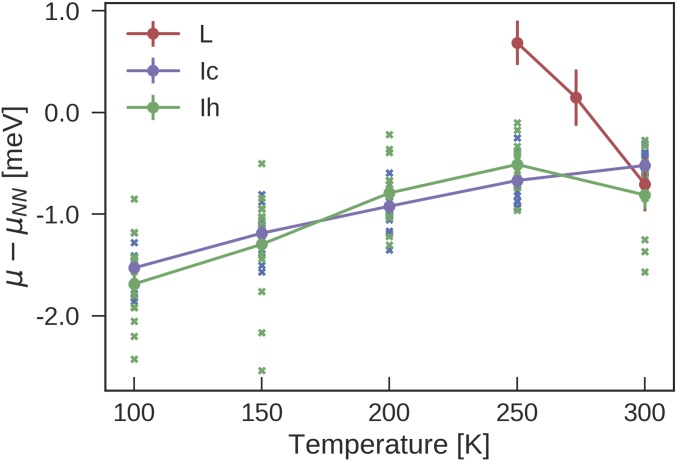
The temperature-dependent DFT corrections to the NN chemical potentials of different phases of water, $\mathrm{\Delta }{\mu }_{NN}\equiv \mu -{\mu }_{\mathrm{N}\mathrm{N}}=\left(G-G_{\text{NN}}\right)/N$, as obtained from free-energy perturbations (Eq. 1) performed on 64-molecule systems, are shown in Fig. 3. For each ice phase (Ic and Ih), 16 different proton-disordered initial configurations with zero net polarization are generated by using the Hydrogen-Disordered Ice Generator (49). The SD of the potential energy for the 16 proton-disordered ice Ic configurations is $0.3\hspace{0.17em}\mathrm{m}\mathrm{e}\mathrm{V}/{\mathrm{H}}_2\mathrm{O}$ ($0.25\hspace{0.17em}\mathrm{m}\mathrm{e}\mathrm{V}/{\mathrm{H}}_2\mathrm{O}$) by using the NN potential (DFT), respectively. For ice Ih, it is $0.4\hspace{0.17em}\mathrm{m}\mathrm{e}\mathrm{V}/{\mathrm{H}}_2\mathrm{O}$ ($0.25\hspace{0.17em}\mathrm{m}\mathrm{e}\mathrm{V}/{\mathrm{H}}_2\mathrm{O}$) by using the NN potential (DFT). Starting from these different initial configurations is crucial here, because (i) the proton order is effectively “frozen-in” at the timescales available to simulation (50) and (ii) there are significant differences between $\mathrm{\Delta }{\mu }_{NN}$ of different proton-disordered states (Fig. 3). For liquid water, 1,000 single-point revPBE0-D3 calculations for uncorrelated configurations generated from NN-based NPT simulations suffice to converge the value of the calibration term $\mathrm{\Delta }{\mu }_{NN}^{\mathrm{L}}$ to $\sim 0.2\hspace{0.17em}\mathrm{m}\mathrm{e}\mathrm{V}/{\mathrm{H}}_2\mathrm{O}$. For each proton-disordered ice structure, 200 such single-point calculations are enough to converge $\mathrm{\Delta }{\mu }_{NN}^{\mathrm{I}\mathrm{c}}$ and $\mathrm{\Delta }{\mu }_{NN}^{\mathrm{I}\mathrm{h}}$ to $0.1\hspace{0.17em}\mathrm{m}\mathrm{e}\mathrm{V}/{\mathrm{H}}_2\mathrm{O}$.

Fig. 3.

The difference in the chemical potential $\mathrm{\Delta }{\mu }_{\mathrm{N}\mathrm{N}}\equiv \mu -{\mu }_{\mathrm{N}\mathrm{N}}$ between revPBE0-D3 and NN-based MD simulations at $P=1\hspace{0.17em}\mathrm{b}\mathrm{a}\mathrm{r}$. Standard errors of the mean are indicated by the error bars. The violet (green) crosses indicate the results from 16 different 64-molecule proton-orderings of Ic (Ih). The violet (green) line shows the average $\mathrm{\Delta }{\mu }_{\mathrm{N}\mathrm{N}}$ across proton orderings.

Results and Discussion

The Relative Stability of Hexagonal and Cubic Ice.

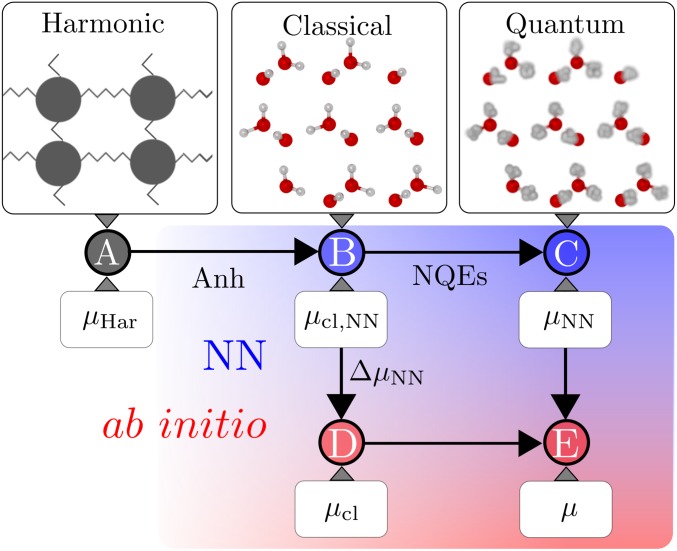
We follow the workflow in Materials and Methods (see Fig. 7 for illustration) to evaluate the chemical potential difference $\mathrm{\Delta }{\mu }^{\text{Ih}\to \text{Ic}}$ at the revPBE0-D3 level of theory, taking into account nuclear quantum fluctuations. We first compute the classical absolute free energies of the two ice phases at the NN level using the TI methods described in ref. 51 and thereby the corresponding chemical potential difference $\mathrm{\Delta }{\mu }_{\text{cl,NN}}^{\text{Ih}\to \text{Ic}}$. The classical chemical potential difference between ice Ih and Ic at the revPBE0-D3 level can then be evaluated as $\mathrm{\Delta }{\mu }_{\text{cl}}^{\text{Ih}\to \text{Ic}}=\mathrm{\Delta }{\mu }_{\text{cl,NN}}^{\text{Ih}\to \text{Ic}}+\mathrm{\Delta }{\mu }_{NN}^{Ic}-\mathrm{\Delta }{\mu }_{NN}^{Ih}$.

Fig. 7.

A schematic of the TI workflow, which starts from a harmonic reference crystal, uses a NN description as an intermediate step, and finally arrives at the underlying ab initio level. The chemical potentials indicated here are related to the absolute Gibbs free energy of the systems by $\mu \equiv G/N$.

Note that the speed and linear scaling of the NN potential allow us to simulate ice systems containing as many as 768 water molecules. Such system size is not only essential to represent the wide spectrum of possible local arrangements realized in proton-disordered ice, but also important for averaging over different proton-disordered structures when correcting for the chemical differences between the NN potential and revPBE0-D3, as demonstrated by the spread of $\mathrm{\Delta }{\mu }_{NN}$ between different structures in Fig. 3.

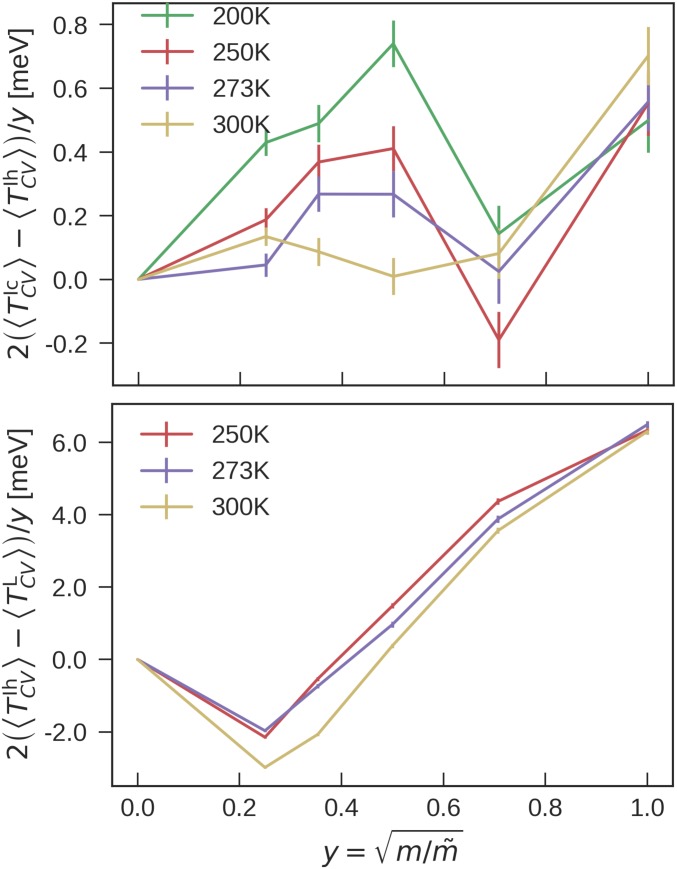
NQEs are taken into account by integrating the quantum centroid virial kinetic energy $⟨T_{CV}⟩$ with respect to the fictitious “atomic” mass from the classical (i.e., infinite) mass to the physical masses of oxygen and hydrogen atoms (Materials and Methods and see Fig. 6). We perform NN-based PIMD simulations within the NPT ensemble and assess the impact of NQEs on the chemical potential at the NN level using $\mathrm{\Delta }{\mu }_{\text{NN}}^{\text{Ih}\to \text{Ic}}-\mathrm{\Delta }{\mu }_{\text{cl,NN}}^{\text{Ih}\to \text{Ic}}$. We note that the NN potential is not “biased” toward Ic or Ih, as the NN to revPBE0-D3 calibration terms $\mathrm{\Delta }{\mu }_{NN}^{\mathrm{I}\mathrm{c}}$ and $\mathrm{\Delta }{\mu }_{NN}^{\mathrm{I}\mathrm{h}}$ are similar (Fig. 3), and that the difference in $⟨T_{CV}⟩$ of difference water phases is found to be very similar for three completely different interatomic potentials (18). Combining all of these terms, we finally arrive at the result $\mathrm{\Delta }{\mu }^{\text{Ih}\to \text{Ic}}=\mathrm{\Delta }{\mu }_{\text{cl}}^{\text{Ih}\to \text{Ic}}+\mathrm{\Delta }{\mu }_{\text{NN}}^{\text{Ih}\to \text{Ic}}-\mathrm{\Delta }{\mu }_{\text{cl,NN}}^{\text{Ih}\to \text{Ic}}$.

Fig. 6.

The integral from the classical limit to the full quantum treatment (Eq. 3), for the case of ice Ic and Ih (Upper) and ice Ih and liquid water (Lower).

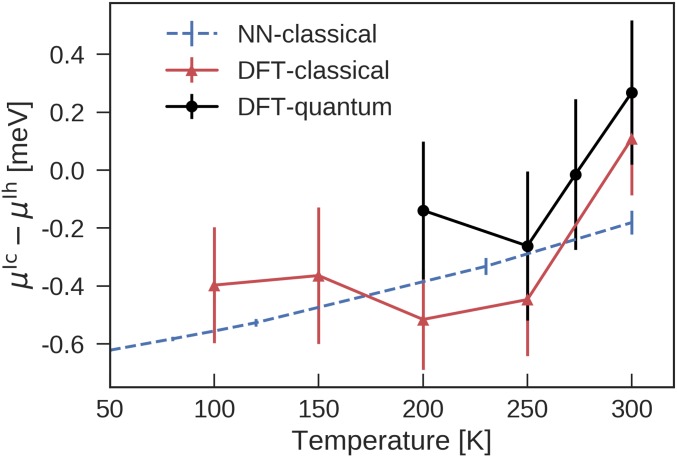
Fig. 4 shows that the NN predictions of $\mathrm{\Delta }{\mu }^{\text{Ih}\to \text{Ic}}$ and the revPBE0-D3 results are statistically indistinguishable. At the classical level, $\mathrm{\Delta }{\mu }_{\text{cl}}^{\text{Ih}\to \text{Ic}}$ is negative, especially at low temperatures. Consistent with the VSCF results of ref. 13, proton disorder introduces substantial variations in the chemical potential of ice Ic and Ih. More importantly, nuclear quantum fluctuations are crucial to stabilize ice Ih. At the quantum-mechanical level $\mathrm{\Delta }{\mu }^{\text{Ih}\to \text{Ic}}$ is close to zero at 200–250 K and increases to $0.2\pm 0.2\hspace{0.17em}\mathrm{m}\mathrm{e}\mathrm{V}/{\mathrm{H}}_2\mathrm{O}$ at 300 K, suggesting that ice Ih is more stable after all. For comparison, at the classical level, the monoatomic water model (52)—which omits hydrogen atoms—predicts a negligible difference [$\mathrm{\Delta }{\mu }^{\text{Ih}\to \text{Ic}}\left(240\hspace{0.17em}K\right)=0.032\pm 0.002\hspace{0.17em}\mathrm{\text{meV}}$ (53)], while the MB-pol force field (54), which includes many-body terms fitted to the coupled-clusters level of theory, predicts a small negative value ($-0.4\hspace{0.17em}\mathrm{m}\mathrm{e}\mathrm{V}/{\mathrm{H}}_2\mathrm{O}$) (see SI Appendix for further details). Assuming that the heat of transition from ice Ic to ice Ih is approximately constant over the temperature range 200–300 K, the temperature dependence of $\mathrm{\Delta }{\mu }^{\text{Ih}\to \text{Ic}}$ implies (using a TI with respect to $T$ analogous to Eq. 2) a transition enthalpy of $H^{\text{Ic}}-H^{\text{Ih}}=1.0\pm 0.5\hspace{0.17em}\mathrm{m}\mathrm{e}\mathrm{V}/{\mathrm{H}}_2\mathrm{O}$, consistent with the wide experimental range $0.1-1.7\hspace{0.17em}\mathrm{m}\mathrm{e}\mathrm{V}/{\mathrm{H}}_2\mathrm{O}$ (55).

Fig. 4.

Temperature dependence of the chemical potential difference between ice Ih and Ic at 1 bar. The errors associated with the classical and quantum-mechanical revPBE0-D3 values arise predominantly from the differences in $\mathrm{\Delta }{\mu }_{\mathrm{N}\mathrm{N}}$ between different proton orderings.

The Relative Stability of Hexagonal Ice and Liquid Water.

Now, we compute the difference in chemical potential $\mathrm{\Delta }{\mu }^{\text{L}\to \text{Ih}}={\mu }^{Ih}-{\mu }^L$ between the proton-disordered ice Ih and liquid water. The approach is, in analogy to the schematics in Fig. 7, to obtain the NN chemical potential difference before promoting it to the DFT level and adding NQEs.

We first compute $\mathrm{\Delta }{\mu }_{\text{cl,NN}}^{\text{L}\to \text{Ih}}$ using the interface-pinning method (56) in classical MD simulations with the NN potential. We then fit $\mathrm{\Delta }{\mu }_{\text{cl,NN}}^{\text{L}\to \text{Ih}}$ from independent simulations at different temperatures to the TI expression

$$\begin{array}{ccc}\hfill \mathrm{\Delta }{\mu }_{\text{cl,NN}}^{\text{L}\to \text{Ih}}\left(T\right)=-k_{BT}{\int }_{T_m}^T\frac{{⟨H_{\mathrm{c}\mathrm{l},\mathrm{N}\mathrm{N}}^{\mathrm{I}\mathrm{h}}⟩}_{P,T}-{⟨H_{\mathrm{c}\mathrm{l},\mathrm{N}\mathrm{N}}^{\mathrm{L}}⟩}_{P,T}}{k_B{T}^2}dT,& \hfill & \hfill \\ \hfill & \hfill & \hfill \end{array}$$ [2]

where $H_{cl,NN}$ is the enthalpy of the classical system described by the NN potential, whose value has been computed from separate NPT simulations (SI Appendix, Fig. S3). Afterward, the calibration terms for chemical potentials $\mathrm{\Delta }{\mu }_{\mathrm{N}\mathrm{N}}^{\mathrm{L}}$ and $\mathrm{\Delta }{\mu }_{\mathrm{N}\mathrm{N}}^{\mathrm{I}\mathrm{h}}$ (Fig. 3) are added to obtain the revPBE0-D3 predictions for the classical systems. Finally, NQEs in ${\mathrm{H}}_2$O water and ${\mathrm{D}}_2$O water are considered by performing a series of PIMD simulations at different fictitious masses using the NN potential.

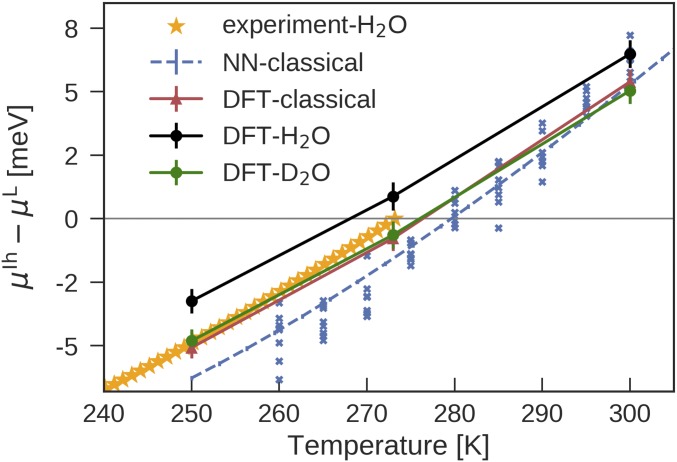
Fig. 5 shows $\mathrm{\Delta }{\mu }^{\text{L}\to \text{Ih}}$ predicted at different levels of theory along with experimental data for ${\mathrm{H}}_2$O (57). A comparison between the melting points $T_{\text{m}}$ and the heat of fusion $H_f=H^{\mathrm{L}}\left(T_{\text{m}}\right)-H^{\mathrm{I}\mathrm{h}}\left(T_{\text{m}}\right)$ of different models is provided in Table 1. For revPBE0-D3 ${\mathrm{H}}_2$O water with NQEs, the predicted $T_{\text{m}}$ has only $\sim$2% of error compared with experiment, and the values of $\mathrm{\Delta }{\mu }^{\text{L}\to \text{Ih}}$ are well within 15% of experimental values at moderate undercoolings of $<20\hspace{0.17em}$ K below $T_{\text{m}}$. $H_f$ is underestimated by using revPBE0-D3 and including NQEs, which may be due to the artifacts of the revPBE0-D3 functional or the limitations of representing proton disorders in natural ice, even when using state-of-the-art methods (49). Overall, the predictions here constitute a substantial improvement over most commonly used empirical water models (6). For instance, TIP4P models underestimate $H_f$ by 20–30% (58).

Fig. 5.

Temperature dependence of the chemical potential difference between liquid water and ice Ih at 1 bar. Blue crosses indicate $\mathrm{\Delta }{\mu }_{\text{cl,NN}}^{\text{L}\to \text{Ih}}$ from independent interface pinning simulations, and the blue dashed line indicates the best fit of these results to the TI expression in Eq. 2. The experimental values were calculated from the heat capacities reported in ref. 57.

Table 1.

Predictions of the melting point ($T_{\text{m}}$) and the heat of fusion ($H_f$)

Model	$T_{\text{m}}$, K	$H_f$, $\mathrm{m}\mathrm{e}\mathrm{V}/{\mathrm{H}}_2\mathrm{O}$
NN-classical	279.6 (4)	67.8 (2)
DFT-classical	275 (2)	58 (2)
DFT-${\mathrm{H}}_2$O	267 (2)	52 (3)
DFT-${\mathrm{D}}_2$O	275 (2)	58 (2)
Experiment-${\mathrm{H}}_2$O	273.15	62.3
Experiment-${\mathrm{D}}_2$O	276.97	64.5

The value in parentheses indicates the statistical uncertainty in the last digit.

NQEs lower the melting point of ${\mathrm{H}}_2$O by $\sim$8 K compared with classical water. The difference in $T_{\text{m}}$ between the ${\mathrm{D}}_2$O and ${\mathrm{H}}_2$O is predicted to be $8\pm 2$ K, consistent with the result obtained by using the q-TIP4P/F water model (15) and in rough agreement with experiment (3.82 K) (40). Curiously, the $T_{\text{m}}$ of ${\mathrm{D}}_2$O is about the same as the classical water. To elucidate the reason, we plot the integral when performing TI from physical masses ($m_{\mathrm{H}}$ for H) to classical masses ($\infty$) in Fig. 6. It can be seen that NQEs initially, from $m_{\mathrm{H}}$ to $\sim 6m_{\mathrm{H}}$, stabilize water relative to ice. Then, from $6m_{\mathrm{H}}$ to $\infty$, they stabilize ice. When performing TI from the atomic mass of deuterium to the classical mass, NQEs thus largely cancel out. This reversal of NQEs at different atomic masses has been observed before for q-TIP4P/F water (15) and for stacked polyglutamine (59) and has been interpreted as a manifestation of competing quantum effects.

Conclusions

We show that a revPBE0-D3 description of the electronic structure predicts properties for ice Ih, ice Ic, and liquid water that are in excellent quantitative agreement with experiment. This is made possible by using a ML potential as an intermediate surrogate model and by using advanced free-energy techniques. We not only rigorously compute but also quantitatively analyze the individual contributions from NQEs, proton disorder, and anharmonicity.

This study demonstrates that it is possible to achieve a submillielectronvolt level of statistical accuracy in predicting the thermodynamic properties of a complex system such as water at a hybrid DFT level of theory. The idea of using ML potentials as sampling devices significantly broadens the applicability and prowess of electronic-structure approaches, making it affordable to use them in the accurate computations of free energies and other thermodynamic properties. The overall framework and the free-energy methods described here provide a general, accurate, and robust way for first-principles predictions of thermodynamic properties of a plethora of physical systems, such as pharmaceutical compounds, hydrogen storage materials, hydrocarbons, and metallic alloys.

Materials and Methods

Simulation Details.

The density isobar in Fig. 1 is computed by using both classical MD and PIMD simulations in the NPT ensemble for ice Ic, ice Ih, and liquid water systems of 64 molecules. We confirm that the equilibrium density computed with 64 water molecules in classical MD simulations is consistent with the values obtained for systems with $\sim$2,000 molecules. All MD simulations and PIMD simulations that use 56 beads are performed by using the i-PI code (60) in conjunction with LAMMPS (61) with a NN potential implementation (62, 63).

Interface Pinning.

The interface pinning simulations (56) are performed by using the PLUMED code (64) on an ice–liquid system containing 5,760 molecules at temperatures ranging from 250 to 300 K and pressure 1 bar, using the NN potential.

Accounting for NQEs.

NQEs on the chemical potential difference between ice Ic and ice Ih at 200, 250, 273, and 300 K are taken into account by integrating the quantum centroid virial kinetic energy $⟨T_{CV}⟩$ with respect to the fictitious atomic mass $\tilde{m}$ from the classical mass (i.e., infinity) to the physical masses of oxygen and hydrogen atoms (18, 65–67)—that is,

$$\mathrm{\Delta }{\mu }_{\text{NN}}^{\text{Ih}\to \text{Ic}}-\mathrm{\Delta }{\mu }_{\text{cl,NN}}^{\text{Ih}\to \text{Ic}}={\int }_m^{\infty }d\tilde{m}\frac{⟨T_{CV}^{Ic}\left(\tilde{m}\right)⟩-⟨T_{CV}^{Ih}\left(\tilde{m}\right)⟩}{\tilde{m}},$$ [3]

where $m$ are the physical masses of the elements. In practice, a change of variable $y=\sqrt{m/\tilde{m}}$ is applied to reduce the discretization error in the evaluation of the integral (65), and the integrand is evaluated by using PIMD simulations for $y=1/\mathrm{4,1}/2\sqrt{2},1/\mathrm{2,1}/\sqrt{2},1$—that is,

$$\mathrm{\Delta }{\mu }_{\text{NN}}^{\text{Ih}\to \text{Ic}}-\mathrm{\Delta }{\mu }_{\text{cl,NN}}^{\text{Ih}\to \text{Ic}}=2{\int }_0^1\frac{⟨T_{CV}^{Ic}\left(1/y^2\right)⟩-⟨T_{CV}^{Ih}\left(1/y^2\right)⟩}{y}dy.$$ [4]

To evaluate this integral, we perform a PIMD simulation that uses 56 beads at the NPT ensemble for systems containing 64 molecules. For the case of ice Ih and liquid water, the treatment is similar.

Workflow for Computing $\mathrm{\Delta }{\mu }^{\text{Ih}\to \text{Ic}}$.

Here, we describe the workflow for computing absolute Gibbs free energy and thereby the chemical potential of an ice system. The first step is a TI from a harmonic reference to a classical ice system ($A\to B$ in Fig. 7). We closely follow the methods described in ref. 51: First integrate from a Debye crystal to classical ice at 25 K in the NVT ensemble, then transition to the NPT ensemble, and, finally, evaluate the temperature dependence of the Gibbs free energy by using MD simulations in the NPT ensemble at temperatures between 25 and 300 K. Subsequently, to reach the ab initio description of classical ice from the NN description ($B\to D$ in Fig. 7), the correction term $\mathrm{\Delta }{\mu }_{\text{NN}}$ (Fig. 3) computed by using the free energy perturbation expression in Eq. 1 is included. Finally, to describe ab initio ice with quantum-mechanical nuclei ($D\to E$ in Fig. 7), NQEs are included by integrating from the infinite atomic mass to the physical masses (Eq. 3). As an alternative strategy, one can also follow the TI route $A\to B\to C\to E$, but this requires reweighting the whole ring-polymer system in PIMD simulations by using Eq. 1, which is more costly.

Datasets.

The NN potential for water based on revPBE0-D3, the training set for the potential, and all necessary simulation input files are included in SI Appendix and are available at https://archive.materialscloud.org/2018.0020/v1.