Predicting RNA-Metal Ion Binding with Ion Dehydration Effects

Abstract

Metal ions play essential roles in nucleic acids folding and stability. The interaction between metal ions and nucleic acids can be highly complicated because of the interplay between various effects such as ion correlation, fluctuation, and dehydration. These effects may be particularly important for multivalent ions such as Mg²⁺ ions. Previous efforts to model ion correlation and fluctuation effects led to the development of the Monte Carlo tightly bound ion model. Here, by incorporating ion hydration/dehydration effects into the Monte Carlo tightly bound ion model, we develop a, to our knowledge, new approach to predict ion binding. The new model enables predictions for not only the number of bound ions but also the three-dimensional spatial distribution of the bound ions. Furthermore, the new model reveals several intriguing features for the bound ions such as the mutual enhancement/inhibition in ion binding between the fully hydrated (diffuse) ions, the outer-shell dehydrated ions, and the inner-shell dehydrated ions and novel features for the monovalent-divalent ion interplay due to the hydration effect.

Introduction

Metal ions, especially multivalent ions such as Mg²⁺, play essential roles in nucleic acids folding by neutralizing RNA backbone charges (1, 2, 3, 4). According to the localization of the bound ions, we can classify two types of bound ions: site-specific bound (SSB) ions and nonspecific bound (NSB) ions (5, 6). SSB ions around a nucleic acid such as an RNA are captured at specific binding sites and often involve direct interactions with the nucleic acid (5). In general, binding sites of specific bound ions usually involve pockets or cavities of the nucleic acid structure (7, 8, 9). Some of the binding sites are narrow and water inaccessible; thus, SSB ions are often partially or even fully dehydrated (10). SSB ion-binding energetics is governed by the competition between the gain in ion-RNA electrostatic and other specific interactions and the penalty of losing water molecule(s). Although SSB ions only neutralize a small fraction of negative charges on RNA backbone (11), they play critical roles in catalysis of ribozymes (12, 13, 14), bistate transition of RNA (15), docking of tetraloop-receptor complex (16), and many other processes (17, 18). In contrast, NSB ions usually remain fully hydrated and form a mobile “sheath” around the RNA (19, 20). The size of this “sheath” could extend up to 20 Å away from the surface of the RNA (21). The large amount of NSB ions leads to significant electrostatic effects for RNA folding stability (22).

With the recognition of the importance of ion binding (NSB and SSB ions) in RNA folding and stability (23, 24), different approaches have been developed to study the ion effects. Among these approaches, molecular dynamics (MD) simulation has the advantage of providing deep insight into atom-scale details for the ion-binding process (21, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43). Indeed, MD simulations have given many novel findings for ion-RNA interactions. For example, simulations have predicted the specific binding sites of the SSB ions in the 5S rRNA loop E motif (26), the hepatitis delta virus ribozyme (27), an RNA kissing loop (28), human immunodeficiency virus-1 TAR RNA (31), and locations of co-binding Mg²⁺ ions in the active site of ribozyme (38), and furthermore the Mg²⁺-ion-assisted catalysis of the ribozyme at the different steps of the reaction (40). However, the application of the MD simulation may be limited by the accuracy of the metal ion force field (44) (especially for SSB ions because of the complication in ion-RNA interactions) and the exceedingly long sampling time (28) (especially for the large number of NSB ions).

For the binding of NSB ions, an early description came from the Manning counterion condensation (CC) theory (45). The CC theory is based on an assumption that the counterions uniformly reduce the effective linear charges on the backbone of a polyelectrolyte. The simplicity of the approach is a great advantage of the CC model (46, 47, 48, 49) and, in the meantime, limits its applicability to problems for nucleic acids with complicated structures. The nonlinear Poisson-Boltzmann (NLPB) model can handle the ion effects for complicated nucleic acid structures (50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61). In NLPB calculation, all of the NSB ions interact with RNA in a “diffuse” manner like a fluid. Meanwhile, the density of the continuous NSB ions obeys the Boltzmann distribution, which is highly dependent on the RNA structure. NLPB experiment comparisons (19, 62) suggested that NLPB model could reliably treat the monovalent ion solutions but may underestimate the effect of multivalent ions such as divalent ions. Moreover, NLPB may also underestimate the ion effects for special monovalent ion solutions such as the NaF solution at a high concentration (63).

One of the possible sources that contribute to the underestimation of the multivalent ion effects by the NLPB model (and CC theory) is the neglect of ion-ion correlation and ion fluctuation effects (20, 64). For a compact tertiary structure of RNA, (NSB) ions would accumulate around the RNA, causing a high local ion concentration near the RNA surface. The high local ion concentration would cause strong ion-ion correlation (coupling) through volume exclusion and Coulombic interaction. The strongly correlated ions thus cannot be regarded as “diffuse” ions (21), and their distribution is subject to ion-ion correlation. The ion-ion correlation effect is more pronounced for multivalent ions such as Mg²⁺ or small ions such as F⁻. The ion-ion correlation is intrinsically tied to many-particle distributions of the ions; therefore, the calculation for correlated ions inevitably requires the sampling of discrete many-ion distributions and, equivalently, fluctuations of ion distributions.

Significant efforts have been directed toward developing models that can treat ion-ion correlation effect in ion-RNA interactions (65, 66, 67), such as the generalized Manning condensation (GMC) model (68), the three-dimensional reference interaction site (3D-RISM) model (69, 70), and the tightly bound ion (TBI) model (20, 71, 72, 73, 74, 75, 76, 77). The GMC model is a new generation of the Manning CC theory (68). In the GMC model, an explicit Mg²⁺-Mg²⁺ correlation term is added to the classical Manning ion condensation theory, and the potential energies for the different types of ion-RNA interactions are achieved from the Langevin dynamics. The 3D-RISM model is another promising model (69, 70). Between the mean-field method (such as NLPB) and the MD simulation, 3D-RISM found a middle ground to balance the computational efficiency of the mean-field method and the ability of the MD simulation to give atomistic insights for ion-ion correlation and the solvent effects. Therefore, it has the potential to provide more accurate predictions than NLPB while costing less computational time than MD simulation. The TBI model is another effective model that can treat ion-ion correlation and ion fluctuations in ion-RNA interactions (20, 71, 72, 73, 74, 75, 76, 77). In the TBI model, the NSB ions are classified into strongly correlated ions and weakly correlated ions. For the strongly correlated ions, an explicit enumeration is used to sample the discrete ion distributions, whereas for the weakly correlated ions, NLPB calculation is used to estimate the average ion distribution. Extensive comparisons between TBI predictions and experimental results proved that the TBI model can provide improved predictions of (NSB) divalent ion-binding effects.

Recently, we developed a, to our knowledge, new TBI model named the Monte Carlo tightly bound ion (MCTBI) model (78). In the MCTBI model, similar to the original TBI model, the NSB ions are classified into two types: the strongly correlated ions, which are treated with explicit sampling of discrete distributions, and the weakly correlated ions, which are treated with an implicit continuum model such as NLPB. However, the MCTBI model, unlike the original TBI model, samples the distributions of the strongly correlated ions using the Monte Carlo “insertion-deletion” (MCID) method, a novel Monte Carlo-based sampling algorithm for strongly correlated ions (78). Compared with the original TBI model, the MCTBI model enhances computational efficiency by at least several hundredfold and in general provides more accurate predictions for ion-binding effects (78). Although the original MCTBI model assumed fully hydrated Mg²⁺ ions (78), it showed potential to make low-resolution predictions for the binding regions for ions, including some dehydrated SSB Mg²⁺ ions, observed in the crystal structures of RNAs.

The ions of strong correlation are distributed in the close vicinity of the RNA surface. Some of the strongly correlated ions can become dehydrated SSB ions. The aforementioned models that can treat ion-ion correlations have the potential to account for the binding of dehydrated ions. For example, the 3D-RISM model solves the Ornstein and Zernike integral equation by averaging the solvent degrees of freedom so the solvation effects for the monovalent ions, which have a simple hydration layer, can be treated (79). Recently, a new model named semiexplicit assembly (SEA), based on the improved field-SEA water models, was developed to compute the solvation free energy of nonpolar, polar, and charged solutes (80, 81, 82). Based on the SEA model, the prediction results for the free energy of monovalent ions are consistent with those predicted from the explicit solvent model (82). However, because of the importance of the divalent ions in RNA folding and stability, we need a reliable model that can simultaneously account for the dehydrated and hydrated states for divalent ions. In general, there are two hydrated layers around divalent ions such as Be²⁺, Mg²⁺, and Ca²⁺ (83), resulting in a more complicated solvation effect than monovalent ions (83).

A fully hydrated Mg²⁺ ion attracts 18 water molecules around it, and these water molecules form two hydrated shells (83, 84). Accordingly, the dehydrated Mg²⁺ ions can be classified into inner-shell dehydrated (ISD) Mg²⁺ and outer-shell dehydrated (OSD) Mg²⁺. Combined with the strongly and weakly correlated NSB Mg²⁺ions, in total, an Mg²⁺ ion can have four states. In this work, based on the MCTBI framework, we develop a, to our knowledge, new model to predict ion-nucleic acids interactions for dehydrated and hydrated Mg²⁺ ions. In the new model developed here, using the MCID algorithm, we sample explicitly the discrete ion distributions for the ISD ions, the OSD ions, and the strongly correlated NSB ions and apply NLPB to treat the weakly correlated NSB ions. This new model allows us to predict the number of bound Mg²⁺ ions, the probable binding sites for the (inner- and outer-shell) dehydrated Mg²⁺ ions, and the cooperative and competitive effects for the hydrated and dehydrated ion binding. Comparison between the theoretical predictions and experimental results further support the validity of the model.

Materials and Methods

RNA structures and ions

We use an all-atom structure model for RNA and DNA duplexes, RNA tertiary structures, and RNA-protein complexes. The structures are downloaded from the Protein Data Bank (PDB) or generated using X3DNA (85). It is important to note that the specific structures are not involved in the parameter optimization in our model. For a given structure, we use a partial-charge model to describe the charge distribution. Specifically, the partial charges are assigned using the “Dock Prep” module in Chimera (86). For a given structure, we run the “Dock Prep” module through several operations, which include solvent deletion, alternate locations deletion (keeping the highest occupancy), hydrogen addition, partial charges addition, and finally, output with the Mol2 format. Charges for standard residues in RNAs are adopted from AMBER ff14SB (87), and charges for nonstandard residues are calculated using the ANTECHAMBER module with AM1-BCC charges (88, 89). In our calculation, to reduce the computational time, all the hydrogen atoms in the structures are deleted, and their charges are shifted to the connected (heavy) atoms.

The ions in this study include divalent cation Mg²⁺, monovalent cation Na⁺ (or K⁺), and monovalent anion Cl⁻. Their bulk concentrations $c_{2+}^0$, $c_{+}^0$, and $c_{-}^0$ satisfy the charge neutrality condition $2c_{2+}^0+c_{+}^0=c_{-}^0$. The monovalent ions are regarded as fully hydrated, with radii $r_{{\text{Na}}^{+}}=3.5\text{Å}$, $r_{{\text{K}}^{+}}=4.0\text{Å}$, and $r_{{\text{Cl}}^{-}}=4.0\text{Å}$ for Na⁺, K⁺, and Cl⁻, respectively (74, 75). The different hydration states of an ion lead to different effective ion radii. In the order model, Mg²⁺ ions can have three radii, corresponding to the fully hydrated Mg²⁺ (with two hydration shells), OSD Mg²⁺ (with one hydration shell), and ISD Mg²⁺ (without any hydration shell). In practice, however, because of the highly sensitive water exchange mechanism (especially in the inner shell) (90), it is difficult to accurately determine the radius of a hydrated Mg²⁺ and the distribution of water molecules in the hydration shells. For simplicity, based on the density functional theory, we set the radii of the three types of Mg²⁺ ions as $r_{{\text{Mg}}^{2+}}=4.5\text{Å}$ (fully hydrated Mg²⁺), 2.65 Å (OSD Mg²⁺), and 0.80 Å (ISD Mg²⁺), respectively (83). Moreover, we also assume that the water molecules are uniformly distributed in each hydration shell. There are six water molecules and 12 water molecules in the inner shell and outer shell, respectively. Theoretical calculations (83) show that the full dehydration of the outer shell (i.e., 12 water molecules) and the inner shell (i.e., six water molecules) would cost 156.9 and 303.9 kcal/mol, respectively. In the ion-binding process, the interplay between the energy gain from ion-nucleic acid interaction and the energy cost for the removal of water molecules from the ion hydration shells can lead to partial dehydration of the bound ions and different stable binding sites for the ions.

Enhanced MCTBI model

In the MCTBI model, ions around an RNA/DNA are classified into two types: the (strongly correlated) tightly bound (TB) ions and the (weakly correlated) diffusely bound (DB) ions. To establish the spatial demarcation between the regions for the TB and DB ions, we first use the NLPB model to calculate the ion-concentration distribution and then estimate the ion-correlation strength (71). The region where the correlation strength is larger than a critical correlation strength (71) is called the TB region, and the ions in the region are TB ions. Outside the TB region is the DB region, where DB ions are distributed. Monovalent ions have negligible TB regions and are thus treated as DB ions.

TB ions, according to the hydration state, can be further classified into three types: the ISD, the OSD, and the strongly correlated nondehydrated (ND, i.e., fully hydrated TB) Mg²⁺, whereas DB ions contain weakly correlated, fully hydrated Mg²⁺ ions and all the monovalent ions such as Na⁺ (or K⁺) and Cl⁻. For the three types of TB ions (ISD, OSD, and ND), the corresponding regions are termed as the ISD, OSD, and ND layers (see Fig. 1 A).

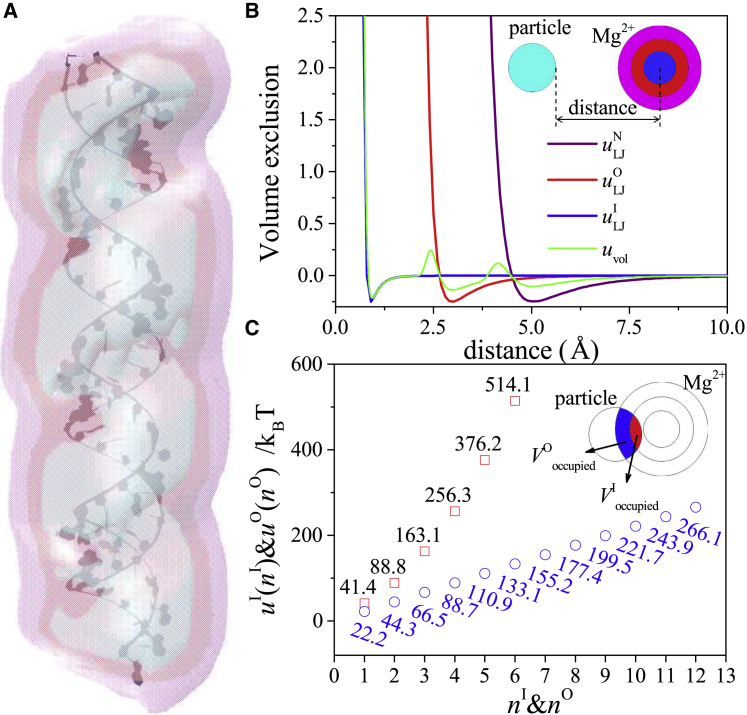
Figure 1.

(A) Three layers of the TB region around an RNA. The nondehydrated (ND) layer for the ND ions, the outer-shell dehydrated (OSD) layer for the OSD ions, and the inner-shell dehydrated (ISD) layer for the ISD ions are shown as the outermost, the middle, and the innermost layers. (B) The volume exclusion energy between a particle and an Mg²⁺ ion. $u_{\text{LJ}}^{\text{N}}$, $u_{\text{LJ}}^{\text{O}}$, and $u_{\text{LJ}}^{\text{I}}$ are the “12-6” LJ potentials between the particle and an ND Mg²⁺ ion, an OSD Mg²⁺ ion, and an ISD Mg²⁺ ion, respectively. u_vol is calculated by the Boltzmann average for the three LJ potentials. Inset: the outer and inner layers around the magnesium ion represent the outer and inner hydration shells, respectively. The dark and light blue balls are the fully dehydrated Mg²⁺ and the other particle. (C) The dehydration energies of the inner and the outer shells as a function of the number of the removed water molecules. Inset: the blue and red regions show the volumes of the outer and inner shells occupied by the other particles. To see this figure in color, go online.

We sample the discrete distributions for the TB ions using the MCID algorithm (78), an enhanced sampling algorithm, and use the NLPB model to calculate the free energy and the mean distribution of the DB ions. Specifically, for a given RNA structure with N_p nucleotides, the partition function of all the ions in the system is given by

$$\begin{array}{c}Z=\sum _{N_{\text{b}}=0}^{N_{\text{p}}}Z\left(N_{\text{b}}\right)\\ =\sum _{N_{\text{b}}=0}^{N_{\text{p}}}\left[Z_{\text{id}}{\left(c_{2+}^0\right)}^{N_{\text{b}}}\frac{W\left(N_{\text{b}}\right)}{N_{\text{b}}!}{e}^{-\mathit{\Delta }{G}_{\text{d}}/k_{\text{B}}T}\right].\end{array}$$ (1)

In the equation above, N_b is the number of TB ions in the TB region, k_B is the Boltzmann constant, and T is the temperature. Z(N_b) and Z_id are the partition functions for the system of N_b TB ions and for the reference system without RNA polyanions. ΔG_d is the free energy of the DB ions in the DB region, including the interaction between the DB and the TB ions. The total statistical weight W(N_b) for a given N_b TB ions involves all the TB ion distribution in TB region. The details of W(N_b) and ΔG_d will be described in the following content.

We use a simple cubic lattice with lattice size l_b in the TB region to configure the ion distributions. Each lattice site is allowed to be occupied by 0 or 1 ion. The distributions of the TB ions are generated by randomly inserting ions one by one, and the sum over all the possible ion distributions gives the total statistical weight:

$$W\left(N_{\text{b}}\right)=\prod _{i=1}^{N_{\text{b}}}w\left(i\right).$$ (2)

Here, the product ${\mathit{\prod }}_{i=1}^{N_{\text{b}}}$ corresponds to the process of adding 1,2…N_b ions. The individual statistical weight of the i-th inserted ion w(i)

$$w\left(i\right)=l_b^3\sum _{k=1}^{m_i}{e}^{-\mathit{\Delta }{U}_i\left(k\right)/k_{\text{B}}T}$$ (3)

is determined by the number of the available (vacant) sites m_i for placing the i-th ion and the interaction energy ΔU_i(k) between the inserted ion at site k and the other preexisting particles, which include the RNA atoms and the (i − 1) preexisting ions.

We use a, to our knowledge, novel Monte Carlo algorithm to sample the distribution of TB ions (including ISD, SSD and ND ions). To sample the distribution of the TB ions, we insert the ions one by one using Monte Carlo sampling and then compute the individual and total statistical weight w(i) and W(N_b) according to Eqs. 2 and 3. However, as a new ion is inserted into the TB region, the newly added ion can perturb the distribution of the preexisting ions. To account for the above feedback effect, we developed the MCID algorithm (78). A key feature of the algorithm is the enhanced sampling for low-energy distributions. Specifically, after inserting the ions, we randomly remove the high-energy ions. In this way, we enhance the sampling for the low-energy distributions. Here, we note that the number of TB ions N_b is assumed to vary from 0 to N_p (the number of nucleotides) in the sampling of the ion distributions. In fact, the number of the bound divalent TB ions hardly exceeds $N_{\text{p}}/2$ (full charge neutralization) (11). Indeed, the overall contribution from the partition functions Z(N_b) for $N_{\text{b}}>N_{\text{p}}/2$ is small and may be ignored (see Eq. 1). However, because the MCID algorithm samples the N_b-ion distributions through deletion of ions from the systems of larger (>N_b) numbers of ions, we set N_b = N_p as the maximal number of the TB ions. See the Section “Sampling of TB ions: the MCID algorithm” in the Supporting Materials and Methods for a detailed description of the MCID sampling algorithm.

We classify the distributions according to the number N_b (= 0,1,2,….,N_p) of TB ions. For a given N_b, we compute the free energy of the DB ions and the interaction between the TB and the DB ions using NLPB (91, 92):

$$\begin{array}{c}\mathit{\Delta }{G}_{\text{d}}=\frac{1}{2}\int \sum _{\alpha }{c}_{\alpha }\left(r\right)z_{\alpha }e\left[\psi \left(r\right)+\psi \text{'}\left(r\right)\right]d^{3}r\\ +\int \sum _{\alpha }\left[c_{\alpha }\left(r\right)\text{ln}\frac{c_{\alpha }\left(r\right)}{c_{\alpha }^0}-c_{\alpha }\left(r\right)+c_{\alpha }^0\right]d^{3}r.\end{array}$$ (4)

Here, α denotes the ion species. ψ(r) and ψ′(r) are the electrical potentials at position r with and without ions in the solution. c_α(r) and $c_{\alpha }^0$ represent the local (at r) and bulk concentrations, respectively. The first integral in the above equation includes the free energy for the interaction between the DB ions and the charged particles (RNA and TB ions) in the TB region and the enthalpic part of the free energy for the DB ions (91). The second integral gives the entropic part of the free energy for the DB ions. In the following subsections, we provide detailed description about the energy functions for the TB ions.

Energy functions for TB ions

In the original MCTBI model, the bound ions are assumed to be fully hydrated, and thus the original model cannot treat the dehydration effect in ion binding. In our model, for the i-th ion at site k, the interaction energy ΔU_i(k) induced by other particles includes the volume exclusion energy u_vol, the Coulombic interaction energy u_ele, and the dielectric polarization energy u_pol. Moreover, the ion involves also the self-polarization energy u_self and the (possible) dehydration energy u_dehy. Therefore, ΔU_i(k) is the sum of the different energy components:

$$\mathit{\Delta }{U}_i\left(k\right)=\sum _j{u}_{\text{vol}}+\sum _j{u}_{\text{ele}}+\sum _j{u}_{\text{pol}}+u_{\text{self}}+{\epsilon }_{\text{dehy}}{u}_{\text{dehy}}.$$ (5)

Here, $\sum _j$ denotes the summation over all the other particles. Two notably novel terms are the excluded volume u_vol and the dehydration ε_dehyu_dehy energies with ε_dehy as the dehydration constant and u_dehy as the dehydration energy (see below for the details).

We consider the volume exclusion interaction u_vol between a TB (Mg²⁺) ion and another particle as a Boltzmann-based average of the “12-6” Lennard-Jones (LJ) potential. Depending on the degree of dehydration, a TB Mg²⁺ ion can be an ISD, OSD, or ND ion. To account for the different sizes of the ion with the different hydration levels, we use radii $r_{{\text{Mg}}^{2+}}$ = 0.8, 2.65, and 4.5 Å for the ISD, OSD, and ND ions, respectively.

$$u_{\text{vol}}=\frac{u_{\text{LJ}}^{\text{I}}{e}^{-u_{\text{LJ}}^{\text{I}}/k_{\text{B}}T}+u_{\text{LJ}}^{\text{O}}{e}^{-u_{\text{LJ}}^{\text{O}}/k_{\text{B}}T}+u_{\text{LJ}}^{\text{N}}{e}^{-u_{\text{LJ}}^{\text{N}}/k_{\text{B}}T}}{e^{-u_{\text{LJ}}^{\text{I}}/k_{\text{B}}T}+e^{-u_{\text{LJ}}^{\text{O}}/k_{\text{B}}T}+e^{-u_{\text{LJ}}^{\text{N}}/k_{\text{B}}T}}.$$ (6)

The volume exclusion energy u_vol and the three types of the “12-6” LJ potentials are shown in Fig. 1 B. In our calculation, the polarization energy is computed from the generalized Born model. u_ele, u_pol, and u_self are given by

$$\begin{array}{l}{u}_{\text{ele}}=\frac{Z_i{Z}_j{e}^2}{{\epsilon }_R{r}_{ij}}\\ u_{\text{pol}}=\left(\frac{1}{{\epsilon }_W}-\frac{1}{{\epsilon }_R}\right)\frac{Z_i{Z}_j{e}^2}{\sqrt{r_{ij}^2+B_i{B}_j\text{exp}\left(-\frac{r_{ij}^2}{4B_i{B}_j}\right)}}.\\ u_{\text{self}}=\left(\frac{1}{{\epsilon }_W}-\frac{1}{{\epsilon }_R}\right)\left(\frac{1}{B_i}-\frac{1}{B_i^0}\right)Z_i^2{e}^2\end{array}$$ (7)

Here, subscripts i and j denote the i-th ion and other particles j, r_ij is the distance between i-th ion and particle j, and Ze is the charge. The Born radius B calculated from a pairwise model (see details in Supporting Materials and Methods) is dependent on the distribution of RNA/DNA atoms. $B_i^0$ denotes the Born radius for an isolated ion. ε_R (= 20) and ε_W (= 78) are the dielectric constants of RNA/DNA and water, respectively. This choice of the dielectric constants for RNA/DNA (ε_R = 20) has been suggested by previous studies (93, 94, 95). In fact, in our previous calculations (75), we found that the prediction results are not sensitive to the change of interior (RNA/DNA) dielectric constant, probably because of two possible reasons: 1) the highly charged atoms, such as the atoms in the phosphate group, are mainly exposed to the solvent, and the solvent dielectric constant may play a dominant role (96); 2) changes in ion-RNA/DNA charge-charge interactions (such as u_ele, u_pol, and u_self) for the different choices of ε_R, to a large extent, may offset each other.

To account for the dehydration energy of a TB Mg²⁺, we develop a new model by including a dehydration energy term ε_dehyu_dehy in Eq. 5. The dehydration energy term u_dehy is given by

$$u_{\text{dehy}}=u^{\text{O}}\left(n^{\text{O}}\right)+u^{\text{I}}\left(n^{\text{I}}\right).$$ (8)

Here, u^O(n^O) and u^I(n^I) denote the dehydration energies for the removal of n^O water molecules from the outer shell and n^I water molecules from the inner shell for a TB Mg²⁺ ion. n^O and n^I are defined as

$$n^{\text{O}\left(\text{or}\text{I}\right)}=\{\begin{array}{ll}0\hfill & \text{the}\text{TB}\text{ion}\text{located}\text{beyond}\text{the}\text{OSD}\left(\text{or}\text{ISD}\right)\text{layer}\hfill \\ \text{int}\left[N^{\text{O}\left(\text{or}\text{I}\right)}\times \frac{V_{\text{occupied}}^{\text{O}\left(\text{or}\text{I}\right)}}{V_{\text{OSD}\left(\text{or}\text{ISD}\right)}}\right]+1\hfill & \text{the}\text{TB}\text{ion}\text{located}\text{within}\text{the}\text{OSD}\left(\text{or}\text{ISD}\right)\text{layer}\hfill \end{array},$$ (9)

where “int[]” denotes the integer part of the number in bracket, and N^O (= 12) and N^I (= 6) are the total number of the water molecules at the outer shell and inner shell of an Mg²⁺ ion, respectively. $V_{\text{occupied}}^{\text{O}}$ and $V_{\text{occupied}}^{\text{I}}$ denote the excluded volume occupied by other particles in the outer and the inner hydration shells, respectively, of the Mg²⁺ ion, as illustrated by the inset of Fig. 1 C. V_OSD and V_ISD denote the total volume of the outer and the inner hydration shell of the Mg²⁺ ion, respectively.

Theoretical calculations (83) suggest that the energy penalty of removing all water molecules at the outer and the inner shells are (u^O(12) =) 266.1 and 514.1 k_BT (156.9 and 303.9 kcal/mol with T = 25°C), respectively. The calculations also provide the inner-shell dehydration energy as a function of the removed number of water molecule (83). The results are used as u^I(n^I) in our model. For the outer-shell dehydration energy, we assume that u^O(n^O) linearly increases with n^I. See Fig. 1 C for the values of u^O(n^O) and u^I(n^I).

In addition to Coulombic interaction, RNA-ion chemical interactions, such as the hydrogen bonds between RNA atoms invading the hydration layers and the nearby water molecules and the covalent bonds between RNA atoms and ions, also contribute to ion dehydration. These chemical energies could offset part of the dehydrated energy. A larger number of RNA atoms that invade into ion hydration layers would cause stronger chemical interactions and, in the meantime, dispel more water molecules from the hydration layers. We introduce a dehydration constant ε_dehy to account for the above offset effect. Comparisons between theoretical predictions and experimental data suggest an estimated value of 0.35 for ε_dehy and the LJ constant ε_LJ (see Eq. S3) of the “12-6” LJ potential (71, 76).

Results and Discussion

We use five structurally distinct nucleic acids to test the, to our knowledge, new MCTBI theory: a 40 base pair (bp) A-RNA helix, a 40 bp B-DNA duplex, an adenine riboswitch (PDB: 4TZX (97)), an rRNA-protein complex (PDB: 1HC8 (98)), and a tRNA (PDB: 1TRA (99)). The new MCTBI model has the advantage of simultaneously treating the ISD ions, the OSD ions, the strongly correlated ND (i.e., the fully hydrated TB) ions, and the DB ions. We note that ISD, OSD, and ND ions belong to the TB ions. Using the current new MCTBI model, we predict the binding fractions, distributions, and the linear density (distribution) for each types of ions.

Ion-binding fractions

Ion-binding fraction f_α per nucleotide for ion species α is an important quantity that gives an overall description for the ion-binding effects. The ion-binding fraction f_α is calculated using the following formula:

$$f_{\alpha }=\frac{1}{N_{\text{p}}}\sum _{N_{\text{b}}=0}^{N_{\text{p}}}\frac{{\text{Γ}}_{\alpha }\left(N_{\text{b}}\right)\times Z\left(N_{\text{b}}\right)}{Z},$$ (10)

where the partition functions Z(N_b) and Z are determined from Eq. 1 and Γ_α(N_b) is the number of excess ions, including the TB ions and DB ions:

$${\text{Γ}}_{\alpha }\left(N_{\text{b}}\right)=\{\begin{array}{c}{N}_{\text{b}}+\int \left(c_{\alpha }-c_{\alpha }^0\right)d^{3}r,\text{if}\alpha \text{is}\text{multivalention},\\ \int \left(c_{\alpha }-c_{\alpha }^0\right)d^{3}r,\text{if}\alpha \text{is}\text{monovalention}\text{.}\end{array}$$ (11)

Here, N_b is the number of TB ions, including the ISD, OSD, and ND ions.

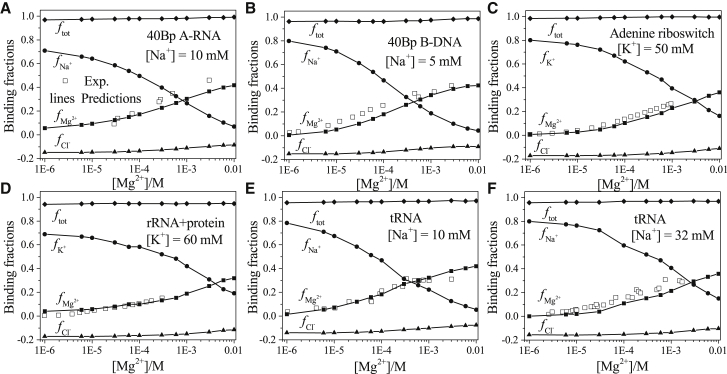
Fig. 2 shows the binding fraction of each ion species as a function of the bulk concentration [Mg²⁺] for the different RNA/DNA structures. The overall agreement between the theoretical predictions and the experimental results (100, 101, 102, 103, 104) supports the reliability of the model. With the increase in [Mg²⁺], more Mg²⁺ ions are attracted to the RNA because the entropic cost for Mg²⁺ binding is smaller for a higher [Mg²⁺]. Meanwhile, an increased number of Mg²⁺ ions around RNA would competitively reduce the accumulation of monovalent cations (Na⁺ or K⁺) and reduce the depletion of monovalent anions (Cl⁻). As a result, $f_{{\text{Na}}^{+}\left(\text{or}{\text{K}}^{+}\right)}$ decreases and $f_{{\text{Cl}}^{-}}$ increases with the increase of [Mg²⁺]. Similarly, the comparisons of $f_{{\text{Mg}}^{2+}}$ between tRNA at [Na⁺] = 10 mM (see Fig. 2 E) and [Na⁺] = 32 mM (see Fig. 2 F) indicate that a high bulk concentration of monovalent ion can inhibit Mg²⁺ binding. In addition, we find that the net binding fraction f_tot (= $2f_{{\text{Mg}}^{2+}}+f_{{\text{Na}}^{+}\left({\text{or K}}^{+}\right)}-f_{{\text{Cl}}^{-}}$) reaches 1, i.e., the bound ions in the solution tend to keep the nucleic acids neutral. Furthermore, because the OSD Mg²⁺ ion radius (Mg²⁺ that retains the first hydration shell) may not have a definitive value (90), to further test our model, we compute the binding fraction $f_{{\text{Mg}}^{2+}}$ using different radius parameters $r_{{\text{Mg}}^{2+}}$ for the OSD Mg²⁺ ion. As shown in Fig. S1, in which $r_{{\text{Mg}}^{2+}}$ varies from 2.45 to 2.75 Å, we find that the results are not sensitive to the small variations of $r_{{\text{Mg}}^{2+}}$.

Figure 2.

The [Mg²⁺]-dependence of the ion-binding fractions per nucleotide for six RNA/DNA-solution systems: (A) 40 bp A-RNA duplex with 10 mM Na⁺, (B) 40 bp B-DNA duplex with 5 mM Na⁺, (C) adenine riboswitch (PDB: 4TZX (97)) with 50 mM K⁺, (D) rRNA-protein complex (PDB: 1HC8 (98)) with 60 mM K⁺, tRNA (PDB: 1TRA (99)) with (E) 10 mM Na⁺ and (F) 32 mM Na⁺. The experimental data are from (100, 101, 102, 103, 104), respectively.

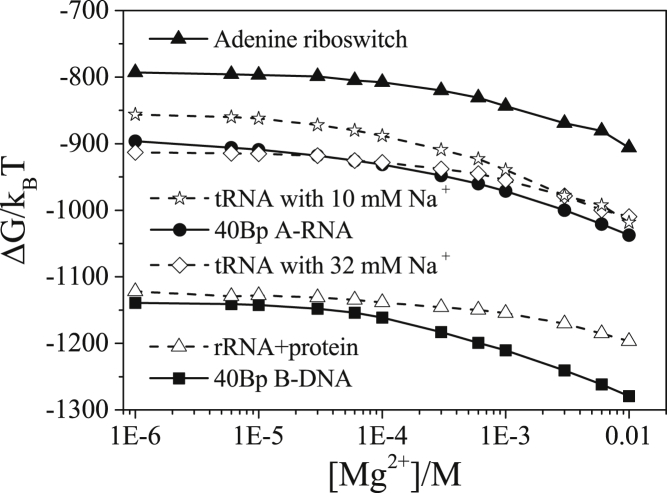
As shown in Fig. 3, we also study the dependence of the electrostatic free energy ΔG(= −k_BT lnZ) on the bulk concentration [Mg²⁺]. We find that for the different nucleic acid systems tested, an increasing [Mg²⁺] leads to a decrease in the free energy ΔG. This illustration of the model is based on the folded states. However, predicting the ion-dependent folding stability involves also the electrostatic free energies for the unfolded states, which requires their conformational ensembles.

Figure 3.

Electrostatic free energy ΔG as a function of [Mg²⁺] for the adenine riboswitch with 50 mM K⁺, tRNA with 10 mM Na⁺, 40 bp A-RNA duplex with 10 mM Na⁺, tRNA with 32 mM Na⁺, rRNA-protein complex with 60 mM K⁺, and 40 bp B-DNA duplex with 5 mM Na⁺, from top to bottom at [Mg²⁺] = 10⁻⁶ M, respectively.

For a mixed solution with monovalent and divalent ions, the electrostatic free energy shows a competition between the monovalent and divalent ions. From the plots for the tRNA with [Na⁺] = 10 mM (line with open stars) and [Na⁺] = 32 mM (line with open diamonds), we find that in a dilute [Mg²⁺], adding Na⁺ would lower the electrostatic free energy, suggesting a dominant role of monovalent ions in stabilizing the RNA structure. In contrast, at a high [Mg²⁺], Mg²⁺ ions become dominant and the electrostatic free energies ΔG are less sensitive to the different Na⁺ concentrations.

Distribution of TB Mg²⁺ ions

The MCTBI model also predicts the spatial distributions for the TB ions. The probability of finding a TB ion at site k is given by

$$p\left(k\right)=\sum _{N_{\text{b}}=0}^{N_{\text{p}}}\frac{n\left(N_{\text{b}},k\right)}{M_{\text{f}}\times M_{\text{b}}}\times \frac{Z\left(N_{\text{b}}\right)}{Z}.$$ (12)

Here, n(N_b, k) is the number of N_b-ion distributions with site k occupied by a TB ion out of the totally M_fM_b sampled distributions, where M_f is the sample number for the N_p-ion distributions and M_b are the repeated deletion times for each N_p-ion distribution (see details in Supporting Materials and Methods). It is important to note that the original MCTBI model (78) could not treat ion dehydration and thus may not give reliable predictions for the binding sites of the dehydrated or partially dehydrated (SSB) ions. The current model can treat the dehydration effects and therefore can predict the binding sites of the SSB ions.

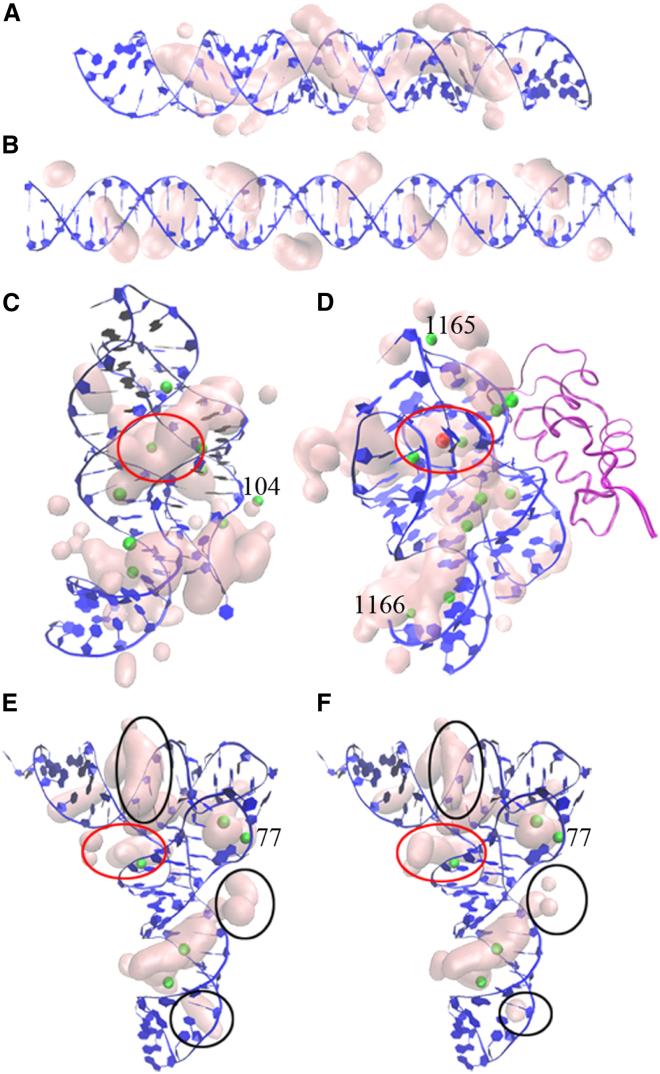
Fig. 4 shows the probability distribution of the TB ions, including the ISD, OSD, and ND ions, around the different nucleic acid structures at [Mg²⁺] = 6 mM. We define the likely binding sites as regions with probability p(k) > 0.01. We find that in general, such binding regions occupy only 2–3$\text{\%}$ of the TB region. Furthermore, as shown in Fig. 4, A and B, metal ions tend to accumulate in/around the deep groove of the helix. In addition, ions also tend to bind to three-dimensional pocket-shaped regions, such as the space within the kissing loop for the adenine riboswitch, the region where a K⁺ ion (large red ball) and two Mg²⁺ ions (small green balls) are buried inside the rRNA-protein complex, and the region near the U8-C13 for the tRNA (labeled by red cycles in Fig. 4, C–F, respectively).

Figure 4.

The highly probable Mg²⁺ ion distribution for (A) 40 bp A-RNA duplex with 10 mM Na⁺, (B) 40 bp B-DNA duplex with 5 mM Na⁺, (C) adenine riboswitch with 50 mM K⁺, (D) rRNA-protein complex with 60 mM K⁺, and tRNA with (E) 10 mM Na⁺ and (F) 32 mM Na⁺. The RNA (DNA) is labeled as blue, and the protein is labeled as purple. The green and red balls show the SSB Mg²⁺ and K⁺ ions, respectively, observed in the crystal structures. The numbers in (C)–(F) are the ion indices in the PDB files (97, 98, 99). To see this figure in color, go online.

Moreover, Fig. 4 shows the results for two comparisons. The first comparison is for the ion distributions around the A-RNA helix (Fig. 4 A) and the B-DNA duplex (Fig. 4 B). Our results show that the A-RNA helix can attract Mg²⁺ ions to enter a deep groove, whereas the B-DNA duplex cannot. The result, as explained in the following, may be attributed to the different sizes of the deep grooves for the A-RNA and B-DNA duplexes. An A-RNA helix has a narrower deep groove and hence a higher charge density than a B-DNA. As a result, the A-RNA helix has a stronger tendency to induce ion dehydration. The dehydrated ions, which are less bulky than hydrated ions, can enter the deep groove of the A-RNA helix. In contrast, the wider groove of the B-DNA cannot provide enough force for ion dehydration. The second comparison is between tRNA at [Na⁺] = 10 mM (Fig. 4 E) and [Na⁺] = 32 mM (Fig. 4 F). As shown in the figures, some ion accumulation regions (labeled by black cycles) for the tRNA at dilute [Na⁺] are larger than that at high [Na⁺], whereas the situation is reversed at other ion accumulation regions (e.g., the pockets of tRNA, labeled by red cycles). We will explain the reason in the next subsection.

Fig. 4, C–F show that the improved MCTBI can predict nearly all binding sites for the SSB ions observed in the crystal structures for RNAs, including some SSB ions not buried in the RNA structures, such as the Mg²⁺ ion (index 104 in the PDB file (97)) around adenine riboswitch, the Mg²⁺ ions (indices 1165 and 1166) around rRNA-protein complex (98), and the Mg²⁺ ion (index 77) for tRNA (99).

Mg²⁺ binding and dehydration

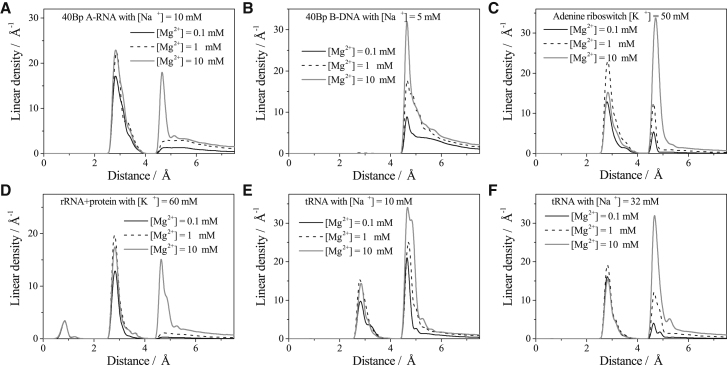
In the above two subsections, we focus on the overall view of Mg²⁺ ion-binding properties. In this subsection, we investigate novel features of the binding of the different types Mg²⁺ ions, specifically, the ISD, OSD, and fully hydrated (ND and DB) Mg²⁺ ions. Fig. 5 shows the linear densities as a function of the distance to surface of the nucleic acids for a series of the different nucleic acid structures at low (0.1 mM; black solid lines), medium (1 mM; black dashed lines), and high (10 mM; gray solid lines) Mg²⁺ concentrations, respectively. In general, for RNA and DNA duplexes, the radial distance of the ion from the helix central axis is treated as the x axis (distance variable) to describe the linear density (79), whereas for RNAs with more complicated structures, the x axis can be the distance between the ion and specific atoms, such as the nonbridging phosphate oxygens, purine N7 atom, and uracil O4 atom (21). Here, to clearly classify the different types of Mg²⁺ ions (6), we simply use the distance between the ion and the closest atom surface as the x axis to describe the linear density. The different types of Mg²⁺ ions show the different characteristics in linear density. According to the number of peaks in linear density, there are three types of nucleic acid structures for ion binding. The A-RNA helix, adenine riboswitch, and tRNA belong to the first type. These RNAs have narrow deep grooves and three-dimensional pockets, which lead to outer-shell dehydration for the bound ions. In the linear density curve, the first peak appears near the radial distance 2.65 Å, which is the radius of the OSD Mg²⁺ ion. The second type is the B-DNA duplex, which has a wide deep groove. Therefore, ion dehydration is less likely. The rRNA-protein complex belongs to the third type. The structure can cause inner-shell dehydration for the bound Mg²⁺ ions, specifically in the cavity, where a K⁺ ion (red ball) and two Mg²⁺ ions (green balls) are buried (labeled with red circles in Fig. 4 D). The RNA atoms around the cavity provide a very strong attraction so that the Mg²⁺ ions can become ISD in the process of entering the cavity.

Figure 5.

The linear density as a function of the distance from the RNA (DNA) surface for (A) 40 bp A-RNA duplex with 10 mM Na⁺, (B) 40 bp B-DNA duplex with 5 mM Na⁺, (C) adenine riboswitch with 50 mM K⁺, (D) rRNA-protein complex with 60 mM K⁺, and tRNA with (E) 10 mM Na⁺ and (F) 32 mM Na⁺.

Furthermore, we find that with the increase of [Mg²⁺], there are three different behaviors for the linear density peaks corresponding to the ISD, OSD, and fully hydrated ions, respectively. For the fully hydrated ions, the increase in [Mg²⁺] leads to the rise of the peak height, indicating an increased accumulation of the fully hydrated ions. For the ISD ions, the cavity in the rRNA-protein complex provides a stable environment that protects the bound ions from the influence of the bulk ion concentration change. Therefore, the peaks of the ISD ions at various [Mg²⁺] remain nearly the same for the different [Mg²⁺] (Fig. 5 D).

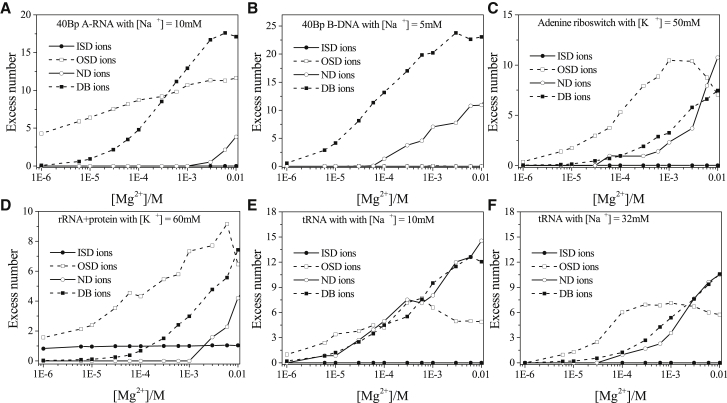
One of the most intriguing features is about the peak for the OSD ions (Fig. 5, A and C–F). The height of the peak first increases, then decreases with the increase of [Mg²⁺] (104). The above behavior is a result of two competitive effects. The increase in bulk Mg²⁺ ion concentration leads to an increase in Mg²⁺ ion binding and thus a higher probability of Mg²⁺ ion dehydration and a higher likelihood for the ions to be trapped in the groove and pockets of the RNA. As the Mg²⁺ ion concentration is further increased, the increased accumulation of the hydrated ions around the RNA surface would exclude further binding of the OSD ions, causing a decrease in OSD binding. The exclusion effect is supported by the results for the [Mg²⁺] dependence of ion binding. As shown in Fig. 6, an increase in [Mg²⁺] would cause an increase in the binding of both ND (fully hydrated TB) and DB ions. However, the change in the binding of DB ions (outside the TB region) does not affect the accumulation of the OSD ions (inside the TB region). In contrast, the increase in ND ion binding leads to significant effect on the inhibition of further accumulation of the OSD ions because the increase of the excess number for ND ions (solid lines with open cycles in Fig. 6) immediately leads to the decrease of the excess number for OSD ions (dashed lines with open squares in Fig. 6).

Figure 6.

The [Mg²⁺] dependence of the excess number of the different types of the dehydrated (or hydrated) Mg²⁺ ions: (A) 40 bp A-RNA duplex with 10mM Na⁺, (B) 40 bp B-DNA duplex with 5 mM Na⁺, (C) adenine riboswitch with 50 mM K⁺, (D) rRNA-protein complex with 60 mM K⁺, and tRNA with (E) 10 mM Na⁺ and (F) 32 mM Na⁺.

Furthermore, as shown in the comparisons between Fig. 5, E and F and between Fig. 6, E and F, divalent ions and monovalent ions show competitive behavior in their binding to RNA. The observation is consistent with the aforementioned inhibition of Mg²⁺ binding because of a high concentration of monovalent ions (Fig. 2, E and F). However, our results for the ion distributions indicate that such an inhibition effect may not occur for all the Mg²⁺ ions. For example, more Mg²⁺ ions would accumulate in some pockets of the tRNA at the high [Na⁺] (Fig. 4, E and F). In fact, the fully hydrated (including ND and DB) Mg²⁺ ions are indeed subjected to the inhibition effect because of the Na⁺ ions of high concentration, as shown by the peak in linear density for the fully hydrated ions (see the peak of the fully hydrated ions in Fig. 5, E and F) as well as the excess number of the ND and DB ions (see the lines of ND and DB ions in Fig. 6, E and F). However, as we explained above, fewer ND ions can lead to more OSD ions. Therefore, with the increase of Na⁺ ion concentration, more OSD Mg²⁺ ions would bind to the RNA (see the peak of OSD ions in Fig. 5, E and F). In other words, a higher bulk concentration of Na⁺ ions can indirectly help the binding of OSD Mg²⁺ ions.

Conclusions

By considering ion correlation and fluctuation effects, the original MCTBI model can predict the ion effects in nucleic acids folding and stability for fully hydrated ions, especially divalent ions such as Mg²⁺. Inspired by the important role of ion dehydration, we here develop a, to our knowledge, new MCTBI model by accounting for the different dehydration states of ions upon binding to an RNA or DNA. The new model developed here may be applied to other biopolymers such as proteins. However, it is important to note that because of the different electric and dielectric properties of nucleic acids and proteins, specific parameters such as the internal dielectric constant may be changed to properly describe ion-protein interactions.

Compared with the monovalent ions such as K⁺ and Na⁺, the divalent ions such as Mg²⁺ have more complicated dehydration/hydration effects. In general, a fully hydrated Mg²⁺ ion has two hydration shells, an inner shell with six water molecules and an outer shell with 12 water molecules. Correspondingly, the Mg²⁺ ions around the nucleic acid can have four different hydration states: ISD, OSD, strongly correlated ND (fully hydrated), and DB (also fully hydrated).

Extensive theory-experiment comparisons on ion-binding numbers and binding sites for various dehydrated Mg²⁺ ions support the reliability of the new MCTBI model. The results suggest that this new model may be useful to treat the ion effects for different nucleic acid structures such as the A-RNA and B-DNA duplexes, tRNA, adenine riboswitch, and rRNA-protein complex. In addition to the model development, this study leads to several intriguing findings:

• 1)Nucleic acids with a wide deep groove, such as B-DNA duplex, can attract the fully hydrated ions, but it is difficult to induce the dehydration for the ions. Nucleic acids such as the A-RNA helix, tRNA, and adenine riboswitch, which have narrow deep grooves and three-dimensional pockets, can more likely cause the ion to be OSD and to enter deeply into the structures. Other systems such as an rRNA-protein complex, whose structure has a cavity with strong attraction but small size for the ions, can cause the Mg²⁺ ions to become ISD and enter the cavity.
• 2)In general, a higher bulk concentration of [Mg²⁺] would lead to more Mg²⁺ ions bound to the nucleic acids. In this study, we find that the increased number of the bound Mg²⁺ ions can inhibit further binding of OSD ions because of the Mg²⁺-Mg²⁺ Coulombic and excluded volume repulsion. Furthermore, we find that the ISD ions are barely affected by the change of the solution environment because the RNA provides a “shield” for the ISD ions.
• 3)A high bulk concentration of monovalent ions such as [Na⁺] could inhibit overall binding of Mg²⁺. We find that the main type of the Mg²⁺ ion that suffers the inhibition is the hydrated Mg²⁺ ion (ND and DB ions). In contrast, the high [Na⁺] may indirectly enhance the accumulation of the OSD ions because of the inhibition effects for the hydrated ions, especially for the ND ions.

It is important to note that the current new MCTBI model can only predict the probable regions for the SSB ions instead of the coordinates of the bound ions. The binding site of an SSB ion is determined not only by the electrostatic and solvation effects but also by other coordinated specific interactions such as the interaction between Mg²⁺ ion and specific oxygen atoms. Further development should consider these effects to predict the specific binding sites for the SSB ions.

Author Contributions

S.-J.C. and L.-Z.S. designed the research. L.-Z.S. performed the computation. L.-Z.S. and S.-J.C. performed the analysis, and both authors contributed to writing the article.

Editor: Margaret Cheung.