Abstract
Objective
Relapse rates are consistently high for stimulant user disorders. In order to obtain prognostic information about individuals in treatment, machine learning models have been applied to neuroimaging and clinical data. Yet few efforts have been made to test these models in independent samples or show that they can outperform linear models. In this exploratory study, we examine whether machine learning models relative to linear models provide greater predictive accuracy and less overfitting.
Method
This longitudinal study included 63 methamphetamine-dependent (training sample) and 29 cocaine-dependent (test sample) individuals who completed an MRI scan during residential treatment. Linear and machine learning models predicting relapse at a one-year follow up that were previously developed in the methamphetamine-dependent sample using neuroimaging and clinical variables were applied to the cocaine-dependent sample. Receiver operating characteristic analysis was used to assess performance using area under the curve (AUC) as the primary outcome.
Results
Twelve individuals in the cocaine-dependent sample remained abstinent, and 17 relapsed. The linear models produced more accurate prediction in the training sample than the machine learning models but showed reduced performance in the testing sample, with AUC decreasing by 0.18. The machine learning models produced similar predictive performance in the training and test samples, with AUC changing by 0.03. In the test sample, neither the linear nor the machine learning model predicted relapse at rates above chance.
Conclusions
Although machine learning algorithms may have advantages, in this study neither model's performance was sufficient to be clinically useful. In order to improve predictive models, stronger predictor variables and larger samples are needed.
Highlights
-
•
Stimulant use disorders are highly relapsing conditions, yet it remains difficult to know which patients are at greatest risk.
-
•
Neuroimaging has been proposed as a tool to assess prognosis for patients.
-
•
Previously published linear and machine-learning models of relapse were tested in a novel sample
-
•
Neither model performed better than chance when applied to novel data.
-
•
Developing accurate models using neuroimaging will require larger samples and stronger predictors.
1. Introduction
Addiction is a chronically relapsing condition (McLellan et al., 2000). One of the fundamental challenges for clinicians is to assess a patients' likelihood for relapse in an effort to help prevent negative outcomes (Marlatt and Donovan, 2005). Prominent theories about substance use disorders hold that they are brain-based diseases (Robinson and Berridge, 1993; Koob and Volkow, 2010; Hyman and Malenka, 2001; Wise, 1996; Paulus, 2007), implying that the brain should contain information about an individual's current disease status and prognosis (Paulus, 2015; Pine and Leibenluft, 2015). Accordingly, a major research goal has been to identify patterns of brain activity that predict relapse following treatment (Volkow et al., 2015). Recently, this search has been aided by machine learning algorithms (Gowin et al., 2015; Breiman, 2001; Pereira et al., 2009) that train computers to iteratively improve performance at uncovering relationships between variables. One application of these algorithms is to classify objects into groups (LeCun et al., 2015), such as labeling substance-dependent individuals as likely to relapse or abstain. Potential advantages of machine learning algorithms relative to binary logistic regression are that they typically incorporate internal cross-validation to increase model-stability, include interactions by default, and are robust to outliers (Breiman, 2001; LeCun et al., 2015; Scholkopf et al., 1997). All these characteristics optimize exploratory analysis. In contrast, standard regression approaches do not automatically include cross-validation, require the researcher to specify interactions, and may be sensitive to outliers. These considerations taken together, machine learning approaches may produce models that have superior predictive ability, which is why these techniques have recently expanded in use. Yet, despite the proliferation of these techniques (Jordan and Mitchell, 2015), few studies have attempted to replicate published models that purport to predict relapse in new samples, which is a necessary step to determine whether they can be developed into useful prognostic tools.
One neural process that has shown promise for assessing substance users' prognosis is assessment of risky decisions (Gowin et al., 2013; Gowin et al., 2014a, 2017a). Colloquially, risk-taking indicates a decision that has a possibility for harm, such as the decision to use substances despite the increased likelihood of legal or medical problems (American Psychiatric Association, 2013). Researchers have operationally defined risk-taking as choosing an option with a higher level of uncertainty in the outcome (Kahneman and Tversky, 1979) and have shown that individuals with stimulant dependence choose risky options at a higher frequency than non-dependent comparison groups (Gowin et al., 2018). Many neuroimaging studies using both PET and fMRI have also observed differences in the neural processing of risky decisions in participants with stimulant dependence relative to healthy comparison participants (Bolla et al., 2003; Tanabe et al., 2007; Cousijn et al., 2013; Gilman et al., 2015). Meta-analytic evidence indicates that differences in processing are present in a variety of brain regions, including the insula, striatum, and anterior cingulate cortex (Gowin et al., 2013). We have previously shown that neural processing of risk has also been shown to distinguish individuals who relapse from those who remain abstinent following treatment (Gowin et al., 2014b). Although promising, this finding has not been replicated, which is crucial for establishing model validity.
Here, we collected a large longitudinal sample of stimulant dependent individuals who had completed a risk-taking task in an MRI scanner during residential treatment. Two classes of stimulant users were included: cocaine- and methamphetamine-dependent individuals. Results from the methamphetamine-dependent sample have been published previously (Gowin et al., 2014b, 2015). The first paper used a linear model to show that insular processing of risk during the decision phase of the task predicts relapse (Gowin et al., 2014b). The second paper used a machine learning model to show that striatal activation during the outcome phase of the task was among the best predictors of relapse (Gowin et al., 2015, 2017b). Longitudinal data from the cocaine-dependent individuals have not been published, and as the groups were demographically similar (Table 1), we believe the cocaine-dependent group constitute a reasonable test sample. We sought to determine which analytic approach would provide more accurate predictions in the test sample and which was least likely to overfit (i.e. perform well in the training sample, but poorly on the test sample). We hypothesized that, relative to the linear model, the machine learning model would produce more accurate predictions in the test sample and show less evidence of overfitting.
Table 1.
Participant characteristics.
| Methamphetamine (N = 63) |
Cocaine (N = 29) |
||||
|---|---|---|---|---|---|
| N | % | N | % | Chi-square p-value | |
| Relapse | 18 | 28.6 | 17 | 58.6 | 0.006 |
| Male | 48 | 76.2 | 25 | 86.2 | 0.270 |
| VA patienta | 43 | 68.3 | 22 | 75.9 | 0.457 |
| Generalized anxiety disorder | 3 | 4.8 | 0 | 0 | 0.232 |
| Major depressive disorder | 2 | 3.2 | 0 | 0 | 0.332 |
| Alcohol dependence | 20 | 31.8 | 9 | 31.0 | 0.792 |
| Cannabis dependence | 13 | 20.6 | 9 | 31.0 | 0.277 |
| Opioid dependence | 2 | 3.2 | 5 | 17.2 | 0.018 |
| Median | IQR | Median | IQR | Mann-Whitney p-value | |
| Age | 37 | 18 | 46 | 12.5 | 0.040 |
| Verbal IQ | 109 | 13 | 105 | 15 | 0.031 |
| Years of education | 12 | 2 | 13 | 3 | 0.252 |
| Days since last use | 27 | 14 | 30 | 15.5 | 0.323 |
| Cigarettes/day | 15 | 12 | 10 | 20 | 0.147 |
| Lifetime uses of cocaine | 150 | 2298 | 6752 | 19,192 | <0.001 |
| Lifetime uses of methamphetamine | 5195 | 9900 | 0 | 128.5 | <0.001 |
Bold font indicates p < .05.
Participants were recruited from either a Veterans Affairs treatment program or a community hospital's treatment program.
2. Methods
2.1. Sample
Sixty-eight participants (Gowin et al., 2014b, 2015) with a diagnosis of methamphetamine dependence (training sample) and thirty-two participants with a diagnosis of cocaine dependence (test sample) were recruited from 28-day inpatient treatment programs at the Veterans Affairs (VA) San Diego Healthcare System and Scripps Green Hospital (La Jolla, CA). Participants underwent study procedures during the second or third week of treatment (days 10–24) and semi-structured clinical interviews revealed that no subjects were experiencing symptoms of withdrawal during neuroimaging sessions. Participants were randomly screened for the presence of drugs throughout the programs. Participants were informed that the goal of the study was to examine behavior and brain characteristics related to stimulant dependence. Written informed consent was obtained from all participants after study procedures were fully explained in accordance with the UC San Diego Human Research Protections Program.
2.2. Intake assessment
Lifetime DSM-IV Axis I diagnoses (including substance abuse and dependence) and Axis II antisocial personality disorder (ASPD) were assessed by experienced interviewers using the Semi Structured Assessment for the Genetics of Alcoholism (SSAGA), a validated, semi-structured interview that allows for quantification of lifetime drug use (Bucholz et al., 1994). Diagnoses were based on consensus meetings with a clinician specialized in substance use disorders (MPP) and trained study personnel. The following were exclusion criteria: (McLellan et al., 2000) antisocial personality disorder; (Marlatt and Donovan, 2005) current (past 6 months) Axis I panic disorder, social phobia, post-traumatic stress disorder, major depressive disorder; (Robinson and Berridge, 1993) lifetime bipolar disorder, schizophrenia, and obsessive compulsive disorder; (Koob and Volkow, 2010) current severe medical disorders requiring inpatient treatment or frequent medical visits; (Hyman and Malenka, 2001) use of medications that affect the hemodynamic response within the past 30 days; (Wise, 1996) current positive urine toxicology test; and (Paulus, 2007) history of head injuries with loss of consciousness for longer than 5 min. Participants in the methamphetamine- and cocaine-dependent groups could have co-morbid substance use disorders so long as their drug of choice was methamphetamine or cocaine, respectively.
During evaluation, participants also performed the North American Adult Reading Test (Uttl, 2002) as a measure of verbal intelligence (VIQ). Characteristics are summarized in Table 1.
2.3. Relapse assessment
Follow-up phone interviews were conducted 3, 6, 9, and 12 months after treatment to assess relapse. The interview was based on the substance use module of the SSAGA. For participants recruited through the VA, their medical records were examined to assess substance use following treatment in addition to the phone interviews. If there were discrepancies between medical records and self-reported responses, we assumed that any report of substance use was accurate, so the earliest date of relapse was used. Relapse was defined based on participants' self-reported substance use, and a single lapse constituted a relapse event. Since the treatment program advocated for abstinence from all substances, the use of any substance (e.g., alcohol) other than nicotine was counted as a relapse event. Five training and three test participants were lost during follow up; complete follow-up data were available for 92% of the sample.
2.4. Risky Gains Task (RGT)
The RGT (Paulus et al., 2003) is a risk-taking task that allows participants to earn money. Participants selected one of three sequentially appearing options—20¢, 40¢, or 80¢—on each of 96 trials. Each option appeared on the screen for 1 s in ascending order, and if the participants pressed the button when the option was shown, they received that amount. Participants were told that choosing 20¢ resulted in a guaranteed gain of 20¢, but choosing 40¢ or 80¢ resulted in a chance of either gaining or losing 40¢ or 80¢, respectively. Probabilities were not disclosed. All trials lasted three-and-a-half seconds regardless of which option was chosen. Participants were notified with text on the screen indicating whether they won or lost. There was no advantage to making risky or safe choices, as the task was designed so that choosing the same option on each trial would earn the same final payment of $19.20.
2.5. Image acquisition
A functional MRI scan was performed using a Signa EXCITE 3 T scanner (GE Healthcare, Milwaukee, Wisconsin T2*-weighted echoplanar imaging; TR = 2000 ms, TE = 32 ms, FoV = 230 × 230 mm2, 64 × 64 matrix, 30 2.6 mm axial slices with 1.4 mm gap, flip angle = 90°, total duration: 8 min, 32 s, 3.59 × 3.59 × 2.6 mm3 voxels). Six resting trials were collected at preset points during the task, which used to establish baseline activity level. For anatomical reference, a high-resolution, T-1 weighted image (TR = 8 ms, TE = 3 msec, FoV = 250 × 250 mm2, 192 × 256 matrix interpolated to a 256 × 256 matrix, flip angle = 12°, 172 sagittally acquired slices, .97×.97 × 1 mm3 voxels) was collected during the same session.
2.6. Structural MRI processing
Cortical reconstruction and volumetric segmentation was performed with the FreeSurfer 6.0.0 image analysis suite, which is documented and freely available for download online (http://surfer.nmr.mgh.harvard.edu/) (FreeSurfer, 2012).
2.7. fMRI processing
Data were preprocessed using Analysis of Functional NeuroImages (AFNI) software (Cox, 1996). Echoplanar images were aligned to anatomical images. Outlier voxels were identified in the aligned images and time points that had two standard deviations above the mean number of outlier voxels were excluded from subsequent analyses. Images were warped to Talairach space using an affine transformation and then visually inspected. Spatial smoothing was conducted using a 4 mm Gaussian kernel at full-width half-maximum. Data were analyzed using a multiple regression model based on a BOLD response function. Separate general linear models were performed using AFNI's 3dDeconvolve function for the decision and outcome phases. For the decision phase, regressors for 20¢, 40¢, and 80¢ choices were defined as starting at trial onset and concluding when the subject made a response. The sequential design meant that a participant could lose 40¢ and have the trial end even if they intended to choose 80¢. Thus, trials that resulted in a loss were excluded since the participant's intent was unknown. For the outcome phase, regressors for −80¢, −40¢, +20¢, +40¢, and + 80¢ were defined as starting when notification of the outcome was delivered and concluding at the end of the trial. Neural response was modeled based on a blood‑oxygenation level dependent (BOLD) signal with a 4–6 s peak after stimulus onset. Baseline activation was calculated from the BOLD signal during intertrial intervals and null trials (i.e., fixation on crosshairs without responding). Six motion parameters (roll, pitch and yaw; x, y, and z drift) were included as regressors of non-interest. Percent signal change was calculated by dividing the regressor of interest by the baseline regressor.
2.8. Linear model of relapse applied to test sample
We previously used a general linear model (the training model) to compare methamphetamine dependent individuals who relapsed with those who remained abstinent (Gowin et al., 2014b). The independent variables in the training model included 1) days since last drug use prior to treatment, 2) total lifetime stimulant uses (log-transformed due to skewness), 3) percentage of risky choices made during the Risky Gains Task, and 4) the difference in right anterior insula activity during a risky relative to a safe decision. A binary logistic regression was conducted, such that the dependent variable was the probability of relapse. A probability >.5 was classified as a relapse and a classification table was generated to assess accuracy.
The estimated probability of relapse was calculated for each individual. We examined probability as a continuous variable and generated receiver operator characteristic curves using the pROC package in R software, version 3.5.1 (Robin et al., 2011). Receiver operating characteristic curves show how classification ability changes as the discrimination threshold varies, as there is an inevitable tradeoff between sensitivity and specificity (Greiner et al., 2000). Area under the curve (AUC) was assessed with bootstrapping to estimate the 95% confidence interval, and this was used to determine whether the model performed better than chance (AUC = 0.5) based on the lower bound of the 95% confidence interval.
The same four variables were obtained for the test sample of cocaine dependent individuals. Using the regression coefficients from the training sample model, estimated probability of relapse was calculated for each cocaine dependent individual. A classification table and receiver operating characteristic analysis was conducted to assess performance.
Lastly, a machine learning model was generated in the training sample using the same four variables. The model we used was random forest (Breiman, 2001), implemented in R software using the randomForest package, with 2000 trees grown and two variables tested at each node. The model was also applied to the test sample. Classification tables and receiver operating characteristic analysis were conducted to assess performance.
2.9. Machine learning model of relapse applied to test sample
We previously used a machine learning technique called random forest (Breiman, 2001) to classify individuals as either relapsed or abstinent in the year after treatment (Gowin et al., 2015). The predictor variables were neural activity during the reward processing phase of the Risky Gains Task, as well as demographic (age, sex), percentage of risky choices made during the Risky Gains Task, psychometrics (Barratt Impulsiveness Scale, Sensation Seeking Scale, Temperament and Character Inventory), and clinical variables (total methamphetamine uses, total cocaine uses, drinks per week, cigarettes per day). For brain activity, the percent signal change was extracted from 72 anatomically-defined regions covering the entire brain (Fonzo et al., 2013). Reward processing activity was defined as the difference between percent signal change during the +80¢ relative to the +20¢ outcomes. The random forest model was generated in R using the randomForest package (Liaw and Wiener, 2002).
The random forest training model consisted of 2000 unpruned classification trees. As there were more individuals who remained abstinent, and this would bias the model toward predicting that every individual would remain abstinent, upsampling was used, such that each tree was generated with a random subsample of the total sample with the restriction that the subsample included equal numbers of individuals who relapsed and remained abstinent. Each decision tree was grown by randomly selecting 10 of the 109 predictor variables, and then determining which of those 10 variables could produce the best split of the sample. Random forest models generated using different numbers of trees or trying different numbers of variables at each node did not produce models that were more accurate. The best split was defined by the greatest increase in purity in the children nodes, such that if the parent node had a 50/50 split of relapsers and abstainers, the best split would produce one child node with a high proportion of relapsed individuals and another child node with a high proportion of abstinent individuals. The tree was grown until every terminal node resulted only a single class, either “relapsed” or “abstinent.” Since each tree was generated with only a subsample of the total training sample, the remaining participants constituted a test sample. Each participant was used in the test sample on approximately 1/3 of all trees, or 666 times. The proportion of trees that classified an individual as “relapse” was the dependent variable of the model, and this value is analogous to the dependent variable from the binary logistic regression: P(relapse). Thus, the same steps were taken to assess model performance. A proportion of relapse votes >0.5 was classified as a relapse in the binary model. A classification table was generated to assess accuracy. The proportion of trees voting for “relapse” for each individual was used for receiver operating characteristic analysis, as described above.
For the test sample of cocaine dependent individuals, the same 109 predictor variables were obtained. Using the collection of decision trees generated from the training sample model, each cocaine dependent individual was classified as either “relapsed” or “abstinent” in all 2000 trees. The proportion of trees voting for relapse was calculated for each cocaine dependent individual. A classification table was generated using a threshold of 0.5 to assess the accuracy of the model. The proportion of trees voting for relapse was used for receiver operating characteristic analysis, as described above.
3. Results
3.1. Sample characteristics
The samples shared similar demographic profiles (see Table 1), but a larger percentage of cocaine-dependent individuals (58.6%) relapsed in the year after treatment relative to methamphetamine-dependent individuals (28.6%). The cocaine dependent group was older and had a lower average IQ (p < .05). However, the groups had a similar percentage of males, patients from the VA hospital, and patients with an alcohol dependence. Cocaine- and methamphetamine-dependent individuals were similar in duration of abstinence prior to treatment and cigarettes smoked per day.
3.2. Linear model of relapse applied to test sample
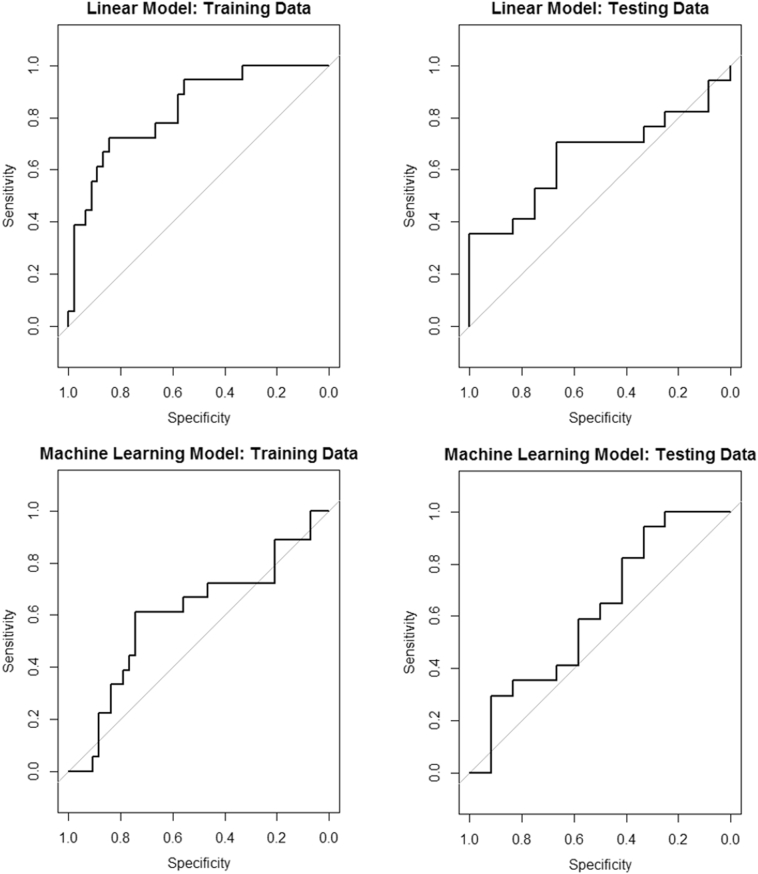
The previously published linear model of relapse for the training sample had an overall accuracy rate of 79.4%, and successfully classified 91.1% of individuals who remained abstinent but only 50.0% of individuals who relapsed (Table 2). The model showed that less differentiation in the right anterior insula for safe versus risky decisions was associated with a greater likelihood for relapse (Table 3). The receiver operating characteristic plot (Fig. 1) showed that predicted values were significantly better than chance (AUC = 0.83, 95% CI: 0.72–0.94). When this model was applied to the test sample, performance decreased by 0.18 and was no longer significantly better than chance (AUC = 0.65, 95% CI: 0.45–0.86).
Table 2.
Performance of the models of relapse prediction.
| Accuracy (%) | Sensitivity | Specificity | AUC | 95% CI | |
|---|---|---|---|---|---|
| Linear | |||||
| Linear implementation | |||||
| Training | 79.4 | 0.50 | 0.91 | 0.83 | 0.72–0.94 |
| Testing | 55.2 | 0.35 | 0.83 | 0.65 | 0.45–0.86 |
| Machine learning implementation | |||||
| Training | 73.0 | 0.33 | 0.89 | 0.69 | 0.54–0.83 |
| Testing | 62.1 | 0.47 | 0.83 | 0.64 | 0.43–0.86 |
| Machine learning | |||||
| Linear implementation | |||||
| Training | 75.4 | 0.27 | 0.95 | 0.72 | 0.57–0.87 |
| Testing | 41.3 | 0.06 | 0.92 | 0.53 | 0.32–0.76 |
| Machine learning implementation | |||||
| Training | 65.6 | 0.39 | 0.77 | 0.59 | 0.42–0.75 |
| Testing | 51.7 | 0.41 | 0.67 | 0.62 | 0.40–0.84 |
The linear model contained four variables (fMRI and clinical) and was applied directly to the test sample. The same four variables were also used in a machine learning implementation of that model. The machine learning model contained 110 variables (fMRI and clinical) and was also applied directly to the test sample. The four variables from the machine learning model that performed best were used to generate a linear model in the training sample, and this linear model was also applied to the test sample.
Table 3.
Linear and machine learning approaches using the variables from the original linear model.
| Linear model specification | ||||
|---|---|---|---|---|
| Coefficient | Odds Ratio | 95% Confidence interval | p value | |
| Risky choices (percent) | −1.97 | 0.14 | 0.01, 2.51 | 0.181 |
| Lifetime stimulant uses (log transformed) | −0.32 | 0.73 | 0.44, 1.21 | 0.216 |
| Days since last use | 0.02 | 1.02 | 0.99, 1.06 | 0.191 |
| Right insula activation to risky decision | −0.09 | 0.91 | 0.86, 0.96 | <0.001 |
| Machine learning model specification | ||
|---|---|---|
| Mean decrease accuracya | Mean decrease in Gini coefficientb | |
| Risky choices (percent) | −0.98 | 4.14 |
| Lifetime stimulant uses (log transformed) | 4.19 | 4.24 |
| Days since last use | −4.33 | 3.15 |
| Right insula activation to risky decision | 25.48 | 6.47 |
Mean decrease in accuracy indicates how much random permutation of a variable's values reduces the performance of the model, where large values for decrease in accuracy indicate that the variable is important.
The Gini coefficient indicates how well splits of the sample on the predictor variable lead to increased purity in the children nodes. High purity is a child node with a large majority of one class, such as 95% of individuals who relapsed.
Fig. 1.
Receiver operating characteristic curves for the predictive models. The linear model produced the best performance in the training sample, but had decreased performance in the test sample as assessed by area under the curve (ΔAUC = −0.18). The machine learning model performed modestly in the training sample, but had a similar performance in the test sample (ΔAUC = 0.03). Neither model produced useful predictions in the test sample.
3.3. Machine learning model using linear model variables
When a random forest model was generated from the four variables in the linear model, the accuracy on the training sample was 73.0%, which was similar to the linear model. Receiver operating characteristic analysis showed that predictions were better than chance (AUC = 0.69, 95%CI: 0.54–0.83). When the model was applied to the test sample, performance was similar to the training sample (AUC = 0.64, 95%CI: 0.43–0.86), with a decrease of 0.05, but predictive accuracy was no longer significantly better than chance. In the training sample, right anterior insula activation was the most important variable in the model (Table 3).
3.4. Machine learning model of relapse applied to test sample
The previously published machine learning model of relapse on the training sample had an overall accuracy rate of 65.6%, and successfully classified 76.7% of individuals who remained abstinent but only 38.9% of individuals who relapsed (Table 2). The receiver operating characteristic analysis (Fig. 1) did not perform significantly better than chance (AUC = 0.59, 95% CI: 0.42–0.75). When this model was applied to the test sample, it performed similarly (AUC = 0.62, 95% CI: 0.40–0.84), with an increase in AUC of 0.03. The four top performing variables in this model were activation levels in the right globus pallidus, the left transverse temporal gyrus, the cingulate, and the right inferior temporal gyrus.
3.5. Linear model using best variables from machine learning model
When the four top performing variables form the machine learning model were used to generate a linear model in the training sample, it produced an overall accuracy rate of 75.4% and successfully classified 95.3% of individuals who remained abstinent but only 27.8% of individuals who relapsed. The model approximated the approach of assuming everyone would remain abstinent, and this led to performance significantly better than chance (AUC = 0.72, 95% CI: 0.57–0.87). While this approach succeeded in the training sample, it produced poor predictions in the testing sample, with an overall accuracy of 41.3%. It performed at chance levels (AUC = 0.53, 95% CI: 0.32–0.76), showing a decrease in AUC of 0.19 relative to the training sample.
4. Discussion
This study investigated whether a machine learning model of functional neuroimaging and clinical variables could produce superior performance at predicting relapse to stimulant use when compared to a linear model. This represents the first study to compare performance across two independent samples using both linear and machine learning models to predict relapse. As expected, the original linear model showed evidence of overfitting to the training sample, as evidenced by a decrease in AUC of 0.18 in the test sample. In contrast, a machine learning model using the same variables resulted in a similar AUC in the test and training samples. Similarly, the original machine learning model produced similar AUC in the training and test samples whereas the linear model performed well in the training sample but poorly in the test sample. However, both models performed poorly overall, with neither model performing better than chance in the test sample. This indicates that relapse models acquired using small training samples may no longer be predictive of relapse when applied to novel clinical samples.
Linear and machine learning models each have advantages. For example, linear models are easier to interpret. As shown in Table 3, the coefficient estimates show how a change in each variable affects the probability of relapse. In our study, the linear model suggests that individuals with greater differentiation in insular processing between risky and safe decisions are more likely to maintain abstinence. In contrast, although the machine learning model also shows that insula activation is important for predicting relapse, it does not specify the direction of the relationship. It is unclear from the measure of variable importance whether increased insula activation increases or decreases the probability of relapse. A strength of the machine learning model is that accuracy was similar in the training and test samples, providing confidence about a model's performance in a novel sample. Machine learning models are also able to test many variables simultaneously without violating model assumptions. For example, the original machine learning model had 109 predictor variables, but linear models should not have more predictor variables than observations. The tradeoff between the mechanistic explanations of the linear model versus the more stable performance of the machine learning model likely depend on the goals of the analysis. If the goal is to generate a robust predictive model, then a machine learning approach is likely preferable. Once the best performing variables are identified, they can be examined with a linear model in an independent sample to understand how the variables affect outcomes.
The limitations of this study included method for relapse assessment, the imaging task design, the largely male, veteran sample, and a relatively small sample size. This study assessed relapse via retrospective self-reported drug use as opposed to urine samples. Nonetheless, allowing for relapse assessment over the phone did facilitate higher retention. We used a risk-taking task that does not involve a jitter between decision and outcome, so the neuroimaging variables are not fully independent, which could influence the results and reduces the ability to draw conclusions about specific neural processes. Methamphetamine and cocaine do not produce identical effects on the brain, so the classes of drugs used may have influenced results. The relapse rate for the methamphetamine-dependent sample was low, whereas the rate for the cocaine-dependent sample was higher. The sample was primarily recruited from a Veterans Affairs hospital and was predominantly male, so it will be important to test these effects in a sample with more females to see if the results generalize. This study also did not measure important predictors of relapse such as environmental and genetic factors, which were therefore not captured in our models. Lastly, with smaller sample sizes, parameter estimates can be imprecise, so all the findings here should be reexamined in larger samples.
Both linear and machine learning models derived from a training sample of individuals with methamphetamine dependence did not accurately predict relapse when applied to a test sample of individuals with cocaine dependence. Future studies should make an effort to include cross-validation regardless of which analytic approach they use. Furthermore, the use of larger samples with more diverse predictor variables that address the wide range of factors which contribute to relapse would likely produce more stable and valid models.
Disclosures
All authors report no conflict of interests.
Acknowledgements
This work was supported by grants from the National Institutes of Health (R01-DA016663, P20-DA027834, R01-DA027797, and R01-DA018307, PI Paulus; K99-AA024778, PI Gowin; K23-MH113708 PI Ball; T32 AA013525, F31 AA027169 May). Sponsors played no role in the design, conduct of the study, collection, management, analysis, and interpretation of the data; or with preparation, review, or approval of the manuscript. We would like to thank Dr. F. Berger, T. Flagan, H. Donovan, D. Leland, M. Mortezaei and B. Friedrich for assistance and support during data acquisition. We would also like to thank Ty Brumback for reviewing VA records to assess relapse in participants.
References
- American Psychiatric Association . 5th ed. American Psychiatric Association; Washington, D.C.: 2013. American Psychiatric Association. DSM-5 Task Force.: Diagnostic and Statistical Manual of Mental Disorders: DSM-5. [Google Scholar]
- Bolla K.I., Eldreth D.A., London E.D., Kiehl K.A., Mouratidis M., Contoreggi C., Matochik J.A., Kurian V., Cadet J.L., Kimes A.S., Funderburk F.R., Ernst M. Orbitofrontal cortex dysfunction in abstinent cocaine abusers performing a decision-making task. NeuroImage. 2003;19:1085–1094. doi: 10.1016/s1053-8119(03)00113-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breiman L. Machine Learning. Vol. 45. 2001. Random forests; pp. 5–32. [Google Scholar]
- Bucholz K.K., Cadoret R., Cloninger C.R., Dinwiddie S.H., Hesselbrock V., Nurnberger J., Jr., Reich T., Schmidt I., Schuckit M.A. A new, semi-structured psychiatric interview for use in genetic linkage studies: a report on the reliability of the SSAGA. J. Stud. Alcohol. 1994;55:149–158. doi: 10.15288/jsa.1994.55.149. [DOI] [PubMed] [Google Scholar]
- Cousijn J., Wiers R.W., Ridderinkhof K.R., Brink W., Veltman D.J., Porrino L.J., Goudriaan A.E. Individual differences in decision making and reward processing predict changes in cannabis use: a prospective functional magnetic resonance imaging study. Addict. Biol. 2013;18:1013–1023. doi: 10.1111/j.1369-1600.2012.00498.x. [DOI] [PubMed] [Google Scholar]
- Cox R.W. AFNI: software for analysis and visualization of functional magnetic resonance neuroimages. Comput. Biomed. Res. 1996;29:162–173. doi: 10.1006/cbmr.1996.0014. [DOI] [PubMed] [Google Scholar]
- Fonzo G.A., Flagan T.M., Sullivan S., Allard C.B., Grimes E.M., Simmons A.N., Paulus M.P., Stein M.B. Neural functional and structural correlates of childhood maltreatment in women with intimate-partner violence-related posttraumatic stress disorder. Psychiatry Res. 2013;211:93–103. doi: 10.1016/j.pscychresns.2012.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- FreeSurfer Fischl B. NeuroImage. 2012;62:774–781. doi: 10.1016/j.neuroimage.2012.01.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilman J.M., Smith A.R., Bjork J.M., Ramchandani V.A., Momenan R., Hommer D.W. Cumulative gains enhance striatal response to reward opportunities in alcohol-dependent patients. Addict. Biol. 2015;20:580–593. doi: 10.1111/adb.12147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gowin J.L., Mackey S., Paulus M.P. Altered risk-related processing in substance users: imbalance of pain and gain. Drug Alcohol Depend. 2013;132:13–21. doi: 10.1016/j.drugalcdep.2013.03.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gowin J.L., Stewart J.L., May A.C., Ball T.M., Wittmann M., Tapert S.F., Paulus M.P. Altered cingulate and insular cortex activation during risk-taking in methamphetamine dependence: losses lose impact. Addiction. 2014;109:237–247. doi: 10.1111/add.12354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gowin J.L., Harle K.M., Stewart J.L., Wittmann M., Tapert S.F., Paulus M.P. Attenuated insular processing during risk predicts relapse in early abstinent methamphetamine-dependent individuals. Neuropsychopharmacology. 2014;39:1379–1387. doi: 10.1038/npp.2013.333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gowin J.L., Ball T.M., Wittmann M., Tapert S.F., Paulus M.P. Individualized relapse prediction: Personality measures and striatal and insular activity during reward-processing robustly predict relapse. Drug Alcohol Depend. 2015;152:93–101. doi: 10.1016/j.drugalcdep.2015.04.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gowin J.L., May A.C., Wittmann M., Tapert S.F., Paulus M.P. Doubling down: increased risk-taking behavior following a loss by individuals with cocaine use disorder is associated with striatal and anterior cingulate dysfunction. Biol. Psychiatry. 2017;2:94–103. doi: 10.1016/j.bpsc.2016.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gowin J.L., Ball T.M., Wittmann M., Tapert S.F., Paulus M.P. Corrigendum to “Individualized relapse prediction: Personality measures and striatal and insular activity during reward-processing robustly predict relapse”[Drug and Alcohol Dependence 152 (2015) 93–101] Drug Alcohol Depend. 2017;175:255. doi: 10.1016/j.drugalcdep.2015.04.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gowin J.L., Sloan M.E., Ramchandani V.A., Paulus M.P., Lane S.D. Differences in decision-making as a function of drug of choice. Pharmacol. Biochem. Behav. 2018;164:118–124. doi: 10.1016/j.pbb.2017.09.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greiner M., Pfeiffer D., Smith R.D. Principles and practical application of the receiver-operating characteristic analysis for diagnostic tests. Prevent. Vet. Med. 2000;45:23–41. doi: 10.1016/s0167-5877(00)00115-x. [DOI] [PubMed] [Google Scholar]
- Hyman S.E., Malenka R.C. Addiction and the brain: the neurobiology of compulsion and its persistence. Nat. Rev. Neurosci. 2001;2:695. doi: 10.1038/35094560. [DOI] [PubMed] [Google Scholar]
- Jordan M.I., Mitchell T.M. Machine learning: Trends, perspectives, and prospects. Science. 2015;349:255–260. doi: 10.1126/science.aaa8415. [DOI] [PubMed] [Google Scholar]
- Kahneman D., Tversky A. Prospect theory: an analysis of decision under risk. Econometrica. 1979:263–291. [Google Scholar]
- Koob G.F., Volkow N.D. Neurocircuitry of addiction. Neuropsychopharmacology. 2010;35:217. doi: 10.1038/npp.2009.110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LeCun Y., Bengio Y., Hinton G. Deep learning. Nature. 2015;521:436. doi: 10.1038/nature14539. [DOI] [PubMed] [Google Scholar]
- Liaw A., Wiener M. R news. Vol. 2. 2002. Classification and regression by randomForest; pp. 18–22. [Google Scholar]
- Marlatt G.A., Donovan D.M. Guilford Press; 2005. Relapse Prevention: Maintenance Strategies in the Treatment of Addictive Behaviors. [Google Scholar]
- McLellan A.T., Lewis D.C., O'Brien C.P., Kleber H.D. Drug dependence, a chronic medical illness: implications for treatment, insurance, and outcomes evaluation. JAMA. 2000;284:1689–1695. doi: 10.1001/jama.284.13.1689. [DOI] [PubMed] [Google Scholar]
- Paulus M.P. Decision-making dysfunctions in psychiatry--altered homeostatic processing? Science. 2007;318:602–606. doi: 10.1126/science.1142997. [DOI] [PubMed] [Google Scholar]
- Paulus M.P. Pragmatism instead of mechanism: a call for impactful biological psychiatry. JAMA Psychiatry. 2015;72:631–632. doi: 10.1001/jamapsychiatry.2015.0497. [DOI] [PubMed] [Google Scholar]
- Paulus M.P., Rogalsky C., Simmons A., Feinstein J.S., Stein M.B. Increased activation in the right insula during risk-taking decision making is related to harm avoidance and neuroticism. NeuroImage. 2003;19:1439–1448. doi: 10.1016/s1053-8119(03)00251-9. [DOI] [PubMed] [Google Scholar]
- Pereira F., Mitchell T., Botvinick M. Machine learning classifiers and fMRI: a tutorial overview. NeuroImage. 2009;45:S199–S209. doi: 10.1016/j.neuroimage.2008.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pine D.S., Leibenluft E. Biomarkers with a mechanistic focus. JAMA Psychiatry. 2015;72:633–634. doi: 10.1001/jamapsychiatry.2015.0498. [DOI] [PubMed] [Google Scholar]
- Robin X., Turck N., Hainard A., Tiberti N., Lisacek F., Sanchez J.-C., Müller M. pROC: an open-source package for R and S+ to analyze and compare ROC curves. BMC Bioinform. 2011;12:77. doi: 10.1186/1471-2105-12-77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson T.E., Berridge K.C. The neural basis of drug craving: an incentive-sensitization theory of addiction. Brain Res. Rev. 1993;18:247–291. doi: 10.1016/0165-0173(93)90013-p. [DOI] [PubMed] [Google Scholar]
- Scholkopf B., Sung K.-K., Burges C.J., Girosi F., Niyogi P., Poggio T., Vapnik V. Comparing support vector machines with Gaussian kernels to radial basis function classifiers. IEEE Trans. Signal Process. 1997;45:2758–2765. [Google Scholar]
- Tanabe J., Thompson L., Claus E., Dalwani M., Hutchison K., Banich M.T. Prefrontal cortex activity is reduced in gambling and nongambling substance users during decision-making. Hum. Brain Mapp. 2007;28:1276–1286. doi: 10.1002/hbm.20344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uttl B. North American Adult Reading Test: age norms, reliability, and validity. J. Clin. Exp. Neuropsychol. 2002;24:1123–1137. doi: 10.1076/jcen.24.8.1123.8375. [DOI] [PubMed] [Google Scholar]
- Volkow N.D., Koob G., Baler R. Biomarkers in substance use disorders. ACS Chem. Neurosci. 2015;6:522–525. doi: 10.1021/acschemneuro.5b00067. [DOI] [PubMed] [Google Scholar]
- Wise R.A. Neurobiology of addiction. Curr. Opin. Neurobiol. 1996;6:243–251. doi: 10.1016/s0959-4388(96)80079-1. [DOI] [PubMed] [Google Scholar]