Fibonacci numbers: A population dynamics perspective

Abstract

Fibonacci numbers or Fibonacci sequence is among the most popular numbers or sequence in Mathematics. In this paper, we discuss the sequence in a population dynamics perspective. We discuss the early development of the sequence and interpret the sequence as a number of a hypothetical population. The governing equation that produces the Fibonacci sequence is written in a matrix form having a square matrix A. We show the relation of the eigenvalues, eigenvectors, and eigenspaces to the matrix with the dynamics of the sequence. We also generalize the matrix equation so that it governs a more realistic model of the hypothetical population. Some results regarding the modified golden ratio are presented.

1. Introduction

Fibonacci numbers or Fibonacci sequence is among the most popular numbers or sequence in mathematics. The sequence is in the form of 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, .... which first appeared in Liber Abaci book of Leonardo Pisano in 1202 (Sigler, 2002). It is often known as the Lame sequence (Roberts, 1992) or Viranka number (Goonatilake, 1998) as many other ancient mathematicians have used this sequence in their document. The first mathematician who called it Fibonacci sequence is Edouard Lucas in 19-th century (Gardner, 1996). Lucas also showed that the Fibonacci sequence appears in the shallow diagonal of the Pascal triangle and he also defines a sequence based on the Fibonacci numbers, which is currently known as Lucas number. The complete information of the sequence can be found in the On-Line Encyclopedia of Integer Sequence (OEIS, 2017).

One of the important features arising from the Fibonacci sequence is the Golden Ratio. It is the ratio of the consecutive numbers in the Fibonacci sequence which converges to 1.61803398875 (Livio, 2002). The ratio has been found in many areas of applications such as in analyzing the proportions of natural objects and man-made systems. The ratio can also be found in modern applications such as financial analysis and plastic surgery (Letzter, 2016). Given that it has many applications, many studies have been conducted to extend the sequence. The extension of the Fibonacci sequence is also widespread and penetrated many branches of mathematics including dynamical system. For example, the Fibonacci sequence has been extended to tribonacci, tetranacci, and other higher order n-nacci sequences (Wolfram, 1998). The n-nacci sequence has found application in coin tossing problem (Weisstein, a, Weisstein, b; Griffiths, 2011). On the other hand, the Fibonacci sequence also has been extended by generalizing the integer to real and complex numbers (Harman, 1981, Asci and Gurel, 2013), quarternion (Halici, 2012), generalized quarternion (Akyigit et al., 2014, Tan et al., 2016).

The other extension of Fibonacci sequence has been done by Bruin (2007) and Bruin and Volkova (2005) who developed a Fibonacci-like map or a kneading map. They show an important dynamical structure in the model that is the properties of the absolute continuous invariant measure. However, Li and Wang (2014) developed a new class of generalized Fibonacci sequence by considering a unimodal maps and show that, in some circumstances, the map has no absolutely continuous invariant probability measure. The result is different from the one found by Bruin and reveals the richness of dynamical properties of mathematical structures developed from Fibonacci sequence – or alike. The brief review above shows that the extension of Fibonacci sequence is directed to a more abstract manner. Historically the Fibonacci sequence appeared in a population problem as the following statement given by Leonardo Pisano (Sigler, 2002) who wrote “A certain man put a pair of rabbits in a place surrounded on all sides by a wall. How many pairs of rabbits can be produced from that pair in a year if it is supposed that every month each pair begets a new pair which from the second month on becomes productive?”. In this paper we review the Fibonacci sequence from population dynamic perspective. We also generalize the sequence in this perspective and give some population interpretation to the model. Some mathematical results are obtained. We begin with a brief explanation on the Fibonacci sequence in a matrix equation in the following section.

2. Theory

Let $X(n)$ and $Y(n)$ be the numbers of adults and juveniles of a hypothetical population, respectively, with the dynamics is given by the recursive equations

$$\begin{array}{cc}\hfill X(n+1)& =X(n)+Y(n),\hfill \\ \hfill Y(n+1)& =X(n)\hfill \end{array}$$ (1)

with $X(0)=1$ and $Y(0)=0$. The system of equations above can be written in the form

$$X(n+1)=X(n)+X(n-1)$$ (2)

which is clearly is Fibonacci recursive equation for the Fibonacci sequence

$$0,1,1,2,3,5,8,13,21,34,55,89,....$$ (3)

The system has an explicit solution in the form Binet Formula (Weisstein, a, Weisstein, b), but some authors claimed this formula is found by de Moivre in 18 century (Knuth, 1997),

$$X(n)=\frac{1}{\sqrt{5}}({\left(\frac{1+\sqrt{5}}{2}\right)}^n-{\left(\frac{1-\sqrt{5}}{2}\right)}^n).$$ (4)

Note that the system of equations (1) can be written in the form

$$\left[\begin{array}{c}\hfill X(n+1)\hfill \\ \hfill Y(n+1)\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill \end{array}\right]\left[\begin{array}{c}\hfill X(n)\hfill \\ \hfill Y(n)\hfill \end{array}\right].$$ (5)

This equation generates the Fibonacci sequence regardless the initial values of the vector ${[X(0),Y(0)]}^t$ where the notation ^t denotes the transpose of the associated vector. As the examples are the following. Suppose that we have different initial values, $X(0)=1$ and $Y(0)=0$, then by considering equation (5) we have the following sequence:

$$\begin{array}{c}\left[\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \end{array}\right]==>\left[\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill \end{array}\right]\left[\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \end{array}\right]=\left[\begin{array}{c}\hfill 1\hfill \\ \hfill 1\hfill \end{array}\right]==>\left[\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill \end{array}\right]\left[\begin{array}{c}\hfill 1\hfill \\ \hfill 1\hfill \end{array}\right]=\left[\begin{array}{c}\hfill 2\hfill \\ \hfill 1\hfill \end{array}\right]==>\hfill \\ \left[\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill \end{array}\right]\left[\begin{array}{c}\hfill 2\hfill \\ \hfill 1\hfill \end{array}\right]=\left[\begin{array}{c}\hfill 3\hfill \\ \hfill 2\hfill \end{array}\right]==>\left[\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill \end{array}\right]\left[\begin{array}{c}\hfill 3\hfill \\ \hfill 2\hfill \end{array}\right]=\left[\begin{array}{c}\hfill 5\hfill \\ \hfill 3\hfill \end{array}\right]==>\left[\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill \end{array}\right]\left[\begin{array}{c}\hfill 5\hfill \\ \hfill 3\hfill \end{array}\right]=\left[\begin{array}{c}\hfill 8\hfill \\ \hfill 5\hfill \end{array}\right].\hfill \end{array}$$

Next suppose that $X(0)=0$ and $Y(0)=1$, then by considering equation (5) we have the following sequence:

$$\begin{array}{c}\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 1\hfill \end{array}\right]==>\left[\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill \end{array}\right]\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 1\hfill \end{array}\right]=\left[\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \end{array}\right]==>\left[\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill \end{array}\right]\left[\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \end{array}\right]=\left[\begin{array}{c}\hfill 1\hfill \\ \hfill 1\hfill \end{array}\right]==>\hfill \\ \left[\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill \end{array}\right]\left[\begin{array}{c}\hfill 1\hfill \\ \hfill 1\hfill \end{array}\right]=\left[\begin{array}{c}\hfill 2\hfill \\ \hfill 1\hfill \end{array}\right]==>\left[\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill \end{array}\right]\left[\begin{array}{c}\hfill 2\hfill \\ \hfill 1\hfill \end{array}\right]=\left[\begin{array}{c}\hfill 3\hfill \\ \hfill 2\hfill \end{array}\right]==>\hfill \\ \left[\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill \end{array}\right]\left[\begin{array}{c}\hfill 3\hfill \\ \hfill 2\hfill \end{array}\right]=\left[\begin{array}{c}\hfill 5\hfill \\ \hfill 3\hfill \end{array}\right]==>\left[\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill \end{array}\right]\left[\begin{array}{c}\hfill 5\hfill \\ \hfill 3\hfill \end{array}\right]=\left[\begin{array}{c}\hfill 8\hfill \\ \hfill 5\hfill \end{array}\right].\hfill \end{array}$$

In the next section we show that any initial value is indeed attracted to the eigenspace of the Fibonacci matrix

$$A=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill \end{array}\right].$$ (6)

3. Results & discussion

In this section we present some results regarding the solution of equation (5), its properties and the relation to the matrix A in (6). A generalization of equation (5) is also considered. To begin with, note that the characteristic equation of matrix A is ${\lambda }^2-\lambda -1=0$, hence it has two eigenvalues ${\lambda }_1=\frac{1}{2}+\frac{1}{2}\sqrt{5}$ and ${\lambda }_1=\frac{1}{2}-\frac{1}{2}\sqrt{5}$ with the corresponding eigenvectors ${[X,Y]}^t={[\frac{1}{2}+\frac{1}{2}\sqrt{5},1]}^t\alpha$ and ${[X,Y]}^t={[\frac{1}{2}-\frac{1}{2}\sqrt{5},1]}^t\alpha$, respectively, with $\alpha \in \Re$ and $\alpha \ne 0$. There are two eigenspaces, corresponding to ${\lambda }_1$ and ${\lambda }_2$. The eigenspace corresponding to the largest eigenvalue ${\lambda }_1$ is $\left\{{[\frac{1}{2}+\frac{1}{2}\sqrt{5},1]}^t\right\}$ which consists of all linear combinations of the vector ${[\frac{1}{2}+\frac{1}{2}\sqrt{5},1]}^t$ plus the zero vector. While the eigenspace corresponding to the other eigenvalue ${\lambda }_2$ is $\left\{{[\frac{1}{2}-\frac{1}{2}\sqrt{5},1]}^t\right\}$ which consists of all linear combinations of the vector ${[\frac{1}{2}-\frac{1}{2}\sqrt{5},1]}^t$ plus the zero vector.

Let us concentrate in the eigenspace associated with the largest eigenvalue ${\lambda }_1$. Figure 1, Figure 2 show the eigenspace as the line in the XY plane. Since the line connects the origin $(0,0)$ with the point of $((1+\sqrt{5})/2,1)$, then the line is given by

$$y=\frac{2}{(1+\sqrt{5})}x\stackrel{def}{=}{E}_{{\lambda }_1}(A).$$ (7)

Let us consider the vector ${[x,y]}^t$ as a point $(x,y)$ in XY plane. Figure 1 shows the iteration of Equation (5) for several initial values, such as (0,1), (1,1), (2,1), and (0,2) (upper figure). Some of the initial values are from the Fibonacci sequence, such as (1,1) and (2,1). Others are arbitrary, such as (0,2). However, all initial values are eventually brought to the eigenspace of the largest eigenvalue by the recurrence equation (5). Even Figure 2 shows that it remains true for the relatively large arbitrary couples of $(X(0),Y(0))$. This observation leads to the following theorems.

Theorem 1

Let $(X_0,Y_0)$ be any point with $X_0$ and $Y_0$ are neighboring Fibonacci numbers. Then for any initial value $(X_0,Y_0)$ the iteration of equation (5) converges to the eigenspace $E_{{\lambda }_1}(A)$.

Figure 1.

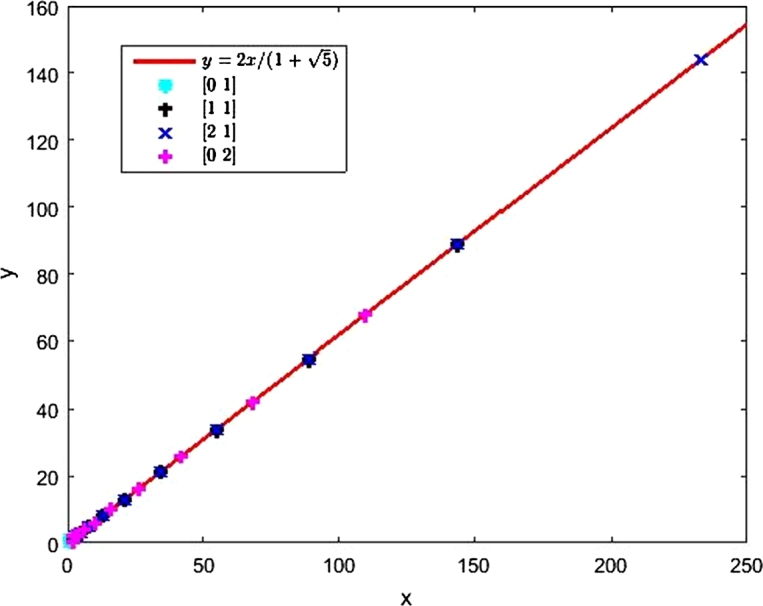
Iterations of equation (5) with small Fibonacci and non Fibonacci numbers as initial values.

Figure 2.

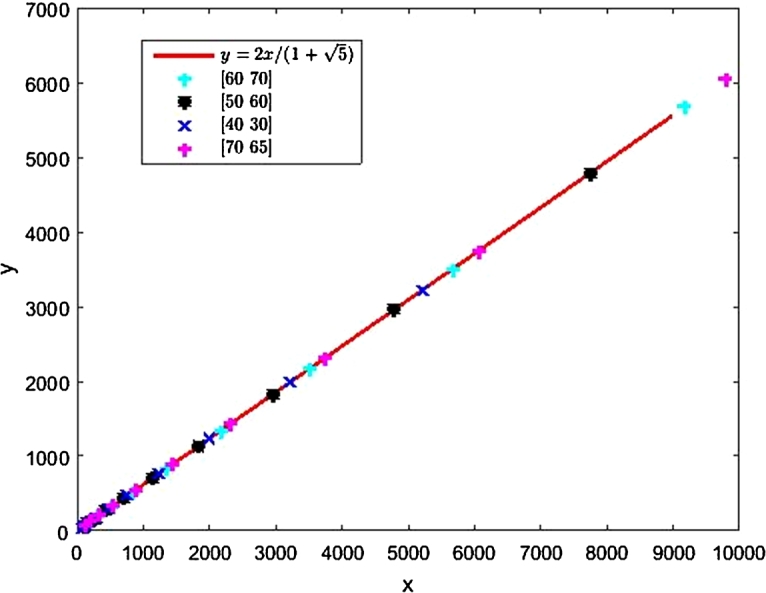
Iterations of equation (5) with relatively large integer as initial values.

Proof

We will show that the distance between the line of eigenspace of the largest eigenvalue and the n-th iteration of the initial value point $(a,b)$ by the recursive Equation (2) is eventually close to zero. To prove this let us start with an initial value $(X_0,Y_0)$ with $X_0$ and $Y_0$ are a neighboring Fibonacci number so that its n-th iteration is $(a,b)$. Hence we have $(a,b)=(x_n,x_{(n-1)})$ where $x_n=\frac{1}{\sqrt{5}}({\left(\frac{1+\sqrt{5}}{2}\right)}^n-{\left(\frac{1-\sqrt{5}}{2}\right)}^n)$. It is known that the distance of $(a,b)$ to any line $px+qy+r=0$ is given by $d=\frac{|pa+qb+r|}{\sqrt{p^2+q^2}}$. We construct the eigenspace linear equation as follows. The line connects the point $(0,0)$ to the eigenspace base point $(\frac{1+\sqrt{5}}{2},1)$, resulting in the equation is $y=\frac{2}{1+\sqrt{5}}x$ which equivalent to $y=\frac{2}{1+\sqrt{5}}x-y=0$. Since $p=\frac{2}{1+\sqrt{5}}x$, $q=-1$, and $r=0$ then we have

$$d=\frac{|\left(\frac{2}{1+\sqrt{5}}\right)a-b|}{\sqrt{{\left(\frac{2}{1+\sqrt{5}}\right)}^2+1}},$$

with $(a,b)=(x_n,x_{(n-1)})$ and $x_n=\frac{1}{\sqrt{5}}({\left(\frac{1+\sqrt{5}}{2}\right)}^n-{\left(\frac{1-\sqrt{5}}{2}\right)}^n)$, and hence d is given by

$$\begin{array}{c}\hfill \frac{\left(\frac{2}{1+\sqrt{5}}\right)\frac{1}{\sqrt{5}}({\left(\frac{1+\sqrt{5}}{2}\right)}^n-{\left(\frac{1-\sqrt{5}}{2}\right)}^n)-\frac{1}{\sqrt{5}}({\left(\frac{1+\sqrt{5}}{2}\right)}^{n-1}-{\left(\frac{1-\sqrt{5}}{2}\right)}^{n-1})}{\sqrt{{\left(\frac{2}{1+\sqrt{5}}\right)}^2+1}}\end{array}\stackrel{def}{=}F(n)$$

It can be shown that ${\lim }_{n\to \infty }F(n)=0$ which proves that eventually the sequence is trapped by the eigenspace $E_{\lambda }(A)$. □

Remark

As pointed out by one of the reviewers, from the dynamical system theory point of view, the dynamic of equation (5) is characterized by the dynamic matrix A that has two eigenvalues. The smaller one is less than unity while then second one is larger. Consequently, “starting from a generic initial point $(X_0,Y_0)$, the state component which is aligned with the eigenvector of the smaller (convergent) eigenvalue will vanish with n, while the one aligned with the eigenvector of the larger (divergent) eigenvalue will grow indefinitely”.

Theorem 2

Let $(X_0,Y_0)$ be any positive integer in the XY plane. Then, starting from $(X_0,Y_0)$ as the initial value, the n-th iteration of Equation (5) converges to the eigenspace $E_{{\lambda }_1}(A)$.

Proof

Consider the matrix A and let us define P and D as follows:

$$P=\left[\begin{array}{cc}\hfill \frac{1+\sqrt{5}}{2}\hfill & \hfill \frac{1-\sqrt{5}}{2}\hfill \\ \hfill 1\hfill & \hfill 1\hfill \end{array}\right]\text{and}D=\left[\begin{array}{cc}\hfill \frac{1+\sqrt{5}}{2}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{1-\sqrt{5}}{2}\hfill \end{array}\right]$$

The columns of P are the eigenvectors of A and the diagonal of D is the eigenvalues of A, and hence we have $A=PD{P}^{-1}$. Furthermore we have $A^n=PD{P}^{-1}PD{P}^{-1}\dots PD{P}^{-1}=P{D}^n{P}^{-1}$ that leads to

$$A^n=\left[\begin{array}{cc}\hfill \frac{\sqrt{5}}{5}{\left(\frac{1+\sqrt{5}}{2}\right)}^{n+1}-\frac{\sqrt{5}}{5}{\left(\frac{1-\sqrt{5}}{2}\right)}^{n+1}\hfill & \hfill \left(\frac{5-\sqrt{5}}{10}\right){\left(\frac{1+\sqrt{5}}{2}\right)}^{n+1}+\left(\frac{5+\sqrt{5}}{10}\right){\left(\frac{1-\sqrt{5}}{2}\right)}^{n+1}\hfill \\ \hfill \frac{\sqrt{5}}{5}{\left(\frac{1+\sqrt{5}}{2}\right)}^n-\frac{\sqrt{5}}{5}{\left(\frac{1-\sqrt{5}}{2}\right)}^n\hfill & \hfill \left(\frac{5-\sqrt{5}}{10}\right){\left(\frac{1+\sqrt{5}}{2}\right)}^n+\left(\frac{5+\sqrt{5}}{10}\right){\left(\frac{1-\sqrt{5}}{2}\right)}^n\hfill \end{array}\right]$$

Let us see for the case $n\to \infty$. In this case ${\lim }_{n\to \infty }{\left(\frac{1-\sqrt{5}}{2}\right)}^n=0$ and hence for large n we have

$$A^n\approx \left[\begin{array}{cc}\hfill \frac{\sqrt{5}}{5}{\left(\frac{1+\sqrt{5}}{2}\right)}^{n+1}\hfill & \hfill \left(\frac{5-\sqrt{5}}{10}\right){\left(\frac{1+\sqrt{5}}{2}\right)}^{n+1}\hfill \\ \hfill \frac{\sqrt{5}}{5}{\left(\frac{1+\sqrt{5}}{2}\right)}^n\hfill & \hfill \left(\frac{5-\sqrt{5}}{10}\right){\left(\frac{1+\sqrt{5}}{2}\right)}^n\hfill \end{array}\right]$$

Further for any initial value $\left[\begin{array}{c}\hfill X_0\hfill \\ \hfill Y_0\hfill \end{array}\right]$ we have

$$\left[\begin{array}{c}\hfill X_n\hfill \\ \hfill Y_n\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill \frac{\sqrt{5}}{5}{\left(\frac{1+\sqrt{5}}{2}\right)}^{n+1}\hfill & \hfill \left(\frac{5-\sqrt{5}}{10}\right){\left(\frac{1+\sqrt{5}}{2}\right)}^{n+1}\hfill \\ \hfill \frac{\sqrt{5}}{5}{\left(\frac{1+\sqrt{5}}{2}\right)}^n\hfill & \hfill \left(\frac{5-\sqrt{5}}{10}\right){\left(\frac{1+\sqrt{5}}{2}\right)}^n\hfill \end{array}\right]\left[\begin{array}{c}\hfill X_0\hfill \\ \hfill Y_0\hfill \end{array}\right]$$

which equivalent to:

$$\begin{array}{cc}\hfill X_n& =\frac{\sqrt{5}}{5}{\left(\frac{1+\sqrt{5}}{2}\right)}^{n+1}{X}_0+\left(\frac{5-\sqrt{5}}{10}\right){\left(\frac{1+\sqrt{5}}{2}\right)}^{n+1}{Y}_0\hfill \\ \hfill Y_n& =\frac{\sqrt{5}}{5}{\left(\frac{1+\sqrt{5}}{2}\right)}^n{X}_0+\left(\frac{5-\sqrt{5}}{10}\right){\left(\frac{1+\sqrt{5}}{2}\right)}^n{Y}_0.\hfill \end{array}$$

It is obvious that

$$Y_n=\left(\frac{2}{1+\sqrt{5}}\right)X_n$$

which is definitely is the equation of the eigenspace in (7). This shows that for any integer initial values ${[X_0,Y_0]}^t$ the iteration of equation (5) is eventually trapped by the eigenspace $E_{{\lambda }_1}(A)$. □

Remark

Theorem 2 actually holds for any real numbers. See Figure 3 that illustrate that the trapping properties of the eigenspace of the largest eigenvalue remains true for arbitrary real initial values.

Figure 3.

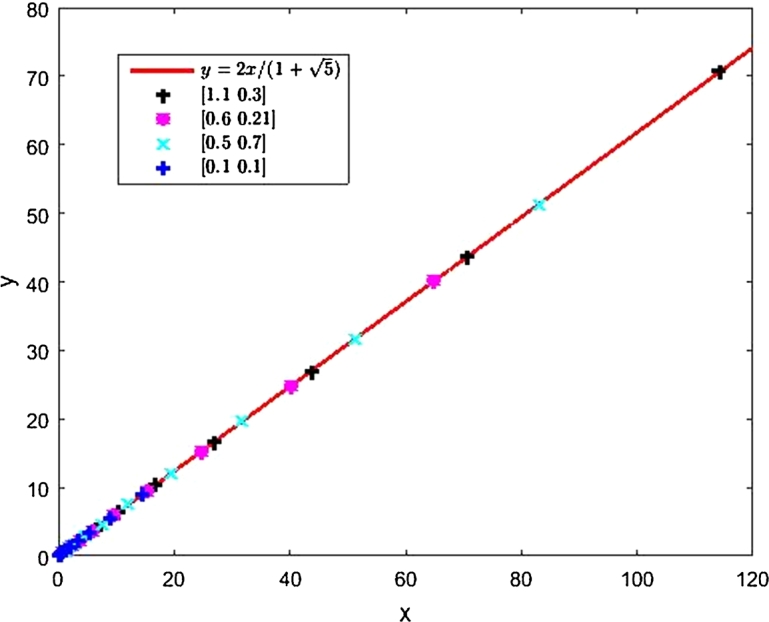
Iterations of equation (5) with arbitrary real numbers as initial values.

3.1. Generalization of the Fibonacci matrix

The Fibonacci matrix $A=A_2=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill \end{array}\right]$ can be generalized into several directions. For examples it can be generalized into the matrices $A_3$ or $A_4$ below:

$$A_3=\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right]\text{or}{A}_4=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right],$$

or even into matrices in higher dimensions. However, from population perspective these generalizations are not realistic. Let us consider the matrix $A_3$. It can be considered as the growth matrix of a population having three age classes. It assumes that there is no mortality in the populations. However if there is a mortality or survival rates in the population, then the matrix should accommodate these factors. For example, let us consider the easiest one, the population having only two age classes, adults and juveniles. Then one of the model that accommodate mortality could be given by the matrix $A_m=\left[\begin{array}{cc}\hfill \alpha \hfill & \hfill \beta \hfill \\ \hfill \gamma \hfill & \hfill 0\hfill \end{array}\right]$. The matrix gives the following recursive equations:

$$\begin{array}{cc}\hfill X(n+1)& =\alpha X(n)+\beta Y(n)\hfill \\ \hfill Y(n+1)& =\gamma X(n)\hfill \end{array}$$ (8)

with $X(0)=X_0$ and $Y(0)=Y_0$. At the first glance, this equation is closely related to the one in Balestrino et al. (2009). Their equation of the generalized Fibonacci sequence forms a dynamical system which motivated by a problem in digital filters and manufacturing of tissue with fractal property. A closer inspection to the equation shows that their equation, motivation, and interpretation are different to ours, in which here we look at a population dynamics perspective. The parameters can be interpreted as follows: α is the survival rate of adults that still alive, β is the survival rate of juveniles that reach adult class, and γ is the birth rate of adults that produce the new juveniles. Here we present some results of the model analysis. The first result is presented in the following theorem.

Theorem 3

The closed form solution of Equation (8) is given by $X_n=\frac{1}{\sqrt{{\alpha }^2+4\beta \gamma }}{(\frac{\alpha }{2}+\frac{1}{2}\sqrt{{\alpha }^2+4\beta \gamma })}^n-\frac{1}{\sqrt{{\alpha }^2+4\beta \gamma }}{(\frac{\alpha }{2}-\frac{1}{2}\sqrt{{\alpha }^2+4\beta \gamma })}^n$ and the associated golden ratio is given by $\phi =\frac{\alpha }{2}+\frac{1}{2}\sqrt{{\alpha }^2+4\beta \gamma }$.

Proof

Let us consider Equation (8) in the form of

$$X(n+1)=\alpha X(n)+\beta \gamma X(n-1).$$ (9)

The characteristic equation for the above recurrence equation is

$$x^2-\alpha x-\beta \gamma =0$$ (10)

with the solution

$$\phi =\frac{\alpha }{2}+\frac{1}{2}\sqrt{{\alpha }^2+4\beta \gamma }\text{and}\psi =\frac{\alpha }{2}-\frac{1}{2}\sqrt{{\alpha }^2+4\beta \gamma }.$$ (11)

Hence, the closed form solution of the generalized Fibonacci Equation (9) is in the form of

$$X_n=s{\phi }^n+t{\psi }^n$$ (12)

with s and t are some real numbers. Suppose that the initial conditions are given by $X_0$ and $X_1$ then we have

$$X_0=s+t\text{and}{X}_1=s\phi +t\psi .$$ (13)

Without loss of generality we assume $X_0=0$ and $X_1=1$, hence solving the last equations gives

$$s=\frac{1}{\sqrt{{\alpha }^2+4\beta \gamma }}\text{and}t=-\frac{1}{\sqrt{{\alpha }^2+4\beta \gamma }}.$$ (14)

Therefore the closed form solution is given by

$$\begin{array}{cc}\hfill X_n& =\frac{1}{\sqrt{{\alpha }^2+4\beta \gamma }}{(\frac{\alpha }{2}+\frac{1}{2}\sqrt{{\alpha }^2+4\beta \gamma })}^n-\hfill \\ \hfill & \frac{1}{\sqrt{{\alpha }^2+4\beta \gamma }}{(\frac{\alpha }{2}-\frac{1}{2}\sqrt{{\alpha }^2+4\beta \gamma })}^n\hfill \end{array}$$ (15)

Let $R(n+1)=\frac{X_{n+2}}{X_{n+1}}$, then we have

$$\begin{array}{cc}\hfill R(n+1)R(n)& =\frac{X_{n+2}}{X_{n+1}}\frac{X_{n+1}}{X_n}\hfill \\ \hfill & =\frac{X_{n+2}}{X_n}\hfill \\ \hfill & =\frac{\alpha X(n+1)+\beta \gamma X(n)}{X_n}\hfill \\ \hfill & =\alpha R_n+\beta \gamma \hfill \end{array}$$ (16)

If the limit of the ratio exists as n approaches infinity, say ${\lim }_{n\to \infty }(R_n)=L$ then we have

$$L^2=\alpha L+\beta \gamma$$ (17)

which is satisfied by $\phi =\frac{\alpha }{2}+\frac{1}{2}\sqrt{{\alpha }^2+4\beta \gamma }$. The existence of the limit can be proved by showing that $R_n$ forms a Cauchy sequence. □

The matrix $A_m$ has the characteristic equation ${\lambda }^2-\alpha \lambda -\beta \lambda =0$ with two eigenvalues ${\lambda }_1=\frac{\alpha }{2}+\frac{1}{2}\sqrt{{\alpha }^2+4\beta \gamma }$ and values ${\lambda }_2=\frac{\alpha }{2}-\frac{1}{2}\sqrt{{\alpha }^2+4\beta \gamma }$ with corresponding eigenvector ${[X,Y]}^t={[\frac{\alpha }{2}+\frac{1}{2}\sqrt{{\alpha }^2+4\beta \gamma },1]}^t\theta$ and ${[X,Y]}^t={[\frac{\alpha }{2}-\frac{1}{2}\sqrt{{\alpha }^2+4\beta \gamma },1]}^t\theta$, respectively, with $\theta \in \Re$ and $\theta \ne 0$. There are two eigenspaces, corresponding to ${\lambda }_1$ and ${\lambda }_2$. The eigenspace corresponding to the largest eigenvalue ${\lambda }_1$ is $\left\{{[\frac{\alpha }{2}+\frac{1}{2}\sqrt{{\alpha }^2+4\beta \gamma },1]}^t\right\}$ which consists of all linear combinations of the eigenvector of the largest eigenvalue ${\lambda }_1$ plus the zero vector. The eigenspace corresponding to the other eigenvalue is $\left\{{[\frac{\alpha }{2}-\frac{1}{2}\sqrt{{\alpha }^2+4\beta \gamma },1]}^t\right\}$ which consists of all linear combinations of the corresponding eigenvector plus the zero vector.

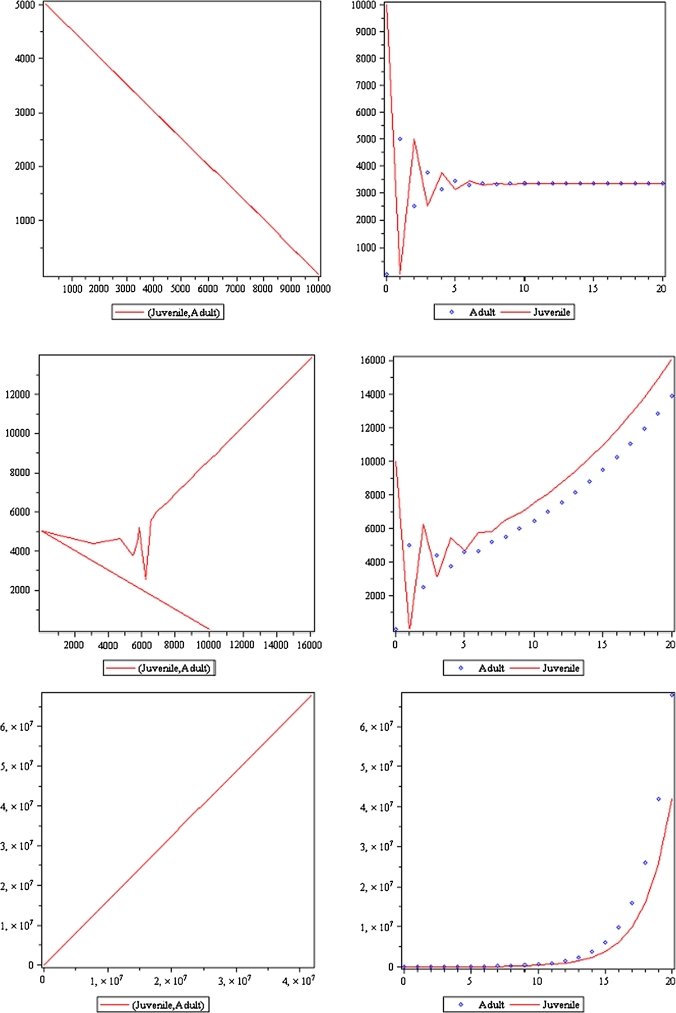
Unlike the original Fibonacci model, in which the population always increasing unbounded with a constant golden ratio $\phi =(1+\sqrt{5})/2\approx 1.618033989$, the modified model of (7) is able to accommodate increasing and decreasing growth, and even a steady state. Figure 4 (upper) shows an example for eventually steady growth with $\alpha =0.5$, $\beta =0.5$ and $\gamma =1$ resulting in the ratio of consecutive population is 1. Other growth (middle and lower graphs in Figure 4) shows the exponential growth with different parameters. The previous theorem shows that the modified golden ratio is given by $\hat{\varphi }=\frac{\alpha }{2}+\frac{1}{2}\sqrt{({\alpha }^2+4\beta \gamma )}$, which for the case of $\alpha =\beta =\gamma =1$ the ratio collapses to $\phi =(1+\sqrt{5})/2\approx 1.618033989$.

Figure 4.

An example for eventually steady growth with α = 0.5, β = 0.5 and γ = 1 resulting in the ratio of consecutive population is 1 (upper figure). The graphs in the middle and lower figures show the exponential growth with different parameters resulting in the ratio of consecutive population 1.079 and 1.618, respectively. All graphs begin with the same population sizes: 10,000 juveniles and 20 adults.

Table 1 reveals that there is an interesting pattern regarding the ratio of two consecutive numbers of the modified Fibonacci sequence. The triple $(\alpha ,\beta ,\gamma )$ is not unique, in the sense that different triples may give the same ratio. For example, the ratio of two consecutive numbers of the modified Fibonacci sequence is exactly the same as the golden ratio (of the original Fibonacci sequence) for several different triples. Some parameters in the triple are the function of the golden ratio φ.

Table 1.

Examples of different triples of (α,β,γ) which result in the same ratios of the long-term two consecutive time of population sizes.

Adult survival	Juvenile survival	Birth rate	Ratio
(α)	(β)	(γ)	($\hat{\phi }$)
0.5	0.5	1	1.000000000
0.5	1	0.5	1.000000000
0.5	0.5	1.25	1.079156198
0.5	1.25	0.5	1.079156198
0.5	0.5	2 + φ	φ
0.5	2 + φ	0.5	φ
0.5 φ	φ	0.5 φ	φ
0.5φ	0.5φ	φ	φ

Table 2, Table 3, Table 4, Table 5 show that if the growth parameters of the population are certain form of function of the golden ratio φ, the pattern of the ratio (we called it the modified golden ratio $\hat{\phi }$) becomes more prevalent as stated in Theorem 3 and Theorem 4. Some numerical example show that the ratio in Table 5 can be expressed in a different form as shown in Table 6. These two expression is equivalent as stated in Theorem 6.

Table 2.

Examples of different triples of (α,β,γ) for α = β = γ = k which result in the same form of ratios of the long-term two consecutive time of population sizes.

Adult survival	Juvenile survival	Birth rate	Ratio
(α)	(β)	(γ)	($\hat{\phi }$)
1	1	1	φ
2	2	2	2 φ
3	3	3	3 φ
⋮	⋮	⋮	⋮
k	k	k	k φ

Table 3.

Examples of different triples of (α,β,γ) for α = β = γ = kφ which result in the same form of ratios of the long-term two consecutive time of population sizes.

Adult survival	Juvenile survival	Birth rate	Ratio
(α)	(β)	(γ)	($\hat{\phi }$)
φ	φ	φ	1 + φ
2 φ	2 φ	2 φ	2 (1 + φ)
3 φ	3 φ	3 φ	3 (1 + φ)
4 φ	4 φ	4 φ	4 (1 + φ)
⋮	⋮	⋮	⋮
k φ	k φ	k φ	k (1 + φ)

Table 4.

Examples of different triples of (α,β,γ) for α = β = γ = k + φ which result in the same form of ratios of the long-term two consecutive time of population sizes.

Adult survival	Juvenile survival	Birth rate	Ratio
(α)	(β)	(γ)	($\hat{\phi }$)
φ	φ	φ	1 + φ
1 + φ	1 + φ	1 + φ	1 + 2 φ
2 + φ	2 + φ	2 + φ	1 + 3 φ
3 + φ	3 + φ	3 + φ	1 + 4 φ
⋮	⋮	⋮	⋮
k + φ	k + φ	k + φ	1 + (k + 1) φ

Table 5.

Examples of different triples of (α,β,γ) for α = β = γ = φ^k which result in the same form of ratios of the long-term two consecutive time of population sizes.

Adult survival	Juvenile survival	Birth rate	Ratio
(α)	(β)	(γ)	($\hat{\phi }$)
φ	φ	φ	φ2
φ2	φ2	φ2	φ3
φ3	φ3	φ3	φ4
φ4	φ4	φ4	φ5
φ5	φ5	φ5	φ6
φ6	φ6	φ6	φ7
φ7	φ7	φ7	φ8
φ8	φ8	φ8	φ9
⋮	⋮	⋮	⋮
φk	φk	φk	φk+1

Table 6.

Examples of different triples of (α,β,γ) for α = β = γ = φ^k in Table 5, which result in the same form of ratios containing F_i, where F_i denotes the i-th term of the original Fibonacci sequence.

Adult survival	Juvenile survival	Birth rate	Ratio
(α)	(β)	(γ)	($\hat{\phi }$)
φ	φ	φ	φ + 1
φ2	φ2	φ2	2 φ + 1
φ3	φ3	φ3	3 φ + 2
φ4	φ4	φ4	5 φ + 3
φ5	φ5	φ5	8 φ + 5
φ6	φ6	φ6	13 φ + 8
φ7	φ7	φ7	21 φ + 13
φ8	φ8	φ8	34 φ + 21
⋮	⋮	⋮	⋮
φk	φk	φk	F(k−1)φ + F(k−2)

Theorem 4

If $\alpha =\beta =\gamma =k$ with $k=1,2,3,\dots$ then the golden ratio $\tilde{\phi }$ of $x_{n+1}/x_n$ of the generalized Fibonacci sequence is given by $\tilde{\phi }=k\phi$ where φ is the golden ratio of the Fibonacci sequence.

Proof

Recall that the ratio of the modified Fibonacci sequence is given by $\tilde{\phi }=\alpha /2+1/2\sqrt{{\alpha }^2+4\beta \gamma }$. If $\alpha =\beta =\gamma =k$ with $k=1,2,3,\dots$ then we have by $\tilde{\phi }=k/2+1/2\sqrt{k^2+4k^2}=k(1/2+(1/2)\sqrt{5})=k\phi$. □

Theorem 5

If $\alpha =\beta =\gamma =f(\phi )$ is a function of the golden ratio φ then the ratio $\tilde{\phi }$ of $x_{n+1}/x_n$ of the generalized Fibonacci sequence is also a function of φ, specifically:

• 1.$\tilde{\phi }=k(\phi +1)$ whenever $f(\phi )=k\phi$,
• 2.$\tilde{\phi }=(k+1)\phi +1$ whenever $f(\phi )=k+\phi$,
• 3.$\tilde{\phi }={\phi }^{(k+1)}$ whenever $f(\phi )={\phi }^k$.

Proof

We present the proof for the above theorem

• 1.As before the ratio of the modified Fibonacci sequence is given by $\tilde{\phi }=\frac{\alpha }{2}+\frac{1}{2}\sqrt{{\alpha }^2+4\beta \gamma }$. If $\alpha =\beta =\gamma =k\phi$ with $k=1,2,3,\dots$ then we have $\tilde{\phi }=\frac{k\phi }{2}+\frac{1}{2}\sqrt{{(k\phi )}^2+4{(k\phi )}^2}=k\phi (\frac{1}{2}+\frac{1}{2}\sqrt{5})=k{\phi }^2$. Since φ is one of the solution of the characteristic equation associated with the Fibonacci sequence, it satisfies ${\phi }^2=\phi +1$. Hence we have $\tilde{\phi }=k(\phi +1)$ as required.
• 2.As before the ratio of the modified Fibonacci sequence is given by $\tilde{\phi }=\frac{\alpha }{2}+\frac{1}{2}\sqrt{{\alpha }^2+4\beta \gamma }$. If $\alpha =\beta =\gamma =k+\phi$ with $k=1,2,3,\dots$ then we have $\tilde{\phi }=\frac{k+\phi }{2}+\frac{1}{2}\sqrt{{(k+\phi )}^2+4{(k+\phi )}^2}=(k+\phi )(\frac{1}{2}+\frac{1}{2}\sqrt{5})=(k+\phi )\phi$. Since φ is one of the solution of the characteristic equation associated with the Fibonacci sequence, it satisfies ${\phi }^2=\phi +1$. Hence we have $\tilde{\phi }=(k+\phi )\phi =k\phi +{\phi }^2=k({\phi }^2-1)+{\phi }^2=k{\phi }^2+{\phi }^2-k=k(\phi +1)+(\phi +1)-k=k\phi +(\phi +1)=(k+1)\phi +1$. Hence we have $\tilde{\phi }=(k+1)\phi +1$ as required.
• 3.As before the ratio of the modified Fibonacci sequence is given by $\tilde{\phi }=\frac{\alpha }{2}+\frac{1}{2}\sqrt{{\alpha }^2+4\beta \gamma }$. If $\alpha =\beta =\gamma ={\phi }^k$ with $k=1,2,3,\dots$ then we have $\tilde{\phi }=\frac{{\phi }^k}{2}+\frac{1}{2}\sqrt{{\phi }^{2k}+4{\phi }^{2k}}={\phi }^k(\frac{1}{2}+\frac{1}{2}\sqrt{5})={\phi }^k\phi ={\phi }^{k+1}$ as required.
  Note: Some numerical experiment also show that the last equation is equivalent to the expression $\tilde{\phi }=F_{(n-1)}\phi +F_{(n-2)}$ whenever $f(\phi )={\phi }^k$, with $F_i$ denotes the i-th term of the Fibonacci sequence. We can observe that it is obvious ${\phi }^2=\phi +1$, and recursively we obtain the following:

  $$\begin{array}{cc}\hfill {\phi }^3& =\phi (\phi +1)={\phi }^2+\phi =(\phi +1)+\phi =2\phi +1,\hfill \\ \hfill {\phi }^4& =\phi (2\phi +1)=2{\phi }^2+\phi =2(\phi +1)+\phi =3\phi +2,\hfill \\ \hfill {\phi }^5& =\phi (\phi +2)=3{\phi }^2+2\phi =3(\phi +1)+2\phi =5\phi +3,\hfill \\ \hfill {\phi }^6& =\phi (5\phi +3)=5{\phi }^2+3\phi =5(\phi +1)+3\phi =8\phi +5\hfill \\ \hfill ⋮\\ \hfill etc\end{array}$$

We can prove in general that ${\phi }^k=F_k\phi +F_{k-1}$. It is clear that the formula true for some integer above. Let us assume that ${\phi }^k=F_k\phi +F_{(k-1)}$ holds for an integer k, we will prove that it also holds for the integer $k+1$ as what the follows.

$$\begin{array}{cc}\hfill {\phi }^{(k+1)}& ={\phi }^k\phi =(F_k\phi +F_{k-1})\phi =F_k{\phi }^2+F_{k-1}\phi \hfill \\ \hfill & =F_k(\phi +1)+F_{k-1}\phi =(F_k+F_{k-1})\phi +F_k=F_{k+1}\phi +F_k\hfill \end{array}$$

Hence we have ${\phi }^k=F_k\phi +F_{k-1}$ for any $k\ge 1$. This is actually proof of the following theorem. □

Theorem 6

If φ is the golden ratio of the Fibonacci sequence then ${\phi }^k=F_k\phi +F_{k-1}$ for any integer $k\ge 1$.

Corollary 1

If $\alpha =\beta =\gamma ={\phi }^k$ then the ratio of $x_{n+1}/x_n$ of the generalized Fibonacci sequence is given by $\tilde{\phi }={\phi }^{k+1}=F_{k+1}\phi +F_k$.

Proof

The proof is clear from Theorem 5 (point 3) and Theorem 6. □

4. Conclusion

We have presented a discussion regarding one way to modify and generalize the Fibonacci sequence via population dynamic perspective. The modified Fibonacci sequence is able to model a steady state growth for certain choice of the triplet demographic parameters. A modified golden ratio is also presented and some interesting patterns are proved.

Declarations

Author contribution statement

Asep K. Supriatna: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Ema Carnia: Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Meksianis Z. Ndii: Contributed reagents, materials, analysis tools or data; Wrote the paper.

Funding statement

This work was supported by the University of Padjadjaran, through the scheme of Academic Leadership Grant (ALG-2018) (2297/UN6.D/KS/2018).

Competing interest statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.