Abstract
In this paper, we demonstrate the ability to 3D print tightly integrated structures with active valves, pumps, and mixers, and we use our compact chip-to-chip interconnects [Gong et al., Lab Chip 18, 639–647 (2018)] to move bulky world-to-chip connections to separate interface chips for both post-print flushing and post-cure device operation. As example devices, we first examine 3D printed pumps, followed by two types of selectable ratio mixer pumps, a linear dilution mixer pump (LDMP) and a parallelized dilution mixer pump (PDMP), which occupy volumes of only and , respectively. The LDMP generates a selectable dilution ratio from a linear set of possibilities, while the PDMP generates a denser set of possible dilutions with a maximum dilution ratio of 1/16. The PDMP also incorporates a new 4-to-1 valve to simultaneously control 4 inlet channels. To characterize LDMP and PDMP operation and performance, we present a new, low-cost video method to directly measure the relative concentration of an absorptive dye on a pixel-by-pixel basis for each video frame. Using this method, we find that 6 periods of the active mixer that forms the core of the LDMP and PDMP are sufficient to fully mix the fluid, and that the generated concentrations track the designed dilution ratios as expected. The LDMP mixes 20 nl per 4.6 s mixer pump period, while the PDMP uses parallelized input pumps to process the same fluid volume with greater choice of dilution ratios in a 3.6 s period.
I. INTRODUCTION
3D printing is widely recognized as a potentially attractive fabrication method for microfluidics.1–3 However, a critical drawback is that to date commercial tools and materials do not lend themselves to achieving truly microfluidic features, or (in the case of two-photon polymerization) volumes large enough for many practical devices.4 Our focus for the past few years has been to develop tools, materials, and methods to address these drawbacks. We have built a first generation custom 3D printer and formulated low-cost custom resins specifically tailored to the needs of microfluidic devices. In our recent work, we have demonstrated 3D printed flow channels as small as ,5 diameter valves that withstand 1 000 000 actuations,6 and high density () chip-to-chip interconnects.6 The latter facilitates delegating bulky world-to-chip interconnects to re-usable 3D printed interface chips to enable further miniaturization of 3D printed device chips. In this paper, we use our 3D printing tools, materials, and methods to explore the miniaturization potential of a common class of microfluidic component, an active fluid mixer, but with the additional ability of directly selecting the desired mixing ratio. Our motivation is to illustrate how the flexibility of 3D printing in combination with the unrestricted 3D layout of individual device elements and routing of fluid channels enables the realization of extremely small, complex microfluidic components.
Microfluidic mixing is a critical operation in many chemical and biological applications7 such as chemical synthesis,8–13 polymerization,14–16 extraction,17–21 DNA analysis,22–26 enzyme assays,25,27–29 and protein folding.30–33 However, mixing is a challenge at the low Reynolds numbers typical of microfluidic device operation since the fluid flow is laminar.34,35 Over several decades, a wide variety of both passive and active mixing strategies have been demonstrated. Comprehensive reviews of such strategies can be found in Refs. 34–36. While demonstrating a 3-to-2 3D printed multiplexer with an earlier, larger version of our technology, we show that a 3D printed valve and displacement chamber (DC) has the potential to achieve mixing in a compact device volume.37 Our purpose here is to use our current capabilities to explore the implementation of an active mixer with a selectable mixing ratio in the minimum possible volume that accomplishes mixing in minimum time for small () fluid volumes. We call such devices selectable dilution mixer pumps (SDMPs).
In this paper, we first establish a low-cost video approach for absorption-based measurement of the local dye concentration in an outlet channel to determine mixing effectiveness. This simplifies data acquisition for SDMP characterization such that the only tools needed beyond pneumatic valve and pump controls are a smartphone for slow motion video capture and a microscope operating in the transmission mode. We also test 3D printed pumps with varying DC dimensions to measure the fluid volume expelled per pumping period, which increases with larger pump DCs. Then, having established pump operational parameters and a direct relative concentration measurement method, we implement and characterize two possible SDMP configurations: (1) a linear dilution mixer pump (LDMP) and (2) a parallelized dilution mixer pump (PDMP). Each configuration contains a number of pumps to inject variable amounts of fluid from two sources into their active mixing units to realize selectable mixing ratios. The volume occupied by the LDMP is only , and its mixing effectiveness is compared to diffusion-driven mixing and optimized by experimenting with different mixing operation sequences. In contrast to a LDMP, a PDMP () is designed to obtain a denser set of dilution ratios and shorten the overall mixing process. The shorter mixing process is achieved by minimizing the pump idle time and synchronizing all pump operations. It also contains a 4-to-1 valve that controls 4 valve inlet channels to reduce the total number of required valves.
II. MATERIALS AND METHODS
A. 3D printer and materials
The 3D printer used in this paper is described in Ref. 5. It has a 385 nm LED light source and a pixel pitch of in the projected image plane. We use a custom photopolymerizable resin which consists of poly(ethylene glycol) diacrylate (PEGDA, MW258) with a 1% (w/w) phenylbis(2,4,6-trimethylbenzoyl)phosphine oxide (Irgacure 819) photoinitiator, and a 2% (w/w) 2-nitrophenyl phenyl sulfide (NPS) UV absorber, details of which are provided in the same reference.
B. 3D printing and sample preparation
We use 25 mm square silanized glass slides as 3D printing substrates. Slides are first rinsed with acetone and isopropyl alcohol (IPA), and then immersed in toluene mixed with 10% 3-(trimethoxysilyl)propyl methacrylate for 2 h. After silanization, we store the glass slides in fresh toluene inside a closed container until use, which ranges from under an hour to several weeks. All 3D prints reported in this paper are fabricated with a layer thickness of . Except where otherwise noted, each layer has an exposure time of 550 ms. The image plane irradiance is with an LED source spectrum as reported in Ref. 5 with a peak at 383 nm.
The fabrication process steps are illustrated in Fig. 1. After printing, the unpolymerized resin must be flushed from all interior voids with IPA prior to optical curing. The flushing process requires that all voids have two means of access so the IPA can flow through each void region (channel, valve chamber, etc.), i.e., there must not be any dead ends in the printed structure since they generally cannot be flushed of unpolymerized resin, which would then become polymerized during optical curing. After flushing, a device is optically cured for 30 min in a custom curing station using a 430 nm LED (Thorlabs, Newton, NJ) having a measured irradiance of in the curing plane.
FIG. 1.
Microfluidic 3D printing fabrication process flow.
We find that IPA works well as a solvent for post-print device flushing and does not seem to affect 3D printed PEGDA. Ethanol likewise appears to be compatible with our PEGDA devices. However, acetone, tetrahydrofuran, and dicholoromethane show varying degrees of incompatibility as evidenced by substantial cracking and/or dissolution of the 3D printed material.
Unless otherwise noted for the DCs used in pumps, the fluid and control chamber heights are both , and the membrane thickness is (2 layers). Also, the actuation pressure and the vacuum pressure used to deflect valve and DC membranes are 20 psi and approximately , respectively.
C. Concentration measurement
There are two commonly used approaches in the literature to measure concentration at the outlet of a mixer, fluorescence-based38–54 and absorption-based.55–61 Both take advantage of the fact that the pixel gray level for any pixel in a digital image of the fluid in an outlet channel is a function of the local concentration of the fluorescent or absorbent species in the small fluid region imaged to that pixel. In a fluorescence-based system, the pixel gray level is linearly proportional to the concentration of fluorescent material, making data processing to directly obtain the local concentration straightforward and intuitive. The downside is that working with a fluorescent material demands a relatively complicated and expensive setup which includes an excitation source and an optical filter in addition to a microscope and digital imager. In contrast, an absorption-based method requires only a digital imager with a microscope operated in the transmission mode and is therefore simpler and less expensive. However, in the literature, numerous papers do not directly measure the local concentration based on the pixel gray level using the absorption-based approach. Instead, the variance of the pixel gray level is calculated and interpreted as an indirect indicator of the degree of mixing,55–59 rather than connecting measurements directly to the local absorber concentration as in Refs. 62 and 63.
In this paper, we develop a low-cost video approach to directly measure relative concentration as a function of time for the absorption-based method. For data collection, we mount an iPhone 8 Plus on a microscope (Olympus BX60) eyepiece to record slow motion () video as the raw output. We chose to use a smartphone as a video camera because nearly every student has one (i.e., no additional cost to use in laboratory setups), and the current smartphone photo and video capabilities are more than adequate for our measurement needs. The two different fluids are DI water (Water) and red-dyed water (Red) consisting of a few drops of Red 40 food coloring in DI water. The outlet of each type of the mixer pump is a wide (), shallow ( unless otherwise noted) 3D printed outlet channel in which the spatially-varying fluid concentration is observed with the iPhone video.
According to Beer’s law, the transmitted light irradiance as a function of pixel location, , is
| (1) |
where is the incident light irradiance, is the spatially-dependent absorption coefficient based on local concentration, and is the thickness of the material the light travels through (in our case, the height of the channel). We can solve for the absorbance, in terms of the irradiance as
| (2) |
where is the irradiance when there is no red dye in a channel (i.e., only water in a channel). We therefore re-label as . is an individual video frame (i.e., image) from any point in the experiment video, typically during operation when dye is introduced to the outlet channel by the mixer pump. Likewise, is an individual video frame near the start of a video when all channels are filled with water and Red has not yet been introduced into the mixer.
Note that in general the absorbance can be written in terms of dye concentration, , as
| (3) |
where is the absorptivity (in suitable units given the units of the concentration, ) and is the channel thickness at pixel position . Clearly, the absorbance, , is linearly dependent on the concentration, . This concentration can be thought of as the integrated concentration through the height of the outlet channel at a given pixel position. As long as the channel height is relatively small, we expect it to be a reasonable approximation of the local concentration.35,64–67
The condition of maximum absorbance, , is when the full red dye concentration is in the outlet channel such that the irradiance is :
| (4) |
In each experiment video, we fill the outlet channel with Red near the end of the video, while at the beginning of each experiment video, the outlet channel is filled with Water. Each video therefore contains the calibration frames needed to determine and , and hence . The frames in the middle of the video track the progress of the mixer pump in creating the desired mixing ratio of the output fluid.
We can define the relative absorbance, in reference to as
| (5) |
| (6) |
| (7) |
| (8) |
is therefore the relative concentration at pixel position . The mean of over some region , , is the average relative concentration and the standard deviation of , , over the same region is a direct measure of how well the solution is mixed, with, in the ideal case, being fully mixed. We defer to future work a rigorous analysis of the limit of detection for our concentration measurement approach. Instead, as we show in Sec. III, noise in the measurement process results in the fully mixed condition being manifested by a small value that does not change systematically in time. Using this as a metric, we can readily measure dilutions down to 1/16 as shown in Sec. III D.
III. RESULTS AND DISCUSSION
A. Pumps
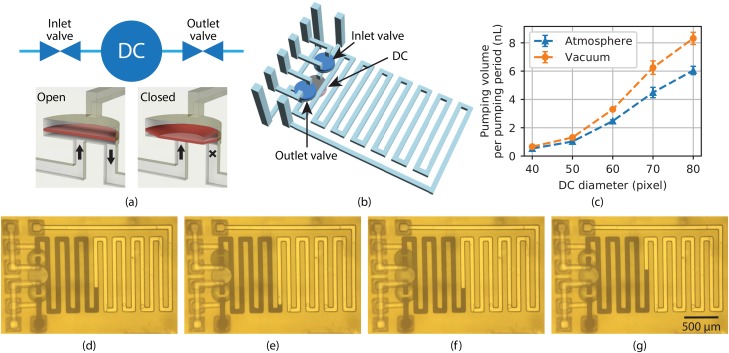
As shown schematically in Fig. 2(a), a 3D printed pump comprises an inlet valve, a DC, and an outlet valve.37 The valves and the DC each have 2 vertically stacked circular chambers, a control chamber and a fluid chamber, separated by a membrane which can be deflected according to the control chamber pressure.68 For valves, fluid channels are located at the center and edge of the fluid chamber, respectively. As shown in Fig. 2(a) lower right, when the control chamber is pressurized, the membrane (denoted by a reddish color even though it is the same material as the rest of the 3D print) deflects into the fluid chamber and blocks the central fluid channel, thereby closing the valve. When the control chamber pressure is released (lower left), the membrane returns to its equilibrium position, opening the valve. Alternatively, vacuum can be applied to open the valve, which pulls the membrane up into the control chamber.
FIG. 2.
(a) (top) Functional illustration of a 3D printed pump and (bottom) a 3D printed valve in open and closed states. See text for details. (b) CAD drawing of a pump with a serpentine outlet channel. (c) Measured pumping volume for DCs with different diameters and height for both the fluid and control chambers. The unit of the x-axis dimension, pixel, is the DLP image plane pixel pitch, . (d)–(g) Microscope photos of a pump at various stages in its operation. The DC has the same diameter as the valves, which is 40 pixels. (d)(e): Outlet valve opens, and the meniscus moves back by the volume of the valve upward membrane displacement, ; (e)(f): DC is actuated, and the meniscus moves forward by the volume of the DC downward membrane displacement, ; (f)(g): outlet valve is actuated, and the meniscus moves further forward by the volume of the valve downward membrane displacement, which is the same as its upward membrane displacement, .
A DC has both fluid channels located at the edges of the fluid chamber such that neither is blocked when the membrane deflects. Instead, the DC membrane movement pulls in or pushes out fluid depending on whether the control chamber is exposed to atmosphere or pressure. Alternatively, vacuum can be applied instead of atmosphere, in which case the volume of fluid pumped per pumping period increases to the degree that the membrane is pulled up into the control chamber by the vacuum. The pump fluid direction is determined by which of the inlet and outlet valves are opened and closed during DC pressurization and de-pressurization.
The pump operates using a 5-phase cycle as detailed in Ref. 37. We call each phase time a clock cycle, , and one 5-phase pump cycle a pumping period, , which equals . In this paper, is 100 ms.
We typically fabricate valve and DC membranes that are only thick. We find that without enough polymer crosslinking during 3D printing, for larger diameters (i.e., for the 4-to-1 valve and mixer), the membrane may not be tough enough to avoid tearing during operation, limiting membrane durability. In the past, when we used commercial 3D printers (and therefore created larger structures), we were forced to use the same exposure time for every layer in a 3D print, and for every pixel within each layer. This lack of flexibility exposes a fundamental trade-off with such printers when trying to print both valves and small channels in the same 3D print. The trade-off is that higher doses are required to improve the mechanical toughness of membranes, but higher doses preclude fabricating small channels, for which a smaller dose is required.5 Since we have full control over all aspects of our custom 3D printer, in this work, we increase the membrane exposure for larger diameter membranes independent of other build layers, and other regions within the same build layer, such that we can achieve both strong membranes and small minimum channel size.
Our approach is for build layers that contain larger diameter membranes, after the normal layer exposure and before moving the build platform to get ready for the next layer, we expose a secondary image which illuminates the larger membrane regions with a circle having a diameter 10 pixels greater than the membrane, thereby giving the membranes a higher dose than the rest of the layer and selectively toughening the membranes and their anchor region in the surrounding material while maintaining a lower dose everywhere else in the layer, consistent with reliably fabricating small channels. In this manner, we are able to achieve excellent membrane durability without sacrificing the minimum channel size. We find that smaller diameter membranes, such as 40 pixel valves, do not need this extra dose or expanded exposure region, but that it noticeably benefits 4-to-1 valves (80 pixel diameter) and mixers (140 pixel diameter). Membrane exposure times are given in the supplementary material, Table S1.
To determine the expelled volume per pumping period, , we connect the pump outlet to a 3D printed serpentine channel as shown in Fig. 2(b). This serpentine channel has a well-defined cross-section area, and is integrated with the pump, which makes measuring the fluid volume pumped as a function of time as convenient as simply measuring the length of channel the fluid has traveled as captured in a video of pump operation. Specifically, we observe the progress of the fluid-air meniscus of black-dyed water during pump operation. Example videos are included as the supplementary material, Videos S1(a) and S1(b).
Representative video frames are shown in Figs. 2(d)–2(g). During pump operation, the outlet valve must be opened before the DC expels fluid, which results in the meniscus initially moving backward as the fluid is drawn into the outlet valve fluid chamber. This can be seen by comparing Fig. 2(d) with Fig. 2(e). The volume drawn into the valve is . Next, the meniscus moves forward according to how much fluid volume is expelled by the DC, [Figs. 2(e)2(f)]. Finally, the outlet valve is closed, which pushes fluid into the outlet channel and further moves the meniscus forward by [Figs. 2(f)2(g)]. This process generates a pulsatile flow with one step back () and two steps forward ( and ). This is clearly seen in Videos S1(a) and S1(b) in the supplementary material for pumps with 40-pixel () diameter valves and 40-pixel and 60-pixel () diameter DCs, respectively. Note that the net forward motion of the meniscus for one pumping period corresponds to the displaced volume, , since the volume drawn in and expelled by the outlet valve during a pumping period is the same. Therefore, the pump volume per pumping period, is just
| (9) |
The specific approach we use to measure is counting dark pixels over the region of the serpentine channel, which is directly proportional to the area filled by the fluid. Based on our previous work,5 the channel height is very consistent in our 3D prints. We can therefore calculate
| (10) |
where is the outlet channel area per image pixel, and and are the dark pixel counts after pump periods and , respectively, and is the channel height. Figure 2(c) shows measured as a function of the DC diameter. We would normally expect to increase as the square of the diameter, which is clearly not the case in the data. The reason is that the actual volume that is pumped is not just a function of the physical DC fluid chamber volume, but it is also affected by the membrane diameter in relation to its thickness and stiffness. Error bars in the figure refer to the standard deviation over numerous pumping periods. We also apply vacuum to the DC such that when it is not pressurized, the membrane is pulled up into the control chamber, creating more space for fluid, and therefore resulting in larger compared to just using atmospheric pressure.
B. Linear dilution mixer pump (LDMP)
1. Concept and design
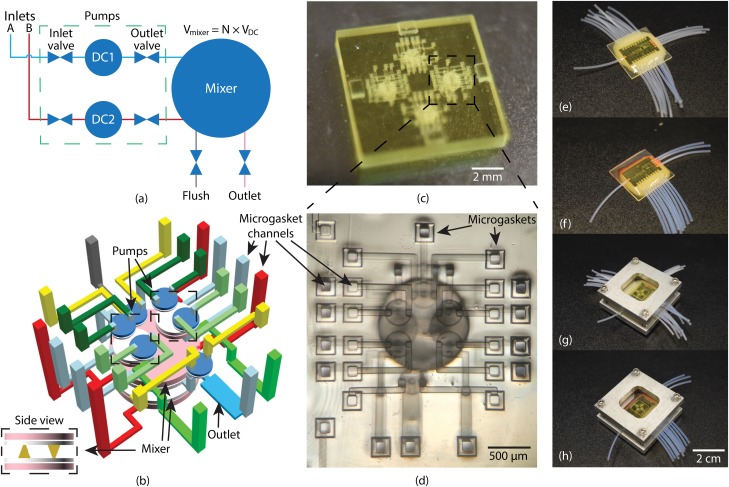
Figure 3(a) depicts the basic idea of a linear dilution mixer pump (LDMP). It utilizes two pumps, Pump 1 (top) and Pump 2 (bottom), to inject fluids A and B, respectively, from their individual inlets into the mixer. These two pumps are designed to be identical so that the mixer receives an equal amount of fluid from either pump for one pumping period. We also design the mixer fluid capacity, , to be , where is an integer, so Pumps 1 and 2 need to operate a total of pumping periods to fill the mixer. In our case, . We design the pumps with DCs that are 60 pixels in diameter with tall fluid and control chambers, and operate the pumps with vacuum. From Fig. 2(c), such that is 19.8 nl.
FIG. 3.
(a) Schematic of LDMP. It contains 2 pumps which are connected to a fluid reservoir. They can selectively pump fluid to the mixer which performs mixing. (b) 3D layout of (a). Pumps are stacked on top of the mixer, and the mixer has 2 large DCs connected to each other via cone-shaped channels. (c) Photograph of a 3D printed device designed for characterization of 4 LDMPs on a single chip. (d) Microscope photo of an LDMP which uses microgaskets developed in Ref. 5. (e) LDMP flushing chip. (f) LDMP operation chip. (g) LDMP device chip assembled with flushing chip. (h) LDMP device chip assembled with operation chip.
A CAD design of an LDMP is shown in Fig. 3(b), in which the two pumps and the flush and outlet valves are located on top of a coupled pair of larger DCs that function as an active mixer. Note the tight 3D layout of valves, pumps, channels, and active mixer, which illustrates a key advantage of 3D printing, namely, arbitrary component placement and channel routing for efficient volume utilization. The LDMP volume is only , not including the connections through the microgasket channels since these are specific to this particular implementation for testing a single LDMP. In general, an LDMP would be connected to other microfluidic components in the same 3D print to comprise a functional device for a particular application.
The mixer side view in Fig. 3(b) shows that the two vertically stacked mixer DCs are connected with 2 oppositely-oriented cone-shaped channels. When the top DC is activated (pressurized) and the bottom DC is deactivated (switched to atmosphere or vacuum), most of the fluid in the mixer is forced from the top DC through these channels into the bottom DC, and vice versa. The mixing effect is achieved by repeatedly activating one mixer DC and releasing the other, and then reversing the process, thereby causing fluid to move back and forth between the mixer DCs. The opposite cone shapes of the connecting channels are intended to provide spatial asymmetry as fluid flows back and forth to aid in the mixing effect. Here, we define actuating each mixer DC once as a mixing period, denoted as , such that
| (11) |
Fluid mixing is accomplished by actuating the mixer some number of mixing periods, , which requires a time . The value of needed to achieve good mixing is experimentally determined later in this section.
2. Mixer pump cycle
A complete mixer pump cycle is illustrated in the supplementary material, Fig. S1 consisting first of two clock cycles, , one to close the outlet valve and one to deactivate both mixer DCs, followed by sequential pumping periods and mixing periods, and, finally, two additional clock cycles, one to open the outlet valve and the other to activate both mixer DCs to expel the mixed fluid through the outlet valve. At this point, the mixer pump cycle repeats. The time for a complete mixer pump cycle, , can be written as
| (12) |
| (13) |
3. Interface chips
As discussed in Ref. 6, we use PTFE tubing as world-to-chip connections in 3D printed interface chips. With this approach, individual tubes are epoxied in cylindrical receptacles fabricated as part of the 3D printed interface chip, and the interface chip has internal channels that route each tube to a specific chip-to-chip interconnect.
Two such interface chips are required for an LDMP, one to facilitate flushing the device immediately after 3D printing and before optical curing, and the other for actual LDMP operation. As explained in Sec. II B during flushing there must be a path to flow IPA into and out of every channel and fluid and control chamber to remove unpolymerized resin. For an LDMP, this requires a total of 24 chip-to-chip interconnects and corresponding PTFE tubes. A fabricated interface chip with attached PTFE tubes is shown in Fig. 3(e), and clamped to an LDMP device chip in Fig. 3(g).
During operation, valve and DC control chambers only need one connection to control the pressure in these chambers (and therefore the associated membrane deflection), rather than two as for flushing. Hence, only 14 connections are needed, 10 pneumatic and 4 fluidic. However, there are still 24 chip-to-chip interconnects on the device chip. We use a simple approach to block the 2nd access channel to each valve and DC control chamber, illustrated in the supplementary material, Fig. S2 and which consists of replacing an unneeded interface chip channel with a blank surface to seal that particular interconnect channel on the device chip. An operational interface chip is shown in Fig. 3(f), and clamped to a device chip in Fig. 3(h).
4. Diffusion-driven mixing
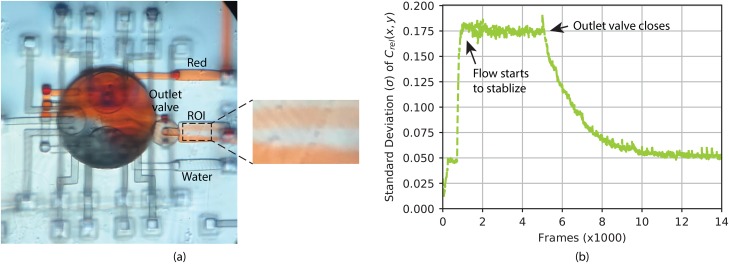
Next, we determine a baseline for LDMP mixing performance by using gravity to freely flow Water and Red through the device while observing the degree of mixing in the output channel. The fluid reservoirs for Water and Red are placed at the same height, higher than the LDMP device, while all of the valves except the flushing valve are opened so that Water and Red can flow through the device, i.e., in through their respective inlet ports and out through the outlet port. After the flow stabilizes, the segregation between Water and Red in the region of interest (ROI) in the outlet channel in Fig. 4(a) indicates an unsurprising lack of mixing. Next, we close the outlet valve and observe the mixing process in the outlet channel driven only by diffusion. Using the method developed in Sec. II C, we calculate in the ROI for each individual frame for the entire process, which is shown in Fig. 4(b). After starting gravity-driven flow around Frame 800 to 900, it stabilizes near Frame 1000, and the flow is allowed to proceed uninterrupted until near Frame 5000, over which time is relatively constant at . Near Frame 5000 the outlet valve is closed, after which starts to drop exponentially as diffusion mixes the fluid that is now static (no flow) in the outlet channel. It takes approximately 7000 frames () for to asymptote to the noise floor of . This experiment confirms the expected problem with diffusion-driven passive mixing of a confined volume of the fluid (in this case the 6 nl in the outlet channel), i.e., slow mixing. For a diffusion coefficient of 62,63 for Red 40 dye and 1D diffusion over the width of the outlet channel, (since the concentration is relatively constant over the length of the channel), the estimated diffusion time is , which agrees well with the measured value.
FIG. 4.
(a) Water and Red flow induced only by gravity. The fluid in the ROI denoted by the dashed box is segregated, as expected. (b) Standard deviation, , of relative concentration, , in the ROI as a function of frames in recorded video.
As noted in Sec. III B 1, the pumps inject of fluid into the mixer during LDMP operation. The mixer is in diameter so if the fluid was to sit in the mixer until it was mixed solely by diffusion, the diffusion time would be approximately . Alternatively, if the 20 nl was injected into a cubic volume, it would take to mix by diffusion. One figure of merit for a mixer is how much faster it mixes a given volume of fluid compared to diffusion-only mixing.
5. Active mixing
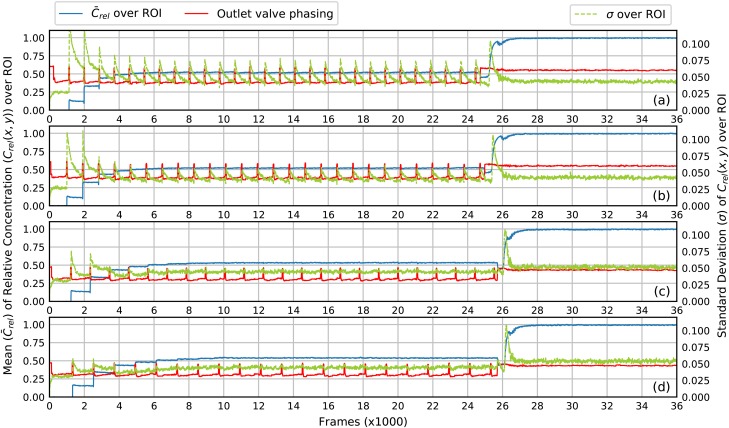
Using our new concentration-based analysis method from Sec. II C, we first investigate how many mixing periods, , guarantee thorough mixing. In a full mixer pump cycle (Sec. III B 2), we sequentially operate Pumps 1 and 2, each for three pumping periods, to achieve 1-to-2 dilution, and examine the degree of mixing as a function of . The results are shown in Figs. 5(a)–5(d) for values of 1, 2, 6, and 8, respectively. A video of the first minute of operation for Fig. 5(c) is shown in the supplementary material, Video S7(a).
FIG. 5.
The mean and standard deviation of relative concentration in the ROI as a function of the frame number. The state (open/closed) of the outlet valve is plotted as the red curve where a pulse corresponds to open. The outlet is initially filled with Water. Near Frame 26 000 () the outlet channel is flushed with Red. (a) . (b) . (c) . (d) . See text for mixing details.
In each plot, the mean relative concentration, (blue curve), in the ROI of the outlet channel is plotted on the left vertical axis as a function of the video frame number. For the first 1000 frames, only Water is in the outlet channel so . For the last 10 000 frames, only Red is in the channel so . In between, the LDMP executes a series of mixer pump cycles. Each cycle can be tracked by the red curve, which indicates the state of the outlet valve as shown in the supplementary material, Fig. S3. An upward pulse of the red curve shows when the outlet valve is open, which happens during one per mixer pump cycle. It can therefore be used to visualize each mixer pump cycle on a plot. As expected, the period between peaks in the red curves increases as increases since becomes correspondingly longer. Also note that during the first few mixer pump cycles, jumps up when the outlet valve opens, indicating that fluid containing at an increasing amount of Red is injected into the outlet channel during that cycle. After 6 mixer pump cycles, stabilizes at a value of just over 0.5, the desired relative concentration, which indicates that mixer pump cycles are required to flush the dead volume from the mixer and outlet channels to reach a stable relative concentration.
The standard deviation of , , over the ROI is shown as a green curve (right vertical axis) in each plot in Fig. 5. It gives a direct measure of the homogeneity (mixing) of the fluid for each frame in the video. For example, consider Fig. 5(a) () after Frame 6000. Every time the outlet valve opens (red curve pulse), the green curve jumps up to about the same level for each mixer pump cycle and then exponentially decays until the outlet valve opens for the next cycle. This indicates that the fluid that enters the outlet channel when the valve opens is not well mixed, and that as it sits statically in the outlet channel after the valve closes, diffusion continues the mixing process until the next time the outlet valve opens and new, not-well-mixed fluid is injected by the mixer. Nonetheless, the peak value of () is significantly less than 0.175 in Fig. 4(b) for gravity-induced continuous flow, which demonstrates that even gives better mixing than diffusion in continuous flow. For mixer pump cycles prior to Frame 6000, is more a measure of poorly mixed fluid due to flushing the dead volume of the mixer.
Note that in Fig. 5(b), () jumps to a lower value when the outlet valve opens than in Fig. 5(a). This means that the fluid entering the outlet channel is better mixed, but still not thoroughly mixed. Examining in Fig. 5(c) () and (d) () shows no evidence of a rapid increase in when the outlet valve opens, meaning that the fluid entering the outlet channel from the mixer is well mixed. For the case of (not shown), there is still a noticeable increase in when new fluid is expelled from the mixer into the outlet channel. We therefore choose for normal LDMP operation to ensure good mixing and avoid larger values of so as to minimize the time it takes to execute a mixer pump cycle, which is
| (14) |
| (15) |
Therefore, a mixer pump cycle with 6 mixing cycles takes , which is 6.5 times faster than diffusion alone for a 20 nl cubic volume, and 150 times faster than if the fluid just sat in the mixer.
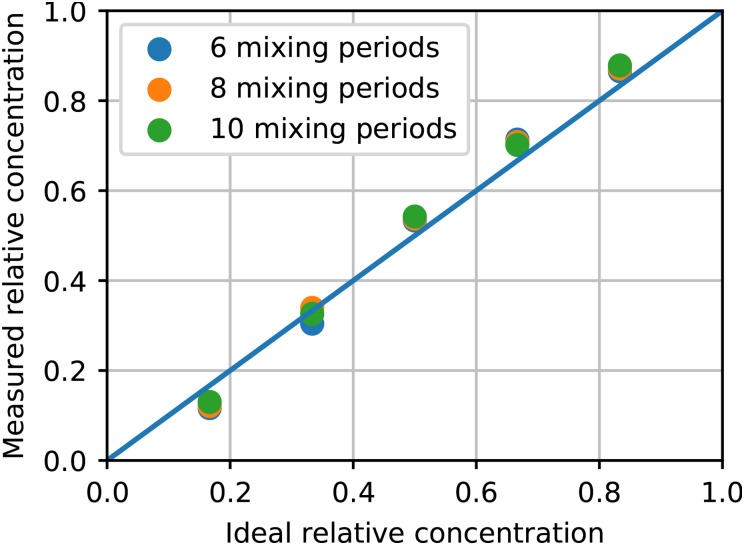
Having determined how many mixing periods are needed to ensure good mixing, we now examine the fidelity of obtaining desired dilution ratios with an LDMP. Since the volume, , is , the possible Red dilution ratios are i/6, where . Figures S4(a)–S4(e) in the supplementary material contain experimental data for each of these cases with . From these, the average relative concentration is calculated and plotted in Fig. 6. We find that the dilution fidelity is reasonably good with the variation from ideal concentration for individual dilutions ranging from 4% to 15%. We also plot the same results for 8 and 10 mixing periods, which shows the same results as for 6 mixing periods and further demonstrates that increasing beyond 6 does not provide a noticeably greater degree of mixing.
FIG. 6.
Measured relative concentration as a function of ideal relative concentration for 6, 8, and 10 mixing periods. The measured relative concentration is averaged over frames in 3 full consecutive mixer pump cycles starting from frame 20 000.
C. 4-to-1 Valve
The 3D printed valves we have discussed so far possess only 1 inlet channel. To simultaneously control 4 inlet channels, 4 such valves would be needed. Alternatively, we can create a 4-to-1 valve that performs the same function. In Fig. 7(a), we show a CAD design of a 4-to-1 valve, which we use in Sec. III D. By placing 4 inlets at the center of the valve, the deflected membrane is designed to seal all of them, simultaneously closing the fluidic pathway between these inlets and the outlet, as shown in Fig. 7(b). To enable the membrane to seal over all four inlet channels, we have increased the valve diameter to 80 pixels (). This 4-to-1 valve is not only smaller than four 40-pixel-diameter valves, but also notably reduces the structural complexity resulting from channel routing. Additionally, combining 4 valves into 1 means only 1 control chamber must be flushed after 3D printing, which simplifies the flushing operation.
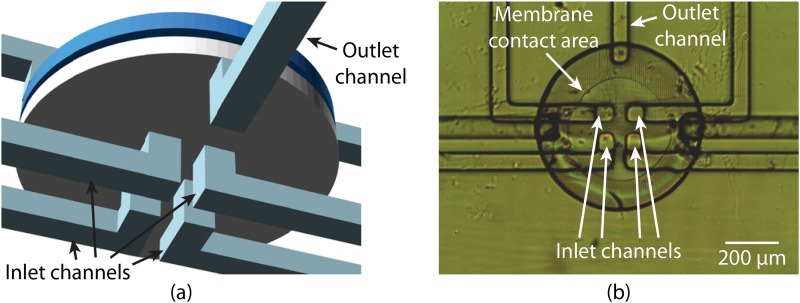
FIG. 7.
(a) CAD design of a 3D printed 4-to-1 valve that contains 4 inlet channels and 1 outlet channel. (b) Microscope photo of a fabricated 4-to-1 valve under pressure. The membrane is deflected such that it is in contact with the central area of the bottom of the valve, covering all 4 inlet channels and therefore closing the valve.
D. Parallelized dilution mixer pump (PDMP)
In an LDMP, inlets A and B are each connected to their own pump. During routine operation if only one pump runs at a time, it takes to fill the mixer. If we operate the 2 pumps simultaneously as much as possible, in the best case for a concentration of 3/6, are needed to fill the mixer. In the worst case (for example, a concentration of 1/6), the Red pump is idle for out of in every mixer pump cycle. To solve this problem, we consider a parallelized dilution mixer pump (PDMP) that exploits its pumps as much as possible to shorten the mixer pump cycle.
In Figs. 8(a)–8(c), we consider several possible configurations for a PDMP. In the extreme case [Fig. 8(a)], there is only 1 pump in the PDMP. However, the pump has a pair of inlet valves, each connected to an individual fluid source such that the pump can be used to pump either fluid. We call this type of pump a dual inlet pump (DIP). If we want its DC to draw fluid from inlet A, we ensure that the inlet B valve is closed. Then the inlet A valve, DC, and 1-to-1 outlet valve together form a regular pump. Since there is only 1 pump, and because , the single DIP must operate times to fill the mixer.
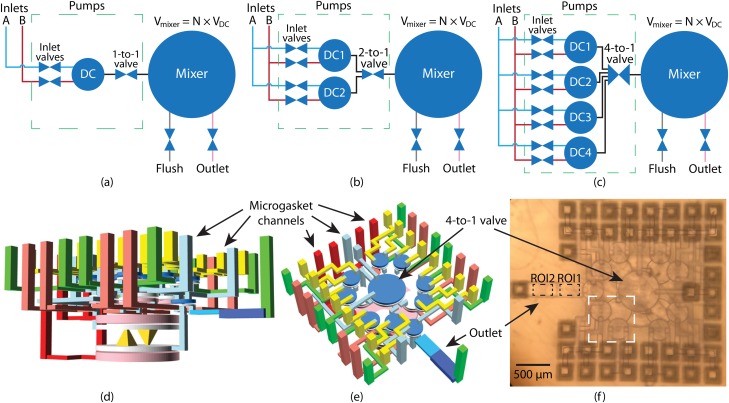
FIG. 8.
(a)–(c) Schematic of PDMPs with 1, 2, and 4 DIPs, respectively. A DIP has 2 inlet valves to enable pumping from either fluid source. The 1-to-1 valve is a normal valve, but a n-to-1 valve controls connecting n inlets to 1 outlet. (d) and (e) Different perspectives of a PDMP CAD design with 4 pumps and a 4-to-1 valve. The green vertical channels are fluidic channels, and the rest are control (pneumatic) channels. The outlet channel consists of two sections with heights of (ROI1) and (ROI2), respectively. (f) Microscope photo of a 3D printed device based on (d) and (e). Inside the white dashed box are 2 inlet valves and a DC.
In Fig. 8(b), we double the number of DIPs and consolidate two 1-to-1 outlet valves into one 2-to-1 outlet valve. Because all of the DIPs in a PDMP are operated in parallel, the time to fill the mixer is cut in half, assuming that is even. The same principle applies to the PDMP in Fig. 8(c) in which 4 DIPs and one 4-to-1 outlet valve are used.
In Table I, we compare the number of valves, DCs, pneumatic lines, and time to fill the mixer for the best case LDMP with PDMPs having various DIP counts. As more DIPs are added to a PDMP, it takes less time to fill the mixer to its maximum capacity if is evenly divisible by the number of DIPs. However, more DIPs increase the complexity of the PDMP 3D layout (for both the PDMP and the interface chips), occupies more volume, and can increase the difficulty of flushing. Therefore, we implement the 4 DIP configuration in Fig. 8(c) as a compromise between faster filling of the mixer and increasing complexity. Our CAD design is shown from two different perspectives in Figs. 8(d) and 8(e), and Fig. 8(f) shows a fabricated device, which occupies a volume of only not counting the various external channels. In the flushing interface chip, we use 41 PTFE tubes, 32 to flush control chambers and 9 to flush fluid chambers and channels. In the operating interface chip, there are 16 tubes, 13 pneumatic and 3 fluidic.
TABLE I.
Comparison of LDMP and PDMPs with different DIP count. Here, we assume the pump DC dimensions are the same for LDMP and PDMPs, and that .
| Inlet | DCs | Outlet | Pneumatic | Shortest time to | |
|---|---|---|---|---|---|
| valves | valves | Lines | fill up mixer | ||
| DMP | 2 | 2 | 2 | 10 | |
| PDMP (1 DIP) | 2 | 1 | 1 | 8 | |
| PDMP (2 DIPs) | 4 | 2 | 1 | 10 | |
| PDMP (4 DIPs) | 8 | 4 | 1 | 14 |
To evaluate this PDMP design, we conduct serial dilutions for the dilution factors listed in Table II. The mixer in the PDMP is the same as in the LDMP, but we shrink the pump DC diameter from 60 pixels to 50 pixels and the fluid and control chamber heights from to to achieve a smaller pump volume, which we can estimate as 80% of (vacuum) from Fig. 2(c), or 1.05 nl. We reduce the pump volume so that more pump volumes can fit in the mixer, which gives us a wider range of possible dilution ratios. We experimentally find that . We choose the denominators in the actual pumped fluid volume ratios in Table II to be as close to 20 as possible for two reasons. First, it allows more fluid to be mixed per mixer pump cycle, and, second, if there is too little fluid in the mixer, the membrane cannot be fully restored to its undeflected state or fully pulled into the control chamber, which limits how much the membrane can move. Limited membrane movement tends to be less effective for active mixing.
TABLE II.
Available serial dilution ratios with various dilution factors for the fabricated PDMP design. A dilution factor of 4 is a subset of a dilution factor of 2.
| Dilution factor | Concentration (actual pumped fluid volume ratios) |
|||
|---|---|---|---|---|
| 2 | 1/2 (8/16) | 1/4 (4/16) | 1/8 (2/16) | 1/16 (1/16) |
| 3 | 1/3 (5/15) | 1/9 (2/18) | … | … |
| 4 | 1/4 (4/16) | 1/16 (1/16) | … | … |
| 5 | 1/5 (3/15) | … | … | … |
An of 6 is used for testing all of the dilution concentrations in Table II. For serial dilution with a dilution factor of 2, a PDMP with 4 DIPs requires 4 pumping periods such that , leading to
| (16) |
| (17) |
which is 8.3 times faster than diffusion alone for a 20 nl cubic volume, and 190 times faster than if the fluid sat statically in the mixer.
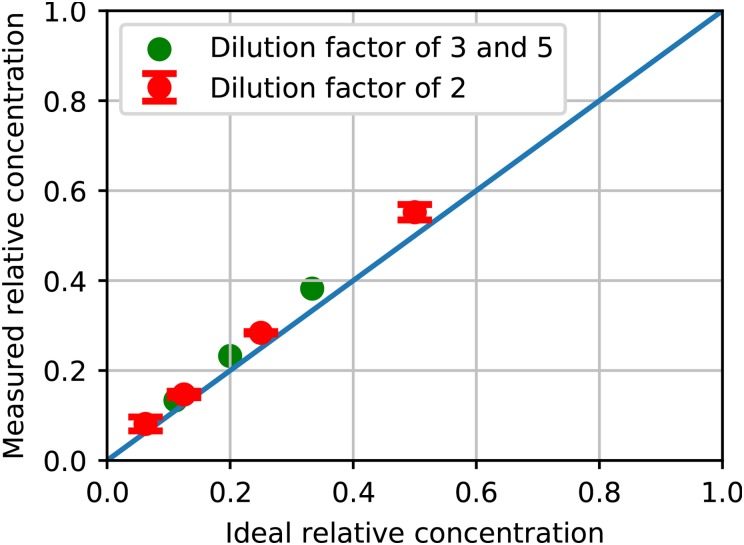
In contrast, an LDMP with the same DC size for the pumps would require 8 pumping periods at minimum for the best case 1/2 dilution ratio, making its 5.6 s, which is over 50% longer than for the PDMP, and 15 pumping periods in the worst case for 1/16 dilution (). Another noteworthy aspect of the PDMP design is that the outlet channel in Figs. 8(e) and 8(f) is divided into 2 sections, the first of which is tall, followed by a tall section. The taller section increases the measurement dynamic range for lower concentration ratios. As shown in Fig. 9, the measured relative concentrations are close to the designed values. For a dilution factor of 2, we test 3 different PDMPs, the results of which are plotted in red in Fig. 9. The error bars for these points represent the standard deviation of the measurements for the 3 different PDMPs, which indicates good repeatability between different fabricated PDMPs. A video of the first minute of operation for a 1:2 dilution ratio is shown in the supplementary material, Video S7(b).
FIG. 9.
Measured relative concentration as a function of ideal relative concentration for different dilution factors using PDMPs. See text for details.
IV. CONCLUSIONS
We have taken advantage of our custom 3D printer and resin to demonstrate highly compact active microfluidic components with tight 3D layouts in only a few cubic millimeters. We have further shown that offloading world-to-chip connections to a separate 3D printed interface chip6 is an important facilitator of such miniaturization. We first examined 3D printed pumps, which can be realized with two valves and a displacement chamber, and demonstrated the relationship between the displacement chamber size and the volume pumped per pumping cycle using a simple video-based analysis method in conjunction with a serpentine channel 3D printed as the pump outlet.
We then integrated 2 pumps with an active mixer to realize a selectable ratio linear dilution mixer pump (LDMP) in only . It is designed to mix 20 nl of fluid in each mixer pump cycle. We have shown that 6 mixer periods are sufficient to fully mix the fluid as evidenced by our new video absorption-based measurement method that uses only a smartphone with a microscope operating in a transmission mode. Using this new method, we are able to process the recorded slow motion videos and obtain the relative dye concentration and its spatial variation in the outlet channel observation region. The measured linear set of concentrations the device can produce are close to the designed dilutions that range from 1/6 to 5/6. Each mixer pump cycle takes 4.6 s.
To speed up the mixing process and achieve a denser set of dilution ratios, we created a parallelized dilution mixer pump (PDMP) which utilizes a new 4-to-1 valve that controls 4 inlets with only 1 pneumatic line. The PDMP shows that we can sacrifice structural simplicity to gain a shorter mixer pump cycle of 3.6 s using 4 dual input pumps. By reducing the pump DC size, we also gain a greater range of dilution possibilities, and demonstrate serial dilutions with dilution factors of 2, 3, and 4, with the highest dilution ratio being 1/16. All measured concentrations are close to the designed values.
SUPPLEMENTARY MATERIAL
See supplementary material for additional videos, tables, and figures referenced in the text.
ACKNOWLEDGMENTS
We are grateful to the National Institutes of Health (R15GM123405 and R01EB006124) for partial support of this work. H.G. acknowledges the support from a Brigham Young University Graduate Research Fellowship.
REFERENCES
- 1.Ho C. M. B., Ng S. H., Li K. H. H., and Yoon Y.-J., “3d printed microfluidics for biological applications,” Lab Chip 15, 3627–3637 (2015). 10.1039/C5LC00685F [DOI] [PubMed] [Google Scholar]
- 2.Au A. K., Huynh W., Horowitz L. F., and Folch A., “3d-printed microfluidics,” Angew. Chem. Int. Ed. 55, 3862–3881 (2016). 10.1002/anie.201504382 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Waheed S., Cabot J. M., Macdonald N. P., Lewis T., Guijt R. M., Paull B., and Breadmore M. C., “3d printed microfluidic devices: Enablers and barriers,” Lab Chip 16, 1993–2013 (2016). 10.1039/C6LC00284F [DOI] [PubMed] [Google Scholar]
- 4.Beauchamp M. J., Nordin G. P., and Woolley A. T., “Moving from millifluidic to truly microfluidic sub-100- cross-section 3d printed devices,” Anal. Bioanal. Chem. 409, 4311–4319 (2017). 10.1007/s00216-017-0398-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Gong H., Bickham B. P., Woolley A. T., and Nordin G. P., “Custom 3d printer and resin for microfluidic flow channels,” Lab Chip 17, 2899–2909 (2017). 10.1039/C7LC00644F [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Gong H., Woolley A. T., and Nordin G. P., “3d printed high density, reversible, chip-to-chip microfluidic interconnects,” Lab Chip 18, 639–647 (2018). 10.1039/C7LC01113J [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Jeong G. S., Chung S., Kim C.-B., and Lee S.-H., “Applications of micromixing technology,” Analyst 135, 460–473 (2010). 10.1039/b921430e [DOI] [PubMed] [Google Scholar]
- 8.Green and sustainable chemical synthesis using flow microreactors,” ChemSusChem 4, 331–340 (2011). 10.1002/cssc.v4.3 [DOI] [PubMed]
- 9.Ehrfeld W., Golbig K., Hessel V., Löwe H., and Richter T., “Characterization of mixing in micromixers by a test reaction: Single mixing units and mixer arrays,” Ind. Eng. Chem. Res. 38, 1075–1082 (1999). 10.1021/ie980128d [DOI] [Google Scholar]
- 10.Mitchell M. C., Spikmans V., and de Mello A. J., “Microchip-based synthesis and analysis: Control of multicomponent reaction products and intermediates,” Analyst 126, 24–27 (2001). 10.1039/b007397k [DOI] [PubMed] [Google Scholar]
- 11.Suga S., Nagaki A., Yoshida J.-i., “Highly selective Friedel–Crafts monoalkylation using micromixing,” Chem. Commun. 34, 354–355 (2003). 10.1039/b211433j [DOI] [PubMed] [Google Scholar]
- 12.Kim H., Min K.-I., Inoue K., Kim D.-P., Yoshida J.-i. et al., “Submillisecond organic synthesis: Outpacing fries rearrangement through microfluidic rapid mixing,” Science 352, 691–694 (2016). 10.1126/science.aaf1389 [DOI] [PubMed] [Google Scholar]
- 13.Lignos I., Stavrakis S., Nedelcu G., Protesescu L., deMello A. J., and Kovalenko M. V., “Synthesis of cesium lead halide perovskite nanocrystals in a droplet-based microfluidic platform: Fast parametric space mapping,” Nano Lett. 16, 1869–1877 (2016). 10.1021/acs.nanolett.5b04981 [DOI] [PubMed] [Google Scholar]
- 14.Nagaki A., Kawamura K., Suga S., Ando T., Sawamoto M., and Yoshida J.-i., “Cation pool-initiated controlled/living polymerization using microsystems,” J. Am. Chem. Soc. 126, 14702–14703 (2004). 10.1021/ja044879k [DOI] [PubMed] [Google Scholar]
- 15.Bally F., Serra C. A., Hessel V., and Hadziioannou G., “Micromixer-assisted polymerization processes,” Chem. Eng. Sci. 66, 1449–1462 (2011). 10.1016/j.ces.2010.07.026 [DOI] [Google Scholar]
- 16.Peng J., Tian C., Zhang L., Cheng Z., and Zhu X., “The in situ formation of nanoparticles via raft polymerization-induced self-assembly in a continuous tubular reactor,” Polym. Chem. 8, 1495–1506 (2017). 10.1039/C6PY02133F [DOI] [Google Scholar]
- 17.Assmann N., Ładosz A., and Rudolf von Rohr P., “Continuous micro liquid-liquid extraction,” Chem. Eng. Technol. 36, 921–936 (2013). 10.1002/ceat.v36.6 [DOI] [Google Scholar]
- 18.Haverkamp V., Ehrfeld W., Gebauer K., Hessel V., Löwe H., Richter T., and Wille C., “The potential of micromixers for contacting of disperse liquid phases,” Fresenius’ J. Anal. Chem. 364, 617–624 (1999). 10.1007/s002160051397 [DOI] [Google Scholar]
- 19.Freitas S., Merkle H. P., and Gander B., “Microencapsulation by solvent extraction/evaporation: Reviewing the state of the art of microsphere preparation process technology,” J. Control Release 102, 313–332 (2005). 10.1016/j.jconrel.2004.10.015 [DOI] [PubMed] [Google Scholar]
- 20.Leblebici M. E., Kuhn S., Stefanidis G. D., and Van Gerven T., “Milli-channel mixer and phase separator for solvent extraction of rare earth elements,” Chem. Eng. J. 293, 273–280 (2016). 10.1016/j.cej.2016.02.083 [DOI] [Google Scholar]
- 21.Jafari O., Rahimi M., and Kakavandi F. H., “Liquid–liquid extraction in twisted micromixers,” Chem. Eng. Process. Process Intensification 101, 33–40 (2016). 10.1016/j.cep.2015.12.013 [DOI] [Google Scholar]
- 22.Liu R. H., Yang J., Lenigk R., Bonanno J., and Grodzinski P., “Self-contained, fully integrated biochip for sample preparation, polymerase chain reaction amplification, and dna microarray detection,” Anal. Chem. 76, 1824–1831 (2004). 10.1021/ac0353029 [DOI] [PubMed] [Google Scholar]
- 23.Lee C.-Y., Lee G.-B., Lin J.-L., Huang F.-C., and Liao C.-S., “Integrated microfluidic systems for cell lysis, mixing/pumping and dna amplification,” J. Micromech. Microeng. 15, 1215 (2005). 10.1088/0960-1317/15/6/011 [DOI] [Google Scholar]
- 24.Chang Y.-H., Lee G.-B., Huang F.-C., Chen Y.-Y., and Lin J.-L., “Integrated polymerase chain reaction chips utilizing digital microfluidics,” Biomed. Microdevices 8, 215–225 (2006). 10.1007/s10544-006-8171-y [DOI] [PubMed] [Google Scholar]
- 25.Kefala I. N., Papadopoulos V. E., Karpou G., Kokkoris G., Papadakis G., and Tserepi A., “A labyrinth split and merge micromixer for bioanalytical applications,” Microfluid. Nanofluidics 19, 1047–1059 (2015). 10.1007/s10404-015-1610-4 [DOI] [Google Scholar]
- 26.Kurita R. and Niwa O., “Microfluidic platforms for dna methylation analysis,” Lab Chip 16, 3631–3644 (2016). 10.1039/C6LC00829A [DOI] [PubMed] [Google Scholar]
- 27.Hadd A. G., Raymond D. E., Halliwell J. W., Jacobson S. C., and Ramsey J. M., “Microchip device for performing enzyme assays,” Anal. Chem. 69, 3407–3412 (1997). 10.1021/ac970192p [DOI] [PubMed] [Google Scholar]
- 28.Burke B. J. and Regnier F. E., “Stopped-flow enzyme assays on a chip using a microfabricated mixer,” Anal. Chem. 75, 1786–1791 (2003). 10.1021/ac026173j [DOI] [PubMed] [Google Scholar]
- 29.Ukita Y., Asano T., Fujiwara K., Matsui K., Takeo M., Negoro S., Kanie T., Katayama M., and Utsumi Y., “Application of vertical microreactor stack with polystylene microbeads to immunoassay,” Sens. Actuators, A 145, 449–455 (2008). 10.1016/j.sna.2008.01.024 [DOI] [Google Scholar]
- 30.Roder H. and Wüthrich K., “Protein folding kinetics by combined use of rapid mixing techniques and NMR observation of individual amide protons,” in NMR in Structural Biology: A Collection of Papers by Kurt Wüthrich (World Scientific, 1995), pp. 691–699. [DOI] [PubMed] [Google Scholar]
- 31.Bilsel O., Kayatekin C., Wallace L. A., and Matthews C. R., “A microchannel solution mixer for studying microsecond protein folding reactions,” Rev. Sci. Instrum. 76, 014302 (2005). 10.1063/1.1834698 [DOI] [Google Scholar]
- 32.Borgia A., Kemplen K. R., Borgia M. B., Soranno A., Shammas S., Wunderlich B., Nettels D., Best R. B., Clarke J., and Schuler B., “Transient misfolding dominates multidomain protein folding,” Nat. Commun. 6, 8861 (2015). 10.1038/ncomms9861 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Jiang L., Zeng Y., Sun Q., Sun Y., Guo Z., Qu J. Y., and Yao S., “Microsecond protein folding events revealed by time-resolved fluorescence resonance energy transfer in a microfluidic mixer,” Anal. Chem. 87, 5589–5595 (2015). 10.1021/acs.analchem.5b00366 [DOI] [PubMed] [Google Scholar]
- 34.Lee C.-Y., Chang C.-L., Wang Y.-N., and Fu L.-M., “Microfluidic mixing: A review,” Int. J. Mol. Sci. 12, 3263–3287 (2011). 10.3390/ijms12053263 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Cai G., Xue L., Zhang H., and Lin J., “A review on micromixers,” Micromachines 8, 274 (2017). 10.3390/mi8090274 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Suh Y. K. and Kang S., “A review on mixing in microfluidics,” Micromachines 1, 82–111 (2010). 10.3390/mi1030082 [DOI] [Google Scholar]
- 37.Gong H., Woolley A. T., and Nordin G. P., “High density 3d printed microfluidic valves, pumps, and multiplexers,” Lab Chip 16, 2450–2458 (2016). 10.1039/C6LC00565A [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Stroock A. D., Dertinger S. K., Ajdari A., Mezić I., Stone H. A., and Whitesides G. M., “Chaotic mixer for microchannels,” Science 295, 647–651 (2002). 10.1126/science.1066238 [DOI] [PubMed] [Google Scholar]
- 39.Luong T.-D., Phan V.-N., and Nguyen N.-T., “High-throughput micromixers based on acoustic streaming induced by surface acoustic wave,” Microfluid. Nanofluidics 10, 619–625 (2011). 10.1007/s10404-010-0694-0 [DOI] [Google Scholar]
- 40.Wang S., Huang X., and Yang C., “Mixing enhancement for high viscous fluids in a microfluidic chamber,” Lab Chip 11, 2081–2087 (2011). 10.1039/c0lc00695e [DOI] [PubMed] [Google Scholar]
- 41.Ahmed D., Mao X., Juluri B. K., and Huang T. J., “A fast microfluidic mixer based on acoustically driven sidewall-trapped microbubbles,” Microfluid. Nanofluidics 7, 727 (2009). 10.1007/s10404-009-0444-3 [DOI] [Google Scholar]
- 42.Lim C. Y., Lam Y. C., and Yang C., “Mixing enhancement in microfluidic channel with a constriction under periodic electro-osmotic flow,” Biomicrofluidics 4, 014101 (2010). 10.1063/1.3279790 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Du Y., Zhang Z., Yim C., Lin M., and Cao X., “A simplified design of the staggered herringbone micromixer for practical applications,” Biomicrofluidics 4, 024105 (2010). 10.1063/1.3427240 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wang Y., Zhe J., Chung B. T., and Dutta P., “A rapid magnetic particle driven micromixer,” Microfluid. Nanofluidics 4, 375–389 (2008). 10.1007/s10404-007-0188-x [DOI] [Google Scholar]
- 45.Lam Y., Gan H., Nguyen N.-T., and Lie H., “Micromixer based on viscoelastic flow instability at low reynolds number,” Biomicrofluidics 3, 014106 (2009). 10.1063/1.3108462 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Huang M.-Z., Yang R.-J., Tai C.-H., Tsai C.-H., and Fu L.-M., “Application of electrokinetic instability flow for enhanced micromixing in cross-shaped microchannel,” Biomed. Microdevices 8, 309–315 (2006). 10.1007/s10544-006-0034-z [DOI] [PubMed] [Google Scholar]
- 47.Tofteberg T., Skolimowski M., Andreassen E., and Geschke O., “A novel passive micromixer: Lamination in a planar channel system,” Microfluid. Nanofluidics 8, 209–215 (2010). 10.1007/s10404-009-0456-z [DOI] [Google Scholar]
- 48.Chen Z., Bown M., O’Sullivan B., MacInnes J., Allen R., Mulder M., Blom M., and van’t Oever R., “Performance analysis of a folding flow micromixer,” Microfluid. Nanofluidics 6, 763–774 (2009). 10.1007/s10404-008-0351-z [DOI] [Google Scholar]
- 49.Tsai R.-T. and Wu C.-Y., “An efficient micromixer based on multidirectional vortices due to baffles and channel curvature,” Biomicrofluidics 5, 014103 (2011). 10.1063/1.3552992 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Ward K. and Fan Z. H., “Mixing in microfluidic devices and enhancement methods,” J. Micromech. Microeng. 25, 094001 (2015). 10.1088/0960-1317/25/9/094001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Lang Q., Ren Y., Hobson D., Tao Y., Hou L., Jia Y., Hu Q., Liu J., Zhao X., and Jiang H., “In-plane microvortices micromixer-based ac electrothermal for testing drug induced death of tumor cells,” Biomicrofluidics 10, 064102 (2016). 10.1063/1.4967455 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Wu Y., Ren Y., Tao Y., Hou L., Hu Q., and Jiang H., “A novel micromixer based on the alternating current-flow field effect transistor,” Lab Chip 17, 186–197 (2017). 10.1039/C6LC01346E [DOI] [PubMed] [Google Scholar]
- 53.Li Y., Liu C., Feng X., Xu Y., and Liu B.-F., “Ultrafast microfluidic mixer for tracking the early folding kinetics of human telomere g-quadruplex,” Anal. Chem. 86, 4333–4339 (2014). 10.1021/ac500112d [DOI] [PubMed] [Google Scholar]
- 54.Yang A.-S., Chuang F.-C., Chen C.-K., Lee M.-H., Chen S.-W., Su T.-L., and Yang Y.-C., “A high-performance micromixer using three-dimensional tesla structures for bio-applications,” Chem. Eng. J. 263, 444–451 (2015). 10.1016/j.cej.2014.11.034 [DOI] [Google Scholar]
- 55.Buchegger W., Wagner C., Lendl B., Kraft M., and Vellekoop M. J., “A highly uniform lamination micromixer with wedge shaped inlet channels for time resolved infrared spectroscopy,” Microfluid. Nanofluidics 10, 889–897 (2011). 10.1007/s10404-010-0722-0 [DOI] [Google Scholar]
- 56.Lin C.-H., Tsai C.-H., and Fu L.-M., “A rapid three-dimensional vortex micromixer utilizing self-rotation effects under low Reynolds number conditions,” J. Micromech. Microeng. 15, 935 (2005). 10.1088/0960-1317/15/5/006 [DOI] [Google Scholar]
- 57.Du M., Ma Z., Ye X., and Zhou Z., “On-chip fast mixing by a rotary peristaltic micropump with a single structural layer,” Sci. China Technol. Sci. 56, 1047–1054 (2013). 10.1007/s11431-013-5140-6 [DOI] [Google Scholar]
- 58.Hardt S., Pennemann H., and Schönfeld F., “Theoretical and experimental characterization of a low-reynolds number split-and-recombine mixer,” Microfluid. Nanofluidics 2, 237–248 (2006). 10.1007/s10404-005-0071-6 [DOI] [Google Scholar]
- 59.Abbas Y., Miwa J., Zengerle R., and von Stetten F., “Active continuous-flow micromixer using an external braille pin actuator array,” Micromachines 4, 80–89 (2013). 10.3390/mi4010080 [DOI] [Google Scholar]
- 60.You J. B., Kang K., Tran T. T., Park H., Hwang W. R., Kim J. M., and Im S. G., “PDMS-based turbulent microfluidic mixer,” Lab Chip 15, 1727–1735 (2015). 10.1039/C5LC00070J [DOI] [PubMed] [Google Scholar]
- 61.Chen K., Lu H., Sun M., Zhu L., and Cui Y., “Mixing enhancement of a novel c-sar microfluidic mixer,” Chem. Eng. Res. Des. 132, 338–345 (2018). 10.1016/j.cherd.2018.01.032 [DOI] [Google Scholar]
- 62.Coelho C. P., Desai S., Freeman D., and White J., “A robust approach for estimating diffusion constants from concentration data in microchannel mixers,” in Proceedings of 2005 NSTI Nanotechnology Conference and Trade Show (Nanotech, 2004) (TechConnect, Anaheim, CA, 2005), Vol. 3, pp. 549–552.
- 63.Werts M. H. V., Raimbault V., Texier-Picard R., Poizat R., Français O., Griscom L., and Navarro J. R. G., “Quantitative full-colour transmitted light microscopy and dyes for concentration mapping and measurement of diffusion coefficients in microfluidic architectures,” Lab Chip 12, 808 (2012). 10.1039/c2lc20889j [DOI] [PubMed] [Google Scholar]
- 64.Liu R. H., Stremler M. A., Sharp K. V., Olsen M. G., Santiago J. G., Adrian R. J., Aref H., and Beebe D. J., “Passive mixing in a three-dimensional serpentine microchannel,” J. Microelectromech. Syst. 9, 190–197 (2000). 10.1109/84.846699 [DOI] [Google Scholar]
- 65.Stroock A. D., Dertinger S. K. W., Ajdari A., Mezić I., Stone H. A., and Whitesides G. M., “Chaotic mixer for microchannels,” Science 295, 647–651 (2002). 10.1126/science.1066238 [DOI] [PubMed] [Google Scholar]
- 66.Hashmi A. and Xu J., “On the quantification of mixing in microfluidics,” J. Assoc. Lab. Autom. 19, 488–491 (2014). 10.1177/2211068214540156 [DOI] [PubMed] [Google Scholar]
- 67.Ansari K.-Y. K. S. M. and Kim M. A., “Numerical and experimental study on mixing performances of simple and vortex micro t-mixers,” Micromachines 9, 204 (2018). 10.3390/mi9050204 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Rogers C. I., Qaderi K., Woolley A. T., and Nordin G. P., “3d printed microfluidic devices with integrated valves,” Biomicrofluidics 9, 016501 (2015). 10.1063/1.4905840 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
See supplementary material for additional videos, tables, and figures referenced in the text.