Integrating Coexpression Networks with GWAS to Prioritize Causal Genes in Maize

Robert J Schaefer; Jean-Michel Michno; Joseph Jeffers; Owen Hoekenga; Brian Dilkes; Ivan Baxter; Chad L Myers

doi:10.1105/tpc.18.00299

. 2018 Nov 8;30(12):2922–2942. doi: 10.1105/tpc.18.00299

Integrating Coexpression Networks with GWAS to Prioritize Causal Genes in Maize^{^[OPEN]}

Robert J Schaefer ^a, Jean-Michel Michno ^a,^b, Joseph Jeffers ^c, Owen Hoekenga ^d, Brian Dilkes ^e, Ivan Baxter ^f,^g,¹, Chad L Myers ^c,¹

PMCID: PMC6354270 PMID: 30413654

Co-expression networks from three diverse maize gene expression data sets were constructed and integrated with genome wide association study data to prioritize genes related to the maize grain ionome.

Abstract

Genome-wide association studies (GWAS) have identified loci linked to hundreds of traits in many different species. Yet, because linkage equilibrium implicates a broad region surrounding each identified locus, the causal genes often remain unknown. This problem is especially pronounced in nonhuman, nonmodel species, where functional annotations are sparse and there is frequently little information available for prioritizing candidate genes. We developed a computational approach, Camoco, that integrates loci identified by GWAS with functional information derived from gene coexpression networks. Using Camoco, we prioritized candidate genes from a large-scale GWAS examining the accumulation of 17 different elements in maize (Zea mays) seeds. Strikingly, we observed a strong dependence in the performance of our approach based on the type of coexpression network used: expression variation across genetically diverse individuals in a relevant tissue context (in our case, roots that are the primary elemental uptake and delivery system) outperformed other alternative networks. Two candidate genes identified by our approach were validated using mutants. Our study demonstrates that coexpression networks provide a powerful basis for prioritizing candidate causal genes from GWAS loci but suggests that the success of such strategies can highly depend on the gene expression data context. Both the software and the lessons on integrating GWAS data with coexpression networks generalize to species beyond maize.

INTRODUCTION

Genome-wide association studies (GWAS) are a powerful tool for understanding the genetic basis of trait variation. This approach has been applied successfully to hundreds of important traits in different species, including important yield-relevant traits in crops. Sufficiently powered GWAS often identify tens to hundreds of loci containing hundreds of single-nucleotide polymorphisms (SNPs) associated with a trait of interest (McMullen et al., 2009). In maize (Zea mays) alone, GWAS have identified nearly 40 genetic loci for flowering time (Buckler et al., 2009), 89 loci for plant height (Peiffer et al., 2014), 36 loci for leaf length (Tian et al., 2011), 32 loci for resistance to southern leaf blight (Kump et al., 2011), and 26 loci for kernel protein (Cook et al., 2012). Despite an understanding of the overall genetic architecture and the ability to statistically associate many loci with a trait of interest, a major challenge has been the identification of causal genes and the biological interpretation of functional alleles associated with these loci.

Linkage disequilibrium (LD), which powers GWAS, acts as a major hurdle limiting the identification of causal genes. Genetic markers are identified by GWAS but often reside outside annotated gene boundaries (Wallace et al., 2014) and can be relatively far from the actual causal polymorphism. Thus, GWAS “hits” can implicate many causal genes at each associated locus. In maize, LD varies between 1 kb to over 1 Mb (Gore et al., 2009), and this range can be even broader in other crop species (Morrell et al., 2005; Caldwell et al., 2006). Moreover, there is increasing evidence that gene regulatory regions play a significant role in functional variation, leading to causal variants falling outside annotated gene boundaries (Wray, 2007; Wallace et al., 2014). Several quantitative trait loci (QTLs) composed of noncoding sequences have been reported previously in maize (Clark et al., 2006; Louwers et al., 2009; Castelletti et al., 2014). These challenging factors mean that even when a marker is strongly associated with a trait, many candidate genes are equally plausible until a causal polymorphism is identified.

graphic file with name TPC_201800299R2_fx1.jpg

The issues with narrowing a large set of candidate genes to likely causal genes are exacerbated in crop species, where gene annotation is largely incomplete. For example, in maize, only ∼1% of genes have functional annotations based on mutant analyses (Andorf et al., 2016). Thus, even when a list of potential candidate genes can be identified for a particular trait, there are very few sources of information that can help identify genes linked to a phenotype. The interpretation and narrowing of large lists of highly associated SNPs with complex traits are now the bottleneck in developing new mechanistic understanding of how genes influence traits.

One informative and easily measurable source of functional information is gene expression. Surveying gene expression profiles in different contexts, such as throughout tissue development or within different genetic backgrounds, helps establish how a gene’s expression is linked to its biological function, including variation in phenotype. Comparing the similarity of two genes’ expression profiles, or coexpression, quantifies the joint response of the genes to various biological contexts, and highly similar expression profiles can indicate shared regulation and function (Eisen et al., 1998). The analysis of coexpression has been used successfully to identify functionally related genes, including in several crop species (Ozaki et al., 2010; Mochida et al., 2011; Swanson-Wagner et al., 2012; Zheng and Zhao, 2013; Obayashi et al., 2014; Sarkar et al., 2014; Schaefer et al., 2014; Michno et al., 2018; Wen et al., 2018), and has been used to characterize GWAS results in Arabidopsis (Arabidopsis thaliana) (Chan et al., 2011; Corwin et al., 2016; Angelovici et al., 2017; Lee and Lee, 2018).

Because coexpression provides a global measure of functional relationships, it can serve as a powerful means for interpreting GWAS candidate loci. Specifically, we expect that variation in several different genes contributing to the same biological process would be associated with a given phenotype (Wolfe et al., 2005; Rotival and Petretto, 2014). Thus, if genetic variation driving the phenotype captured by GWAS is encoded by coregulated genes, these data sets will overlap nonrandomly. Although not all functional relationships are captured with coexpression relationships (Ritchie et al., 2015), these data still provide a highly informative, and sometimes the only, set of clues about genes that otherwise have not been studied. This principle has been used successfully with other types of networks, for example, protein-protein interactions (Li et al., 2008), and coexpression has been used as a basis for understanding GWAS in mouse and human (Bunyavanich et al., 2014; Taşan et al., 2015; Calabrese et al., 2017; Shim et al., 2017; Baillie et al., 2018).

We developed a freely available, open-source computational framework called Camoco (Coanalysis of molecular components) designed specifically to integrate results from GWAS with gene coexpression networks to prioritize individual candidate genes. Camoco evaluates candidate SNPs derived from a typical GWAS, and then identifies sets of high-confidence candidate genes with strong coexpression where multiple members of the set are associated with the phenotype of interest.

We applied this approach to maize, one of the most important agricultural crops in the world, yielding 15.1 billion bushels of grain in the United States alone in 2016 (USDA, 2016). We specifically focused on quantitative phenotypes measuring the accumulation of 17 different elements in the maize grain ionome (Al, As, B, Ca, Cd, Fe, K, Mg, Mn, Mo, Na, Ni, Rb, S, Se, Sr, and Zn). Plants must take up all elements except carbon and oxygen from the soil, making the plant ionome a critical component in understanding the plant environmental response (Baxter, 2010), grain nutritional quality (Guerinot and Salt, 2001), and plant physiology (Baxter et al., 2008).

We evaluated the utility of three different types of coexpression networks to support the application of Camoco and demonstrate the efficacy of our approach by simulating GWAS to establish maize-specific SNP-to-gene mapping parameters as well as a robust null model for GWAS-network overlap. Our study does indeed confirm overlap between functional modules captured by coexpression networks and GWAS candidate SNPs for the maize grain ionome. We present high-confidence candidate genes identified for a variety of different ionomic traits, test single-gene mutants demonstrating the utility of this approach, and, more generally, highlight lessons about the connection between coexpression and GWAS loci from our study that are likely to generalize to other traits and other species.

RESULTS

Camoco: A Framework for Integrating GWAS Results and Comparing Coexpression Networks

We developed a computational framework called Camoco that integrates the outputs of GWAS with coexpression networks to prioritize high-confidence causal genes associated with a phenotype of interest. The rationale for our approach is that genes that function together in a biological process that are identified by GWAS also should have nonrandom structure in coexpression networks that capture the same biological function. Our approach takes, as input, a list of SNPs associated with a trait of interest and a table of gene expression values and produces, as output, a list of high-priority candidate genes that are near GWAS peaks having evidence of strong coexpression with other genes associated with the trait of interest.

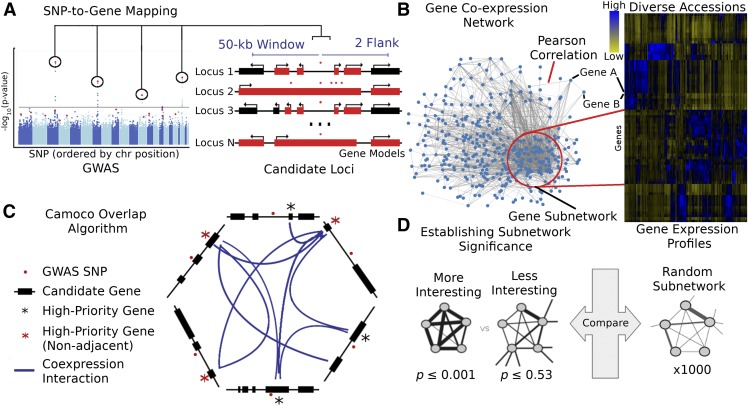
There are three major components of the Camoco framework: a module for SNP-to-gene mapping (Figure 1A), tools for the construction and analysis of coexpression networks (Figure 1B), and an “overlap” algorithm that integrates GWAS-derived candidate genes with the coexpression networks to identify high-priority candidate genes with strong coexpression support across multiple GWAS loci (Figure 1C) (see Methods for details on each component).

The overlap algorithm uses two network scoring metrics: subnetwork density and subnetwork locality. Subnetwork density measures the average interaction strength between all pairwise combinations (i.e., unthresholded) of genes near GWAS peaks. Specifically, density is obtained by computing the mean of raw interaction scores among all pairs of genes in the subnetwork and normalizing by the subnetwork size (Equation 1). Subnetwork locality measures the proportion of significant (Z ≥ 3) coexpression interactions among genes within a GWAS-derived subnetwork (local interactions) as compared with the number of global interactions with other genes in the genome (global interactions). Specifically, locality is obtained by first fitting a linear regression between all genes’ local degree (among the subnetwork of interest) and their global degree and measuring the mean of the residual for genes in the subnetwork (Equation 2). Density and locality metrics can be calculated on whole subnetworks or on a gene-specific basis to prioritize candidate genes by factoring out each gene’s contribution to the subnetwork (Equations 3 and 4) (see Methods for details). For a given input GWAS trait and coexpression network, the statistical significance for both density and locality is determined by generating a null distribution based on randomly generated GWAS traits (n = 1000) with the same number of implicated loci and corresponding candidate genes. The resulting null distribution is then used to derive a P value for the observed subnetwork density and locality for all putative causal genes (Figure 1D). Thus, for a given input GWAS trait, Camoco produces a ranked list of candidate causal genes for both network metrics and a corresponding false discovery rate (FDR) that indicates the significance of the observed overlap between each candidate causal gene’s coexpression network neighbors and the set of genes under implicated loci. Using this integrated approach, the number of candidate genes prioritized for follow-up validation is reduced substantially relative to the initial set of genes under implicated loci.

Camoco allows users to build, validate, and analyze data sets using common file types for gene expression, GWAS, and species-specific reference data (e.g., OBO, FASTA, and GFF). Our tool formalizes the integration of GWAS data with coexpression networks by offering systematic SNP-to-gene mapping parameters, which can be evaluated using simulated GWAS gold standard data sets. Camoco also corrects for artifacts (such as cis coexpression bias) that arise from integrating GWAS and coexpression data. The framework offers a unified command line interface to the components described above but also can be used through its Python API to integrate into other workflows. Our method can be applied to any trait and species for which GWAS has been completed and sufficient gene expression data exist to construct a coexpression network.

Generating Coexpression Networks from Diverse Transcriptional Data

A coexpression network that is derived from the biological context generating the phenotypic variation subjected to GWAS is a key component of our approach. A well-matched coexpression network will describe the most relevant functional relationships and identify coherent subsets of GWAS-implicated genes. We and others have shown previously that coexpression networks generated from expression data derived from different contexts capture different functional information (Swanson-Wagner et al., 2012; Schaefer et al., 2014). For example, experiments measuring changes in gene expression can explore environmental adaptation, developmental and organ-based variation, or variation in expression that arises from population and ecological dynamics (reviewed in Schaefer et al., 2017). For some species, published data contain enough experimental accessions to build networks from these different types of expression experiments (the term accession is used here to differentiate samples, tissues, conditions, etc.). We reasoned that these different sources of expression profiles likely have a strong influence on the utility of the coexpression network for interpreting genetic variation captured by GWAS. Using this rationale, we constructed several coexpression networks independently and assessed the ability of each to produce high-confidence discoveries using our Camoco framework.

Three coexpression networks representing three different biological contexts were built. The first data set targeted expression variation that exists between diverse maize accessions built from whole-seedling transcriptomes on a panel of 503 diverse inbred lines from a previously published data set characterizing the maize pan-genome (called the ZmPAN network hereafter; Hirsch et al., 2014). Briefly, Hirsch et al. (2014) chose these lines to represent major heterotic groups within the United States, sweet corn, popcorn, and exotic maize lines, and measured gene expression profiles for seedling tissue as a representative tissue for all lines. The second data set examined gene expression variation from a previous study characterizing different tissues and developmental time points (Stelpflug et al., 2016). Whole-genome RNA sequencing (RNA-Seq) transcriptome profiles from 76 different tissues and developmental time points from the maize reference accession B73 were used to build a network representing a single-accession expression map (called the ZmSAM network hereafter). Finally, we created a third data set as part of the ionomics GWAS research program. These data measure gene expression variation in the root, which serves as the primary uptake and delivery system for all the measured elements (Baxter, 2010; Chao et al., 2011; Baxter and Dilkes, 2012). Gene expression was measured from mature roots in a collection of 46 genotypically diverse maize inbreds (called the ZmRoot network hereafter). All data sets used here were generated from whole-genome RNA-Seq analysis, although Camoco also could be applied to microarray-derived expression data.

Coexpression networks for each data set were constructed from gene expression matrices using Camoco (see Methods for specific details on building these networks). Once built, several summary statistics were evaluated from interactions that arise between genes in the network (Supplemental Figures 1–3). Coexpression was measured among genes within the same Gene Ontology (GO) term to establish how well density and locality captured terms with annotated biological functions (Table 1; Supplemental Data Set 1). Indeed, we observed enrichment for a large number of GO terms for both metrics in all three networks as well as similar levels of enriched modules derived from a graph clustering approach (Table 2; Supplemental Data Set 2; van Dongen, 2000), supporting their ability to capture functionally related genes (see Discussion; Supplemental Text and Supplemental Data Set 3).

Table 1. Significantly Coexpressed GO Terms.

	No. of Significant (P ≤ 0.01) GO Terms (n = 1078)
Network	Density	Locality	Both Scores	Either Score
ZmPAN	451 (41%)	539 (50%)	312 (29%)	678 (63%)
ZmSAM	365 (34%)	437 (40%)	234 (21%)	568 (53%)
ZmRoot	573 (53%)	331 (31%)	278 (26%)	626 (58%)

Open in a new tab

Coexpression was measured among genes within each GO term that had coexpression data in each network using both density (Equation 1) and locality (Equation 2). The significance of coexpression metrics was assessed by comparing values with 1000 random gene sets of the same size.

Table 2. Gene Coexpression Network Cluster Assignments.

	Network Clusters
Network	No. of Clusters (10 ≥ n > 100)	No. of Clusters  (n ≥ 100)	No. of Clusters (n ≥ 10) Enriched for GO Terms  (P ≤ 0.01)
ZmPAN	76	18	71
ZmSAM	160	10	115
ZmRoot	150	10	106

Open in a new tab

Gene clusters were calculated by running the Markov Cluster (MCL) algorithm on the coexpression matrix. Cluster values designate network-specific gene clusters and are not compared across networks.

Accounting for cis Gene Interactions

Camoco integrates GWAS candidates with coexpression interactions by directly assessing the density or locality of interactions among candidate genes near GWAS SNPs. However, the process of mapping SNPs to surrounding candidate genes has inherent complications that can strongly influence subnetwork coexpression calculations. While we assume that the majority of informative interactions among candidate genes are between GWAS loci, cis-regulatory elements and other factors can lead to coexpression between linked genes and produce skewed distributions in density and locality calculations, which in turn can bias coexpression statistics. Identifying significant overlap between GWAS loci and coexpression networks requires a distinction between coexpression among genes that are in close proximity to one another on a chromosome (cis) compared with those genes that are not (trans).

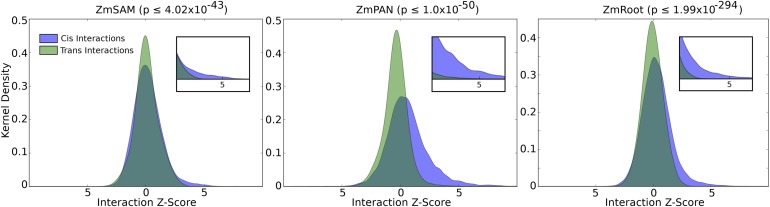
To assess the influence of cis coexpression, network interactions for genes located on different chromosomes (trans interactions) were compared with cis interactions for pairs of genes less than 50 kb apart. The distributions of the two groups indicate that cis genes are more likely to have a strong coexpression interaction score than trans genes (Figure 2). This bias toward cis genes is especially pronounced for strong positive coexpression, where we observed substantially stronger enrichment for linked gene pairs compared with trans genes (e.g., z score ≥ 3; Figure 2, insets).

Figure 2. — *Cis* Versus *trans* Coexpression Network Interactions.

The distributions of coexpression network interaction scores between *cis* and *trans* sets of genes were compared. Distribution densities of *trans* gene pairs (green) show interactions between genes on separate chromosomes. Distribution densities of *cis* gene pairs (blue) show interactions between genes with less than 50-kb intergenic distance. Inset graphs show z score values greater than 3. Nonparametric P values were calculated between coexpression values taken from *cis* and *trans* distributions (Mann-Whitney U test).

The enrichment of significant coexpression among cis genes, likely due to shared cis-regulatory sequences or closely encoded clusters of functionally related genes, prompted us to remove cis interactions when examining coexpression relationships among candidate genes identified by GWAS SNPs in Camoco. To account for the bias of strong coexpression among cis genes, only interactions among pairs of genes originating from unlinked SNPs (i.e., trans) were included in density and locality calculations when evaluating GWAS results (see Methods).

Evaluation of the Camoco Framework

To explore the limits of our approach, we examined factors that influence overlap detection between coexpression networks and genes linked to GWAS loci. In an idealized scenario, SNPs identified by GWAS map directly to true causal genes, all of which exhibit strong coexpression network interactions with each other (Figure 3). In practice, SNPs can affect regulatory sequences or be in LD with the functionally important allele, leading to a large proportion of SNPs occurring outside of genic regions (Wallace et al., 2014).

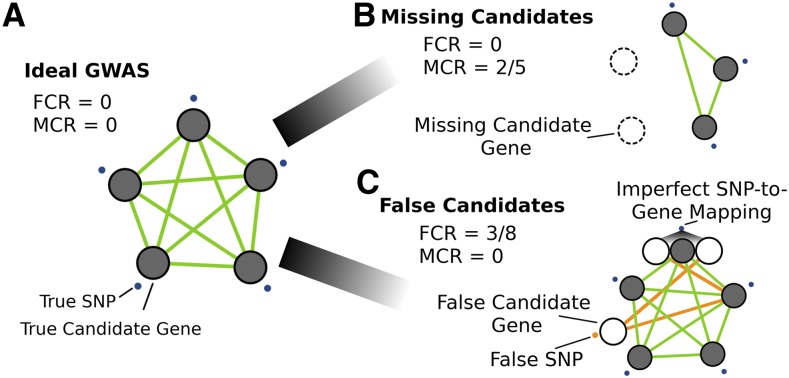
Figure 3. — Simulating GWAS Network Overlap Using GO Terms.

Several GWAS scenarios were simulated to assess the effect of noise on coexpression network overlap.

**(A)** Ideal GWAS, where SNPs (blue points) map directly to candidate genes within the same biological process (i.e., a GO term) and have strong coexpression (green lines). Signal is defined as the coexpression among the genes exclusive to the GO term. Noise in the overlap between GWAS and coexpression networks was introduced by varying two parameters: the MCR and FCR.

**(B)** Effect of a large proportion of missing candidate genes (MCR = 2/5) on network signal.

**(C)** Effect of false candidate genes (FCR) on network overlap, either through false-positive GWAS SNPs (orange point) or through imperfect SNP-to-gene mapping (FCR = 3/8). Orange lines designate the additional candidate genes that introduce coexpression noise that impedes the identification of network structure.

We evaluated two major challenges that influence SNP-to-gene mapping. The first is the total number of functionally related genes in a subnetwork, representing the fraction of genes involved in a biological process that are identified simultaneously by GWAS. In cases where too few genes represent any one of the underlying causal processes, our proposed approach is not likely to perform well; for example, consider the situation when GWAS identifies a single locus in a 10-gene biological process due to incomplete penetrance, limited allelic variation in the mapping population, or extensive gene-by-environment interactions. We refer to this source of noise as the missing candidate gene rate (MCR) or, in other words, the fraction of genes involved in the causal process not identified by the GWAS in question (Figure 3B; Equation 5).

The second key challenge in identifying causal genes from GWAS loci is instances where associated SNPs each implicate a large number of noncausal candidate genes. Thus, in cases where the linked regions are large (i.e., imperfect SNP-to-gene mapping), the framework’s ability to confidently identify subnetworks of highly coexpressed causal genes may be compromised. One would expect to find scenarios where the proposed approach does not work simply because there are too many noncausal genes implicated by linkage within each GWAS locus, such that the coexpression signal among the true causal genes is diminished by the false candidates linked to those regions. We refer to this source of noise as the false candidate gene rate (FCR), the fraction of all genes linked to GWAS-implicated loci that are not causal genes (Figure 3C; Equation 6).

To explore the limits of our coexpression-based approach with respect to these factors, we simulated scenarios where we could precisely control both MCR and FCR. In practice, neither of these quantities can be controlled; MCR is a function of the genetic architecture of the phenotype as well as the degree of power within the study population of interest, and FCR is a function of recombination frequency in the GWAS population.

We evaluated the expected performance of the Camoco framework for a range of each of these parameters by simulating ideal GWAS scenarios using GO terms with significantly coexpressed genes (P ≤ 0.05; Table 1). These ideal cases were then subjected to processes where either a subset of genes was replaced by random genes (i.e., to simulate MCR but conserve term size) or additional functionally unrelated genes were added using SNP-to-gene mapping (i.e., to simulate FCR introduced by linkage). In both cases, simulated GWAS candidates (i.e., genes annotated to our selected GO terms) were subjected to varying levels of either FCR or MCR while tracking the number of GO terms that remained significantly coexpressed at each level. These simulations enabled us to explore a broad range of settings for these key parameters and establish whether our proposed approach had the potential to be applied in maize.

Simulated GWAS Data Sets Show Robust Coexpression Signal to MCR and FCR

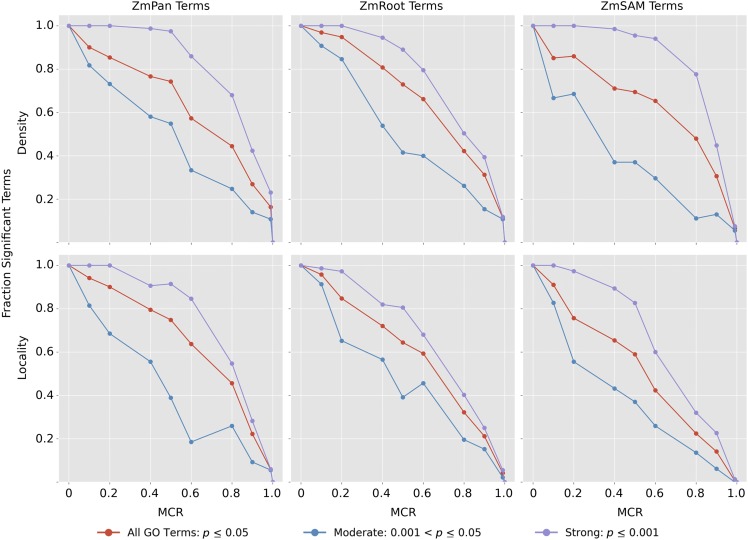
Subnetwork density and locality were measured for GO terms with significantly coexpressed genes containing between 50 and 150 genes in each network at varying levels of MCR (Supplemental Data Set 4). At each MCR level, density and locality among the remaining genes were compared with 1000 random sets of genes of the same size. The proportion of initial GO terms that remained significantly coexpressed was recorded for each network (Figure 4, red curves; see Supplemental Figure 4A for absolute term numbers). GO terms also were split into two starting groups based on the strength of the initial coexpression: moderate (0.001 < P ≤ 0.05; blue curves) and strong (P ≤ 0.001; violet curves).

As expected, the strength of coexpression among GO terms decreased as MCR increased. Figure 4 shows the decay in the proportion of GO terms that exhibit significant coexpression at increasing levels of MCR (red curves). In general, the decay of signal is similar between density and locality, where signal initially decays slowly until ∼60% MCR, when signal quickly diminishes.

In all three networks, GO terms with stronger initial coexpression were more robust to MCR. Signal among GO terms with strongly coexpressed genes (P ≤ 0.001; violet curves) decayed at a substantially lower rate than GO terms with a more moderate signal, indicating that this approach is robust for GWAS data sets with moderate levels of missing genes when coexpression among true candidate genes is strong. Coexpression signal in relation to MCR also was compared between GO terms split by the number of genes within the term (Supplemental Figures 4B and 4C), which did not influence the rate at which the coexpression signal decayed.

Likewise, the effect of FCR was simulated. GO terms with between 50 and 150 genes (MCR = 0) with significant coexpression among member genes (P ≤ 0.05; Supplemental Data Set 4) were selected. The nucleotide position of the starting base pair of each true GO term gene was used as input for our SNP-to-gene mapping protocol to identify GWAS candidates (see Methods). Subnetwork density and locality were calculated for the simulated candidate genes corresponding to each SNP-to-gene mapping combination, in each network, to evaluate the decay of coexpression signal as FCR increases (Figure 5).

Figure 5. — Strength of Coexpression among GO Terms at Varying Levels of FCR.

GO terms with significantly coexpressed genes (density or locality P ≤ 0.05) were used to simulate the effect of FCR on GWAS results. False candidates were added to GO terms by including flanking genes near true GO term genes according to SNP-to-gene mapping (window) parameters. Box plots show effective FCR of GO terms at each SNP-to-gene mapping parameter. Signal plots show the proportional number of GO terms that remain significant at FCR ≥ x (red curves). GO terms in each network also were split into two subsets based on initial coexpression strength: strong (initial coexpression P ≤ 0.001; blue curves) and moderate (initial coexpression 0.001 < P ≤ 0.05; violet curves).

Candidate genes were added by varying the window size for each SNP up to 50, 100, and 500 kb upstream and downstream and by varying the maximum number of flanking genes on each side to one, two, and five. Given the number of additional candidate genes introduced at each SNP-to-gene mapping combination, FCR was calculated for each GO term at each window size (Figure 5, box plots).

Coexpression signal in relation to FCR was assessed by comparing subnetwork density and locality for each GO term at different SNP-to-gene mapping parameters for each of the three coexpression networks to random subnetworks with the same number of genes (n = 1000) (Figure 5, top). The proportion of GO terms with significantly coexpressed genes decayed at higher levels of FCR (see Supplemental Figure 5A for absolute term numbers). The minimum FCR level ranged from 1 to 80% across all GO terms but for most GO terms was ∼50%, as the most stringent SNP-to-gene mapping (50 kb/one flank) approximately doubled the number of candidate genes. Two additional scenarios were considered in which signal was split further based on the initial coexpression strength: moderate (0.001 < P < 0.05; blue curves) and strong (P ≤ 0.001; violet curves).

Despite high initial false candidate rates, coexpression signal among GO terms remained significant even at 60 to 70% FCR. Similar to the results with MCR, GO terms with stronger initial coexpression were more likely to remain significantly coexpressed at higher FCR levels. Coexpression signal in relation to FCR also was compared between GO terms split by the number of genes in the term (Supplemental Figures 5B and 5C), which did not differentiate the rate at which coexpression signal decayed.

In cases where true candidate genes identified by GWAS were strongly coexpressed, as simulated here, a substantial number of false-positive SNPs or an introduction of false candidate genes through uncertainty in SNP-to-gene mapping can be tolerated, and network metrics still detected the underlying coexpressed gene sets using our method. These results indicate that, in GWAS scenarios where the majority of SNPs do not resolve perfectly to candidate genes, systematic integration with coexpression networks can efficiently filter out false candidates introduced by SNP-to-gene mapping if the underlying causal loci are linked to genes that are strongly coexpressed with each other. Moreover, in instances where several intervening genes exist between strongly associated SNPs in LD with each other and the true causative allele, true causal candidates can be detected using coexpression networks as a functional filter for candidate gene identification.

The potential for using this approach, however, is highly dependent on the LD of the organism in question, the genetic architecture of the trait being studied, and the degree of coexpression between causative loci. Simulations provide insight into the feasibility of using Camoco to evaluate overlap between coexpression networks and GWAS as well as a survey of the SNP-to-gene mapping parameters that should be used when using this approach (see Discussion for more details). In the context of maize, the simulations performed here suggest that systematic integration of coexpression networks to interpret GWAS results will increase the precision with which causal genes associated with quantitative traits in true GWAS scenarios can be identified.

High-Priority Candidate Causal Genes under Ionomic GWAS Loci

Identifying the biological processes underlying the elemental composition of plant tissues, also known as the ionome, can lead to a better understanding of plant adaptation as well as improved crops (Baxter and Dilkes, 2012). High-throughput analytic approaches such as inductively coupled plasma mass spectrometry (ICP-MS) are capable of measuring elemental concentrations for multiple elements and are scalable to thousands of accessions per week. Using ICP-MS, we analyzed the accumulation of 17 elements in maize kernels described in depth by Ziegler et al. (2017). Briefly, kernels from the nested association mapping (NAM) population were grown in four geographic locations (McMullen et al., 2009). To reduce environment-specific factors, the SNPs used in this study were from the GWAS performed on the all-location models. Approximately 30 million SNPs and small-copy-number variants were projected onto the association panel and used to perform a GWAS for each of the 17 elements. SNPs were tested for the significance of association for each trait using resampling model inclusion probability (Valdar et al., 2009) (RMIP ≤ 0.05; see Methods). For each element (trait), significantly associated SNPs were used as input to Camoco to generate candidate genes from the maize filtered gene set (FGS; n = 39,656) using a range of SNP-to-gene mapping parameters: 50-, 100-, and 500-kb windows (upstream/downstream) limited each to one, two, or five flanking genes (upstream/downstream of SNP; Figure 1A). In total, 4243 statistically significant SNPs were associated with maize grain ionome traits. Summing the potential candidate genes across all 17 traits implicates between 5272 and 22,927 unique genes depending on the SNP-to-gene mapping parameters used (between 13 and 57% of the maize FGS, respectively; Supplemental Data Set 5). On average, each trait’s significantly associated SNPs identified 119 nonoverlapping windows across the 10 chromosomes of maize (i.e., effective loci; see Methods), and these implicate an average of 613 candidate genes per element (see Methods).

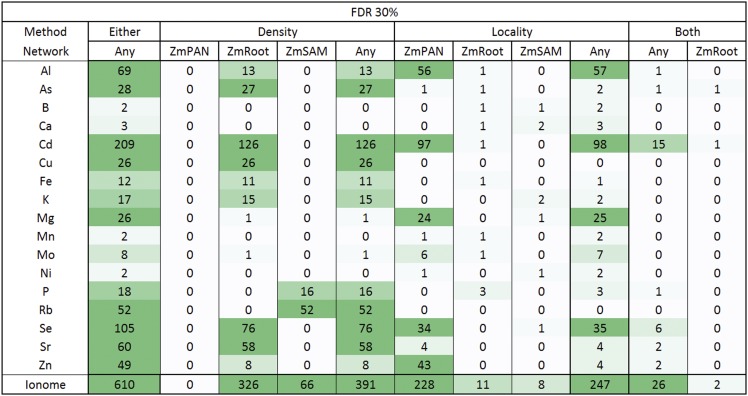
Given the large number of candidate genes associated with elemental accumulation, we used Camoco to integrate network coexpression with effective loci identified by GWAS for each of the 17 elemental traits separately. By combining candidate gene lists with the three gene expression data sets (ZmPAN, ZmRoot, and ZmSAM) and two coexpression network metrics (locality and density), high-priority candidate genes driving elemental accumulation in maize were identified (Figure 1C). For each network-trait combination, Camoco identified a ranked list of prioritized candidate causal genes, each associated with an FDR that reflects the significance of coexpression connecting that candidate gene to genes near other loci associated with the same trait (Supplemental Data Set 6). We defined a set of high-confidence discoveries by reporting candidates that were discovered at FDR ≤ 30% in at least two SNP-to-gene mapping parameter settings (e.g., 50 kb/one flank and 100 kb/one flank), denoted as the high-priority overlap (HPO) set (Supplemental Data Set 7; see Methods).

By these criteria, we found strong evidence of coexpression for 610 HPO genes that were positional candidates across the 17 ionomic traits measured (1.5% maize FGS). The number of HPO genes discovered varied significantly across the traits we examined, with between 2 and 209 HPO genes for a given element considering either density or locality in any network (Figure 6, Either/Any column). HPO genes discovered by Camoco often were nonadjacent to GWAS effective loci, either having genes intervening between the HPO candidate or that were closer to the GWAS-implicated locus (Figure 1C), demonstrating that Camoco often identifies candidates with strong coexpression evidence that would not have been selected by choosing the closest positional candidate.

Figure 6. — Maize Grain Ionome High-Priority Candidate Gene Heat Map Summary.

Gene-specific density and locality metrics were compared with random sets of genes (n = 1000) of the same size to establish a 30% FDR. Genes were considered candidates if they were observed at two or more SNP-to-gene mappings (i.e., HPO). Candidates in the Either column are HPO genes discovered by either density or locality in any network. The number of genes discovered for each element is further broken down by coexpression method (density, locality, and both) and by network (ZmPAN, ZmSAM, and ZmRoot). Candidates in the Both column were discovered by density and locality in the same network or in different networks (Any). The shading of the heat map indicates more HPO genes. Note that zero elements had HPO genes using both methods in the ZmPAN and ZmSAM networks.

Genotypically Diverse Networks Support Stronger Candidate Gene Discoveries Than Tissue Atlases

The variation in the number of genes discovered by Camoco depended on which coexpression network was used as the basis for discovery. The ZmRoot coexpression network proved to be the strongest input, discovering genes for 15 of the 17 elements (absent in Ni and Rb) for a total of 335 HPO genes, ranging from 1 to 126 per trait (Supplemental Data Set 7). In contrast, the ZmSAM network, which was constructed based on a tissue and developmental expression atlas collected exclusively from the B73 accession, supported the discovery of candidate genes for only 8 elements (B, Ca, K, Mg, Ni, P, Rb, and Se) for a total of 74 HPO genes, ranging from 1 to 52 per trait (Supplemental Data Set 7). The ZmPAN network, which was constructed from whole seedlings (pooled tissue) across 503 different accessions, provided intermediate results, supporting high-confidence candidate discoveries for 10 elements (Al, As, Cd, Mg, Mn, Mo, Ni, Se, Sr, and Zn) for a total of 228 HPO genes, ranging from 1 to 97 per trait (Supplemental Data Set 7). The relative strengths of the different networks for discovering candidate causal genes were consistent even at stricter FDR thresholds (e.g., FDR ≤ 0.10; Supplemental Data Set 7).

Network Coexpression Metrics Provide Complementary Information, and Most Candidate Causal Genes Are Trait Specific

Both density and locality were assessed on a gene-specific level to measure the strength of a given candidate causal gene’s coexpression relationships with genes in other GWAS-identified loci (Equations 3 and 4) (Figure 6, Density/Any and Locality/Any). Interestingly, the high-confidence genes identified by the two approaches were largely complementary, in terms of both which traits and which network they produced results for. Indeed, when we measured the direct correlation of gene-specific density and locality measures across several GWAS traits and GO terms, we observed very weak positive but significant correlations (Supplemental Figure 6). We observed that the utility of the locality metric appeared to be associated with the number of accessions used to construct the network (Supplemental Data Set 8; see Discussion). One important question is the extent to which putative causal genes overlap across different ionomic traits. It is plausible that some mechanisms affecting elemental accumulation are shared by multiple elements. However, most of the discovered HPO genes are element specific, with relatively little overlap between elements (Supplemental Figure 7 and Supplemental Data Set 9).

Camoco Identifies Genes with Known Roles in Elemental Accumulation

To explore the broader biological processes represented among HPO genes, we performed GO enrichment analysis on the candidate lists, revealing enrichments for five elements (Supplemental Data Set 10). For example, Sr was enriched for genes involved in anion transport (GO:0006820; P ≤ 0.008) and metal ion transmembrane transporter activity (GO:0046873; P ≤ 0.015) (see Supplemental Text for in-depth summary). Possibly due to insufficient functional annotation of the maize genome, these enrichment results were limited, and zero elements passed a strict multiple-test correction (Bonferroni). We created a larger set of genes, including genes highly connected to the HPO genes, and compared those with GO terms (Supplemental Text). As detailed in the Supplemental Text, several GO terms were enriched in this set, including genes that act in previously described pathways known to impact elemental traits (Supplemental Figure 8 and Supplemental Data Set 11). However, GO terms were too broad or insufficiently specific to distinguish causal genes.

We also manually examined literature support for the association of candidate genes with ionomic traits (see Supplemental Text for in-depth summary). Complementing genes with known roles in elemental homeostasis, HPO gene sets for some ionomic traits included multiple genes encoding known members of the same pathway or protein complex. For example, one gene with highly pleiotropic effects on the maize kernel ionome is sugary1 (GRMZM2G138060) (Baxter et al., 2014), which was present among the HPO genes for Se accumulation (Supplemental Data Set 7) based on the root coexpression network (ZmRoot-Se) but was linked to significant NAM GWAS SNPs for the elements P, K, and As. Previous analysis of lines segregating the sugary1 allele demonstrated effects on the levels of P, S, K, Ca, Mn, Fe, As, Se, and Rb in the seed. A number of transporters with known roles in ionome homeostasis also were identified among the HPO genes. Among these were a P-type ATPase transporter of the ACA P2B subfamily 4 (GRMZM2G140328; ZmRoot-Sr) encoding a homolog of known plasma membrane-localized Ca transporters in multiple species (Baxter et al., 2003), an ABC transporter homolog of the family involved in organic acid secretion in the roots from the As HPO set (GRMZM2G415529; ZmRoot-As) (Badri et al., 2008), and a pyrophosphate-energized pump (GRMZM2G090718; ZmPAN-Cd). These candidates suggest that biological signal was enriched by combining coexpression with GWAS data and provided evidence of associations between multiple pathways and elemental homeostasis.

Mutant Analysis Validates That Gibberellin-Signaling DELLA Domain Transcription Factors Influence the Maize Ionome

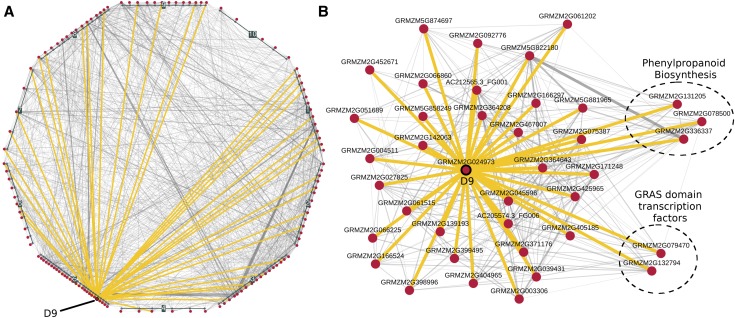
One of the high-confidence candidate genes that appeared in the HPO sets comparing Cd and the ZmRoot network is the gibberellin (GA)-signaling component and DELLA and GRAS domain transcription factor dwarf9 (d9; GRMZM2G024973) (Winkler and Freeling, 1994). d9 is one of two DELLA paralogs in the maize genome, the other being d8 (GRMZM2G144744); both can be mutated to dominant-negative forms that display dwarf phenotypes and dramatic suppression of GA responses (Lawit et al., 2010). Camoco ranked d9 but not d8 among the high-confidence candidates for Cd, although both are present in the root-based coexpression network (ZmRoot). In the ZmRoot network, D9 was strongly coexpressed with 38 other HPO genes (Figure 7; Supplemental Text). There was only moderate, but positive, coexpression between D8 and D9 transcripts (ZmRoot, z = 1.03; ZmPAN, z = 1.04). Given the indistinguishable phenotypes of the known dominant mutants of d8 and d9, the most likely explanation for this result is that there was allelic variation for d9 but not d8 in the GWAS panel. These results suggested that GA signaling in the roots might shape the ionome and alter the accumulation of Cd in seeds, with potential implications for human health.

Figure 7. — Coexpression Network for D9 and Cd HPO Genes.

Coexpression interactions among HPO genes were identified in the ZmRoot network for Cd and visualized at several levels.

**(A)** Local interactions among the 126 Cd HPO genes (red nodes). Genes are grouped and positioned based on chromosomal location. Interactions among HPO genes and D9 (GRMZM2G024973) are highlighted in yellow.

**(B)** Force-directed layout of D9 with HPO neighbors. Circled genes are sets of genes with previously known roles in elemental accumulation.

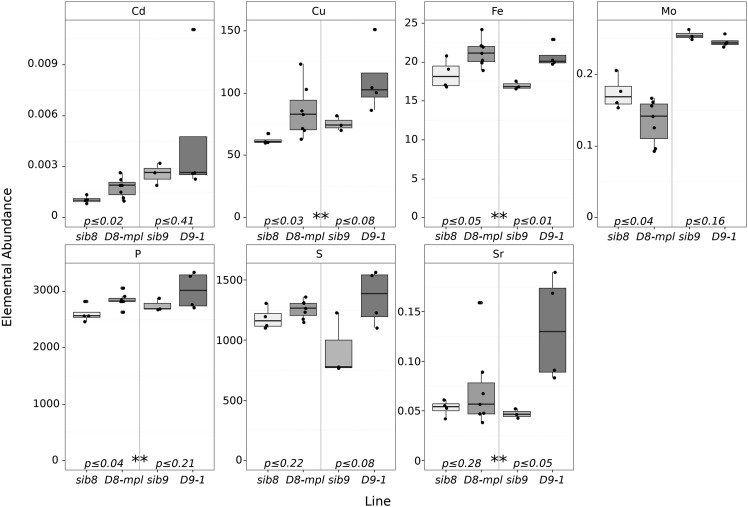
To test for an influence of GA signaling on the ionome and provide single-locus tests, we grew two dominant GA-insensitive mutants, D9-1 and D8-mpl, and their congenic wild-type siblings (sib9 and sib8). The dominant D8-mpl and D9-1 alleles have nearly equivalent effects on aboveground plant growth and similar GA-insensitivity phenotypes in the shoots (Winkler and Freeling, 1994). Both mutants were obtained from the maize genetics coop and crossed three times to inbred B73 to generate BC2F1 families segregating 1:1 for the dwarf phenotype. Ears from phenotypically dwarf and phenotypically wild-type siblings were collected and processed for single-seed ionomic profiling using ICP-MS (Figure 8). Both dwarf lines had significantly different elemental compositions compared with their wild-type siblings. A joint analysis by Student’s t tests between least-squared means comparing dwarfs and wild types revealed that Cu, Fe, P, and Sr were higher in the dwarf than in wild-type seeds (designated with two asterisks in Figure 8). Transcripts encoded by d8 are expressed at lower levels than d9 in the root but at manyfold higher levels in the shoot (Wang et al., 2009; QTeller, 2018). D8-mpl also was significantly different from its sibling in Cd and Mo accumulation. It is possible that D8-mpl has a shoot-driven effect on Mo accumulation in the seed, but we note that previous work (Asaro et al., 2016) identified a large-effect QTL affecting Mo and containing the mot1 gene a mere 22 Mb away from d8. As the allele at mot1 is uncharacterized in the original D8-mpl genetic background, linkage drag carrying a mot1 allele cannot be ruled out. The other dominant-negative allele, D9-1, did not recapitulate the Cd accumulation effect of the linked GWAS QTL that was the basis for its discovery as a high-confidence candidate gene by Camoco. However, the D8-mpl allele did recapitulate the accumulation effect, and our data demonstrate that both D8 and D9 have broad effects on other ionomic phenotypes.

Figure 8. — Ionomic Profiles of *D8-mpl* and *D9-1* Mutants.

Box plots display ICP-MS values for *D8-mpl* and *D9-1* along with congenic wild-type siblings (*sib8* and *sib9*). Embedded P values indicate statistical differences between mutants and wild-type siblings, while asterisks (**) indicate significant differences in a joint analysis between dwarf and the wild type.

Genes coexpressed with D9 that have annotated functions were investigated to determine which were further associated with ionomic traits, in particular seed Cd levels (see Supplemental Text for an in-depth report). Genes linked to the cell cycle, root development, and Fe uptake suggest the hypothesis that maize DELLA domain transcription factors regulate root architecture or the type II Fe uptake mechanism used by grasses to affect the maize ionome.

Camoco Produces High-Confidence Candidate Genes on a Large Collection of Nonionomic GWAS

To assess the generalizability of our approach, we applied it to a separate collection of GWAS surveying a compendium of phenotypes using the maize NAM population (Supplemental Data Set 12). Using Camoco, SNPs were mapped to genes using two different window sizes (50 and 100 kb) and two flanking gene limits (one and two genes). Gene-specific density and locality were calculated for each trait in all three coexpression networks, and HPO genes were identified as genes with less than 10% FDR in at least two SNP-to-gene mappings. Between 0 (fructose, leaf length, malate, northern leaf blight, second principal component of metabolites PC2, protein, stalk strength, and total amino acid) and 302 (average internode length [below ear]) HPO genes were discovered for the 41 traits examined (Supplemental Data Set 12), with candidates produced for 33 of the 41 traits (80%). The candidate genes prioritized for these traits were largely nonoverlapping with those discovered for the ionome traits: only 14 of 697 possible trait pairings (2%) overlapped significantly in terms of the candidate gene sets (Bonferroni-corrected P < 0.05; Supplemental Data Set 13). As with our maize ionome Camoco results, the genotype networks (ZmPAN and ZmRoot) outperformed the single-accession map network (ZmSAM), supporting our earlier conclusion that genotypically diverse tissue networks support stronger candidate gene discovery for interpreting GWAS than tissue atlases. A full list of Wallace HPO genes can be found in Supplemental Data Set 14.

DISCUSSION

Our approach addresses a challenging bottleneck in the process of translating large sets of statistically associated loci into shorter lists based on a more mechanistic understanding of these traits. Marker SNPs identified by a GWAS provide an initial lead on a region of interest, but due to LD, the candidate region can be quite broad and implicate many potentially causal genes. In addition to LD, many SNPs identified by GWAS studies lie in regulatory regions quite far from their target genes (Clark et al., 2006; Louwers et al., 2009; Castelletti et al., 2014). Previous studies in maize found that, while LD decays rapidly in maize (∼1 kb), the variance can be large due to the functional allele segregating in a small number of lines (Wallace et al., 2014). Additionally, Wallace et al. (2014) showed that the causal polymorphism is likely to reside in regulatory regions, that is, outside of exonic regions.

Relying solely on window-based SNP-to-gene mapping can result in a very large (here, upward of 57% of all genes) and ambiguous set of candidate genes. Until we precisely understand the regulatory landscape in the species being studied, even the most powerful GWAS will identify polymorphisms that implicate genes many base pairs away. Here, we surveyed several different SNP-to-gene parameters, finding that the large majority of HPO genes often were not the closest genes to the identified SNPs (Supplemental Figure 9). These genes likely would not have been identified using the common approach of prioritizing the genes closest to each marker SNP.

A common approach to interpreting lists of significant SNPs is through manual inspection of the genome region of interest with a goal of identifying candidate genes whose function is consistent with the phenotype of interest. This can introduce bias into the discovery process and necessarily ignores uncharacterized genes. For nonhuman and nonmodel species, like maize, this manual approach is especially ineffective, because the large majority of the genome remains functionally undercharacterized. Functional validation is expensive and time consuming. Combining data-driven approaches such as network integration with expert biological curation is an efficient means for the prioritization of genes driving complex traits like elemental accumulation, so that functional validation can be applied to only those best candidates. Camoco leverages orthogonal gene expression data, which can now be readily collected for most species of interest, to add an additional layer of relevant biological context to the interpretation of GWAS data and the prioritization of potentially causal variants for further experimental validation. In this way, Camoco complements approaches taken in model organisms and humans, where probabilistic functional gene networks have been used to analyze GWAS data sets (Lee et al., 2010; Shim et al., 2017; Lee and Lee, 2018). Using RNA-Seq or other high-throughput sequencing methods, high-quality functional networks can be readily constructed even in species that have limited existing genomic datasets. We evaluated our framework under simulated conditions as well as applied to a large-scale GWAS in order to define different coexpression metrics and networks, biases such as cis coexpression, and network parameters needed to be considered in order to identify coexpression signal.

Camoco successfully identified subsets of genes linked to candidate SNPs that also exhibit strong coexpression with genes near other candidate SNPs. Integrating GWAS data with coexpression networks resulted in a set of 610 HPO genes that are primed for functional validation (1.5% of the maize FGS). The resulting prioritized gene sets reflect groups of coregulated genes that potentially can be used to infer a broader biological process in which genetic variation affects the phenotype of interest. Indeed, using Camoco, we found strong evidence for HPO gene sets in 13 of the 17 elemental accumulation phenotypes we examined (with five or more HPO genes). These high-priority sets of genes represent a small, high-confidence subset of the candidates implicated by the GWAS for each phenotype (Figure 6; Supplemental Data Set 6).

It is important to note caveats of our approach. The core assumption underpinning Camoco is that there are multiple variants in different genes, each contributing to a phenotype’s variation through a shared biological process. We expect that this assumption holds for many phenotypes influenced by natural variation (supported by the fact that we have discovered strong candidates for most traits examined here), but exceptional traits and causal alleles will violate this assumption. In such cases, Camoco will not perform well. For example, phenotypes caused by genetic variation in a single or small number of genes or, alternatively, caused by a diverse set of otherwise functionally unrelated genes are not good candidates for our approach.

Also, we note that it is possible that some of the coexpression measured across a set of genetically diverse individuals is derived from the nonrandom inheritance of alleles. As a result, both population structure and LD could lead to coexpressed genes. We designed Camoco to correct for the coexpression among cis-linked genes (e.g., produced by coinherited cis-regulatory variants), which was shown to be present in all three networks (Figure 2). However, the extent to which population structure drives the coexpression of physically unlinked genes near GWAS SNPs is unclear, and we do not yet have an approach to detect or correct this potential source of confounding. Population structure, however, was accounted for in the identification of the GWAS-implicated loci. The extent to which unaccounted population or demographic parameters inflate GWAS and network overlap should be considered when interpreting any gene coexpression networks derived from diverse sets of natural accessions, including in the context of Camoco.

Finally, expression data used to build networks do not fully overlap with genomic data included in GWAS. For example, of the 39,656 genes in the maize FGS, 11,718 genes did not pass quality-control filters and were absent from the three coexpression networks analyzed here; thus, they could not be analyzed despite the possibility that there were potentially significant GWAS SNPs nearby.

Relationship between Camoco and Previous Tools for GWAS Analysis

It is important to note that previous studies have leveraged the complementarity of gene expression and/or other functional genomic data to interpret GWAS. For example, one powerful previously described approach is GWAB (Lee et al., 2011; Shim et al., 2017; Lee and Lee, 2018), which integrates functional networks and GWAS results to prioritize candidate genes, with applications described in Arabidopsis and human. These studies focus on the use of integrated functional networks, which incorporate data from a diverse set of sources (e.g., protein-protein interaction networks, phylogenetic similarity, and sequence similarity). Such networks have been built for Arabidopsis and human (and several other “data-rich” species), but their construction is not possible in many plant species where functional genomic data beyond expression simply do not exist. Here, we focus exclusively on coexpression networks as the basis for GWAS interpretation, as these can be built for the majority of species where research communities are performing GWAS (because gene expression compendia have already been produced or can be readily produced).

Another series of studies describe the use of coexpression networks from ATTED-II to interpret GWAS results in Arabidopsis (Chan et al., 2011; Corwin et al., 2016). There are two notable distinctions between our work and these studies. First, these studies focus on analyzing SNPs very near or within coding regions of genes (<1 kb for Chan et al. [2011] and two significant SNPs in a coding region for Corwin et al. [2016]). Here, we provide evidence for many traits where the coexpression network clustering of causal candidate genes is much stronger when one considers genes encoded quite far (e.g., >100 kb) from the associated SNPs, including genes that are not directly adjacent. Second, both of these studies leverage a single coexpression network from the ATTED-II database. Here, we explore the important issue of which gene expression data provide the most informative context for GWAS candidate gene prioritization (tissue/developmental assays versus profiling of diverse individuals).

We note that there also has been previous work integrating coexpression networks with GWAS, focused on interpreting human traits (Bunyavanich et al., 2014; Calabrese et al., 2017; Baillie et al., 2018). Most of these studies first cluster the coexpression network using no GWAS information, define modules, and then assess the overlap between GWAS-identified loci and these modules. These studies are generally less focused on prioritizing individual candidate causal genes and instead focus on characterizing broad modules with connections to traits of interest.

Our study explores several important issues affecting the integration of coexpression and GWAS results and provides insights about best practices. Importantly, we provide a complete, scalable computational pipeline for constructing coexpression networks and integrating GWAS results, which can be used in many different species as long as gene expression data are available.

Camoco-Discovered Gene Sets Are as Coherent as GO Terms

In evaluating the expected performance of our approach, we simulated the effect of imperfect SNP-to-gene mapping by assuming that GO terms were identified by a simulated GWAS trait. Neighboring genes (encoded nearby on the genome) were added to simulate the scenario where we could not resolve the causal gene from linked neighboring genes. This analysis was useful, as it established the boundaries of possibility for our approach: that is, how much noise in terms of false candidate genes can be tolerated before our approach fails. As described in Figure 5, this analysis suggests a sensitivity of ∼40% using a ±500-kb window to map SNPs to genes (two flanking genes maximum) or a tolerance of nearly 75% false candidates due to SNP-to-gene mapping. Therefore, if linkage regions implicated by GWAS extend so far as to include more than 75% false candidates, we would not be likely to discover processes as coherent as GO terms.

At the same window/flank parameter setting noted above, we were able to make significant discoveries (genes with FDR ≤ 0.30) for 7 of 17 elements (41%) using the density metric in the ZmRoot network. This success rate is remarkably consistent with what was predicted by our GO simulations at the same window/flanking gene parameter setting. Intriguingly, HPO gene sets alone were not enriched significantly for GO term genes, indicating that, while the HPO gene sets and GO terms exhibited strikingly similar patterns of gene expression, the gene sets they described do not overlap significantly. It was not until the HPO gene sets were supplemented with coexpression neighbors that gene sets exhibited GO term enrichment, although the resulting terms were not very specific. We speculate that this is due to discovery bias in the GO annotations that were used for our evaluation, which were largely curated from model species and assigned to maize through orthology. There are likely a large number of maize-specific processes and phenotypes that are not yet characterized but that have strong coexpression evidence and can be given functional annotations through GWAS.

Our analysis shows that loci implicated by ionomic GWAS loci exhibit patterns of coexpression as strong as many of the maize genes coannotated to GO terms. Additionally, gene sets identified by Camoco have strong literature support for being involved in elemental accumulation despite not exhibiting GO enrichment. Indeed, one of the key motivations of our approach was that crop genomes like maize have limited species-specific gene ontologies, and this result emphasizes the extent of this limitation. Where current functional annotations, such as GO, rely highly on orthology, future curation schemes could rely on species-specific data obtained from GWAS and coexpression.

Beyond highlighting the challenges of a genome lacking precise functional annotation, these results also suggest an interesting direction for future work. Despite maize genes’ limited ontological annotations, many GWAS have been enabled by powerful mapping populations (e.g., NAM; McMullen et al., 2009). Our results suggest that these sets of loci, combined with a proper mapping to the causal genes they represent using coexpression, could serve as a powerful resource for gene function characterization. Furthermore, our simulations using FCR indicate that researchers could use more permissive genome-wide significance cutoffs from GWAS, as the networks act as robust filters against false-positive genes. Systematic efforts to curate the results from such GWAS using Camoco and similar tools, then providing public access in convenient forms, would be worthwhile. Maize is exceptional in this regard due to its excellent genomic tools and powerful mapping populations. There are several other crop species with rich population genetic resources but limited genome functional annotations that also could benefit from this approach.

Coexpression Context Matters

Using our approach, we evaluated 17 ionomic traits for overlap with three different coexpression networks. Two of the coexpression networks were generated from gene expression profiles collected across a diverse set of individuals (ZmRoot and ZmPAN) and performed substantially better than the ZmSAM network, which was based on a large collection of expression profiles across different tissues and developmental stages derived from a single reference line (B73). We emphasize that this result is not a reflection of the data quality or even the general utility of the coexpression network used to derive the tissue/developmental atlas. Evaluations of this network showed a similar level of enrichment for coexpression relationships among genes involved in the same biological processes (Table 1) and had very similar network structure (Table 2). Instead, our results indicate that the underlying processes driving genotypic variation associated with traits captured by GWAS are better captured by transcriptional variation observed across genetically diverse individuals. Indeed, despite networks having similar levels of GO term enrichment (Table 1), the actual GO terms that drove that enrichment are quite different (Supplemental Data Set 1), which is consistent with our previous analysis demonstrating that the experimental context of coexpression networks strongly influences which biological processes it captures (Schaefer et al., 2014).

Between the two coexpression networks based on expression variation across genotypically diverse individuals, we also observed differences depending on which tissues were profiled. Our coexpression network derived from sampling of root tissue across a diverse set of individuals (ZmRoot) provided the best performance at the FDR we analyzed (Figure 6), producing a total of 335 (326 from density and 11 from locality, 2 in both) HPO candidate genes as compared with 228 (all from locality) HPO candidate genes produced by the ZmPAN network, which was derived from expression profiles of whole seedlings. This result affirms our original motivation for collecting tissue-specific gene expression profiles: we expected that processes occurring in the roots would be central to elemental accumulation phenotypes, which were measured in kernels. However, the difference between the performance of these two networks was modest and much less significant than the difference between the developmental/tissue atlas-derived network and the diverse genotype-derived networks. Furthermore, we expect neither the ZmRoot nor the ZmPAN network to fully describe elemental accumulation processes. While ions are initially acquired from the soil via the root system, we do not directly observe their accumulation in the seed. The data sets presented here could be further complemented by additional tissue-specific data, such as genotypically diverse seed, stalk, or leaf networks.

The performance of the ZmRoot versus the ZmPAN network also was quite different depending on which network metric we used. Specifically, HPO gene discovery in the ZmRoot network was driven by the density metric, while the performance of the ZmPAN network relied on the locality metric (Figure 6). Locality and density were positively correlated, but only modestly, in both networks (Supplemental Figure 6), implying that these two metrics are likely complementary. Indeed, this relationship also was observed for the density and locality of GO terms. Table 1 shows that both metrics had similar overall performance, each capturing ∼40% of GO terms in each network; however, only ∼25% were captured by both metrics, indicating that there are certain biological processes where one metric is more appropriate than the other. In addition to the tissue source differing between the ZmRoot and ZmPAN networks, the number of experimental accessions differed drastically as well (503 accessions in ZmPAN and 48 in ZmRoot), and this influenced the performance of network metrics. We showed that locality was sensitive to the number of accessions used to calculate coexpression (Supplemental Data Set 8), which could partially explain the bias between network metrics and the number of input accessions. This result also suggests that the 46 accessions in ZmRoot did not saturate this approach for coexpression signal and that expanding the ZmRoot data set to include more accessions would result in greater power to detect overlap and the identification of more true positives using the locality metric. In future work, it would be worthwhile to further explore the relationship between the network data source and which subnetwork metrics perform the best.

In general, our results strongly suggest that coexpression networks derived from expression experiments profiling genetically diverse individuals, as opposed to deep expression atlases derived from a single reference genotype, will be more powerful for interpreting candidate genetic loci identified in a GWAS. Furthermore, our findings suggest that where it is possible to identify relevant tissues for a phenotype of interest, tissue-specific expression profiling across genetically diverse individuals is an effective strategy. Identifying the best coexpression context for a given GWAS is an important consideration for data generation efforts in future studies.

METHODS

Availability of Data and Material

Full GWAS information for all maize (Zea mays) ionome traits studied here is publicly available from Ziegler et al. (2017). Fragments per kilobase per million reads (FPKM) values from RNA-Seq data for the ZmSAM network were used from Stelpflug et al. (2016). FPKM values for the ZmPAN network are available from Hirsch et al. (2014). Raw RNA-Seq data used to build the ZmRoot network are available in National Center for Biotechnology Information BioProject PRJNA304663. All computer source code used in this study is available from http://www.github.com/schae234/Camoco.

Software Implementation of Camoco

Camoco is a python library that includes a suite of command line tools to interrelate and coanalyze different layers of genomic data. Specifically, it integrates genes present near GWAS loci with functional information derived from gene coexpression networks. Camoco was developed to build and analyze coexpression networks from gene transcript expression data (i.e., RNA-Seq), but it also can be utilized on other expression data such as metabolite, protein abundance, or microarray data.

This software implements three main routines: (1) construction and validation of coexpression networks from a counts or abundance matrix; (2) mapping SNPs (or other loci) to genes; and (3) an algorithm that assesses the overlap of coexpression among candidate genes near significant GWAS peaks.

Camoco is open source and freely available under the terms of the "MIT license" (see source code for full terms). Full source code, software examples, as well as instructions on how to install and run Camoco are available on GitHub (Camoco Software Repository, 2018). Camoco version 0.5.0 (DOI: 10.5281/zenodo.1049133) was used for this article.

Construction and Quality Control of Coexpression Networks

Camoco Parameters

All networks were built using the command line interface (CLI) with the following Camoco quality control parameters: min_expr_level, 0.001 (expression [FPKM] below this is set to NaN [not a number]); max_gene_missing_data, 0.3 (genes missing expression data more than this percentage were removed from analysis); max_accession_missing data, 0.08 (accessions missing expression data in more than this percentage were removed from analysis); and min_single_sample_expr, 1.0 (genes must have at least this amount of expression [FPKM] in one accession).

ZmPAN: A Genotypically Diverse, Pan-Genome Coexpression Network

Camoco was used to process the FPKM table reported by Hirsch et al. (2014) and to build a coexpression network. The raw gene expression data were passed through the quality control pipeline in Camoco. After quality control, 24,756 genes were used to build the network. For each pairwise combination of genes, a Pearson correlation coefficient was calculated across FPKM profiles to produce ∼306 million network edge scores (Supplemental Figure 1A), which were then Fisher transformed and standard normalized (z score hereafter) to allow cross-network comparison (Supplemental Figure 1B) (Huttenhower et al., 2006; Schaefer et al., 2014). A global significance threshold of z ≥ 3 was set on coexpression interactions to calculate gene degree and other conventional network measures.

To assess overall network health, several approaches were taken. First, the z scores of edges between genes coannotated in the maize GO terms were compared with edges in 1000 random terms containing the same number of genes. Supplemental Figure 1C shows the distribution of P values compared with empirical z scores of edges within a GO term. With a nominal P value cutoff of 0.05, the PAN coexpression network had 11.9-fold more GO terms than expected with P ≤ 0.05, suggesting that edges within this coexpression network capture meaningful biological variation. Degree distribution also is as expected within the network. Supplemental Figure 1D shows empirical degree distributions compared with the power law, exponential, and truncated power law distributions. Typically, the degree distributions of biological networks are best fit by a truncated power law distribution, which is consistent with the ZmPAN genome coexpression network (Ghazalpour et al., 2006).

ZmSAM: A Maize Single-Accession Map Coexpression Network

Publicly available gene expression data were generated from Stelpflug et al. (2016). In total, 22,691 genes passed quality control metrics. Similar to the ZmPAN network described above, gene interactions were calculated between each pairwise combination of genes to produce ∼257 million network edges. A global significance threshold of z ≥ 3 was set on coexpression interactions in order to differentiate significantly coexpressed gene pairs.

Supplemental Figure 2A shows the distribution of edge scores before they were Fisher transformed and standard normalized (Supplemental Figure 2B). The ZmSAM network shows a 10.8-fold enrichment for strong edge scores (P ≤ 0.05) between genes annotated to the same GO terms (Supplemental Figure 2C). A final network health check shows that the empirical degree distribution of the ZmSAM network is consistent with previously characterized biological networks (Supplemental Figure 2D).

ZmRoot: A Genotypically Diverse Maize Root Coexpression Network

Plants were grown from 48 diverse maize accessions: A5554, B57, B73, B76, B97, CML103, CML108, CML157Q, CML158Q, CML228, CML277, CML311, CML322, CML341, CML69, CMl333, F2834T, F70NY2011, H84, H95 HP301, HY, IL14H, KY21, KY228, Ki11, Ki3, Ki44, M162W, M37W, MO17, MO18W, MS71, NC260, NC350, NC358, NC360, OH40B, OH43, OH7B, P39, SC357, T2I16, TX303, TZi8, U267Y, W22, and W64A. Lines were selected to span a diverse panel starting with the 25 NAM parents, then adding more diverse lines that were at the extreme of accumulation for at least one element. Two to three plants per genotype were distributed to independent trays and grown in the greenhouse soil mixture for 2 weeks, and a 1- to 2-inch section of the root ∼1 inch below the soil surface was collected and frozen in liquid nitrogen. Roots were ground in liquid nitrogen, and RNA was extracted using Trizol. Sample quality was checked on a Bioanalyzer, and then two samples per genotype were pooled before library construction. Library construction and sequencing were done at the University of Minnesota sequencing core. RNA was extracted and sequenced in triplicate and multiplexed across 11 barcoded, multiplexed sequencing lanes using TruSeq Stranded RNA Library Prep and Illumina HiSeq 100-bp paired-end RNA-Seq reads. Each library was split across two different Illumina HiSeq2000 lanes (between 6 and 10 lines multiplexed per lane) totaling 10 lanes, with a final lane including all the libraries to help eliminate technical artifacts. Raw reads were deposited into the Short Read Archive under project number PRJNA304663.

Raw reads were passed through quality control using the program AdapterRemoval (Lindgreen, 2012), which collapses overlapping reads into high-quality single reads while also trimming residual PCR adapters. Reads were then mapped to the maize 5b reference genome using BWA (Li and Durbin, 2009; Schubert et al., 2014), PCR duplicates were detected and removed, and then realignment was performed across detected insertions and deletions, resulting in between 14 and 30 million high-quality, unique nuclear reads per accession. Two accessions (H84 and H95) were dropped due to low coverage, bringing the total number to 46.

The quantification of gene expression levels into FPKM was done using a modified version of HTSeq that quantifies both paired- and unpaired-end reads (Anders et al., 2015) available on GitHub (MixedHTSeq Software Repository, 2018). Raw FPKM tables were imported into Camoco and passed through the quality control pipeline. After quality control steps, 25,260 genes were included in coexpression network construction containing ∼319 million interactions. Supplemental Figure 3A shows raw Pearson correlation coefficient scores, while Supplemental Figure 3B shows z scores after standard normal transformation. Similar to ZmPAN and ZmSAM, coexpression among GO terms was compared with random gene sets of the same size as GO terms (1000 instances), showing a 13.5-fold enrichment for GO terms with significantly coexpressed genes (Supplemental Figure 3C). The degree distribution of the ZmRoot network closely follows a truncated power law similar to the other networks built here (Supplemental Figure 3D).

SNP-to-Gene Mapping and Effective Loci

Two parameters are used during SNP-to-gene mapping: candidate window size and maximum number of flanking genes. Windows were calculated both upstream and downstream of input SNPs. SNPs having overlapping windows were collapsed down into effective loci containing the contiguous genomic intervals of all overlapping SNPs, including windows both upstream and downstream of the effective locus’ flanking SNPs (e.g., locus 2 in Figure 1A). Effective loci were cross referenced with the maize 5b FGS GFF file (http://ftp.maizesequence.org/release-5b/filtered-set/ZmB73_5b_FGS.gff.gz) to convert effective loci to candidate gene sets containing all candidate genes within the interval of the effective SNP and also including up to a certain number of flanking genes both upstream and downstream from the effective SNP. For each candidate gene identified by an effective locus, the number of intervening genes was calculated from the middle of the candidate gene to the middle of the effective locus. Candidate genes were ranked by the absolute value of their distance to the center of their parental effective locus. Algorithms implementing the SNP-to-gene mapping used here are accessible through the Camoco command line interface.

Calculating Subnetwork Density and Locality

Coexpression was measured among candidate genes using two metrics: density and locality. Subnetwork density is formulated as the average interaction strength between all (unthresholded) pairwise combinations of input genes, normalized for the total number of input gene pairs:

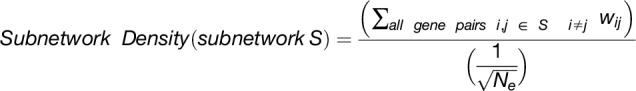graphic file with name TPC_201800299R2_equ1.jpg

(1)

where w_ij is the coexpression score between genes i and j and N_e is the total number of pairwise, nonself gene interactions in the subnetwork.

Network locality assesses the proportion of significant coexpression interactions (z ≥ 3) that are connected locally to other subnetwork genes compared with the number of global network interactions. To quantify network locality, both local and global degree are calculated for each gene within a subnetwork where local degree is the number of interactions to other genes in the subnetwork and global degree is the total number of interactions a gene has. To account for degree bias, where genes with a high global degree are more likely to have more local interactions, a linear regression is calculated on local degree using global degree (designated local ∼ global), and regression residuals for each gene are analyzed:

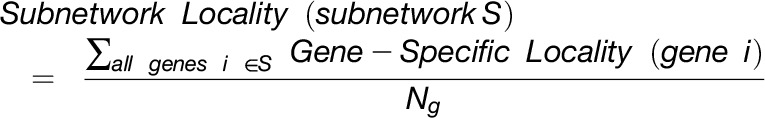graphic file with name TPC_201800299R2_equ2.jpg

(2)

where the gene-specific locality measure is defined below (Equation 4) and N_g is the number of genes in the subnetwork of interest.

Gene-specific density is calculated by considering subnetwork interactions on a per-gene basis:

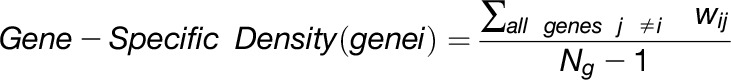graphic file with name TPC_201800299R2_equ3.jpg

(3)

where w_ij is the coexpression score between genes i and j and N_g is the total number of genes in the coexpression network.

Gene locality residuals can be interpreted independently to identify gene-specific locality:

(4)

where 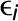Inline graphic is the residual for gene i derived from fitting the following regression model on the entire genome:

where degree_local(gene j) is the total number of interactions between gene j and the subnetwork of interest meeting the threshold and degree_global(gene j) is the total number of interactions between gene j and any other gene in the genome.

Interactions among genes that originate from the same effective GWAS locus (i.e., cis interactions) were removed from density and locality calculations due to biases in cis coexpression. During SNP-to-gene mapping, candidate genes retained information containing a reference back to the parental GWAS SNP. A software flag within Camoco allows for interactions derived from the same parental SNP to be discarded from coexpression score calculations.

The statistical significance of subnetwork density and locality metrics (for both individual genes and whole subnetworks) was assessed by comparing the observed statistic with the distribution of 1000 randomly sampled sets of candidate genes, conserving the number of input genes. This sampling was used to derive a null distribution, which was used to calculate an empirical P value.

Simulating GWAS Using GO Terms

GO (Harris et al., 2004) annotations were downloaded for maize genes from http://ftp.maizesequence.org/release-4a.53/functional_annotations/. Coannotated genes within a GO term were treated as true causal genes identified by a hypothetical GWAS. Terms between 50 and 100 genes were included to simulate the genetic architecture of a multigenic trait. In each coexpression network, terms having genes with significant coexpression (P ≤ 0.05; density or locality) were retained for further analysis. Noise introduced by imperfect GWAS was simulated using two different methods to decompose how noise affects significantly coexpressed networks. These methods were the MCR

graphic file with name TPC_201800299R2_equ5.jpg

(5)

and the FCR

(6)

Simulating MCR

The effects of MCR were evaluated by subjecting GO terms with significant coexpression (P ≤ 0.05; described above) to varying levels of MCRs. True GO term genes were replaced with random genes at varying rates (MCR: 0, 10, 20, 50, 80, 90, and 100%). The effect of MCR was evaluated by assessing the number of GO terms that retained significant coexpression (compared with 1000 randomizations) at each level of MCR.

Adding False Candidate Genes by Expanding SNP-to-Gene Mapping Parameters

To determine how false candidates due to imperfect SNP-to-gene mapping affected the ability to detect coexpressed candidate genes linked to a GWAS trait, GO terms with significantly coexpressed genes were reassessed after incorporating false candidate genes. Each gene in a GO term was treated as an SNP and remapped to a set of candidate genes using the different SNP-to-gene mapping parameters (all combinations of 50, 100, and 500 kb and one, two, or five flanking genes). Effective FCR at each SNP-to-gene mapping parameter setting was calculated by dividing the number of true GO genes with candidates identified after SNP-to-gene mapping. Since varying SNP-to-gene mapping parameters changes the number of candidate genes considered within a term, each term was considered independently for each parameter combination.

Maize Ionome GWAS

Elemental concentrations were measured for 17 different elements in the maize kernel using ICP-MS as described by Ziegler et al. (2017). Outliers were removed from single-seed measurements using median absolute deviation (Davies and Gather, 1993). Basic linear unbiased predictors for each elemental concentration were calculated across different environments and used to estimate variance components (Hung et al., 2012). Joint-linkage analysis was run using TASSEL version 3.0 (Bradbury et al., 2007) with over 7000 SNPs obtained by a genotype-by-sequencing approach (Elshire et al., 2011). An empirical P value cutoff was determined by performing 1000 permutations in which the basic linear unbiased predictor phenotype data were shuffled within each NAM family before joint-linkage analysis was performed. The P value corresponding to a 5% FDR was used for inclusion of a QTL in the joint-linkage model.

Genome-wide association was performed using stepwise forward regression implemented in TASSEL version 4.0 similar to other studies (Tian et al., 2011; Cook et al., 2012; Wallace et al., 2014). Briefly, genome-wide association was performed on a chromosome-by-chromosome basis. To account for the variance explained by QTLs on other chromosomes, the phenotypes used were the residuals from each chromosome calculated from the joint-linkage model fit with all significant joint-linkage QTLs except those on the given chromosome. Association analysis for each trait was performed 100 times by randomly sampling, without replacement, 80% of the lines from each population.

The final input SNP data set contained 28.9 million SNPs obtained from the maize HapMap1 (Gore et al., 2009), the maize HapMap2 (Chia et al., 2012), as well as an additional ∼800,000 putative copy-number variants from an analysis of read depth counts in HapMap2 (Chia et al., 2012; Wallace et al., 2014). These ∼30 million markers were projected onto all 5000 lines in the NAM population using low-density markers obtained through a genotype-by-sequencing approach. A cutoff P value (P ≤ 1e-6) was used from inclusion in the final model. SNPs associated with elemental concentrations were considered significant if they were selected in more than 5 of the 100 models (resample model inclusion probability) (Valdar et al., 2009).

Identifying Ionome HPO Genes and HPO+ Genes

Gene-specific density and locality were calculated for candidate genes identified from the 17 ionome GWAS traits as well as for 1000 random sets of genes of the same size. Gene-specific metrics were converted to the standard normal scale (z score) by subtracting the average gene-specific score from the randomized set and dividing by the average randomized sd. An FDR was established by incrementally evaluating the number of GWAS candidates discovered at a z score threshold compared with the average number discovered in the random sets. For example, if 10 GWAS genes had a gene-specific z score of 3 and an average of 2.5 randomized genes (in the 1000 random sets) had a score of 3 or above, the FDR would be 25%.

HPO candidate genes for each element were identified by requiring candidate genes to have a coexpression FDR ≤ 30% in two or more SNP-to-gene mapping scenarios in the same coexpression network using the same coexpression metric (i.e., density or locality).

HPO+ candidate gene sets were identified by taking the number of HPO genes discovered in each element (n genes) and querying each coexpression network for the set of n genes that had the strongest aggregate coexpression. For example, of the 18 HPO genes for P, an additional 18 genes (36 total) were added to the HPO+ set based on coexpression in each of the networks. Genes were added based on the sum of their coexpression to the original HPO set.

Reduced-Accession ZmPAN Networks

Both the ZmPAN and ZmRoot networks were rebuilt using only the 20 accessions in common between the 503 ZmPAN and 46 ZmRoot experimental data sets. The ZmPAN network also was built using the common set of 20 accessions as well as 26 accessions selected from the broader set of 503 to simulate the number of accessions used in the ZmRoot network. Density and locality were assessed in these reduced-accession networks using the same approach as the full data sets.

Identifying High-Priority Genes from 41 Nonionomic GWAS

Camoco was used to identify HPO candidate genes from 41 GWAS traits reported previously by Wallace et al. (2014): 100 kernel weight, anthesis-silking interval, average internode length (above ear), average internode length (below ear), average internode length (whole plant), boxcox-transformed leaf angle, chlorophyll a, chlorophyll b, cob diameter, days to anthesis, days to silk, ear height, ear row number, fructose, fumarate, glucose, glutamate, height above ear, height per day (until flowering), leaf length, leaf width, malate, nitrate, nodes above ear, nodes per plant, nodes to ear, northern leaf blight, PCA of metabolites: PC1, PCA of metabolites: PC2, photoperiod growing-degree days to silk, photoperiod growing-degree days to anthesis, plant height, protein, ratio of ear height to total height, southern leaf blight, stalk strength, starch, sucrose, tassel branch number, tassel length, and total amino acids. SNPs were mapped to genes using two window sizes (50 and 100 kb) as well as two flanking gene parameters (one and two genes). Overlap was calculated using both density and locality in all three coexpression networks, and FDR was calculated for candidate genes in each GWAS subnetwork as described above. HPO candidate genes were identified as described above as candidate genes with less than 10% FDR in at least two SNP-to-gene mappings (Supplemental Data Set 12).

Accession Numbers

Raw RNA-Seq data used to build the ZmRoot network (A5554, B57, B73, B76, B97, CML103, CML108, CML157Q, CML158Q, CML228, CML277, CML311, CML322, CML341, CML69, CMl333, F2834T, F70NY2011, H84, H95 HP301, HY, IL14H, KY21, KY228, Ki11, Ki3, Ki44, M162W, M37W, MO17, MO18W, MS71, NC260, NC350, NC358, NC360, OH40B, OH43, OH7B, P39, SC357, T2I16, TX303, TZi8, U267Y, W22, and W64A) are available in National Center for Biotechnology Information BioProject PRJNA304663. All computer source code used in this study is available from GitHub (http://www.github.com/schae234/Camoco), version 0.5.0, and from Zenodo (DOI: 10.5281/zenodo.1049133).

Supplemental Data

Supplemental Figure 1. ZmPAN network health.
Supplemental Figure 2. ZmSAM network health.
Supplemental Figure 3. ZmRoot network health.
Supplemental Figure 4. Absolute and size-selected GO term MCR.
Supplemental Figure 5. Absolute and size-selected GO term FCR.
Supplemental Figure 6. Distribution of pearson correlation coefficients between gene-specific density and locality.
Supplemental Figure 7. Element HPO candidate gene overlap heat map.
Supplemental Figure 8. GO biological process enrichment for the ionome.
Supplemental Figure 9. Number of intervening genes between HPO gene and GWAS locus.
Supplemental Text. Validating density and locality; enrichment analysis of HPO and HPO+ candidate gene sets; gene coexpression analysis of D9; previously described HPO genes and their effects on the ionome.
Supplemental Data Set 1. Full GO term density and locality p values.
Supplemental Data Set 2. Network MCL cluster gene assignments.
Supplemental Data Set 3. Network MCL cluster GO enrichment.
Supplemental Data Set 4. Network signal of GO terms with various levels of MCR/FCR.
Supplemental Data Set 5. Maize grain ionome SNP-to-gene mapping results.
Supplemental Data Set 6. Maize grain ionome GWAS network overlap candidate genes.
Supplemental Data Set 7. Maize grain ionome GWAS HPO candidate genes.
Supplemental Data Set 8. Locality HPO genes discovered with networks built from accession subsets.
Supplemental Data Set 9. Multiple-element HPO gene list.
Supplemental Data Set 10. Element GO enrichment.
Supplemental Data Set 11. HPO plus neighbors’ GO enrichment.
Supplemental Data Set 12. HPO genes discovered from nonionomic traits.
Supplemental Data Set 13. Overlap between Wallace et al. (2014) and Ionome HPO genes.
Supplemental Data Set 14. ZmWallace GWAS network overlap candidate genes.

Acknowledgments

We thank Ben VanderSluis, Henry Ward, and Joanna Dinsmore for their helpful comments and feedback in writing this article. We also thank Abby Cabunoc-Mayes and other members of the Mozilla Science Lab for their mentorship and help in making Camoco a free and open scientific resource. This work was supported by funding from the National Science Foundation (IOS-1126950, IOS-1444503, and IOS-1450341), the USDA Agricultural Research Service (5070-21000-039-00D), and the USDA National Institute for Food and Agriculture (2016-67012-24841).

AUTHOR CONTRIBUTIONS

Experimental concept and design: C.L.M., O.H., and I.B. Sample collection and data contribution: I.B. Data analysis and interpretation: R.J.S., J.-M.M., O.H., B.D., I.B., and C.L.M. Computational support: J.J. Manuscript writing and figures: R.S., B.D., I.B., and C.L.M. Manuscript review: all authors read and approved the final manuscript.

Footnotes

^[OPEN]

Articles can be viewed without a subscription.

References

Anders S., Pyl P.T., Huber W. (2015). HTSeq: A Python framework to work with high-throughput sequencing data. Bioinformatics 31: 166–169. [DOI] [PMC free article] [PubMed] [Google Scholar]
Andorf C.M., Cannon E.K., Portwood J.L. II, Gardiner J.M., Harper L.C., Schaeffer M.L., Braun B.L., Campbell D.A., Vinnakota A.G., Sribalusu V.V., Huerta M., Cho K.T., et al. (2016). MaizeGDB update: New tools, data and interface for the maize model organism database. Nucleic Acids Res. 44: D1195–D1201. [DOI] [PMC free article] [PubMed] [Google Scholar]
Angelovici R., Batushansky A., Deason N., Gonzalez-Jorge S., Gore M.A., Fait A., DellaPenna D. (2017). Network-guided GWAS improves identification of genes affecting free amino acids. Plant Physiol. 173: 872–886. [DOI] [PMC free article] [PubMed] [Google Scholar]
Asaro A., Ziegler G., Ziyomo C., Hoekenga O.A., Dilkes B.P., Baxter I. (2016). The interaction of genotype and environment determines variation in the maize kernel ionome. G3 Genes Genomes Genetics 6: 4175–4183. [DOI] [PMC free article] [PubMed] [Google Scholar]
Badri D.V., Loyola-Vargas V.M., Broeckling C.D., De-la-Peña C., Jasinski M., Santelia D., Martinoia E., Sumner L.W., Banta L.M., Stermitz F., Vivanco J.M. (2008). Altered profile of secondary metabolites in the root exudates of Arabidopsis ATP-binding cassette transporter mutants. Plant Physiol. 146: 762–771. [DOI] [PMC free article] [PubMed] [Google Scholar]
Baillie J.K., Bretherick A., Haley C.S., Clohisey S., Gray A., Neyton L.P.A., Barrett J., Stahl E.A., Tenesa A., Andersson R., Brown J.B., Faulkner G.J., et al. (2018). Shared activity patterns arising at genetic susceptibility loci reveal underlying genomic and cellular architecture of human disease. PLOS Comput. Biol. 14: e1005934. [DOI] [PMC free article] [PubMed] [Google Scholar]
Baxter I. (2010). Ionomics: The functional genomics of elements. Brief. Funct. Genomics 9: 149–156. [DOI] [PubMed] [Google Scholar]
Baxter I., Dilkes B.P. (2012). Elemental profiles reflect plant adaptations to the environment. Science 336: 1661–1663. [DOI] [PubMed] [Google Scholar]
Baxter I., Tchieu J., Sussman M.R., Boutry M., Palmgren M.G., Gribskov M., Harper J.F., Axelsen K.B. (2003). Genomic comparison of P-type ATPase ion pumps in Arabidopsis and rice. Plant Physiol. 132: 618–628. [DOI] [PMC free article] [PubMed] [Google Scholar]
Baxter I.R., Vitek O., Lahner B., Muthukumar B., Borghi M., Morrissey J., Guerinot M.L., Salt D.E. (2008). The leaf ionome as a multivariable system to detect a plant’s physiological status. Proc. Natl. Acad. Sci. USA 105: 12081–12086. [DOI] [PMC free article] [PubMed] [Google Scholar]
Baxter I.R., Ziegler G., Lahner B., Mickelbart M.V., Foley R., Danku J., Armstrong P., Salt D.E., Hoekenga O.A. (2014). Single-kernel ionomic profiles are highly heritable indicators of genetic and environmental influences on elemental accumulation in maize grain (Zea mays). PLoS ONE 9: e87628. [DOI] [PMC free article] [PubMed] [Google Scholar]
Bradbury P.J., Zhang Z., Kroon D.E., Casstevens T.M., Ramdoss Y., Buckler E.S. (2007). TASSEL: Software for association mapping of complex traits in diverse samples. Bioinformatics 23: 2633–2635. [DOI] [PubMed] [Google Scholar]
Buckler E.S., Holland J.B., Bradbury P.J., Acharya C.B., Brown P.J., Browne C., Ersoz E., Flint-Garcia S., Garcia A., Glaubitz J.C., Goodman M.M., Harjes C., et al. (2009). The genetic architecture of maize flowering time. Science 325: 714–718. [DOI] [PubMed] [Google Scholar]
Bunyavanich S., Schadt E.E., Himes B.E., Lasky-Su J., Qiu W., Lazarus R., Ziniti J.P., Cohain A., Linderman M., Torgerson D.G., Eng C.S., Pino-Yanes M., et al. (2014). Integrated genome-wide association, coexpression network, and expression single nucleotide polymorphism analysis identifies novel pathway in allergic rhinitis. BMC Med. Genomics 7: 48. [DOI] [PMC free article] [PubMed] [Google Scholar]
Calabrese G.M., Mesner L.D., Stains J.P., Tommasini S.M., Horowitz M.C., Rosen C.J., Farber C.R. (2017). Integrating GWAS and co-expression network data identifies bone mineral density genes SPTBN1 and MARK3 and an osteoblast functional module. Cell Syst. 4: 46–59.e4. [DOI] [PMC free article] [PubMed] [Google Scholar]
Caldwell K.S., Russell J., Langridge P., Powell W. (2006). Extreme population-dependent linkage disequilibrium detected in an inbreeding plant species, Hordeum vulgare. Genetics 172: 557–567. [DOI] [PMC free article] [PubMed] [Google Scholar]
Camoco Software Repository (2018). GitHub http://github.com/schae234/Camoco.
Castelletti S., Tuberosa R., Pindo M., Salvi S. (2014). A MITE transposon insertion is associated with differential methylation at the maize flowering time QTL Vgt1. G3 Genes Genomes Genetics 4: 805–812. [DOI] [PMC free article] [PubMed] [Google Scholar]
Chan E.K.F., Rowe H.C., Corwin J.A., Joseph B., Kliebenstein D.J. (2011). Combining genome-wide association mapping and transcriptional networks to identify novel genes controlling glucosinolates in Arabidopsis thaliana. PLoS Biol. 9: e1001125. [DOI] [PMC free article] [PubMed] [Google Scholar]
Chao D.-Y., Gable K., Chen M., Baxter I., Dietrich C.R., Cahoon E.B., Guerinot M.L., Lahner B., Lü S., Markham J.E., Morrissey J., Han G., et al. (2011). Sphingolipids in the root play an important role in regulating the leaf ionome in Arabidopsis thaliana. Plant Cell 23: 1061–1081. [DOI] [PMC free article] [PubMed] [Google Scholar]
Chia J.-M., Song C., Bradbury P.J., Costich D., de Leon N., Doebley J., Elshire R.J., Gaut B., Geller L., Glaubitz J.C., Gore M., Guill K.E., et al. (2012). Maize HapMap2 identifies extant variation from a genome in flux. Nat. Genet. 44: 803–807. [DOI] [PubMed] [Google Scholar]
Clark R.M., Wagler T.N., Quijada P., Doebley J. (2006). A distant upstream enhancer at the maize domestication gene tb1 has pleiotropic effects on plant and inflorescent architecture. Nat. Genet. 38: 594–597. [DOI] [PubMed] [Google Scholar]
Cook J.P., McMullen M.D., Holland J.B., Tian F., Bradbury P., Ross-Ibarra J., Buckler E.S., Flint-Garcia S.A. (2012). Genetic architecture of maize kernel composition in the nested association mapping and inbred association panels. Plant Physiol. 158: 824–834. [DOI] [PMC free article] [PubMed] [Google Scholar]
Corwin J.A., Copeland D., Feusier J., Subedy A., Eshbaugh R., Palmer C., Maloof J., Kliebenstein D.J. (2016). The quantitative basis of the Arabidopsis innate immune system to endemic pathogens depends on pathogen genetics. PLoS Genet. 12: e1005789. [DOI] [PMC free article] [PubMed] [Google Scholar]
Davies L., Gather U. (1993). The identification of multiple outliers. J. Am. Stat. Assoc. 88: 782. [Google Scholar]
Eisen M.B., Spellman P.T., Brown P.O., Botstein D. (1998). Cluster analysis and display of genome-wide expression patterns. Proc. Natl. Acad. Sci. USA 95: 14863–14868. [DOI] [PMC free article] [PubMed] [Google Scholar]
Elshire R.J., Glaubitz J.C., Sun Q., Poland J.A., Kawamoto K., Buckler E.S., Mitchell S.E. (2011). A robust, simple genotyping-by-sequencing (GBS) approach for high diversity species. PLoS ONE 6: e19379. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ghazalpour A., Doss S., Zhang B., Wang S., Plaisier C., Castellanos R., Brozell A., Schadt E.E., Drake T.A., Lusis A.J., Horvath S. (2006). Integrating genetic and network analysis to characterize genes related to mouse weight. PLoS Genet. 2: e130. [DOI] [PMC free article] [PubMed] [Google Scholar]
Gore M.A., Chia J.M., Elshire R.J., Sun Q., Ersoz E.S., Hurwitz B.L., Peiffer J.A., McMullen M.D., Grills G.S., Ross-Ibarra J., Ware D.H., Buckler E.S. (2009). A first-generation haplotype map of maize. Science 326: 1115–1117. [DOI] [PubMed] [Google Scholar]
Guerinot M.L., Salt D.E. (2001). Fortified foods and phytoremediation: Two sides of the same coin. Plant Physiol. 125: 164–167. [DOI] [PMC free article] [PubMed] [Google Scholar]
Harris M.A., Clark J., Ireland A., Lomax J., Ashburner M., Foulger R., Eilbeck K., Lewis S., Marshall B., Mungall C., Richter J., Rubin G.M., et al. (2004). The Gene Ontology (GO) database and informatics resource. Nucleic Acids Res. 32: D258–D261. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hirsch C.N., Foerster J.M., Johnson J.M., Sekhon R.S., Muttoni G., Vaillancourt B., Peñagaricano F., Lindquist E., Pedraza M.A., Barry K., de Leon N., Kaeppler S.M., et al. (2014). Insights into the maize pan-genome and pan-transcriptome. Plant Cell 26: 121–135. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hung H.-Y., Browne C., Guill K., Coles N., Eller M., Garcia A., Lepak N., Melia-Hancock S., Oropeza-Rosas M., Salvo S., Upadyayula N., Buckler E.S., et al. (2012). The relationship between parental genetic or phenotypic divergence and progeny variation in the maize nested association mapping population. Heredity (Edinb) 108: 490–499. [DOI] [PMC free article] [PubMed] [Google Scholar]
Huttenhower C., Hibbs M., Myers C., Troyanskaya O.G. (2006). A scalable method for integration and functional analysis of multiple microarray datasets. Bioinformatics 22: 2890–2897. [DOI] [PubMed] [Google Scholar]
Kump K.L., Bradbury P.J., Wisser R.J., Buckler E.S., Belcher A.R., Oropeza-Rosas M.A., Zwonitzer J.C., Kresovich S., McMullen M.D., Ware D., Balint-Kurti P.J., Holland J.B. (2011). Genome-wide association study of quantitative resistance to southern leaf blight in the maize nested association mapping population. Nat. Genet. 43: 163–168. [DOI] [PubMed] [Google Scholar]
Lawit S.J., Wych H.M., Xu D., Kundu S., Tomes D.T. (2010). Maize DELLA proteins dwarf plant8 and dwarf plant9 as modulators of plant development. Plant Cell Physiol. 51: 1854–1868. [DOI] [PubMed] [Google Scholar]
Lee T., Lee I. (2018). araGWAB: Network-based boosting of genome-wide association studies in Arabidopsis thaliana. Sci. Rep. 8: 2925. [DOI] [PMC free article] [PubMed] [Google Scholar]
Lee I., Ambaru B., Thakkar P., Marcotte E.M., Rhee S.Y. (2010). Rational association of genes with traits using a genome-scale gene network for Arabidopsis thaliana. Nat. Biotechnol. 28: 149–156. [DOI] [PMC free article] [PubMed] [Google Scholar]
Lee I., Blom U.M., Wang P.I., Shim J.E., Marcotte E.M. (2011). Prioritizing candidate disease genes by network-based boosting of genome-wide association data. Genome Res. 21: 1109–1121. [DOI] [PMC free article] [PubMed] [Google Scholar]
Li H., Durbin R. (2009). Fast and accurate short read alignment with Burrows-Wheeler transform. Bioinformatics 25: 1754–1760. [DOI] [PMC free article] [PubMed] [Google Scholar]
Li M., Chen J.E., Wang J.X., Hu B., Chen G. (2008). Modifying the DPClus algorithm for identifying protein complexes based on new topological structures. BMC Bioinformatics 9: 398. [DOI] [PMC free article] [PubMed] [Google Scholar]
Lindgreen S. (2012). AdapterRemoval: Easy cleaning of next-generation sequencing reads. BMC Res. Notes 5: 337. [DOI] [PMC free article] [PubMed] [Google Scholar]
Louwers M., Bader R., Haring M., van Driel R., de Laat W., Stam M. (2009). Tissue- and expression level-specific chromatin looping at maize b1 epialleles. Plant Cell 21: 832–842. [DOI] [PMC free article] [PubMed] [Google Scholar]
McMullen M.D., Kresovich S., Villeda H.S., Bradbury P., Li H., Sun Q., Flint-Garcia S., Thornsberry J., Acharya C., Bottoms C., Brown P., Browne C., et al. (2009). Genetic properties of the maize nested association mapping population. Science 325: 737–740. [DOI] [PubMed] [Google Scholar]
Michno J.-M., Burghardt L.T., Liu J., Jeffers J.R., Tiffin P., Stupar R., Myers C.L. (2018). Identification of candidate genes underlying nodulation-specific phenotypes in Medicago truncatula through integration of genome-wide association studies and co-expression networks. bioRxiv. [Google Scholar]
MixedHTSeq Software Repository (2018). GitHub. http://github.com/schae234/MixedHTSeq.
Mochida K., Uehara-Yamaguchi Y., Yoshida T., Sakurai T., Shinozaki K. (2011). Global landscape of a co-expressed gene network in barley and its application to gene discovery in Triticeae crops. Plant Cell Physiol. 52: 785–803. [DOI] [PMC free article] [PubMed] [Google Scholar]
Morrell P.L., Toleno D.M., Lundy K.E., Clegg M.T. (2005). Low levels of linkage disequilibrium in wild barley (Hordeum vulgare ssp. spontaneum) despite high rates of self-fertilization. Proc. Natl. Acad. Sci. USA 102: 2442–2447. [DOI] [PMC free article] [PubMed] [Google Scholar]
Obayashi T., Okamura Y., Ito S., Tadaka S., Aoki Y., Shirota M., Kinoshita K. (2014). ATTED-II in 2014: Evaluation of gene coexpression in agriculturally important plants. Plant Cell Physiol. 55: e6. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ozaki S., Ogata Y., Suda K., Kurabayashi A., Suzuki T., Yamamoto N., Iijima Y., Tsugane T., Fujii T., Konishi C., Inai S., Bunsupa S., et al. (2010). Coexpression analysis of tomato genes and experimental verification of coordinated expression of genes found in a functionally enriched coexpression module. DNA Res. 17: 105–116. [DOI] [PMC free article] [PubMed] [Google Scholar]
Peiffer J.A., Romay M.C., Gore M.A., Flint-Garcia S.A., Zhang Z., Millard M.J., Gardner C.A.C., McMullen M.D., Holland J.B., Bradbury P.J., Buckler E.S. (2014). The genetic architecture of maize height. Genetics 196: 1337–1356. [DOI] [PMC free article] [PubMed] [Google Scholar]
QTeller (2018). http://qteller.com.
Ritchie M.D., Holzinger E.R., Li R., Pendergrass S.A., Kim D. (2015). Methods of integrating data to uncover genotype-phenotype interactions. Nat. Rev. Genet. 16: 85–97. [DOI] [PubMed] [Google Scholar]
Rotival M., Petretto E. (2014). Leveraging gene co-expression networks to pinpoint the regulation of complex traits and disease, with a focus on cardiovascular traits. Brief. Funct. Genomics 13: 66–78. [DOI] [PubMed] [Google Scholar]
Sarkar N.K., Kim Y.-K., Grover A. (2014). Coexpression network analysis associated with call of rice seedlings for encountering heat stress. Plant Mol. Biol. 84: 125–143. [DOI] [PubMed] [Google Scholar]
Schaefer R.J., Briskine R., Springer N.M., Myers C.L. (2014). Discovering functional modules across diverse maize transcriptomes using COB, the Co-expression Browser. PLoS ONE 9: e99193. [DOI] [PMC free article] [PubMed] [Google Scholar]
Schaefer R.J., Michno J.-M., Myers C.L. (2017). Unraveling gene function in agricultural species using gene co-expression networks. Biochim. Biophys. Acta. Gene Regul. Mech. 1860: 53–63. [DOI] [PubMed] [Google Scholar]
Schubert M., Ermini L., Der Sarkissian C., Jónsson H., Ginolhac A., Schaefer R., Martin M.D., Fernández R., Kircher M., McCue M., Willerslev E., Orlando L. (2014). Characterization of ancient and modern genomes by SNP detection and phylogenomic and metagenomic analysis using PALEOMIX. Nat. Protoc. 9: 1056–1082. [DOI] [PubMed] [Google Scholar]
Shim J.E., Bang C., Yang S., Lee T., Hwang S., Kim C.Y., Singh-Blom U.M., Marcotte E.M., Lee I. (2017). GWAB: A web server for the network-based boosting of human genome-wide association data. Nucleic Acids Res. 45: W154–W161. [DOI] [PMC free article] [PubMed] [Google Scholar]
Stelpflug S.C., Sekhon R.S., Vaillancourt B., Hirsch C.N., Buell C.R., de Leon N., Kaeppler S.M. (2016). An expanded maize gene expression atlas based on RNA sequencing and its use to explore root development. Plant Genome 9: 314–362. [DOI] [PubMed] [Google Scholar]
Swanson-Wagner R., Briskine R., Schaefer R., Hufford M.B.M.B., Ross-Ibarra J., Myers C.L.L., Tiffin P., Springer N.M.M. (2012). Reshaping of the maize transcriptome by domestication. Proc. Natl. Acad. Sci. USA 109: 11878–11883. [DOI] [PMC free article] [PubMed] [Google Scholar]
Taşan M., Musso G., Hao T., Vidal M., Macrae C.A., Roth F.P. (2015). Selecting causal genes from genome-wide association studies via functionally coherent subnetworks. Nat. Methods 12: 154–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
Tian F., Bradbury P.J., Brown P.J., Hung H., Sun Q., Flint-Garcia S., Rocheford T.R., McMullen M.D., Holland J.B., Buckler E.S. (2011). Genome-wide association study of leaf architecture in the maize nested association mapping population. Nat. Genet. 43: 159–162. [DOI] [PubMed] [Google Scholar]
USDA (2016). USDA Crop Production 2015 Summary. U.S. Department of Agriculture National Agricultural Statistics Service
Valdar W., Holmes C.C., Mott R., Flint J. (2009). Mapping in structured populations by resample model averaging. Genetics 182: 1263–1277. [DOI] [PMC free article] [PubMed] [Google Scholar]
van Dongen S. (2000). MCL: A Cluster Algoithm for Graphs. https://micans.org/mcl/.
Wallace J.G., Bradbury P.J., Zhang N., Gibon Y., Stitt M., Buckler E.S. (2014). Association mapping across numerous traits reveals patterns of functional variation in maize. PLoS Genet. 10: e1004845. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wang X., Elling A.A., Li X., Li N., Peng Z., He G., Sun H., Qi Y., Liu X.S., Deng X.W. (2009). Genome-wide and organ-specific landscapes of epigenetic modifications and their relationships to mRNA and small RNA transcriptomes in maize. Plant Cell 21: 1053–1069. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wen Z., Tan R., Zhang S., Collins P.J., Yuan J., Du W., Gu C., Ou S., Song Q., An Y.-Q.C., Boyse J.F., Chilvers M.I., et al. (2018). Integrating GWAS and gene expression data for functional characterization of resistance to white mold in soya bean. Plant Biotechnol. J. 16: 1825–1835. [DOI] [PMC free article] [PubMed] [Google Scholar]
Winkler R.G., Freeling M. (1994). Physiological genetics of the dominant gibberellin-nonresponsive maize dwarfs, Dwart8 and Dwart9. Planta 193: 341–348. [Google Scholar]
Wolfe C.J., Kohane I.S., Butte A.J. (2005). Systematic survey reveals general applicability of “guilt-by-association” within gene coexpression networks. BMC Bioinformatics 6: 227. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wray G.A. (2007). The evolutionary significance of cis-regulatory mutations. Nat. Rev. Genet. 8: 206–216. [DOI] [PubMed] [Google Scholar]
Zheng Z.-L., Zhao Y. (2013). Transcriptome comparison and gene coexpression network analysis provide a systems view of citrus response to ‘Candidatus Liberibacter asiaticus’ infection. BMC Genomics 14: 27. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ziegler G., Kear P.J., Wu D., Ziyomo C., Lipka A.E., Gore M., Hoekenga O., Baxter I. (2017). Elemental accumulation in kernels of the maize nested association mapping panel reveals signals of gene by environment interactions. bioRxiv. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Data Availability Statement

[bib1] Anders S., Pyl P.T., Huber W. (2015). HTSeq: A Python framework to work with high-throughput sequencing data. Bioinformatics 31: 166–169. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib2] Andorf C.M., Cannon E.K., Portwood J.L. II, Gardiner J.M., Harper L.C., Schaeffer M.L., Braun B.L., Campbell D.A., Vinnakota A.G., Sribalusu V.V., Huerta M., Cho K.T., et al. (2016). MaizeGDB update: New tools, data and interface for the maize model organism database. Nucleic Acids Res. 44: D1195–D1201. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib3] Angelovici R., Batushansky A., Deason N., Gonzalez-Jorge S., Gore M.A., Fait A., DellaPenna D. (2017). Network-guided GWAS improves identification of genes affecting free amino acids. Plant Physiol. 173: 872–886. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib4] Asaro A., Ziegler G., Ziyomo C., Hoekenga O.A., Dilkes B.P., Baxter I. (2016). The interaction of genotype and environment determines variation in the maize kernel ionome. G3 Genes Genomes Genetics 6: 4175–4183. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib5] Badri D.V., Loyola-Vargas V.M., Broeckling C.D., De-la-Peña C., Jasinski M., Santelia D., Martinoia E., Sumner L.W., Banta L.M., Stermitz F., Vivanco J.M. (2008). Altered profile of secondary metabolites in the root exudates of Arabidopsis ATP-binding cassette transporter mutants. Plant Physiol. 146: 762–771. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib6] Baillie J.K., Bretherick A., Haley C.S., Clohisey S., Gray A., Neyton L.P.A., Barrett J., Stahl E.A., Tenesa A., Andersson R., Brown J.B., Faulkner G.J., et al. (2018). Shared activity patterns arising at genetic susceptibility loci reveal underlying genomic and cellular architecture of human disease. PLOS Comput. Biol. 14: e1005934. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib7] Baxter I. (2010). Ionomics: The functional genomics of elements. Brief. Funct. Genomics 9: 149–156. [DOI] [PubMed] [Google Scholar]

[bib8] Baxter I., Dilkes B.P. (2012). Elemental profiles reflect plant adaptations to the environment. Science 336: 1661–1663. [DOI] [PubMed] [Google Scholar]

[bib9] Baxter I., Tchieu J., Sussman M.R., Boutry M., Palmgren M.G., Gribskov M., Harper J.F., Axelsen K.B. (2003). Genomic comparison of P-type ATPase ion pumps in Arabidopsis and rice. Plant Physiol. 132: 618–628. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib10] Baxter I.R., Vitek O., Lahner B., Muthukumar B., Borghi M., Morrissey J., Guerinot M.L., Salt D.E. (2008). The leaf ionome as a multivariable system to detect a plant’s physiological status. Proc. Natl. Acad. Sci. USA 105: 12081–12086. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib11] Baxter I.R., Ziegler G., Lahner B., Mickelbart M.V., Foley R., Danku J., Armstrong P., Salt D.E., Hoekenga O.A. (2014). Single-kernel ionomic profiles are highly heritable indicators of genetic and environmental influences on elemental accumulation in maize grain (Zea mays). PLoS ONE 9: e87628. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib12] Bradbury P.J., Zhang Z., Kroon D.E., Casstevens T.M., Ramdoss Y., Buckler E.S. (2007). TASSEL: Software for association mapping of complex traits in diverse samples. Bioinformatics 23: 2633–2635. [DOI] [PubMed] [Google Scholar]

[bib13] Buckler E.S., Holland J.B., Bradbury P.J., Acharya C.B., Brown P.J., Browne C., Ersoz E., Flint-Garcia S., Garcia A., Glaubitz J.C., Goodman M.M., Harjes C., et al. (2009). The genetic architecture of maize flowering time. Science 325: 714–718. [DOI] [PubMed] [Google Scholar]

[bib14] Bunyavanich S., Schadt E.E., Himes B.E., Lasky-Su J., Qiu W., Lazarus R., Ziniti J.P., Cohain A., Linderman M., Torgerson D.G., Eng C.S., Pino-Yanes M., et al. (2014). Integrated genome-wide association, coexpression network, and expression single nucleotide polymorphism analysis identifies novel pathway in allergic rhinitis. BMC Med. Genomics 7: 48. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib15] Calabrese G.M., Mesner L.D., Stains J.P., Tommasini S.M., Horowitz M.C., Rosen C.J., Farber C.R. (2017). Integrating GWAS and co-expression network data identifies bone mineral density genes SPTBN1 and MARK3 and an osteoblast functional module. Cell Syst. 4: 46–59.e4. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib16] Caldwell K.S., Russell J., Langridge P., Powell W. (2006). Extreme population-dependent linkage disequilibrium detected in an inbreeding plant species, Hordeum vulgare. Genetics 172: 557–567. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib17] Camoco Software Repository (2018). GitHub http://github.com/schae234/Camoco.

[bib18] Castelletti S., Tuberosa R., Pindo M., Salvi S. (2014). A MITE transposon insertion is associated with differential methylation at the maize flowering time QTL Vgt1. G3 Genes Genomes Genetics 4: 805–812. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib19] Chan E.K.F., Rowe H.C., Corwin J.A., Joseph B., Kliebenstein D.J. (2011). Combining genome-wide association mapping and transcriptional networks to identify novel genes controlling glucosinolates in Arabidopsis thaliana. PLoS Biol. 9: e1001125. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib20] Chao D.-Y., Gable K., Chen M., Baxter I., Dietrich C.R., Cahoon E.B., Guerinot M.L., Lahner B., Lü S., Markham J.E., Morrissey J., Han G., et al. (2011). Sphingolipids in the root play an important role in regulating the leaf ionome in Arabidopsis thaliana. Plant Cell 23: 1061–1081. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib21] Chia J.-M., Song C., Bradbury P.J., Costich D., de Leon N., Doebley J., Elshire R.J., Gaut B., Geller L., Glaubitz J.C., Gore M., Guill K.E., et al. (2012). Maize HapMap2 identifies extant variation from a genome in flux. Nat. Genet. 44: 803–807. [DOI] [PubMed] [Google Scholar]

[bib22] Clark R.M., Wagler T.N., Quijada P., Doebley J. (2006). A distant upstream enhancer at the maize domestication gene tb1 has pleiotropic effects on plant and inflorescent architecture. Nat. Genet. 38: 594–597. [DOI] [PubMed] [Google Scholar]

[bib23] Cook J.P., McMullen M.D., Holland J.B., Tian F., Bradbury P., Ross-Ibarra J., Buckler E.S., Flint-Garcia S.A. (2012). Genetic architecture of maize kernel composition in the nested association mapping and inbred association panels. Plant Physiol. 158: 824–834. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib24] Corwin J.A., Copeland D., Feusier J., Subedy A., Eshbaugh R., Palmer C., Maloof J., Kliebenstein D.J. (2016). The quantitative basis of the Arabidopsis innate immune system to endemic pathogens depends on pathogen genetics. PLoS Genet. 12: e1005789. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib25] Davies L., Gather U. (1993). The identification of multiple outliers. J. Am. Stat. Assoc. 88: 782. [Google Scholar]

[bib26] Eisen M.B., Spellman P.T., Brown P.O., Botstein D. (1998). Cluster analysis and display of genome-wide expression patterns. Proc. Natl. Acad. Sci. USA 95: 14863–14868. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib27] Elshire R.J., Glaubitz J.C., Sun Q., Poland J.A., Kawamoto K., Buckler E.S., Mitchell S.E. (2011). A robust, simple genotyping-by-sequencing (GBS) approach for high diversity species. PLoS ONE 6: e19379. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib28] Ghazalpour A., Doss S., Zhang B., Wang S., Plaisier C., Castellanos R., Brozell A., Schadt E.E., Drake T.A., Lusis A.J., Horvath S. (2006). Integrating genetic and network analysis to characterize genes related to mouse weight. PLoS Genet. 2: e130. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib29] Gore M.A., Chia J.M., Elshire R.J., Sun Q., Ersoz E.S., Hurwitz B.L., Peiffer J.A., McMullen M.D., Grills G.S., Ross-Ibarra J., Ware D.H., Buckler E.S. (2009). A first-generation haplotype map of maize. Science 326: 1115–1117. [DOI] [PubMed] [Google Scholar]

[bib30] Guerinot M.L., Salt D.E. (2001). Fortified foods and phytoremediation: Two sides of the same coin. Plant Physiol. 125: 164–167. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib31] Harris M.A., Clark J., Ireland A., Lomax J., Ashburner M., Foulger R., Eilbeck K., Lewis S., Marshall B., Mungall C., Richter J., Rubin G.M., et al. (2004). The Gene Ontology (GO) database and informatics resource. Nucleic Acids Res. 32: D258–D261. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib32] Hirsch C.N., Foerster J.M., Johnson J.M., Sekhon R.S., Muttoni G., Vaillancourt B., Peñagaricano F., Lindquist E., Pedraza M.A., Barry K., de Leon N., Kaeppler S.M., et al. (2014). Insights into the maize pan-genome and pan-transcriptome. Plant Cell 26: 121–135. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib33] Hung H.-Y., Browne C., Guill K., Coles N., Eller M., Garcia A., Lepak N., Melia-Hancock S., Oropeza-Rosas M., Salvo S., Upadyayula N., Buckler E.S., et al. (2012). The relationship between parental genetic or phenotypic divergence and progeny variation in the maize nested association mapping population. Heredity (Edinb) 108: 490–499. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib34] Huttenhower C., Hibbs M., Myers C., Troyanskaya O.G. (2006). A scalable method for integration and functional analysis of multiple microarray datasets. Bioinformatics 22: 2890–2897. [DOI] [PubMed] [Google Scholar]

[bib35] Kump K.L., Bradbury P.J., Wisser R.J., Buckler E.S., Belcher A.R., Oropeza-Rosas M.A., Zwonitzer J.C., Kresovich S., McMullen M.D., Ware D., Balint-Kurti P.J., Holland J.B. (2011). Genome-wide association study of quantitative resistance to southern leaf blight in the maize nested association mapping population. Nat. Genet. 43: 163–168. [DOI] [PubMed] [Google Scholar]

[bib36] Lawit S.J., Wych H.M., Xu D., Kundu S., Tomes D.T. (2010). Maize DELLA proteins dwarf plant8 and dwarf plant9 as modulators of plant development. Plant Cell Physiol. 51: 1854–1868. [DOI] [PubMed] [Google Scholar]

[bib37] Lee T., Lee I. (2018). araGWAB: Network-based boosting of genome-wide association studies in Arabidopsis thaliana. Sci. Rep. 8: 2925. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib38] Lee I., Ambaru B., Thakkar P., Marcotte E.M., Rhee S.Y. (2010). Rational association of genes with traits using a genome-scale gene network for Arabidopsis thaliana. Nat. Biotechnol. 28: 149–156. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib39] Lee I., Blom U.M., Wang P.I., Shim J.E., Marcotte E.M. (2011). Prioritizing candidate disease genes by network-based boosting of genome-wide association data. Genome Res. 21: 1109–1121. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib40] Li H., Durbin R. (2009). Fast and accurate short read alignment with Burrows-Wheeler transform. Bioinformatics 25: 1754–1760. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib41] Li M., Chen J.E., Wang J.X., Hu B., Chen G. (2008). Modifying the DPClus algorithm for identifying protein complexes based on new topological structures. BMC Bioinformatics 9: 398. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib42] Lindgreen S. (2012). AdapterRemoval: Easy cleaning of next-generation sequencing reads. BMC Res. Notes 5: 337. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib43] Louwers M., Bader R., Haring M., van Driel R., de Laat W., Stam M. (2009). Tissue- and expression level-specific chromatin looping at maize b1 epialleles. Plant Cell 21: 832–842. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib44] McMullen M.D., Kresovich S., Villeda H.S., Bradbury P., Li H., Sun Q., Flint-Garcia S., Thornsberry J., Acharya C., Bottoms C., Brown P., Browne C., et al. (2009). Genetic properties of the maize nested association mapping population. Science 325: 737–740. [DOI] [PubMed] [Google Scholar]

[bib45] Michno J.-M., Burghardt L.T., Liu J., Jeffers J.R., Tiffin P., Stupar R., Myers C.L. (2018). Identification of candidate genes underlying nodulation-specific phenotypes in Medicago truncatula through integration of genome-wide association studies and co-expression networks. bioRxiv. [Google Scholar]

[bib46] MixedHTSeq Software Repository (2018). GitHub. http://github.com/schae234/MixedHTSeq.

[bib47] Mochida K., Uehara-Yamaguchi Y., Yoshida T., Sakurai T., Shinozaki K. (2011). Global landscape of a co-expressed gene network in barley and its application to gene discovery in Triticeae crops. Plant Cell Physiol. 52: 785–803. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib48] Morrell P.L., Toleno D.M., Lundy K.E., Clegg M.T. (2005). Low levels of linkage disequilibrium in wild barley (Hordeum vulgare ssp. spontaneum) despite high rates of self-fertilization. Proc. Natl. Acad. Sci. USA 102: 2442–2447. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib49] Obayashi T., Okamura Y., Ito S., Tadaka S., Aoki Y., Shirota M., Kinoshita K. (2014). ATTED-II in 2014: Evaluation of gene coexpression in agriculturally important plants. Plant Cell Physiol. 55: e6. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib50] Ozaki S., Ogata Y., Suda K., Kurabayashi A., Suzuki T., Yamamoto N., Iijima Y., Tsugane T., Fujii T., Konishi C., Inai S., Bunsupa S., et al. (2010). Coexpression analysis of tomato genes and experimental verification of coordinated expression of genes found in a functionally enriched coexpression module. DNA Res. 17: 105–116. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib51] Peiffer J.A., Romay M.C., Gore M.A., Flint-Garcia S.A., Zhang Z., Millard M.J., Gardner C.A.C., McMullen M.D., Holland J.B., Bradbury P.J., Buckler E.S. (2014). The genetic architecture of maize height. Genetics 196: 1337–1356. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib52] QTeller (2018). http://qteller.com.

[bib53] Ritchie M.D., Holzinger E.R., Li R., Pendergrass S.A., Kim D. (2015). Methods of integrating data to uncover genotype-phenotype interactions. Nat. Rev. Genet. 16: 85–97. [DOI] [PubMed] [Google Scholar]

[bib54] Rotival M., Petretto E. (2014). Leveraging gene co-expression networks to pinpoint the regulation of complex traits and disease, with a focus on cardiovascular traits. Brief. Funct. Genomics 13: 66–78. [DOI] [PubMed] [Google Scholar]

[bib55] Sarkar N.K., Kim Y.-K., Grover A. (2014). Coexpression network analysis associated with call of rice seedlings for encountering heat stress. Plant Mol. Biol. 84: 125–143. [DOI] [PubMed] [Google Scholar]

[bib56] Schaefer R.J., Briskine R., Springer N.M., Myers C.L. (2014). Discovering functional modules across diverse maize transcriptomes using COB, the Co-expression Browser. PLoS ONE 9: e99193. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib57] Schaefer R.J., Michno J.-M., Myers C.L. (2017). Unraveling gene function in agricultural species using gene co-expression networks. Biochim. Biophys. Acta. Gene Regul. Mech. 1860: 53–63. [DOI] [PubMed] [Google Scholar]

[bib58] Schubert M., Ermini L., Der Sarkissian C., Jónsson H., Ginolhac A., Schaefer R., Martin M.D., Fernández R., Kircher M., McCue M., Willerslev E., Orlando L. (2014). Characterization of ancient and modern genomes by SNP detection and phylogenomic and metagenomic analysis using PALEOMIX. Nat. Protoc. 9: 1056–1082. [DOI] [PubMed] [Google Scholar]

[bib59] Shim J.E., Bang C., Yang S., Lee T., Hwang S., Kim C.Y., Singh-Blom U.M., Marcotte E.M., Lee I. (2017). GWAB: A web server for the network-based boosting of human genome-wide association data. Nucleic Acids Res. 45: W154–W161. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib60] Stelpflug S.C., Sekhon R.S., Vaillancourt B., Hirsch C.N., Buell C.R., de Leon N., Kaeppler S.M. (2016). An expanded maize gene expression atlas based on RNA sequencing and its use to explore root development. Plant Genome 9: 314–362. [DOI] [PubMed] [Google Scholar]

[bib61] Swanson-Wagner R., Briskine R., Schaefer R., Hufford M.B.M.B., Ross-Ibarra J., Myers C.L.L., Tiffin P., Springer N.M.M. (2012). Reshaping of the maize transcriptome by domestication. Proc. Natl. Acad. Sci. USA 109: 11878–11883. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib62] Taşan M., Musso G., Hao T., Vidal M., Macrae C.A., Roth F.P. (2015). Selecting causal genes from genome-wide association studies via functionally coherent subnetworks. Nat. Methods 12: 154–159. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib63] Tian F., Bradbury P.J., Brown P.J., Hung H., Sun Q., Flint-Garcia S., Rocheford T.R., McMullen M.D., Holland J.B., Buckler E.S. (2011). Genome-wide association study of leaf architecture in the maize nested association mapping population. Nat. Genet. 43: 159–162. [DOI] [PubMed] [Google Scholar]

[bib64] USDA (2016). USDA Crop Production 2015 Summary. U.S. Department of Agriculture National Agricultural Statistics Service

[bib65] Valdar W., Holmes C.C., Mott R., Flint J. (2009). Mapping in structured populations by resample model averaging. Genetics 182: 1263–1277. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib66] van Dongen S. (2000). MCL: A Cluster Algoithm for Graphs. https://micans.org/mcl/.

[bib67] Wallace J.G., Bradbury P.J., Zhang N., Gibon Y., Stitt M., Buckler E.S. (2014). Association mapping across numerous traits reveals patterns of functional variation in maize. PLoS Genet. 10: e1004845. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib68] Wang X., Elling A.A., Li X., Li N., Peng Z., He G., Sun H., Qi Y., Liu X.S., Deng X.W. (2009). Genome-wide and organ-specific landscapes of epigenetic modifications and their relationships to mRNA and small RNA transcriptomes in maize. Plant Cell 21: 1053–1069. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib69] Wen Z., Tan R., Zhang S., Collins P.J., Yuan J., Du W., Gu C., Ou S., Song Q., An Y.-Q.C., Boyse J.F., Chilvers M.I., et al. (2018). Integrating GWAS and gene expression data for functional characterization of resistance to white mold in soya bean. Plant Biotechnol. J. 16: 1825–1835. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib70] Winkler R.G., Freeling M. (1994). Physiological genetics of the dominant gibberellin-nonresponsive maize dwarfs, Dwart8 and Dwart9. Planta 193: 341–348. [Google Scholar]

[bib71] Wolfe C.J., Kohane I.S., Butte A.J. (2005). Systematic survey reveals general applicability of “guilt-by-association” within gene coexpression networks. BMC Bioinformatics 6: 227. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib72] Wray G.A. (2007). The evolutionary significance of cis-regulatory mutations. Nat. Rev. Genet. 8: 206–216. [DOI] [PubMed] [Google Scholar]

[bib73] Zheng Z.-L., Zhao Y. (2013). Transcriptome comparison and gene coexpression network analysis provide a systems view of citrus response to ‘Candidatus Liberibacter asiaticus’ infection. BMC Genomics 14: 27. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib74] Ziegler G., Kear P.J., Wu D., Ziyomo C., Lipka A.E., Gore M., Hoekenga O., Baxter I. (2017). Elemental accumulation in kernels of the maize nested association mapping panel reveals signals of gene by environment interactions. bioRxiv. [Google Scholar]

PERMALINK

Integrating Coexpression Networks with GWAS to Prioritize Causal Genes in Maize[OPEN]

Robert J Schaefer

Jean-Michel Michno

Joseph Jeffers

Owen Hoekenga

Brian Dilkes

Ivan Baxter

Chad L Myers